Reliability Improvement of a Hybrid Electric Vehicle Integrated Distribution System
Abstract
:1. Introduction
2. Literature Survey
Research Gap
- The VCS integration in the distribution system is considered an additional load to charge the EVs.
- The impact of the increased load (VCS) in the distribution system is rectified by the optimal integration of DG.
- Reliability analysis is performed to study the effectiveness of the system.
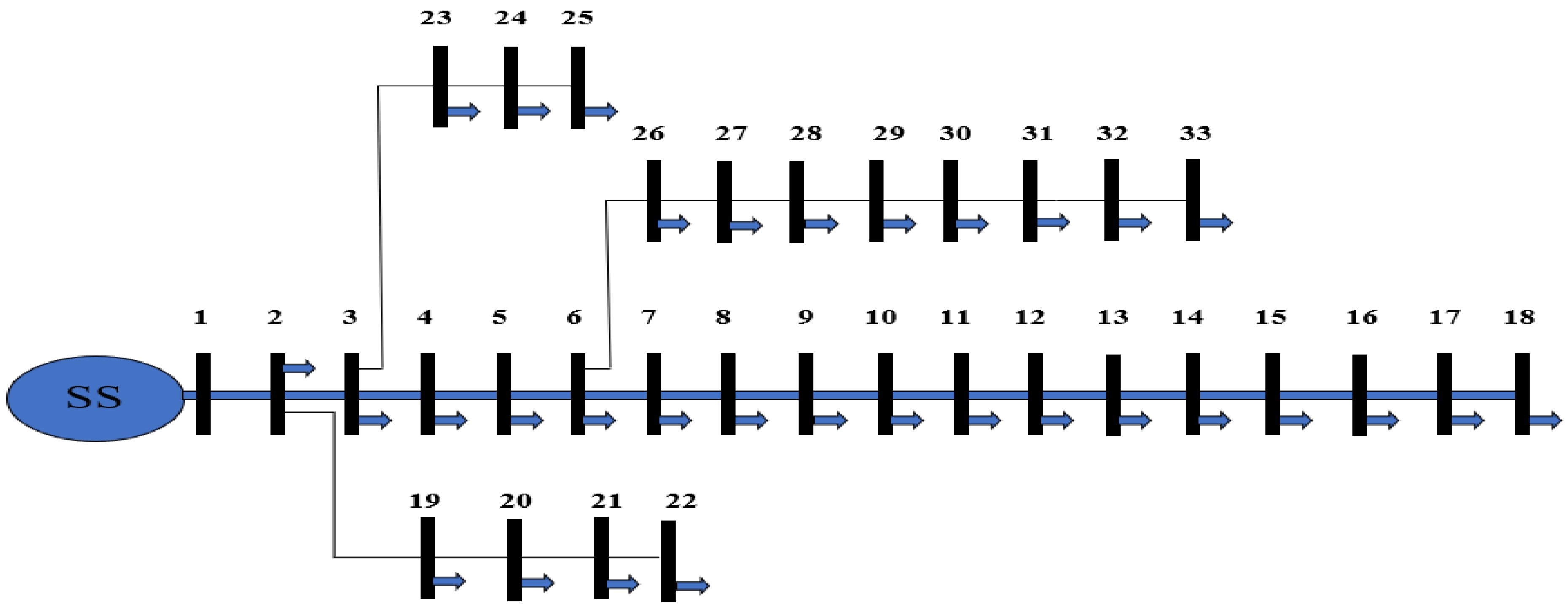
3. System Description
Hybrid Electric Vehicle
4. Problem Formulation
4.1. Voltage Stability Index (VSI)
4.2. Reliability Index
4.3. Objective Function
- Power Balance Constraint
- Voltage Constraint
- DG Penetration Constraint
4.4. Forward and Backward Sweep Algorithm
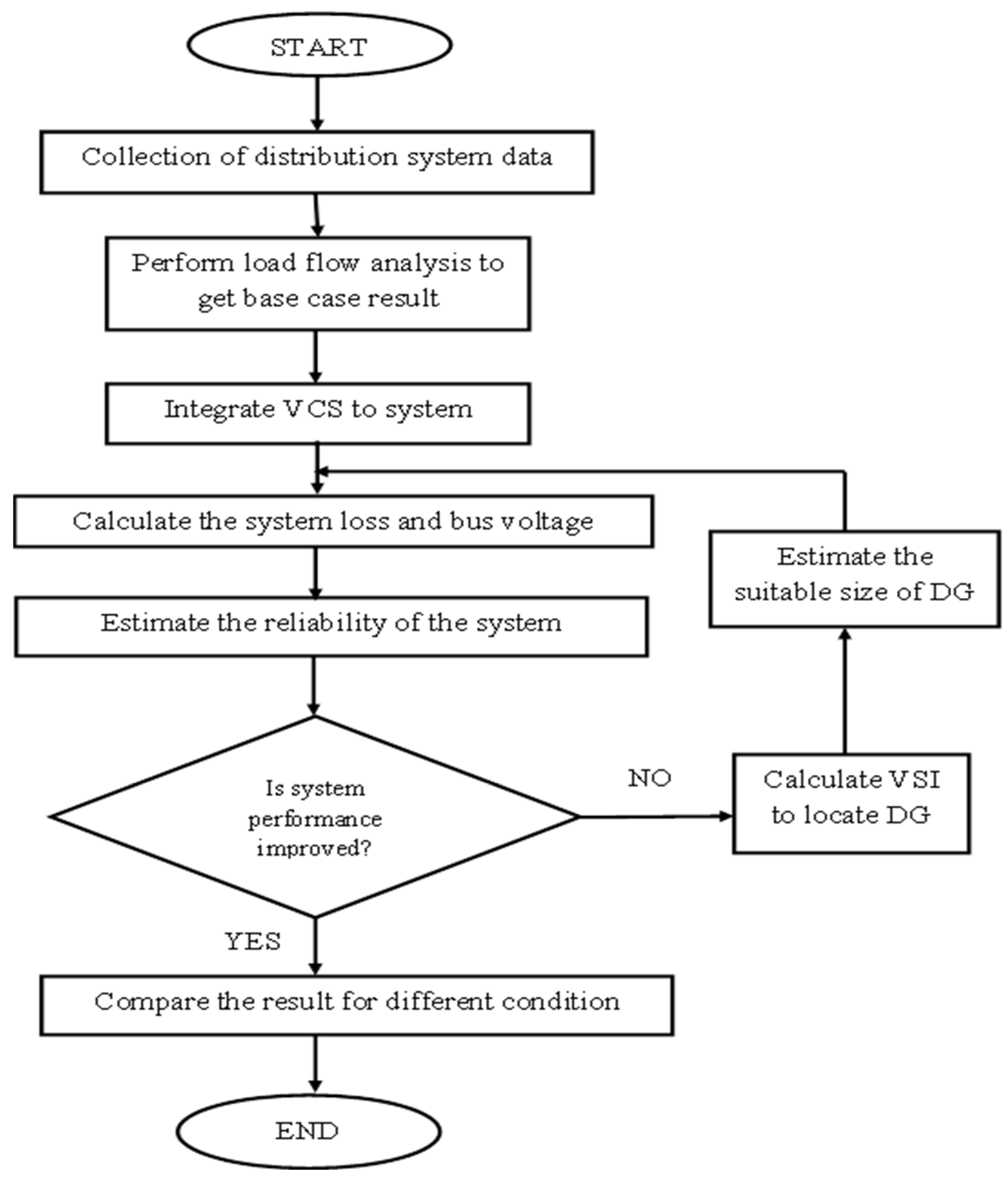
5. Methodology
| Algorithm 1. Proposed methodology to analyze system performance. |
| STEP 1: The location of the substation, number of feeders and their interconnected branches with main and lateral feeders are noted from the IEEE radial distribution system. |
| STEP 2: The power demand in each load bus is noted for the IEEE system. |
| STEP 3: The impedance values of the distribution lines between the buses are noted for the IEEE system. |
| STEP 4: Forward and backward sweep load flow analysis is performed with the collected data. |
| STEP 5: The voltage at each bus and the current through each branch is calculated through the forward and backward sweep, respectively. |
| STEP 6: Power flow, voltage, current and losses are obtained through load flow analysis. |
| STEP 7: VCS is placed arbitrarily in the last bus of the selected distribution system. The power demand in the VCS location is changed from P to (P + PVCS). |
| STEP 8: Along with VCS in the system, VSI is calculated to place the DG in an optimal location. In this case, PVCS is included in calculating the current and voltage for load flow using Equations (19)–(21). |
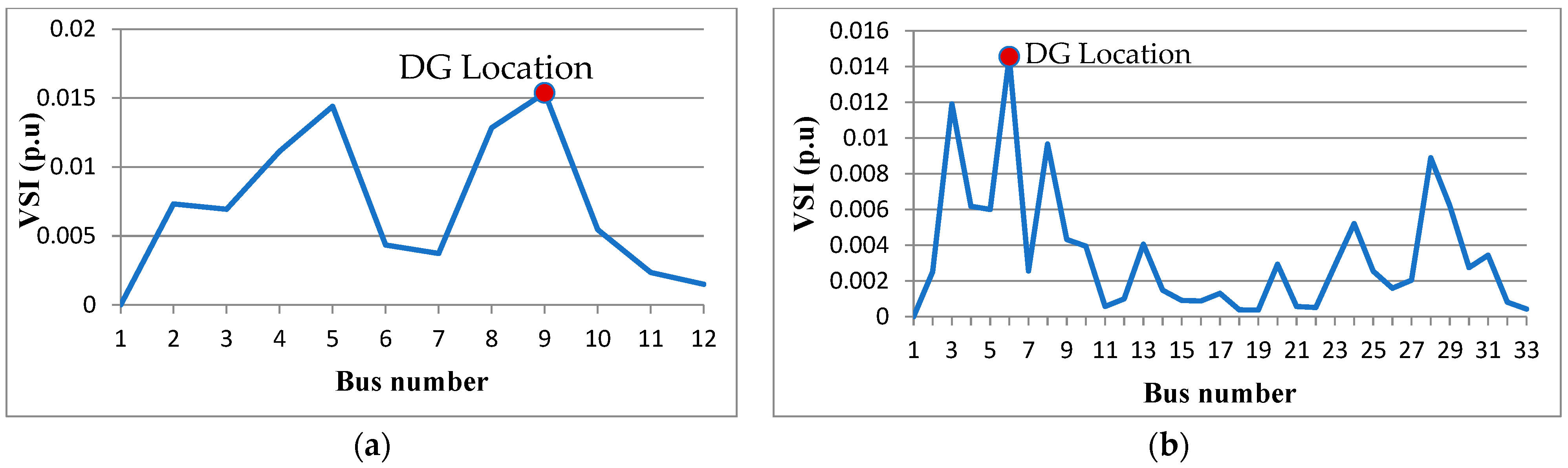
| STEP 9: The optimal location for DG is selected by VSI using Equations (12) and (13). |
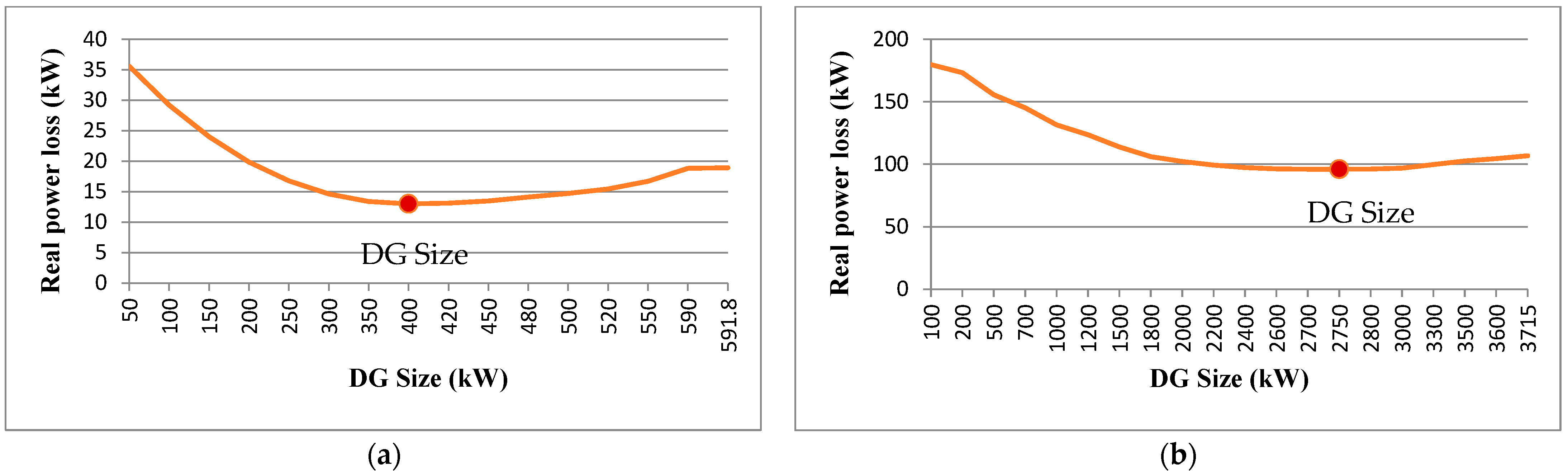
| STEP 10: The DG size is determined by analytical method with the objective of power loss minimization using Equation (15). |
| STEP 11: The DG size should satisfy all the power system constraints Equations (16)–(18). Here, PDG and PVCS are included in calculating the current and voltage for load flow using Equations (19)–(21). |
| STEP 12: LOLP is calculated to estimate the system reliability Equation (14). |
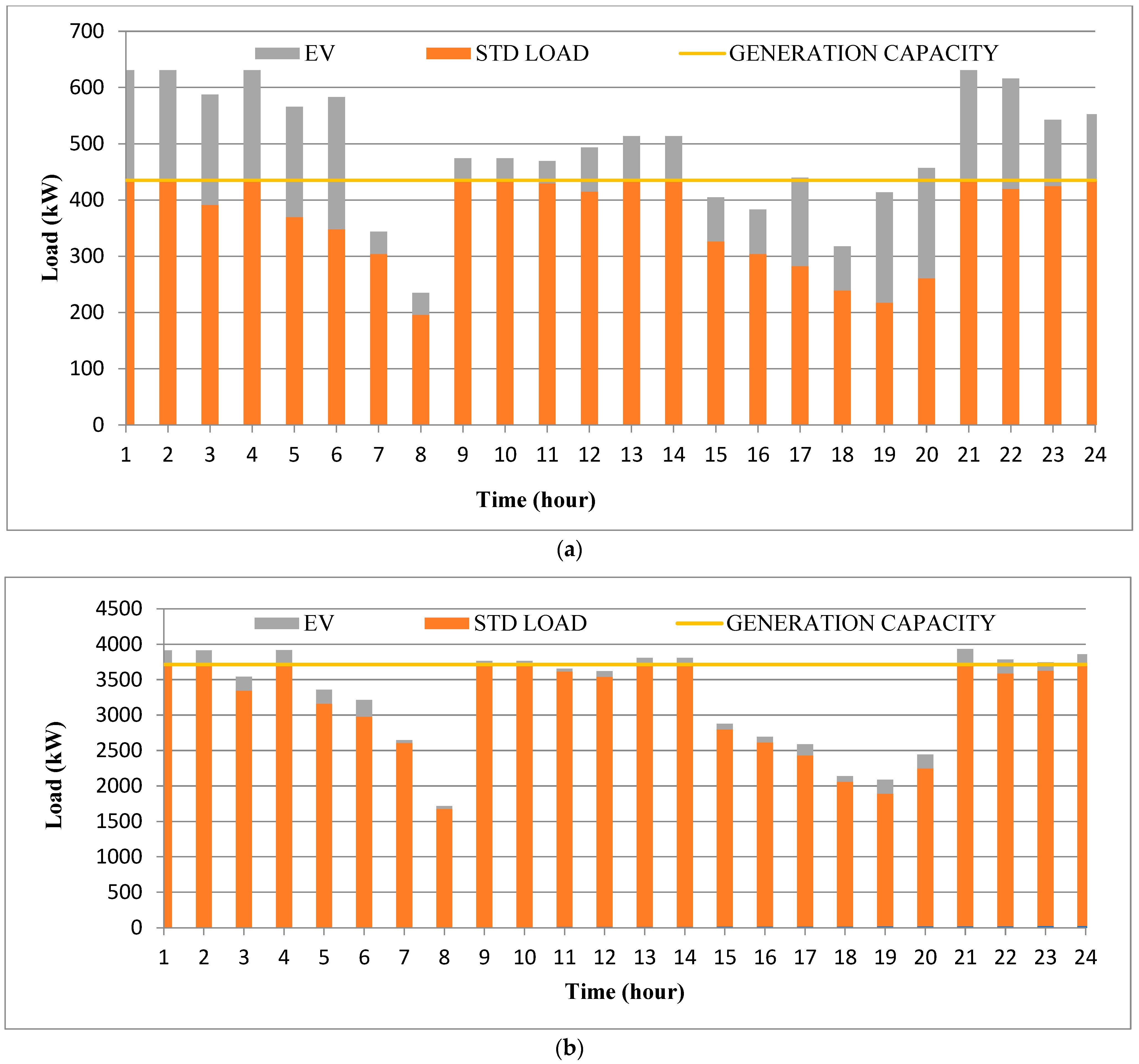
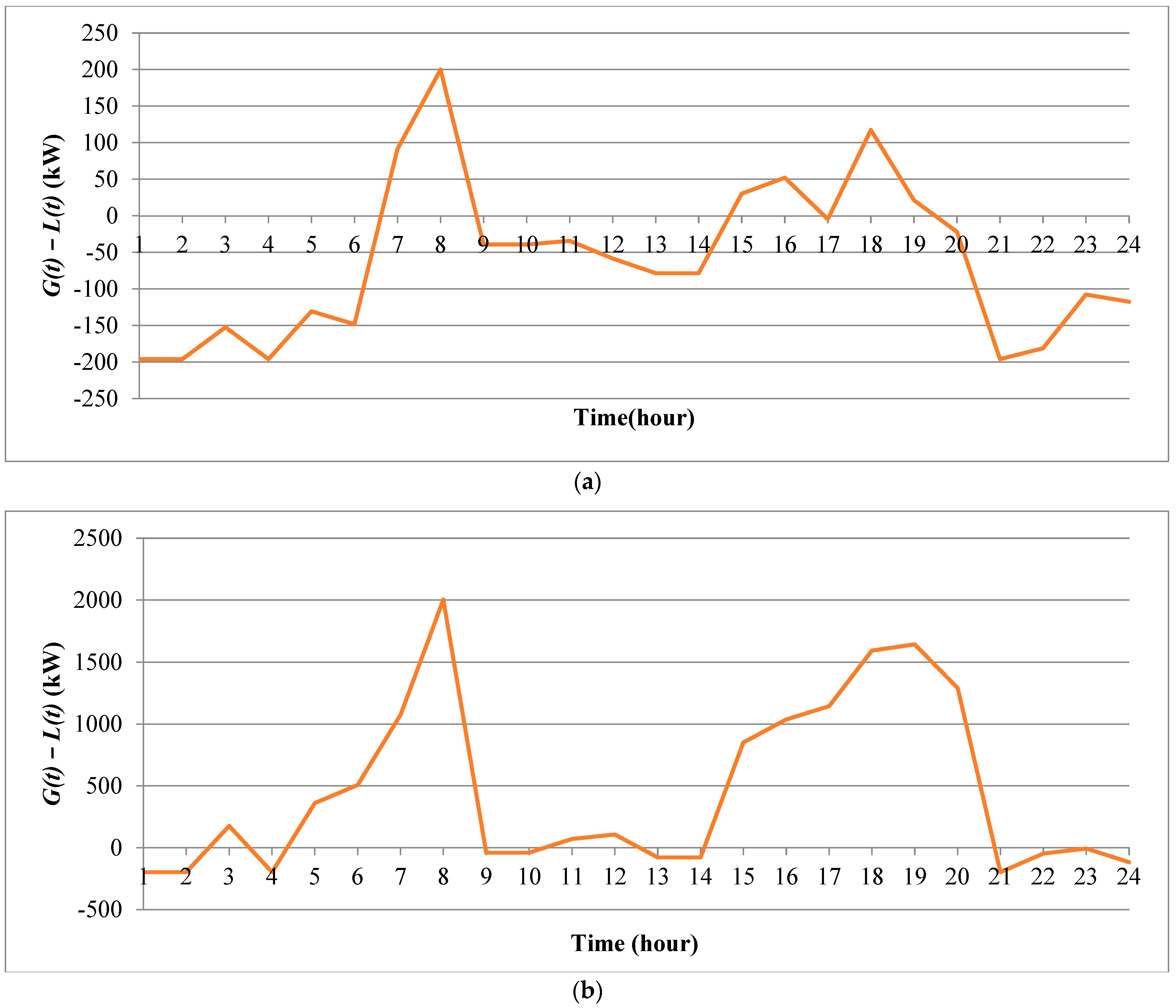
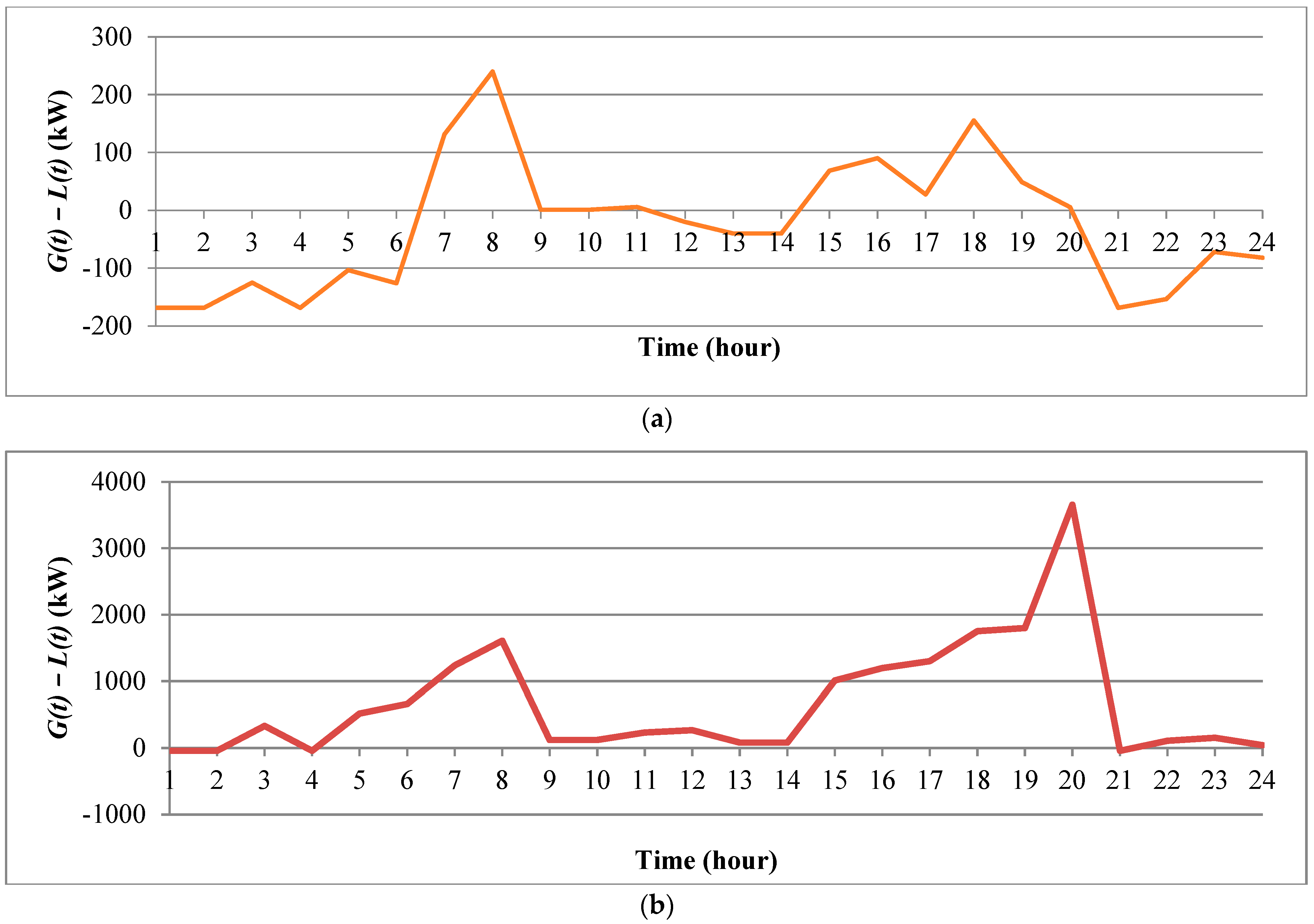
| STEP 13: The system reliability is analyzed for one complete day by considering only VCS and both VCS and DG. Here, for only VCS, G(t) includes the power source (Pin) and losses, whereas L(t) includes the load connected (standard load and EV load). In the case of both VCS and DG, G(t) includes the power sources (PDG and Pin) and losses, whereas L(t) includes the load connected (standard load and EV load). |
| STEP 14: A comparative study is performed to identify the system which has higher reliability. |
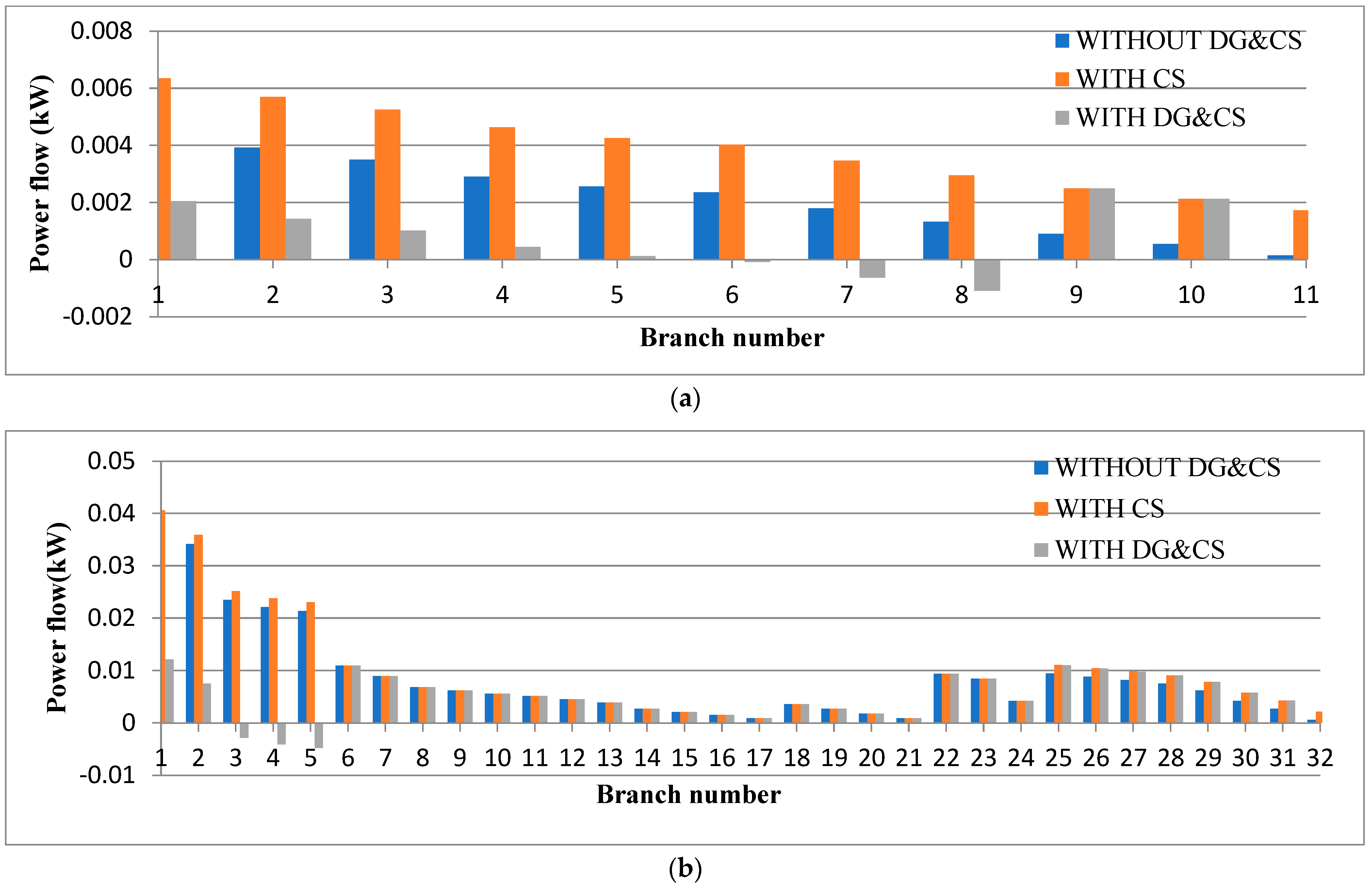
| STEP 15: Further, all the power flow parameters are compared between the two systems. |
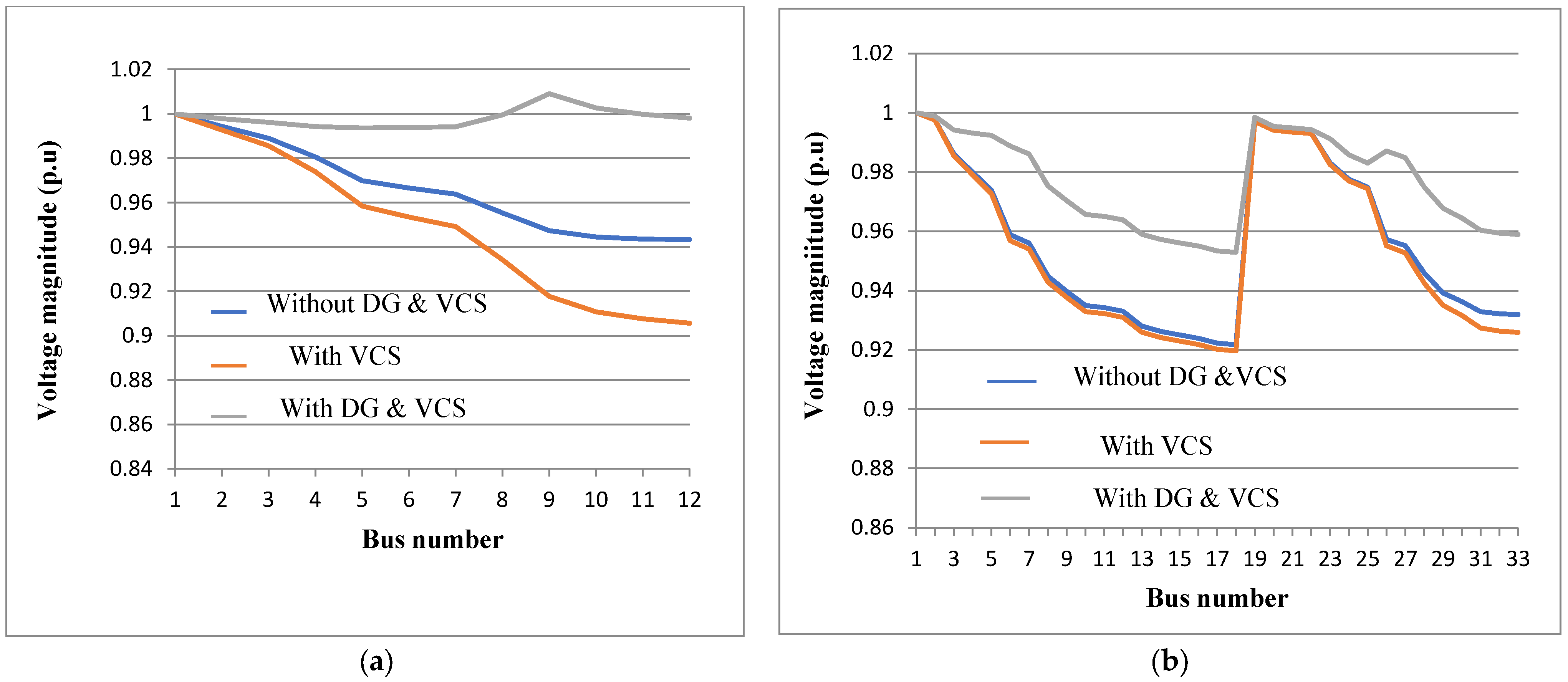
| STEP 16: The system, which has both VCS and DG, has improved voltage, improved reliability and reduced loss. |
6. Results and Discussion
6.1. System Analysis
6.1.1. Integration of VCS and DG
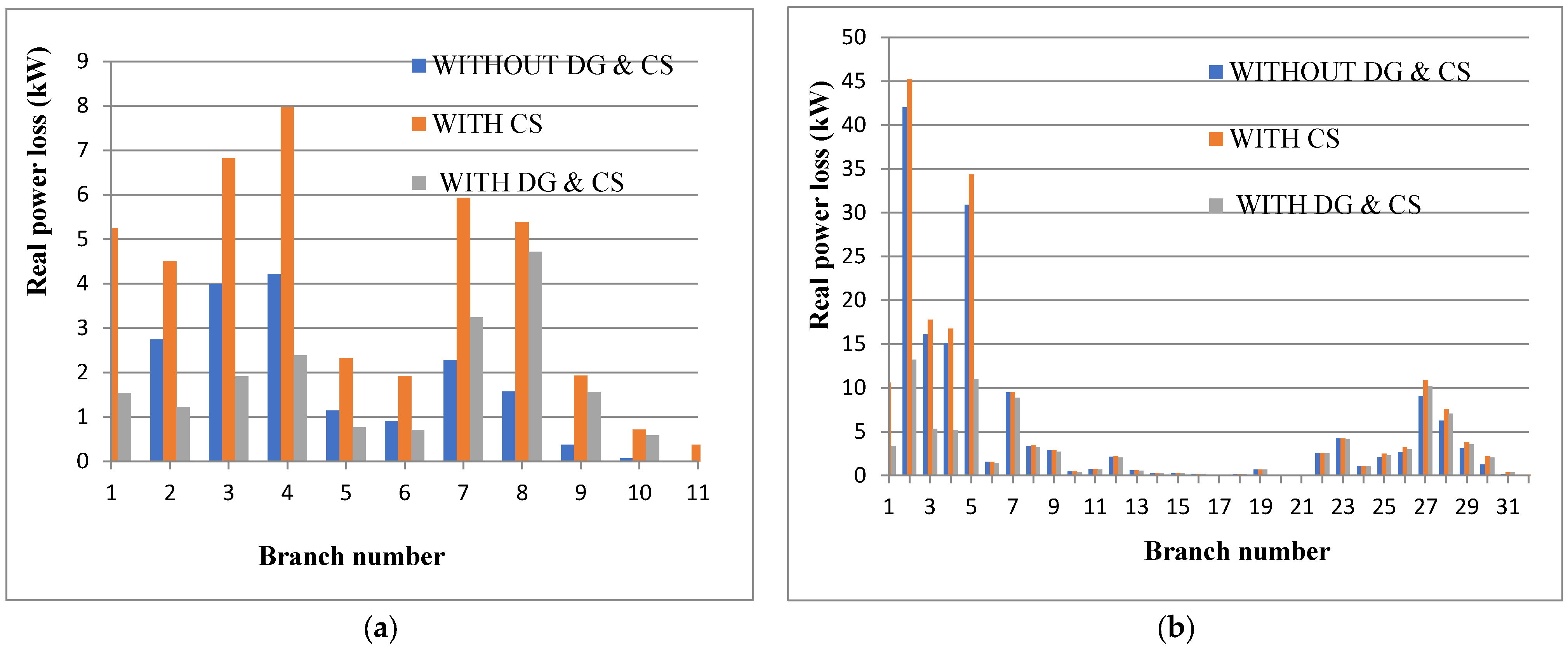
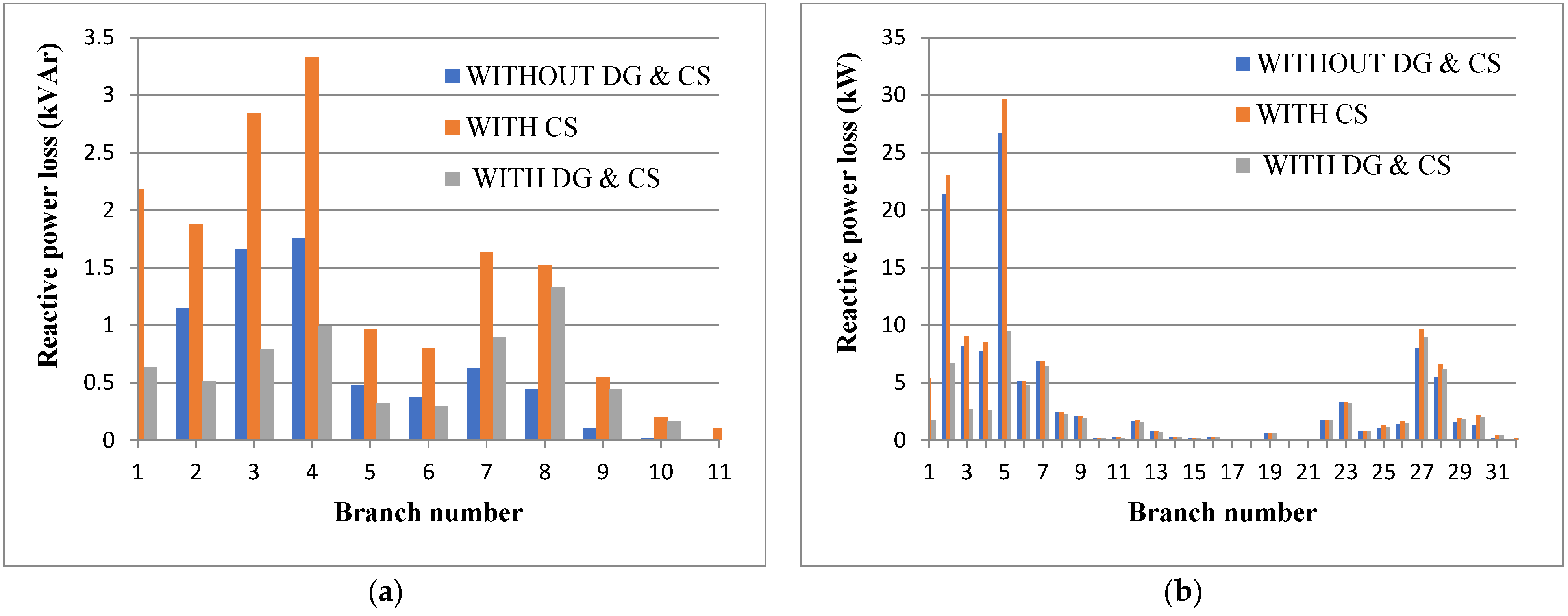
6.1.2. Performance Evaluation
6.1.3. Reliability Evaluation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| HEV | Hybrid Electric Vehicle |
| DG | Distributed Generation |
| VCS | Vehicle Charging Station |
| VSI | Voltage Stability Index |
| LOLP | Loss Of Load Probability |
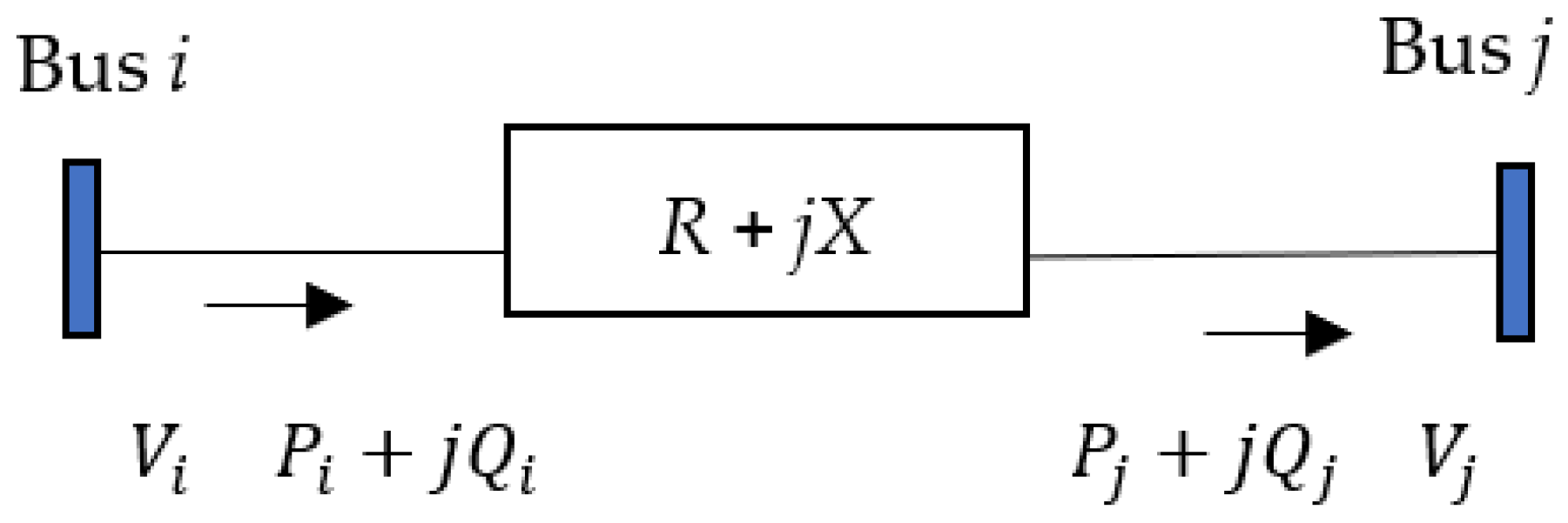
| Pi | Real power injected at bus i |
| Qi | Reactive power injected at bus i |
| Ri | Resistance between the buses in branch i |
| Xi | Reactance between the buses in branch i |
| PDG | Real power supplied through DG |
| PVCS | Real power absorbed through VCS |
| Pin | Real power injected in the substation |
References
- Atwa, Y.M.; El-Saadany, E.F.; Salama, M.M.A.; Seethapathy, R. Optimal Renewable Resources Mix for Distribution System Energy Loss Minimization. IEEE Trans. Power Syst. 2010, 25, 360–370. [Google Scholar] [CrossRef]
- Wang, X.; Karki, R. Exploiting PHEV to Augment Power System Reliability. IEEE Trans. Smart Grid 2017, 8, 2100–2108. [Google Scholar] [CrossRef]
- Gao, Y.; Ehsani, M. Design and Control Methodology of Plug-in Hybrid Electric Vehicles. IEEE Trans. Ind. Electron. 2010, 57, 633–640. [Google Scholar] [CrossRef]
- Alizadeh, S.M.; Ozansoy, C.; Alpcan, T. The impact of X/R ratio on voltage stability in a distribution network penetrated by wind farms. In Proceedings of the 2016 Australasian Universities Power Engineering Conference, Brisbane, Australia, 25–28 September 2016. [Google Scholar] [CrossRef]
- Jha, B.K.; Kumar, A.; Singh, D.; Misra, R.K. Coordinated effect of PHEVs with DGs on distribution network. Int. Trans. Electr. Energy Syst. 2018, 29, e2800. [Google Scholar] [CrossRef]
- Falahati, B.; Shahverdi, M.; Fajri, P.; Kargarian, A. Loss of Load Probability of Power Systems Considering the High PHEV Penetration Rates. In Proceedings of the 2018 IEEE Conference on Technologies for Sustainability, Long Beach, CA, USA, 11–13 November 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Abdel-Akher, M.; Eid, A.; Ali, A. Effective Demand Side Scheme for PHEVs Operation Considering Voltage Stability of Power Distribution Systems. Int. J. Emerg. Electr. Power Syst. 2017, 18, 114268588. [Google Scholar] [CrossRef]
- Reddy, G.H.; Chakrapani, P.; Goswami, A.K.; Choudhury, N.B.D. Optimal distributed generation placement in distribution system to improve reliability and critical loads pick up after natural disasters. Int. J. Eng. Sci. Technol. 2017, 20, 825–832. [Google Scholar] [CrossRef]
- Quiroga, G.A.; Kagan, H.; Amasifen, J.C.C.; Almeida, C.F.M.; Kagan, N.; Vicentini, E. Study of the Distributed Generation impact on distributed networks, focused on quality of power. In Proceedings of the 2016 17th International Conference on Harmonics and Quality of Power (ICHQP), Belo Horizonte, Brazil, 16–19 October 2016; pp. 855–860. [Google Scholar] [CrossRef]
- Reddy, G.H.; Goswami, A.K.; Choudhury, N.B.D. Impact of plug-in electric vehicles and distributed generation on reliability of distribution systems. Int. J. Eng. Sci. Technol. 2018, 21, 50–59. [Google Scholar] [CrossRef]
- Sarma, S.S.; Madhusudhan, V.; Ganesh, V. Evaluation and enhancement of reliability of electrical distribution system in the presence of dispersed generation. In Proceedings of the 2016 International Conference on Signal Processing, Communication, Power and Embedded System, Paralakhemundi, India, 3–5 October 2016; pp. 357–362. [Google Scholar] [CrossRef]
- Aljanad, A.; Mohamed, A. Power quality impacts of plug-in hybrid electric vehicles on distribution network. In Proceedings of the 2016 International Conference on Advances in Electrical, Electronic and Systems Engineering, Putrajaya, Malaysia, 14–16 November 2016; pp. 616–620. [Google Scholar] [CrossRef]
- Adefarati, T.; Bansal, R. Integration of renewable distributed generators into the distribution system: A review. IET Renew. Power Gener. 2016, 10, 873–884. [Google Scholar] [CrossRef]
- Sa’ed, J.A.; Amer, M.; Bodair, A.; Baransi, A.; Favuzza, S.; Zizzo, G. A Simplified Analytical Approach for Optimal Planning of Distributed Generation in Electrical Distribution Networks. Appl. Sci. 2019, 9, 5446. [Google Scholar] [CrossRef]
- Purlu, M.; Turkay, B.E. Optimal Allocation of Renewable Distributed Generations Using Heuristic Methods to Minimize Annual Energy Losses and Voltage Deviation Index. IEEE Access 2022, 10, 21455–21474. [Google Scholar] [CrossRef]
- Sultana, B.; Mustafa, M.W.; Sultana, U.; Bhatti, A.R. Review on reliability improvement and power loss reduction in distribution system via network reconfiguration. Renew. Sustain. Energy Rev. 2016, 66, 297–310. [Google Scholar] [CrossRef]
- de Sousa, R.S.; Martins, C.C.; Sperandio, M. Distribution System Reliability Assessment Using Sequential Monte Carlo Simulation. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Conference, Gramado, Brazil, 15–18 September 2019. [Google Scholar] [CrossRef]
- Li, Z.; Wu, W.; Zhang, B.; Tai, X. Analytical Reliability Assessment Method for Complex Distribution Networks Considering Post-Fault Network Reconfiguration. IEEE Trans. Power Syst. 2020, 35, 1457–1467. [Google Scholar] [CrossRef]
- López-Prado, J.L.; González-Sánchez, J.W.; Vélez, J.I.; Garcia-Llinás, G.A. Reliability Assessment in Rural Distribution Systems with Microgrids: A Computational-Based Approach. IEEE Access 2022, 10, 43327–43340. [Google Scholar] [CrossRef]
- Tur, M.R. Reliability Assessment of Distribution Power System When Considering Energy Storage Configuration Technique. IEEE Access 2020, 8, 77962–77971. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.; Yan, N.; Ma, R. Cooperative Dispatch of Distributed Energy Storage in Distribution Network with PV Generation Systems. IEEE Trans. Appl. Supercond. 2021, 31, 0604304. [Google Scholar] [CrossRef]
- Talukdar, B.K.; Deka, B.C.; Bhuyan, M.P. Reliability Analysis of Electric Vehicle integrated Distribution Network. In Proceedings of the 2021 International Conference on Computational Performance Evaluation, Shillong, India, 1–3 December 2021; pp. 858–862. [Google Scholar] [CrossRef]
- Sadeghian, O.; Nazari-Heris, M.; Abapour, M.; Taheri, S.S.; Zare, K. Improving reliability of distribution networks using plug-in electric vehicles and demand response. J. Mod. Power Syst. Clean Energy 2019, 7, 1189–1199. [Google Scholar] [CrossRef]
- Khan, R.; Mehmood, K.K.; Bukhari, S.B.A.; Imran, K.; Wadood, A.; Rhee, S.B.; Park, S. An Optimization-Based Reliability Enhancement Scheme for Active Distribution Systems Utilizing Electric Vehicles. IEEE Access 2021, 9, 157247–157258. [Google Scholar] [CrossRef]
- Zanjani, S.M.H.; Shahinzadeh, H.; Pourmirza, Z.; Kabalci, E.; Muyeen, S.M.; Benbouzid, M. Optimal Operation of a Residential Energy Hub in the Presence of an Electric Vehicle using Whale Optimization Algorithm. In Proceedings of the 2022 26th International Electrical Power Distribution Conference (EPDC), Tehran, Iran, 11–12 May 2022; pp. 84–89. [Google Scholar] [CrossRef]
- Wu, Y.; Ravey, A.; Chrenko, D.; Miraoui, A. Demand side energy management of EV charging stations by approximate dynamic programming. Energy Convers. Manag. 2019, 196, 878–890. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, J.; Ravey, A.; Chrenko, D.; Miraoui, A. Real-time energy management of photovoltaic-assisted electric vehicle charging station by markov decision process. J. Power Sources 2020, 476, 228504. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, Z.; Huangfu, Y.; Ravey, A.; Chrenko, D.; Gao, F. Hierarchical Operation of Electric Vehicle Charging Station in Smart Grid Integration Applications—An Overview. Int. J. Electr. Power Energy Syst. 2022, 139, 108005. [Google Scholar] [CrossRef]
- Aslani, M.; Imanloozadeh, A.; Hashemi-Dezaki, H.; Hejazi, M.A.; Nazififard, M.; Ketabi, A. Optimal probabilistic reliability-oriented planning of islanded microgrids considering hydrogen-based storage systems, hydrogen vehicles, and electric vehicles under various climatic conditions. J. Power Sources 2022, 525, 231100. [Google Scholar] [CrossRef]
- Bagherzadeh, L.; Shahinzadeh, H.; Gharehpetian, G.B. Scheduling of Distributed Energy Resources in Active Distribution Networks Considering Combination of Techno-Economic and Environmental Objectives. In Proceedings of the International Power System Conference (PSC), Tehran, Iran, 9–11 December 2019; pp. 687–695. [Google Scholar] [CrossRef]
- Senthil Kumar, J.; Raja, S.C.; Srinivasan, D.; Venkatesh, P. Hybrid renewable energy-based distribution system for seasonal load variations. Int. J. Energy Res. 2018, 42, 1066–1087. [Google Scholar] [CrossRef]


| Reference Number | Objective | Summary |
|---|---|---|
| [6,8,10,11,16,17,18,19,20] | Reliability analysis |
|
| [7,9] | Voltage profile improvement |
|
| [12] | Power quality analysis |
|
| [13,14,15,21] | Power loss minimization |
|
| Parameters | Standard System (without VCS/DG) | VCS Connected | VCS and DG Connected |
|---|---|---|---|
| Location of DG | - | - | 9 |
| Size of DG (kW) | - | - | 400 |
| Location of VCS | - | 12 | 12 |
| Size of VCS (kW) | - | 156.8 | 156.8 |
| Substation real power (kW) | 455.7138 | 634.9223 | 85.6682 |
| Substation Reactive Power (kVAr) | 413.0411 | 421.0105 | 413.1343 |
| Real power loss (kW) | 20.7138 | 43.1223 | 18.922 |
| Reactive power loss (kVAr) | 8.0411 | 16.0105 | 6.4721 |
| Parameters | Standard System | VCS Connected | VCS and DG Connected |
|---|---|---|---|
| Location of DG | - | - | 6 |
| Size of DG (kW) | - | - | 2750 |
| Location of VCS | - | 33 | 33 |
| Size of VCS (kW) | - | 156.8 | 156.8 |
| Substation real power (kW) | 3884.5 | 4058.2 | 1217.9 |
| Substation Reactive Power (kVAr) | 2414.8 | 2426.5 | 2371.1 |
| Real power loss (kW) | 169.5135 | 186.3839 | 96.0627 |
| Reactive power loss (kVAr) | 114.8382 | 126.541 | 71.0985 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sripriya, R.; Kumar, C.; Xavier, F.J.; Kumar, J.S.; Kotsampopoulos, P.; Fayek, H.H. Reliability Improvement of a Hybrid Electric Vehicle Integrated Distribution System. Energies 2023, 16, 3984. https://doi.org/10.3390/en16103984
Sripriya R, Kumar C, Xavier FJ, Kumar JS, Kotsampopoulos P, Fayek HH. Reliability Improvement of a Hybrid Electric Vehicle Integrated Distribution System. Energies. 2023; 16(10):3984. https://doi.org/10.3390/en16103984
Chicago/Turabian StyleSripriya, Ramalingam, Chandrasekaran Kumar, Felix Joseph Xavier, Jeyaraj Senthil Kumar, Panos Kotsampopoulos, and Hady H. Fayek. 2023. "Reliability Improvement of a Hybrid Electric Vehicle Integrated Distribution System" Energies 16, no. 10: 3984. https://doi.org/10.3390/en16103984
APA StyleSripriya, R., Kumar, C., Xavier, F. J., Kumar, J. S., Kotsampopoulos, P., & Fayek, H. H. (2023). Reliability Improvement of a Hybrid Electric Vehicle Integrated Distribution System. Energies, 16(10), 3984. https://doi.org/10.3390/en16103984









