A Review of Research on Dynamic and Static Economic Dispatching of Hybrid Wind–Thermal Power Microgrids
Abstract
1. Introduction
2. The Significance of Wind Power Grid Connection
2.1. The Development of Thermal Power Generation
2.2. Development of Renewable Energy Power Generation
2.3. Development of Wind Power Generation
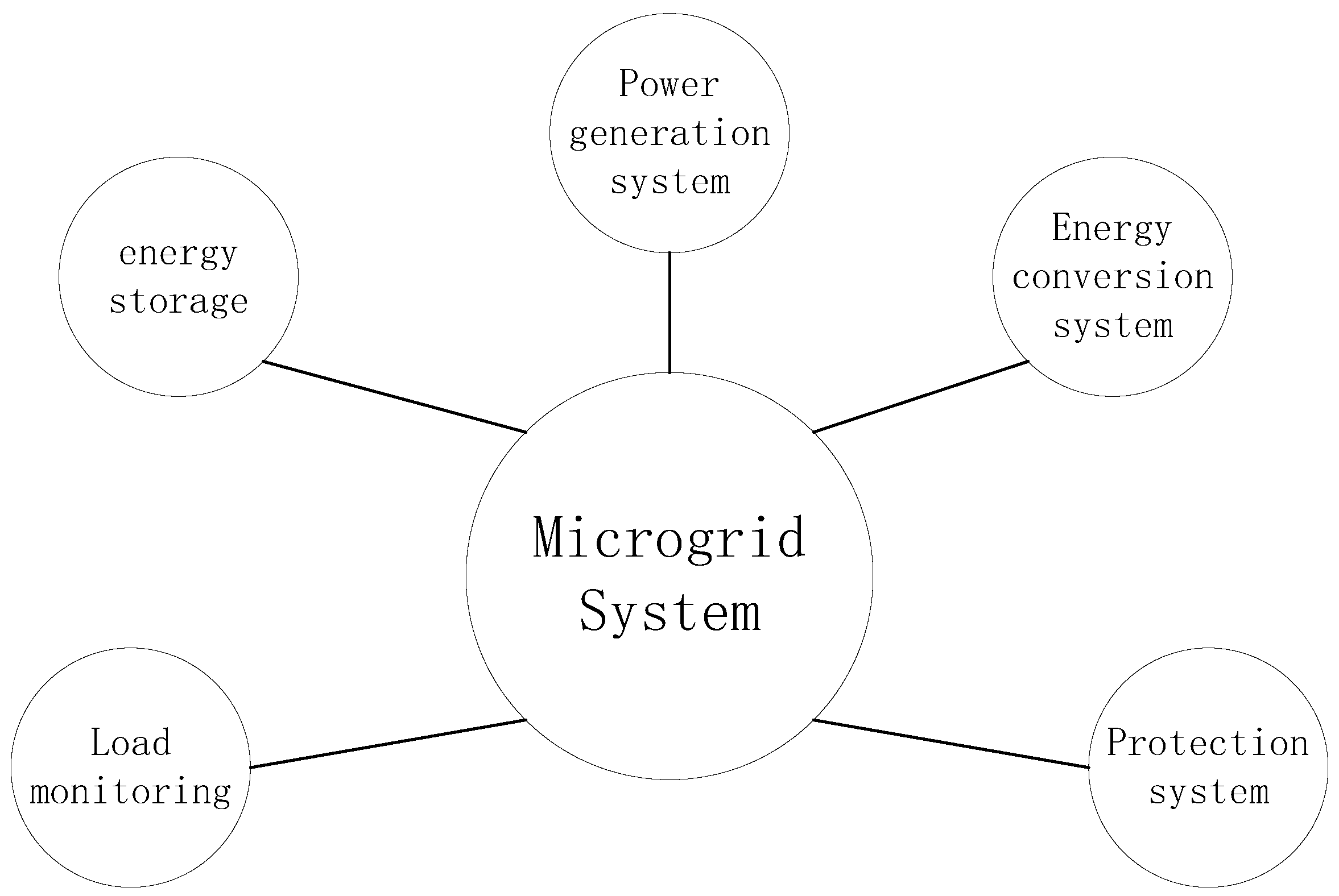
2.4. Development of A Microgrid
3. Concept and Research Significance of Economic Dispatching
3.1. Concept of Economic Dispatching
3.2. Research Significance and the Direction of Economic Dispatching
3.3. The Economic Dispatch Calculation Method
3.3.1. Calculation Methods and the Steps for Static Economic Dispatch
- (1)
- Determine the objective function. Usually, minimizing costs is used as the objective function or multiple indicators such as cost and emissions are considered simultaneously;
- (2)
- Establish a power system model. Establish a feasible mathematical model of the power system. This model typically includes load equations, unit generation equations, transmission loss equations, and constraint conditions;
- (3)
- Perform optimization solution. Substitute the objective function into the power system model and use mathematical optimization methods to obtain the optimal solution, which is to achieve economic dispatch;
3.3.2. Calculation Methods and the Steps for Dynamic Economic Dispatch
- (1)
- Predicting load and power output. For short-term dynamic economic scheduling, it is necessary to predict the load and power output for a period of time in the future. Time series analysis and other methods can be used for prediction;
- (2)
- Dynamic programming. Input the current state and prediction information in a future period of time into the dynamic programming model and obtain a group of optimal solutions by optimizing the decision of each time step, that is, to achieve dynamic economic scheduling;
- (3)
- Model predictive control. Using the predicted results of load and power output as inputs for dynamic economic scheduling, economic scheduling is achieved through two steps: prediction and control. Among them, prediction uses algorithms such as ARIMA and LSTM, while control uses optimization algorithms for decision making.
4. Current Status of Static Economic Dispatch Research on Wind–Thermal Power Hybrid Microgrids
4.1. Static Economic Scheduling Model
- (1)
- Objective function
- Power balance equation constraint
- B.
- Power generation capacity constraints
- C.
- Slope rate constraint
- D.
- The constraint of prohibited operating zone of the unit
4.2. Solution Method of Static Economic Scheduling
5. Current Status of Dynamic Economic Dispatch Research on Wind–Thermal Power Hybrid Microgrids
5.1. Dynamic Economic Scheduling Model and Algorithm
- (1)
- Objective functionwhere is the total number of scheduling periods, generally taken to be 24, and contained energy storage equipment, such as batteries. The other parameters are the same Formulas (1)–(5).
- (2)
- Constraint conditionThe battery output is added to the equation constraint to become:where is the charging and discharging power of the battery in the t period, negative values indicate charge and positive values indicate discharge.
- Climbing constraint of controllable unit:where and are the upward and downward climbing rates of the generator set, respectively.
- Energy storage equipment operation constraints, here to the battery (BT) as the representative.where and are the minimum and maximum charging and discharging powers of the battery, respectively; and are the minimum and maximum stored energy of the battery, respectively; is the initial energy storage of the battery.
- Considering the utilization rate of wind power, the grid-connected power and wind abandon power need to be met:where is the actual generating power (MW) of the wind farm, is the wind abandon power (MW), and is the grid-connected power (MW) of the wind power generation.
5.2. The Random Volatility of Wind Energy
5.3. Dynamic Economic Scheduling of Environmental Benefit Objectives
5.4. Optimization of Bidding Strategy of Wind Power Suppliers and the Improvement of Wind Power Absorption Capacity
6. Application Prospect
7. Summary and Outlook
- (1)
- A good algorithm can provide the technical basis for solving the dynamic and static economic dispatching model of wind–thermal power hybrid microgrids and provide methods for solving the problems of high complexity and high dimension in economic dispatching. Some existing algorithms such as the basic sailfish optimization algorithm (SFO), the particle swarm optimization algorithm (PSO), and the multiverse algorithm (MVO) can be applied to many simple optimization problems in science and engineering due to their flexibility and simplicity. However, with the increase in problem complexity and data dimension, there will be some problems in the process of data processing of these algorithms, such as low solving accuracy and slow convergence speed. Therefore, some improvements should be made to the original algorithm when solving problems. The algorithm can be improved from the three aspects of solving ability, exploration diversity, and convergence speed. Three methods, namely weight inertia, global search factor, and population diversity maintenance strategy, were used, respectively;
- (2)
- To solve the static economic dispatching problem of wind–thermal power hybrid microgrids, we can start with the establishment of its optimization mathematical model, reduce the impact of its volatility on system stability by limiting the grid-connected capacity of wind energy, and take the low cost of wind energy into account so as to further guarantee the economy of microgrid system dispatching. At the same time, more constraints should be considered in future research of hybrid dynamic and static economic scheduling models so that the solution of the model can be closer to the actual operation of the system;
- (3)
- The non-stationary characteristics of wind energy should be taken into account when establishing the dynamic economic dispatching model of wind–thermal power hybrid microgrids so as to make the power output estimation of the microgrid system more realistic and make full use of wind energy, in order to ensure the economy and environmental protection of microgrid dispatching;
- (4)
- At present, research on the static economic dispatch of wind power thermal power hybrid microgrids lacks a global and refined evaluation of system economy and environmental protection. Based on the comparison and demonstration of previous operation plans, it can be seen that proposing methods and indicators that can finely evaluate the long-term operating cost, energy consumption, and efficiency of the system are urgently needed for future research.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Debnath, K.B.; Mourshed, M. Challenges and gaps for energy planning models in the developing-world context. Nat. Energy 2018, 3, 172–184. [Google Scholar] [CrossRef]
- Yuan, J.; Na, C.; Lei, Q.; Xiong, M.; Guo, J.; Hu, Z. Coal use for power generation in China. Resour. Conserv. Recycl. 2018, 129, 443–453. [Google Scholar] [CrossRef]
- Yao, L. New energy utilization in environmental design and realization. Energy Rep. 2022, 8, 9211–9220. [Google Scholar] [CrossRef]
- Østergaard, P.A.; Duic, N.; Noorollahi, Y.; Kalogirou, S. Renewable energy for sustainable development. Renew. Energy 2022, 199, 1145–1152. [Google Scholar] [CrossRef]
- Lu, X.; Zhou, K.; Yang, S. Multi-objective optimal dispatch of microgrid containing electric vehicles. J. Clean. Prod. 2017, 165, 1572–1581. [Google Scholar] [CrossRef]
- Ahmethodžić, L.; Musić, M.; Huseinbegović, S. Microgrid energy management: Classification, review and challenges. CSEE J. Power Energy Syst. 2022, 2022, 1–13. [Google Scholar]
- Zou, Y.; Wang, Q.; Hu, B.; Chi, Y.; Zhou, G.; Xu, F.; Zhou, N.; Xia, Q. Hierarchical evaluation framework for coupling effect enhancement of renewable energy and thermal power coupling generation system. Int. J. Electr. Power Energy Syst. 2023, 146, 108717. [Google Scholar] [CrossRef]
- Weishang, G.; Yihua, M.; Xuexing, Z.; Huan, Y. Internal benefit optimization model of gas-thermal power virtual power plant under china’s carbon neutral target. Energy Sci. Eng. 2022, 10, 1227–1239. [Google Scholar] [CrossRef]
- Al Kindi, A.A.; Aunedi, M.; Pantaleo, A.M.; Strbac, G.; Markides, C.N. Thermo-economic assessment of flexible nuclear power plants in future low-carbon electricity systems: Role of thermal energy storage. Energy Convers. Manag. 2022, 258, 115484. [Google Scholar] [CrossRef]
- Zhang, G.-X.; Yang, Y.; Su, B.; Nie, Y.; Duan, H.-B. Electricity production, power generation structure, and air pollution: A monthly data analysis for 279 cities in China (2015–2019). Energy Econ. 2023, 120, 106597. [Google Scholar] [CrossRef]
- Santillán-Lemus, F.D.; Minor-Popocatl, H.; Aguilar-Mejía, O.; Tapia-Olvera, R. Optimal Economic Dispatch in Microgrids with Renewable Energy Sources. Energies 2019, 12, 181. [Google Scholar] [CrossRef]
- Barbosa-Ayala, O.I.; Montañez-Barrera, J.A.; Damian-Ascencio, C.E.; Saldaña-Robles, A.; Alfaro-Ayala, J.A.; Padilla-Medina, J.A.; Cano-Andrade, S. Solution to the Economic Emission Dispatch Problem Using Numerical Polynomial Homotopy Continuation. Energies 2020, 13, 4281. [Google Scholar] [CrossRef]
- Wang, X.; Chen, S.; Zhou, Y.; Wang, J.; Cui, Y. Optimal Dispatch of Microgrid with Combined Heat and Power System Considering Environmental Cost. Energies 2018, 11, 2493. [Google Scholar] [CrossRef]
- Fan, W.; Huang, L.; Cong, B.; Degejirifu; Tan, Z.; Xing, T. Research on an optimization model for wind power and thermal power participating in two-level power market transactions. Int. J. Electr. Power Energy Syst. 2022, 134, 107423. [Google Scholar] [CrossRef]
- Roy, S. The maximum likelihood optima for an economic load dispatch in presence of demand and generation variability. Energy 2018, 147, 915–923. [Google Scholar] [CrossRef]
- Wen, G.; Yu, X.; Liu, Z. Recent progress on the study of distributed economic dispatch in smart grid: An overview. Front. Inf. Technol. Electron. Eng. 2021, 22, 25–39. [Google Scholar] [CrossRef]
- Gaing, Z. Particle swarm optimization to solving the economic dispatch considering the generator constraints. IEEE Trans. Power Syst. 2003, 18, 1187–1195. [Google Scholar] [CrossRef]
- Bulbul, S.M.A.; Pradhan, M.; Roy, P.K.; Pal, T. Opposition-based krill herd algorithm applied to economic load dispatch problem. Ain Shams Eng. J. 2018, 9, 423–440. [Google Scholar] [CrossRef]
- Chen, X.; Wang, P.; Wang, Q.; Dong, Y. A Two-Stage strategy to handle equality constraints in ABC-based power economic dispatch problems. Soft Comput. 2019, 23, 6679–6696. [Google Scholar] [CrossRef]
- Li, X.; Fu, L.; Lu, Z. A novel constraints handling mechanism based on virtual generator unit for economic dispatch problems with valve point effects. Int. J. Electr. Power Energy Syst. 2021, 129, 106825. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, S.; Verma, A. Optimal sizing and multi-energy management strategy for PV-biofuel-based off-grid systems. IET Smart Grid 2019, 3, 83–97. [Google Scholar]
- Rodríguez, F.; Galarza, A.; Vasquez, J.C.; Guerrero, J.M. Using deep learning and meteorological parameters to forecast the photovoltaic generators intra-hour output power interval for smart grid control. Energy 2022, 239, 122116. [Google Scholar] [CrossRef]
- Chang, X.; Xu, Y.; Sun, H.; Khan, I. A distributed robust optimization approach for the economic dispatch of flexible resources. Int. J. Electr. Power Energy Syst. 2021, 124, 106360. [Google Scholar] [CrossRef]
- Shafie-khah, M.; Parsa Moghaddam, M.; Sheikh-El-Eslami, M.K. Unified solution of a non-convex SCUC problem using combination of modified Branch-and-Bound method with Quadratic Programming. Energy Convers. Manag. 2011, 52, 3425–3432. [Google Scholar] [CrossRef]
- Dayev, Z.A.; Kairakbayev, A.K.; Sultanov, N.Z. Development of humidity of natural gas control system based on linear programming methods. Energy Syst. 2019, 12, 233–245. [Google Scholar] [CrossRef]
- Fan, W.; Liao, Y.; Lee, J.-B.; Kim, Y.-K. Evaluation of two lagrangian dual optimization algorithms for large-scale unit commitment problems. J. Electr. Eng. Technol. 2012, 7, 17–22. [Google Scholar] [CrossRef]
- Dai, W.; Yang, Z.; Yu, J.; Cui, W.; Li, W.; Li, J.; Liu, H. Economic dispatch of interconnected networks considering hidden flexibility. Energy 2021, 223, 120054. [Google Scholar] [CrossRef]
- Jebaraj, L.; Venkatesan, C.; Soubache, I. Application of differential evolution algorithm in static and dynamic economic or emission dispatch problem: A review. Renew. Sustain. Energy Rev. 2017, 77, 1206–1220. [Google Scholar] [CrossRef]
- Selvakumar, A.I.; Thanushkodi, K. A new particle swarm optimization solution to nonconvex economic dispatch problems. IEEE Trans. Power Syst. 2007, 22, 42–51. [Google Scholar] [CrossRef]
- Pothiya, S.; Ngamroo, I.; Kongprawechnon, W. Application of multiple tabu search algorithm to solve dynamic economic dispatch considering generator constraints. Energy Convers. Manag. 2008, 49, 506–516. [Google Scholar] [CrossRef]
- Xiong, Z.; Chen, Y.; Ban, G.; Zhuo, Y.; Huang, K. A Hybrid Algorithm for Short-Term Wind Power Prediction. Energies 2022, 15, 7314. [Google Scholar] [CrossRef]
- Nawaz, A.; Saleem, N.; Mustafa, E.; Khan, U.A. An efficient global technique for solving the network constrained static and dynamic economic dispatch problem. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 73–82. [Google Scholar] [CrossRef]
- Xu, J.; Yan, F.; Yun, K.; Su, L.; Li, F.; Guan, J. Noninferior Solution Grey Wolf Optimizer with an Independent Local Search Mechanism for Solving Economic Load Dispatch Problems. Energies 2019, 12, 2274. [Google Scholar] [CrossRef]
- Guo, F.; Li, G.; Wen, C.; Wang, L.; Meng, Z. An Accelerated Distributed Gradient-Based Algorithm for Constrained Optimization With Application to Economic Dispatch in a Large-Scale Power System. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2041–2053. [Google Scholar] [CrossRef]
- Sakthivel, V.P.; Suman, M.; Sathya, P.D. Squirrel search algorithm for economic dispatch with valve-point effects and multiple fuels. Energy Sources Part B Econ. Plan. Policy 2020, 15, 351–382. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Z.; Dannier, A. Day-Ahead and Intra-Day Optimal Scheduling of Integrated Energy System Considering Uncertainty of Source & Load Power Forecasting. Energies 2021, 14, 2539. [Google Scholar]
- Cazzaro, D.; Fischetti, M.; Fischetti, M. Heuristic algorithms for the Wind Farm Cable Routing problem. Appl. Energy 2020, 278, 115617. [Google Scholar] [CrossRef]
- Li, Z.; Zou, D.; Kong, Z. A harmony search variant and a useful constraint handling method for the dynamic economic emission dispatch problems considering transmission loss. Eng. Appl. Artif. Intell. 2019, 84, 18–40. [Google Scholar] [CrossRef]
- Vijay, R. Quorum Sensing Driven Bacterial Swarm Optimization to Solve Practical Dynamic Power Ecological Emission Economic Dispatch. Int. J. Comput. Methods 2018, 15, 1850089. [Google Scholar] [CrossRef]
- Song, Y.; Shi, L. Dynamic Economic Dispatch With CHP and Wind Power Considering Different Time Scales. IEEE Trans. Ind. Appl. 2022, 58, 5734–5746. [Google Scholar] [CrossRef]
- Xie, M.; Luo, W.; Cheng, P.; Ke, S.; Ji, X.; Liu, M. Multidisciplinary collaborative optimisation-based scenarios decoupling dynamic economic dispatch with wind power. IET Renew. Power Gener. 2018, 12, 727–734. [Google Scholar] [CrossRef]
- Zhou, W.; Peng, Y.; Sun, H.; Wei, Q.H. Dynamic Economic Dispatch in Wind Power Integrated System. Proc. CSEE 2009, 29, 13–18. [Google Scholar]
- Liu, Y.X.; Guo, L.; Wang, C.S. Economic Dispatch of Microgrid Based on Two Stage Robust Optimization. Proc. CSEE 2018, 38, 4013–4022. [Google Scholar]
- Talari, S.; Haghifam, M.-R.; Yazdaninejad, M. Stochastic-based scheduling of the microgrid operation including wind turbines, photovoltaic cells, energy storages and responsive loads. IET Gener. Transm. Distrib. 2015, 9, 1498–1509. [Google Scholar] [CrossRef]
- Tu, Q.; Miao, S.; Yao, F.; Li, Y.; Yin, H.; Han, J.; Zhang, D.; Yang, W. Forecasting Scenario Generation for Multiple Wind Farms Considering Time-series Characteristics and Spatial-temporal Correlation. J. Mod. Power Syst. Clean Energy 2021, 9, 837–848. [Google Scholar] [CrossRef]
- Matevosyan, J.; Soder, L. Minimization of imbalance cost trading wind power on the short-term power market. IEEE Trans. Power Syst. 2006, 21, 1396–1404. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, M.; Wang, X.; Li, C.; Hu, M. Bi-level robust dynamic economic emission dispatch considering wind power uncertainty. Electr. Power Syst. Res. 2016, 135, 35–47. [Google Scholar] [CrossRef]
- Mukherjee, S.; Chakrabortty, A.; Babaei, S. Modeling and Quantifying the Impact of Wind Penetration on Slow Coherency of Power Systems. IEEE Trans. Power Syst. 2021, 36, 1002–1012. [Google Scholar] [CrossRef]
- Tang, C.; Xu, J.; Sun, Y.; Liu, J.; Li, X.; Ke, D.; Yang, J.; Peng, X. A versatile mixture distribution and its application in economic dispatch with multiple wind farms. IEEE Trans. Sustain. Energy 2017, 8, 1747–1762. [Google Scholar] [CrossRef]
- Teimourian, H.; Abubakar, M.; Yildiz, M.; Teimourian, A. A Comparative Study on Wind Energy Assessment Distribution Models: A Case Study on Weibull Distribution. Energies 2022, 15, 5684. [Google Scholar] [CrossRef]
- Luo, Y.; Nie, Q.; Yang, D.; Zhou, B. Robust Optimal Operation of Active Distribution Network Based on Minimum Confidence Interval of Distributed Energy Beta Distribution. J. Mod. Power Syst. Clean Energy 2021, 9, 423–430. [Google Scholar] [CrossRef]
- Ponciroli, R.; Stauff, N.E.; Ramsey, J.; Ganda, F.; Vilim, R.B. An Improved Genetic Algorithm Approach to the Unit Commitment/Economic Dispatch Problem. IEEE Trans. Power Syst. 2020, 35, 4005–4013. [Google Scholar] [CrossRef]
- Yang, J.; Liu, Y.; Jiang, S.; Luo, Y.; Liu, N.; Ke, D. A Method of Probability Distribution Modeling of Multi-Dimensional Conditions for Wind Power Forecast Error Based on MNSGA-II-Kmeans. Energies 2022, 15, 2462. [Google Scholar] [CrossRef]
- Zhang, H.; Lei, X.; Wang, C.; Yue, D.; Xie, X. Adaptive grid based multi-objective Cauchy differential evolution for stochastic dynamic economic emission dispatch with wind power uncertainty. PLoS ONE 2017, 12, e0185454. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Luh, P.B.; Gribik, P.; Peng, T.; Zhang, L. Commitment Cost Allocation of Fast-Start Units for Approximate Extended Locational Marginal Prices. IEEE Trans. Power Syst. 2016, 31, 4176–4184. [Google Scholar] [CrossRef]
- Chiodo, E.; Fantauzzi, M.; Mazzanti, G. The Compound Inverse Rayleigh as an Extreme Wind Speed Distribution and Its Bayes Estimation. Energies 2022, 15, 861. [Google Scholar] [CrossRef]
- Yan, L.; Zhu, Z.; Kang, X.; Qu, B.; Qiao, B.; Huan, J.; Chai, X. Multi-Objective Dynamic Economic Emission Dispatch with Electric Vehicle–Wind Power Interaction Based on a Self-Adaptive Multiple-Learning Harmony-Search Algorithm. Energies 2022, 15, 4942. [Google Scholar] [CrossRef]
- Jiang, K.; Wu, F.; Shi, L.; Lin, K. Distributed Hierarchical Consensus-Based Economic Dispatch for Isolated AC/DC Hybrid Microgrid. Energies 2020, 13, 3209. [Google Scholar] [CrossRef]
- Liang, H.; Liu, Y.; Li, F.; Shen, Y. Dynamic Economic/Emission Dispatch Including PEVs for Peak Shaving and Valley Filling. IEEE Trans. Ind. Electron. 2019, 66, 2880–2890. [Google Scholar] [CrossRef]
- Qiao, B.; Liu, J. Multi-objective dynamic economic emission dispatch based on electric vehicles and wind power integrated system using differential evolution algorithm. Renew. Energy Int. J. 2020, 154, 316–336. [Google Scholar] [CrossRef]
- Azizivahed, A.; Arefi, A.; Naderi, E.; Narimani, H.; Fathi, M.; Narimani, M.R. An Efficient Hybrid Approach to Solve Bi-objective Multi-area Dynamic Economic Emission Dispatch Problem. Electr. Power Compon. Syst. 2020, 48, 485–500. [Google Scholar] [CrossRef]
- Qu, B.Y.; Liang, J.J.; Zhu, Y.S.; Suganthan, P.N. Solving dynamic economic emission dispatch problem considering wind power by multi-objective differential evolution with ensemble of selection method. Nat. Comput. 2019, 18, 695–703. [Google Scholar] [CrossRef]
- Hu, F.; Hughes, K.J.; Ingham, D.B.; Ma, L.; Pourkashanian, M. Dynamic economic and emission dispatch model considering wind power under Energy Market Reform: A case study. Int. J. Electr. Power Energy Syst. 2019, 110, 184–196. [Google Scholar] [CrossRef]
- Ding, C.; Zhou, Y.; Ding, Q.; Li, K. Integrated Carbon-Capture-Based Low-Carbon Economic Dispatch of Power Systems Based on EEMD-LSTM-SVR Wind Power Forecasting. Energies 2022, 15, 1613. [Google Scholar] [CrossRef]
- Narimani, H.; Razavi, S.-E.; Azizivahed, A.; Naderi, E.; Fathi, M.; Ataei, M.H.; Narimani, M.R. A multi_objective framework for multi_area economic emission dispatch. Energy 2018, 154, 126–142. [Google Scholar] [CrossRef]
- Boudab, S.; Goléa, N. Combined economic-emission dispatch problem: Dynamic neural networks solution approach. J. Renew. Sustain. Energy 2017, 9, 035503. [Google Scholar] [CrossRef]
- Zhang, R.; Aziz, S.; Farooq, M.U.; Hasan, K.N.; Mohammed, N.; Ahmad, S.; Ibadah, N. A Wind Energy Supplier Bidding Strategy Using Combined EGA-Inspired HPSOIFA Optimizer and Deep Learning Predictor. Energies 2021, 14, 3059. [Google Scholar] [CrossRef]
- Zhang, G.; Zhu, Y.; Xie, T.; Zhang, K.; He, X. Wind Power Consumption Model Based on the Connection between Mid- and Long-Term Monthly Bidding Power Decomposition and Short-Term Wind-Thermal Power Joint Dispatch. Energies 2022, 15, 7201. [Google Scholar] [CrossRef]
- Chu, S.; Ge, W.S.; Teng, Y.; Liu, C.; Cai, G.W.; Dong, H. Multi-time-scale Scheduling Strategy for Combined Accommodation of Wind Power by Seawater Desalination and Electric Heating Loads. Autom. Electr. Power Syst. 2023, 47, 1–16. [Google Scholar]
- Cheng, T.; Chen, M.; Wang, Y.; Li, B.; Hassan, M.; Chen, T.; Xu, R. Adaptive Robust Method for Dynamic Economic Emission Dispatch Incorporating Renewable Energy and Energy Storage. Complexity 2018, 2018, 2517987. [Google Scholar] [CrossRef]
- Chinnadurrai, C.L.; Victoire, T.A.A. Enhanced multi-objective crisscross optimization for dynamic economic emission dispatch considering demand response and wind power uncertainty. Soft Comput. 2020, 24, 9021–9038. [Google Scholar] [CrossRef]
| Types of Energy | Installed Capacity (Gigawatts) | Proportion (%) | Newly Installed Capacity (Million kW) | Proportion (%) |
|---|---|---|---|---|
| Hydroelectric power Generation | 4.13 | 16.1 | 2387 | 11.9 |
| Wind power Generation | 3.65 | 14.2 | 3763 | 18.8 |
| Photovoltaic power | 3.93 | 15.3 | 8741 | 43.7 |
| biomass power generation Generation | 0.41 | 1.6 | 334 | 1.67 |
| total | 12.13 | 47.3 | 15225 | 76.2 |
| Area | Installed Capacity (Gigawatts) | Proportion (%) | Newly Installed Capacity (Million kW) | Proportion (%) |
|---|---|---|---|---|
| Onshore wind power | 3.34 | 91.5 | 4360 | 89.3 |
| Offshore wind power | 0.31 | 8.5 | 520 | 10.7 |
| total | 3.65 | 100 | 4880 | 100 |
| Scenario | Total Cost (Yuan) | Electricity Purchase Cost (Yuan) | Gas Purchase Cost (Yuan) |
|---|---|---|---|
| 1 | 2,380,977.356 | 308,359.0327 | 1,700,017.44 |
| 2 | 2,221,565.65 | 287,023.3357 | 1,572,484.016 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Pei, J.; Shen, Q. A Review of Research on Dynamic and Static Economic Dispatching of Hybrid Wind–Thermal Power Microgrids. Energies 2023, 16, 3985. https://doi.org/10.3390/en16103985
Li L, Pei J, Shen Q. A Review of Research on Dynamic and Static Economic Dispatching of Hybrid Wind–Thermal Power Microgrids. Energies. 2023; 16(10):3985. https://doi.org/10.3390/en16103985
Chicago/Turabian StyleLi, Lingling, Jiarui Pei, and Qiang Shen. 2023. "A Review of Research on Dynamic and Static Economic Dispatching of Hybrid Wind–Thermal Power Microgrids" Energies 16, no. 10: 3985. https://doi.org/10.3390/en16103985
APA StyleLi, L., Pei, J., & Shen, Q. (2023). A Review of Research on Dynamic and Static Economic Dispatching of Hybrid Wind–Thermal Power Microgrids. Energies, 16(10), 3985. https://doi.org/10.3390/en16103985






