PSO-Based Identification of the Li-Ion Battery Cell Parameters
Abstract
1. Introduction
- Proposed method for OCV characteristic determination based on HPPC tests.
- Developed universal, PSO-based optimization method, suitable both for OCV characteristic and HPPC pulses approximation.
- Comparison and evaluation of various OCV approximation functions.
- Comparison and evaluation of a one-time-constant and a two-time-constant Thevenin model of the same battery cell.
2. Methods
3. Results
3.1. Battery Cell OCV Characteristic
3.2. Battery Cell Thevenin Impedance
3.3. Particle Swarm Optimization
3.3.1. Particle Swarm Dynamics
3.3.2. Cognition Process
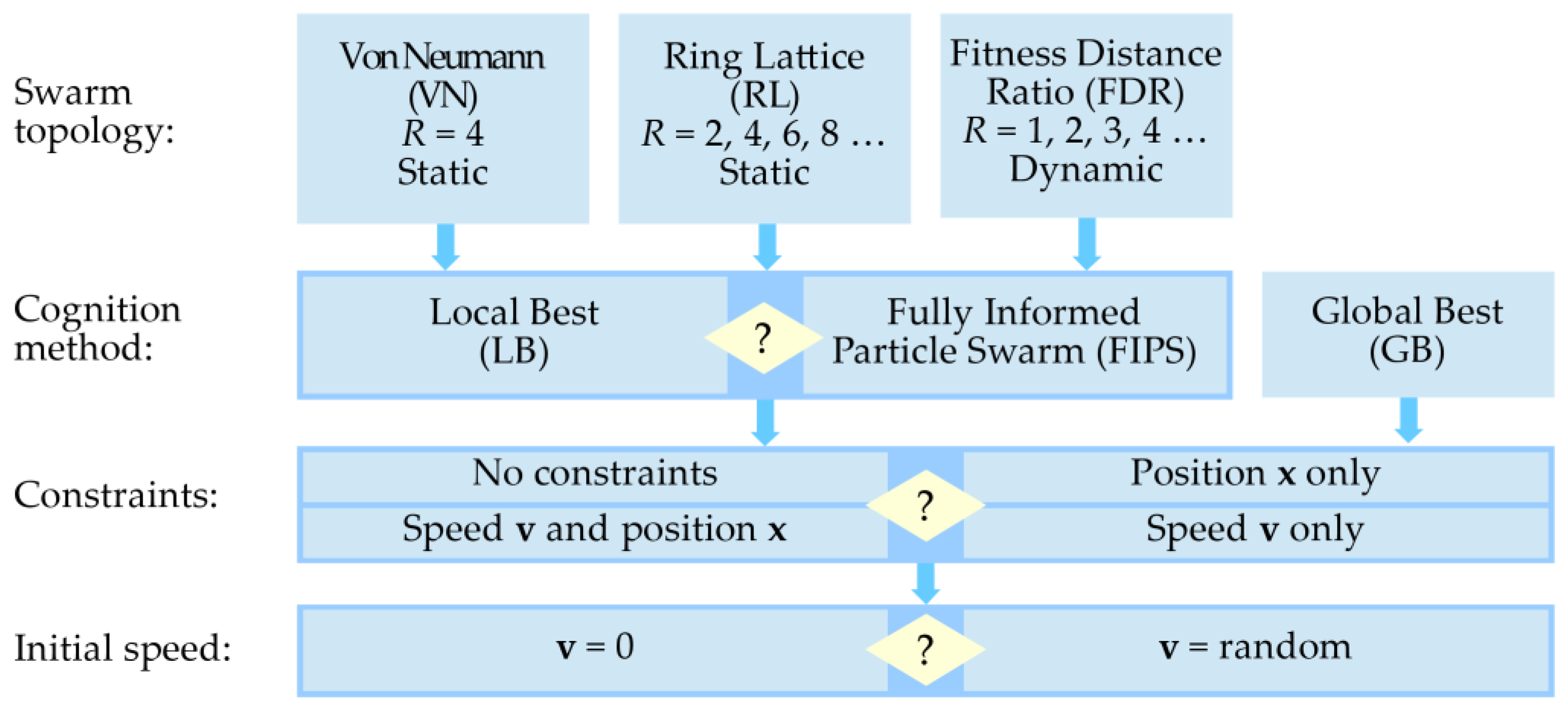
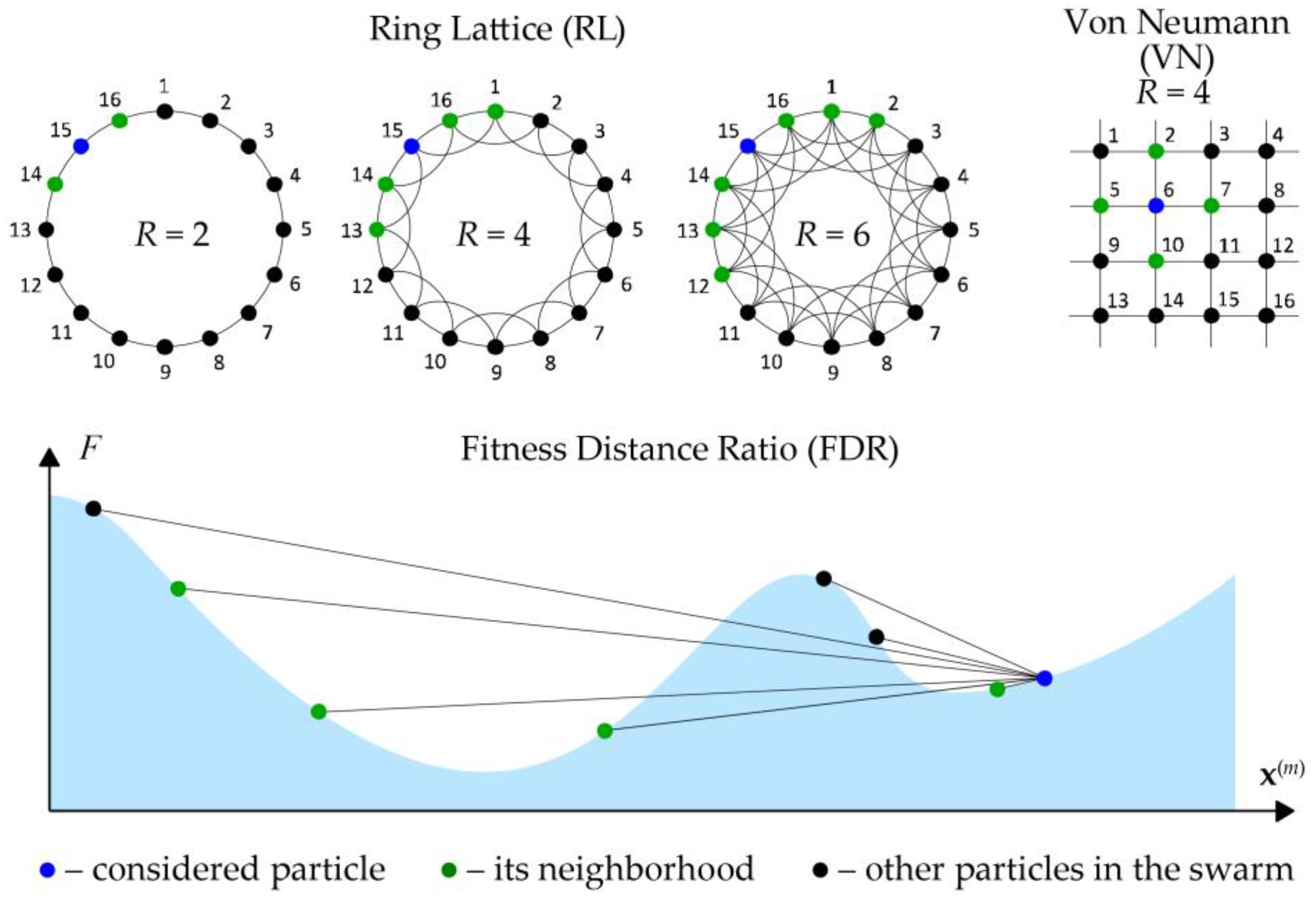
3.3.3. Swarm Topology
3.3.4. Initial Conditions and Constraints
3.3.5. Convergence and Stability
3.4. Optimization and Simulation Results
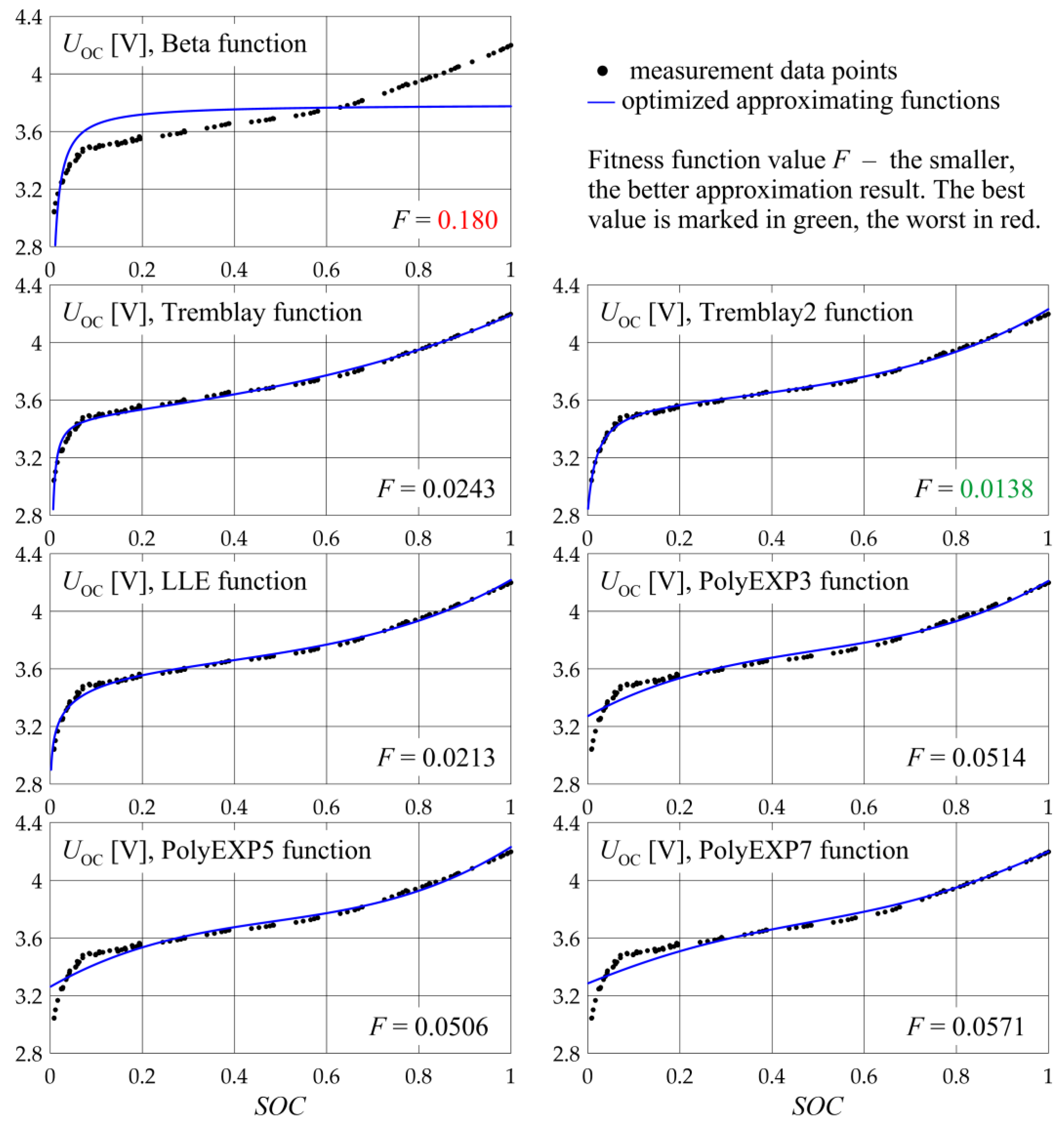
3.4.1. OCV Characteristic Approximation
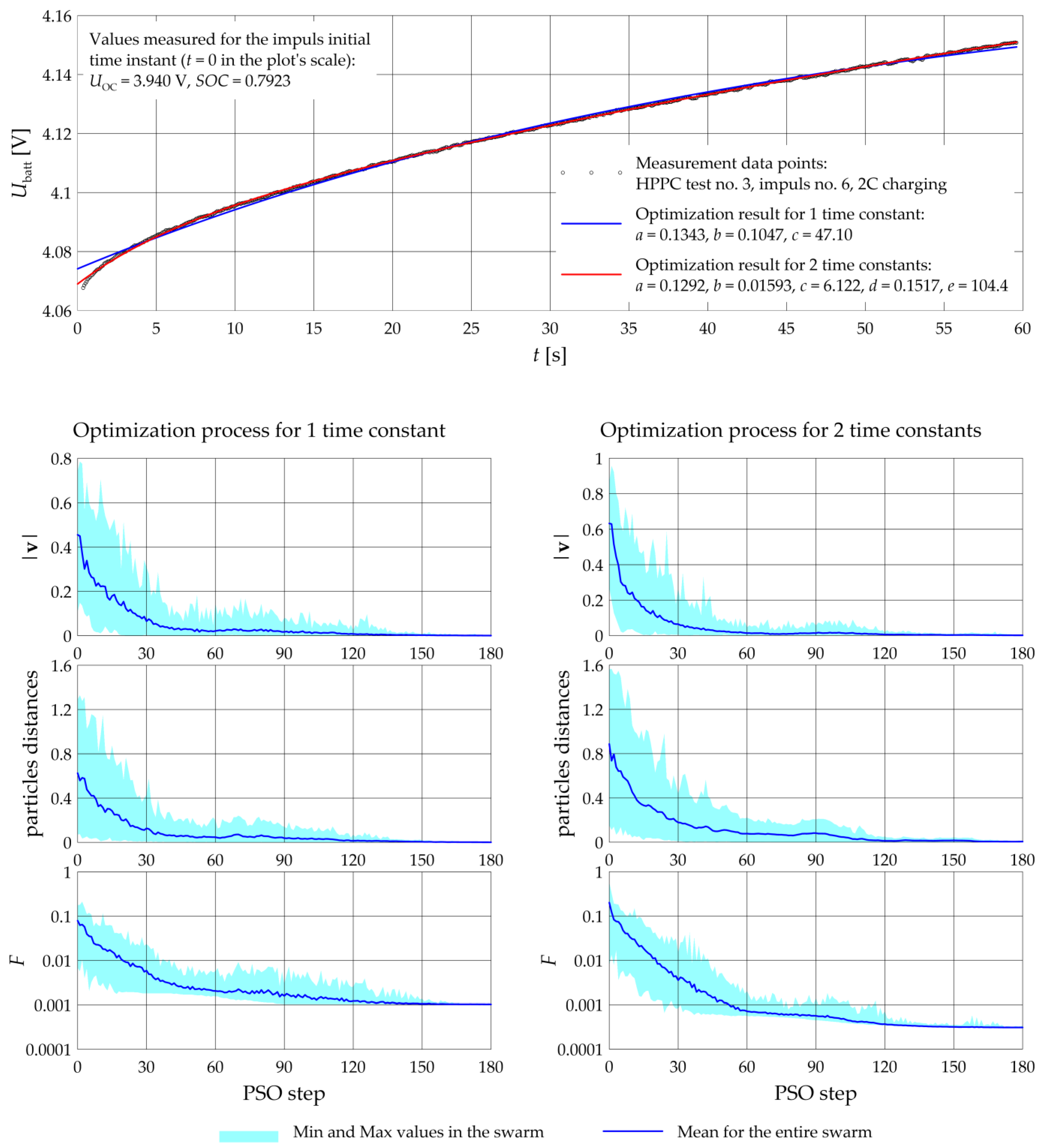
3.4.2. HPPC Pulses Approximation
3.4.3. Simulations Compared to Measurements
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shi, J.; Guo, H.; Chen, D. Parameter identification method for lithium-ion batteries based on recursive least square with sliding window difference forgetting factor. J. Energy Storage 2021, 44, 103485. [Google Scholar] [CrossRef]
- Stroe, D.I.; Swierczynski, M.; Stroe, A.I.; Knudsen Kær, S. Generalized Characterization Methodology for Performance Modelling of Lithium-Ion Batteries. Batteries 2016, 2, 37. [Google Scholar] [CrossRef]
- Davis, K.; Hayes, J.G. Comparison of Lithium-Ion Battery Pack Models Based on Test Data from Idaho and Argonne National Laboratories. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 5626–5632. [Google Scholar] [CrossRef]
- Rahmoun, A.; Biechl, H. Modelling of li-ion batteries using equivalent circuit diagrams. Electr. Rev. 2012, 2, 152–156. [Google Scholar]
- Tremblay, O.; Dessaint, L.; Dekkiche, A. A Generic Battery Model for the Dynamic Simulation of Hybrid Electric Vehicles. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Arlington, TX, USA, 9–12 September 2007; pp. 274–279. [Google Scholar] [CrossRef]
- Cipin, R.; Toman, M.; Prochazka, P.; Pazdera, I. Identification of Li-ion Battery Model Parameters. In Proceedings of the International Conference on Electrical Drives & Power Electronics (EDPE), The High Tatras, Slovakia, 24–26 September 2019; pp. 225–229. [Google Scholar] [CrossRef]
- Chen, S.X.; Tseng, K.J.; Choi, S.S. Modeling of Lithium-Ion Battery for Energy Storage System Simulation. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 28–30 March 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Huang, K.; Wang, Y.; FENG, J. Research on equivalent circuit Model of Lithium-ion battery for electric vehicles. In Proceedings of the 3rd World Conference on Mechanical Engineering and Intelligent Manufacturing (WCMEIM), Shanghai, China, 4–6 December 2020; pp. 492–496. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Fan, J. Evaluation of Lithium-Ion Battery Equivalent Circuit Models for State of Charge Estimation by an Experimental Approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Sibi Krishnan, K.; Pathiyil, P.; Sunitha, R. Generic Battery model covering self-discharge and internal resistance variation. In Proceedings of the IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Wu, W.; Qin, L.; Wu, G. State of power estimation of power lithium-ion battery based on an equivalent circuit model. J. Energy Storage 2022, 51, 104538. [Google Scholar] [CrossRef]
- Li, Z.; Shi, X.; Shi, M.; Wei, C.; Di, F.; Sun, H. Investigation on the Impact of the HPPC Profile on the Battery ECM Parameters’ Offline Identification. In Proceedings of the Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 28–31 May 2020; pp. 753–757. [Google Scholar] [CrossRef]
- Khattak, A.A.; Khan, A.N.; Safdar, M.; Basit, A.; Zaffar, N.A. A Hybrid Electric Circuit Battery Model Capturing Dynamic Battery Characteristics. In Proceedings of the IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 13–14 July 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Baczyńska, A.; Niewiadomski, W.; Gonçalves, A.; Almeida, P.; Luís, R. Li-NMC Batteries Model Evaluation with Experimental Data for Electric Vehicle Application. Batteries 2018, 4, 11. [Google Scholar] [CrossRef]
- Somakettarin, N.; Funaki, T. Study on Factors for Accurate Open Circuit Voltage Characterizations in Mn-Type Li-Ion Batteries. Batteries 2017, 3, 8. [Google Scholar] [CrossRef]
- Gao, Y.; Ji, W.; Zhao, X. SOC Estimation of E-Cell Combining BP Neural Network and EKF Algorithm. Processes 2022, 10, 1721. [Google Scholar] [CrossRef]
- Hemi, H.; M’Sirdi, N.K.; Naamane, A.; Ikken, B. Open Circuit Voltage of a Lithium ion Battery Model Adjusted by Data Fitting. In Proceedings of the 6th International Renewable and Sustainable Energy Conference (IRSEC), Rabat, Morocco, 5–8 December 2018; pp. 1–5. [Google Scholar]
- Zhang, Q.; Shang, Y.; Li, Y.; Cui, N.; Duan, B.; Zhang, C. A novel fractional variable-order equivalent circuit model and parameter identification of electric vehicle Li-ion batteries. ISA Trans. 2020, 97, 448–457. [Google Scholar] [CrossRef]
- Navas, S.J.; Cabello González, G.M.; Pino, F.J.; Guerra, J.J. Modelling Li-ion batteries using equivalent circuits for renewable energy applications. Energy Rep. 2023, 9, 4456–4465. [Google Scholar] [CrossRef]
- Wang, J.; Jia, Y.; Yang, N.; Lu, Y.; Shi, M.; Ren, X.; Lu, D. Precise equivalent circuit model for Li-ion battery by experimental improvement and parameter optimization. J. Energy Storage 2022, 52, 104980. [Google Scholar] [CrossRef]
- Haghjoo, Y.; Khaburi, D.A. Modeling, simulation, and parameters identification of a lithium-ion battery used in electric vehicles. In Proceedings of the 9th Iranian Conference on Renewable Energy & Distributed Generation (ICREDG), Mashhad, Iran, 23–24 February 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Yu, Q.; Wan, C.; Li, J.; E, L.; Zhang, X.; Huang, Y.; Liu, T. An Open Circuit Voltage Model Fusion Method for State of Charge Estimation of Lithium-Ion Batteries. Energies 2021, 14, 1797. [Google Scholar] [CrossRef]
- Gao, L.; Liu, S.; Dougal, R.A. Dynamic lithium-ion battery model for system simulation. IEEE Trans. Compon. Packag. Technol. 2002, 25, 495–505. [Google Scholar] [CrossRef]
- Wen, F.; Duan, B.; Zhang, C.; Zhu, R.; Shang, Y.; Zhang, J. High-Accuracy Parameter Identification Method for Equivalent-Circuit Models of Lithium-Ion Batteries Based on the Stochastic Theory Response Reconstruction. Electronics 2019, 8, 834. [Google Scholar] [CrossRef]
- Feng, D.; Huang, J.; Jin, P.; Chen, H.; Wang, A.; Zheng, M. Parameter Identification and Dynamic Simulation of Lithium-Ion Power Battery Based on DP Model. In Proceedings of the 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 1275–1279. [Google Scholar] [CrossRef]
- Baccouche, I.; Jemmali, S.; Manai, B.; Omar, N.; Amara, N.E.B. Improved OCV Model of a Li-Ion NMC Battery for Online SOC Estimation Using the Extended Kalman Filter. Energies 2017, 10, 764. [Google Scholar] [CrossRef]
- Pillai, P.; Sundaresan, S.; Kumar, P.; Pattipati, K.R.; Balasingam, B. Open-Circuit Voltage Models for Battery Management Systems: A Review. Energies 2022, 15, 6803. [Google Scholar] [CrossRef]
- Wang, C.; Xu, M.; Zhang, Q.; Feng, J.; Jiang, R.; Wei, Y.; Liu, Y. Parameters identification of Thevenin model for lithium-ion batteries using self-adaptive Particle Swarm Optimization Differential Evolution algorithm to estimate state of charge. J. Energy Storage 2021, 44, 103244. [Google Scholar] [CrossRef]
- Tran, M.K.; Mathew, M.; Janhunen, S.; Panchal, S.; Raahemifar, K.; Fraser, R.; Fowler, M. A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters. J. Energy Storage 2021, 43, 103252. [Google Scholar] [CrossRef]
- Deng, S.D.; Liu, S.Y.; Wang, L.; Xia, L.L.; Chen, L. An improved second-order electrical equivalent modeling method for the online high power Li-ion battery state of charge estimation. In Proceedings of the IEEE 12th Energy Conversion Congress & Exposition—Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 1725–1729. [Google Scholar] [CrossRef]
- Parthasarathy, C.; Laaksonen, H.; Halagi, P. Characterisation and Modelling Lithium Titanate Oxide Battery Cell by Equivalent Circuit Modelling Technique. In Proceedings of the IEEE PES Innovative Smart Grid Technologies—Asia (ISGT Asia), Brisbane, Australia, 5–8 December 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Nemes, R.; Ciornei, S.; Ruba, M.; Hedesiu, H.; Martis, C. Modeling and simulation of first-order Li-Ion battery cell with experimental validation. In Proceedings of the 8th International Conference on Modern Power Systems (MPS), Cluj-Napoca, Romania, 21–23 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Nemes, R.O.; Ciornei, S.M.; Ruba, M.; Martis, C. Parameters identification using experimental measurements for equivalent circuit Lithium-Ion cell models. In Proceedings of the 11th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 28–30 March 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Tang, A.; Gong, P.; Li, J.; Zhang, K.; Zhou, Y.; Zhang, Z. A State-of-Charge Estimation Method Based on Multi-Algorithm Fusion. World Electr. Veh. J. 2022, 13, 70. [Google Scholar] [CrossRef]
- Jarrraya, I.; Degaa, L.; Rizoug, N.; Chabchoub, M.H.; Trabelsi, H. Comparison study between hybrid Nelder-Mead particle swarm optimization and open circuit voltage—Recursive least square for the battery parameters estimation. J. Energy Storage 2022, 50, 104424. [Google Scholar] [CrossRef]
- Mueller, K.; Schwiederik, E.; Tittel, D. Analysis of parameter identification methods for electrical Li-Ion battery modelling. In Proceedings of the World Electric Vehicle Symposium and Exhibition (EVS27), Barcelona, Spain, 17–20 November 2013; pp. 1–9. [Google Scholar] [CrossRef]
- Jamali, S.; Eftekhari, A. PSO-Vegas: Algorytm Vegas z poprawioną PSO. Electr. Rev. 2011, 87, 199–203. [Google Scholar]
- Shaheen, A.M.; Hamida, M.A.; El-Sehiemy, R.A.; Elattar, E.E. Optimal parameter identification of linear and non-linear models for Li-Ion Battery Cells. Energy Rep. 2021, 7, 7170–7185. [Google Scholar] [CrossRef]
- Pizarro-Carmona, V.; Castano-Solís, S.; Cortés-Carmona, M.; Fraile-Ardanuy, J.; Jimenez-Bermejo, G. GA-based approach to optimize an equivalent electric circuit model of a Li-ion battery-pack. Expert Syst. Appl. 2021, 172, 114647. [Google Scholar] [CrossRef]
- Hamida, M.A.; El-Sehiemy, R.A.; Ginidi, A.R.; Elattar, E.; Shaheen, A.M. Parameter identification and state of charge estimation of Li-Ion batteries used in electric vehicles using artificial hummingbird optimizer. J. Energy Storage 2022, 51, 104535. [Google Scholar] [CrossRef]
- Huang, Y.; Li, Y.; Jiang, L.; Qiao, X.; Cao, Y.; Yu, J. Research on Fitting Strategy in HPPC Test for Li-ion battery. In Proceedings of the IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019; pp. 1776–1780. [Google Scholar] [CrossRef]
- Castanho, D.; Guerreiro, M.; Silva, L.; Eckert, J.; Antonini Alves, T.; Tadano, Y.d.S.; Stevan, S.L., Jr.; Siqueira, H.V.; Corrêa, F.C. Method for SoC Estimation in Lithium-Ion Batteries Based on Multiple Linear Regression and Particle Swarm Optimization. Energies 2022, 15, 6881. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization: An overview. Swarm Intell 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Li, W.; Fan, Y.; Jiang, Q.; Xu, Q. Velocity-Driven Particle Swarm Optimization. In Proceedings of the 8th International Conference on Computing and Pattern Recognition (ICCPR ‘19), Beijing, China, 23–25 October 2019; pp. 9–16. [Google Scholar] [CrossRef]
- Cleghorn, C.W.; Engelbrecht, A.P. Fitness-distance-ratio particle swarm optimization: Stability analysis. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO), Berlin, Germany, 15–19 July 2017; pp. 12–18. [Google Scholar] [CrossRef]
- Fernandes, C.M.; Rosa, A.C.; Fachada, N.; Laredo, J.L.J.; Merelo, J.J. Particle swarm and population structure. In Proceedings of the Genetic and Evolutionary Computation Conference Companion (GECCO), Kyoto, Japan, 15–19 July 2018; pp. 85–86. [Google Scholar] [CrossRef]
- Peram, T.; Veeramachaneni, K.; Mohan, C.K. Fitness-distance-ratio based particle swarm optimization. In Proceedings of the IEEE Swarm Intelligence Symposium (SIS), Indianapolis, IN, USA, 26 April 2003; pp. 174–181. [Google Scholar] [CrossRef]
- Clerc, M.; Kennedy, J. The particle swarm—Explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Diampovesa, S.; Hubert, A.; Yvars, P.A. Designing physical systems through a model-based synthesis approach. Example of a Li-ion battery for electrical vehicles. Comput. Ind. 2021, 129, 103440. [Google Scholar] [CrossRef]
- Skarka, W. Model-Based Design and Optimization of Electric Vehicles. In Proceedings of the 25th ISPE International Conference on Transdisciplinary Engineering, Modena, Italy, 3–6 July 2018; Volume 7, pp. 566–575. [Google Scholar]
- Peciak, M.; Skarka, W. Assessment of the Potential of Electric Propulsion for General Aviation Using Model-Based System Engineering (MBSE) Methodology. Aerospace 2022, 9, 74. [Google Scholar] [CrossRef]
- Mateja, K.; Skarka, W.; Peciak, M.; Niestrój, R.; Gude, M. Energy Autonomy Simulation Model of Solar Powered UAV. Energies 2023, 16, 479. [Google Scholar] [CrossRef]
- Peciak, M.; Skarka, W.; Mateja, K.; Gude, M. Impact Analysis of Solar Cells on Vertical Take-Off and Landing (VTOL) Fixed-Wing UAV. Aerospace 2023, 10, 247. [Google Scholar] [CrossRef]
- Niestrój, R.; Rogala, T.; Skarka, W. An Energy Consumption Model for Designing an AGV Energy Storage System with a PEMFC Stack. Energies 2020, 13, 3435. [Google Scholar] [CrossRef]
- Belt, J.R. Battery Test Manual for Plug-In Hybrid Electric Vehicles, 2nd ed.; U.S. Department of Energy Vehicle Technologies Program: Idaho Falls, ID, USA, 2010. [CrossRef]
- Yang, Z.; Wang, X. An improved parameter identification method considering multi-timescale characteristics of lithium-ion batteries. J. Energy Storage 2023, 59, 106462. [Google Scholar] [CrossRef]
- Karimi, D.; Behi, H.; Van Mierlo, J.; Berecibar, M. Equivalent Circuit Model for High-Power Lithium-Ion Batteries under High Current Rates, Wide Temperature Range, and Various State of Charges. Batteries 2023, 9, 101. [Google Scholar] [CrossRef]
- Plett, G.L. High-performance battery-pack power estimation using a dynamic cell model. IEEE Trans. Veh. Technol. 2004, 53, 1586–1593. [Google Scholar] [CrossRef]
- Marušić, D.; Vašak, M. Efficient Method of Identifying a Li-Ion Battery Model for an Electric Vehicle. In Proceedings of the IEEE 20th International Power Electronics and Motion Control Conference (PEMC), Brasov, Romania, 25–28 September 2022; pp. 421–426. [Google Scholar] [CrossRef]
- Guenther, C.; Barillas, J.K.; Stumpp, S.; Danzer, M.A. A dynamic battery model for simulation of battery-to-grid applications. In Proceedings of the 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Berlin, Germany, 14–17 October 2012; pp. 1–7. [Google Scholar] [CrossRef]
- Sörés, M.A.; Hartmann, B. Overview of possible methods of determining self-discharge. In Proceedings of the IEEE International Conference on Environment and Electrical Engineering and IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, Y.; Lyden, S.; de la Barra, B.A.L.; Haque, M.E. Optimization of Tremblay’s battery model parameters for plug-in hybrid electric vehicle applications. In Proceedings of the Australasian Universities Power Engineering Conference (AUPEC), Melbourne, Australia, 19–22 November 2017; pp. 1–6. [Google Scholar]
- Li, R.; Wang, Z.; Yu, J.; Lei, Y.; Zhang, Y.; He, J. Dynamic Parameter Identification of Mathematical Model of Lithium-Ion Battery Based on Least Square Method. In Proceedings of the IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, R.; Pan, Z. Model Identification of Lithium-Ion Batteries Considering Current-Rate Effects on battery impedance. In Proceedings of the 4th International Conference on Power and Renewable Energy (ICPRE), Chengdu, China, 21–23 September 2019; pp. 305–309. [Google Scholar] [CrossRef]
- Einhorn, M.; Conte, V.F.; Kral, C.; Fleig, J.; Permann, R. Parameterization of an electrical battery model for dynamic system simulation in electric vehicles. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; pp. 1–7. [Google Scholar] [CrossRef]


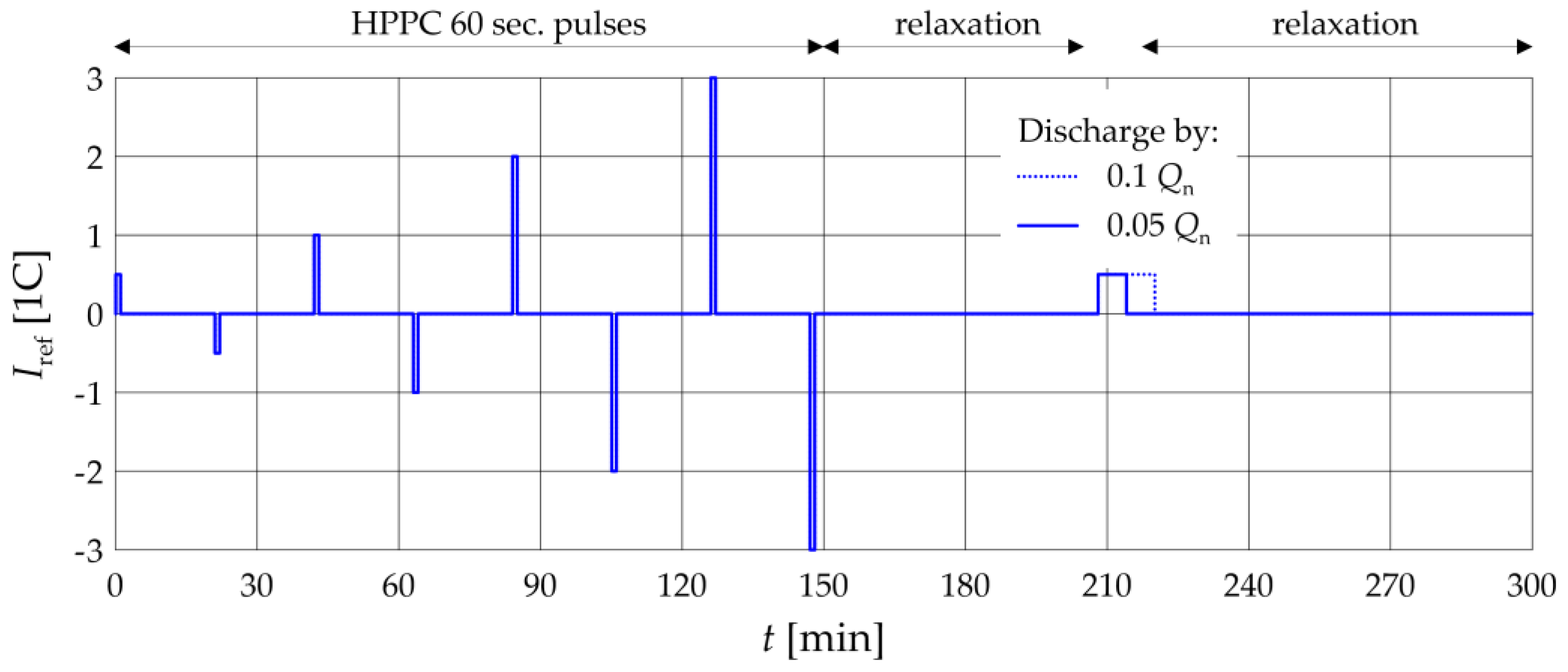
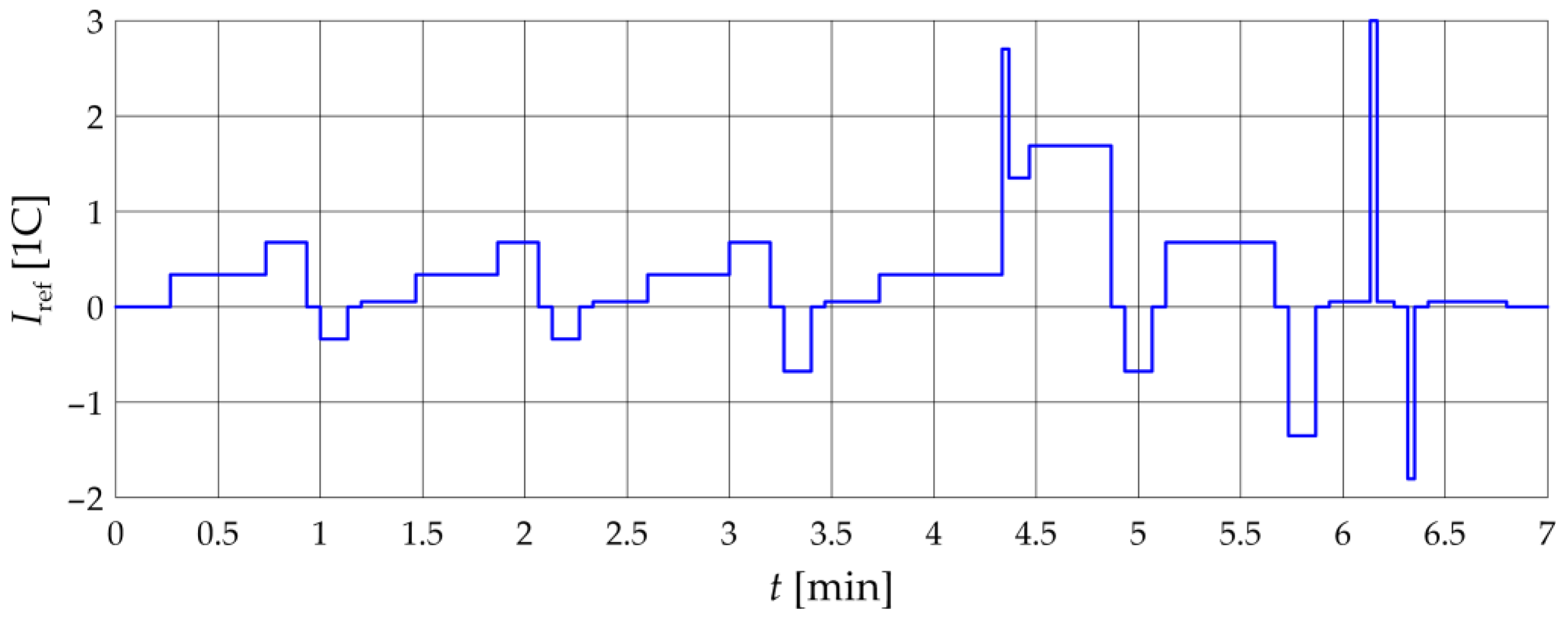
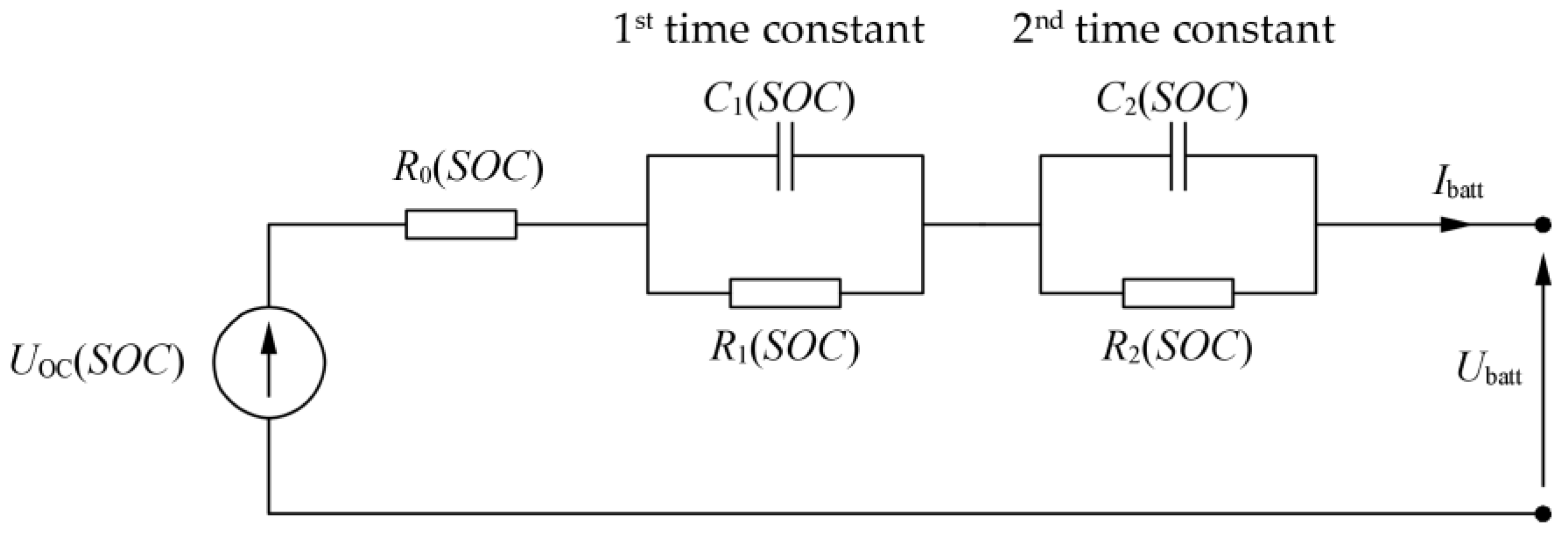
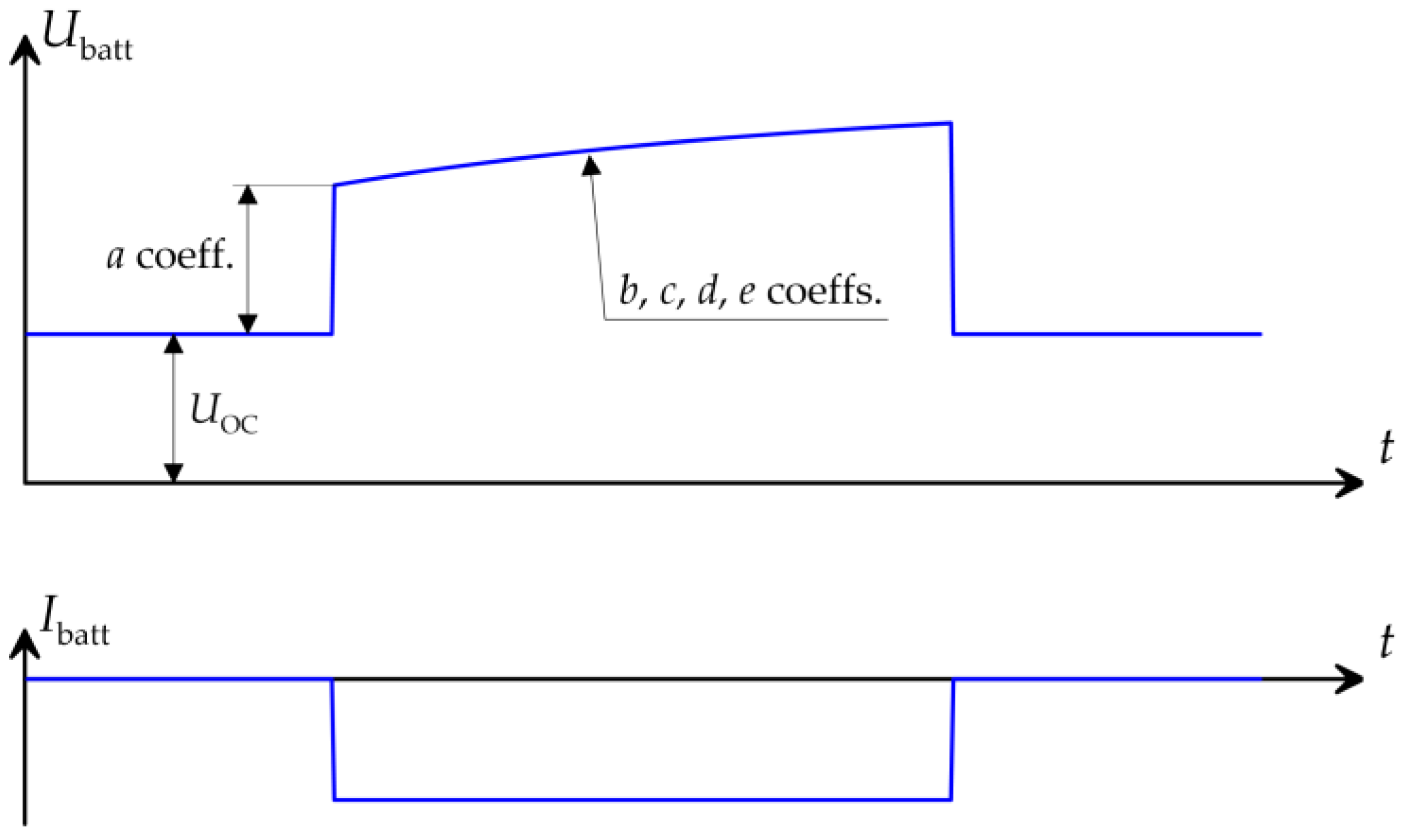
| Type | KOKAM SLPB78205130H |
| Chemistry | Nickel Manganese Cobalt (NMC) |
| Rated capacity Qn | 16 Ah |
| Energy density | 146 Wh/kg |
| Dimensions (width/length/thickness) | 220 mm/132 mm/7.8 mm |
| Voltage (min./average/max.) | 2.7 V/3.7 V/4.2 V |
| Continues current (charge/discharge) | 48 A (3C *)/128 A (8C *) |
| Peak discharge current (max. 10 s at SOC > 50%) | 240 A (15C *) |
| OCV Characteristic Approximating Functions | ||||||||
|---|---|---|---|---|---|---|---|---|
| Beta | Tremblay | Tremblay2 | LLE | PolyEXP3 | PolyEXP5 | PolyEXP7 | ||
| Optimization results—function parameters and fitness function | a [limits] | 3.775 [2.5, 4] | 3.302 [2.5, 4] | 3.563 [2.5, 4] | 3.760 [2.5, 4] | 3.271 [2.5, 5] | 3.261 [2.5, 5] | 3.250 [2.5, 5] |
| b [limits] | 0.9962 [0.9, 1] | 0.8931 [0.1, 4] | 0.6842 [0.1, 5] | 0.1474 [0, 2] | 3.564 × 10−3 [0, 5] | 0 [0, 5] | 1.219 [0, 5] | |
| c [limits] | – | 1.564 [0.1, 5] | 2.773 [2, 100] | 1.583 × 10−7 [0, 0.3] | 2.783 [0, 5] | 2.990 [0, 5] | 3.574 [0, 5] | |
| d [limits] | – | 0.004545 [0, 0.1] | 0.01618 [0, 1] | −0.3078 [−0.5, 0.5] | 1.768 [−3, 3] | 1.823 [−3, 3] | 1.170 [−3, 3] | |
| e [limits] | – | – | 0.02028 [0, 0.1] | 2.618 [0.1, 10] | −2.581 [−3, 3] | −2.475 [−3, 3] | −0.8740 [−3, 3] | |
| f [limits] | – | – | – | 1.102 [0.85, 1.5] | 1.749 [−3, 3] | 0.8092 [−3, 3] | −1.844 [−3, 3] | |
| g [limits] | – | – | – | – | – | 1.366 [−3, 3] | 2.736 [−3, 3] | |
| h [limits] | – | – | – | – | – | −0.5519 [−3, 3] | −1.397 [−3, 3] | |
| i [limits] | – | – | – | – | – | – | 0.3985 [−3, 3] | |
| j [limits] | – | – | – | – | – | – | −0.4576 [−3, 3] | |
| F | 0.180 1 | 0.0243 | 0.0138 1 | 0.0213 | 0.0514 | 0.0506 | 0.0571 | |
| PSO total time (relative) | 1 | 58.7 | 3.89 | 5.06 | 5.08 | 5.04 | 5.10 | |
| PSO settings | I | 120 | 120 | 120 | 120 | 120 | 120 | 120 |
| N | 36 | 64 | 64 | 64 | 100 | 100 | 100 | |
| Topology (R) | – | FDR (4) | VN (4) | RL (6) | VN (4) | VN (4) | VN (4) | |
| Cognition (φ) | GB (4.1) | LB (4.15) | FIPS (4.1) | FIPS (4.15) | LB (4.25) | LB (4.25) | LB (4.25) | |
| Constraints | v and x | only x | v and x | v and x | v and x | v and x | v and x | |
| Thevenin Time Constants Number | 1 | 2 | |
|---|---|---|---|
| PSO settings | I | 180 | 180 |
| N | 36 | 64 | |
| Topology (R) | VN (4) | RL (8) | |
| Cognition (φ) | FIPS (4.1) | FIPS (4.1) | |
| Constraints | v and x | v and x | |
| Fitness function statistics | min(F) * | 3.07 × 10−4 | 1.73 × 10−4 |
| max(F) * | 3.84 × 10−3 | 2.80 × 10−3 | |
| mean(F) * | 9.87 × 10−4 | 4.73 × 10−4 | |
| median(F) * | 7.91 × 10−4 | 3.95 × 10−4 | |
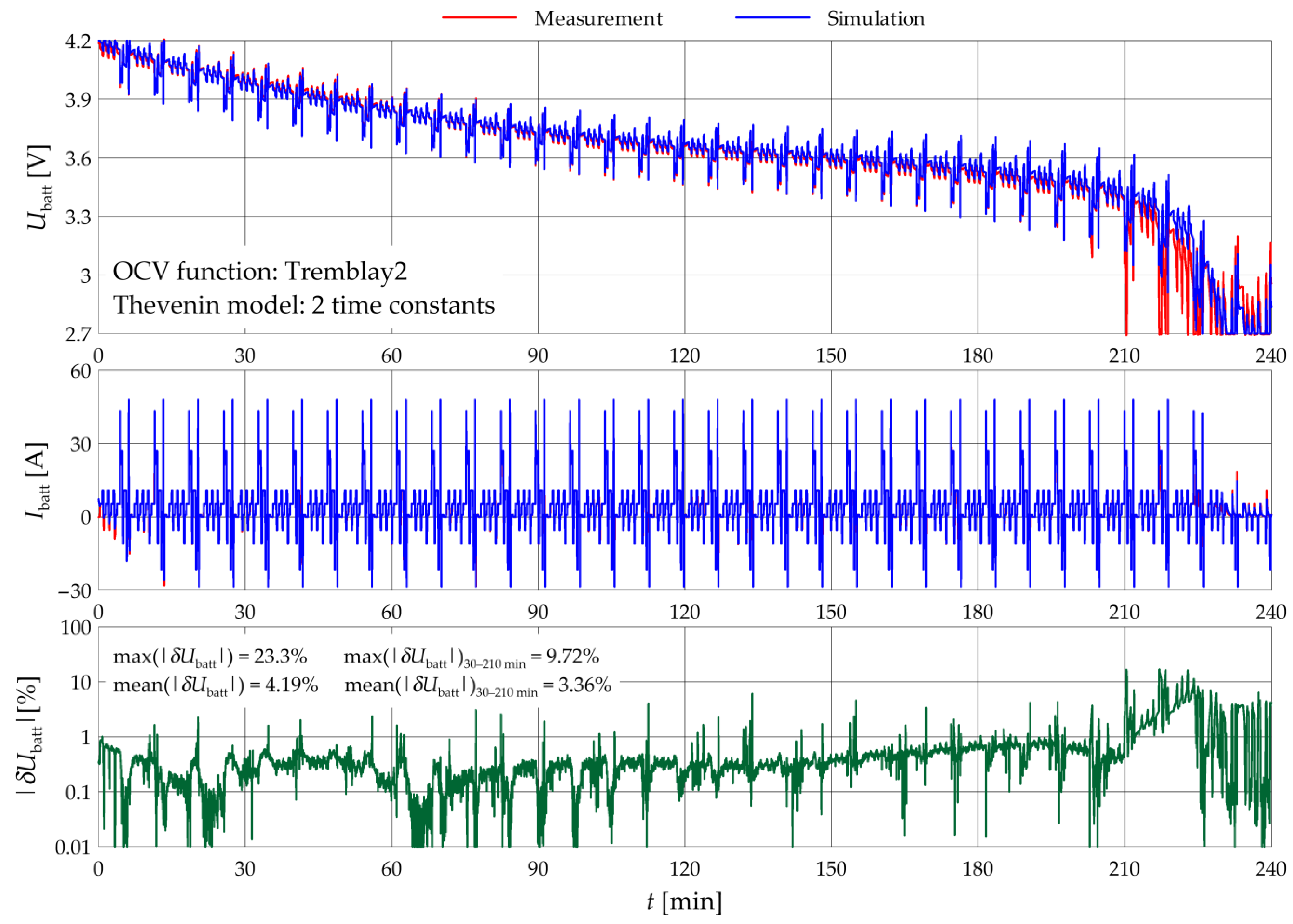
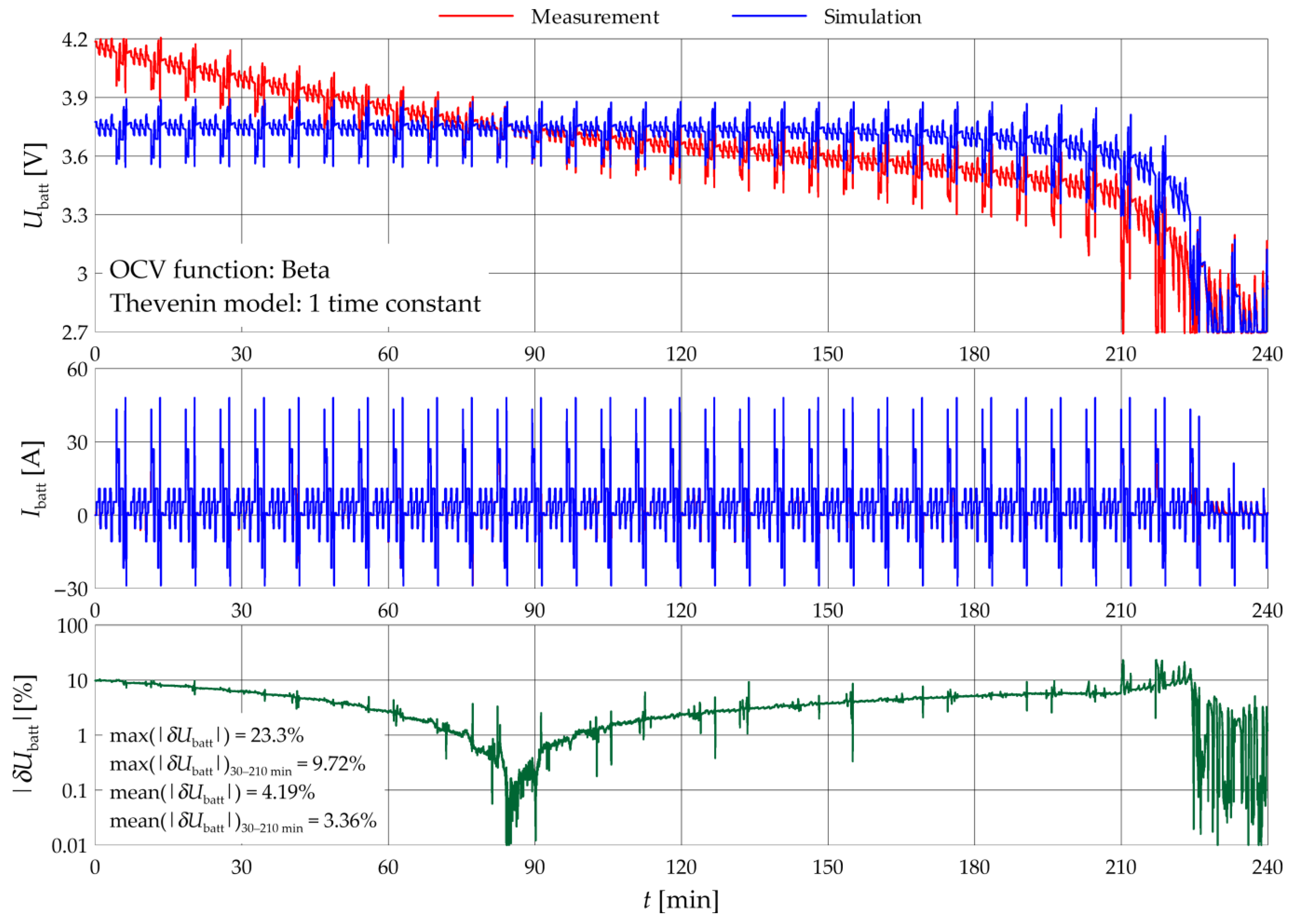
| OCV Function | Thevenin Time Constants | max(|δUbatt|) [%] | mean(|δUbatt|) [%] | max(|δUbatt|)30–210 min [%] | mean(|δUbatt|)30–210 min [%] |
|---|---|---|---|---|---|
| Beta | 1 2 | 23.31 23.31 | 4.191 4.15 | 9.721 9.42 | 3.361 3.30 |
| Tremblay | 1 2 | 19.4 19.3 | 0.758 0.684 1 | 6.14 5.77 1 | 0.359 0.284 1 |
| Tremblay2 | 1 2 | 17.0 16.9 1 | 0.771 0.684 1 | 6.45 6.08 | 0.466 0.377 |
| LEE | 1 2 | 17.0 16.9 1 | 0.800 0.722 | 6.69 6.32 | 0.505 0.420 |
| PolyEXP3 | 1 2 | 18.5 18.2 | 1.53 1.46 | 7.22 6.85 | 0.716 0.671 |
| PolyEXP5 | 1 2 | 17.9 17.6 | 1.42 1.37 | 7.08 6.71 | 0.645 0.620 |
| PolyEXP7 | 1 2 | 19.0 18.6 | 1.54 1.46 | 6.72 6.35 | 0.688 0.635 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Białoń, T.; Niestrój, R.; Korski, W. PSO-Based Identification of the Li-Ion Battery Cell Parameters. Energies 2023, 16, 3995. https://doi.org/10.3390/en16103995
Białoń T, Niestrój R, Korski W. PSO-Based Identification of the Li-Ion Battery Cell Parameters. Energies. 2023; 16(10):3995. https://doi.org/10.3390/en16103995
Chicago/Turabian StyleBiałoń, Tadeusz, Roman Niestrój, and Wojciech Korski. 2023. "PSO-Based Identification of the Li-Ion Battery Cell Parameters" Energies 16, no. 10: 3995. https://doi.org/10.3390/en16103995
APA StyleBiałoń, T., Niestrój, R., & Korski, W. (2023). PSO-Based Identification of the Li-Ion Battery Cell Parameters. Energies, 16(10), 3995. https://doi.org/10.3390/en16103995







