A Pre-Synchronization Method for Parallel VSGs of Distributed Microgrid Based on Control Mode Switching
Abstract
:1. Introduction
2. Microgrid Structure and Control Mode
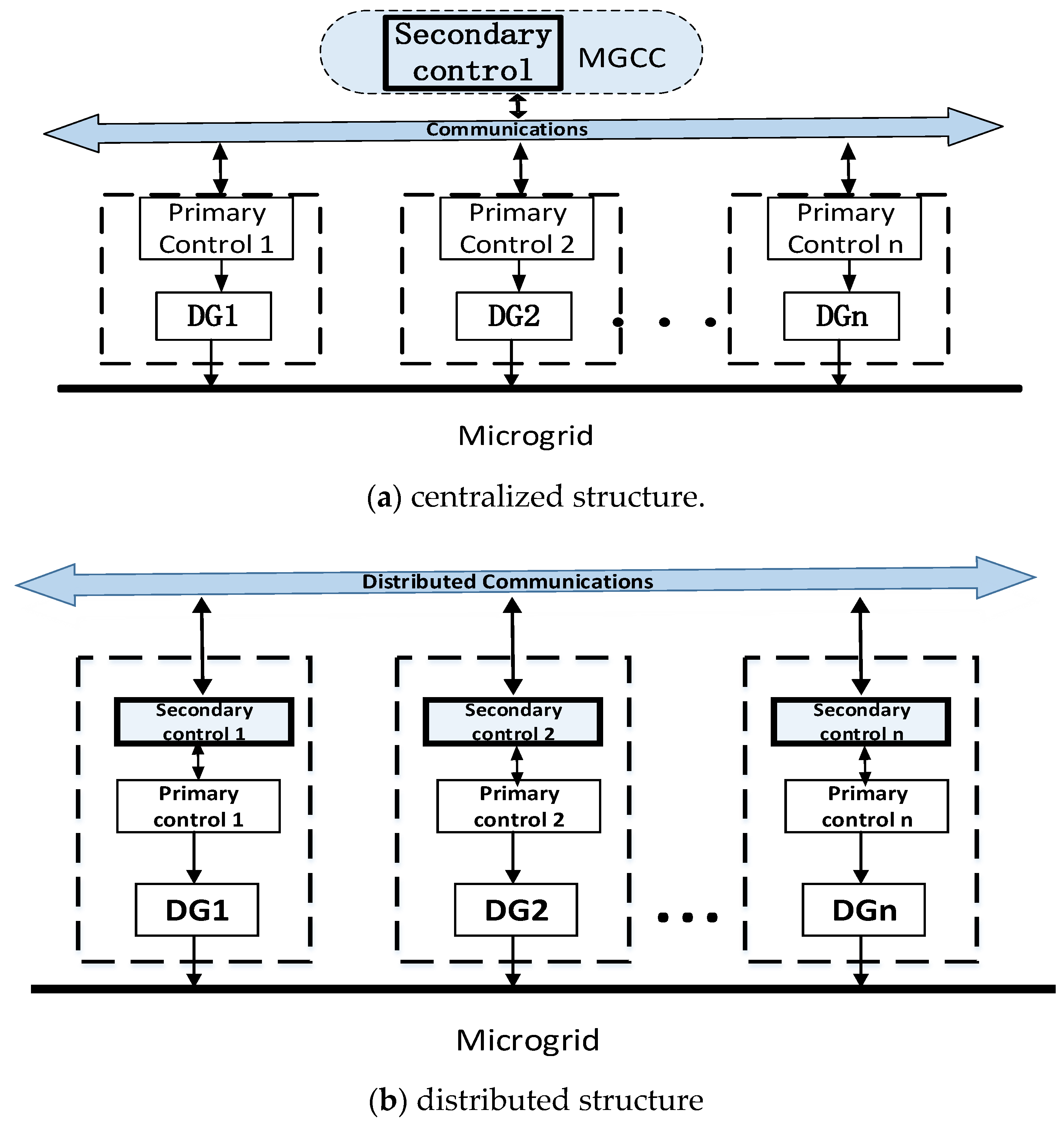
2.1. Microgrid Structure
2.2. Control Mode of DG
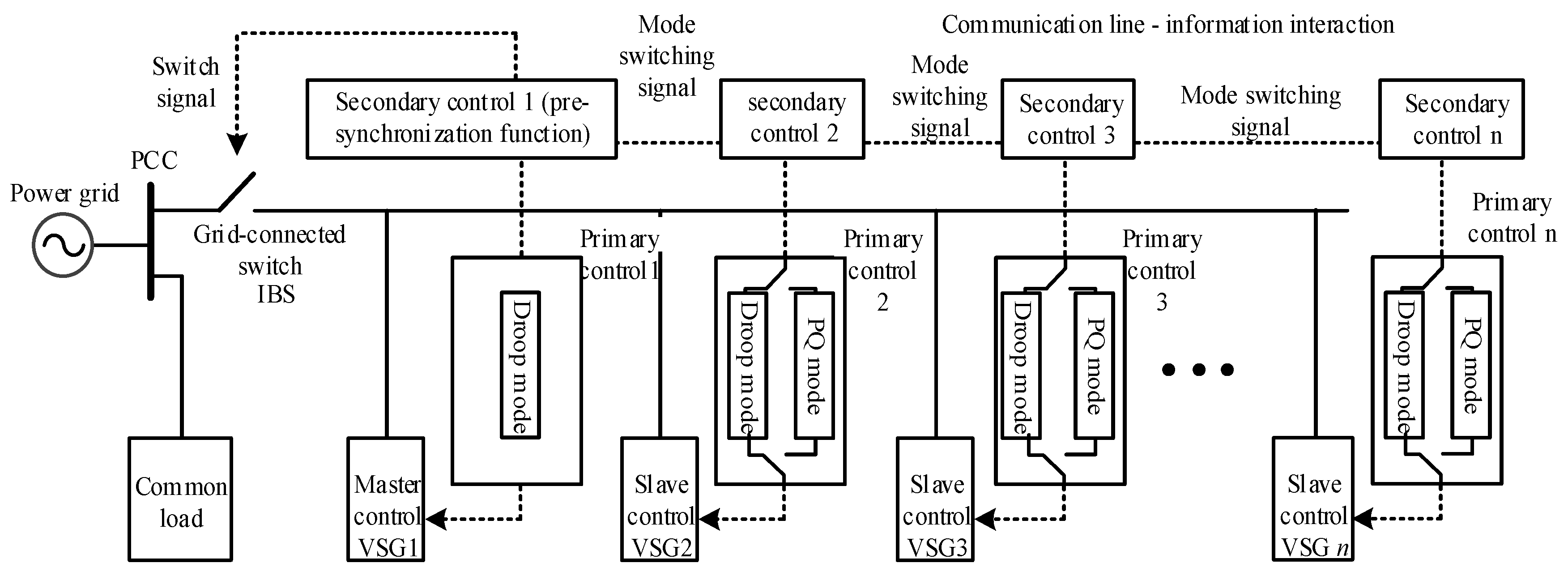
3. Pre-Synchronization Method Based on Control Mode Switching
3.1. Switching Mechanism of Control Modes
3.2. Multi-VSG Pre-Synchronization Steps
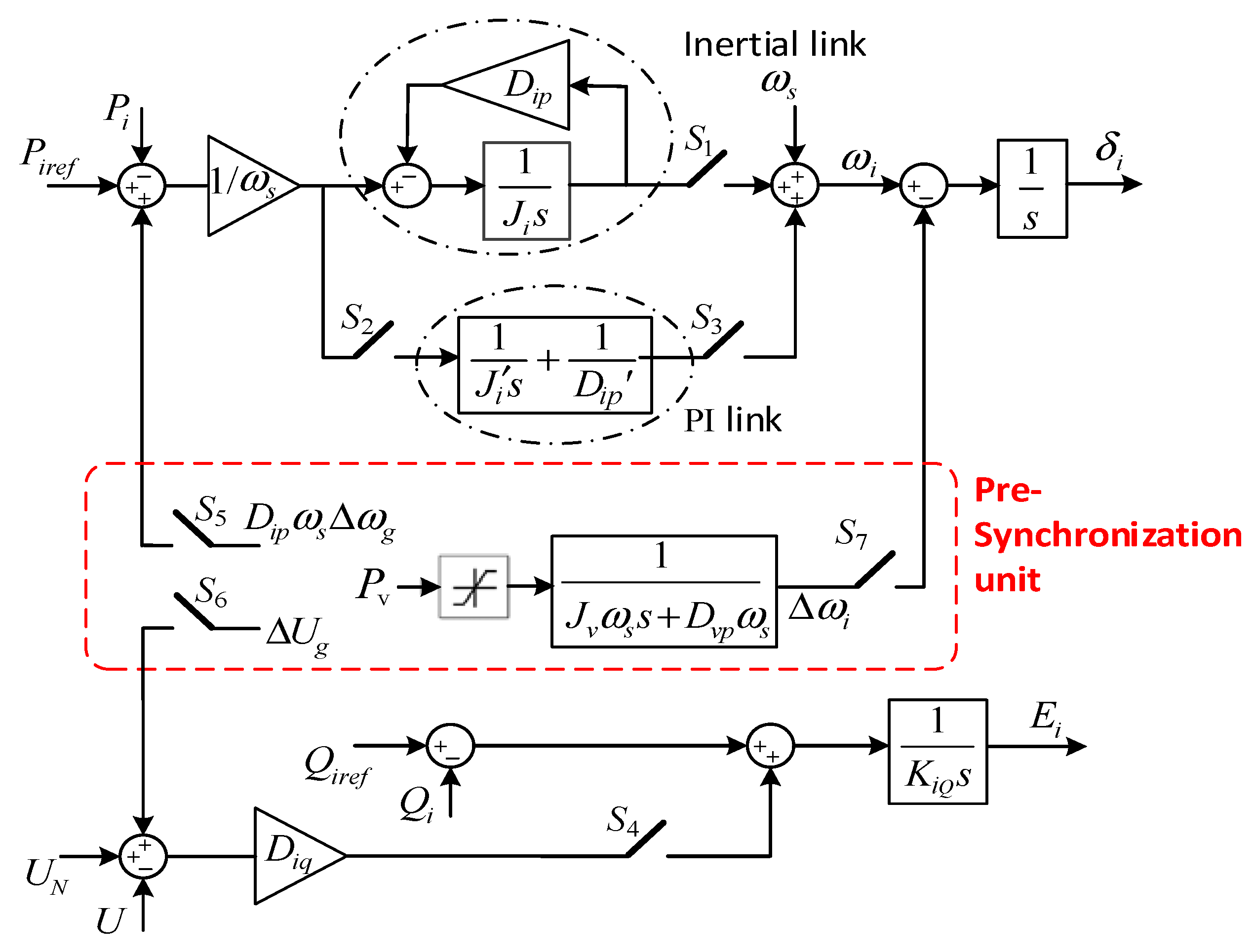
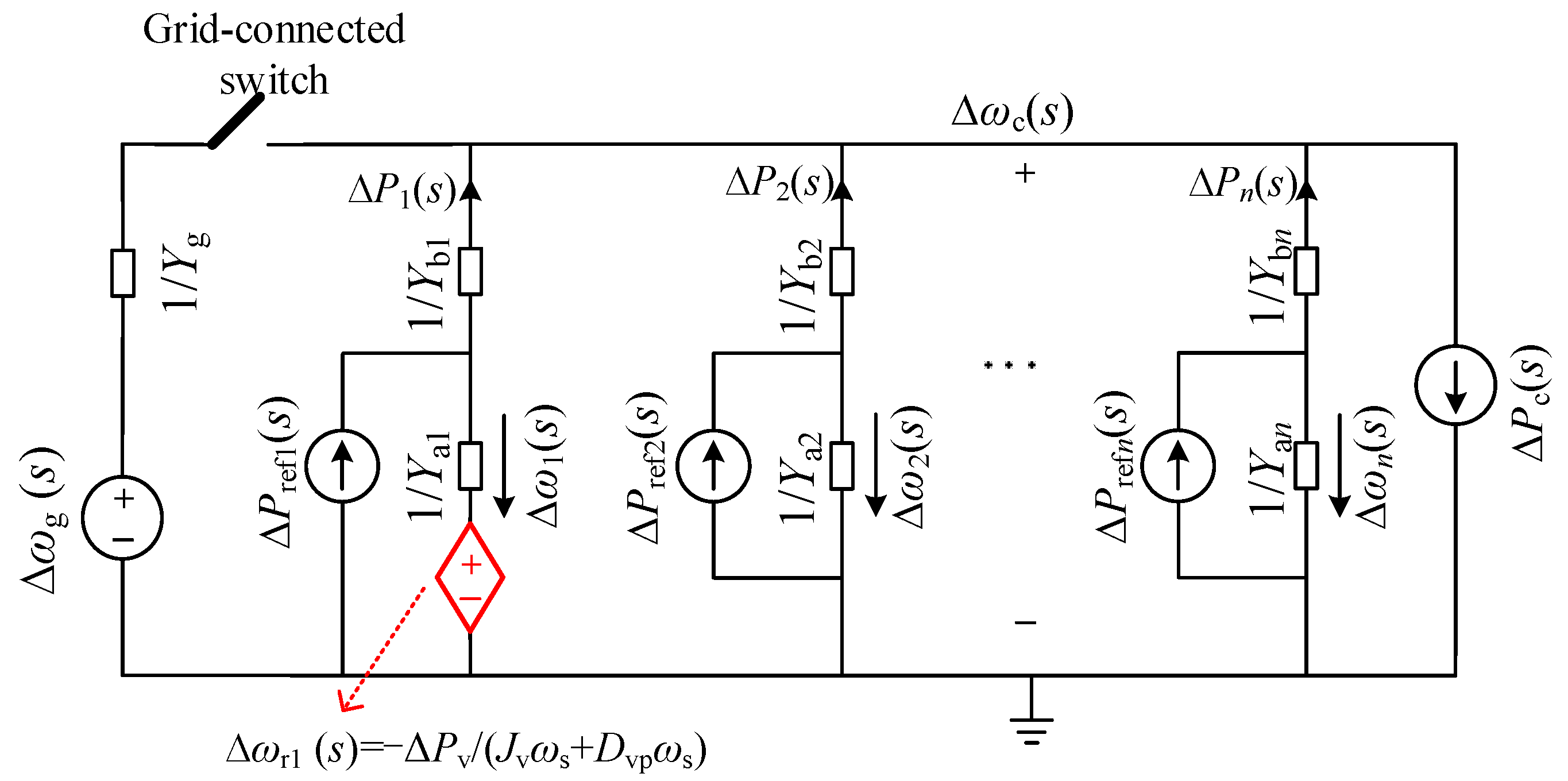
4. Model Analysis of Pre-Synchronization Control for Multi-VSG Parallel System
4.1. Decomposition of Phase Pre-Synchronization Process
4.2. Modeling of Phase Pre-Synchronization Process
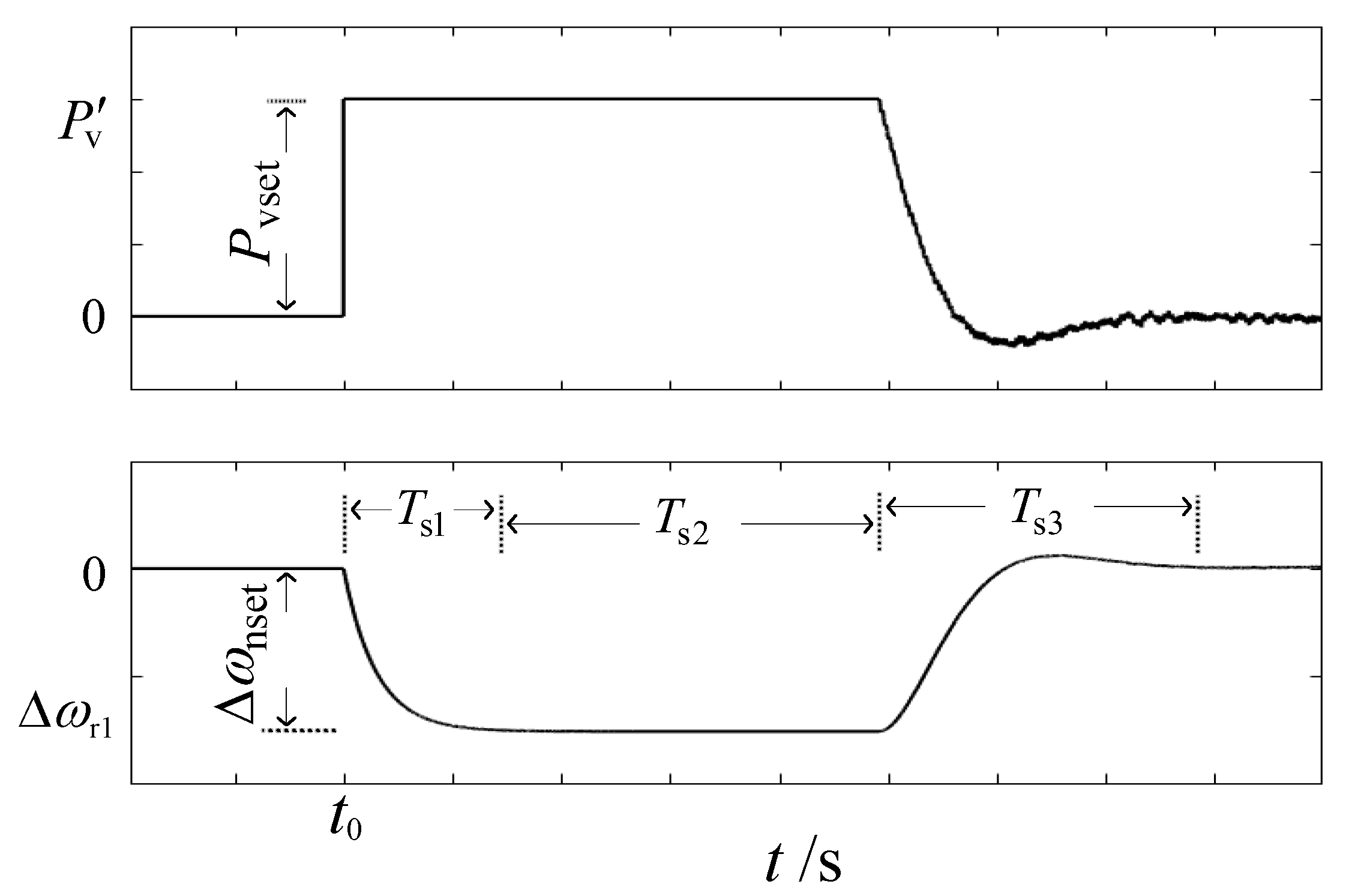
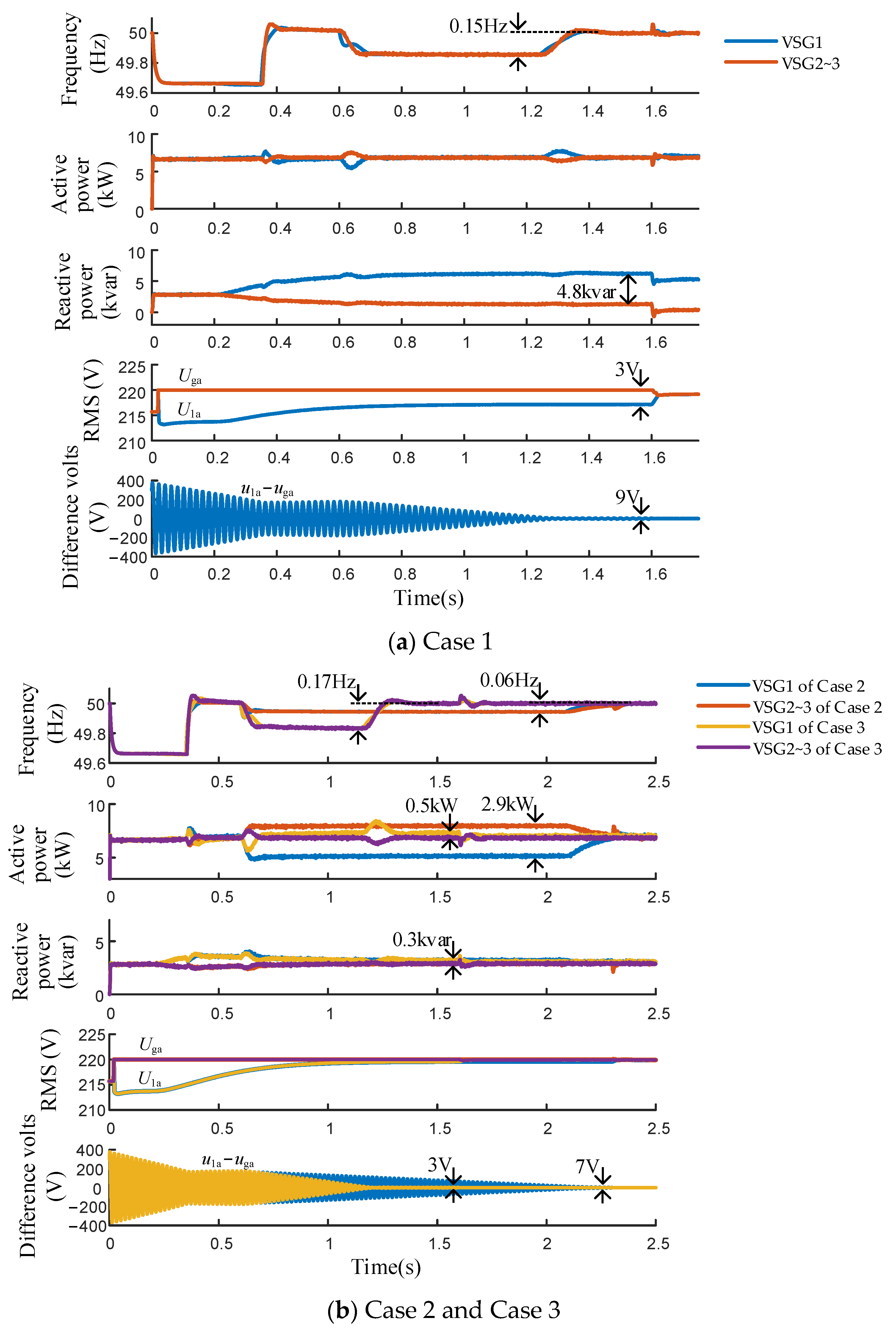
5. Simulation Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Chen, K.; Cai, G. Research on the Operation Control Strategy of a Low-Voltage Direct Current Microgrid Based on a Disturbance Observer and Neural Network Adaptive Control Algorithm. Energies 2019, 12, 1162. [Google Scholar] [CrossRef]
- IEEE Standard 1547.4-2011; IEEE Guide for Design, Operation, and Integration of Distributed Resource Island Systems with Electric Power Systems. IEEE: Piscataway, NJ, USA, 2011; pp. 1–54.
- Shi, J.; Wu, D.; Qian, Y. A Novel Pre-Synchronization Control Method Based on Open-Loop Phase Detection for the Maritime VSC-HVDC System. Front. Energy Res. 2022, 10, 932971. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Ise, T. Comparison of dynamic characteristics between virtual synchronous generator and droop control in inverter-based distributed generators. IEEE Trans. Power Electron. 2016, 31, 3600–3611. [Google Scholar] [CrossRef]
- Ashabani, M.; Freijedo, F.D.; Golestan, S.; Guerrero, J.M. Inducverters: PLL-Less Converters with Auto- Synchronization and Emulated Inertia Capability. IEEE Trans. Smart Grid 2016, 7, 1660–1674. [Google Scholar] [CrossRef]
- Meng, X.; Liu, J.; Liu, Z. A Generalized Droop Control for Grid-Supporting Inverter Based on Comparison between Traditional Droop Control and Virtual Synchronous Generator Control. IEEE Trans. Power Electron. 2019, 34, 5416–5438. [Google Scholar] [CrossRef]
- Gu, W.; Lou, G.; Tan, W. A nonlinear state estimator-based decentralized secondary voltage control scheme for autonomous microgrids. IEEE Trans. Power Syst. 2017, 32, 4794–4804. [Google Scholar] [CrossRef]
- Zheng, W.; Liu, L.; Zeng, J. Smooth Switching Strategy between Grid-Connected and Islanded Microgrid Using Improved Phase Control Method. Power Syst. Technol. 2016, 40, 1155–1162. [Google Scholar]
- Zhong, Q.; Nguyen, P.H.; Ma, Z. Self-synchronized synchronverters: Inverters without a dedicated synchronization unit. IEEE Trans. Power Electron. 2014, 29, 617–630. [Google Scholar] [CrossRef]
- Hariharan, R.; Mishra, M.K. Analysis and design of gradient descent based pre-synchronization control for synchronverter. IET Renew. Power Gener. 2021, 15, 297–312. [Google Scholar]
- Cheng, Q.; Chu, S.; Cheng, Y. Multiple Master-slave Mixed Coordinated Control for Microgrid Based on Improved Droop Control. Autom. Electr. Power Syst. 2016, 40, 69–75. [Google Scholar]
- Vasquez, J.C.; Guerrero, J.M.; Savaghebi, M. Modeling, Analysis, and Design of Stationary-Reference-Frame Droop-Controlled Parallel Three-Phase Voltage Source Inverters. IEEE Trans. Ind. Electron. 2013, 60, 1271–1280. [Google Scholar] [CrossRef]
- Wen, C.; Xiong, Q.; Jia, J. Research on multi-VSG fast pre-synchronization grid connection with dual power loop. Energy Rep. 2020, 6, 1226–1236. [Google Scholar] [CrossRef]
- Lou, G.; Gu, W.; Xu, Y.; Jin, W.; Du, X. Stability Robustness for Secondary Voltage Control in Autonomous Microgrids with Consideration of Communication Delays. IEEE Trans. Power Syst. 2018, 33, 4164–4178. [Google Scholar] [CrossRef]
- Shafiee, Q.; Guerrero, J.M.; Vasquez, J.C. Distributed secondary control for islanded microgrids—A novel approach. IEEE Trans. Power Electron. 2013, 29, 1018–1031. [Google Scholar] [CrossRef]
- Wu, T.; Liu, J.; Liu, Z. Load Power Estimation Based Secondary Control for Microgrids. In Proceedings of Ninth International Conference on Power Electronics-ECCE Asia, Seoul, Republic of Korea, 1–5 June 2015; pp. 722–727. [Google Scholar]
- Doost Mohammadi, F.; Keshtkar Vanashi, H.; Feliachi, A. State-Space Modeling, Analysis, and Distributed Secondary Frequency Control of Isolated Microgrids. IEEE Trans. Energy Convers. 2018, 33, 155–165. [Google Scholar] [CrossRef]
- Shao, B.; Xiao, Q.; Xiong, L.; Wang, L.; Yang, Y.; Chen, Z.; Frede, B.; Josep, M.G. Power coupling analysis and improved decoupling control for the VSC connected to a weak AC grid. Int. J. Electr. Power Energy Syst. 2023, 145, 108645. [Google Scholar] [CrossRef]
- Yan, X.; Jia, J.; Wang, D. Synchronous power control and mode smooth switching of virtual synchronous generator. Autom. Electr. Power Syst. 2018, 42, 91–99. [Google Scholar]
- Qin, B.; Xu, Y.; Yuan, C.; Jia, J. A Unified Method of Frequency Oscillation Characteristic Analysis for Multi-VSG Grid-Connected System. IEEE Trans. Power Deliv. 2022, 37, 279–289. [Google Scholar] [CrossRef]



| Communication Cycle | Main Control Signal 1 | Slave Signal 1 | Slave Signal 2 | Slave Signal 3 | Slave Signal 4 | Slave Signal 5 |
|---|---|---|---|---|---|---|
| 0 | 0 | 0+ | 0+ | 0+ | 0+ | 0+ |
| 1 | 1 | 0+ | 0+ | 0+ | 0+ | 0+ |
| 2 | 1 | 1+ | 1+ | 0+ | 0+ | 0+ |
| 3 | 1 | 1+ | 1+ | 1+ | 1+ | 0+ |
| 4 | 1 | 1X | 1X | 1X | 1+ | 1+ |
| 5 | 1 | 1X | 1X | 1X | 1X | 1X |
| 6 | 0 | 1X | 1X | 1X | 1X | 1X |
| 7 | 0 | 0X | 0X | 1X | 1X | 1X |
| 8 | 0 | 0X | 0X | 0X | 0X | 1X |
| 9 | 0 | 0+ | 0+ | 0+ | 0X | 0X |
| 10 | 0 | 0+ | 0+ | 0+ | 0+ | 0+ |
| Working Condition | 1 | 2 | 3 |
|---|---|---|---|
| Control model | VSG2~3:P mode; Q-V droop mode | VSG2~3:P-ω droop mode; Q mode | VSG2~3:P mode; Q mode |
| Initial phase difference | 46° | 46° | 46° |
| Pre-synchronization time | 1.2 s | 2.1 s | 1.2 s |
| Frequency deviation | 0.15 Hz | 0.06 Hz | 0.17 Hz |
| Maximum value of circulation | ΔP: 0 kW ΔQ: 4.8 kvar | ΔP: 2.9 kW ΔQ: 0 kvar | ΔP: 0.5 kW ΔQ: 0.3 kvar |
| RMS deviation U1a−Uga | 3 V | 0 V | 0 V |
| Instantaneous maximum of u1a−uga | 9 V | 7 V | 3 V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, K.; Jia, J. A Pre-Synchronization Method for Parallel VSGs of Distributed Microgrid Based on Control Mode Switching. Energies 2023, 16, 4069. https://doi.org/10.3390/en16104069
Dong K, Jia J. A Pre-Synchronization Method for Parallel VSGs of Distributed Microgrid Based on Control Mode Switching. Energies. 2023; 16(10):4069. https://doi.org/10.3390/en16104069
Chicago/Turabian StyleDong, Kunyu, and Jiaoxin Jia. 2023. "A Pre-Synchronization Method for Parallel VSGs of Distributed Microgrid Based on Control Mode Switching" Energies 16, no. 10: 4069. https://doi.org/10.3390/en16104069




