Locating and Sizing Electric Vehicle Chargers Considering Multiple Technologies

Abstract

In order to foster electric vehicle (EV) adoption rates, the availability of a pervasive and efficient charging network is a crucial requirement. In this paper, we provide a decision support tool for helping policymakers to locate and size EV charging stations. We consider a multi-year planning horizon, taking into account different charging technologies and different time periods (day and night). Accounting for these features, we propose an optimization model that minimizes total investment costs while ensuring a predetermined adequate level of demand coverage. In particular, the setup of charging stations is optimized every year, allowing for an increase in the number of chargers installed at charging stations set up in previous years. We have developed a tailored heuristic algorithm for the resulting problem. We validated our algorithm using case study instances based on the village of Gardone Val Trompia (Italy), the city of Barcelona (Spain), and the country of Luxembourg. Despite the variability in the sizes of the considered instances, our algorithm consistently provided high-quality results in short computational times, when compared to a commercial MILP solver. Produced solutions achieved optimality gaps within 7.5% in less than 90 s, often achieving computational times of less than 5 s.

1. Introduction

Due to environmental concerns, electric vehicles (EVs) are increasingly gaining importance as efficient and clean transport modes. Indeed, the widespread adoption of EVs is prioritized by various policymakers to mitigate climate change impacts and foster sustainability. However, the diffusion of these vehicles is challenged by several adoption barriers, such as relatively high prices, safety concerns, and relatively poor performance [1]. Additionally, sparse public charging infrastructure is one of the most significant adoption barriers for private EV users [2]. Therefore, a well-planned design of a pervasive charging network is crucial to facilitating users’ recharging access and stimulating EV adoption. Furthermore, Sustainable Development Goal 7 (SDG7) calls for ensuring “universal access to affordable, reliable and modern energy services”, expanding infrastructure, and upgrading suitable technologies, so as to make energy supply available to everyone.

Planning the locations and capacities of public charging infrastructure is a complex task as it encompasses various intertwined issues. Namely, EV chargers should be spread out in a way that facilitates easy access to users. However, the construction and maintenance of charging infrastructure can be costly. The magnitude of such investments, coupled with the projected growth in EV adoption, suggests that the strategic planning of charging infrastructure should be done by considering a multi-year planning horizon. Furthermore, different charging technologies should be evaluated, according to user preferences and needs.

We investigate the problem of locating and sizing public charging stations (CSs) for private EV users; we consider a multi-year planning horizon as well as multiple charging technologies. In particular, we consider slow and fast charging technologies. The former is more suited for EVs parked for long durations, such as at home or work [2], whereas the latter is suited for major urban motorways and dense road traffic areas. The specifications of our problem were identified through the eCharge4Drivers project, which is funded by the European Union Horizon 2020 program.

The design process of an adequate network of public CSs can be decomposed into three major conceptual steps. The first step consists of estimating the charging demand for different technologies in the considered area. Two main modeling approaches are used for this purpose [3]: (a) estimating origin–destination traffic flows, with the aim of intercepting recharging needs during trips, and (b) aggregating demand in zones (e.g., neighborhoods) considered as nodes of a network. We use demand estimates derived from the second approach, which is suitable for vehicles parked for long durations (e.g., at home or work) in urban and semi-urban areas. The second step identifies a set of potential locations for CSs. This is done on the basis of land-use planning, environmental effects, and safety requirements. Furthermore, the compatibility of locations with charging technologies (e.g., fast chargers) is identified. This typically includes the consideration of energy grid capabilities and possible upgrades. Given the input from the first two steps, the third step consists of optimizing the locations of CSs along with their sizing. The latter entails establishing the number of chargers of each technology to install at a CS. This paper is centered on modeling and developing an efficient solution algorithm for the third step. However, we validate our model using input from the first two steps, which is derived from the eCharge4Drivers project. We were provided with demand estimates for each technology for two daily periods (i.e., daytime and nighttime), for a set of zones. As we investigate the problem of locating and sizing public CSs, we presume that the demand (used as input to our problem) already discounts the charging demand that is satisfied by home charging. Moreover, zones were also classified as potential CS locations in terms of their ability to accommodate fast and slow charging technologies. Finally, the existing CSs were also provided as input.

We modeled a multi-year charger location and sizing problem. We simultaneously considered expanding the charging capacities of existing CSs by installing more chargers, setting up new CSs, and determining their number of chargers. To this end, we considered costs related to setting up a new CS and the costs of installing chargers in a setup CS. These costs depend on the installed technology. Moreover, the capacity of each charging technology was modeled via an input parameter expressed as the amount of kWh it could provide in a period. As such, our model is general and can work with any charging technology, which is specified through input parameter values. For more details concerning the latest developments in charging technologies, we refer the reader to the following surveys [4,5,6,7]. The objective of the problem is to minimize the total investment costs while guaranteeing a target level of demand converge, expressed as a percentage of total demand. Given the multi-year aspect of the problem, we assume that location and sizing decisions are performed at the beginning of each year, and that installed chargers at a given CS remain operational for the subsequent years. We denote the resulting problem as the incremental charger location problem (ICLP).

We propose a mixed-integer linear programming (MILP) model for the ICLP. We derive a maximum flow formulation for a subproblem of ICPL, in which the charging infrastructure is fixed. Such a subproblem can efficiently be solved in polynomial time using well-established algorithms. We use this result in developing an efficient heuristic algorithm for the ICLP based on iteratively installing CSs and chargers at promising locations until the desired level of coverage is reached. Finally, we accelerate our proposed algorithm by using a priority-based strategy, which significantly reduces the computational effort associated with the identification of promising locations at each iteration of the algorithm. We validate the algorithm on three case study instances obtained through the eCharge4Drivers project. Specifically, we show that our algorithm consistently produces high-quality results in a fraction of the time required by a state-of-the-art commercial MILP solver. Finally, we note that maximum flow problems can be very efficiently solved by existing open-source algorithms. Thus, our algorithm can be easily implemented by a broad audience, as it does not necessitate the use of commercial MILP solvers that often require costly software licenses.

To summarize, the contributions of this paper are as follows.

• We model a multi-year charger location and sizing problem by considering multiple charging technologies and periods (ICLPs). Specifically, we consider that the demand for each year, technology, and period is provided for a set of zones.
• We reformulate the single-year ICLP with a fixed charger infrastructure as a maximum flow problem.
• We utilize the maximum flow subproblem in developing an efficient heuristic algorithm for the ICLP.
• We validate the proposed heuristic on three realistic case studies.

The rest of the paper is organized as follows. In Section 2, we briefly outline related works on the charging location problem. In Section 3, we present MILP models for the ICPL and several of its subproblems. We describe our proposed algorithm in Section 4, and validate its performance through computational experiments in Section 5. Finally, we discuss our conclusions and possible future research directions in Section 6.

2. Literature Review

Optimizing the location of CSs has received considerable attention in recent years (see Kchaou-Boujelben [3] for a comprehensive survey). An important aspect of such problems is related to the estimation and modeling of EV charging demand. In particular, the models proposed in the literature often fall into one of two categories: flow-based models and node-based models. In the former case, the demand is modeled through a set of origin–destination trips, whose charging requirements are satisfied at possible locations that intercept the traffic flow. This is suitable for locating CSs on motorways, where the objective is to capture EV flows. In the latter case, the demand is assumed to be located on a set of given nodes. Such demand models are suitable for locating CSs in inhabited areas (e.g., neighborhoods) where EV users live or work. In this paper, we adopt a node-based demand model. This choice stems from the addressed cases in the eCharge4Drivers project. Furthermore, we assume that the energy demand is given as an input to the problem. Thus, the problem of estimating energy demand is beyond the scope of this paper. However, we remark that different methodologies can be applied to estimate the demand for EV charging, such as data-driven techniques, machine learning, spatial statistical analysis (e.g., [8,9,10,11,12]). In what follows, we focus on contributions related to optimizing CS locations considering node-based demand.

A variety of modeling techniques has been employed in CS location optimization, such as fixed-charge models [13], set covering models [8], and p-median models [14]. Those models have been solved using a wide range of approaches, including exact methods [8,14], approximate methods [15], spatial analysis techniques [10], evolutionary algorithms [16,17], and neural networks [11]. The extensive survey by Kchaou-Boujelben [3] provides details on the used solution methods.

An important distinction between models pertains to the choice of objective functions used in the optimization. Several types of objective functions have been considered in the literature, such as minimizing investment costs [15], maximizing covered demands [10], and maximizing service levels. This last objective is typically achieved by minimizing the users’ traveling costs/distances to installed chargers [14]. Several authors have considered multiple objectives in the optimization simultaneously. Bai et al. [16] introduced a bi-objective function by accounting for investment costs and service levels, determined by the users’ driving time to the chargers as well as recharging times. Given a fixed budget, Cavadas et al. [9] maximized the satisfied demand, which was weighted to prevent users from having to travel long distances for recharging. Analogously, Vazifeh et al. [12] ensured demand satisfaction, minimized the user’s total excess driving distance to reach installed CSs, and minimized the number of CSs. We consider minimizing investment costs while guaranteeing that a given percentage of the demand is satisfied.

Two main cost components may be considered when minimizing investment costs. Firstly, a setup cost, comprising land, construction, and grid upgrades; secondly, an installation cost, associated with each installed charger. The setup cost may vary depending on the specific location, e.g., setting up a CS in the city center may be expensive, due to the cost of renting/purchasing land in that area. Conversely, the installation cost is roughly proportional to the number of installed chargers. When considering expanding the number of chargers at an existing CS, the setup cost may be ignored. This possibility was explicitly modeled by Bai et al. [16], who included a “saving cost” in their objective function, which occurs whenever a CS is based at an existing gas station. We note that the installation cost is meaningfully distinct from the setup cost when the optimization problem also considers the sizing of chargers (i.e., determining the number of chargers to be installed at each CS); thus, the problem explicitly models the charging capacity of the infrastructure.

The enforcement of capacity constraints is often done through an allocation-based approach, where the charging demand is directly allocated to CSs to measure capacity consumption. This is often done through a system optimum approach, where the model is free to determine the allocation of demand to chargers as part of the optimization, e.g., [9,13,18]. Ko and Shim [14] considered the nearest allocation rule, where demand is allocated to the nearest open charger, whereas Xie et al. [15] and Hu et al. [11] considered a simulation-based approach to allocate the demand. Furthermore, demand is usually allowed to be allocated to any CS within a maximum distance [9,13], with some authors opting to limit the amount of demand that can be allocated to distant chargers [18].

In some cases, locating and sizing decisions are not made simultaneously but are addressed sequentially. For example, Xie et al. [15] proposed a two-stage approach for locating renewable-powered charging stations on a highway network, where the locations of CSs are first determined and then the capacities of the CSs and energy storage units are established. Several authors simultaneously optimized the setup costs and the installation costs (e.g., [19]). Sadeghi-Barzani et al. [20] minimized these costs by considering fast chargers. They proposed a mixed-integer non-linear model for the resulting problem. Frade et al. [18] defined a maximum covering model that establishes the number and capacities of CSs, in order to satisfy morning and peak hour requests within acceptable levels of service. Zhu et al. [17] considered setup costs and installation costs while accounting for user access costs. The authors formulated an integer programming model for the resulting problem and solved the model via a genetic algorithm.

Considering the previously discussed literature, three additional features are fundamental to optimizing CS locations. First, the demand volume depends on different periods of the day, e.g., day and night. Such a distinction was made in models by Frade et al. [18], Dong et al. [10], and Cavadas et al. [9]. We considered distinct demand input values for day and night periods. Second, several charging technologies exist (e.g., slow and fast), inducing different costs and demand coverage characteristics. This was considered in [13,16]. We consider the option of simultaneously installing fast and slow chargers at a single location. Third, given the strategic nature of the problem, a multi-year planning horizon should be considered. A multi-year planning horizon was considered by Hu et al. [11]. We adopt a similar setting multi-year setting. Furthermore, we allow setting up new locations every year, as well as expanding the capacities of locations installed in previous years.

We summarize the main features of the surveyed literature review in

Table 1. Comparison with representative papers.

Paper	Application	Coverage Requirement	Coverage Condition	Demand Allocation	Existing Infrastructure	Capacity	Objective	Problem Characteristics
Frade et al. (2011) [18]	city block	max	distance dependent	optimal allocation		sizing	maximize coverage	P
Baouche et al. (2014) [13]	city	full	max range	optimal allocation		fixed capacity	minimize setup plus travel costs	T
Sadeghi-Barzani et al. (2014) [20]	city block	full	max range	minimum distance		sizing	minimize setup plus energy loss (grid plus EVs)
Cavadas et al. (2015) [9]	city	max	max range	optimal allocation		fixed capacity	maximize coverage	P
Asamer et al. (2016) [8]	city	max	max range	no	yes	no	maximize coverage
Ko and Shim (2016) [14]	city (taxi network)	full	none	nearest		sizing (capacity scenarios)	minimize travel cost
Zhu et al. (2016) [17]	metropolitan area	full	max range	optimal allocation		sizing	minimize installation plus travel costs
Xie et al. (2018) [15]	highway network	full	max range	simulation		sizing (2-step)	minimize setup plus installation costs
Bai et al. (2019) [16]	city	full	none	optimal allocation	yes	sizing	minimize setup plus installation plus travel costs	T
Bouguerra and Layeb (2019) [19]	city	full	max range	optimal allocation		sizing	minimize setup plus installation plus travel costs
Dong et al. (2019) [10]	city	max	max range	no		no	maximize coverage	P
Vazifeh et al. (2019) [12]	metropolitan area	full	distance dependent	no		fixed capacity	minimize travel cost
Hu et al. (2020) [11]	metropolitan area	max	max range	simulation		sizing	maximize coverage	Y
This paper	metropolitan area, city, village	full/partial	max range	optimal allocation	yes	sizing	minimize setup plus installation costs	P Y T

Problem characteristics: Y multiple years; P multiple periods; T multiple technologies.

. The last line of the table positions our paper with respect to the literature.

3. Problem Statement and Formulations

The ICLP is a multi-year planning problem centered on determining the locations of CSs and sizing their installed chargers. We consider minimizing the setup costs and installation costs, while guaranteeing that a target level of coverage is reached. Furthermore, we account for multiple demand periods (day and night) and multiple charging technologies (slow and fast).

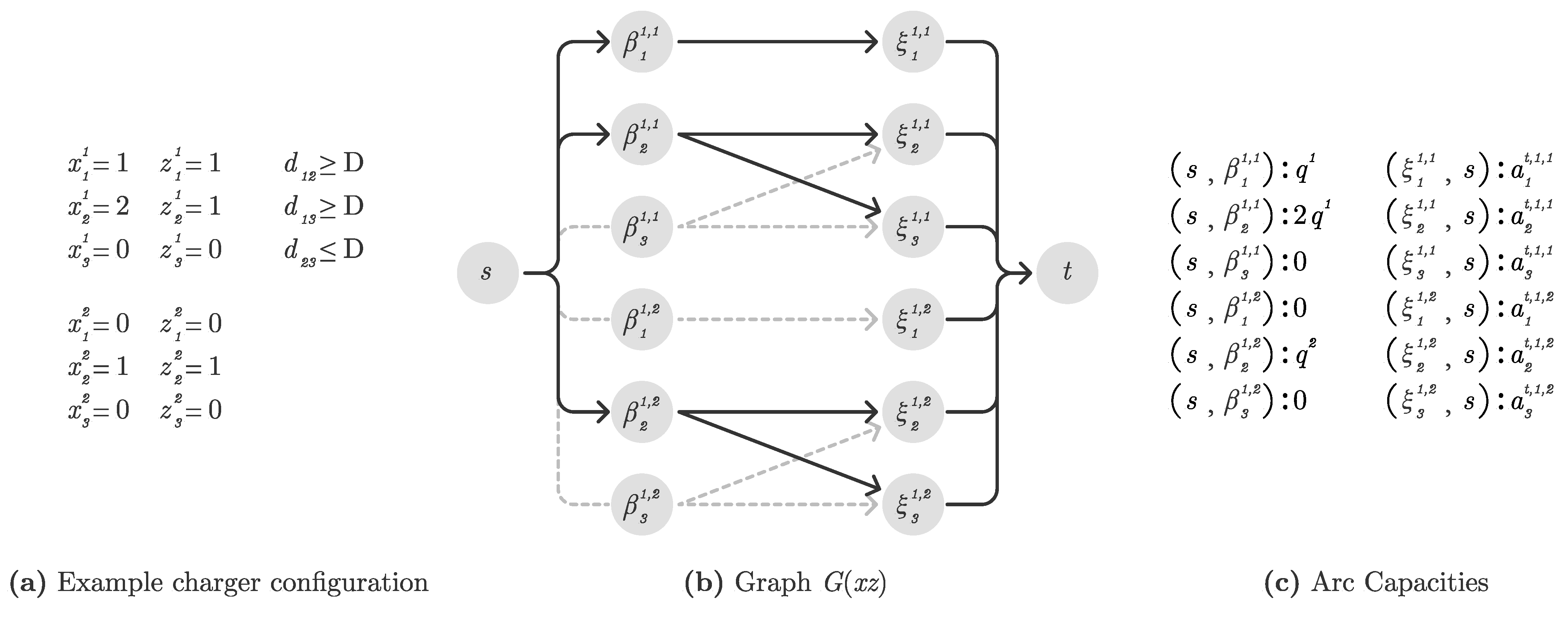
We denote by P the set of periods, the set of available charging technologies as K, and the set of years as T. The objective of the problem involves the minimization of the total infrastructure investment cost while reaching a target level of coverage of ${\Psi }^t$ percent of the total demand for each year $t\in T$. Let J denote the set of locations where CSs may be built, including locations already setup with existing CSs and chargers. Let I be the set of locations to be served (i.e., demand zones). We denote by $d_{ij}$ the distance between location $i\in I$ and $j\in J$. Users are willing to walk for a maximum range of D to reach a CS. Thus, the charging demand of location $i\in I$ may only be allocated to locations within a D radius, i.e., $j\in J:d_{ij}\le D$. We note that this potential coverage can be easily changed by the user. Indeed, what is needed in terms of input is a parameter indicating if location $i\in I$ could potentially be served by location $j\in J$. Thus, if the user possesses such information, it can easily be used instead of the maximum range.

A fixed cost of $f_j^k$ is paid to set up location j for technology k. Each location $j\in J$ may have up to $M_j^k$ chargers of technology k installed in total, and installing each charger entails a cost of $c_j^k$. We consider that certain charging infrastructures may exist before the start of the planning horizon. To capture this, parameter ${\overline{z}}_j^{0k}$ is one if location j is already setup for technology k at the start of the planning horizon. Similarly, parameter ${\overline{x}}_j^{0k}$ indicates the number of chargers with technology k that are already installed at location j at the start of the planning horizon. We denote by $a_i^{tpk}$ the charging demand for location i for technology k, in period p, in year t. The demand for each node is expressed in kWh per period. We assume that demand is allocated to chargers in a system optimum approach. Thus, the optimization model establishes the assignment of demands to CSs, while respecting the range and capacity constraints. Furthermore, we consider that a single charger using technology k may provide up to $q^k$ kWh per period.

3.1. Incremental Charger Location Problem Formulation

We formulate the ICLP as a MILP. We denote by $x_j^{tk}$ the number of chargers installed at location j with technology k at the beginning of year t. Variable $z_j^{tk}$ is one if location j is setup for technology k in year t, and zero otherwise. Variable $y_{ij}^{tpk}$ is the percentage of allocated demand from location i for technology k in year t and period p to chargers at location j.

$$\begin{array}{ccc}\hfill \left[ICLP\right]min& \sum _{t\in T}\sum _{k\in K}\sum _{j\in J}(f_j^k{z}_j^{tk}+c_j^k{x}_j^{tk})\hfill & \hfill \end{array}$$

(1)

$$\begin{array}{ccc}\sum _{j\in J:d_{ij}\le D}{y}_{ij}^{tpk}\le 1\hfill & \hfill & \hfill \forall t\in T,p\in P,k\in K,i\in I\end{array}$$

(2)

$$\begin{array}{ccccc}\sum _{p\in P}\sum _{k\in K}\sum _{i\in I}\sum _{j\in J:d_{ij}\le D}{a}_i^{tpk}{y}_{ij}^{tpk}\ge {\mathsf{\Psi }}^t\sum _{p\in P}\sum _{k\in K}\sum _{i\in I}{a}_i^{tpk}\hfill & \hfill & \hfill & \hfill & \hfill \forall t\in T\end{array}$$

(3)

$$\begin{array}{ccc}\hfill & \sum _{i\in I:d_{ij}\le D}{a}_i^{tpk}{y}_{ij}^{tpk}\le q^k(\sum _{t^{\prime }\in T:t^{\prime }\le t}{x}_j^{t^{\prime }k}+{\overline{x}}_j^{0k})\hfill & \hfill \forall t\in T,p\in P,k\in K,j\in J\end{array}$$

(4)

$$\begin{array}{ccc}\hfill & (\sum _{t^{\prime }\in T:t^{\prime }\le t}{x}_j^{t^{\prime }k}+{\overline{x}}_j^{0k})\le M_j^k(\sum _{t^{\prime }\in T:t^{\prime }\le t}{z}_j^{t^{\prime }k}+{\overline{z}}_j^{0k})\hfill & \hfill \forall t\in T,p\in P,k\in K,j\in J\end{array}$$

(5)

$$\begin{array}{ccc}\hfill & (\sum _{t\in T}{z}_j^{tk}+{\overline{z}}_j^{0k})\le 1\hfill & \hfill \forall k\in K,j\in J\end{array}$$

(6)

$$\begin{array}{ccc}\hfill & 0\le y_{ij}^{tpk}\le 1\hfill & \hfill \forall t\in T,p\in P,k\in K,i\in I,j\in J:d_{ij}\le D\end{array}$$

(7)

$$\begin{array}{ccc}\hfill & z_j^{tk}\in \{0,1\},x_j^{tk}\ge 0\hfill & \hfill \forall t\in T,k\in K,j\in J\end{array}$$

(8)

Objective function (1) minimizes the total setup costs and installation costs. Constraint (2) ensures that no more than the available charging demand is allocated to chargers. Constraint (3) enforces the target level of coverage for each year. Constraint (4) sets the available charging supply of the chargers. Constraint (5) links the setup activation variables with the charger installation variables. Constraint (6) ensures that the setup cost for each location is accounted for at most once.

Our proposed algorithm is based on iteratively solving subproblems of the ICLP. We present the relevant subproblems in the following subsections.

3.2. Single-Year Incremental Charger Location Problem

In this section, we present a rolling horizon approach to solving the ICLP. This entails optimizing the location of CSs and their installed chargers one year at a time. We use this approach to benchmark the performance of our proposed algorithm in the computational experiments.

When solving the ICLP in a rolling horizon fashion, all chargers installed in the previous years are considered fixed for the subsequent years. Thus, parameter ${\overline{z}}_j^{tk}$ is one if location j is setup for technology k before the beginning of year t. Note that parameter ${\overline{z}}_j^{0k}$ is a special case of this notation, as it denotes whether or not a location has been setup for technology k before the start of the planning horizon, i.e., year 0. Similarly, parameter ${\overline{x}}_j^{tk}$ represents the number of chargers with technology k installed at location j before the beginning of year t. We solve the ICLP for each year sequentially until the end of the planning horizon. We refer to the single-year version of the problem as the ICPL(t), where t is the year that is being optimized.

We formulate the ICLP(t) as a MILP. We denote by $x_j^k$ the number of chargers installed at location j with technology k. Variable $z_j^k$ is one if location j is setup for technology k, and zero otherwise. Variable $y_{ij}^{pk}$ is the percentage of allocated demand from location i for technology k at period p to chargers at location j.

$$\begin{array}{ccc}\hfill \left[\mathrm{ICLP}\right(t\left)\right]min& \sum _{k\in K}\sum _{j\in J}(f_j^k{z}_j^k+c_j^k{x}_j^k)\hfill & \hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill & \sum _{j\in J:d_{ij}\le D}{y}_{ij}^{pk}\le 1\hfill & \hfill \forall p\in P,k\in K,i\in I\end{array}$$

(10)

$$\begin{array}{cc}\hfill & \sum _{p\in P}\sum _{k\in K}\sum _{i\in I}\sum _{j\in J:d_{ij}\le D}{a}_i^{tpk}{y}_{ij}^{pk}\ge {\mathsf{\Psi }}^t\sum _{p\in P}\sum _{k\in K}\sum _{i\in I}{a}_i^{tpk}\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill & \sum _{i\in I:d_{ij}\le D}{a}_i^{tpk}{y}_{ij}^{pk}\le q^k(x_j^k+{\overline{x}}_j^{t-1,k})\hfill & \hfill \forall p\in P,k\in K,j\in J\end{array}$$

(12)

$$\begin{array}{ccc}\hfill & (x_j^k+{\overline{x}}_j^{t-1,k})\le M_j^k(z_j^k+{\overline{z}}_j^{t-1,k})\hfill & \hfill \forall p\in P,k\in K,j\in J\end{array}$$

(13)

$$\begin{array}{ccc}\hfill & (z_j^k+{\overline{z}}_j^{t-1,k})\le 1\hfill & \hfill \forall k\in K,j\in J\end{array}$$

(14)

$$\begin{array}{ccc}\hfill & 0\le y_{ij}^{pk}\le 1\hfill & \hfill \forall p\in P,k\in K,i\in I,j\in J:d_{ij}\le D\end{array}$$

(15)

$$\begin{array}{ccc}\hfill & z_j^k\in \{0,1\},x_j^k\ge 0\hfill & \hfill \forall k\in K,j\in J\end{array}$$

(16)

Objective function (9) minimizes the setup costs and installation costs for year t. Constraint (10) ensures that no more than the available charging demand is allocated to chargers for each location. Constraint (11) enforces the target level of coverage. Constraint (12) sets the available charging supply of the chargers. Constraint (13) links the setup activation variables with the charger installation variables. Constraint (14) ensures that the setup cost for each location is accounted for at most once.

3.3. ICLP(t) with Fixed Infrastructure

If all infrastructure variables are fixed (i.e., variables x and z are fixed), the ICLP(t) becomes a feasibility problem. Specifically, the problem pertains to whether or not the target level of demand coverage can be reached with a feasible allocation of the demand to chargers. Thus, it is possible to prove the feasibility of a given configuration of chargers by maximizing the total demand covered by the fixed infrastructure, and comparing it to ${\Psi }^t{\sum }_{p\in P}{\sum }_{k\in K}{\sum }_{i\in I}{a}_i^{tpk}$. We recall that ${\overline{z}}_j^{tk}$ is one if location j is setup for technology k before the beginning of year t and that parameter ${\overline{x}}_j^{tk}$ represents the number of chargers with technology k installed at location j before the beginning of year t. Thus, given the existing infrastructure at year t described by $\overline{x}$ and $\overline{z}$, the formulation of the problem of maximizing the covered demand is as follows:

$$\begin{array}{ccc}\hfill \left[ICLP\left(t\right|\overline{x}\overline{z})\right]max& \sum _{p\in P}\sum _{k\in K}\sum _{i\in I}\sum _{j\in J:d_{ij}\le D}{a}_i^{tpk}{y}_{ij}^{pk}\hfill & \hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill & \sum _{j\in J:d_{ij}\le D}{y}_{ij}^{pk}\le 1\hfill & \hfill \forall p\in P,k\in K,i\in I\end{array}$$

(18)

$$\begin{array}{ccc}\hfill & \sum _{i\in I:d_{ij}\le D}{a}_i^{tpk}{y}_{ij}^{pk}\le q^k{\overline{x}}_j^{tk}\hfill & \hfill \forall p\in P,k\in K,j\in J\end{array}$$

(19)

$$\begin{array}{ccc}\hfill & 0\le y_{ij}^{pk}\le {\overline{z}}_j^{tk}\hfill & \hfill \forall p\in P,k\in K,i\in I,j\in J:d_{ij}\le D\end{array}$$

(20)

3.4. Maximum Flow Formulation of $\left[ICLP\left(t\right|\overline{x}\overline{z})\right]$

We now reformulate $\left[\mathrm{ICLP}\left(t\right|\overline{x}\overline{z})\right]$ as a maximum flow problem on a directed graph $G\left(\overline{x}\overline{z}\right)=(N,A\left(\overline{x}\overline{z}\right))$. We note that maximum flow problems can be very efficiently solved by existing algorithms. Thus, the subsequent formulation is instrumental to our proposed algorithm in Section 4. Let s denote the source node, and t denote the sink node of the graph. Each potential charger location $j\in J$, for each technology $k\in K$ and each period $p\in P$, is associated with node ${\beta }_j^{pk}$. Similarly, each demand location $i\in I$ for each technology $k\in K$ and each period $p\in P$ is associated with node ${\xi }_i^{pk}$. Thus, the node set of the graph is $N=\{s,t\}\cup \{{\beta }_j^{pk}\forall j\in J,k\in K,p\in P\}\cup \{{\xi }_i^{pk}\forall i\in I,k\in K,p\in P\}$.

The arcs of $G\left(\overline{x}\overline{z}\right)$ express how the demand is assigned to chargers. The source node s is connected through a directed arc to each charger node ${\beta }_j^{pk}$ with capacity $q^k{\overline{x}}_j^{tk}$, $\forall j\in J,k\in K$. The flow on arc $(s,{\beta }_j^{pk})$ represents the total charging demand that is supplied by the chargers at location j with technology k in period p. Similarly, each demand node ${\xi }_i^{pk}$ is connected to the sink node t with capacity $a_i^{tpk}$, $\forall i\in I,p\in P,k\in K$. The flow of those arcs represents the amount of charging demand of location i for technology k in period p, which is satisfied by the installed chargers. Lastly, each charger node ${\beta }_j^{pk}$ is connected by an arc to all demand nodes in the range of j with technology k in period p, i.e., ${\xi }_i^{pk}$, $\forall i\in I:d_{ij}\le D$. The flow on arc $({\beta }_j^{pk},{\xi }_i^{pk})$ represents the amount of charging demand at location i for technology k in period p, which is satisfied by chargers installed at location j. The capacity of an arc $({\beta }_j^{pk},{\xi }_i^{pk})$ is $min(a_i^{tpk},q^k{\overline{x}}_j^{tk})$, i.e., the minimum between the demand of location i for technology k in period p and the capacity of the chargers installed at j. Note, however, that the capacity of this last class of arcs can be relaxed without loss of generality. In Figure 1, we present a visual example of the construction of graph $G\left(\overline{x}\overline{z}\right)$, for fixed infrastructure described by $\overline{x}\overline{z}$.

The maximum amount of demand covered by the charging infrastructure described by $\overline{x}\overline{z}$ equals the maximum flow on graph $G\left(\overline{x}\overline{z}\right)$ from s to t. The charging infrastructure described by $\overline{x}\overline{z}$ is then feasible if the maximum flow is greater or equal to ${\Psi }^t{\sum }_{p\in P}{\sum }_{k\in K}{\sum }_{i\in I}{a}_i^{tpk}$.

4. Successive Incremental Algorithm

We propose an efficient successive incremental heuristic algorithm for the $\mathrm{ICLP}\left(t\right)$. We present our algorithm in two phases. We first present the main elements of the algorithm. Then, in Section 4.1, we introduce algorithmic enhancements to these elements.

Starting from the already existing infrastructure at year t, the heuristic iteratively installs chargers at promising locations, until the targeted level of demand coverage is reached. We use variable $x_j^k$, initialized to zero, to indicate the current number of chargers installed at location j with technology k in the solution. Thus, the value $x_j^k+{\overline{x}}_j^{t-1,k}$ represents the total number of chargers installed at location j with technology k at the current iteration of the heuristic. Similarly, we use variable $z_j^k$, initialized to zero, to indicate whether location j has been set up for technology k in the heuristic solution, and $z_j^k+{\overline{z}}_j^{t-1,k}$ to indicate whether location j is currently setup for technology k. At each iteration, we select a location, technology, and number of chargers, and update the corresponding x and z variables accordingly. Then, we measure the level of demand coverage achieved by the current solution and, if the targeted level of coverage has not been reached, the algorithm is iterated.

The location, technology, and number of installed chargers are selected at each iteration based on the two-step approach. In the first step, a restricted set of candidate locations is selected. This is done by identifying up to two locations for each technology: one representing the most promising location that has already been set up for that technology, and one for the most promising location that has not yet been set up for that technology.

The selection is based on the total uncovered demand that could be covered by installing any number of additional chargers at those locations. Formally, the computation of the total uncovered demand that could be covered is performed for each location i and technology k, by temporarily installing a single charger of infinite capacity at location i using technology k and measuring the increase in covered demand compared to the current solution. This results in a set of up to $2|K$ locations to be considered for the next step.

In the second step, for each location in the restricted set of candidate locations, we consider each possible number of installed chargers, and measure the increase in coverage, achieved by installing the number of chargers, divided by the required installation and setup cost (if necessary). Once all locations have been evaluated in this way, we select the best combination of location, technology, and number of installed chargers according to the measured coverage increase per unit investment. Then, those chargers are installed at the selected location. Afterward, if the targeted level of coverage is not achieved, the procedure is iterated. In the following, we will detail each step of the algorithm.

To perform the selection of the restricted set of candidate locations (performed in the first step of the algorithm), let us denote by ${\delta }_j^{pk}$ the maximum amount of additional charging demand that could be covered in period p by installing additional chargers with technology k at location j. To measure it, we consider a modified version of $G\left(\overline{x}\overline{z}\right)$ where the capacity of arc $(s,{\beta }_j^{pk})$ is set to $+\infty$ and solves the associated maximum flow problem. The difference between the current covered demand and the maximum flow computed on the modified graph corresponds to ${\delta }_j^{pk}$. For ease of notation, let ${\delta }_j^k={\sum }_{p\in P}{\delta }_j^{pk}$. For each technology $k\in K$, we identify the most promising new location (${\pi }^{0k}$) and the most promising already setup location (${\pi }^{1k}$) as follows.

$$\begin{array}{cc}\hfill & {\pi }^{0k}=\underset{j\in J:z_j^k+{\overline{z}}_j^{t-1,k}=0}{arg\; max}{\delta }_j^k;\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & {\pi }^{1k}=\underset{j\in J:z_j^k+{\overline{z}}_j^{t-1,k}>0}{arg\; max}{\delta }_j^k.\hfill \end{array}$$

(22)

For the second step of the algorithm, each of the $2|K$ candidate locations is then evaluated by considering each possible number of chargers that could be installed at that location and dividing the achieved increase in covered demand reached by installing the number of chargers against the required installation and setup costs. Note that the setup cost is only accounted for when evaluating new locations. For each candidate location $\pi$ with technology k, the possible number of chargers that could be installed is $\theta \in 1,\dots ,(M_{\pi }^k-x_{\pi }^k-{\overline{x}}_{\pi }^{t-1,k})$. The amount of the charging demand that could be covered by installing $\theta$ chargers at location $\pi$ for technology k is computed based on ${\delta }_{\pi }^{pk}$, $\forall p\in P$ as follows:

$$\begin{array}{cc}\hfill & \sum _{p\in P}min(q^k\theta ,{\delta }_{\pi }^{pk}).\hfill \end{array}$$

(23)

We denote by $\nu (k,\pi ,\theta )$ the increase in covered demand divided by the potential setup and installation cost associated with installing $\theta$ chargers with technology k at location $\pi$:

$$\begin{array}{cc}\hfill & \nu (k,\pi ,\theta )=\left\{\begin{array}{cc}\frac{{\sum }_{p\in P}min(q^k\theta ,{\delta }_{\pi }^{pk})}{f_j^k+\theta c_j^k}\hfill & \mathrm{if}{z}_{\pi }^k+{\overline{z}}_{\pi }^{t-1,k}=0;\hfill \\ \frac{{\sum }_{p\in P}min(q^k\theta ,{\delta }_{\pi }^{pk})}{\theta c_j^k}\hfill & \mathrm{if}{z}_{\pi }^k+{\overline{z}}_{\pi }^{t-1,k}>0.\hfill \end{array}\right.\hfill \end{array}$$

(24)

Out of the candidate locations that we previously identified, we select the location, technology, and number of chargers according to the most promising value of $\nu$. Thus, formally:

$$\begin{array}{c}\hfill (k,\pi ,\theta )=\underset{k\in K,\pi \in \{{\pi }^{0k},{\pi }^{1k}\},\theta \in 1,\dots ,(M_{\pi }^k-z_{\pi }^k-{\overline{z}}_{\pi }^{t-1,k})}{arg\; max}\nu (k,\pi ,\theta ).\end{array}$$

(25)

Then, we install $\theta$ chargers of type k at location $\pi$, update the associated variables (i.e., $x_j^k$ and $z_j^k$), and compute the total coverage achieved by adding these chargers via the maximum flow problem. If the achieved coverage reaches ${\Psi }^t{\sum }_{p\in P}{\sum }_{k\in K}{\sum }_{i\in I}{a}_i^{tpk}$, then we terminate; otherwise, the procedure is repeated until the targeted level of coverage is reached. The developed heuristic is described in Algorithm 1.

Algorithm 1: The successive incremental algorithm.

4.1. Priority-Based Successive Incremental Algorithm

The increase in the maximum demand that can be met by installing more chargers at a specific location, represented by ${\delta }_j^{pk}$, is an important factor in the developed heuristic. We recall that the computation of ${\delta }_j^{pk}$ involves solving a maximum flow problem, which can be done very efficiently. However, lines 6 and 7 of Algorithm 1 require the computation of all values ${\delta }_j^{pk}$, $\forall p\in P,k\in K,j\in J$, which is still very computationally expensive. Therefore, we modify Algorithm 1 to take advantage of the fact that the value of ${\delta }_j^{pk}$ may only decrease at each iteration, $\forall p\in P,k\in K,j\in J$. For each technology $k\in K$, we introduce two priority queues: $Q^{k0}$ and $Q^{k1}$. A priority queue is a queue data structure that is similar to a standard queue, with the additional feature that each element has a priority associated with it. When an element is added to the queue, it is added based on its priority, so that the element with the highest priority is at the front of the queue and the element with the lowest priority is at the back. The purpose of queues $Q^{k0}$ is to facilitate the evaluation of expression (21), whereas queues $Q^{k1}$ do so for expression (22). Within $Q^{k0}$, each location $j\in J:z_j^k+{\overline{z}}_j=0$ is stored in the queue with priority ${\overline{\delta }}_j^k$, where ${\overline{\delta }}_j^k$ is an upper bound to ${\delta }_j^k$. To compute ${\pi }^{0k}$, we examine the first element of the queue: $\overline{\pi }$. The priority associated with $\overline{\pi }$ is an upper bound to ${\delta }_{\overline{\pi }}^k$. Then, we compute ${\delta }_{\overline{\pi }}^k$ by solving the associated maximum flow problem and updating the priority of $\overline{\pi }$. If $\overline{\pi }$ is still the first element of the queue, ${\pi }^{0k}=\overline{\pi }$; otherwise, the process is repeated until the first element remains unchanged. Indeed, since the priority values of each element stored in $Q^{k0}$ are upper bounds to their respective ${\delta }_j^k$, we can conclude that $\overline{\pi }={\pi }^{0k}={arg\; max}_{j\in J:z_j^k+{\overline{z}}_j^{t-1,k}=0}{\delta }_j^k$. This significantly reduces the number of times the ${\delta }_j^k$ needs to be computed and reduces the overall runtime of our algorithm. At the start of the algorithm, we populate $Q^{k0}$ with each element $j\in J:z_j^k+{\overline{z}}_j^{t-1,k}=0$ with priority ${\sum }_{p\in P}{\sum }_{i\in I:d_{ij}\le D}{a}_i^{tpk}$. Similar considerations hold for $Q^{k1}$. We update Algorithm 1 to use these queues in Algorithm 2. We use Algorithm 2 in our experiments in a rolling horizon fashion, i.e., we optimize the location of chargers one year at a time. To solve the maximum flow problem in the heuristic, we use a push–relabel algorithm. This results in the worst-case complexity of $\mathcal{O}\left(M\right|K\left|\right|P\left|\right|T\left|\right|I{|}^5)$ for the entire algorithm, where M corresponds to the maximum number of chargers of a single technology that may be installed at a single location. We remark however that, in practice, the effective computational complexity of the algorithm is much lower.

Algorithm 2: The priority-based successive incremental algorithm.

5. Computational Results

The successive incremental algorithm was implemented in Python version 3.9 using python-igraph version 0.10.2 [21] to solve the maximum flow problem used to evaluate the $ICLP\left(t\right|\overline{x}\overline{z})$. To validate the performance of our proposed algorithm, we compared its solutions to the exact solutions obtained by solving the $ICLP$ and the $ICLP\left(t\right)$ in a rolling horizon fashion using the CPLEX solver version 12.10. We considered a planning horizon of three years. Both formulations were implemented in Julia version 1.8, using the JuMP modeling interface version 1.7. The $ICLP$ formulation was run with a three-hour time limit, whereas for each year, the $ICLP\left(t\right)$ was solved with a one-hour time limit (totaling a maximum run time of three hours for three years). All experiments were run on 3.20 Ghz AMD Ryzen 5 1600, with 16 GB of RAM and 12 cores, running Windows 10, using a single thread.

We validated our algorithm on three test cases considered in the eCharge4Drivers; namely, the village of Gardone Val Trompia (Italy), the city of Barcelona (Spain), and the country of Luxembourg. Each of those instances is solved across a three-year planning horizon (2024–2026), considering two demand periods (day and night) per year and two charging technologies (fast and slow). The area of each instance is partitioned into the set of locations to be served I. After discussions with the project partners, the costs of setting up a location to accommodate chargers were set at EUR 20,000 for slow chargers and EUR 100,000 for fast chargers. Additionally, the cost of a single slow charger was set to EUR 7500 and EUR 80,000 for a single fast charger. Lastly, after discussions with the project partners, the charging capacities of the slow charger and fast charger were estimated (from charging session data) to be 28 kWh/day and 300 kWh/day, respectively. We note that these values correspond to about 25% of the theoretical capacity of the assumed chargers. This reduction is meant to capture the fact that chargers should not be assumed to be operational at full capacity, as users are not willing to wait for a CS to be free. Thus, this reduction implicitly acts as a buffer against demand uncertainty. An estimation of the demand (expressed in kWh/day) for each combination of location, period, and technology was provided to us by project partners. These data are not publicly available, as they were derived from confidential data.

The Gardone Val Trompia instance represents a small-sized instance (with $\left|I\right|=113$ locations) in the context of a village area; the Barcelona instance represents a medium-sized instance (with $\left|I\right|=656$ locations) within the context of a city, and lastly, the Luxembourg instance represents a country (with $\left|I\right|=2674$ locations). The demand for each year was computed by assuming a linear growth of 5% per year over the estimated demand from the year 2023. For generality, the set of potential charger locations J was set equal to I, while accounting for all exiting charging infrastructure in J. For each area, we conducted tests with coverage target levels of 70%, 80%, and 90%.

Considering the three coverage target levels,

Table 2. Computational results of the Gardone Val Trompia instance.

		ICLP-[C1]			ICLP(t)-[C2]				ICLP(t)-H-[C3]			Comparison
Target Coverage Level (%)	Year	Cost	Gap(%)	t(s)	Cost	Gap(%)	Total Cost	Total t(s)	Cost	Total Cost	Total t(s)	Gap(C2,C1)(%)	Gap(C3,C1)(%)	Gap(C3,C2)(%)
70	1				280	0.0	280	204	280	280				0.0
	2				0	0.0	280	204	0	280				0.0
	3	295.0	3.1	10,800	15	0.0	295	204	15	295	1	0.0	0.0	0.0
80	1				330	0.0	330	464	350	350				5.7
	2				0	0.0	330	464	0	350				5.7
	3	345.0	2.2	10,800	15	0.0	345	464	0	350	1	0.0	1.4	1.4
90	1				400	0.0	400	2282	420	420				4.8
	2				0	0.0	400	2282	0	420				4.8
	3	415.0	3.0	10,800	15	0.0	415	2282	0	420	1	0.0	1.2	1.2

Tested approaches: C1: 3-year ICLP using CPLEX; C2: rolling horizon ICLP(t) using CPLEX; C3: rolling horizon ICLP(t) using a constructive heuristic.

,

Table 3. Computational results of the Barcelona instance.

		ICLP-[C1]			ICLP(t)-[C2]				ICLP(t)-H-[C3]			Comparison
Target Coverage Level (%)	Year	Cost	Gap(%)	t(s)	Cost	Gap(%)	Total Cost	Total t(s)	Cost	Total Cost	Total t(s)	Gap(C2,C1)(%)	Gap(C3,C1)(%)	Gap(C3,C2)(%)
70	1				6260	0.0	6260	16	6625	6625				5.5
	2				360	0.0	6620	53	310	6935				4.5
	3	6940.0	0.1	10,800	345	0.0	6965	64	505	7440	3	0.4	6.7	6.4
80	1				7490	0.0	7490	11	7885	7885				5.0
	2				415	0.0	7905	21	490	8375				5.6
	3	8285.0	0.0	515	420	0.0	8325	26	260	8635	3	0.5	4.1	3.6
90	1				8905	0.0	8905	388	9275	9275				4.0
	2				790	0.0	9695	399	890	10,165				4.6
	3	10,120.0	0.3	10,800	510	0.0	10,205	407	780	10,945	4	0.8	7.5	6.8

Tested approaches: C1: 3-year ICLP using CPLEX; C2: rolling horizon ICLP(t) using CPLEX; C3: rolling horizon ICLP(t) using a constructive heuristic.

and

Table 4. Computational results of the Luxembourg instance.

		ICLP-[C1]			ICLP(t)-[C2]				ICLP(t)-H-[C3]			Comparison
Target Coverage Level (%)	Year	Cost	Gap(%)	t(s)	Cost	Gap(%)	Total cost	Total t(s)	Cost	Total cost	Total t(s)	Gap(C2,C1)(%)	Gap(C3,C1)(%)	Gap(C3,C2)(%)
70	1				18,690	0.2	18,690	3600	19,905	19,905				6.1
	2				1000	0.0	19,690	3842	1135	21,040				6.4
	3	20,430.0	1.0	10,800	755	0.0	20,445	4216	915	21,955	67	0.1	6.9	6.9
80	1				23,245	0.2	23,245	3600	24,540	24,540				5.3
	2				1195	0.0	24,440	3902	1255	25,795				5.3
	3	672,545.0	96.3	10,800	1025	0.0	25,465	3956	1055	26,850	77	−2541.1	−2404.8	5.2
90	1				28,260	0.5	28,260	3600	29,895	29,895				5.5
	2				1370	0.7	29,630	7200	1485	31,380				5.6
	3	672,545.0	95.6	10,801	1075	0.5	30,705	10,800	1130	32,510	89	−2090.3	−1968.7	5.6

Tested approaches: C1: 3-year ICLP using CPLEX; C2: rolling horizon ICLP(t) using CPLEX; C3: rolling horizon ICLP(t) using a constructive heuristic.

show the results for Gardone Val Trompia, Barcelona, and Luxembourg, respectively. Under the title ICLP-[C1], the tables report the best-obtained cost values via CPLEX within the allotted time (i.e., three hours), where the costs include the setup and installation costs. The Gap column (%) shows the final optimality gap reported by CPLEX, while the t(s) column reports the runtime in seconds. The latter is lower than 10,800 only in cases where CPLEX found the optimal solution. Under the title ICLP(t)-[C2], we report CPLEX’s results on the $ICLP\left(t\right)$ run in a rolling horizon of three years. Under the cost column, we report the best-obtained cost values via CPLEX for each year within the allotted time (i.e., one hour per year). The Gap(%) column shows the final optimality gap reported by CPLEX for each year. The Total cost column reports the cumulative yearly setup costs and installation costs, while the Total t(s) column shows the cumulative run time over the three years. The ICLP(t)-H -[C3] columns report the results of our proposed algorithm. The columns under this title have an analogous meaning to those presented by ICLP(t)-[C2]. The last three columns of Table 2, Table 3 and Table 4 compare the solutions obtained by the three methods. Specifically, we report the gaps computed as follows: $\mathrm{Gap}(\mathrm{A},\mathrm{B})=\frac{({\cos \mathrm{t}}_A-{\cos \mathrm{t}}_B)}{{\cos \mathrm{t}}_A}$. For the sake of convenience, in the tables, we use C1 to refer to the solutions computed using the ICPL (considering all three years), C2 to refer to the solutions computed using the ICPL(t) (considering a single year in a rolling horizon fashion), and C3 to refer to the solutions computed using the proposed algorithm.

We observe that our proposed algorithm produces solutions that are approximately $7\%$ from optimality in a fraction of the computational time required by CPLEX to solve the same instances. In the large instances of the country of Luxembourg, the proposed heuristic produces solutions that are within 6.9% of the best solutions obtained using CPLEX in less than 90 s, whereas the same instances required well over one hour of computational time when using CPLEX. Additionally, we remark that when solving the $ICLP$, and considering all three years, CPLEX fails to converge to an optimal solution. In particular, for the large Luxembourg instances with target coverage levels of 80% and 90%, the solver performed very poorly. In those instances, CPLEX only managed to compute the naive solution obtained by installing the maximum number of chargers at each location, therefore trivially guaranteeing complete coverage of the demand. In the medium- and small-scale instances based in the city of Barcelona and the village of Gardone Val Trompia, we achieved solutions within 7.5% of the best solutions found by CPLEX in less than 5 s.

Thus, we conclude that our algorithm is effective at generating high-quality solutions within a short computational time.

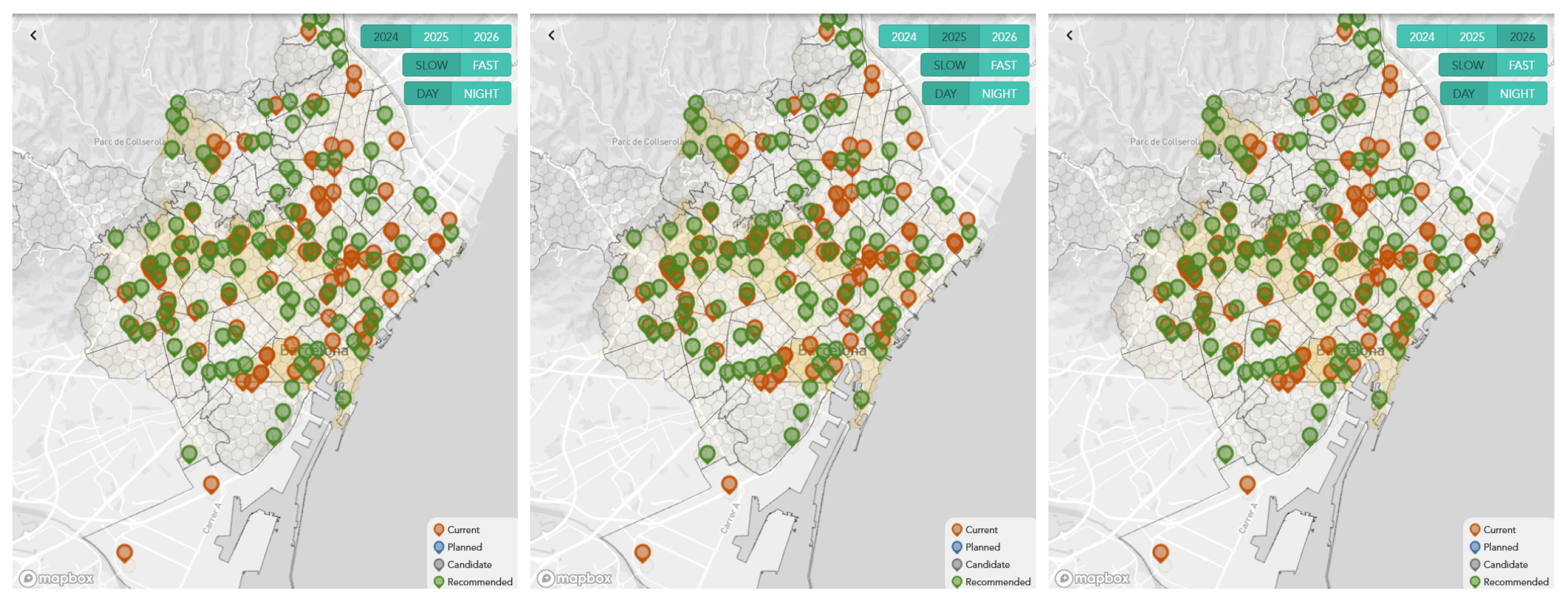
Finally, the developed algorithm was also implemented in an online tool as part of the eCharge4Drivers project. In Figure 2 and Figure 3, we show a visualization produced by the online tool of the solutions for the Barcelona and Luxembourg instances with 80% required coverage. Each panel displays the installed chargers by the end of a single year.

6. Conclusions

We modeled a multi-year charger location and sizing problem, referred to as ICLP. This problem combines a number of realistic features, including multiple charging technologies and a distinction between the demand periods of the day. Furthermore, the setting up of new locations every year was considered along with increasing the number of chargers installed at locations set up in previous years. The objective of the ICLP is to minimize the total costs entailed by setting up new locations and installing chargers while guaranteeing a given service level. This is measured as the percentage of the total demand that is served by the charging infrastructure.

We developed MILP models for the ICLP and several of its subproblems. In particular, we showed that the single-year subproblem with a given charging infrastructure can be modeled as a maximum flow problem. We used this result to design a tailored successive incremental algorithm for the ICPL. This algorithm does not require the use of MILP solvers and, thus, may easily be applied in practice at no investment.

We validated the performance of our algorithm using a series of instances derived from realistic case studies. Specifically, we compared our algorithm against a commercial solver. We conclude that our algorithm achieves high-quality results in reasonable computational times.

Our algorithm could be used to provide guidelines for local authorities or private entities that are concerned with locating and sizing CSs. Such users would mainly need to possess demand estimates for the zones of a considered area and estimates of the effective capacity of the considered chargers.

Our model and proposed algorithm can be expanded to handle more realistic features of the problem. First, the demand of a zone can potentially be split and covered by two or more locations, which may not necessarily be within its vicinity. Furthermore, demand uncertainty could be incorporated by introducing appropriate uncertainty sets that model the operational behaviors of users. Moreover, various utilization rates can be further elaborated by assuming different input values for the effective capacity level for each location for each period. One of the assumptions made in our model entails that a charger installed at a given year will remain operational in the subsequent years of the considered planning horizon. Technological advances in terms of EVs, as well as their charging infrastructure, can make certain technologies obsolete. Therefore, a valid extension of our model may involve replacing (or removing) chargers during the planning period. Additionally, accounting for bidirectional charging in CS location problems would be an interesting extension. Finally, a highly relevant future research direction would be to include aspects related to the production of energy from renewable energy sources for the charging needs of electric vehicles.