Hybrid Driving Training and Particle Swarm Optimization Algorithm-Based Optimal Control for Performance Improvement of Microgrids
Abstract
1. Introduction
- Improving the microgrid’s performance by optimizing the PI and PIA gains to improve the voltage profile and the system stability.
- Introducing driving training-based optimization (DTBO), a relatively new optimization method. This is used along with particle swarm optimization (PSO) in a hybrid approach toward maximizing the terminal voltages of various distributed energy generation (DEG) systems located in the microgrid model by optimizing the controller gain values.
- The proposed PIA controller is compared with the traditional PI controller.
- The optimization problem is formulated using a central composite response surface methodology (CCRSM), which generates an objective function in every case.
2. System Modeling
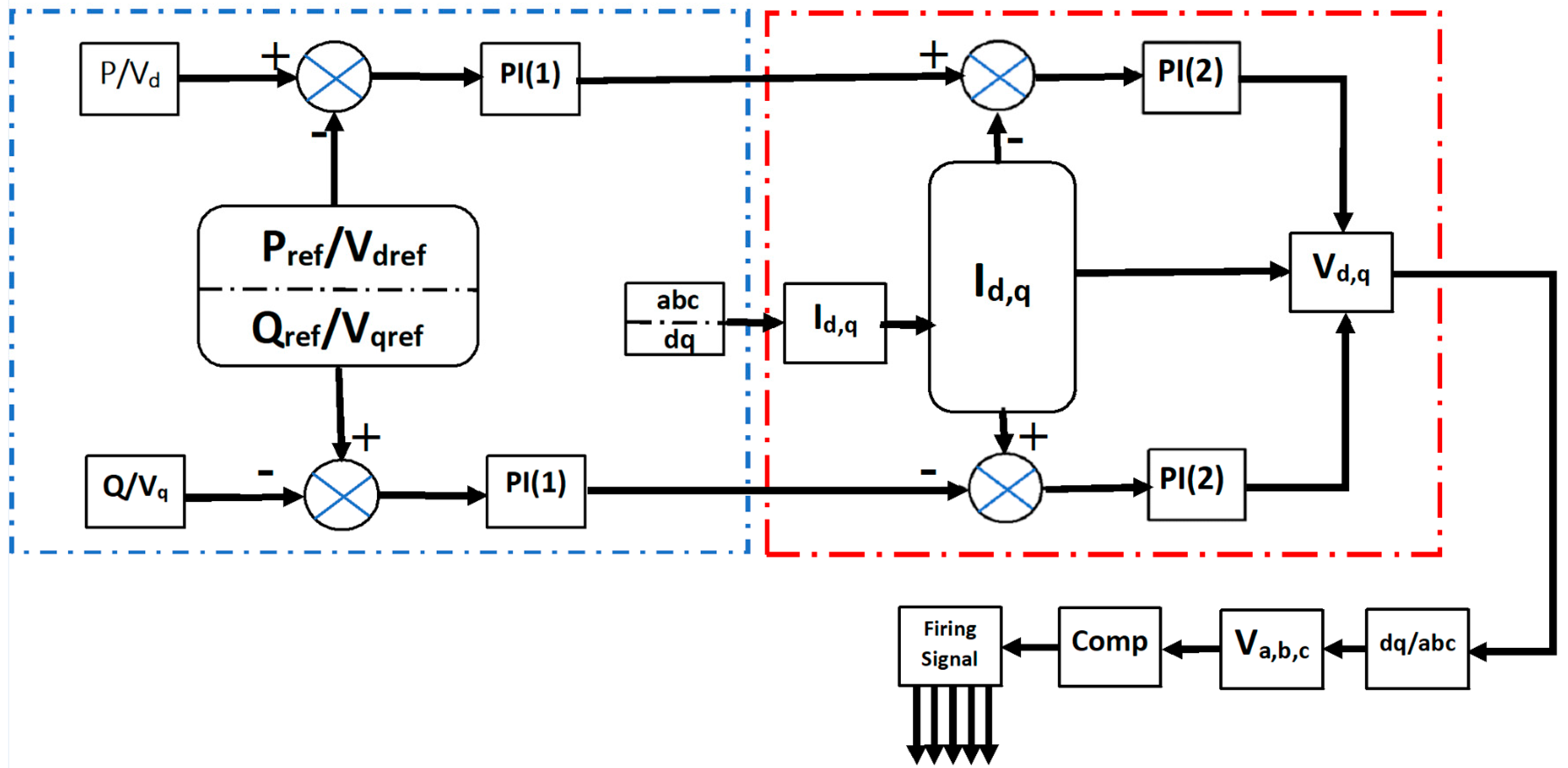
3. Controllers and the Control Strategy
3.1. Proportional Integral Controller
3.2. The Proportional-Integral Accelerator Controller
3.3. The Control Strategy
4. Modeling Stage
4.1. Variables and Levels Selection
4.2. PSCAD/EMTDC Program Calculation
4.3. Central Composite Response Surface Empirical Target Determination
5. Optimizing Stage
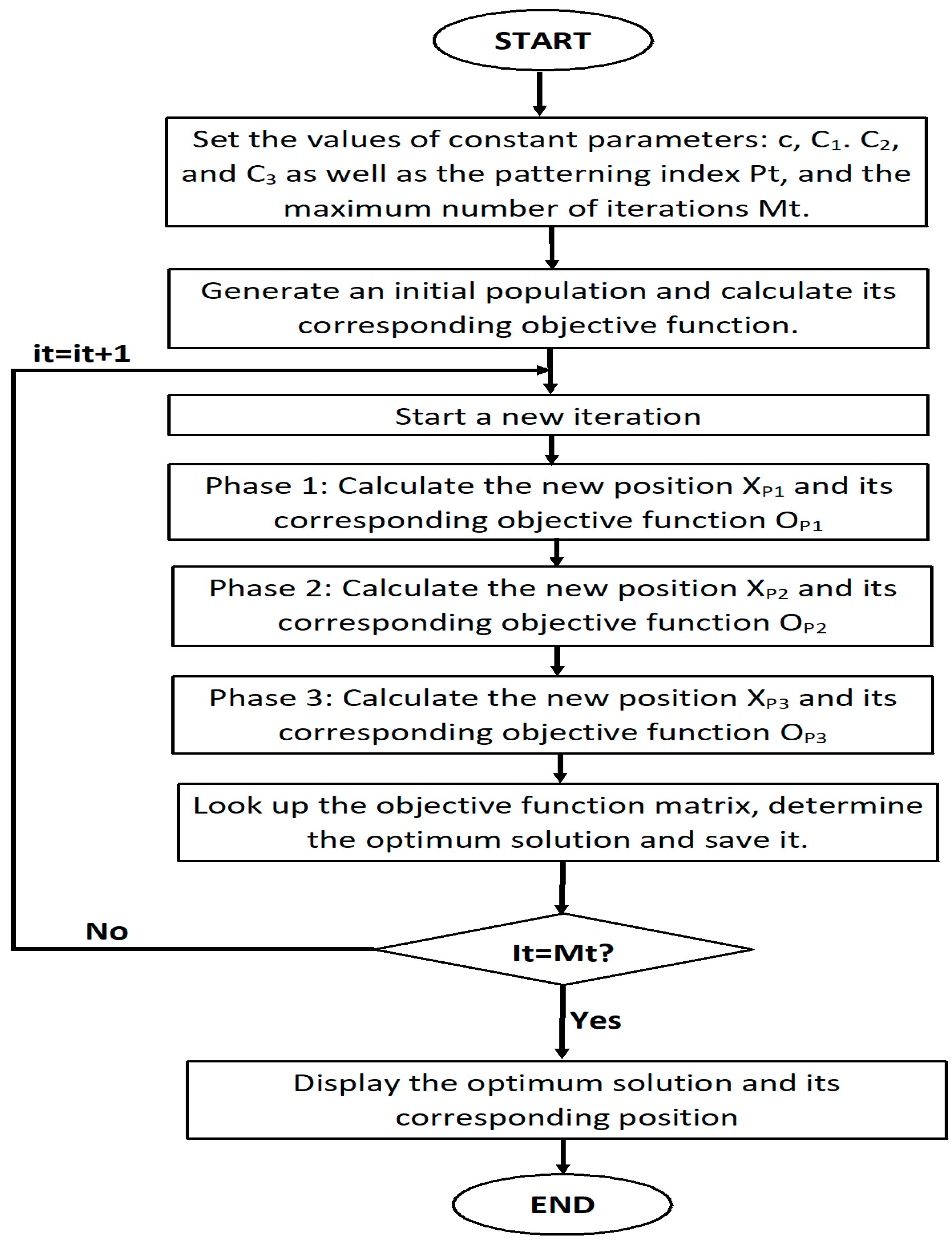
5.1. Driving Training-Based Optimization (DTBO)
5.2. HDTPS
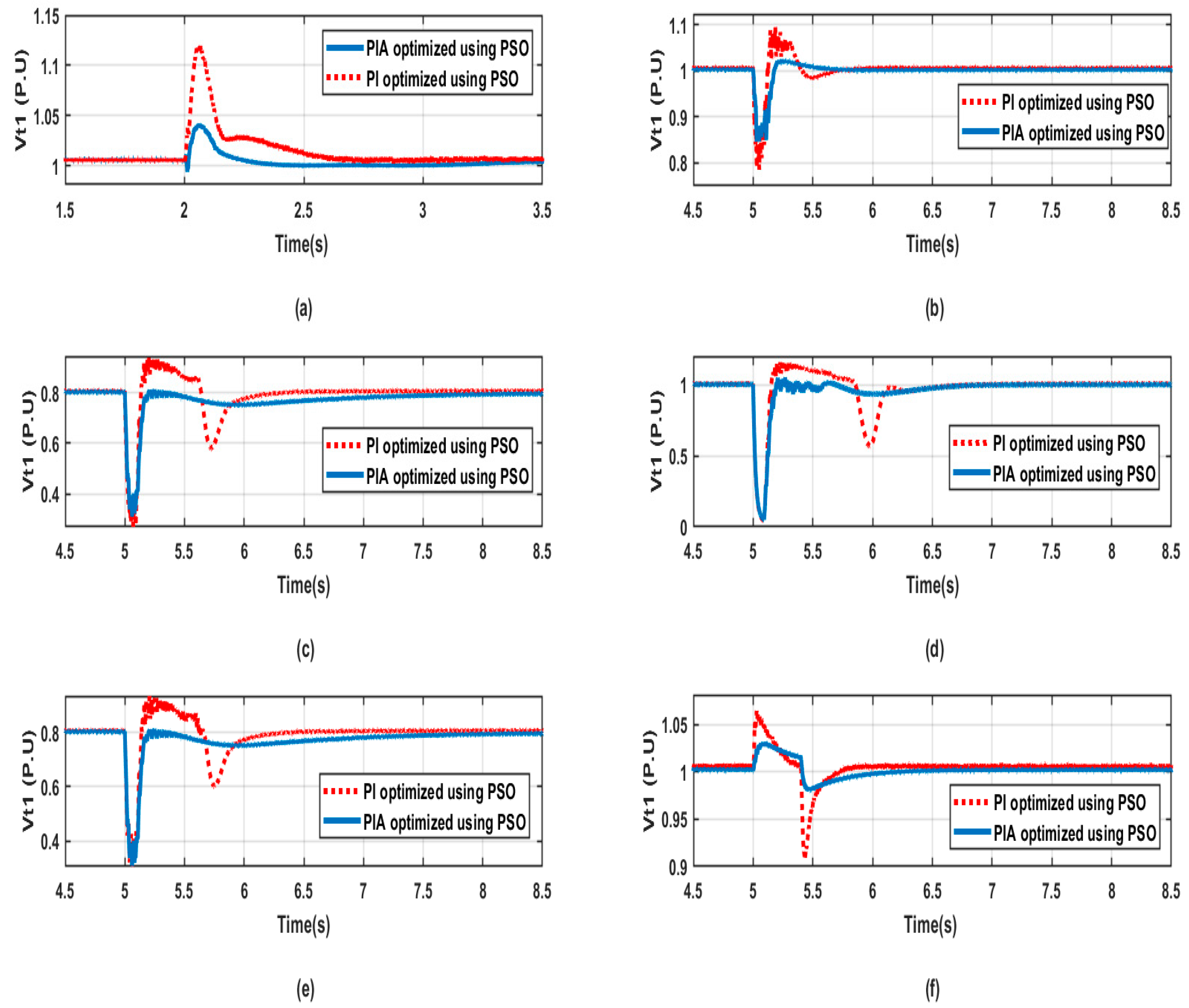
6. Simulation Results
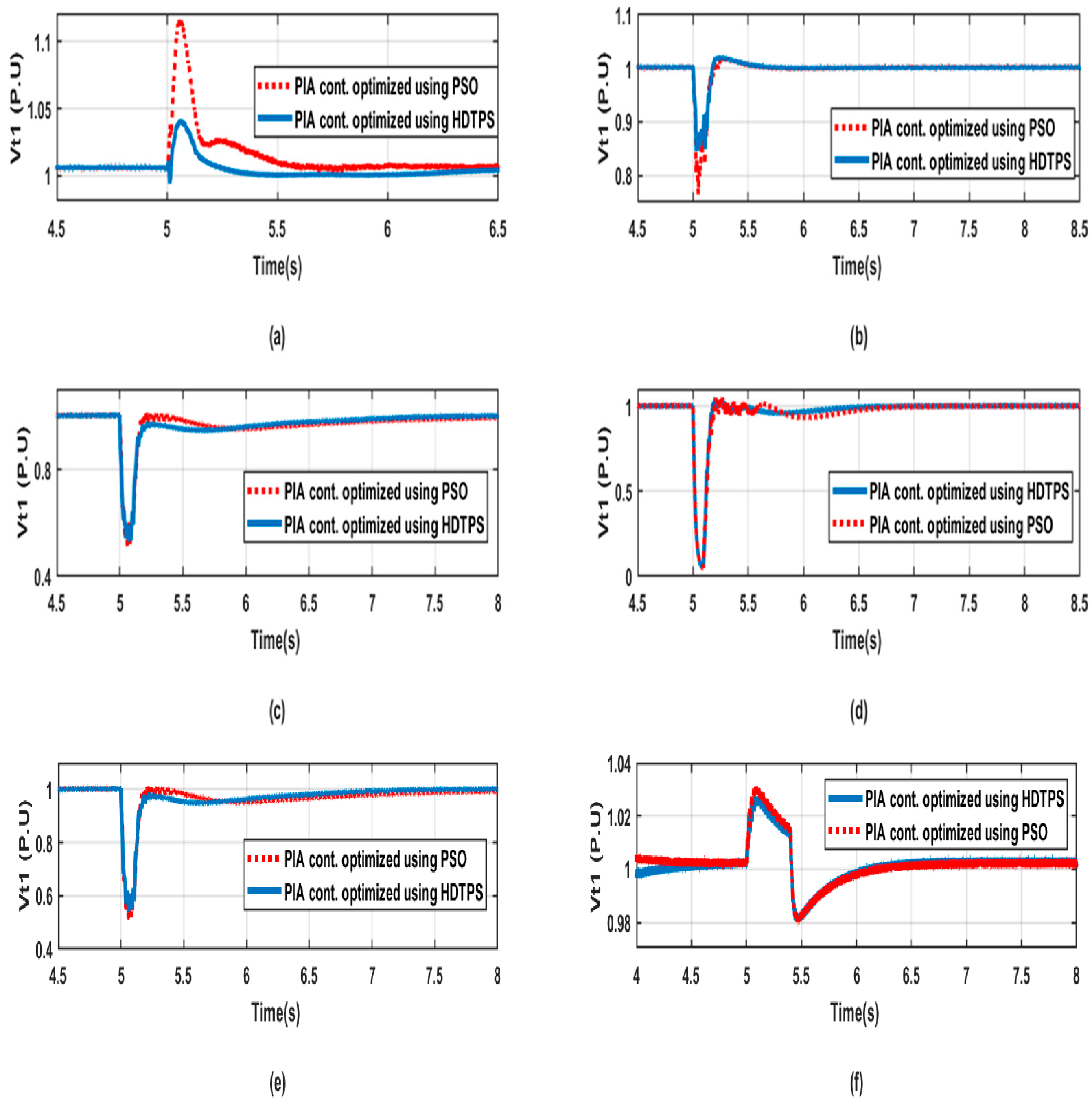
6.1. Controller Performance Comparison Using HDTPS and PSO
6.2. Optimization Technique Comparison (HDTPS and PSO)
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Muqeet, H.A.; Javed, H.; Akhter, M.N.; Shahzad, M.; Munir, H.M.; Nadeem, M.U.; Bukhari, S.S.; Huba, M. Sustainable Solutions for Advanced Energy Management System of Campus Microgrids: Model Opportunities and Future Challenges. Sensors 2022, 22, 2345. [Google Scholar] [CrossRef] [PubMed]
- Zaki, D.A.; Hasanien, H.M.; El-Amary, N.H.; Abdelaziz, A.Y. Performance Enhancement of an Inverter-Based Decentralized energy generation System Using Evaporation Rate Based Water Cycle Algorithm. In Proceedings of the IEEE Conference on Power Electronics and Renewable Energy (CPERE), Aswan, Egypt, 23–25 October 2019; pp. 270–277. [Google Scholar]
- Liu, X.; Zhang, P.; Deng, X.; Sun, D. Hierarchical overvoltage predictive control scheme for a DFIG-based wind farm. Electr. Power Syst. Res. 2023, 217, 109172. [Google Scholar] [CrossRef]
- Chakraborty, A.; Maity, T. Integrated control algorithm for fast and accurate detection of the voltage sag with low voltage ride-through (LVRT) enhancement for doubly-fed induction generator (DFIG) based wind turbines. Control. Eng. Pract. 2023, 131, 105393. [Google Scholar] [CrossRef]
- Zolfaghari, M.; Gharehpetian, G.B.; Shafie-khah, M.; Catalão, J.P. Comprehensive review on the strategies for controlling the interconnection of AC and DC microgrids. Int. J. Electr. Power Energy Syst. 2022, 136, 107742. [Google Scholar] [CrossRef]
- Du, W.; Chen, Z.; Schneider, K.P.; Lasseter, R.H.; Nandanoori, S.P.; Tuffner, F.K.; Kundu, S. A Comparative Study of Two Widely Used Grid-Forming Droop Controls on Microgrid Small-Signal Stability. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 963–975. [Google Scholar] [CrossRef]
- Tan, K.H.; Li, M.Y.; Weng, X.Y. Droop Controlled Microgrid with DSTATCOM for Reactive Power Compensation and Power Quality Improvement. IEEE Access 2022, 10, 121602–121614. [Google Scholar] [CrossRef]
- Benadli, R.; Khiari, B.; Memni, M.; Bjaoui, M.; Sellami, A. An Improved Super-Twisting Sliding Mode Control for Standalone Hybrid Wind/Photovoltaic/Fuel Cell System Based on Energy Management of Battery/Hydrogen. J. Sol. Energy Eng. 2022, 144, 031003. [Google Scholar] [CrossRef]
- Trivedi, R.; Khadem, S. Implementation of artificial intelligence techniques in microgrid control environment: Current progress and future scopes. Energy AI 2022, 2, 100147. [Google Scholar] [CrossRef]
- Zaki, D.A.; Hasanien, H.M.; El-Amary, N.H.; Abdelaziz, A.Y. Tuning PI controllers for optimal migrogrid operation based on Artificial Neural Network. In Proceedings of the IEEE Conference on Power Electronics and Renewable Energy (CPERE), Aswan, Egypt, 23–25 October 2019; pp. 371–378. [Google Scholar]
- Sindi, H.F.; Alghamdi, S.; Rawa, M.; Omar, A.I.; Elmetwaly, A.H. Robust control of adaptive power quality compensator in Multi-Microgrids for power quality enhancement using puzzle optimization algorithm. Ain Shams Eng. J. 2022, 17, 102047. [Google Scholar] [CrossRef]
- Saxena, N.K.; Gao, W.D.; Kumar, A.; Mekhilef, S.; Gupta, V. Frequency regulation for microgrid using genetic algorithm and particle swarm optimization tuned STATCOM. Int. J. Circuit Theory Appl. 2022, 50, 3231–3250. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Performance evolution of different controllers for frequency regulation of a hybrid energy power system employing chaotic crow search algorithm. ISA Trans. 2022, 120, 128–146. [Google Scholar] [CrossRef] [PubMed]
- Rostom, D.Z.; Hasanien, H.M.; El Amary, N.H.; Abdelaziz, A.Y. Adaptive PI Control Strategy for Microgrid Performance Enhancement. Int. J. Energy Conv. 2019, 7. [Google Scholar] [CrossRef]
- Nagaraja, Y.; Devaraju, T.; Sankar, A.M.; Narasimhulu, V. PV and Wind Energy Conversion Exploration based on Grid Integrated Hybrid Generation Using the Cuttlefish Algorithm. Eng. Technol. Appl. Sci. Res. 2022, 12, 9670–9675. [Google Scholar] [CrossRef]
- Hasan, R.; Masud, M.S.; Haque, N.; Abdussami, M.R. Frequency control of nuclear-renewable hybrid energy systems using optimal PID and FOPID controllers. Heliyon 2022, 8, e11770. [Google Scholar] [CrossRef]
- Jagatheesan, K.; Shah, P.; Sekhar, R. Fractional Order PiλDµ Controller for Microgrid Power System Using Cohort Intelligence Optimization. Results Control. Optim. 2023, 11, 100218. [Google Scholar]
- Miret, J.; Balestrassi, P.P.; Camacho, A.; Guzmán, R.; Castilla, M. Optimal tuning of the control parameters of an inverter-based microgrid using the methodology of design of experiments. IET Power Electron. 2020, 13, 3651–3660. [Google Scholar] [CrossRef]
- Rey, J.M.; Vergara, P.P.; Castilla, M.; Camacho, A.; Velasco, M.; Martí, P. Droop-free hierarchical control strategy for inverter-based AC microgrids. IET Power Electron. 2020, 13, 1403–1415. [Google Scholar] [CrossRef]
- Zhang, Y.; Mohammadpour, S.A.; Wang, L.; Mohammadi-Ivatloo, B. Enhanced PI control and adaptive gain tuning schemes for distributed secondary control of an islanded microgrid. IET Renew. Power Gener. 2021, 15, 854–864. [Google Scholar] [CrossRef]
- Kavitha, P.; Karuvelam, P. A highly efficient optimized pi controller fed sepic converter for hybrid renewable sources based microgrid system. Microprocess. Microsyst. 2023, 16, 104797. [Google Scholar] [CrossRef]
- Gope, S.; Reddy, G.H.; Singh, K.M. Frequency regulation analysis for renewable bio generated autonomous multi-microgrid using moth flame optimized fractional order controller. Mater. Today Proc. 2022, 80, 753–761. [Google Scholar] [CrossRef]
- Jaber, A.S.; Abdulbari, H.A.; Shalash, N.A.; Abdalla, A.N. Garra Rufa-inspired optimization technique. Int. J. Intell. Syst. 2020, 35, 1831–1856. [Google Scholar] [CrossRef]
- Mansoorhoseini, P.; Mozafari, B.; Mohammadi, S. Islanded AC/DC microgrids supervisory control: A novel stochastic optimization approach. Electr. Power Syst. Res. 2022, 209, 108028. [Google Scholar] [CrossRef]
- Nafeh, A.A.; Heikal, A.; El-Sehiemy, R.A.; Salem, W.A. Intelligent fuzzy-based controllers for voltage stability enhancement of AC-DC micro-grid with D-STATCOM. Alex. Eng. J. 2022, 61, 2260–2293. [Google Scholar] [CrossRef]
- Anuraj, U.; Hameed, S.H.; Arunprakash, N.; Sajeeva, J.; Thanihaichelvan, T.; Kokulavasan, T.; Rajan, R.; Yuvaraj, M.; Thananjeyan, S.; Ahilan, K.; et al. Micro-grid Concept for Coordinated Control of Renewable Energy Power Plants and a Way to Integrate with Main Grid. In Proceedings of the 7th International Conference on Environment Friendly Energies and Applications (EFEA), Bagatelle Moka MU, Mauritius, 14–16 December 2022; pp. 1–6. [Google Scholar]
- Litwin, M.; Zieliński, D.; Styński, S. Remote synchronization of the microgrid to the utility grid without access to point of common coupling in the presence of disturbances. IEEE Access 2022, 10, 27819–27831. [Google Scholar] [CrossRef]
- Kaur, A.; Kaushal, J.; Basak, P. A review on microgrid central controller. Renew. Sustain. Energy Rev. 2016, 55, 338–345. [Google Scholar] [CrossRef]
- Arefi, A.; Shahnia, F. Tertiary controller-based optimal voltage and frequency management technique for multi-microgrid systems of large remote towns. IEEE Trans. Smart Grid 2018, 9, 5962–5974. [Google Scholar] [CrossRef]
- Shahnia, F.; Arefi, A. Defining the suitable adjacent microgrids to form a temporary system of coupled microgrids. In Proceedings of the IEEE Region 10 Conference, Singapore, 22–26 November 2016; pp. 1216–1219. [Google Scholar]
- Wu, P.; Huang, W.; Tai, N.; Liang, S. A novel design of architecture and control for multiple microgrids with hybrid AC/DC connection. Appl. Energy 2018, 210, 1002–1016. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, J.; Sun, Q.; Guerrero, J.M.; Ma, D. Data-driven control for interlinked AC/DC microgrids via model-free adaptive control and dual-droop control. IEEE Trans. Smart Grid 2017, 8, 557–571. [Google Scholar] [CrossRef]
- Nabatirad, M.; Razzaghi, R.; Bahrani, B. Autonomous power balance in hybrid AC/DC microgrids. Int. J. Electr. Power Energy Syst. 2023, 146, 108752. [Google Scholar] [CrossRef]
- Yu, H.; Niu, S.; Shao, Z.; Jian, L. A scalable and reconfigurable hybrid AC/DC microgrid clustering architecture with decentralized control for coordinated operation. Int. J. Electr. Power Energy Syst. 2022, 135, 107476. [Google Scholar] [CrossRef]
- Aryani, D.R.; Adi, F.S.; Kim, J.S.; Song, H. An improved model-based interlink converter control design in hybrid AC/DC microgrids. Energy Rep. 2022, 8, 520–531. [Google Scholar] [CrossRef]
- Li, S.; Li, Y.; Li, T. An autonomous flexible power management for hybrid AC/DC microgrid with multiple subgrids under the asymmetric AC side faults. Int. J. Electr. Power Energy Syst. 2022, 142, 107985. [Google Scholar] [CrossRef]
- Jithin, S.; Rajeev, T. Novel adaptive power management strategy for hybrid AC/DC microgrids with hybrid energy storage systems. J. Power Electron. 2022, 10, 1–3. [Google Scholar]
- Kamal, F.; Chowdhury, B. Model predictive control and optimization of networked microgrids. Int. J. Electr. Power Energy Syst. 2022, 138, 107804. [Google Scholar] [CrossRef]
- Manitoba HVDC Research Center. PSCAD/EMTDC Manual; HVDC Research Center: Winnipeg, MB, Canada, 2018. [Google Scholar]
- Milanesi, M.; Mirandola, E.; Visioli, A. A comparison between PID and PIDA controllers. In Proceedings of the IEEE 27th International Conference on Emerging Technologies and Factory Automation (ETFA), Stuttgart, Germany, 6–9 September 2022; pp. 1–6. [Google Scholar] [CrossRef]
- López-Meraz, R.A.; Hernández-Callejo, L.; Boza, L.O.; Ramos, J.A.; Hernández, J.J.; Gómez, V.A. Electric power management in a microgrid analyzing photovoltaic arrays and a turbine-generator system. Rev. Fac. Ing. Univ. Antioq. 2022, 104, 129–139. [Google Scholar] [CrossRef]
- Mansouri, S.; Zishan, F.; Montoya, O.D.; Azimizadeh, M.; Giral-Ramírez, D.A. Using an intelligent method for microgrid generation and operation planning while considering load uncertainty. Results Eng. 2023, 17, 100978. [Google Scholar] [CrossRef]
- Hussien, A.M.; Turky, R.A.; Alkuhayli, A.; Hasanien, H.M.; Tostado-Véliz, M.; Jurado, F.; Bansal, R.C. Coot bird algorithms-based tuning PI controller for optimal microgrid autonomous operation. IEEE Access 2022, 10, 6442–6458. [Google Scholar] [CrossRef]
- Hussien, A.M.; Kim, J.; Alkuhayli, A.; Alharbi, M.; Hasanien, H.M.; Tostado-Véliz, M.; Turky, R.A.; Jurado, F. Adaptive PI Control Strategy for Optimal Microgrid Autonomous Operation. Sustainability 2022, 14, 14928. [Google Scholar] [CrossRef]
- Dehghani, M.; Trojovská, E.; Trojovský, P. A new human-based metaheuristic algorithm for solving optimization problems on the base of simulation of driving training process. Sci. Rep. 2022, 12, 9924. [Google Scholar] [CrossRef]
- Feng, L.; Sun, X.; Tian, X.; Diao, K. Direct torque control with variable flux for an SRM based on hybrid optimization algorithm. IEEE Trans. Power Electron. 2022, 37, 6688–6697. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Keawsawasvong, S.; Sarir, P.; Khailany, D.K. Seismic analysis of earth slope using a novel sequential hybrid optimization algorithm. Period. Polytech. Civ. Eng. 2022, 66, 355–366. [Google Scholar]
- Kim, H.; Lee, T.H. Design-target-based optimization using input variable selection and penalty-Lagrange multiplier for high-dimensional design problems. Struct. Multidiscip. Optim. 2022, 65, 258. [Google Scholar] [CrossRef]
- Dey, B.; Raj, S.; Mahapatra, S.; Márquez, F.P. Optimal scheduling of distributed energy resources in microgrid systems based on electricity market pricing strategies by a novel hybrid optimization technique. Int. J. Electr. Power Energy Syst. 2022, 134, 107419. [Google Scholar] [CrossRef]
- Bakry, O.M.; Alhabeeb, A.; Ahmed, M.; Alkhalaf, S.; Senjyu, T.; Mandal, P.; Dardeer, M. Improvement of distribution networks performance using renewable energy sources-based hybrid optimization techniques. Ain Shams Eng. J. 2022, 13, 101786. [Google Scholar] [CrossRef]
- Shaheen, M.A.; Hasanien, H.M.; Alkuhayli, A. A novel hybrid GWO-PSO optimization technique for optimal reactive power dispatch problem solution. Ain Shams Eng. J. 2021, 12, 621–630. [Google Scholar] [CrossRef]
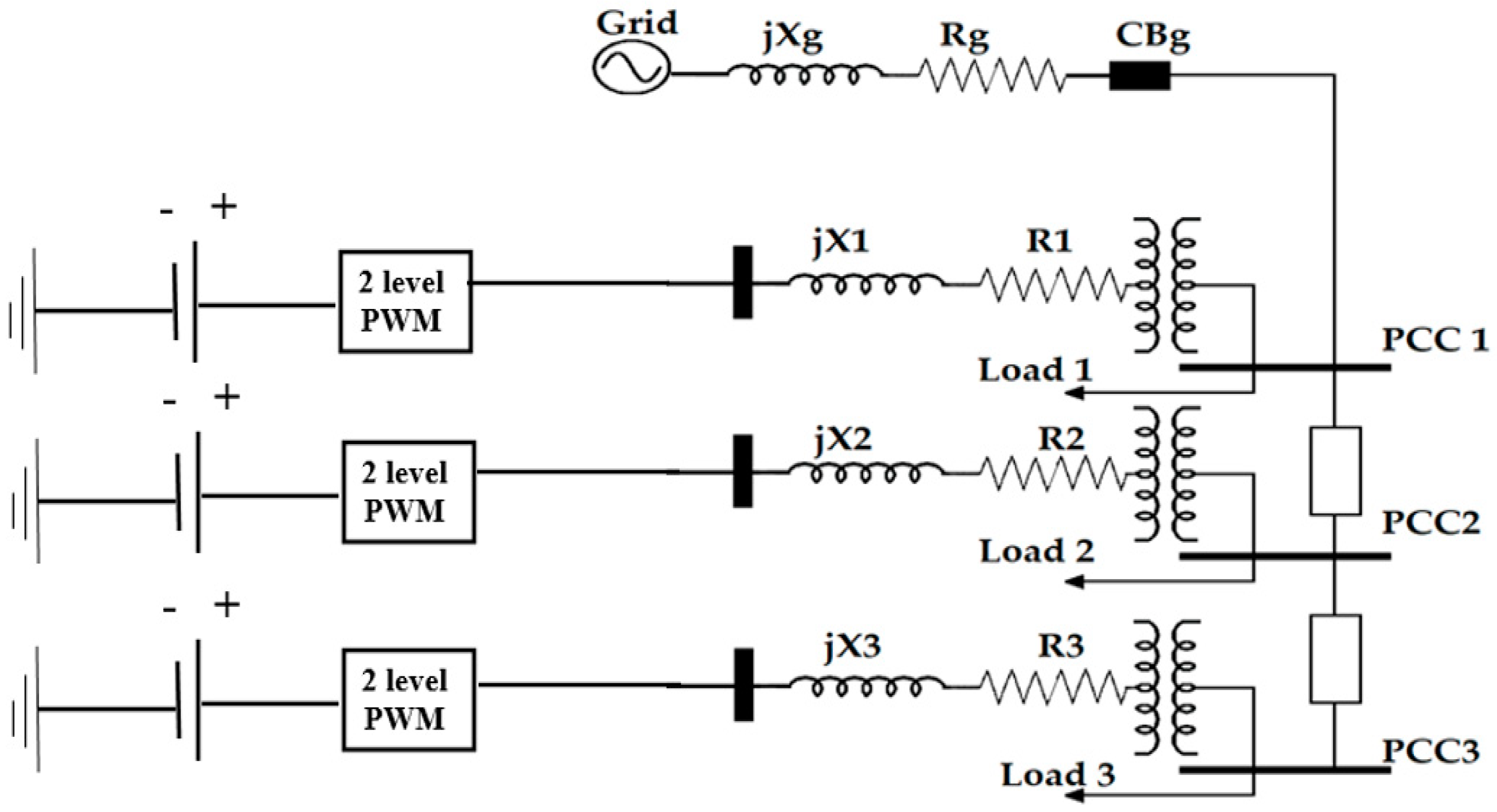

| DEG data | Vbase, low = 0.600 kV, Vbase, high = 13.800 kV, | ||
| Sb1 = 5 MVA | Sb2 = 7.5 MVA | Sb3 = 3.75 MVA | |
| Transformer data | ∆/Y = 0.60/13.80 kV | ||
| Connected load data | Load t1: Cl = 34 µF, Rl1 = 8.0 Ω, Rl2 = 150.0 Ω, Ll = 0.40 H | ||
| Load t2: C2 = 45.3 µF, R22 = 6.0 Ω, Rl2 = 150.0 Ω, L2 = 0.30 H | |||
| Load t3: C3 = 11.3 µF, R33 = 24 Ω, Rl2 = 150 Ω, L3 = 1.2 H | |||
| Transmission line data | T.L1: R1= 0.5 Ω, L1 = 0.0003 H | ||
| TL2: R2 = 1 Ω, L2 = 0.00070 H | |||
| Filter parameters | Rf = 1.5 mΩ, Xf = 3 mΩ, Quality factor = 50.0 | ||
| Main network data | V = 13.80 KV, f = 60.0 Hz, Rg = 0.20 Ω, Lg = 0.00030 H | ||
| DEG 1 | DEG 2 | DEG 3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Design Variable Level (PI) | kp11 | ti11 | kp12 | ti12 | kp21 | ti21 | kp22 | ti22 | kp31 | ti31 | kp32 | ti32 |
| Level 1 (−1) | 0.5 | 0.04 | 0.5 | 0.04 | 0.5 | 0.04 | 0.5 | 0.04 | 0.5 | 0.04 | 0.5 | 0.04 |
| Level 2 (0) | 1 | 0.12 | 1 | 0.12 | 1 | 0.12 | 1 | 0.12 | 1 | 0.12 | 1 | 0.12 |
| Level 3 (1) | 1.5 | 0.2 | 1.5 | 0.2 | 1.5 | 0.2 | 1.5 | 0.2 | 1.5 | 0.2 | 1.5 | 0.2 |
| Design Variable Level (PIA) | Level 1 (−1) | Level 2 (0) | Level 3 (1) | Design Variable Level (PIA) | Level 1 (−1) | Level 2 (0) | Level 3 (1) |
|---|---|---|---|---|---|---|---|
| kp11 | 5 | 4 | 3 | kp22 | 5 | 4 | 3 |
| ti11 | 0.2 | 0.1 | 0 | ti22 | 0.2 | 0.1 | 0 |
| ka11 | 5 | 3.5 | 2 | ka22 | 5 | 3.5 | 2 |
| a11 | 1300 | 1250 | 1200 | a22 | 1300 | 1250 | 1200 |
| b11 | 300 | 250 | 200 | b22 | 300 | 250 | 200 |
| kp12 | 5 | 4 | 3 | kp31 | 5 | 4 | 3 |
| ti12 | 0.2 | 0.1 | 0 | ti31 | 0.2 | 0.1 | 0 |
| ka12 | 5 | 3.5 | 2 | ka31 | 5 | 3.5 | 2 |
| a12 | 1300 | 1250 | 1200 | a31 | 1300 | 1250 | 1200 |
| b12 | 300 | 250 | 200 | b31 | 300 | 250 | 200 |
| kp21 | 5 | 4 | 3 | kp32 | 5 | 4 | 3 |
| ti21 | 0.2 | 0.1 | 0 | ti32 | 0.2 | 0.1 | 0 |
| ka21 | 5 | 3.5 | 2 | ka32 | 5 | 3.5 | 2 |
| a21 | 1300 | 1250 | 1200 | a32 | 1300 | 1250 | 1200 |
| b21 | 300 | 250 | 200 | b32 | 300 | 250 | 200 |
| kp1 | ti1 | kp2 | ti2 | Vt1-lllg | Vt2-lllg | Vt3-lllg |
|---|---|---|---|---|---|---|
| 1 | 0.12 | 1 | 0.2 | 0.098 | 0.1133 | 0.128 |
| 1.5 | 0.04 | 1.5 | 0.2 | 0.097 | 0.11324 | 0.128 |
| 0.5 | 0.2 | 0.5 | 0.2 | 0.0668 | 0.083 | 0.66 |
| 0.5 | 0.04 | 1.5 | 0.04 | 0.074 | 0.08534 | 0.1014 |
| 1.5 | 0.04 | 0.5 | 0.04 | 0.0975 | 0.1128 | 0.128 |
| 1 | 0.12 | 1 | 0.12 | 0.9344 | 0.1133 | 0.1285 |
| 1 | 0.12 | 1.5 | 0.12 | 0.097 | 0.11245 | 0.12752 |
| 1 | 0.04 | 1 | 0.12 | 0.097 | 0.1132 | 0.128 |
| 1 | 0.12 | 1 | 0.04 | 0.0978 | 0.11322 | 0.1285 |
| 1.5 | 0.2 | 0.5 | 0.2 | 0.0975 | 0.11276 | 0.13 |
| 1 | 0.12 | 1 | 0.12 | 0.9344 | 0.1133 | 0.1285 |
| 0.5 | 0.2 | 1.5 | 0.2 | 0.07125 | 0.08 | 0.095 |
| 1.5 | 0.2 | 0.5 | 0.04 | 0.0974 | 0.1127 | 0.128 |
| 1 | 0.12 | 1 | 0.12 | 0.9344 | 0.1133 | 0.1285 |
| 1 | 0.12 | 0.5 | 0.12 | 0.098 | 0.1134 | 0.1287 |
| 0.5 | 0.04 | 0.5 | 0.2 | 0.069 | 0.0806 | 0.097 |
| 0.5 | 0.04 | 0.5 | 0.04 | 0.071 | 0.082 | 0.098 |
| 1 | 0.12 | 1 | 0.12 | 0.9344 | 0.1133 | 0.1285 |
| 0.5 | 0.2 | 1.5 | 0.04 | 0.071 | 0.082 | 0.095 |
| 1 | 0.12 | 1 | 0.12 | 0.9344 | 0.1133 | 0.1285 |
| 0.5 | 0.12 | 1 | 0.12 | 0.07 | 0.082 | 0.0966 |
| 1.5 | 0.04 | 0.5 | 0.2 | 0.0975 | 0.112 | 0.128 |
| 1.5 | 0.12 | 1 | 0.12 | 0.097 | 0.1122 | 0.127 |
| 1 | 0.12 | 1 | 0.12 | 0.9344 | 0.1133 | 0.1285 |
| 0.5 | 0.2 | 0.5 | 0.04 | 0.07 | 0.0785 | 0.093 |
| 1 | 0.12 | 1 | 0.12 | 0.9344 | 0.1133 | 0.1285 |
| 0.5 | 0.04 | 1.5 | 0.2 | 0.073 | 0.0852 | 0.101 |
| 1.5 | 0.04 | 1.5 | 0.04 | 0.0975 | 0.112 | 0.13 |
| 1 | 0.2 | 1 | 0.12 | 0.0984 | 0.113 | 0.128 |
| 1.5 | 0.2 | 1.5 | 0.04 | 0.098 | 0.1134 | 0.128 |
| 1.5 | 0.2 | 1.5 | 0.2 | 0.09 | 0.12 | 0.146 |
| kp1 | ti1 | ka1 | a1 | b1 | kp2 | ti2 | ka2 | a2 | b2 | Vt1-lllg | Vt2-lllg | Vt3-lllg |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 0.101 | 5 | 1200 | 200 | 4 | 0.101 | 3.5 | 1250 | 200 | 0.004424 | 0.05717 | 0.07 |
| 5 | 0.101 | 3.5 | 1250 | 250 | 4 | 0.101 | 2 | 1200 | 300 | 0.04399 | 0.568 | 0.06982 |
| 4 | 0.002 | 2 | 1250 | 250 | 4 | 0.2 | 5 | 1250 | 250 | 0.045025 | 0.0604 | 0.06397 |
| 4 | 0.2 | 3.5 | 1300 | 250 | 5 | 0.101 | 3.5 | 1300 | 250 | 0.449 | 0.5798 | 0.6708 |
| 4 | 0.101 | 5 | 1300 | 300 | 4 | 0.101 | 3.5 | 1250 | 200 | 0.0443 | 0.05714 | 0.07 |
| 3 | 0.101 | 3.5 | 1250 | 250 | 4 | 0.101 | 5 | 1200 | 300 | 0.0439 | 0.0568 | 0.0696 |
| 4 | 0.002 | 2 | 1250 | 250 | 4 | 0.002 | 2 | 1250 | 250 | 0.05284 | 0.06842 | 0.0839 |
| 4 | 0.2 | 3.5 | 1200 | 250 | 3 | 0.101 | 3.5 | 1300 | 250 | 0.0443 | 0.0569 | 0.0697 |
| 4 | 0.101 | 3.5 | 1300 | 200 | 3 | 0.101 | 5 | 1250 | 250 | 0.04406 | 0.0567 | 0.0696 |
| 3 | 0.101 | 3.5 | 1300 | 250 | 4 | 0.2 | 2 | 1250 | 250 | 0.047 | 0.0604 | 0.0745 |
| 4 | 0.002 | 5 | 1250 | 250 | 4 | 0.002 | 5 | 1250 | 250 | 0.05284 | 0.06866 | 0.08384 |
| 4 | 0.101 | 2 | 1250 | 300 | 4 | 0.002 | 3.5 | 1200 | 250 | 0.0525 | 0.06824 | 0.0834 |
| 4 | 0.101 | 5 | 1200 | 300 | 4 | 0.101 | 3.5 | 1250 | 300 | 0.044322 | 0.057131 | 0.07 |
| 4 | 0.2 | 3.5 | 1200 | 250 | 5 | 0.101 | 3.5 | 1200 | 250 | 0.04487 | 0.058 | 0.0709 |
| 5 | 0.101 | 2 | 1250 | 250 | 5 | 0.101 | 3.5 | 1300 | 250 | 0.0454 | 0.05874 | 0.07138 |
| 3 | 0.101 | 3.5 | 1250 | 250 | 4 | 0.101 | 2 | 1300 | 300 | 0.043926 | 0.056764 | 0.0696 |
| 4 | 0.101 | 2 | 1200 | 300 | 4 | 0.101 | 3.5 | 1250 | 200 | 0.044382 | 0.0572 | 0.07 |
| 4 | 0.2 | 3.5 | 1300 | 250 | 3 | 0.101 | 3.5 | 1200 | 250 | 0.443 | 0.056936 | 0.06978 |
| 4 | 0.002 | 5 | 1250 | 250 | 4 | 0.2 | 2 | 1250 | 250 | 0.045 | 0.0604 | 0.069687 |
| 5 | 0.101 | 3.5 | 1250 | 250 | 4 | 0.101 | 5 | 1300 | 300 | 0.043986 | 0.05809 | 0.069762 |
| 3 | 0.002 | 3.5 | 1250 | 200 | 4 | 0.101 | 3.5 | 1250 | 200 | 0.044584 | 0.057453 | 0.07019 |
| 3 | 0.2 | 3.5 | 1250 | 200 | 4 | 0.101 | 3.5 | 1250 | 300 | 0.044417 | 0.057232 | 0.070062 |
| 4 | 0.101 | 3.5 | 1300 | 300 | 5 | 0.101 | 5 | 1250 | 250 | 0.044727 | 0.057849 | 0.07086 |
| 5 | 0.101 | 3.5 | 1300 | 250 | 4 | 0.002 | 2 | 1250 | 250 | 0.053026 | 0.06857 | 0.084176 |
| 3 | 0.101 | 2 | 1250 | 250 | 3 | 0.101 | 3.5 | 1300 | 250 | 0.043713 | 0.05638 | 0.069116 |
| 4 | 0.101 | 2 | 1250 | 200 | 4 | 0.2 | 3.5 | 1200 | 250 | 0.046465 | 0.059818 | 0.07325 |
| 4 | 0.2 | 3.5 | 1250 | 250 | 3 | 0.2 | 3.5 | 1250 | 200 | 0.0457 | 0.058757 | 0.072287 |
| 4 | 0.002 | 3.5 | 1250 | 250 | 3 | 0.2 | 3.5 | 1250 | 300 | 0.04717 | 0.060933 | 0.07714 |
| 3 | 0.101 | 5 | 1250 | 250 | 5 | 0.101 | 3.5 | 1300 | 250 | 0.04518 | 0.058315 | 0.071161 |
| 5 | 0.2 | 5 | 1300 | 300 | 5 | 0.2 | 5 | 1300 | 300 | 0.4792 | 0.485 | 0.4909 |
| 3 | 0.002 | 2 | 1200 | 200 | 3 | 0.002 | 2 | 1200 | 200 | 0.55147 | 0.556 | 0.5642 |
| Constants | DEG1 | DEG2 | DEG3 |
|---|---|---|---|
| c1 | 0.905 | 0.02117 | 0.085 |
| c2 | 1.27 | 0.15478 | 0.015 |
| c3 | 2.99 | −0.0348 | 1.09 |
| c4 | 1.13 | 0.00132 | −0.141 |
| c5 | 2.99 | −0.0215 | 1.12 |
| c6 | −0.619 | −0.06329 | 0.024 |
| c7 | 14.6 | 0.018 | 1.06 |
| c8 | −0.563 | 1 × 10−5 | 0.041 |
| c9 | −14.6 | 0.035 | 1.09 |
| c10 | 0.001 | 0.02355 | −0.673 |
| c11 | −0.005 | −2 × 10−5 | 0.1434 |
| c12 | −0.001 | 0.00783 | −0.698 |
| c13 | −0.001 | 8 × 10−5 | −0.71 |
| c14 | −0.05 | 0.0668 | 3.84 |
| c15 | −0.01 | 0.00426 | −0.705 |
| Constant | DEG1 | DEG2 | DEG3 |
|---|---|---|---|
| c1 | 159.9 | 264 | 170.5 |
| c2 | −1.889 | 2.357 | −3.785 |
| c3 | −45.42 | −26.55 | −33.95 |
| c4 | 0.138 | 1.323 | 1.115 |
| c5 | −0.1373 | −0.151 | −0.1018 |
| c6 | 0.004150 | −0.01289 | 0.002202 |
| c7 | 0.1348 | −0.7729 | 0.2179 |
| c8 | −0.5257 | 4.521 | −3.511 |
| c9 | −0.07814 | −0.1635 | −0.07251 |
| c10 | −0.1071 | −0.2619 | −0.1519 |
| c11 | −0.01333 | −0.07532 | −0.04382 |
| c12 | 0.04909 | −0.2753 | 0.324 |
| c13 | 10.15 | 6.597 | −1.027 |
| c14 | 0.008846 | −0.02901 | −0.0358 |
| c15 | 0.000051 | 0.000058 | 0.000034 |
| c16 | 0.00008 | 0.000026 | 0.000005 |
| c17 | −0.01030 | 0.1297 | −0.1527 |
| c18 | 2.407 | 22.18 | 16.95 |
| c19 | 0.01168 | 0.1216 | 0.06735 |
| c20 | 0.000043 | 0.00011 | 0.000062 |
| c21 | 0.000015 | 0.000083 | 0.000035 |
| c22 | −0.3417 | −2.934 | −1.791 |
| c23 | −0.04992 | −0.2799 | −0.2159 |
| c24 | 0.001460 | 0.000674 | 0.003491 |
| c25 | 0.05449 | 0.4195 | 0.3234 |
| c26 | −0.000901 | −0.1720 | −0.09998 |
| c27 | −1 × 10−8 | −0.002551 | 0.000029 |
| c28 | 0.001506 | 0.008395 | 0.006566 |
| c29 | −0.1405 | 0.000444 | −0.03273 |
| c30 | 0.03634 | 0.02639 | 0.02961 |
| c31 | 0.004169 | 1.319 | 1.48 |
| PIA Controller | PI Controller | ||
|---|---|---|---|
| Optimized Gains Using HDTPS | Optimized Gains Using PSO | Optimized Gains Using HDTPS | Optimized Gains Using PSO |
| kp11 = 4.6382 | kp11 = 3.41862 | kp11 = 1.5612 | kp11 = 1.4673 |
| ti11 = 0.13994 | ti11 = 0.19731334 | ||
| ka11 = 4.3485 | ka11 = 2.2254873 | ||
| a11 = 1223.49 | a11 = 1376.7431 | ti11 = 0.22646 | ti11 = 0.1985 |
| b11 = 292.3687 | b11 = 339.77794 | ||
| kp12 = 3.14 | kp12 = 4.6312007 | ||
| ti12 = 0.1130817 | ti12 = 0.19295647 | kp12 = 0.64132 | kp12 = 0.6135 |
| ka12 = 2.11283 | ka12 = 2.6077231 | ||
| a12 = 1244.535 | a12 = 1307.3856 | ti12 = 0.13742 | ti12 = 0.1537 |
| b12 = 246.9423 | b12 = 259.24443 | ||
| kp21 = 3.859339 | kp21 = 3.4101114 | kp21 = 0.42163 | kp21 = 0.5039 |
| ti21 = 0.18897325 | ti21 = 0.057683216 | ||
| ka21 = 2.1731026 | ka21 = 2.4704053 | ||
| a21 = 1297.5596 | a21 = 1342.5901 | ti21= 0.060711 | ti21 = 0.0716 |
| b21 = 290.04226 | b21 = 258.99485 | ||
| kp22 = 4.4601331 | kp22 = 3.5387 | ||
| ti22 = 0.16837334 | ti22 = 0.059242033 | kp22 = 0.82882 | kp22 = 0.8051 |
| ka22 = 3.2468467 | ka22 = 2.6917 | ||
| a22 = 1259.8421 | a22 = 1358.8685 | ti22 = 0.069886 | ti22 = 0.0711 |
| b22 = 246.1586 | b22 = 235.72769 | ||
| kp31 = 3.6314382 | kp31 = 4.1937448 | kp31 = 0.4648 | kp31 = 0.5548 |
| ti31 = 0.04777053 | ti31 = 0.15264061 | ||
| ka31 = 2.4095915 | ka31 = 3.5112517 | ||
| a31 = 1194.0056 | a31 = 1107.0271 | ti31 = 0.035788 | ti31 = 0.0442 |
| b31 = 221.69729 | b31 = 180.10337 | ||
| kp32 = 3.7879111 | kp32 = 4.0073627 | ||
| ti32 = 0.05891 | ti32 = 0.1091544 | kp32 = 1.5369 | kp32 = 1.3686 |
| ka32 = 2.4789045 | ka32 = 3.4360098 | ||
| a32 = 1289.379 | a32 = 1282.3392 | ti32 = 0.091197 | ti32 = 0.1125 |
| b32 = 207.19588 | b32 = 267.846 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaki, D.A.; Hasanien, H.M.; Alharbi, M.; Ullah, Z.; Sameh, M.A. Hybrid Driving Training and Particle Swarm Optimization Algorithm-Based Optimal Control for Performance Improvement of Microgrids. Energies 2023, 16, 4355. https://doi.org/10.3390/en16114355
Zaki DA, Hasanien HM, Alharbi M, Ullah Z, Sameh MA. Hybrid Driving Training and Particle Swarm Optimization Algorithm-Based Optimal Control for Performance Improvement of Microgrids. Energies. 2023; 16(11):4355. https://doi.org/10.3390/en16114355
Chicago/Turabian StyleZaki, Dina A., Hany M. Hasanien, Mohammed Alharbi, Zia Ullah, and Mariam A. Sameh. 2023. "Hybrid Driving Training and Particle Swarm Optimization Algorithm-Based Optimal Control for Performance Improvement of Microgrids" Energies 16, no. 11: 4355. https://doi.org/10.3390/en16114355
APA StyleZaki, D. A., Hasanien, H. M., Alharbi, M., Ullah, Z., & Sameh, M. A. (2023). Hybrid Driving Training and Particle Swarm Optimization Algorithm-Based Optimal Control for Performance Improvement of Microgrids. Energies, 16(11), 4355. https://doi.org/10.3390/en16114355










