1. Introduction
Off-road vehicles often need high-power systems in order to reach their working point; this implies that fluid power systems have to process elevated thermal loads on the heat exchanger with suitable cooling systems attached, frequently characterized by a high fan speed. In this respect, the correct installation of the fan and an optimized design of the air vents’ position could bring the fan to operating close to the maximum-efficiency operating point.
The experimental approach is important and some researchers tested the effects of different fan rotational speeds, radiator water flows, and underhood geometries, demonstrating that an optimum underhood cooling system can reduce the vehicle fuel consumption [
1]. However, the simulation approach based on Computational Fluid Dynamics (CFD) is surely a more valuable tool for analyzing the air that flows under the vehicle hood and predicting how the fluid interacts with the components of the engine.
A CFD analysis has been used in several studies related to the automotive field [
2,
3,
4], where the underhood flow was studied in different types of cars, showing temperature, pressure, and velocity fields of the air flow at different conditions. With these kinds of studies, it is possible to reduce the vehicle drag [
5] or increase the heat exchanger efficiency, for example by changing the design of the air intake [
6]. In 2011, [
7] referred to the influence of the shroud position on the automotive cooling fan: the relative position between the fan and the conveyor was a critical design aspect, as the fan ducting into the shroud conveyor directly influenced the performance of the heat exchanger. The influence of the cooling system’s component position on a flow field of a cooling fan was also studied [
8].
Thermal analyses for underhood air-flow are also an important aspect for other kind of vehicles. In buses, [
9] studied the overheating issue by analyzing numerical aspects of the air flow field (e.g., velocity, recirculation, and temperature); they demonstrated that a new underhood layout may bring a temperature reduction that improves the power performance and fuel economy. In heavy-duty transportation, a detailed numerical study was presented by [
10], where a structural thermal fluid dynamics model was developed for a parametric analysis of a heat exchanger of the cooling system. This latter work helped in understanding that, with a coupled structural/fluid dynamics approach, it is possible to take into account the influence of the fluid temperature on the stress and displacement of the radiator, raising the degree of optimization. A further work used CFD to design the cooling fan and heat shield and optimize the distance between the fan and heat exchanger [
11].
As for agricultural tractors, their underhood air flows are fundamental in prevent ingoverheating issues, because higher working powers need efficient cooling systems. Some studies have analyzed different fan installation positions and cooling packages in an agricultural tractor, with a three-dimensional numerical approach [
12,
13]. A similar approach, coupled with one-dimensional thermal fluid model, was also used to assess the cooling requirements of an off-road equipment using experimental data [
14].
CFD applied to fans has been largely studied, and [
15] presented a comparison between commercial and open-source codes, in which their numerical results were compared with an ISO 5801 Type A experimental test. Moreover, some studies have analyzed the influence of the pitch blade angle [
16] and of the tip leakage [
17] on the fan design. As for the tip clearances, they affect the fan noise [
18,
19], as well as the fan performance [
20]. Fan CFD models have been developed to predict the noise emitted, either with the Reynolds-averaged Navier–Stokes (RANS) approach [
21,
22,
23,
24,
25,
26], or a more accurate Large eddy Simulation (LES) approach [
27,
28,
29,
30,
31].
An incorrect installation of the fan and wrong design of the air vents’ position may cause additional sources of noise and vibrations due to the pressure waves of the air under the vehicle hood. This fact reduces the comfort for the users, both in the driver cabin and outside the chassis, and increases the power losses of the whole hydraulic system. The noise emission of the cooling fan is then an important performance aspect to be considered. In some working conditions, the rotational velocity of the fan can reach high values and the air flow at the blade tip can be a relevant noise source. These noise emissions of the cooling fan have been studied in heavy-duty [
32] and fuel cell [
33] vehicles, as well as in the automotive field [
34].
Some computational simulations carried out for the engine cooling system of an off-road vehicle under different resistance coefficients have permitted the obtainment of the flow field and pressure distribution of different components. The results showed that the greater the resistance, the higher the velocity radical component. In addition, due to the asymmetric shape of the baffle plane, the flow behind the fan shows an asymmetric behavior too [
35].
In the design of a vehicle cooling system, each component (heat exchanger, fan, and conveyor) is often chosen based on its fixed operating point [
36]. Unfortunately, these vehicles work in variable conditions and the performance of each component is different when they are working as a whole under the hood [
37].
In this paper, we want to show how it is possible to optimize the entire system only by varying the installation positions of the key components. An underhood airflow CFD analysis is performed on an off-road compact machine, where overheating and noise emission are important design aspects that have been scarcely addressed by the scientific community.
2. Description of the Compact Off-Road Vehicle
The machine is an off-road vehicle designed to be a multifunctional machine (
Figure 1). This vehicle is self-propelled, with a compact structure capable of many functions; it can be connected through a plate and hydraulic connector to a series of attachments, characterized by different functionalities. The field of use of the machine is therefore determined by the final user who decides which attachment to connect, according to the work to be fulfilled: earth-moving, farming, gardening, and the maintenance of public areas, etc.
The common rail diesel engine, with 2500 cc displacement and 75 hp, is equipped with four cylinders in line and a liquid cooling system. During the working cycle, the engine speed varies from 1800 to 2600 rpm. Four-wheel drives with hydrostatic direct motors ensure its mobility in off-road conditions and the engine is compliant with the Tier-IV emission regulations. With the update of directives and standards, it often happens that the heat rejection data, the radiator, and other cooling components have to be re-designed and validated in order to fulfill these updated requirements.
The underhood layout components are shown in
Figure 2, in particular the fan and conveyor. These components are normally set between the engine vane and radiator. In this position, the suction air for the cooling fan flows inside the engine vane from lateral and frontal air vents. The air is pushed against the radiator and then flows out from the outflow vents positioned on the rear of the vehicle. The coolant fluid inside the radiator is a water–glycol mixture and the pressure drop is a 0.24–0.25 bar, depending on the working conditions. The relative position of the fan, with respect to the engine and the radiator, is shown in
Figure 3. The tip clearance between the fan blade and conveyor is 10 mm and the relative overlap is 6 mm.
The axial fan has eight forward blades with an incidence angle of 35° and an external diameter of 435 mm; some other characteristics are reported in
Table 1.
3. Physical Phenomena Involved
Since the cooling air flow comes from the air vents and passes through the engine surfaces and other heat exchangers (i.e., condenser and charged air cooler), the velocity distribution at the face of the radiator is highly non-uniform. For optimized thermal management, it is necessary to have the proper positioning of all the components, upstream and downstream of the fan and conveyor position [
38].
In the automotive sector, there are two main sources of energy that contribute to the cooling air flow through the underhood: one is ram air and another is the radiator fan. For vehicles at high speeds, the main driving force for the cooling air flow is the ram air. For vehicles at low speeds, the main driving force for the cooling air is the radiator fan. The mini-loader vehicle works with a very low velocity and the cooling flow is generated only from the fan, suctioning air from the air vent and pushing it to the radiator.
As the free-flowing air approaches the air vent, passes through it, and touches all the underhood components, the air velocity or dynamic pressure decreases while the static pressure increases, in order to maintain the same total pressure (Bernoulli Law). On the other hand, the air acceleration resulting from the Venturi Effect (lower cross-sectional area and higher velocity) creates low static pressure areas at the underhood.
Meanwhile, the electric fan, acting as a momentum source, generates a static pressure jump and total pressure jump to the air flowing through the fan. The fans work with the cooling air by supplying both static and dynamic energy to the air.
Furthermore, the spectral distribution and magnitude of the aerodynamic noise that originates from the fluctuating forces exerted by the blades is closely linked to the inflow characteristics. These are commonly referred to as aerodynamic installation effects. Thus, the study of the sound-generating mechanisms and acoustic propagation from the ducted fans involves an examination of both installation effects.
4. Simplified Geometries for the CFD Analysis
One of the main sources of noise emission in the vehicle is the axial fan of the heat exchanger. The targets are to find the losses provided by the airflow inside the motor vane and define the best operating point of the fan using the CFD analysis. The 3D geometries are courtesy of MultiOne s.r.l.
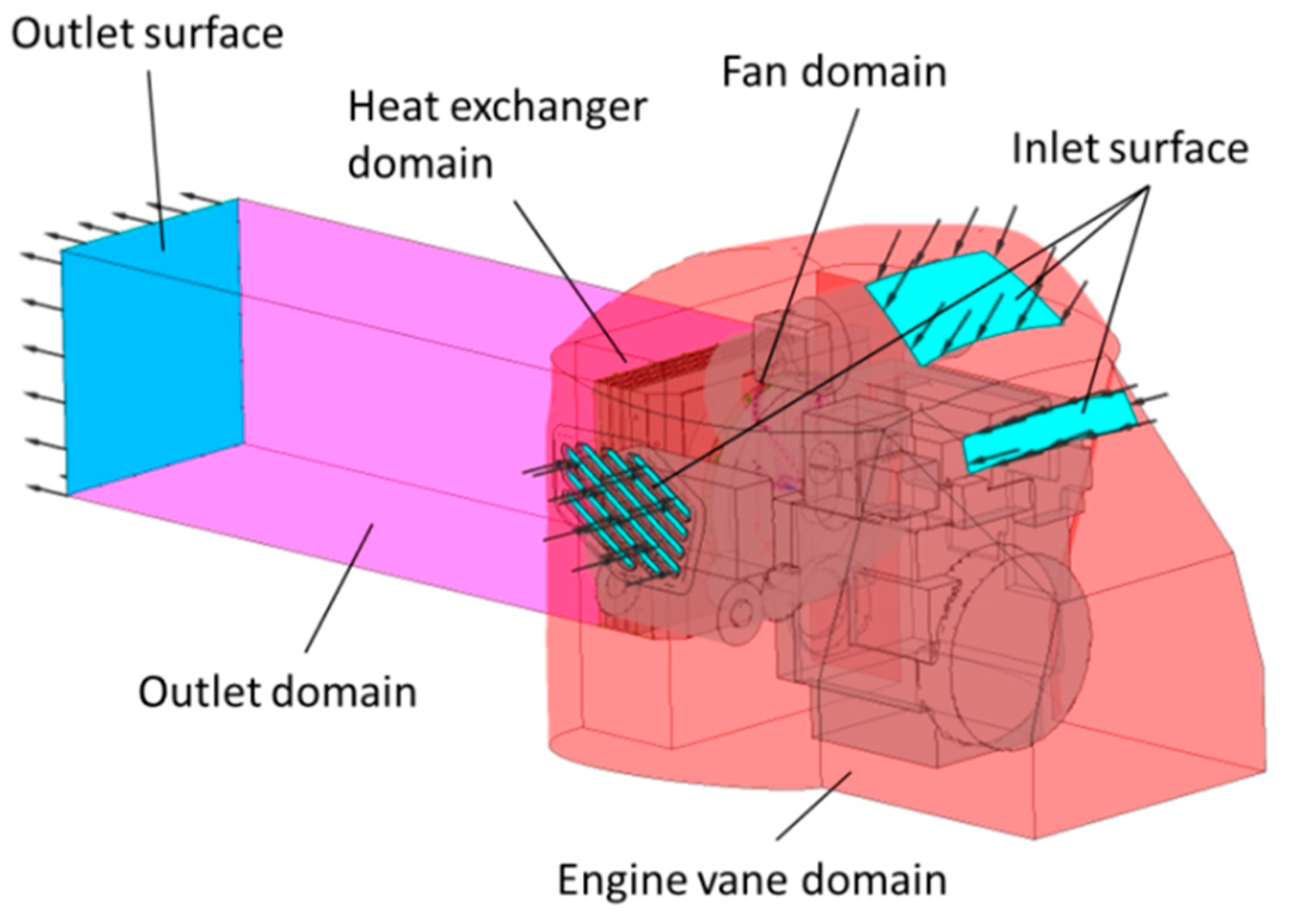
The geometries of the vehicle hood, engine, and heat exchanger are simplified, in order to better achieve a numerical convergence and physically reliable results in an affordable CPU simulation time. For the computational analysis, the simulated global domain is divided into three domains: the engine vane domain, fan domain, and heat exchanger domain. This subdivision is performed in order to better discretize each volume and their surfaces for all the different geometries analyzed in the solid design modeler, separately.
The engine vane domain is composed of three main parts: the upperhood surface, external chassis surface, and engine envelope. The hood and the external chassis are simplified, in order to reproduce the development of the global volume that the air occupies during the intake process. The simulated air vents are located on the upperhood surface. The global vehicle engine is modelled as a “shaped closed box”, in order to simulate only the main clearances between the fan, air vents, and main path of the airflow under the hood (
Figure 4).
The fan domain is composed of a rotating and stationary part, called multiple reference frames (MRF) (
Figure 5A), and a conveyor (
Figure 5B), respectively. The remaining volume is the heat exchanger domain (
Figure 5C).
5. Validation of the Model
To overcome the experimental tests on a “real” operating machine, the experimental validation was performed only on the fan model, using its characteristic pressure curve (virtual test). The validation of the entire underhood model was performed with a mesh-independent analysis for each calculated variable.
5.1. Virtual Test for the Validation of the Fan Model
Since the experimental characteristic pressure curve was obtained following an ISO 5801 Type A configuration [
39], the simulation should be done in the same conditions. For this reason, as shown in
Figure 6, the bell-mouth inlet Test Space (iTS), in green, and the cylindrical outlet Test Chamber (oTC), in purple, were added to the fan domain to simulate the undisturbed flow condition. The measurement was taken in the dark purple cylinder and the space behind it served the purpose of having an undisturbed outgoing flow.
Four meshes (1, 2, 3, and 4) were generated with the characteristics shown in
Table 2. The four meshes varied from each other by their number of elements; the greater the number, the more accurate the result should be, but with more computation time.
The mesh quality was measured by analyzing the orthogonality angle, the expansion, and the aspect ratio. In
Figure 7, some characteristics of cell vertex centered based code are shown in order to identify these mesh parameters. The grey area represents the control volume. The orthogonality angle is the angle between the vector s, that joins two mesh nodes, and the normal vector n, for each integration surface point associated with that edge (
Figure 7). In other words, the orthogonality is how close the angles between the adjacent element faces or adjacent element edges are to some optimal angle (for example, 90° for quadrilateral-faced elements and 60° for triangular-faced elements). The expansion factor is the ratio of the largest to smallest volume elements surrounding a node. The aspect ratio is the ratio of the largest, A
max, to the smallest, A
min, areas of the integration points for each element surrounding a node.
The orthogonality angle and aspect ratio are criteria used to measure the distortion of the elements, while the expansion factor is used to measure the mesh uniformity.
Keeping these quality parameters in specific ranges (orthogonality angle > 20°, expansion factor < 20, and aspect ratio < 100) leads to a better stability and convergence of the calculation, but it often involves an exponential increase in the number of elements, which is not acceptable; therefore, these criteria are just taken as an overall guide for the mesh quality measurement.
An unstructured grid with tetrahedral elements was used for the discretization of the analyzed domain. To improve the surface discretization near the blade and conveyor, the tetrahedral elements were cut with six prismatic layers. The prismatic elements that were generated in this way had a height lower than the original elements; therefore, it was possible to perform a high mesh local refinement, keeping the number of global elements approximately constant. The height of the first prismatic layer was 0.01 mm for a better boundary layer resolution. For all the following simulations performed, the y+ value was systematically checked to be lower than 2, as recommended [
41,
42] for the adopted turbulence model.
For the four meshes, the pressure rise of the fan was calculated by the difference of the total pressure calculated in the outlet and inlet sections,
p02 [Pa] and
p01 [Pa], respectively [
43].
where
p0 is the static pressure averaged over the local mass flow that can be obtained by the general expression reported in Equation (2) [
41], where ϕ represents any variable or expression being averaged (
p0 in this case) and m represents the local mass flow:
The boundary conditions are those reported in
Table 3; in particular, the atmospheric pressure and mass flow rate were set at the inlet and outlet surfaces, respectively.
In
Figure 8, the curves of the pressure rise of the fan, as a function of the volumetric flow rate calculated for the four meshes, are reported against the experimental curve.
The curves related to mesh 1 and mesh 2 have trends different from that of the experimental curve and, in some points, the differences are greater than 10%. On the contrary, mesh 3 and mesh 4 are in good agreement with the experimental curve, with a deviation almost always within 3%. In order to reduce the computational effort, mesh 3 was chosen for the next step of the calculation and the fan with the conveyor was considered to be validated.
5.2. Mesh-Independent Analysis for the Validation of the Underhood Model
The fan model previously validated with the virtual test (mesh 3) was used.
As shown in
Figure 9, the outlet domain, in pink, was added to the initial three-domain subdivision (engine vane domain, fan domain, and heat exchanger domain) to improve the stability of the simulation. The figure also makes it clear where the input and output surfaces of the flow are.
Four meshes (A, B, C, and D) with the characteristics shown in
Table 4 were generated in order to compute an independent mesh analysis. The same boundary conditions used for the validation of the fan model were set (
Table 3).
Figure 10 shows the results of the mesh-independent analysis. Meshes A and B were the reverse of each other at some points; the different trends between the two curves meant that one of the two was not mesh-independent. Moreover, the trend of meshes A and B differed from that of meshes C and D for the non-identification of the relative maximum point at Q = 8000 m
3/h.
In conclusion, the trend of C or D was more replicable, as there was no specific influence given by the numbers of the points of the mesh. The third mesh (mesh C) was finally adopted, since it allowed for a lower computational effort with a comparable result accuracy.
6. Numerical Simulation
The numerical simulations were carried out with the commercial CFD code ANSYS CFX 19.2 [
41]. This code solved the 3D Reynolds-averaged form of the Navier–Stokes equations by using a finite element approach based on finite volume method. A second-order high-resolution advection scheme was adopted to calculate the advection terms in the discrete finite-volume equations. The meshes used in the calculations were hybrid tetrahedral and hexahedral elements, generated by means of ANSYS ICEM CFD 19.2 [
44].
It is well known that RANS models do not accurately predict all the flow details in massively separated flow regions. In addition, the RANS formulation has some limitations if used to predict flow-induced noise or vibrations [
26]. For these problems, the flow-field resolution with an LES (Large eddy simulation) or DES (Detached eddy simulation) approach can provide valuable details far exceeding RANS simulations. While the grid resolution requirements are not significantly higher than those for RANS, the time resolution with LES or DES imposes high CPU demands. On the other hand, DES is a computer-intensive method, because large (detached) turbulent structures need to be resolved in space and time. In cases of complex fluid domain geometries, as in this case, DES or LES approaches are hardly applicable. However, when low-frequency tones are sought, as in this study, the acoustic sources for tonal noise can be computed in RANS simulations.
The shear stress transport (SST) k-ω two-equation model [
24,
25,
34] was used to solve the turbulent flow. The k-ω-based SST model was designed to provide highly accurate predictions of the onset and amount of flow separation under adverse pressure gradients by the inclusion of transport effects into the formulation of the eddy viscosity. In SST, k-ω blending functions are present, whose formulation is based on the flow variables and the distance to the nearest surface.
Near-wall effects were modeled by means of automatic wall functions based on the analytical wall function approach [
44]. The simulations were performed in steady-state conditions. When both stator and rotor are present in the simulation, the simulations are performed in an MRF (multiple reference frame) to take into account the contemporary presence of moving and stationary domains. In particular, a mixing-plane approach was imposed at the rotor/stator interface. In this approach, a single-pass steady-state solution was calculated, exchanging the flow-field variables at the interface. The flow-field data were averaged circumferentially for both frames of reference at the interface and passed to the adjacent zone as boundary conditions.
The inlet and outlet boundary conditions were set with a normal direction and medium intensity of turbulence, in order to improve the numerical stability. Every wall was modeled as an ideal “No Slip” smooth wall, in order to disregard the effect of the wall roughness on the results.
The advection scheme imposed was a high-resolution, second-order backward Euler. The convergence criteria for the equations’ residual values were set to 10−4. With these settings for the steady-state simulations, the global imbalances were normally kept below ±3%. With these settings, the convergence was achieved in about 500 iterations and the necessary time calculation was around 6 h with an Intel Xeon CPU.
7. Parametric Analysis and Simulated Test Cases
Once the numerical model was validated, the parametric analysis was carried out. The parameters studied were the relative positions between the engine, fan, and conveyor (six cases), the conveyor geometry (three cases), and the blade angle (two cases). The choice of the various cases will be discussed in the following paragraphs. Each case was simulated with the boundary conditions already indicated and reported in
Table 3.
7.1. Test Cases with Different Positions
In order to investigate the influence of the position, different engine–fan and engine–radiator distances were considered. These distances are indicated in
Figure 3 with dimensions
a and
b, respectively. In order to limit the overall dimensions, the engine–fan distance can be increased by a maximum of two mechanical spacers, 18 mm each, while the engine–radiator distance should not be increased more than 30 mm. This generates six different test cases, which are identified in
Table 5 with letters “a” to “f”.
7.2. Test Cases with Different Conveyor Geometries
The analysis of the pressure gradient on the conveyor surface led to the idea of modifying the standard geometry (test case a) and designing two new optimized geometries (test cases g and h), as shown in
Figure 11.
The first geometry (test case g) was designed with a curved profile on the right side. The analysis of the pressure peaks on the original geometry showed that the different alignment between the fan and radiator generated a lateral stagnation volume. The outflow was stuck in that region and increased the pressure force on the conveyor surface, creating an additional and unwanted noise source. For this reason, a circular guide profile was designed in order to reduce the air logging and increase the overall efficiency.
The second geometry (test case h) was designed with a divergent conveyor section on the inlet area. The standard conveyor had a squared geometry, which generated a recirculation zone near the edges. With the new geometry, a pressure-wave reduction near the conveyor edges was expected.
7.3. Test Cases with Different Blade Angles
The blade angle of the original axial fan was 35° and could be changed with pitches of 5°. From a noise emission point of view, it is well known [
41] that the angle of incidence has a direct influence on the sound pressure. In fact, a greater blade angle increases the air pressure on the surface of the radiator, increasing the sound intensity at the same time. For this reason, it was decided to investigate the influence of the blade angle by reducing it from 35° (test case a) to 30° (test case i), as shown in
Figure 12.
7.4. Additional Test Case
An additional test case (case j) was obtained by combining some of the previous designs. In particular, the engine–fan distance was increased by 36 mm compared to the standard configuration, the geometry chosen for the conveyor was curved and diverging, and the blade angle was 30°.
The increased performance expected for a greater engine–fan distance and from a different conveyor geometry should balance the decrease in the static pressure expected for the lower pitch blade angle. The latter should, however, limit the noise emission.
8. Results and Discussion
As shown in
Table 6, from the numerical model, several parameters were calculated for all the test cases:
the hydraulic and mechanical powers, as defined in [
41]:
where Δ
p0 is difference in the static pressure,
Q is the flow rate,
Mt is the torque acting on the impeller, and
ω is the fan rotational velocity.
the fan efficiency
η [
41]
the sound pressure level
SPL, both in terms of peak and averaged values. The acoustics pressure,
pa, is computed by the Lowson model [
45].
where
paref is the acoustic reference pressure of 20 µPa.
8.1. Test Cases a to f—Different Positions
Regarding the different distances, the numerical results (
Table 6) show that an increase in the engine–fan distance (test cases b and c) led to lower efficiency η, while a simultaneous increase in the engine–radiator distance (test cases e and f) produced an increase in the efficiency combined with a decrease in the averaged SPL. Case f had an estimated attenuation of 10 dB with respect to case a.
The simultaneous presence of two countertrending effects implies the need to find the optimum setting to maximize the performance: the insertion of spacers between the engine and fan improved the inlet air flow to the fan, increasing its axial component and moving the operating point closer to the theoretical design one. On the other hand, when the distance between the fan and the conveyor was reduced, the recirculation phenomena due to the air reflected by the radiator walls was increased. If, however, at the same time, the distance between the fan and conveyor was increased, the system reached a higher performance level in terms of the uniformity of the air flow, with an optimum heat exchange performance and lower noise emitted by the fan.
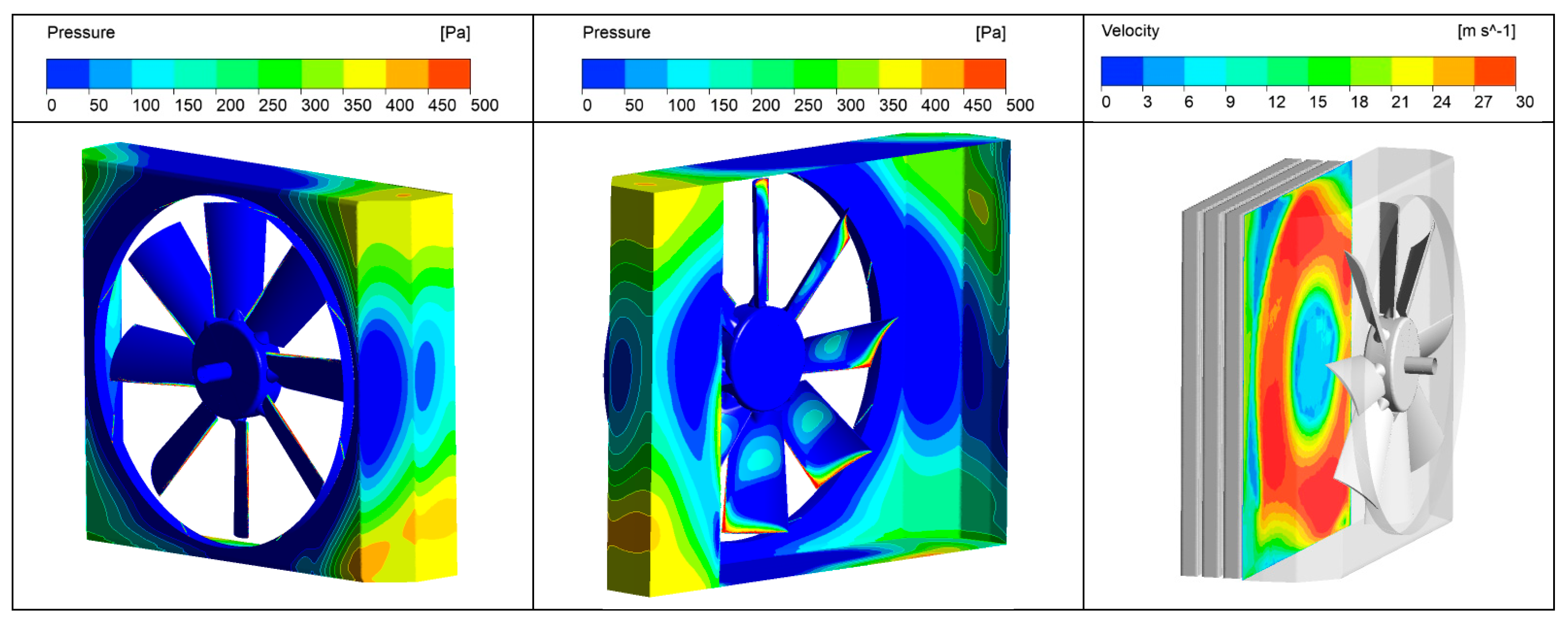
As for the simulation contour plots,
Figure 13 shows the results of the standard geometry (case a): the static pressure on the fan and conveyor wall with two different views (upper left and center) and the velocity contour plot on the inlet plane of the heat exchanger (upper right). It is possible to see the high pressure on the tip blade and the high-flow velocity.
The comparison with the results shown in
Figure 14 (case f) reveals the improvement obtained when both distances (engine–fan and fan–conveyor) were increased up to the maximum possible, in order to completely duct the blades in the conveyor, decreasing the radial incidence phenomena and leaving more space at the fan outlet, in order to minimize the recirculation effects.
8.2. Test Cases g and h—Different Conveyor Geometries
Regarding the conveyor geometry, the results (
Table 6) show that the tested geometries (case g and h) improved the internal fluid dynamics of the system, increasing its performance in terms of the pressure difference and overall efficiency. A slight increase (1.5–3 dB) in the averaged sound pressure level was observed.
The simulations of case g and h are shown in
Figure 15 and
Figure 16, respectively. The simulation contour plots of
Figure 16. show that, in case h, the velocity and pressure gradients were more uniform, probably due to the best geometry of the conveyor. In fact, the pitch pressure that was evident in case g (
Figure 15) in the angle of the conveyor (red area on the left and central plots) disappeared.
8.3. Test Case i—Different Blade Angles
Regarding the blade angle of incidence, the results (
Table 6) show that case i had an estimated averaged sound pressure level almost 3 dB lower than that of case a, as expected.
As for the simulation contour plots shown in
Figure 17, looking at the static pressure contour on the fan and conveyor wall (left and center), it is evident that the maximum value of the pressure was on the blade-leading edge, while on the blade surface, there was a pressure gradient that increased from the hub to the blade tip.
As for the flow velocity reported in the right side, a high gradient on the heat exchanger surface can be observed. In addition, the fan discharged less pressure forces to the conveyor walls than all the previous simulations (cases a, f, g, and h).
8.4. Test Case j
All the improved parameters were combined into a final synthesis geometry (case j). The results were that the chosen configuration implemented two spacers between the engine and the fan, a greater distance between the fan and the conveyor, a conveyor with an optimized internal geometry, and a blade with a reduced pitch angle. The results (
Figure 18) show a significant drop in the surface pressures to the conveyor and a significant reduction in the noise emitted by the fan (
Table 6), without affecting the performance required by the radiator for the needed thermal power.
Therefore, with the aim of noise reduction, the geometry must be optimized by inserting changes aimed at increasing the relative distances between all the components involved and reducing the effects of decentralization. By doing this, it is possible to improve the fluid dynamics of the system and, consequently, to set a lower pitch angle for the blades, which would allow for less noise to be emitted by the fan.
Figure 19 shows the contour plot of the flow velocity in a cross-section of the under-hood for the different test cases (a, i, and j). It can be seen that the air flow entering from the air vent touches the upper side of the engine and then enters into the upper area of the fan conveyor. The engine position causes a strong blockage to the flow and generates a high-velocity gradient at the outlet fan conveyor. In this way, the fan is probably working in off-design conditions. The best efficiency point (BEP) was measured for an air flow rate of 2.5 m
3/s and reached 42%. Conversely, in all the simulated cases, the efficiency was between 28% and 35%, due to the off-design conditions.
The best configuration is that shown in case i, where the flow acceleration at the top of the fan is lower and the gradient is more uniform. Case j and all the other simulated test cases, although not reported as plots, are similar to case a. The improvement in the flow condition at the inlet of the fan could be reached by modifying the position of the air vent and adding another one, for example on the underside of the motor, but this is beyond the scope of this study.
9. Conclusions and Future Perspectives
A fan is normally designed to operate at the point of maximum efficiency, but the relative positions between the air intakes, engine, and other underhood components cause the fan to operate in off-design conditions. Indeed, the engine dimension generates a blockage of the inflow and a vortex stagnation.
In off-design conditions, a high fan velocity is necessary to ensure the engine cooling effect and a high trailing edge tip velocity generates noise. Furthermore, considering the radiator, a high-velocity gradient on the heat exchanger causes a low efficiency of the heat exchange, leading to the oversizing of the exchanger during the design phase of the vehicle. It is not worth studying the position and dimension of the components separately. The underhood air flow should be the results of three combined aspects: the dimension and position of the air intakes, the dimension and position of the mechanical parts involved (engine, duct, and filters, etc.), and the design of the axial flow fan geometry.
The fan operating point is much influenced by the geometry of the vehicle system: if this effect is not taken into account during the design operations, it would lead to an unbalanced air flow on the heat exchanger, with overheating problems as a consequence. Moreover, the high flow velocity and fan off-design behavior can cause high noise emissions during the working cycle, due to unwanted air pressure waves. This could cause problems in complying with the current regulations/directives on noise emission.
This work demonstrates how it is possible to optimize the underhood flow and other performance characteristics by simply changing some key parameters, such as the fan position, the geometry of conveyor, and the blade angle. These parameters can affect up to 10% of the fan efficiency and up to 13 dB of the averaged sound pressure level.
This work highlights the need to consider the impact of the vehicle’s system geometry during the design phase to better balance the air flow on the heat exchanger and avoid noise emission issues. These results should sensitize designers to save time and prototype costs, testing any innovative underhood system design using a CFD analysis not for a single component, but for the entire system. These considerations are applicable to many off-road vehicles, where there is a need to generate high power under heavy load conditions.
In this work, all the numerical analyses were completed at a fixed fan operating point, which is representative of the heaviest working condition of the machine. In this working condition, the efficiency, noise, and other characteristics have a greater impact on the vehicle performance than with other working points. A future work would analyze different fan working points, depending on the working cycle.