Cryogenic Hydrogen Jet and Flame for Clean Energy Applications: Progress and Challenges
Abstract
:1. Introduction
1.1. Background and Motivation
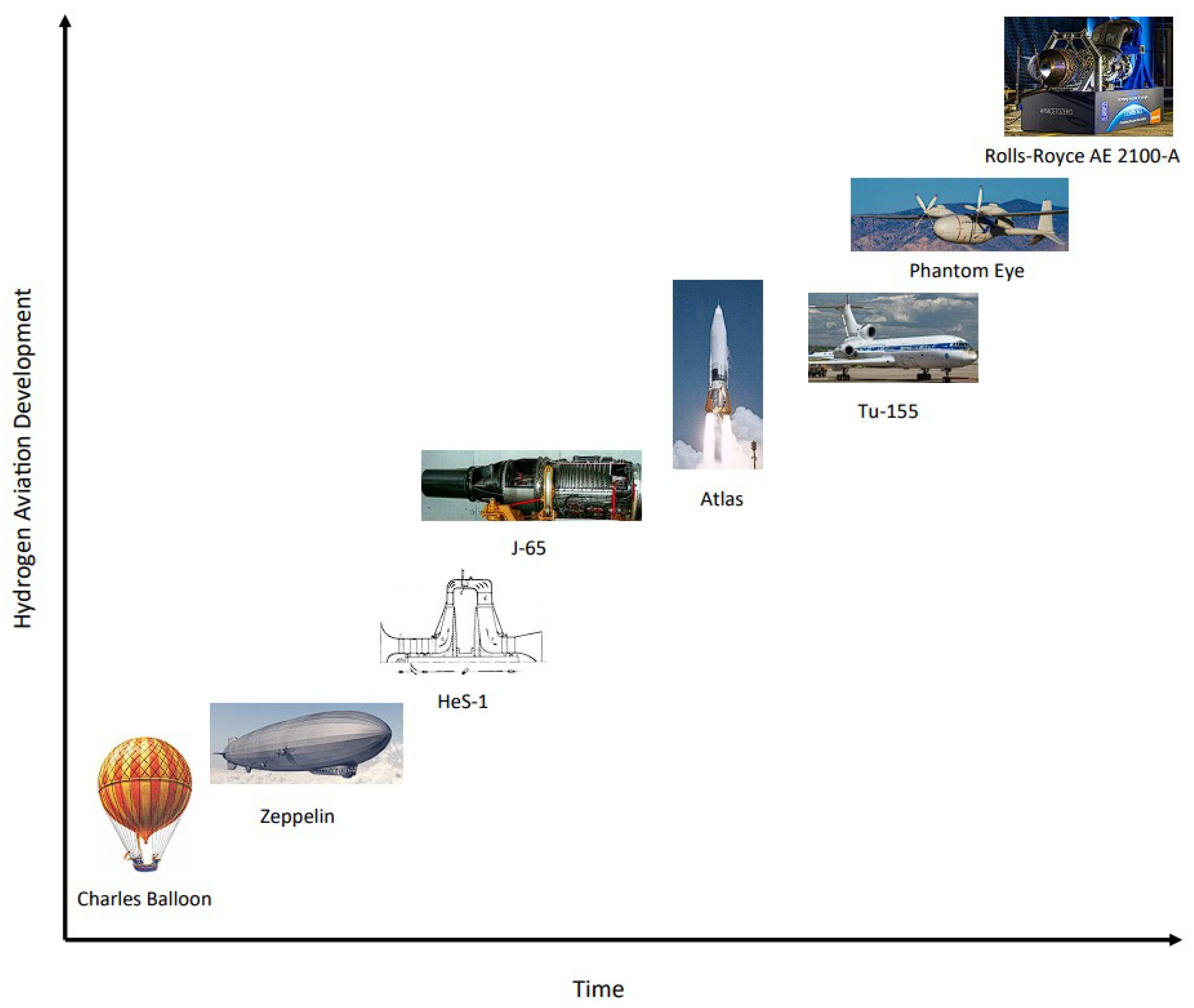
1.2. The History of Hydrogen in the Aerospace Industry
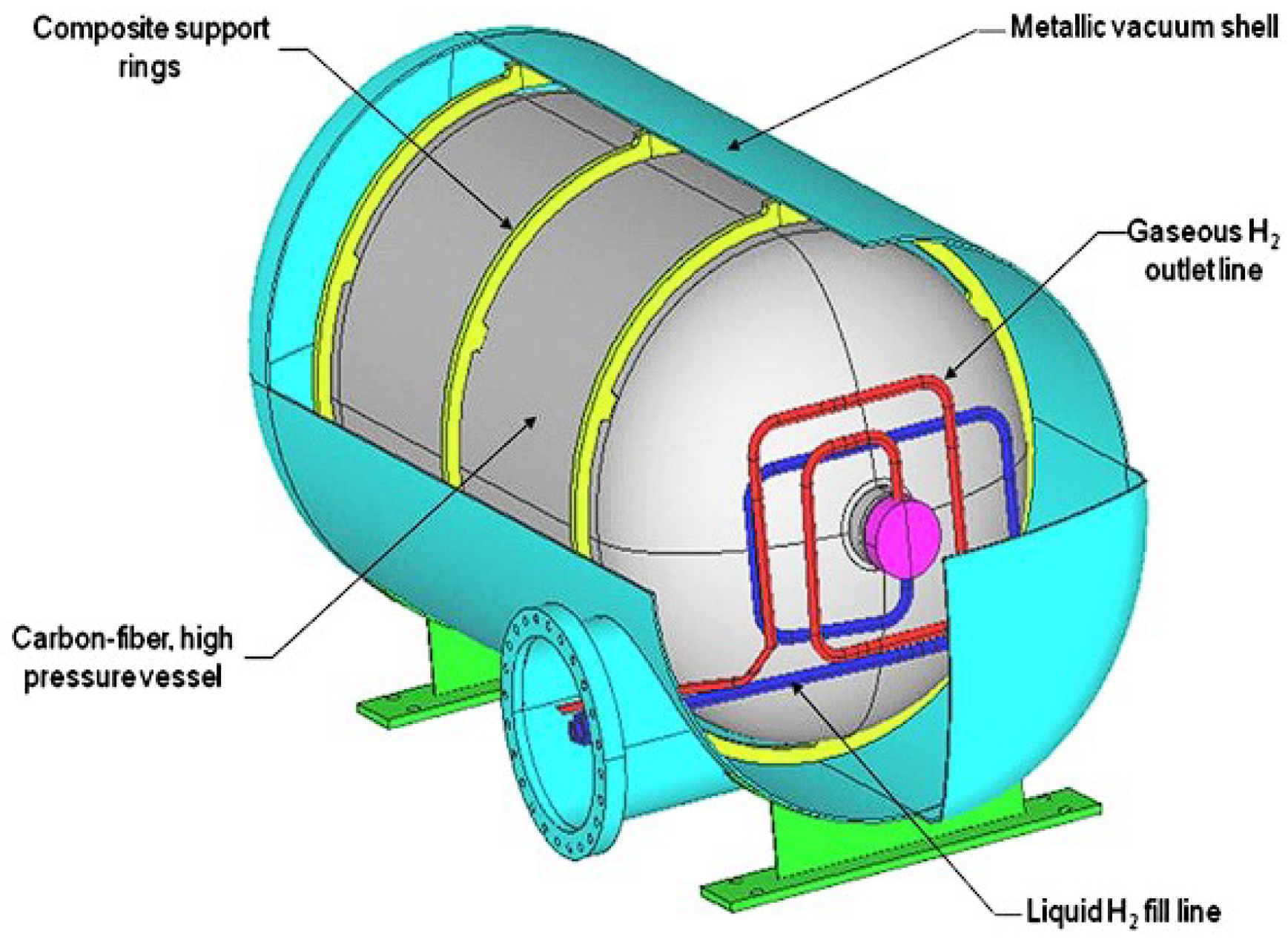
1.3. Hydrogen Storage Methods
2. Physics and Theoretical Models
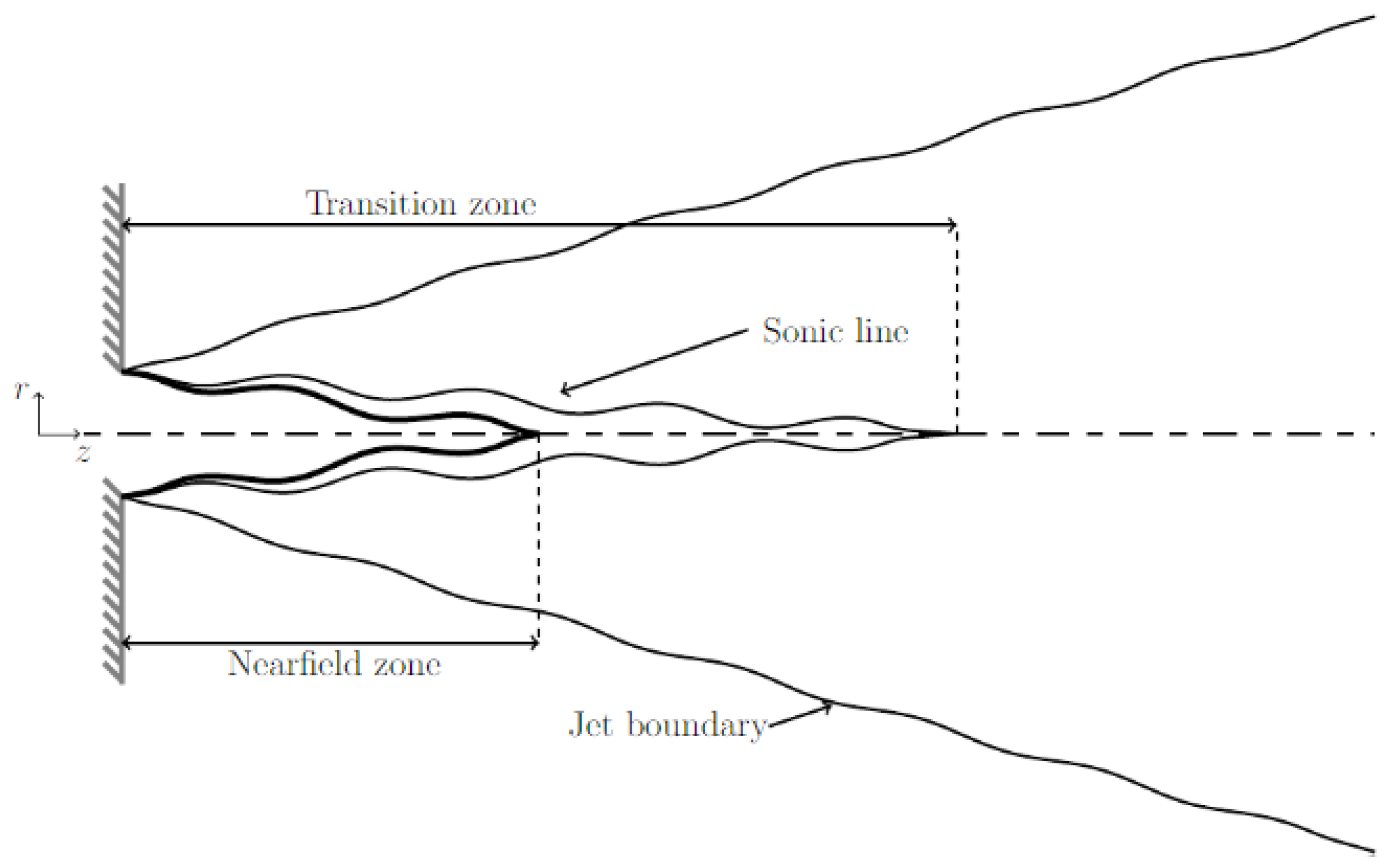
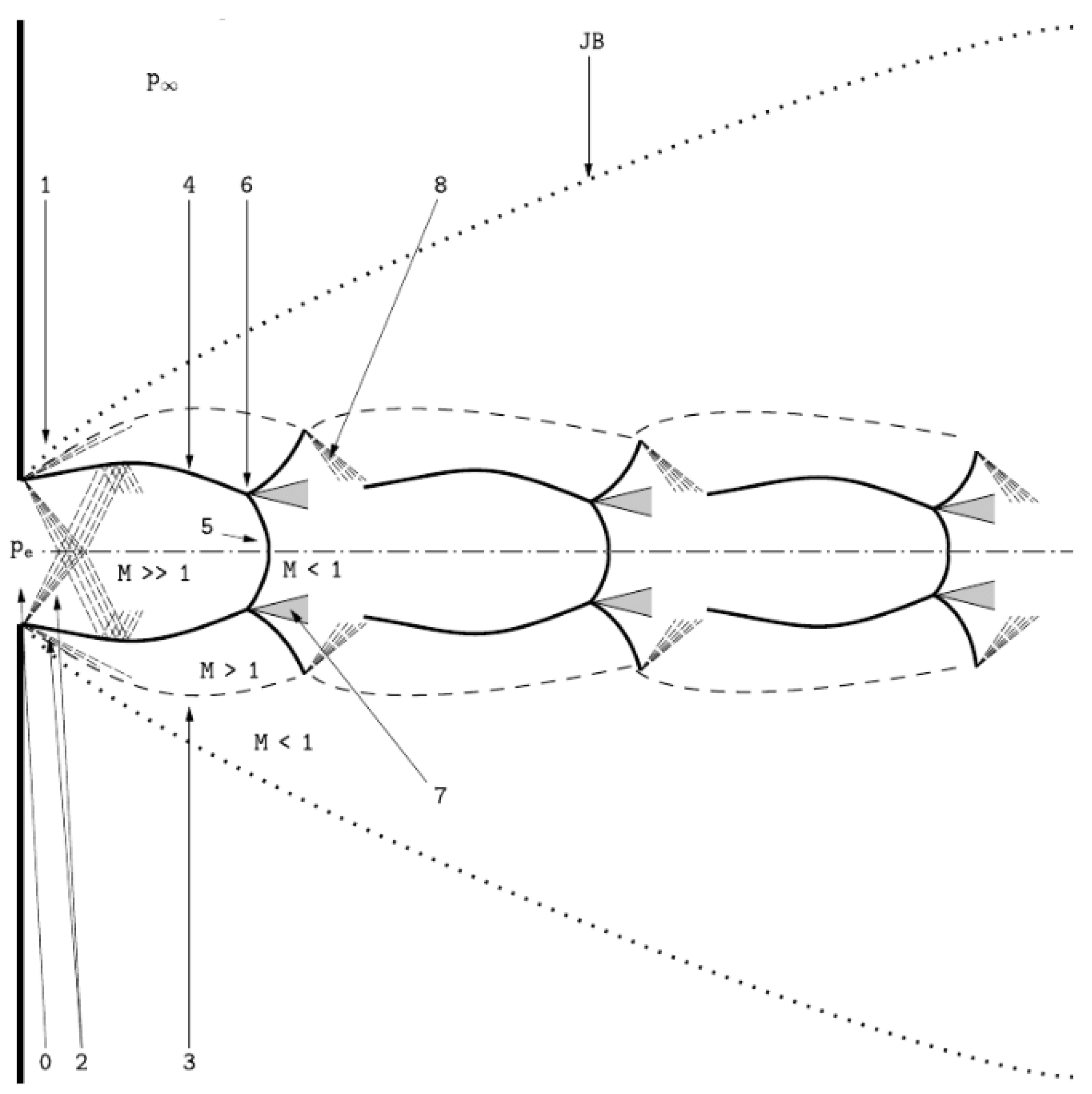
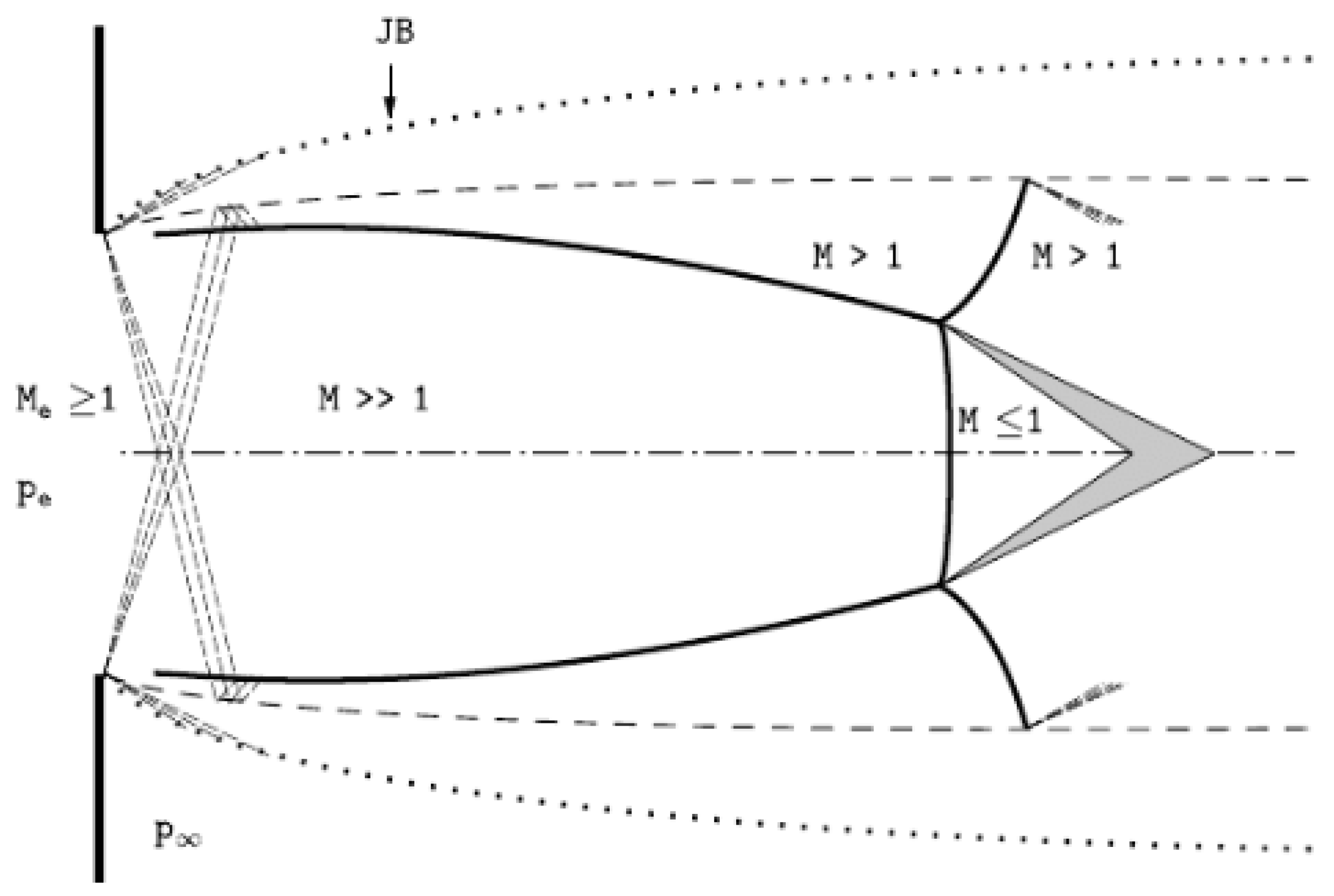
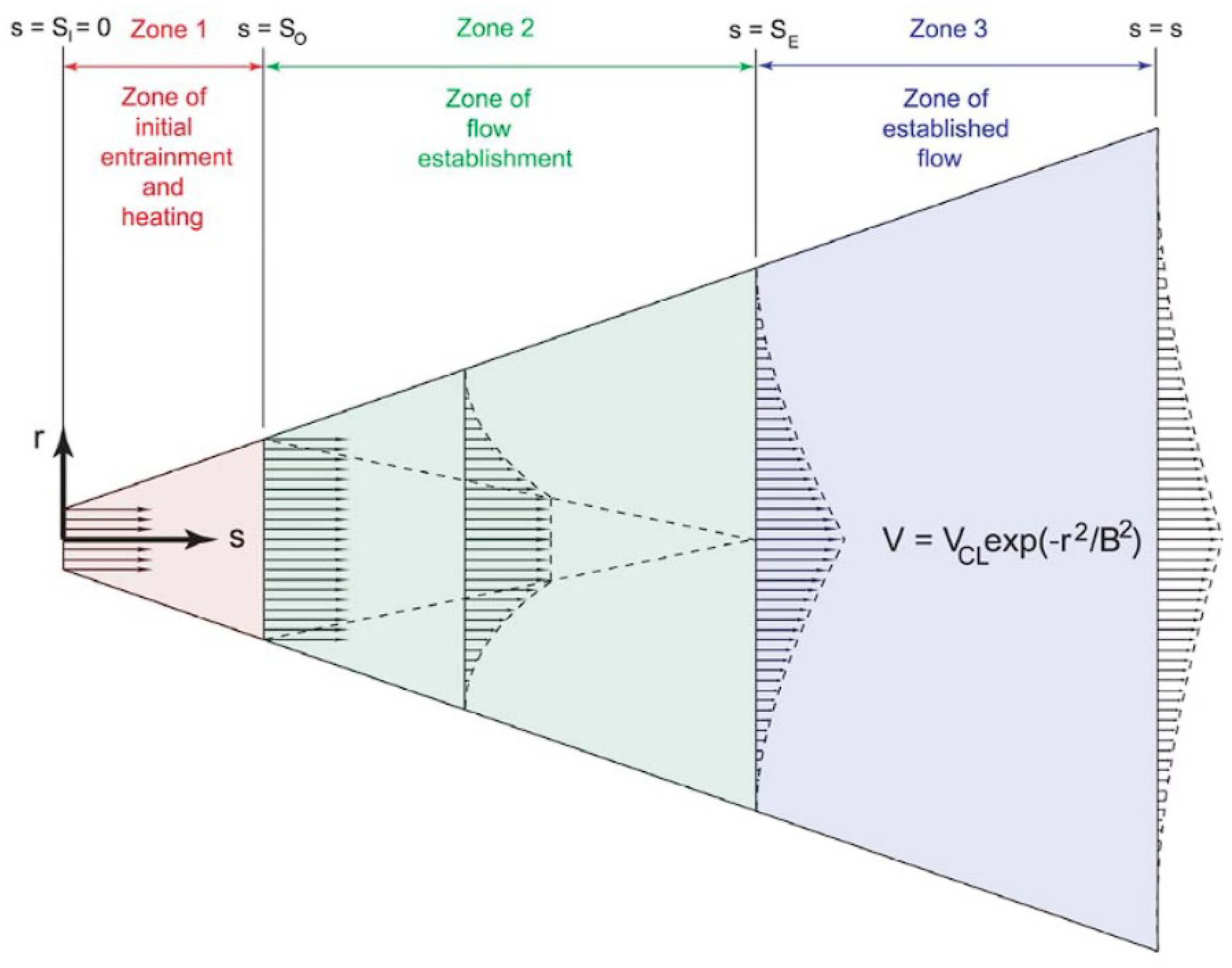
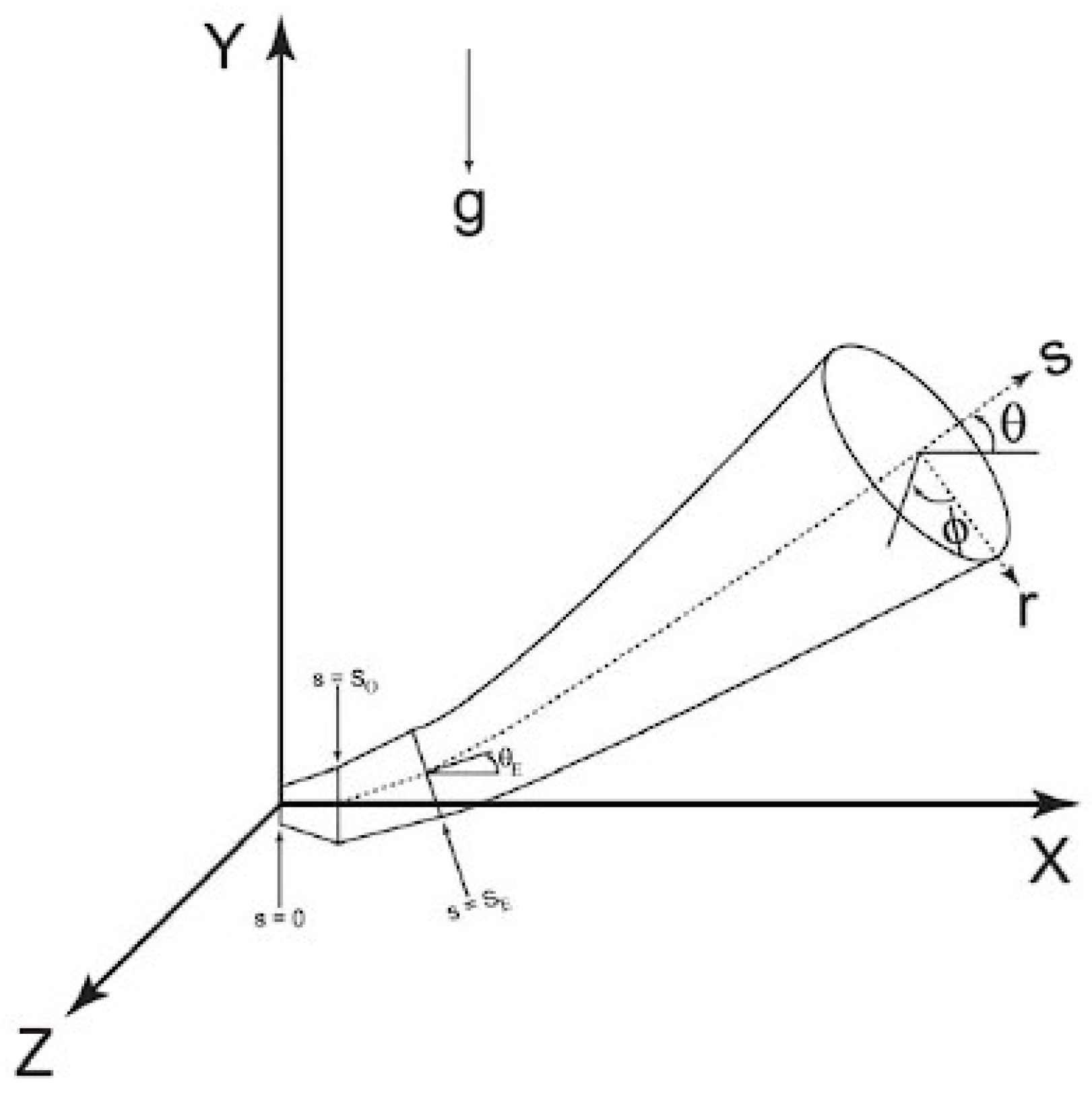
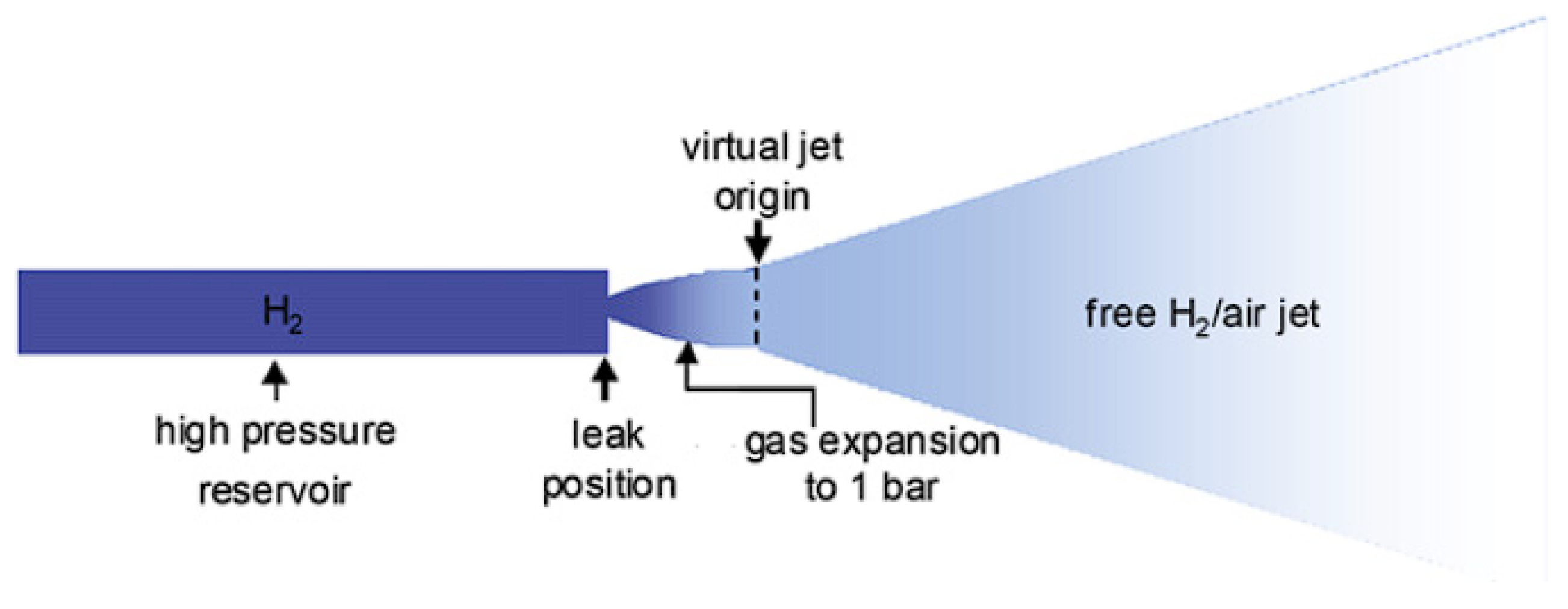
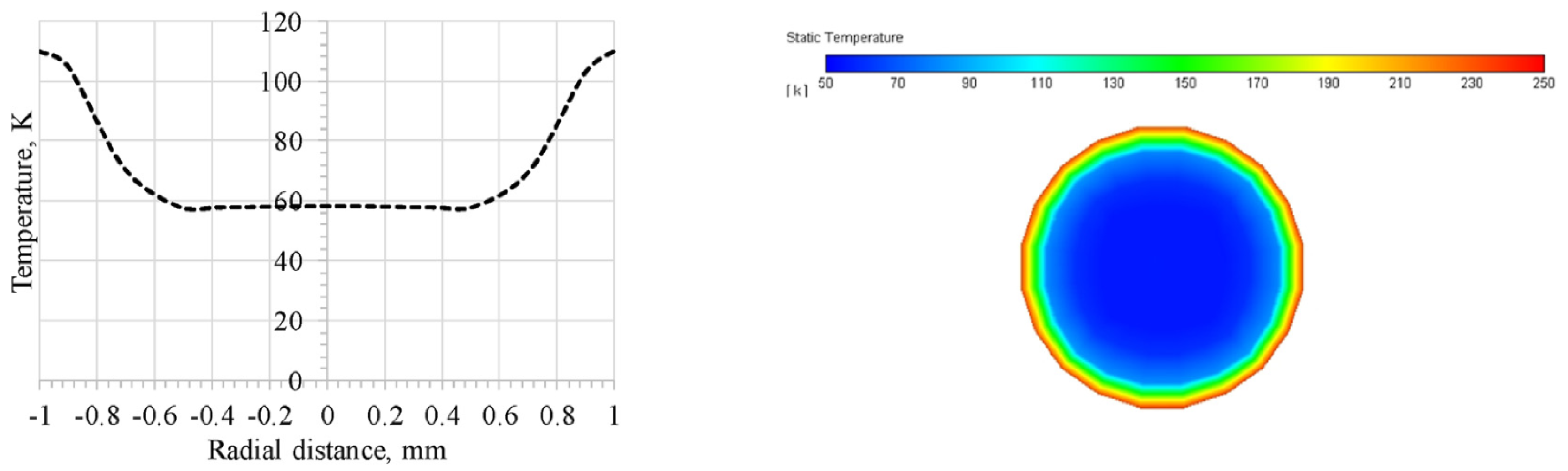
2.1. The Underexpanded Jet
2.2. Hydrogen Jet Theoretical Studies
3. Overview of Experimental Studies
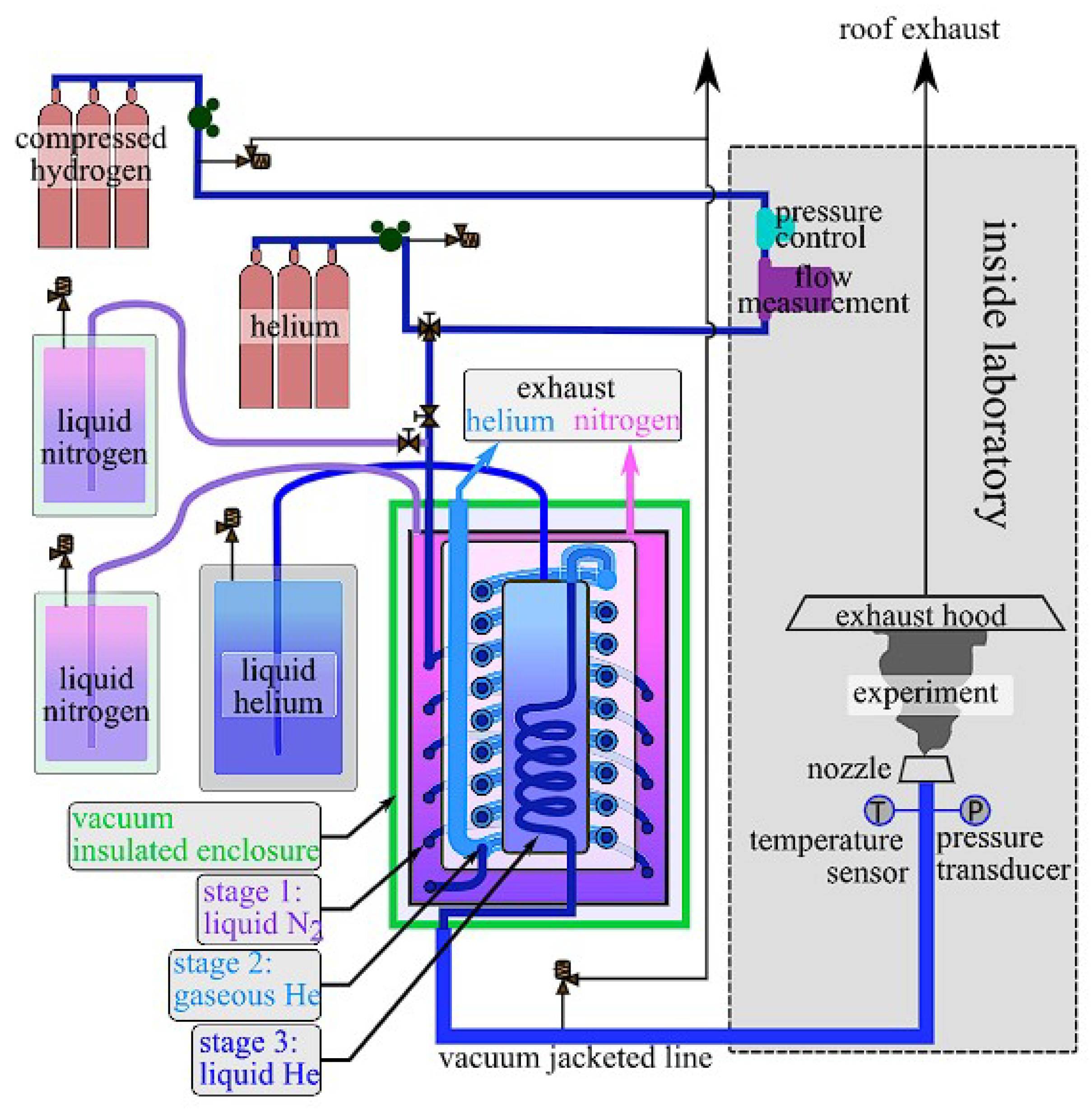
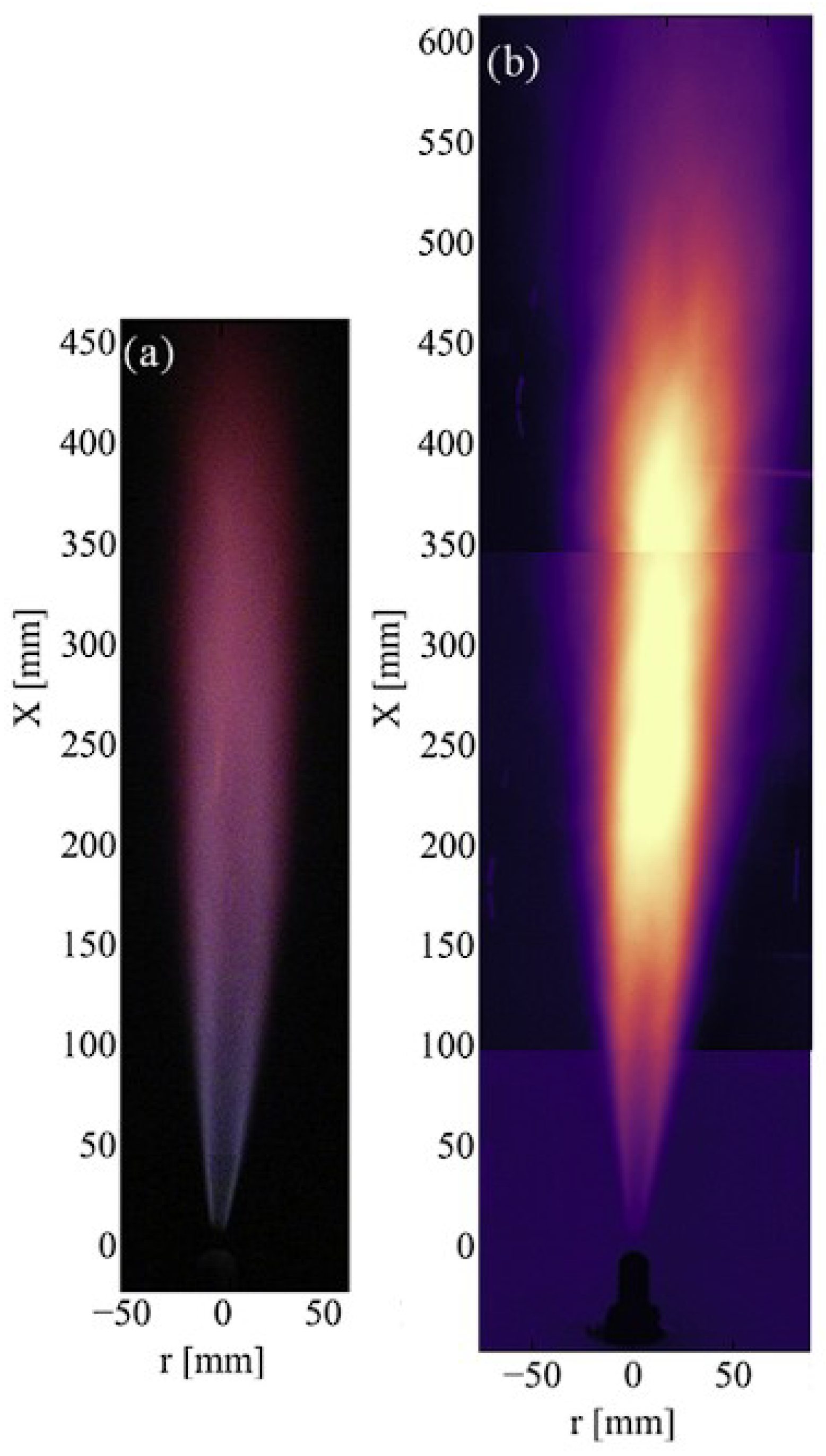
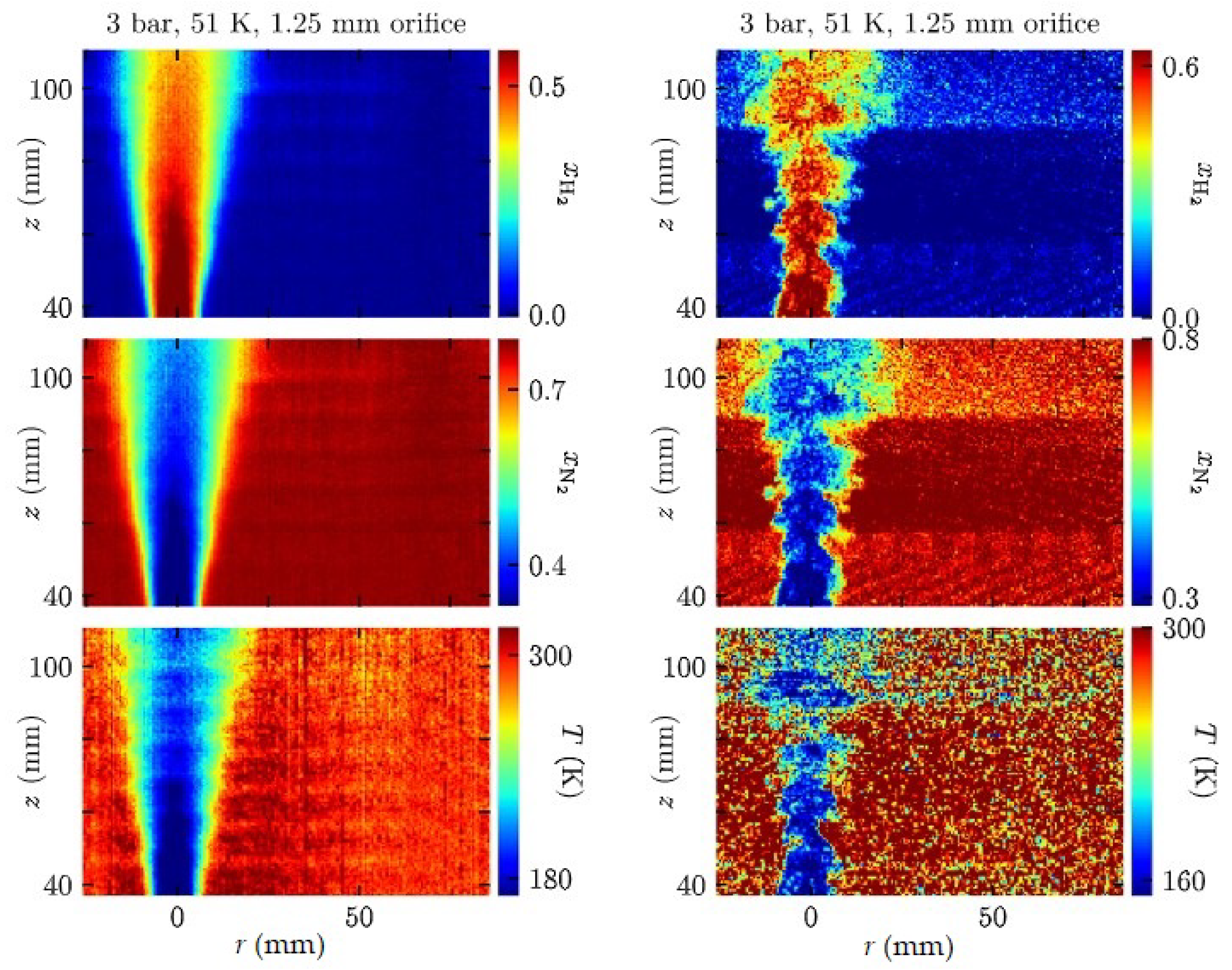
3.1. Sandia National Laboratories (SNL)
3.2. Karlsruhe Institute for Technology (KIT)
3.3. New Energy and Industrial Technology Development Organization (NEDO)
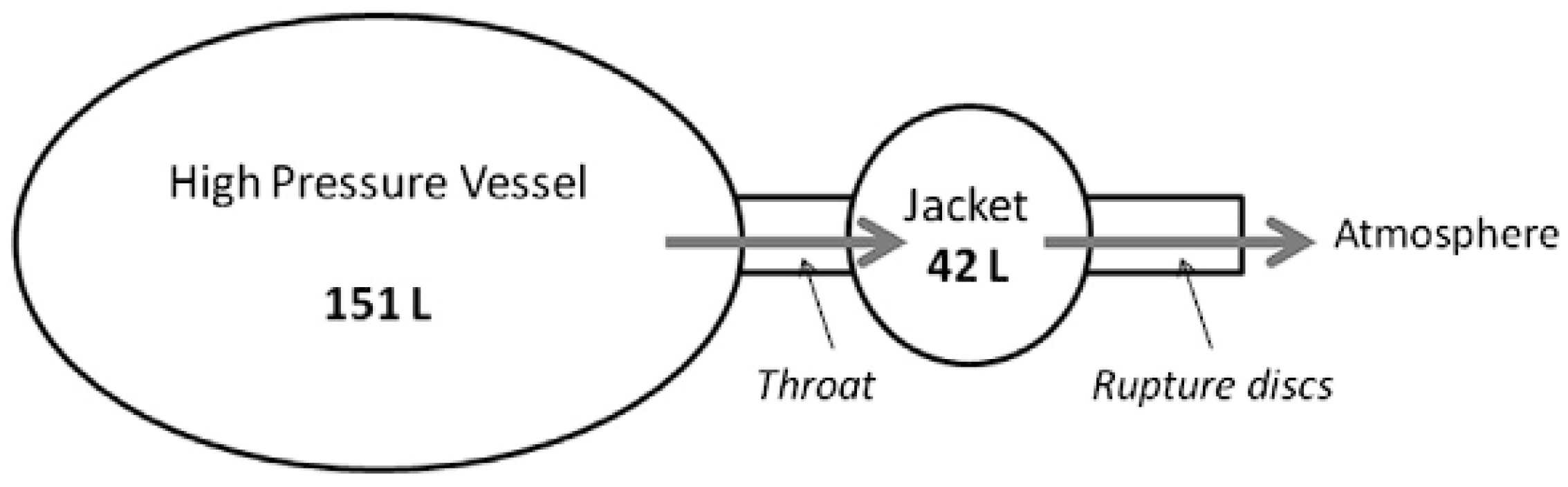
3.4. Health and Safety Executive (HSE) Science and Research Centre
3.5. National Aeronautics and Space Administration (NASA)
3.6. Additional Experimental Studies
4. Overview of Numerical Simulation Studies
4.1. Equations of State
4.2. Multiphase Flow Models
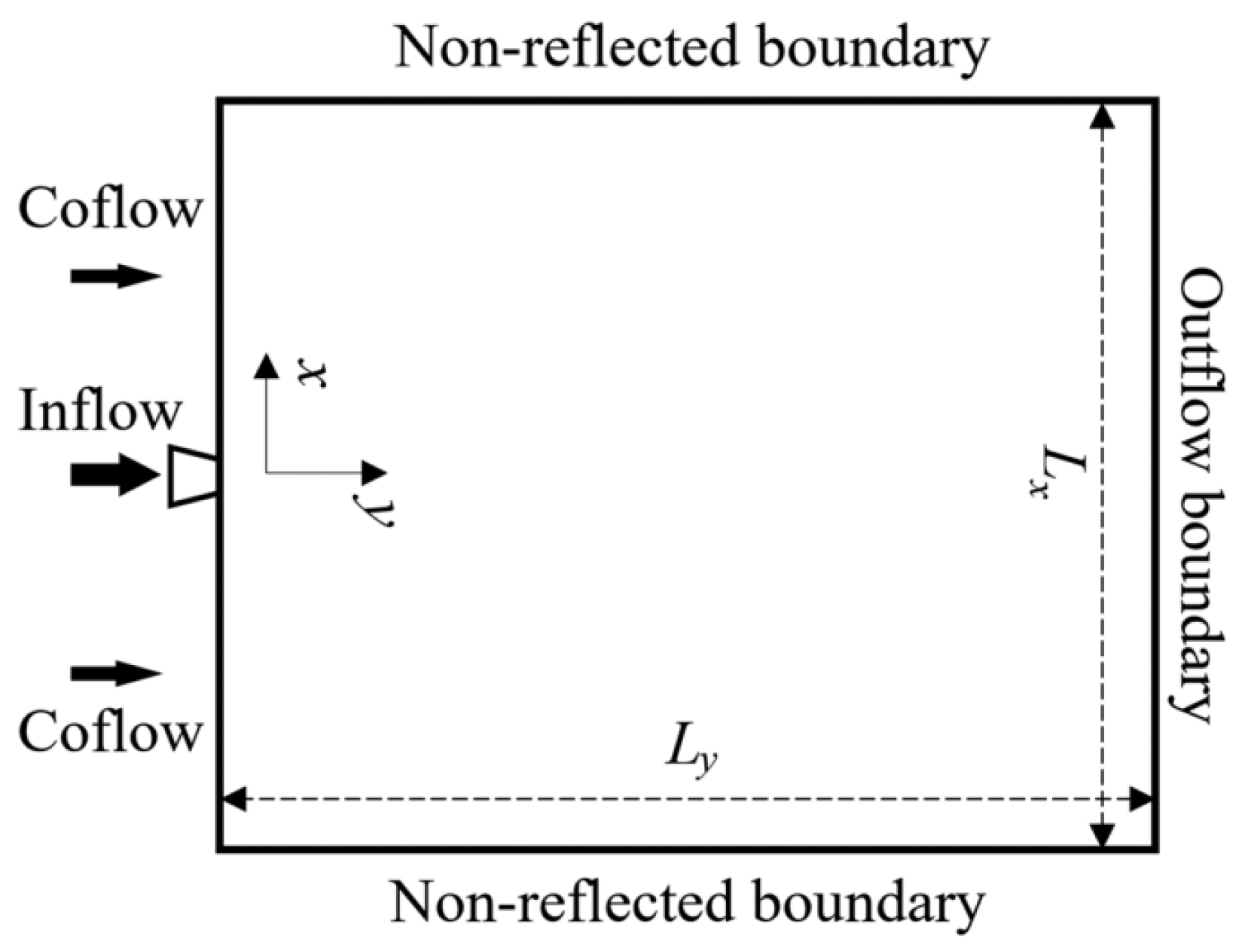
4.3. Unignited Hydrogen Jet
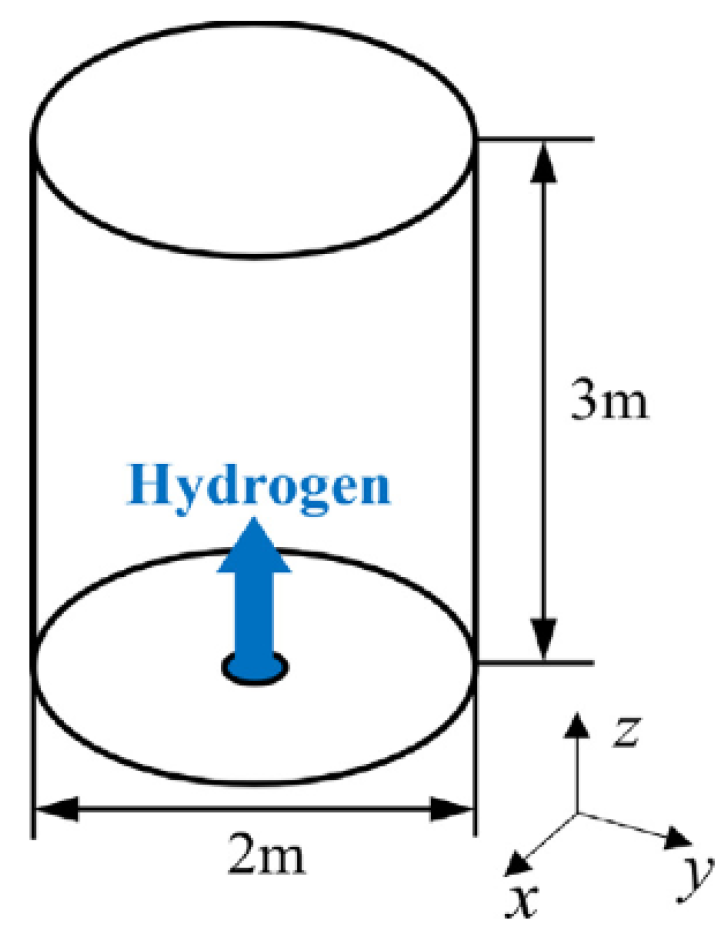
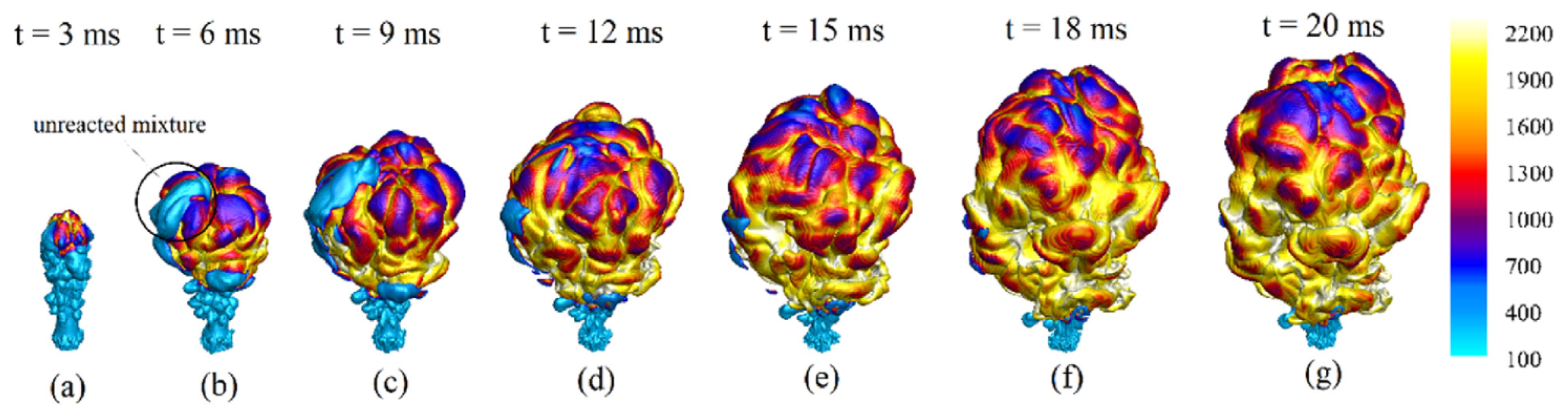
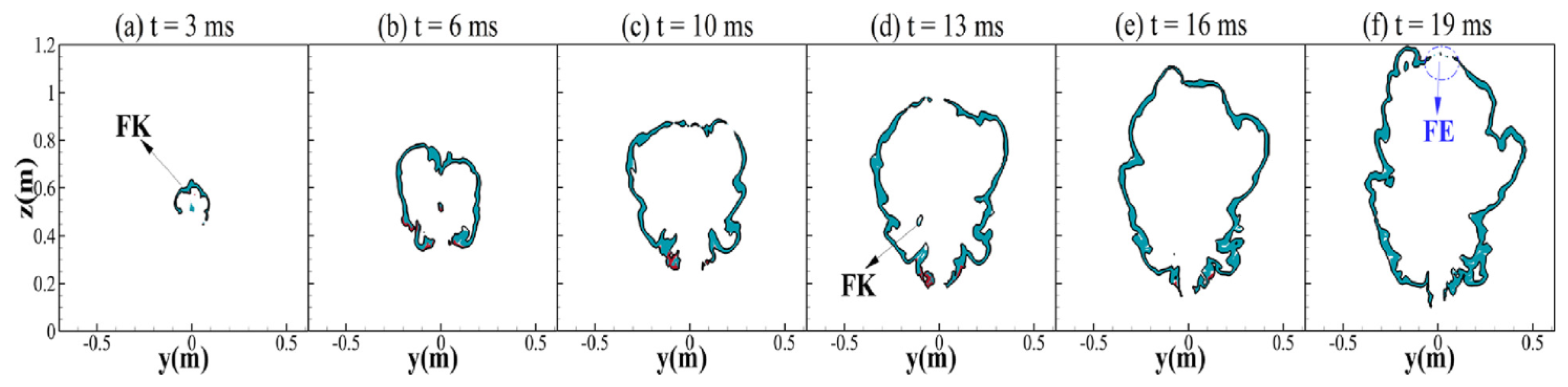
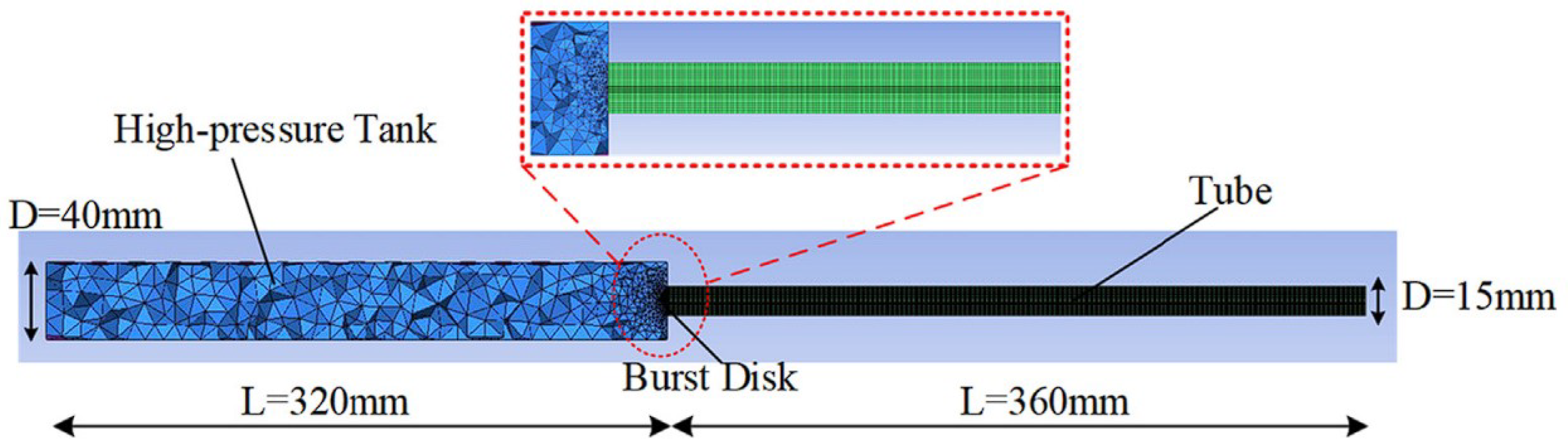
4.4. Ignited Hydrogen Jet and Flame
5. Conclusions
5.1. Summary and Current Progress
5.2. Challenges for Future Research
5.2.1. Experiments
5.2.2. Numerical Simulations
- There is a lack of a database containing all hydrogen release experiments for numerical model validation;
- There are few simulations carried out on real, industrial-scale problems with complex geometry and variable weather conditions;
- There are few studies on highly underexpanded hydrogen jets;
- There are few studies on multiphase hydrogen jets;
- There are few studies that account for the non-ideal behaviour of liquid and gaseous hydrogen at very low temperatures;
- There are few studies that investigate indoor confined hydrogen flames and fires;
- There does not exist a CFD model evaluation and validation protocol for hydrogen safety that is similar to that for liquefied natural gas (LNG) [128].
Funding
Conflicts of Interest
Abbreviations
| LH2 | Liquid Hydrogen |
| EoS | Equation of State |
| SNL | Sandia National Laboratories |
| KIT | Karlsruhe Institute of Technology |
| NASA | National Aeronautics and Space Administration |
| CFD | Computational Fluid Dynamics |
| RANS | Reynolds-Averaged Navier–Stokes |
| LES | Large-Eddy Simulation |
References
- Callendar, G.S. The artificial production of carbon dioxide and its influence on temperature. J. R. Meteorol. Soc. 1938, 64, 223–240. [Google Scholar] [CrossRef]
- UK Government. Net Zero Strategy: Build Back Greener; UK Government: London, UK, 2021.
- Department for Transport. Jet Zero Consultation: Summary of Responses and Government Response; UK Government: London, UK, 2022.
- Department for Transport. Decarbonising Transport: A Better, Greener Britain; UK Government: London, UK, 2021.
- UK Government. UK Hydrogen Strategy; UK Government: London, UK, 2021.
- Crowl, D.; Jo, Y.-D. The hazards and risks of hydrogen. J. Loss Prev. Process. Ind. 2007, 20, 158–164. [Google Scholar] [CrossRef]
- Acar, C.; Dincer, I. Review and evaluation of hydrogen production options for better environment. J. Clean. Prod. 2019, 218, 835–849. [Google Scholar] [CrossRef]
- Acar, C.; Dincer, I. Review and evaluation of hydrogen production methods for better sustainability. Int. J. Hydrogen Energy 2015, 40, 11094–11111. [Google Scholar]
- Holladay, J.; Hu, J.; King, D.; Wang, Y. An overview of hydrogen production technologies. Catal. Today 2009, 139, 244–260. [Google Scholar] [CrossRef]
- Nikolaidis, P.; Poulikkas, A. A comparative overview of hydrogen production processes. Renew. Sustain. Energy Rev. 2017, 67, 597–611. [Google Scholar] [CrossRef]
- Abdalla, A.M.; Hossain, S.; Nisfindy, O.B.; Azad, A.T.; Dawood, M.; Azad, A.K. Hydrogen production, storage, transportation and key challenges with applications: A review. Energy Conserv. Manag. 2018, 165, 602–627. [Google Scholar] [CrossRef]
- Watson, E. The First Hydrogen Balloon. Eng. Sci. 1946, 9, 12–16. [Google Scholar]
- Eckener, H. Count Zeppelin: The Man and His Work; Massie Publishing Company Limited: Auckland, New Zealand, 1938. [Google Scholar]
- DiLisi, G. The Hindenburg Disaster: Combining Physics and History in the Laboratory. Phys. Teach. 2017, 55, 268–273. [Google Scholar] [CrossRef]
- Mattingly, J. Elements of Gas Turbine Propulsion; McGraw-Hill: New York, NY, USA, 2017; Volume 1. [Google Scholar]
- Sloop, J. Liquid Hydrogen as a Propulsion Fuel, 1945–1959; Scientific and Technical Information Office, NASA: Hampton, VI, USA, 1978; Volume 4404.
- Heald, D. 50 Years of Atlas Propulsion Systems. In Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Hartford, CT, USA, 21–23 July 2008; Volume 44, p. 5223. [Google Scholar]
- Khandelwal, B. Hydrogen powered aircraft: The future of air transport. Prog. Aerosp. Sci. 2013, 60, 45–59. [Google Scholar] [CrossRef]
- Heinz, G.; Faass, K. CRYOPLANE: Hydrogen fuelled aircraft—Status and challenges. Air Space Eur. 2001, 3, 252–254. [Google Scholar]
- Boyce, R.; Gerard, S.; Paull, A. The HyShot Scramjet Flight Experiment—Flight Data and CFD Calculations Compared. AIAA Int. Space Planes Hypersonic Syst. Technol. 2003, 12, 7029. [Google Scholar]
- McClinton, C. Preliminary X-43 flight test results. Acta Astronaut. 2005, 57, 266–276. [Google Scholar] [CrossRef]
- Mills, G.; Buchholtz, B.; Olsen, A. Design, fabrication and testing of a liquid hydrogen fuel tank for a long duration aircraft. AIP Conf. Proc. 2012, 1434, 773–780. [Google Scholar]
- Yilmaz, I. Investigation of hydrogen usage in aviation industry. Energy Conserv. Manag. 2012, 63, 63–69. [Google Scholar] [CrossRef]
- Bruce, S.; Temminghoff, M.; Hayward, J.; Palfreyman, D.; Munnings, C.; Burke, N.; Creasey, S. Opportunities for Hydrogen in Aviation; CSIRO: Canberra, NSW, Australia, 2020.
- Bicer, Y.; Dincer, I. Life cycle evaluation of hydrogen and other potential fuels for aircrafts. Int. J. Hydrogen Energy 2017, 42, 10722–10738. [Google Scholar] [CrossRef]
- Contreras, A. Hydrogen as aviation fuel: A comparison with hydrocarbon fuels. Int. J. Hydrogen Energy 1997, 22, 1053–1060. [Google Scholar] [CrossRef]
- Baroutaji, A.; Wilberforce, T.; Ramadan, M.; Olabi, A.G. Comprehensive investigation on hydrogen and fuel cell technology in the aviation and aerospace sectors. Renew. Sustain. Energy Rev. 2019, 106, 31–40. [Google Scholar] [CrossRef]
- Petrescu, R.; Machin, A.; Fontanez, K.; Arango, J.C.; Marquez, F.M.; Petrescu, F.I.T. Hydrogen for aircraft power and propulsion. Int. J. Hydrogen Energy 2020, 45, 20740–20764. [Google Scholar] [CrossRef]
- Rondinelli, S.; Gardi, A.; Kapoor, R.; Sabatini, R. Benefits and challenges of liquid hydrogen fuels in commercial aviation. Int. J. Sustain. Aviat. 2017, 3, 200–211. [Google Scholar] [CrossRef]
- Hua, T.; Ahluwalia, R.K.; Peng, J.K.; Kromer, M.; Lasher, S.; McKenney, K.; Law, K.; Sinha, J. Technical assessment of compressed hydrogen storage tank systems for automotive applications. Int. J. Hydrogen Energy 2011, 36, 3037–3049. [Google Scholar] [CrossRef]
- Yanxing, Z.; Maoqiong, G.; Yuan, Z.; Xueqiang, D.; Jun, S. Thermodynamics analysis of hydrogen storage based on compressed gaseous hydrogen, liquid hydrogen and cryo-compressed hydrogen. Int. J. Hydrogen Energy 2019, 44, 16833–16840. [Google Scholar] [CrossRef]
- Aceves, S.; Petitpas, G.; Espinosa-Loza, F.; Matthews, M.J.; Ledesma-Orozco, E. Safe, long range, inexpensive and rapidly refuelable hydrogen vehicles with cryogenic pressure vessels. Int. J. Hydrogen Energy 2013, 38, 2480–2489. [Google Scholar] [CrossRef]
- Ahluwalia, R.; Hua, T.Q.; Peng, J.K.; Lasher, S.; McKenney, K.; Sinha, J.; Gardiner, M. Technical assessment of cryo-compressed hydrogen storage tank systems for automotive applications. Int. J. Hydrogen Energy 2010, 35, 4171–4184. [Google Scholar] [CrossRef]
- Petitpas, G.; Aceves, S. Modeling of sudden hydrogen expansion from cryogenic pressure vessel failure. Int. J. Hydrogen Energy 2013, 38, 8190–8198. [Google Scholar] [CrossRef]
- Winnefeld, C.; Kadyk, T.; Bensmann, B.; Krewer, U.; Hanke-Rauschenbach, R. Modelling and Designing Cryogenic Hydrogen Tanks for Future Aircraft Applications. Energies 2018, 11, 105. [Google Scholar] [CrossRef]
- Sorensen, B. Hydrogen and Fuel Cells: Emerging Technologies and Applications; Academic Press: Cambridge, MA, USA, 2018; Volume 3. [Google Scholar]
- Abohamzeh, E. Review of hydrogen safety during storage, transmission, and applications processes. J. Loss Prev. Process. Ind. 2021, 72, 104569. [Google Scholar] [CrossRef]
- Groth, K.; Hecht, E. HyRAM: A methodology and toolkit for quantitative risk assessment of hydrogen systems. Int. J. Hydrogen Energy 2017, 42, 7485–7493. [Google Scholar] [CrossRef]
- Franquet, E.; Perrier, V.; Gibout, S.; Bruel, P. Free underexpanded jets in a quiescent medium: A review. Prog. Aerosp. Sci. 2015, 77, 25–53. [Google Scholar] [CrossRef]
- Cumber, P.; Fairweather, M.; Falle, S.A.E.G.; Giddings, J.R. Predictions of the structure of turbulent, moderately underexpanded jets. J. Fluids Eng. 1994, 116, 707–713. [Google Scholar] [CrossRef]
- Cumber, P.; Fairweather, M.; Falle, S.A.E.G.; Giddings, J.R. Predictions of the structure of turbulent, highly underexpanded jets. J. Fluids Eng. 1995, 117, 599–604. [Google Scholar] [CrossRef]
- Ewan, B.; Moodie, K. Structure and velocity measurements in underexpanded jets. Combust. Sci. Technol. 1986, 45, 275–288. [Google Scholar] [CrossRef]
- Winters, W. Modeling Leaks from Liquid Hydrogen Storage Systems; Sandia National Laboratories: Albuquerque, NM, USA, 2009.
- Winters, W.; Houf, W. Simulation of small-scale releases from liquid hydrogen storage systems. Int. J. Hydrogen Energy 2011, 36, 3913–3921. [Google Scholar] [CrossRef]
- Schefer, R.; Houf, W. Analytical and experimental investigation of small-scale unintended releases of hydrogen. Int. J. Hydrogen Energy 2008, 33, 1435–1444. [Google Scholar]
- Winters, W.; Evans, G. Final Report for the ASC Gas-Powder Two-Phase Flow Modeling Project AD2006-09; Sandia National Laboratories: Albuquerque, NM, USA, 2007.
- Winters, W.; Houf, W. Simulation of High-Pressure Liquid Hydrogen Releases; Sandia National Laboratories: Albuquerque, NM, USA, 2013.
- Xiao, J.; Travis, J.; Breitung, W. Hydrogen release from a high pressure gaseous hydrogen reservoir in case of a small leak. Int. J. Hydrogen Energy 2011, 36, 2545–2554. [Google Scholar] [CrossRef]
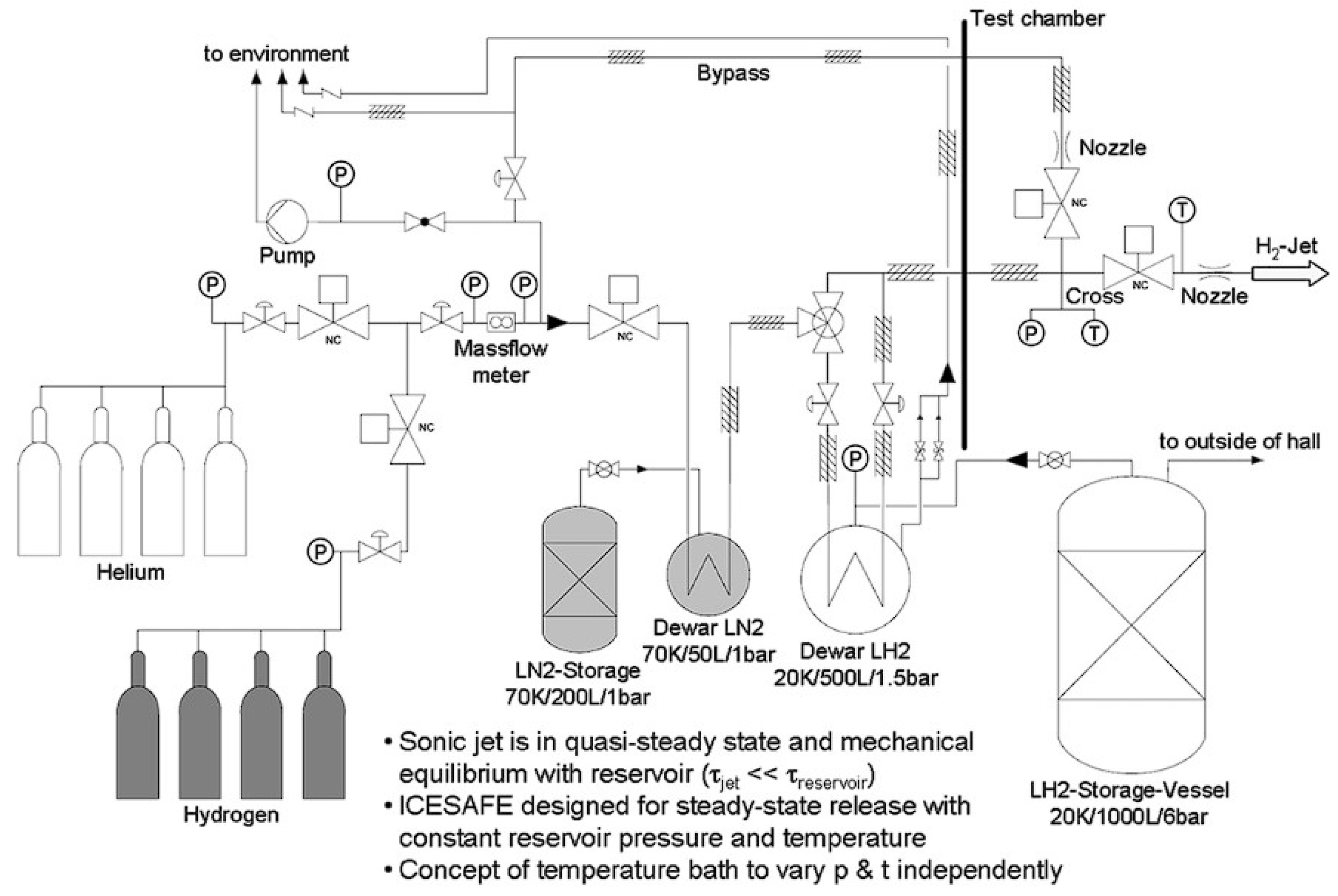
- Venetsanos, A.; Cirrone, D.; Coldrick, S.; Giannissi, S.; Jordan, T.; Mauri, L.; Molkov, V.; Xiao, J. Theory and Analysis of Cryogenic Hydrogen Release and Dispersion. Preshly Deliv. D 2019, 3, 1. [Google Scholar]
- Lyons, K. Theory and analysis of ignition with specific conditions related to cryogenic hydrogen. Preshly 2020. [Google Scholar]
- Correa-Jullian, C.; Groth, K. Data requirements for improving the Quantitative Risk Assessment of liquid hydrogen storage systems. Int. J. Hydrogen Energy 2022, 47, 4222–4235. [Google Scholar] [CrossRef]
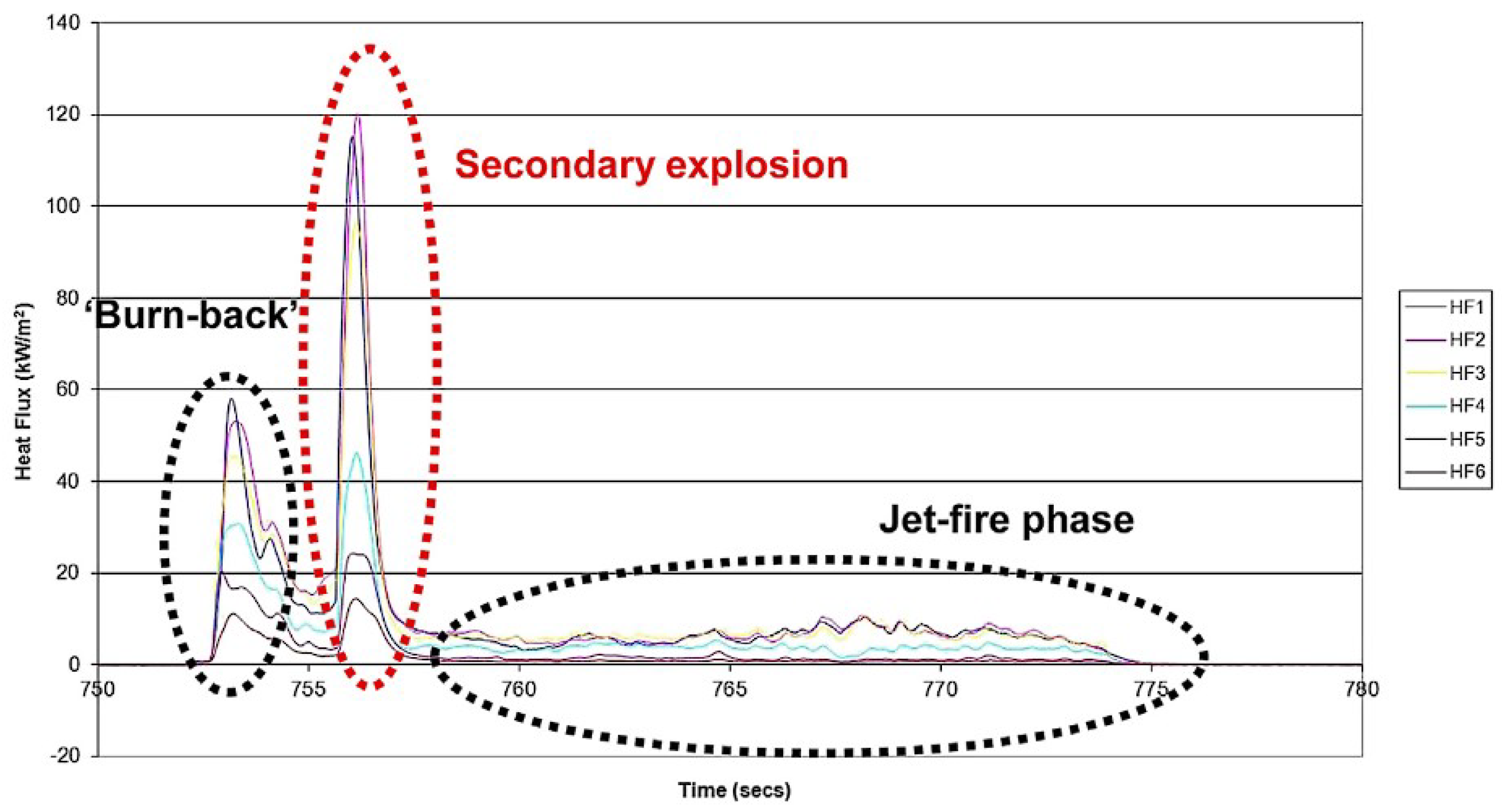
- Cirrone, D.; Makarov, D.; Friedrich, A.; Grune, J.; Takeno, K.; Molkov, V. Blast Wave Generated by Delayed Ignition of Under-Expanded Hydrogen Free Jet at Ambient and Cryogenic Temperatures. Hydrogen 2022, 3, 433–449. [Google Scholar] [CrossRef]
- Hecht, E.; Panda, P. Ignition and flame characteristics of cryogenic hydrogen releases. Int. J. Hydrogen Energy 2017, 42, 775–785. [Google Scholar]
- Hecht, E.; Panda, P.; Chowdhury, B.; Ye, D. Characteristics of Cryogenic Hydrogen Releases Under Unignited and Ignited Conditions; Sandia National Laboratories: Albuquerque, NM, USA, 2019.
- Hecht, E.; Panda, P. Mixing and warming of cryogenic hydrogen releases. Int. J. Hydrogen Energy 2019, 44, 8960–8970. [Google Scholar] [CrossRef]
- Hecht, E.; Chowdhury, B. Dispersion of Cryogenic Hydrogen Through High-Aspect Ratio Nozzles; Sandia National Laboratories: Albuquerque, NM, USA, 2019.
- Li, X.; Yao, C.; Egbert, S.C.; He, Q.; Zhao, Z.; Christopher, D.M.; Hecht, E.S. Self-similar characteristics of underexpanded, cryogenic hydrogen and methane jets. Int. J. Hydrogen Energy 2023, 48, 4104–4117. [Google Scholar] [CrossRef]
- Veser, A.; Kuznetsov, M.; Fast, G.; Friedrich, A.; Kotchourko, N.; Stern, G.; Schwall, M.; Breitung, W. The structure and flame propagation regimes in turbulent hydrogen jets. Int. J. Hydrogen Energy 2010, 36, 2351–2359. [Google Scholar] [CrossRef]
- Klinge, F.; Kirmse, T.; Kompenhans, J. Application of quantitative background oriented schlieren (BOS). In Proceedings of the PSFVIP-4, Chamonix, France, 3–5 June 2003; Volume 4097, pp. 3–5. [Google Scholar]
- Grant, I. Particle image velocimetry: A review. Proc. Inst. Mech. Eng. Part J. Mech. Eng. Sci. 2016, 211, 55–76. [Google Scholar] [CrossRef]
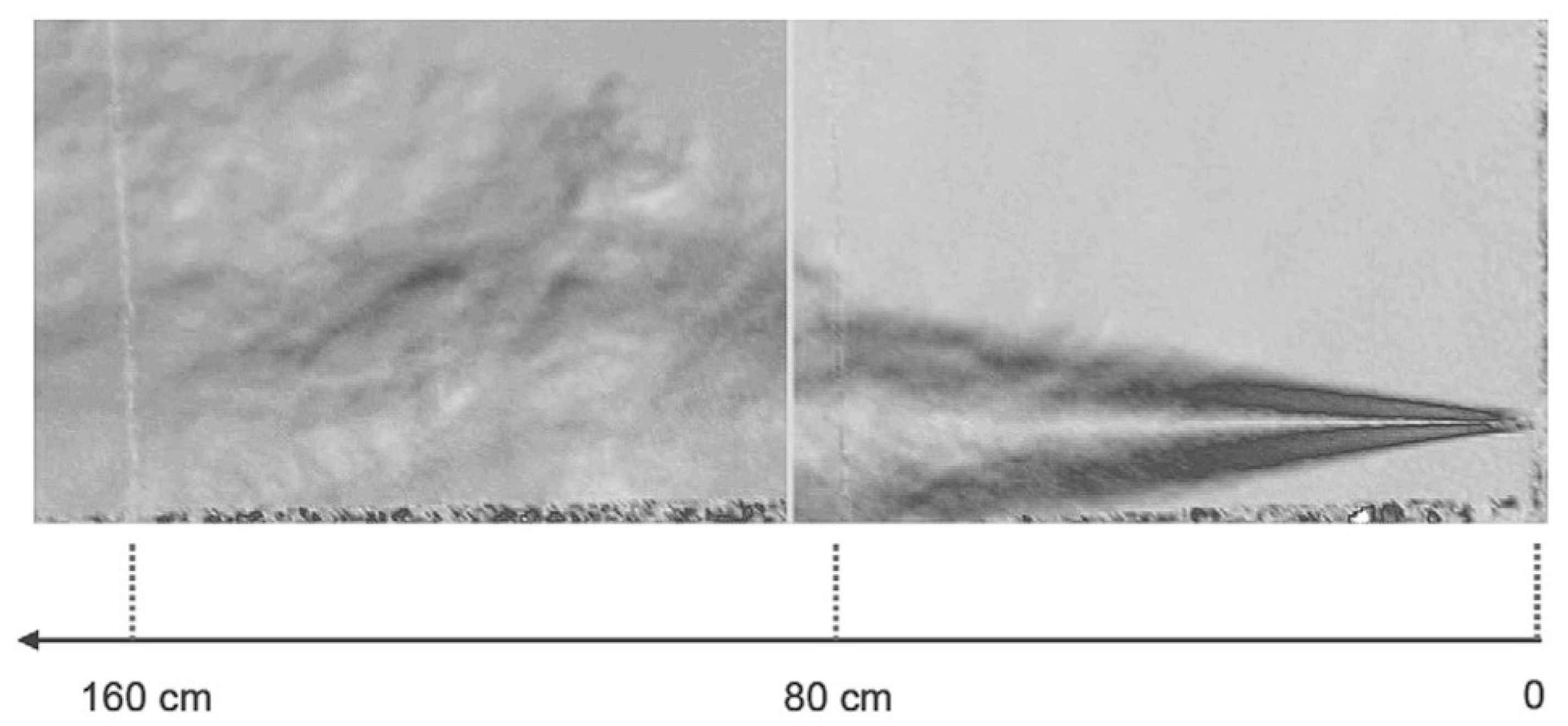
- Friedrich, A. Ignition and heat radiation of cryogenic hydrogen jets. Int. J. Hydrogen Energy 2012, 37, 17589–17598. [Google Scholar] [CrossRef]
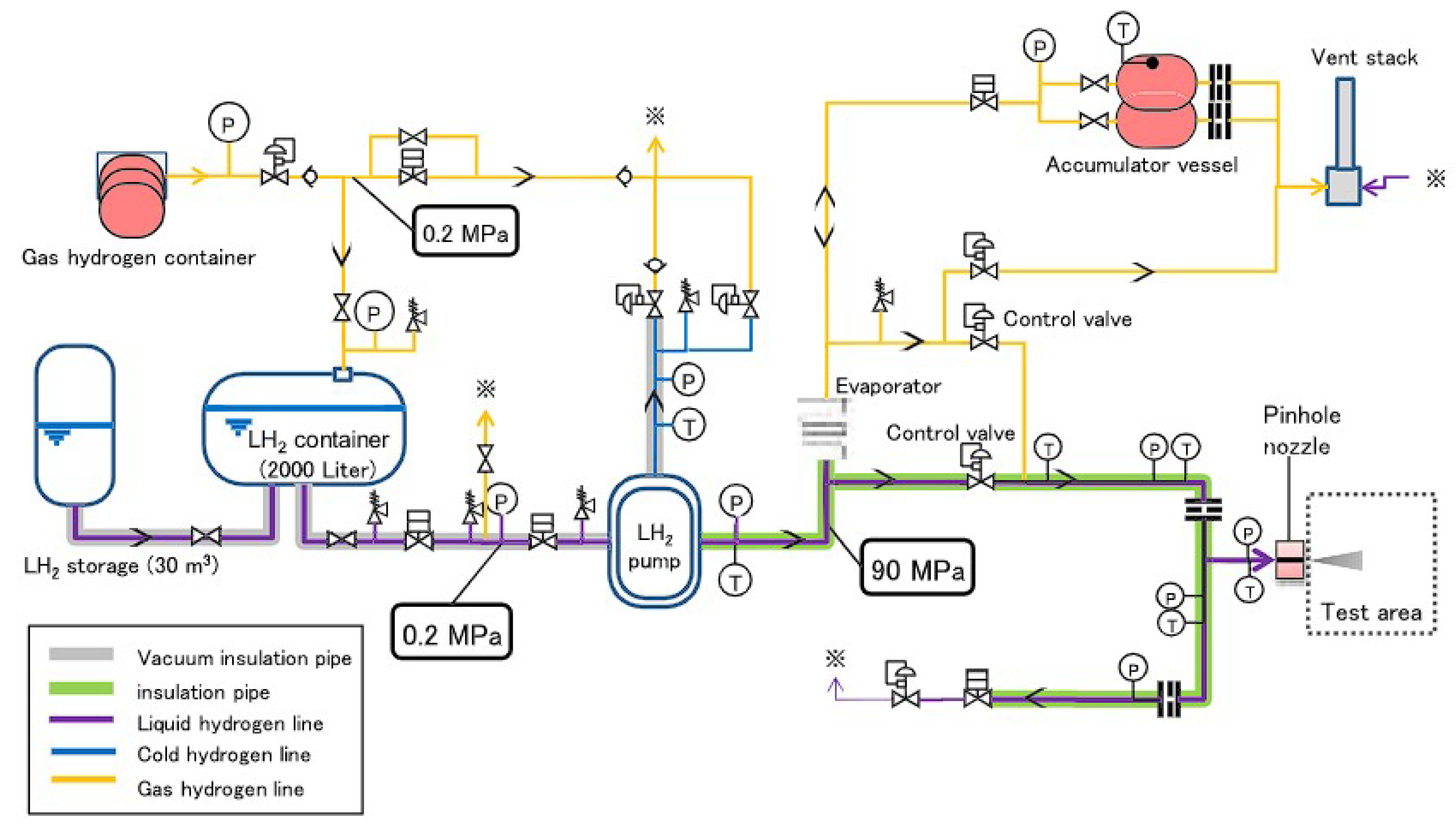
- Kobayashi, H. Experiment of cryo-compressed (90-MPa) hydrogen leakage diffusion. Int. J. Hydrogen Energy 2018, 43, 17928–17937. [Google Scholar] [CrossRef]
- Kobayashi, H. Experimental study on cryo-compressed hydrogen ignition and flame. Int. J. Hydrogen Energy 2020, 45, 5098–5109. [Google Scholar] [CrossRef]
- Hooker, P.; Willoughby, D.; Royle, M. Experimental Releases of Liquid Hydrogen. In Proceedings of the International Conference on Hydrogen Safety, San Francisco, CA, USA, 12–14 September 2011. [Google Scholar]
- Hooker, P.; Willoughby, D.; Hall, J. Ignited releases of liquid hydrogen: Safety considerations of thermal and overpressure effects. Int. J. Hydrogen Energy 2014, 39, 20547–20553. [Google Scholar]
- Cassutt, L.; Maddocks, F.; Sawyer, W. A study of the hazards in the storage and handling of liquid hydrogen. Adv. Cryog. Eng. 1960, 55–61. [Google Scholar]
- Witcofski, R.; Chirivella, J. Experimental and analytical analyses of the mechanisms governing the dispersion of flammable clouds formed by liquid hydrogen spills. Int. J. Hydrogen Energy 1984, 9, 425–435. [Google Scholar] [CrossRef]
- Nakamichi, K.; Kihara, Y.; Okamura, T. Observation of liquid hydrogen jet on flashing and evaporation characteristics. Cryogenics 2007, 48, 26–30. [Google Scholar] [CrossRef]
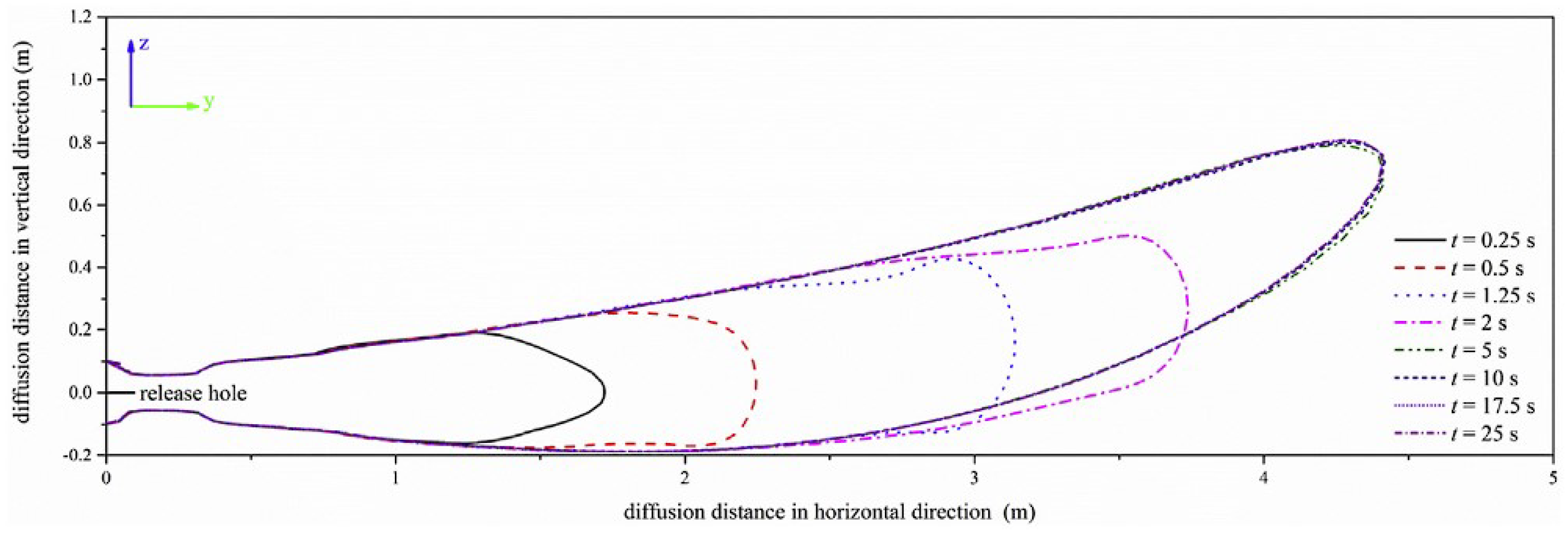
- Gong, L.; Yang, S.; Han, Y.; Jin, K.; Lu, L.; Gao, Y.; Zhang, Y. Experimental investigation on the dispersion characteristics and concentration distribution of unignited low-temperature hydrogen release. Process. Saf. Environ. Prot. 2022, 160, 676–682. [Google Scholar] [CrossRef]
- Yu, X.; Wu, Y.; Zhao, Y.; Wang, C. Flame characteristics of under-expanded, cryogenic hydrogen jet fire. Combust. Flame 2022, 244, 112294. [Google Scholar] [CrossRef]
- Mironov, V.; Penyazkov, O.; Ignatenko, D. Self-ignition and explosion of a 13-MPa pressurized unsteady hydrogen jet under atmospheric conditions. Int. J. Hydrogen Energy 2015, 40, 5749–5762. [Google Scholar] [CrossRef]
- Kitabayashi, N.; Wada, Y.; Mogi, T.; Saburi, T.; Hayashi, A.K. Experimental study on high pressure hydrogen jets coming out of tubes of 0.1–4.2 m in length. Int. J. Hydrogen Energy 2013, 38, 8100–8107. [Google Scholar] [CrossRef]
- Duan, Q.; Xiao, H.; Gao, W.; Wang, Q.; Shen, X.; Jiang, L.; Sun, J. An experimental study on shock waves and spontaneous ignition produced by pressurized hydrogen release through a tube into atmosphere. Int. J. Hydrogen Energy 2015, 40, 8281–8289. [Google Scholar] [CrossRef]
- Kessler, A.; Schreiber, A.; Wassmer, C.; Deimling, L.; Knapp, S.; Weiser, V.; Sachsenheimer, K.; Langer, G.; Eisenreich, N. Ignition of hydrogen jet fires from high pressure storage. Int. J. Hydrogen Energy 2014, 39, 20554–20559. [Google Scholar] [CrossRef]
- Fortov, V. Thermodynamics and Equations of State for Matter: From Ideal Gas to Quark-Gluon Plasma; World Scientific: Singapore, 2016. [Google Scholar]
- Chiapolino, A.; Boivin, P.; Saurel, R. A simple phase transition relaxation solver for liquid–vapor flows. Int. J. Numer. Methods Fluids 2016, 83, 583–605. [Google Scholar] [CrossRef]
- Wangxia, W.; Bing, W.; Gaoming, X. Impingement of high-speed cylindrical droplets embedded with an air/vapour cavity on a rigid wall: Numerical analysis. J. Fluid Mech. 2019, 864, 1058–1087. [Google Scholar]
- Menikoff, R.; Plohr, B. The Riemann problem for fluid flow of real materials. Rev. Mod. Phys. 1989, 61, 75. [Google Scholar] [CrossRef]
- Aslani, M.; Regele, J. A localized artificial diffusivity method to simulate compressible multiphase flows using the stiffened gas equation of state. Int. J. Numer. Methods Fluids 2018, 88, 413–433. [Google Scholar] [CrossRef]
- Haller, K.; Ventikos, Y.; Poulikakos, D. Wave structure in the contact line region during high speed droplet impact on a surface: Solution of the Riemann problem for the stiffened gas equation of state. J. Appl. Phys. 2003, 93, 3090–3097. [Google Scholar] [CrossRef]
- Neron, L.; Saurel, R. Noble-Abel/First-order virial equations of state for gas mixtures resulting of multiple condensed reactive materials combustion. Phys. Fluids 2021, 34, 016107. [Google Scholar] [CrossRef]
- Johnston, I. The Noble-Abel Equation of State: Thermodynamic Derivations for Ballistics Modelling; Defence Science and Technology Organisation Edinburgh Weapons Systems Division: Edinburgh, SA, Australia, 2005.
- Métayer, O.; Saurel, R. The Noble-Abel Stiffened-Gas equation of state. Phys. Fluids 2016, 28, 046102. [Google Scholar] [CrossRef]
- Métayer, O.; Saurel, R. Extended Noble—Abel Stiffened-Gas Equation of State for Sub-and-Supercritical Liquid-Gas Systems Far from the Critical Point. Fluids 2018, 3, 48. [Google Scholar]
- Redlich, O.; Kwong, J. On the thermodynamics of solutions. An equation of state: Fugacity of gaseous solutions. Chem. Rev. 1949, 44, 233–244. [Google Scholar] [CrossRef]
- Soave, G. Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci. 1972, 27, 1197–1203. [Google Scholar] [CrossRef]
- Peng, D.; Robinson, D. A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Patel, N.; Teja, A. A new cubic equation of state for fluids and fluid mixtures. Chem. Eng. Sci. 1982, 37, 463–473. [Google Scholar] [CrossRef]
- Beattie, J.; Ikehara, S. An Equation of State for Gas Mixtures. II. A Study of the Methods of Combination of the Constants of the Beattie-Bridgeman Equation of State. Proc. Am. Acad. Arts Sci. 1930, 64, 127–176. [Google Scholar] [CrossRef]
- Mie, G. Zur kinetischen theorie der einatomigen körper. Ann. Phys. 1903, 316, 657–697. [Google Scholar] [CrossRef]
- Gruneisen, E. Theorie des festen zustandes einatomiger elemente. Ann. Phys. 1912, 344, 257–306. [Google Scholar] [CrossRef]
- Leachman, J.W.; Jacobsen, R.T.; Penoncello, S.; Lemmon, E.W. Fundamental Equations of State for Parahydrogen, Normal Hydrogen, and Orthohydrogen. J. Phys. Chem. Ref. Data 2009, 38, 721–748. [Google Scholar] [CrossRef]
- Saurel, R.; Petitpas, F.; Abgrall, R. Modelling phase transition in metastable liquids: Application to cavitating and flashing flows. J. Fluid Mech. 2008, 607, 313–350. [Google Scholar] [CrossRef]
- Zein, A. Numerical Methods for Multiphase Mixture Conservation Laws with Phase Transition. Doctoral Dissertation, Magdeburg University, Magdeburg, Germany, 2010. [Google Scholar]
- Downar-Zapolski, P.; Bilicki, Z.; Bolle, L.; Franco, J. The non-equilibrium relaxation model for one-dimensional flashing liquid flow. Int. J. Multiph. Flow 1996, 22, 473–483. [Google Scholar] [CrossRef]
- Chiapolino, A.; Boivin, P.; Saurel, R. A simple and fast phase transition relaxation solver for compressible multicomponent two-phase flows. Comput. Fluids 2017, 150, 31–45. [Google Scholar] [CrossRef]
- Boivin, P.; Cannac, M.; le Metayer, O. A thermodynamic closure for the simulation of multiphase reactive flows. Int. J. Therm. Sci. 2019, 137, 640–649. [Google Scholar] [CrossRef]
- Boivin, P.; Deng, X. Diffuse interface modelling of reactive multi-phase flows applied to a sub-critical cryogenic jet. Appl. Math. Model. 2020, 84, 405–424. [Google Scholar]
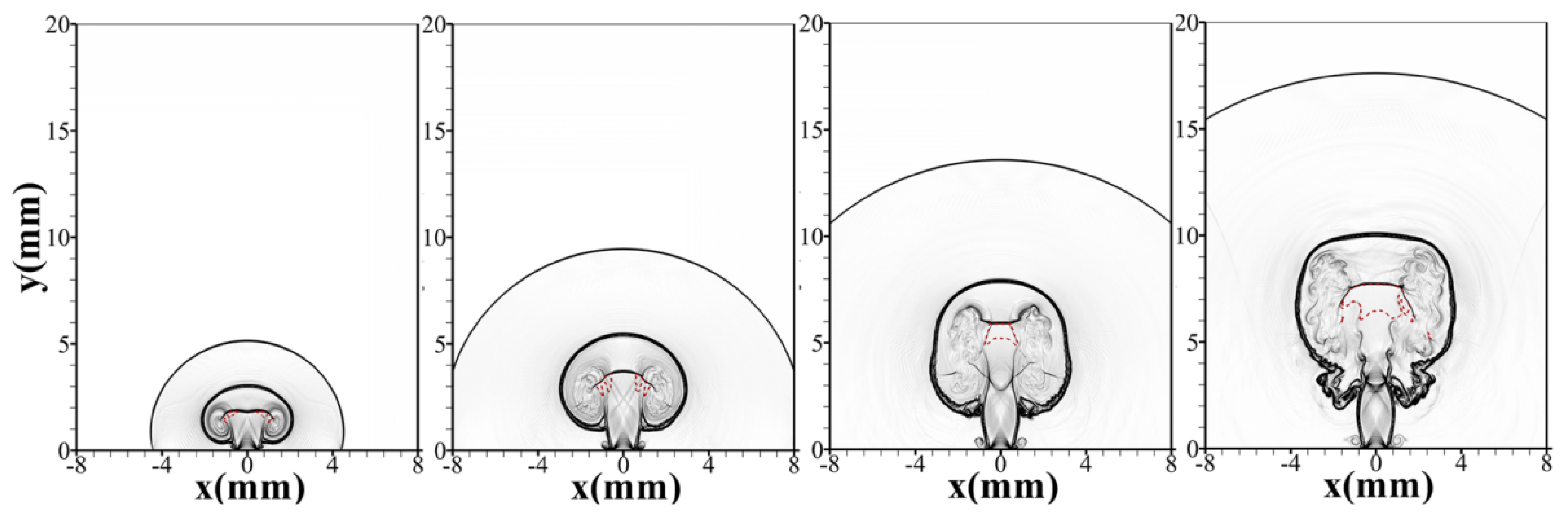
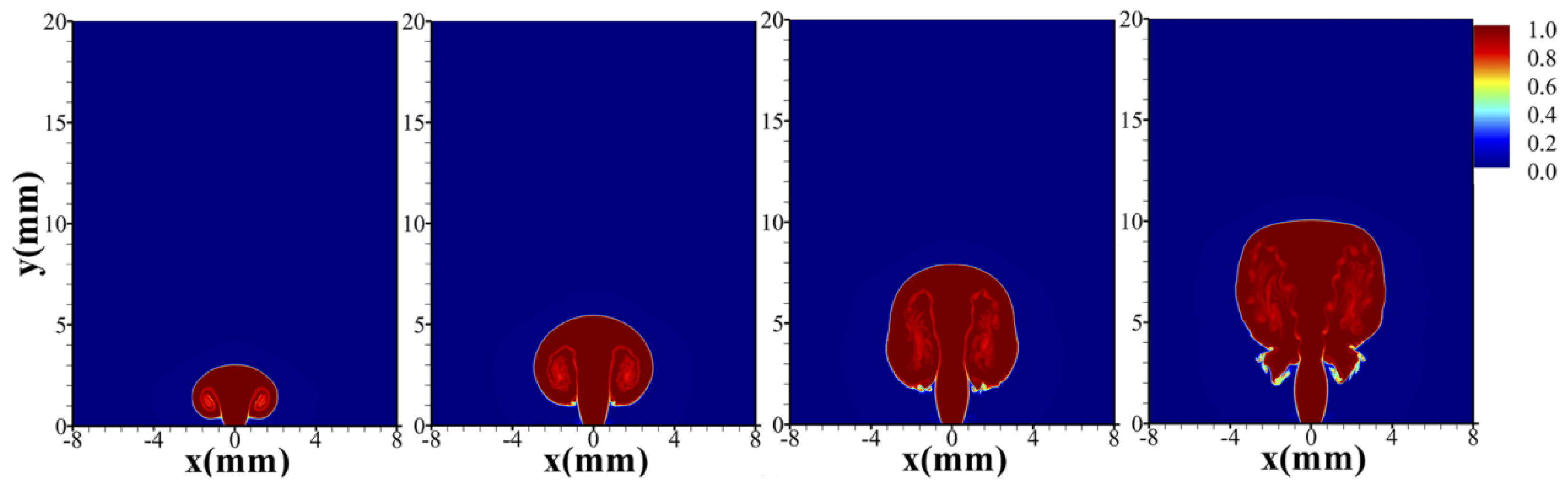
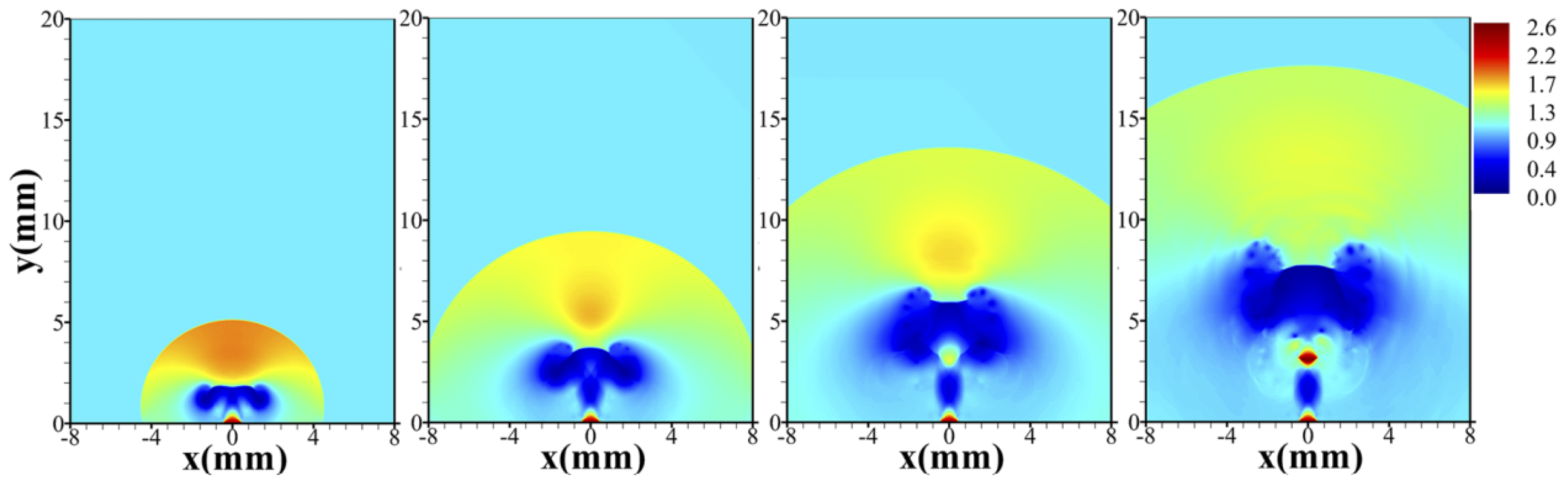
- Ren, Z.; Wen, J. Numerical characterization of underexpanded cryogenic hydrogen gas jets. AIP Adv. 2020, 10, 095303. [Google Scholar] [CrossRef]
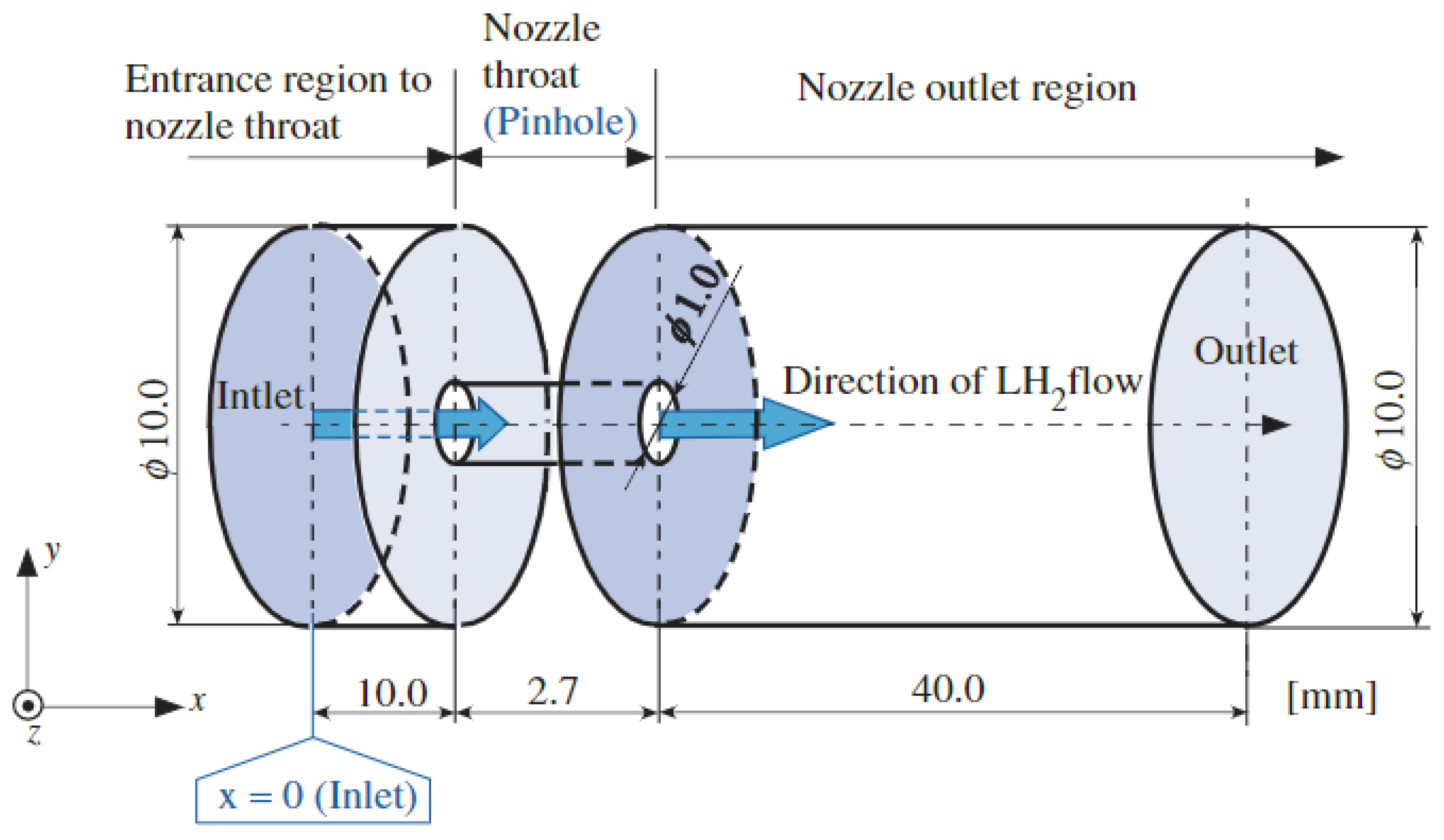
- Ishimoto, J.; Ohira, K.; Okabayashi, K.; Chitose, K. Integrated numerical prediction of atomization process of liquid hydrogen jet. Cryogenics 2008, 48, 238–247. [Google Scholar] [CrossRef]
- Dou, Y.; Sun, L.; Ren, J.; Dong, L. Opportunities and future challenges in hydrogen economy for sustainable development. Hydrogen Econ. 2023, 1, 537–569. [Google Scholar]
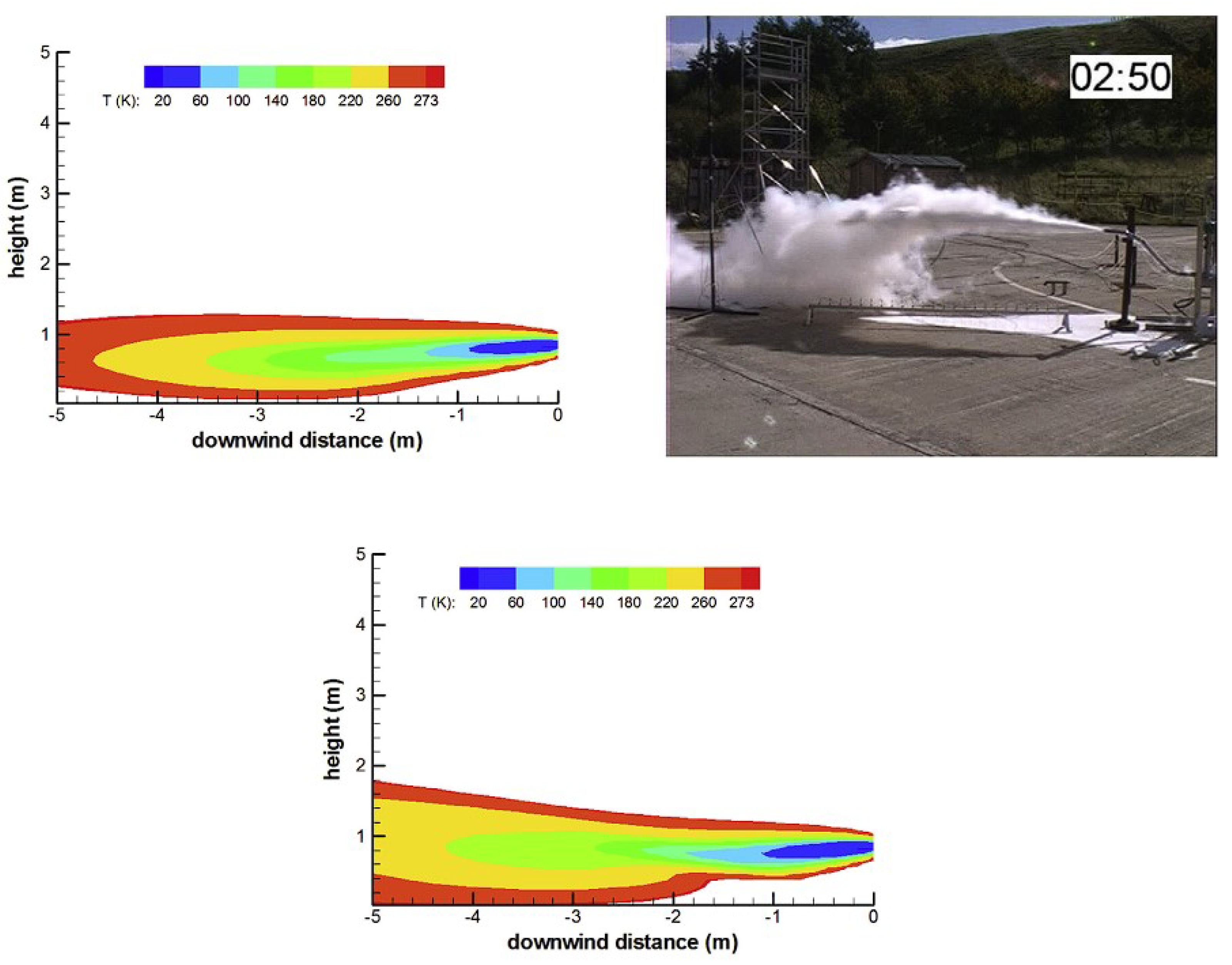
- Ichard, M.; Hansen, O.R.; Middha, P.; Willoughby, D. CFD computations of liquid hydrogen releases. Int. J. Hydrogen Energy 2006, 37, 17380–17389. [Google Scholar] [CrossRef]
- Giannissi, S.G.; Venetsanos, A.G.; Markatos, N.; Bartzis, J.G. CFD modeling of hydrogen dispersion under cryogenic release conditions. Int. J. Hydrogen Energy 2014, 39, 15851–15863. [Google Scholar] [CrossRef]
- Giannissi, S.G.; Venetsanos, A.G.; Markatos, N. Modeling of cryogenic hydrogen jets. In Proceedings of the International Conference on Hydrogen Safety, Yokohama, Japan, 14–17 October 2015. [Google Scholar]
- Giannissi, S.G.; Venetsanos, A.G. Release and dispersion modeling of cryogenic under-expanded hydrogen jets. Int. J. Hydrogen Energy 2017, 42, 7672–7682. [Google Scholar]
- Giannissi, S.G.; Venetsanos, A.G. Study of key parameters in modeling liquid hydrogen release and dispersion in open environment. Int. J. Hydrogen Energy 2018, 43, 455–467. [Google Scholar] [CrossRef]
- Giannissi, S.G.; Venetsanos, A.G. A comparative CFD assessment study of cryogenic hydrogen and LNG dispersion. Int. J. Hydrogen Energy 2019, 44, 9018–9030. [Google Scholar] [CrossRef]
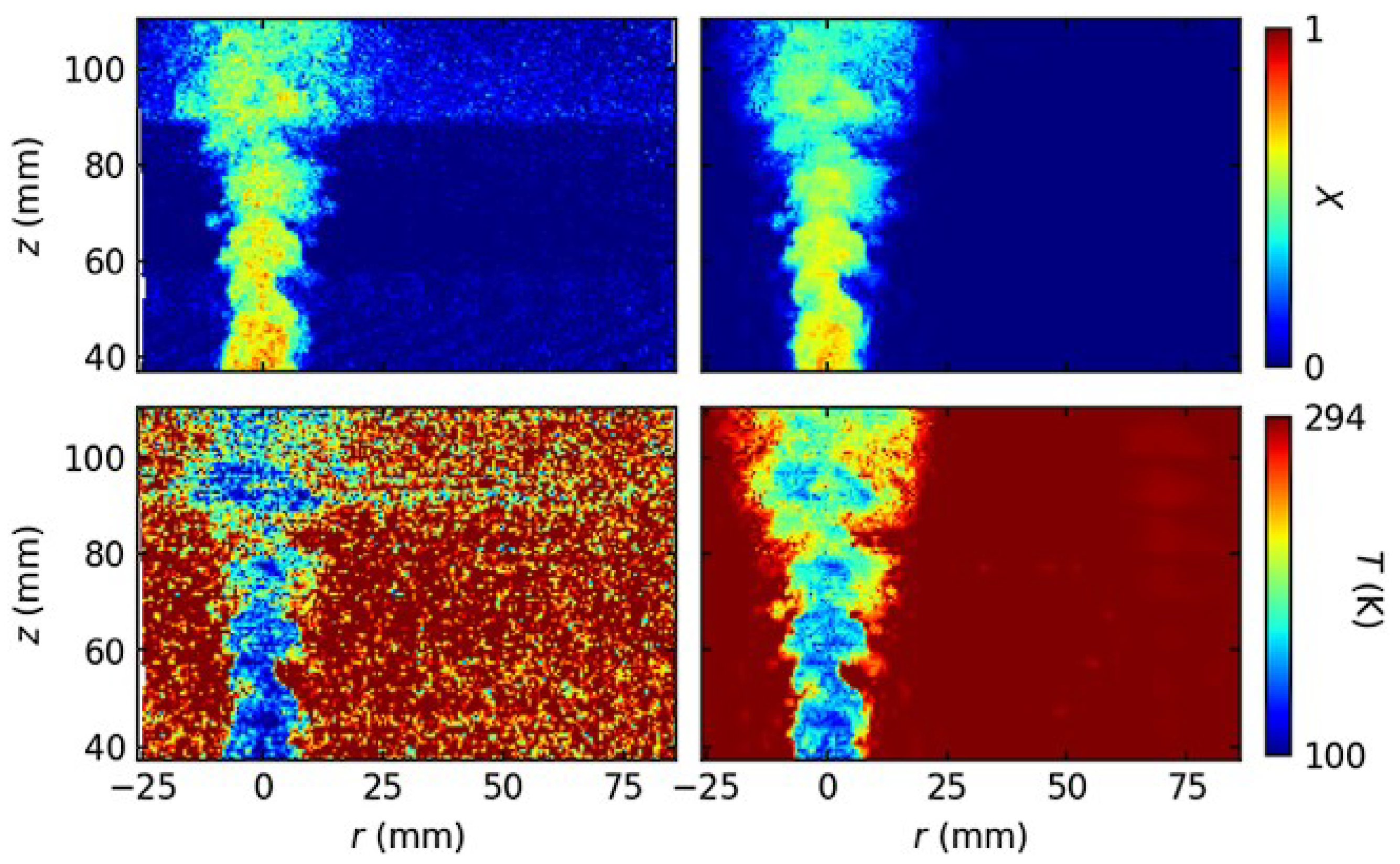
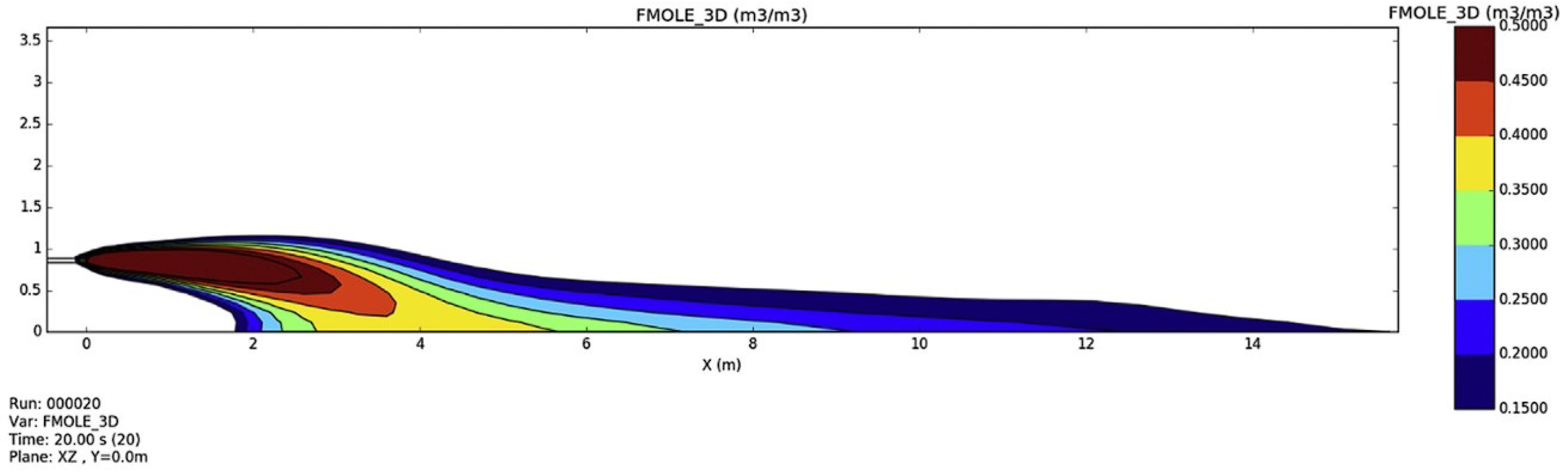
- Giannissi, S.G.; Venetsanos, A.G.; Hecht, E.S. Numerical predictions of cryogenic hydrogen vertical jets. Int. J. Hydrogen Energy 2021, 46, 12566–12576. [Google Scholar] [CrossRef]
- Jin, T.; Liu, Y.; Wei, J.; Wu, M.; Lei, G.; Chen, H.; Lan, Y. Modeling and analysis of the flammable vapor cloud formed by liquid hydrogen spills. Int. J. Hydrogen Energy 2017, 42, 26762–26770. [Google Scholar] [CrossRef]
- Jäkel, C.; Kelm, S.; Verfondern, K.; Allelein, H.-J. Validation of a 3D multiphase-multicomponent CFD model for accidental liquid and gaseous hydrogen releases. Int. J. Hydrogen Energy 2019, 44, 8807–8818. [Google Scholar] [CrossRef]
- Brennan, C. Fundamentals of Multiphase Flows; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
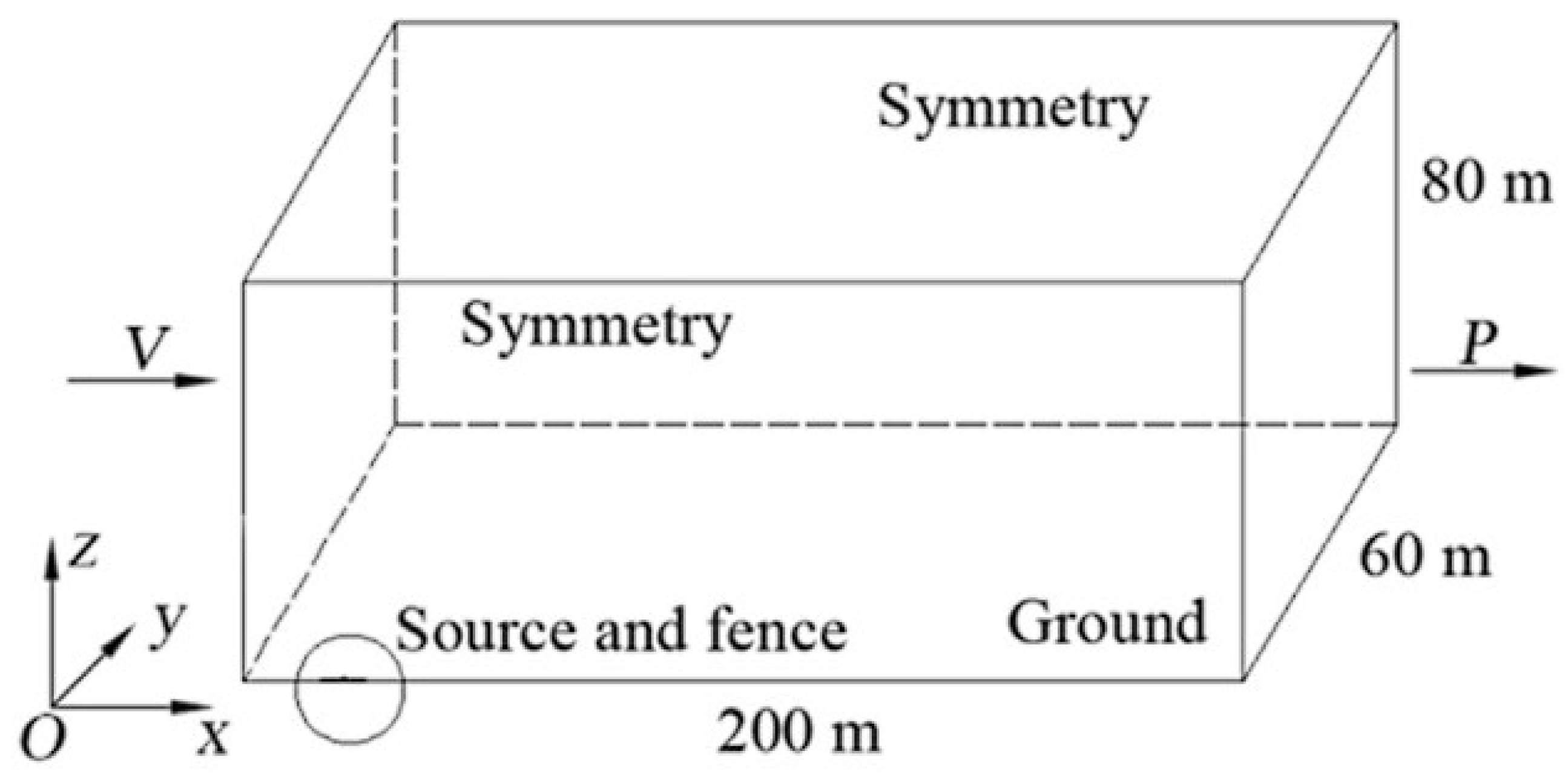
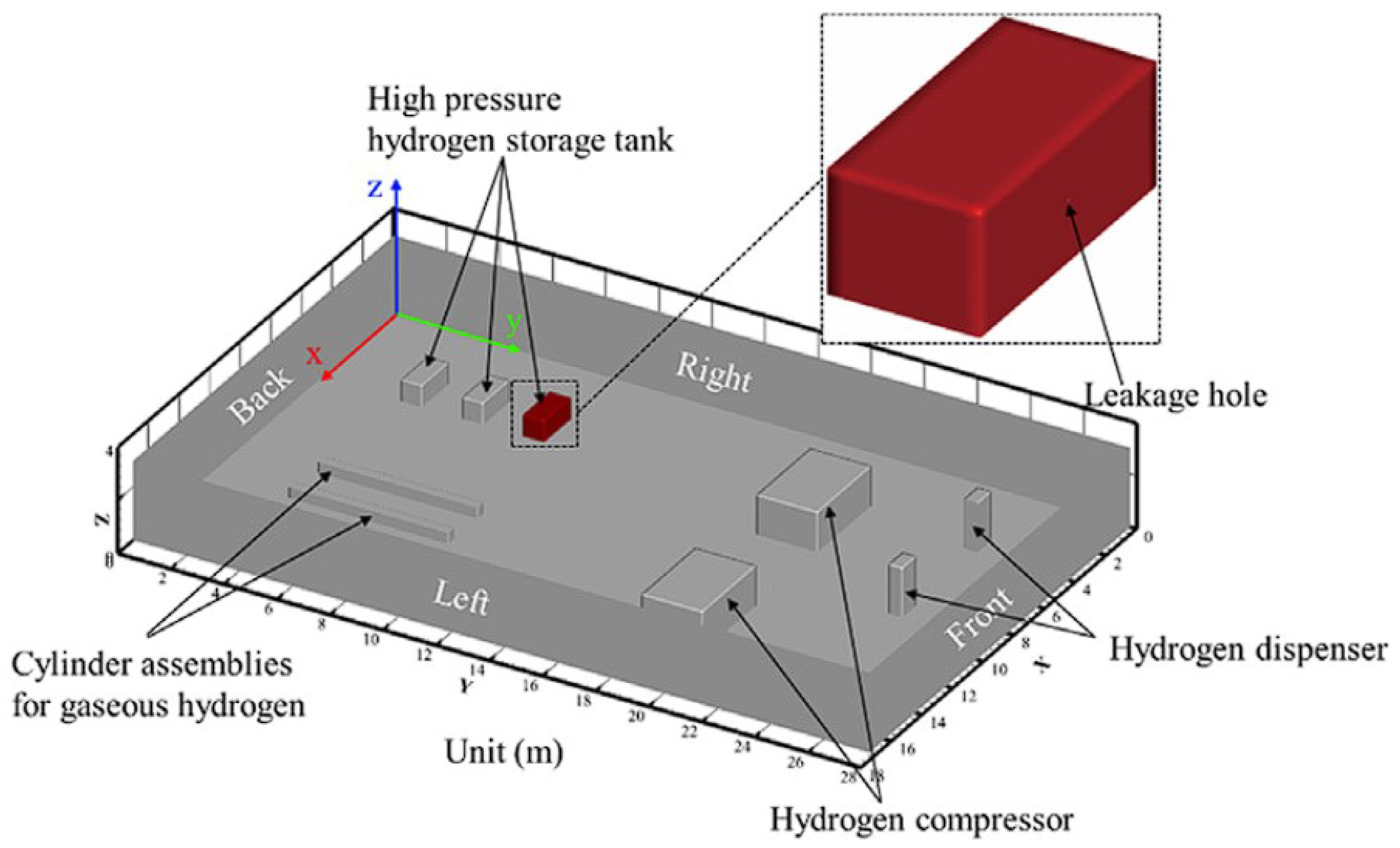
- Qian, J.; Li, X.; Jin, Z. A numerical study of unintended hydrogen release in a hydrogen refueling station. Int. J. Hydrogen Energy 2020, 45, 20142–20152. [Google Scholar] [CrossRef]
- Schefer, R.; Houf, W.; Williams, T. Investigation of small-scale unintended releases of hydrogen: Momentum-dominated regime. Int. J. Hydrogen Energy 2008, 33, 6373–6384. [Google Scholar] [CrossRef]
- Swain, M.R.; Swain, M.N.; Grilliot, E.S. Risks Incurred by Hydrogen Escaping from Containers and Conduits; National Renewable Energy Lab: Golden, CO, USA, 1998.
- Hansen, O. Liquid hydrogen releases show dense gas behavior. Int. J. Hydrogen Energy 2020, 45, 1343–1358. [Google Scholar] [CrossRef]
- Ren, Z.; Giannissi, S.; Venetsanos, A.G.; Friedrich, A.; Kuznetsov, M.; Jordan, T.; Wen, J.X. The evolution and structure of ignited high-pressure cryogenic hydrogen jets. Int. J. Hydrogen Energy 2022, 47, 29184–29194. [Google Scholar] [CrossRef]
- Jordan, T.; Bernard, L.; Cirrone, D.; Coldrick, S.; Friedrich, A.; Jallais, S.; Kuznetsov, M.; Proust, C.; Venetsanos, A.G.; Wen, J.X. Results of the pre-normative research project PRESLHY for the safety use of liquid hydrogen. Preshly 2021. [Google Scholar]
- Keenan, J.; Makarov, D.; Molkov, V. Modelling and simulation of high-pressure hydrogen jets using notional nozzle theory and open source code OpenFOAM. Int. J. Hydrogen Energy 2017, 42, 7447–7456. [Google Scholar] [CrossRef]
- Yoshizawa, A. Bridging between eddy-viscosity-type and second-order turbulence models through a two-scale turbulence theory. Phys. Rev. 1993, 48, 273. [Google Scholar] [CrossRef]
- Parente, A.; Malik, M.R.; Contino, F.; Cuoci, A.; Dally, B.B. Extension of the Eddy Dissipation Concept for turbulence/chemistry interactions to MILD combustion. Fuel 2016, 163, 98–111. [Google Scholar] [CrossRef]
- Gong, L.; Li, Z.; Jin, K.; Gao, Y.; Duan, Q.; Zhang, Y.; Sun, J. Numerical study on the mechanism of spontaneous ignition of high-pressure hydrogen during its sudden release into a tube. Saf. Sci. 2020, 129, 104807. [Google Scholar] [CrossRef]
- Cirrone, D.; Makarov, D.; Molkov, V. Spontaneous ignition of cryo-compressed hydrogen in a T-shaped channel system. Hydrogen 2022, 3, 348–360. [Google Scholar] [CrossRef]
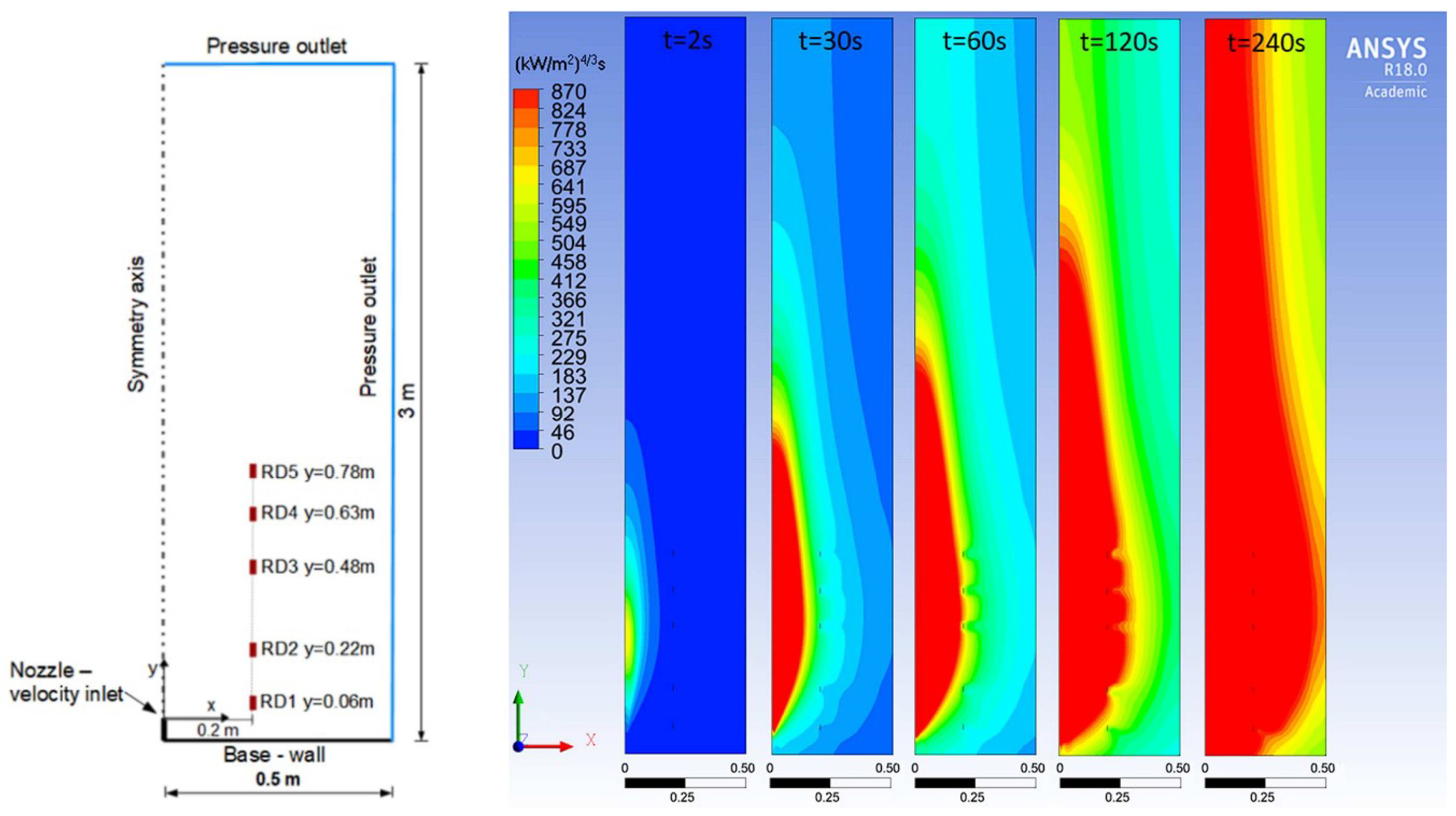
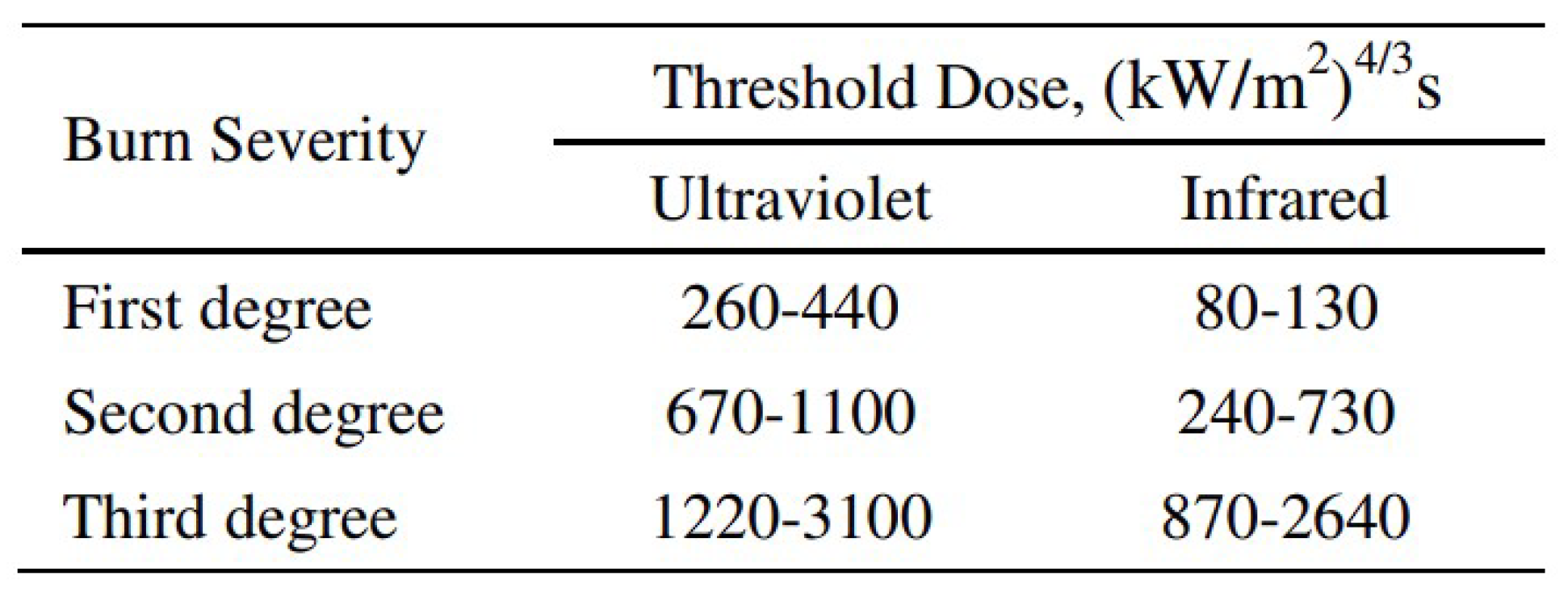
- Cirrone, D.; Makarov, D.; Molkov, V. Near field thermal dose of cryogenic hydrogen jet fires. Int. Semin. Fire Explos. Hazards 2019, 9, 1361–1367. [Google Scholar]
- Cirrone, D.; Makarov, D.; Molkov, V. Thermal radiation from cryogenic hydrogen jet fires. Int. J. Hydrogen Energy 2019, 44, 8874–8885. [Google Scholar] [CrossRef]
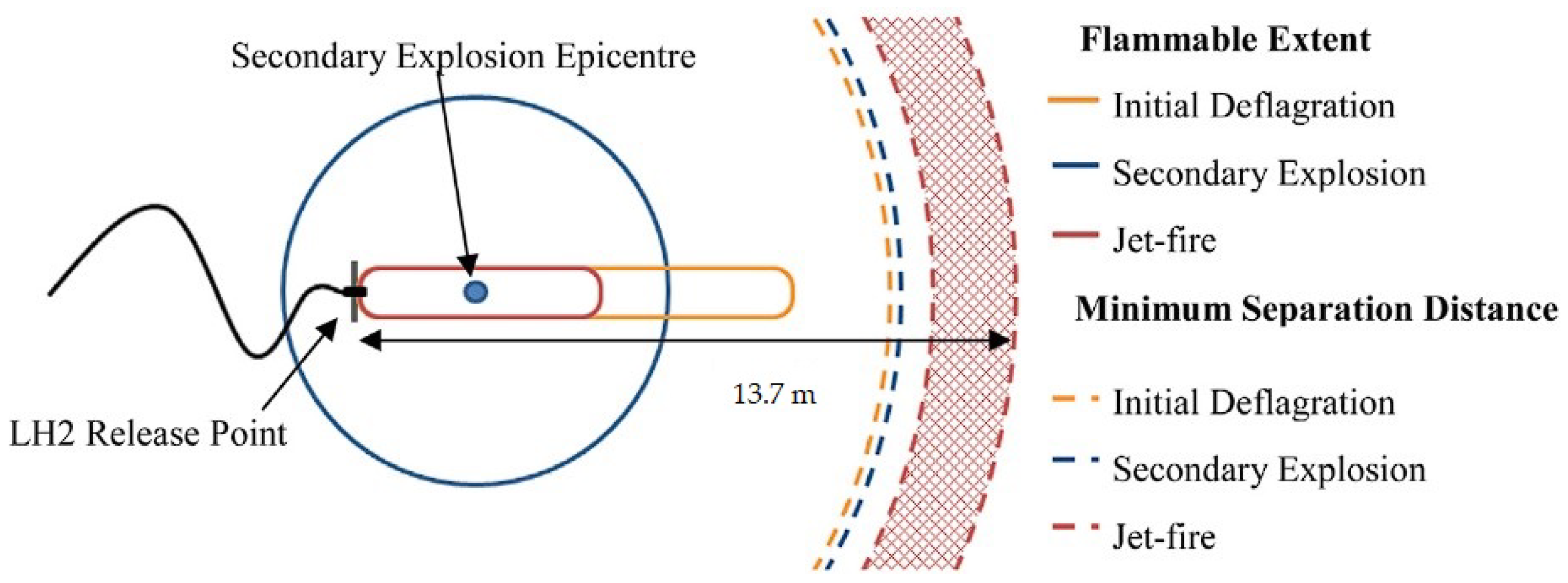
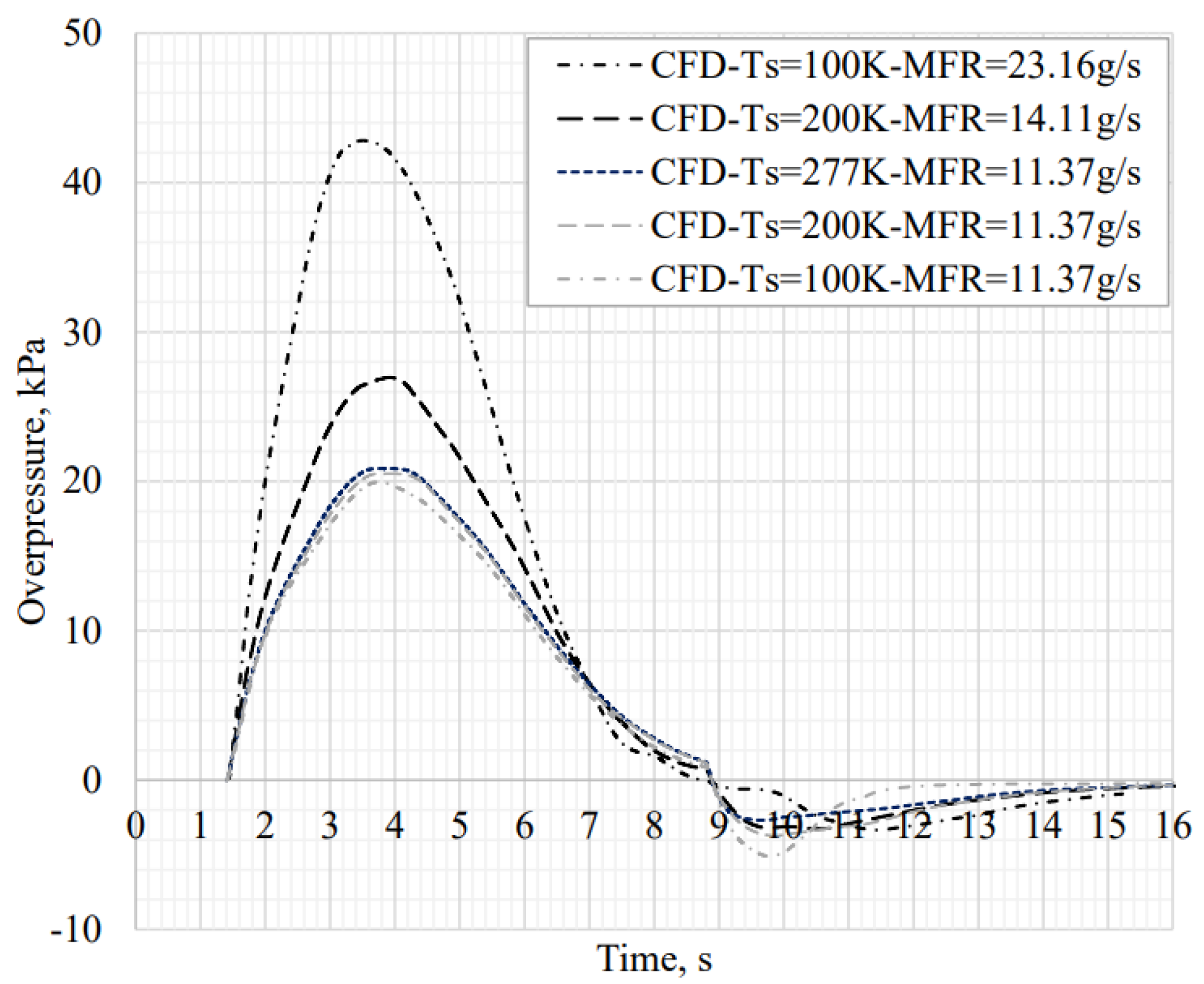
- Cirrone, D.; Makarov, D.; Lach, A.; Gaathaug, A.; Molkov, V. The Pressure Peaking Phenomenon for Ignited Under-Expanded Hydrogen Jets in the Storage Enclosure: Experiments and Simulations for Release Rates of up to 11.5 g/s. Energies 2022, 15, 271. [Google Scholar] [CrossRef]
- Brennan, S.; Molkov, V.; Makarov, D. The Pressure Peaking Phenomenon for ignited dynamics of flammable hydrogen-air mixture formation in an enclosure with a single vent. Proc. Int. Semin. Fire Explos. 2011, 6, 493–503. [Google Scholar]
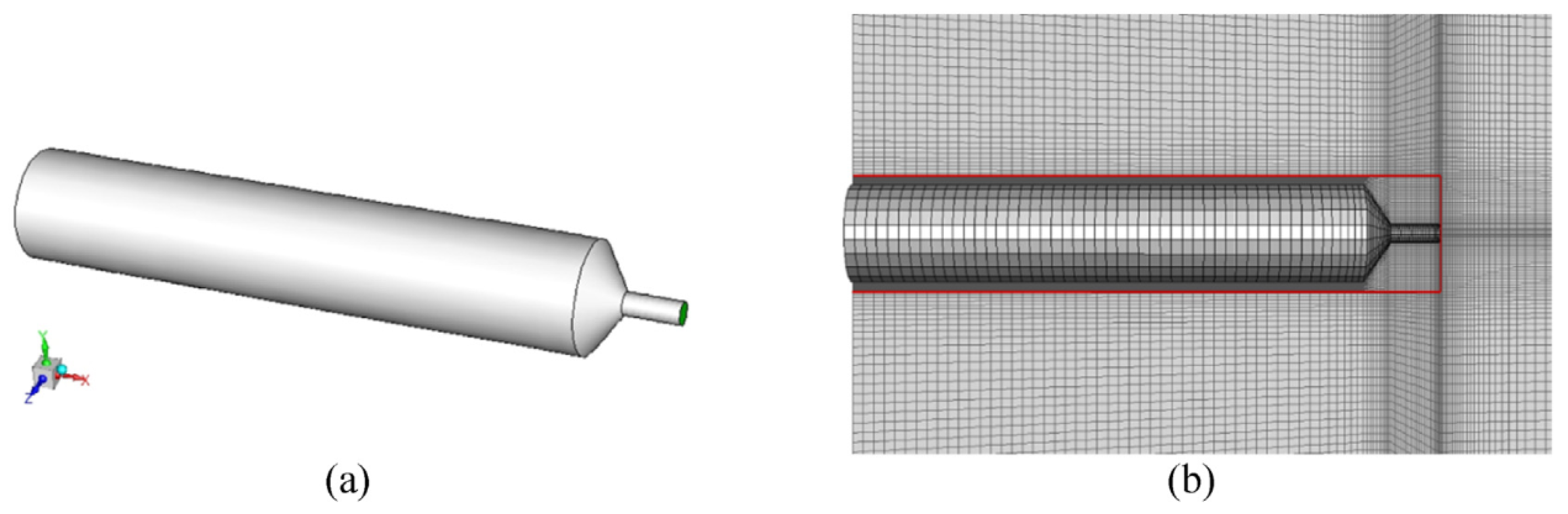
- Cirrone, D.; Makarov, D.; Kuznetsov, M.; Friedrich, A.; Molkov, V. Effect of heat transfer through the release pipe on simulations of cryogenic hydrogen jet fires and hazard distances. Int. J. Hydrogen Energy 2022, 47, 21596–21611. [Google Scholar] [CrossRef]
- Ivings, M.J.; Jagger, S.F.; Lea, C.J.; Webber, D.M. Evaluating vapor dispersion models for safety analysis of LNG facilities. Fire Prot. Res. Found. 2016. [Google Scholar]












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clarke, J.; Dettmer, W.; Wen, J.; Ren, Z. Cryogenic Hydrogen Jet and Flame for Clean Energy Applications: Progress and Challenges. Energies 2023, 16, 4411. https://doi.org/10.3390/en16114411
Clarke J, Dettmer W, Wen J, Ren Z. Cryogenic Hydrogen Jet and Flame for Clean Energy Applications: Progress and Challenges. Energies. 2023; 16(11):4411. https://doi.org/10.3390/en16114411
Chicago/Turabian StyleClarke, Jac, Wulf Dettmer, Jennifer Wen, and Zhaoxin Ren. 2023. "Cryogenic Hydrogen Jet and Flame for Clean Energy Applications: Progress and Challenges" Energies 16, no. 11: 4411. https://doi.org/10.3390/en16114411





