3D Solar Irradiance Model for Non-Uniform Shading Environments Using Shading (Aperture) Matrix Enhanced by Local Coordinate System
Abstract
:1. Introduction
- The curved surface [31];
- Frequent variation in the orientation angle of a VIPV during driving [31];
- Relatively higher probability for VIPVs to be shaded by objects [31];
- Relatively small size of shading objects, such as street trees and signals, and the consequent high influence of partial shading loss on these [31];
- Temperature variation (parking and driving) [31];
- Dynamic fluctuation of the solar spectrum [31];
- Rapid fluctuations in solar irradiance (in milliseconds) owing to dynamic partial shading [31].
- Solar irradiance onto the VIPV (orthogonal five orientations-roof and four sides, front, left, tail, and right);
- Distribution of shaded objects, estimation of solar irradiance, and irradiation on an arbitrary reference plane tangential to the curved surface of the VIPV.
- Partial shading impact;
- Dynamic shading impact (only for the VIPV);
- Testing the VIPV indoors or outdoors for rating;
- I–V curve measurement during driving (only for the VIPV);
- Influence of power on the curved surface;
- Transient output of the modules, which is affected by the capacitance and other transient characteristics of the device (only for the VIPV);
- Temperature measurements;
- Spectrum correction.
- Solar irradiance in other zones such as residential and open zones;
- Solar irradiance on car sides;
- Simultaneous validation of the five orthogonal orientations (i.e., evidence on only one axis may not be substantial);
- Pathway to the energy rating of the VIPV;
- Consistency among different shading environments, car orientations, and car sides.
2. Methods
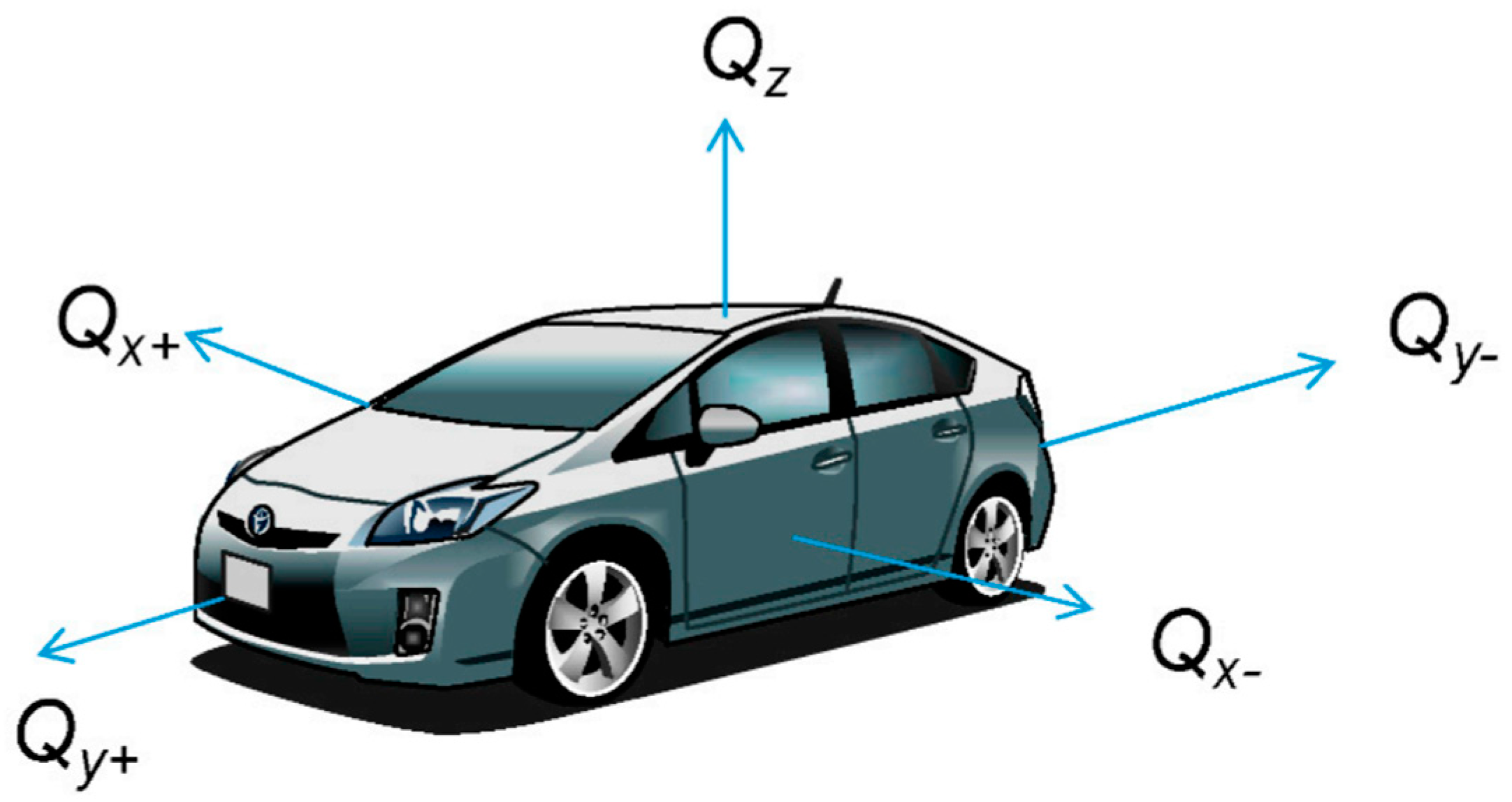
2.1. Local Coordinate System
2.2. Solar Irradiance Measurement Influenced by Shading Objects
2.3. Measurement Methods of the Distribution of Shading Objects
- A fisheye image of the sky was captured. Without blue-colored structures, such as blue signs and walls, the best capturing condition was a clear-sky day (no clouds) with certain shading objects shading the sun. In this case, a fisheye video or camera were used to generate the RGB images. The alternative timings were sunrise or sunset (Figure 4). The recommended fisheye video system is the model WV-S4550L made by Panasonic, Japan;
- A median filter was applied to remove spot-like image noise;
- If obtained under blue-sky conditions, decomposition into red, green, and blue images were effective. A differential image matrix (gray-scale matrix), such as 2B − (G + R), converted the sky into white and building walls into black regardless of whether these reflected sunlight (Figure 4). B, G, and R represented the image matrices decomposed from RGB images. A median image filter could erase spot-like noise by applying the median number of five adjacent elements. Note that differential image matrix calculations, such as 2B − (G + R), induced errors in the image, including bright-blue walls or signs. A typical mistake was considering bright-blue objects as part of the sky. In such cases, the image may have been replaced with the ones captured at low sun height (dark sky condition), as shown in Figure 4;
- The filtered fisheye images were then binarized. The best threshold was determined conveniently using the median point of the two peaks of the brightness histogram (one peak corresponded to the open sky and the other corresponded to shading objects) (Figure 5);
- The aperture matrix E was generated using a 2D histogram. The matrix elements ranged from zero to one (0: shaded, 1: unshaded). Shading implied shading a point in a hemispherical sky, instead of “shading the sun”. That is, the (i, j) elements, Ei,j, were the densities of the unshaded points in the 2D bin of the elevation angles [i°, (i + 1)°] (i = 0, 1, …. 89) and orientation angles [4j°, 4(j + 1)°] (j = 0, 1, …., 89). The image matrix could be conveniently converted from a polar coordinate system to an orthogonal coordinate system before the elements were counted in 2D bins (Figure 4). Occasionally, the reflection by a window was identified as the sky. However, it may have been filled in black (or zero in the matrix) manually, or erosion may have been applied using image processing.
2.4. Definition of the Aperture (Shading) Matrix
2.5. 3D Solar Irradiance Calculation Using the Aperture Matrix
3. Results
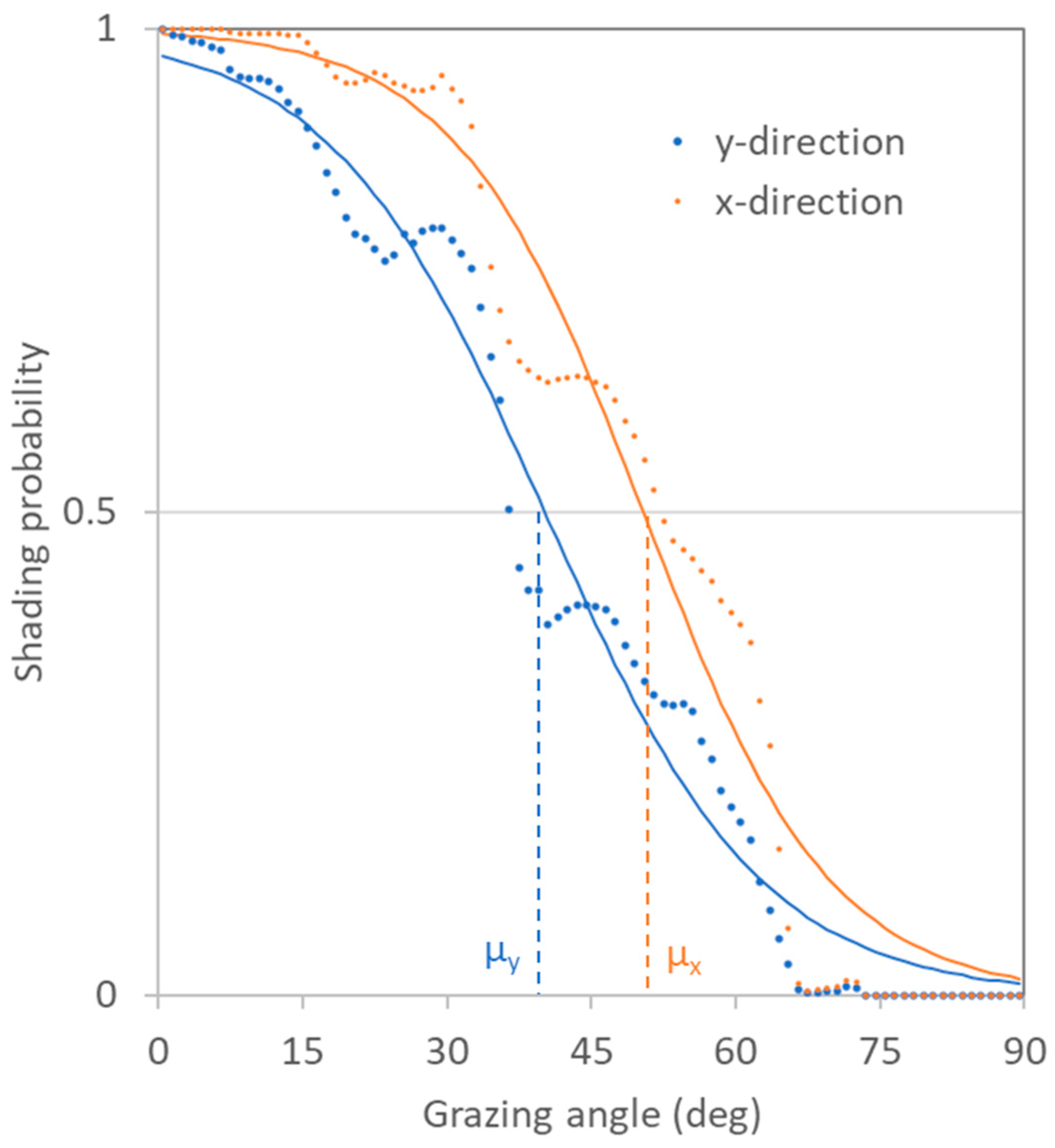
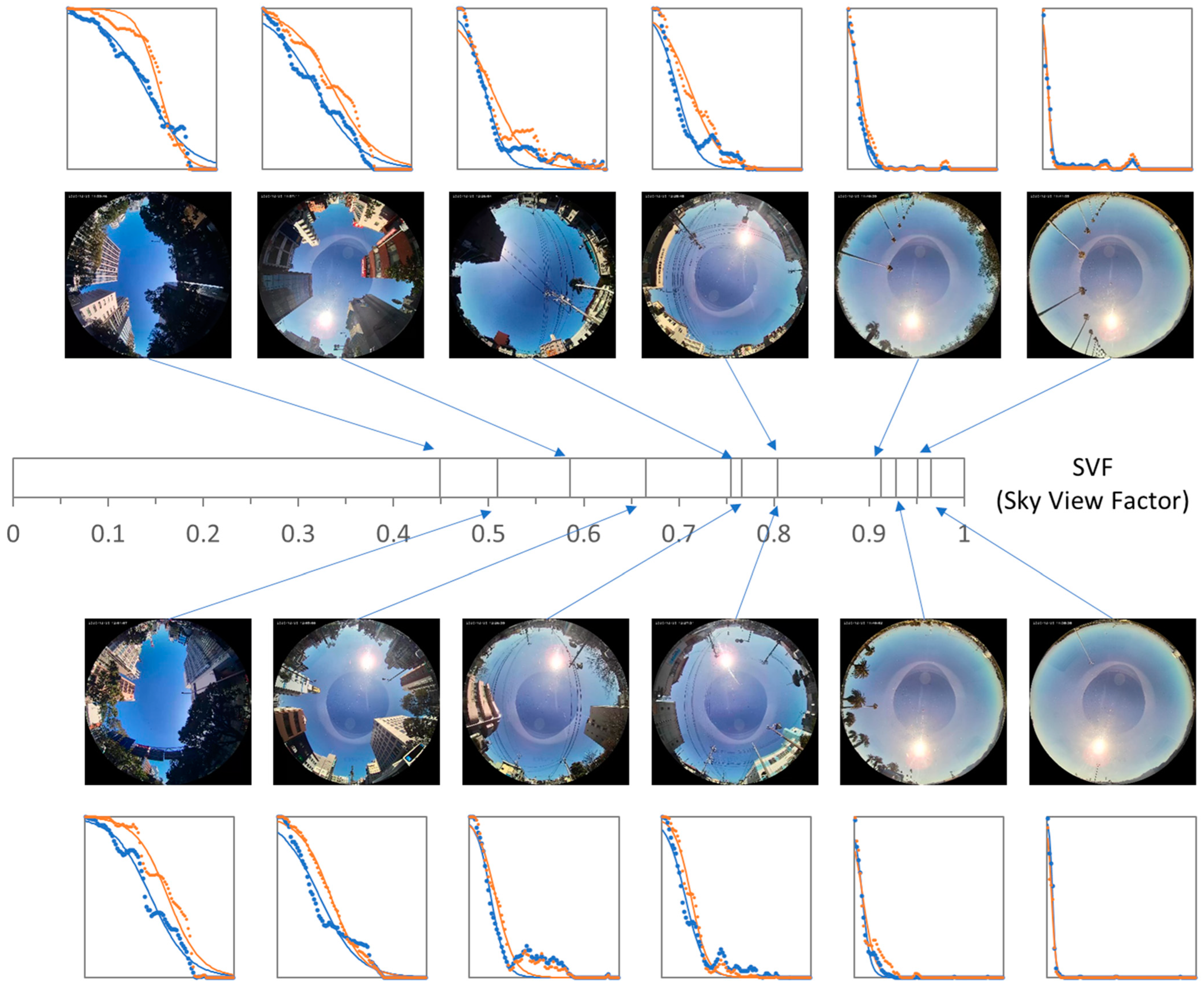
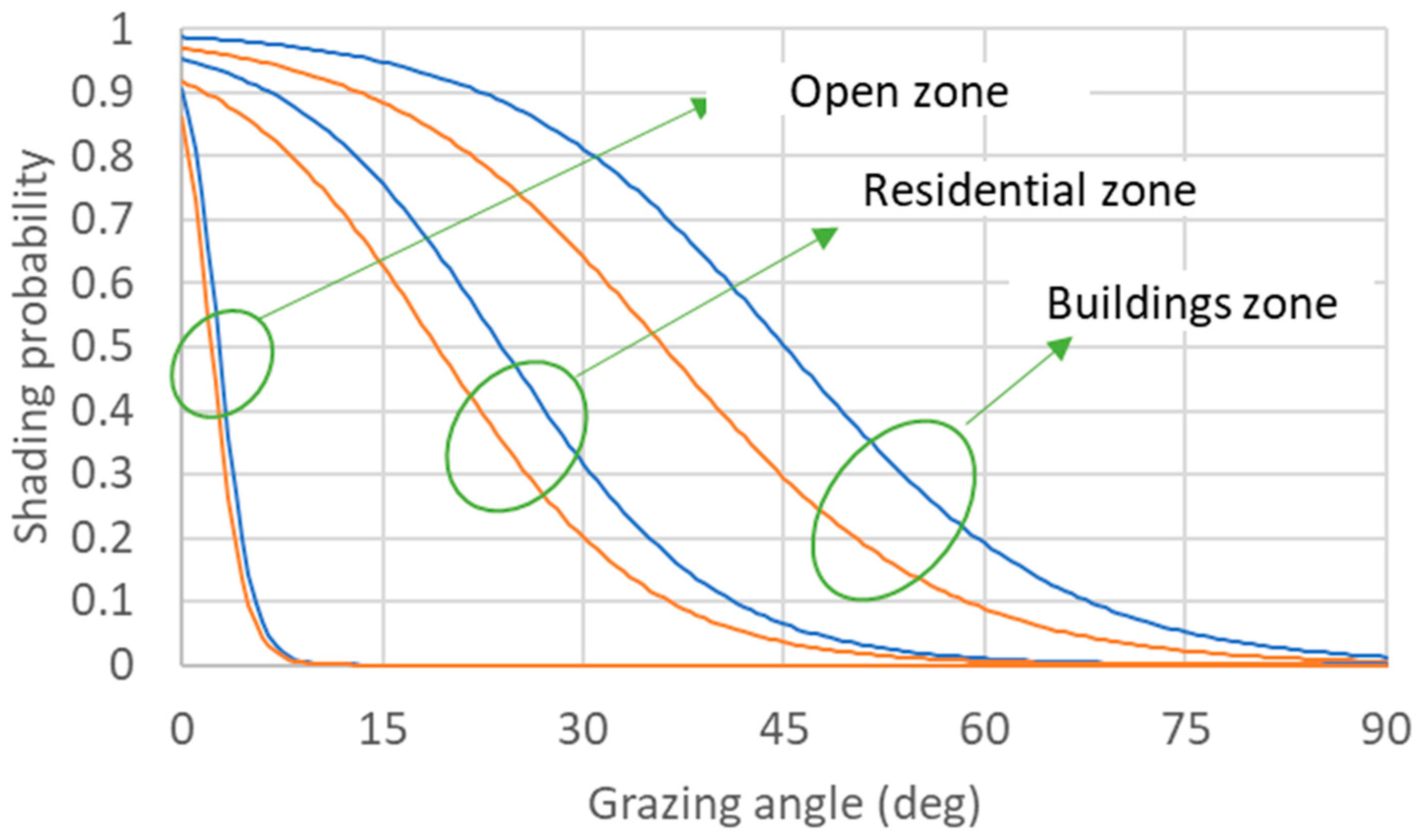
3.1. Shading Probability Distribution
3.2. Model Validation by Measurements
4. Discussion
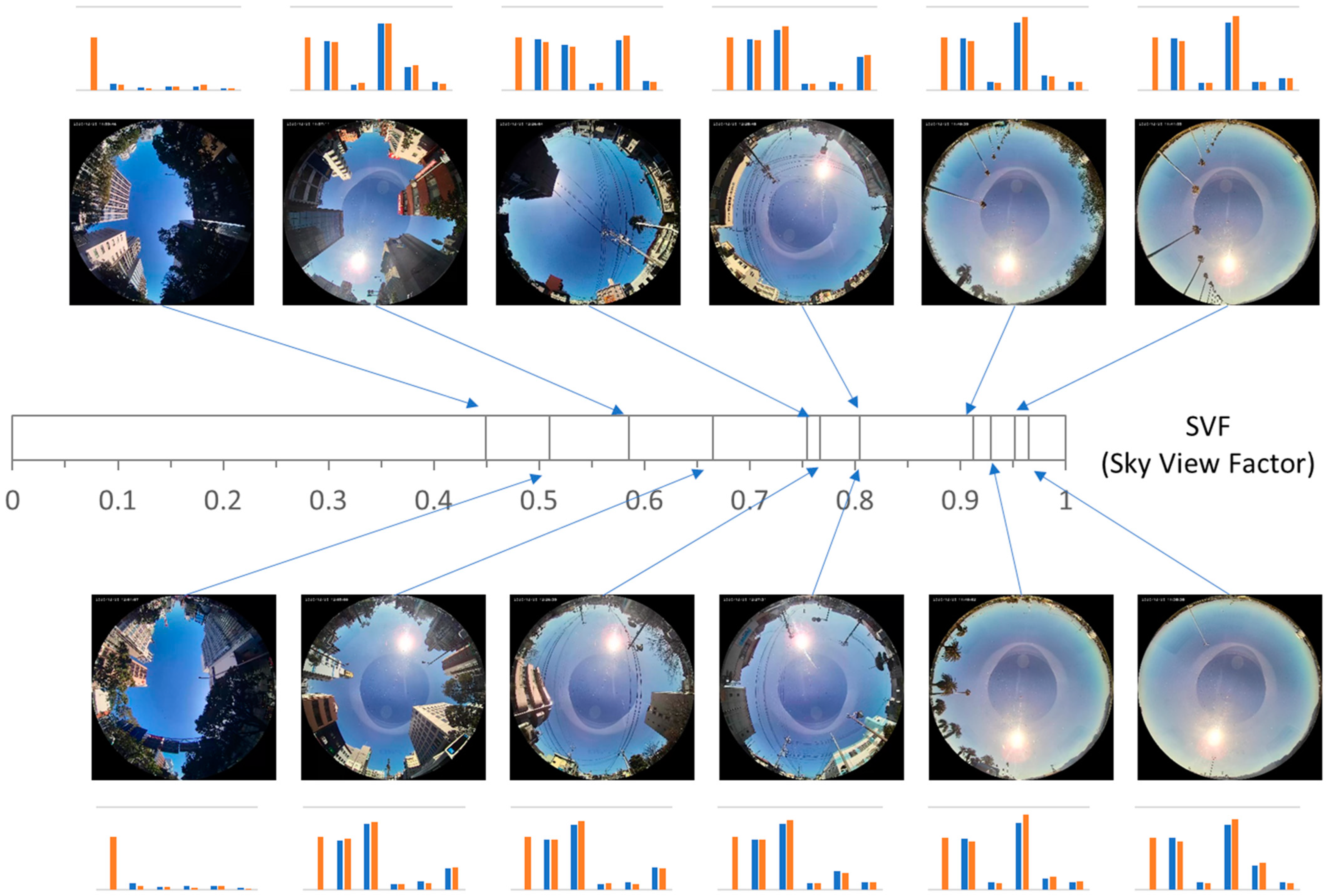
4.1. Categorizing the Shading Environment
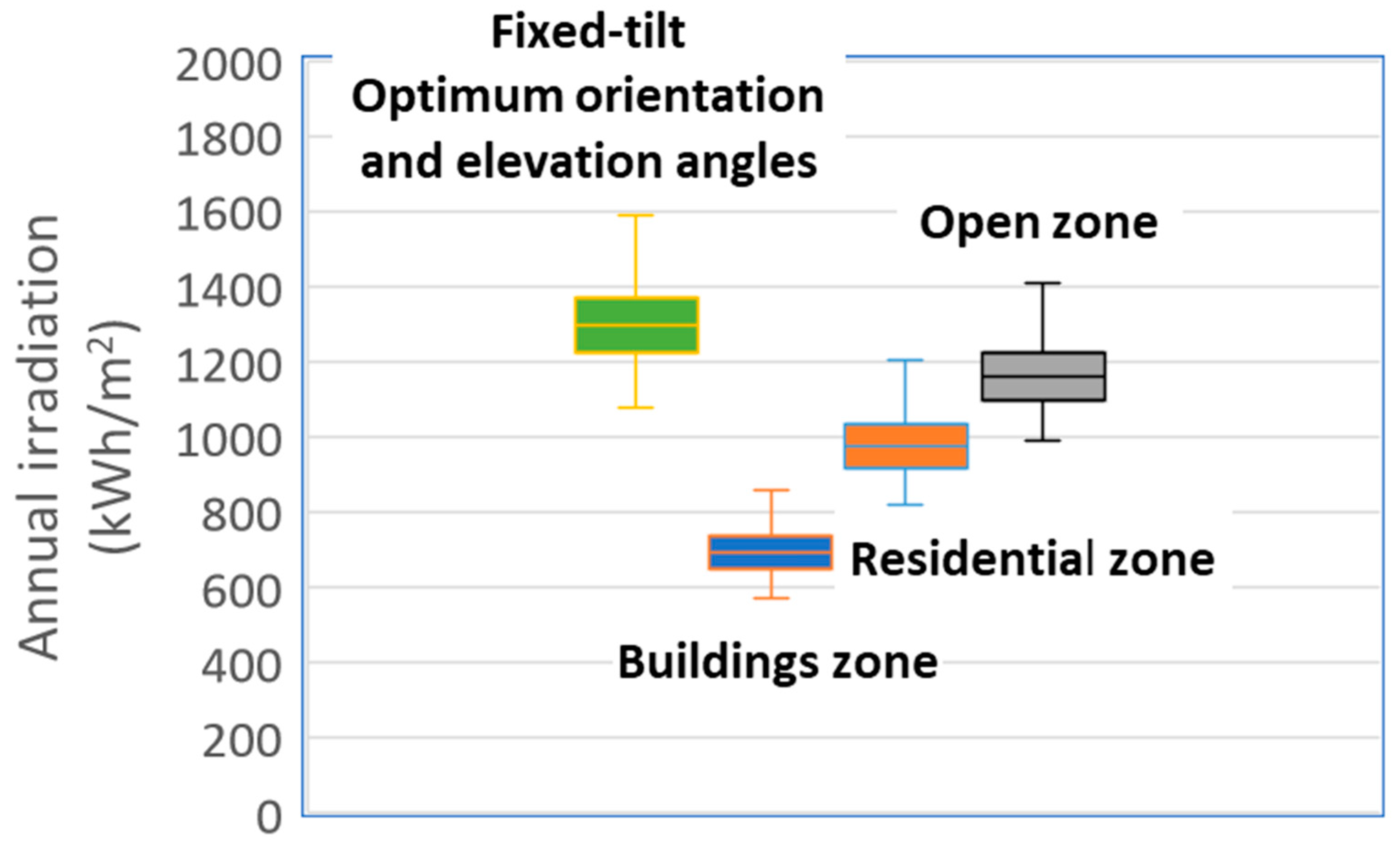
4.2. Estimation of Annual Solar Irradiance Using Shading Probability Distribution
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | two-dimensional |
| 3D | three-dimensional |
| BEV | battery electric vehicle |
| BIPV | building-integrated photovoltaics |
| DC | direct current |
| DNI | direct normal irradiance |
| ECU | electronic control unit |
| EV | electric vehicle |
| GHI | global horizonal irradiance |
| GPS | global positioning system |
| IEC | International Electrotechnical Commission |
| I-V | current-voltage |
| MPPT | maximum power point tracking |
| PV | photovoltaic |
| RGB | red-green-blue |
| SEV | solar electric vehicle |
| Si | silicon |
| SVF | sky view factor |
| VIPV | vehicle-integrated photovoltaics |
References
- Thiel, C.; Amillo, A.G.; Tansini, A.; Tsakalidis, A.; Fontaras, G.; Dunlop, E.; Taylor, N.; Jäger-Waldau, A.; Araki, K.; Nishioka, K.; et al. Impact of climatic conditions on prospects for integrated photovoltaics in electric vehicle. Renew. Sustain. Energy Rev. 2022, 158, 112109. [Google Scholar] [CrossRef]
- Araki, K.; Ji, L.; Kelly, G.; Yamaguchi, M. To Do List for Research and Development and International Standardization to Achieve the Goal of Running a Majority of Electric Vehicles on Solar Energy. Coatings 2018, 8, 251. [Google Scholar] [CrossRef] [Green Version]
- Muntwyler, U. Towards 100% renewable energy supplies. In Proceedings of the 2015 Tenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 31 March–2 April 2015; pp. 1–8. [Google Scholar] [CrossRef]
- Masuda, T.; Araki, K.; Okumura, K.; Urabe, S.; Kudo, Y.; Kimura, K.; Nakado, T.; Sato, A.; Yamaguchi, M. Static concentrator photovoltaics for automotive applications. Sol. Energy 2017, 146, 523–531. [Google Scholar] [CrossRef]
- NEDO. Interim Report of the Exploratory Committee on the Automobile Using Photovoltaic System. Available online: http://www.nedo.go.jp/news/press/AA5_100909.html (accessed on 9 May 2018).
- Masuda, T.; Araki, K.; Okumura, K.; Urabe, S.; Kudo, Y.; Kimura, K.; Nakado, T.; Sato, A.; Yamaguchi, M. Next environment-friendly cars: Application of solar power as automobile energy source. In Proceedings of the IEEE 43rd Photovoltaic Specialists Conference (PVSC), Portland, OR, USA, 5–10 June 2016. [Google Scholar] [CrossRef]
- Araki, K.; Sato, D.; Masuda, T.; Lee, K.-H.; Yamada, N.; Yamaguchi, M. Why and how does car-roof PV create 50 GW/year of new installations? Also, why is a static CPV suitable to this application? AIP Conf. Proc. 2019, 2149, 050003. [Google Scholar] [CrossRef]
- Stutzmann, M. Role of mechanical stress in the light-induced degradation of hydrogenated amorphous silicon. Appl. Phys. Lett. 1985, 47, 21–23. [Google Scholar] [CrossRef]
- Moeini, I.; Ahmadpour, M.; Mosavi, A.; Alharbi, N.; Gorji, N.E. Modeling the time-dependent characteristics of perovskite solar cells. Sol. Energy 2018, 170, 969–973. [Google Scholar] [CrossRef]
- Lindroos, J.; Savin, H. Review of light-induced degradation in crystalline silicon solar cells. Sol. Energy Mater. Sol. Cells 2016, 147, 115–126. [Google Scholar] [CrossRef]
- Meyer, E.L.; Van Dyk, E.E. Assessing the reliability and degradation of photovoltaic module performance parameters. IEEE Trans. Reliab. 2004, 53, 83–92. [Google Scholar] [CrossRef]
- Letendre, S.; Perez, R.; Herig, C. Vehicle integrated PV: A clean and secure fuel for hybrid electric vehicles. In Proceedings of the Solar Conference; American Solar Energy Society: Boulder, CO, USA; American Institute of Architects: Washington, DC, USA, 2003; pp. 201–206. [Google Scholar]
- De Pinto, S.; Lu, Q.; Camocardi, P.; Chatzikomis, C.; Sorniotti, A.; Ragonese, D.; Iuzzolino, G.; Perlo, P.; Lekakou, C. Electric vehicle driving range extension using photovoltaic panels. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Hangzhou, China, 17–20 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Wang, Y.; Pedram, M.; Chang, N. Fast photovoltaic array reconfiguration for partial solar powered vehicles. In Proceedings of the International Symposium on Low Power Electronics and Design, La Jolla, CA, USA, 11–13 August 2014; pp. 357–362. [Google Scholar] [CrossRef]
- Alhammad, Y.A.; Al-Azzawi, W.F. Exploitation the waste energy in hybrid cars to improve the efficiency of solar cell panel as an auxiliary power supply. In Proceedings of the 10th International Symposium on Mechatronics and Its Applications (ISMA), Sharjah, United Arab Emirates, 8–10 December 2015; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar] [CrossRef]
- The Ford Motor Company. Let the Sun In: Ford C-MAX Solar Energi Concept Goes Off the Grid, Gives Glimpse of Clean Vehicle Future. Available online: https://media.ford.com/content/fordmedia/fna/us/en/news/2014/01/02/let-the-sun-in--ford-c-max-solar-energi-concept-goes-off-the-gri.html (accessed on 9 May 2018).
- Automotive News, Next-Generation Toyota Prius Has Solar Roof for Europe, Japan. Available online: http://www.autonews.com/article/20160616/OEM05/160619900/next-generation-toyota-prius-has-solar-roof-for-europe-japan (accessed on 3 March 2023).
- Automotive News. Available online: http://www.autonews.com/article/20160811/OEM04/308119912/karma-targets-tesla-with-$115000-solar-boosted-hybrid (accessed on 3 March 2023).
- Hanergy Holding Group Ltd. Available online: https://www.autoevolution.com/news/china-s-hanergy-unveils-four-solar-powered-concept-cars-109094.html (accessed on 3 March 2023).
- Nissan Motor Corporation. Nissan Sustainability Report 2014. Available online: https://www.nissan-global.com/EN/SUSTAINABILITY/LIBRARY/SR/2014/ (accessed on 3 March 2023).
- Sierra, A.; Reinders, A. Designing innovative solutions for solar-powered electric mobility applications. Prog. Photovolt. Res. Appl. 2021, 29, 802–818. [Google Scholar] [CrossRef]
- Kanz, O.; Reinders, A.; May, J.; Ding, K. Environmental Impacts of Integrated Photovoltaic Modules in Light Utility Electric Vehicles. Energies 2020, 13, 5120. [Google Scholar] [CrossRef]
- Araki, K.; Ota, Y.; Maeda, A.; Kumano, M.; Nishioka, K. Solar Electric Vehicles as Energy Sources in Disaster Zones: Physical and Social Factors. Energies 2023, 16, 3580. [Google Scholar] [CrossRef]
- Kim, S.; Holz, M.; Park, S.; Yoon, Y.; Cho, E.; Yi, J. Future Options for Lightweight Photovoltaic Modules in Electrical Passenger Cars. Sustainability 2021, 13, 2532. [Google Scholar] [CrossRef]
- Macias, J.; Herrero, R.; Nunez, R.; Anton, I. On the effect of cell interconnection in Vehicle Integrated Photovoltaics: Modelling energy under different scenarios. In Proceedings of the 2021 IEEE 48th Photovoltaic Specialists Conference (PVSC), Fort Lauderdale, FL, USA, 20–25 June 2021. [Google Scholar] [CrossRef]
- Sagaria, S.; Duarte, G.; Neves, D.; Baptista, P. Photovoltaic integrated electric vehicles: Assessment of synergies between solar energy, vehicle types and usage patterns. J. Clean. Prod. 2022, 348, 131402. [Google Scholar] [CrossRef]
- Mallon, K.R.; Assadian, F.; Fu, B. Analysis of On-Board Photovoltaics for a Battery Electric Bus and Their Impact on Battery Lifespan. Energies 2017, 10, 943. [Google Scholar] [CrossRef] [Green Version]
- Conti, S.; Di Mauro, S.; Raciti, A.; Rizzo, S.A.; Susinni, G.; Musumeci, S.; Tenconi, A. Solar electric vehicles: State-of-the-art and perspectives. In Proceedings of the 2018 AEIT International Annual Conference, Bari, Italy, 3–5 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Available online: https://metro.co.uk/2019/06/26/lightyear-one-solar-powered-electric-car-thatll-450-miles-10072219/ (accessed on 1 March 2023).
- Available online: https://sonomotors.com/ (accessed on 1 March 2023).
- Araki, K.; Ota, Y.; Yamaguchi, M. Measurement and Modeling of 3D Solar Irradiance for Vehicle-Integrated Photovoltaic. Appl. Sci. 2020, 10, 872. [Google Scholar] [CrossRef] [Green Version]
- Heinrich, M.; Kutter, C.; Basler, F.; Mittag, M.; Alanis, L.E.; Eberlein, D.; Schmid, A.; Reise, C.; Kroyer, T.; Neuhaus, D.H.; et al. Yield Potential of Vehicle Integrated Photovoltaics on Commercial Trucks and Vans. In Proceedings of the 37th European PV Solar Energy Conference and Exhibition, Online, 7–11 September 2020; Volume 7, pp. 1695–1700. [Google Scholar] [CrossRef]
- Abdelhamid, M.; Pilla, S.; Singh, R.; Haque, I.; Filipi, Z. A comprehensive optimized model for on-board solar photovoltaic system for plug-in electric vehicles: Energy and economic impacts: On-board solar photovoltaic system for plug-in electric vehicles. Int. J. Energy Res. 2016, 40, 1489–1508. [Google Scholar] [CrossRef]
- Ota, Y.; Araki, K.; Nagaoka, A.; Nishioka, K. Curve correction of vehicle-integrated photovoltaics using statistics on commercial car bodies. Prog. Photovolt. Res. Appl. 2022, 30, 152–163. [Google Scholar] [CrossRef]
- Tayagaki, T.; Araki, K.; Yamaguchi, M.; Sugaya, T. Impact of Nonplanar Panels on Photovoltaic Power Generation in the Case of Vehicles. IEEE J. Photovolt. 2019, 9, 1721–1726. [Google Scholar] [CrossRef]
- Ota, Y.; Araki, K.; Nagaoka, A.; Nishioka, K. Facilitating vehicle-integrated photovoltaics by considering the radius of curvature of the roof surface for solar cell coverage. Clean. Eng. Technol. 2022, 7, 100446. [Google Scholar] [CrossRef]
- Nagaoka, A.; Ota, Y.; Sakai, K.; Araki, K.; Matsuo, H.; Kadota, N.; Maeda, K.; Nakajima, A.; Nishioka, K. Performance evaluation and spectrum-based analysis of a wall-mounted photovoltaic system for zero-energy building. Renew. Energy 2021, 174, 147–156. [Google Scholar] [CrossRef]
- Ekins-Daukes, N.; Betts, T.R.; Kemmoku, Y.; Araki, K.; Lee, H.; Gottschalg, R.; Boreland, M.; Infield, D.; Yamaguchi, M. Syracuse—A multi-junction concentrator system computer model. In Proceedings of the Conference Record of the Thirty-First IEEE Photovoltaic Specialists Conference 2005, Lake Buena Vista, FL, USA, 3–7 January 2005; pp. 651–654. [Google Scholar] [CrossRef] [Green Version]
- Celik, B.; Karatepe, E.; Silvestre, S.; Gokmen, N.; Chouder, A. Analysis of Spatial Fixed PV Arrays Configurations to Maximize Energy Harvesting in BIPV Applications. Renew. Energy 2015, 75, 534–540. [Google Scholar] [CrossRef] [Green Version]
- Gurupira, T.; Rix, A.J. PV Simulation Software Comparisons: Pvsyst, Nrel Sam and Pvlib. In Proceedings of the 25th Southern African Universities Power Engineering Conference (SAUPEC 2017), Stellenbosch, South Africa, 30 January–1 February 2017; Available online: https://www.researchgate.net/publication/313249367_PV_SIMULATION_SOFTWARE_COMPARISONS_PVSYST_NREL_SAM_AND_PVLIB?enrichId=rgreq-e788d259e0b7f587850acc24621c272d-XXX&enrichSource=Y292ZXJQYWdlOzMxMzI0OTM2NztBUzo0NTc1OTY3NTE2MTgwNDhAMTQ4NjExMDk3NTM2Nw%3D%3D&el=1_x_2&_esc=publicationCoverPdf (accessed on 29 May 2023).
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M.D. A Review and Evaluation of the State-of-the-Art in PV Solar Power Forecasting: Techniques and Optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]
- Wang, F.; Xuan, Z.; Zhen, Z.; Li, K.; Wang, T.; Shi, M. A Day-Ahead PV Power Forecasting Method Based on LSTM-RNN Model and Time Correlation Modification under Partial Daily Pattern Prediction Framework. Energy Convers. Manag. 2020, 212, 112766. [Google Scholar] [CrossRef]
- Landelius, T.; Andersson, S.; Abrahamsson, R. Modelling and Forecasting PV Production in the Absence of Behind-the-Meter Measurements. Prog. Photovolt. Res. Appl. 2019, 27, 990–998. [Google Scholar] [CrossRef] [Green Version]
- Jakica, N.; Ynag, R.J.; Eisenlohr, J. BIPV Design and Performance Modelling: Tools and Methods; Report IEA-PVPS T15-09:2019; International Energy Agency: Paris, France, 2019; ISBN 9783906042862. Available online: http://iea-pvps.org/ (accessed on 29 May 2023).
- Dorman, M.; Erell, E.; Vulkan, A.; Kloog, I. Shadow: R Package for Geometric Shadow Calculations in an Urban Environment. R J. 2020, 11, 287. [Google Scholar] [CrossRef] [Green Version]
- De Sousa Freitas, J.; Cronemberger, J.; Soares, R.M.; Amorim, C.N.D. Modeling and Assessing BIPV Envelopes Using Parametric Rhinoceros Plugins Grasshopper and Ladybug. Renew. Energy 2020, 160, 1468–1479. [Google Scholar] [CrossRef]
- Polo, J.; Martín-Chivelet, N.; Sanz-Saiz, C. BIPV Modeling with Artificial Neural Networks: Towards a BIPV Digital Twin. Energies 2022, 15, 4173. [Google Scholar] [CrossRef]
- Behera, M.K.; Majumder, I.; Nayak, N. Solar Photovoltaic Power Forecasting Using Optimized Modified Extreme Learning Machine Technique. Eng. Sci. Technol. Int. J. 2018, 21, 428–438. [Google Scholar] [CrossRef]
- Zhang, Y.; Waibel, C.; Schlüter, A. Stochastic Solar Irradiance from Deep Generative Networks and their Application in BIPV Design. IOP Conf. Ser. Earth Environ. Sci. 2022, 1078, 012040. [Google Scholar] [CrossRef]
- Brito, M.; antos, T.; Moura, F.; Pera, D.; Rocha, J. Urban solar potential for vehicle integrated photovoltaics. Transp. Res. D Trans. Environ. 2021, 94, 102810. [Google Scholar] [CrossRef]
- Ota, Y.; Masuda, K.; Araki, K.; Yamaguchi, M. A mobile multipyranometer array for the assessment of solar irradiance incident on a photovoltaic-powered vehicle. Sol. Energy 2019, 184, 84–90. [Google Scholar] [CrossRef]
- von Hinüber, E. Inertial measuring systems with fibre-optic gyroscopes. ATZ Worldw. 2002, 104, 17–20. [Google Scholar] [CrossRef]
- Araki, K.; Ota, Y.; Nishioka, K.; Tobita, H.; Ji, L.; Kelly, G.; Yamaguchi, M. Toward the Standardization of the Car-roof PV–The challenge to the 3-D Sunshine Modeling and Rating of the 3-D Continuously Curved PV Panel. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa, HI, USA, 10–15 June 2018; pp. 0368–0373. [Google Scholar] [CrossRef]
- Itagaki, A.; Okumura, H.; Yamada, A. Preparation of meteorological data set throughout Japan for suitable design of PV systems Photovoltaic Energy Conversion. In Proceedings of the 3rd World Conference on Photovoltaic Energy Conversion, Osaka, Japan, 11–18 May 2003; pp. 11–18. [Google Scholar]
- Shirakawa, K.; Itagaki, A.; Utsunomiya, T. Preparation of hourly solar radiation data on inclined surface (METPV-11) throughout Japan. In Proceedings of the JSES/JWEA Joint Conference, Wakkanai, Japan, 21–22 September 2011. [Google Scholar]








| Conditions | |
|---|---|
| Pyranometer mount | The angular error should be at most 1°. The pyranometers should be fixed tightly to the vehicle structure, with no vibration resonance during driving. The absorber of pyranometers should capture the entire hemisphere and not be shaded by the vehicle body. |
| Pyranometer performance | The time constant should be at most 5 s. The temperature error should be at most ±5%/K. Class B or better |
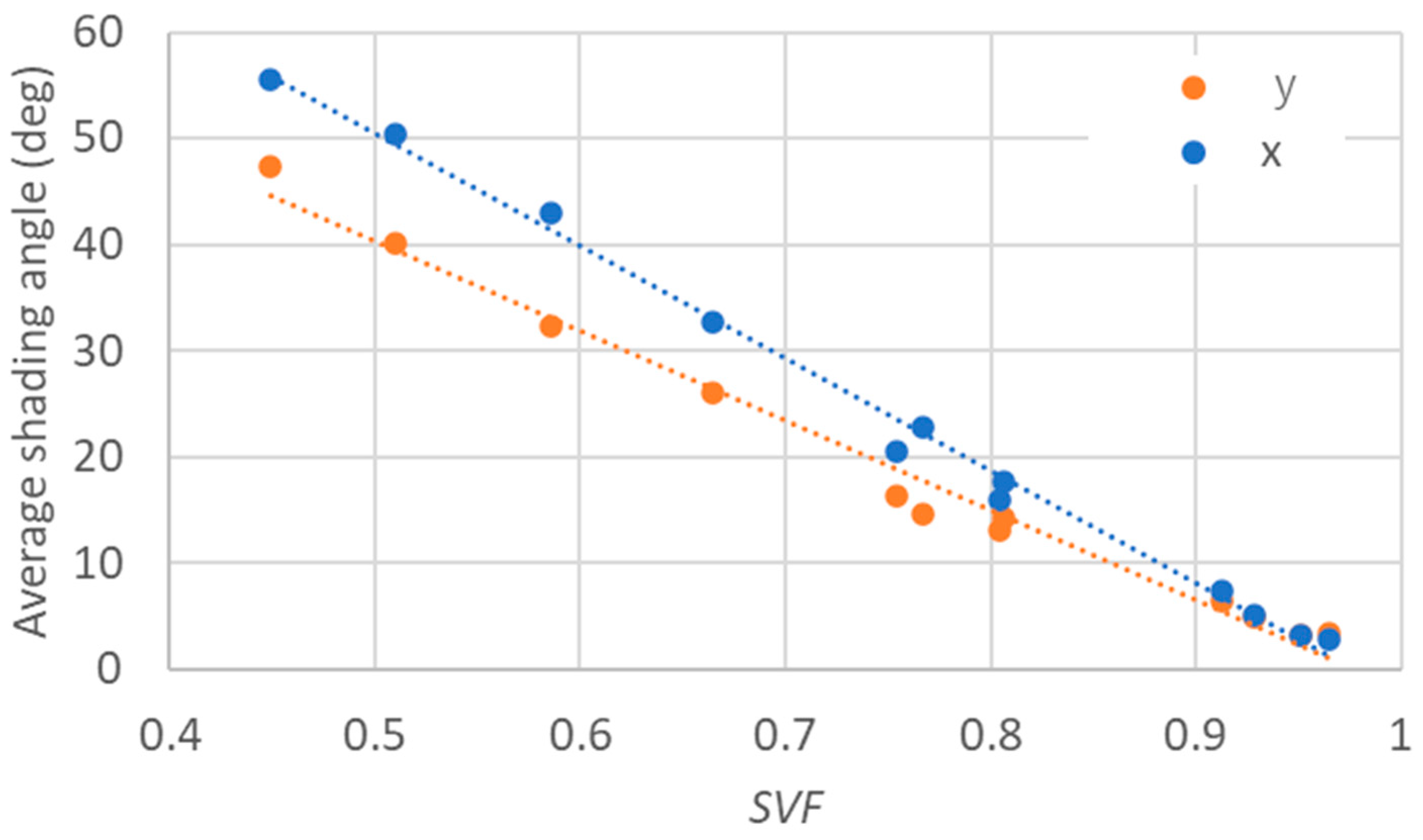
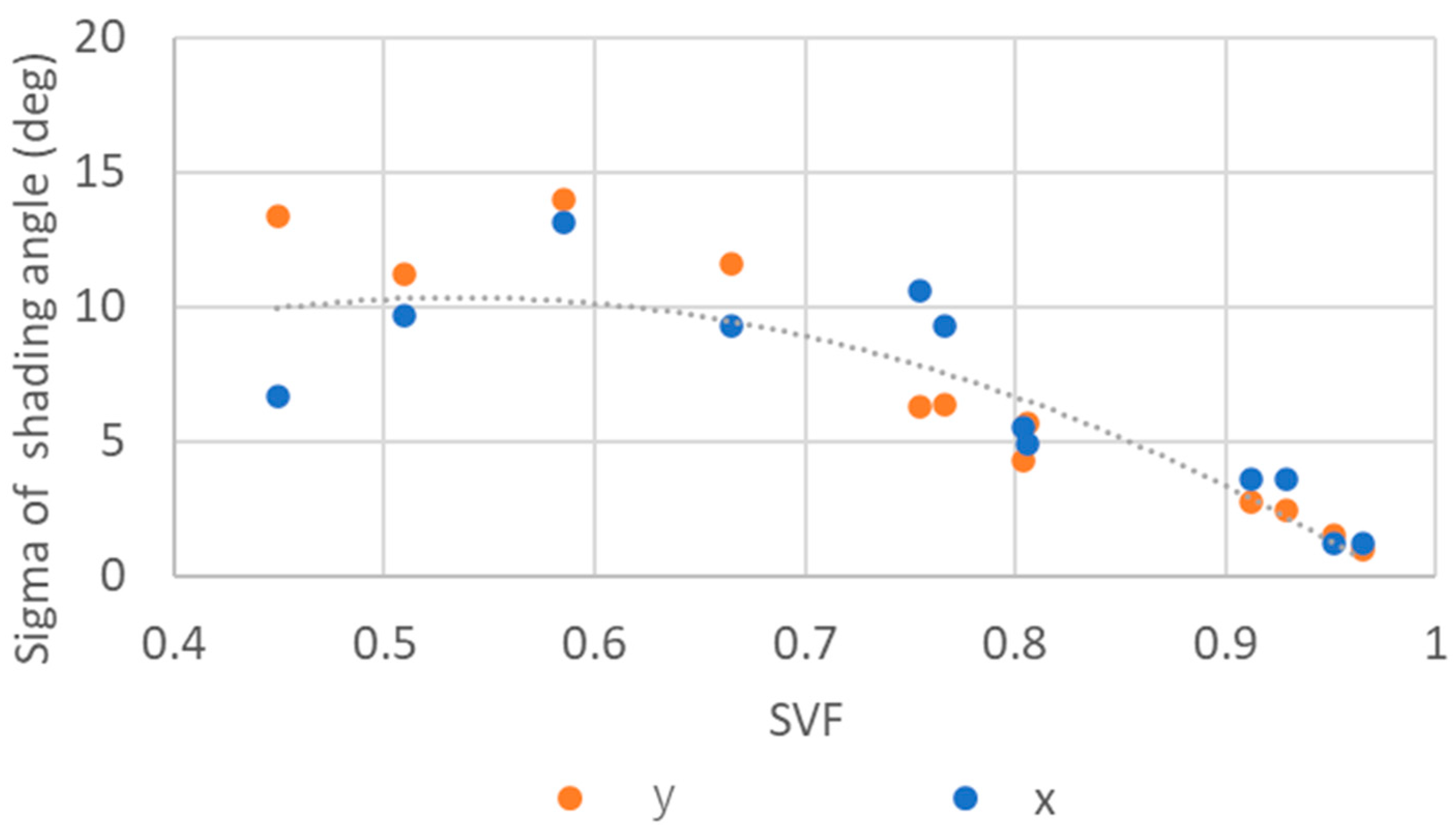
| Category | Orientation | SVF | ||
|---|---|---|---|---|
| Open zone | X | 0.95 | 2.8° | 1.2° |
| Y | 2.2° | |||
| Residential zone | X | 0.75 | 24.0° | 7.9° |
| Y | 19.1° | |||
| Building zone | X | 0.55 | 45.1° | 10.3° |
| Y | 36.0° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Araki, K.; Ota, Y.; Nagaoka, A.; Nishioka, K. 3D Solar Irradiance Model for Non-Uniform Shading Environments Using Shading (Aperture) Matrix Enhanced by Local Coordinate System. Energies 2023, 16, 4414. https://doi.org/10.3390/en16114414
Araki K, Ota Y, Nagaoka A, Nishioka K. 3D Solar Irradiance Model for Non-Uniform Shading Environments Using Shading (Aperture) Matrix Enhanced by Local Coordinate System. Energies. 2023; 16(11):4414. https://doi.org/10.3390/en16114414
Chicago/Turabian StyleAraki, Kenji, Yasuyuki Ota, Akira Nagaoka, and Kensuke Nishioka. 2023. "3D Solar Irradiance Model for Non-Uniform Shading Environments Using Shading (Aperture) Matrix Enhanced by Local Coordinate System" Energies 16, no. 11: 4414. https://doi.org/10.3390/en16114414









