Distributed Generation Forecasting Based on Rolling Graph Neural Network (ROLL-GNN)
Abstract
1. Introduction
- Facing the feature that ‘the fluctuation of the predicted value always lags behind the fluctuation of the real value in the time axis’, this paper attempts to use generation power from neighboring PV panels surrounding the target panel to indicate the lagging information in the prediction model.
- The indicated lagging information is generated by a proposed lead–lag relationship analysis on the correlation model. The output of this model is set to the adjacency matrix in the graph neural network.
- As the sun position and the cloud condition change in real time, this paper creates a rolling graph neural network, which uses the latest real-time lead–lag relationship result. The numerical study shows that the proposed rolling graph neural network performs better than typical traditional prediction models.
2. Model Architecture and Mathematical Modeling
2.1. ROLL-GNN
2.2. Similarity Analysis
2.3. Graph Convolution
3. Experiment
3.1. Dataset
3.2. Experimental Background Information
3.3. Data Preprocessing
3.4. Evaluation and Metrics
3.5. Training
3.6. Baselines
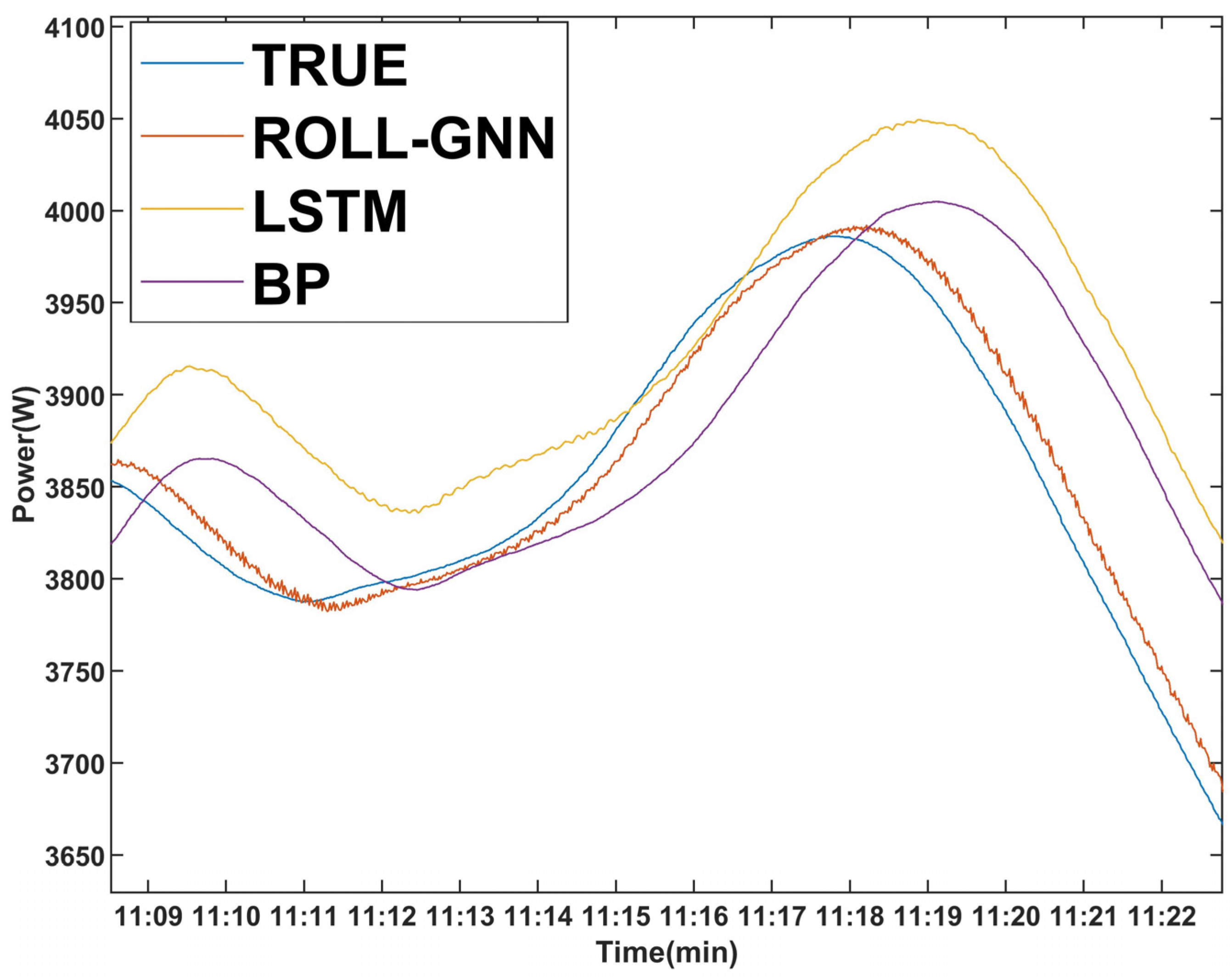
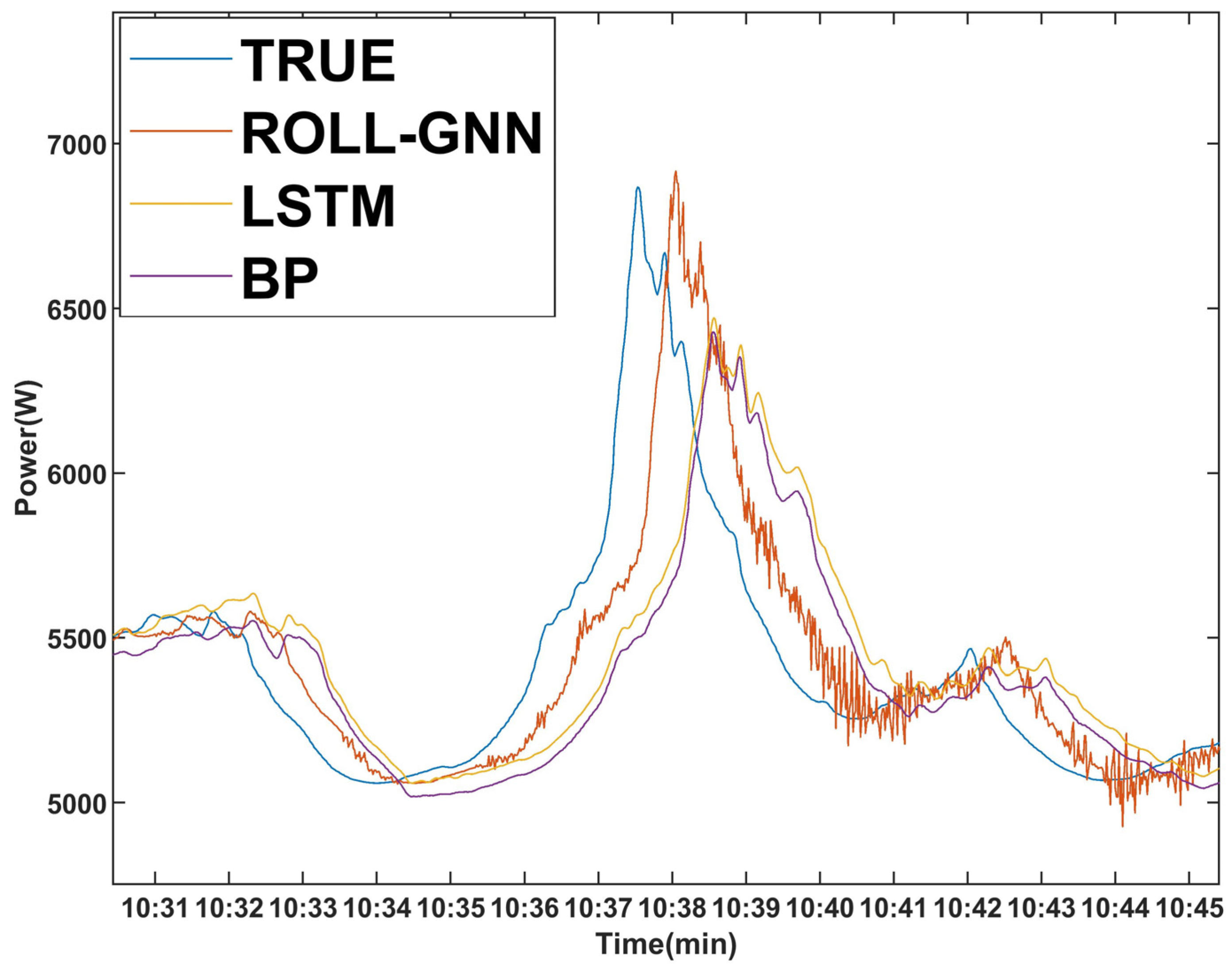
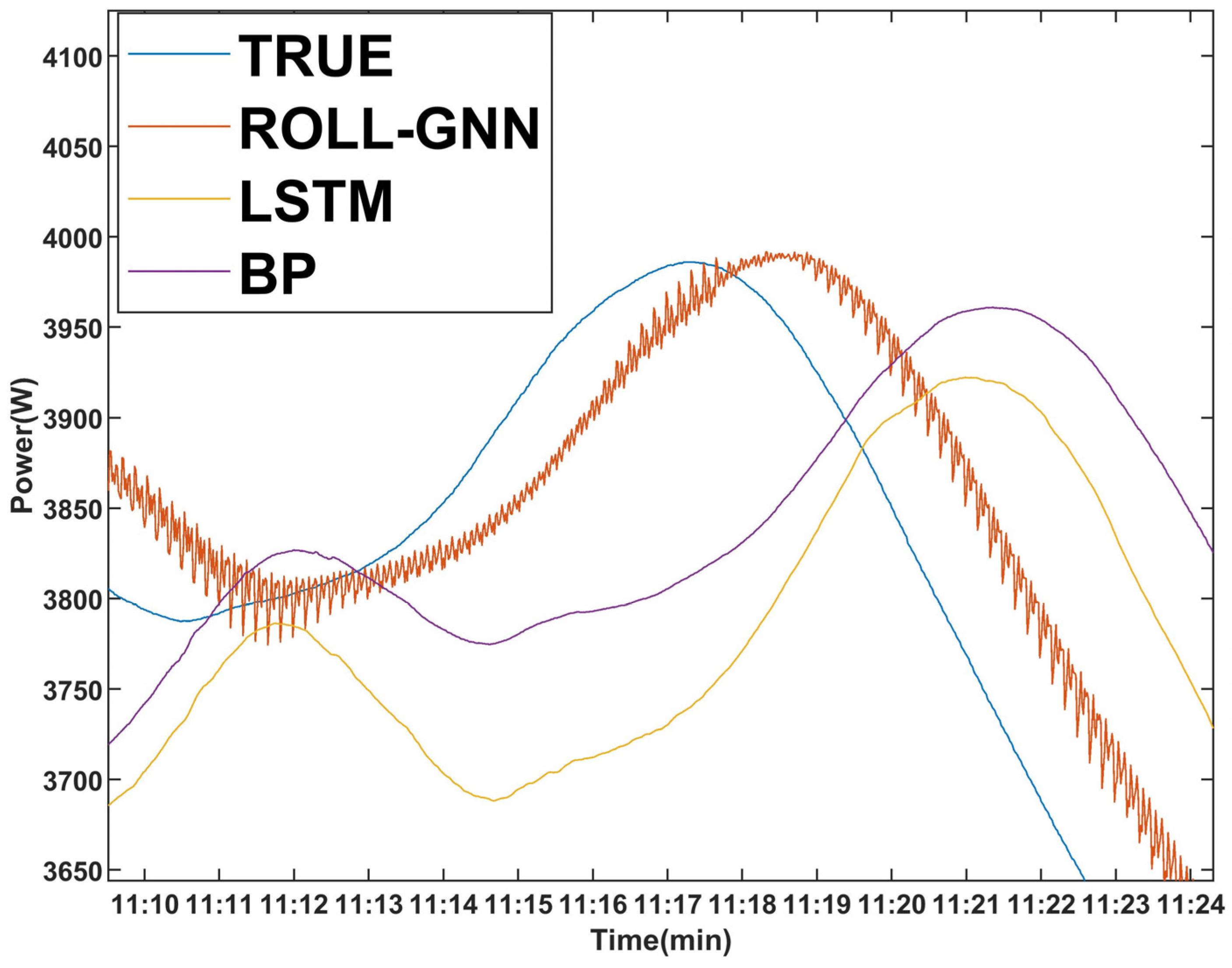
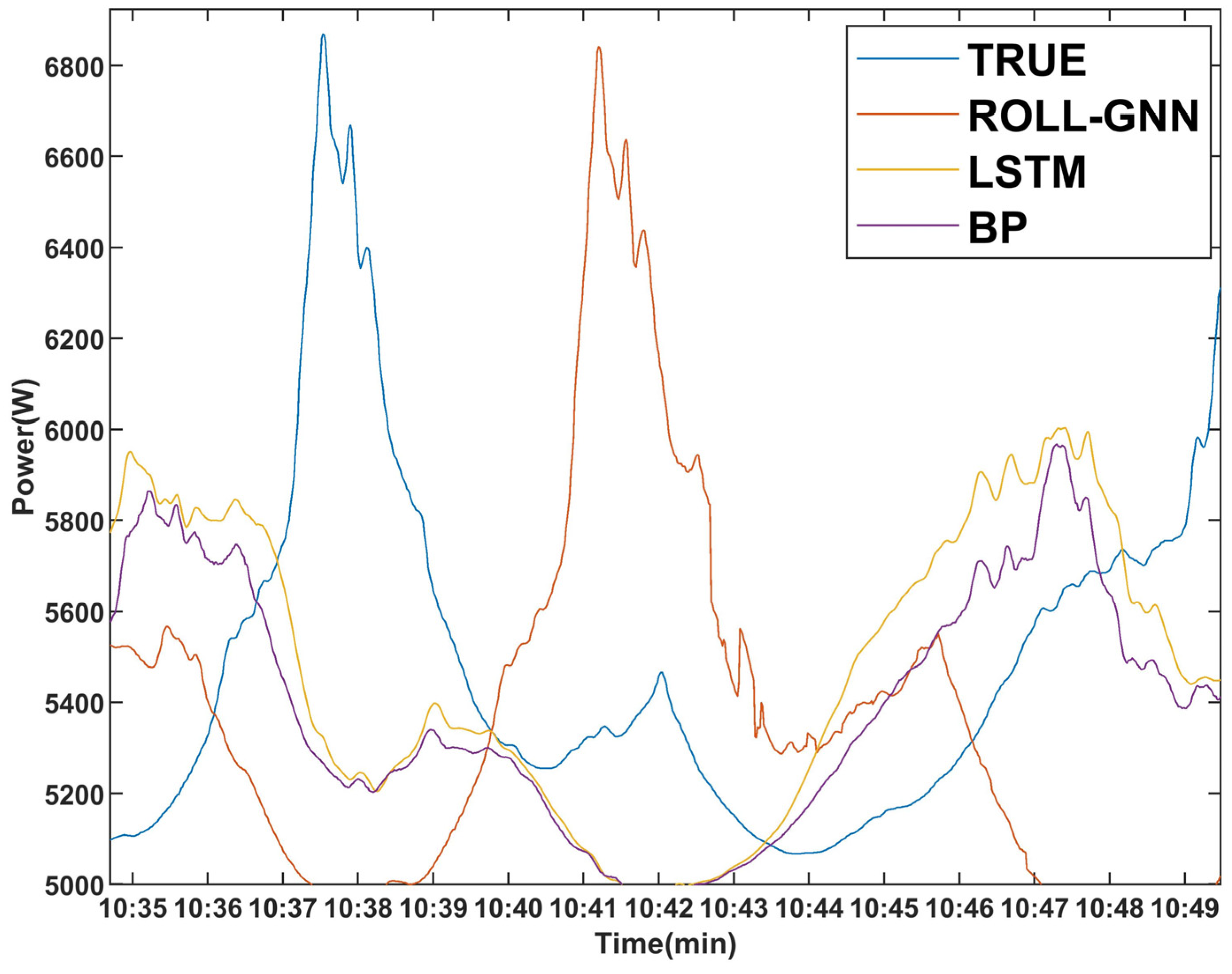
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chaturvedi, D.K.; Isha, I. Solar power forecasting: A review. Int. J. Comput. Appl. 2016, 145, 28–50. [Google Scholar]
- Wu, Y.K.; Chen, C.R.; Abdul Rahman, H. A novel hybrid model for short-term forecasting in PV power generation. Int. J. Photoenergy 2014, 2014, 569249. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, Y.; Wang, H. Review on Monitoring and Operation-Maintenance Technology of Far-Reaching Sea Smart Wind Farms. J. Mar. Sci. Eng. 2022, 10, 820. [Google Scholar] [CrossRef]
- Kou, L.; Li, Y.; Zhang, F.; Gong, X.; Hu, Y.; Yuan, Q.; Ke, W. Review on Monitoring, Operation and Maintenance of Smart Offshore Wind Farms. Sensors 2022, 22, 2822. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Ge, L.; Li, H.; Chi, F. A review on characteristic analysis and prediction method of distributed PV. Electr. Power Constr. 2017, 38, 1–9. [Google Scholar]
- Tan, J.; Deng, C.; Yang, W.; Liang, N.; Li, F. Ultra-short-term photovoltaic power forecasting in microgrid based on adaboost clustering. Autom. Electr. Power Syst. 2017, 41, 33–39. [Google Scholar]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-De-Pison, F.J.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Huang, J.; Perry, M. A semi-empirical approach using gradient boosting and k-nearest neighbors regression for GEFCom2014 probabilistic solar power forecasting. Int. J. Forecast. 2016, 32, 1081–1086. [Google Scholar] [CrossRef]
- Li, Z.; Rahman, S.M.; Vega, R.; Dong, B. A hierarchical approach using machine learning methods in solar photovoltaic energy production forecasting. Energies 2016, 9, 55. [Google Scholar] [CrossRef]
- Sperati, S.; Alessandrini, S.; Delle Monache, L. An application of the ECMWF Ensemble Prediction System for short-term solar power forecasting. Sol. Energy 2016, 133, 437–450. [Google Scholar] [CrossRef]
- Pierro, M.; De Felice, M.; Maggioni, E.; Moser, D.; Perotto, A.; Spada, F.; Cornaro, C. A new approach for regional photovoltaic power estimation and forecast. In Proceedings of the 33rd European Photovoltaic Solar Energy Conference and Exhibition (EUPVSEC), Amsterdam, The Netherlands, 25–29 September 2017. [Google Scholar]
- Chu, Y.; Urquhart, B.; Gohari, S.M.; Pedro, H.T.; Kleissl, J.; Coimbra, C.F. Short-term reforecasting of power output from a 48 MWe solar PV plant. Sol. Energy 2015, 112, 68–77. [Google Scholar] [CrossRef]
- Jang, H.S.; Bae, K.Y.; Park, H.S.; Sung, D.K. Solar power prediction based on satellite images and support vector machine. IEEE Trans. Sustain. Energy 2016, 7, 1255–1263. [Google Scholar] [CrossRef]
- Schmidt, T.; Calais, M.; Roy, E.; Burton, A.; Heinemann, D.; Kilper, T.; Carter, C. Short-term solar forecasting based on sky images to enable higher PV generation in remote electricity networks. Renew. Energy Environ. Sustain. 2017, 2, 23. [Google Scholar] [CrossRef]
- Hu, K.; Cao, S.; Wang, L.; Li, W.; Lv, M. A new ultra-short-term photovoltaic power prediction model based on ground-based cloud images. J. Clean. Prod. 2018, 200, 731–745. [Google Scholar] [CrossRef]
- Geraldi, E.; Romano, F.; Ricciardelli, E. An advanced model for the estimation of the surface solar irradiance under all atmospheric conditions using MSG/SEVIRI data. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2934–2953. [Google Scholar] [CrossRef]
- Wang, F.; Xuan, Z.; Zhen, Z.; Li, K.; Wang, T.; Shi, M. A day-ahead PV power forecasting method based on LSTM-RNN model and time correlation modification under partial daily pattern prediction framework. Energy Convers. Manag. 2020, 212, 112766. [Google Scholar] [CrossRef]
- Wang, L.; Mao, M.; Xie, J.; Liao, Z.; Zhang, H.; Li, H. Accurate solar PV power prediction interval method based on frequency-domain decomposition and LSTM model. Energy 2023, 262, 125592. [Google Scholar] [CrossRef]
- Kleissl, J.; Bosch, J.L.; Kurtz, B.; Lave, M.; Lopez, I.; Mathiesen, P.; Nguyen, A.; Urquhart, B. Recent Advances in Solar Variability Modeling and Solar Forecasting at UC San Diego. In Proceedings of the American Solar Energy Society, 2013 Solar Conference, Baltimore, MD, USA, 16–20 April 2013. [Google Scholar]
- McCandless, T.C.; Haupt, S.E.; Young, G.S. A model tree approach to forecasting solar irradiance variability. Sol. Energy 2015, 120, 514–524. [Google Scholar] [CrossRef]
- Monjoly, S.; André, M.; Calif, R.; Soubdhan, T. Forecast horizon and solar variability influences on the performances of multiscale hybrid forecast model. Energies 2019, 12, 2264. [Google Scholar] [CrossRef]
- Wang, F.; Xuan, Z.; Zhen, Z.; Li, Y.; Li, K.; Zhao, L.; Shafie-khah, M.; Catalão, J.P. A minutely solar irradiance forecasting method based on real-time sky image-irradiance mapping model. Energy Convers. Manag. 2020, 220, 113075. [Google Scholar] [CrossRef]
- Lappalainen, K.; Valkealahti, S. Output power variation of different PV array configurations during irradiance transitions caused by moving clouds. Appl. Energy 2017, 190, 902–910. [Google Scholar] [CrossRef]
- Liu, X.; Wang, J.; Yao, T.; Zhang, P.; Chi, X. Ultra Short Term Distributed Photovoltaic Power Prediction Based on Satellite Remote Sensing. Trans. China Electrotech. Soc. 2022, 31, 1800–1809. [Google Scholar]
- Guanjun, B.; Liubin, T.; Shibo, C.; Jianjun, T.; Linwei, Z.; Fang, X. An ultra-short-term power prediction model based on machine vision for distributed photovoltaic system. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 1148–1152. [Google Scholar]
- Simeunovic, J.; Schubnel, B.; Alet, P.-J.; Carrillo, R.E. Spatio-temporal graph neural networks for multi-site PV power forecasting. IEEE Trans. Sustain. Energy 2021, 13, 1210–1220. [Google Scholar] [CrossRef]
- Tiwari, S.; Sabzehgar, R.; Rasouli, M. Short term solar irradiance forecast based on image processing and cloud motion detection. In Proceedings of the 2019 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 7–8 February 2019; pp. 1–6. [Google Scholar]
- Kong, W.; Jia, Y.; Dong, Z.Y.; Meng, K.; Chai, S. Hybrid approaches based on deep whole-sky-image learning to photovoltaic generation forecasting. Appl. Energy 2020, 280, 115875. [Google Scholar] [CrossRef]
- Pothineni, D.; Oswald, M.R.; Poland, J.; Pollefeys, M. Kloudnet: Deep learning for sky image analysis and irradiance forecasting. In Proceedings of the Pattern Recognition: 40th German Conference, GCPR 2018, Stuttgart, Germany, 9–12 October 2018; Proceedings 40. Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 535–551. [Google Scholar]
- Xu, X.; Niu, D.; Wang, Q.; Wang, P.; Wu, D.D. Intelligent forecasting model for regional power grid with distributed generation. IEEE Syst. J. 2015, 11, 1836–1845. [Google Scholar] [CrossRef]
- Changsong, C.; Shanxu, D.; Jinjun, Y. Research of energy management system of distributed generation based on power forecasting. In Proceedings of the 2008 International Conference on Electrical Machines and Systems, Wuhan, China, 17–20 October 2008; pp. 2734–2737. [Google Scholar]
- Agoua, X.G.; Girard, R.; Kariniotakis, G. Short-term spatio-temporal forecasting of photovoltaic power production. IEEE Trans. Sustain. Energy 2017, 9, 538–546. [Google Scholar] [CrossRef]
- Yang, C.; Thatte, A.A.; Xie, L. Multitime-scale data-driven spatio-temporal forecast of photovoltaic generation. IEEE Trans. Sustain. Energy 2014, 6, 104–112. [Google Scholar] [CrossRef]
- Chai, S.; Xu, Z.; Jia, Y.; Wong, W.K. A robust spatiotemporal forecasting framework for photovoltaic generation. IEEE Trans. Smart Grid 2020, 11, 5370–5382. [Google Scholar] [CrossRef]
- Jeong, J.; Kim, H. Multi-site photovoltaic forecasting exploiting spacetime convolutional neural network. Energies 2019, 12, 4490. [Google Scholar] [CrossRef]
- Zhu, Q.; Chen, J.; Zhu, L.; Duan, X.; Liu, Y. Wind speed prediction with spatio–temporal correlation: A deep learning approach. Energies 2018, 11, 705. [Google Scholar] [CrossRef]
- Zhang, C.; Peng, T.; Nazir, M.S. A novel integrated photovoltaic power forecasting model based on variational mode decomposition and CNN-BiGRU considering meteorological variables. Electr. Power Syst. Res. 2022, 213, 108796. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, Y.; Yang, L.; Liu, Q.; Yan, K.; Du, Y. Short-term photovoltaic power forecasting based on long short term memory neural network and attention mechanism. IEEE Access 2019, 7, 78063–78074. [Google Scholar] [CrossRef]
- Shih, S.-Y.; Sun, F.-K.; Lee, H.-Y. Temporal pattern attention for multivariate time series forecasting. Mach. Learn. 2019, 108, 1421–1441. [Google Scholar] [CrossRef]
- Ortega, A.; Frossard, P.; Kovăcevi’c, J.; Moura, J.M.F.; Vandergheynst, P. Graph signal processing: Overview, challenges, and applications. Proc. IEEE 2018, 106, 808–828. [Google Scholar] [CrossRef]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A. review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4–24. [Google Scholar] [CrossRef]
- Zhang, R.; Ma, H.; Hua, W.; Saha, T.K.; Zhou, X. Data-driven photovoltaic generation forecasting based on a Bayesian network with spatial–temporal correlation analysis. IEEE Trans. Ind. Inform. 2019, 16, 1635–1644. [Google Scholar] [CrossRef]
- Lai, C.S.; Tao, Y.; Xu, F.; Ng, W.W.; Jia, Y.; Yuan, H.; Huang, C.; Lai, L.L.; Xu, Z.; Locatelli, G. A robust correlation analysis framework for imbalanced and dichotomous data with uncertainty. Inf. Sci. 2019, 470, 58–77. [Google Scholar] [CrossRef]
- Chaudhary, P.; Rizwan, M. Short term solar energy forecasting using GNN integrated wavelet-based approach. Int. J. Renew. Energy Technol. 2019, 10, 229–246. [Google Scholar] [CrossRef]
- Chaturvedi, D.K. Forecasting of solar power using quantum ga-gnn. Int. J. Comput. Appl. 2015, 975, 8887. [Google Scholar] [CrossRef]
- Wu, D.; Lin, W. Efficient residential electric load forecasting via transfer learning and graph neural networks. IEEE Trans. Smart Grid 2022, 14, 2423–2431. [Google Scholar] [CrossRef]
- Zhang, D.; Ren, Z.; Bi, Y.; Zhou, D.; Bi, Y. Power load forecasting based on grey neural network. In Proceedings of the 2008 IEEE International Symposium on Industrial Electronics, Cambridge, UK, 30 June–2 July 2008; pp. 1885–1889. [Google Scholar]
- Chaudhary, P.; Rizwan, M. Short-term PV power forecasting using generalized neural network and weather-type classification. In Advances in Energy and Power Systems: Select Proceedings of ICAEDC 2017; Springer: Singapore, 2018; pp. 13–20. [Google Scholar]
- Karimi, A.M.; Wu, Y.; Koyuturk, M.; French, R.H. Spatiotemporal graph neural network for performance prediction of photovoltaic power systems. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 15323–15330. [Google Scholar]
- Chaturvedi, D.K.; Premdayal, S.A.; Chandiok, A. Short-term load forecasting using soft computing techniques. Int. J. Commun. Netw. Syst. Sci. 2010, 3, 273. [Google Scholar] [CrossRef]






| Model Metrics | Model Parameter |
|---|---|
| Number of graph convolutional layers | 2 |
| Number of hidden neurons in graph convolutional layer | 80 |
| Number of fully connected layers | 2 |
| Number of hidden neurons in the fully connected layer | 20 |
| The number of input neurons | 500 |
| The number of output neurons | 1 |
| Algebra of iterations | 50 |
| Advance Time | Type of Algorithm | MSE (W) | MAPE (%) |
|---|---|---|---|
| 60 s | ROLL-GNN | 8273.69 | 1.72 |
| LSTM | 15,353.03 | 3.82 | |
| BP | 25,066.60 | 5.73 | |
| 180 s | ROLL-GNN | 18,643.24 | 4.65 |
| LSTM BP | 44,720.29 33,028.18 | 8.51 6.24 | |
| 300 s | ROLL-GNN | 41,969.19 | 7.86 |
| LSTM BP | 48,628.93 38,282.85 | 10.79 7.98 |
| Advance Time | Type of Algorithm | MSE (W) | MAPE (%) |
|---|---|---|---|
| 60 s | ROLL-GNN | 8110.58 | 1.68 |
| LSTM | 15,944.51 | 3.21 | |
| BP | 24,608.95 | 5.34 | |
| 180 s | ROLL-GNN | 18,272.51 | 3.96 |
| LSTM BP | 40,646.83 32,191.51 | 7.65 6.52 | |
| 300 s | ROLL-GNN | 31,641.34 | 7.36 |
| LSTM BP | 49,869.71 35,665.77 | 8.96 7.56 |
| Advance Time | Type of Algorithm | MSE (W) | MAPE (%) |
|---|---|---|---|
| 60 s | ROLL-GNN | 15,708.30 | 3.11 |
| LSTM | 19,995.35 | 4.52 | |
| BP | 26,807.99 | 5.63 | |
| 180 s | ROLL-GNN | 20,159.35 | 4.23 |
| LSTM BP | 43,766.11 37,250.11 | 8.13 7.36 | |
| 300 s | ROLL-GNN | 33,036.11 | 8.56 |
| LSTM BP | 44,821.59 43,763.56 | 9.25 8.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, J.; Kang, Z.; Lai, C.S.; Wang, Y.; Xu, F.; Yuan, H. Distributed Generation Forecasting Based on Rolling Graph Neural Network (ROLL-GNN). Energies 2023, 16, 4436. https://doi.org/10.3390/en16114436
Xue J, Kang Z, Lai CS, Wang Y, Xu F, Yuan H. Distributed Generation Forecasting Based on Rolling Graph Neural Network (ROLL-GNN). Energies. 2023; 16(11):4436. https://doi.org/10.3390/en16114436
Chicago/Turabian StyleXue, Jizhong, Zaohui Kang, Chun Sing Lai, Yu Wang, Fangyuan Xu, and Haoliang Yuan. 2023. "Distributed Generation Forecasting Based on Rolling Graph Neural Network (ROLL-GNN)" Energies 16, no. 11: 4436. https://doi.org/10.3390/en16114436
APA StyleXue, J., Kang, Z., Lai, C. S., Wang, Y., Xu, F., & Yuan, H. (2023). Distributed Generation Forecasting Based on Rolling Graph Neural Network (ROLL-GNN). Energies, 16(11), 4436. https://doi.org/10.3390/en16114436







