Modeling Annual Electricity Production and Levelized Cost of Energy from the US East Coast Offshore Wind Energy Lease Areas
Abstract
:1. Introduction
1.1. Offshore Wind Energy
1.2. Predicting Power Production: The Role of Wakes
1.3. Levelized Cost of Energy Modeling
1.4. Objectives and Structure
2. Methods
2.1. Wind Farm Power Production and Wake Modeling
- (i)
- To generate the freestream wind climate, 40 years of hourly u (west–east) and v (south–north) wind components at 100 m height from ERA5 reanalysis [10] in the center of each LA group were used to compute the wind direction frequency and Weibull scale and shape distribution parameters (c and k) [49,50] of the wind speed probability distribution in 30° sectors using maximum likelihood estimation:This wind climate (Figure 2) was used for both microscale wake models. However, it must be acknowledged that the assumption of an average wind speed and direction distribution may not reflect the variability of offshore wind conditions. In the ERA5 data, all LA groups were dominated by flow from the southwest sector, but the highest wind speeds (and, hence, Weibull scale factor) in LA groups NE, NJ and VA were associated with northwesterly flow due, in part, to longer over water fetch for northwesterly than southwesterly flow (Figure 1).
- (ii)
- In the NOJ model, k was set to 0.04 (Equations (4) and (5)).
- (iii)
- For the Fuga wake model, default parameters were used. Offshore roughness length (z0) was set to 0.0001 m, the atmospheric boundary layer was assumed to be near-neutral and the PBLH = 400 m.
- (iv)
- The wind turbine power (P) and thrust (Ct) coefficients that describe the power production and thrust on the flow as a function of inflow wind speed derive from the 15 MW IEA reference wind turbine [24]. Thus, annual energy production (AEP) is the total power from wind turbines in each LA group computed as the sum of power from all wind turbines derived using the Weibull distributed wind speeds in each wind direction sector.
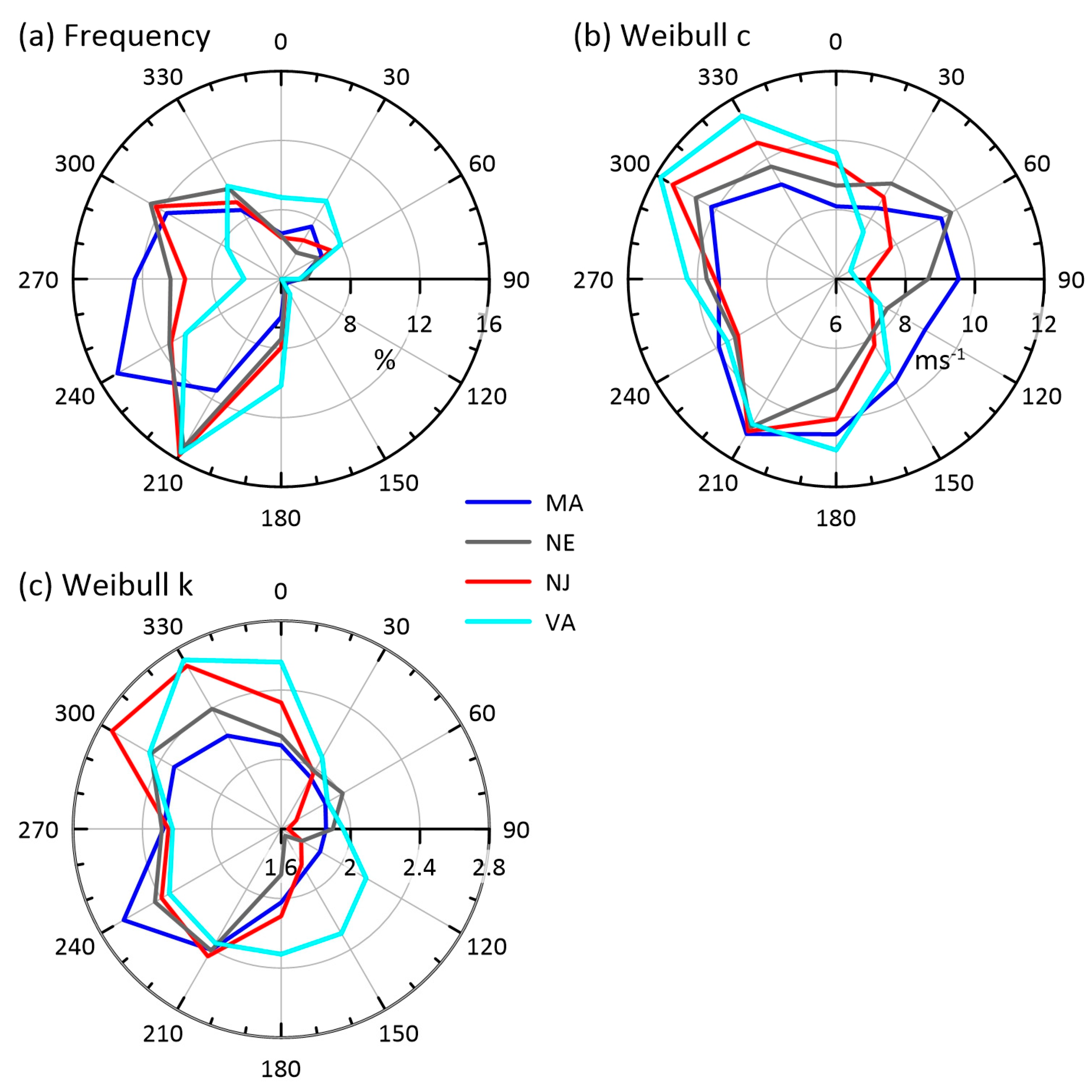
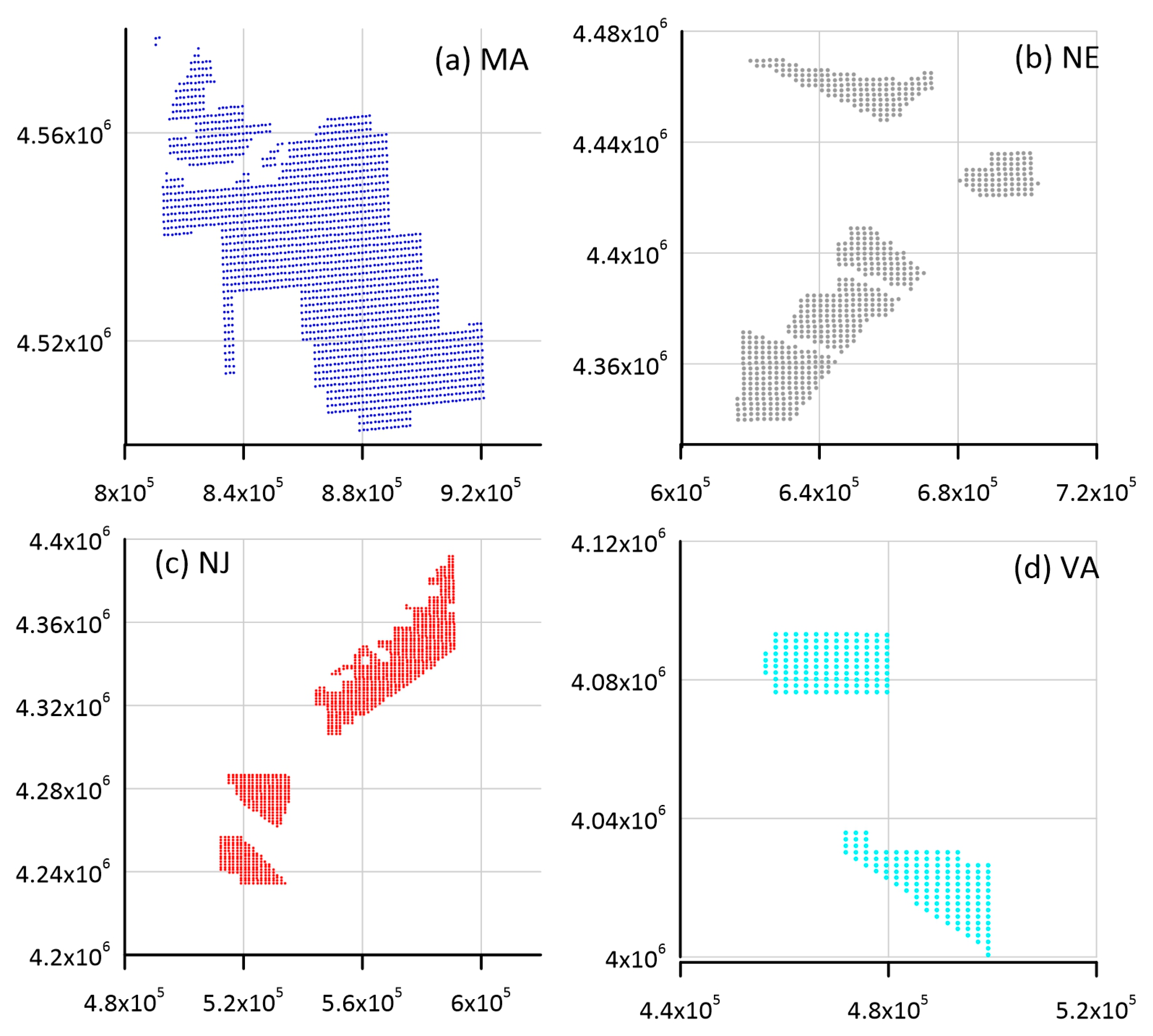
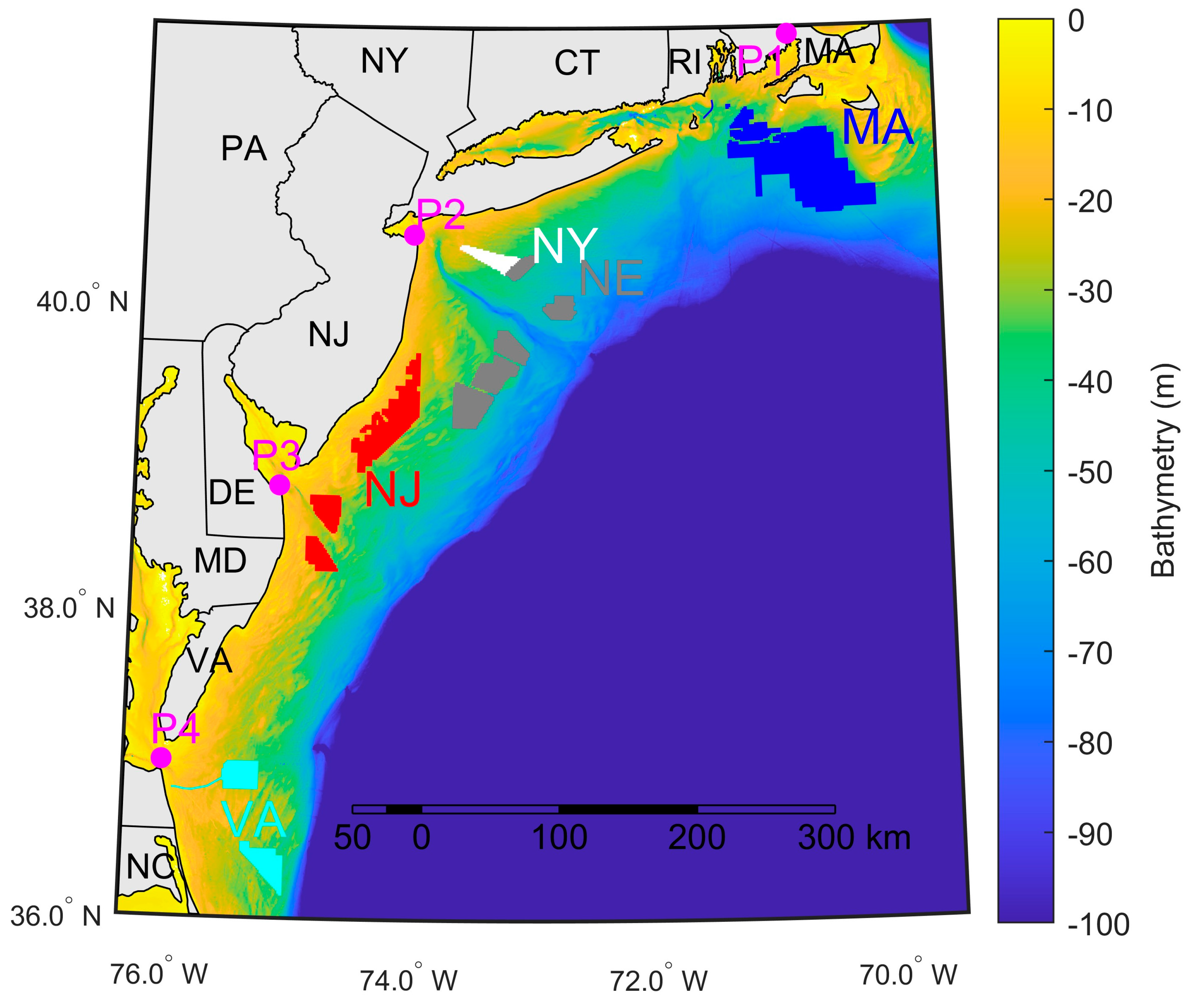
2.2. Lease Areas and Wind Turbine Layouts
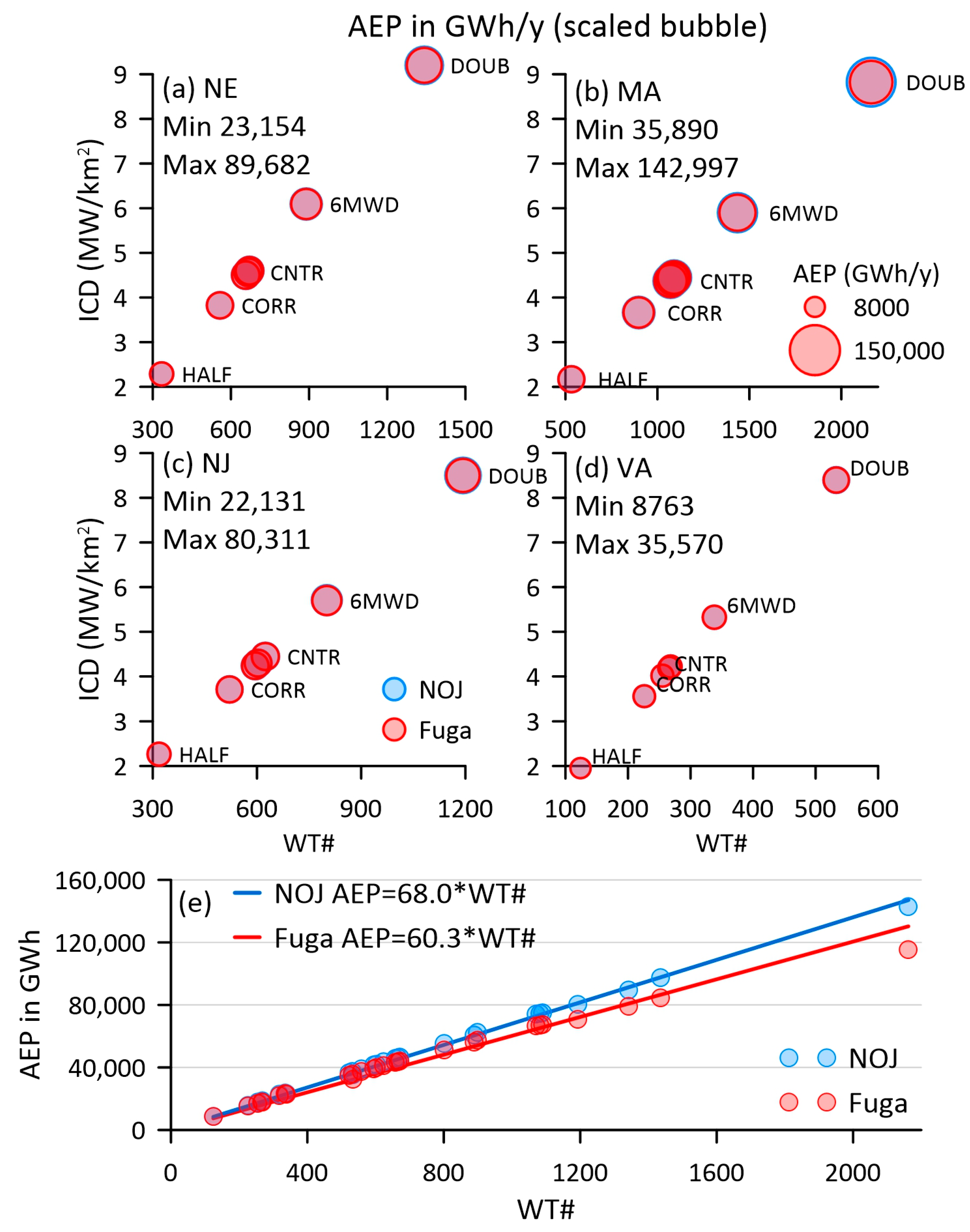
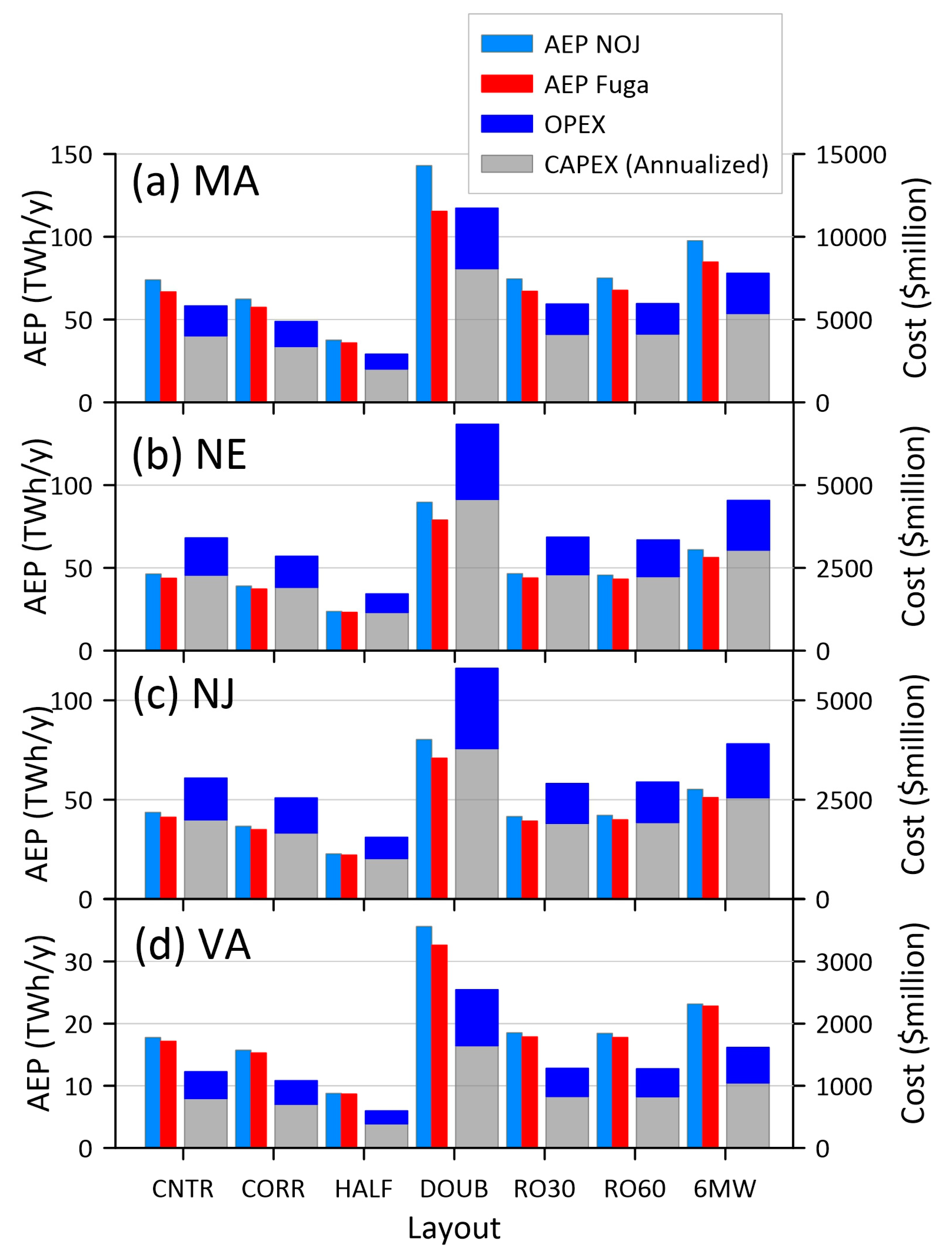
- CNTR: In this layout, wind turbines were deployed on an equally spaced north–south and east–west grid with a spacing of 1.85 km. For the 15 MW IEA reference wind turbines, this equated to a spacing of 7.7 D and an ICD of approximately 4.3 MW/km2. The LA groups; MA, NE, NJ and VA had 1071, 666, 624 and 255 wind turbines, respectively, for this layout (Figure 3).
- CORR: In this layout, every sixth north–south column of wind turbines was removed to generate a marine corridor. This led to an average ICD of approximately 3.5 MW/km2. Implementation of these corridors may enable multiple use of these areas [51] (e.g., enable fishing), address shipping safety concerns [52] and mitigate wildlife impacts [53].
- HALF: In this layout, wind turbines were deployed with increased spacing in the west–east and north–south directions to reduce to half the number of turbines relative to CNTR. The resulting ICD was approximately 2.1 MW/km2.
- DOUBLE: In this layout, wind turbines were deployed with decreased spacing in the west–east and north–south directions to double the number of turbines relative to CNTR. The resulting ICD was approximately 8.6 MW/km2.
- RO30: In this layout, wind turbines were deployed on an equally spaced north–south and east–west grid with a turbine spacing of 1.85 km (as in CNTR), the locations were then rotated by +30° (i.e., in a clockwise direction) around a center axis in order to increase the wind turbine separation along the south-southwest to north-northeast prevailing wind direction (Figure 2).
- RO60: In this layout, wind turbines were deployed on an equally spaced north–south and east–west grid with a turbine spacing of 1.85 km (as in CNTR), the locations were then rotated by +60° (i.e., in a clockwise direction) around a center axis in order to increase the wind turbine separation along the west-southwest to east-northeast prevailing wind direction (Figure 2).
- 6MWD: In this layout, wind turbines were deployed on an equally spaced north–south and east–west grid with an approximate separation of 1.6 km for an ICD of approximately 6 MW/km2.
| Lease Area Group (Area km2) | CNTR | CORR | HALF | DOUB | RO30 | RO60 | 6MWD |
|---|---|---|---|---|---|---|---|
| MA (3675) | 1071 | 898 | 532 | 2162 | 1082 | 1090 | 1475 |
| NE (2188) | 666 | 558 | 334 | 1342 | 671 | 657 | 889 |
| NJ (2105) | 624 | 521 | 318 | 1193 | 595 | 603 | 801 |
| VA (952) | 255 | 226 | 124 | 533 | 268 | 266 | 338 |
2.3. Levelized Cost of Energy (LCoE)
3. Results
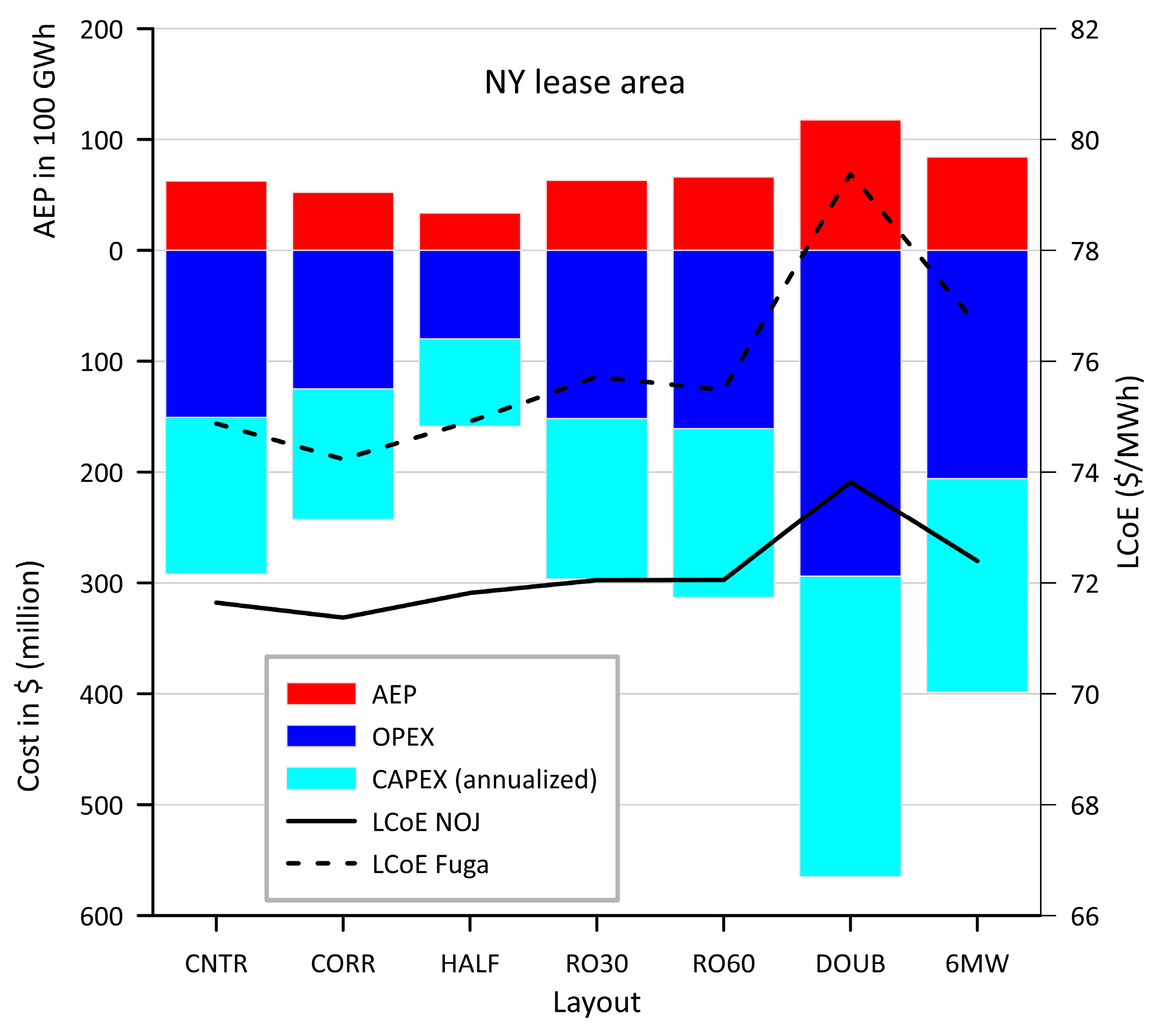
3.1. Illustrative Example of Research Methodology and Results: NY Lease Area
3.2. Wind Farm Modeling of Wakes and AEP for the LA Groups
- Differences in the driving wind climate—here, we used 40 years of ERA5 output, while the simulations with WRF used representative flow conditions that were frequency weighted to generate a representative CF.
- The disparity in modeled CF may also reflect the fundamental differences in terms of the ability of WRF to capture variations in PBLH and the propagation of wakes from remote lease areas. The WRF simulations indicated that, under some flow conditions, the wind farm wake (defined as the area with velocity deficits due to wakes of over 5% of the freestream wind speed) extended up to 90 km from the largest wind farm clusters, and the frequency weighted net wake extent was 2.6 times the areal extent of the lease areas.
- Conversely, here, the LA groups were modeled individually with NOJ and Fuga. Furthermore, the NOJ parameterization, which used the sum of squares of the velocity deficit when wakes were merged, tended to generate wake recovery within a few kilometers of the downstream edge of a lease area. Fuga tended to generate more persistent wakes but still did not capture the full extent of the modification of the boundary-layer and the downwind propagation of whole wind farm wakes.

3.3. LCoE Modeling
3.4. Modeling Uncertainties
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| LA Group | Wake Model | Layout | LA Area (km2) | WT | AEP (GWh) | AEP per WT (GWh) | AEP/km2 (GWh) | ICD MW/km2 | CF (%) | Min Dist (km) | Min Dist D |
|---|---|---|---|---|---|---|---|---|---|---|---|
| NY | NOJ | CNTR | 321 | 89 | 6242 | 70 | 19 | 4.2 | 53.4 | 1.85 | 7.7 |
| NY | NOJ | CORR | 321 | 74 | 5216 | 70 | 16 | 3.5 | 53.6 | 1.85 | 7.7 |
| NY | NOJ | HALF | 321 | 47 | 3357 | 71 | 10 | 2.2 | 54.4 | 2.62 | 10.9 |
| NY | NOJ | DOUB | 321 | 174 | 11,775 | 68 | 37 | 8.1 | 51.5 | 1.31 | 5.5 |
| NY | NOJ | RO30 | 321 | 90 | 6298 | 70 | 20 | 4.2 | 53.3 | 1.85 | 7.7 |
| NY | NOJ | RO60 | 321 | 95 | 6649 | 70 | 21 | 4.4 | 53.3 | 1.85 | 7.7 |
| NY | NOJ | 6MWD | 321 | 122 | 8446 | 69 | 26 | 5.7 | 52.7 | 1.57 | 6.5 |
| NY | Fuga | CNTR | 321 | 89 | 6105 | 69 | 19 | 4.2 | 52.2 | 1.85 | 7.7 |
| NY | Fuga | CORR | 321 | 74 | 5126 | 69 | 16 | 3.5 | 52.7 | 1.85 | 7.7 |
| NY | Fuga | HALF | 321 | 47 | 3326 | 71 | 10 | 2.2 | 53.9 | 2.62 | 10.9 |
| NY | Fuga | DOUB | 321 | 174 | 11,173 | 64 | 35 | 8.1 | 48.9 | 1.31 | 5.5 |
| NY | Fuga | RO30 | 321 | 90 | 6154 | 68 | 19 | 4.2 | 52.0 | 1.85 | 7.7 |
| NY | Fuga | RO60 | 321 | 95 | 6499 | 68 | 20 | 4.4 | 52.1 | 1.85 | 7.7 |
| NY | Fuga | 6MWD | 321 | 122 | 8162 | 67 | 25 | 5.7 | 50.9 | 1.57 | 6.5 |
| MA | NOJ | CNTR | 3675 | 1071 | 73,975 | 69 | 20 | 4.4 | 52.6 | 1.85 | 7.7 |
| MA | NOJ | CORR | 3675 | 898 | 62,382 | 69 | 17 | 3.7 | 52.9 | 1.85 | 7.7 |
| MA | NOJ | HALF | 3675 | 532 | 37,610 | 71 | 10 | 2.2 | 53.8 | 2.62 | 10.9 |
| MA | NOJ | DOUB | 3675 | 2162 | 142,997 | 66 | 39 | 8.8 | 50.3 | 1.31 | 5.5 |
| MA | NOJ | RO30 | 3675 | 1082 | 74,570 | 69 | 20 | 4.4 | 52.4 | 1.85 | 7.7 |
| MA | NOJ | RO60 | 3675 | 1090 | 75,105 | 69 | 20 | 4.4 | 52.4 | 1.85 | 7.7 |
| MA | NOJ | 6MWD | 3675 | 1475 | 97,651 | 66 | 27 | 6.0 | 50.4 | 1.57 | 6.5 |
| MA | Fuga | CNTR | 3675 | 1071 | 66,753 | 62 | 18 | 4.4 | 47.4 | 1.85 | 7.7 |
| MA | Fuga | CORR | 3675 | 898 | 57,360 | 64 | 16 | 3.7 | 48.6 | 1.85 | 7.7 |
| MA | Fuga | HALF | 3675 | 532 | 35,890 | 67 | 10 | 2.2 | 51.3 | 2.62 | 10.9 |
| MA | Fuga | DOUB | 3675 | 2162 | 115,393 | 53 | 31 | 8.8 | 40.6 | 1.31 | 5.5 |
| MA | Fuga | RO30 | 3675 | 1082 | 67,057 | 62 | 18 | 4.4 | 47.2 | 1.85 | 7.7 |
| MA | Fuga | RO60 | 3675 | 1090 | 67,657 | 62 | 18 | 4.4 | 47.2 | 1.85 | 7.7 |
| MA | Fuga | 6MWD | 3675 | 1513 | 84,757 | 56 | 23 | 6.0 | 42.6 | 1.57 | 6.5 |
| NJ | NOJ | CNTR | 2105 | 624 | 43,635 | 70 | 21 | 4.4 | 53.2 | 1.85 | 7.7 |
| NJ | NOJ | CORR | 2105 | 521 | 36,616 | 70 | 17 | 3.7 | 53.5 | 1.85 | 7.7 |
| NJ | NOJ | HALF | 2105 | 318 | 22,708 | 71 | 11 | 2.3 | 54.3 | 2.62 | 10.9 |
| NJ | NOJ | DOUB | 2105 | 1193 | 80,311 | 67 | 38 | 8.5 | 51.2 | 1.31 | 5.5 |
| NJ | NOJ | RO30 | 2105 | 595 | 41,524 | 70 | 20 | 4.2 | 53.1 | 1.85 | 7.7 |
| NJ | NOJ | RO60 | 2105 | 603 | 42,143 | 70 | 20 | 4.3 | 53.2 | 1.85 | 7.7 |
| NJ | NOJ | 6MWD | 2105 | 801 | 55,321 | 69 | 26 | 5.7 | 52.6 | 1.57 | 6.5 |
| NJ | Fuga | CNTR | 2105 | 624 | 41,191 | 66 | 20 | 4.4 | 50.2 | 1.85 | 7.7 |
| NJ | Fuga | CORR | 2105 | 521 | 34,963 | 67 | 17 | 3.7 | 51.1 | 1.85 | 7.7 |
| NJ | Fuga | HALF | 2105 | 318 | 22,131 | 70 | 11 | 2.3 | 53.0 | 2.62 | 10.9 |
| NJ | Fuga | DOUB | 2105 | 1193 | 70,894 | 59 | 34 | 8.5 | 45.2 | 1.31 | 5.5 |
| NJ | Fuga | RO30 | 2105 | 595 | 39,239 | 66 | 19 | 4.2 | 50.2 | 1.85 | 7.7 |
| NJ | Fuga | RO60 | 2105 | 603 | 39,865 | 66 | 19 | 4.3 | 50.3 | 1.85 | 7.7 |
| NJ | Fuga | 6MWD | 2105 | 813 | 51,109 | 63 | 24 | 5.8 | 47.8 | 1.57 | 6.5 |
| VA | NOJ | CNTR | 952 | 255 | 17,763 | 70 | 19 | 4.0 | 53.0 | 1.85 | 7.7 |
| VA | NOJ | CORR | 952 | 226 | 15,731 | 70 | 17 | 3.6 | 53.0 | 1.85 | 7.7 |
| VA | NOJ | HALF | 952 | 124 | 8786 | 71 | 9 | 2.0 | 53.9 | 2.62 | 10.9 |
| VA | NOJ | DOUB | 952 | 533 | 35,570 | 67 | 37 | 8.4 | 50.8 | 1.31 | 5.5 |
| VA | NOJ | RO30 | 952 | 268 | 18,525 | 69 | 19 | 4.2 | 52.6 | 1.85 | 7.7 |
| VA | NOJ | RO60 | 952 | 266 | 18,439 | 69 | 19 | 4.2 | 52.8 | 1.85 | 7.7 |
| VA | NOJ | 6MWD | 952 | 338 | 23,153 | 69 | 24 | 5.3 | 52.1 | 1.57 | 6.5 |
| VA | Fuga | CNTR | 952 | 255 | 17,169 | 67 | 18 | 4.0 | 51.2 | 1.85 | 7.7 |
| VA | Fuga | CORR | 952 | 226 | 15,731 | 70 | 17 | 3.6 | 53.0 | 1.85 | 7.7 |
| VA | Fuga | HALF | 952 | 124 | 8763 | 71 | 9 | 2.0 | 53.8 | 2.62 | 10.9 |
| VA | Fuga | DOUB | 952 | 533 | 32,627 | 61 | 34 | 8.4 | 46.6 | 1.31 | 5.5 |
| VA | Fuga | RO30 | 952 | 268 | 17,875 | 67 | 19 | 4.2 | 50.8 | 1.85 | 7.7 |
| VA | Fuga | RO60 | 952 | 266 | 17,780 | 67 | 19 | 4.2 | 50.9 | 1.85 | 7.7 |
| VA | Fuga | 6MWD | 952 | 338 | 23,153 | 69 | 24 | 5.3 | 52.1 | 1.57 | 6.5 |
| NE | NOJ | CNTR | 2188 | 666 | 46,317 | 70 | 21 | 4.6 | 52.9 | 1.85 | 7.7 |
| NE | NOJ | CORR | 2188 | 558 | 39,018 | 70 | 18 | 3.8 | 53.2 | 1.85 | 7.7 |
| NE | NOJ | HALF | 2188 | 334 | 23,736 | 71 | 11 | 2.3 | 54.1 | 2.62 | 10.9 |
| NE | NOJ | DOUB | 2188 | 1342 | 89,682 | 67 | 41 | 9.2 | 50.9 | 1.31 | 5.5 |
| NE | NOJ | RO30 | 2188 | 671 | 46,555 | 69 | 21 | 4.6 | 52.8 | 1.85 | 7.7 |
| NE | NOJ | RO60 | 2188 | 657 | 45,657 | 69 | 21 | 4.5 | 52.9 | 1.85 | 7.7 |
| NE | NOJ | 6MWD | 2188 | 889 | 61,005 | 69 | 28 | 6.1 | 52.2 | 1.57 | 6.5 |
| NE | Fuga | CNTR | 2188 | 666 | 43,738 | 66 | 20 | 4.6 | 50.0 | 1.85 | 7.7 |
| NE | Fuga | CORR | 2188 | 558 | 37,252 | 67 | 17 | 3.8 | 50.8 | 1.85 | 7.7 |
| NE | Fuga | HALF | 2188 | 334 | 23,154 | 69 | 11 | 2.3 | 52.8 | 2.62 | 10.9 |
| NE | Fuga | DOUB | 2188 | 1342 | 78,948 | 59 | 36 | 9.2 | 44.8 | 1.31 | 5.5 |
| NE | Fuga | RO30 | 2188 | 671 | 43,945 | 65 | 20 | 4.6 | 49.8 | 1.85 | 7.7 |
| NE | Fuga | RO60 | 2188 | 657 | 43,209 | 66 | 20 | 4.5 | 50.1 | 1.85 | 7.7 |
| NE | Fuga | 6MWD | 2188 | 889 | 56,304 | 63 | 26 | 6.1 | 48.2 | 1.57 | 6.5 |
References
- Barthelmie, R.J.; Pryor, S.C. Climate Change Mitigation Potential of Wind Energy. Climate 2021, 9, 136. [Google Scholar] [CrossRef]
- The White House. FACT SHEET: Biden Administration Jumpstarts Offshore Wind Energy Projects to Create Jobs. 2021. Available online: https://www.whitehouse.gov/briefing-room/statements-releases/2021/03/29/fact-sheet-biden-administration-jumpstarts-offshore-wind-energy-projects-to-create-jobs/ (accessed on 26 October 2022).
- WindEurope. Offshore Wind in Europe Key Trends and Statistics 2020. 2021. p. 38. Available online: https://windeurope.org/intelligence-platform/product/wind-energy-in-europe-in-2020-trends-and-statistics/ (accessed on 27 February 2020).
- WindEurope. Wind Energy in Europe. 2022 Statistics and Outlook for 2023–2027. 2023. p. 58. Available online: https://windeurope.org/intelligence-platform/product/wind-energy-in-europe-2022-statistics-and-the-outlook-for-2023-2027/#overview (accessed on 24 March 2023).
- Barthelmie, R.J.; Folkerts, L.; Ormel, F.; Sanderhoff, P.; Eecen, P.; Stobbe, O.; Nielsen, N.M. Offshore wind turbine wakes measured by SODAR. J. Atmos. Ocean. Technol. 2003, 30, 466–477. [Google Scholar] [CrossRef]
- Musial, W.; Spitsen, P.; Duffy, P.; Beiter, P.; Marquis, M.; Hammond, R.; Shields, M. 2022 Offshore Wind Technologies Market Report DOE/GO-102022-5765; Department of Energy: Washington, DC, USA, 2022; p. 126. Available online: https://www.energy.gov/eere/wind/articles/offshore-wind-market-report-2022-edition (accessed on 4 April 2023).
- Barthelmie, R.J.; Dantuono, K.; Renner, E.; Letson, F.; Pryor, S.C. Extreme wind and waves in U.S. east coast offshore wind energy lease areas. Energies 2021, 14, 1053. [Google Scholar] [CrossRef]
- Volcovici, V.U.S. Offshore Wind Auction Draws Record $4.37 Billion in Bids. 2022. Available online: https://www.reuters.com/business/energy/us-offshore-wind-auction-nears-4bln-third-day-bidding-2022-02-25/ (accessed on 28 February 2022).
- BOEM. Outer Continental Shelf Renewable Energy Leases Map Book. July 2022; p. 33. Available online: https://www.boem.gov/sites/default/files/documents/renewable-energy/Leases-Map-Book-July%202022.pdf (accessed on 23 March 2023).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- BOEM. Outer Continental Shelf Renewable Energy Leases Map Book. 2019; p. 19. Available online: https://www.boem.gov/sites/default/files/renewable-energy-program/Mapping-and-Data/Renewable_Energy_Leases_Map_Book_March_2019.pdf (accessed on 22 July 2020).
- Barthelmie, R.J. The effects of atmospheric stability on coastal wind climates. Meteorol. Appl. 1998, 6, 39–47. [Google Scholar] [CrossRef]
- Larsen, G.C.; Réthoré, P.-E. TOPFARM a tool for wind farm optimization. Energy Procedia 2013, 35, 317–324. [Google Scholar] [CrossRef] [Green Version]
- Barthelmie, R.J.; Jensen, L.E. Evaluation of wind farm efficiency and wind turbine wakes at the Nysted offshore wind farm. Wind. Energy 2010, 13, 573–586. [Google Scholar] [CrossRef]
- Doekemeijer, B.M.; Simley, E.; Fleming, P. Comparison of the Gaussian Wind Farm Model with Historical Data of Three Offshore Wind Farms. Energies 2022, 15, 1964. [Google Scholar] [CrossRef]
- Pryor, S.C.; Barthelmie, R.J.; Shepherd, T.J. Wind power production from very large offshore wind farms. Joule 2021, 5, 2663–2686. [Google Scholar] [CrossRef]
- Aird, J.A.; Barthelmie, R.J.; Shepherd, T.J.; Pryor, S.C. Occurrence of Low-Level Jets over the Eastern US Coastal Zone at Heights Relevant to Wind Energy. Energies 2022, 15, 445. [Google Scholar] [CrossRef]
- Pryor, S.C.; Barthelmie, R.J.; Shepherd, T.J.; Hahmann, A.H.; Garcia Santiago, O.M. Wakes in and between very large offshore arrays. J. Phys. Conf. Ser. 2022, 2265, 022037. [Google Scholar] [CrossRef]
- Nygaard, N.G.; Newcombe, A.C. Wake behind an offshore wind farm observed with dual-Doppler radars. J. Phys. Conf. Ser. 2018, 1037, 072008. [Google Scholar] [CrossRef]
- Eriksson, O.; Nilsson, K.; Breton, S.P.; Ivanell, S. Large-eddy simulations of wind farm production and long distance wakes. J. Phys. Conf. Ser. 2015, 625, 012022. [Google Scholar] [CrossRef]
- Barthelmie, R.J.; Pryor, S.C. Wake model evaluation using data from the Virtual Wakes Laboratory. Appl. Energy 2013, 104, 834–844. [Google Scholar] [CrossRef]
- Barthelmie, R.J.; Hansen, K.S.; Pryor, S.C. Meteorological controls on wind turbine wakes. Proc. IEEE 2013, 101, 1010–1019. [Google Scholar] [CrossRef]
- Barthelmie, R.J.; Frandsen, S.T.; Nielsen, N.M.; Pryor, S.C.; Rethore, P.E.; Jørgensen, H.E. Modelling and measurements of power losses and turbulence intensity in wind turbine wakes at Middelgrunden offshore wind farm. Wind. Energy 2007, 10, 217–228. [Google Scholar] [CrossRef]
- Gaertner, E.; Rinker, J.; Sethuraman, L.; Zahle, Z.; Anderson, B.; Barter, G.; Abbas, B.; Meng, F.; Bortolotti, F.; Skrzypinski, W.; et al. Definition of the IEA 15-Megawatt Offshore Reference Wind Turbine; NREL/TP-5000-75698; National Renewable Energy Laboratory: Golden, CO, USA, 2020. Available online: https://www.nrel.gov/docs/fy20osti/75698.pdf (accessed on 11 May 2020).
- Borrmann, R.; Rehfeldt, K.; Wallasch, A.K.; Lüers, S. Capacity Densities of European Offshore Wind Farms; SP18004A1; Deutsche Windguard GmbH: Hamburg, Germany, 2018; p. 86. Available online: https://www.msp-platform.eu/practices/capacity-densities-european-offshore-wind-farms (accessed on 20 January 2021).
- Ahsbahs, T.; Maclaurin, G.; Draxl, C.; Jackson, C.; Monaldo, F.; Badger, M. US East Coast synthetic aperture radar wind atlas for offshore wind energy. Wind. Energy Sci. 2020, 5, 1191–1210. [Google Scholar] [CrossRef]
- Pryor, S.C.; Shepherd, T.; Volker, P.; Hahmann, A.; Barthelmie, R.J. ‘Wind theft’ from onshore arrays: Sensitivity to wind farm parameterization and resolution. J. Appl. Meteorol. Climatol. 2020, 59, 153–174. [Google Scholar] [CrossRef]
- Fitch, A.C. Notes on using the mesoscale wind farm parameterization of Fitch et al. (2012) in WRF. Wind Energy 2016, 19, 1757–1758. [Google Scholar] [CrossRef]
- Wind Europe. Wind Energy in Europe in 2019: Trends and Statistics; Wind Europe: Brussels, Belgium, 2020; p. 25. Available online: https://windeurope.org/wp-content/uploads/files/about-wind/statistics/WindEurope-Annual-Statistics-2019.pdf (accessed on 6 October 2020).
- Enevoldsen, P.; Jacobson, M.Z. Data investigation of installed and output power densities of onshore and offshore wind turbines worldwide. Energy Sustain. Dev. 2021, 60, 40–51. [Google Scholar] [CrossRef]
- Jorgensen, B.H.; Holtinnen, H.; D’ahlgaard, K.; Rosenfeldt Jakobson, K.; Marti, I. IEA Wind TCP Annual Report 2019; International Energy Agency: Pairs, France, 2020; p. 53. ISBN 978-87-93549-78-4. Available online: http://community.ieawind.org (accessed on 11 May 2020).
- Larsen, T.J.; Madsen, H.; Larsen, G.; Hansen, K.S. Validation of the Dynamic Wake Meander Model for Loads and Power Production in the Egmond aan Zee Wind Farm. Wind Energy 2012, 16, 605–624. [Google Scholar] [CrossRef] [Green Version]
- Barthelmie, R.J.; Larsen, G.C.; Mølgaard Pedersen, M.; Pryor, S.C. Microscale modelling of wind turbines in the New York offshore lease area. J. Phys. Conf. Ser. 2022, 2265, 022040. [Google Scholar] [CrossRef]
- Mahulja, S.; Larsen, G.C.; Elham, A. Engineering an optimal wind farm using surrogate models. Wind Energy 2018, 21, 1296–1308. [Google Scholar] [CrossRef]
- Réthoré, P.-E.; Fuglsang, P.; Larsen, P.C.; Buhl, T.; Larsen, T.J.; Madsen, H.A. TOPFARM: Multi-fidelity optimization of wind farms. Wind Energy 2014, 17, 1797–1816. [Google Scholar] [CrossRef] [Green Version]
- National Renewable Energy Laboratory. 2022 Annual Technology Baseline (ATB) Cost and Performance Data for Electricity Generation Technologies [Data Set]; National Renewable Energy Laboratory: Golden, CO, USA, 2022. Available online: https://data.openei.org/submissions/5716 (accessed on 6 April 2023).
- Sørensen, J.N.; Larsen, G.C. A Minimalistic Prediction Model to Determine Energy Production and Costs of Offshore Wind Farms. Energies 2021, 14, 448. [Google Scholar] [CrossRef]
- Nunemaker, J.; Matt, S.; Hammond, R.; Duffy, P. ORBIT: Offshore Renewables Balance-of-System and Installation Tool. NREL/TP-5000-77081; National Renewable Energy Laboratory: Golden, CO, USA, 2020. Available online: https://www.nrel.gov/docs/fy20osti/77081.pdf (accessed on 26 October 2022).
- Richards, H. Energy Prices Threaten Mass. Offshore Wind Project. Energy Wire 11/01/202. 2022. Available online: https://www.eenews.net/articles/energy-prices-threaten-mass-offshore-wind-project/ (accessed on 24 March 2023).
- Pedersen, M.M.; van der Laan, P.; Friis-Møller, M.; Rinker, J.; Réthoré, P.-E. DTUWindEnergy/PyWake: PyWake (Version v1.0.10). Zenodo. 2019. Available online: https://zenodo.org/record/2562662 (accessed on 3 August 2021).
- Jensen, N.O. A Note on Wind Turbine Interaction; Risø-M-2411; Risø National Laboratory: Roskilde, Denmark, 1983; p. 16.
- Barthelmie, R.J.; Folkerts, L.; Rados, K.; Larsen, G.C.; Pryor, S.C.; Frandsen, S.; Lange, B.; Schepers, G. Comparison of wake model simulations with offshore wind turbine wake profiles measured by sodar. J. Atmos. Ocean. Technol. 2006, 23, 888–901. [Google Scholar] [CrossRef]
- Katic, I.; Højstrup, J.; Jensen, N.O. A simple model for cluster efficiency. In Proceedings of the European Wind Energy Association, Rome, Italy, 7–9 October 1986; pp. 407–409. [Google Scholar]
- Barthelmie, R.J.; Pryor, S.C.; Frandsen, S.T.; Hansen, K.; Schepers, J.G.; Rados, K.; Schlez, W.; Neubert, A.; Jensen, L.E.; Neckelmann, S. Quantifying the impact of wind turbine wakes on power output at offshore wind farms. J. Atmos. Ocean. Technol. 2010, 27, 1302–1317. [Google Scholar] [CrossRef]
- Cañadillas, B.; Foreman, R.; Steinfeld, G.; Robinson, N. Cumulative Interactions between the Global Blockage and Wake Effects as Observed by an Engineering Model and Large-Eddy Simulations. Energies 2023, 16, 2949. [Google Scholar] [CrossRef]
- Ott, S.; Berg, J.; Nielsen, M. Linearised CFD Models for Wakes; Risoe-R-1772(EN); DTU: Roskilde, Denmark, 2011; Available online: https://orbit.dtu.dk/en/publications/linearised-cfd-models-for-wakes(c29803f3-a1eb-45ab-b73f-ede444928477).html: (accessed on 26 July 2019).
- Troen, I.; Petersen, E.L. European Wind Atlas; Risø National Laboratory: Roskilde, Denmark, 1989; p. 656.
- Ott, S.; Sogachev, A.; Mann, J.; Jørgensen, H.E.; Frandsen, S.T. Applying Flow Models of Different Complexity for Estimation of Wind Turbine Wakes. In Proceedings of the European Wind Energy Conference and Exhibition, Marseilles, France, 16–19 March 2009; p. 8. Available online: https://backend.orbit.dtu.dk/ws/portalfiles/portal/3740046/2009_17.pdf (accessed on 26 April 2022).
- Pryor, S.C.; Nielsen, M.; Barthelmie, R.J.; Mann, J. Can satellite sampling of offshore wind speeds realistically represent wind speed distributions? Part II: Quantifying uncertainties associated with sampling strategy and distribution fitting methods. J. Appl. Meteorol. 2004, 43, 739–750. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Oxford, UK, 2011; Volume 100. [Google Scholar]
- Gusatu, L.F.; Yamu, C.; Zuidema, C.; Faaij, A. A spatial analysis of the potentials for offshore wind farm locations in the North Sea region: Challenges and opportunities. ISPRS Int. J. Geo-Inf. 2020, 9, 96. [Google Scholar] [CrossRef] [Green Version]
- Mehdi, R.A.; Schröder-Hinrichs, J.-U.; van Overloop, J.; Nilsson, H.; Pålsson, J. Improving the coexistence of offshore wind farms and shipping: An international comparison of navigational risk assessment processes. WMU J. Marit. Aff. 2018, 17, 397–434. [Google Scholar] [CrossRef] [Green Version]
- Petruny, L.M.; Wright, A.J.; Smith, C.E. Getting it right for the North Atlantic right whale (Eubalaenaglacialis): A last opportunity for effective marine spatial planning? Mar. Pollut. Bull. 2014, 85, 24–32. [Google Scholar] [CrossRef] [PubMed]
- Maness, M.; Maples, B.; Smith, A. NREL Offshore Balance-of-System Model; NREL/TP-6A20-66874. 2017; p. 56. Available online: https://www.nrel.gov/docs/fy17osti/66874.pdf (accessed on 7 July 2022).
- Beiter, P.; Musial, W.; Kilcher, L.; Maness, M.; Smith, A. An Assessment of the Economic Potential of Offshore Wind in the United States from 2015 to 2030; Technical Report NREL/TP-6A20-67675. 2017; p. 77. Available online: https://tethys.pnnl.gov/sites/default/files/publications/Beiter-et-al-2017-NETL.pdf (accessed on 1 May 2020).
- BVG Associates. Guide to an Offshore Wind Farm; The Crown Estate and the Offshore Renewable Energy Catapult: 2019. p. 128. Available online: https://guidetoanoffshorewindfarm.com (accessed on 10 June 2022).
- Liang, Y.; Ma, Y.; Wang, H.; Mesbahi, A.; Jeong, B.; Zhou, P. Levelised cost of energy analysis for offshore wind farms—A case study of the New York State development. Ocean. Eng. 2021, 239, 109923. [Google Scholar] [CrossRef]
- Stehly, T.; Duffy, P. 2020 Cost of Wind Energy Review; NREL/TP-5000-81209; National Renewable Energy Laboratory: Golden, CO, USA, 2022; p. 77. Available online: https://www.nrel.gov/docs/fy22osti/81209.pdf (accessed on 3 June 2022).
- Shields, M.; Beiter, P.; Nunemaker, J.; Cooperman, A.; Duffy, P. Impacts of turbine and plant upsizing on the levelized cost of energy for offshore wind. Appl. Energy 2021, 298, 117189. [Google Scholar] [CrossRef]
- Smart, G.; Smith, A.; Warnr, E.; Sperstad, I.B.; Prinsen, B.; Lacal-Arántegui, R. IEA Task 26—Offshore Wind Farm Baseline Documentation; IEA Wind: 2016. p. 30. Available online: www.nrel.gov/docs/fyosti/66262.pdf (accessed on 7 July 2022).
- Wang, L.; Kolios, A.; Liu, X.; Venetsanos, D.; Rui, C. Reliability of offshore wind turbine support structures: A state-of-the-art review. Renew. Sustain. Energy Rev. 2022, 161, 112250. [Google Scholar] [CrossRef]
- Fischetti, M.; Pisinger, D. Optimal wind farm cable routing: Modeling branches and offshore transformer modules. Networks 2018, 72, 42–59. [Google Scholar] [CrossRef] [Green Version]
- Rowell, D.; Jenkins, B.; Carroll, J.; McMillan, D. How Does the Accessibility of Floating Wind Farm Sites Compare to Existing Fixed Bottom Sites? Energies 2022, 15, 8946. [Google Scholar] [CrossRef]
- Hand, M.M. (Ed.) IEA Wind TCP Task 26–Wind Technology, Cost, and Performance Trends in Denmark, Germany, Ireland, Norway, Sweden, the European Union, and the United States: 2008–2016; NREL/TP-6A20.71844; National Renewable Energy Laboratory: Golden, CO, USA, 2018; p. 104. Available online: https://www.nrel.gov/docs/fy19osti/71844.pdf (accessed on 13 July 2020).
- Noonan, M.; Stehly, T.; Mora, D.; Kitzing, L.; Smart, G.; Berkhout, V.; Kikuchi, Y. IEA Wind TCP Task 26: Offshore Wind Energy International Comparative Analysis. Updated January 2020; IEA Wind: 2018. p. 71. Available online: https://www.nrel.gov/docs/fy23osti/81246.pdf: (accessed on 19 March 2023).
- Barthelmie, R.J.; Rathmann, O.; Frandsen, S.T.; Hansen, K.; Politis, E.; Prospathopoulos, J.; Rados, K.; Cabezón, D.; Schlez, W.; Phillips, J.; et al. Modelling and measurements of wakes in large wind farms. J. Phys. Conf. Ser. 2007, 75, 012049. [Google Scholar] [CrossRef]
- Wade, B. Offshore Wind Farm Layout Strategies; WindTech International: New Delhi, India, 2019. [Google Scholar]
- Agora Energiewende, A.V. Technical University of Denmark and Max-Planck-Institute for Biogeochemistry. Making the Most of Offshore Wind: Re-Evaluating the Potential of Offshore Wind in the German North Sea; 176/01-S-2020/EN. 2020. p. 84. Available online: https://static.agora-energiewende.de/fileadmin/Projekte/2019/Offshore_Potentials/176_A-EW_A-VW_Offshore-Potentials_Publication_WEB.pdf (accessed on 14 September 2021).
- Wood McKenzie. United States Levelized Cost of Electricity (LCOE) Report. Analysis of Power Technology and Generation Cost Trends and Competitiveness. 2021. p. 136. Available online: https://www.woodmac.com/reports/power-markets-united-states-levelized-cost-of-electricity-lcoe-2021-523092/ (accessed on 1 December 2021).
- Beiter, P.; Spitsen, P.; Musial, W.; Lantz, E. The Vineyard Wind Power Purchase Agreement: Insights for Estimating Costs of U.S. Offshore Wind Projects; NREL/TP-5000-72981; National Renewable Energy Laboratory: Golden, CO, USA, 2019; p. 27. Available online: https://www.nrel.gov/docs/fy19osti/72981.pdf (accessed on 19 March 2023).
- Fleming, P.; King, J.; Simley, E.; Roadman, J.; Scholbrock, A.; Murphy, P.; Lundquist, J.K.; Moriarty, P.; Fleming, K.; van Dam, J.; et al. Continued results from a field campaign of wake steering applied at a commercial wind farm—Part 2. Wind Energy Sci. 2020, 5, 945–958. [Google Scholar] [CrossRef]
- Cooperman, A.; Duffy, P.; Hall, M.; Lozon, E.; Shields, M.; Musial, W. Assessment of Offshore Wind Energy Leasing Areas for Humboldt and Morro Bay Wind Energy Areas; NREL/TP-5000-82341; National Renewable Energy Laboratory: Golden, CO, USA, 2022; p. 85. Available online: https://www.nrel.gov/docs/fy22osti/82341.pdf (accessed on 19 March 2023).
- GustoMSC. U.S. Jones Act Compliant Offshore Wind Turbine Installation Vessel Study; GustoMSC: Houston, TX, USA, 2022; p. 86. Available online: https://www.cleanegroup.org/wp-content/uploads/US-Jones-Act-Compliant-Offshore-Wind-Study.pdf (accessed on 19 March 2023).
- Nikkanen, M. How Offshore Weather Awareness Enhances Saftey and Optimizes Operation. Windower Engineering and Development, 8–13 February 2022. [Google Scholar]
- Shields, M.; Stefek, J.; Oteri, F.; Maniak, S.; Kreider, M.; Gill, E.; Gould, R.; Malvik, C.; Tirone, S.; Hines, E. A Supply Chain Road Map for Offshore Wind Energy in the United States; NREL/TP-5000-84710; National Renewable Energy Laboratory: Golden, CO, USA, 2023; p. 209. Available online: https://www.nrel.gov/docs/fy23osti/84710.pdf (accessed on 19 March 2023).
- Lazard. Lazards Levelized Cost of Energy Analysis—Version 15.0. 2021. p. 21. Available online: https://www.lazard.com/research-insights/levelized-cost-of-energy-levelized-cost-of-storage-and-levelized-cost-of-hydrogen-2021/ (accessed on 10 April 2022).





| LA Group | Project Name (Lessee) | Area (km2) | Identifier | Lease Date | Center Latitude (N) | Center Longitude (E) |
|---|---|---|---|---|---|---|
| MA | Sea2shore The Renewable Link | - | OCS-A 0506 | 2014 | - | - |
| Revolution Wind | 339 | OCS-A 0486 | 2013 | 41.16 | −71.12 | |
| South Fork Wind | 55 | OCS-A 0517 | 2013 | 41.10 | −71.13 | |
| Sunrise Wind | 445 | OCS-A 0487 | 2013 | 40.94 | −71.08 | |
| Bay State Wind | 586 | OCS-A 0500 | 2015 | 40.98 | −70.84 | |
| Vineyard Wind | 264 | OCS-A 0501 | 2015 | 41.11 | −70.51 | |
| New England Wind | 411 | OCS-A 0534 | 2015 | 40.95 | −70.62 | |
| Beacon Wind | 521 | OCS-A 0520 | 2018 | 40.84 | −70.52 | |
| (Mayflower) | 516 | OCS-A 0521 | 2019 | 40.75 | −70.43 | |
| Vineyard NE Wind | 536 | OCS-A 0522 | 2019 | 40.70 | −70.20 | |
| NE | Empire Wind | 321 | OCS-A 0512 | 2017 | 40.27 | −73.32 |
| (Mid-Atlantic Offshore Wind) | 174 | OCS-A 0544 | 2022 | 40.24 | −73.08 | |
| (OW Ocean Winds East) | 289 | OCS-A 0537 | 2022 | 39.95 | −72.74 | |
| (Attentive Energy) | 341 | OCS-A 0538 | 2022 | 39.71 | −73.17 | |
| (Bight Wind Holdings/Community Offshore Wind) | 510 | OCS-A 0539 | 2022 | 39.53 | −73.32 | |
| (Invenergy Wind Offshore) | 340 | OCS-A 0542 | 2022 | 39.31 | −73.47 | |
| (Atlantic Shores Offshore Wind Bight) | 321 | OCS-A 0541 | 2022 | 39.35 | −73.60 | |
| NJ | Atlantic Shores North | 328 | OCS-A 0549 | 2016 | 39.50 | −74.00 |
| Atlantic Shores South | 413 | OCS-A 0499 | 2016 | 39.30 | −74.13 | |
| Ocean Wind NJ | 305 | OCS-A 0498 | 2016 | 39.15 | −74.20 | |
| Ocean Wind 2 | 343 | OCS-A 0532 | 2016 | 39.10 | −74.42 | |
| Garden State Offshore Energy I | 284 | OCS-A 0482 | 2012 | 38.60 | −74.70 | |
| Skipjack Wind Farm | 107 | OCS-A 0519 | 2018 | 38.56 | −74.67 | |
| MarWin | 323 | OCS-A 0490 | 2014 | 38.38 | −74.78 | |
| VA | Coastal Virginia Offshore Wind Pilot | 9 | OCS-A 0497 | 2015 | 36.91 | −75.50 |
| Coastal Virginia Offshore Wind | 456 | OCS-A 0483 | 2013 | 36.91 | −75.36 | |
| Kitty Hawk | 496 | OCS-A 0508 | 2017 | 36.34 | −75.11 |
| Liang [57] | % | NREL 3 [54,55,58,59] | % | BVG 2 [56] | % | IEA [60] | BOSi 4 Equation (8) | % | ||
|---|---|---|---|---|---|---|---|---|---|---|
| CAPEX/MW ($ million) | 3.05 | 3.77 | 3.38 | 3.54 | 3.84 | |||||
| Project management 1 | 0.45 | 14.80 | 0.67 | 17.8 | 0.58 | 17.11 | 0.52 | 14.69 | 0.67 | 17.45 |
| Turbine | 1.2 | 39.30 | 1.3 | 34.6 | 1.44 | 42.77 | 1.5 | 42.37 | 1.37 | 35.68 |
| BOS | 1.4 | 45.90 | 1.8 | 47.5 | 1.36 | 40.12 | 1.52 | 42.94 | 1.80 | 46.88 |
| Foundation | 0.8 | 26.23 | 0.52 | 15.48 | 0.7 | 19.77 | 1.02 | 26.56 | ||
| Internal cable | 0.01 | 0.33 | 0.06 | 1.73 | 0.13 | 3.67 | 0.08 | 2.08 | ||
| Export cable | 0.08 | 2.62 | 0.49 | 14.36 | 0.37 | 10.45 | 0.04 | 1.04 | ||
| Sub-station offshore | 0.34 | 11.15 | 0.21 | 6.22 | 0.2 | 5.65 | 0.44 | 11.46 | ||
| Sub-station onshore | 0.17 | 5.57 | 0.08 | 2.368 | 0.14 | 3.95 | 0.22 | 5.73 |
| Wake Model → | NOJ | Fuga | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Layout | #WT | ICD (MW/km2) | Min. Distance between WT (km) | AEP (GWh/y) | AEP (GWh/y) per WT | AEP (GWh/y) per km2 | CF (%) | AEP (GWh/y) | AEP (GWh/y) per WT | AEP (GWh/y) per km2 | CF (%) |
| CNTR | 89 | 4.2 | 1.85 | 6242 | 70 | 19 | 53.4 | 6105 | 69 | 19 | 52.2 |
| CORR | 74 | 3.5 | 1.85 | 5216 | 70 | 16 | 53.6 | 5126 | 69 | 16 | 52.7 |
| HALF | 47 | 2.2 | 2.62 | 3357 | 71 | 10 | 54.4 | 3326 | 71 | 10 | 53.9 |
| DOUB | 174 | 8.1 | 1.31 | 11775 | 68 | 37 | 51.5 | 11173 | 64 | 35 | 48.9 |
| RO30 | 90 | 4.2 | 1.85 | 6298 | 70 | 20 | 53.3 | 6154 | 68 | 19 | 52.0 |
| RO60 | 95 | 4.4 | 1.85 | 6649 | 70 | 21 | 53.3 | 6499 | 68 | 20 | 52.1 |
| 6MWD | 122 | 5.7 | 1.57 | 8446 | 69 | 26 | 52.7 | 8162 | 67 | 25 | 50.9 |
| Layout | Minimum Turbine Spacing (D) | Internal Cable Length (ITD) (km) | Internal Cable Cost (Million $ per km Top Row, Remaining Rows Total Cost Million $) | Total CAPEX (Million $) | Total OPEX (Million $/yr) | ||
|---|---|---|---|---|---|---|---|
| 0.465 | 0.544 | 0.632 | |||||
| CNTR | 7.7 | 163 | 76 | 89 | 103 | 4487 | 151 |
| DOUB | 5.5 | 230 | 107 | 125 | 145 | 8695 | 296 |
| HALF | 10.9 | 123 | 57 | 67 | 78 | 2444 | 80 |
| Lease Area Group | Wake Parameterization | Area (km2) | WT | AEP (GWh/y) | CF (%) |
|---|---|---|---|---|---|
| NE | NOJ | 2188 | 666 | 46,317 | 52.9 |
| NE | Fuga | 2188 | 666 | 43,738 | 50.0 |
| MA | NOJ | 3675 | 1071 | 73,975 | 52.6 |
| MA | Fuga | 3675 | 1071 | 66,753 | 47.4 |
| NJ | NOJ | 2105 | 624 | 43,635 | 53.2 |
| NJ | Fuga | 2105 | 624 | 41,191 | 50.2 |
| VA | NOJ | 952 | 255 | 17,763 | 52.7 |
| VA | Fuga | 952 | 255 | 9024 | 50.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barthelmie, R.J.; Larsen, G.C.; Pryor, S.C. Modeling Annual Electricity Production and Levelized Cost of Energy from the US East Coast Offshore Wind Energy Lease Areas. Energies 2023, 16, 4550. https://doi.org/10.3390/en16124550
Barthelmie RJ, Larsen GC, Pryor SC. Modeling Annual Electricity Production and Levelized Cost of Energy from the US East Coast Offshore Wind Energy Lease Areas. Energies. 2023; 16(12):4550. https://doi.org/10.3390/en16124550
Chicago/Turabian StyleBarthelmie, Rebecca J., Gunner C. Larsen, and Sara C. Pryor. 2023. "Modeling Annual Electricity Production and Levelized Cost of Energy from the US East Coast Offshore Wind Energy Lease Areas" Energies 16, no. 12: 4550. https://doi.org/10.3390/en16124550
APA StyleBarthelmie, R. J., Larsen, G. C., & Pryor, S. C. (2023). Modeling Annual Electricity Production and Levelized Cost of Energy from the US East Coast Offshore Wind Energy Lease Areas. Energies, 16(12), 4550. https://doi.org/10.3390/en16124550








