Operation Control Method for High-Speed Maglev Based on Fractional-Order Sliding Mode Adaptive and Diagonal Recurrent Neural Network
Abstract
:1. Introduction
2. Dynamic Model of High-Speed Maglev Train
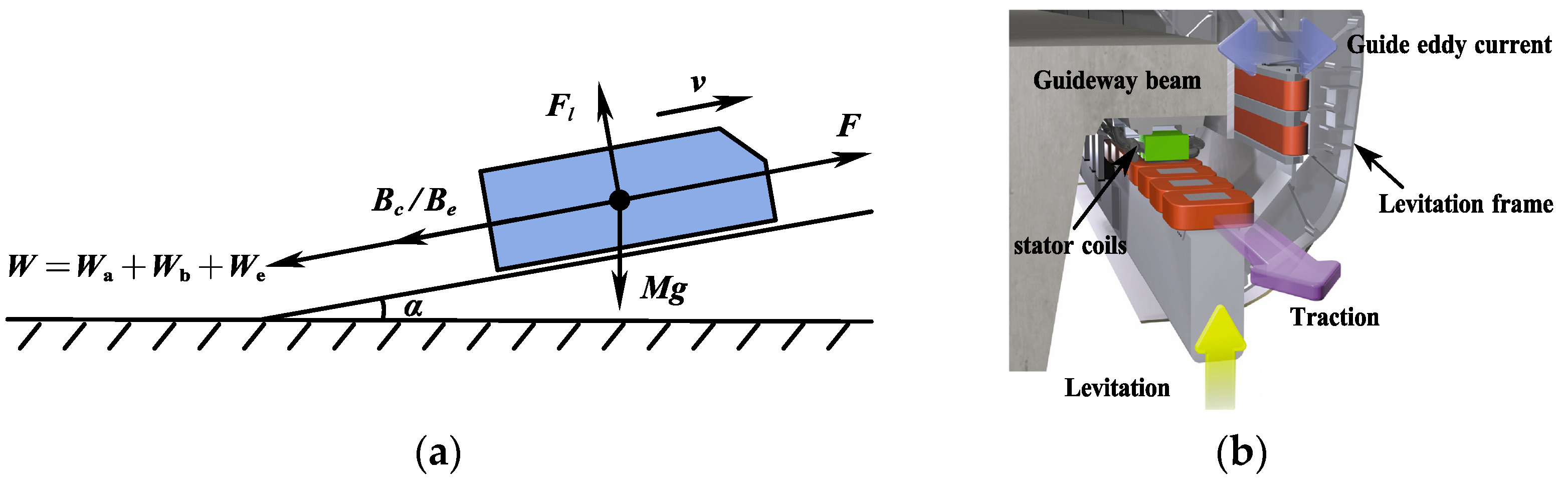
2.1. Tractive Force Model
2.2. Braking Force Model
2.3. Running Resistance Model
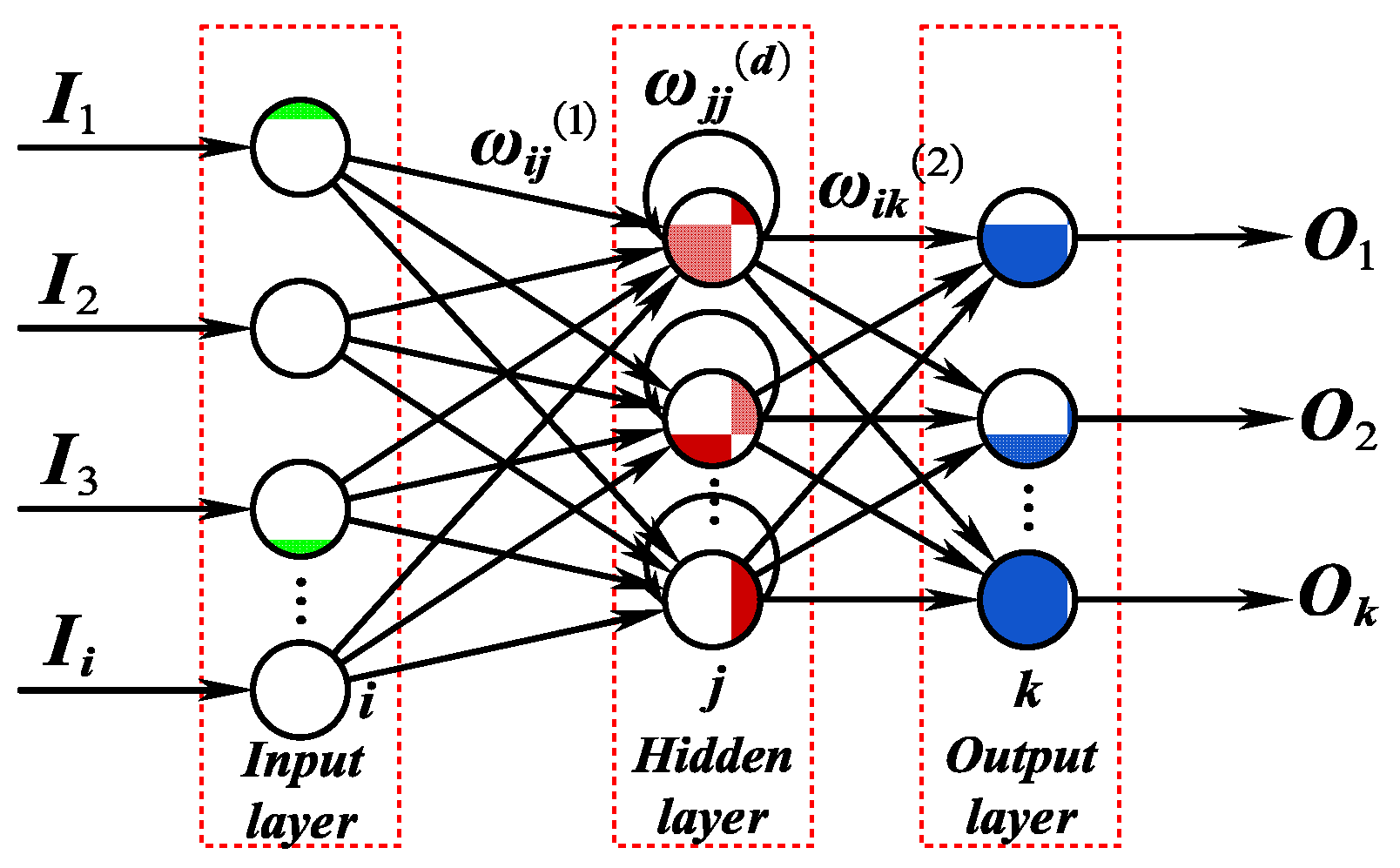
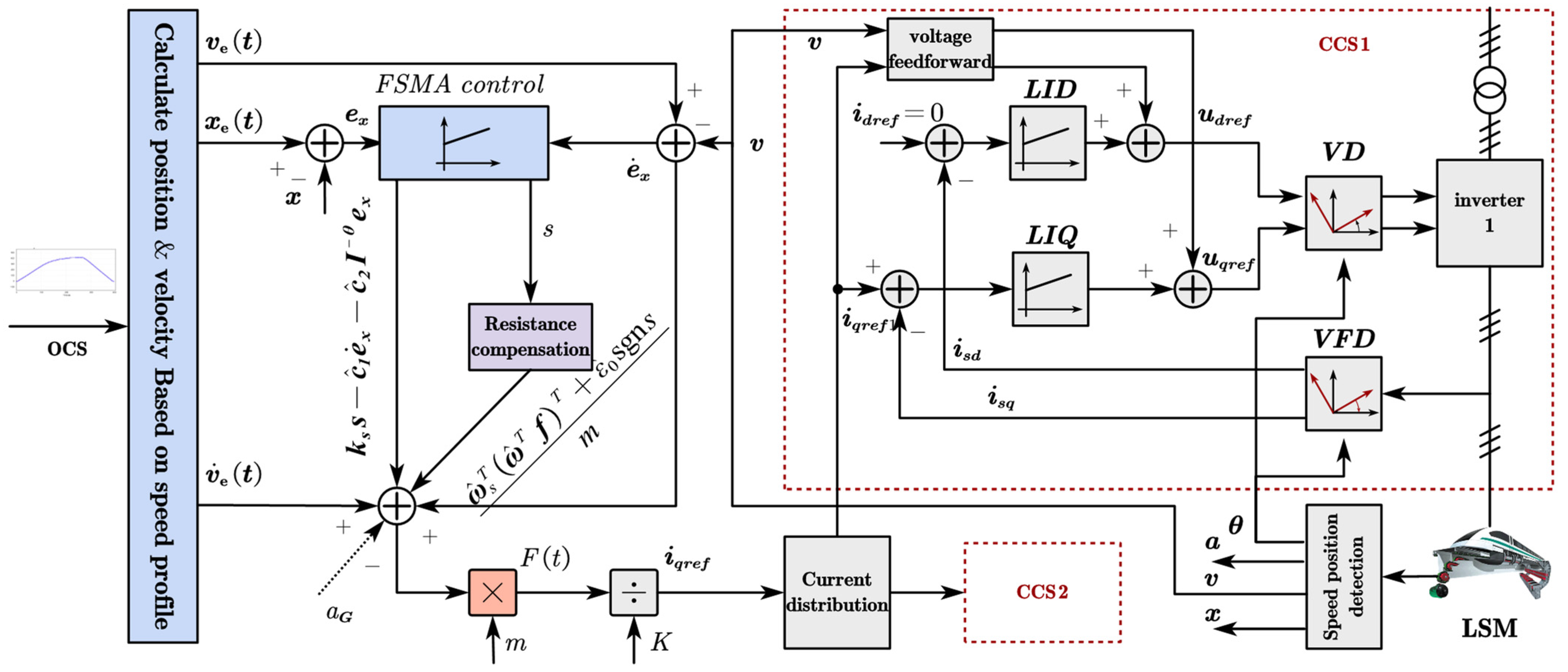
3. FSMA-DRNN Operation Controller Design
3.1. FSMA-DRNN Control Law
3.2. Controller Structure Design Process
3.3. Stability Analysis of the Controller
4. Experimental Verification
4.1. Test Line and Train Parameters
4.1.1. Line Parameter
4.1.2. Train Parameters
4.2. Controller Parameter Setting
4.2.1. FSMA-DRNN and PID Control Parameter Setting
4.2.2. Adaptive Control Parameter Setting
4.3. Experimental Platform
5. Comparison of Experimental Results
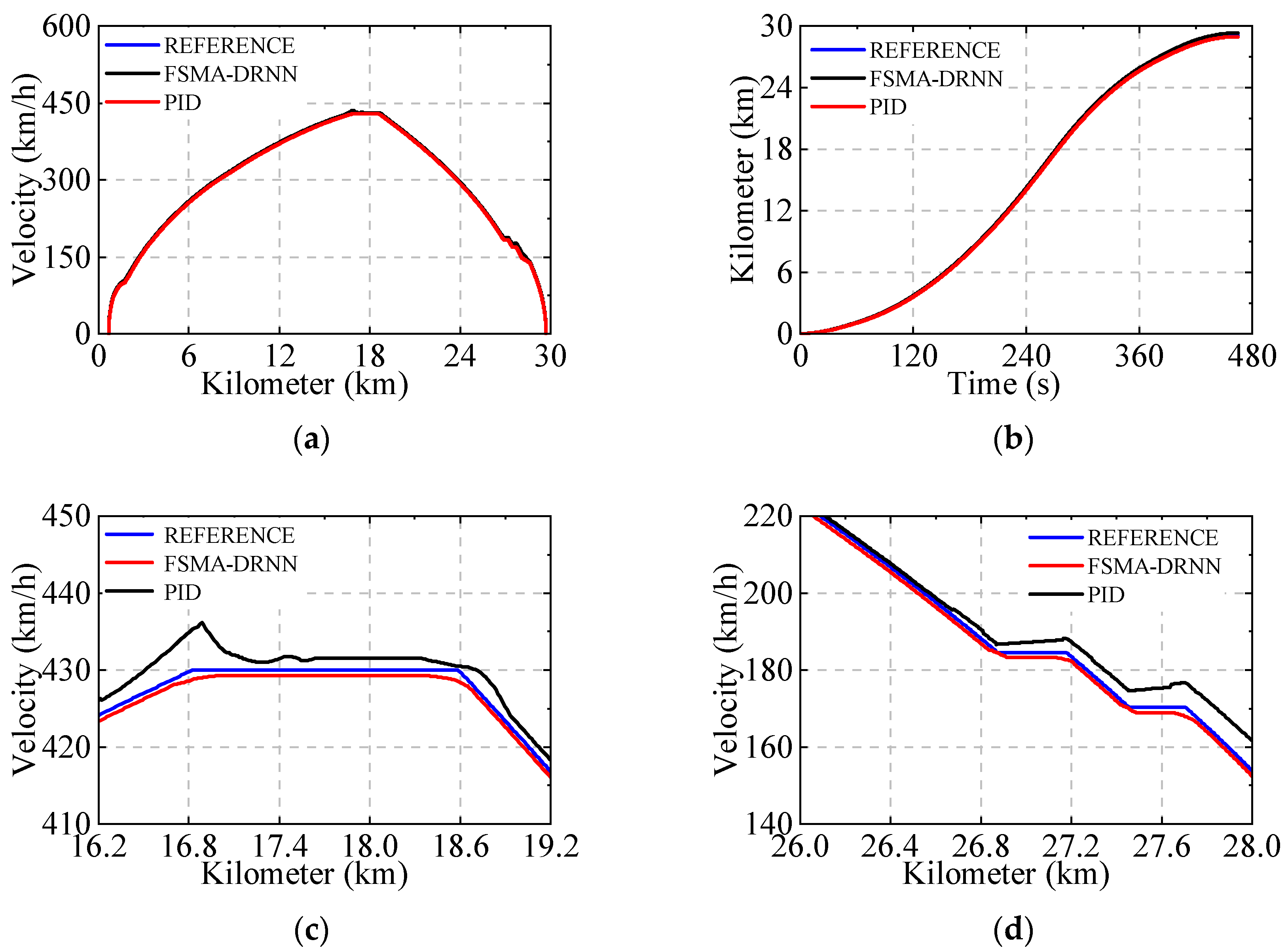
5.1. Comparison of Speed and Position Tracking Performance
5.2. Comparison of Speed and Position Tracking Errors
5.3. Estimated Effect of Running Resistance
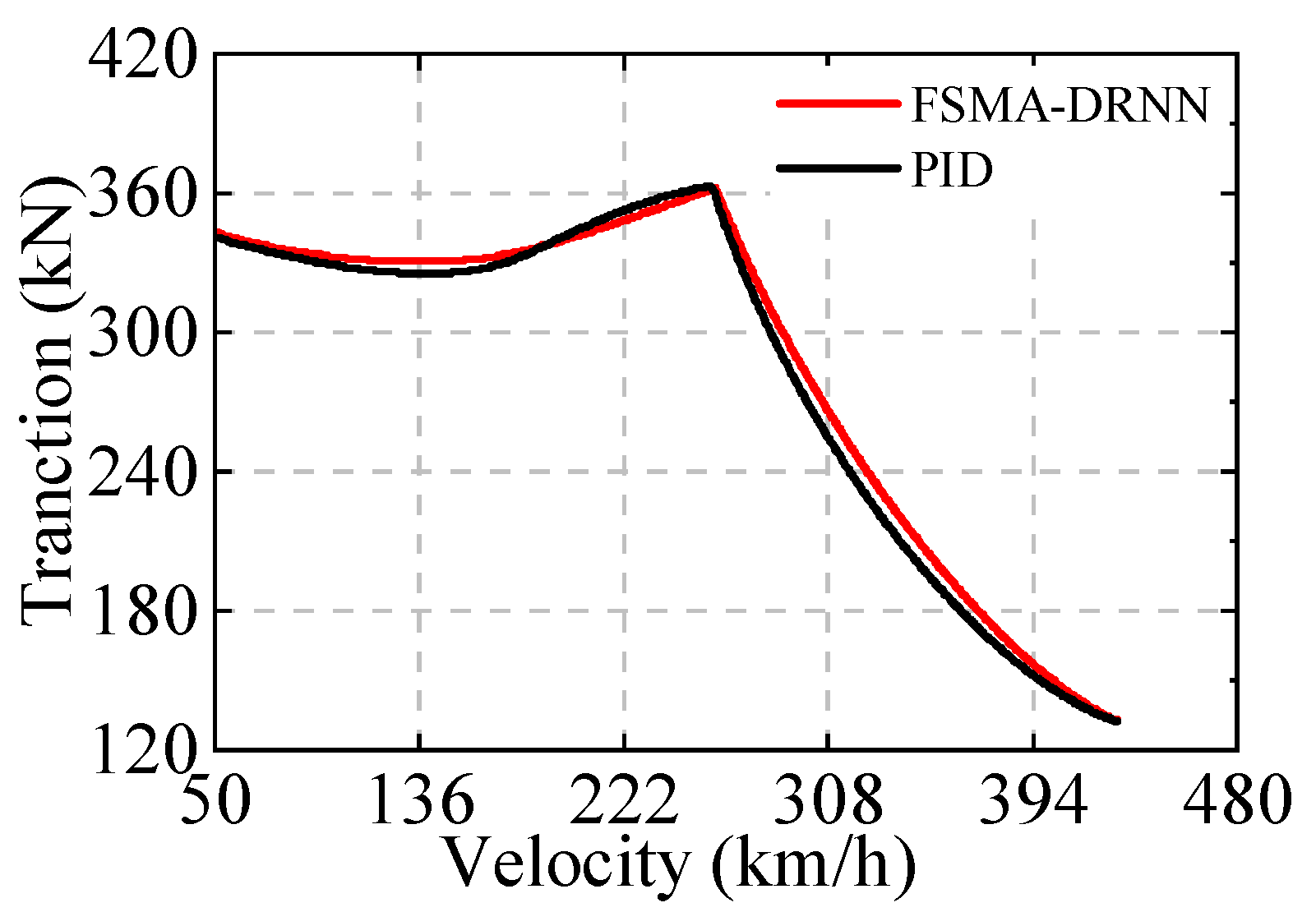
5.4. Comparison of Tractive Force Output Effects
6. Conclusions
- A kinematics model for neural network recognition is established based on adopting the tractive force, braking force, and running resistance. A novel algorithm called DRNN is presented to predict the resistance for compensating for the output acceleration.
- A new fractional-order sliding mode adaptive control algorithm (FSMA) is proposed to track the optimal speed profile. By using the corresponding traction generated by FSMA, the speed profile can be tracked more effectively and robustly.
- The real data sets from the Shanghai maglev line are used on a hardware-in-the-loop platform for experimental simulations. Comparative studies for different control strategies validate the effectiveness and superiority of the proposed operation controller.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ding, S. 600 Km/h High-Speed Maglev Transportation System; Shanghai Scientific & Technical Publishers: Shanghai, China, 2022. [Google Scholar]
- Wu, X. Maglev Train; Shanghai Scientific & Technical Publishers: Shanghai, China, 2003. [Google Scholar]
- Gang, L.; Zhi, R.; Cui, L.; Zhang, Z.; Liu, Y. Analysis on the Air-Gap Magnetic Flux Density and Propulsion of the TFLSM Considering Cogging Effect. IEEE Trans. Magn. 2023, 59, 1–7. [Google Scholar]
- Liao, Z.; Yue, J.; Lin, G. Application Research of HTS Linear Motor Based on Halbach Array in High Speed Maglev System. IEEE Trans. Appl. Supercond. 2021, 31, 1–7. [Google Scholar] [CrossRef]
- Zhao, Y.; Peng, F.; Ren, L.; Lin, G.; Xu, J. A Levitation Condition Awaeness Architecture for Low-Speed Maglev Train Based on Data-Driven Random Matrix Analysis. IEEE Access 2020, 8, 176575–176587. [Google Scholar] [CrossRef]
- Chen, C.; Xu, J.; Sun, Y.; Zhao, X. Sliding Mode Bifurcation Control Based on Acceleration Feedback Correction Adaptive Compensation for Maglev Train Suspension System With Time-Varying Disturbance. IEEE Trans. Transp. Electrif. 2022, 8, 2273–2287. [Google Scholar] [CrossRef]
- Chen, C.; Xu, J.; Rong, L.; Ji, W.; Lin, G.; Sun, Y. Neural-Network-State-Observation-Based Adaptive Inversion Control Method of Maglev Train. IEEE Trans. Veh. Technol. 2022, 71, 3660–3669. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, Z.; Sun, M. Design of a Novel Claw Pole Transverse Flux Permanent Magnet Motor Based on Hybrid Stator Core. IEEE Trans. Magn. 2021, 57, 1–5. [Google Scholar] [CrossRef]
- Xu, Y.; Zhao, X.; Yin, S.; Long, Z. Real-Time Performance Optimization of Electromagnetic Levitation Systems and the Experimental Validation. IEEE Trans. Ind. Electron. 2023, 70, 3035–3044. [Google Scholar] [CrossRef]
- Jiang, S.; Xu, H.; Zhang, T.; Yao, X.; Long, Z. Lazy Prescribed-Time Synchronization Control of Half Bogie for High-Speed Maglev Train Considering Track Irregularities and Input Constraints. IEEE Trans. Veh. Technol. 2022, 71, 6924–6937. [Google Scholar] [CrossRef]
- Lv, G.; Cui, L.; Zhi, R.; Zhou, T.; Liu, Y. Investigation of the Transverse Flux Linear Synchronous Motor Integrated with Propulsion, Levitation and Guidance for the Maglev Train. IEEE Trans. Transp. Electrif. 2023, 1. [Google Scholar] [CrossRef]
- Yang, J.; Jia, L.; Lu, S.; Li, Z. Energy-efficient Operation of Electric Freight Trains-Part I: Speed Profile Optimization. J. China Railw. Soc. 2016, 38, 22–31. [Google Scholar]
- Yang, J.; Jia, L.; Fu, Y.; Luo, Y. Energy-efficient Freight Train Operation-Part II: Combined Control of Speed Tracking. J. China Railw. Soc. 2016, 38, 23–31. [Google Scholar]
- He, H.; Yang, Z.; Lv, J. Braking Control Algorithm for Accurate Train Stopping Based on Adaptive Fuzzy Sliding Mode. China Railw. Sci. 2019, 40, 122–129. [Google Scholar]
- Kim, J.; Park, J.; Eun, Y. Precise Stop Control and Experimental Validation for Metro Train Overcoming Delays and Nonlinearities. IEEE Trans. Veh. Technol. 2022, 71, 4776–4787. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, C.; Liu, F.; Li, P.; Xie, G. Bio-Inspired Speed Curve Optimization and Sliding Mode Tracking Control for Subway Trains. IEEE Trans. Veh. Technol. 2019, 68, 6331–6342. [Google Scholar] [CrossRef]
- Meng, J.; Xu, R.; Li, D.; Chen, X. Combining the Matter-Element Model With the Associated Function of Performance Indices for Automatic Train Operation Algorithm. IEEE Trans. Intell. Transp. Syst. 2019, 20, 253–263. [Google Scholar] [CrossRef]
- Pu, Q.; Zhu, X.; Liu, J.; Cai, D.; Fu, G.; Wei, D.; Sun, J.; Zhang, R. Integrated Optimal Design of Speed Profile and Fuzzy PID Controller for Train With Multifactor Consideration. IEEE Access 2020, 8, 152146–152160. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, K.; Ouyang, Q. Intelligent Traction Control Method Based on Model Predictive Fuzzy PID Control and Online Optimization for Permanent Magnetic Maglev Trains. IEEE Access 2021, 9, 29032–29046. [Google Scholar] [CrossRef]
- Pu, Q.; Zhu, R.; Zhang, R.; Liu, J.; Cai, D.; Fu, G. Speed Profile Tracking by an Adaptive Controller for Subway Train Based on Neural Network and PID Algorithm. IEEE Trans. Veh. Technol. 2020, 69, 10656–10667. [Google Scholar] [CrossRef]
- Zheng, J.; Hou, Z. Model Free Adaptive Iterative Learning Control Based Fault-Tolerant Control for Subway Train With Speed Sensor Fault and Over-Speed Protection. IEEE Trans. Autom. Sci. Eng. 2022, 1–13. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, Z.; Cheng, F.; Su, S. Trajectory optimization for high-speed trains via a mixed integer linear programming approach. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17666–17676. [Google Scholar] [CrossRef]
- Wang, X.; Su, S.; Cao, Y.; Wang, X. Robust control for dynamic train regulation in fully automatic operation system under uncertain wireless transmissions. IEEE Trans. Intell. Transp. Syst. 2022, 23, 20721–20734. [Google Scholar] [CrossRef]
- Liu, G.; Hou, Z. RBFNN-Based Adaptive Iterative Learning Fault-Tolerant Control for Subway Trains With Actuator Faults and Speed Constraint. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 5785–5799. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, Z.; Li, Z. An Intelligent Train Operation Method Based on Event-Driven Deep Reinforcement Learning. IEEE Trans. Ind. Inform. 2022, 18, 6973–6980. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, Z.; Yang, F. Elastic Tracking Operation Method for High-speed Railway using Deep Reinforcement Learning. IEEE Trans. Consum. Electron. 2023, 1. [Google Scholar] [CrossRef]
- Yin, J.; Chen, D.; Li, L. Intelligent train operation algorithms for subway by expert system and reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2561–2571. [Google Scholar] [CrossRef]
- Zhu, Q.; Su, S.; Tang, T.; Liu, W.; Zhang, Z.; Tian, Q. An eco-driving algorithm for trains through distributing energy: A Q-learning approach. ISA Trans. 2021, 122, 24–37. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.-C.; Deng, D.-J.; Chih, Y.-L.; Chiu, H.-T. Smart manufacturing scheduling with edge computing using multiclass deep Q network. IEEE Trans. Ind. Informat. 2019, 15, 4276–4284. [Google Scholar] [CrossRef]
- Han, X.; Liu, H.; Sun, F.; Zhang, X. Active object detection with multistep action prediction using deep Q-network. IEEE Trans. Ind. Informat. 2019, 15, 3723–3731. [Google Scholar] [CrossRef]
- Zhou, K.; Song, S.; Xue, A.; You, K.; Wu, H. Smart Train Operation Algorithms Based on Expert Knowledge and Reinforcement Learning. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 716–727. [Google Scholar] [CrossRef]
- Zhang, W.; Cao, B.; Liu, Y.; Yue, Q.; Xu, H. Operation Control Method for Medium-Speed Maglev Trains Based on Fractional Order Sliding Mode Adaptive Neural Network. China Railw. Sci. 2022, 43, 152–160. [Google Scholar]
- Cao, B.; Gao, Y.; Li, K.; Zhang, J.; Zhang, Z.; Zhang, W. A Fractional Order Operation Control Method for Medium-speed Maglev Trains. J. China Railw. Soc. 2022, 44, 42–48. [Google Scholar]
- Zhang, W.; Nan, N.; Cao, B.; Li, M.; Yue, Q.; Xu, H. Operation Control Method for Medium-low-speed Maglev Train Based on Periodic Adaptive Learning. J. China Railw. Soc. 2021, 43, 88–94. [Google Scholar]
- Tang, L.; He, K.; Liu, Y. Adaptive Output Feedback Fuzzy Event-triggered Control for Fractional-order Nonlinear Switched Systems. IEEE Trans. Fuzzy Syst. 2023, 1–10. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, H.; Sun, J.; Wang, Y. Sliding Mode Control Based on Reinforcement Learning for T-S Fuzzy Fractional-Order Multiagent System With Time-Varying Delays. IEEE Trans. Neural Netw. Learn. Syst. 2023, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Shen, Y.; Li, D.; Lin, S.; Muyeen, S.; Zhai, H.; Zhao, J. Fractional-Order Sliding Mode Load Frequency Control and Stability Analysis for Interconnected Power Systems With Time-Varying Delay. IEEE Trans. Power Syst. 2023, 1–11. [Google Scholar] [CrossRef]
- Wang, J.; Wang, S.; Deng, C.; Zeng, Y.; Song, H.; Huang, H. A super high speed HTS maglev vehicle. Int. J. Mod. Phys. B 2005, 19, 399–401. [Google Scholar] [CrossRef]
- Lu, Y.; Dang, Q.; Liu, M. Levitation Performance Study of Bulk HTSC over Monopole PMG Consider Different Cross-Section Configuration with 3D-Modeling Numerical Method. J. Low Temp. Phys. 2013, 173, 45–53. [Google Scholar] [CrossRef]
- Davey, K.R.; Dalian, Z. Prediction and use of impedance matrices for eddy-current problems. IEEE Trans. Magn. 1997, 33, 2478–2485. [Google Scholar] [CrossRef]
- Che, T.; Gou, Y.F.; Deng, Z.G.; Zheng, J.; Zheng, B.T.; Chen, P. A method to enhance the curve negotiation performance of HTS Maglev. Int. J. Mod. Phys. B 2015, 29, 1542037. [Google Scholar] [CrossRef]
- Qin, W.; Bird, J.Z. Electrodynamic Wheel Magnetic Rolling Resistance. IEEE Trans. Magn. 2017, 53, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Deng, Z.; Zhang, W.; Wang, L.; Wang, Y.; Zhou, W.; Zhao, J.; Lu, K.; Guo, J.; Zhang, W.; Zhou, X.; et al. High-Speed Running Test Platform for High-Temperature Superconducting Maglev. IEEE Trans. Appl. Supercond. 2022, 32, 1–5. [Google Scholar] [CrossRef]
- Wu, J.; Hu, F. Monitoring Ground Subsidence Along the Shanghai Maglev Zone Using TerraSAR-X Images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 117–121. [Google Scholar] [CrossRef]



| Parameters | Value |
|---|---|
| Total length of main line (km) | 29.86 |
| Number of curves | 6 |
| Curve line extension (km) | 18.51 |
| Curve in the total line (%) | 62.0 |
| Maximum curve radius (m) | 7997.45 |
| Minimum curve radius (m) | 1292.52 |
| Maximum transition curve (m) | 2399.32 |
| Minimum transition curve (m) | 290.00 |
| Parameters | Value |
|---|---|
| Total number of slope sections | 7 |
| Average slope section length (km) | 4.28 |
| Average slope section length in total line length (%) | 14.3 |
| Maximum slope (%) | −1.076 |
| Maximum slope length (m) | 14,105.55 |
| Minimum slope length (m) | 650.55 |
| Maximum vertical curve radius (m) | 80,000 |
| Minimum vertical curve radius (m) | 45,000 |
| Maximum transition curve (m) | 100 |
| Minimum transition curve (m) | 20 |
| Parameters | Value |
|---|---|
| Formation/car | 5, (2 head/tail, 3 middle) |
| Head/tail car—no-load weight (t) | 52.9 |
| Middle car—no-load weight (t) | 50.3 |
| Head/tail car—maximum allowable gross weight (t) | 67.0 |
| Middle car—maximum allowable gross weight (t) | 69.5 |
| Total weight of train (t) | 342.5 |
| Maximum speed (km/h) | 430 |
| Maximum acceleration during acceleration (m/s2) | 1 |
| Maximum acceleration during deceleration (m/s2) | 12.5 |
| Controller | Parameter | Values |
|---|---|---|
| FSMA-DRNN | ks, θ | −397, 2.59 |
| PID | kp, ki, kd | 1200, 1310, 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Lin, G.; Hu, K.; Liao, Z.; Wang, H. Operation Control Method for High-Speed Maglev Based on Fractional-Order Sliding Mode Adaptive and Diagonal Recurrent Neural Network. Energies 2023, 16, 4566. https://doi.org/10.3390/en16124566
Zhang W, Lin G, Hu K, Liao Z, Wang H. Operation Control Method for High-Speed Maglev Based on Fractional-Order Sliding Mode Adaptive and Diagonal Recurrent Neural Network. Energies. 2023; 16(12):4566. https://doi.org/10.3390/en16124566
Chicago/Turabian StyleZhang, Wenbai, Guobin Lin, Keting Hu, Zhiming Liao, and Huan Wang. 2023. "Operation Control Method for High-Speed Maglev Based on Fractional-Order Sliding Mode Adaptive and Diagonal Recurrent Neural Network" Energies 16, no. 12: 4566. https://doi.org/10.3390/en16124566
APA StyleZhang, W., Lin, G., Hu, K., Liao, Z., & Wang, H. (2023). Operation Control Method for High-Speed Maglev Based on Fractional-Order Sliding Mode Adaptive and Diagonal Recurrent Neural Network. Energies, 16(12), 4566. https://doi.org/10.3390/en16124566







