Chemical Modeling of Constant-Volume Combustion of the Mixture of Methane and Hydrogen Used in Spark Ignition Otto Cycles
Abstract
:1. Introduction
2. The Approach of the Closed Constant-Volume Combustion in Otto Engine Cycles
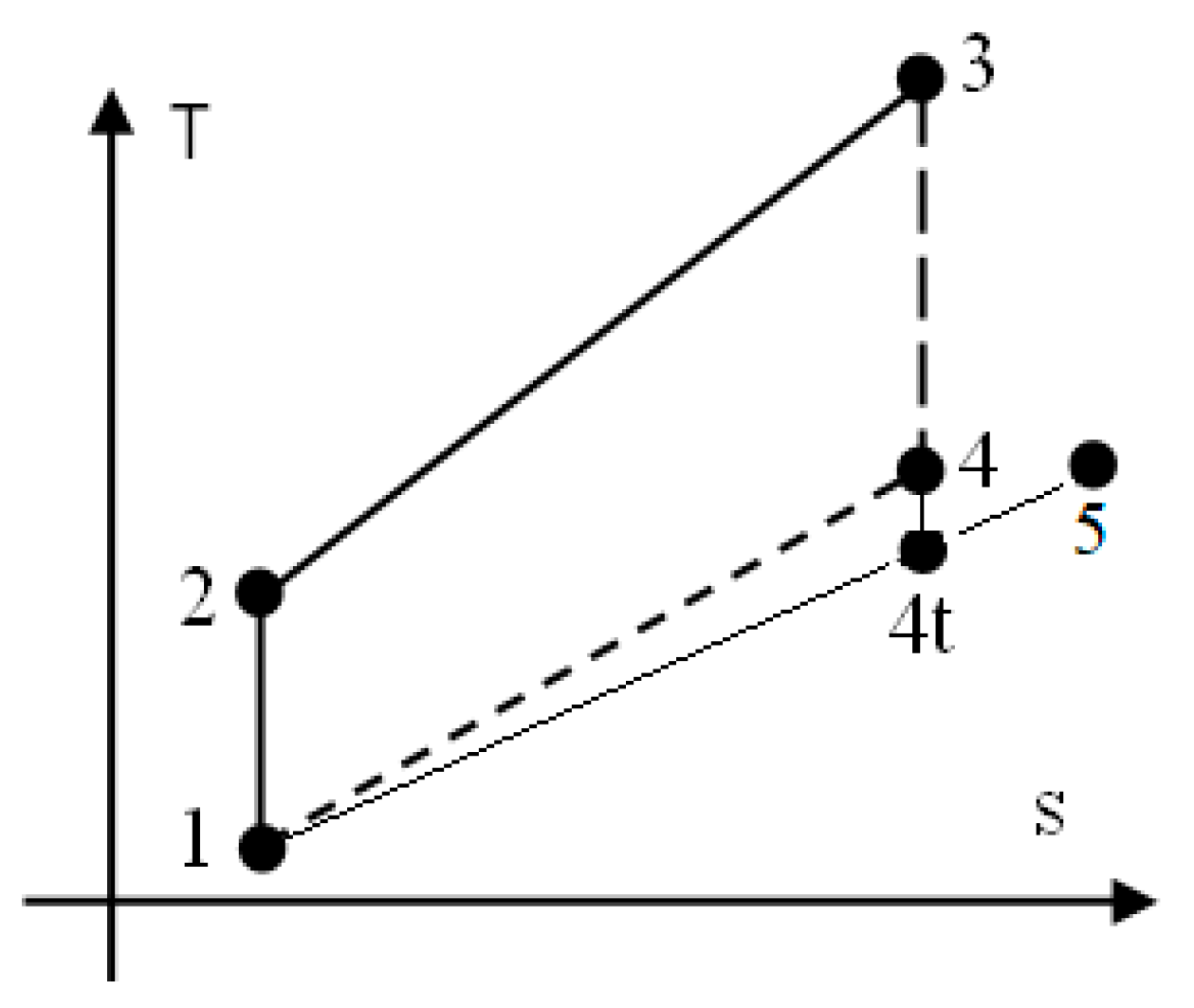
2.1. The Assumptions for the Otto Cycle
- 1–2: isentropic compression of homogeneous mixture CH4/H2/air prepared by a specific device;
- 2–3: closed constant-volume combustion;
- 3–4: isentropic expansion of flue gas;
- 4–5: exhaust of flue gas, assimilated via a throttling process (succession of 4−4t isentropic expansion through flow section of exhaust valves and 4t–5 constant pressure stagnation);
- 5–1: final constant-pressure exhaust of flue gas.
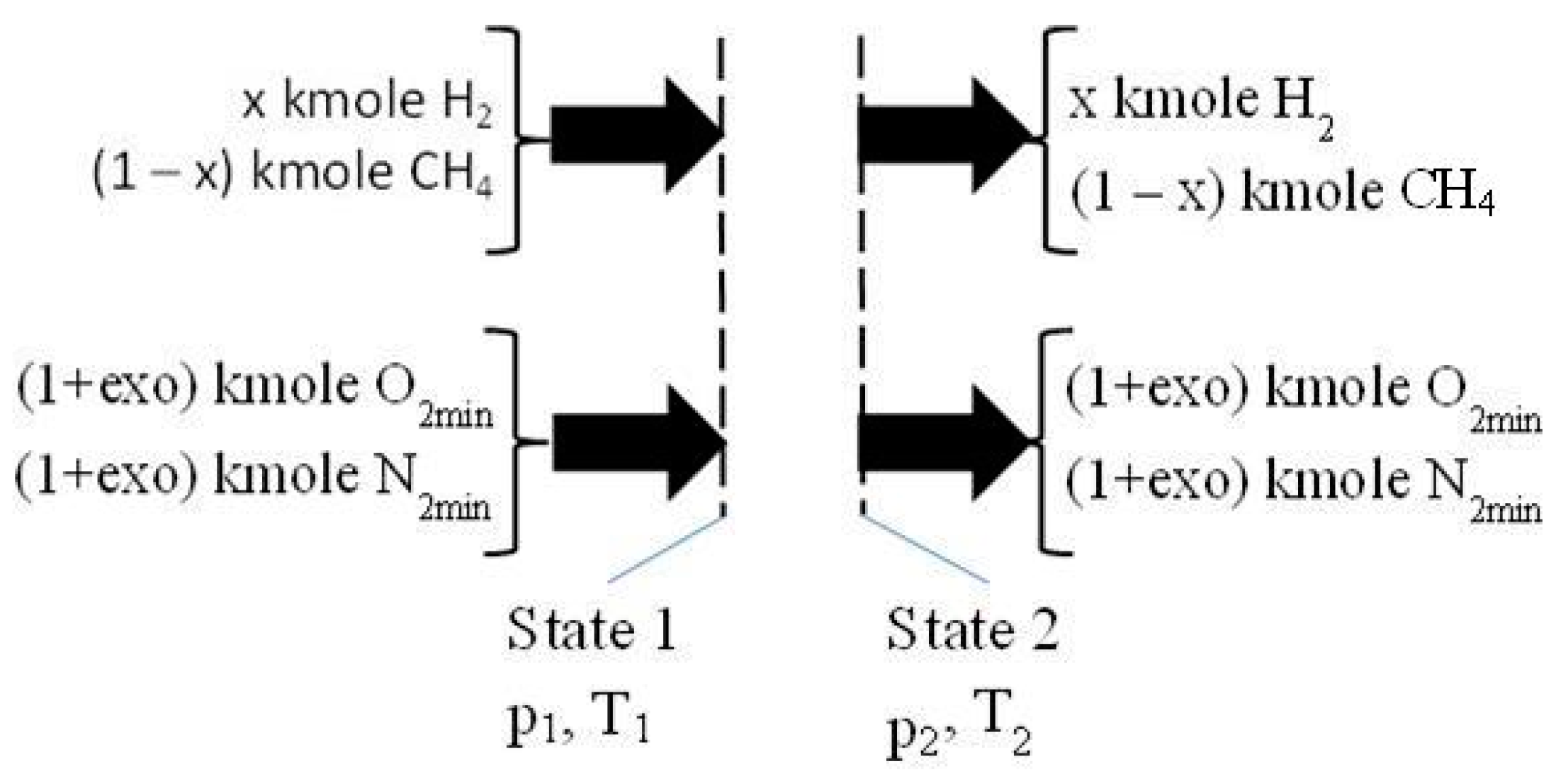
2.2. The Isentropic Compression of Homogeneous Mixture of CH4/H2/Air
- −
- one kmole fuel with x kmole H2 and (1 − x) kmole CH4 was considered;
- −
- the air required for combustion was evaluated using the imposed hydrogen ratio in one kmole fuel, x, and excess oxygen, exo, respectively: (1 + exo)·(2 − 1.5·x) kmole O2 and 3.7619·(1 + exo)·(2 − 1.5·x) kmole N2;
- −
- the imposed x and exo: x = (0, 0.25, 0.5, 0.75, 1), and exo = (0, 0.25, 0.5, 0.75, 1, 1.5, 2);
- −
- the volumetric compression ratio: π12 = V2/V1 = 10.
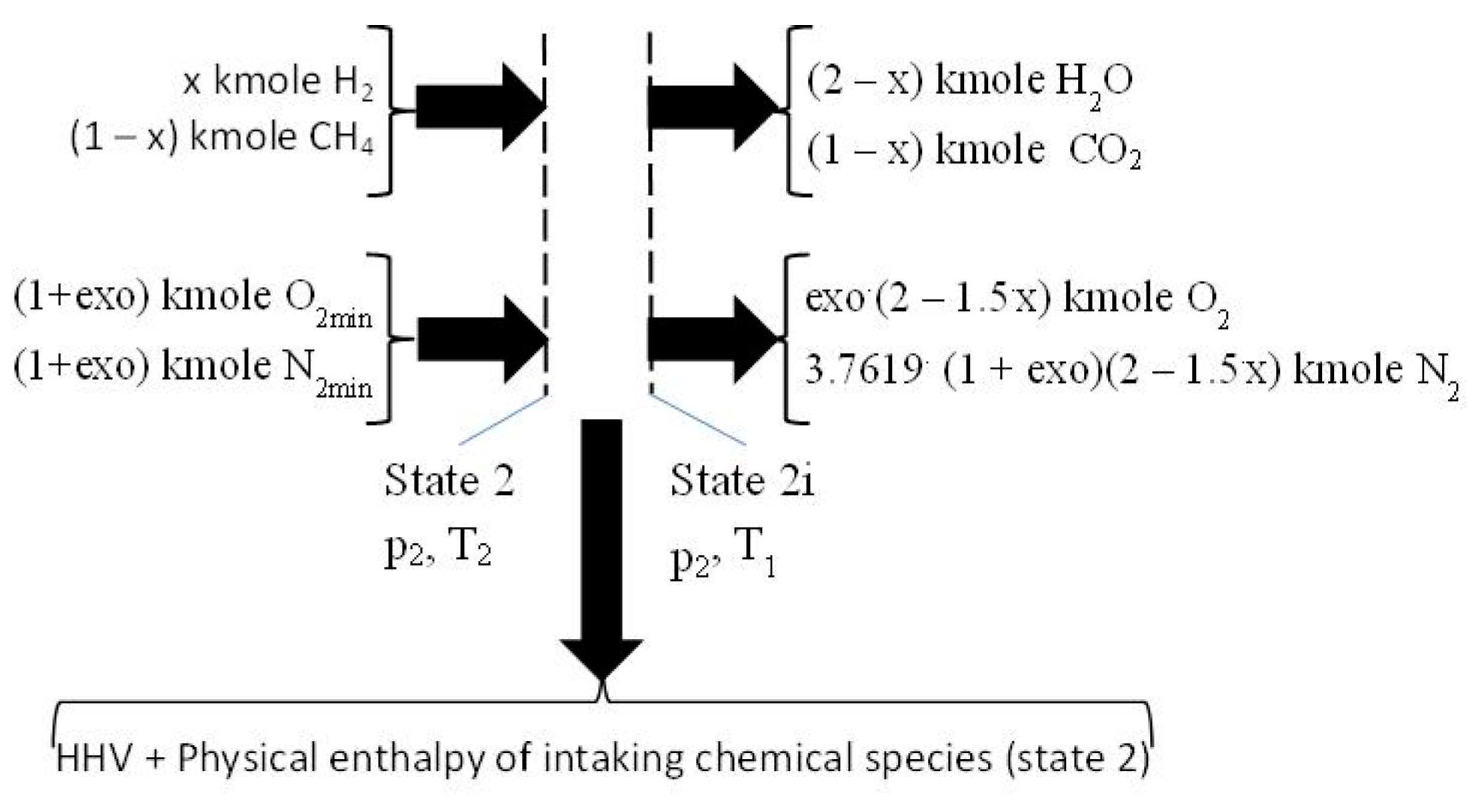
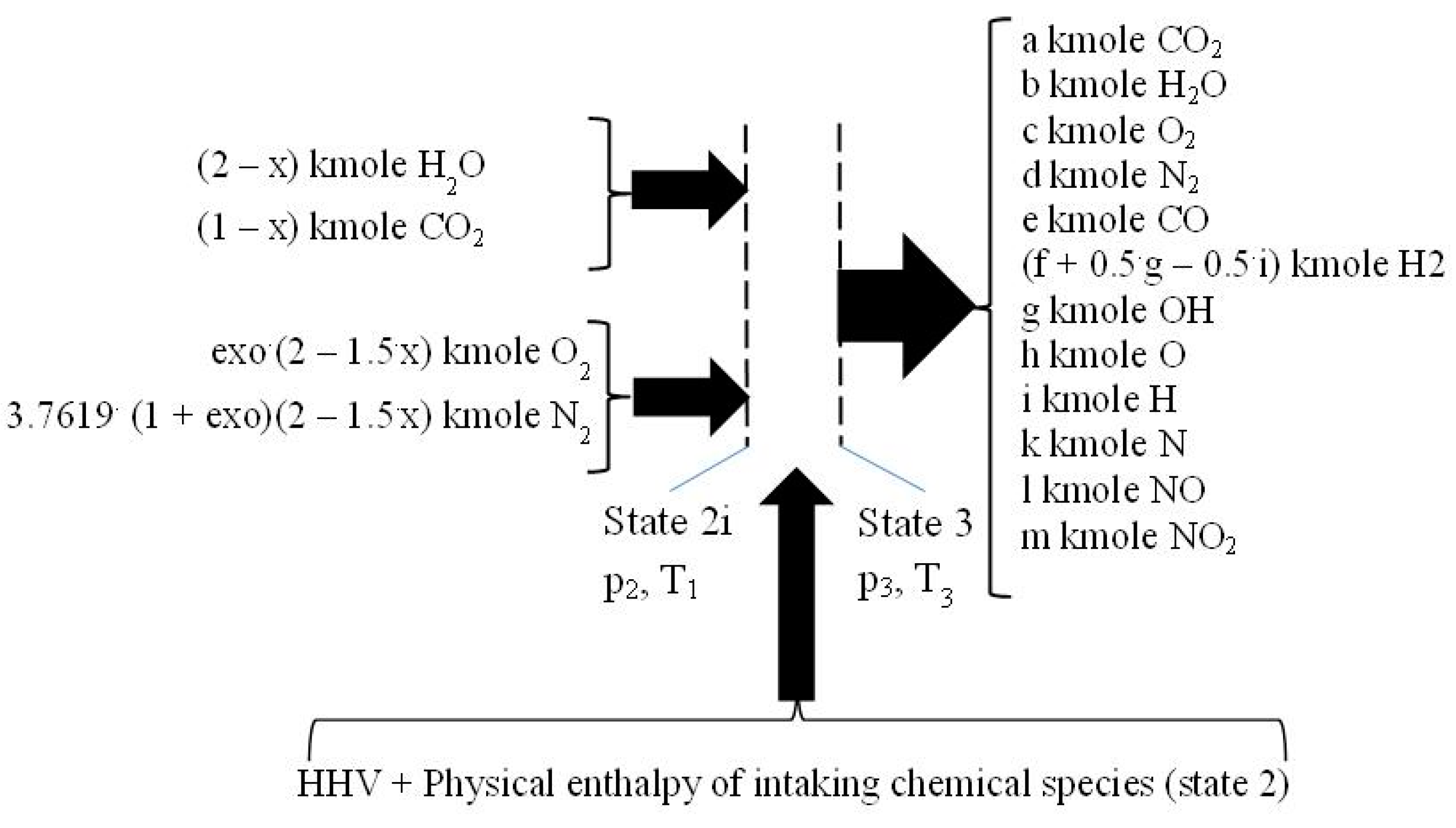
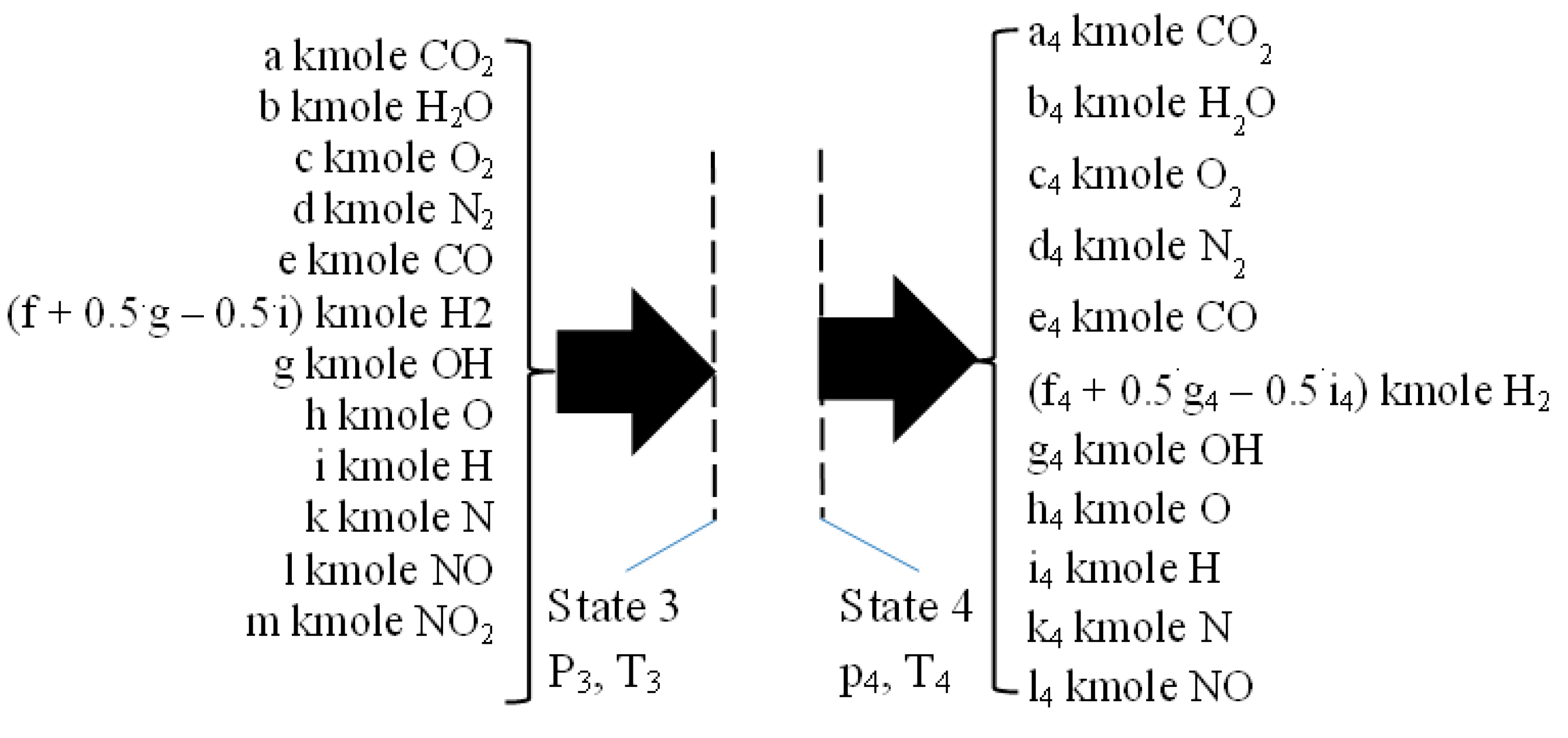
2.3. The Closed Constant-Volume Combustion
- −
- four equations related to the balance of the kmole numbers of major chemical species, such as CO2, H2O, O2, and N2;
- −
- eight equations interrelating all chemical species through chemical equilibrium relations;
- −
- one mass balance for the whole process 2i − 3.
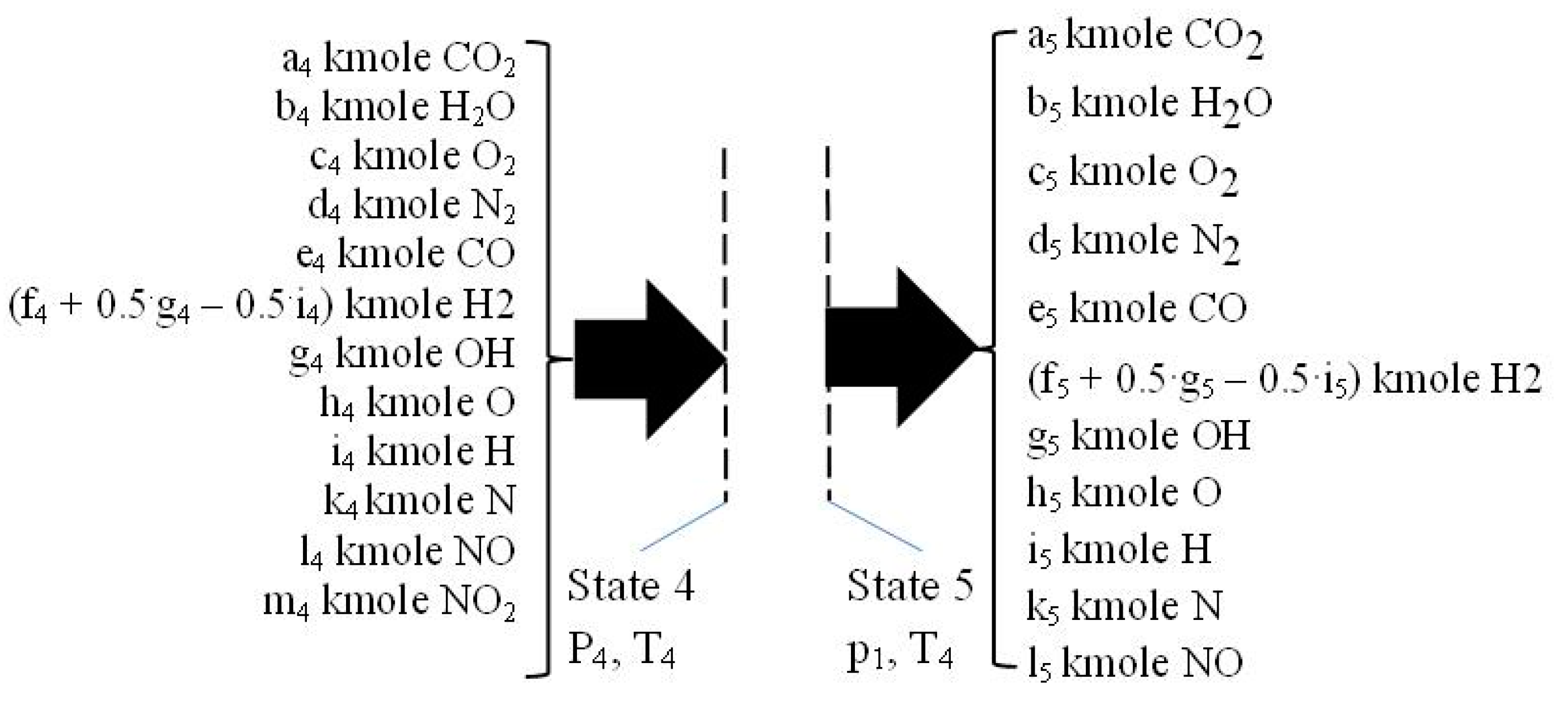
2.4. Isentropic Expansion 3–4
2.5. The Flue Exhaust Process 4–5
3. The Numerical Solving and Results
3.1. Numerical Solving
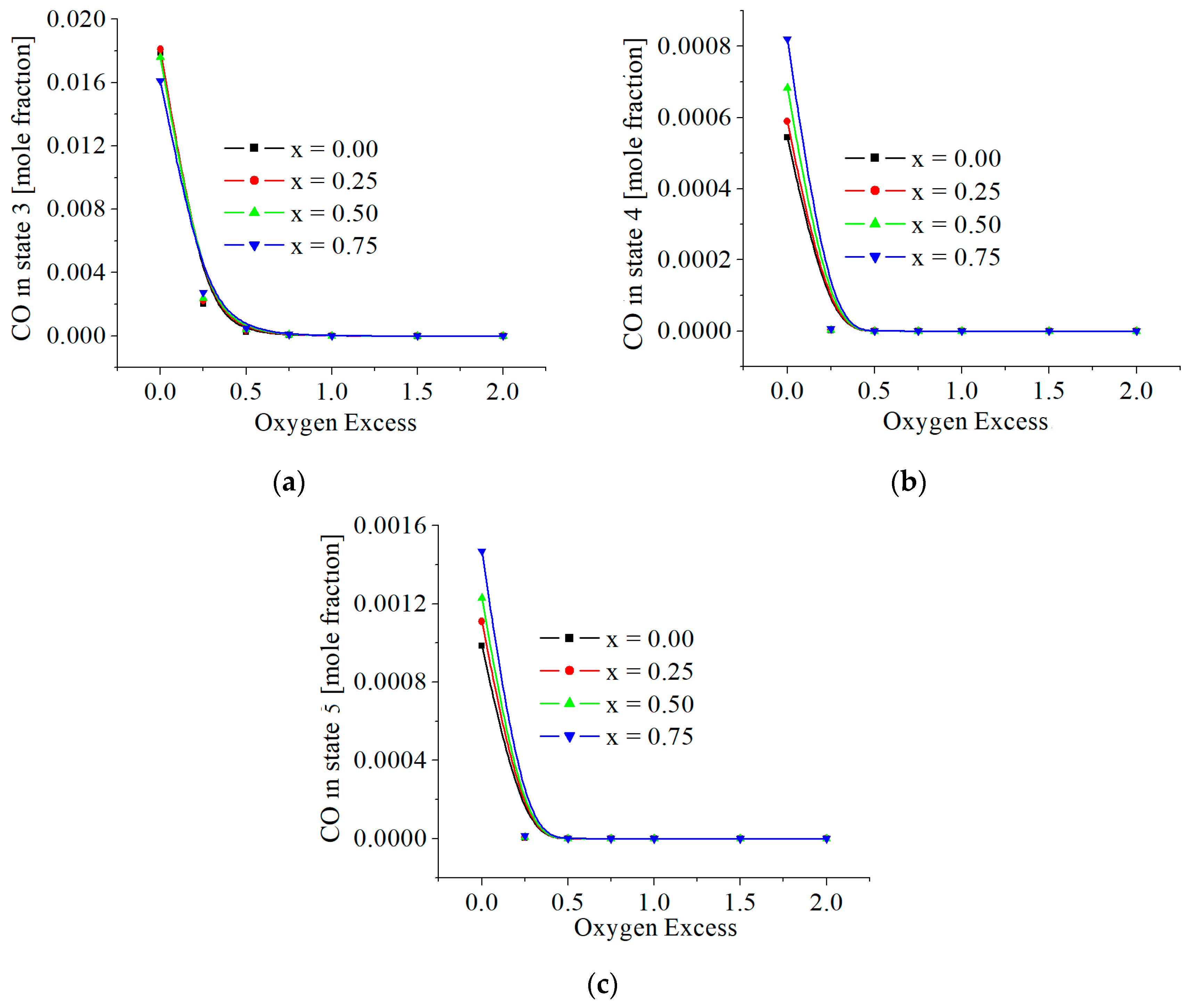
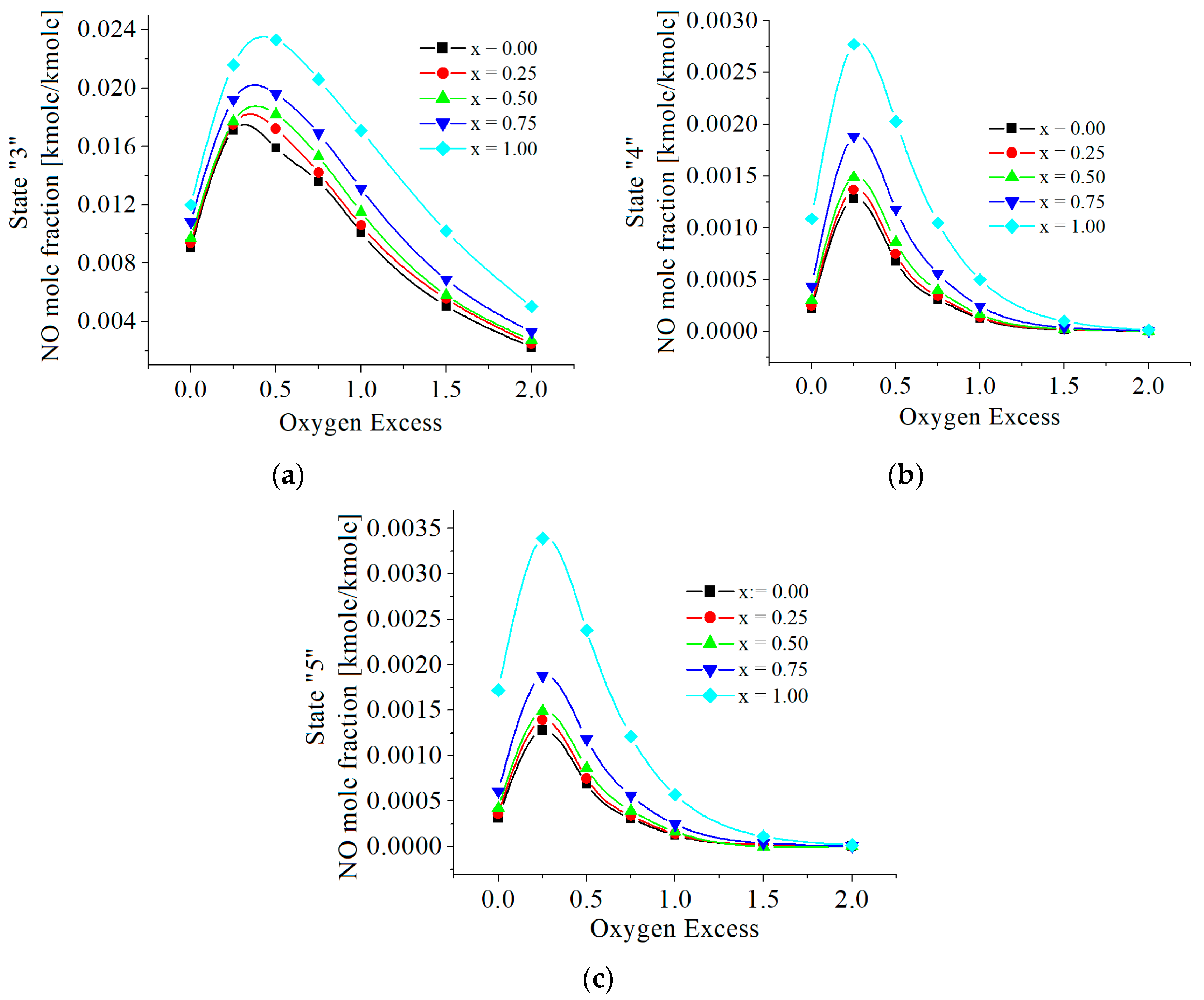
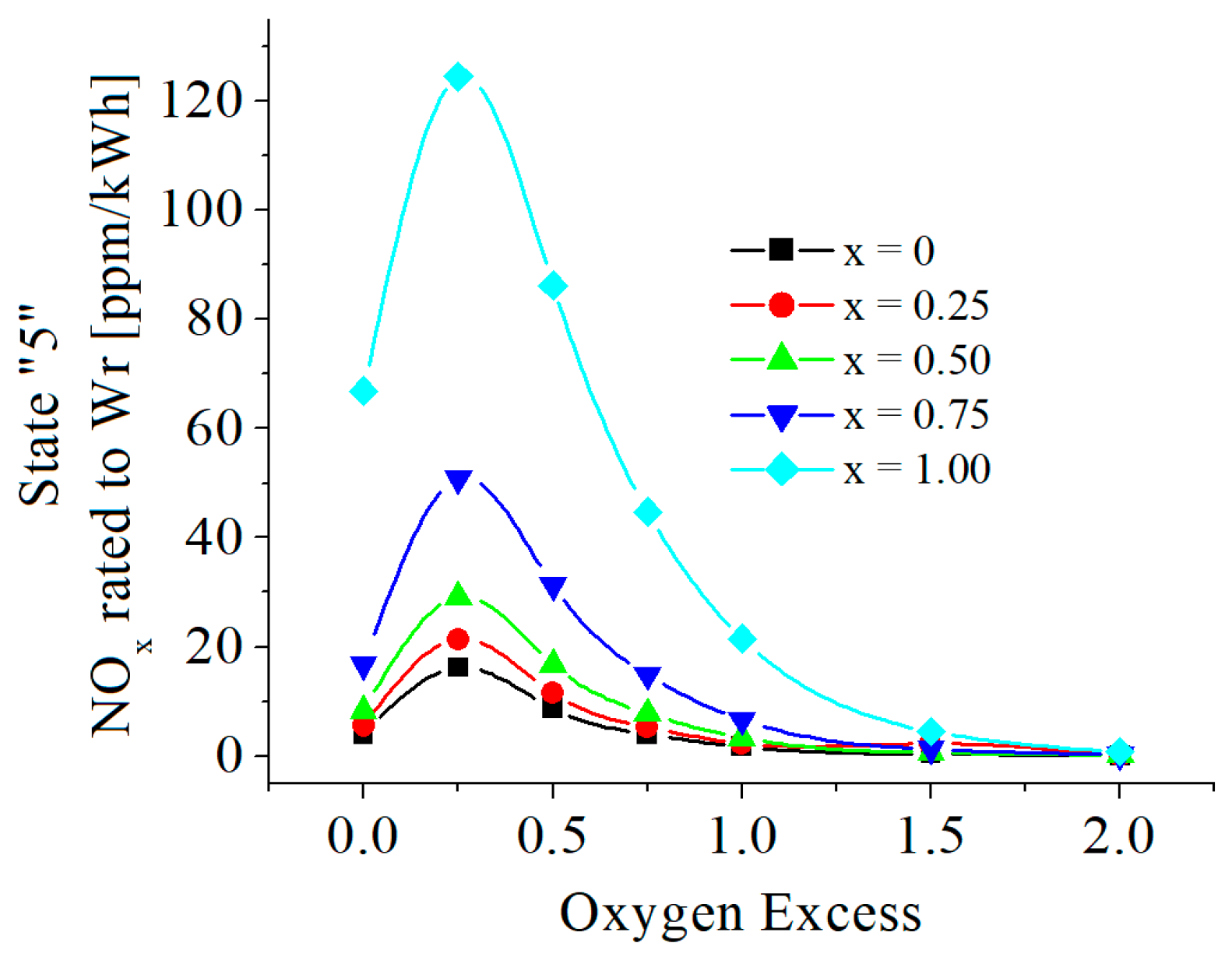
3.2. Numerical Results
4. Critical Comparison with Results Reported Elsewhere
4.1. Comparison 1
4.2. Comparison 2
4.3. Comparison 3
4.4. Comparison 4
4.5. Comparison 5
- NOx 19.65 (mg/kg), 8.86 (ppmvd, 15% O2)
- CO 1.4 × 10−7 (mg/kg), 7 × 10−8 (ppmvd, 15% O2)
5. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Di Sarli, V.; Di Benedetto, A. Laminar burning velocity of hydrogen–methane/air premixed flames. Int. J. Hydrogen Energy 2007, 32, 637–646. [Google Scholar] [CrossRef]
- Di Sarli, V.; Di Benedetto, A.; Long, E.; Hargrave, G. Time-Resolved Particle Image Velocimetry of dynamic interactions between hydrogen-enriched methane/air premixed flames and toroidal vortex structures. Int. J. Hydrogen Energy 2012, 37, 16201–16213. [Google Scholar] [CrossRef] [Green Version]
- Krebs, S.; Biet, C. Predictive model of a premixed, lean hydrogen combustion for internal combustion engines. Transp. Eng. 2021, 5, 100086. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, Y.; Wang, R.; Lu, W.; Liu, W.; Zhang, Y. Investigation on the effects of blending hydrogen-rich gas in the spark-ignition engine. Energy Rep. 2022, 8, 797–803. [Google Scholar] [CrossRef]
- Qadiri, U.; AlFantazi, A. Numerical 1-D simulations on Single-Cylinder stationary spark ignition engine using Micro-Emulsions, gasoline, and hydrogen in dual fuel mode. Clean. Chem. Eng. 2022, 2, 100009. [Google Scholar] [CrossRef]
- Yu, X.; Hu, Z.; Guo, Z.; Li, D.; Wang, T.; Li, Y.; Zhang, J.; Gong, T.; Li, Y. Research on combustion and emission characteristics of a hydrous ethanol/hydrogen combined injection spark ignition engine under lean-burn conditions. Int. J. Hydrogen Energy 2022, 47, 27223–27236. [Google Scholar] [CrossRef]
- Barbu, M.C.; Birta, A.; Chiriac, R. On the improvement of performance and pollutant emissions of a spark ignition engine fuelled by compressed natural gas and hydrogen. Energy Rep. 2022, 8, 978–991. [Google Scholar] [CrossRef]
- Suresh, D.; Porpatham, E. Influence of high compression ratio and hydrogen addition on the performance and emissions of a lean burn spark ignition engine fueled by ethanolgasoline. Int. J. Hydrogen Energy 2023, 48, 14433–14448. [Google Scholar] [CrossRef]
- Gonca, G.; Sahin, B.; Hocaoglu, M.F. Influences of hydrogen and various gas fuel addition to different liquid fuels on the performance characteristics of a spark ignition engine. Int. J. Hydrogen Energy 2022, 47, 12421–12431. [Google Scholar] [CrossRef]
- Bui, V.G.; Bui, T.M.T.; Tran, V.N.; Huang, Z.; Hoang, A.T.; Tarelko, W.; Bui, V.H.; Pham, X.M.; Nguyen, P.Q.P. Flexible syngas-biogas-hydrogen fueling spark-ignition engine behaviors with optimized fuel compositions and control parameters. Int. J. Hydrogen Energy 2023, 18, 6722–6737. [Google Scholar] [CrossRef]
- Naruke, M.; Morie, K.; Sakaida, S.; Tanaka, K.; Konno, M. Effects of hydrogen addition on engine performance in a spark ignition engine with a high compression ratio under lean burn conditions. Int. J. Hydrogen Energy 2019, 44, 15565–15574. [Google Scholar] [CrossRef]
- Sanli, A.; Yılmaz, I.T.; Gümüs, M. Assessment of combustion and exhaust emissions in a common-rail diesel engine fueled with methane and hydrogen/methane mixtures under different compression ratio. Int. J. Hydrogen Energy 2020, 45, 3263–3283. [Google Scholar] [CrossRef]
- Ali, G.; Zhang, T.; Wu, W.; Zhou, Y. Effect of hydrogen addition on NOx formation mechanism and pathways in MILD combustion of H2-rich low calorific value fuels. Int. J. Hydrogen Energy 2020, 45, 9200–9210. [Google Scholar] [CrossRef]
- Pashchenko, D. Hydrogen-rich fuel combustion in a swirling flame: CFD-modeling with experimental verification. Int. J. Hydrogen Energy 2020, 45, 19996–20003. [Google Scholar] [CrossRef]
- García, C.P.; Abril, S.O.; León, J.P. Analysis of performance, emissions, and lubrication in a spark-ignition engine fueled with hydrogen gas mixtures. Heliyon 2022, 8, e11353. [Google Scholar] [CrossRef]
- Pan, H.; Geng, S.; Yang, H.; Zhang, G.; Bian, H.; Liu, Y. Influence of H2 blending on NOx production in natural gas combustion: Mechanism comparison and reaction routes. Int. J. Hydrogen Energy 2023, 48, 784–797. [Google Scholar] [CrossRef]
- Taamallah, S.; Vogiatzaki, K.; Alzahrani, F.M.; Mokheimer, E.M.A.; Habib, M.A.; Ghoniem, A.F. Fuel flexibility, stability and emissions in premixed hydrogen-rich gas turbine combustion: Technology, fundamentals, and numerical simulations. Appl. Energy 2015, 154, 1020–1047. [Google Scholar] [CrossRef]
- Peng, Q.; Ye, J.; Tu, Y.; Yang, W.; Jiaqiang, E.; Kang, Z.; Fu, G. Experimental and numerical investigation on premixed H2/C3H8/air combustion and thermal performance in a burner with partially filled porous media. Fuel 2022, 328, 125227. [Google Scholar] [CrossRef]
- Maio, G.; Boberic, A.; Giarracca, L.; Aubagnac-Karkar, D.; Colin, O.; Duffour, F.; Deppenkemper, K.; Virnich, L.; Pischinger, S. Experimental and numerical investigation of a direct injection spark ignition hydrogen engine for heavy-duty applications. Int. J. Hydrogen Energy 2022, 47, 29069–29084. [Google Scholar] [CrossRef]
- Yosri, M.; Palulli, R.; Talei, M.; Mortimer, J.; Poursadegh, F.; Yang, Y.; Brear, M. Numerical investigation of a large bore, direct injection, spark ignition, hydrogen-fuelled engine. Int. J. Hydrogen Energy 2023, 48, 17689–17702. [Google Scholar] [CrossRef]
- Urroz, J.C.; Diéguez, P.M.; Arzamendi, G.; Arana, M.; Gandía, L.M. Gaseous fueling of an adapted commercial automotive spark-ignition engine: Simplified thermodynamic modeling and experimental study running on hydrogen, methane, carbon monoxide and their mixtures. Fuel 2023, 337, 127178. [Google Scholar] [CrossRef]
- Xu, L.; Sun, X.; Ku, C.; Liu, J.; Lai, M.-C.; Duan, X. Effects of control strategies for mixture activity and chemical reaction pathway coupled with exhaust gas recirculation on the performance of hydrogen-enriched natural-gas fueled spark ignition engine. Fuel 2022, 322, 124153. [Google Scholar] [CrossRef]
- Ganesan, N.; Sahni, I.; Samuel, O.D.; Enweremadu, C.C.; Veza, I.; Chandran, D. Optimization and sustainability of gasohol/hydrogen blends for operative spark ignition engine utilization and green environment. Case Stud. Therm. Eng. 2022, 39, 102381. [Google Scholar] [CrossRef]
- Salvi, B.L.; Subramanian, K.A. A novel approach for experimental study and numerical modeling of combustion characteristics of a hydrogen fuelled spark ignition engine. Sustain. Energy Technol. Assess. 2022, 51, 101972. [Google Scholar] [CrossRef]
- Kosmadakis, G.M.; Rakopoulos, D.C.; Rakopoulos, C.D. Assessing the cyclic-variability of spark-ignition engine running on methane-hydrogen blends with high hydrogen contents of up to 50%. Int. J. Hydrogen Energy 2021, 46, 17955–17968. [Google Scholar] [CrossRef]
- Li, D.; Wang, H.; Yu, X.; Yang, H. Combustion and emission characteristics of an Acetone-Butanol-Ethanol (ABE) spark ignition engine with hydrogen direct injection. Int. J. Hydrogen Energy 2021, 46, 30145–30157. [Google Scholar] [CrossRef]
- Bundele, H.; Kurien, C.; Varma, P.S.; Mittal, M. Experimental and computational study on the enhancement of engine characteristics by hydrogen enrichment in a biogas fuelled spark ignition engine. Int. J. Hydrogen Energy 2022, 47, 30671–30686. [Google Scholar] [CrossRef]
- Borgnakke, C.; Sonntag, R.E. Fundamentals of Thermodynamics, 8th ed.; Wiley: Hoboken, NJ, USA, 2012; ISBN 978-1-118-13199-2. Available online: https://www.academia.edu/32941529/Fundamentals_of_Thermodynamics_8th_ed (accessed on 1 April 2023).

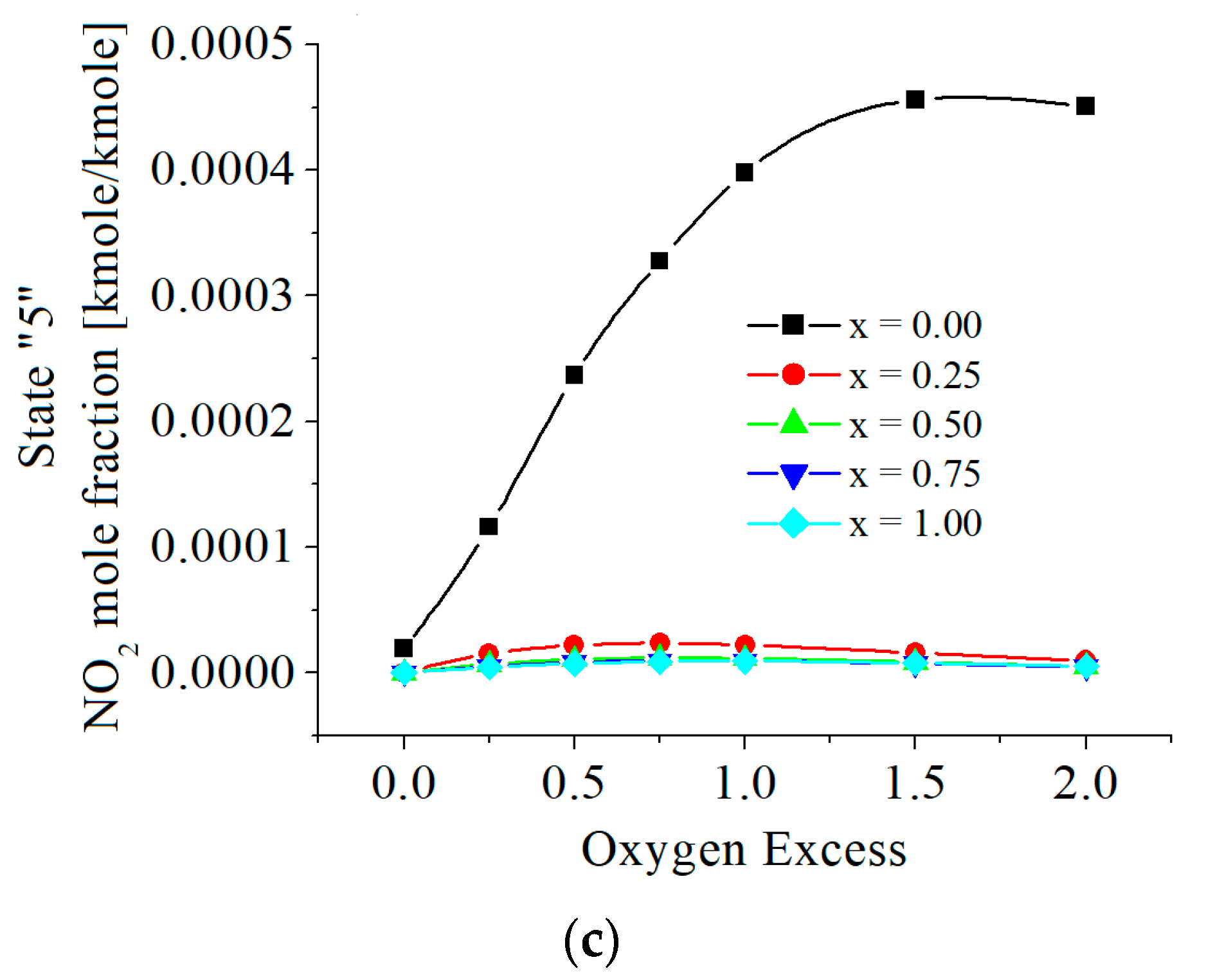
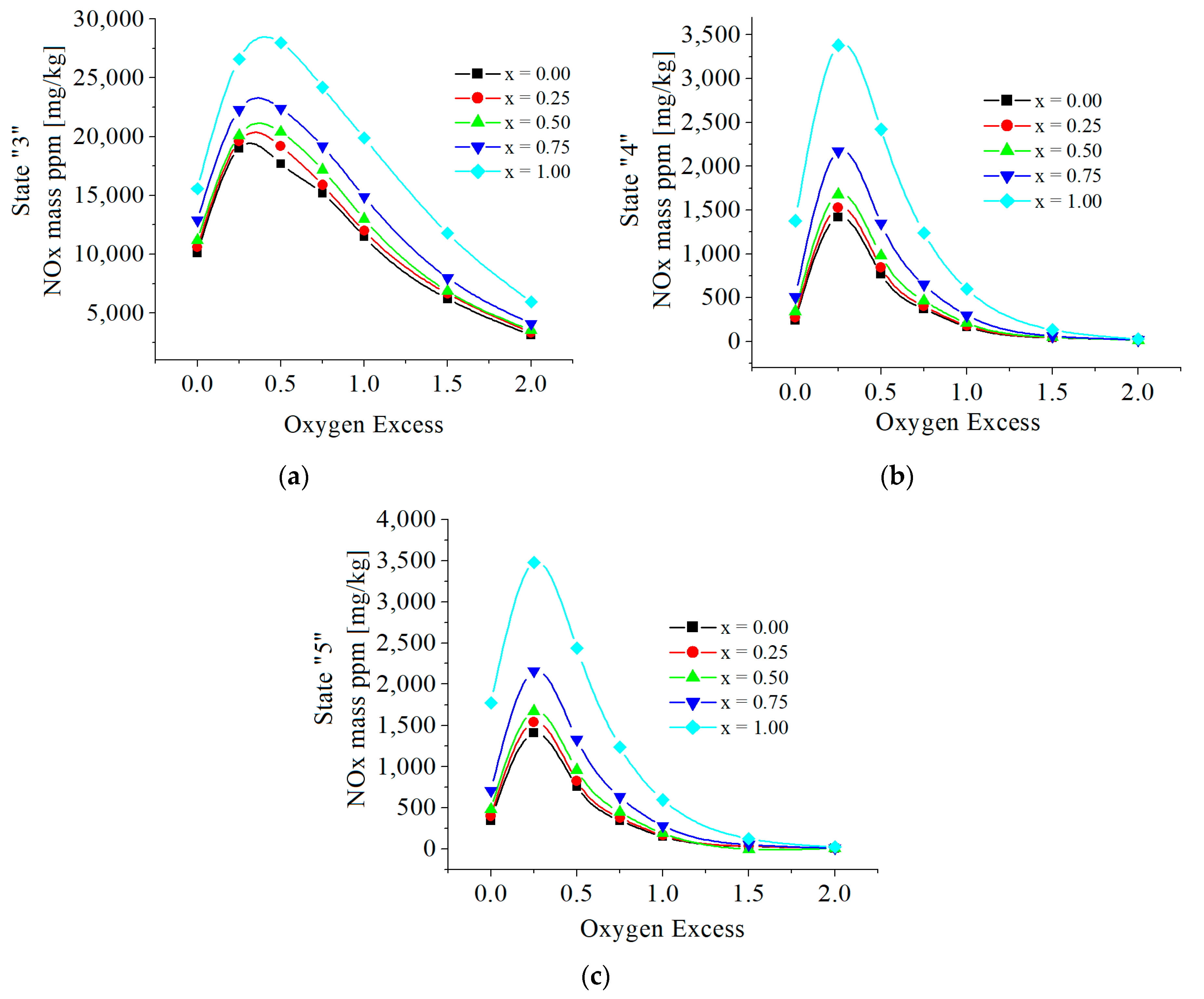
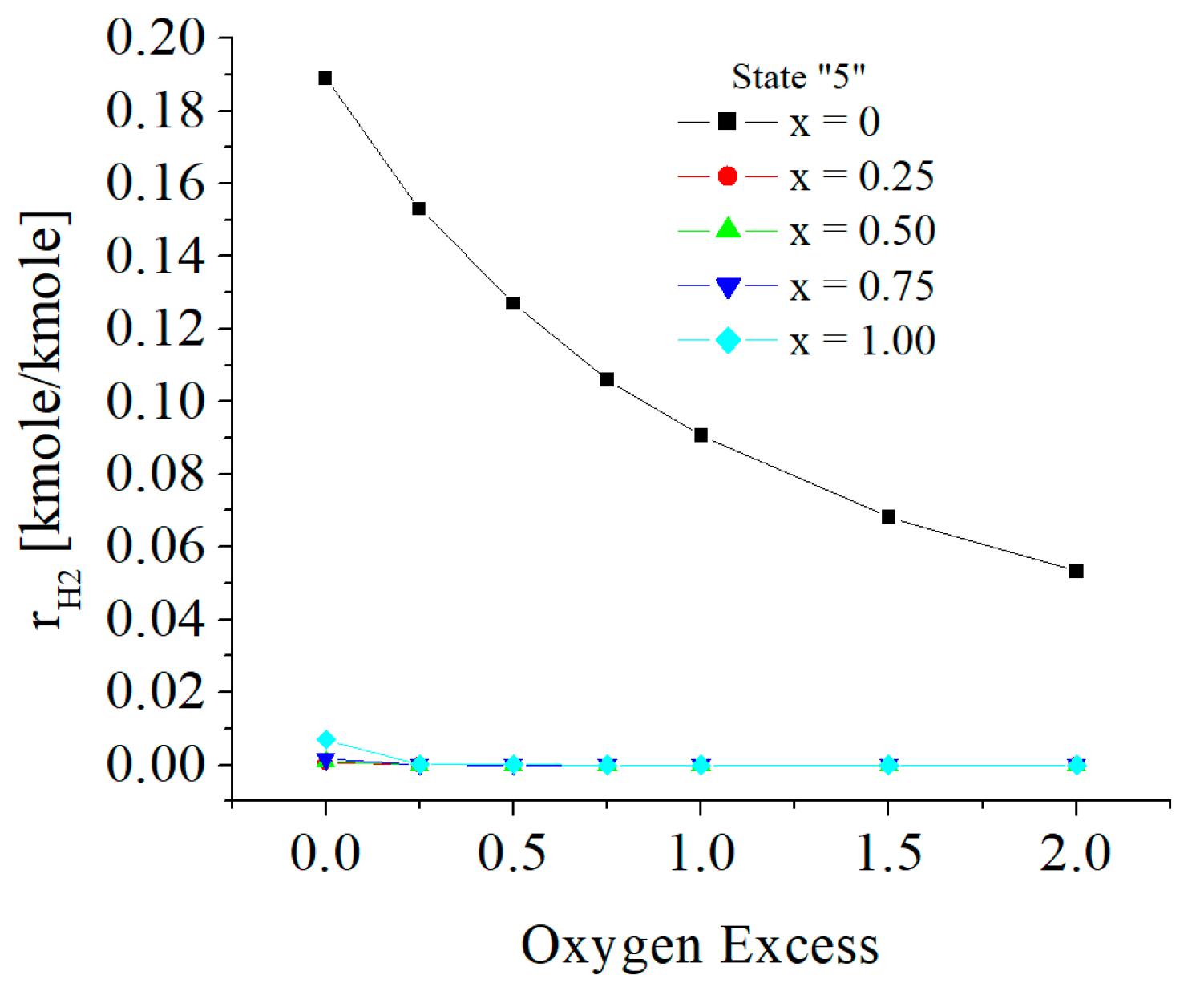
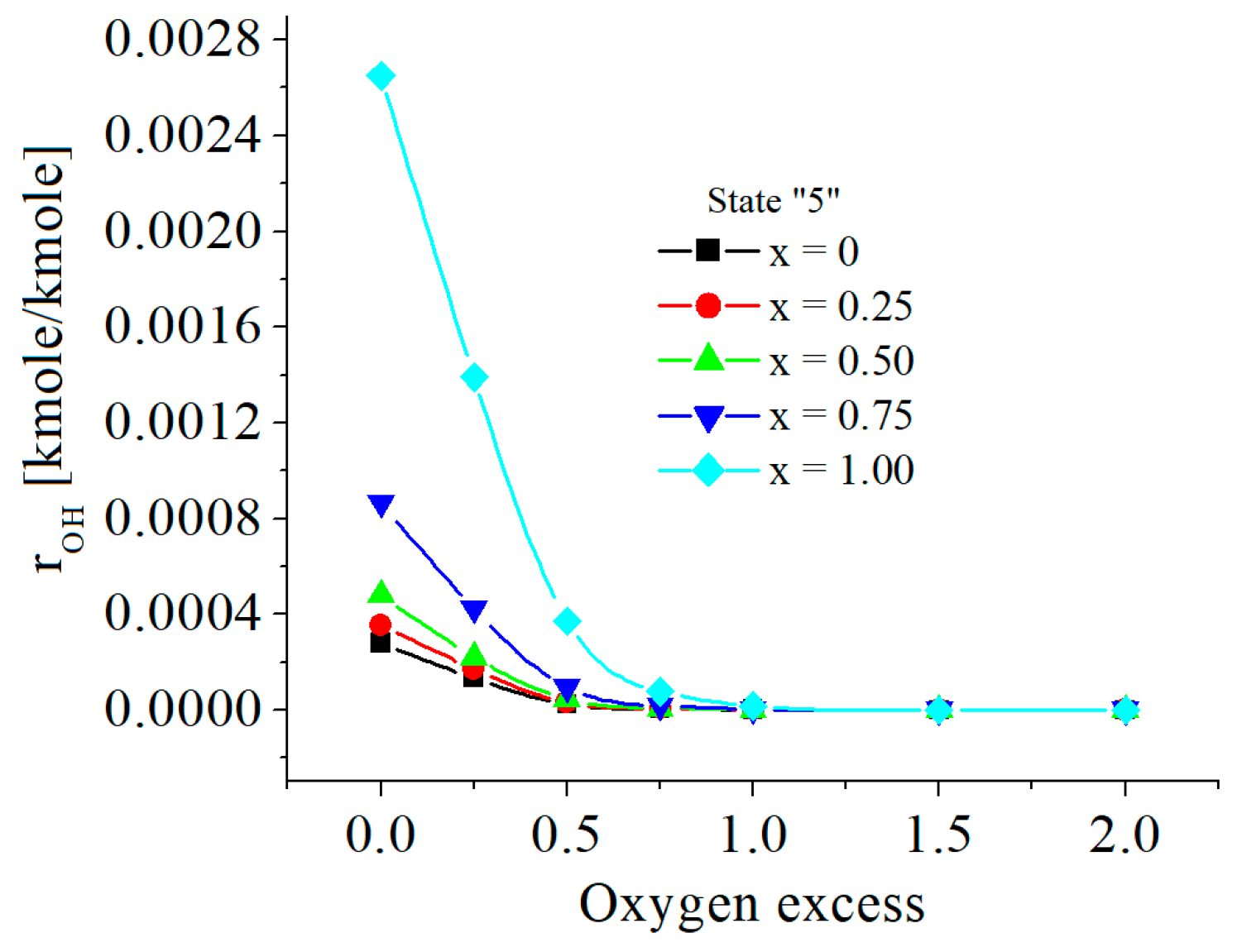
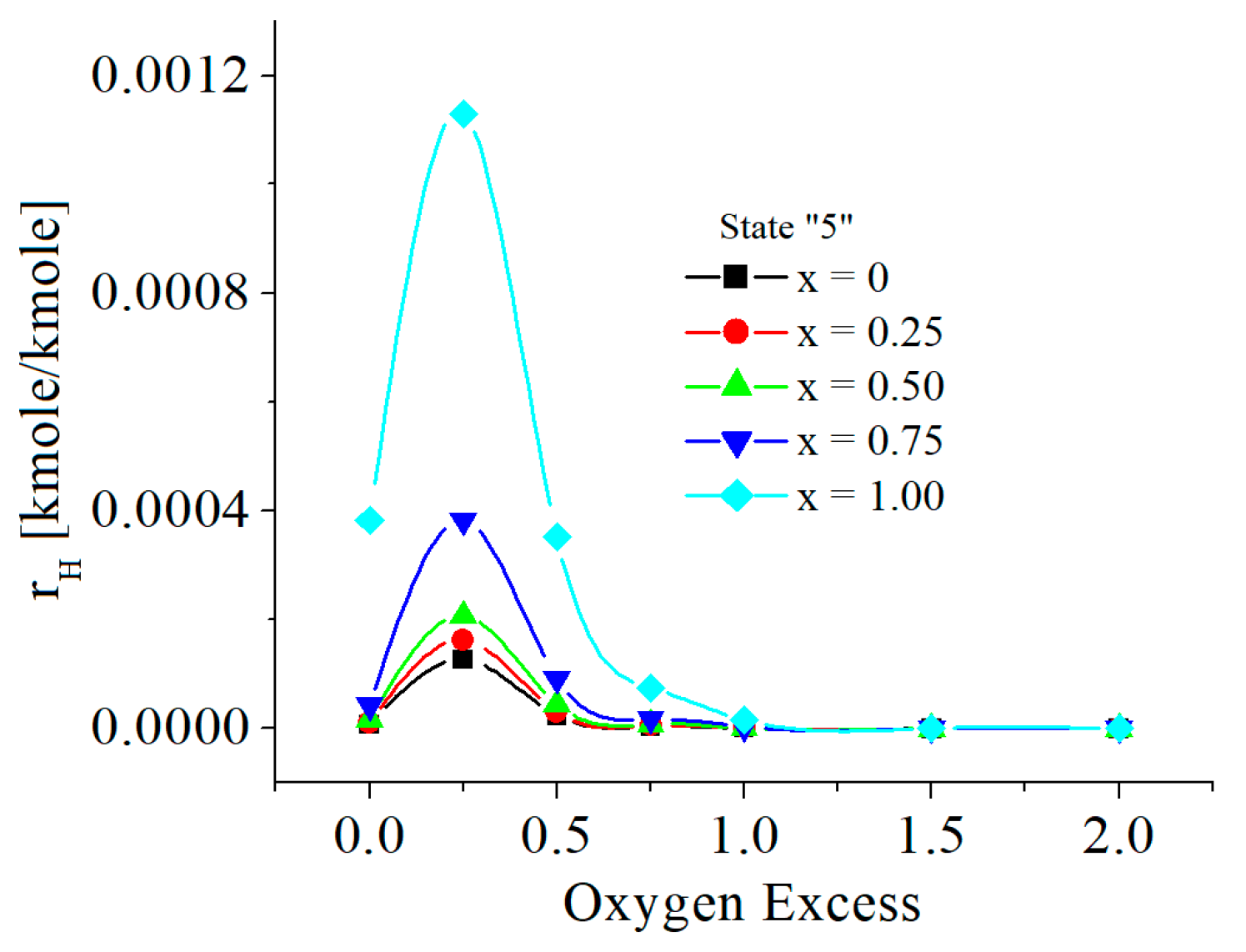
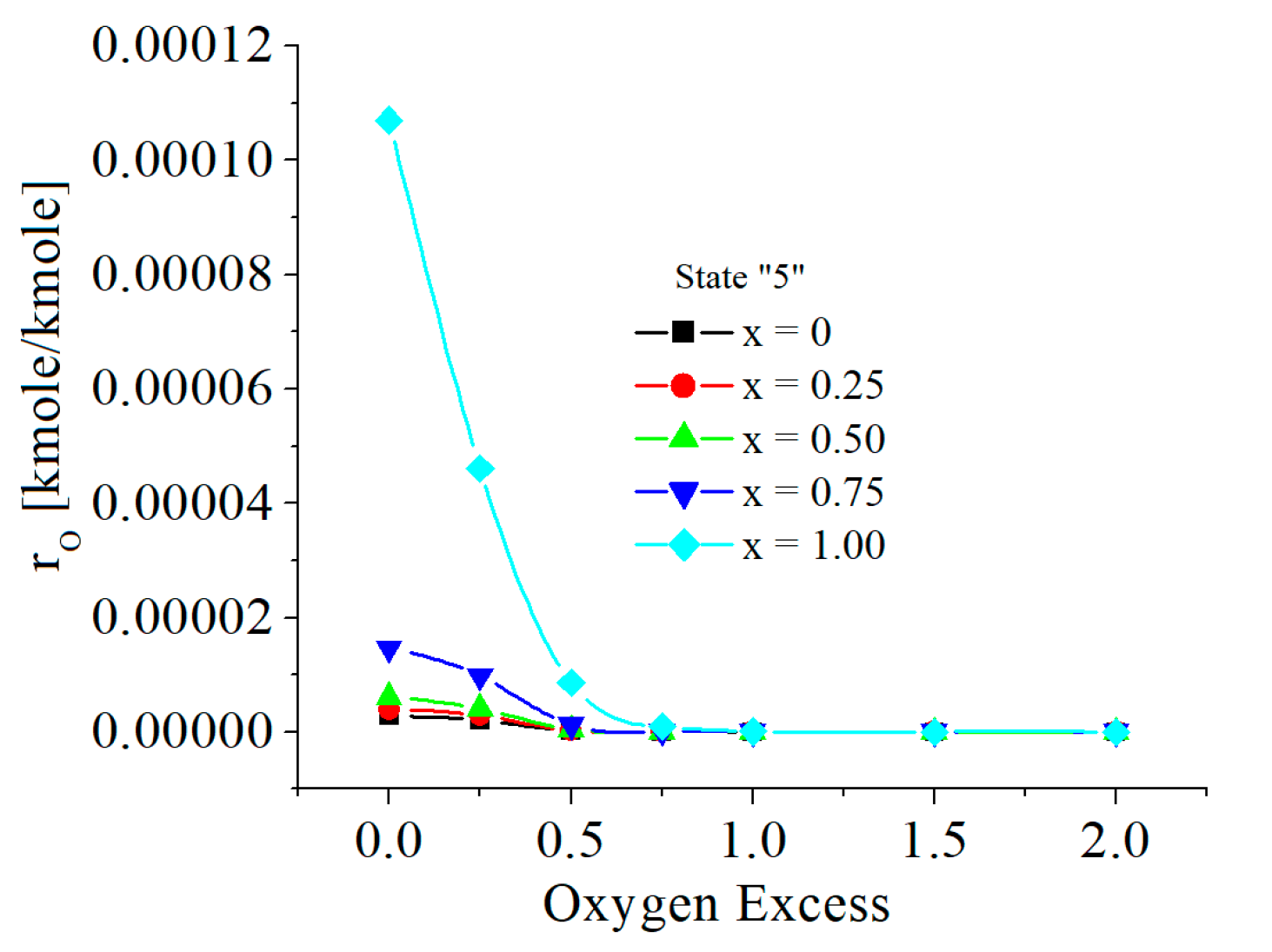
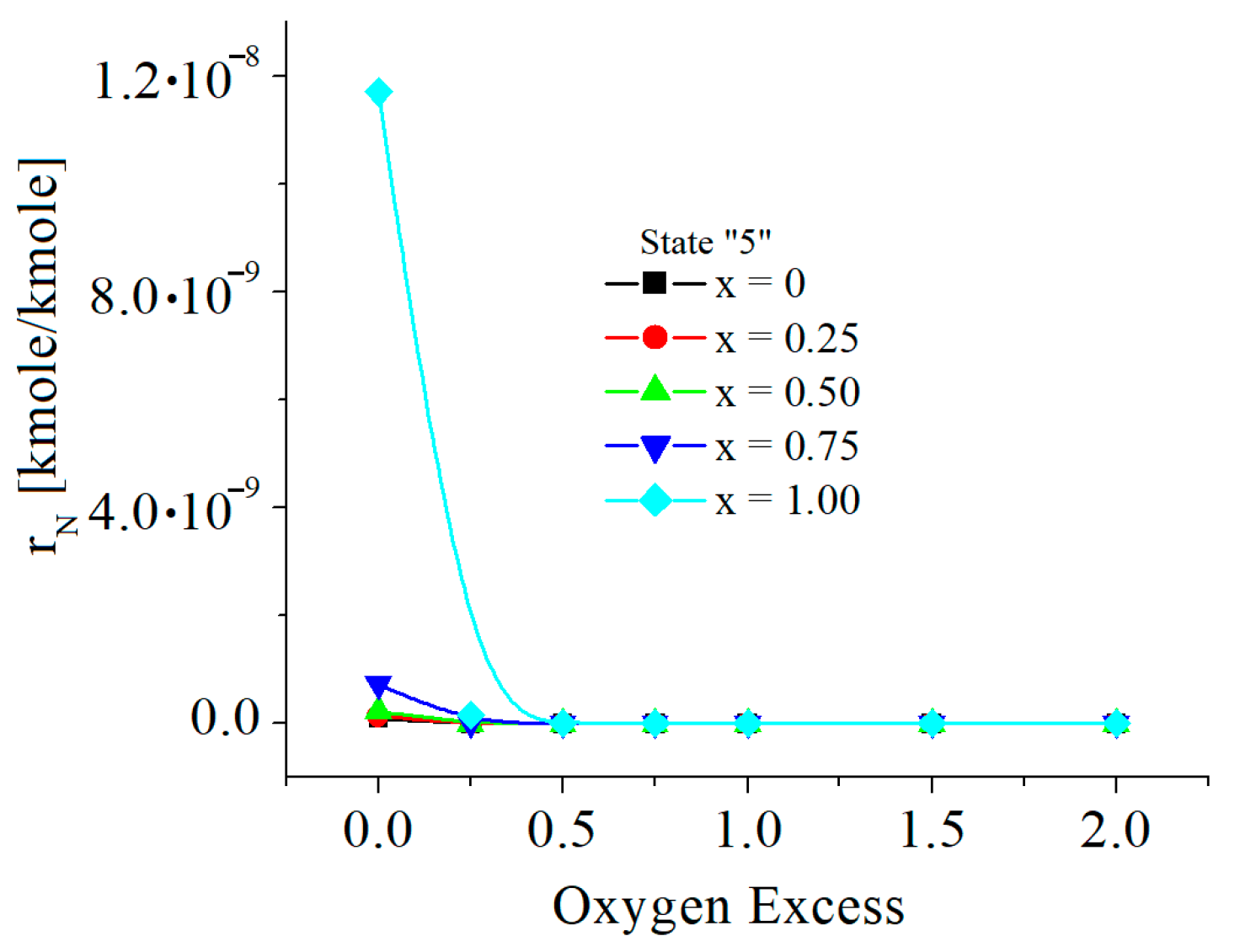
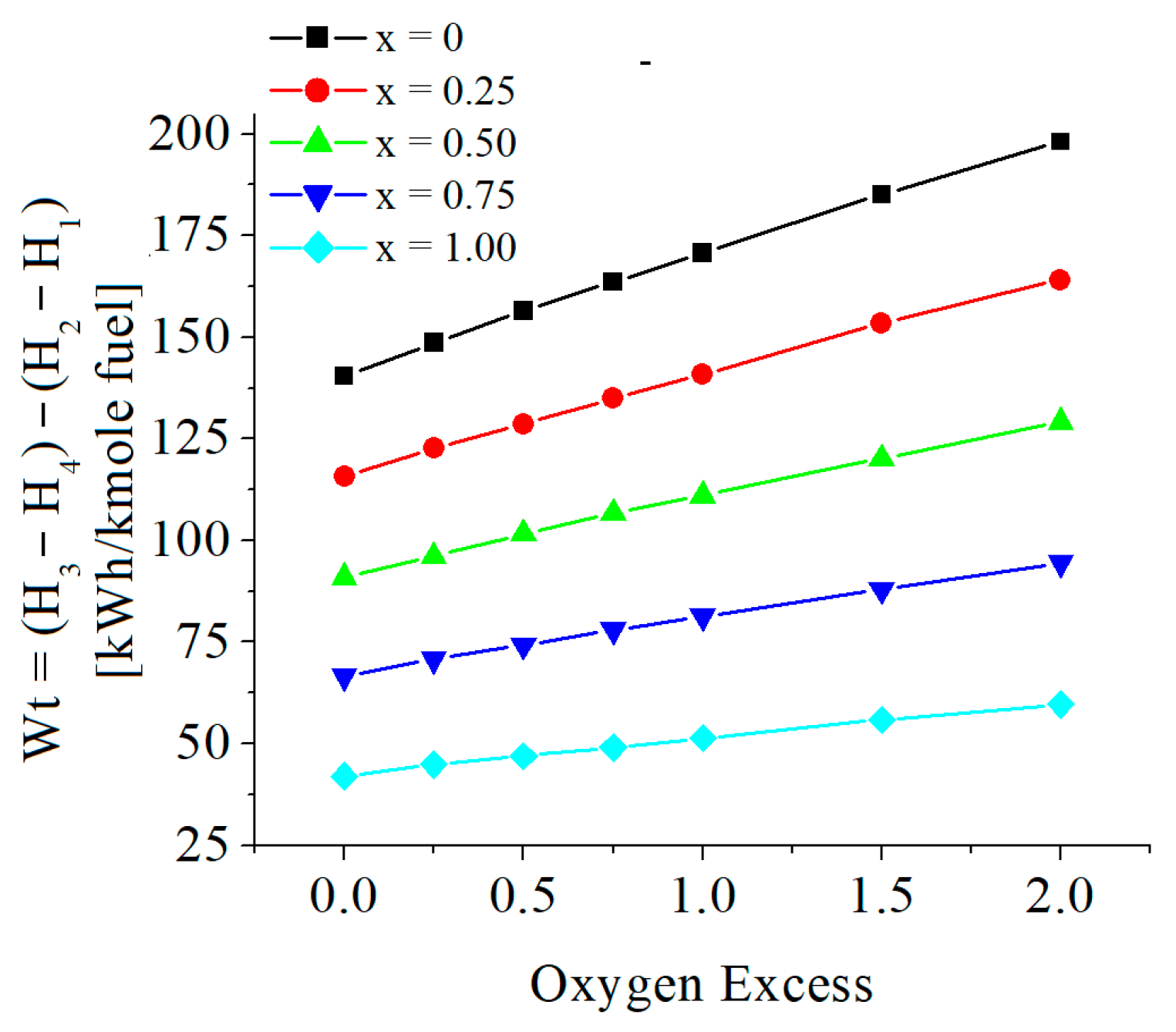
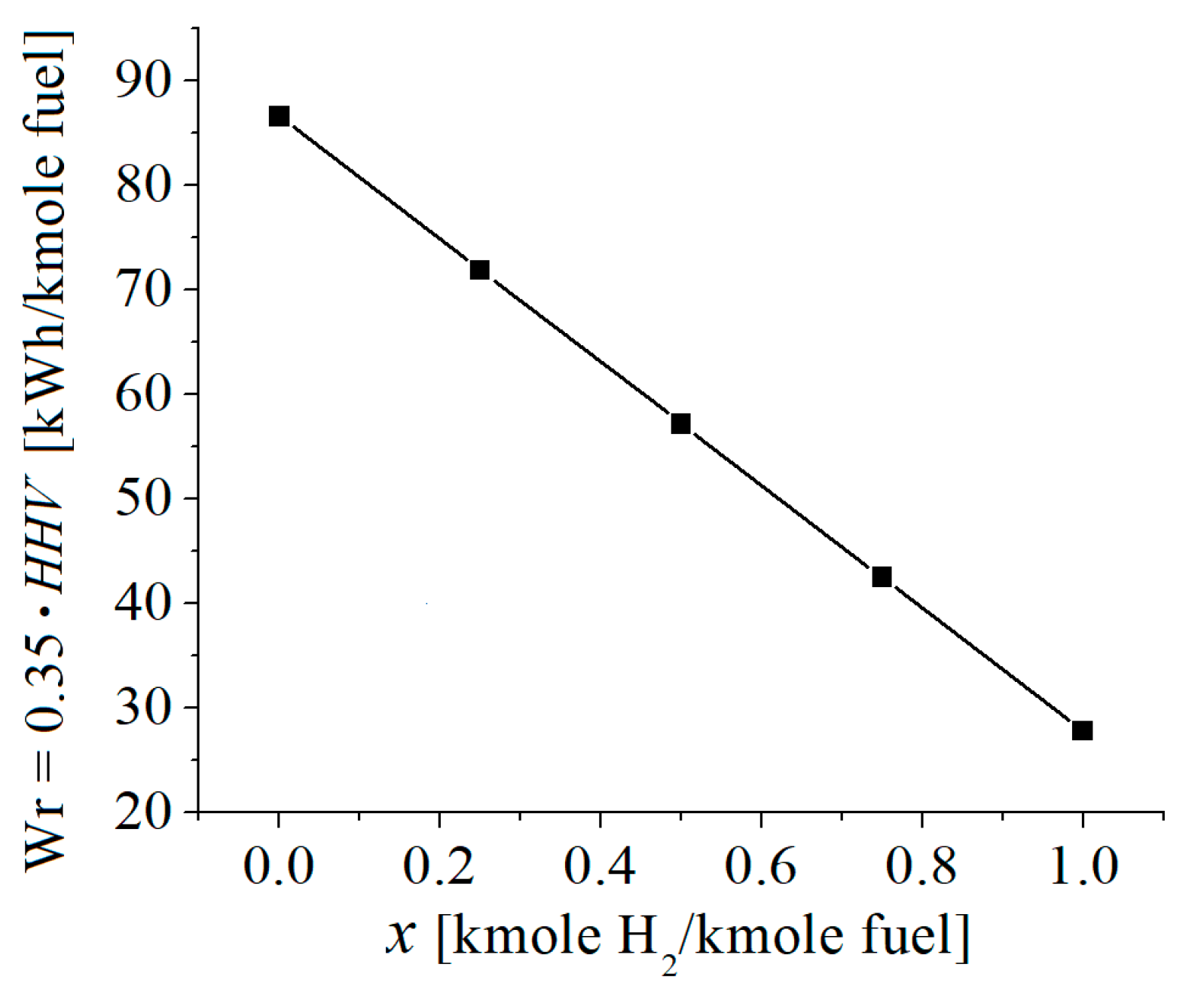
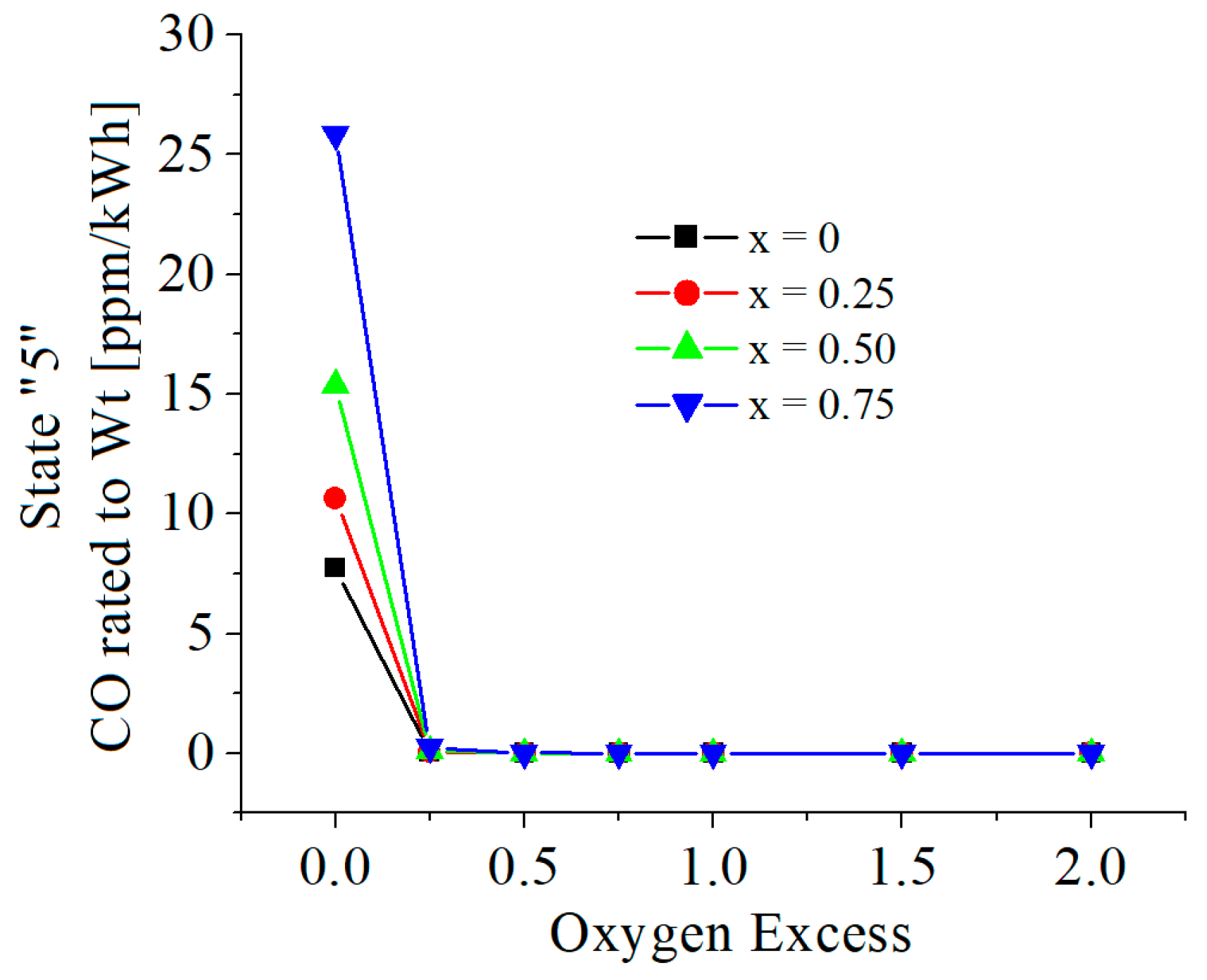
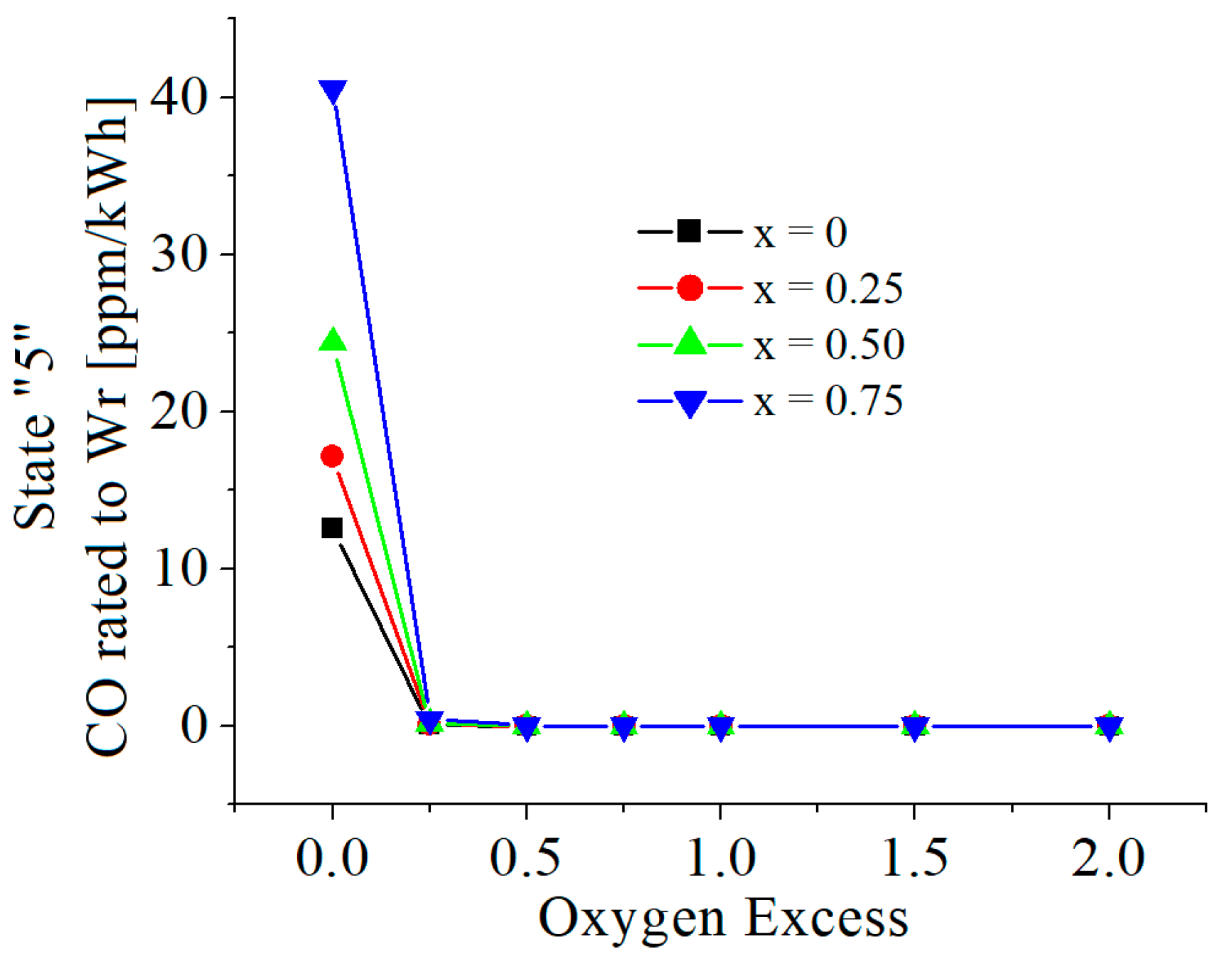
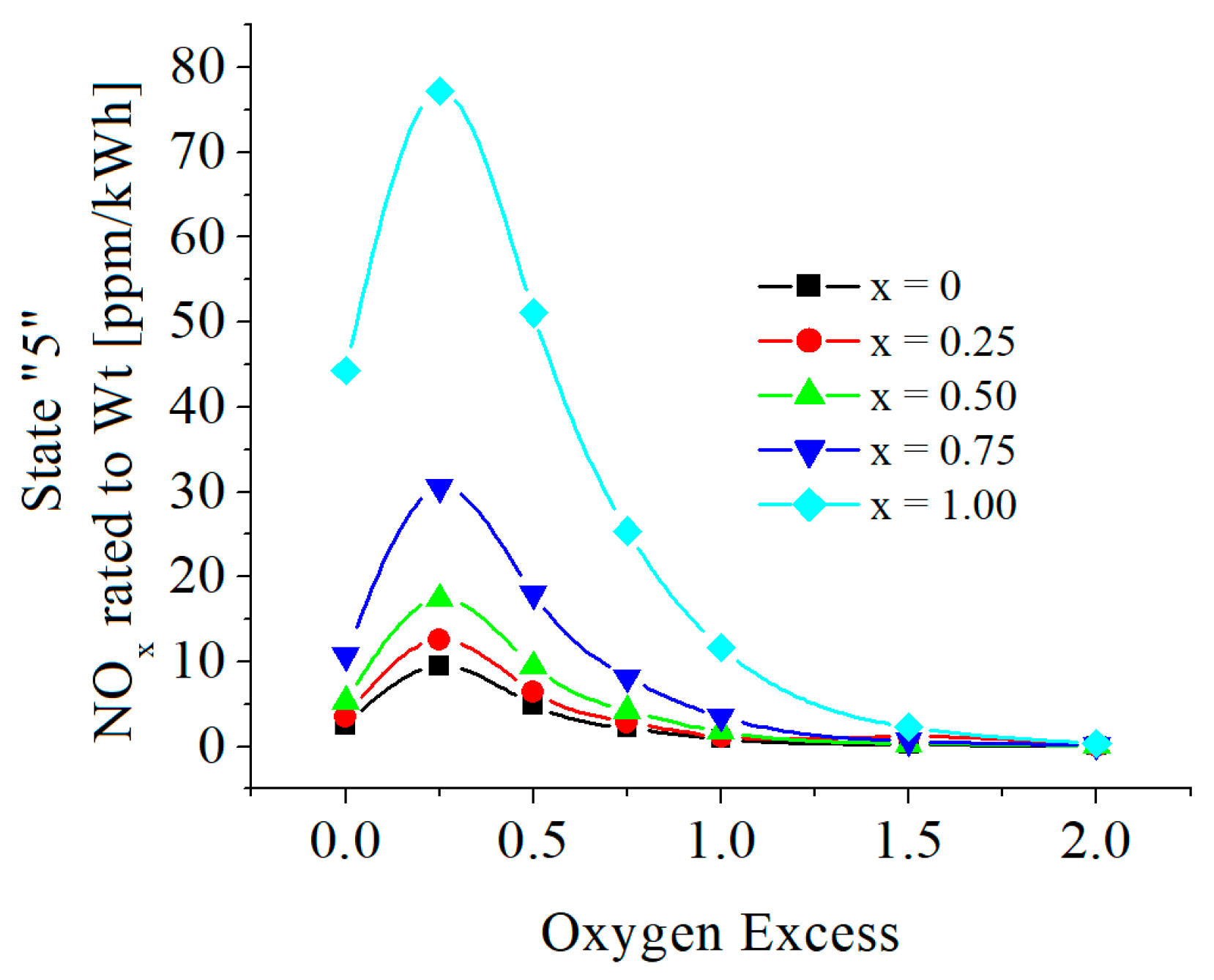

| c0 | c1 | c2 | c3 | c4 | c5 | |
|---|---|---|---|---|---|---|
| −10,295.73122 | +29.18222805 | +0.01976308361 | −0.000006164587807 | +9.718495272 × 10−10 | −5.984216612 × 10−14 | |
| −7820.523838 | +24.56140839 | +0.006095193576 | −0.000001576697822 | +2.155196747 × 10−10 | −1.189998347 × 10−14 | |
| −8310.810038 | +26.11440421 | +0.006486554878 | −0.000001879231979 | +3.125634850 × 10−10 | −2.048055699 × 10−14 | |
| −7820.523838 | +24.56140839 | +0.006095193576 | −0.000001576607822 | +2.155196747 × 10−10 | −1.189998347 × 10−14 | |
| −77,895.91761 | 24.23615845 | +0.006957194766 | −0.000002000452191 | +3.006868933 × 10−10 | −1.79961500 × 10−14 | |
| −8523.602676 | +28.58874847 | −0.0002520099380 | +0.000001072813673 | −2.405013187 × 10−10 | +1.755178738 × 10−14 | |
| −8479.625232 | +28.19400310 | +0.0006776079283 | +7.234592056 × 10−7 | −1.956721062 × 10−10 | +1.522710549 × 10−14 | |
| −6430.497036 | +21.74597694 | −0.0006119709133 | +1.784585133 × 10−7 | −2.341992360 × 10−11 | +1.452421376 × 10−15 | |
| −6191.086828 | +20.77251773 | +0.00001104663432 | −4.160102635 × 10−9 | +7.310338752 × 10−13 | +4.846517103 × 10−17 | |
| −6167.889202 | +20.64973571 | +0.0001887590700 | −9.970607532 × 10−8 | +1.832411454 × 10−11 | −2.236164634 × 10−16 | |
| −8047.826762 | +25.12271666 | +0.006900181303 | −0.000002036851415 | +3.093429512 × 10−10 | −1.856273997 × 10−14 | |
| 10,209.25264 | +29.28985710 | +0.01839187998 | −0.000006044547788 | +9.772891559 × 10−10 | −6.122580161 × 10−14 | |
| −8143.263322 | +21.07695175 | +0.01570851794 | +0.00002221853471 | −1.604634302 × 10−8 | +3.367601937 × 10−12 | |
| CH4 | CO2 | H2O | H2 | O2 | N2 | CO | H | O | N | OH | NO | NO2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| hf0 (kJ/kmole) | −74,873 | −393,522 | −285,830 | 0 | 0 | 0 | −110,527 | +217,999 | +249,170 | +472,680 | +38,897 | +90,921 | +33,100 |
| ln(K1) | ln(K2) | ln(K3) | ln(K4) | ln(K5) | ln(K6) | ln(K7) | ln(K8) | |
|---|---|---|---|---|---|---|---|---|
| a7 | +9.2326311289 × 10−22 | +1.136595616 × 10−21 | +7.643759089 × 10−22 | +8.166909930 × 10−22 | +1.543529198 × 10−21 | +7.070194312 × 10−22 | +2.948541681 × 10−22 | +1.070424351 × 10−22 |
| a6 | −1.469466515 × 10−17 | −1.77695367 × 10−17 | −1.219664280 × 10−17 | −1.298258556 × 10−17 | −2.454651317 × 10−17 | −1.125159755 × 10−17 | −4.688934093 × 10−18 | −1.700672496 × 10−18 |
| a5 | +9.908436246 × 10−14 | +1.173485363 × 10−13 | +8.256023802 × 10−14 | +8.743314794 × 10−14 | +1.653766691 × 10−13 | +7.586041432 × 10−14 | +3.159040657 × 10−14 | +1.144079969 × 10−14 |
| a4 | −3.683648801 × 10−10 | −4.258599458 × 10−10 | −3.081726001 × 10−10 | −3.246702476 × 10−10 | −6.143247539 × 10−10 | −2.282012344 × 10−10 | −1.173468673 × 10−10 | −4.240167126 × 10−11 |
| a3 | +8.221477783 × 10−7 | +9.246236875 × 10−7 | +6.907189777 × 10−7 | +7.238919496 × 10−7 | +0.000001370114593 | +6.294886934 × 10−7 | +2.616956936 × 10−7 | +9.424074844 × 10−8 |
| a2 | −0.001121518545 | −0.001223384239 | −0.0009467177073 | −0.0009868881509 | −0.001868142287 | −0.0008592308402 | −0.0003567351418 | −0.0001278633183 |
| a1 | +0.9056894246 | +0.9575982855 | +0.7698066320 | +0.7977691487 | +1.509735517 | +0.695832294 | +0.2880804502 | +0.1027180385 |
| a0 | −370.3187386 | −385.6441663 | −323.0833734 | −330.5159532 | −638.9027541 | −289.1945752 | −121.5994613 | −59.57996704 |
| This paper | Ref. [16] | This Paper | Ref. [16] | This Paper | Ref. [16] | Ref. [16] | |
|---|---|---|---|---|---|---|---|
| x | 1 | Figure 7 | 0.75 | Figure 7 | 0.5 | Figure 7 | Figure 10 |
| exo | 1.5 | residence time 0.02 to 0.14 s | 0.428571 | residence time 0.02 to 0.14 s | 0 | residence time 0.02 to 0.14 s | residence time up to 3 s |
| T (K) | 1700 | 1700 | 1700 | 1700 | 1700 | 1700 | 1700 |
| p (bar) | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Φ | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 |
| NOx (mole/J) | 7.97 × 10−8 | 2 × 10−10 to 1.35 × 10−9 | 2.77 × 10−8 | 3 × 10−10 to 1.6 × 10−9 | 7.99 × 10−10 | 3.5 × 10−10 to 1.7 × 10−9 | 1 × 10−7 to 4 × 10−7 |
| This Model | Ref. [10] | This Model | Ref. [10] | This Model | Ref. [10] | This Model | Ref. [10] | This Model | Ref. [10] | |
|---|---|---|---|---|---|---|---|---|---|---|
| exo | 0.952515 | 0.695605 | 0.481218 | 0.28866 | 0.171509 | |||||
| (°CA) | - | 300 | - | 300 | - | 300 | - | 300 | - | 300 |
| T (K) (approx.) | 1250 | 1250 | 1400 | 1400 | 1550 | 1550 | 1725 | 1725 | 1800 | 1800 |
| p (bar) (approx.) | 5 | 5 | 5 | 5 | 5.5 | 5.5 | 6 | 6 | 6.25 | 6.25 |
| Φ | 0.66 | 0.66 | 0.76 | 0.76 | 0.87 | 0.87 | 1 | 1 | 1.1 | 1.1 |
| NOx (mg/kg) | 299 | 50 | 622 | 280 | 1081 | 850 | 1688 | 1400 | 1676 | 1650 |
| This Paper | Ref. [14] | ||
|---|---|---|---|
| T (K) | 1090 | 1100 | ~1100 K, Figure 5 and Figure 6 |
| p (bar) | 1 | 1 | 1 |
| exo | 0.1 | 0.1 | 0.1 |
| NOx (mg/kg) | 88.38 | 95.64 | 89 to 93 |
| This Paper (Specific Power = HHV·0.35/3600 (kWh)) | Ref. [15] | |||
|---|---|---|---|---|
| Φ | 0.8 | 1 | 1.2 | unknown |
| exo | 0.782094595 | 0.425676 | 0.188063 | unknown |
| T (K) | 1850 | 1850 | 1850 | 1850 |
| p (bar) | 4 | 4 | 4 | 4 |
| NOx (mole/J) | 4.91E–08 | 3.18E–08 | 7.73E–09 | unknown |
| NOx (mg/kg) | 3946.125733 | 2253.72 | 976.2172 | unknown |
| NOx (ppmvd 15%O2) | 2128.171993 | 4058.322 | 9521.072 | unknown |
| CO (mg/kg) | 28.47564843 | 77.82024 | 231.9931 | unknown |
| NOx (g/kWh) | 15.18732844 | 6.559401 | 2.385153 | cca 6 |
| CO (g/kWh) | 0.109593321 | 0.226494 | 0.56682 | cca 1.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feidt, M.; Dumitrascu, G.; Lupu, A.-G. Chemical Modeling of Constant-Volume Combustion of the Mixture of Methane and Hydrogen Used in Spark Ignition Otto Cycles. Energies 2023, 16, 4578. https://doi.org/10.3390/en16124578
Feidt M, Dumitrascu G, Lupu A-G. Chemical Modeling of Constant-Volume Combustion of the Mixture of Methane and Hydrogen Used in Spark Ignition Otto Cycles. Energies. 2023; 16(12):4578. https://doi.org/10.3390/en16124578
Chicago/Turabian StyleFeidt, Michel, Gheorghe Dumitrascu, and Ana-Georgiana Lupu. 2023. "Chemical Modeling of Constant-Volume Combustion of the Mixture of Methane and Hydrogen Used in Spark Ignition Otto Cycles" Energies 16, no. 12: 4578. https://doi.org/10.3390/en16124578
APA StyleFeidt, M., Dumitrascu, G., & Lupu, A.-G. (2023). Chemical Modeling of Constant-Volume Combustion of the Mixture of Methane and Hydrogen Used in Spark Ignition Otto Cycles. Energies, 16(12), 4578. https://doi.org/10.3390/en16124578









