CFD Simulation and Experimental Study on a Thermal Energy Storage–Updraft Solid Waste Gasification Device
Abstract
:1. Introduction
2. Operation Experiment of Gasification Reactor
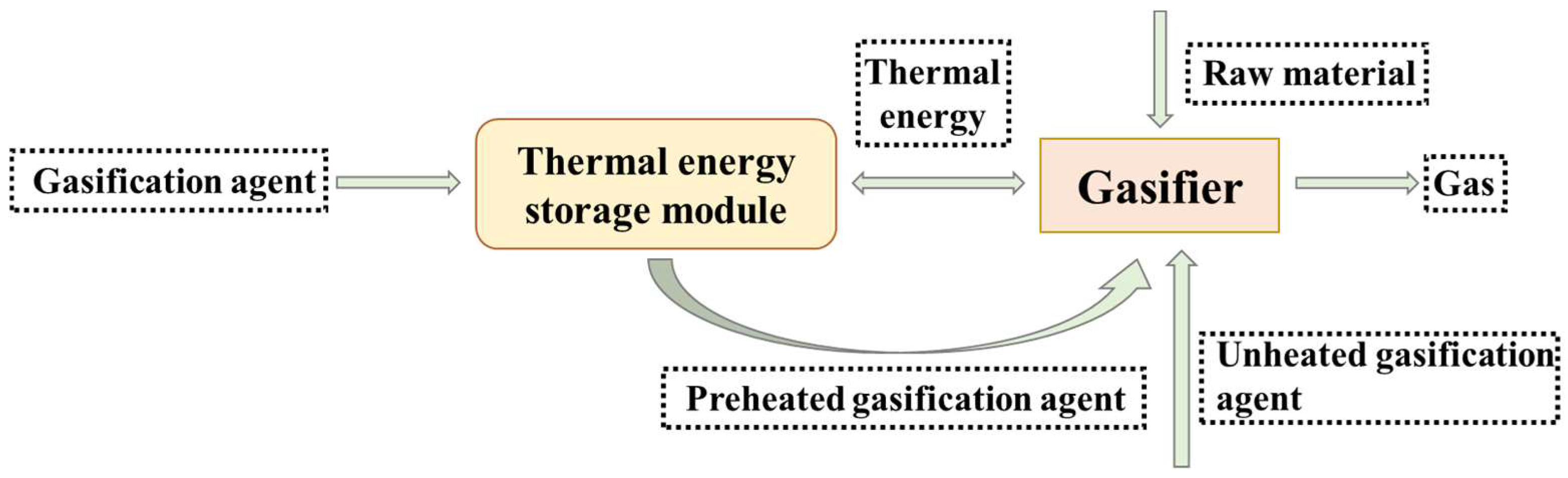
2.1. Introduction
2.2. Physical Analysis of Raw Materials
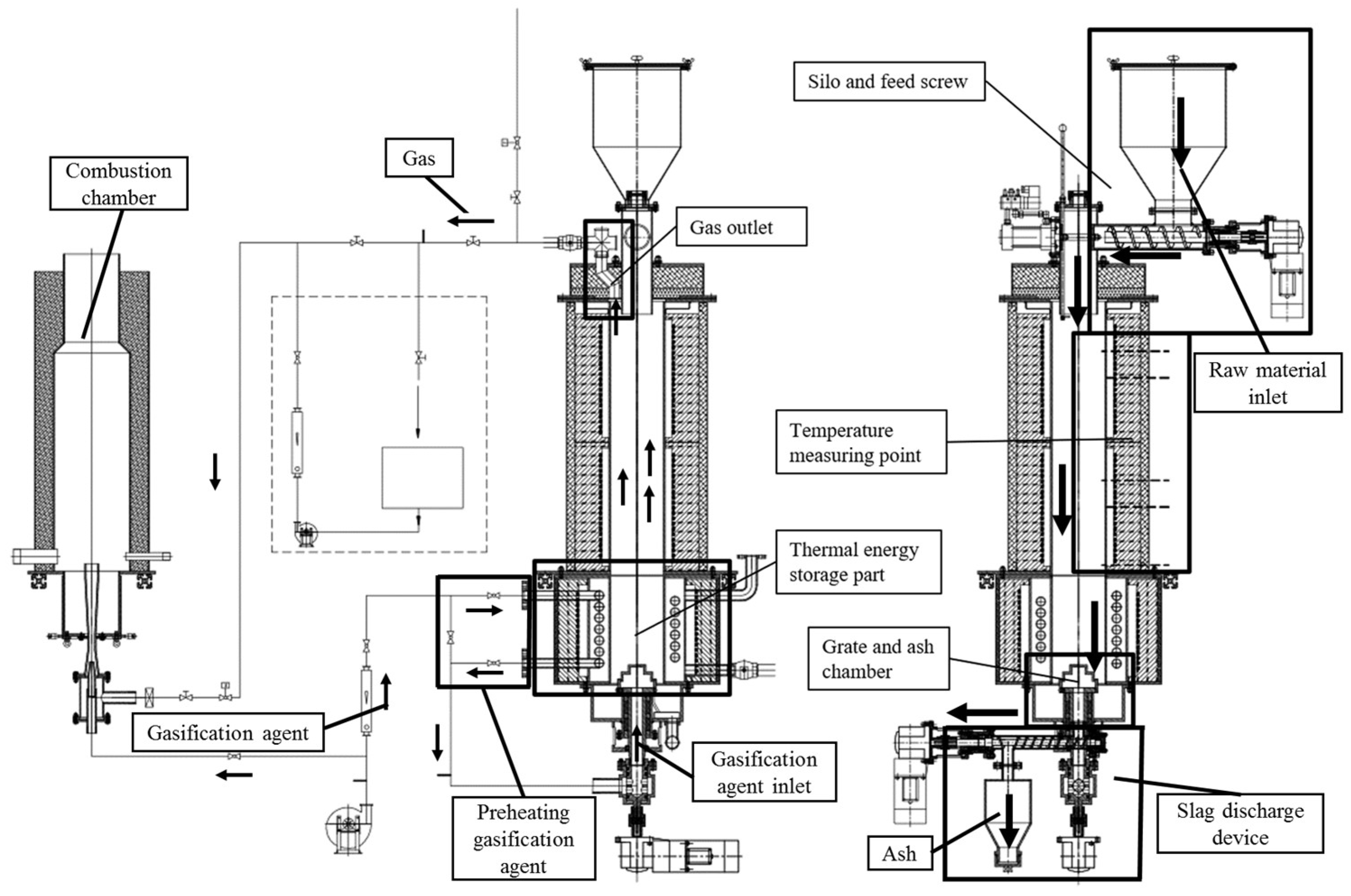
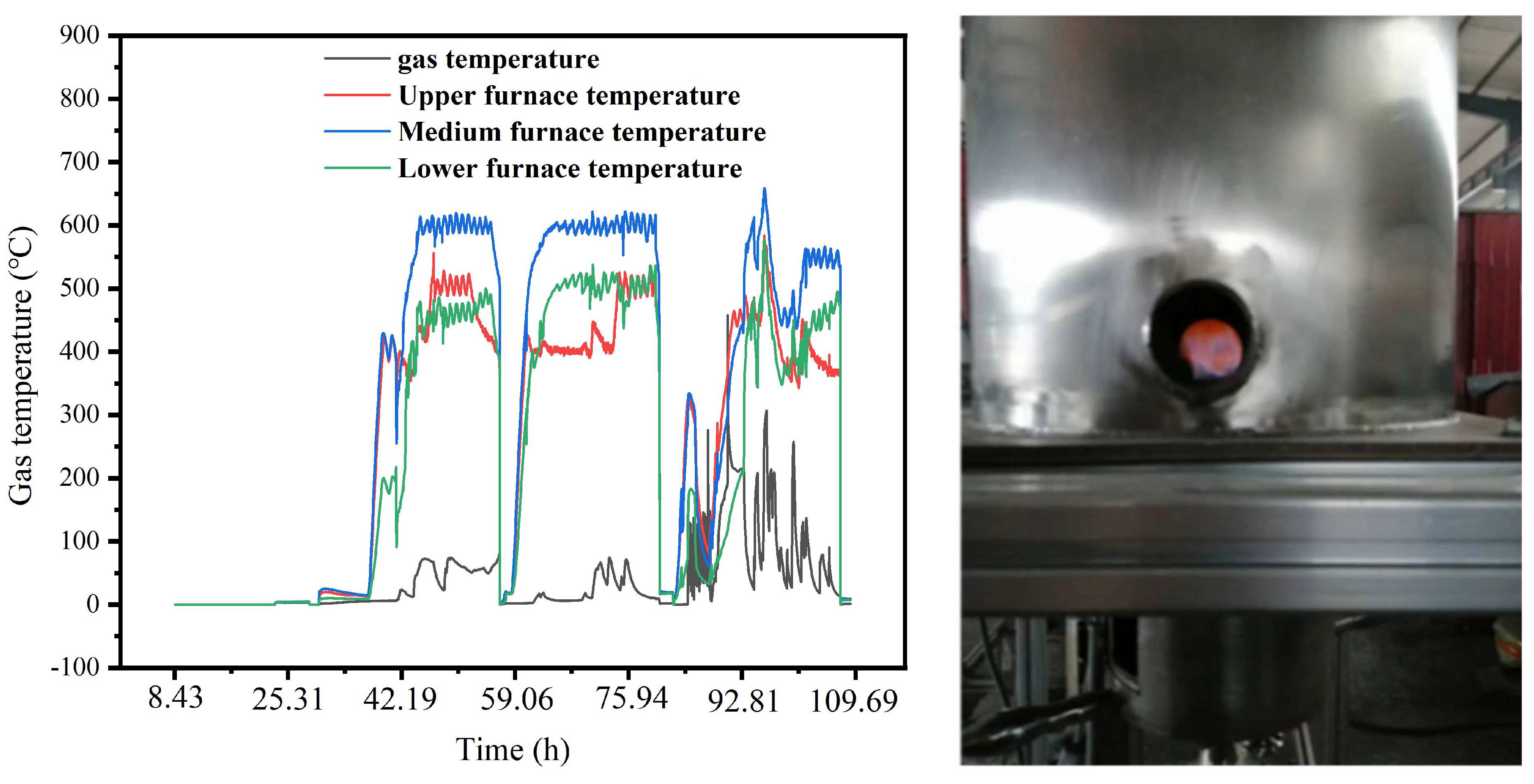
2.3. Gasification Device Operation Experiment
3. Mathematical Modeling
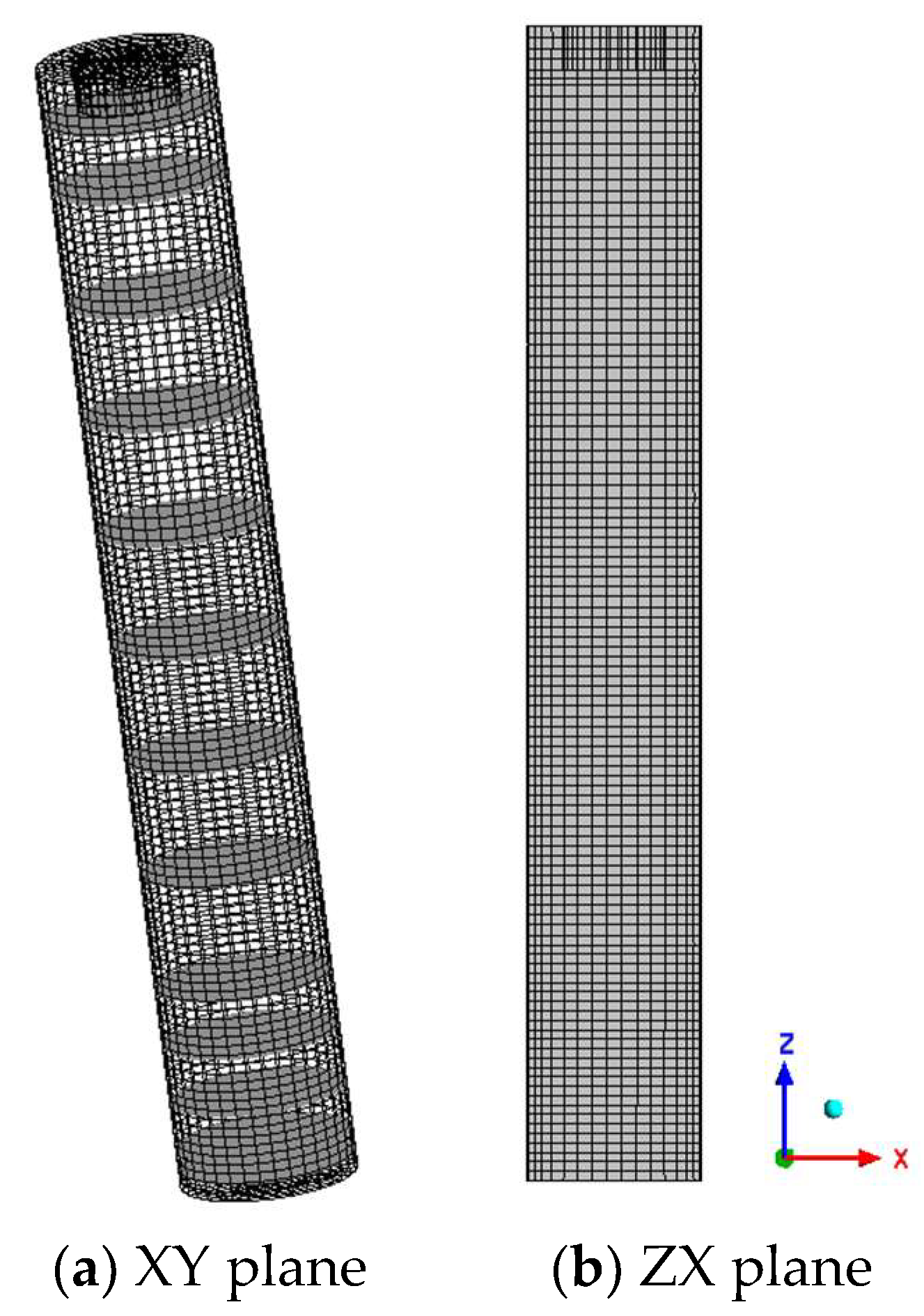
3.1. Meshing
3.2. Continuous Phase Mathematical Model
- 3.
- Energy equation [23]:
- 4.
- Species transport equation [23]:
3.3. Discrete Phase Mathematical Model
4. Pre-Processing Settings
5. Results and Discussion
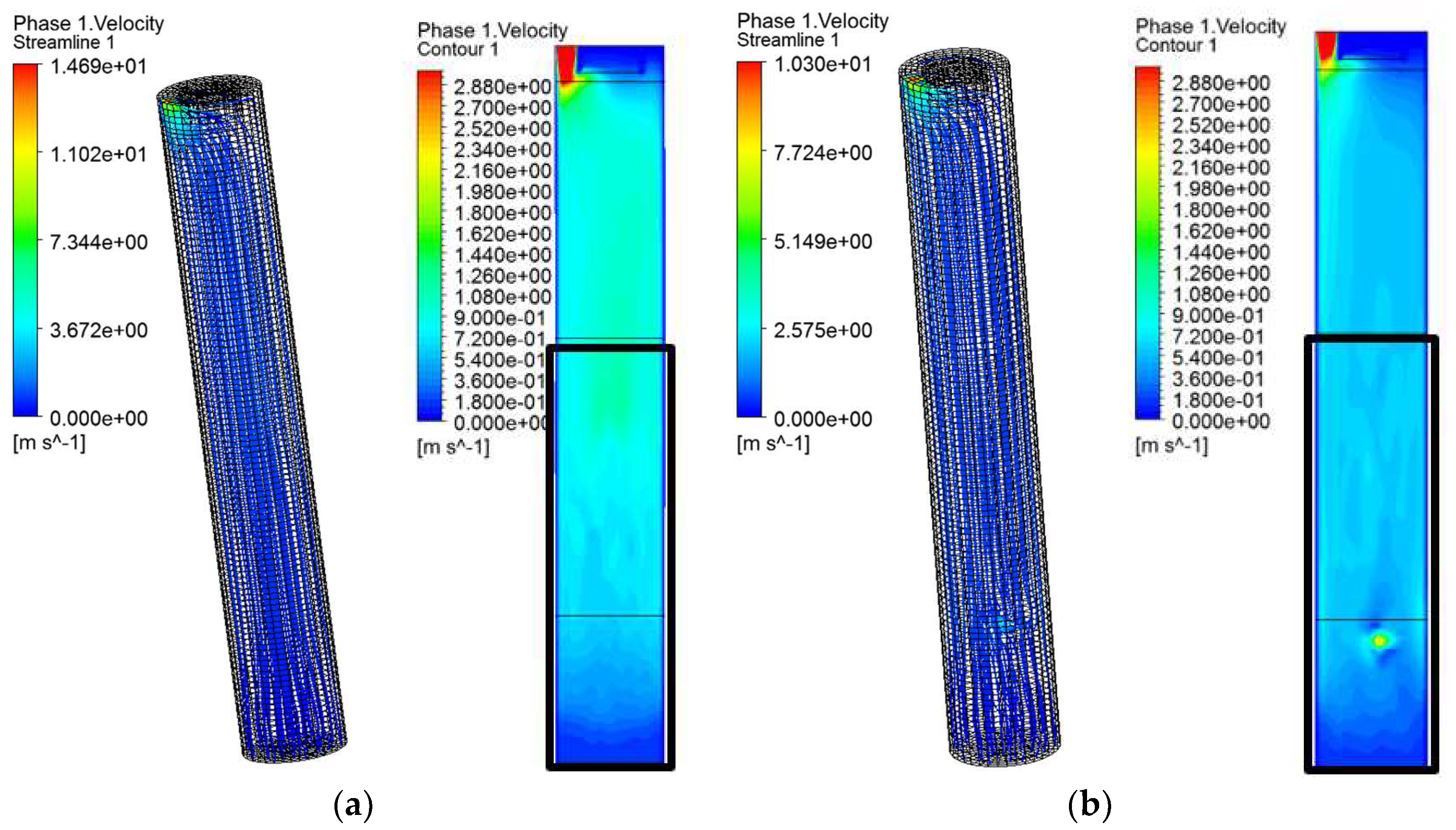
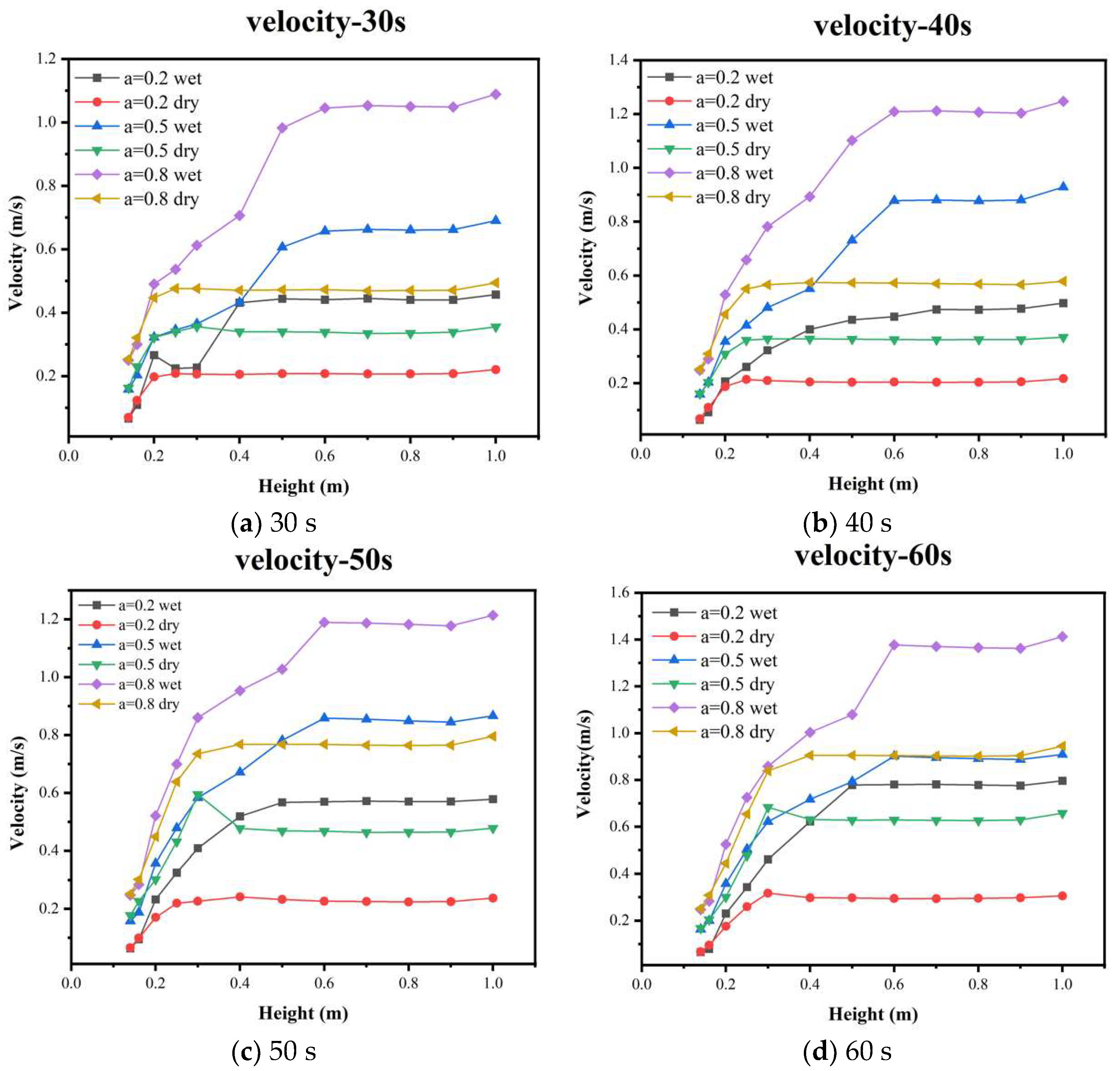
5.1. Flow Field Structure Analysis
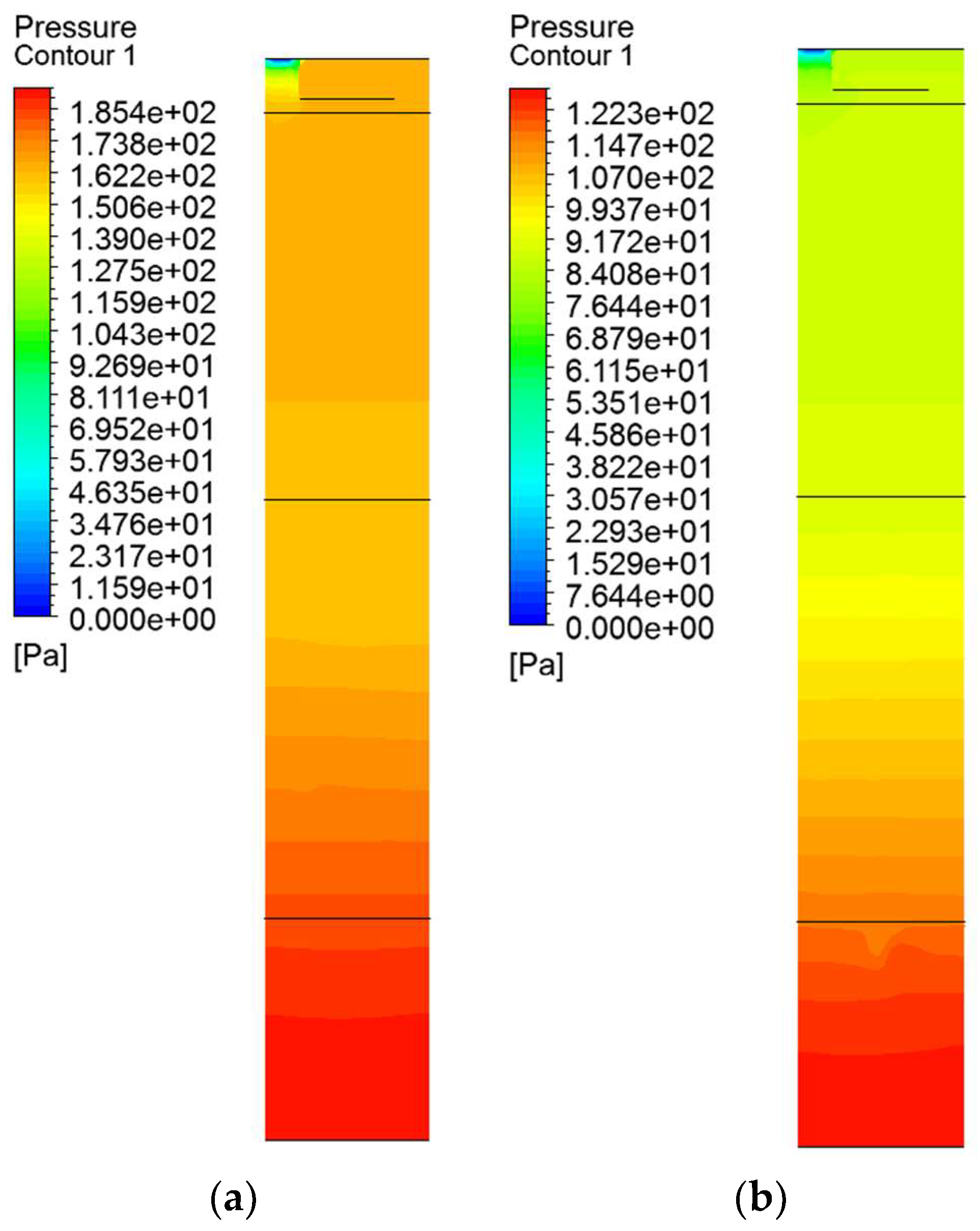
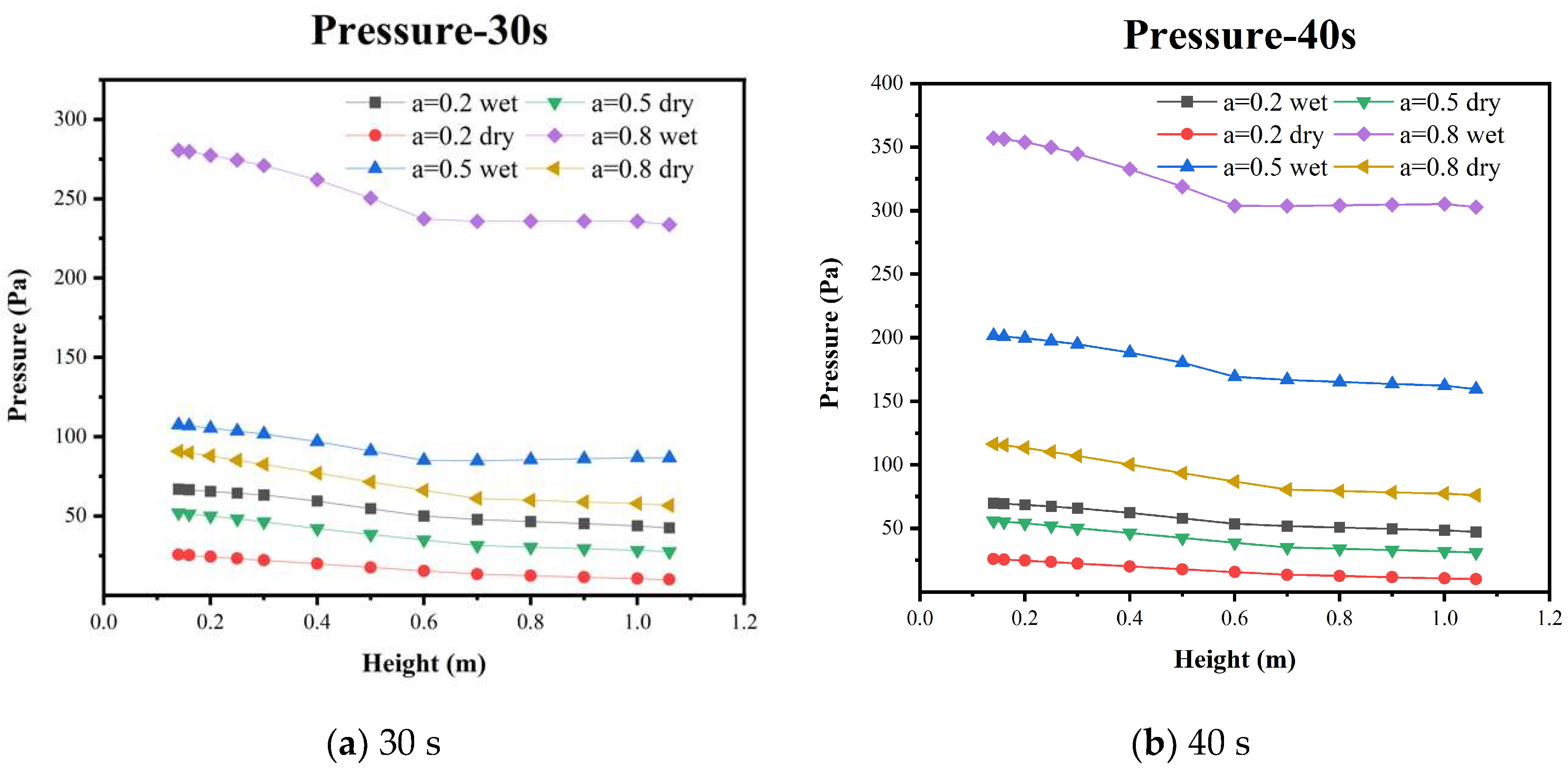
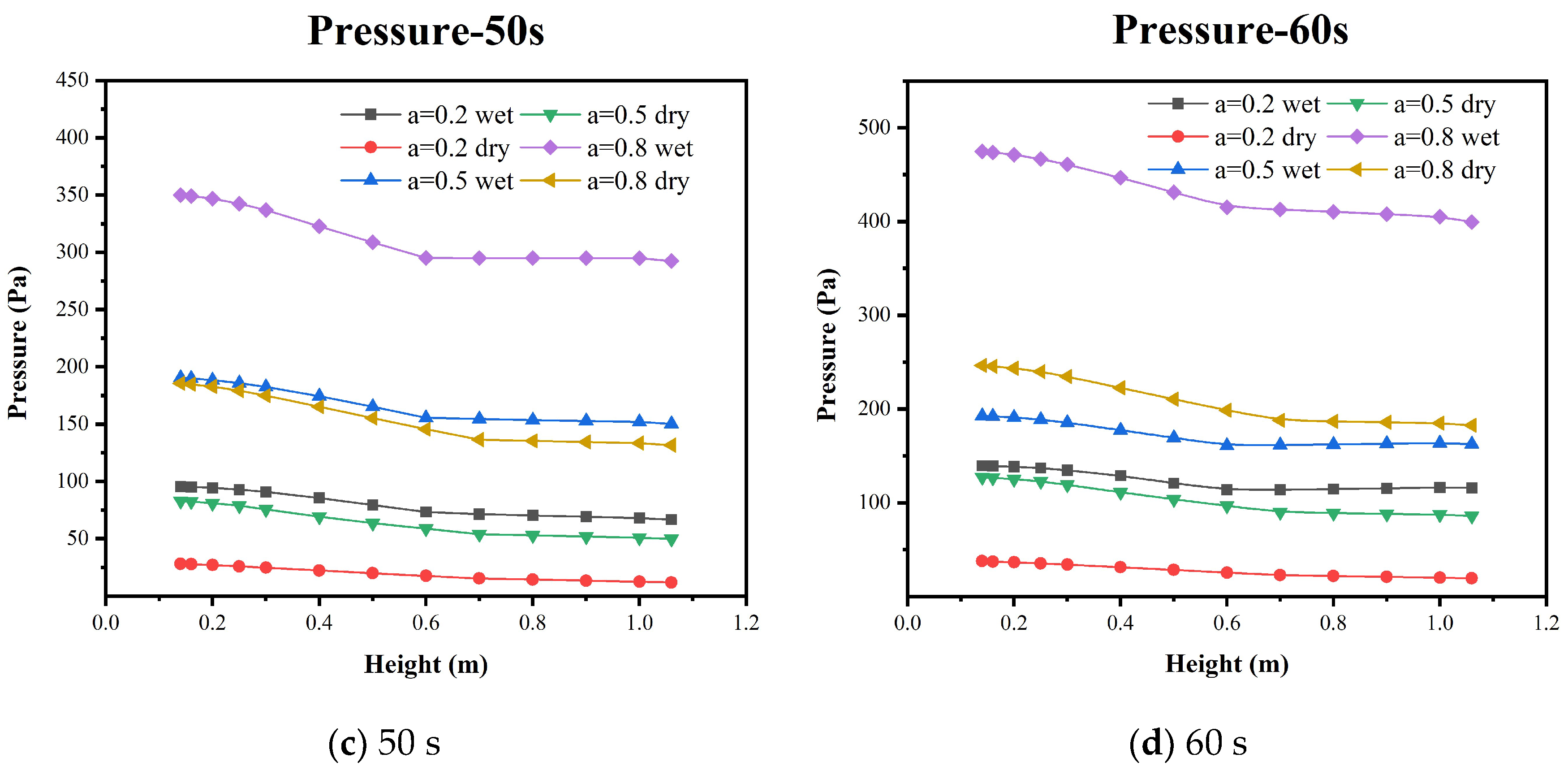
5.2. Pressure Distribution
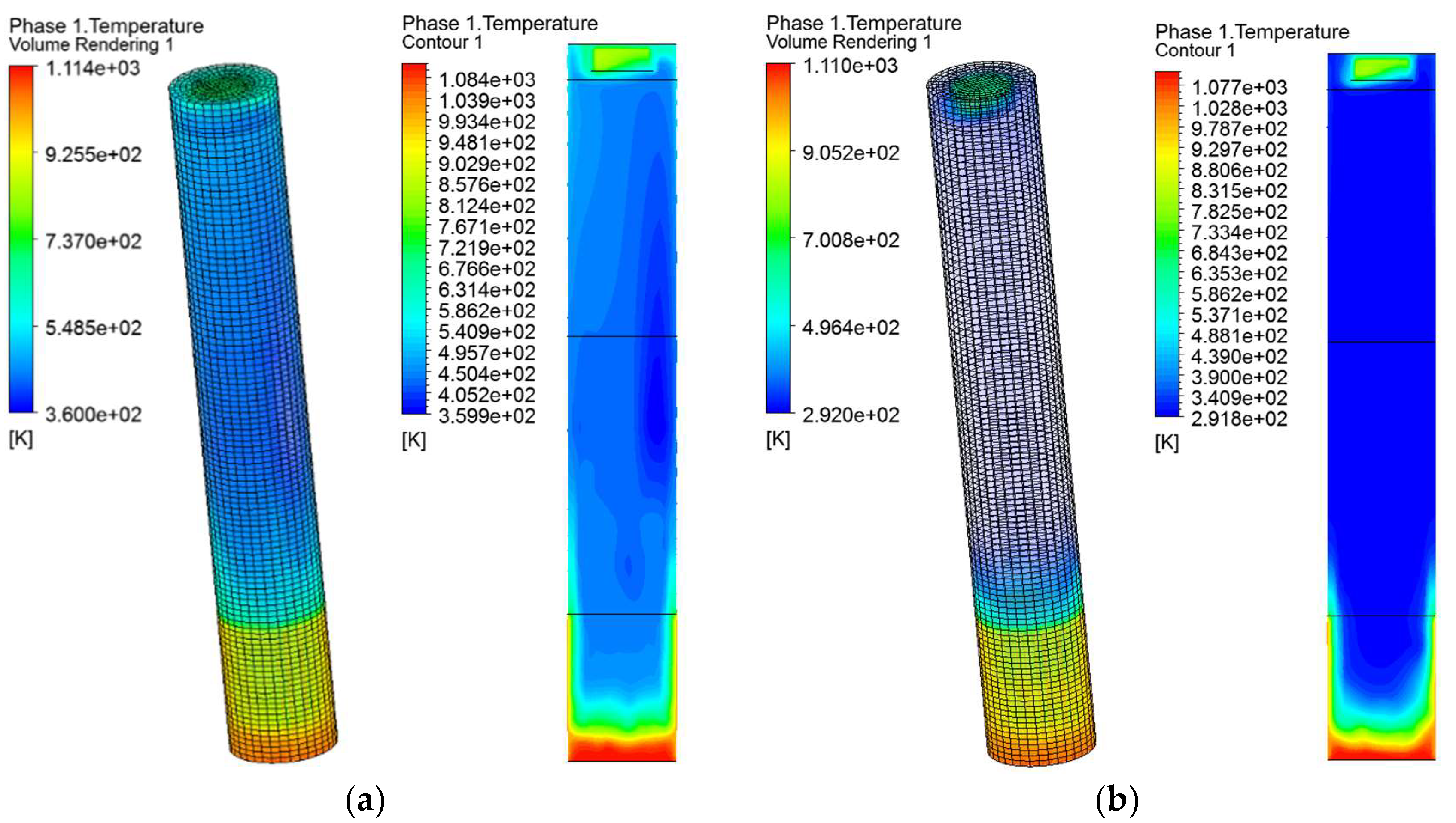
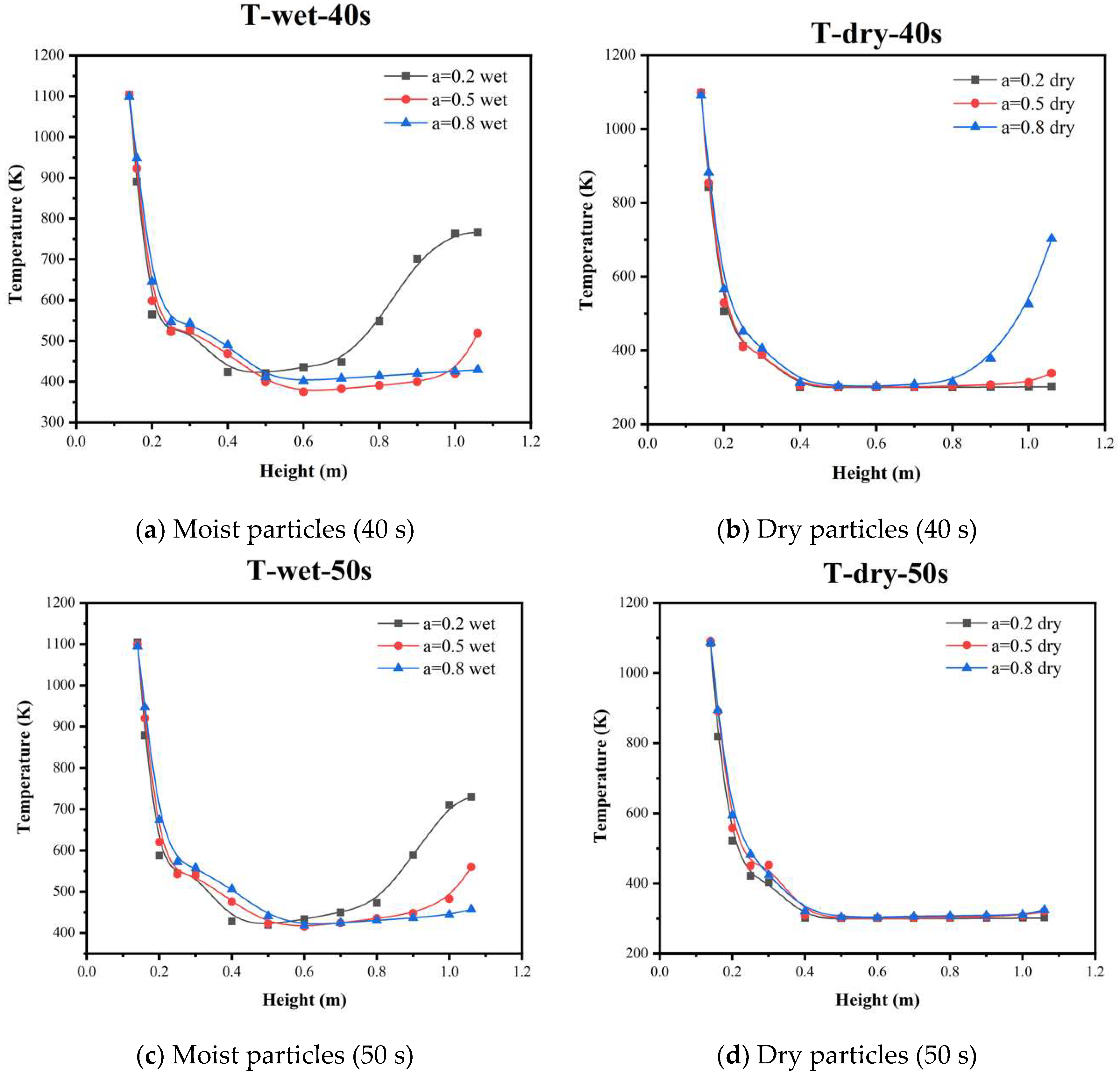
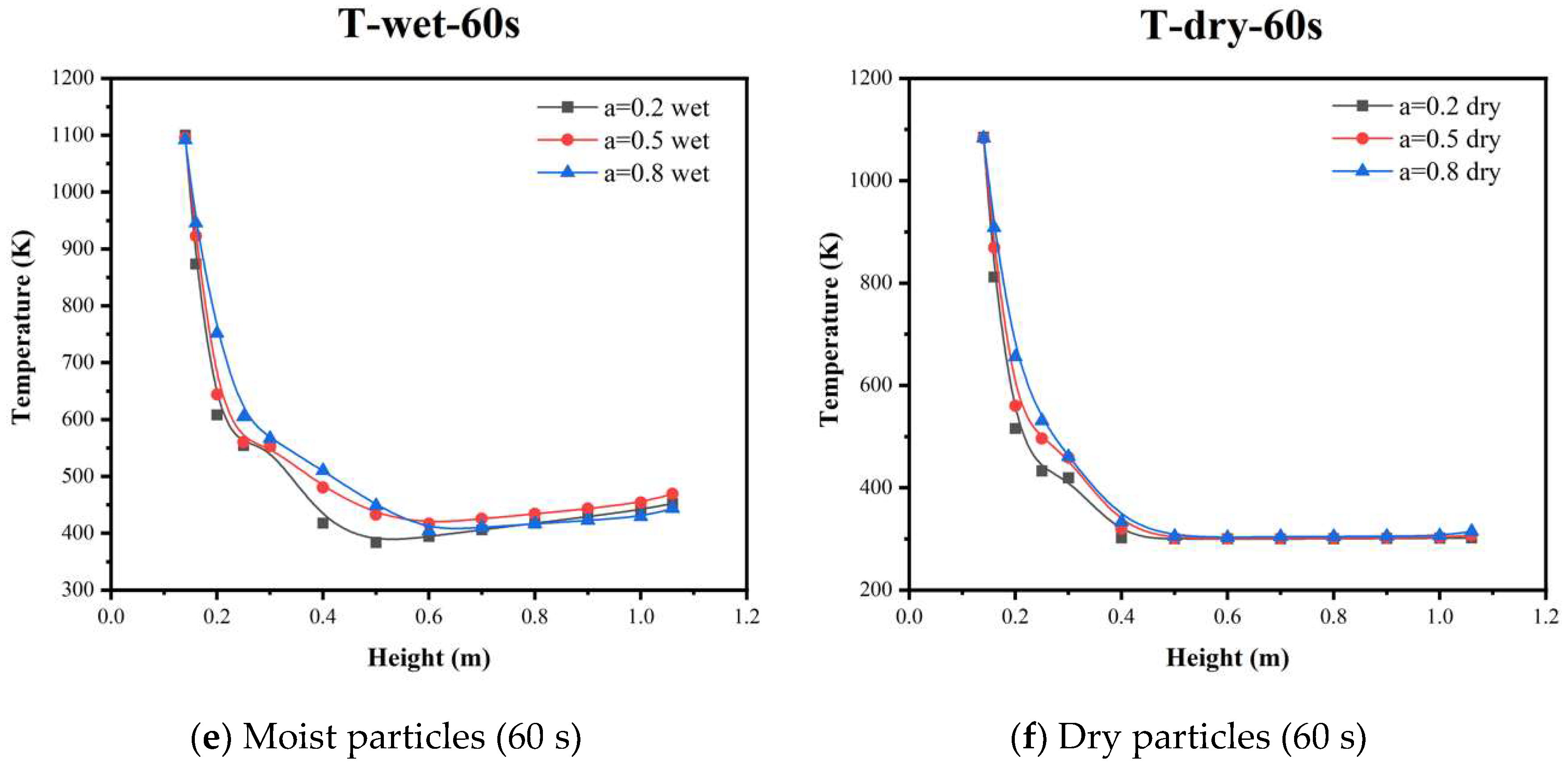
5.3. Temperature Distribution
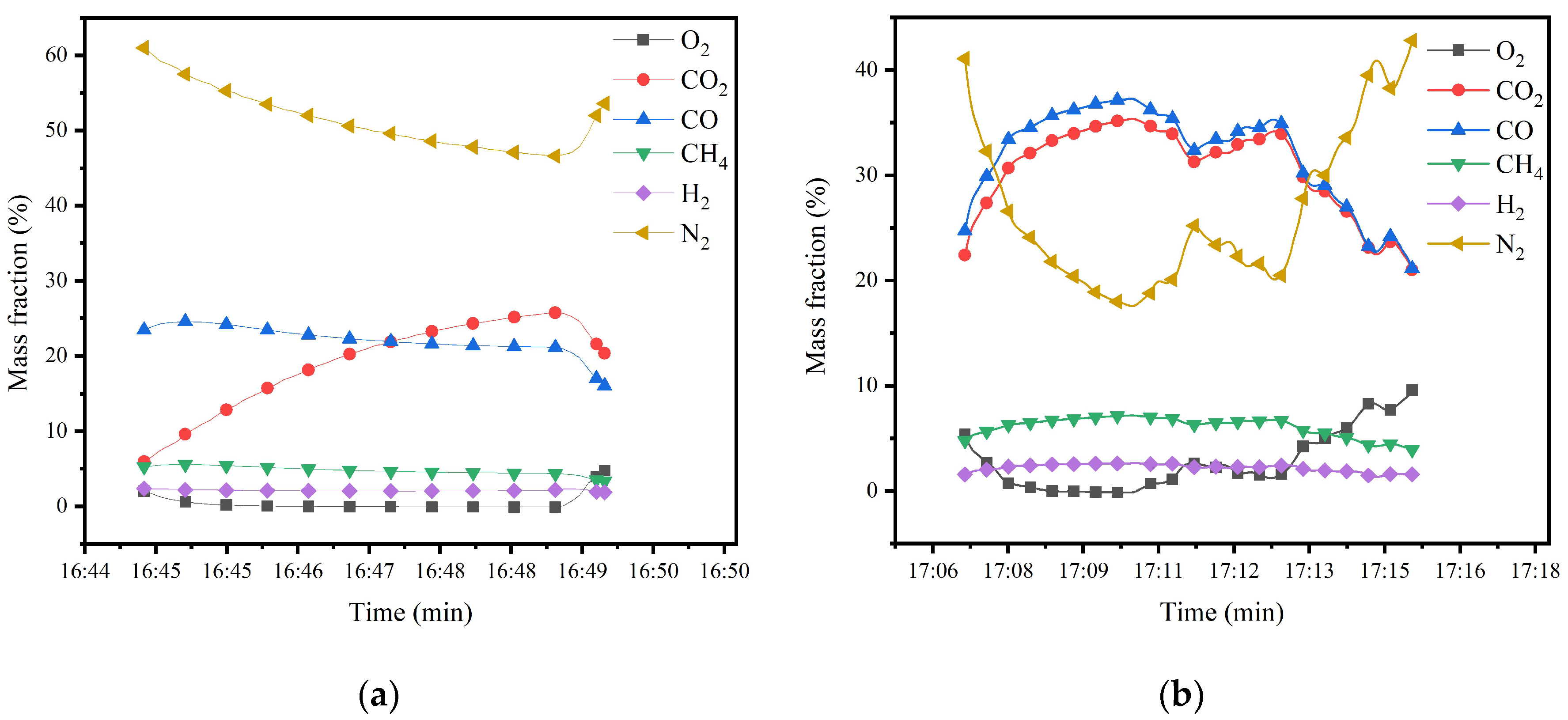
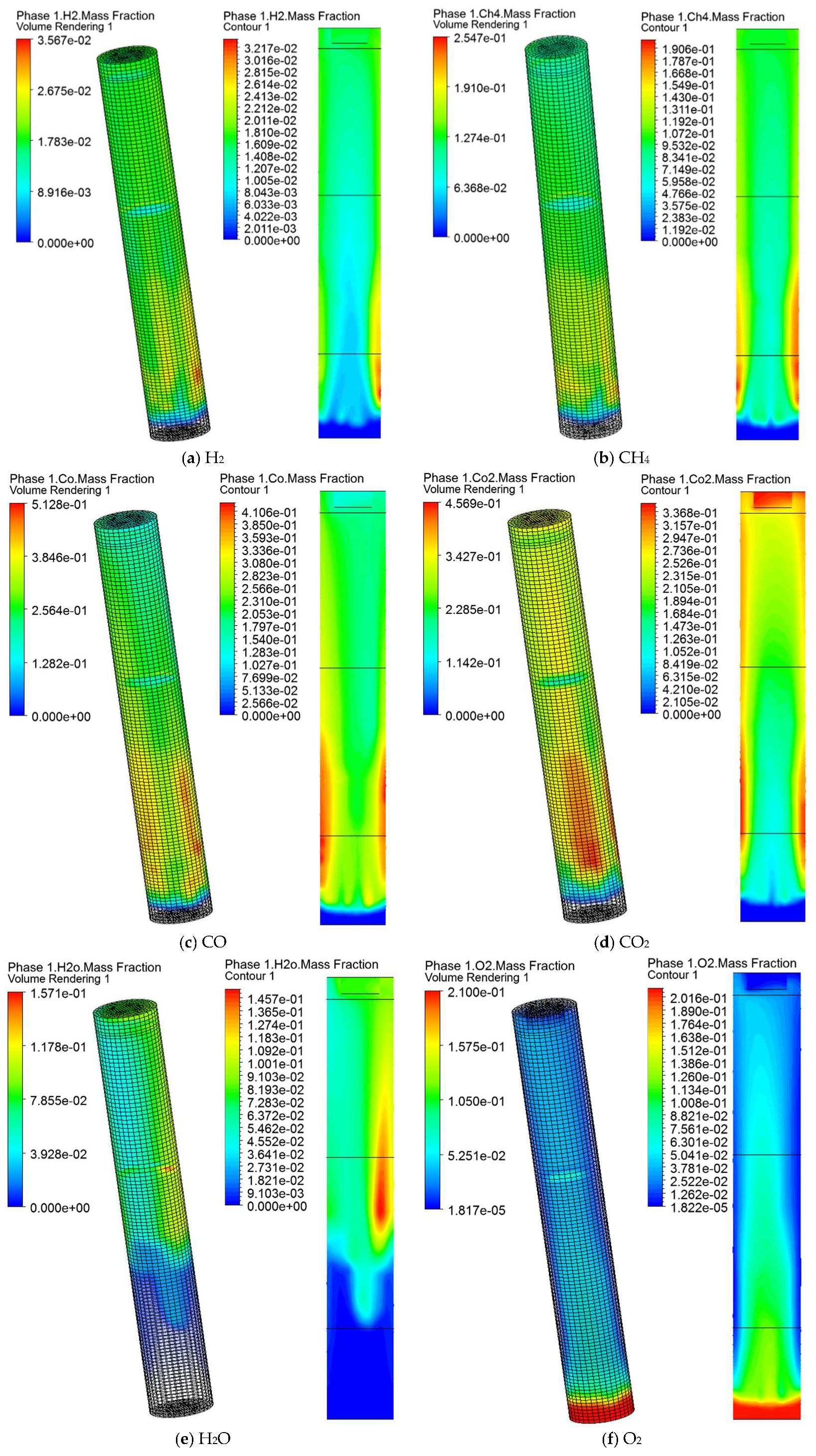
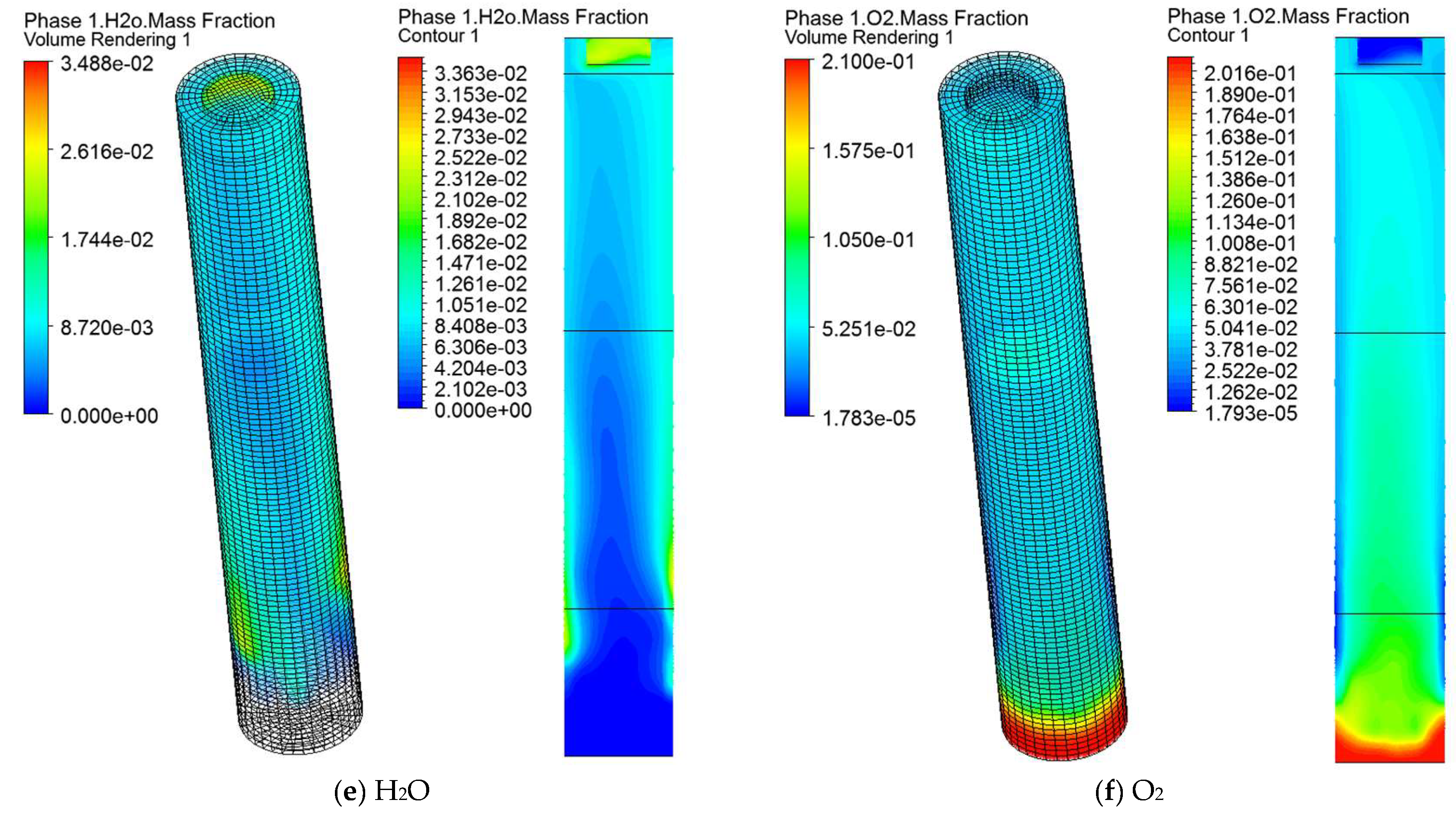
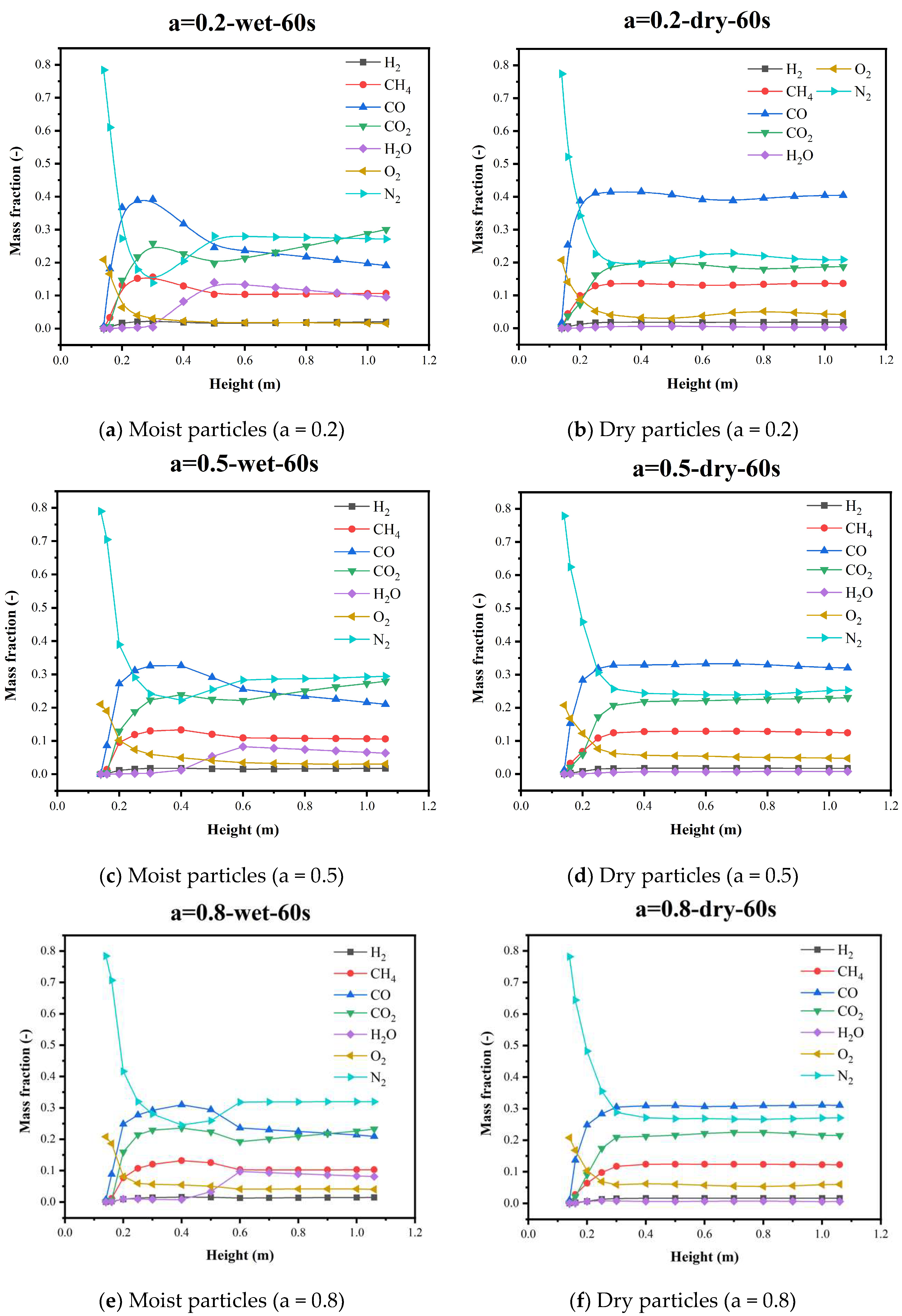
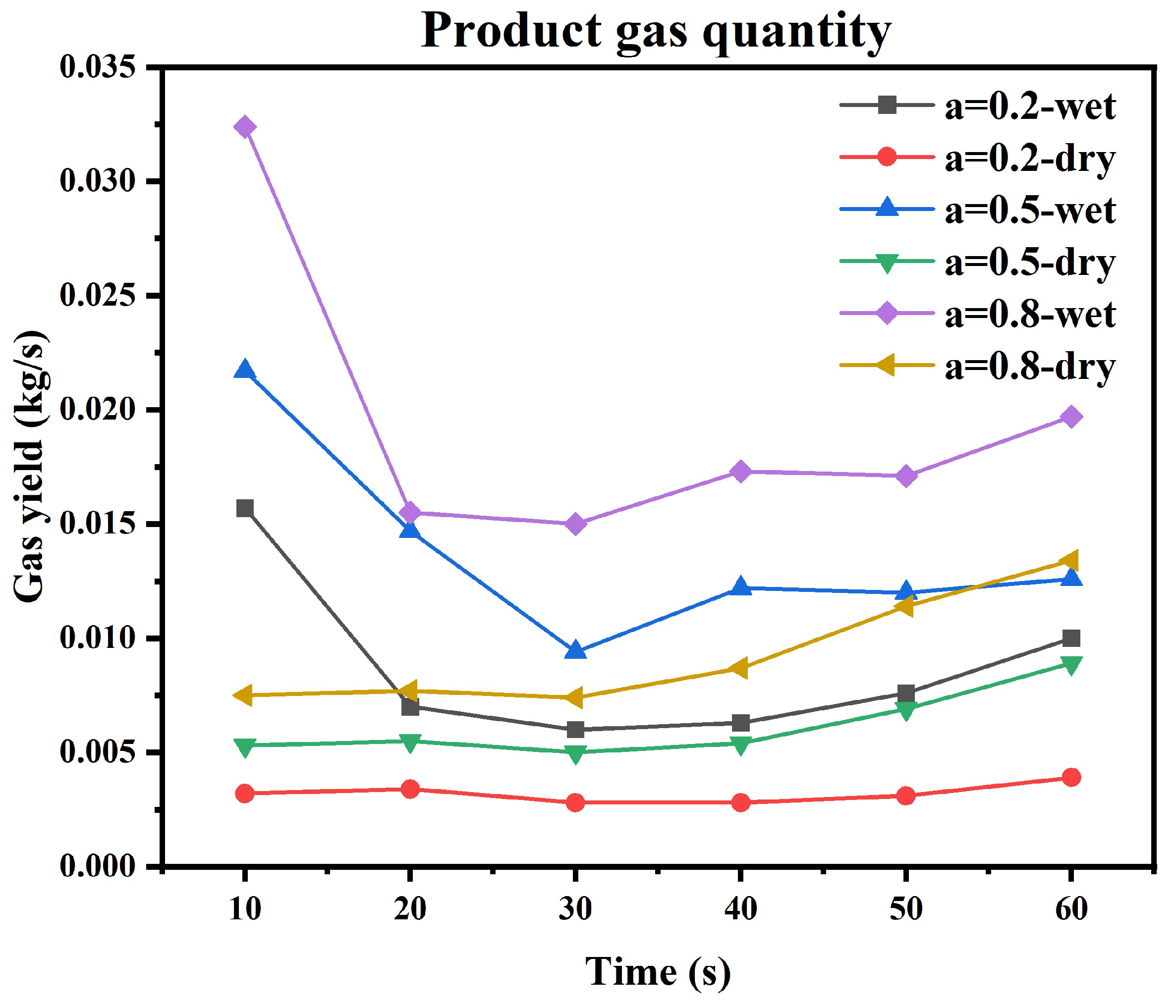
5.4. Gas Species Distribution and Gasification Reaction Characteristics
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Antimiani, A.; Costantini, V.; Paglialunga, E. Fossil fuels subsidy removal and the EU carbon neutrality policy. Energy Econ. 2023, 119, 6524. [Google Scholar] [CrossRef]
- Pao, H.-T.; Chen, H.; Li, Y.-Y. Competitive dynamics of energy, environment, and economy in the U.S. Energy 2015, 89, 449–460. [Google Scholar] [CrossRef]
- Lu, J.S.; Chang, Y.; Poon, C.S.; Lee, D.J. Slow pyrolysis of municipal solid waste (MSW): A review. Bioresour Technol. 2020, 312, 123615. [Google Scholar] [CrossRef]
- Galán-Martín, Á.; Contreras, M.d.M.; Romero, I.; Ruiz, E.; Bueno-Rodríguez, S.; Eliche-Quesada, D.; Castro-Galiano, E. The potential role of olive groves to deliver carbon dioxide removal in a carbon-neutral Europe: Opportunities and challenges. Renew. Sustain. Energy Rev. 2022, 165, 112609. [Google Scholar] [CrossRef]
- Ma, Y.; Li, Y.P.; Huang, G.H. Planning China’s non-deterministic energy system (2021–2060) to achieve carbon neutrality. Appl. Energy 2023, 334, 120673. [Google Scholar] [CrossRef]
- Dogu, O.; Pelucchi, M.; Van de Vijver, R.; Van Steenberge, P.H.M.; D’Hooge, D.R.; Cuoci, A.; Mehl, M.; Frassoldati, A.; Faravelli, T.; Van Geem, K.M. The chemistry of chemical recycling of solid plastic waste via pyrolysis and gasification: State-of-the-art, challenges, and future directions. Prog. Energy Combust. Sci. 2021, 84, 100901. [Google Scholar] [CrossRef]
- Heidenreich, S.; Foscolo, P.U. New concepts in biomass gasification. Prog. Energy Combust. Sci. 2015, 46, 72–95. [Google Scholar] [CrossRef]
- Mazaheri, N.; Akbarzadeh, A.H.; Madadian, E.; Lefsrud, M. Systematic review of research guidelines for numerical simulation of biomass gasification for bioenergy production. Energy Convers. Manag. 2019, 183, 671–688. [Google Scholar] [CrossRef]
- Cerone, N.; Zimbardi, F.; Contuzzi, L.; Baleta, J.; Cerinski, D.; Skvorčinskienė, R. Experimental investigation of syngas composition variation along updraft fixed bed gasifier. Energy Convers. Manag. 2020, 221, 113116. [Google Scholar] [CrossRef]
- Anca-Couce, A.; Archan, G.; Buchmayr, M.; Essl, M.; Hochenauer, C.; Scharler, R. Modelling fuel flexibility in fixed-bed biomass conversion with a low primary air ratio in an updraft configuration. Fuel 2021, 296, 120687. [Google Scholar] [CrossRef]
- Kurkela, E.; Kurkela, M.; Hiltunen, I. Pilot-scale development of pressurized fixed-bed gasification for synthesis gas production from biomass residues. Biomass Convers. Biorefinery 2021. [Google Scholar] [CrossRef]
- Ali, M.; Alkaabi, A.K.; Alameri, S.A.; Addad, Y. Overall efficiency analysis of an innovative load-following nuclear power plant-thermal energy storage coupled cycle. Int. J. Exergy 2021, 36, 98–122. [Google Scholar] [CrossRef]
- Alameri, S.A.; King, J.C.; Alkaabi, A.K.; Addad, Y. Prismatic-core advanced high temperature reactor and thermal energy storage coupled system–A preliminary design. Nucl. Eng. Technol. 2020, 52, 248–257. [Google Scholar] [CrossRef]
- Ali, M.; Alkaabi, A.K.; Lee, J.I. CFD simulation of an integrated PCM-based thermal energy storage within a nuclear power plant connected to a grid with constant or variable power demand. Nucl. Eng. Des. 2022, 394. [Google Scholar] [CrossRef]
- Ali, M.; Alkaabi, A.K.; Addad, Y. Numerical investigation of a vertical triplex-tube latent heat storage/exchanger to achieve flexible operation of nuclear power plants. Int. J. Energy Res. 2021, 46, 2970–2987. [Google Scholar] [CrossRef]
- Deepak Selvakumar, R.; Wu, J.; Ding, Y.; Alkaabi, A.K. Melting behavior of an organic phase change material in a square thermal energy storage capsule with an array of wire electrodes. Appl. Therm. Eng. 2023, 228. [Google Scholar] [CrossRef]
- Alobaid, F.; Almohammed, N.; Massoudi Farid, M.; May, J.; Rößger, P.; Richter, A.; Epple, B. Progress in CFD Simulations of Fluidized Beds for Chemical and Energy Process Engineering. Prog. Energy Combust. Sci. 2022, 91, 100930. [Google Scholar]
- Adnan, M.; Sun, J.; Ahmad, N.; Wei, J.J. Multiscale modeling of bubbling fluidized bed reactors using a hybrid Eulerian-Lagrangian dense discrete phase approach. Powder Technol. 2020, 376, 296–319. [Google Scholar] [CrossRef]
- Adnan, M.; Sun, J.; Ahmad, N.; Wei, J.J. Verification and validation of the DDPM-EMMS model for numerical simulations of bubbling, turbulent and circulating fluidized beds. Powder Technol. 2021, 379, 69–88. [Google Scholar] [CrossRef]
- Adnan, M.; Sun, J.; Ahmad, N.; Wei, J.J. Comparative CFD modeling of a bubbling bed using a Eulerian–Eulerian two-fluid model (TFM) and a Eulerian-Lagrangian dense discrete phase model (DDPM). Powder Technol. 2021, 383, 418–442. [Google Scholar] [CrossRef]
- Hwang, I.S.; Jeong, H.J.; Hwang, J. Numerical simulation of a dense flow cyclone using the kinetic theory of granular flow in a dense discrete phase model. Powder Technol. 2019, 356, 129–138. [Google Scholar] [CrossRef]
- Kong, D.; Luo, K.; Wang, S.; Yu, J.; Fan, J. Particle behaviours of biomass gasification in a bubbling fluidized bed. Chem. Eng. J. 2022, 428, 131847. [Google Scholar] [CrossRef]
- Ostermeier, P.; Fischer, F.; Fendt, S.; DeYoung, S.; Spliethoff, H. Coarse-grained CFD-DEM simulation of biomass gasification in a fluidized bed reactor. Fuel 2019, 255, 115790. [Google Scholar] [CrossRef]
- Chen, T.; Li, T.; Sjöblom, J.; Ström, H. A reactor-scale CFD model of soot formation during high-temperature pyrolysis and gasification of biomass. Fuel 2021, 303, 121240. [Google Scholar] [CrossRef]
- Timsina, R.; Thapa, R.K.; Moldestad, B.M.E.; Eikeland, M.S. Computational particle fluid dynamics simulation of biomass gasification in an entrained flow gasifier. Chem. Eng. Sci. X 2021, 12, 100112. [Google Scholar] [CrossRef]
- Wu, H.; Yang, C.; Zhang, Z.; Zhang, Q. Simulation of Two-Phase Flow and Syngas Generation in Biomass Gasifier Based on Two-Fluid Model. Energies 2022, 15, 4800. [Google Scholar] [CrossRef]
- Assoumani, N.; Simo-Tagne, M.; Kifani-Sahban, F.; Tagne Tagne, A.; El Marouani, M.; Obounou Akong, M.B.; Rogaume, Y.; Girods, P.; Zoulalian, A. Numerical Study of Cylindrical Tropical Woods Pyrolysis Using Python Tool. Sustainability 2021, 13, 13892. [Google Scholar] [CrossRef]
- Horsfall, I.T.; Ndukwu, M.C.; Abam, F.; Simo-Tagne, M.; Nwachukwu, C.C. Parametric studies of heat and mass transfer process for two-stage biochar production from poultry litter pellet biomass. Biomass Convers. Biorefinery 2022, 1–13. [Google Scholar] [CrossRef]
- Ismail, T.M.; El-Salam, M.A. Numerical and experimental studies on updraft gasifier HTAG. Renew. Energy 2015, 78, 484–497. [Google Scholar] [CrossRef]
- Kumar, U.; Paul, M.C. CFD modelling of biomass gasification with a volatile break-up approach. Chem. Eng. Sci. 2019, 195, 413–422. [Google Scholar] [CrossRef] [Green Version]
- Ngamsidhiphongsa, N.; Ponpesh, P.; Shotipruk, A.; Arpornwichanop, A. Analysis of the Imbert downdraft gasifier using a species-transport CFD model including tar-cracking reactions. Energy Convers. Manag. 2020, 213, 112808. [Google Scholar] [CrossRef]
- Lu, D.; Yoshikawa, K.M.; Ismail, T.; El-Salam, M.A. Computational Fluid Dynamics Model on Updraft Gasifier Using Carbonized Woody Briquette as Fuel. Energy Procedia 2017, 142, 166–171. [Google Scholar] [CrossRef]
- Manek, B.; Javia, M.S.; Harichandan, A.; Ramani, H. A CFD based comprehensive study of coal-fired updraft gasifier in ceramic industry. Therm. Sci. Eng. Prog. 2019, 9, 11–20. [Google Scholar] [CrossRef]
- Janajreh, I.; Al Shrah, M. Numerical and experimental investigation of downdraft gasification of wood chips. Energy Convers. Manag. 2013, 65, 783–792. [Google Scholar] [CrossRef]
- Lu, D.; Yoshikawa, K.; Ismail, T.M.; Abd El-Salam, M. Assessment of the carbonized woody briquette gasification in an updraft fixed bed gasifier using the Euler-Euler model. Appl. Energy 2018, 220, 70–86. [Google Scholar] [CrossRef]
- Murgia, S.; Vascellari, M.; Cau, G. Comprehensive CFD model of an air-blown coal-fired updraft gasifier. Fuel 2012, 101, 129–138. [Google Scholar] [CrossRef]
- Zhang, H.; Baeyens, J.; Cáceres, G.; Degrève, J.; Lv, Y. Thermal energy storage: Recent developments and practical aspects. Prog. Energy Combust. Sci. 2016, 53, 1–40. [Google Scholar] [CrossRef]
- Ku, X.; Li, T.; Løvås, T. Eulerian–Lagrangian Simulation of Biomass Gasification Behavior in a High-Temperature Entrained-Flow Reactor. Energy Fuels 2014, 28, 5184–5196. [Google Scholar] [CrossRef] [Green Version]
- Zhong, W.; Yu, A.; Zhou, G.; Xie, J.; Zhang, H. CFD simulation of dense particulate reaction system: Approaches, recent advances and applications. Chem. Eng. Sci. 2016, 140, 16–43. [Google Scholar] [CrossRef]
- Klimanek, A.; Adamczyk, W.; Katelbach-Woźniak, A.; Węcel, G.; Szlęk, A. Towards a hybrid Eulerian–Lagrangian CFD modeling of coal gasification in a circulating fluidized bed reactor. Fuel 2015, 152, 131–137. [Google Scholar] [CrossRef]
- Subramaniam, S. Lagrangian–Eulerian methods for multiphase flows. Prog. Energy Combust. Sci. 2013, 39, 215–245. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Shen, Y. CFD-DEM study of biomass gasification in a fluidized bed reactor: Effects of key operating parameters. Renew. Energy 2020, 159, 1146–1164. [Google Scholar] [CrossRef]
- Wan, Z.; Hu, J.; Qi, X. Numerical analysis of hydrodynamics and thermochemical property of biomass gasification in a pilot-scale circulating fluidized bed. Energy 2021, 225, 120254. [Google Scholar] [CrossRef]
- Yang, S.; Liu, X.; Wang, S.; Zhang, K.; Wang, H. Eulerian-Lagrangian simulation study of the gas-solid reacting flow in a bubbling fluidized coal gasifier. Chem. Eng. J. 2021, 426, 130825. [Google Scholar] [CrossRef]
- Muhammad, A.; Zhang, N.; Wang, W. CFD simulations of a full-loop CFB reactor using coarse-grained Eulerian–Lagrangian dense discrete phase model: Effects of modeling parameters. Powder Technol. 2019, 354, 615–629. [Google Scholar] [CrossRef]
- Wang, S.; Shen, Y. Coarse-grained CFD-DEM modelling of dense gas-solid reacting flow. Int. J. Heat Mass Transf. 2022, 184, 122302. [Google Scholar] [CrossRef]
- Stroh, A.; Alobaid, F.; von Bohnstein, M.; Ströhle, J.; Epple, B. Numerical CFD simulation of 1 MWth circulating fluidized bed using the coarse grain discrete element method with homogenous drag models and particle size distribution. Fuel Process. Technol. 2018, 169, 84–93. [Google Scholar] [CrossRef]
- Hong, K.; Shi, Z.; Ullah, A.; Wang, W. Extending the bubble-based EMMS model to CFB riser simulations. Powder Technol. 2014, 266, 424–432. [Google Scholar] [CrossRef]
- Qin, Z.; Zhou, Q.; Wang, J. An EMMS drag model for coarse grid simulation of polydisperse gas–solid flow in circulating fluidized bed risers. Chem. Eng. Sci. 2019, 207, 358–378. [Google Scholar] [CrossRef]
- Lu, L.; Xu, J.; Ge, W.; Yue, Y.; Liu, X.; Li, J. EMMS-based discrete particle method (EMMS–DPM) for simulation of gas–solid flows. Chem. Eng. Sci. 2014, 120, 67–87. [Google Scholar] [CrossRef]
- Tricomi, L.; Melchiori, T.; Chiaramonti, D.; Boulet, M.; Lavoie, J.M. Numerical investigation of a cold bubbling bed throughout a dense discrete phase model with KTGF collisional closure. Biofuels Eng. 2017, 2, 32–50. [Google Scholar] [CrossRef]
- Ku, X.; Li, T.; Løvås, T. CFD–DEM simulation of biomass gasification with steam in a fluidized bed reactor. Chem. Eng. Sci. 2015, 122, 270–283. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Luo, K.; Fan, J. CFD-DEM coupled with thermochemical sub-models for biomass gasification: Validation and sensitivity analysis. Chem. Eng. Sci. 2020, 217, 115550. [Google Scholar] [CrossRef]
- Behrendt, M.O.S.G.F. Euler–Lagrange/DEM simulation of wood gasification in a bubbling fluidized bed reactor. Particuology 2009, 7, 307–316. [Google Scholar]
- Chen, L.; He, A.; Zhao, J.; Kang, Q.; Li, Z.-Y.; Carmeliet, J.; Shikazono, N.; Tao, W.-Q. Pore-scale modeling of complex transport phenomena in porous media. Prog. Energy Combust. Sci. 2022, 88, 100968. [Google Scholar] [CrossRef]
- Fernando, N.; Narayana, M. A comprehensive two dimensional Computational Fluid Dynamics model for an updraft biomass gasifier. Renew. Energy 2016, 99, 698–710. [Google Scholar] [CrossRef]
- Umeki, K.; Namioka, T.; Yoshikawa, K. Analysis of an updraft biomass gasifier with high temperature steam using a numerical model. Appl. Energy 2012, 90, 38–45. [Google Scholar] [CrossRef]







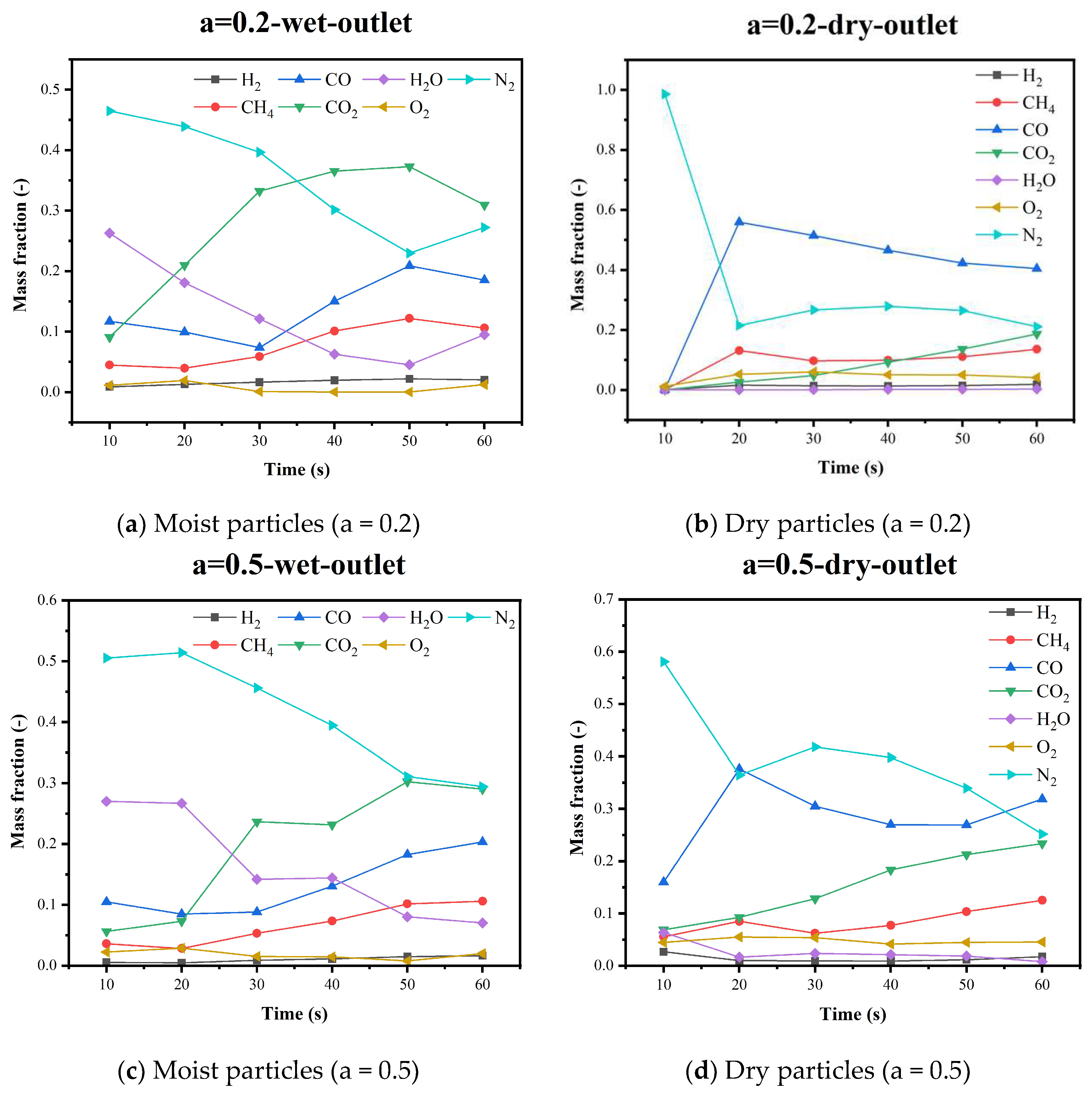
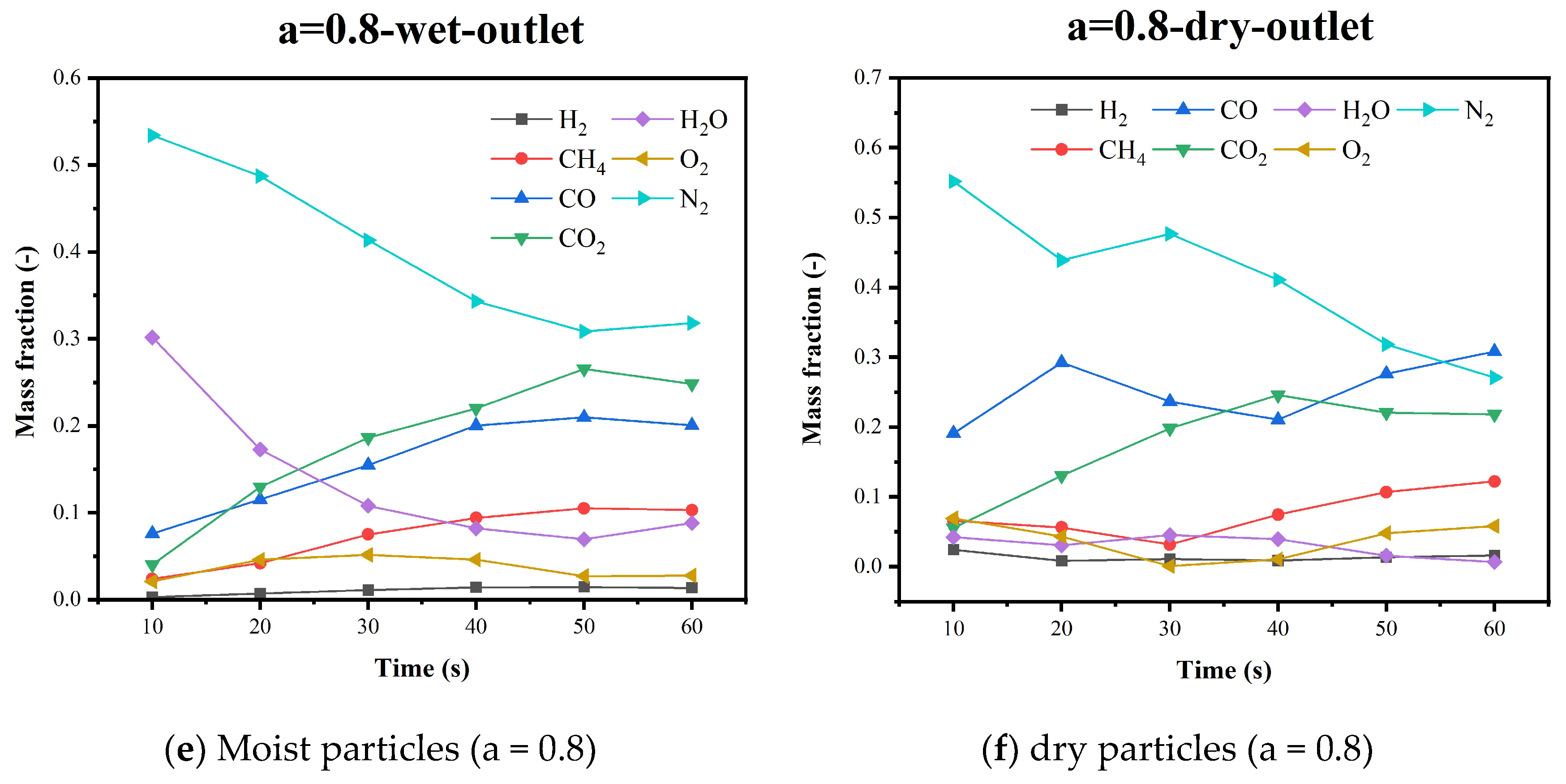
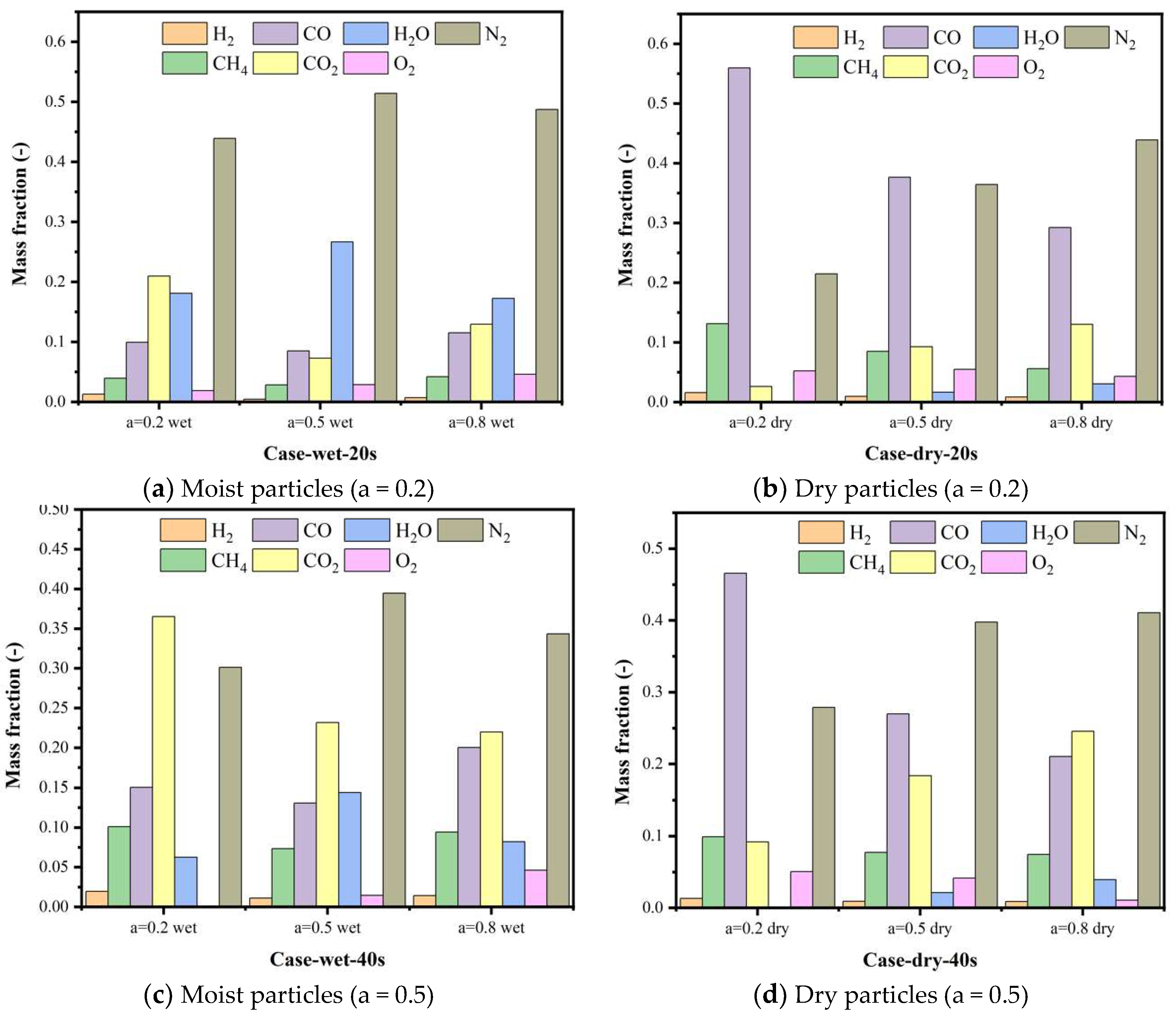

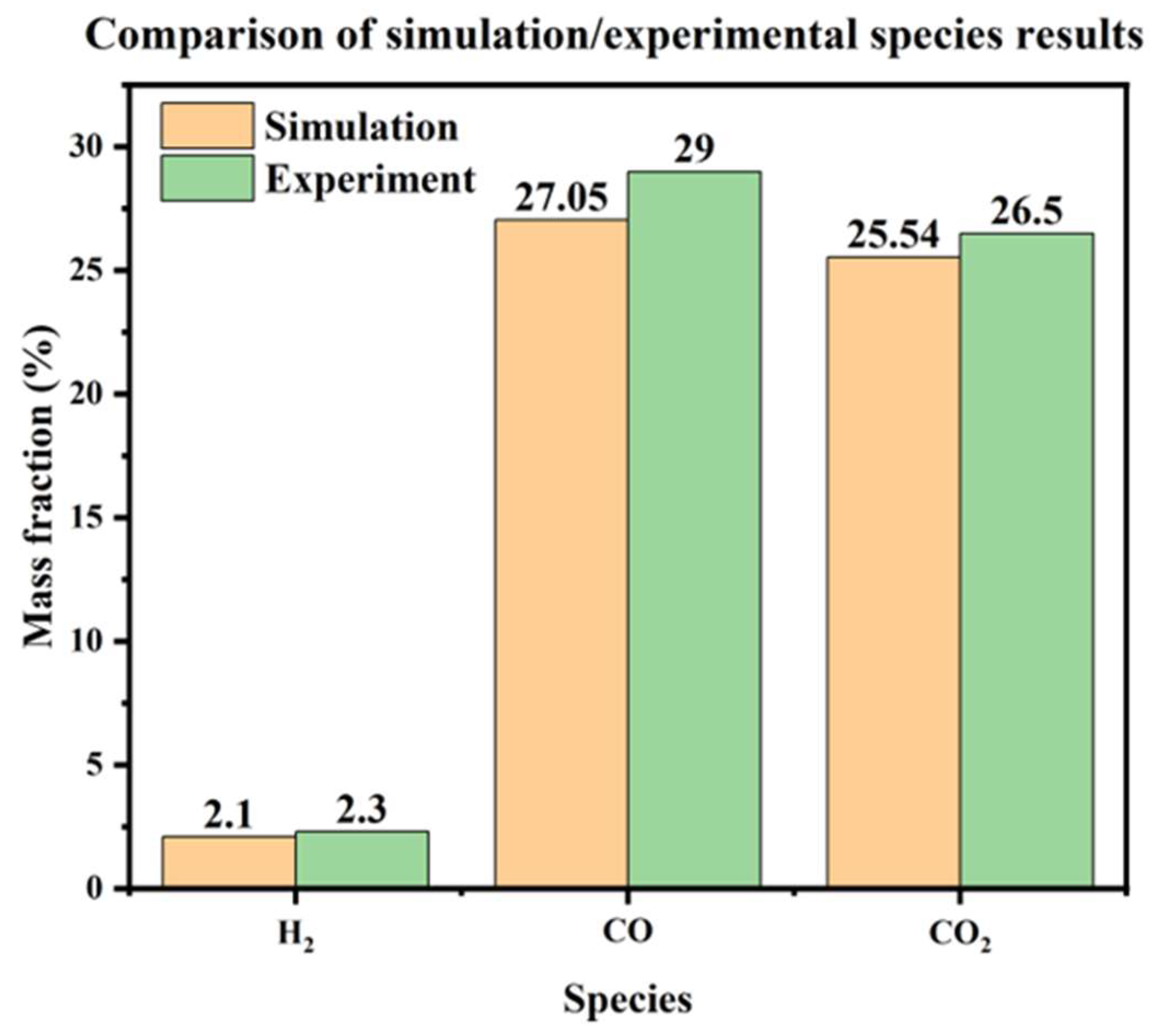
| Research | Device Type | Raw Material | Simulation Method | Spatial Scale |
|---|---|---|---|---|
| [30] | Downdraft fixed bed | biomass | DPM | 2D |
| [29] | Updraft fixed bed | biomass | DEM | 2D |
| [10] | Updraft fixed bed | biomass | - | 1D |
| [34] | Downdraft fixed bed | biomass | DPM | 2D |
| [35] | Updraft fixed bed | biomass | TFM | 2D |
| [36] | Updraft fixed bed | coal | TFM | 2D |
| [31] | Downdraft fixed bed | biomass | DPM | 2D |
| Industrial Analysis | Elemental Analysis | ||||
|---|---|---|---|---|---|
| Volatile (%) | Fixed Carbon (%) | Ash (%) | C (%) | H (%) | N (%) |
| 82.951 ± 0.531 | 16.677 ± 0.124 | 0.372 ± 0.002 | 48 ± 0.681 | 6.35 ± 0.037 | 0.02 ± 0.0001 |
| Data Record Point | H2 (%) | CH4 (%) | CO (%) | CO2 (%) | O2 (%) | Calorific Value (MJ/m3) |
|---|---|---|---|---|---|---|
| 1 | 2.51 | 6.662 | 35.496 | 33.09 | 0.03 | 7.1 |
| 2 | 2.19 | 6.432 | 33.198 | 32.08 | 2.42 | 6.7 |
| 3 | 2.52 | 6.701 | 35.676 | 33.28 | 0.00 | 7.2 |
| 4 | 2.41 | 6.424 | 34.267 | 31.74 | 0.48 | 6.9 |
| H2 | CH4 | CO | CO2 |
|---|---|---|---|
| 2.225 | 18.85 | 37.65 | 41.275 |
| Reactions | Pre-Exponential Factor Ahete (s·m−1·K−1) | Activation Energy Ehete (J·kmol−1) |
|---|---|---|
| C(s) + H2O → H2 + CO | 45.6 | 4.37 × 107 |
| C(s) + CO2→2CO | 8.3 | 4.37 × 107 |
| Reactions | Pre-Exponential Factor Ahete (kmol/m3) | Activation Energy Ehete (J·kmol−1) |
|---|---|---|
| CO + H2O → CO2 + H2 | 2.78 × 103 | 1.26 × 107 |
| CO2 + H2 → CO + H2O | 9.59 × 104 | 4.66 × 107 |
| CH4 + H2O → 3H2 + CO | 3 × 108 | 1.26 × 108 |
| CO + 0.5O2 → CO2 | 3.987 × 1014 | 1.6738 × 108 |
| CH4 + 2O2 → CO2 + 2H2O | 1.585 × 1013 | 2.025 × 108 |
| H2 + 0.5O2 → H2O | 1.9953 × 1012 | 1.092 × 108 |
| Work Conditions | Water Content (%) | Excess Air Coefficient (−) | Mass Flow Rate (kg/s) |
|---|---|---|---|
| 1 | 10 | 0.2 | 0.001268 |
| 2 | 10 | 0.5 | 0.00317 |
| 3 | 10 | 0.8 | 0.005072 |
| 4 | 0 | 0.2 | 0.001268 |
| 5 | 0 | 0.5 | 0.00317 |
| 6 | 0 | 0.8 | 0.005072 |
| Turbulence Model | Realizable k-ε |
|---|---|
| Wall function | Scalable wall functions |
| Radiation model | Discrete ordinates (DOs) |
| Gasification agent temperature | 1100 K |
| Thermal energy storage wall temperature | 1000 K |
| Fluid time step | 2 × 10−4 s |
| Discrete phase time step | 2 × 10−5 s |
| Study | Particle Type | Gasification Agent Type | H2 (%) | CO (%) | CO2 (%) |
|---|---|---|---|---|---|
| This study | biomass | air | 3.84 | 49.46 | 46.7 |
| [36] | coal | air–steam | 2.27 | 68.6 | 29.13 |
| [56] | biomass | air | 1.46 | 51.64 | 46.9 |
| [35] | biomass | air | 1.31 | 68.8 | 29.89 |
| [10] | biomass | air | 1.36 | 51 | 47.64 |
| [9] | biomass | air; air–steam | 3 | 63.47 | 33.53 |
| [57] | biomass | steam | 5.9 | 11.3 | 82.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Wang, Y.; Gu, J.; Yuan, H.; Liu, Z.; Cheng, L.; Li, X.; Li, X. CFD Simulation and Experimental Study on a Thermal Energy Storage–Updraft Solid Waste Gasification Device. Energies 2023, 16, 4580. https://doi.org/10.3390/en16124580
Sun Z, Wang Y, Gu J, Yuan H, Liu Z, Cheng L, Li X, Li X. CFD Simulation and Experimental Study on a Thermal Energy Storage–Updraft Solid Waste Gasification Device. Energies. 2023; 16(12):4580. https://doi.org/10.3390/en16124580
Chicago/Turabian StyleSun, Zepeng, Yazhuo Wang, Jing Gu, Haoran Yuan, Zejian Liu, Leilei Cheng, Xiang Li, and Xian Li. 2023. "CFD Simulation and Experimental Study on a Thermal Energy Storage–Updraft Solid Waste Gasification Device" Energies 16, no. 12: 4580. https://doi.org/10.3390/en16124580
APA StyleSun, Z., Wang, Y., Gu, J., Yuan, H., Liu, Z., Cheng, L., Li, X., & Li, X. (2023). CFD Simulation and Experimental Study on a Thermal Energy Storage–Updraft Solid Waste Gasification Device. Energies, 16(12), 4580. https://doi.org/10.3390/en16124580






