Analysis and Optimization Strategy of Active Power Dynamic Response for VSG under a Weak Grid
Abstract
1. Introduction
- (1)
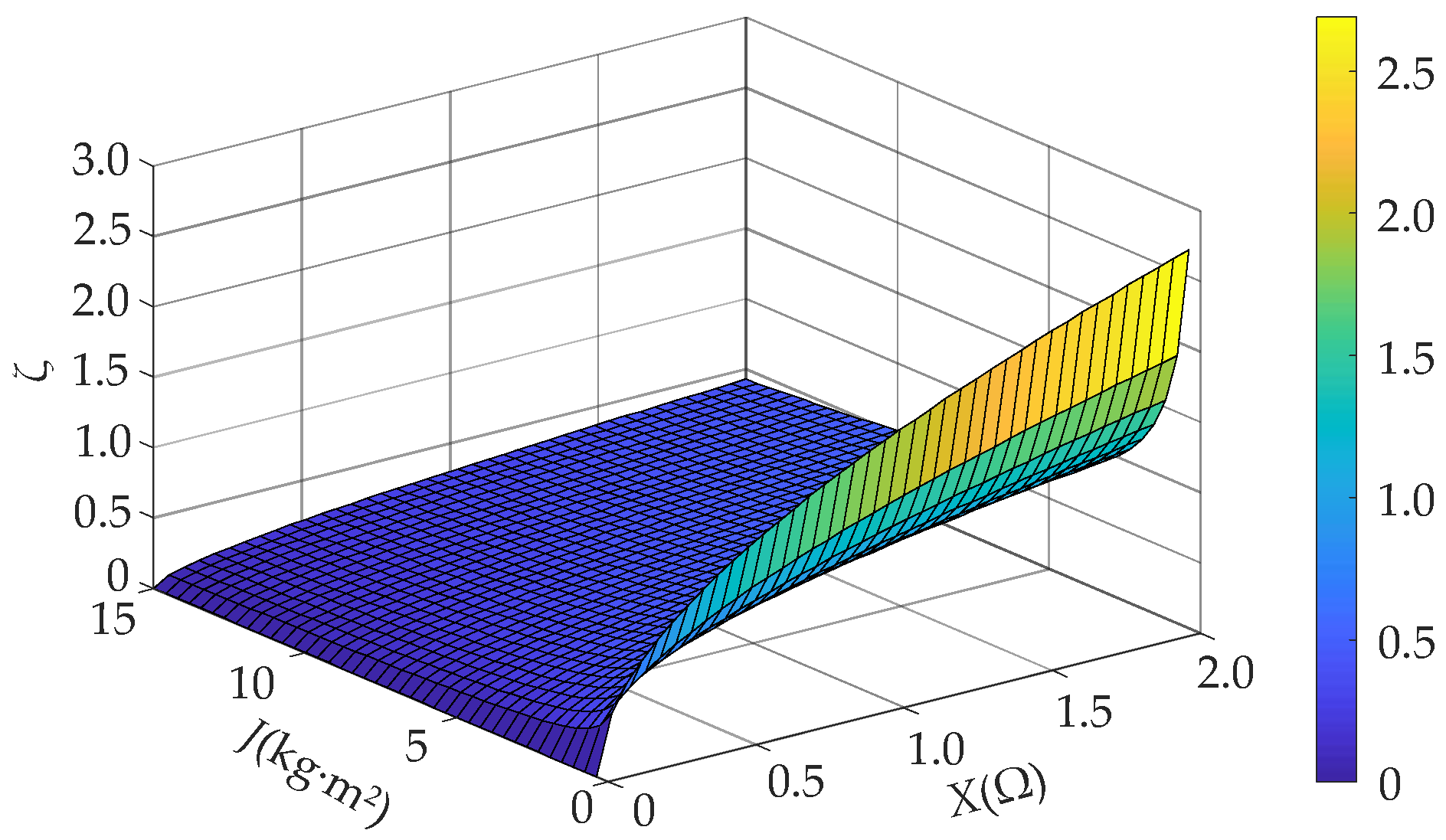
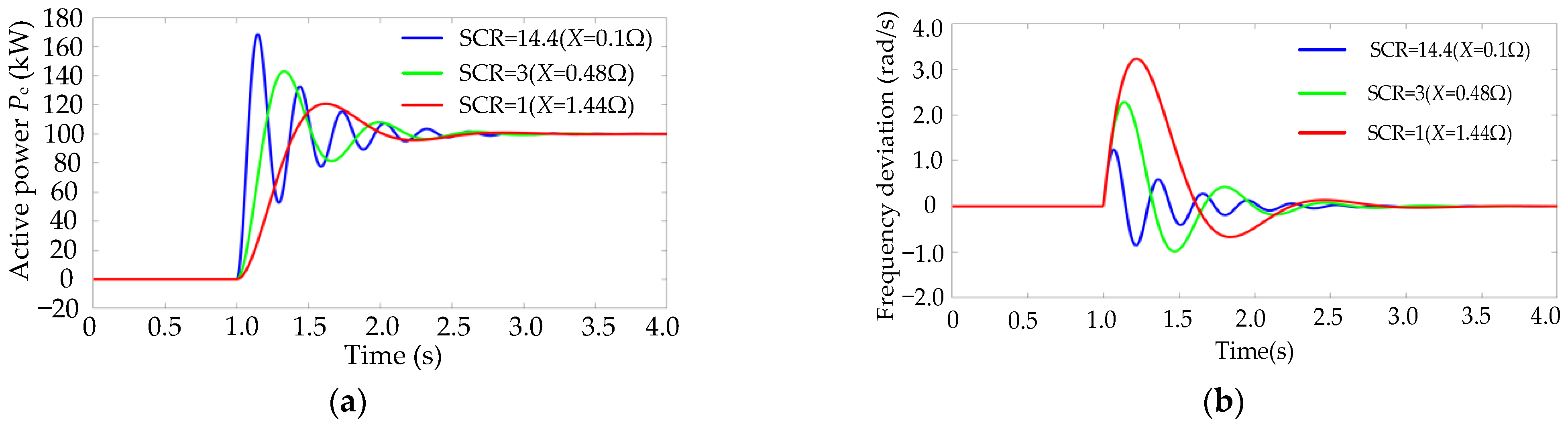
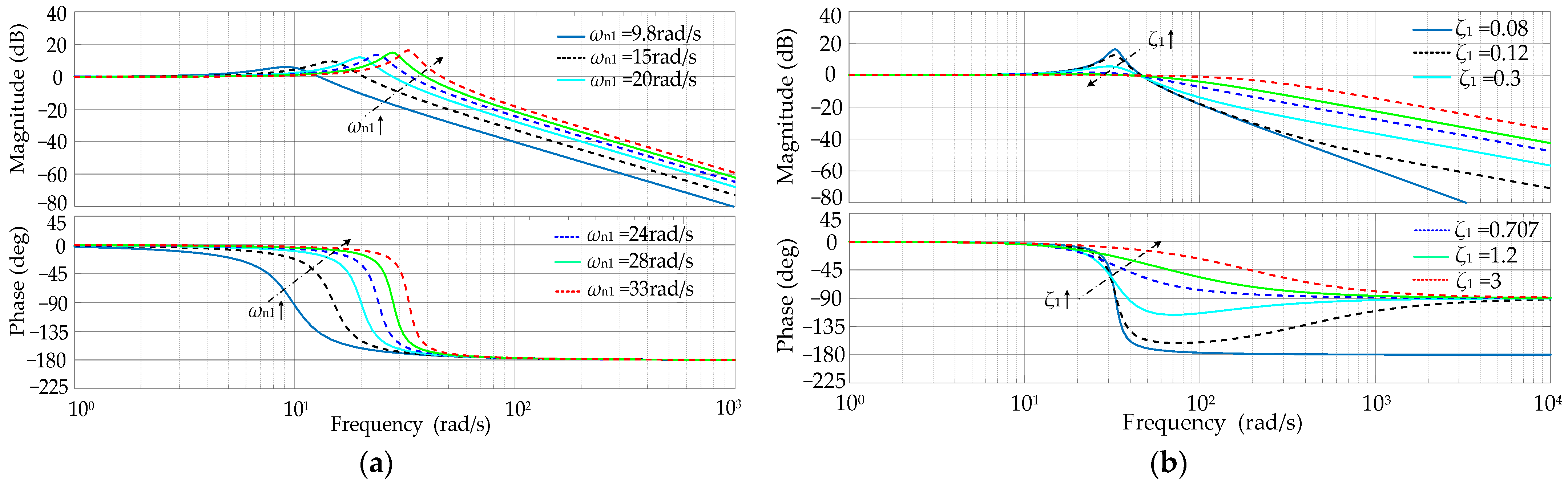
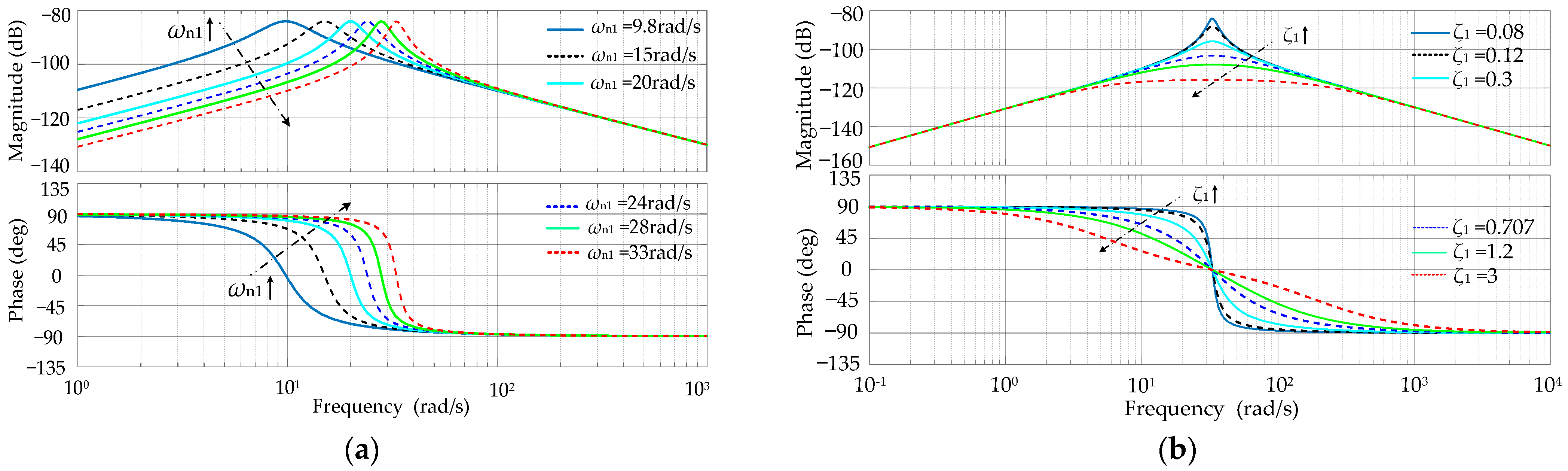
- The small signal model of the GCAP closed-loop system of the VSG is established when the VSG is incorporated into a weak grid. Accordingly, it reflects that the dynamic oscillation amplitude of GCAP decreases with the increase of the short circuit ratio (SCR) but the GCAP dynamic response speed slows down yet the output frequency overshoot increases under the active power command step.
- (2)
- The proposed control method builds a novel mechanism for improving transient damping for the grid-connected VSG system and breaks through the limitation of simulating the SG. Therefore, the tradeoff of multiple control objectives is avoided and the inherent control contradictions of the VSG are fundamentally solved, thus, improving the dynamic response performances of the VSG as well as greatly simplifying the controller design.
- (3)
- The proposed VNIAPTD control algorithm is simple, intuitive, does not use differential operation, and is easy to be implemented in engineering. As such, the dynamic response performances of the GCAP as well as the output frequency for the VSG can be significantly improved simultaneously when the VSG is incorporated into a weak grid.
2. Small Signal Model and Dynamic Response Characteristics of the TVSG
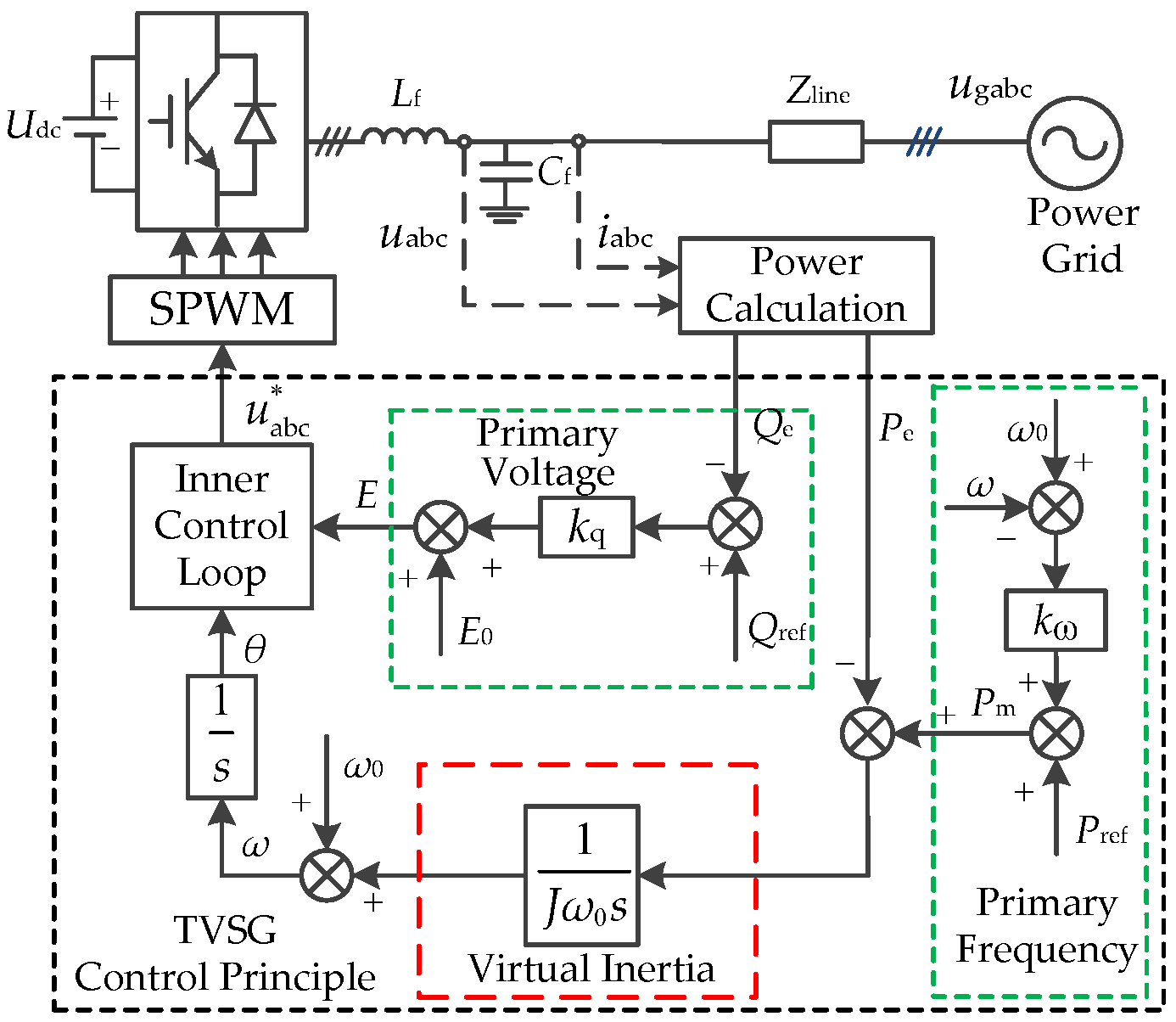
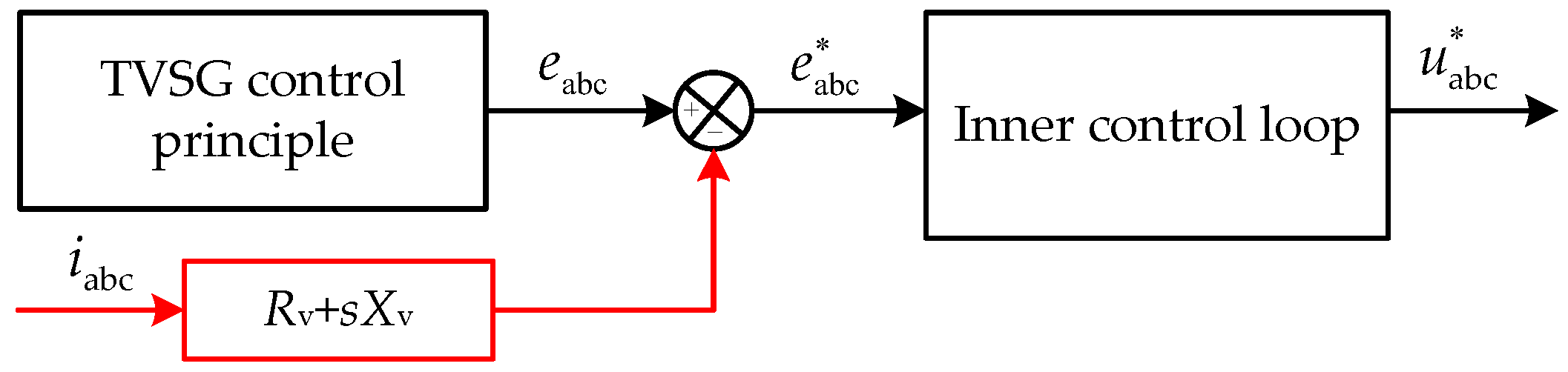
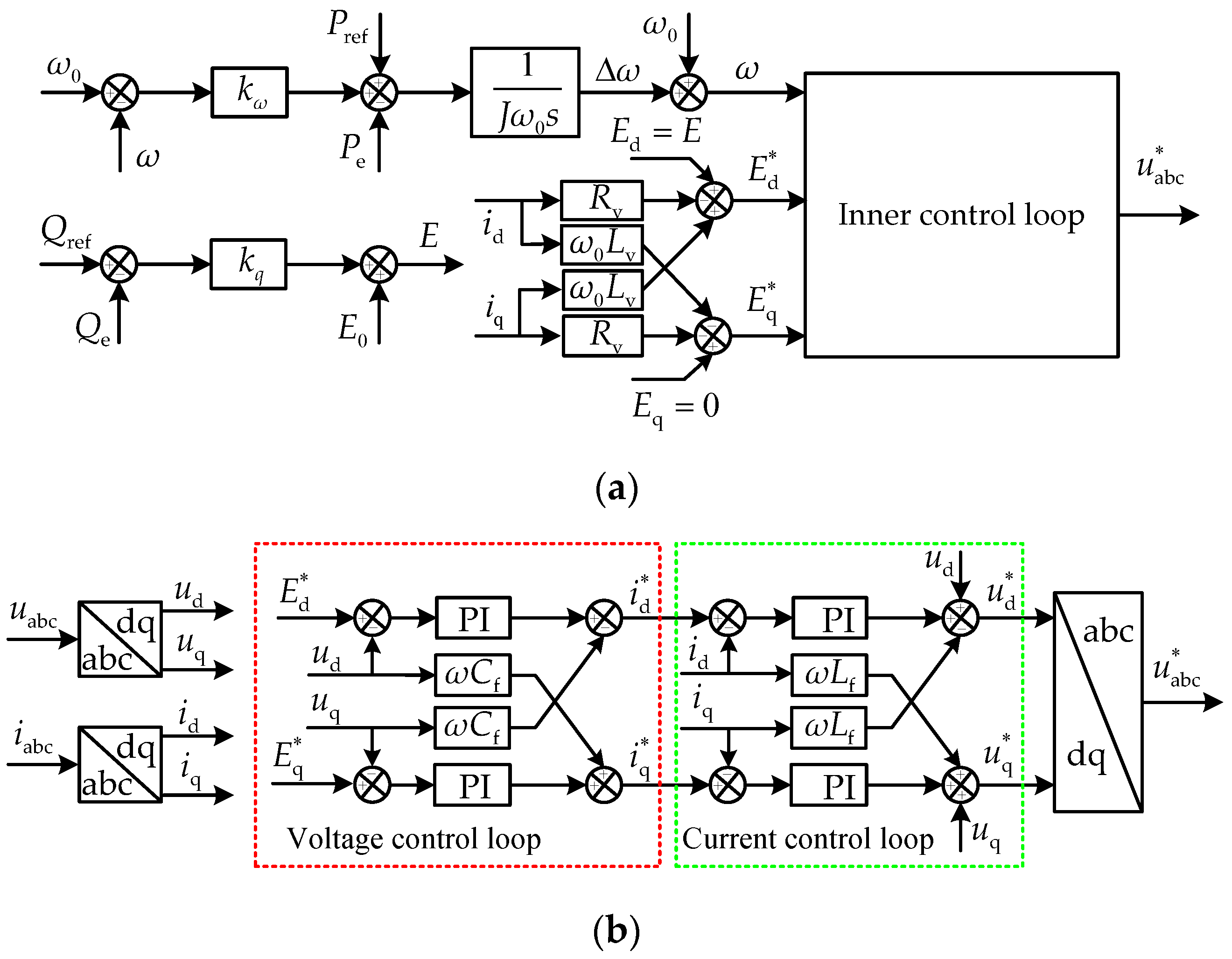
2.1. Control Principle of the TVSG
2.2. Small Signal Model of TVSG
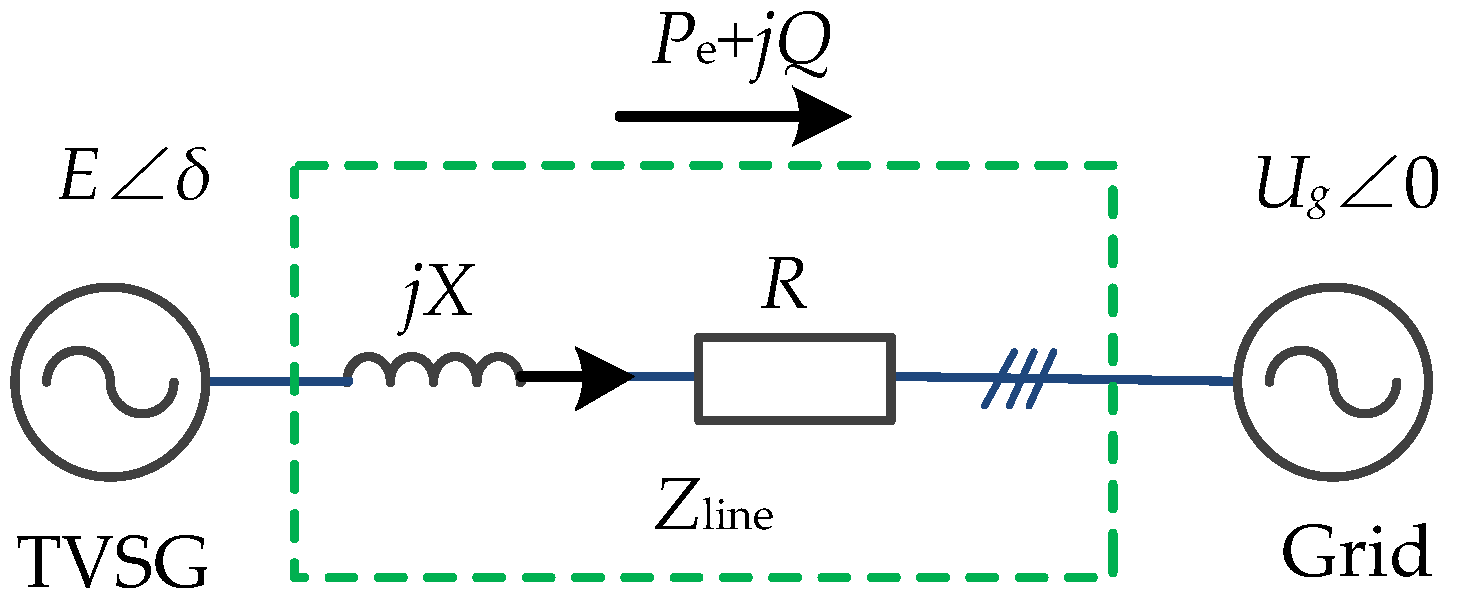
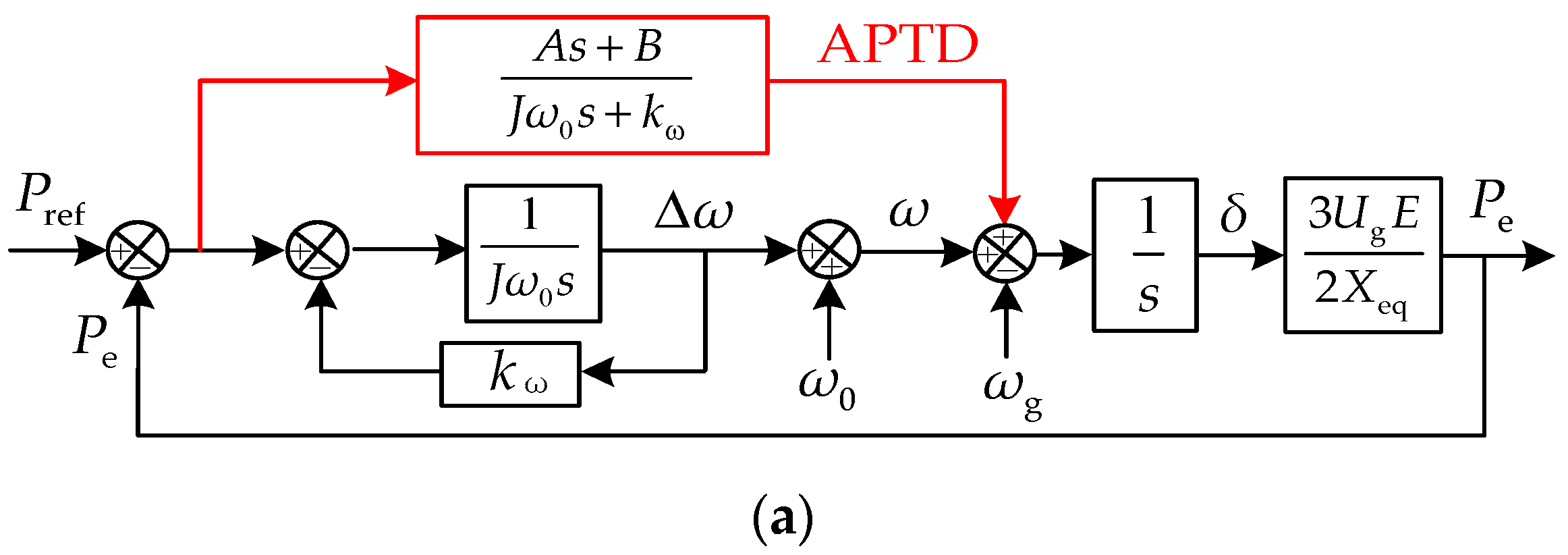
2.3. Dynamic Response Characteristics of the TVSG under a Weak Grid
3. VNIAPTD-VSG Control Strategy
3.1. Virtual Negative Impedance Control Algorithm
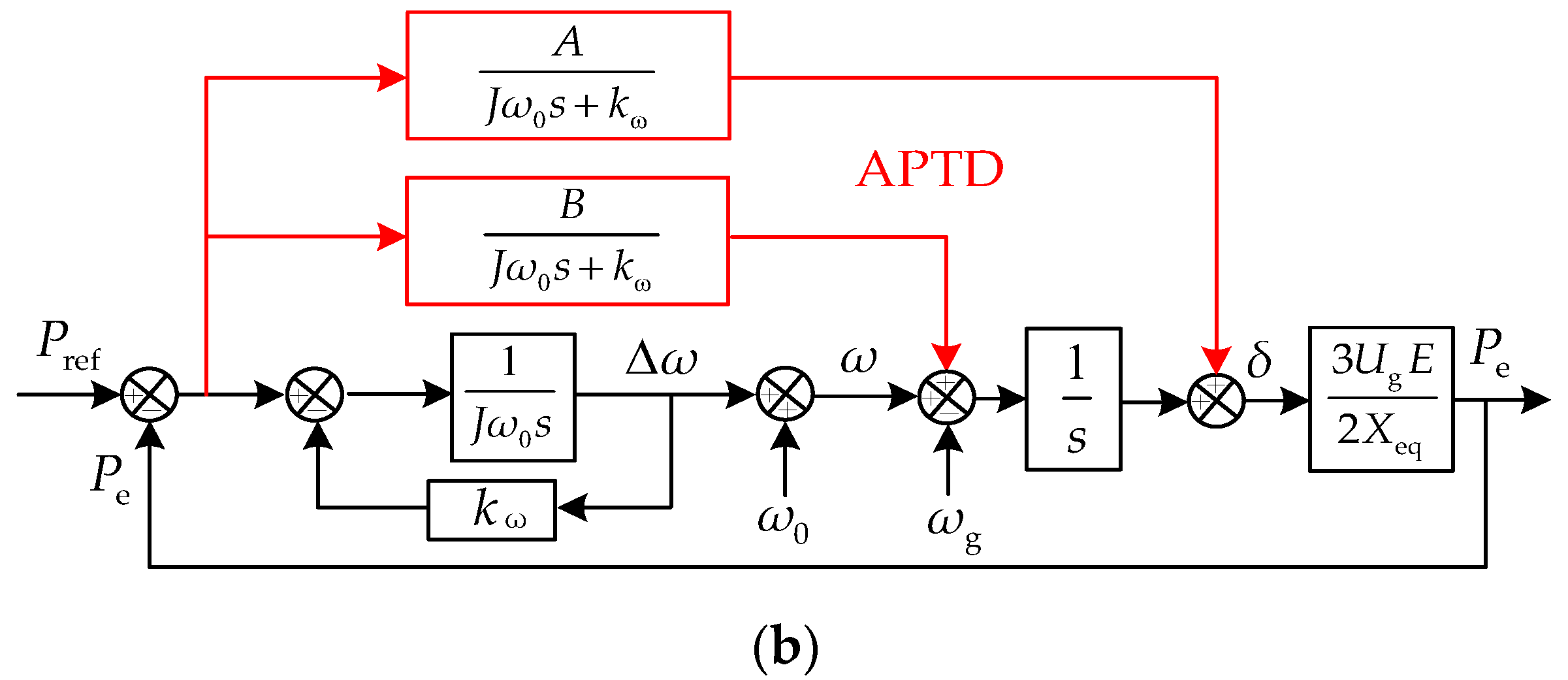
3.2. Active Power Transient Damping (APTD) Control Algorithm
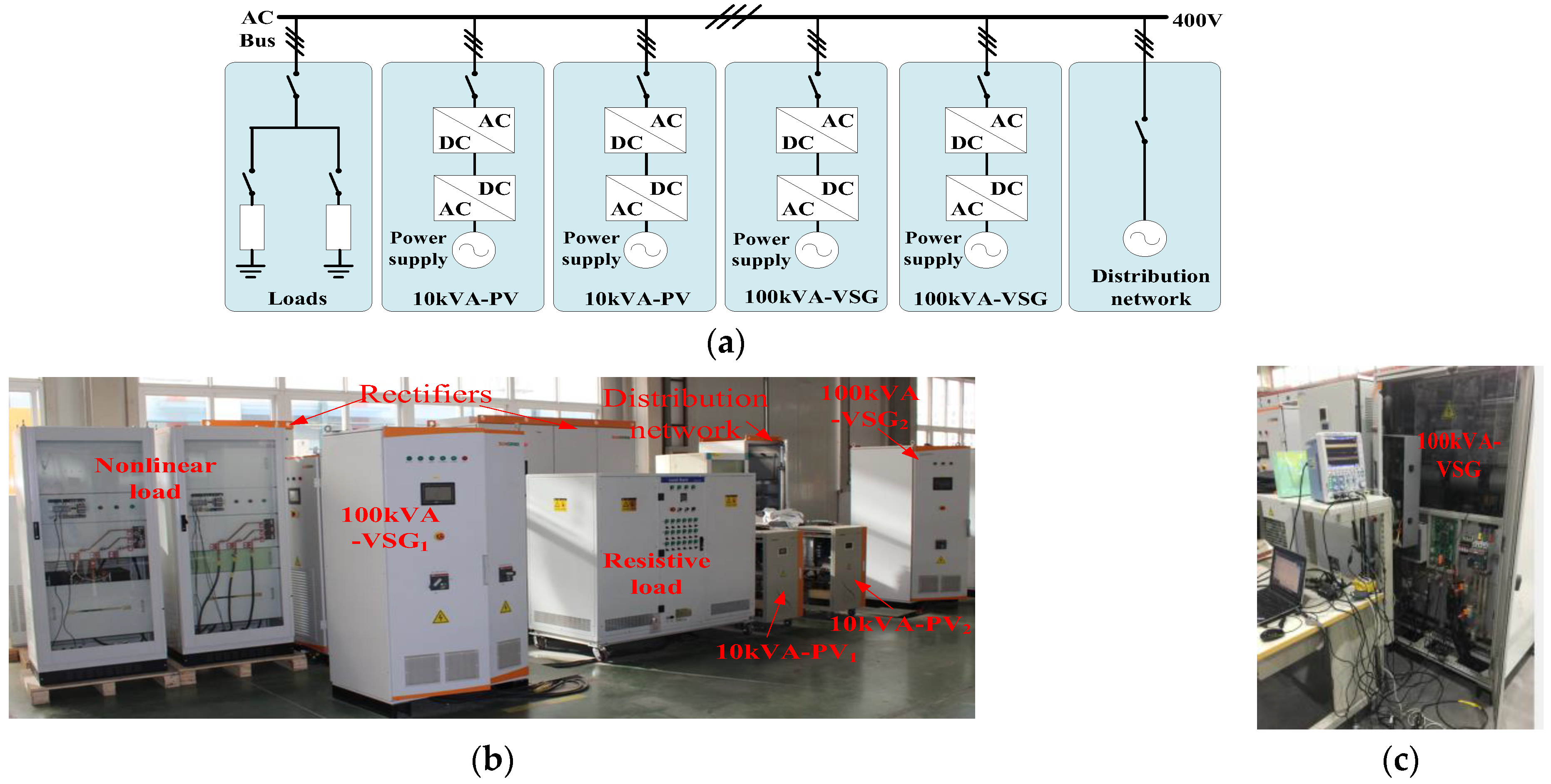
4. Simulation and Experimental Verifications
4.1. Simulation Results and Analysis
4.2. Experimental Results and Analysis
5. Conclusions
- (1)
- When the TVSG is connected to a weak grid, the dynamic oscillation amplitude of Pe decreases with SCR but its Pe dynamic response speed slows down, yet its f overshoot amplitude increases under the Pref step disturbance.
- (2)
- Although the control strategy based on the virtual negative impedance algorithm can reduce the equivalent line inductance of the grid-connected TVSG system and the Pe dynamic response time, it can increase the Pe dynamic oscillation amplitude and the f dynamic oscillation degree under a disturbance of Pref when the TVSG is operating and connected to a weak grid.
- (3)
- The proposed VNIAPTD-VSG can solve the inherent contradiction between the overshoot suppression ability and dynamic response speed of Pe, thereby obtaining a better Pe overshoot suppression ability and faster Pe dynamic response speed compared with the TVSG. The VNIAPTD-VSG can solve the inherent contradiction among the overshoot suppression ability, RoCoF, and dynamic response speed of f, thereby obtaining a better f dynamic oscillation suppression ability and shorter f regulation time without affecting the RoCoF compared to the TVSG. The VNIAPTD-VSG can solve the inherent contradiction between the control objectives of Pe and f, thereby achieving desirable dynamic response performances of Pe and f simultaneously.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Pref, Qref | Command of active power and reactive power |
| Pe, Qe | Grid-connected active power and grid-connected reactive power |
| J | Virtual inertia |
| ω0, ω | Rated angular frequency and output angular frequency |
| f | Output frequency |
| X | Circuit equivalent reactance |
| kω | Primary frequency modulation coefficient |
| kq | Primary voltage modulation coefficient |
| E0, E | Rated voltage amplitude and output voltage amplitude |
| Ug, ωg | Grid voltage amplitude and gird angular frequency |
| ωn, ωn1 | Natural oscillation angular frequency |
| ζ, ζ1 | Damping ratio |
| Rv, Xv | Virtual resistance and virtual inductance |
| Lv | Virtual negative inductor |
| A | Dynamic compensation coefficient of APTD |
| B | Proportional compensation coefficient of APTD |
| RESs | Renewable energy sources |
| SG | Synchronous generator |
| VSG | Virtual synchronous generator |
| GCAP | Grid-connected active power |
| GCRP | Grid-connected reactive power |
| APTD | Active power transient damping |
| VNIAPTD | Virtual negative impedance combined with the active power transient damping |
| TVSG | Typical VSG |
| VNIAPTD-VSG | VSG with VNIAPTD control algorithm |
| SCR | Short circuit ratio |
References
- Liu, Y.Q.; Chen, L.X.; Han, X.Q. The key problem analysis on the alternative new energy under the energy transition. Proc. CSEE 2022, 42, 515–523. [Google Scholar]
- Zhong, Q.C. Power-electronics-enabled autonomous power systems: Architecture and technical routes. IEEE Trans. Ind. Electron. 2017, 64, 5907–5918. [Google Scholar] [CrossRef]
- Yuan, X.M.; Zhang, M.Q.; Chi, Y.N.; Ju, P. Basic challenges of and technical roadmap to power-electronized power system dynamics issues. Proc. CSEE 2022, 42, 1904–1916. [Google Scholar]
- Wang, X.F.; Taul, M.G.; Wu, H.; Liao, Y.C.; Blaabjerg, F.; Harnefors, L. Grid-synchronization stability of converter- based resources—An overview. IEEE Open J. Ind. Appl. 2020, 1, 115–134. [Google Scholar] [CrossRef]
- Wang, X.F.; Blaabjerg, F. Harmonic stability in power electronic-based power systems: Concept, modeling, and analysis. IEEE Trans. Smart Grid 2019, 10, 2858–2870. [Google Scholar] [CrossRef]
- Laaksonen, H. Improvement of power system frequency stability with universal grid-forming battery energy storages. IEEE Access 2023, 11, 10826–10841. [Google Scholar] [CrossRef]
- Chen, S.M.; Sun, Y.; Han, H.; Fu, S.Q.; Luo, S.H.; Shi, G.Z. A modified VSG control scheme with virtual resistance to enhance both small-signal stability and transient synchronization stability. IEEE Trans. Power Electron. 2023, 38, 6005–6014. [Google Scholar] [CrossRef]
- Lu, S.; Zhu, Y.; Dong, L.; Na, G.; Hao, Y.; Zhang, G.; Zhang, W.; Cheng, S.; Yang, J.; Sui, Y. Small-signal stability research of grid-connected virtual synchronous generators. Energies 2022, 15, 7158. [Google Scholar] [CrossRef]
- Sang, W.; Guo, W.; Dai, S.; Tian, C.; Yu, S.; Teng, Y. Virtual synchronous generator, a comprehensive overview. Energies 2022, 15, 6148. [Google Scholar] [CrossRef]
- Sun, P.; Yao, J.; Zhao, Y.; Fang, X.; Cao, J.Y. Stability assessment and damping optimization control of multiple grid connected virtual synchronous generators. IEEE Trans. Energy Convers. 2021, 36, 3555–3567. [Google Scholar] [CrossRef]
- Wu, G.T.; He, Y.Y.; Zhang, H.; Wang, X.H.; Pan, D.H.; Ruan, X.B.; Yao, C. Passivity-based stability analysis and generic controller design for grid-forming inverter. IEEE Trans. Power Electron. 2023, 38, 5832–5843. [Google Scholar] [CrossRef]
- Li, M.X.; Yu, P.; Hu, W.H.; Wang, Y.; Shu, S.R.; Zhang, Z.Y.; Blaabjerg, F. Phase feedforward damping control method for virtual synchronous generators. IEEE Trans. Power Electron. 2022, 37, 9790–9806. [Google Scholar] [CrossRef]
- Fang, J.Y.; Lin, P.F.; Li, H.C.; Yang, Y.H.; Tang, Y. An improved virtual inertia control for three-phase voltage source converters connected to a weak grid. IEEE Trans. Power Electron. 2019, 34, 8660–8670. [Google Scholar] [CrossRef]
- Rathnayake, D.B.; Me, S.P.; Razzaghi, R.; Bahrani, B. H∞-based control design for grid-forming inverters with enhanced damping and virtual inertia. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 2311–2325. [Google Scholar] [CrossRef]
- Liu, H.; Yang, B.; Xu, S.; Du, M.J.; Lu, S. Universal virtual synchronous generator based on extended virtual inertia to enhance power and frequency response. Energies 2023, 16, 2983. [Google Scholar] [CrossRef]
- Xu, H.Z.; Yu, C.Z.; Liu, C.; Wang, Q.L.; Zhang, X. An improved virtual inertia algorithm of virtual synchronous generator. J. Mod. Power Syst. Clean Energy 2020, 8, 377–386. [Google Scholar] [CrossRef]
- Li, M.X.; Wang, Y.; Xu, N.Y.; Niu, R.G.; Lei, W.J. Control strategy of virtual synchronous generator based on band-pass damped power feedback. Trans. China Electrotech. Soc. 2018, 33, 2176–2185. [Google Scholar]
- Shuai, Z.K.; Huang, W.; Shen, Z.J.; Luo, A.; Tian, Z. Active power oscillation and suppression techniques between two parallel synchronverters during load fluctuations. IEEE Trans. Power Electron. 2020, 35, 4127–4142. [Google Scholar] [CrossRef]
- Jiang, J.Y.; Wang, W.; Tang, F.; Wu, X.Z.; Yang, Z.W. d-axis current differential feedforward control for improving the dynamic characteristic of energy storage virtual synchronous generator. Power Syst. Tech. 2022, 46, 2510–2523. [Google Scholar]
- Zhang, Y.N.; Zhou, X.M. Virtual synchronous generator control technology with fractional virtual inertia for grid-connected inverters. Control Dec. 2021, 36, 463–468. [Google Scholar]
- Lan, Z.; Long, Y.; Zeng, J.H.; Tu, C.M.; Xiao, F. Transient power oscillation suppression strategy of virtual synchronous generator considering overshoot. Auto. Elect. Power Syst. 2022, 46, 131–141. [Google Scholar]
- Lan, Z.; Long, Y.; Zeng, J.H.; Lv, Z.P.; He, D. VSG control strategy introducing transient electromagnetic power compensation. Power Syst. Tech. 2022, 46, 1421–1429. [Google Scholar]
- Yu, Y.; Chaudhary, S.K.; Tinajero, G.D.; Xu, L.N.; Bakar, N.; Vasquez, J.C.; Guerrero, J.M. A reference-feedforward-based damping method for virtual synchronous generator control. IEEE Trans. Power Electron. 2022, 37, 7566–7571. [Google Scholar] [CrossRef]
- Li, M.; Zhang, X.; Guo, Z.X.; Wang, J.L.; Wang, Y.; Li, F.; Zhao, W. The control strategy for the grid-connected inverter through impedance reshaping in q-axis and its stability analysis under a weak grid. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3229–3242. [Google Scholar] [CrossRef]
- Arco, S.D.; Suul, J.A.; Fosso, O.B. A virtual synchronous machine implementation for distributed control of power converters in SmartGrids. Elect. Power Syst. Res. 2015, 122, 180–197. [Google Scholar]
- Liu, J.; Miura, Y.; Ise, T. Comparison of dynamic characteristics between virtual synchronous generator and droop control in inverter-based distributed denerators. IEEE Trans. Power Electron. 2016, 31, 3600–3611. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Bevrani, H.; Ise, T. A unified modeling method of virtual synchronous generator for multi-operation-mode analyses. IEEE J. Emerg. Sel. Topics Power Electron. 2021, 9, 2394–2409. [Google Scholar] [CrossRef]
- Shi, R.L.; Zhang, X.; Hu, C.; Xu, H.Z.; Gu, J.; Cao, W. Self-tuning virtual synchronous generator control for improving frequency stability in autonomous photovoltaic-diesel microgrids. J. Mod. Power Syst. Clean Energy 2018, 6, 482–494. [Google Scholar] [CrossRef]
- Li, M.; Zhang, X.; Guo, Z.X.; Pan, H.L.; Ma, M.Y.; Zhao, W. Impedance adaptive dual-mode control of grid-connected inverters with large fluctuation of SCR and its stability analysis based on D-partition method. IEEE Trans. Power Electron. 2021, 36, 14420–14435. [Google Scholar] [CrossRef]
- Huang, L.B.; Xin, H.H.; Yuan, H.; Wang, G.Z.; Ju, P. Damping effect of virtual synchronous machines provided by a dynamical virtual impedance. IEEE Trans. Energy Conver. 2021, 36, 570–573. [Google Scholar] [CrossRef]
- Ren, M.W.; Li, T.; Shi, K.; Xu, P.F.; Sun, Y.X. Coordinated control strategy of virtual synchronous generator based on adaptive moment of inertia and virtual impedance. IEEE J. Emerg. Sel. Topics Cir. Syst. 2021, 11, 99–110. [Google Scholar] [CrossRef]
- Shi, R.L.; Zhang, X. VSG-based dynamic frequency support control for autonomous PV-diesel microgrids. Energies 2018, 11, 1814–1829. [Google Scholar] [CrossRef]





| Symbol | Parameter | Value |
|---|---|---|
| E0 | Rated voltage amplitude | 311 V |
| Udc | DC bus voltage | 700 V |
| ω0 | Rated angular frequency | 314.15 rad/s |
| J | Virtual inertia | 10 kg·m2 |
| kq | Primary voltage regulation coefficient | 1.4 × 10−4 V/var |
| kω | Primary frequency modulation coefficient | 15,915.5 J/rad |
| Lf | Filter inductance | 50.6 mH |
| Cf | Filter capacitor | 270 uF |
| fs | Sampling frequency | 5 kHz |
| Numbers | Advantages | Reasons |
|---|---|---|
| 1 | VNIAPTD-VSG can obtain better Pe overshoot suppression ability and faster Pe dynamic response speed compared with TVSG. | VNIAPTD-VSG can solve the inherent contradiction between the overshoot suppression ability and dynamic response speed of Pe. |
| 2 | VNIAPTD-VSG can obtain better f dynamic oscillation suppression ability and shorter f regulation time without affecting RoCoF compared with TVSG. | VNIAPTD-VSG can solve the inherent contradiction among the overshoot suppression ability, RoCoF and dynamic response speed of f. |
| 3 | VNIAPTD-VSG can obtain desirable dynamic response performances of Pe and f simultaneously, i.e., fast Pe dynamic response speed without overshoot or oscillation yet small f overshoot amplitude without affecting RoCoF. | VNIAPTD-VSG can solve the inherent contradiction between the control objectives of Pe and f under the Pref step disturbance when TVSG is connected to a weak grid. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, R.; Lan, C.; Huang, J.; Ju, C. Analysis and Optimization Strategy of Active Power Dynamic Response for VSG under a Weak Grid. Energies 2023, 16, 4593. https://doi.org/10.3390/en16124593
Shi R, Lan C, Huang J, Ju C. Analysis and Optimization Strategy of Active Power Dynamic Response for VSG under a Weak Grid. Energies. 2023; 16(12):4593. https://doi.org/10.3390/en16124593
Chicago/Turabian StyleShi, Rongliang, Caihua Lan, Ji Huang, and Chengwei Ju. 2023. "Analysis and Optimization Strategy of Active Power Dynamic Response for VSG under a Weak Grid" Energies 16, no. 12: 4593. https://doi.org/10.3390/en16124593
APA StyleShi, R., Lan, C., Huang, J., & Ju, C. (2023). Analysis and Optimization Strategy of Active Power Dynamic Response for VSG under a Weak Grid. Energies, 16(12), 4593. https://doi.org/10.3390/en16124593






