Real-Time Control of Gas Supply System for a PEMFC Cold-Start Based on the MADDPG Algorithm
Abstract
:1. Introduction
- (1)
- Linear control methods: linear control methods have been developed for many years. Earlier methods included quadratic Gaussian controllers and multivariate quadratic controllers and, more recently linear parametric control methods have been developed. However, these methods have many drawbacks, so researchers have gradually turned to the study of nonlinear control methods [11].
- (2)
- Model-based control methods: model-based control methods can comprehensively simulate the controlled system, such as state-space predictive control methods. However, these methods have a limited scope because they cannot be used for nonlinear systems [12].
- (3)
- Adaptive control methods: adaptive control methods are characterized by high robustness and real-time performance and are widely used in control domain development. Recent research includes data-oriented adaptive control methods, parameter identification-based adaptive control methods, etc. [13].
- (4)
- PID control methods: various PID controllers have been developed, including neural network PID controllers, fuzzy PID controllers, etc. Due to their excellent robustness and real-time feedback performance, they have become a mainstream technology in the field of control engineering [14].
- (1)
- Unlike traditional PEMFC gas supply system control strategies, this paper presents a control strategy based on the MADDPG algorithm and designs corresponding air and hydrogen supply controllers. As a gas supply system control strategy, MADDPG provides feedback on various stack states during the PEMFC cold-start process and optimizes the gas supply system operating parameters in real time, effectively improving the PEMFC cold-start performance.
- (2)
- This study is the first to apply Deep Reinforcement Learning to the PEMFC cold-start research. It improves the control method of such a complex coupled nonlinear system in PEMFC cold-start and opens new avenues for research in this field.
2. PEMFC Cold-Start Model
2.1. Framework of the Model
- (1)
- Mesh validation
- (2)
- Solution algorithm settings
2.2. Assumptions
- (1)
- All gases are considered ideal.
- (2)
- Water produced by electrochemical reactions initially exists as membrane-bound water.
- (3)
- Heat and mass transfer in the direction of stack thickness are neglected, with diffusion being the primary transfer mode.
- (4)
- Changes in internal pressure of the stack are ignored.
- (5)
- Gravity effects are not considered.
- (6)
- Ice formed by saturation of membrane-bound water in the cathode and anode catalyst layers is entirely present in the pores.
- (7)
- The physical parameters of each layer are concentrated at the center position of each layer.
2.3. Boundary Conditions
2.3.1. Electromotive Force Boundary Condition
- (1)
- The initial inlet gas is dry gas;
- (2)
- The initial voltage is
- (3)
- The initial water content in the electrolyte membrane and catalyst layer is .
2.3.2. Mass Boundary Condition
2.3.3. Heat Transfer Boundary Conditions
3. Control Strategy of Gas Supply System Based on MADDPG
3.1. Deep Reinforcement Learning
- (1)
- At each successive time step, the agent interacts with the environment and perceives its state features through deep learning.
- (2)
- Based on the expected reward, the value function of the current state and action is evaluated, and the current state is mapped to an action by a certain strategy.
- (3)
- The environment responds to the issued action and proceeds to the next time step.
- (4)
- The above process is repeated in a loop.
3.2. Common DRL Algorithms
3.2.1. Deep Q-Learning Network
3.2.2. Actor-Critic
3.2.3. Deep Deterministic Policy Gradient
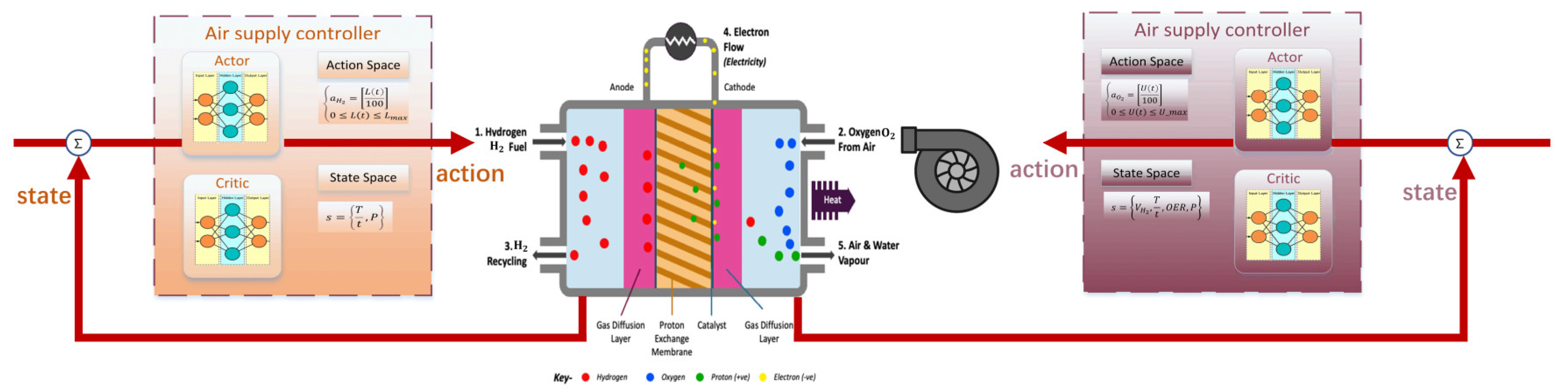
3.3. Controller Design Based on MADDPG
3.3.1. Air Supply Controller
- (1)
- Oxygen excess ratio
- (2)
- Air supply controller
3.3.2. Hydrogen Supply Controller
3.4. Framework of MADDPG Algorithms
| Algorithm 1: Multi-Agent Deep Deterministic Policy Gradient. |
| Initialize critic networks for each agent Initialize actor networks for each agent Initialize target critic networks and target actor networks for each agent Initialize replay buffer for to do Reset environment for to do for to do Observe state Choose action from the Ornstein–Uhlenbeck process Take action and observe reward and next state Store transition in replay buffer end for Sample a random minibatch of transitions from replay buffer for to do Update critic network parameters using: Update actor network parameters using policy gradient: Update target critic and actor networks: end for end for end for |
4. Simulation
4.1. Offline Training
4.2. Online Application
- (1)
- Strategy 1: In Strategy 1, this study uses air supply and hydrogen supply controllers based on the MADDPG control strategy to control the gas supply system. The specific control methodology can be found in Section 3.4.
- (2)
- Strategy 2: The PID control method used in this strategy is currently the most widely used approach in the PEMFC control domain. It offers advantages such as a simple structure and strong processing capability [32]. The PID control strategy can be modeled as follows:
4.2.1. Cold-Start Time
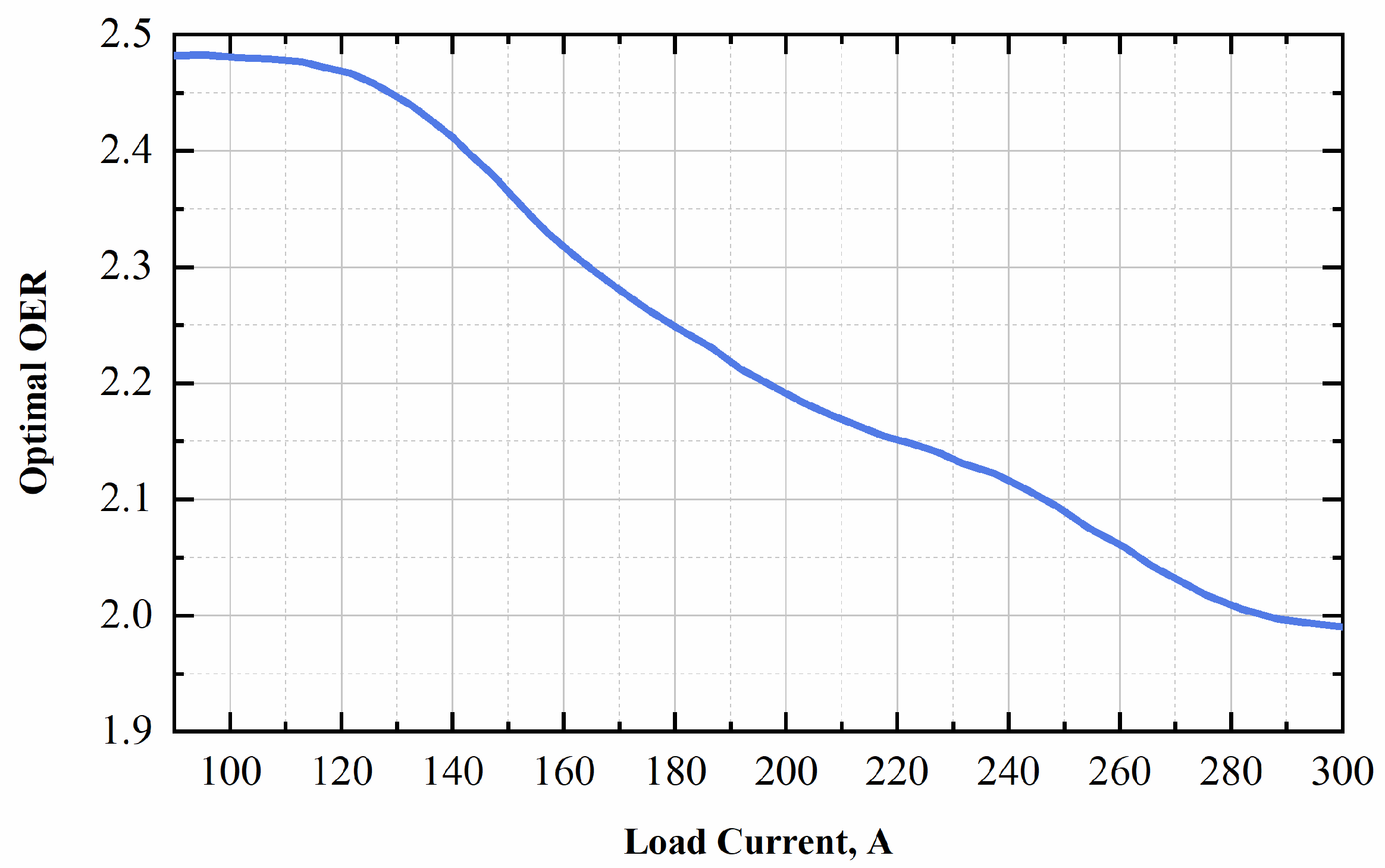
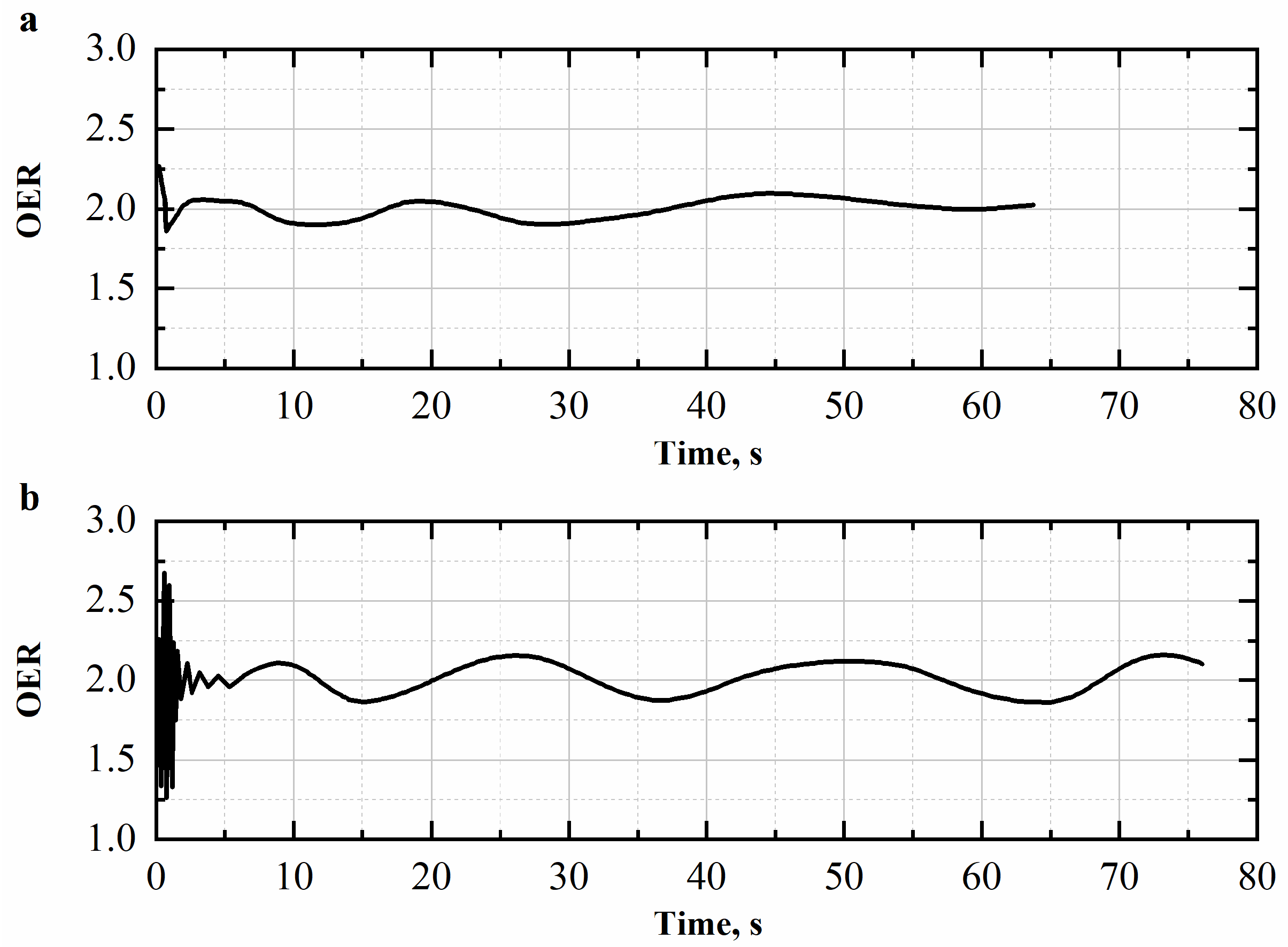
4.2.2. OER
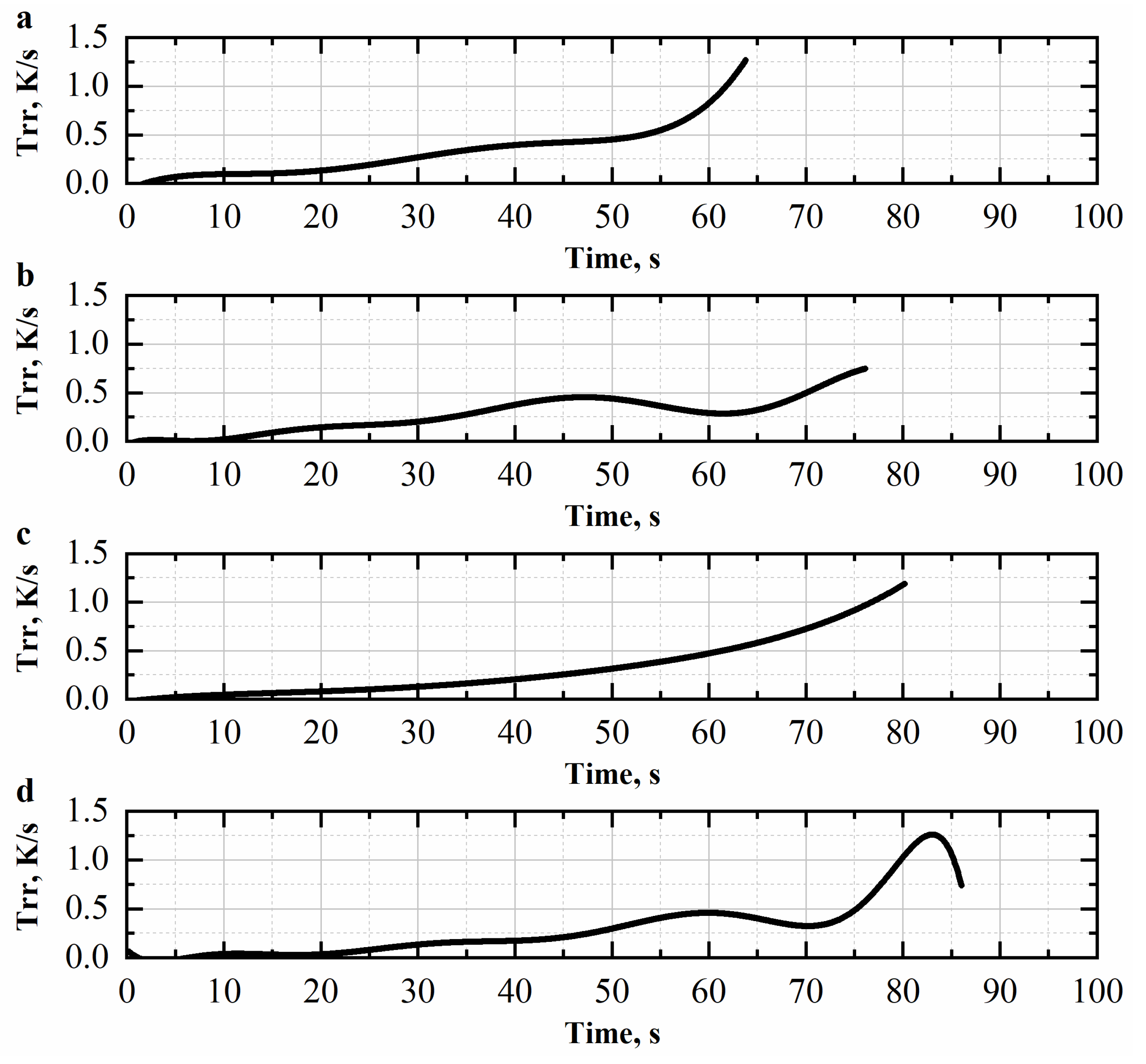
4.2.3. Voltage and Ice Volume Fraction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| PEMFC | Proton exchange membrane fuel cell |
| MADDPG | Multi-agent deep deterministic policy gradient |
| DDPG | Deep deterministic policy gradient |
| DQN | Deep q-learning network |
| AC | Actor-Critic |
| PID | Proportional–Integral–Derivative |
| OER | Oxygen excess ratio |
| Ivf | Ice volume fraction |
| GDL | Gas diffusion layer |
| CL | Catalyst layer |
| Trr | Temperature rise rate |
References
- Kim, D.J.; Jo, M.J.; Nam, S.Y. A review of polymer–nanocomposite electrolyte membranes for fuel cell application. J. Ind. Eng. Chem. 2015, 21, 36–52. [Google Scholar] [CrossRef]
- Luo, Y.; Jiao, K. Cold start of proton exchange membrane fuel cell. Prog. Energy Combust. Sci. 2018, 64, 29–61. [Google Scholar] [CrossRef]
- Li, L.; Wang, S.; Yue, L.; Wang, G. Cold-start icing characteristics of proton-exchange membrane fuel cells. Int. J. Hydrogen Energy 2019, 44, 12033–12042. [Google Scholar] [CrossRef]
- Zalba, B.; Marín, J.M.; Cabeza, L.F.; Mehling, H. Review on thermal energy storage with phase change: Materials, heat transfer analysis and applications. Appl. Therm. Eng. 2003, 23, 251–283. [Google Scholar] [CrossRef]
- Sasmito, A.P.; Shamim, T.; Mujumdar, A.S. Passive thermal management for PEM fuel cell stack under cold weather condition using phase change materials (PCM). Appl. Therm. Eng. 2013, 58, 615–625. [Google Scholar] [CrossRef]
- Li, Y.; Xu, S.; Yang, Z.; Li, Y. Experiment and simulation study on cold start of automotive PEMFC. In Proceedings of the 2011 International Conference on Electric Information and Control Engineering, Wuhan, China, 15–17 April 2011. [Google Scholar]
- Li, L.J.; Wang, S.X.; Yue, L.K.; Wang, G.Z. Cold-start method for proton-exchange membrane fuel cells based on locally heating the cathode. Appl. Energy 2019, 254, 113716. [Google Scholar] [CrossRef]
- Jiang, F.M.; Wang, C.-Y. Potentiostatic Start-Up of PEMFCs from Subzero Temperatures. J. Electrochem. Soc. 2008, 155, B743–B751. [Google Scholar] [CrossRef]
- Chen, H.C.; Zhao, X.; Zhang, T.; Pei, P.C. The reactant starvation of the proton exchange membrane fuel cells for vehicular applications: A review. Energy Convers. Manag. 2019, 182, 282–298. [Google Scholar] [CrossRef]
- Sabharwal, M.; Büchi, F.N.; Nagashima, S.; Marone, F.; Eller, J. Investigation of the transient freeze start behavior of polymer electrolyte fuel cells. J. Power Sources 2021, 489, 229447. [Google Scholar] [CrossRef]
- Bianchi, F.D.; Kunusch, C.; Ocampo-Martinez, C.; Sanchez-Pena, R.S. A Gain-Scheduled LPV Control for Oxygen Stoichiometry Regulation in PEM Fuel Cell Systems. IEEE Trans. Control Syst. Technol. 2014, 22, 1837–1844. [Google Scholar] [CrossRef] [Green Version]
- Guo, A.; Chen, W.R.; Liu, Z.X.; Li, Q.; Zhang, J.F. Temperature model and predictive control for fuel cells in switcher locomotive. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 4235–4240. [Google Scholar] [CrossRef]
- Sun, L.; Shen, J.; Hua, Q.; Lee, K.Y. Data-driven oxygen excess ratio control for proton exchange membrane fuel cell. Appl. Energy 2018, 231, 866–875. [Google Scholar] [CrossRef]
- Zhao, D.; Li, F.; Ma, R.; Zhao, G.; Huangfu, Y. An Unknown Input Nonlinear Observer Based Fractional Order PID Control of Fuel Cell Air Supply System. IEEE Trans. Ind. Appl. 2020, 56, 5523–5532. [Google Scholar] [CrossRef]
- Meraghni, S.; Terrissa, L.S.; Yue, M.; Ma, J.; Jemei, S.; Zerhouni, N. A data-driven digital-twin prognostics method for proton exchange membrane fuel cell remaining useful life prediction. Int. J. Hydrogen Energy 2021, 46, 2555–2564. [Google Scholar] [CrossRef]
- Ma, R.; Yang, T.; Breaz, E.; Li, Z.; Briois, P.; Gao, F. Data-driven proton exchange membrane fuel cell degradation predication through deep learning method. Appl. Energy 2018, 231, 102–115. [Google Scholar] [CrossRef]
- Zuo, J.; Lv, H.; Zhou, D.; Xue, Q.; Jin, L.; Zhou, W.; Yang, D.; Zhang, C. Deep learning based prognostic framework towards proton exchange membrane fuel cell for automotive application. Appl. Energy 2021, 281, 115937. [Google Scholar] [CrossRef]
- Khajeh-Hosseini-Dalasm, N.; Ahadian, S.; Fushinobu, K.; Okazaki, K.; Kawazoe, Y. Prediction and analysis of the cathode catalyst layer performance of proton exchange membrane fuel cells using artificial neural network and statistical methods. J. Power Sources 2011, 196, 3750–3756. [Google Scholar] [CrossRef]
- Huo, W.; Li, W.; Zhang, Z.; Sun, C.; Zhou, F.; Gong, G. Performance prediction of proton-exchange membrane fuel cell based on convolutional neural network and random forest feature selection. Energy Convers. Manag. 2021, 243, 114367. [Google Scholar] [CrossRef]
- Yan, F.; Li, W.; Yang, W.; He, Y. Prediction of fuel cell performance based on Bagging neural network ensemble model. Sci. Sin. Technol. 2019, 49, 391–401. [Google Scholar] [CrossRef]
- Lin-Kwong-Chon, C.; Damour, C.; Benne, M.; Kadjo, J.-J.A.; Grondin-Pérez, B. Adaptive neural control of PEMFC system based on data-driven and reinforcement learning approaches. Control Eng. Pract. 2022, 120, 105022. [Google Scholar] [CrossRef]
- Khadhraoui, A.; Selmi, T.; Cherif, A. Energy Management and Performance Evaluation of Fuel Cell Battery Based Electric Vehicle. Int. J. Comput. Sci. Net. 2022, 22, 37–44. [Google Scholar]
- Qi, X. Rotor resistance and excitation inductance estimation of an induction motor using deep-Q-learning algorithm. Eng. Appl. Artif. Intell. 2018, 72, 67–79. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous Control with Deep Reinforcement Learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Chen, P.; He, Z.; Chen, C.; Xu, J. Control Strategy of Speed Servo Systems Based on Deep Reinforcement Learning. Algorithms 2018, 11, 65. [Google Scholar] [CrossRef] [Green Version]
- Zhu, M.; Wang, X.; Wang, Y. Human-like autonomous car-following model with deep reinforcement learning. Transp. Res. Part C Emerg. Technol. 2018, 97, 348–368. [Google Scholar] [CrossRef] [Green Version]
- Tabe, Y.; Saito, M.; Fukui, K.; Chikahisa, T. Cold start characteristics and freezing mechanism dependence on start-up temperature in a polymer electrolyte membrane fuel cell. J. Power Sources 2012, 208, 366–373. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Li, W.; Xu, K.; Zahid, T.; Qin, F.; Li, C. Energy Management Strategy for a Hybrid Electric Vehicle Based on Deep Reinforcement Learning. Appl. Sci. 2018, 8, 187. [Google Scholar] [CrossRef] [Green Version]
- Xi, L.; Wu, J.; Xu, Y.; Sun, H. Automatic Generation Control Based on Multiple Neural Networks With Actor-Critic Strategy. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 2483–2493. [Google Scholar] [CrossRef]
- Peng, H.; Shen, X. Multi-Agent Reinforcement Learning Based Resource Management in MEC- and UAV-Assisted Vehicular Networks. IEEE J. Sel. Areas Commun. 2021, 39, 131–141. [Google Scholar] [CrossRef]
- Zhu, Y.; Zou, J.; Li, S.; Peng, C. An adaptive sliding mode observer based near-optimal OER tracking control approach for PEMFC under dynamic operation condition. Int. J. Hydrogen Energy 2022, 47, 1157–1171. [Google Scholar] [CrossRef]
- Chen, J.; Zhan, Y.D.; Guo, Y.G.; Zhu, J.G.; Li, L.; Liang, B. Fuzzy Adaptive PI Decoupling Control for Gas Supply System of Proton Exchange Membrane Fuel Cell. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Republic of Korea, 7–10 October 2018; pp. 1145–1150. [Google Scholar] [CrossRef]






| Parts | Parameters (mm) |
|---|---|
| Length of channel | 50 |
| Width of channel | 1.0 |
| Depth of channel | 1.0 |
| Width of ridge | 1.0 |
| Thickness of proton exchange membrane | 0.128 |
| Thickness of GDL | 0.2 |
| Thickness of CL | 0.01 |
| Description | Value | Symbol |
|---|---|---|
| Number of cells in fuel cell stack | ||
| Membrane thickness | ||
| Fuel cell active area | ||
| Compressor diameter | ||
| Compressor motor inertia | ||
| Anode volume | ||
| Cathode volume | ||
| Faraday constant | ||
| Atmospheric pressure | ||
| Air molar mass | ||
| Oxygen molar mass | ||
| Nitrogen molar mass | ||
| Universal gas constant | ||
| Air gas constant | ||
| Oxygen gas constant | ||
| Nitrogen gas constant | ||
| Hydrogen gas constant | ||
| Ratio of specific heat of air | ||
| Motor parameter | ||
| Motor constant |
| Parameter | Value |
|---|---|
| Critic learning rate | 0.002 |
| Actor learning rate | 0.002 |
| Discount factor | 0.9 |
| Probability of selecting samples in experience pool | 0.9 |
| Size of experience pool | 1,000,000 |
| Target action noise variance | 0.01 |
| Policy network update interval | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, L.; Zhang, T.; Gao, Y. Real-Time Control of Gas Supply System for a PEMFC Cold-Start Based on the MADDPG Algorithm. Energies 2023, 16, 4655. https://doi.org/10.3390/en16124655
Pan L, Zhang T, Gao Y. Real-Time Control of Gas Supply System for a PEMFC Cold-Start Based on the MADDPG Algorithm. Energies. 2023; 16(12):4655. https://doi.org/10.3390/en16124655
Chicago/Turabian StylePan, Lei, Tong Zhang, and Yuan Gao. 2023. "Real-Time Control of Gas Supply System for a PEMFC Cold-Start Based on the MADDPG Algorithm" Energies 16, no. 12: 4655. https://doi.org/10.3390/en16124655
APA StylePan, L., Zhang, T., & Gao, Y. (2023). Real-Time Control of Gas Supply System for a PEMFC Cold-Start Based on the MADDPG Algorithm. Energies, 16(12), 4655. https://doi.org/10.3390/en16124655








