Validation of the CFD Tools against In-House Experiments for Predicting Condensing Steam Flows in Nozzles
Abstract
1. Introduction
2. Experimental Facility
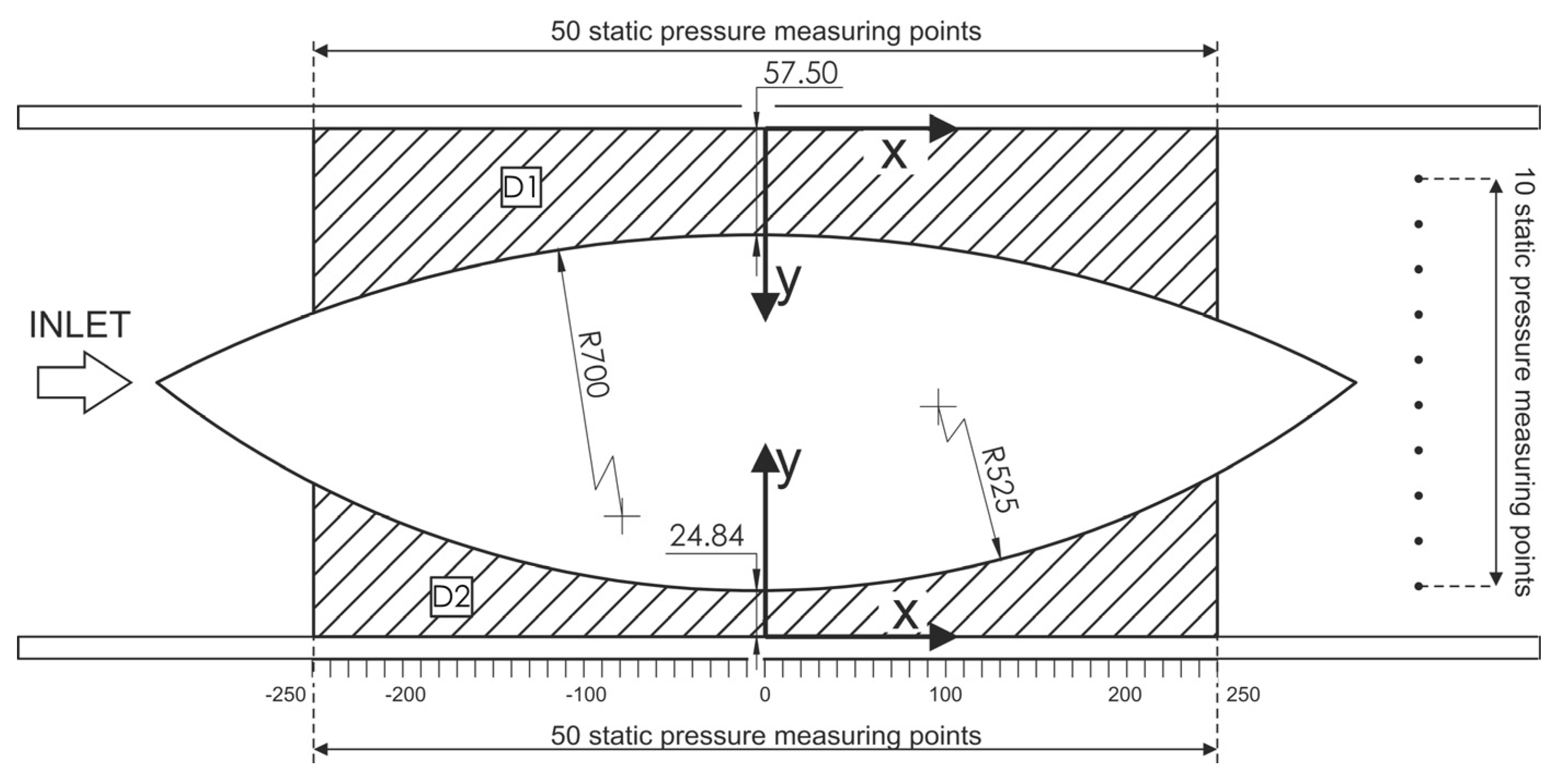
2.1. The Half Nozzles
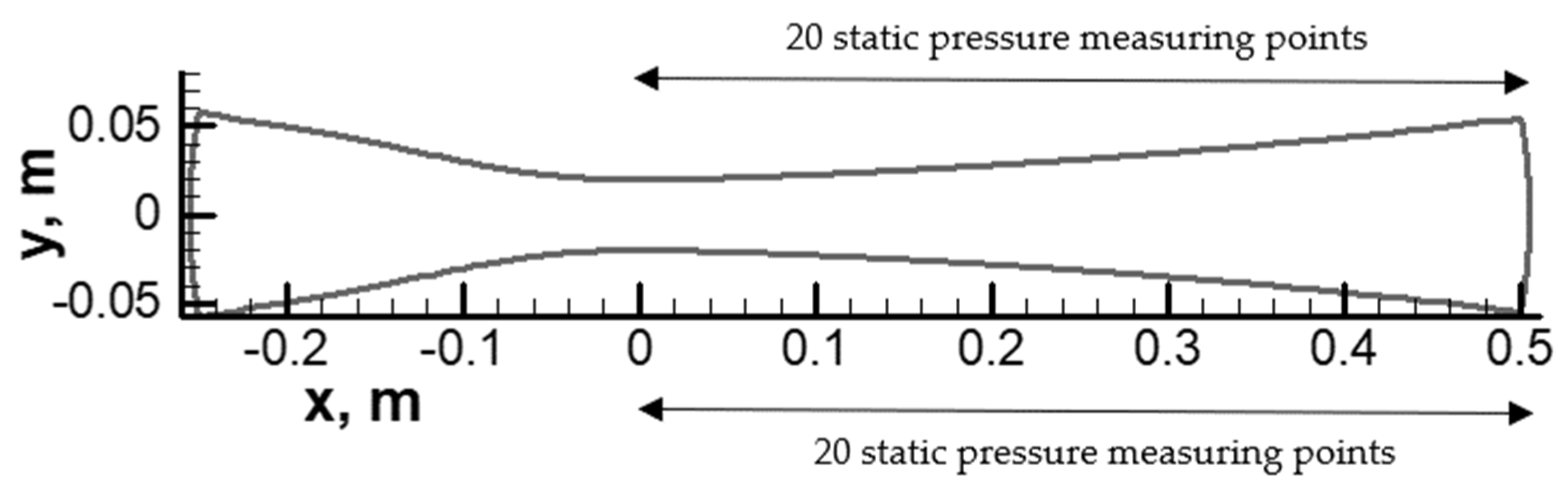
2.2. The IWSEP Nozzle
3. Numerical Model
3.1. Flow-Governing Equations
- The mass, momentum, and energy conservation equations (compressible Navier–Stokes equations) for the vapor–liquid mixture (RANS in Table 1) in the in-house code and for the vapor and liquid separately in ANSYS CFX;
- The turbulence model equations;
- The transport equations for the liquid phase arising due to homogeneous condensation (transport equations in Table 1);
- The equation of state (EOS in Table 1);
- The relations modeling the condensation process (condensation model in Table 1).
| Case 1—Implemented in In-House Code | Case 2—Implemented in ANSYS CFX | ||
|---|---|---|---|
| RANS | Mass conservation equations | ||
| Momentum conservation equations | |||
| Energy conservation equations | |||
| Transport equations | |||
| Equation of state (EOS) | Local real gas EOS: | IAPWS-IF97 The database implemented in CFX covers temperatures ranging from 273.15 to 1073.15 K and pressures ranging from 611 Pa to 100 MPa. | |
| Condensation model | Nucleation rate | ||
| Droplet growth rate | Gyarmathy model: | ||
3.2. Numerical Mesh and Boundary Conditions
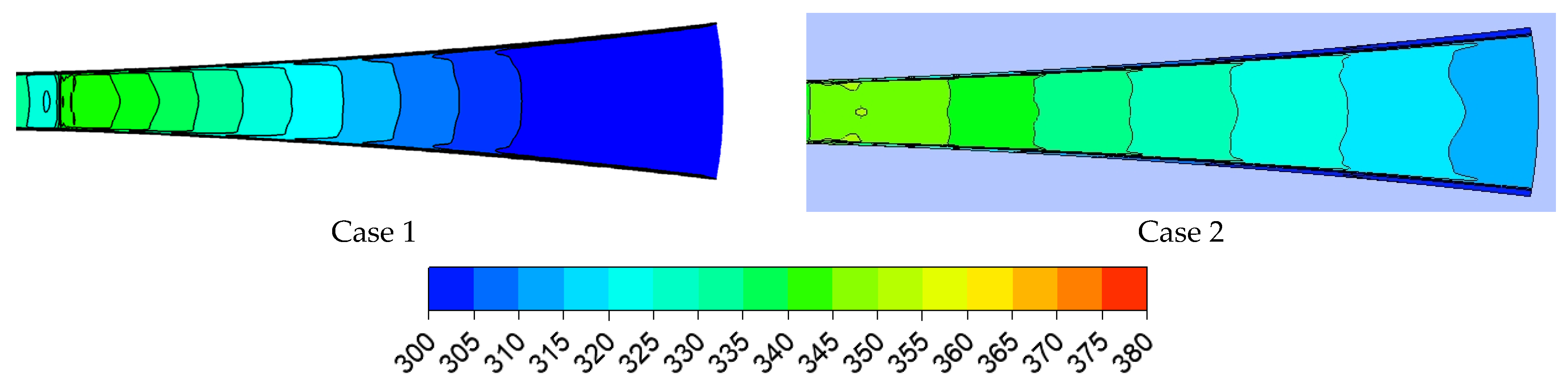
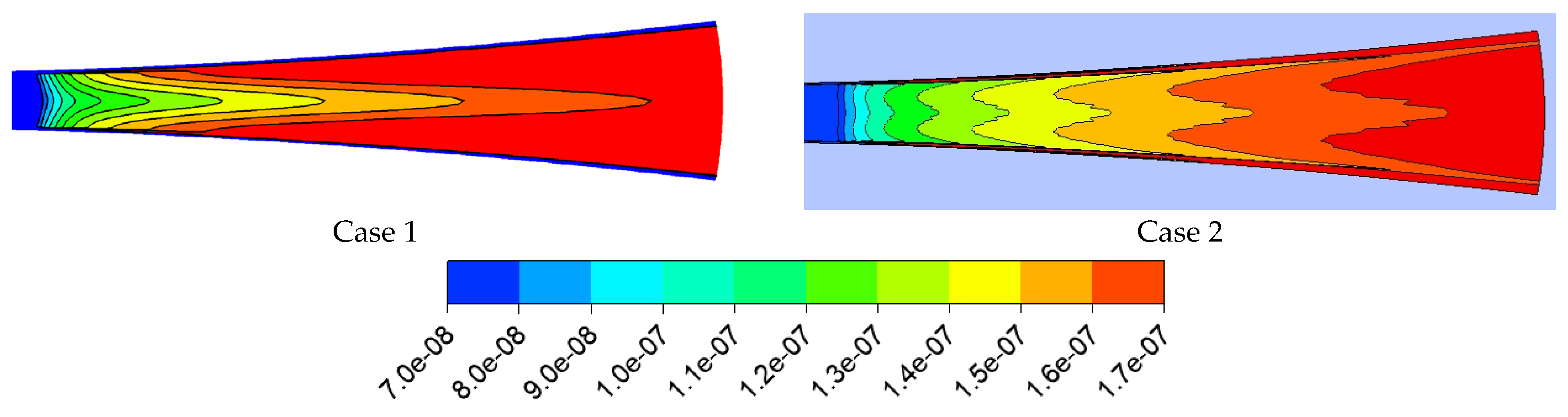
4. Results and Discussion
4.1. The Half Nozzles
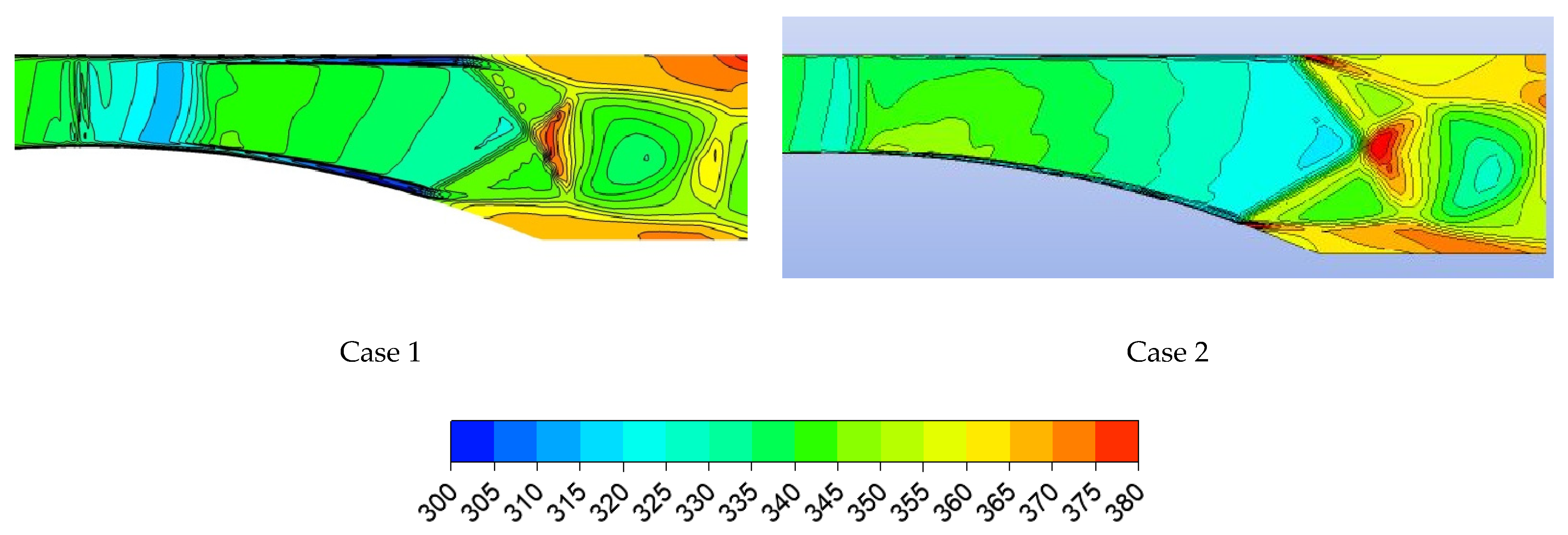
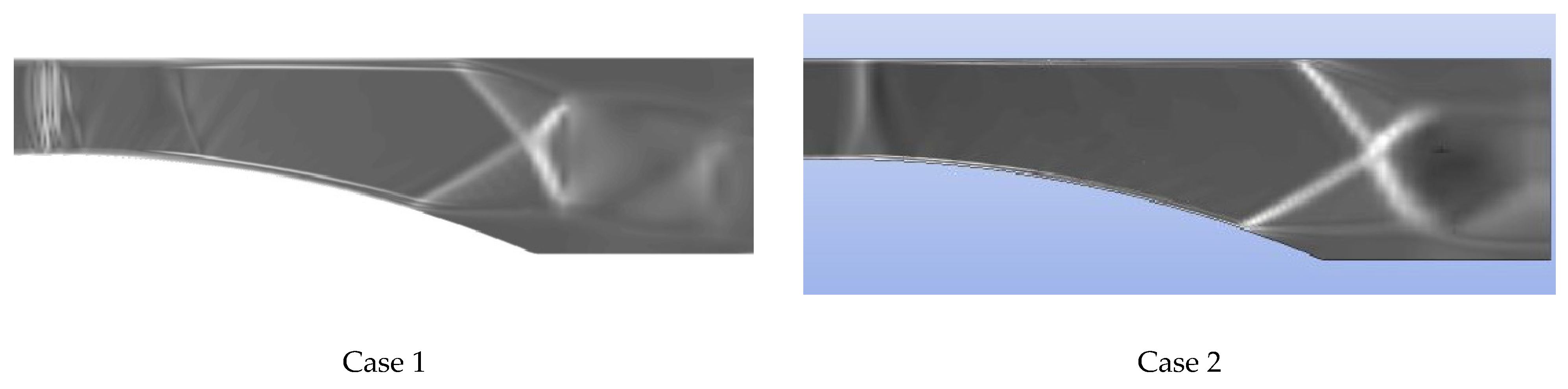
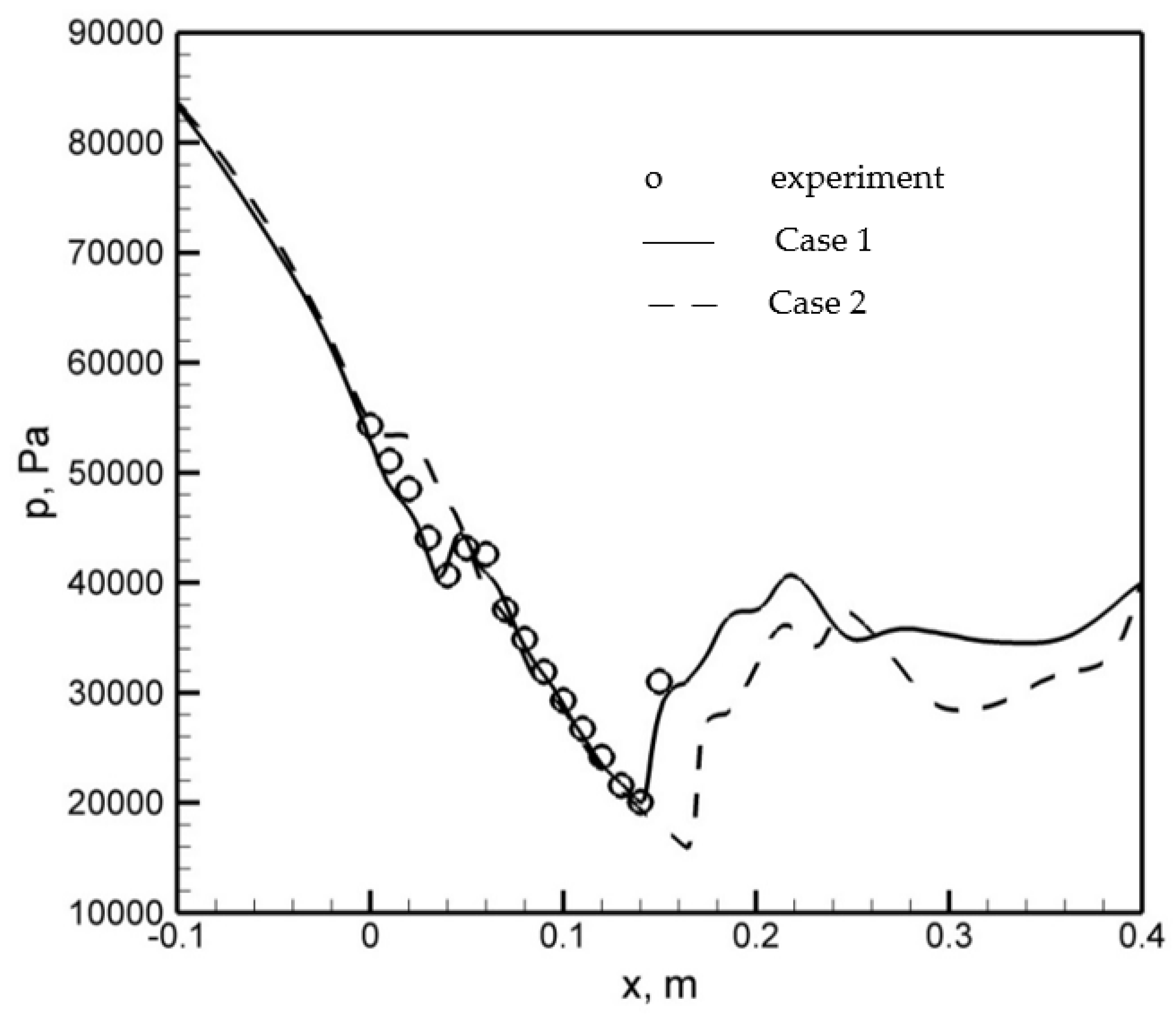
4.1.1. D1 Nozzle
4.1.2. D2 Nozzle
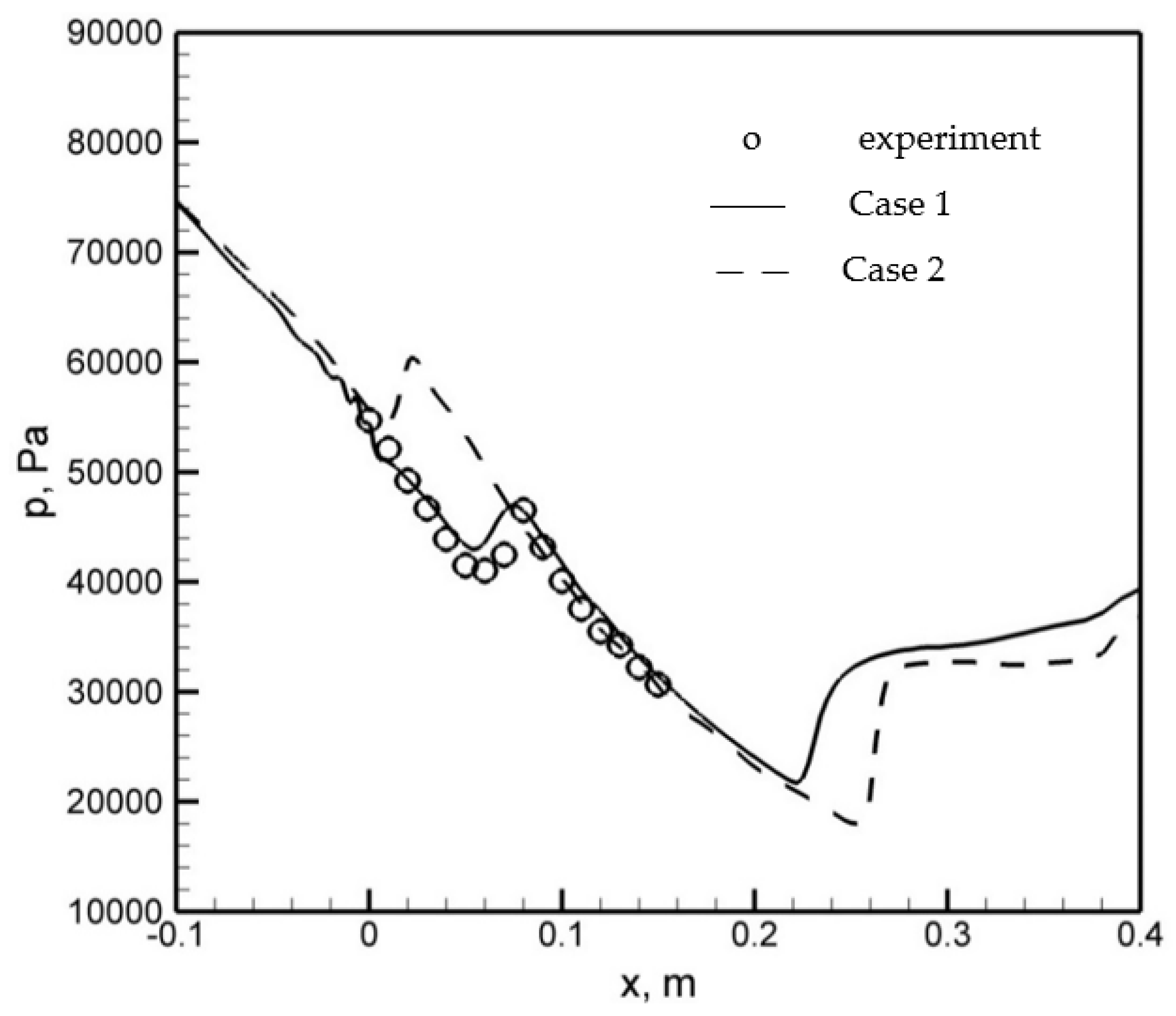
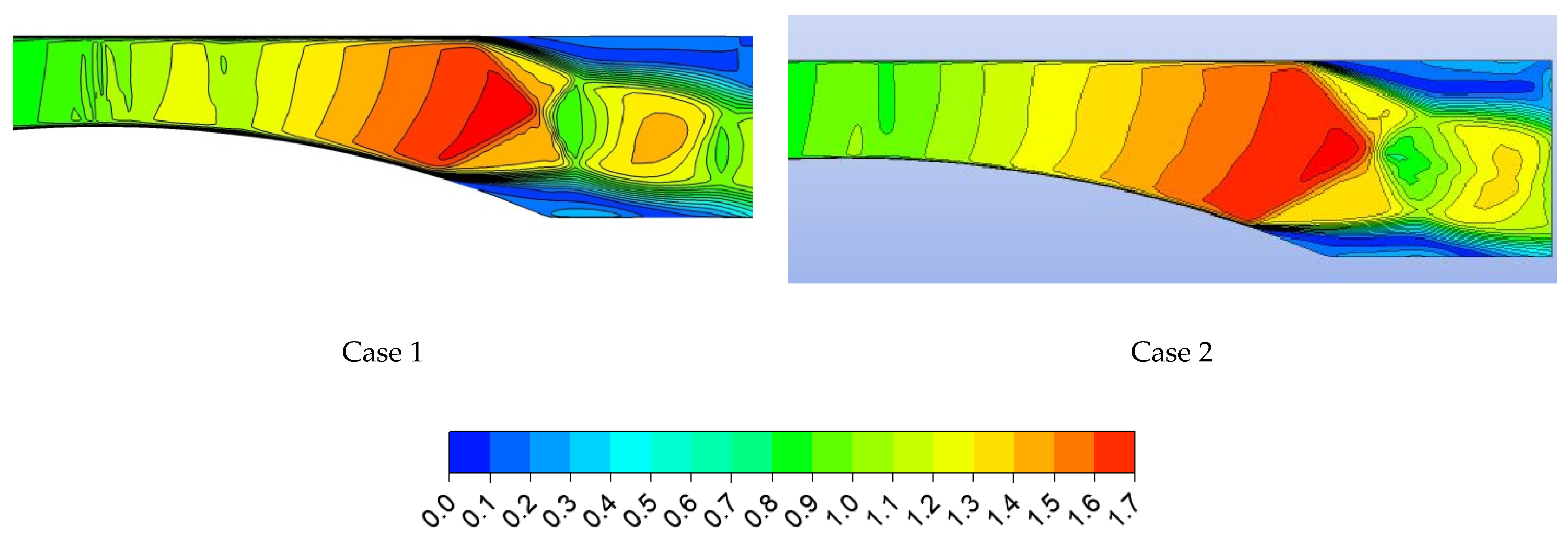
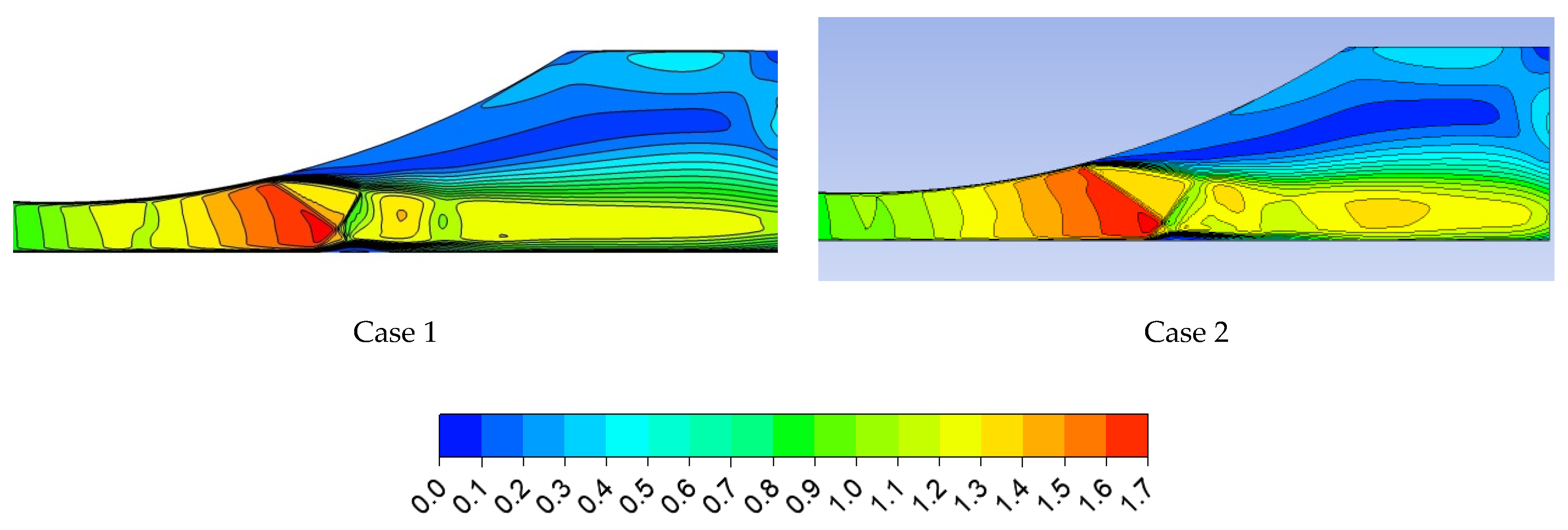
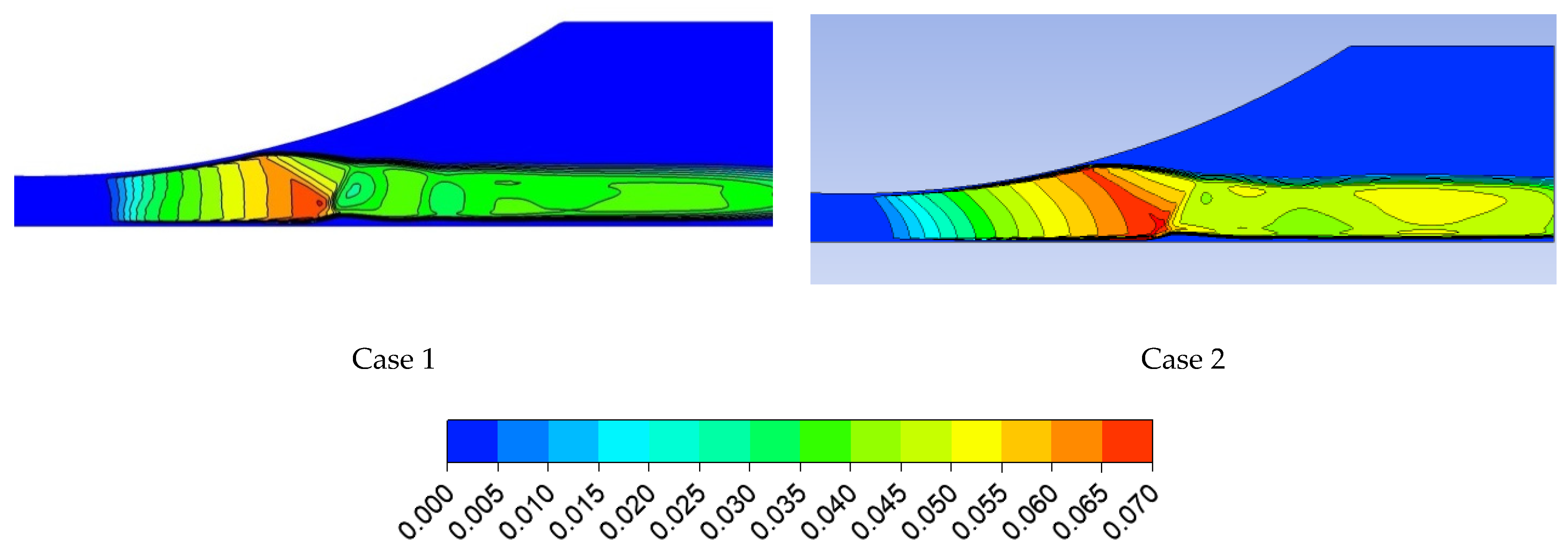
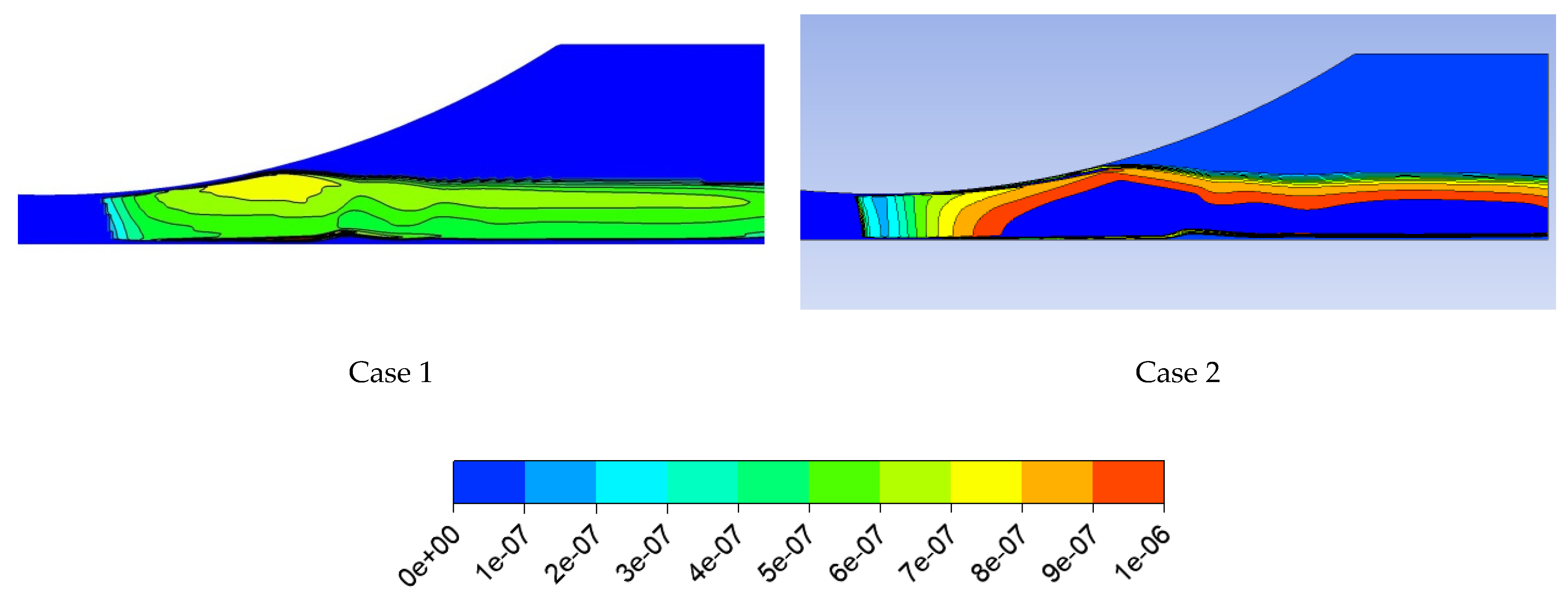
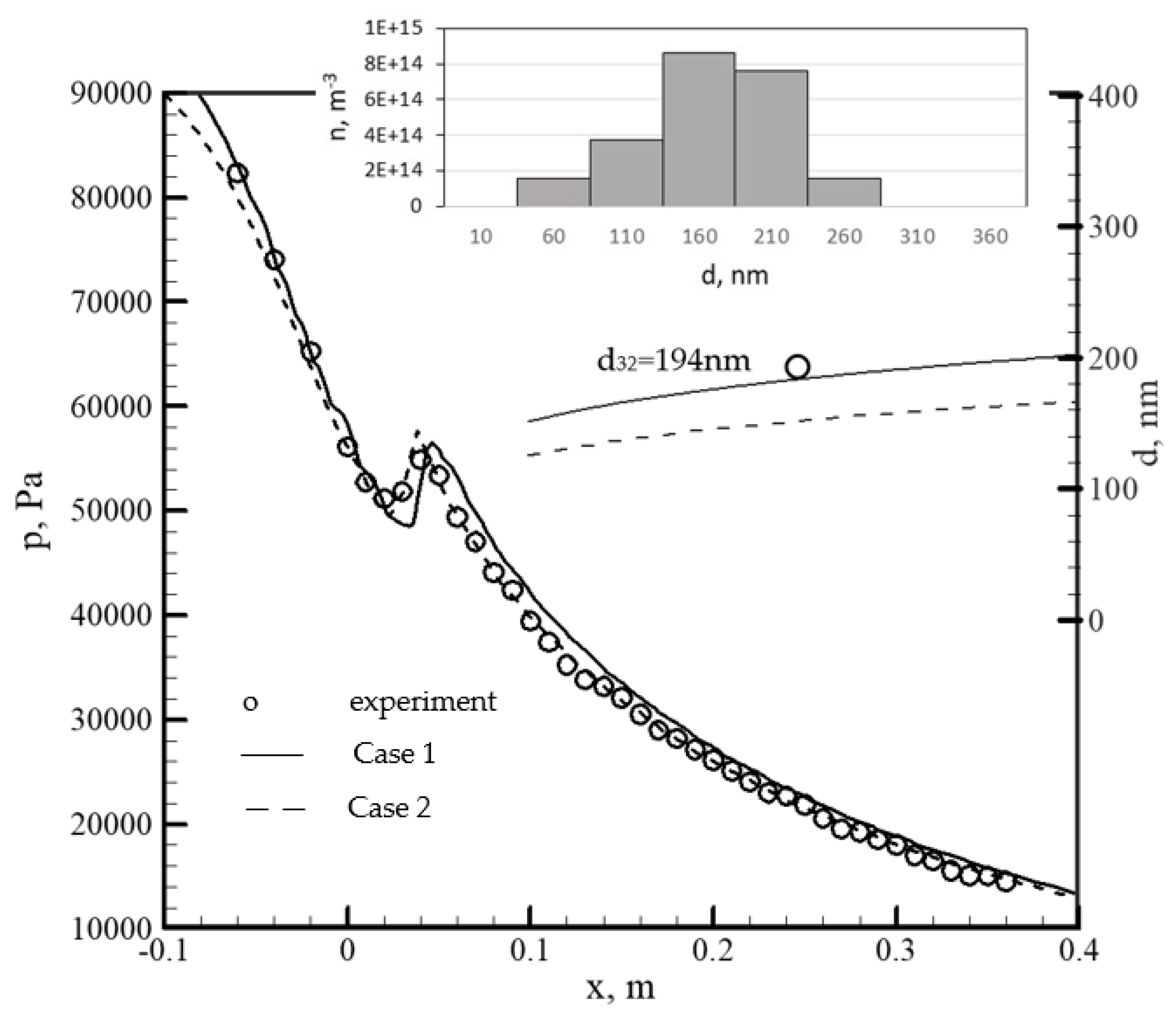
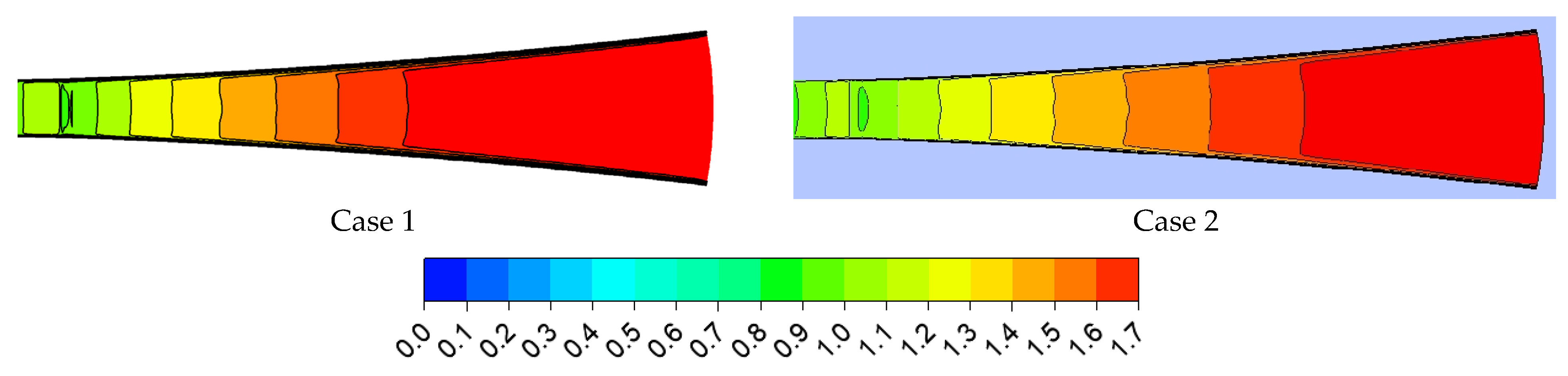
4.2. IWSEP Nozzle
5. Conclusions
- Some differences were observed between the two codes in the parameter distributions, especially in the areas of the flow field strong discontinuities; i.e., in the area of the occurrence of condensation waves. This was due to the different methods used in the two codes to calculate the steam thermodynamic properties below the saturation line.
- For the half nozzles, in ANSYS CFX commercial code, the condensation wave location occurred much earlier (just after the critical cross section of the nozzle), while the in-house CFD code had a good agreement with the experiments in this region.
- For the IWSEP nozzle, the results of the two codes for the static pressure distribution had a good agreement with the experiments. ANSYS CFX predicted the condensation wave location very well, but the in-house code predicted it a bit later than the ANSYS CFX results and experiments. However, the results of the in-house code for the mean droplet diameter were closer to the experimental data.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| d | Droplet diameter, m |
| E | Total internal energy, J kg−1 |
| H | Total enthalpy, J kg−1 |
| J | Nucleation rate, m−3s−1 |
| kB | Boltzmann constant, J K−1 |
| Kn | Knudsen number |
| L | Latent heat, J kg−1 |
| m | Molecular mass, kg |
| n | Number of droplets, m−3 |
| p | Pressure, pa |
| r | Droplet radius, m |
| r* | Critical droplet radius, m |
| R | Gas constant, J kg−1K−1 |
| T | Temperature, K |
| t | Time, s |
| u | Velocity vector, m s−1 |
| V | Volume of the phases, m3 |
| x | Axial coordinate, m |
| y | Liquid mass fraction |
| Greek symbols | |
| α | Liquid volume fraction |
| γ | Ratio of specific heat |
| δ | Kronecker delta |
| λ | Thermal conductivity, W m−1K−1 |
| μ | Dynamic viscosity, kg m−1s−1 |
| ρ | Density, kg m−3 |
| σ | Surface tension, N m−1 |
| τ | Stress tensor, Pa |
| Subscripts | |
| l | Liquid |
| m | Mixture |
| s | Saturation |
| v | Vapor |
References
- Vijayan, V.; Vivekanandan, M.; Venkatesh, R.; Rajaguru, K.; Godwin, A. CFD modeling and analysis of a two-phase vapor separator. J. Therm. Anal. Calorim. 2021, 145, 2719–2726. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, G.; Jin, R.; Zhang, Y.; Dong, K.; Cheng, T.; Wang, B. Water vapor distribution and particle condensation growth in turbulent pipe flow. Powder Technol. 2022, 403, 117401. [Google Scholar] [CrossRef]
- Pakhomov, M.A.; Lobanov, P.D. Gas-Liquid Two-Phase Flow in a Pipe or Channel. Water 2021, 13, 3382. [Google Scholar] [CrossRef]
- Liu, H.; Wen, C.; Yuen, A.C.Y.; Han, Y.; Cheung, S.C.-P.; Kook, S.; Yeoh, G.H. A novel thermal management system for battery packs in hybrid electrical vehicles utilising waste heat recovery. Int. J. Heat Mass Transf. 2022, 195, 123199. [Google Scholar] [CrossRef]
- Young, J.B. The spontaneous condensation of steam in supersonic nozzles. Phys. Chem. Hydrodyn. 1982, 3, 57–82. [Google Scholar]
- Babenko, V.A.; Habibulin, V.S. Formation of water droplets in steam turbines. Heat Transf. Res. 2016, 47, 485–497. [Google Scholar]
- Chen, C.-K.; Yang, S.-A. Laminar film condensation inside a horizontal elliptical tube with variable wall temperature. Int. J. Heat Fluid Flow 1994, 15, 75–78. [Google Scholar] [CrossRef]
- Li, Z.; Yang, W.; Chen, X. Experimental study on the mechanism of water droplets formation in steam turbines. J. Energy Resour. Technol. 2016, 138. [Google Scholar] [CrossRef]
- Sumer, B.M.; Bayraktar, H. Droplet formation in steam turbine flow channels. ASME J. Fluids Eng. 2003, 125, 467–474. [Google Scholar]
- Denton, J.D. Loss Mechanisms in Turbomachines. In Proceedings of the ASME 1993 International Gas Turbine and Aeroengine Congress and Exposition, Cincinnati, OH, USA, 24–27 May 1993. [Google Scholar] [CrossRef]
- Srinivasan, N.R.; Suresh, S.; Kumar, T.D. Steam Turbine Condensation Effects on Power Plant Performance. Int. J. Appl. Eng. Res. 2014, 9, 20557–20572. [Google Scholar]
- Gupta, A.K.; Bhatnagar, A.K. Condensation Phenomenon and Its Effect on the Performance of Steam Turbines. Int. J. Therm. Sci. 2009, 48, 213–222. [Google Scholar]
- Starzmann, J.; Hughes, F.R.; Schuster, S.; White, A.J.; Halama, J.; Hric, V.; Kolovratník, M.; Lee, H.; Sova, L.; Št’astný, M.; et al. Results of the International Wet Steam Modeling Project. Proc. Inst. Mech. Eng. Part A J. Power Energy 2018, 232, 550–570. [Google Scholar] [CrossRef]
- Halama, J.; Benkhaldoun, F.; Fořt, J. Numerical modeling of two-phase transonic flow. Math. Comput. Simul. 2010, 80, 1624–1635. [Google Scholar] [CrossRef]
- Halama, J.; Benkhaldoun, F.; Fořt, J. Flux schemes based finite volume method for internal transonic flow with condensation. Int. J. Numer. Methods Fluids 2011, 65, 953–968. [Google Scholar] [CrossRef]
- Zhang, G.; Dykas, S.; Majkut, M.; Smołka, K.; Cai, X. Experimental and numerical research on the effect of the inlet steam superheat degree on the spontaneous condensation in the IWSEP nozzle. Int. J. Heat Mass Transf. 2021, 165, 120654. [Google Scholar] [CrossRef]
- Grübel, M.; Starzmann, J.; Schatz, M.; Eberle, T.; Vogt, D.M.; Sieverding, F. Two-Phase Flow Modeling and Measurements in Low-Pressure Turbines—Part I: Numerical Validation of Wet Steam Models and Turbine Modeling. J. Eng. Gas Turbines Power 2015, 137, 042602. [Google Scholar] [CrossRef]
- Ihm, S.-W.; Kim, C. Computations of Homogeneous-Equilibrium Two-Phase Flows with Accurate and Efficient Shock-Stable Schemes. AIAA J. 2008, 46, 3012–3037. [Google Scholar] [CrossRef]
- Li, L.; Feng, Z.; Li, G. Study on Effects of Spontaneous Condensation on Performance of Low Pressure Stages in a Steam Turbine. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; pp. 1545–1553. [Google Scholar] [CrossRef]
- Yamamoto, S. Computation of practical flow problems with release of latent heat. Energy 2005, 30, 197–208. [Google Scholar] [CrossRef]
- Wu, X.; Li, L.; Li, G.; Feng, Z. Numerical investigation of the effect of inlet condition on self-excited oscillation of wet steam flow a supersonic turbine cascade. Int. J. Numer. Methods Fluids 2009, 60, 1334–1350. [Google Scholar]
- Dykas, S.; Majkut, M.; Smołka, K.; Strozik, M. An attempt to make a reliable assessment of the wet steam flow field in the de Laval nozzle. Heat Mass Transf. 2018, 54, 2675–2681. [Google Scholar] [CrossRef]
- Dykas, S.; Majkut, M.; Smolka, K.; Strozik, M. Experimental Research on Wet Steam Flow With Shock Wave. Exp. Heat Transf. 2014, 28, 417–429. [Google Scholar] [CrossRef]
- Dykas, S.; Majkut, M.; Strozik, M.; Smołka, K. Experimental study of condensing steam flow in nozzles and linear blade cascade. Int. J. Heat Mass Transf. 2015, 80, 50–57. [Google Scholar] [CrossRef]
- Majkut, M.; Dykas, S.; Smołka, K.; Strozik, M. Identification of the liquid mass fraction content in the wet steam. E3S Web Conf. 2019, 137, 01003. [Google Scholar] [CrossRef]
- ANSYS CFX-Solver Theory Guide, release 15 November 2013.
- Shabani, S.; Majkut, M.; Dykas, S.; Wiśniewski, P.; Smołka, K.; Cai, X.; Zhang, G. Numerical Analysis of the Condensing Steam Flow by Means of ANSYS Fluent and in-House Academic Codes with Respect to the Capacity for Thermodynamic Assessment. Front. Energy Res. 2022, 10, 2629. [Google Scholar] [CrossRef]
- Bakhtar, F.; Young, J.B.; White, A.; Simpson, D.A. Classical Nucleation Theory and Its Application to Condensing Steam Flow Calculations. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2005, 219, 1315–1333. [Google Scholar] [CrossRef]
- Kantrowitz, A. Nucleation in very rapid vapor expansions. J. Chem. Phys. 1951, 19, 1097–1100. [Google Scholar] [CrossRef]
- Gyarmathy, G. Grundlagen einer Theorie der Nassdampfturbine. Ph.D. Thesis, Eidgenössische Technische Hochschule Zürich, Zürich, Switzerland, 1962. [Google Scholar] [CrossRef]












| Case 1—Implemented in In-House Code | Case 2—Implemented in ANSYS CFX | |
|---|---|---|
| RANS | is an upwinded total enthalpy; its value either for the continuous or dispersed phase depends on the direction of the interphase mass transfer. is the heat transfer between the liquid and vapor phase: , where is the empirical constant. | |
| Transport equations | ------------ | |
| EOS | . Coefficients a0..2 and b0..2 of polynomials A(T) and B(T) depend on temperature only and can be found by extrapolating steam properties (given in the IAPWS-IF97) from the superheated region into the supercooled one. | ------------ |
| Nucleation rate | is the condensation coefficient, which is equal to 1. is empirical correction factor, which is equal to 1. This coefficient strongly depends on the pressure at the starting point of spontaneous nucleation. is non-isothermal Kantrowitz correction factor: | |
| Droplet growth rate | is the Knudsen number as follows, where is the mean free path of steam molecules. | |
| Case 1—Implemented in In-House Code | Case 2—Implemented in ANSYS CFX | |
|---|---|---|
| Calculations | In series | Parallel |
| Solver | Density-based | Pressure-based |
| Integration with respect to time | Second-order Runge–Kutta explicit method | Second-order Euler backward implicit scheme |
| Space discretization | Finite volume method (FVM) | Finite volume method (FVM) |
| Control volume central to a node—cell-centered method | Balance of fluxes in the node—cell vortices scheme | |
| Upwind scheme with the third-order Riemann-MUSCL exact solution | Second-order high-resolution scheme |
| Half Nozzles | IWSEP Nozzle | |
|---|---|---|
| Nozzle inlet | P0 = 98 kPa T0 = 105 °C Turbulent intensity = 5% | P0 = 105.8 kPa T0 = 111.2 °C Turbulent intensity = 5% |
| Nozzle walls | Adiabatic, smooth, and no-slip | Adiabatic, smooth, and no-slip |
| Nozzle outlet | Pout = 40 kPa | Supersonic |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shabani, S.; Majkut, M.; Dykas, S.; Smołka, K.; Lakzian, E.; Zhang, G. Validation of the CFD Tools against In-House Experiments for Predicting Condensing Steam Flows in Nozzles. Energies 2023, 16, 4690. https://doi.org/10.3390/en16124690
Shabani S, Majkut M, Dykas S, Smołka K, Lakzian E, Zhang G. Validation of the CFD Tools against In-House Experiments for Predicting Condensing Steam Flows in Nozzles. Energies. 2023; 16(12):4690. https://doi.org/10.3390/en16124690
Chicago/Turabian StyleShabani, Sima, Mirosław Majkut, Sławomir Dykas, Krystian Smołka, Esmail Lakzian, and Guojie Zhang. 2023. "Validation of the CFD Tools against In-House Experiments for Predicting Condensing Steam Flows in Nozzles" Energies 16, no. 12: 4690. https://doi.org/10.3390/en16124690
APA StyleShabani, S., Majkut, M., Dykas, S., Smołka, K., Lakzian, E., & Zhang, G. (2023). Validation of the CFD Tools against In-House Experiments for Predicting Condensing Steam Flows in Nozzles. Energies, 16(12), 4690. https://doi.org/10.3390/en16124690








