The Effect of Collector Azimuth on Inter-Row Shading in Photovoltaic Fields—A Comprehensive Point of View

Abstract

Rooftop buildings, mountain terrains, rivers, and lake beds may be oriented at different azimuths other than due south (in the northern hemisphere), on which photovoltaic (PV) systems may be installed. The present study presents a comprehensive point of view on the relation between the inter-row spacing and the inter-row shading in multiple-row collectors of PV fields; it analytically formulates the inter-row spacing and the associated shading losses for collectors deployed at any azimuth on horizontal, sloped-planed, and oriented toward the south and north, and is supported by the numerical results. Several criteria for the inter-row spacing are applied in the study; among them is a newly introduced criterion appropriate for the collectors deployed at a given azimuth. This study indicates that shorter spacing results in increased shading; minimum shading is obtained for collectors oriented toward the equator; inter-row spacing for maintenance purposes is used in limited dimensions of the PV fields and, usually, in optimal PV system designs; less shading occurs for systems deployed on sloped planes oriented toward the south; less shading is obtained for collectors based on the new criterion, where collectors are deployed at azimuth equal to the solar azimuth, and larger spacing is required for collectors deployed on northern slopes.

1. Introduction

The inter-row spacing in multiple-row deployments of the PV collectors affects the shading losses and, hence, affects the performance and economics of the photovoltaic (PV) systems. The inter-row shading reduces the generated electric energy of the system, and the means to mitigate the shading losses is an objective for PV system designs. Increasing the spacing results in a reduction in these losses, however, at the expense of the available land area. The inter-row spacing depends on the dimension of the available PV plant land, limited or unlimited. For limited land (e.g., rooftops), the PV collector rows are usually dense-deployed, with smaller inter-row spacing, as the objective of the PV system design is to meet some desired electric output power as an example, thus settling for a larger percentage of shading losses. Dense deployment of the collector rows may also result from using constraint optimization methods for limited land, depending on the objective of the system design, whether energetic or economic [1,2,3,4,5]. The optimization process results, among others, in optimal inter-row spacing and optimal inclination of the collectors. The common approaches to determine the inter-row spacing are as follows: minimum required distance for maintenance purposes of the PV system and no shading on collectors on the winter solstice at solar noon or at different times. A few references mention the inter-row spacing in the topic of the articles [6,7], although shading in PV fields is dealt with in many very early studies [8,9,10,11]. Analytical expressions were developed in [12] for the spacing between PV rows on horizontal and sloping grounds. Minimum spacing between the rows to avoid shadings is presented in [13]. A vector analysis method for the row spacing in PV systems on horizontal and non-horizontal planes is presented in [14]. Most studies on inter-row spacing and shading of PV systems deal with the deployment of the PV collectors on horizontal and inclined planes, including flat rooftops, that are oriented toward the equator. The effect of the collector azimuth on the energy yield was analyzed on monitored installed systems [15]. Mountain terrains, riverbeds, rooftop buildings, lakes, and ponds may have slopes oriented at any azimuth on which a PV system may be installed. An analytical approach to investigate the effect of the collector azimuth on the inter-row spacing and on the inter-row shading in photovoltaic fields was not investigated thoroughly in the previous studies. The present study investigates the effect of the azimuth angle on the inter-row spacing and shading for four criteria: maintenance spacing, spacing for no shading on solstice day, spacing for optimal deployment of a PV system, and spacing for newly introduced criteria—no shading on collectors at collector azimuth equal to solar azimuth. The new criteria may result in a reduction in shading losses. The effect of collector azimuth on inter-row spacing and shading in photovoltaic fields deployed on horizontal and inclined planes oriented toward the south and the north are investigated.

2. Methods and Materials

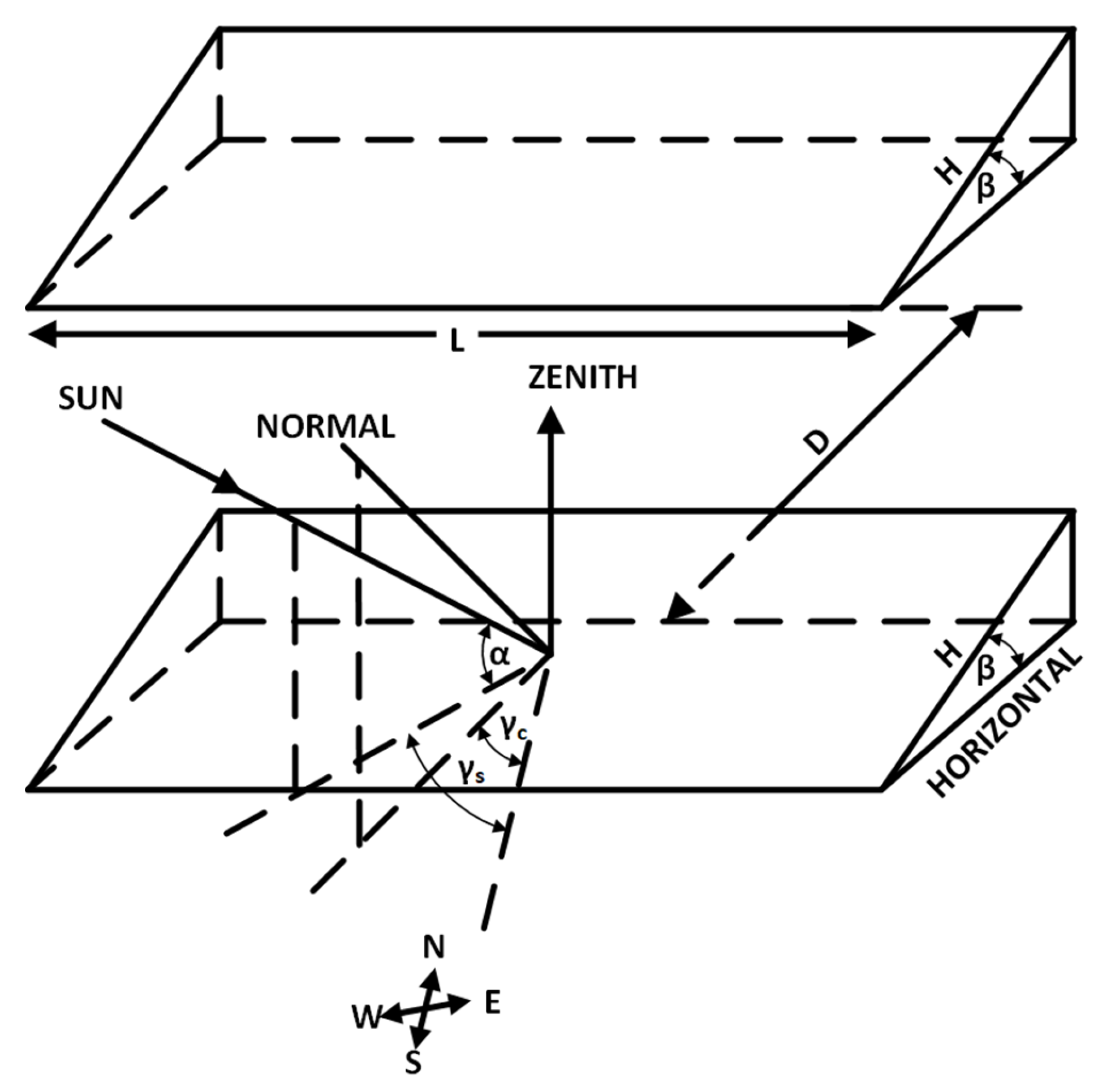
The angles involved in solar calculations of multiple collector rows of PV systems are indicated in Figure 1, where $\beta$ is the collector inclination angle with respect to horizontal; ${\gamma }_c,{\gamma }_s$ are the collector and sun azimuth angles with respect to south, and $\alpha$ is the sun altitude angle. The calculations of the shadow height $H_s$ and length $L_s$ on the second and on the subsequent collector rows, deployed on a horizontal plane and oriented at any azimuth angle ${\gamma }_c$, are based on [16], respectively:

$$H_s=H(1-\frac{D+H\cos \beta }{H\cos \beta +H\sin \beta \cos ({\gamma }_s-{\gamma }_c)/\tan \alpha })$$

(1)

$$L_s=L-(D+H\cos \beta )\frac{\sin \beta \left|\sin ({\gamma }_s-{\gamma }_c)\right|/\tan \alpha }{\cos \beta +\sin \beta \cos ({\gamma }_s-{\gamma }_c)/\tan \alpha }$$

(2)

where $H$ and $L$ are the collector width and length, respectively, and $D$ is the inter-row spacing.

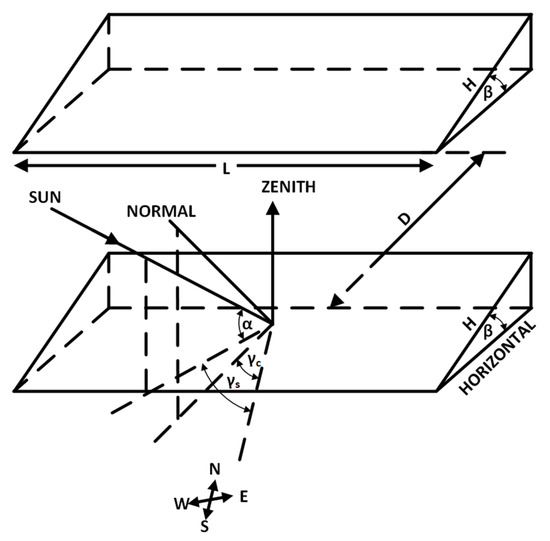
Figure 1. Angles involved in solar calculations.

Four spacing criteria are applied to estimate the inter-row spacing and shading: spacing for maintenance purposes; spacing for “no shading” on winter solstice day at solar noon; spacing based on optimal deployment of PV systems in a solar field; and spacing based on new criteria for “no shading” for ${\gamma }_s={\gamma }_c$. The shadow height depends on the parameters $H,D,\beta ,{\gamma }_c,{\gamma }_s,\alpha$. No shading on collectors; $H_s=0$ (see Equation (1)) occurs for collectors oriented toward the equator $({\gamma }_c=0^{°})$ at solar noon (${\gamma }_s=0$). Equation (1) then reduces to

$$D=H\frac{\sin \beta }{{\tan \alpha }_{{\gamma }_s=0}}$$

(3)

The sun altitude angle $\alpha$ is related to the collector site latitude $\varphi$, to the solar declination angle $\delta$, and to the solar time angle $\omega$ by [9]:

$$\sin \alpha =\sin \varphi \sin \delta +\cos \varphi \cos \delta \cos \omega$$

(4)

In winter solstice at solar noon, $\delta ={\delta }_0=-{23.45}^{°}$, and $\omega =0$; Equation (4) becomes

$$\sin \alpha =\sin \varphi \sin {\delta }_0+\cos \varphi \cos {\delta }_0=\cos (\varphi -{\delta }_0)$$

(5)

By substituting Equation (5) into Equation (3) the inter-row spacing is obtained.

$$D=\frac{H\sin \beta }{\tan [{\sin }^{-1}(\cos (\varphi -{\delta }_0))]}$$

(6)

The percentage of the annual shading losses of the PV system is defined by the difference between the direct beam radiation of the first and the second collector rows, relative to the global radiation on the first collector row:

$$shading losses [\%]=100\frac{first row beam radiation\left(\frac{kWh/m^2}{year}\right)-\sec ond row beam radiation\left(\frac{kWh/m^2}{year}\right)}{first row global radiation\left(\frac{kWh/m^2}{year}\right)}$$

(7)

The shading losses in this study are based on hourly solar radiation data (direct beam and diffuse radiation, Israel, Meteorological Service–IMS) for Tel Aviv; latitude $\varphi ={32}^{°}{6}^{\prime }\mathrm{N}$; longitude ${34}^{°}{51}^{\prime }\mathrm{E}$. Four criteria are examined for the effect of the azimuth angle on the inter-row spacing and shading: maintenance spacing; spacing for no shading on solstice day; spacing for optimal deployment of a PV system; and spacing for no shading on collectors at collector azimuth equal to solar azimuth. This study deals with collectors deployed on horizontal and sloped planes.

To indicate the effect of the azimuth angle on the inter-row spacing and shading in a totally different geographical location, this study investigated the deployment of collectors at Lindenberg, Germany; latitude $\varphi ={52}^{°}{12}^{\prime }$ N; longitude ${14}^{°}{7}^{\prime }$ E, based on solar radiation data from Meteorologisches Observatorium Lindenberg, Richard Aßmann Observatorium, PANGAEA, Monitoring station no.12, https://dataportals.pangaea.de/bsrn/?q=LR1300 (accessed on 1 January 2019); ten minutes of solar radiation data, the year 2006. The assumed lower limit for the inter-row spacing, in this study, is dictated by the maintenance requirement of $D=0.8$ m. The assumed range for the collector azimuth angles ${\gamma }_c$ is from $0^{°}$ to ${85}^{°}$, relative to the south for latitude $\varphi ={32}^{°}{6}^{\prime }$ N and from $0^{°}$ to ${70}^{°}$ for latitude $\varphi ={52}^{°}{12}^{\prime }$ N. For comparison, the assumed collector inclination angle for both latitudes is $\beta ={20}^{°}$. The value of the upper limit of the inter-row spacing $D$ depends on the differently applied criteria for the inter-row spacing.

2.1. Collectors Deployed on Horizontal Planes

This section deals with the inter-row spacing and shading of the PV collectors deployed on horizontal planes for different criteria for the inter-row pacing at different collector azimuth angles.

2.1.1. Maintenance Criteria for Inter-Row Spacing

The maintenance inter-row spacing approach is used in limited areas, for example, on rooftops. The PV collector rows are densely deployed, with smaller inter-row spacing to meet some desired electric output power of the available land area, thus settling for a larger percent of shading losses. It is assumed a maintenance spacing of $D=0.8$ m.

2.1.2. No-Shading Criteria for Inter-Row Spacing on Winter Solstice at Solar Noon

The spacing $D$ is determined by Equation (6). The shadow height and length are given in Equations (1) and (2), respectively. The inter-row spacing is $D=1.05$ m for $H=2.12$ m, $\beta ={20}^{°}$; the declination angle at solar noon is ${\delta }_0=-{23.45}^{°}$ at latitude $\varphi ={32}^{°}{6}^{\prime }$ N.

2.1.3. ${\gamma }_s={\gamma }_c$ Criterion for Inter-Row Spacing on day December 21

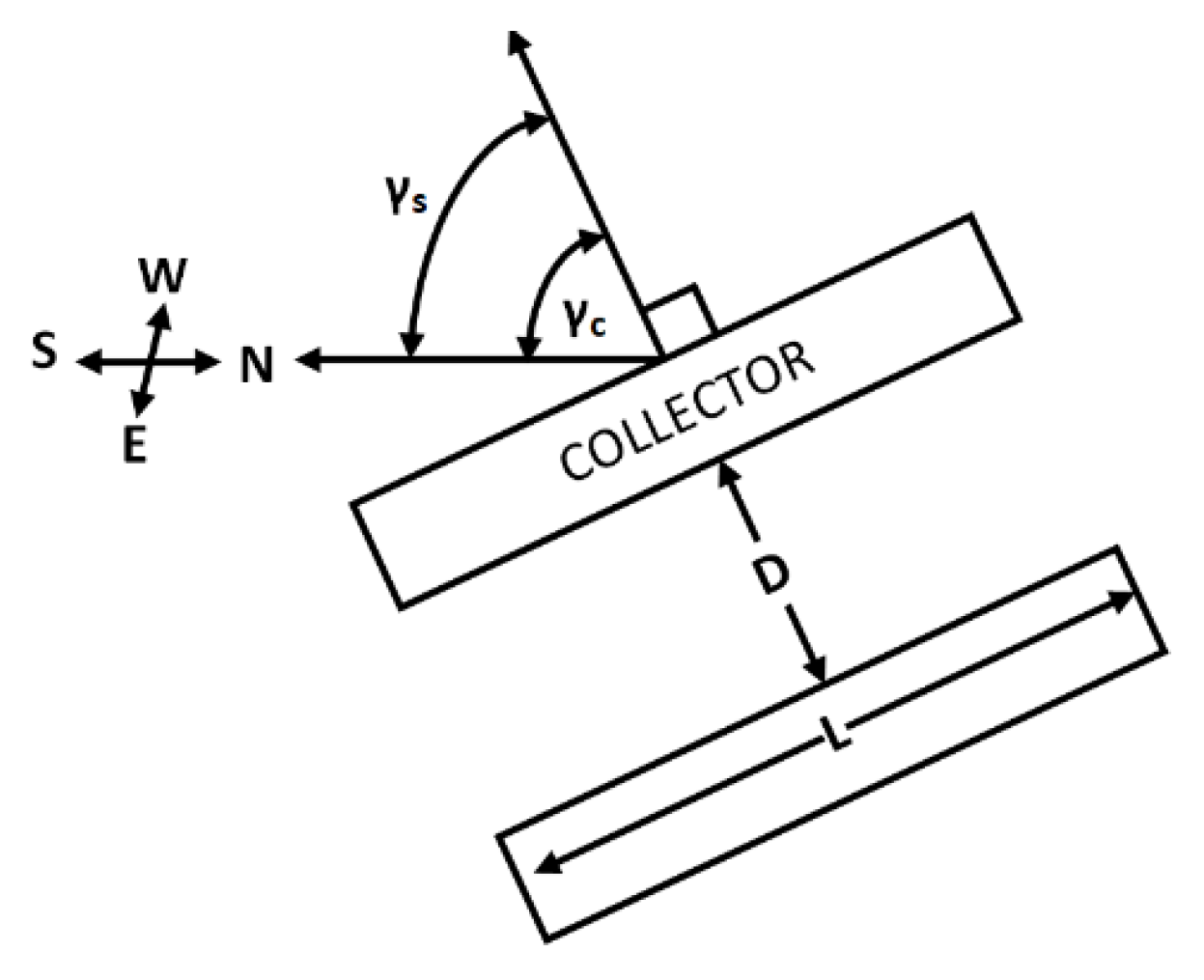
Collectors oriented toward the southwest at angle ${\gamma }_c$, with respect to the south, are shown in Figure 2, where the direction of ${\gamma }_c$ is normal to the collector. The criteria for which the inter-row spacing is defined is when ${\gamma }_s={\gamma }_c$. The sun azimuth angle ${\gamma }_s$ is related to the sun declination angle $\delta$, to the sun hour angle $\omega$, and to the sun altitude angle $\alpha$ by [1]).

$$\sin {\gamma }_s=\frac{\sin \delta \sin \omega }{\cos \alpha }$$

(8)

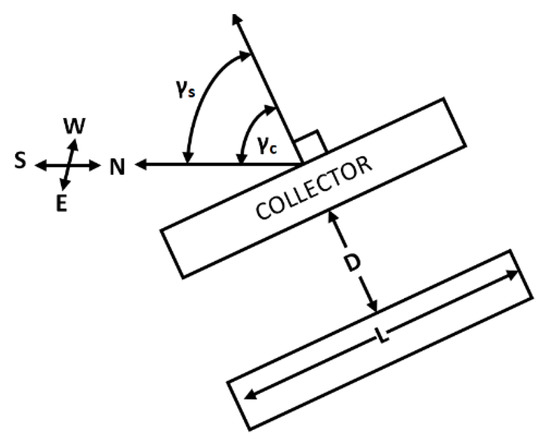
Figure 2. Collectors oriented southwest.

The inter-row spacing $D$ for “no shading” (shadow height $H_s=0$, Equation (1)), therefore, becomes

$$1=\frac{D+H\cos \beta }{H\cos \beta +H\sin \beta /\tan \alpha }$$

(9)

and for ${\gamma }_s={\gamma }_c$, Equation (8) becomes

$$\sin {\gamma }_c=\frac{\sin \delta \sin \omega }{\cos \alpha }$$

(10)

The sun altitude angle $\alpha$ is related to the collector latitude $\varphi$ and to the angles $\delta ,\omega$ by (see Equation (4))

$$\sin \alpha =\sin \varphi \sin \delta +\cos \varphi \cos \delta \cos \omega$$

(11)

and by using Equations (10) and (11) for winter solstice day, ${\delta }_0$, thus obtaining

$${[1-{\cos }^2\alpha ]}^{1/2}=\sin \varphi \sin {\delta }_0+\cos \varphi \cos {\delta }_0{\left[1-\frac{{\sin }^2{\gamma }_c{\cos }^2\alpha }{{\cos }^2{\delta }_0}\right]}^{1/2}$$

(12)

The solution for $\alpha$ is obtained by using the algorithm [17] (https://www.wolframalpha.com/ (accessed on 30 March 2023)).

$$\sin (x)=\sin (a)\sin (b)+\cos (a)\cos (b){\left[1-{\left(\cos (x)\frac{\sin (d)}{\cos (b)}\right)}^2\right]}^{1/2}$$

Substituting into Equation (9) and solving for $D$, we obtain

$$D=H\frac{\sin \beta }{\tan ({\alpha }_{{\gamma }_s={\gamma }_c})}$$

(13)

For a given $H,\beta$, the inter-row spacing depends on the sun altitude angle $\alpha$ at ${\gamma }_s$.

2.1.4. Inter-Row Spacing and Shading Losses in Optimal PV Systems Designs

An optimal design of a Photovoltaics system may be formulated by an objective function and a set of constraints. The optimal design may be based on energy or economic criteria, and the constraints are bounding conditions imposed on the field and on the collector parameters. In this section, the maximum annual incident energy on the collectors is the objective function.

The optimization problem is formulated as follows:

Maximize yearly energy $E$: $\mathrm{C}(\overline{\mathrm{X}})$ with respect to $\overline{\mathrm{X}}$ ($D,H,K,\beta$)

Subject to

$$H\times K\times \cos \beta +(K-1)\times D\le W$$

(14)

$$K\ge 2,\hspace{1em}D\ge D_{\min },\hspace{1em}H\le H_{\max },\hspace{1em}{0}^{°}\le \beta \le {90}^{°}$$

(15)

where $K$ (integer) is the number of the collector rows in the PV field, and $W$ is the field width.

2.2. Collectors Deployed on Sloped Planes Facing the South

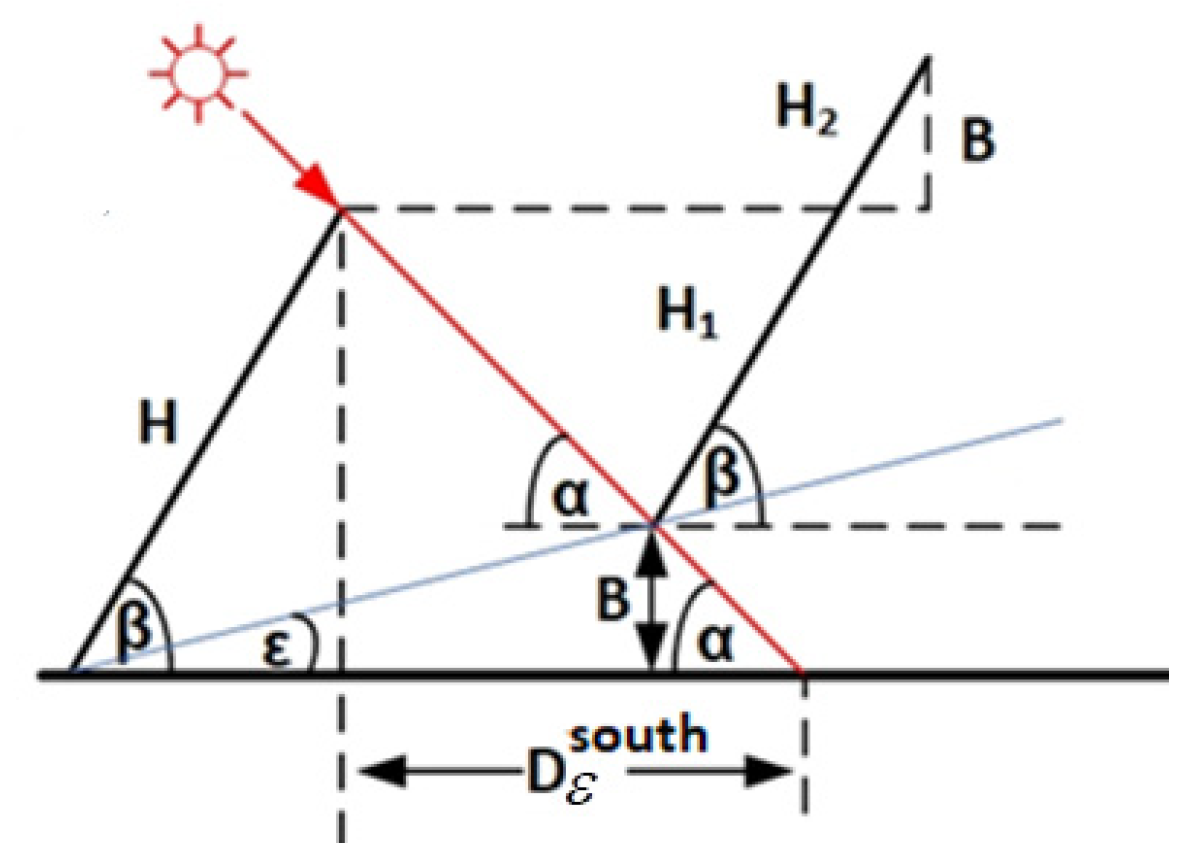
Multiple collector rows deployed on an inclined plane $\epsilon$, facing the south, are shown in Figure 3. The second collector is raised by an amount $B$, relative to the first collector, thus resulting in shading that takes place only on part $H_1$ of the collector.

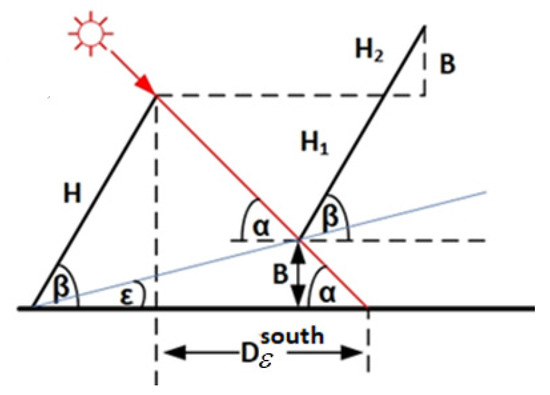
Figure 3. Collectors deployed on inclined plane $\epsilon$ facing the south.

The inter-row spacing for collectors mounted on inclined planes facing the south is developed in [18]

$$D_{\epsilon }^{south}=\frac{H_1\sin \beta }{\tan [{\sin }^{-1}(\cos (\varphi -{\delta }_0))]}$$

(16)

where

$$H_1=H-B/\sin \beta$$

(17)

$$B=(D_{\epsilon }^{south}+H\cos \beta )\tan \epsilon$$

(18)

Inserting Equation (18) into Equation (17), we obtain

$$H_1=H-\frac{(D_{\epsilon }^{south}+H\cos \beta )\tan \epsilon }{\sin \beta }$$

(19)

By substituting Equation (19) into Equation (16), we, thus, obtain the inter-row spacing for collectors deployed on south facing slope $\epsilon$:

$$D_{\epsilon }^{south}=\frac{H\sin \beta -H\cos \beta \tan \epsilon }{\tan [{\sin }^{-1}(\cos (\varphi -{\delta }_0))]+\tan \epsilon },\hspace{1em}\hspace{1em}\hspace{1em}\epsilon \le \beta$$

(20)

The shadow height $H_s$ on the second and on the subsequent collector rows is given in Equation (1), where $H$ is replaced by $H_1$ (see [16]):

$$H_s=H_1(1-\frac{D_{\epsilon }^{south}+H_1\cos \beta }{H_1\cos \beta +H_1\sin \beta \cos ({\gamma }_s-{\gamma }_c)/\tan \alpha })$$

(21)

${\gamma }_s={\gamma }_c$ Criterion for Inter-Row Spacing on day December 21

The collector height of the second and subsequent collectors subject to shading is $H_1$(see Figure 3)); therefore, based on Equation (13), the spacing is given by

$$D_{\epsilon }^{south}=H_1\frac{\sin \beta }{\tan {\alpha }_{{\gamma }_s={\gamma }_c}}$$

(22)

where $H_1$ is given in Equation (17). By solving for $D_{\epsilon }^{south}$, we, thus, obtain:

$$D_{\epsilon }^{south}=H\left(\frac{\sin \beta }{\tan {\alpha }_{{\gamma }_s={\gamma }_c}}\right)\frac{\left(1-\tan \epsilon /\tan \beta \right)}{\left(1+\tan \epsilon /\tan {\alpha }_{{\gamma }_s={\gamma }_c}\right)}, \epsilon \le \beta$$

(23)

2.3. Collectors Deployed on Sloped Planes Facing the North

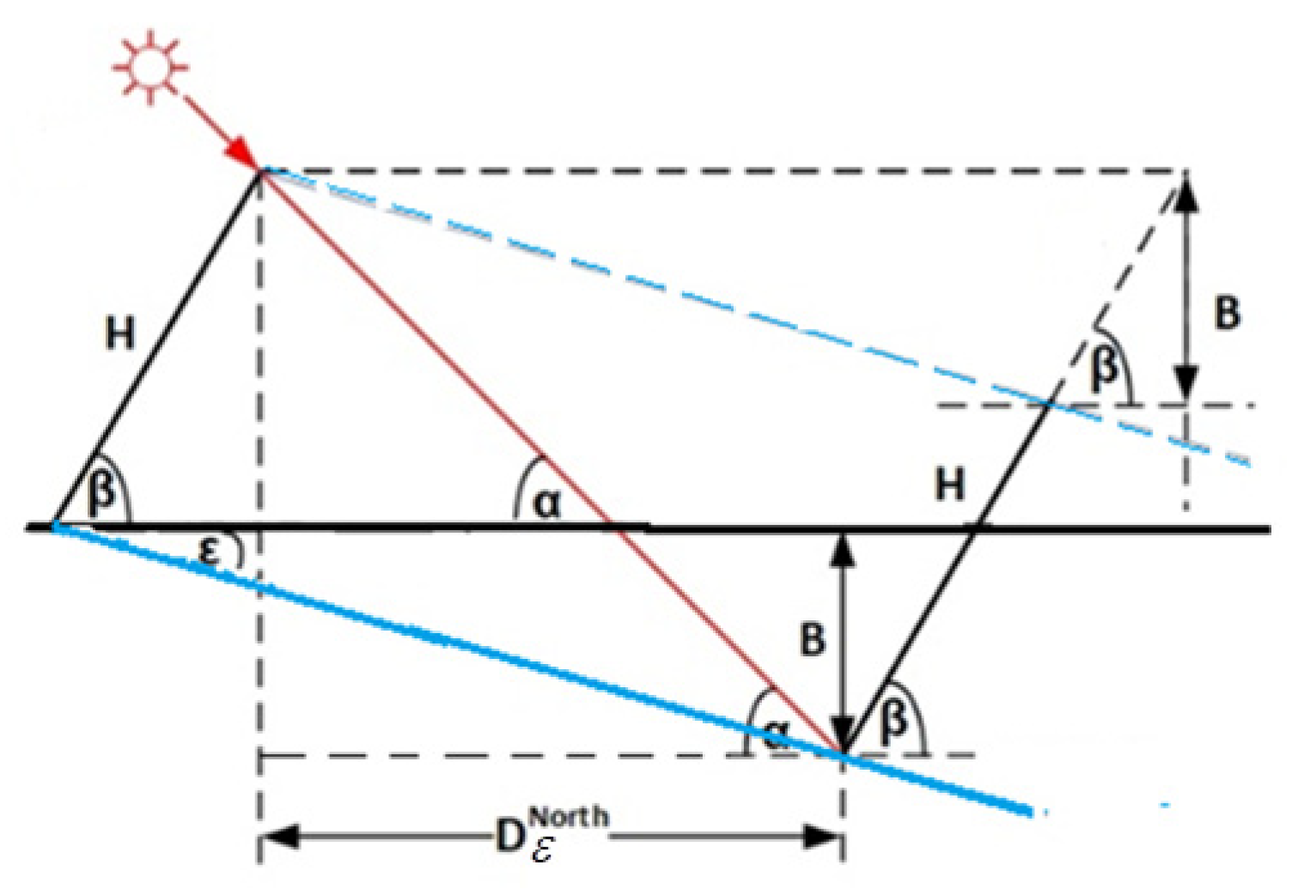
A deployment of two collectors on an inclined plane $\epsilon$ facing north is shown in Figure 4. From the figure, we obtain

$$\tan {\alpha }_{{\gamma }_{s=0}}=(H\sin \beta +B)/D_{\epsilon }^{north}$$

(24)

where

$$B=(H\cos \beta +D^{north})\tan \epsilon$$

(25)

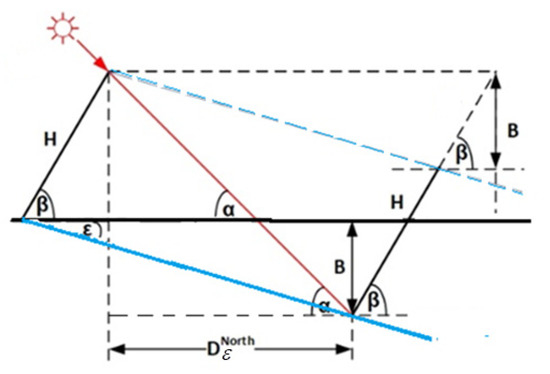
Figure 4. Collectors deployed on inclined plane $\epsilon$ facing north.

By substituting Equations (5) and (25) into Equation (24) and solving for $D_{\epsilon }^{north}$, we obtain

$$D_{\epsilon }^{north}=\frac{H\sin \beta +H\cos \beta \tan \epsilon }{\tan [{\sin }^{-1}(\cos (\varphi -{\delta }_0))]-\tan \epsilon },\hspace{1em}\hspace{1em}\epsilon \le \beta \hspace{1em}$$

(26)

${\gamma }_s={\gamma }_c$ Criterion for Inter-Row Spacing on day December 21

Based on Figure 4, the second and subsequent collectors are subject to shading for height

$$H^{*}=H+B/\sin \beta$$

(27)

where $B=(D_{\epsilon }^{north}+H\cos \beta )\tan \epsilon$; therefore, the inter-row spacing, see Equation (13), is given by

$$D_{\epsilon }^{north}=H^{*}\frac{\sin \beta }{\tan {\alpha }_{{\gamma }_s={\gamma }_c}}$$

(28)

where $H^{*}$ is given in Equation (27). Solving for $D_{\epsilon }^{n°rth}$ thus obtaining:

$$D_{\epsilon }^{north}=H\left(\frac{\sin \beta }{\tan {\alpha }_{{\gamma }_s={\gamma }_c}}\right)\frac{\left(1+\tan \epsilon /\tan \beta \right)}{\left(1-\tan \epsilon /\tan {\alpha }_{{\gamma }_s={\gamma }_c}\right)},\hspace{1em}\epsilon \le \beta$$

(29)

3. Results

The results of the effect of the azimuth angle on the inter-row spacing and shading pertain to the deployment of collectors on horizontal and sloped planes applying four spacing criteria. The deployments are at latitudes $\varphi ={32}^{°}{6}^{\prime }$ N and $\varphi ={52}^{°}{1}^{\prime }$ N.

3.1. Maintenance Criteria for Inter-Row Spacing, $\varphi ={32}^{°}{6}^{\prime }$ N

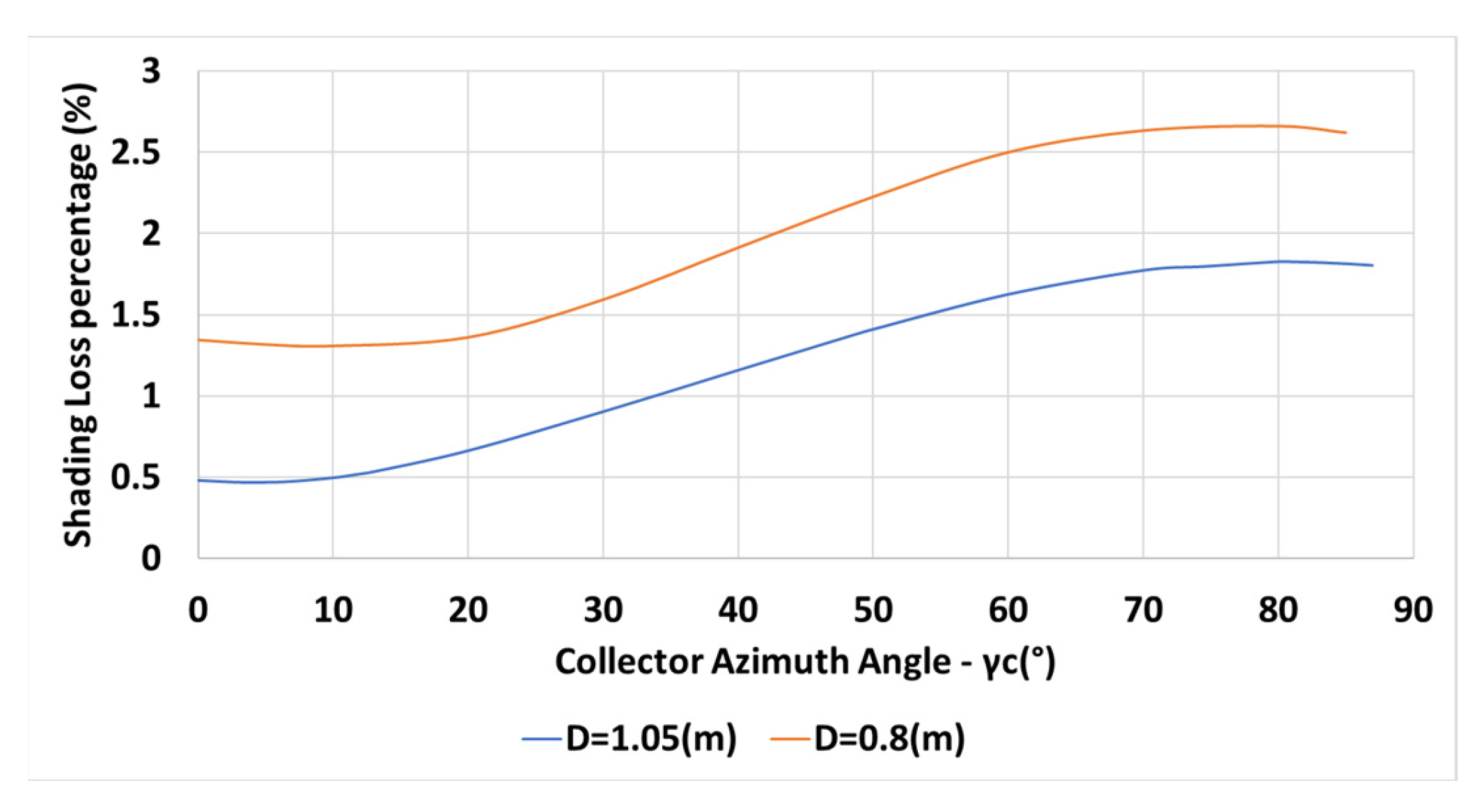
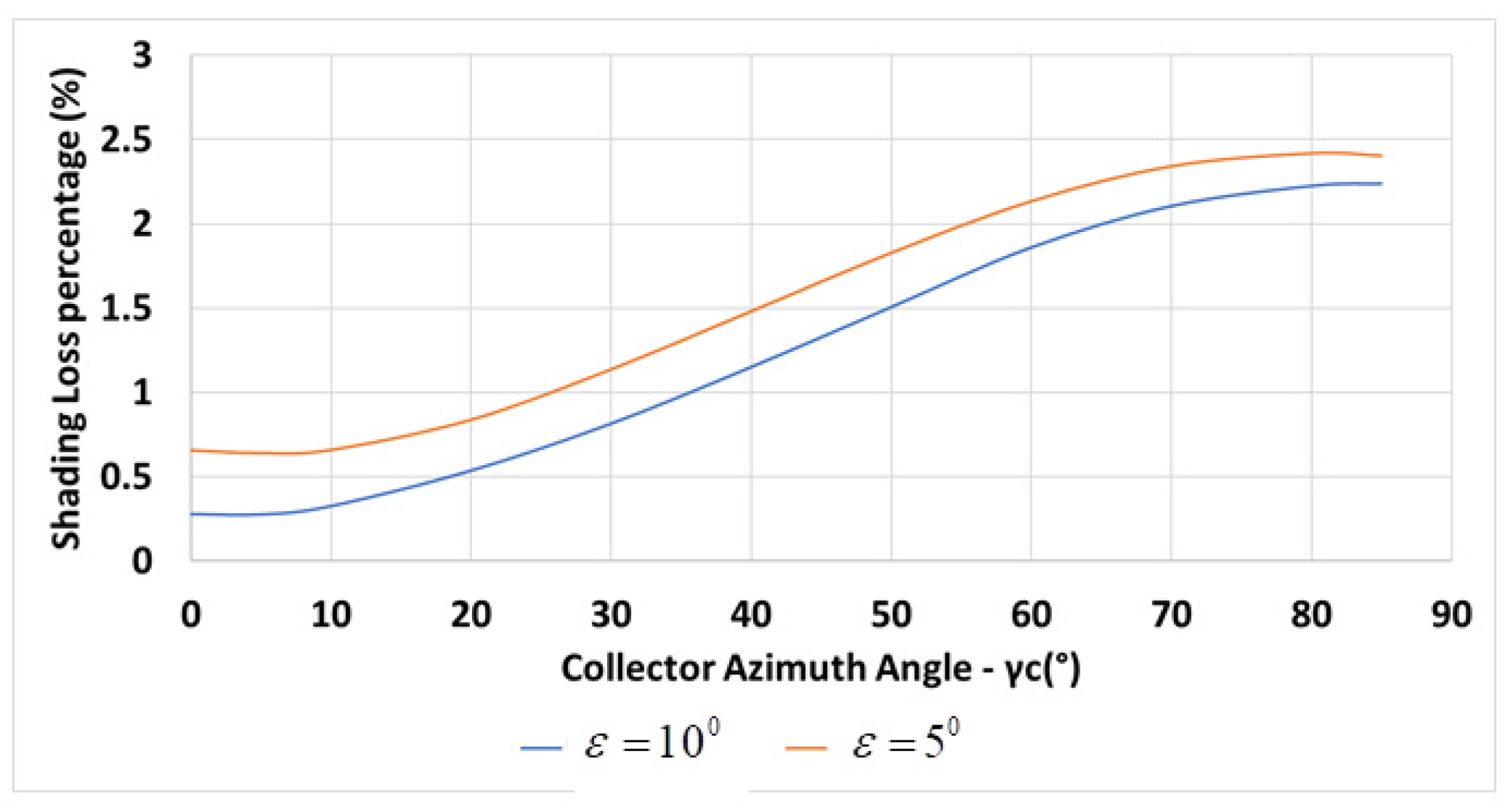
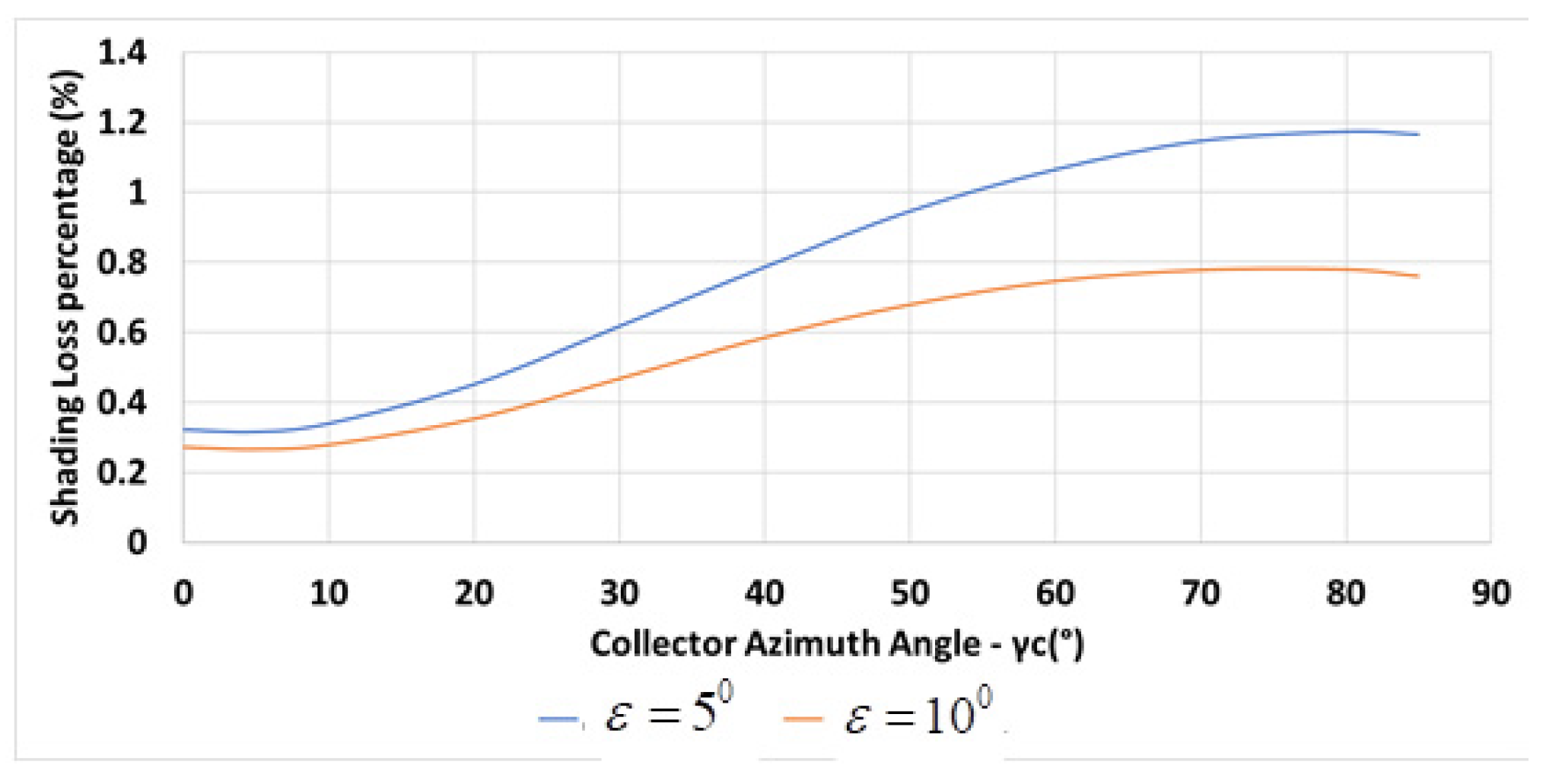
The variation of the annual shading losses percentage with collector azimuth angle ${\gamma }_c$ for $H=2.12$ m, $\beta ={20}^{°}$, $L=40$ m, $\varphi ={32}^{°}{6}^{\prime }$ N, and for a constant inter-row spacing $D=0.8 \mathrm{m}$ is depicted in Figure 5 (orange line).

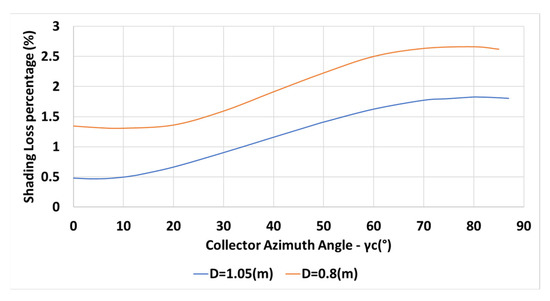
Figure 5. Variation of the annual shading losses percentage with collector azimuth ${\gamma }_c$, $H=2.12$ m, $\beta ={20}^{°}$, $L=40$ m, $\varphi ={32}^{ }{6}^{\prime }$ N, (Equations (6) and (7)).

3.2. No-Shading Criteria for Inter-Row Spacing and Shading on Winter Solstice at Solar Noon, $\varphi ={32}^{°}{6}^{\prime }N$

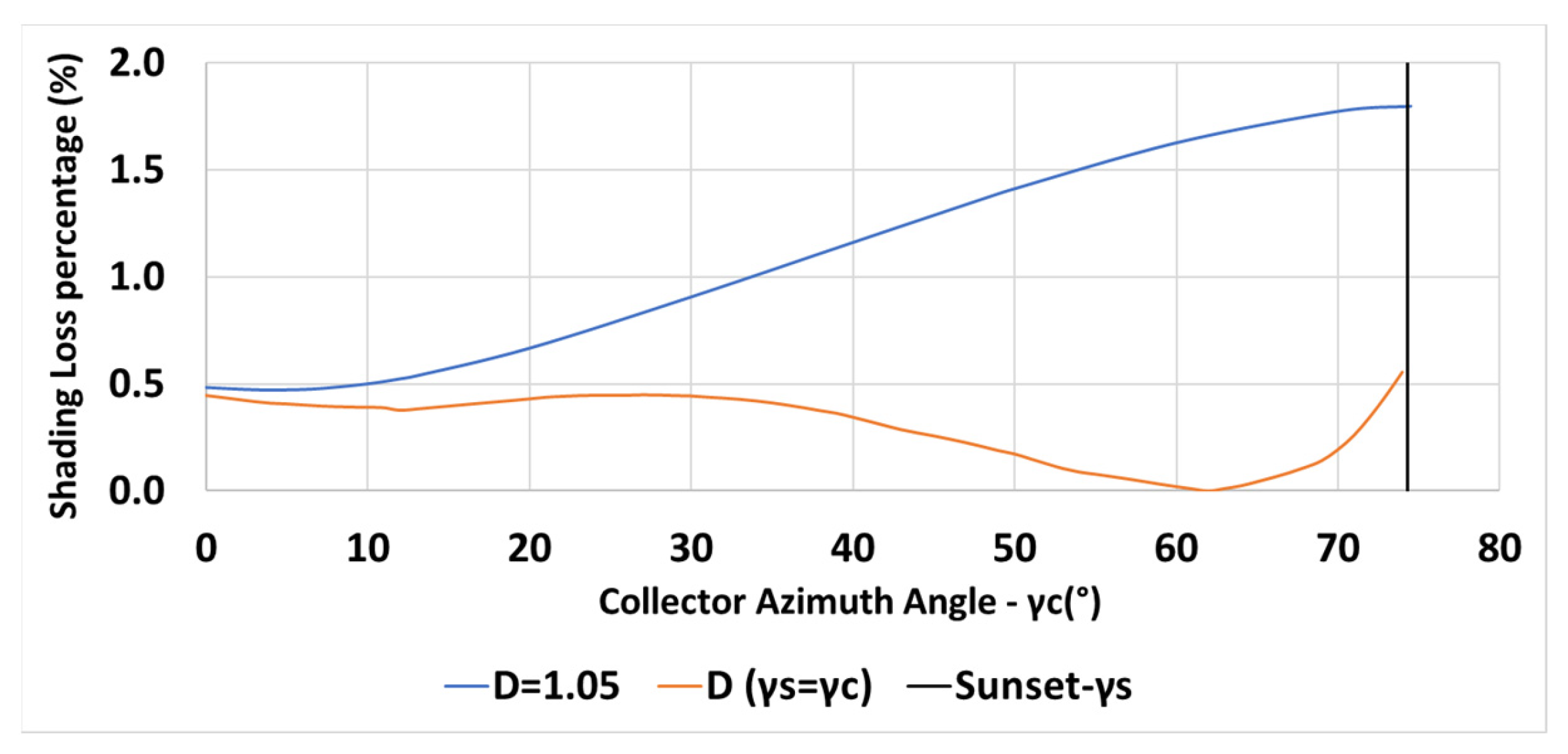
The spacing $D$ is determined by Equation (6). The shadow height and length are given in Equations (1) and (2), respectively. The inter-row spacing is $D=1.05$ m for $H=2.12$ m, $\beta ={20}^{°}$, declination angle at solar noon ${\delta }_0=-{23.45}^{°}$, at latitude $\varphi ={32}^{°}{6}^{\prime }$ N. The variation of the percentage of the shading losses, Equation (7), with the collectors’ azimuth angle ${\gamma }_c$ is shown in Figure 5 for $D=1.05$ m (blue line) and $L=40$ m. The figure shows that the shading losses increase with the increase in the collector azimuth angle ${\gamma }_c$. Shorter inter-row spacing, $D=0.8$ m (in orange) results in higher shading losses.

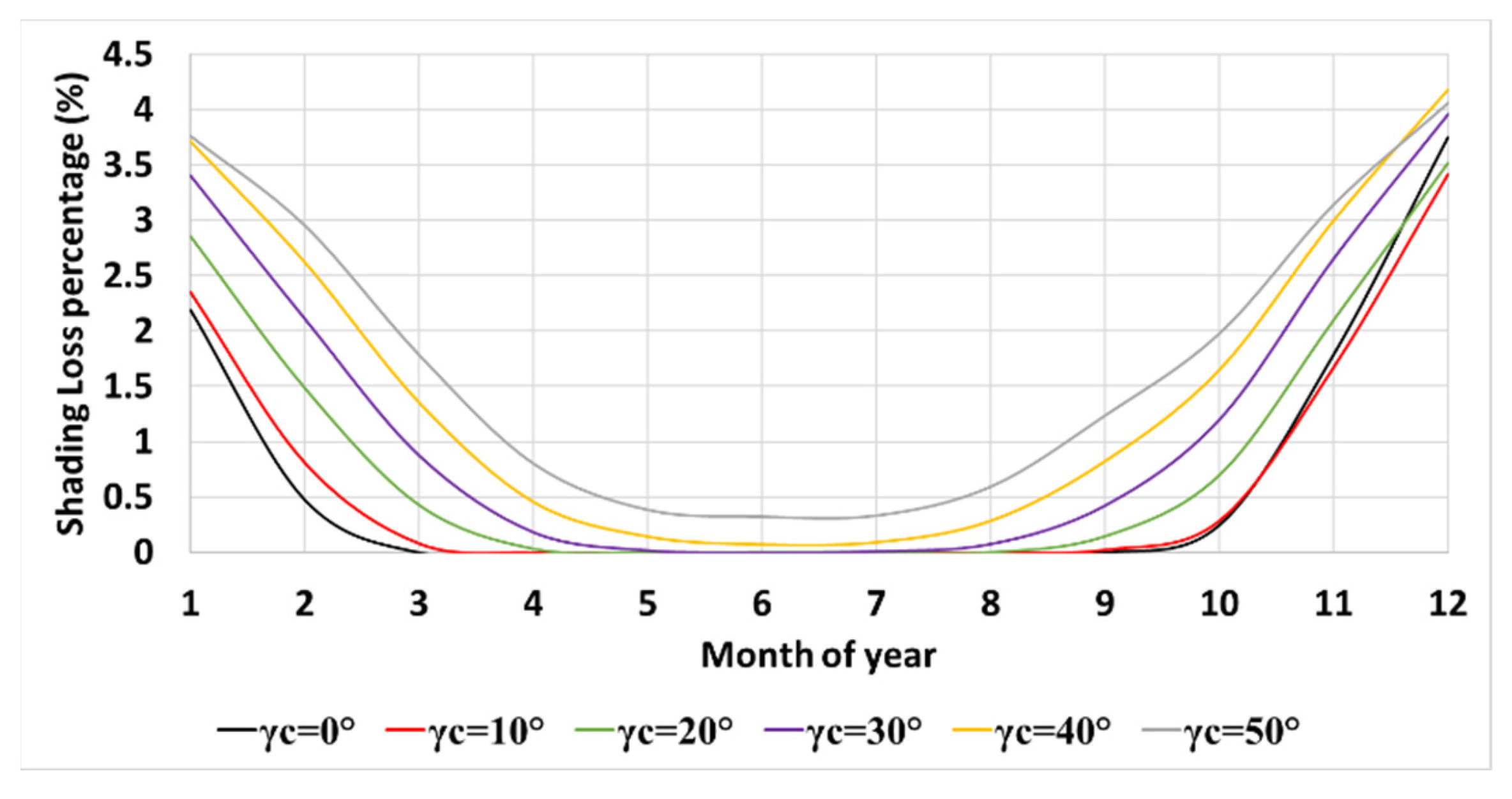
It is also interesting to compare the shading losses on a monthly basis. Figure 6 shows that the time for “no shading” decreases as the collector azimuth increases. For ${\gamma }_c=0^{°}$, no shading occurs for seven months; for ${\gamma }_c={10}^{°}$—for five months; for ${\gamma }_c={20}^{°}$—for four months; for ${\gamma }_c={30}^{°}$—for one month; and for larger azimuths, shading takes place for the entire year.

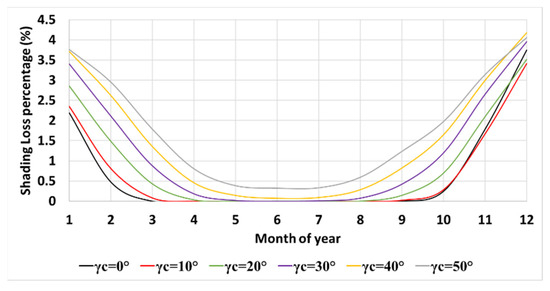
Figure 6. Monthly shading losses percentage for $H=2.12$ m, $\beta ={20}^{°}$, $L=40$ m $\varphi ={32}^{°}{6}^{\prime }$ N, and inter-row spacing $D=1.05$ m, (Equation (6)).

3.3. ${\gamma }_s={\gamma }_c$ Criterion for Inter-Row Spacing on day December 21

The results for the ${\gamma }_s={\gamma }_c$ criterion are depicted for latitudes $\varphi ={32}^{°}{6}^{\prime }$ N and $\varphi ={52}^{°}{12}^{\prime }$ N

3.3.1. Latitude $\varphi ={32}^{°}{6}^{\prime }$ N

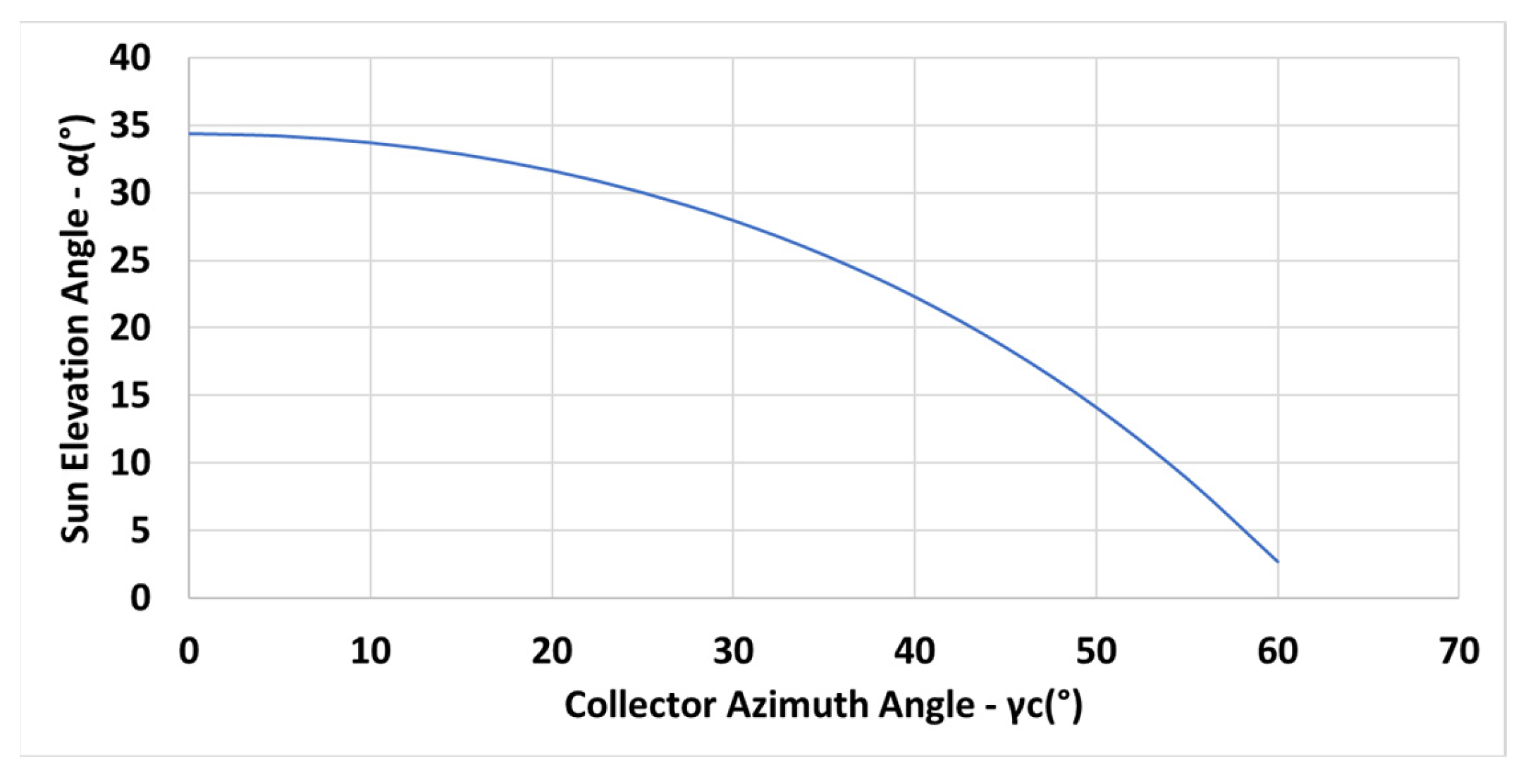
The variation of the sun elevation angle for the criteria ${\gamma }_c={\gamma }_s$ on winter solstice day needed for Equation (13) is depicted in Figure 7.

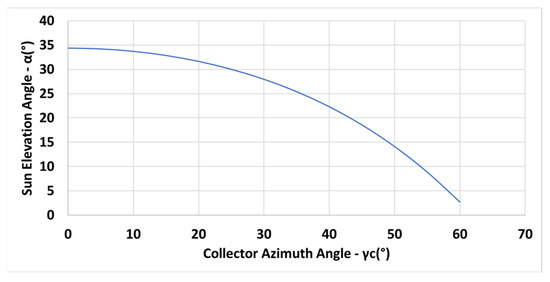
Figure 7. Sun elevation angle on winter solstice for criteria ${\gamma }_c={\gamma }_s={32}^{°}{6}^{\prime }$ N (Equations (11)).

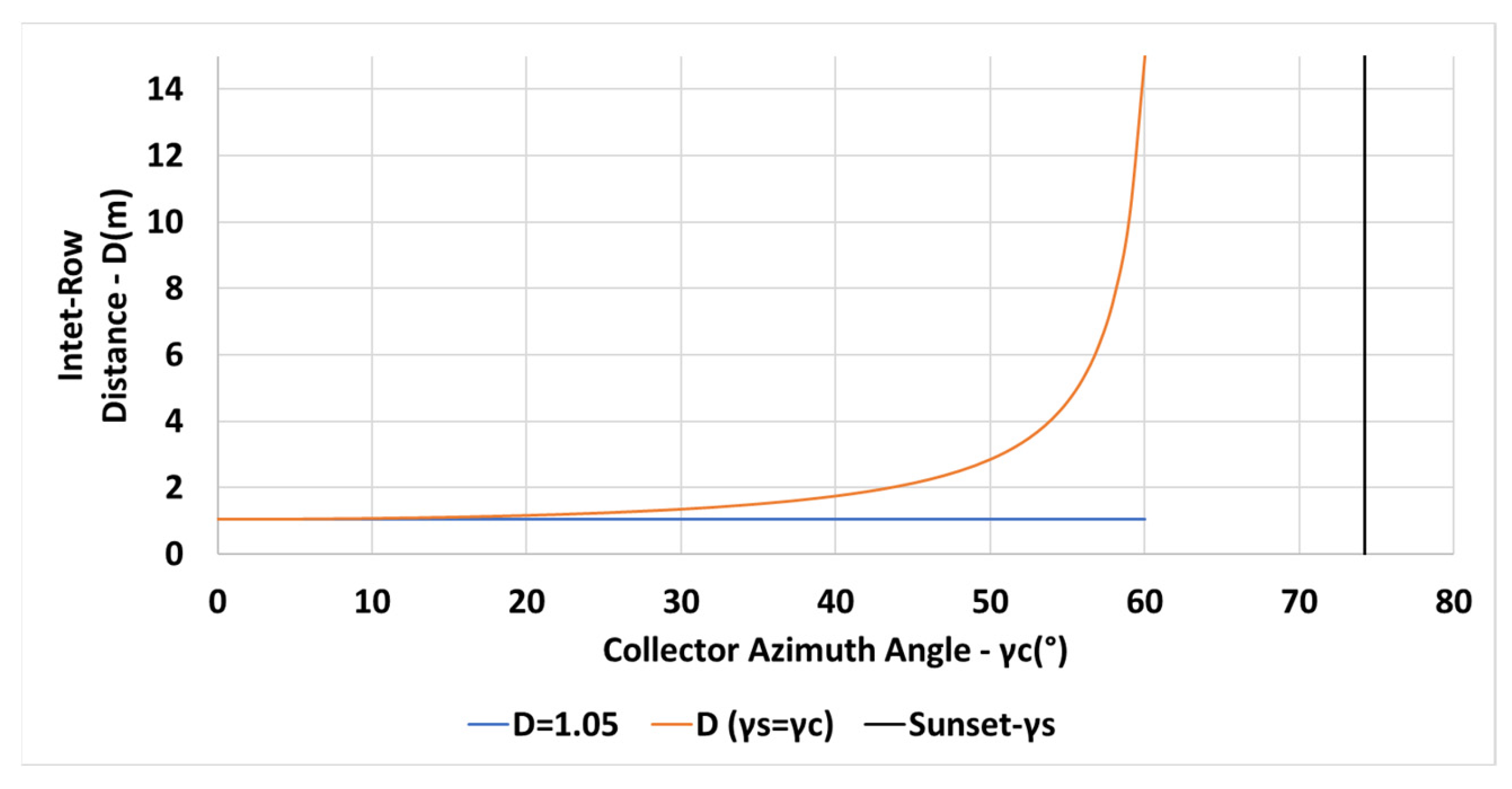
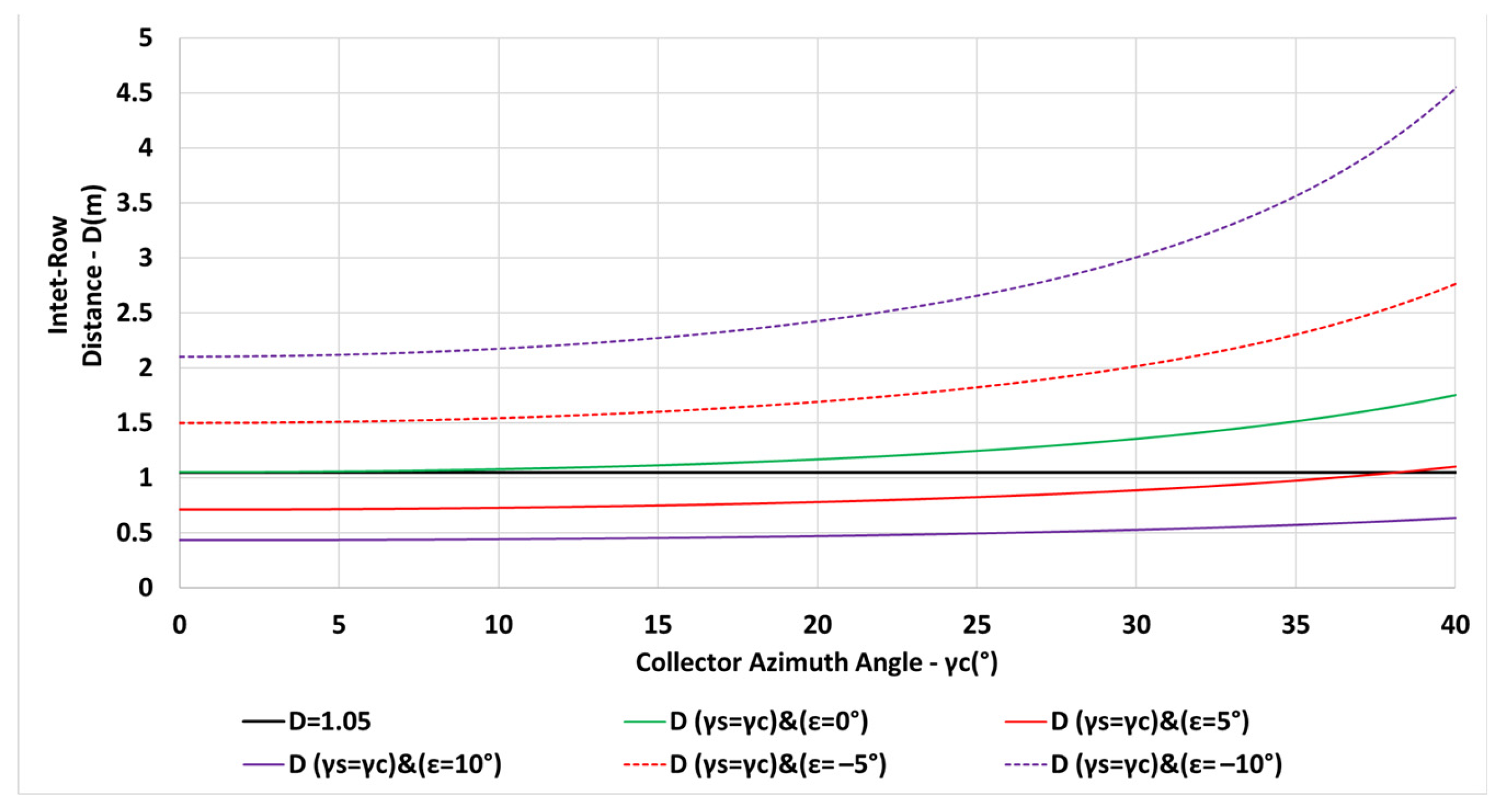
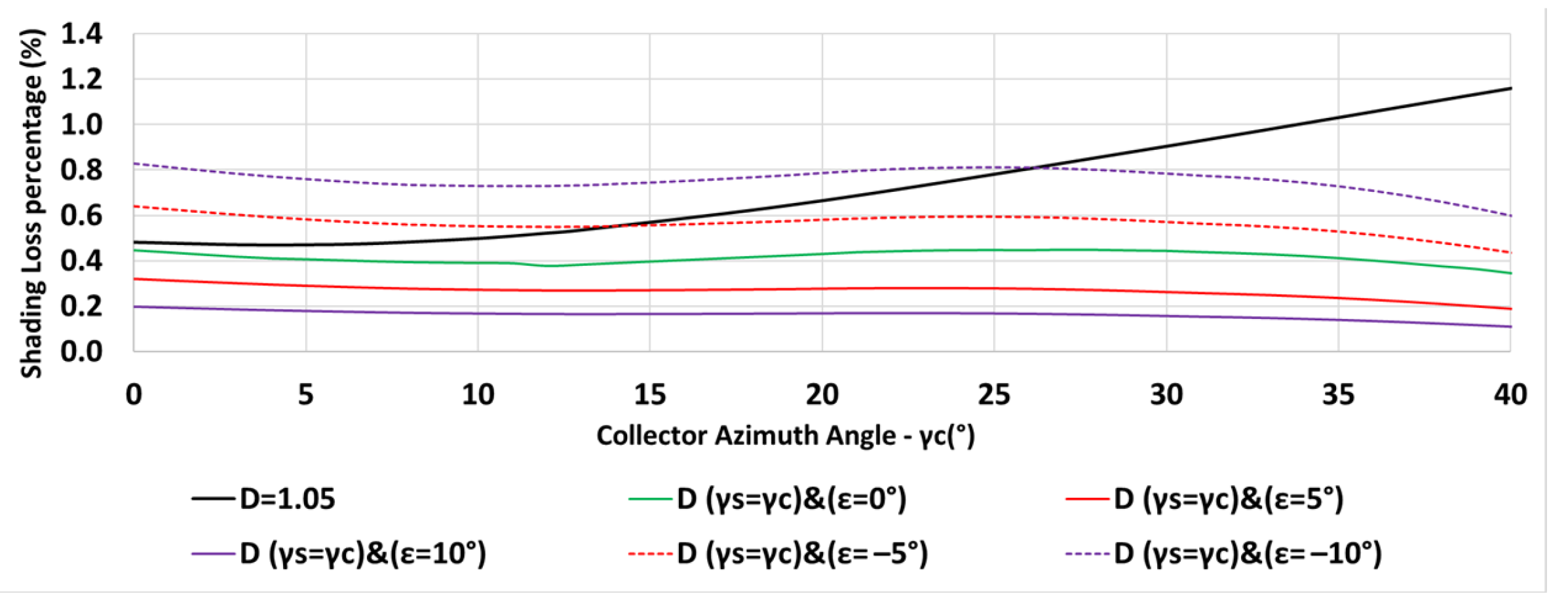
The variation of the inter-row spacing with the collector azimuth angle is depicted in Figure 8 for a constant spacing $D=1.05$ m (in blue—Equation (6)) and for the spacing criterion ${\gamma }_c={\gamma }_s$ (in orange—Equation (13)). The vertical black line indicates the sunset azimuth angle on day December 21. Figure 8 reveals that the inter-row spacing may be equally determined by Equation (6) or by Equation (13) up to the collector azimuths ${\gamma }_c={20}^{°}$. The inter-row spacing based on Equation (13) increases rapidly for ${\gamma }_c>{40}^{°}$, resulting in a large spacing. Figure 9 describes the shading losses percentage as a function of the collector azimuth for a constant spacing $D=1.05$ m (in blue) and for a spacing criterion ${\gamma }_c={\gamma }_s$ (in orange). The figure clearly emphasizes the reduction in the shading losses by applying the criteria ${\gamma }_c={\gamma }_s$.

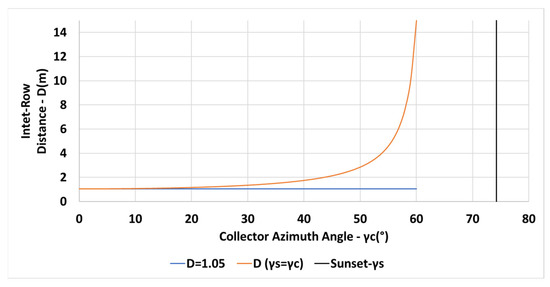
Figure 8. Variation of the inter-row spacing D with collector azimuth ${\gamma }_c$ for $H=2.12$ m, $\beta ={20}^{°}$, $\varphi ={52}^{°}{12}^{\prime }$ N, constant $D=2.386$ m (in blue), $D$ for ${\gamma }_c={\gamma }_s$ (in orange) (see Equations (6) and (13)).

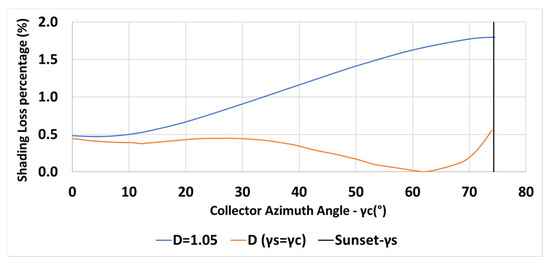
Figure 9. Variation of shading losses percentage with collector azimuth ${\gamma }_c$ for $H=2.12$ m, $\beta ={20}^{°}$, $\varphi ={32}^{°}{6}^{\prime }$ N, constant $D=1.05$ m (in blue), $D$ for ${\gamma }_c={\gamma }_s$ (in orange) (Equations (6), (7) and (13)).

3.3.2. Latitude $\varphi ={52}^{°}{12}^{\prime }$ N

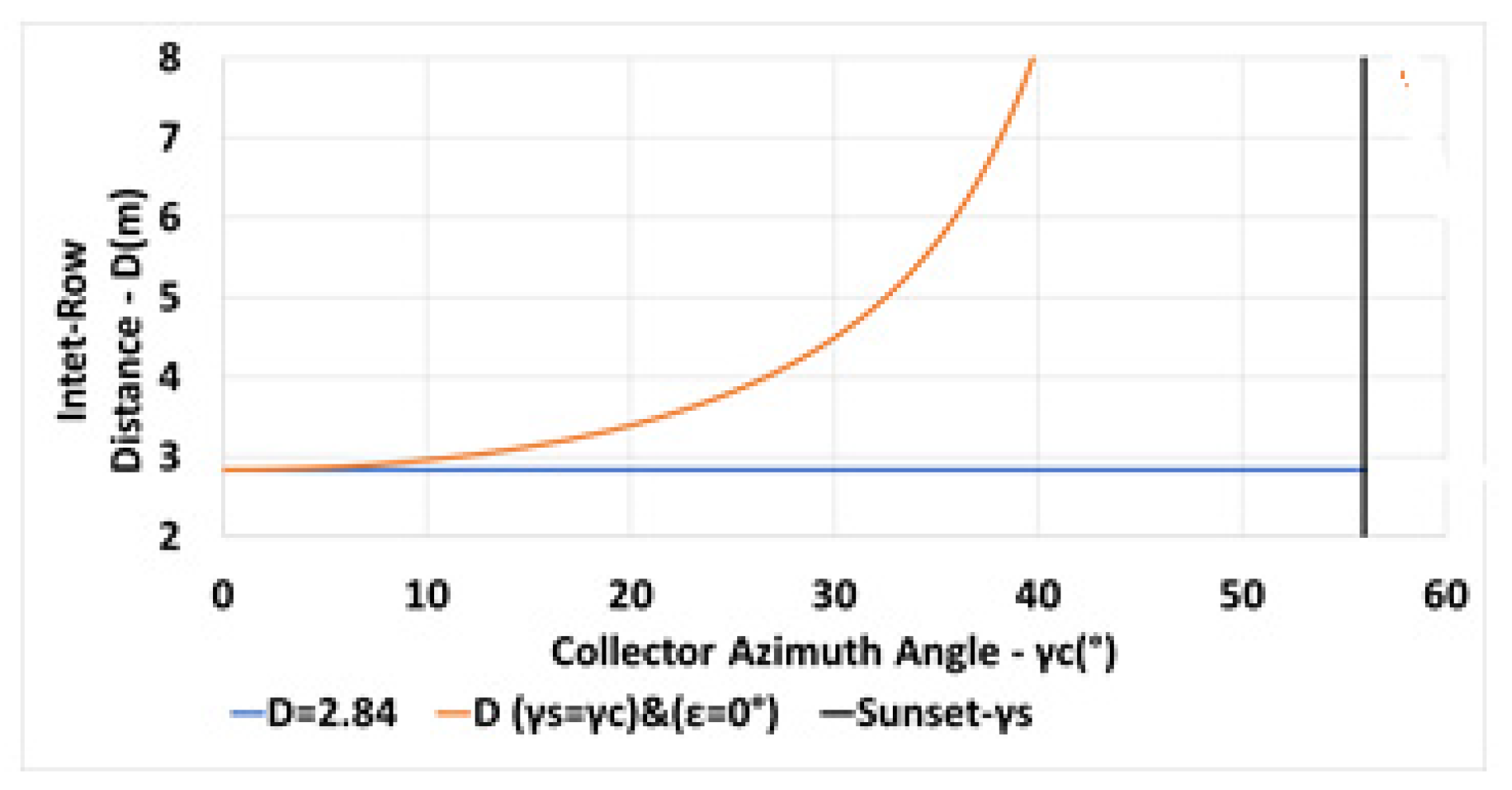
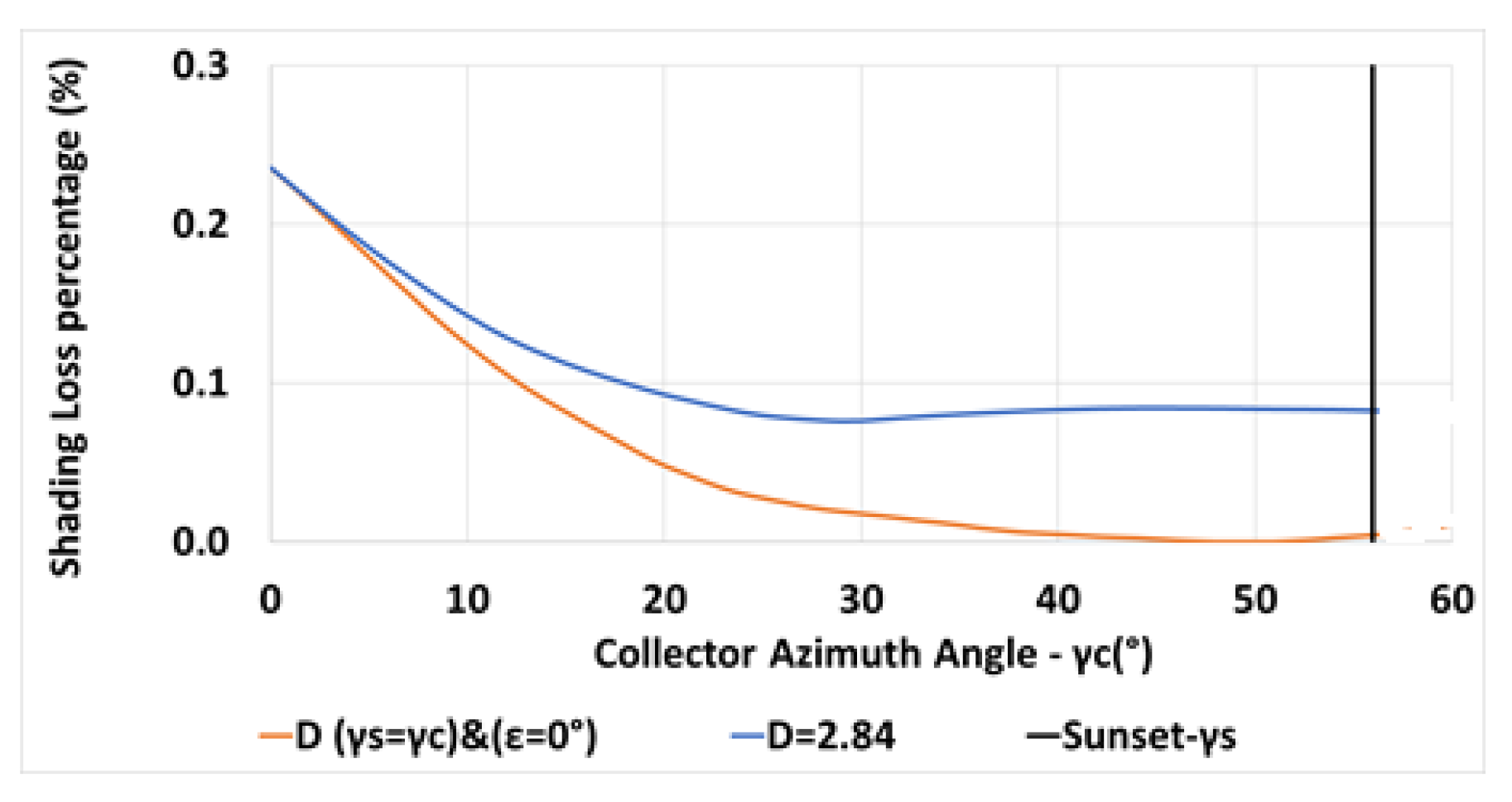
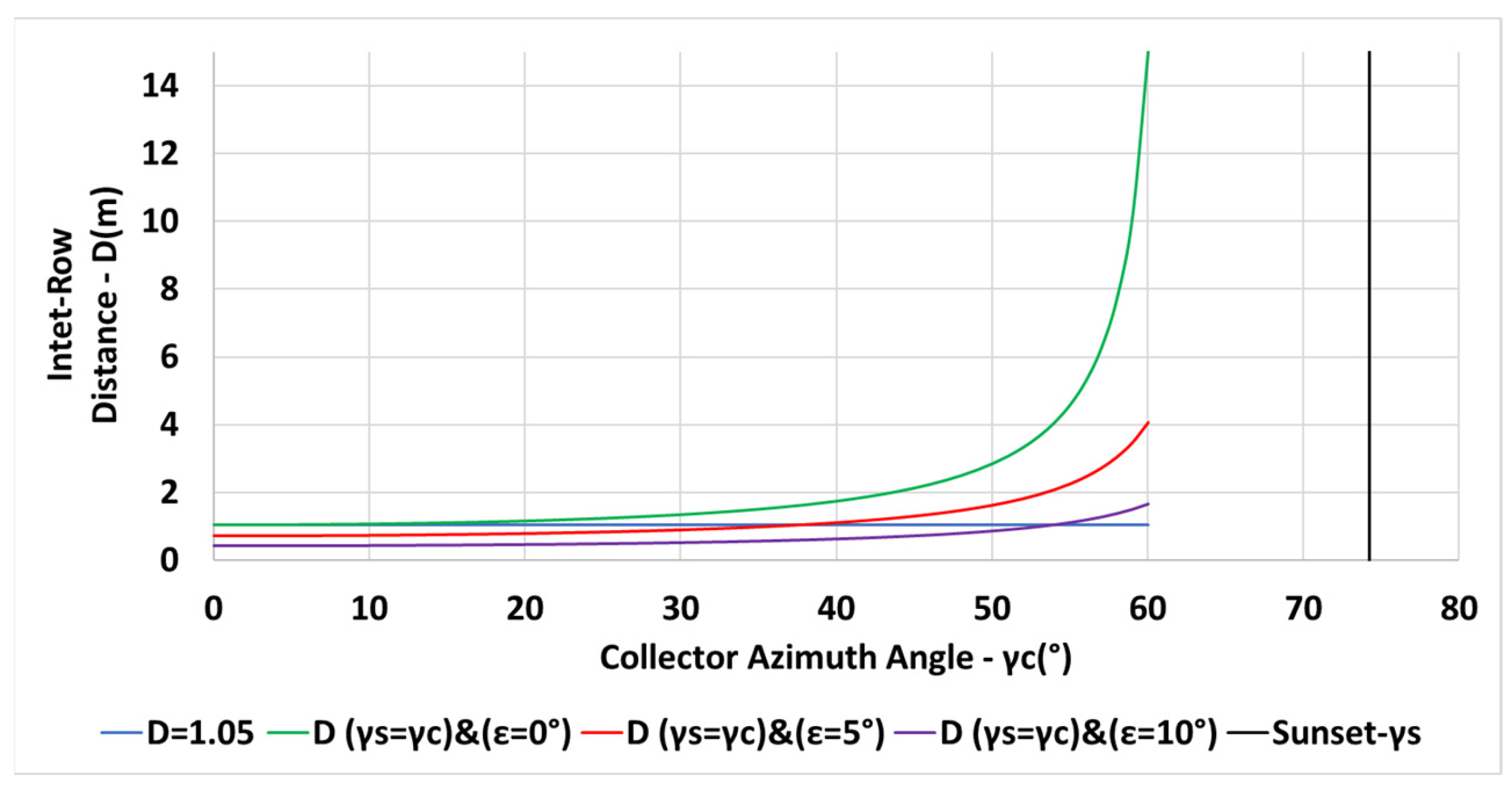
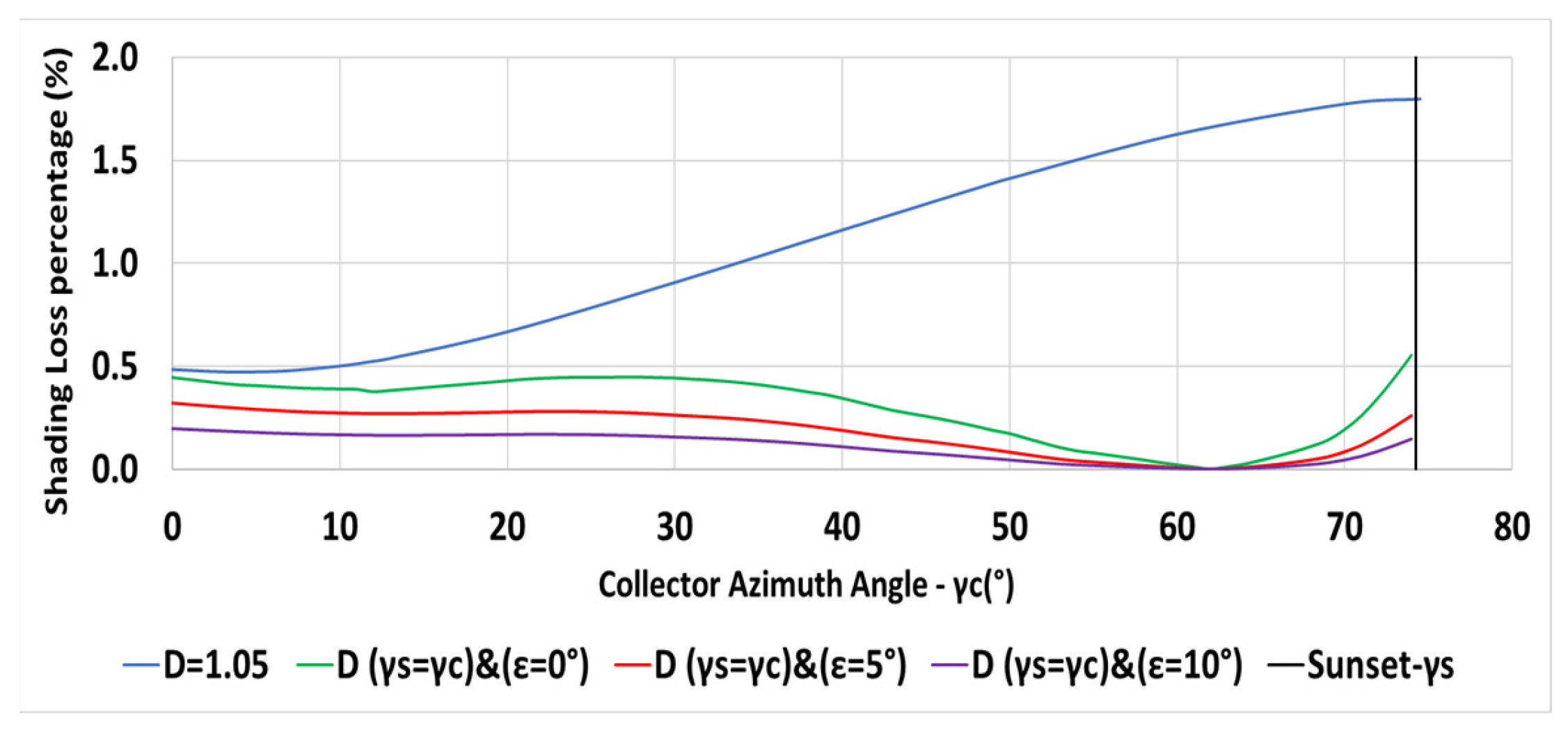
The variation of the inter-row spacing with the collector azimuth angle is depicted in Figure 10 for a constant spacing $D=2.836$ m (in blue—Equation (6)) and for the spacing criterion ${\gamma }_c={\gamma }_s$ (in orange—Equation (13)). The vertical black line indicates the sunset azimuth angle on day December 21. Figure 11 describes the shading losses percentage as a function of the collector azimuth for a constant spacing $D=2.386$ m (in blue) and for a spacing criterion ${\gamma }_c={\gamma }_s$ (in orange). Less shading losses may be obtained by applying the criteria ${\gamma }_c={\gamma }_s$.

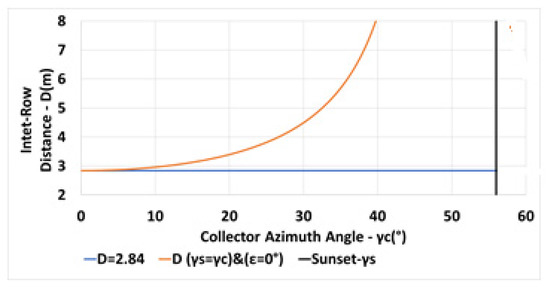
Figure 10. Variation of the inter-row spacing D with collector azimuth ${\gamma }_c$ for $H=2.12 \mathrm{m}, \beta ={20}^{°}$, $\varphi ={52}^{°}{12}^{\prime }$ N, constant $D=2.386$ m (in blue), $D$ for ${\gamma }_c={\gamma }_s$ (in orange) see (Equations (6) and (13)).

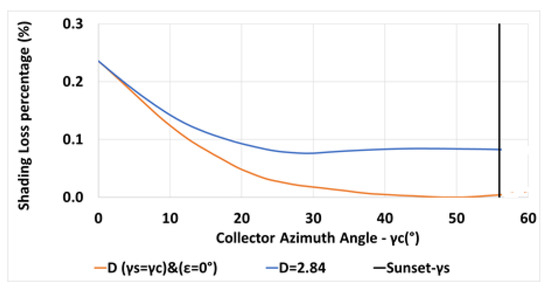
Figure 11. Variation of shading losses percentage with collector azimuth ${\gamma }_c$ for $H=2.12$ m, $\beta ={20}^{°}$, $\varphi ={52}^{°}{12}^{\prime }$ N, constant $D=2.386$ (in bue), $D$ for ${\gamma }_c={\gamma }_s$ (in orange) (Equations (6), (7) and (13)).

3.4. Inter-Row Spacing and Shading Losses in Optimal PV Systems Designs

The optimal design is performed at two locations $\varphi ={32}^{°}{6}^{\prime }$ N (Tel Aviv, Israel) and $\varphi ={52}^{°}{12}^{\prime }$ N (Lindenberg, Germany).

3.4.1. Latitude $\varphi ={32}^{°}{6}^{\prime }$ N

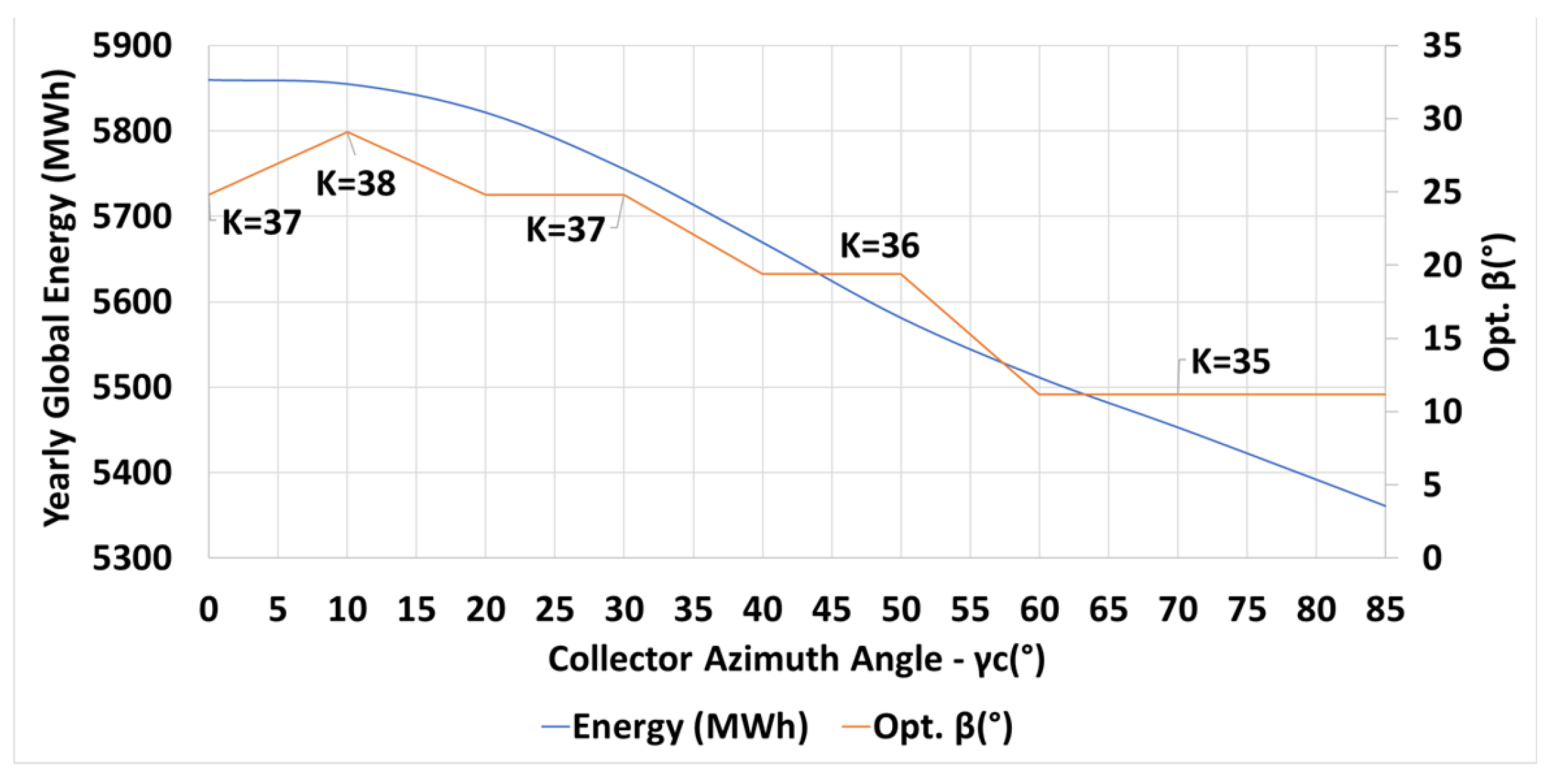
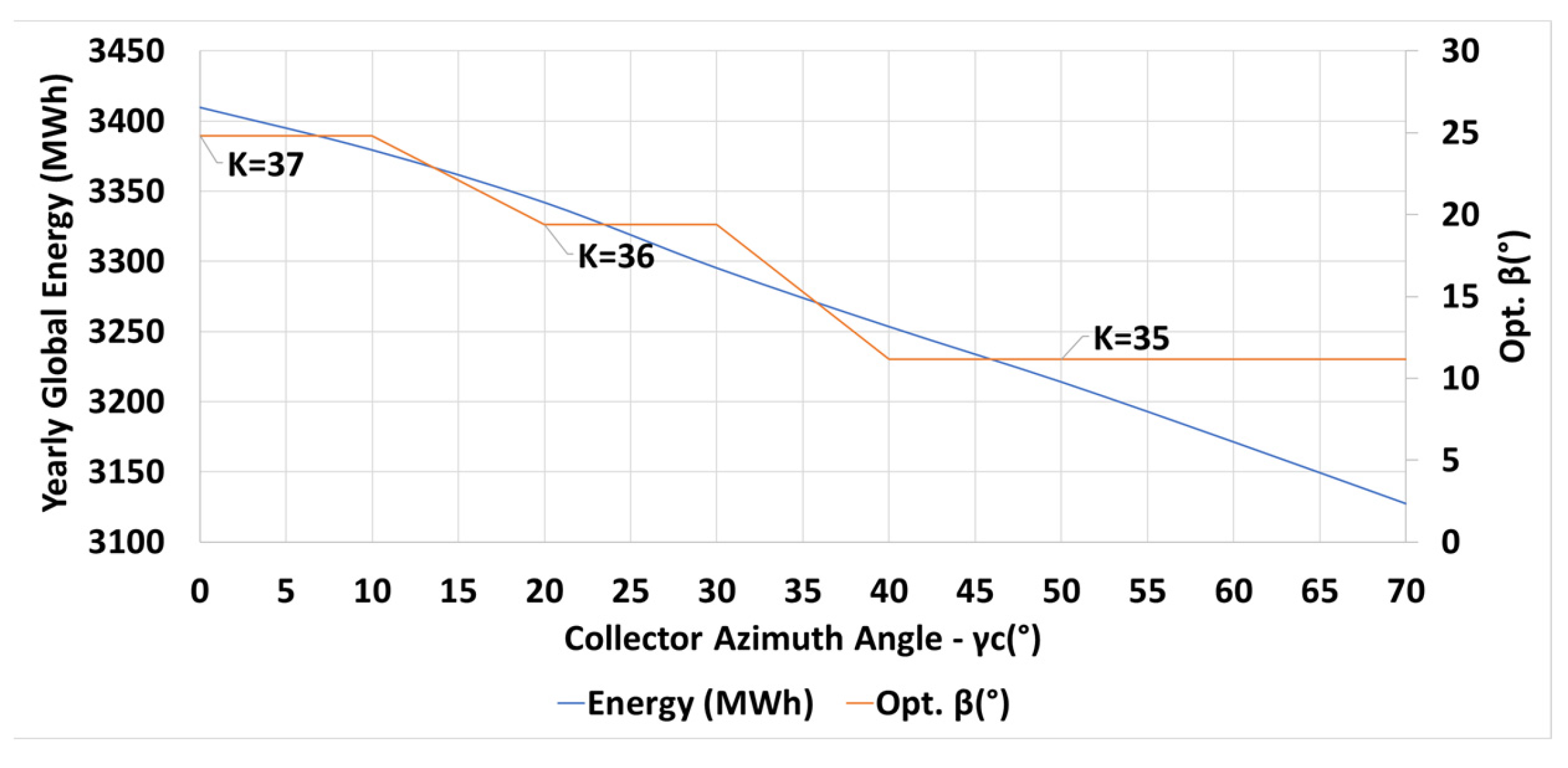
The inter-row spacing $D$ is bounded by a lower limit of $0.8$ m for maintenance purposes. The results for maximum yearly incident energy, the optimal number of the collector rows $K$, and the optimal collector inclination angle $\beta$, for different azimuth angles of the collector ${\gamma }_c$ are depicted in Figure 12 for the latitude $\varphi ={32}^{°}{6}^{\prime }$ N. The optimization process tends to a minimum inter-row spacing of $0.8$ m for all azimuth angles of the collectors in order to increase the number of collector rows in the given field and, hence, to obtain high incident energies. The relation between the optimal inclination angle $\beta$ (in orange) and the azimuth angle ${\gamma }_c$, as depicted in Figure 12, is of a stepwise shape. Therefore, the relationship between shading losses (in blue) and the parameters $\beta$ and ${\gamma }_c$ is complicated. For example, shading losses of 1.91% correspond to $\beta ={20}^{°},{\gamma }_c={40}^{°}$; 2.68% losses correspond to $\beta ={25}^{°},{\gamma }_c={20}^{°}$, and 4.40% losses correspond to $\beta ={30}^{°},{\gamma }_c={10}^{°}$.

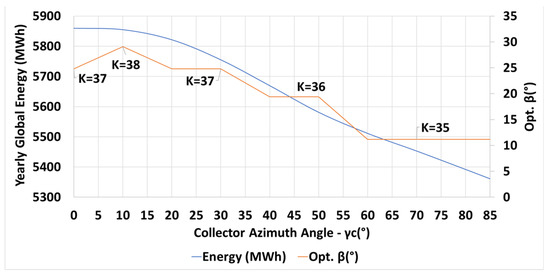
Figure 12. Optimal design parameters for yearly maximum incident energy (in blue) on a PV field as a function of the collector azimuth angle ${\gamma }_c$: number of collector rows $K$, optimal inclination angle $\beta$ (in orange), $\varphi ={32}^{°}{6}^{\prime }$ N (Equations (14) and (15)).

3.4.2. Latitude $\varphi ={52}^{°}{12}^{\prime }$ N

The results for maximum yearly incident energy, the optimal number of the collector rows $K$, and the optimal collector inclination angle $\beta$, for different azimuth angles of the collector ${\gamma }_c$ are depicted in Figure 13 for the latitude $\varphi ={52}^{°}{12}^{\prime }$ N.

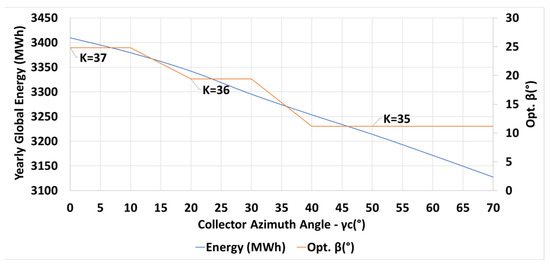
Figure 13. Optimal design parameters for yearly maximum incident energy (in blue) on a PV field as a function of the collector azimuth angle ${\gamma }_c$: number of collector rows $K$, optimal inclination angle $\beta$ (in orange), $\varphi ={52}^{°}{12}^{\prime }$ N (Equations (14) and (15)).

The field and collector parameters at Lindenberg are the same as for Tel Aviv: $W_{\max }=100$ m, $L_{\max }=40$ m, $H_{\max }=2.12$ m, $0.8$ m $\le D\le 5.0$ m, $0.0001\le \beta \le {90}^{°}$, $2\le K\le 100$. The optimization process tends to a minimum inter-row spacing of $0.8$ m for all azimuth angles of the collectors in order to increase the number of collector rows in the given field.

3.5. Collectors Deployed on Sloped Planes Facing the South

3.5.1. Constant Inter-Row Spacing-Maintenance Spacing, $D=0.8$ m, $\varphi ={32}^{°}{6}^{\prime }$ N

The inter-row spacing $D_{\epsilon }^{south}$ for collectors deployed on inclined planes facing the south is shorter than for the collectors deployed on horizontal planes [18]; therefore, the inter-row spacing in this section is determined by the spacing for maintenance purposes, e.g., $D=0.8$ m. Figure 14 shows the variation of the percentage of the annual shading losses with the collector azimuth ${\gamma }_c$ for $H=2.12$ m, $\beta ={20}^{°}$, $L=40$ m, $\varphi ={32}^{°}{6}^{\prime }$ N, and for a constant inter-row spacing $D=0.8$ m, for two plane inclination angles, $\epsilon =5^{°}$ and $\epsilon ={10}^{°}$. The figure shows that a larger inclination angle $\epsilon$ results in less shading.

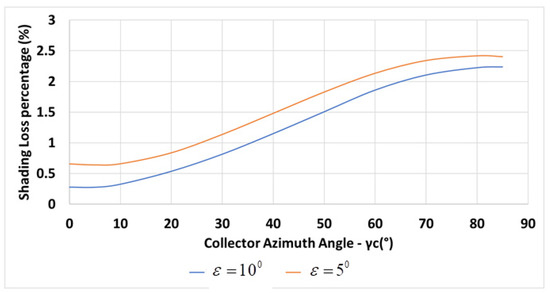
Figure 14. Variation of the annual shading losses percentage with collector azimuth ${\gamma }_c$ for $H=2.12$ m, $\beta ={20}^{°}$, $L=40$ m, $\varphi ={32}^{°}{6}^{\prime }$ N, and for a constant inter-row spacing $D=0.8$ m, (Equation (7)).

3.5.2. ${\gamma }_s={\gamma }_c$ Criterion for Inter-Row Spacing on day December 21, $\varphi ={32}^{°}{6}^{\prime }$ N

The variation of the inter-row spacing with the collector azimuth angle is depicted in Figure 15 for a constant spacing $D=1.05$ m, for spacing criterion ${\gamma }_c={\gamma }_s$ (for $\epsilon =0$), and for $\epsilon =5^{°}$ and $\epsilon ={10}^{°}$, respectively for given parameters $H=2.12$ m, $\beta ={20}^{°}$, $L=40$ m, $\varphi ={32}^{°}{6}^{\prime }$ N. The vertical black line indicates the sunset azimuth angle on day December 21. Figure 15 reveals that the inter-row spacing may be reduced for sloped planes. Figure 16 describes the annual shading losses percentage as a function of the collector azimuth for a constant spacing $D=1.05$ m (Equation (6)), for spacing criterion ${\gamma }_c={\gamma }_s$ (Equation (13)), and for $\epsilon =5^{°}$ and $\epsilon ={10}^{°}$, respectively. The figure clearly emphasizes the reduction in the shading losses by applying the criteria ${\gamma }_c={\gamma }_s$, and larger slopes $\epsilon$ result in less shading.

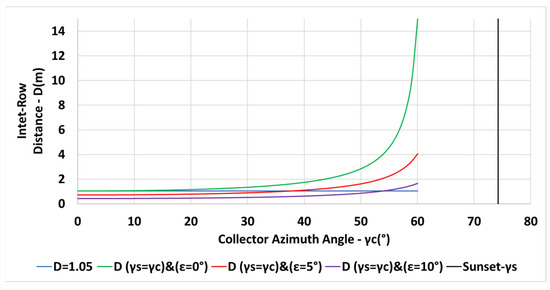
Figure 15. Variation of the inter-row spacing $D_{\epsilon }^{south}$ with collector azimuth ${\gamma }_c$ for $H=2.12$ m, $\beta ={20}^{°}$, $L=40$ m $\varphi ={32}^{°}{6}^{\prime }$ N, constant $D=1.05$ m, $D$ for ${\gamma }_c={\gamma }_s$ ($\epsilon =0^{°}$), and for $\epsilon =5^{°}$ and $\epsilon ={10}^{°}$ (Equations (6) and (23)).

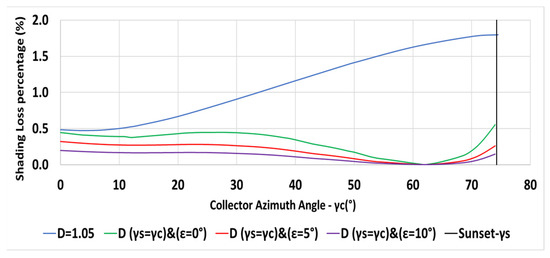
Figure 16. Variation of the annual shading losses percentage with collector azimuth ${\gamma }_c$ for $H=2.12$ m, $\beta ={20}^{°}$, $L=40$ m $\varphi ={32}^{°}{6}^{\prime }$ N, constant $D=1.05$ m, $D$ for ${\gamma }_c={\gamma }_s$ ($\epsilon =0^{°}$), and for $\epsilon =5^{°}$ and $\epsilon ={10}^{°}$ (Equations (6), (7) and (23)).

3.6. Collectors Deployed on Sloped Planes Facing the North

3.6.1. No-Shading Criteria for Inter-Row Spacing and Shading on Winter Solstice at Solar Noon, $\varphi ={32}^{°}{6}^{\prime }$ N

The inter-row spacing $D_{\epsilon }^{north}$ for collectors deployed on inclined planes facing north is longer than for collectors deployed on horizontal planers [18]; therefore, the inter-row spacing, in this section, is determined by Equation (6) for winter solstice at solar noon, ${\delta }_0=-{23.45}^{°}$ and $\omega =0$, i.e., $D=1.05$ m. Figure 17 shows the variation of the percentage of the annual shading losses with the collector azimuth ${\gamma }_c$ for $H=2.12$ m, $\beta ={20}^{°}$, $L=40$ m, $\varphi ={32}^{°}{6}^{\prime }$ N, and for a constant inter-row spacing $D=1.05$ m, for two plane inclination angles, $\epsilon =5^{°}$ and $\epsilon ={10}^{°}$. The figure shows that a larger inclination angle $\epsilon$ results in less shading.

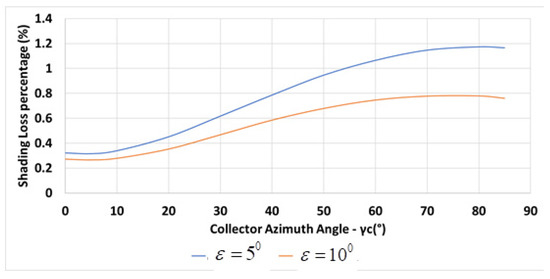
Figure 17. Variation of the annual shading losses percentage with collector azimuth ${\gamma }_c$ for $H=2.12$ m, $\beta ={20}^{°}$, $L=40$ m, $\varphi ={32}^{°}{6}^{\prime }$ N, and for a constant inter-row spacing $D=1.05$ m (Equations (6), (7) and (29)).

3.6.2. ${\gamma }_s={\gamma }_c$ Criterion for Inter-Row Spacing on December 21, $\varphi ={32}^{°}{6}^{\prime }N$

The variation of the inter-row spacing with the collector azimuth angle is depicted in Figure 18 for a constant spacing $D=1.05$ m, for spacing criterion ${\gamma }_c={\gamma }_s$ (for $\epsilon =0^{°}$), and for $\epsilon =\pm 5^{°}$ and $\epsilon =\pm {10}^{°}$, respectively, for given parameters $H=2.12$ m, $\beta ={20}^{°}$, $L=40$ m, $\varphi ={32}^{°}{6}^{\prime }$ N, where the (+) pertains to a southern plane and the (−) pertains to a northern plane. The inter-row spacing (Figure 18) and the annual shading percentage (Figure 19) are drawn up to the azimuth ${\gamma }_c={40}^{°}$ for the collectors because the required spacing becomes impractical even for smaller azimuths. Smaller inter-row spacing is required for collectors deployed on southern slopes and larger for northern slopes, with respect to horizontal planes. Figure 19 describes the annual shading losses percentage as a function of the collector azimuth ${\gamma }_c$ for a constant spacing $D=1.05$ m (Equation (6)), for spacing criterion ${\gamma }_c={\gamma }_s$ (Equation (13)), and for $\epsilon =\pm 5^{°}$ and $\epsilon =\pm {10}^{°}$, respectively. The figure clearly emphasizes the reduction in the shading losses by applying the criteria ${\gamma }_c={\gamma }_s$, and larger southern slopes $+\epsilon$ result in less shading. Collectors may be deployed on northern slopes with acceptable inter-row spacing on account of increasing shading.

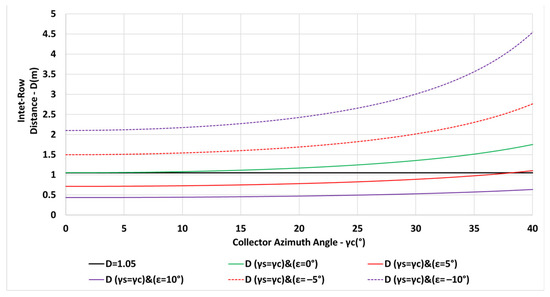
Figure 18. Variation of the inter-row spacing $D_{\epsilon }^{south}$ with collector azimuth ${\gamma }_c$ for $H=2.12$ m, $\beta ={20}^{°}$, $\varphi ={32}^{°}{6}^{\prime }$ N, constant $D=1.05$ m, $D$ for ${\gamma }_c={\gamma }_s$ ($\epsilon =0^{°}$), and for $\epsilon =\pm 5^{°}$ and $\epsilon =\pm {10}^{°}$ (see Equation (6)).

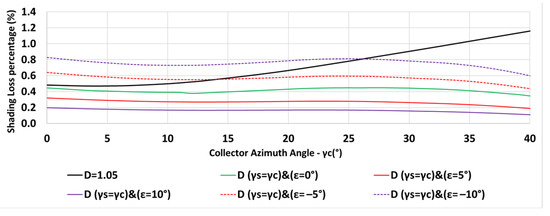
Figure 19. Variation of the annual shading losses percentage with collector azimuth ${\gamma }_c$ for $H=2.12$ m, $\beta ={20}^{°}$, $L=40$ m, $\varphi ={32}^{°}{6}^{\prime }$ N, constant $D=1.05$ m, $D$ for ${\gamma }_c={\gamma }_s$($\epsilon =0^{°}$), and for $\epsilon =\pm 5^{°}$ and $\epsilon =\pm {10}^{°}$, (Equations (6) and (7)).

4. Discussion and Conclusions

The effect of collector azimuth on inter-row spacing and on inter-row shading in photovoltaic fields was not investigated analytically in previous studies, to the best of our knowledge. The present study presents a comprehensive point of view of the relation between the inter-row spacing and the inter-row shading in multiple-row collectors of the PV fields for any azimuthal deployment of the collector rows. PV collectors may be deployed at any azimuth to exploit available structures and land to promote the utilization of renewable energy. Rooftop buildings, mountain terrains, rivers, lakes, and water pond beds may be oriented at different azimuths other than to the equator, on which PV systems may be installed. The inter-row spacing plays an important role in the design of PV systems affecting the generated electric energy. The inter-row spacing determines the number of collector rows in the given dimensions of the field and, hence, determines the shading and masking losses and the electric output energy of the PV system. The common approach to determine the inter-row spacing is based on the “winter solstice rule” (“shading angle”), where the inter-row spacing is determined by the shadow length on day December 21 at solar noon. This general rule is used in practice and in theoretical studies of PV system designs. For limited land (e.g., rooftops), the inter-row spacing is usually dictated by the required maintenance distance, and hence, the PV collector rows are usually densely deployed. The approach of optimal deployment of collectors in a given field may lead to the inter-row spacing that is dictated by the objective function and by the constraints on the problem parameters. A new criterion for the inter-row spacing is introduced in the present study, namely, no shading on collectors for collector azimuth equal to solar azimuth; ${\gamma }_c={\gamma }_s$ on the winter solstice. Applying the new criteria decreases the shading losses. The present study deals with the inter-row spacing and inter-row shading in the PV fields as affected by the collector azimuth angle for horizontal and sloped planes oriented toward the south and the north. Generally, shorter spacing results in increased shading; minimum shading is obtained for collectors oriented toward the equator; inter-row spacing for maintenance purposes is used in limited land of the PV fields and, usually, also in optimal PV system designs; less shading occurs for systems deployed on inclined planes oriented toward the equator; less shading is obtained for the collectors facing the south and oriented at azimuth ${\gamma }_c$ by applying the criterion ${\gamma }_c={\gamma }_s$, and larger spacing is required for collectors deployed on the northern slopes than on the southern slopes.

Conclusions for the PV collectors of width $H=2.12$ m, deployed with an inclination angle of $\beta ={20}^{°}$ with respect to horizontal at latitude $\varphi ={32}^{°}{6}^{\prime }$ N (Tel Aviv, Israel), have the following characteristics:

• For collectors deployed on horizontal planes, the inter-row distance $D$ may be determined nearly equally by the “winter solstice rule” (for example, $D=1.05$ m) or by the criterion ${\gamma }_c={\gamma }_s$, up to collector azimuth ${\gamma }_c={20}^{°}$; however, the inter-row spacing, based on ${\gamma }_c={\gamma }_s$ criterion, then increases rapidly for ${\gamma }_c>{40}^{°}$, resulting in large spacing; however, less shading losses are obtained;
• Reduction in shading losses is obtained by applying the new ${\gamma }_c={\gamma }_s$ criterion for collector deployment with an azimuth $\ne 0^{°}$; see Figure 9, for example;
• The inter-row spacing for collectors deployed on south-facing slopes is usually determined by the distance required for maintenance; for example, $D=0.8$ m;
• Collectors may be deployed on northern slopes with acceptable spacing on account of increasing shading;
• Optimal PV system designs for maximum annual incident solar energy tend to result in minimum inter-row spacing (for example $D=0.8$ m—maintenance distance) for all azimuth angles of the collectors in order to increase the number of collector rows in the given solar field, and hence, to obtain high incident energies;
• At the latitude $\varphi ={52}^{°}{12}^{\prime }$ N, it was assumed that an inclination angle $\beta ={20}^{°}$, and collector width $H=2.12$ m for comparison with the results for $\varphi ={32}^{°}{6}^{\prime }$ N. A low percentage of shading losses is obtained for ${\gamma }_c={\gamma }_s$ criterion due to large inter-row spacing.