Investing in Wind Energy Using Bi-Level Linear Fractional Programming
Abstract
1. Introduction
1.1. Backgrounds
1.2. Literature Survey
1.3. Aims and Contributions
2. Problem Statement
3. Solution Strategy
| Algorithm 1 Newton’s method to find |
| Read: Data and |
| Initialization: , , |
| While do |
| Solve problem (41)–(42). Denote its optimal solution as and its optimal objective function as . |
| ,, |
| End while |
| Return optimal values of and decision variables of problem (32)–(40) |
4. Numerical Results
- Investment in wind energy is increased by around 135% in case (b). The wind investment grows to increase the wind power generation, thereby reducing the fractional objective function defined by Equation (4). However, the profit of wind farms in case (b) is lower than that in case (a) by 33%.
- As expected, the annual energy production of thermal units in case (a) is 49% higher compared with case (b), which is due to the higher number of wind farms installation in the power system in case (b). Note that the production cost of a wind farm is assumed to be negligible. It is inferred that the carbon emission would be much less in case (b).
- It would be interesting to compare the ratio of expected operation cost to the expected wind power generation, i.e., for both cases. This value for case (a) is 78.5, while it is 28.1 for case (b), which shows a significant decrease of 64%, indicating that the model is an effective way to accommodate more wind power.
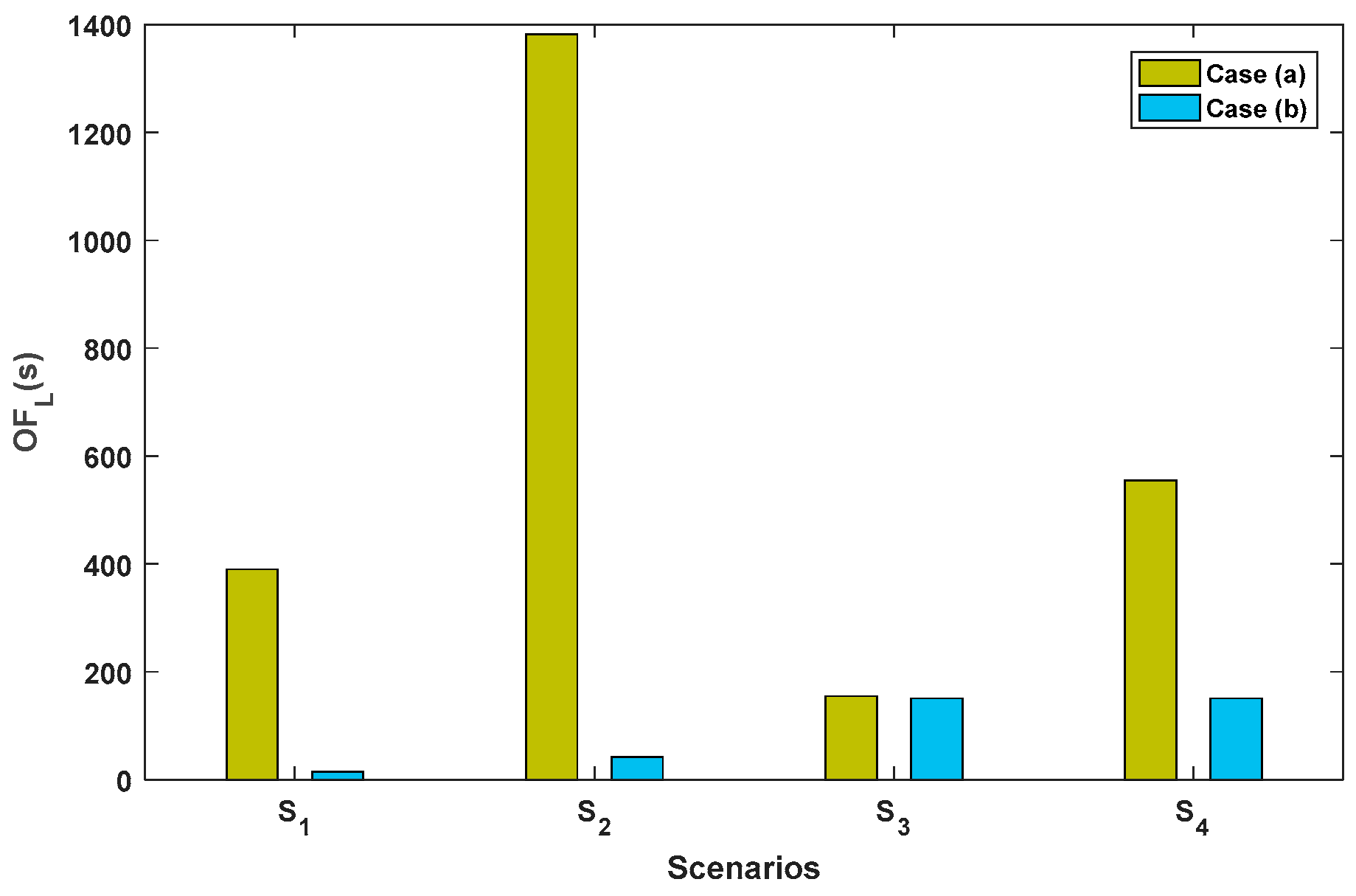
- Scenario 1 (denoted by S1): load demand () and wind intensity () are at their maximum values: .
- Scenario 2 (denoted by S2): load demand is at its maximum value, and wind intensity is at its minimum value: .
- Scenario 3 (denoted by S3): load demand is at its minimum value, and wind intensity is at its maximum value: .
- Scenario 4 (denoted by S4): load demand and wind intensity are at their minimum value: .
5. Conclusions
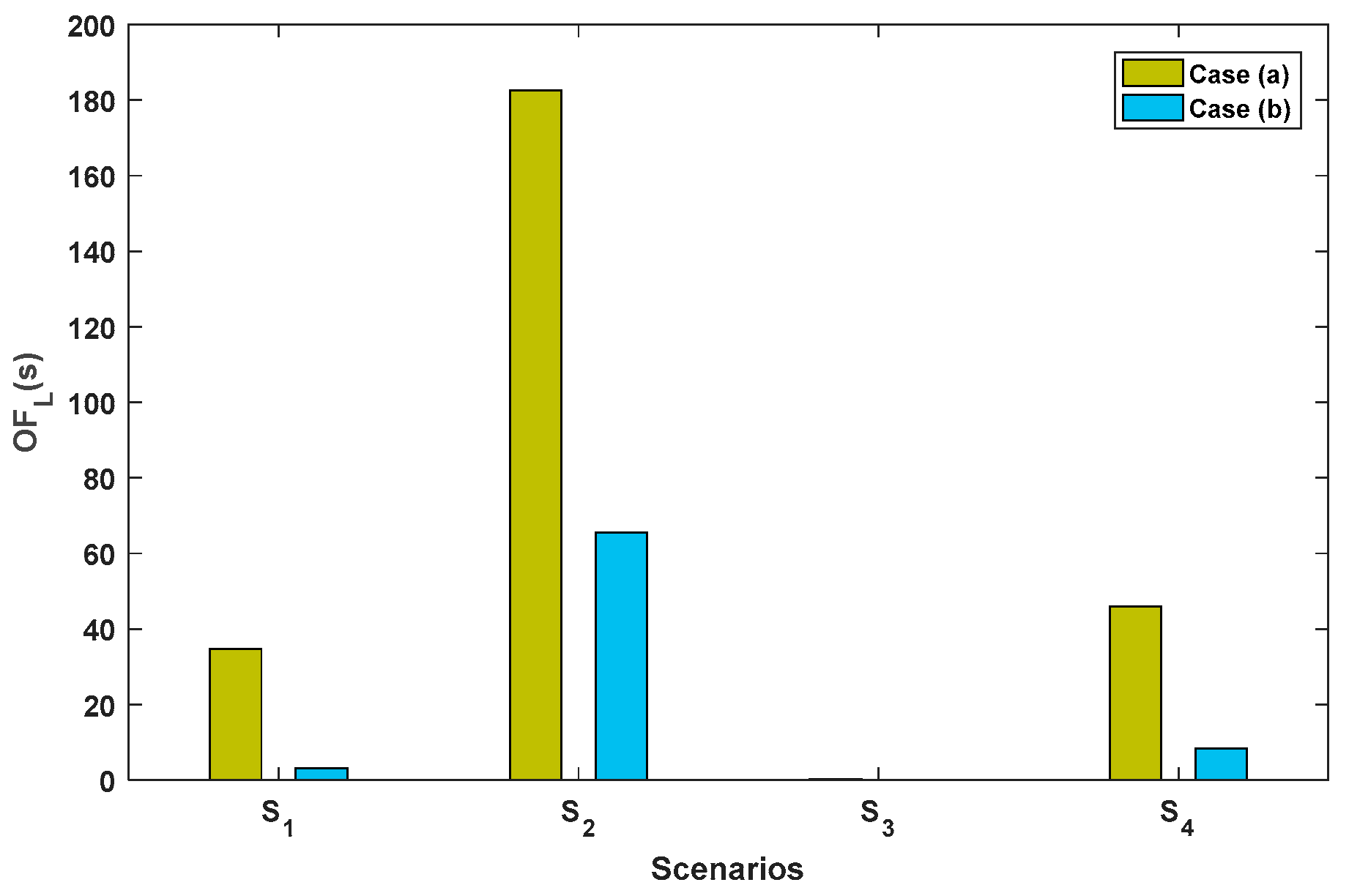
- The lower level’s objective function, i.e., is the same for scenario 3, where load demand is at its minimum value, and wind intensity is at its maximum.
- The ratio has the largest difference between cases (a) and (b) in scenario 2, where load demand is at its maximum value, and wind intensity is at its minimum.
- As the load grows, is first reduced in case (a). However, after reaching a particular point in which has its minimum amount, this ratio increases. For a sufficient amount of load growth, would be the same for both cases (a) and (b).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
- Indices and sets:
Index of blocks and set of all blocks. , Index of buses and set of all buses. s, Index of scenarios and set of all scenarios. - Parameters:
Susceptance of lines (1/). Generation cost of thermal units ($/MWh). Annualized investment cost of wind farm ($). Available investment budget ($). Coefficient related to different levels of electric load . Wind intensity . Maximum of the electric demand (MW). Capacity of a line (MW). Maximum and minimum generation of a thermal unit (MW). Wind capacity of the th block (MW). Number of hours in scenario s. Maximum voltage angle (Rad). Electricity price ($/MWh). - Variables:
Power flow through lines (MW). Power output of thermal units (MW). Power output of wind farms (MW). Capacity of a wind farm (MW). Binary variable equal to 1 if the bth block specify the wind farm capacity. , Voltage angle at node i and at the reference bus (Rad).
References
- IRENA (International Renewable Energy Agency). Wind Energy. 2020. Available online: https://www.irena.org/wind (accessed on 20 June 2023).
- National Energy Administration. Reports on Wind Power Annual Operation. Available online: http://www.nea.gov.cn/2019-01/28/c_137780779.htm (accessed on 20 June 2023).
- Xia, F.; Lu, X.; Song, F. The Role of Feed-in Tariff in the Curtailment of Wind Power in China. Energy Econ. 2020, 86, 104661. [Google Scholar] [CrossRef]
- Baringo, L.; Conejo, A.J. Wind Power Investment within a Market Environment. Appl. Energy 2011, 88, 3239–3247. [Google Scholar] [CrossRef]
- Baringo, L.; Conejo, A.J. Wind Power Investment: A Benders Decomposition Approach. IEEE Trans. Power Syst. 2012, 27, 433–441. [Google Scholar] [CrossRef]
- Baringo, L.; Conejo, A.J. Risk-Constrained Multi-Stage Wind Power Investment. IEEE Trans. Power Syst. 2013, 28, 401–411. [Google Scholar] [CrossRef]
- Li, C.; Lu, G.; Wu, S. The Investment Risk Analysis of Wind Power Project in China. Renew. Energy 2013, 50, 481–487. [Google Scholar] [CrossRef]
- Baringo, L.; Conejo, A.J. Strategic Wind Power Investment. IEEE Trans. Power Syst. 2014, 29, 1250–1260. [Google Scholar] [CrossRef]
- Baringo, L.; Conejo, A.J. Transmission and Wind Power Investment. IEEE Trans. Power Syst. 2012, 27, 885–893. [Google Scholar] [CrossRef]
- Zolfaghari, S.; Akbari, T. Bilevel Transmission Expansion Planning Using Second-Order Cone Programming Considering Wind Investment. Energy 2018, 154, 455–465. [Google Scholar] [CrossRef]
- Barforoushi, T. Strategic Wind Power Investment in Competitive Electricity Markets Considering the Possibility of Participation in Intraday Market. IET Gener. Transm. Distrib. 2020, 14, 2676–2686. [Google Scholar]
- Nikkhah, S.; Rabiee, A. Optimal Wind Power Generation Investment, Considering Voltage Stability of Power Systems. Renew. Energy 2018, 115, 308–325. [Google Scholar] [CrossRef]
- Lam, J.C.K.; Woo, C.K.; Kahrl, F.; Yu, W.K. What Moves Wind Energy Development in China? Show Me the Money! Appl. Energy 2013, 105, 423–429. [Google Scholar] [CrossRef]
- Hitaj, C.; Löschel, A. The Impact of a Feed-in Tariff on Wind Power Development in Germany. Resour. Energy Econ. 2019, 57, 18–35. [Google Scholar] [CrossRef]
- Arabpour, A.; Besmi, M.R.; Maghouli, P. Transmission Expansion and Reactive Power Planning Considering Wind Energy Investment Using a Linearized AC Model. J. Electr. Eng. Technol. 2019, 14, 1035–1043. [Google Scholar] [CrossRef]
- Alishahi, E.; Moghaddam, M.P.; Sheikh-El-Eslami, M.K. A System Dynamics Approach for Investigating Impacts of Incentive Mechanisms on Wind Power Investment. Renew. Energy 2012, 37, 310–317. [Google Scholar] [CrossRef]
- Li, H.; Qiao, Y.; Lu, Z.; Zhang, B.; Teng, F. Frequency-Constrained Stochastic Planning Towards a High Renewable Target Considering Frequency Response Support from Wind Power. IEEE Trans. Power Syst. 2021, 36, 4632–4644. [Google Scholar] [CrossRef]
- Ullmark, J.; Göransson, L.; Chen, P.; Bongiorno, M.; Johnsson, F. Inclusion of Frequency Control Constraints in Energy System Investment Modeling. Renew. Energy 2021, 173, 249–262. [Google Scholar] [CrossRef]
- Gil-González, W.; Montoya, O.D.; Grisales-Noreña, L.F.; Perea-Moreno, A.-J.; Hernandez-Escobedo, Q. Optimal Placement and Sizing of Wind Generators in AC Grids Considering Reactive Power Capability and Wind Speed Curves. Sustainability 2020, 12, 2983. [Google Scholar] [CrossRef]
- Baringo, L.; Conejo, A.J. Correlated Wind-Power Production and Electric Load Scenarios for Investment Decisions. Appl. Energy 2013, 101, 475–482. [Google Scholar] [CrossRef]
- Spyridonidou, S.; Vagiona, D.G.; Loukogeorgaki, E. Strategic Planning of Offshore Wind Farms in Greece. Sustainability 2020, 12, 905. [Google Scholar] [CrossRef]
- Xu, M.; Zhuan, X. Optimal Planning for Wind Power Capacity in an Electric Power System. Renew. Energy 2013, 53, 280–286. [Google Scholar] [CrossRef]
- Zhao, X.; Yao, J.; Sun, C.; Pan, W. Impacts of Carbon Tax and Tradable Permits on Wind Power Investment in China. Renew. Energy 2019, 135, 1386–1399. [Google Scholar] [CrossRef]
- Zhu, M.; Qi, Y.; Belis, D.; Lu, J.; Kerremans, B. The China Wind Paradox: The Role of State-Owned Enterprises in Wind Power Investment versus Wind Curtailment. Energy Policy 2019, 127, 200–212. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhai, Q.; Yuan, W.; Wu, J. Capacity Expansion Planning for Wind Power and Energy Storage Considering Hourly Robust Transmission Constrained Unit Commitment. Appl. Energy 2021, 302, 117570. [Google Scholar] [CrossRef]
- Ouammi, A.; Dagdougui, H.; Sacile, R. Optimal Planning with Technology Selection for Wind Power Plants in Power Distribution Networks. IEEE Syst. J. 2019, 13, 3059–3069. [Google Scholar] [CrossRef]
- Ayvaz, A.; Genc, I. A Novel Optimization Method for Wind Power Investment Considering Economic and Security Concerns. J. Renew. Sustain. Energy 2022, 14, 16301. [Google Scholar] [CrossRef]
- García Mazo, C.M.; Olaya, Y.; Botero Botero, S. Investment in Renewable Energy Considering Game Theory and Wind-Hydro Diversification. Energy Strateg. Rev. 2020, 28, 100447. [Google Scholar] [CrossRef]
- Alshamrani, A.M.; Alrasheedi, A.F.; Alnowibet, K.A. A Game-Theoretic Model for Wind Farm Planning Problem: A Bi-Level Stochastic Optimization Approach. Sustain. Energy Technol. Assess. 2022, 53, 102539. [Google Scholar] [CrossRef]
- Aquila, G.; de Queiroz, A.R.; Balestrassi, P.P.; Rotella Junior, P.; Rocha, L.C.S.; Pamplona, E.O.; Nakamura, W.T. Wind Energy Investments Facing Uncertainties in the Brazilian Electricity Spot Market: A Real Options Approach. Sustain. Energy Technol. Assess. 2020, 42, 100876. [Google Scholar] [CrossRef]
- Liu, Q.; Sun, Y.; Liu, L.; Wu, M. An Uncertainty Analysis for Offshore Wind Power Investment Decisions in the Context of the National Subsidy Retraction in China: A Real Options Approach. J. Clean. Prod. 2021, 329, 129559. [Google Scholar] [CrossRef]
- Xu, G.; Cheng, H.; Fang, S.; Ma, Z.; Zeng, P.; Yao, L. Optimal Size and Location of Battery Energy Storage Systems for Reducing the Wind Power Curtailments. Electr. Power Compon. Syst. 2018, 46, 342–352. [Google Scholar] [CrossRef]
- Neto, D.P.; Domingues, E.G.; Calixto, W.P.; Alves, A.J. Methodology of Investment Risk Analysis for Wind Power Plants in the Brazilian Free Market. Electr. Power Compon. Syst. 2018, 46, 316–330. [Google Scholar] [CrossRef]
- Zeng, B.; Zhang, J.; Ouyang, S.; Yang, X.; Dong, J.; Zeng, M. Two-Stage Combinatory Planning Method for Efficient Wind Power Integration in Smart Distribution Systems Considering Uncertainties. Electr. Power Compon. Syst. 2014, 42, 1661–1672. [Google Scholar] [CrossRef]
- Liu, Q.; Sun, Y.; Wu, M. Decision-Making Methodologies in Offshore Wind Power Investments: A Review. J. Clean. Prod. 2021, 295, 126459. [Google Scholar] [CrossRef]
- Huang, S.; Suo, C.; Guo, J.; Lv, J.; Jing, R.; Yu, L.; Fan, Y.; Ding, Y. Balancing the Water-Energy Dilemma in Nexus System Planning with Bi-Level and Multi-Uncertainty. Energy 2023, 278, 127720. [Google Scholar] [CrossRef]
- Yang, J.; Shi, X.; Prokopyev, O.A. Exact Solution Approaches for a Class of Bilevel Fractional Programs. Optim. Lett. 2022, 17, 191–210. [Google Scholar] [CrossRef]
- Radzik, T. Fractional Combinatorial Optimization. In Handbook of Combinatorial Optimization; Springer: Berlin/Heidelberg, Germany, 1998; pp. 429–478. [Google Scholar]
- Borrero, J.S.; Gillen, C.; Prokopyev, O.A. Fractional 0–1 Programming: Applications and Algorithms. J. Glob. Optim. 2017, 69, 255–282. [Google Scholar] [CrossRef]
- Dinkelbach, W. On Nonlinear Fractional Programming. Manag. Sci. 1967, 13, 492–498. [Google Scholar] [CrossRef]
- A Guide for GAMS software, G.U.; GAMS Development Corporation: Washington, DC, USA, 2014.
- Gurobi Optimization, “Gurobi Optimizer Reference Manual”. Available online: http://www.gurobi.com (accessed on 20 June 2023).
- Investing in Wind Energy Using Bi-Level Linear Fractional Programming. 2022. Available online: https://drive.google.com/file/d/1qar6r8vlf3mfgk2u91jll69t6ccmyght/view?usp=sharing (accessed on 20 June 2023).



| Case (a): Bi-Level Linear Programming | Case (b): Bi-Level Fractional Programming | |
|---|---|---|
| Optimal wind farms location and capacity (MW) | 27 (500), 42 (200), 48 (200), 59 (500), 75 (150), 82 (50), 83 (50), 100 (450) | 12 (350), 24 (500), 27 (500), 31 (300), 42 (500), 48 (400), 59 (500), 75 (500), 82 (400), 83 (300), 95 (400), 99 (250), 100 (50) |
| Wind investment capacity (MW) | 2100 | 4950 |
| Wind annualized investment cost ($) | 2.52 × 108 | 5.94 × 108 |
| Expected annual revenue ($) | 2.95 × 108 | 6.23 × 108 |
| Expected annual profit ($) | 4.3 × 107 | 2.9 × 107 |
| Expected annual operation cost ($) | 8.71 × 108 | 6.20 × 108 |
| Expected annual production of thermal units (MWh) | 3.37 × 107 | 2.26 × 107 |
| Expected annual production of wind farms (MWh) | 1.11 × 107 | 2.21 × 107 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alrasheedi, A.F.; Alshamrani, A.M.; Alnowibet, K.A. Investing in Wind Energy Using Bi-Level Linear Fractional Programming. Energies 2023, 16, 4952. https://doi.org/10.3390/en16134952
Alrasheedi AF, Alshamrani AM, Alnowibet KA. Investing in Wind Energy Using Bi-Level Linear Fractional Programming. Energies. 2023; 16(13):4952. https://doi.org/10.3390/en16134952
Chicago/Turabian StyleAlrasheedi, Adel F., Ahmad M. Alshamrani, and Khalid A. Alnowibet. 2023. "Investing in Wind Energy Using Bi-Level Linear Fractional Programming" Energies 16, no. 13: 4952. https://doi.org/10.3390/en16134952
APA StyleAlrasheedi, A. F., Alshamrani, A. M., & Alnowibet, K. A. (2023). Investing in Wind Energy Using Bi-Level Linear Fractional Programming. Energies, 16(13), 4952. https://doi.org/10.3390/en16134952







