Abstract
Heating, ventilation, and air conditioning (HVAC) systems play a crucial role in either increasing or decreasing the risk of airborne disease transmission. High ventilation, for instance, is a common method used to control and reduce the infection risk of airborne diseases such as COVID-19. On the other hand, high ventilation will increase energy consumption and cost. This paper proposes an optimal HVAC controller to assess the trade-off between energy consumption and indoor infection risk of COVID-19. To achieve this goal, a nonlinear model predictive controller (NMPC) is designed to control the HVAC systems of a university building to minimize the risk of COVID-19 transmission while reducing building energy consumption. The NMPC controller uses dynamic models to predict future outputs while meeting system constraints. To this end, a set of dynamic physics-based models are created to capture heat transfer and conservation of mass, which are used in the NMPC controller. Then, the developed models are experimentally validated by conducting experiments in the ETLC building at the University of Alberta, Canada. A classroom in the building is equipped with a number of sensors to measure indoor and outdoor environmental parameters such as temperature, relative humidity, and concentration. The validation results show that the model can predict room temperature and concentration by 0.8%, and 2.4% mean absolute average errors, respectively. Based on the validated models, the NMPC controller is designed to calculate the optimal airflow and supply air temperature for every 15 min. The results for real case studies show that the NMPC controller can reduce the infection risk of COVID-19 transmission below 1% while reducing energy consumption by 55% when compared to the existing building controller.
1. Introduction
Healthy indoor air quality (IAQ) is always critically important, especially when humans struggle with airborne diseases such as influenza (H1N1), severe acute respiratory syndrome (SARS), Middle East respiratory syndrome (MERS), and now SARS-CoV-2 (COVID-19), which have caused considerable damage to the lives of millions of people around the world [1]. For example, by 6 April 2023, there were 762,201,169 confirmed COVID-19 cases, including 6,893,190 deaths, reported by the World Health Organization (WHO) (https://www.who.int/, accessed on 6 April 2023). Micro-organisms can become airborne when droplets are generated during coughing, breathing, talking, sneezing, singing, etc., which can lead to infectious aerosols. These infectious aerosols can infect many hosts in indoor environments, as people spend nearly 90 percent of their time inside buildings such as homes, schools, offices, shops, and other indoor environments [2,3,4]. Some initial steps such as wearing masks, washing and sanitizing hands, being quarantined, and keeping social distance can help to reduce the infection risk of contact transmissions [5]. However, improving indoor air quality in enclosed areas is an efficient and fundamental approach to ease or dilute the concentration of viral aerosols.
Heating, ventilation, and air conditioning (HVAC) systems can significantly reduce infection risk. These systems prepare comfortable zones by controlling the relative humidity, temperature, and airflow, while removing pollutants from buildings’ indoor and outdoor air. HVAC systems have a dual role in maintaining thermal comfort and acceptable indoor air quality. Thus, improving and controlling the design and operation parameters of HVAC systems by using high-efficiency filters or ultraviolet irradiation (UV) lights, advanced air distribution, personal ventilation, controlling ventilation rate (dilution), relative humidity, temperature, and air distribution (directional airflow) can be some of the best steps to reduce and deactivate the aerosol particles in indoor environments.
Many articles have investigated the role of HVAC parameters in reducing airborne diseases; some articles [6,7] reviewed the role of high-efficiency particulate air (HEPA) filtration in removing or deactivating infectious particles. Several studies [8,9,10] have shown that using UV lights in HVAC systems can reduce the airborne infection risk in indoor environments. Qian et al. [11,12] compared three common ventilation systems: downward, displacement, and mixing. They investigated three locations for the exhaust to notice which one of them performs better to decrease the risk of infection.
On the other hand, HVAC systems consume about 40% of buildings’ energy [13,14,15]. As mentioned before, ventilation is critical in reducing the transmission of airborne disease in indoor environments. Still, increasing ventilation to minimize the infection transmission probability causes high energy consumption and costs; thus, a suitable HVAC controller is desired to provide required IAQ and desired thermal comfort while decreasing energy consumption.
Different control approaches have been used in buildings to control HVAC systems. These approaches include two-position on and off control, proportional–integral (PI) control, proportional–integral–derivative (PID) control, model predictive control (MPC), etc. [16,17,18]. Compared with other controllers, the MPC controller can reduce energy consumption and maintain proper IAQ [18,19]. The MPC controller can predict states with reasonable accuracy by using dynamic models of buildings while being tuned to system constraints. The dynamic models of building and HVAC systems are often nonlinear. However, in most studies, nonlinear dynamic models were simplified to linear ones using linear MPC controllers. Another approach is using nonlinear model predictive controllers (NMPC) that use the nonlinear models directly and provide better control results compared to the linear MPC approach. Figure 1 outlines some of the prior HVAC control studies and the types of controllers used.
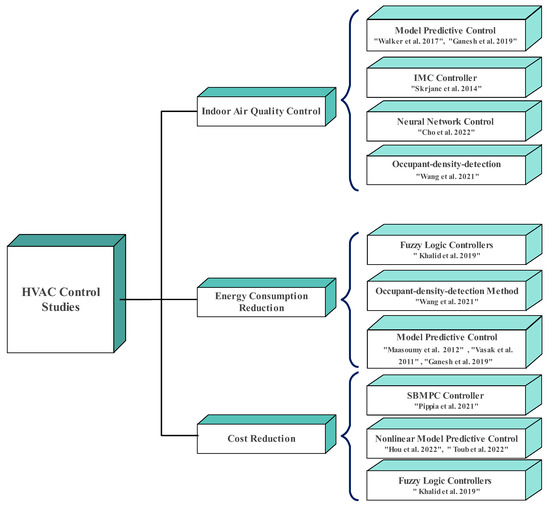
Figure 1.
Classification of the control methods in HVAC systems including some of the prior studies [20,21,22,23,24,25,26,27,28,29,30].
Many studies support the role of HVAC systems in reducing airborne infectious diseases; however, only a few studies have investigated the control of HVAC systems to minimize both the infection transmission risk and energy consumption. For instance, Wang et al. [20] used an intelligent ventilation control according to occupant densities. They studied a new detection algorithm to recognize the distance of occupancy to decrease the infection risk of COVID-19. On the other hand, many articles have studied the role of controllers in preparing the proper IAQ (i.e., level, formaldehyde, ozone, etc.) or thermal comfort with minimizing energy consumption. There is a lack of multi-objective studies in HVAC optimal control literature to (i) minimize HVAC energy consumption, (ii) control IAQ, and (iii) minimize risk of COVID virus transmission by maintaining the risk level less than 1%. This work aims to address this important gap in the HVAC control studies.
Walker et al. [21] compared the performance of two methods of MPC, centralized and distributed methods, for indoor temperature and level with natural ventilation. Maasoumy et al. [22] presented an MPC approach to reduce energy consumption in the HVAC system of a university campus building by controlling the air mass flow rate. Vasak et al. [23] developed an MPC algorithm using a resistor-capacitor (RC) thermal model to control the HVAC system of a residential household. Pippia et al. [24] proposed that combining a stochastic scenario-based MPC (SBMPC) controller with a nonlinear Modelica model can provide more accurate results for buildings heating systems than the linear models. Ganesh et al. [25] used model predictive control to calculate the optimal ventilation rate to decrease indoor pollutant concentrations, such as formaldehyde (HCHO), ozone, and particulate matter (PM) while minimizing total energy consumption. Hou et al. [26] proposed the nonlinear model predictive control to decrease heating costs in university building heating systems while satisfying indoor temperatures. Toub et al. [27] proposed a nonlinear model predictive controller to control MicroCSP and building HVAC systems to optimize energy usage and reduce costs. Skrjanc et al. [28] designed an internal model controller (IMC) with an internal loop to control the level in an indoor environment. Cho et al. [29] developed an integrated model based on an artificial neural network to predict the indoor concentrations of , , and . They showed that the model has high accuracy in predicting these values. Khalid et al. [30] used a fuzzy logic controller for an HVAC system to reduce energy consumption, cost, and peak-to-average ratio (PAR).
A critical review of the papers cited in Figure 1 and the papers discussed in this section shows (i) most HVAC optimal control studies used linear or linearized models inside model-based optimal controllers to reduce computational cost. This adversely affects the performance of these controllers outside the calibrated region, and increases controller calibration efforts, (ii) data-driven HVAC controllers (e.g., fuzzy logic controllers) suffer from their capability for scalability and substantial efforts are required for tuning membership functions by changing building types and building applications, (iii) there is lack of multi-objective optimal control studies that takes into account “all” major factors including energy consumption, temperature, and relative humidity comfort levels of occupants in a building, IAQ, and airborne virus transmission risk, (iv) there are missing“control-oriented” HVAC models that include inter-relations among room air temperature, relative humidity, risk of airborne virus transmission, and supply air velocity, (v) there is need for model-based real-time HVAC controllers to adjust “flow velocity and flow direction” in a building to reduce the virus transmission via airborne particles and droplets, and (vi) it is challenging to estimate and control airborne virus transmission risk by only knowing the number of occupants in a room. This paper aims to provide contributions in the identified research gaps of (i) to (iii) by using “physics-based” scalable building models, design of a multi-objective nonlinear model predictive control (NMPC) for a building HVAC system, and use of statistical models to estimate COVID virus transmission risk by considering the number of occupants in a room and adjusting air flow rate and supply air temperature.
To the best of the authors’ knowledge, this is the first study undertaken to design and implement NMPC on HVAC systems to minimize the infection risk of airborne diseases such as COVID-19, while reducing the energy consumption of HVAC systems and meeting thermal comforts of occupants. The NMPC will enable a constrained optimal solution for complex coupled HVAC and air quality control problems.
The primary objectives of this paper are to investigate the effect of optimal controllers on reducing the transmission risk of airborne diseases and HVAC energy consumption. The main new contributions of this work are (i) modeling of a large classroom in order to predict room temperature, indoor air quality, and energy consumption, (ii) designing a nonlinear model predictive HVAC controller to adjust airflow and supply air temperature to reduce the concentrations of deadly airborne droplets under low risk level and provide a thermal comfort zone while also minimizing the energy consumption of the HVAC system, (iii) experimental data from the HVAC operation and classroom participation during COVID-19 time, and (iv) simulation for the real case studies and comparison with the actual building controller.
This paper is organized as follows. Mathematical models are built in Section 3.4 to determine the concentrations of deadly airborne droplets, temperature, and concentration. Next, based on these dynamic models, a nonlinear model predictive control (NMPC) will be designed in Section 3 to determine the optimal airflow and supply air temperature in real-time. Finally, NMPC results are presented in Section 4, and then the potential of NMPC controllers for building energy saving will be discussed in a real case study.
2. Test Setup
The test bed in this study is a lecture hall located on the ground floor of the north side of the ETLC building at the University of Alberta, Edmonton, Canada. The ETLC building, depicted in Figure 2a, is situated on the western edge of the University of Alberta in Edmonton, Canada. This six-story building primarily serves as an educational facility, housing offices and laboratories. Regarding the HVAC systems of the building, there is a central mechanical ventilation system to provide the required conditioned air to ensure a comfortable indoor environment in the building. Figure 2b provides a photo of the classroom and its location in the ETLC building. The lecture hall area is about 300 and it can accommodate up to 120 people. This classroom has 15 supply air diffusers and 8 return air grills and it is surrounded by two corridors, a neighboring lecture classroom, and a thick concrete wall connected to the outdoor area (Figure 2b). The classroom has three entrances but no window (Figure 2a).
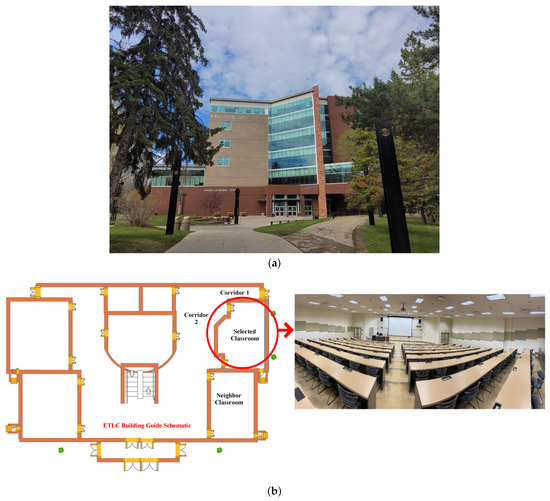
Figure 2.
Testbed in this study: (a) ETLC building, (b) the classroom on the ground floor of the ETLC building at the University of Alberta.
An AHU is the heart of central air conditioning, responsible for blending outside air with the recirculated air from the building within a mixing box. It employs various types of air filters to effectively eliminate dust, mold, bacteria, and other harmful particles from the combined air. Subsequently, the AHU utilizes a cooling coil, heating coil, and a humidifier to regulate the air temperature and relative humidity to desired levels. Finally, the AHU distributes the comfortable and clean air to individual rooms through ductwork. The AHU under study consists of several components, including a mixing box, pleated filters (primary filters), a water heating coil, a water cooling coil, a humidifier, supply and return fans, and access doors for each section. Each class in the ETLC building is equipped with variable air volume (VAV) boxes. The fresh air is propelled by the supply fans to go through the VAV boxes for air conditioning before entering the ETLC building classrooms.
The air volume flow rate and the supply air temperature can be controlled by adjusting the dampers and reheating coils of the VAV boxes. The air volume that flows through the VAV boxes relates to the damper’s position inside the VAV. The VAV reheating coils in the ETLC building receive hot water from central steam boilers on the main campus of the University of Alberta.
The selected lecture classroom is equipped with three VAV boxes, as shown in Figure 3.
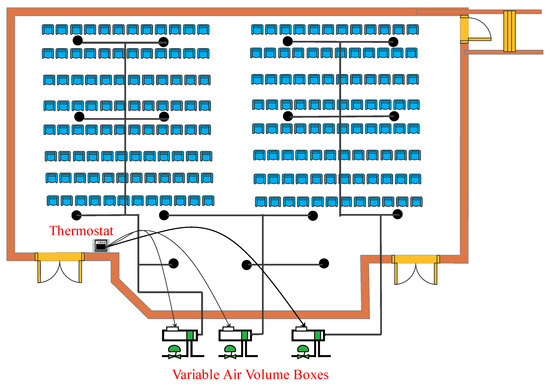
Figure 3.
Air supply layout in the classroom, showing the location of supply-air diffusers (i.e., black circles in the image) and the duct line in the classroom.
The existing building HVAC controller regulates the VAV damper’s position and the reheating coil’s valve based on feedback from the thermostat installed in each classroom. The control logic of the HVAC controller is shown in Figure 4. This controller tracks the given set point, and it does not have any ability to improve energy consumption by predicting the temperature trajectory. However, during the COVID-19 pandemic, in order to decrease the transmission of infection risk, the position of VAV dampers was kept constant to provide the maximum ventilation, and the classroom’s temperature was only controlled by the valves of heating coil in the VAV boxes.
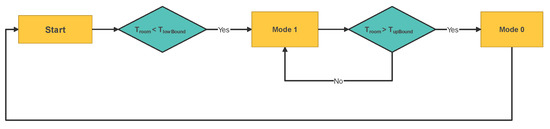
Figure 4.
Control logic of the rule-based HVAC controller in the building. Mode 1 corresponds to the initiation of a reheat cycle, whereas Mode 0 identifies the heating coil idle state. During the COVID time in winter 2022, a constant high air volume flow rate of 4400 CFM was applied during week days to minimize COVID transmission risk.
During the test, the lecture classroom is equipped with nine sensors shown in Figure 5. These sensors can measure indoor and outdoor environmental parameters including temperature, relative humidity, and levels. These sensors were responsible for measuring the temperatures of the neighbor classroom, corridors, outdoor air, and supplied air. In addition, two of the sensors can monitor both concentration and air temperature.

Figure 5.
Location of installed sensors (S) in the testbed.
The measurement devices included three Omega wireless sensors OM-EL-WIFI-TH, four Elitech RC-4HC, one Airthings carbon dioxide meter, and one DOEATOOW indoor monitor. The sensors constantly measured and reported the temperature in C, relative humidity in RH %, and carbon dioxide levels in parts per million (ppm).
Three wireless sensors were placed inside supply ducts to measure the supply air temperature from each VAV box. Additionally, two sensors, labeled as and , were positioned in different height level of the classroom to measure the temperature and concentration of the classroom.
3. Plant Models for Use in Controller
To design of HVAC model-based controller in this study, access to dynamic models is required to predict changes in the classroom temperature, concentration (ventilation requirement), and the risk of COVID virus transmission. Specifically, in Section 4, a nonlinear model predictive controller (NMPC) will be designed, which necessitates simulating the classroom temperature, concentration, and risk of COVID virus transmission over specific prediction horizons. There are demands for developing models that are computationally efficient for embedding inside the ” real-time” NMPC that has limited computational power, which it requires to simulate these nonlinear models for the required prediction horizon (e.g., the next 60 min or 24 h). These models will be included as equality constraints in the NMPC framework to consider the classroom thermal dynamics and air ventilation dynamics. In this section, well-recognized computationally efficient accurate models for HVAC and COVID transmission risk calculation are selected and parameterized for the ETLC classroom.
In this work, physical models are used wherever possible to allow easier understanding of HVAC control actions along with their link to the system states, and also providing better scalability for different building types and HVAC applications. To this end, the building thermal behavior and variations in concentrations of the room are simulated by using physical models; however, statistical models are used for estimating airborne virus transmission. For control purpose in this work, the models are selected such that they can be represented in the form of ordinary differential equations (ODEs) that are preferred for the controller design.
In this section, first, a dynamic model is developed to gain insight into the infection risk on the classroom based on the number of people in the classroom and the supply airflow. Then, another model is developed to estimate the concentration of , which is based on the ventilation rate and the number of people. Furthermore, a thermal model of the classroom is developed to predict how the classroom temperature changes through adjusting the supply air temperature and air flow rate. Subsequently, all these models are integrated together inside the NMPC controller to find the optimal control actions for maintaining indoor air quality, mitigating infection risks, and minimizing HVAC system energy consumption.
All equations in the paper are shown in continuous time domain, except for equations shown with index (k) that refers to discrete time domain.
3.1. Dynamic Model of Airborne COVID-19 Transmission Risk
One of the well-known models for estimating the infection risk assessment in indoor environments is the Wells–Riley equation [31]. This model is based on the “quantum of infection,” defined as the number of infectious airborne particles required to cause infection in 63% of susceptible persons [32]. Regarding the Wells–Riley equation, the probability (P) of infection can be defined by the following equation [33]:
where, C is the number of new infection cases, and S is the number of susceptible people. n is the number of quanta inhaled, which depends on the time-average quanta concentration (, ), the volumetric breathing rate of an occupant (, ) and the duration of the event (D, h) [33]:
Volumetric breathing rate () depends on the type of activities and age; in this study, by considering a light activity in the classroom, the value of is defined as 0.3 [34]. In order to calculate the average quanta concentration, a mathematical model is used to estimate the airborne disease transmission rate in the zone. This model will also be utilized in the model predictive controller.
One of the assumptions of the Wells–Riley equation is that the air is well mixed, causing a uniform concentration of particles inside the space. By considering this assumption as well as the conservation of mass principle, the infection risk model is defined as [33]:
where C is the quanta concentration (quanta per ), ER is the quanta emission rate (quanta per hour), I is the number of infected people, presents the ventilation rate (per hour), which is calculated by dividing the air volume flow rate by the volume of the room, is the volume of the zone (), and t is time (h). The quanta emission rate (ER) relies on factors such as viral load, inhalation rate, and droplet volume concentration, which depends on occupant activities; the ER can vary over an extensive range of 3–300 quanta/h [35]. In this paper, by considering light activity in the classroom such as speaking, the quanta emission rate is considered equal to 58 quanta/h [34]. Regarding the Wells–Riley Equation (1), infection probability is related to the number of quanta inhaled by susceptible people. Thus, decreasing the concentration of quanta in an enclosed area reduces the infection risk. In most studies, the number of infected people is considered one, whereas in reality, the number of infected people in a zone may be more than one person. To determine how many infected people may be inside, the prevalence rate of the disease, , can be estimated by the following equation [36]:
where presents daily new COVID cases, is the fraction of unreported COVID cases, PP is the population, and is the length of the time infectious to COVID-19, and is the number of people in the classroom. For example, by considering the Edmonton population of about 1.519 million, the value of is 75% [37], the length of time for the infectious period (D) is 10 days [38], and the new cases of COVID-19 during March 2022, the population prevalence rate is calculated to be . Therefore, equals of people is considered for March 2022 when this study was conducted.
3.2. Concentration Model
By using the mass balance equation for concentrations and assuming a well-mixed single zone model, the equation to capture changes will be [39]:
where is the room volume (), is the indoor concentration (), represents the outdoor concentration (), and is the volume flow rate of air (). By assuming that the density of air remains constant, it can be defined where is the mass flow rate. E is the emission rate of indoor sources; generally, E is calculated by , where is the number of individuals in the classroom and is generation rate per person (). The generation rate by a person is considered about 7.83 [39].
3.3. Building Thermal Model
Here, the concept of equivalent thermal resistance-capacitance (RC) modeling [13] is used to predict room temperature variations. The temperature of the classroom depends not only on the supply air temperature and air mass flow rate but also on the temperatures of neighboring classrooms, outside air temperature, and the thermal properties of the walls and windows surrounding the classroom. The heat transfer and heat storage equations will be used to define the classroom’s temperature changes by using the RC model for the classroom:
where is the temperature of the classroom neighbors, is the temperature of the classroom, is the temperature of the walls, is the supply air temperature, is the mass flow rate of the supply air , is radiation heat transfer coefficient, represents the total radiation heat flow that reaches the wall, are the neighboring room temperatures, is thermal resistance, which includes and (thermal resistances for indoor and outdoor walls), and and are the heat storage capacity of the classroom and walls, respectively. In the dynamic thermal model of the classroom, , which has the lower thermal capacitance, represents the fast-dynamic mass (e.g., supply air), and , which has the higher thermal capacitance, represents the slow dynamic mass (e.g., solid parts including walls). is the internal heat generation in the classroom, like metabolic heat gain from students’ bodies; which is calculated by ; where is the number of students, and 80.3 W is the metabolic heat generation per occupant for conditions of clothing insulation of 1.0 clo, and metabolic activity at 1.2 met, at 22 , in classrooms [40]. is the thermal resistance between the classroom and other zones. is calculated by the sum of the thermal resistance for conduction () for each side of the wall and the thermal resistance for convection () according to the internal or external side of the walls. Thus, it can be written as follows [41]:
where , , , and are the thermal conductivity, the convection heat transfer coefficient, area and thickness of the wall, respectively.
The thermal resistance-capacitance (RC) model for the classroom is illustrated in Figure 6. The building network has two types of nodes, walls, and classrooms. There are total l nodes, m of which represent walls, and the rest represent classrooms.

Figure 6.
Equivalent resistance capacitance model for the classroom.
Here are the simplifying assumptions made in deriving the Equations (7) and (8):
- Air in the classroom is thoroughly mixed. Thus, the classroom’s temperature and air density are constant across the classroom;
- As the classroom does not have any windows, the effect of solar radiation is negligible;
- Specific heat capacity of air, is equal to 1.007 at 300 ;
- All internal walls have the same properties such as , L, and h.
3.4. State Space Models
For control purposes, the dynamic models (Equations (3) and (6)–(8)) are converted into state space equations:
where is the state vector, is the control input vectors including supply air temperature and mass flow rate, y is the output vectors, and represents the disturbance vector including the temperature of the neighboring zones, is the number of individuals in the classroom, and I is the number of infected people. The state equations for the states in the nonlinear dynamic model (Equation (10)) are:
where represents the rate of changes in the classroom air temperature, represent the rate of changes in the temperature of the wall, the rate of concentration of quanta, and the rate of concentration.
3.5. HVAC Energy Consumption
The energy consumption of the HVAC system includes energy consumption by the fans and energy consumption by the air-conditioning systems, including the air handling unit and VAV boxes. The power consumption of fans, , is estimated by [20]:
where is the power coefficient of the fan and it is set to 0.8 based on the fan specifications. The models to calculate power consumption from the fan and AHU will be used in the designed controller to penalize the control actions that lead to large energy consumption.
The power consumption of air-conditioning systems, which includes the heating coil of the AHU () and the heating coil of VAV boxes (), is calculated by the following equations:
where is the total power consumption of the heating coils, and present the efficiencies of the steam-water/glycol heating system and boilers, respectively, and they are assumed 0.85 based on typical data of similar boilers. is mass flow rate and is the temperature difference through the heating coils.
The total HVAC energy consumption (), including the energy consumption by the fan wall and the heating coils, during the 24 h is calculated by:
4. Controller Design
In this section, a nonlinear model predictive controller (NMPC) is designed for the HVAC system control. Here, the concept of NMPC [42] is exploited to create real-time optimal solutions for the nonlinear, constrained, multi-objective HVAC optimization problem. The nonlinear MPC controller in this work is a discrete-time controller. The NMPC controller automatically discretizes the continuous time models (Section 3), using the implicit trapezoidal rule.
Important factors in the NMPC design include prediction models to simulate system dynamics, optimizer to obtain feasible optimal solutions, optimization constraints, cost function, and selection of prediction horizon and control horizon. Prediction models were discussed in Section 3. Here, the remaining important items in the NMPC design are briefly explained.
- Cost Function: The cost (objective) function in the designed NMPC in this work should be represented by formulations that lead to minimum HVAC energy consumption and minimize the COVID transmission risk. There are different forms of cost functions such as terminal control, minimum control effort, trajectory tracking, minimizing energy consumption, or a combination of them [18]. The cost function in this paper is presented by Equation (15) that includes a combination of minimizing HVAC energy use, minimum control efforts, and trajectory tracking.
- Constraints: Constraints can be defined as rate or range limits, such as upper and lower bounds of zone temperature or maximum and minimum limits of supply airflow rate [18]. In this paper, inequality constraints are included to enforce (i) low risk of COVID transmission, (ii) meeting ASHRAE comfort level for occupants in terms of room temperature, (iii) minimum ventilation requirement set by level in the room, and iv) control actuators operational constraints (i.e., AHU flow rate, supply air temperature).
- Prediction Horizon, Control Horizon, and Control Time Step: The control horizon is often selected to be less than the prediction horizon to minimize computation cost [18]. In this paper, the sample time, is chosen as 15 min by considering slow room temperature dynamics; the prediction horizon, is 96, which provides the prediction time of 1440 min or 24 h; the control horizon, is chosen as 19.
- Optimizer: Selection of an appropriate optimizer for an NMPC is critical to ensure that a feasible optimal solution can be found in real-time within each control time step. The HVAC control problem in this work includes nonlinear programming (NLP) consisting of a quadratic cost function. Some of the methods to solve NLP problems include active set (AS) methods, first order methods (FOM), interior point (IP) methods, and sequential quadratic programming (SQP) methods [43]. In this work, the SQP algorithm is implemented in Matlab to find feasible solution at each control time step.
Figure 7 shows the structure of the designed NMPC for the classroom. Supply air mass flow rate (), and supply air temperature () are the manipulated variables () that define control actions. The nonlinear dynamic building models are run inside the NMPC optimizer to help find the optimal MVs based on the NMPC cost function.

Figure 7.
Structure of the designed nonlinear MPC in this study.
In this paper, the cost function is composed of three terms (Equation (15a)): (i) output reference tracking including tracking desired temperature, CO level, and concentration of quanta (i.e., term ), (ii) minimizing energy consumption by minimizing control actions including values for supply air temperature and air flow rate to the classroom (i.e., term ), and (iii) manipulated variable move suppression to minimize control efforts including changes in the supply air temperature and AHU flow rate (i.e., term ). By considering these three terms, the cost function in the NMPC is defined by the following equation.
where and are the number of plant (i.e., classroom model) outputs and input variables, respectively; y and u are outputs and inputs from the plant; is the desired value for outputs; and are the lower and upper slack variables for outputs; and are the lower and upper constraints on the volumetric airflow rate; and are the lower and upper constraints on the supply air temperature; , and , and are limits on the rate of change of the volume air flow rate and the supply air temperature, respectively. is the tuning weights corresponding to inputs and outputs. These weights emphasize the preference for the input and output variables over others. In this work, a larger weight is used for the second output (i.e., the concentration of quanta), as reducing the quanta concentrations has more priority than the other outputs.
The following numerical values for parameters are used for the constraints, including = [20 22] C during occupied hours and = [18 24] C during unoccupied hours, = [400 800] ppm and = [0 0.025] quanta per , = [19 25] C. Based on the ASHRAE requirements for air change per hour (ACH) of the classroom, there has to be a minimum non-zero airflow during occupied/unoccupied hours for ventilation purposes; the maximum volumetric airflow is = 4400 CFM.
The term in Equation (15a) represents feedback control by considering the plant feedback “y”, including measured/calculated outputs from the classroom. The “y” values include the measured classroom temperature, concentration, and calculated risk of COVID virus transmission based on the ventilation rate and number of people in the classroom. The value of “y” at step is based on actual measurements, whereas the remaining to steps will be based on simulated plant (i.e., classroom model) outputs.
5. Results and Discussions
5.1. Experimental Data
The data collection was conducted in March 2022 since lecture classrooms resumed regular in-person courses during COVID-19 time. The number of occupants in the room was visually counted and recorded every 5 min. The actual number of occupants in the classroom, which varied from 1 to 59, is shown in Figure 8.
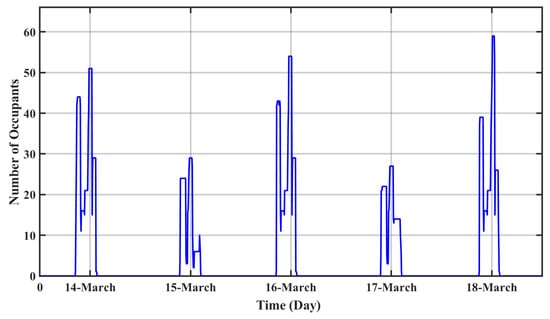
Figure 8.
Number of occupants during the week of experiments, 14–18 March 2022.
The outdoor concentration was considered to be a constant value of about 400 ppm [44]. The sampling period for collecting temperature and relative humidity data was fixed at 60 s.
Figure 9a depicts the measured temperatures for the supply air and the classroom. Because three VAV boxes provide the supply air to the classroom, three sensors were used to measure the supply air temperature of each VAV box. As can be seen, the temperature of the supply air from the two VAV boxes is almost the same. Figure 9b illustrates the measured temperature of the neighboring zones and the outside temperature. During the tests, the temperature of the corridors was almost constant, whereas the temperature of the neighbor classroom () showed some fluctuation.
5.2. Model Validation
The system dynamics are modeled in MATLAB/ Simulink using Equation (11a–f). These represent computationally-efficient, also denoted as control-oriented models, that provide a compromise between accuracy and computation cost. The required level of accuracy in model prediction depends on control objectives. Considering the prior HVAC control studies [41,45], the HVAC models with prediction error less than 10% have the capability to control room air temperature and level accurately. Here, the accuracy of the developed models are assessed against experimental measurements. Next step on verification for the suitability of the developed models for the NMPC can be done by testing the NMPC in a simulation environment (Section 5.3) and then on the actual testbed by assessing the performance of the designed model-based controller for reducing HVAC energy consumption while maintaining a safe condition in the classroom to avoid high risk of COVID virus transmission.
Figure 10 shows the simulation result compared with the recorded concentration data in the classroom. By comparing the results, it can be seen that the validation result shows that the model can predict the concentration by 2.4% average absolute error, confirming a good agreement with the experimental data.

Figure 10.
Simulated concentration versus measured concentration of the classroom (16 March 2022).
The classroom thermal model in this work considers occupants, neighboring zones’ temperatures, and the outside temperature as disturbances. The thermal model from this work is assessed against experimental measurements. The experimental validations of the model for predicting classroom temperature are shown for (i) constant HVAC set point temperature conditions in Figure 11 and (ii) variable HVAC set point temperature conditions in Figure 12. The results show the average prediction errors are less than 1%, confirming the capability of the model to predict classroom air temperature accurately.

Figure 11.
(a) Simulated temperature versus measured temperature of the classroom with a constant set point temperature, (b) Supply air temperature with . The data represent 14 to 21 March 2022. The measured classroom temperature in the plot (a) is from the sensor previously shown in Figure 6.

Figure 12.
(a) Simulated temperature versus measured temperature of the classroom under variable set point temperature conditions, (b) Supply air temperature, (c) Constant supply air flow rate, . The data represent the HVAC operation from 23 to 28 March 2022.
5.3. Control Results
Here, the control results for the classroom, including the quanta concentration, room temperature, concentration, and infection risk are explained. The NMPC controller was designed and simulated in Matlab/Simulink (R2022a). In particular, Matlab Model Predictive Control Toolbox™ was exploited as part of the controller design and implementation. The controller was tested in a model-in-the-loop (MIL) environment on a desktop computer with an Intel Core i7, 32 GB RAM, 3.2 GHz CPU processor. The computation time for the designed NMPC controller was less than 4 min for simulating 24 h. Figure 13 shows the control results over 24 h. As can be seen, the quanta concentrations and infection risk are below the desired bound (i.e., 1% infection probability). In addition, the room temperature and concentration meet the ASHRAE comfort and ventilation constraints, even at the lower limit of their bounds. By comparing Figure 14b,c, it is clear that by increasing the number of students, the ventilation rate is increased immediately to prevent the transmission of infection. The probability of infection in the classroom always stays under one percent. Subplot (d) of Figure 14 illustrates the HVAC system’s power and energy consumption variation depending on the controller inputs during the day. By increasing the volumetric airflow, energy consumption increased.

Figure 13.
Designed NMPC controller results for the control of indoor air quality (IAQ) and minimizing energy consumption): (a) the probability of the infection, (b) quanta concentration, (c) room air temperature, and (d) concentration in the classroom.

Figure 14.
Designed NMPC controller actions, number of occupants, and energy consumption for the results in Figure 13. (a) Control input #1, supply air temperature, (b) control input #2, supply air volume flow rate, (c) number of occupants in the classroom, (d) the HVAC power and energy consumption. This simulation represents the real test conditions (i.e., number of students, and outside temperature) for 16 March 2022.
Figure 15 shows the power and energy consumption of the existing building controller. The comparison between the designed NMPC and the building’s existing controller is shown in Table 1. The results show that the NMPC controller could reduce the total energy consumption by 55% compared to the existing building controller and keep the infection risk below one percent. By considering the electricity cost of $0.1/kWh, the daily cost of HVAC operation is shown in Table 1. Using the designed NMPC results in $56.4 savings per day of HVAC operation for the studied classroom. Considering the winter season in Edmonton spanning 6 months and the estimated daily cost savings of $56.4 as calculated in Table 1, it becomes evident that implementing these savings in just one classroom of a university building could result in a total savings of $10,152.
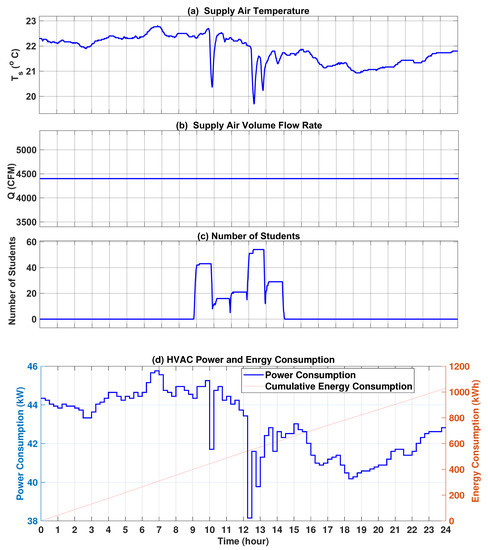
Figure 15.
Existing building controller results: (a) control input #1, Supply air temperature (average of temperature of three VAVs), (b) control input #2, Supply air volume flow rate, (c) number of occupants in the classroom, (d) the daily HVAC power and energy consumption.

Table 1.
Energy and cost savings of the NMPC compared to the existing building controller.
The results of the existing building controller for a whole week of operation are shown in Figure 16. As can be seen, the supply air volume flow rate remained consistently at its maximum value throughout the week, leading to use high power consumption. The results of using NMPC for a whole week of operation are shown in Figure 17 and Figure 18. As seen in the Figure 17, the designed NMPC can keep the infection probability always below 1%, while meeting the required temperature comfort bound and maximum allowed level. Figure 18 demonstrates the simulation results for manipulated variables and energy consumption. As can be seen, by adjusting the air flow rate and supply air temperature, the power consumption show the significant variations during the week.

Figure 16.
Existing building controller results: (a) Control input #1, supply air temperature, (b) control input #2, supply air volume flow rate, (c) the weekly HVAC power and energy consumption.
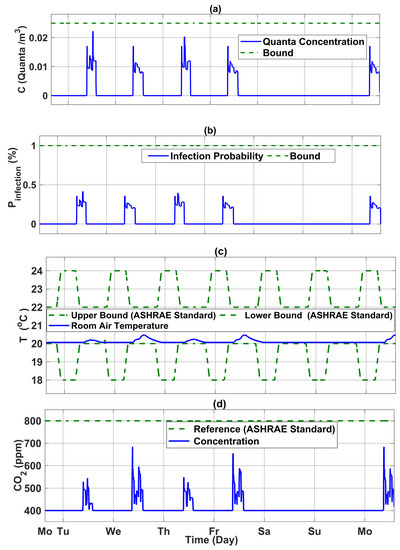
Figure 17.
NMPC results for the IAQ and temperature control for 14 to 21 March 2022: (a) Quanta concentration, (b) the infection probability, (c) room air temperature, (d) concentration.

Figure 18.
NMPC results: (a) Control input #1, supply air temperature, (b) control input #2, supply air volume flow rate, (c) number of occupants in the classroom, (d) the weekly HVAC power and energy consumption.
Figure 14c and Figure 16d show the weekly HVAC power and energy consumption results for the NMPC and the existing building controllers, respectively. The results showed that the NMPC controller could provide 61.97% savings for the classroom of building weekly energy consumption compared to the existing building controller.
6. Summary and Conclusions
This paper investigated the importance of optimal controllers’ critical role in decreasing the energy consumption of the HVAC system while reducing the infection risk of airborne diseases. First, a lecture hall located on the ground floor of the ETLC building at the University of Alberta was selected as a testbed in this study. Then, physics-based dynamic models, including thermal and IAQ models, were developed to be embedded into the NMPC controller to predict the system’s outputs by considering the disturbances like occupants and the outside temperature. The validation results showed that the model could predict the temperatures and concentration by 0.84% and 2.4% average error, respectively, offering a good match with the experimental data. The NMPC controller was designed on nonlinear models, including the infection risk and thermal models. The results showed that the NMPC controller could remarkably mitigate the infection risk and energy consumption while satisfying all the constraints and the cost function. By comparing the energy consumption results from two controllers, NMPC and existing building controllers, it was clear that the NMPC controller has an integral role in saving energy and preparing better indoor air quality, i.e., the NMPC controller can save energy and cost at least about 55% and 57$ per day, respectively.
Author Contributions
Conceptualization, N.S. and M.S.; Methodology, N.S. and M.S.; Software, N.S.; Experimental data collection, N.S.; Writing—original draft preparation, N.S.; Writing—review and editing, N.S. and M.S.; Supervision, M.S.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data reported in this paper is made publicly available at https://sites.ualberta.ca/mahdi/Docs/N_Samadi_MScThesis.pdf.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations and Nomenclature
| ACH | Air Change Per Hour |
| AHU | Air Handling Unit |
| ASHRAE | American Society of Heating, Refrigerating and Air-Conditioning Engineers |
| COVID-19 | Coronavirus |
| ETLC | Engineering Teaching and Learning Complex |
| H1N1 | Influenza |
| HVAC | Heating, Ventilation, and Air Conditioning |
| IAQ | Indoor Air Quality |
| IMC | Internal Model Controller |
| MD | Measurement Disturbance |
| MERS | Middle East Respiratory Syndrome |
| MPC | Model Predictive Control |
| MV | Manipulated Variable |
| NLP | Nonlinear Programming Problem |
| NMPC | Nonlinear Model Predictive Control |
| PAR | Peak to Average Ratio |
| PI | Proportional-Integral |
| PID | Proportional–Integral–Derivative |
| PM | Particulate Matter |
| PPM | Parts Per Million |
| RBC | Rule-based Control |
| RC | Resistance-Capacitance |
| SARS | Severe Acute Respiratory Syndrome |
| SBMPC | Stochastic Scenario-Based MPC |
| SQP | Sequential Quadratic Programming |
| VAV | Variable Air Volume |
| WHO | World Health Organization |
| Symbols | |
| Prevalence rate of disease (-) | |
| Absorption coefficient of the wall between room i, j (-) | |
| Fan power coefficient (-) | |
| Slack variable | |
| Efficiency of the boilers (-) | |
| Thermal conductivity () | |
| Air change per hour () | |
| Air mass flow rate () | |
| Heat transfer rate (W) | |
| Temperature gradient () | |
| Constant pressure specific heat () | |
| Heat storage capacity () | |
| Stefan-Boltzmann constant () | |
| Duration of event ( | |
| Quanta emission rate (quanta/h) | |
| emission rate of indoor source (mg/s) | |
| Fraction of unreported COVID-19 cases | |
| Generation rate by occupants () | |
| Energy consumption | |
| Conductivity of walls () | |
| Control horizon | |
| Prediction horizon | |
| Daily new COVID-19 cases | |
| Power consumption by fans ( | |
| Power consumption by heating coils ( | |
| Probability of being infected (%) | |
| Volumetric breathing rate of an occupant () | |
| Internal thermal resistance of walls ( | |
| Thermal resistance of outside wall ( | |
| Time step (min) | |
| Temperature () | |
| Velocity (m/s) | |
| Constraint violation penalty weight | |
| Density of air () | |
| Q | Air volume flow rate () |
| Wall density () | |
| Area of walls () | |
| Heat storage capacity of the room () | |
| Heat storage capacity of walls () | |
| Convection heat-transfer coefficient () | |
| Number of infected people (-) | |
| Thickness of wall () | |
| Mass () | |
| Number of students (-) | |
| Volume of the classroom () | |
| Wall volume () |
References
- Falode, A.J.; Bolarinwa, J.O.; Yakubu, M. History of pandemics in the twentieth and twenty-first century. Synesis J. Humanit. Soc. Sci. 2021, 2, 9–26. [Google Scholar] [CrossRef]
- Greenhalgh, T.; Jimenez, J.L.; Prather, K.A.; Tufekci, Z.; Fisman, D.; Schooley, R. Ten scientific reasons in support of the airborne transmission of SARS-CoV-2. Lancet 2021, 397, 1603–1605. [Google Scholar] [CrossRef] [PubMed]
- Prather, K.A.; Marr, L.C.; Schooley, R.T.; McDiarmid, M.A.; Wilson, M.E.; Milton, D.K. Airborne transmission of SARS-CoV-2. Science 2020, 370, 303–304. [Google Scholar] [CrossRef] [PubMed]
- Noorimotlagh, Z.; Jaafarzadeh, N.; Martínez, S.S.; Mirzaee, S.A. A systematic review of possible airborne transmission of the COVID-19 virus (SARS-CoV-2) in the indoor air environment. Environ. Res. 2021, 193, 110612. [Google Scholar] [CrossRef]
- Chu, D.K.; Akl, E.A.; Duda, S.; Solo, K.; Yaacoub, S.; Schünemann, H.J. Physical distancing, face masks, and eye protection to prevent person-to-person transmission of SARS-CoV-2 and COVID-19: A systematic review and meta-analysis. Lancet 2020, 395, 1973–1987. [Google Scholar] [CrossRef]
- Azimi, P.; Stephens, B. HVAC filtration for controlling infectious airborne disease transmission in indoor environments: Predicting risk reductions and operational costs. Build. Environ. 2013, 70, 150–160. [Google Scholar] [CrossRef]
- Thuresson, S.; Fraenkel, C.J.; Sasinovich, S.; Soldemyr, J.; Widell, A.; Medstrand, P.; Alsved, M.; Löndahl, J. Airborne severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) in hospitals: Effects of aerosol-generating procedures, HEPA-filtration units, patient viral load, and physical distance. Clin. Infect. Dis. 2022, 75, e89–e96. [Google Scholar] [CrossRef]
- Feng, Z.; Cao, S.J.; Haghighat, F. Removal of SARS-CoV-2 using UV+ Filter in built environment. Sustain. Cities Soc. 2021, 74, 103226. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, H.; Chan, V.; Lai, A.C. Development and experimental validation of a mathematical model for the irradiance of in-duct ultraviolet germicidal lamps. Build. Environ. 2019, 152, 160–171. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, H.; Nunayon, S.S.; Chan, V.; Lai, A.C. Disinfection efficacy of ultraviolet germicidal irradiation on airborne bacteria in ventilation ducts. Indoor Air 2018, 28, 806–817. [Google Scholar] [CrossRef] [PubMed]
- Qian, H.; Zheng, X. Ventilation control for airborne transmission of human exhaled bio-aerosols in buildings. J. Thorac. Dis. 2018, 10, S2295. [Google Scholar] [CrossRef]
- Qian, H.; Li, Y. Removal of exhaled particles by ventilation and deposition in a multibed airborne infection isolation room. Indoor Air 2010, 20, 284–297. [Google Scholar] [CrossRef]
- Razmara, M.; Maasoumy, M.; Shahbakhti, M.; Robinett, R., III. Optimal exergy control of building HVAC system. Appl. Energy 2015, 156, 555–565. [Google Scholar] [CrossRef]
- Razmara, M.; Maasoumy, M.; Shahbakhti, M.; Robinett, R.D. Exergy-based model predictive control for building HVAC systems. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1677–1682. [Google Scholar]
- Pérez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- Harrold, M.; Lush, D. Automatic controls in building services. In Proceedings of the IEE Proceedings B (Electric Power Applications); IET: Rochester, NY, USA, 1988; Volume 135, pp. 105–133. [Google Scholar] [CrossRef]
- Al-Rabghi, O.M.; Akyurt, M.M. A survey of energy-efficient strategies for effective air conditioning. Energy Convers. Manag. 2004, 45, 1643–1654. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Theory and applications of HVAC control systems—A review of model predictive control (MPC). Build. Environ. 2014, 72, 343–355. [Google Scholar] [CrossRef]
- Arguello-Serrano, B.; Velez-Reyes, M. Nonlinear control of a heating, ventilating, and air conditioning system with thermal load estimation. IEEE Trans. Control Syst. Technol. 1999, 7, 56–63. [Google Scholar] [CrossRef]
- Wang, J.; Huang, J.; Feng, Z.; Cao, S.J.; Haghighat, F. Occupant-density-detection based energy efficient ventilation system: Prevention of infection transmission. Energy Build. 2021, 240, 110883. [Google Scholar] [CrossRef]
- Walker, S.S.; Lombardi, W.; Lesecq, S.; Roshany-Yamchi, S. Application of distributed model predictive approaches to temperature and CO2 concentration control in buildings. IFAC—PapersOnLine 2017, 50, 2589–2594. [Google Scholar] [CrossRef]
- Maasoumy, M.; Sangiovanni-Vincentelli, A. Total and peak energy consumption minimization of building HVAC systems using model predictive control. IEEE Des. Test Comput. 2012, 29, 26–35. [Google Scholar] [CrossRef]
- Vašak, M.; Starčić, A.; Martinčević, A. Model predictive control of heating and cooling in a family house. In Proceedings of the 2011 Proceedings of the 34th International Convention MIPRO, Opatija, Croatia, 23–27 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 739–743. [Google Scholar]
- Pippia, T.; Lago, J.; De Coninck, R.; De Schutter, B. Scenario-based nonlinear model predictive control for building heating systems. Energy Build. 2021, 247, 111108. [Google Scholar] [CrossRef]
- Ganesh, H.S.; Fritz, H.E.; Edgar, T.F.; Novoselac, A.; Baldea, M. A model-based dynamic optimization strategy for control of indoor air pollutants. Energy Build. 2019, 195, 168–179. [Google Scholar] [CrossRef]
- Hou, J.; Li, H.; Nord, N. Nonlinear model predictive control for the space heating system of a university building in Norway. Energy 2022, 253, 124157. [Google Scholar] [CrossRef]
- Toub, M.; Robinett, R.D., III; Shahbakhti, M. Building-to-grid optimal control of integrated MicroCSP and building HVAC system for optimal demand response services. Optim. Control Appl. Methods 2022, 44, 866–884. [Google Scholar] [CrossRef]
- Škrjanc, I.; Šubic, B. Control of indoor CO2 concentration based on a process model. Autom. Constr. 2014, 42, 122–126. [Google Scholar] [CrossRef]
- Cho, J.H.; Moon, J.W. Integrated artificial neural network prediction model of indoor environmental quality in a school building. J. Clean. Prod. 2022, 344, 131083. [Google Scholar] [CrossRef]
- Khalid, R.; Javaid, N.; Rahim, M.H.; Aslam, S.; Sher, A. Fuzzy energy management controller and scheduler for smart homes. Sustain. Comput. Inform. Syst. 2019, 21, 103–118. [Google Scholar] [CrossRef]
- Riley, E.; Murphy, G.; Riley, R. Airborne spread of measles in a suburban elementary school. Am. J. Epidemiol. 1978, 107, 421–432. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, T.; Haas, C.N. A quantitative microbial risk assessment model for Legionnaires’ disease: Animal model selection and dose-response modeling. Risk Anal. Int. J. 2007, 27, 1581–1596. [Google Scholar] [CrossRef]
- Miller, S.L.; Nazaroff, W.W.; Jimenez, J.L.; Boerstra, A.; Buonanno, G.; Dancer, S.J.; Kurnitski, J.; Marr, L.C.; Morawska, L.; Noakes, C. Transmission of SARS-CoV-2 by inhalation of respiratory aerosol in the Skagit Valley Chorale superspreading event. Indoor Air 2021, 31, 314–323. [Google Scholar] [CrossRef]
- Shen, J.; Kong, M.; Dong, B.; Birnkrant, M.J.; Zhang, J. A systematic approach to estimating the effectiveness of multi-scale IAQ strategies for reducing the risk of airborne infection of SARS-CoV-2. Build. Environ. 2021, 200, 107926. [Google Scholar] [CrossRef] [PubMed]
- Buonanno, G.; Stabile, L.; Morawska, L. Estimation of airborne viral emission: Quanta emission rate of SARS-CoV-2 for infection risk assessment. Environ. Int. 2020, 141, 105794. [Google Scholar] [CrossRef] [PubMed]
- Hou, D.; Katal, A.; Wang, L.L. Bayesian calibration of using CO2 sensors to assess ventilation conditions and associated COVID-19 airborne aerosol transmission risk in schools. medRxiv 2021. [Google Scholar] [CrossRef]
- Li, B.; Cai, W. A novel CO2-based demand-controlled ventilation strategy to limit the spread of COVID-19 in the indoor environment. Build. Environ. 2022, 219, 109232. [Google Scholar] [CrossRef]
- Hu, Z.; Song, C.; Xu, C.; Jin, G.; Chen, Y.; Xu, X.; Ma, H.; Chen, W.; Lin, Y.; Zheng, Y.; et al. Clinical characteristics of 24 asymptomatic infections with COVID-19 screened among close contacts in Nanjing, China. Sci. China Life Sci. 2020, 63, 706–711. [Google Scholar] [CrossRef]
- Batterman, S. Review and extension of CO2-based methods to determine ventilation rates with application to school classrooms. Int. J. Environ. Res. Public Health 2017, 14, 145. [Google Scholar] [CrossRef]
- Ahmed, K.; Akhondzada, A.; Kurnitski, J.; Olesen, B. Occupancy schedules for energy simulation in new prEN16798-1 and ISO/FDIS 17772-1 standards. Sustain. Cities Soc. 2017, 35, 134–144. [Google Scholar] [CrossRef]
- Maasoumy, M.; Razmara, M.; Shahbakhti, M.; Vincentelli, A.S. Handling model uncertainty in model predictive control for energy efficient buildings. Energy Build. 2014, 77, 377–392. [Google Scholar] [CrossRef]
- Grüne, L.; Pannek, J. Nonlinear Model Predictive Control: Theory and Algorithms; Springer: Berlin/Heidelberg, Germany, 2011; ISBN 978-0-85729-500-2. [Google Scholar] [CrossRef]
- Norouzi, A.; Heidarifar, H.; Shahbakhti, M.; Koch, C.R.; Borhan, H. Model Predictive Control of Internal Combustion Engines: A Review and Future Directions. Energies 2021, 14, 6251. [Google Scholar] [CrossRef]
- Lawrence, T.M. Selecting C. criteria for outdoor air monitoring. Ashrae J. 2008, 50, 18–26. [Google Scholar]
- Yang, S.; Wan, M.P.; Ng, B.F.; Dubey, S.; Henze, G.P.; Chen, W.; Baskaran, K. Experimental study of model predictive control for an air-conditioning system with dedicated outdoor air system. Appl. Energy 2020, 257, 113920. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
