Recent Achievements in the Control of Interior Permanent-Magnet Synchronous Machine Drives: A Comprehensive Overview of the State of the Art
Abstract
:1. Introduction
- Section 2 lays down the necessary theoretical background. This section presents the construction, the mathematical modeling and the operating regions of IPMSMs. Furthermore, it gives a short overview about voltage source inverters. The section also presents the recent trends for the given field.
- Section 3 evaluates the different control approaches used for IPMSM drives, which have been grouped as linear, nonlinear, predictive, robust, intelligent and adaptive.
- Section 4 offers a brief overview about different reference signal generation techniques in the constant-torque and the field-weakening regions.
- Section 5 concludes the article and summarizes future trends and challenges.
2. Theoretical Background
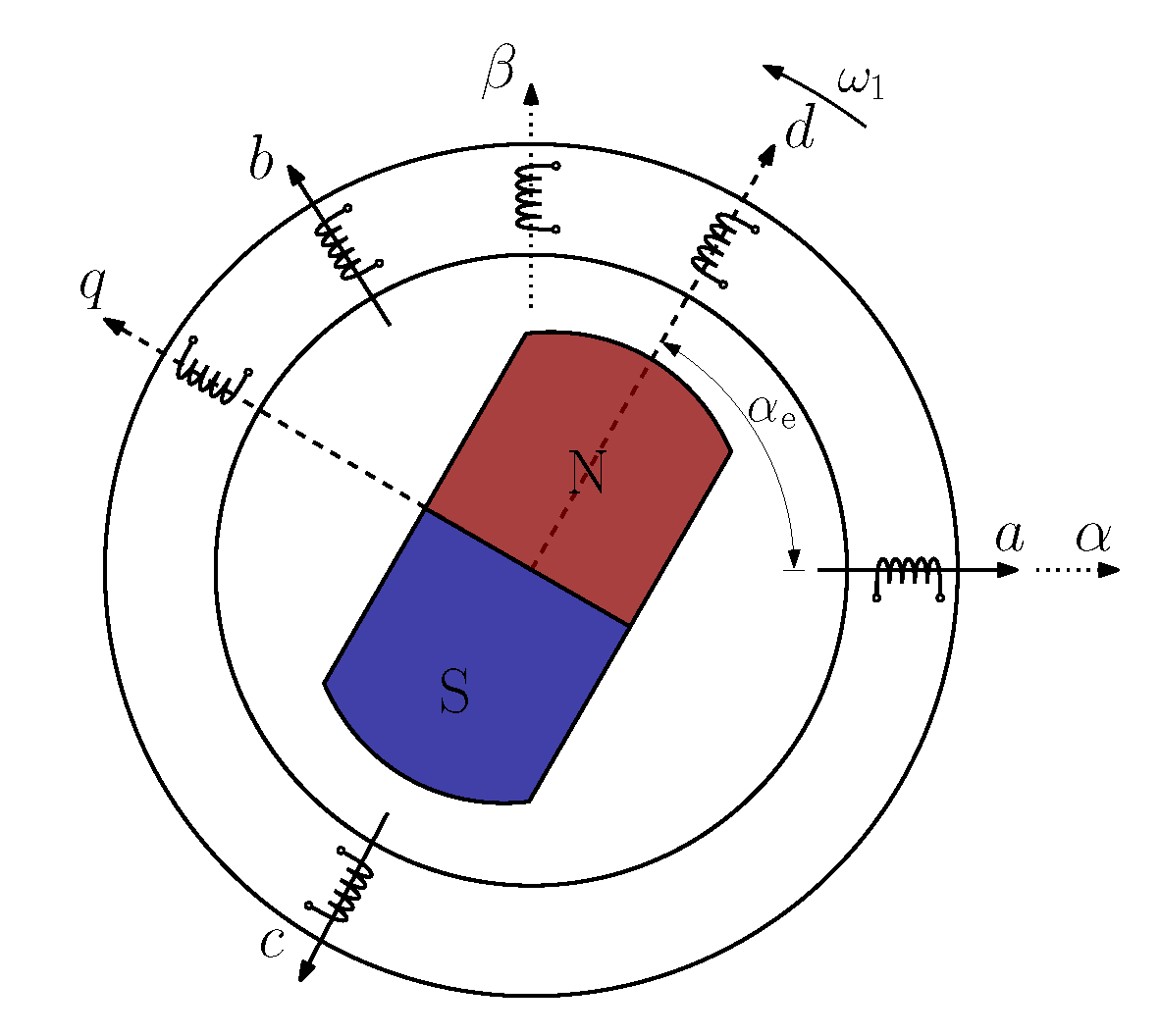
2.1. Construction
2.2. Mathematical Model of IPMSM
2.3. Operation Regions
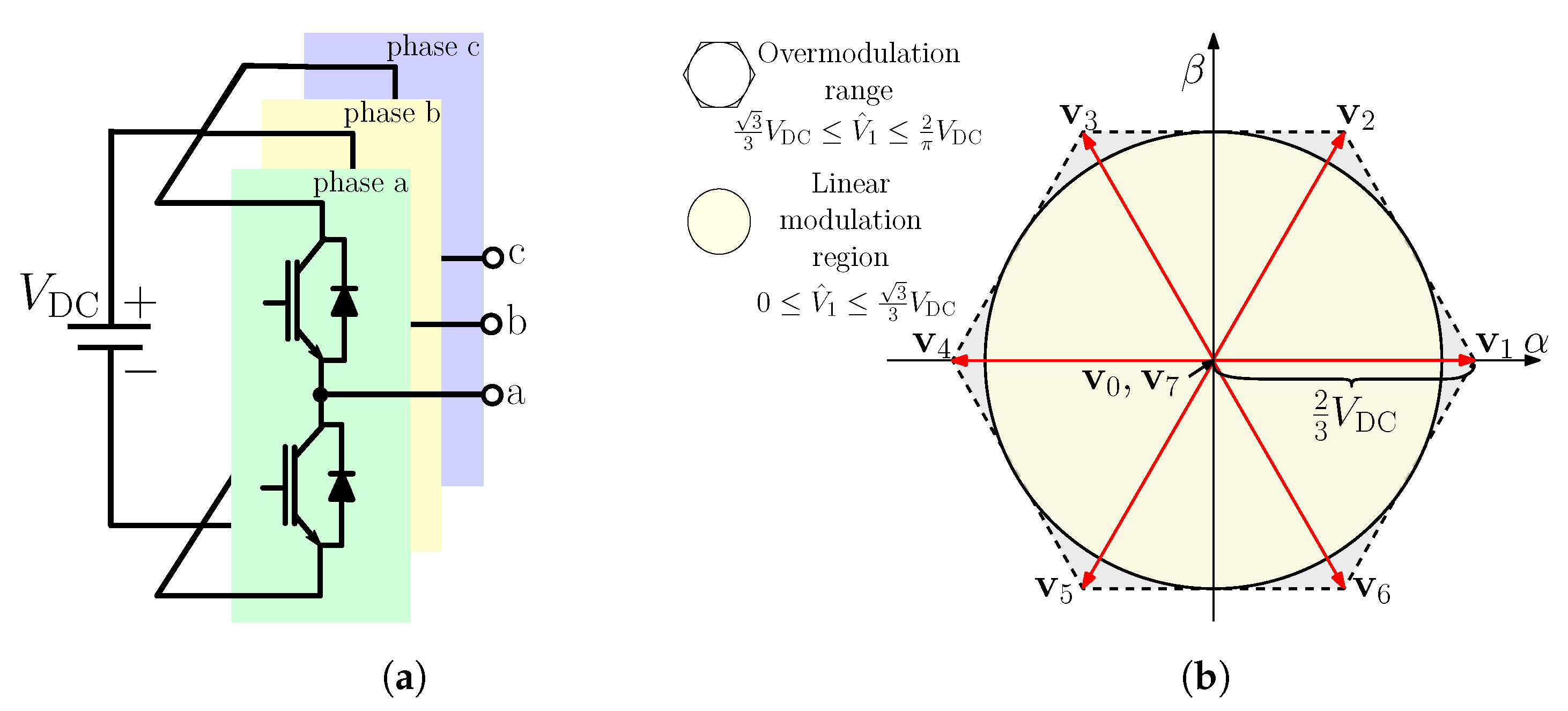
2.4. Voltage Source Inverters
3. Control Techniques of IPMSM Drives
3.1. Linear Controllers
3.1.1. PI Controller
3.1.2. State Feedback
3.2. Nonlinear Controllers
3.2.1. Feedback Linearization
3.2.2. Sliding Mode Control
3.2.3. Backstepping
3.2.4. Gain Scheduling
3.2.5. Hysteresis Control
3.3. Predictive Control
3.3.1. Model Predictive Control
3.3.2. Predictive Deadbeat Control
3.4. Intelligent Control
3.4.1. Fuzzy Logic Control
3.4.2. Reinforcement Learning
3.5. Robust Controllers
3.5.1. H-Synthesis Control
3.5.2. -Synthesis Control
3.6. Adaptive Controllers
3.6.1. Iterative Learning Control
3.6.2. Model Reference Adaptive Control
3.7. Summary
- Developing general design guidelines for control approaches with higher level of complexity;
- Incorporating control approaches with disturbance observers, parameter estimation and adaptive control gain tuning;
- Further reducing computational demand with novel approaches;
- Investigation and improvements of the performance of the control techniques in the overmodulation region and at low-frequency ratios;
- Eliminating model dependency by focusing on model-free and data-driven control techniques
4. Reference Calculation Methods
5. Conclusions, Future Trends
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2L-VSI | Two-Level VSI |
| AI | Artificial Intelligence |
| CS-MPC | Continuous Set Model Predictive Control |
| DTC | Direct Torque Control |
| EV | Electric Vehicle |
| FBL | Feedback Linearization |
| FB | Feedback |
| FF | Feedforward |
| FLC | Fuzzy Logic Control |
| FOC | Field Oriented Control |
| FSCW | Fractional-Slot Concentrated Winding |
| FS-MPC | Finite Set Model Predictive Control |
| FW | Field Weakening |
| HC | Hysteresis Control |
| HEPMa-SynRM | Hybrid-Excited Permanent-Magnet-Assisted SynRM |
| HE-PMSM | Hybrid-Excited PMSM |
| HEV | Hybrid Electric Vehicle |
| ILC | Iterative Learning Controller |
| IPMSM | Interior Permanent-Magnet Synchronous Machine |
| ISDW | Integer-Slot Distributed Winding |
| LQR | Linear Quadratic Regulator |
| LUT | Lookup table |
| MC | Maximum Current |
| ML-VSI | Multilevel Voltage Source Inverter |
| MMB | Mathematical-Model-Based |
| MPC | Model Predictive Control |
| MPCC | Model Predictive Current Control |
| MPTC | Model Predictive Torque Control |
| MRAA | Model Reference Adaptive Algorithm |
| MTPA | Maximum Torque Per Ampere |
| MTPC | Maximum Torque Per Current |
| MTPF | Maximum Torque Per Flux |
| MTPV | Maximum Torque Per Voltage |
| PC | Predictive Control |
| PDBC | Predictive Deadbeat Control |
| PI | Proportional-Integral |
| PM | Permanent Magnet |
| PMa-SynRM | Permanent-Magnet-Assisted SynRM |
| PMSM | Permanent-Magnet Synchronous Machine |
| PWM | Pulse Width Modulation |
| RE | Rare-Earth |
| RL | Reinforcement Learning |
| RRF | Rotating Reference Frame |
| SFC | State Feedback Control |
| SIB | Signal-Injection-Based |
| SM | Synchronous Machine |
| SMB | Searching-Method-Based |
| SMC | Sliding Mode Control |
| SP | Salient Pole |
| SRF | Stationary Reference Frame |
| SVM | Space Vector Modulation |
| SynRM | Synchronous Reluctance Machine |
| THD | Total Harmonic Distortion |
| VE | Voltage Ellipse |
| VSI | Voltage Source Inverter |
| WRSM | Wound Rotor Synchronous Machine |
References
- Miguel-Espinar, C.; Heredero-Peris, D.; Villafafila-Robles, R.; Montesinos-Miracle, D. Review of Flux-Weakening Algorithms to Extend the Speed Range in Electric Vehicle Applications with Permanent Magnet Synchronous Machines. IEEE Access 2023, 11, 22961–22981. [Google Scholar] [CrossRef]
- Hussain, A.; Baig, Z.; Toor, W.T.; Ali, U.; Idrees, M.; Shloul, T.A.; Ghadi, Y.Y.; Alkahtani, H.K. Wound Rotor Synchronous Motor as Promising Solution for Traction Applications. Electronics 2022, 11, 4116. [Google Scholar] [CrossRef]
- Murataliyev, M.; Degano, M.; Di Nardo, M.; Bianchi, N.; Gerada, C. Synchronous Reluctance Machines: A Comprehensive Review and Technology Comparison. Proc. IEEE 2022, 110, 382–399. [Google Scholar] [CrossRef]
- Jahns, T.M.; Kliman, G.B.; Neumann, T.W. Interior Permanent-Magnet Synchronous Motors for Adjustable-Speed Drives. IEEE Trans. Ind. Appl. 1986, IA-22, 738–747. [Google Scholar] [CrossRef]
- Fontana, M.; Bianchi, N. Design and Analysis of Normal Saliency IPM Spoke Motor. IEEE Trans. Ind. Appl. 2020, 56, 3625–3635. [Google Scholar] [CrossRef]
- Khatab, M.F.H.; Zhu, Z.Q.; Li, H.Y.; Liu, Y. Comparative study of novel axial flux magnetically geared and conventional axial flux permanent magnet machines. CES Trans. Electr. Mach. Syst. 2018, 2, 392–398. [Google Scholar] [CrossRef]
- Wu, F.; EL-Refaie, A.M. Permanent Magnet Vernier Machines: A Review. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 372–378. [Google Scholar] [CrossRef]
- Cinti, L.; Bianchi, N. Hybrid-Excited PM Motor for Electric Vehicle. Energies 2021, 14, 916. [Google Scholar] [CrossRef]
- Huynh, T.A.; Hsieh, M.F. Performance Analysis of Permanent Magnet Motors for Electric Vehicles (EV) Traction Considering Driving Cycles. Energies 2018, 11, 1385. [Google Scholar] [CrossRef] [Green Version]
- Wardach, M.; Prajzendanc, P.; Palka, R.; Cierzniewski, K.; Pstrokonski, R.; Cichowicz, M.; Pacholski, S.; Ciurus, J.; Hao, C. Hybrid-Excited Permanent Magnet-Assisted Synchronous Reluctance Machine. Energies 2022, 15, 2997. [Google Scholar] [CrossRef]
- Abhijith, V.; Hossain, M.J.; Lei, G.; Sreelekha, P.A.; Monichan, T.P.; Rao, S.V. Hybrid Switched Reluctance Motors for Electric Vehicle Applications with High Torque Capability without Permanent Magnet. Energies 2022, 15, 7931. [Google Scholar] [CrossRef]
- Cui, W.; Wang, D.; Ren, L.; Zhang, Y. A New Optimized IPMSM for EVs with Reduced Magnet Loss for Over-Modulation Operation. IEEE Trans. Magn. 2023, 59, 8200104. [Google Scholar] [CrossRef]
- Ahsanullah, K.; Dutta, R.; Rahman, M. Distributed and concentrated winding Interior PM Synchronous Machine (IPMSM) for direct drive wind turbine. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society (IECON 2013), Vienna, Austria, 10–13 November 2013; pp. 2762–2767. [Google Scholar] [CrossRef]
- Mukundan, S.; Dhulipati, H.; Li, Z.; Toulabi, M.S.; Tjong, J.; Kar, N.C. Coupled Magnetic Circuit-Based Design of an IPMSM for Reduction of Circulating Currents in Asymmetrical Star-Delta Windings. IEEE Trans. Transp. Electrif. 2022, 8, 2971–2984. [Google Scholar] [CrossRef]
- Song, P.; Toulabi, M.S.; Li, W.; Mukundan, S.; Byczynski, G.; Tjong, J.; Kar, N.C. Improvement of Electromagnetic Force and Acceleration in an Asymmetrical Star-Delta Winding IPMSM through Stator and Rotor Geometrical Modifications. In Proceedings of the 47th Annual Conference of the IEEE Industrial Electronics Society (IECON 2021), Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Islam, M.S.; Husain, I.; Ahmed, A.; Sathyan, A. Asymmetric Bar Winding for High-Speed Traction Electric Machines. IEEE Trans. Transp. Electrif. 2020, 6, 3–15. [Google Scholar] [CrossRef]
- Liu, X.; Chen, H.; Zhao, J.; Belahcen, A. Research on the Performances and Parameters of Interior PMSM Used for Electric Vehicles. IEEE Trans. Ind. Electron. 2016, 63, 3533–3545. [Google Scholar] [CrossRef]
- Oh, S.Y.; Cho, S.Y.; Han, J.H.; Lee, H.J.; Ryu, G.H.; Kang, D.; Lee, J. Design of IPMSM Rotor Shape for Magnet Eddy-Current Loss Reduction. IEEE Trans. Magn. 2014, 50, 841–844. [Google Scholar] [CrossRef]
- Tahanian, H.; Aliahmadi, M.; Faiz, J. Ferrite Permanent Magnets in Electrical Machines: Opportunities and Challenges of a Non-Rare-Earth Alternative. IEEE Trans. Magn. 2020, 56, 900120. [Google Scholar] [CrossRef]
- Cui, W.; Ren, L.; Zhou, J.; Zhang, Q. A New IPMSM With Hybrid Rotor Structure for Electrical Vehicle with Reduced Magnet Loss. IEEE Trans. Magn. 2022, 58, 8700406. [Google Scholar] [CrossRef]
- Xu, R.; Tong, W. Multi-objective Hierarchical Optimization of Interior Permanent Magnet Synchronous Machines Based on Rotor Surface Modification. CES Trans. Electr. Mach. Syst. 2022, 6, 352–358. [Google Scholar] [CrossRef]
- Liang, X.; Liu, F.; Li, W.; Wang, M.; Zheng, P.; Gu, Z. A Novel Rotor Re-Construction Method for Improving the Electromagnetic Performance of the Interior PMSM. In Proceedings of the 2022 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November–2 December 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Krause, P.; Wasynczuk, O.; Sudhoff, S.; Pekarek, S. Analysis of Electric Machinery and Drive Systems, 3rd ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Mubarok, M.S.; Liu, T.H. An Adjustable Wide-Range Speed-Control Method for Sensorless IPMSM Drive Systems. IEEE Access 2022, 10, 42727–42738. [Google Scholar] [CrossRef]
- Yang, R.; Sun, T.; Feng, W.; He, S.; Zhu, S.; Chen, X. Accurate online MTPA control of IPMSM considering derivative terms. Chin. J. Electr. Eng. 2021, 7, 100–110. [Google Scholar] [CrossRef]
- Li, S.; Sarlioglu, B.; Jurkovic, S.; Patel, N.R.; Savagian, P. Analysis of Temperature Effects on Performance of Interior Permanent Magnet Machines for High Variable Temperature Applications. IEEE Trans. Ind. Appl. 2017, 53, 4923–4933. [Google Scholar] [CrossRef]
- Muazzam, H.; Ishak, M.K.; Hanif, A.; Bhatti, A.I. Compensating Thermal Derated Torque of IPMSM Centric Electric Vehicles. IEEE Access 2022, 10, 24468–24480. [Google Scholar] [CrossRef]
- Englert, T.; Graichen, K. Nonlinear model predictive torque control of PMSMs for high performance applications. Control Eng. Pract. 2018, 81, 43–54. [Google Scholar] [CrossRef]
- Elsherbiny, H.; Szamel, L.; Ahmed, M.K.; Elwany, M.A. High Accuracy Modeling of Permanent Magnet Synchronous Motors Using Finite Element Analysis. Mathematics 2022, 10, 3880. [Google Scholar] [CrossRef]
- Watthewaduge, G.; Toulabi, M.S.; Filizadeh, S.; Gole, A.M. Performance Analysis and Operating Limits of a Dual-Inverter Open-Winding IPMSM Drive. IEEE Trans. Energy Convers. 2019, 34, 1655–1666. [Google Scholar] [CrossRef]
- Englert, T.; Graichen, K. A Fixed-Point Iteration Scheme for Model Predictive Torque Control of PMSMs. IFAC-PapersOnLine 2018, 51, 568–573. [Google Scholar] [CrossRef]
- Fasil, M.; Antaloae, C.; Mijatovic, N.; Jensen, B.B.; Holboll, J. Improved dq-Axes Model of PMSM Considering Airgap Flux Harmonics and Saturation. IEEE Trans. Appl. Supercond. 2016, 26, 5202705. [Google Scholar] [CrossRef] [Green Version]
- Di Tommaso, A.O.; Miceli, R.; Nevoloso, C.; Scaglione, G.; Schettino, G. Improved High-Fidelity IPMSM mathematical model Including Saturation, Cross-Coupling, Torque Ripple and Iron Loss effects. In Proceedings of the 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 5–8 September 2022; pp. 21–27. [Google Scholar] [CrossRef]
- Seilmeier, M.; Ebersberger, S.; Piepenbreier, B. PMSM model for sensorless control considering saturation induced secondary saliencies. In Proceedings of the 2013 IEEE International Symposium on Sensorless Control for Electrical Drives and Predictive Control of Electrical Drives and Power Electronics (SLED/PRECEDE), Munich, Germany, 17–19 October 2013; pp. 1–8. [Google Scholar] [CrossRef]
- Cai, H.; Hu, D. On PMSM Model Fidelity and its Implementation in Simulation. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 1674–1681. [Google Scholar] [CrossRef]
- Buettner, M.A.; Monzen, N.; Hackl, C.M. Artificial Neural Network Based Optimal Feedforward Torque Control of Interior Permanent Magnet Synchronous Machines: A Feasibility Study and Comparison with the State-of-the-Art. Energies 2022, 15, 1838. [Google Scholar] [CrossRef]
- Bianchi, N. Chapter 6—Permanent Magnet Synchronous Motors. In Power Electronics and Motor Drives; Bogdan, M., Wilamowski, J.d.I., Eds.; CRC Press: Boca Raton, FL, USA, 2010; pp. 1–42. [Google Scholar]
- Eldeeb, H.; Hackl, C.M.; Horlbeck, L.; Kullick, J. A unified theory for optimal feedforward torque control of anisotropic synchronous machines. Int. J. Control 2018, 91, 2273–2302. [Google Scholar] [CrossRef] [Green Version]
- Inoue, T.; Inoue, Y.; Morimoto, S.; Sanada, M. Mathematical Model for MTPA Control of Permanent-Magnet Synchronous Motor in Stator Flux Linkage Synchronous Frame. IEEE Trans. Ind. Appl. 2015, 51, 3620–3628. [Google Scholar] [CrossRef]
- Morimoto, S.; Sanada, M.; Takeda, Y. Wide-speed operation of interior permanent magnet synchronous motors with high-performance current regulator. IEEE Trans. Ind. Appl. 1994, 30, 920–926. [Google Scholar] [CrossRef]
- Wang, S.; Kang, J.; Degano, M.; Galassini, A.; Gerada, C. An Accurate Wide-Speed Range Control Method of IPMSM Considering Resistive Voltage Drop and Magnetic Saturation. IEEE Trans. Ind. Electron. 2020, 67, 2630–2641. [Google Scholar] [CrossRef]
- Zhang, Z.; Nahid-Mobarakeh, B.; Emadi, A. A Simplified Space Vector Overmodulation Strategy for PMSM Drive System. In Proceedings of the 48th Annual Conference of the IEEE Industrial Electronics Society (IECON 2022), Brussels, Belgium, 17–20 October 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Park, H.J.; Ahn, H.W.; Go, S.C. A Study on Performance and Characteristic Analysis According to the Operating Point of IPMSM Drive. Energies 2023, 16, 1219. [Google Scholar] [CrossRef]
- Holtz, J. Advanced PWM and Predictive Control—An Overview. IEEE Trans. Ind. Electron. 2016, 63, 3837–3844. [Google Scholar] [CrossRef]
- Kumar, K.; Santra, S.B. Performance Analysis of a Three-Phase Propulsion Inverter for Electric Vehicles Using GaN Semiconductor Devices. IEEE Trans. Ind. Appl. 2018, 54, 6247–6257. [Google Scholar] [CrossRef]
- Han, D.; Li, S.; Wu, Y.; Choi, W.; Sarlioglu, B. Comparative Analysis on Conducted CM EMI Emission of Motor Drives: WBG Versus Si Devices. IEEE Trans. Ind. Electron. 2017, 64, 8353–8363. [Google Scholar] [CrossRef]
- Thao, N.G.M.; Naruse, K.; Fujisaki, K. Reduction of Harmonics and Inverter Temperature in Experimental GaN-based Motor Drive System at High Frequencies Using LC Filter. In Proceedings of the 2022 IEEE Ninth International Conference on Communications and Electronics (ICCE), Nha Trang City, Vietnam, 27–29 July 2022; pp. 507–512. [Google Scholar] [CrossRef]
- Costa, P.; Pinto, S.; Silva, J.F. A Novel Analytical Formulation of SiC-MOSFET Losses to Size High-Efficiency Three-Phase Inverters. Energies 2023, 16, 818. [Google Scholar] [CrossRef]
- Hakami, S.S.; Lee, K.B. Four-Level Hysteresis-Based DTC for Torque Capability Improvement of IPMSM Fed by Three-Level NPC Inverter. Electronics 2020, 9, 1558. [Google Scholar] [CrossRef]
- Alsofyani, I.M.; Halabi, L.M. Unidirectional Finite Control Set-Predictive Torque Control of IPMSM Fed by Three-Level NPC Inverter with Simplified Voltage-Vector Lookup Table. Electronics 2023, 12, 252. [Google Scholar] [CrossRef]
- Bouarfa, A.; Bodson, M.; Fadel, M. A fast active-balancing method for the 3-phase multilevel flying capacitor inverter derived from control allocation theory. IFAC-PapersOnLine 2017, 50, 2113–2118. [Google Scholar] [CrossRef]
- Schettino, G.; Nevoloso, C.; Miceli, R.; Tommaso, A.D.; Viola, F. Impact Evaluation of Innovative Selective Harmonic Mitigation Algorithm for Cascaded H-Bridge Inverter on IPMSM Drive Application. IEEE Open J. Ind. Appl. 2021, 2, 347–365. [Google Scholar] [CrossRef]
- Eswar, K.N.D.V.S.; Doss, M.A.N.; Vishnuram, P.; Selim, A.; Bajaj, M.; Kotb, H.; Kamel, S. Comprehensive Study on Reduced DC Source Count: Multilevel Inverters and Its Design Topologies. Energies 2023, 16, 18. [Google Scholar] [CrossRef]
- Vinay Kumar, N.V.; GowriManohar, T. A comprehensive survey on reduced switch count multilevel inverter topologies and modulation techniques. J. Electr. Syst. Inf. Technol. 2023, 10, 3. [Google Scholar] [CrossRef]
- Zhu, C.; Zeng, Z.; Zhao, R. Comprehensive Analysis and Reduction of Torque Ripples in Three-Phase Four-Switch Inverter-Fed PMSM Drives Using Space Vector Pulse-Width Modulation. IEEE Trans. Power Electron. 2017, 32, 5411–5424. [Google Scholar] [CrossRef]
- Lu, J.; Hu, Y.; Liu, J. Analysis and Compensation of Sampling Errors in TPFS IPMSM Drives with Single Current Sensor. IEEE Trans. Ind. Electron. 2019, 66, 3852–3855. [Google Scholar] [CrossRef]
- Lee, K. Flying Capacitor-Assisted Two-Leg Inverter for Permanent Magnet Synchronous Motor Drive. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5429–5440. [Google Scholar] [CrossRef]
- Zhang, B.; Song, Z.; Liu, S.; Huang, R.; Liu, C. Overview of Integrated Electric Motor Drives: Opportunities and Challenges. Energies 2022, 15, 8299. [Google Scholar] [CrossRef]
- Matsumori, H.; Maeda, Y.; Kosaka, T.; Matsui, N.; Saha, S. Dual Inverter-Fed Open Winding IPMSM Drive System for High-Power Premium Class EV. IEEE Trans. Ind. Appl. 2023, 59, 2069–2080. [Google Scholar] [CrossRef]
- Kafi, M.R.; Hamida, M.A.; Chaoui, H.; Belkacemi, R. Sliding Mode Self-Sensing Control of Synchronous Machine Using Super Twisting Interconnected Observers. Energies 2020, 13, 4199. [Google Scholar] [CrossRef]
- Al-Kaf, H.A.G.; Hakami, S.S.; Lee, K.B. Hybrid Current Controller for Permanent-Magnet Synchronous Motors Using Robust Switching Techniques. IEEE Trans. Power Electron. 2023, 38, 3711–3724. [Google Scholar] [CrossRef]
- Bocker, J.; Beineke, S.; Bahr, A. On the control bandwidth of servo drives. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–10. [Google Scholar]
- Yepes, A.G.; Vidal, A.; Malvar, J.; López, O.; Doval-Gandoy, J. Tuning Method Aimed at Optimized Settling Time and Overshoot for Synchronous Proportional-Integral Current Control in Electric Machines. IEEE Trans. Power Electron. 2014, 29, 3041–3054. [Google Scholar] [CrossRef]
- Diab, A.M.; Bozhko, S.; Guo, F.; Rashed, M.; Buticchi, G.; Xu, Z.; Yeoh, S.S.; Gerada, C.; Galea, M. Fast and Simple Tuning Rules of Synchronous Reference Frame Proportional-Integral Current Controller. IEEE Access 2021, 9, 22156–22170. [Google Scholar] [CrossRef]
- Yang, S.M.; Lin, K.W. Automatic Control Loop Tuning for Permanent-Magnet AC Servo Motor Drives. IEEE Trans. Ind. Electron. 2016, 63, 1499–1506. [Google Scholar] [CrossRef]
- Yang, S.C.; Hsu, Y.L.; Chou, P.H.; Chen, J.Y.; Chen, G.R. Digital Implementation Issues on High Speed Permanent Magnet Machine FOC Drive Under Insufficient Sample Frequency. IEEE Access 2019, 7, 61484–61493. [Google Scholar] [CrossRef]
- Zhu, S.; Huang, W.; Yan, Y.; Niu, Z. High-Damped Complex Vector Current Regulator for PMSM Based on Active Damping Function. IEEE Trans. Power Electron. 2023, 38, 5204–5216. [Google Scholar] [CrossRef]
- Vukosavic, S.N.; Peric, L.S.; Levi, E. Digital Current Controller with Error-Free Feedback Acquisition and Active Resistance. IEEE Trans. Ind. Electron. 2018, 65, 1980–1990. [Google Scholar] [CrossRef] [Green Version]
- Briz, F.; Degner, M.; Lorenz, R. Analysis and design of current regulators using complex vectors. IEEE Trans. Ind. Appl. 2000, 36, 817–825. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.Q.; Liang, D.; Liu, K. Online Parameter Estimation for Permanent Magnet Synchronous Machines: An Overview. IEEE Access 2021, 9, 59059–59084. [Google Scholar] [CrossRef]
- Liu, X.; Du, Y. Torque Control of Interior Permanent Magnet Synchronous Motor Based on Online Parameter Identification Using Sinusoidal Current Injection. IEEE Access 2022, 10, 40517–40524. [Google Scholar] [CrossRef]
- Dang, D.Q.; Rafaq, M.S.; Choi, H.H.; Jung, J.W. Online Parameter Estimation Technique for Adaptive Control Applications of Interior PM Synchronous Motor Drives. IEEE Trans. Ind. Electron. 2016, 63, 1438–1449. [Google Scholar] [CrossRef]
- Rafaq, M.S.; Mohammed, S.A.Q.; Jung, J.W. Online Multiparameter Estimation for Robust Adaptive Decoupling PI Controllers of an IPMSM Drive: Variable Regularized APAs. IEEE/ASME Trans. Mechatronics 2019, 24, 1386–1395. [Google Scholar] [CrossRef]
- Lin, F.J.; Chen, S.Y.; Lin, W.T.; Liu, C.W. An Online Parameter Estimation Using Current Injection with Intelligent Current-Loop Control for IPMSM Drives. Energies 2021, 14, 8138. [Google Scholar] [CrossRef]
- Yang, J.; Chen, W.H.; Li, S.; Guo, L.; Yan, Y. Disturbance/Uncertainty Estimation and Attenuation Techniques in PMSM Drives—A Survey. IEEE Trans. Ind. Electron. 2017, 64, 3273–3285. [Google Scholar] [CrossRef] [Green Version]
- Sarsembayev, B.; Suleimenov, K.; Do, T.D. High Order Disturbance Observer Based PI-PI Control System With Tracking Anti-Windup Technique for Improvement of Transient Performance of PMSM. IEEE Access 2021, 9, 66323–66334. [Google Scholar] [CrossRef]
- Huber, T.; Peters, W.; Bocker, J. Voltage controller for flux weakening operation of interior permanent magnet synchronous motor in automotive traction applications. In Proceedings of the 2015 IEEE International Electric Machines and Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 10–13 May 2015; pp. 1078–1083. [Google Scholar] [CrossRef]
- Brosch, A.; Wallscheid, O.; Böcker, J. Model Predictive Control of Permanent Magnet Synchronous Motors in the Overmodulation Region Including Six-Step Operation. IEEE Open J. Ind. Appl. 2021, 2, 47–63. [Google Scholar] [CrossRef]
- Kwon, Y.C.; Kim, S.; Sul, S.K. Six-Step Operation of PMSM with Instantaneous Current Control. IEEE Trans. Ind. Appl. 2014, 50, 2614–2625. [Google Scholar] [CrossRef]
- Nakai, H.; Ohtani, H.; Inaguma, Y. Novel Torque Control Technique for High Efficiency/High Power Interior Permanent Magnet Synchronous Motors. R&D Rev. Toyota CRDL 2005, 40, 44–49. [Google Scholar]
- Lerdudomsak, S.; Kadota, M.; Doki, S.; Okuma, S. Harmonic Currents Estimation and Compensation Method for Current Control System of IPMSM in Overmodulation Range. In Proceedings of the 2007 Power Conversion Conference, Nagoya, Japan 2–5 April 2007; pp. 1320–1326. [Google Scholar] [CrossRef]
- Gemaßmer, T.; Schnarrenberger, M.; Späth, H.; Braun, M. Simple Strategy of Overmodulation in Control of Interior Permanent Magnet Synchronous Machines for Improving Efficiency in Automotive Applications. In Proceedings of the International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management (PCIM EUROPE 2013), Nuremburg, Germany, 14–16 May 2013; pp. 231–238. [Google Scholar]
- Tarczewski, T.; Grzesiak, L.M. Constrained State Feedback Speed Control of PMSM Based on Model Predictive Approach. IEEE Trans. Ind. Electron. 2016, 63, 3867–3875. [Google Scholar] [CrossRef]
- Brasel, M. A gain-scheduled multivariable LQR controller for permanent magnet synchronous motor. In Proceedings of the 2014 19th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 2–5 September 2014; pp. 722–725. [Google Scholar] [CrossRef]
- Paponpen, K.; Konghirun, M. LQR state feedback controller based on particle swarm optimization for IPMSM drive system. In Proceedings of the 2015 IEEE 10th Conference on Industrial Electronics and Applications (ICIEA), Auckland, New Zealand, 15–17 June 2015; pp. 1175–1180. [Google Scholar] [CrossRef]
- Sun, X.; Hu, C.; Lei, G.; Guo, Y.; Zhu, J. State Feedback Control for a PM Hub Motor Based on Gray Wolf Optimization Algorithm. IEEE Trans. Power Electron. 2020, 35, 1136–1146. [Google Scholar] [CrossRef]
- Madanzadeh, S.; Abedini, A.; Radan, A.; Ro, J.S. Application of quadratic linearization state feedback control with hysteresis reference reformer to improve the dynamic response of interior permanent magnet synchronous motors. ISA Trans. 2020, 99, 167–190. [Google Scholar] [CrossRef]
- Hinkkanen, M.; Asad Ali Awan, H.; Qu, Z.; Tuovinen, T.; Briz, F. Current Control for Synchronous Motor Drives: Direct Discrete-Time Pole-Placement Design. IEEE Trans. Ind. Appl. 2016, 52, 1530–1541. [Google Scholar] [CrossRef] [Green Version]
- Matsuki, Y.; Doki, S. High response torque control of IPMSM using state feedback control based on n-t coordinate system. Electr. Eng. Jpn. 2019, 206, 51–62. [Google Scholar] [CrossRef]
- Tarczewski, T.; Grzesiak, L.M. An Application of Novel Nature-Inspired Optimization Algorithms to Auto-Tuning State Feedback Speed Controller for PMSM. IEEE Trans. Ind. Appl. 2018, 54, 2913–2925. [Google Scholar] [CrossRef]
- Meirinho, C.J.; Bartsch, A.; de Oliveira, J.; Santos Matos Cavalca, M. An optimal MIMO control approach for PMSM drives. In Proceedings of the 2017 Brazilian Power Electronics Conference (COBEP), Juiz de Fora, Brazil, 19–22 November 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Xia, C.; Liu, N.; Zhou, Z.; Yan, Y.; Shi, T. Steady-State Performance Improvement for LQR-Based PMSM Drives. IEEE Trans. Power Electron. 2018, 33, 10622–10632. [Google Scholar] [CrossRef]
- Wu, C.; Blaabjerg, F. Chapter 1—Advanced control of power electronic systems—An overview of methods. In Control of Power Electronic Converters and Systems; Blaabjerg, F., Ed.; Academic Press: Cambridge, MA, USA, 2021; pp. 1–33. [Google Scholar] [CrossRef]
- Aghili, F. Optimal Feedback Linearization Control of Interior PM Synchronous Motors Subject to Time-Varying Operation Conditions Minimizing Power Loss. IEEE Trans. Ind. Electron. 2018, 65, 5414–5421. [Google Scholar] [CrossRef]
- Zhou, K.; Ai, M.; Sun, D.; Jin, N.; Wu, X. Field Weakening Operation Control Strategies of PMSM Based on Feedback Linearization. Energies 2019, 12, 4526. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Xu, N.; Yao, M.; Cai, F.; Wu, M. Efficient feedback linearization control for an IPMSM of EVs based on improved firefly algorithm. ISA Trans. 2023, 134, 431–441. [Google Scholar] [CrossRef]
- Choi, Y.S.; Choi, H.H.; Jung, J.W. Feedback Linearization Direct Torque Control with Reduced Torque and Flux Ripples for IPMSM Drives. IEEE Trans. Power Electron. 2016, 31, 3728–3737. [Google Scholar] [CrossRef]
- Li, H.; Wang, Z.; Xu, Z.; Wang, X.; Hu, Y. Feedback Linearization Based Direct Torque Control for IPMSMs. IEEE Trans. Power Electron. 2021, 36, 3135–3148. [Google Scholar] [CrossRef]
- Choi, A.; Kim, H.; Hu, M.; Kim, Y.; Ahn, H.; You, K. Super-Twisting Sliding Mode Control with SVR Disturbance Observer for PMSM Speed Regulation. Appl. Sci. 2022, 12, 10749. [Google Scholar] [CrossRef]
- Liu, X.; Yu, H.; Yu, J.; Zhao, L. Combined Speed and Current Terminal Sliding Mode Control with Nonlinear Disturbance Observer for PMSM Drive. IEEE Access 2018, 6, 29594–29601. [Google Scholar] [CrossRef]
- Mani, P.; Rajan, R.; Shanmugam, L.; Joo, Y.H. Adaptive Fractional Fuzzy Integral Sliding Mode Control for PMSM Model. IEEE Trans. Fuzzy Syst. 2019, 27, 1674–1686. [Google Scholar] [CrossRef]
- Xu, B.; Shen, X.; Ji, W.; Shi, G.; Xu, J.; Ding, S. Adaptive Nonsingular Terminal Sliding Model Control for Permanent Magnet Synchronous Motor Based on Disturbance Observer. IEEE Access 2018, 6, 48913–48920. [Google Scholar] [CrossRef]
- Huang, H.; Tu, Q.; Pan, M.; Jiang, C.; Xue, J. Fast Terminal Sliding Mode Control of Permanent Magnet In-Wheel Motor Based on a Fuzzy Controller. Energies 2020, 13, 188. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Li, D.; Li, Y.; Yang, L. A Novel Discrete Compound Integral Terminal Sliding Mode Control with Disturbance Compensation For PMSM Speed System. IEEE/ASME Trans. Mechatron. 2022, 27, 549–560. [Google Scholar] [CrossRef]
- Yang, T.; Deng, Y.; Li, H.; Sun, Z.; Cao, H.; Wei, Z. Fast integral terminal sliding mode control with a novel disturbance observer based on iterative learning for speed control of PMSM. ISA Trans. 2023, 134, 460–471. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.; Yin, Y.; Zhao, K. Improved Super-Twisting Non-Singular Fast Terminal Sliding Mode Control of Interior Permanent Magnet Synchronous Motor Considering Time-Varying Disturbance of the System. IEEE Access 2023, 11, 17485–17496. [Google Scholar] [CrossRef]
- Junejo, A.K.; Xu, W.; Mu, C.; Ismail, M.M.; Liu, Y. Adaptive Speed Control of PMSM Drive System Based a New Sliding-Mode Reaching Law. IEEE Trans. Power Electron. 2020, 35, 12110–12121. [Google Scholar] [CrossRef]
- Kim, E.K.; Kim, J.; Nguyen, H.T.; Choi, H.H.; Jung, J.W. Compensation of Parameter Uncertainty Using an Adaptive Sliding Mode Control Strategy for an Interior Permanent Magnet Synchronous Motor Drive. IEEE Access 2019, 7, 11913–11923. [Google Scholar] [CrossRef]
- Wang, A.; Jia, X.; Dong, S. A New Exponential Reaching Law of Sliding Mode Control to Improve Performance of Permanent Magnet Synchronous Motor. IEEE Trans. Magn. 2013, 49, 2409–2412. [Google Scholar] [CrossRef]
- Wang, A.; Wei, S. Sliding Mode Control for Permanent Magnet Synchronous Motor Drive Based on an Improved Exponential Reaching Law. IEEE Access 2019, 7, 146866–146875. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, Y.; Zhang, X.; Liang, J. A New Reaching Law for Antidisturbance Sliding-Mode Control of PMSM Speed Regulation System. IEEE Trans. Power Electron. 2020, 35, 4117–4126. [Google Scholar] [CrossRef]
- Hou, Q.; Ding, S.; Yu, X. Composite Super-Twisting Sliding Mode Control Design for PMSM Speed Regulation Problem Based on a Novel Disturbance Observer. IEEE Trans. Energy Convers. 2021, 36, 2591–2599. [Google Scholar] [CrossRef]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S. Disturbance-Observer-Based Control and Related Methods—An Overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Reitz, M.; Yaz, E.E. Field Oriented Sliding Mode Control of Surface-Mounted Permanent Magnet AC Motors: Theory and Applications to Electrified Vehicles. IEEE Trans. Veh. Technol. 2018, 67, 10343–10356. [Google Scholar] [CrossRef] [Green Version]
- Gabbi, T.S.; de Araujo, M.B.; Rocha, L.R.; Scalcon, F.P.; Gründling, H.A.; Vieira, R.P. Discrete-time sliding mode controller based on backstepping disturbance compensation for robust current control of PMSM drives. ISA Trans. 2022, 128, 581–592. [Google Scholar] [CrossRef]
- Rahman, M.; Vilathgamuwa, D.; Uddin, M.; Tseng, K.J. Nonlinear control of interior permanent-magnet synchronous motor. IEEE Trans. Ind. Appl. 2003, 39, 408–416. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Azar, A.T. Chapter 1—An introduction to backstepping control. In Backstepping Control of Nonlinear Dynamical Systems; Vaidyanathan, S., Azar, A.T., Eds.; Advances in Nonlinear Dynamics and Chaos (ANDC); Academic Press: Cambridge, MA, USA, 2021; pp. 1–32. [Google Scholar] [CrossRef]
- Wang, W.; Tan, F.; Wu, J.; Ge, H.; Wei, H.; Zhang, Y. Adaptive Integral Backstepping Controller for PMSM with AWPSO Parameters Optimization. Energies 2019, 12, 2596. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Lei, Y.; Sha, D. Backstepping direct torque control of permanent magnet synchronous motor with RLS parameter identification. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014; pp. 573–578. [Google Scholar] [CrossRef]
- Salah, N.; Samira, B.; Moreau, S. Modified backstepping control of IPMSM: Experimental tests. Proc. Inst. Mech. Eng. Part I 2022, 236, 1590–1602. [Google Scholar] [CrossRef]
- Kim, S.K.; Lee, J.S.; Lee, K.B. Offset-Free Robust Adaptive Back-Stepping Speed Control for Uncertain Permanent Magnet Synchronous Motor. IEEE Trans. Power Electron. 2016, 31, 7065–7076. [Google Scholar] [CrossRef]
- Sun, X.; Yu, H.; Yu, J.; Liu, X. Design and implementation of a novel adaptive backstepping control scheme for a PMSM with unknown load torque. IET Electr. Power Appl. 2019, 13, 445–455. [Google Scholar] [CrossRef]
- Mousavi, M.; Karami, M.; Ahmadi, M. Robust speed controller design for permanent magnet synchronous motor based on gain-scheduled control method via LMI approach. SN Appl. Sci. 2020, 2, 1699. [Google Scholar] [CrossRef]
- Lakhe, R.K.; Chaoui, H.; Alzayed, M.; Liu, S. Universal Control of Permanent Magnet Synchronous Motors with Uncertain Dynamics. Actuators 2021, 10, 49. [Google Scholar] [CrossRef]
- Lopez-Santos, O.; Dantonio, D.S.; Flores-Bahamonde, F.; Torres-Pinzón, C.A. Chapter 2—Hysteresis control methods. In Multilevel Inverters; Kabalcı, E., Ed.; Academic Press: Cambridge, MA, USA, 2021; pp. 35–60. [Google Scholar] [CrossRef]
- Son, D.I.; Han, J.S.; Park, J.S.; Lim, H.S.; Lee, G.H. Performance Improvement of DTC-SVM of PMSM with Compensation for the Dead Time Effect and Power Switch Loss Based on Extended Kalman Filter. Electronics 2023, 12, 966. [Google Scholar] [CrossRef]
- Lezana, P.; Norambuena, M.; Aguilera, R.P. Dual-Stage Control Strategy for a Flying Capacitor Converter Based on Model Predictive and Linear Controllers. IEEE Trans. Ind. Inform. 2022, 18, 2203–2212. [Google Scholar] [CrossRef]
- Cortes, P.; Kazmierkowski, M.P.; Kennel, R.M.; Quevedo, D.E.; Rodriguez, J. Predictive Control in Power Electronics and Drives. IEEE Trans. Ind. Electron. 2008, 55, 4312–4324. [Google Scholar] [CrossRef]
- Rodriguez, J.; Garcia, C.; Mora, A.; Flores-Bahamonde, F.; Acuna, P.; Novak, M.; Zhang, Y.; Tarisciotti, L.; Davari, S.A.; Zhang, Z.; et al. Latest Advances of Model Predictive Control in Electrical Drives—Part I: Basic Concepts and Advanced Strategies. IEEE Trans. Power Electron. 2022, 37, 3927–3942. [Google Scholar] [CrossRef]
- Elmorshedy, M.F.; Xu, W.; El-Sousy, F.F.M.; Islam, M.R.; Ahmed, A.A. Recent Achievements in Model Predictive Control Techniques for Industrial Motor: A Comprehensive State of the Art. IEEE Access 2021, 9, 58170–58191. [Google Scholar] [CrossRef]
- Rodriguez, J.; Garcia, C.; Mora, A.; Davari, S.A.; Rodas, J.; Valencia, D.F.; Elmorshedy, M.; Wang, F.; Zuo, K.; Tarisciotti, L.; et al. Latest Advances of Model Predictive Control in Electrical Drives—Part II: Applications and Benchmarking with Classical Control Methods. IEEE Trans. Power Electron. 2022, 37, 5047–5061. [Google Scholar] [CrossRef]
- Carlet, P.G.; Toso, F.; Favato, A.; Bolognani, S. A speed and current cascade Continuous Control Set Model Predictive Control architecture for synchronous motor drives. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 5682–5688. [Google Scholar] [CrossRef]
- Jose Rodriguez, P.C. Predictive Control of Power Converters and Electrical Drives; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Karamanakos, P.; Geyer, T. Guidelines for the Design of Finite Control Set Model Predictive Controllers. IEEE Trans. Power Electron. 2020, 35, 7434–7450. [Google Scholar] [CrossRef]
- Hassan, M.; Ge, X.; Woldegiorgis, A.T.; Mastoi, M.S.; Shahid, M.B.; Atif, R.; Shaikh, M.S.; Kumar, S. A look-up table-based model predictive torque control of IPMSM drives with duty cycle optimization. ISA Trans. 2023, 138, 670–686. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, D.; Huang, L. Generalized Multiple-Vector-Based Model Predictive Control for PMSM Drives. IEEE Trans. Ind. Electron. 2018, 65, 9356–9366. [Google Scholar] [CrossRef]
- Qu, J.; Jatskevich, J.; Zhang, C.; Zhang, S. Improved multiple vector model predictive torque control of permanent magnet synchronous motor for reducing torque ripple. IET Electr. Power Appl. 2021, 15, 681–695. [Google Scholar] [CrossRef]
- Yang, Y.; Wen, H.; Fan, M.; Zhang, X.; He, L.; Chen, R.; Xie, M.; Norambuena, M.; Rodriguez, J. Low Complexity Finite-Control-Set MPC Based on Discrete Space Vector Modulation for T-Type Three-Phase Three-Level Converters. IEEE Trans. Power Electron. 2022, 37, 392–403. [Google Scholar] [CrossRef]
- Niu, S.; Luo, Y.; Fu, W.; Zhang, X. An Indirect Reference Vector-Based Model Predictive Control for a Three-Phase PMSM Motor. IEEE Access 2020, 8, 29435–29445. [Google Scholar] [CrossRef]
- Lin, H.; Niu, S.; Xue, Z.; Wang, S. A Simplified Virtual-Vector-Based Model Predictive Control Technique with a Control Factor for Three-Phase SPMSM Drives. IEEE Trans. Power Electron. 2023, 38, 7546–7557. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, C.; Gu, X.; Wang, Z.; Li, X. An Improved Model Predictive Torque Control for a Two-Level Inverter Fed Interior Permanent Magnet Synchronous Motor. Electronics 2019, 8, 769. [Google Scholar] [CrossRef] [Green Version]
- Yang, Q.; Karamanakos, P.; Tian, W.; Gao, X.; Li, X.; Geyer, T.; Kennel, R. Computationally Efficient Fixed Switching Frequency Direct Model Predictive Control. IEEE Trans. Power Electron. 2022, 37, 2761–2777. [Google Scholar] [CrossRef]
- Cimini, G.; Bernardini, D.; Levijoki, S.; Bemporad, A. Embedded Model Predictive Control with Certified Real Time Optimization for Synchronous Motors. IEEE Trans. Control. Syst. Technol. 2021, 29, 893–900. [Google Scholar] [CrossRef]
- De Martin, I.D.; Pasqualotto, D.; Tinazzi, F. aVsIs: An Analytical-Solution-Based Solver for Model-Predictive Control with Hexagonal Constraints in Voltage-Source Inverter Applications. IEEE Trans. Power Electron. 2022, 37, 14375–14383. [Google Scholar] [CrossRef]
- Favato, A.; Carlet, P.G.; Toso, F.; Torchio, R.; Bolognani, S. Integral Model Predictive Current Control for Synchronous Motor Drives. IEEE Trans. Power Electron. 2021, 36, 13293–13303. [Google Scholar] [CrossRef]
- Jiang, X.; Yang, Y.; Fan, M.; Ji, A.; Xiao, Y.; Zhang, X.; Zhang, W.; Garcia, C.; Vazquez, S.; Rodriguez, J. An Improved Implicit Model Predictive Current Control with Continuous Control Set for PMSM Drives. IEEE Trans. Transp. Electrif. 2022, 8, 2444–2455. [Google Scholar] [CrossRef]
- Bándy, K.; Stumpf, P. Quadratic Regression Model-Based Indirect Model Predictive Control of AC Drives. IEEE Trans. Power Electron. 2022, 37, 13158–13177. [Google Scholar] [CrossRef]
- Brosch, A.; Wallscheid, O.; Böcker, J. Torque and Inductances Estimation for Finite Model Predictive Control of Highly Utilized Permanent Magnet Synchronous Motors. IEEE Trans. Ind. Inform. 2021, 17, 8080–8091. [Google Scholar] [CrossRef]
- Wang, L.; Tan, G.; Meng, J. Research on Model Predictive Control of IPMSM Based on Adaline Neural Network Parameter Identification. Energies 2019, 12, 4803. [Google Scholar] [CrossRef] [Green Version]
- Niu, S.; Luo, Y.; Fu, W.; Zhang, X. Robust Model Predictive Control for a Three-Phase PMSM Motor with Improved Control Precision. IEEE Trans. Ind. Electron. 2021, 68, 838–849. [Google Scholar] [CrossRef]
- Ke, D.; Wang, F.; He, L.; Li, Z. Predictive Current Control for PMSM Systems Using Extended Sliding Mode Observer with Hurwitz-Based Power Reaching Law. IEEE Trans. Power Electron. 2021, 36, 7223–7232. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Y.; Shen, W. Predictive Current Control and Field-Weakening Operation of SPMSM Drives without Motor Parameters and DC Voltage. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 5635–5646. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, J.; Huang, L. Model-Free Predictive Current Control of PMSM Drives Based on Extended State Observer Using Ultralocal Model. IEEE Trans. Ind. Electron. 2021, 68, 993–1003. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Z.; Yan, Q.; Huang, N.; Du, G. An Improved Model-Free Current Predictive Control of Permanent Magnet Synchronous Motor Based on High-Gain Disturbance Observer. Energies 2023, 16, 141. [Google Scholar] [CrossRef]
- Rodríguez, J.; Heydari, R.; Rafiee, Z.; Young, H.A.; Flores-Bahamonde, F.; Shahparasti, M. Model-Free Predictive Current Control of a Voltage Source Inverter. IEEE Access 2020, 8, 211104–211114. [Google Scholar] [CrossRef]
- Lin, C.K.; Liu, T.H.; Yu, J.t.; Fu, L.C.; Hsiao, C.F. Model-Free Predictive Current Control for Interior Permanent-Magnet Synchronous Motor Drives Based on Current Difference Detection Technique. IEEE Trans. Ind. Electron. 2014, 61, 667–681. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, F.; Young, H.; Ke, D.; Rodríguez, J. Autoregressive Moving Average Model-Free Predictive Current Control for PMSM Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 1. [Google Scholar] [CrossRef]
- Yang, H.; Li, M.; Zhang, Y.; Xu, A. FCS-MPC for Three-Level NPC Inverter-Fed SPMSM Drives without Information of Motor Parameters and DC Capacitor. IEEE Trans. Ind. Electron. 2023, 1–10. [Google Scholar] [CrossRef]
- Carlet, P.G.; Favato, A.; Bolognani, S.; Dörfler, F. Data-Driven Continuous-Set Predictive Current Control for Synchronous Motor Drives. IEEE Trans. Power Electron. 2022, 37, 6637–6646. [Google Scholar] [CrossRef]
- Carlet, P.G.; Favato, A.; Torchio, R.; Toso, F.; Bolognani, S.; Dörfler, F. Real-Time Feasibility of Data-Driven Predictive Control for Synchronous Motor Drives. IEEE Trans. Power Electron. 2023, 38, 1672–1682. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, S.; Huang, X.; Liao, W.; Zhang, J.; Ma, B. An Angle-Based Virtual Vector Model Predictive Current Control for IPMSM Considering Overmodulation. IEEE Trans. Transp. Electrif. 2023, 1. [Google Scholar] [CrossRef]
- Yu, F.; Li, K.; Zhu, Z.; Liu, X. An Over-Modulated Model Predictive Current Control for Permanent Magnet Synchronous Motors. IEEE Access 2022, 10, 40391–40401. [Google Scholar] [CrossRef]
- Zhang, Y.; Qi, R. Flux-Weakening Drive for IPMSM Based on Model Predictive Control. Energies 2022, 15, 2543. [Google Scholar] [CrossRef]
- Xia, C.; Zhou, Z.; Wang, Z.; Yan, Y.; Shi, T. Computationally efficient multi-step direct predictive torque control for surface-mounted permanent magnet synchronous motor. IET Electr. Power Appl. 2017, 11, 805–814. [Google Scholar] [CrossRef]
- Acuna, P.; Rojas, C.A.; Baidya, R.; Aguilera, R.P.; Fletcher, J.E. On the Impact of Transients on Multistep Model Predictive Control for Medium-Voltage Drives. IEEE Trans. Power Electron. 2019, 34, 8342–8355. [Google Scholar] [CrossRef]
- Dorfling, T.; Mouton, H.d.T.; Geyer, T. Generalized Model Predictive Pulse Pattern Control Based on Small-Signal Modeling—Part 1: Algorithm. IEEE Trans. Power Electron. 2022, 37, 10476–10487. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Babayomi, O.; Li, Z. Weighting Factor Design Techniques for Predictive Control of Power Electronics and Motor Drives. Symmetry 2023, 15, 1219. [Google Scholar] [CrossRef]
- Gong, C.; Hu, Y.; Ma, M.; Gao, J.; Shen, K. Novel Analytical Weighting Factor Tuning Strategy Based on State Normalization and Variable Sensitivity Balance for PMSM FCS-MPTC. IEEE/ASME Trans. Mechatronics 2020, 25, 1690–1694. [Google Scholar] [CrossRef]
- Sahin, M. Optimization of Model Predictive Control Weights for Control of Permanent Magnet Synchronous Motor by Using the Multi Objective Bees Algorithm. In Model-Based Control Engineering-Recent Design and Implementations for Varied Applications; IntechOpen: London, UK, 2021. [Google Scholar]
- Novak, M.; Xie, H.; Dragicevic, T.; Wang, F.; Rodriguez, J.; Blaabjerg, F. Optimal Cost Function Parameter Design in Predictive Torque Control (PTC) Using Artificial Neural Networks (ANN). IEEE Trans. Ind. Electron. 2021, 68, 7309–7319. [Google Scholar] [CrossRef]
- Bándy, K.; Stumpf, P. Finite Set Model Predictive Control of PMSM drives with LC filter using dynamic weighting factor assignment. In Proceedings of the 2022 20th International Conference on Mechatronics—Mechatronika (ME), Pilsen, Czech Republic, 7–9 December 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Mei, X.; Zu, R.; Wang, F.; Kennel, R. Variable Cost Functions’ Sequence Design for Model Predictive Control of IPMSM without Weighting Factor. In Proceedings of the 2018 IEEE International Conference on Information and Automation (ICIA), Wuyishan, China, 11–13 August 2018; pp. 500–505. [Google Scholar] [CrossRef]
- Xie, H.; Novak, M.; Wang, F.; Dragicevic, T.; Rodríguez, J.; Blaabjerg, F.; Kennel, R.; Heldwein, M.L. Cooperative Decision-making Approach for Multi-objective Finite Control Set Model Predictive Control without Weighting Parameters. IEEE Trans. Ind. Electron. 2023, 1–11. [Google Scholar] [CrossRef]
- Norambuena, M.; Rodriguez, J.; Zhang, Z.; Wang, F.; Garcia, C.; Kennel, R. A Very Simple Strategy for High-Quality Performance of AC Machines Using Model Predictive Control. IEEE Trans. Power Electron. 2019, 34, 794–800. [Google Scholar] [CrossRef]
- Dai, S.; Wang, J.; Sun, Z.; Chong, E. Deadbeat Predictive Current Control for High-Speed Permanent Magnet Synchronous Machine Drives with Low Switching-To-Fundamental Frequency Ratios. IEEE Trans. Ind. Electron. 2022, 69, 4510–4521. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, Y.; Zhang, X.; Tian, B.; Wang, K.; Liang, J. Antidisturbance Sliding Mode-Based Deadbeat Direct Torque Control for PMSM Speed Regulation System. IEEE Trans. Transp. Electrif. 2021, 7, 2705–2714. [Google Scholar] [CrossRef]
- Alexandrou, A.D.; Adamopoulos, N.K.; Kladas, A.G. Development of a Constant Switching Frequency Deadbeat Predictive Control Technique for Field-Oriented Synchronous Permanent-Magnet Motor Drive. IEEE Trans. Ind. Electron. 2016, 63, 5167–5175. [Google Scholar] [CrossRef]
- Gu, X.; Li, Y.; Chen, W.; Jin, X. Improved Deadbeat Predictive Control Based Current Harmonic Suppression Strategy for IPMSM. Energies 2022, 15, 3943. [Google Scholar] [CrossRef]
- Fan, S.; Zhang, Y.; Jin, J.; Wang, X.; Tong, C. Deadbeat predictive current control of PMSM drives with an adaptive flux-weakening controller. IET Power Electron. 2022, 15, 753–763. [Google Scholar] [CrossRef]
- Agoro, S.; Husain, I. Robust Deadbeat Finite-Set Predictive Current Control with Torque Oscillation and Noise Reduction for PMSM Drives. IEEE Trans. Ind. Appl. 2022, 58, 365–374. [Google Scholar] [CrossRef]
- Lee, J.S. Stability Analysis of Deadbeat-Direct Torque and Flux Control for Permanent Magnet Synchronous Motor Drives with Respect to Parameter Variations. Energies 2018, 11, 2027. [Google Scholar] [CrossRef] [Green Version]
- Ofoli, A.R. Fuzzy-Logic Applications in Electric Drives and Power Electronics. In Power Electronics Handbook, 4th ed.; Rashid, M.H., Ed.; Butterworth-Heinemann: Oxford, UK, 2018; pp. 1221–1243. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, S.H.; Chung, C.C. LPV H∞ Control with Disturbance Estimation for Permanent Magnet Synchronous Motors. IEEE Trans. Ind. Electron. 2018, 65, 488–497. [Google Scholar] [CrossRef]
- Uddin, M.N.; Rebeiro, R.S. Online Efficiency Optimization of a Fuzzy-Logic-Controller-Based IPMSM Drive. IEEE Trans. Ind. Appl. 2011, 47, 1043–1050. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, Z.Q. Fuzzy Logic Speed Control of Permanent Magnet Synchronous Machine and Feedback Voltage Ripple Reduction in Flux-Weakening Operation Region. IEEE Trans. Ind. Appl. 2020, 56, 1505–1517. [Google Scholar] [CrossRef]
- Wang, M.S.; Hsieh, M.F.; Lin, H.Y. Operational Improvement of Interior Permanent Magnet Synchronous Motor Using Fuzzy Field-Weakening Control. Electronics 2018, 7, 452. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.H.; Chen, Y.; Wu, M.J.; Dai, B.C. Adaptive controller for an MTPA IPMSM drive system without using a high-frequency sinusoidal generator. J. Eng. 2017, 2017, 13–25. [Google Scholar] [CrossRef]
- Kakouche, K.; Oubelaid, A.; Mezani, S.; Rekioua, D.; Rekioua, T. Different Control Techniques of Permanent Magnet Synchronous Motor with Fuzzy Logic for Electric Vehicles: Analysis, Modelling, and Comparison. Energies 2023, 16, 3116. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, A.; Li, X.; Zhang, G.; Xia, C. A Novel Current Predictive Control Based on Fuzzy Algorithm for PMSM. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 990–1001. [Google Scholar] [CrossRef]
- Usama, M.; Kim, J. Improved Self-Sensing Speed Control of IPMSM Drive Based on Cascaded Nonlinear Control. Energies 2021, 14, 2205. [Google Scholar] [CrossRef]
- Bouguenna, I.F.; Azaiz, A.; Tahour, A.; Larbaoui, A. Robust neuro-fuzzy sliding mode control with extended state observer for an electric drive system. Energy 2019, 169, 1054–1063. [Google Scholar] [CrossRef]
- Zhao, S.; Blaabjerg, F.; Wang, H. An Overview of Artificial Intelligence Applications for Power Electronics. IEEE Trans. Power Electron. 2021, 36, 4633–4658. [Google Scholar] [CrossRef]
- Zhang, S. Artificial Intelligence in Electric Machine Drives: Advances and Trends. arXiv 2021, arXiv:2110.05403. [Google Scholar]
- Zhang, S.; Wallscheid, O.; Porrmann, M. Machine Learning for the Control and Monitoring of Electric Machine Drives: Advances and Trends. IEEE Open J. Ind. Appl. 2023, 4, 188–214. [Google Scholar] [CrossRef]
- Book, G.; Traue, A.; Balakrishna, P.; Brosch, A.; Schenke, M.; Hanke, S.; Kirchgässner, W.; Wallscheid, O. Transferring Online Reinforcement Learning for Electric Motor Control From Simulation to Real-World Experiments. IEEE Open J. Power Electron. 2021, 2, 187–201. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Schenke, M.; Kirchgässner, W.; Wallscheid, O. Controller Design for Electrical Drives by Deep Reinforcement Learning: A Proof of Concept. IEEE Trans. Ind. Inform. 2020, 16, 4650–4658. [Google Scholar] [CrossRef]
- Traue, A.; Book, G.; Kirchgässner, W.; Wallscheid, O. Toward a Reinforcement Learning Environment Toolbox for Intelligent Electric Motor Control. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 919–928. [Google Scholar] [CrossRef]
- Jegan, J.; Karuppasamy, I. Simulation and Validation of Permanent Magnet Synchronous Motor Drives Using Reinforcement Learning. In Proceedings of the 2023 IEEE 8th International Conference for Convergence in Technology (I2CT), Mumbai, India, 7–9 April 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, S.; Du, Y.; Viswanathan, V.; Su, R.; Ramakrishna, S.; Gajanayake, C.; Gupta, A.K. Application of Off-policy Integral Reinforcement Learning for H-infinity, Input Constrained Control of Permanent Magnet Synchronous Machine. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 2570–2576. [Google Scholar] [CrossRef]
- Jakobeit, D.; Schenke, M.; Wallscheid, O. Meta-Reinforcement-Learning-Based Current Control of Permanent Magnet Synchronous Motor Drives for a Wide Range of Power Classes. IEEE Trans. Power Electron. 2023, 38, 8062–8074. [Google Scholar] [CrossRef]
- Dendaluce Jahnke, M.; Cosco, F.; Novickis, R.; Pérez Rastelli, J.; Gomez-Garay, V. Efficient Neural Network Implementations on Parallel Embedded Platforms Applied to Real-Time Torque-Vectoring Optimization Using Predictions for Multi-Motor Electric Vehicles. Electronics 2019, 8, 250. [Google Scholar] [CrossRef] [Green Version]
- Ullah, K.; Guzinski, J.; Mirza, A.F. Critical Review on Robust Speed Control Techniques for Permanent Magnet Synchronous Motor (PMSM) Speed Regulation. Energies 2022, 15, 1235. [Google Scholar] [CrossRef]
- Ko, P.J.; Tsai, M.C. H∞ Control Design of PID-Like Controller for Speed Drive Systems. IEEE Access 2018, 6, 36711–36722. [Google Scholar] [CrossRef]
- Li, L.; Pei, G.; Liu, J.; Du, P.; Pei, L.; Zhong, C. 2-DOF Robust H∞ Control for Permanent Magnet Synchronous Motor with Disturbance Observer. IEEE Trans. Power Electron. 2021, 36, 3462–3472. [Google Scholar] [CrossRef]
- Rigatos, G.; Abbaszadeh, M.; Wira, P.; Siano, P. A nonlinear optimal control approach for voltage source inverter-fed three-phase PMSMs. In Proceedings of the 47th Annual Conference of the IEEE Industrial Electronics Society (IECON 2021), Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Pohl, L.; Buchta, L. H-infinity tuning technique for PMSM cascade PI control structure. In Proceedings of the 2016 6th IEEE International Conference on Control System, Computing and Engineering (ICCSCE), Penang, Malaysia, 25–27 November 2016; pp. 119–124. [Google Scholar] [CrossRef]
- Cai, R.; Zheng, R.; Liu, M.; Li, M. Optimal selection of PI parameters of FOC for PMSM using structured H∞-synthesis. In Proceedings of the 43rd Annual Conference of the IEEE Industrial Electronics Society (IECON 2017), Beijing, China, 29 October–1 November 2017; pp. 8602–8607. [Google Scholar] [CrossRef]
- Mihaly, V.; Susca, M.; Morar, D.; Stanese, M.; Dobra, P. μ-Synthesis for Fractional-Order Robust Controllers. Mathematics 2021, 9, 911. [Google Scholar] [CrossRef]
- Liu, H.; Ma, L.; Peng, L.; Song, W.; Cheng, S. Robust current control scheme for single-phase PWM rectifiers based on improved μ-synthesis in electric locomotive. IET Power Electron. 2020, 13, 4068–4078. [Google Scholar] [CrossRef]
- Cai, R.; Zheng, R.; Liu, M.; Li, M. Robust Control of PMSM Using Geometric Model Reduction and μ-Synthesis. IEEE Trans. Ind. Electron. 2018, 65, 498–509. [Google Scholar] [CrossRef]
- Ahn, H.S.; Chen, Y.; Moore, K.L. Iterative Learning Control: Brief Survey and Categorization. IEEE Trans. Syst. Man, Cybern. Part 2007, 37, 1099–1121. [Google Scholar] [CrossRef]
- Rafaq, M.S.; Midgley, W.; Steffen, T. A Review of the State of the Art of Torque Ripple Minimization Techniques for Permanent Magnet Synchronous Motors. IEEE Trans. Ind. Inform. 2023, 1–13. [Google Scholar] [CrossRef]
- Qian, W.; Panda, S.; Xu, J.X. Torque ripple minimization in PM synchronous motors using iterative learning control. IEEE Trans. Power Electron. 2004, 19, 272–279. [Google Scholar] [CrossRef]
- Xu, J.X.; Panda, S.; Pan, Y.J.; Lee, T.H.; Lam, B. A modular control scheme for PMSM speed control with pulsating torque minimization. IEEE Trans. Ind. Electron. 2004, 51, 526–536. [Google Scholar] [CrossRef]
- Toloue, S.F.; Moallem, M. PMSM Torque Ripple Minimization Using an Adaptive Iterative Learning Control. In Proceedings of the 46th Annual Conference of the IEEE Industrial Electronics Society (IECON 2020), Singapore, 18–21 October 2020; pp. 335–340. [Google Scholar] [CrossRef]
- Xia, C.; Deng, W.; Shi, T.; Yan, Y. Torque ripple minimization of PMSM using parameter optimization based iterative learning control. J. Electr. Eng. Technol. 2016, 11, 425–436. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Li, H.; Deng, Y. Torque Ripple Minimization of PMSM Based on Robust ILC Via Adaptive Sliding Mode Control. IEEE Trans. Power Electron. 2018, 33, 3655–3671. [Google Scholar] [CrossRef]
- Xia, X.; Zhang, B.; Li, X. High Precision Low-Speed Control for Permanent Magnet Synchronous Motor. Sensors 2020, 20, 1526. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, S.A.Q.; Lee, K.B. Improved adaptive iterative learning current control approach for IPMSM drives. J. Power Electron. 2023, 23, 284–295. [Google Scholar] [CrossRef]
- Golea, N.; Golea, A.; Kadjoudj, M. Robust MRAC Adaptive Control of PMSM drive under General Parameters Uncertainties. In Proceedings of the 2006 IEEE International Conference on Industrial Technology, Mumbai, India, 15–17 December 2006; pp. 1533–1537. [Google Scholar] [CrossRef]
- Amornwongpeeti, S.; Kiselychnyk, O.; Wang, J.; Shah, N.; Soumelidis, M. Speed control of IPMSM motor drives using Model Reference Adaptive technique. In Proceedings of the 2017 International Conference on Applied System Innovation (ICASI), Sapporo, Japan, 13–17 May 2017; pp. 672–675. [Google Scholar] [CrossRef]
- Guo, T.; Chen, Y.; Chen, Q.; Lin, T.; Ren, H. An IPMSM Control Structure Based on a Model Reference Adaptive Algorithm. Machines 2022, 10, 575. [Google Scholar] [CrossRef]
- Su, G.; Wang, P.; Guo, Y.; Cheng, G.; Wang, S.; Zhao, D. Multiparameter Identification of Permanent Magnet Synchronous Motor Based on Model Reference Adaptive System—Simulated Annealing Particle Swarm Optimization Algorithm. Electronics 2022, 11, 159. [Google Scholar] [CrossRef]
- Khlaief, A.; Boussak, M.; Châari, A. A MRAS-based stator resistance and speed estimation for sensorless vector controlled IPMSM drive. Electr. Power Syst. Res. 2014, 108, 1–15. [Google Scholar] [CrossRef]
- Feng, W.; Bai, J.; Zhang, Z.; Zhang, J. A Composite Variable Structure PI Controller for Sensorless Speed Control Systems of IPMSM. Energies 2022, 15, 8292. [Google Scholar] [CrossRef]
- Sanz, A.; Oyarbide, E.; Gálvez, R.; Bernal, C.; Molina, P.; San Vicente, I. Analytical maximum torque per volt control strategy of an interior permanent magnet synchronous motor with very low battery voltage. IET Electr. Power Appl. 2019, 13, 1042–1050. [Google Scholar] [CrossRef]
- Meyer, M.; Grote, T.; Bocker, J. Direct torque control for interior permanent magnet synchronous motors with respect to optimal efficiency. In Proceedings of the 2007 European Conference on Power Electronics and Applications, Aalborg, Denmark, 2–5 September 2007; pp. 1–9. [Google Scholar] [CrossRef]
- Huang, S.; Chen, Z.; Huang, K.; Gao, J. Maximum torque per ampere and flux-weakening control for PMSM based on curve fitting. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Jeong, I.; Gu, B.G.; Kim, J.; Nam, K.; Kim, Y. Inductance Estimation of Electrically Excited Synchronous Motor via Polynomial Approximations by Least Square Method. IEEE Trans. Ind. Appl. 2015, 51, 1526–1537. [Google Scholar] [CrossRef]
- Lin, F.J.; Liao, Y.H.; Lin, J.R.; Lin, W.T. Interior Permanent Magnet Synchronous Motor Drive System with Machine Learning-Based Maximum Torque per Ampere and Flux-Weakening Control. Energies 2021, 14, 346. [Google Scholar] [CrossRef]
- Sun, T.; Wang, J.; Koc, M.; Chen, X. Self-learning MTPA control of interior permanent magnet synchronous machine drives based on virtual signal injection. In Proceedings of the 2015 IEEE International Electric Machines and Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 10–13 May 2015; pp. 1056–1062. [Google Scholar] [CrossRef]
- Li, K.; Wang, Y. Maximum Torque per Ampere (MTPA) Control for IPMSM Drives Using Signal Injection and an MTPA Control Law. IEEE Trans. Ind. Inform. 2019, 15, 5588–5598. [Google Scholar] [CrossRef]
- Chen, Z.; Yan, Y.; Shi, T.; Gu, X.; Wang, Z.; Xia, C. An Accurate Virtual Signal Injection Control for IPMSM with Improved Torque Output and Widen Speed Region. IEEE Trans. Power Electron. 2021, 36, 1941–1953. [Google Scholar] [CrossRef]
- Li, K.; Sun, T.; Jiang, F.; Feng, W.; Li, H. MTPA Control for IPMSM Drives Based on Pseudorandom Frequency-Switching Sinusoidal Signal Injection. Machines 2022, 10, 231. [Google Scholar] [CrossRef]
- Xia, Z.; Nalakath, S.; Tarvirdilu-Asl, R.; Sun, Y.; Wiseman, J.; Emadi, A. Online Optimal Tracking Method for Interior Permanent Magnet Machines with Improved MTPA and MTPV in Whole Speed and Torque Ranges. IEEE Trans. Power Electron. 2020, 35, 9753–9769. [Google Scholar] [CrossRef]
- Xia, Z.; Filho, S.R.; Xiao, D.; Fang, G.; Sun, Y.; Wiseman, J.; Emadi, A. Computation-Efficient Online Optimal Tracking Method for Permanent Magnet Synchronous Machine Drives for MTPA and Flux-Weakening Operations. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5341–5353. [Google Scholar] [CrossRef]
- Bianchini, C.; Franceschini, G.; Torreggiani, A. Improvement on Flux Weakening Control Strategy for Electric Vehicle Applications. Appl. Sci. 2021, 11, 2422. [Google Scholar] [CrossRef]
- Jahns, T.M. Flux-Weakening Regime Operation of an Interior Permanent-Magnet Synchronous Motor Drive. IEEE Trans. Ind. Appl. 1987, IA-23, 681–689. [Google Scholar] [CrossRef]
- Hu, D.; Zhu, L.; Xu, L. Maximum Torque per Volt operation and stability improvement of PMSM in deep flux-weakening Region. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 1233–1237. [Google Scholar] [CrossRef]
- Fadel, M.; Sepulchre, L.; Pietrzak-David, M.; Porte, G. MTPV Flux Weakening Strategy for PMSM High Speed Drive. IEEE Trans. Ind. Appl. 2018, 54, 6081–6089. [Google Scholar] [CrossRef]
- Miguel-Espinar, C.; Heredero-Peris, D.; Gross, G.; Llonch-Masachs, M.; Montesinos-Miracle, D. Maximum Torque per Voltage Flux-Weakening Strategy with Speed Limiter for PMSM Drives. IEEE Trans. Ind. Electron. 2021, 68, 9254–9264. [Google Scholar] [CrossRef]











| MTPA 1 | |
| MTPV 1 | |
| MTPF 2 | |
| Method | Typ. App. 1,2 | Benefits | Limitations |
|---|---|---|---|
| PI | C/S/F |
|
|
| SFC | C/S |
|
|
| FBL | C/S/T/F |
|
|
| SMC | S |
|
|
| BS | C/T |
|
|
| HC | C/T/F |
|
|
| FS-MPC | C/T/F |
|
|
| CS-MPC | C/T/F |
|
|
| PDBC | C/T/F |
|
|
| FLC | S |
|
|
| RL | C/S/F |
|
|
| ILC | S |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stumpf, P.; Tóth-Katona, T. Recent Achievements in the Control of Interior Permanent-Magnet Synchronous Machine Drives: A Comprehensive Overview of the State of the Art. Energies 2023, 16, 5103. https://doi.org/10.3390/en16135103
Stumpf P, Tóth-Katona T. Recent Achievements in the Control of Interior Permanent-Magnet Synchronous Machine Drives: A Comprehensive Overview of the State of the Art. Energies. 2023; 16(13):5103. https://doi.org/10.3390/en16135103
Chicago/Turabian StyleStumpf, Peter, and Tamás Tóth-Katona. 2023. "Recent Achievements in the Control of Interior Permanent-Magnet Synchronous Machine Drives: A Comprehensive Overview of the State of the Art" Energies 16, no. 13: 5103. https://doi.org/10.3390/en16135103
APA StyleStumpf, P., & Tóth-Katona, T. (2023). Recent Achievements in the Control of Interior Permanent-Magnet Synchronous Machine Drives: A Comprehensive Overview of the State of the Art. Energies, 16(13), 5103. https://doi.org/10.3390/en16135103










