Use of Park’s Vector Method for Monitoring the Rotor Condition of an Induction Motor as a Part of the Built-In Diagnostic System of Electric Drives of Transport
Abstract
:1. Introduction
1.1. Motivation and Relevance
1.2. Literature Review
1.3. Contribution
1.4. Organization of the Paper
2. The Main Elements of Monitoring the State of an Induction Electric Motor
3. Development of an Algorithm for Determining the State of the Squirrel-Cage Rotor Winding of an Induction Motor
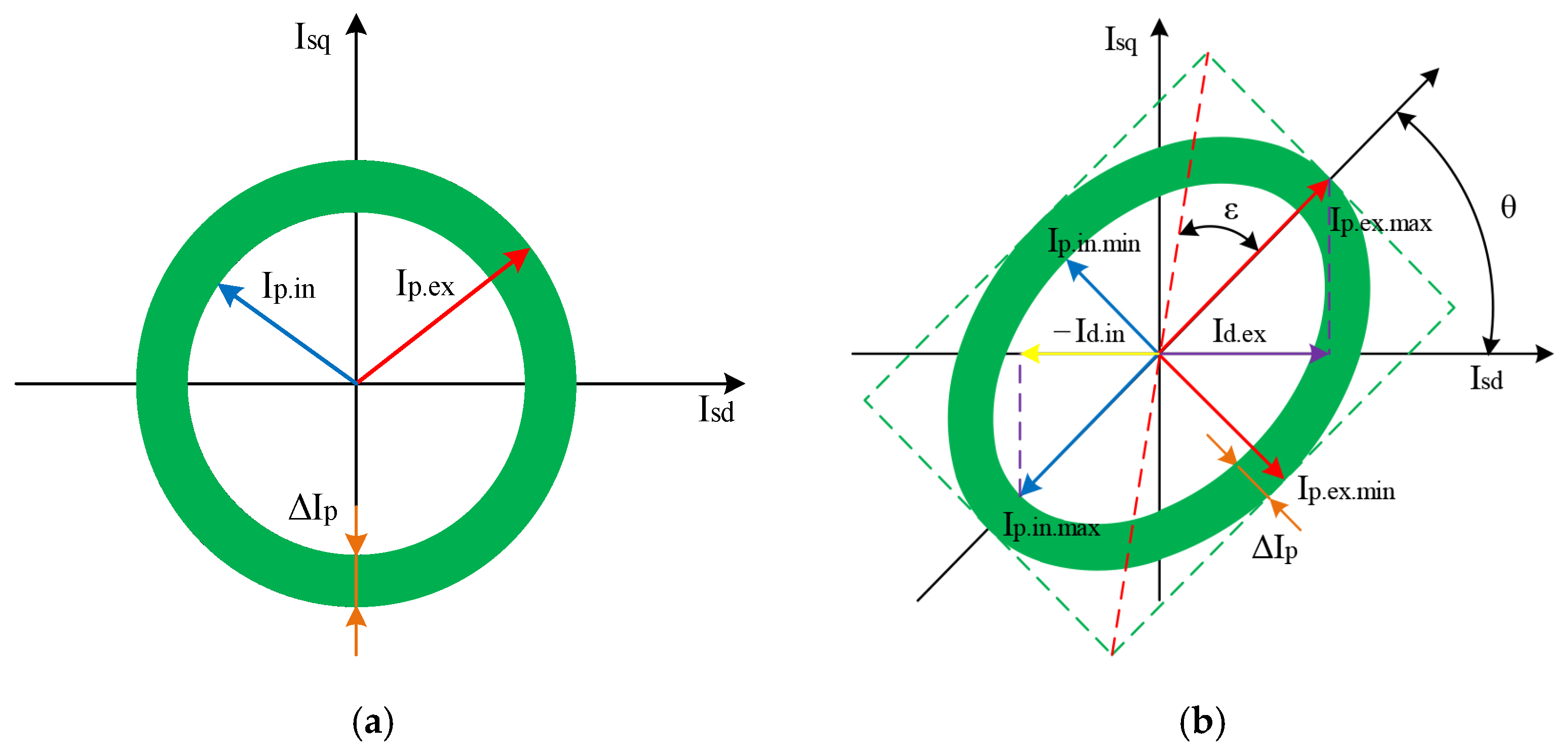
3.1. Using the Park’s Vector Method for Rotor Diagnostics
3.2. Development of a Technique for Determining Rotor Damage by the Park’s Vector Hodograph Method
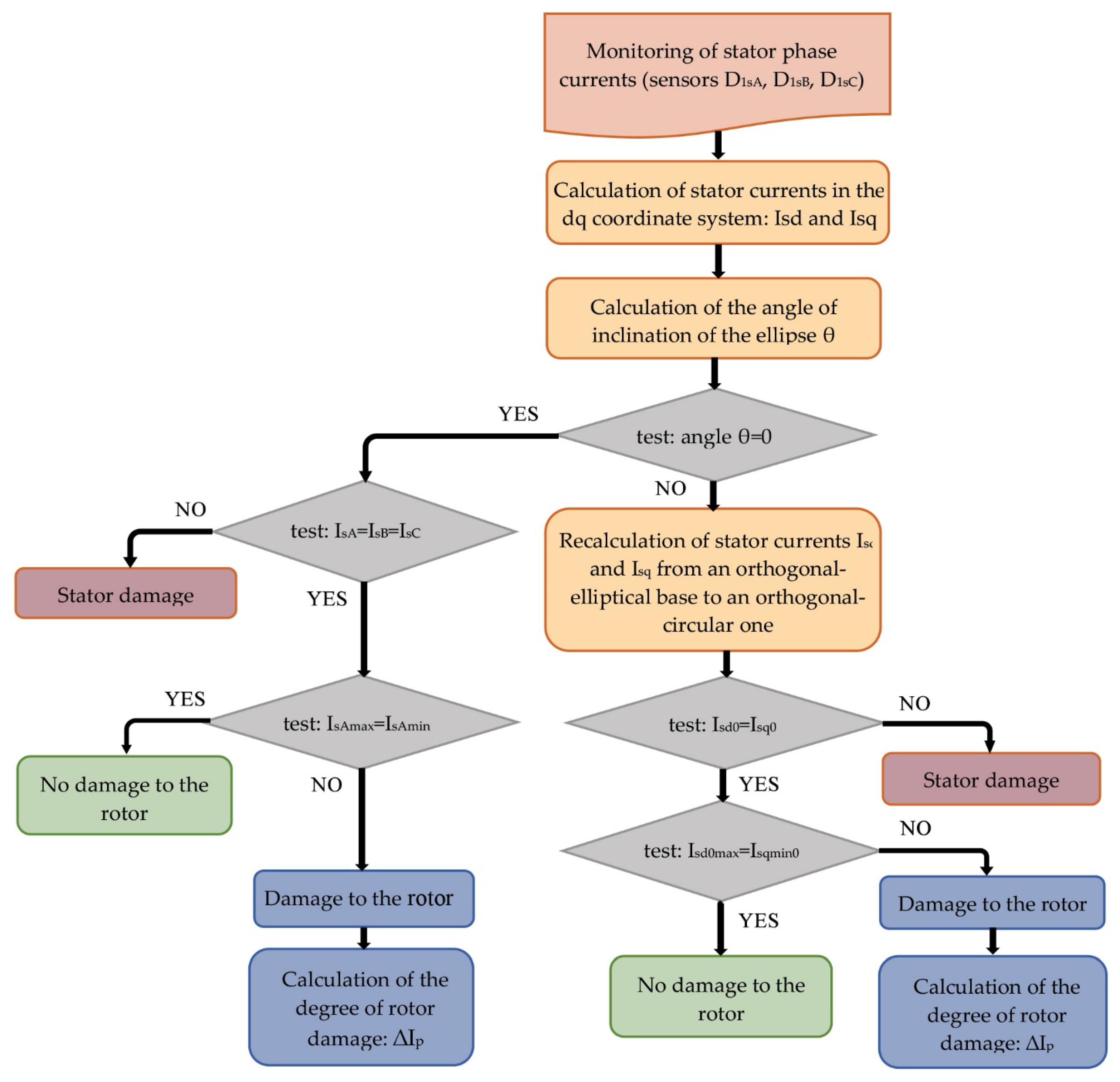
3.3. Algorithm for Using Park’s Method for Rotor Diagnostics in Built-In Diagnostic Systems
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tuychieva, M. Control of electric locomotives with asynchronous electric motors under asymmetric operating conditions in Uzbekistan. IOP Conf. Ser. Earth Environ. Sci. 2020, 614, 012060. [Google Scholar] [CrossRef]
- Lovska, A.; Fomin, O.; Píštěk, V.; Kučera, P. Dynamic load modelling within combined transport trains during transportation on a railway ferry. Appl. Sci. 2020, 10, 5710. [Google Scholar] [CrossRef]
- Kuznetsov, V.; Kardas-Cinal, E.; Gołębiowski, P.; Liubarskyi, B.; Gasanov, M.; Riabov, I.I.; Kondratieva, L.; Opala, M. Method of Selecting Energy-Efficient Parameters of an Electric Asynchronous Traction Motor for Diesel Shunting Locomotives—Case Study on the Example of a Locomotive Series ChME3 (ЧMЭ3, ČME3, ČKD S200). Energies 2022, 15, 317. [Google Scholar] [CrossRef]
- Goolak, S.; Tkachenko, V.; Šťastniak, P.; Sapronova, S.; Liubarskyi, B. Analysis of Control Methods for the Traction Drive of an Alternating Current Electric Locomotive. Symmetry 2022, 14, 150. [Google Scholar] [CrossRef]
- Balakrishna, P.; Khan, U. An Autonomous Electrical Signature Analysis-Based Method for Faults Monitoring in Industrial Motors. IEEE Trans. Instrum. Meas. 2021, 70, 1–8. [Google Scholar] [CrossRef]
- Wu, Y.; Jiang, B.; Wang, Y. Incipient winding fault detection and diagnosis for squirrel-cage induction motors equipped on CRH trains. ISA Trans. 2020, 99, 488–495. [Google Scholar] [CrossRef] [PubMed]
- Kondratieva, L.; Bogdanovs, A.; Overianova, L.; Riabov, I.; Goolak, S. Determination of the Working Energy Capacity of the On-Board Energy Storage System of an Electric Locomotive for Quarry Railway Transport During Working with a Limitation of Consumed Power. Arch. Transp. 2023, 65, 119–135. [Google Scholar] [CrossRef]
- Turpak, S.M.; Taran, I.O.; Fomin, O.V.; Tretiak, O.O. Logistic technology to deliver raw material for metallurgical production. Sci. Bull. Natl. Min. Univ. 2018, 1, 162–169. [Google Scholar] [CrossRef]
- Bodnar, B.; Ochkаsov, O.; Bodnar, E.; Hryshechkina, T.; Keršys, R. Safety performance analysis of the movement and operation of locomotives. In Proceedings of the Transport means 2018: 22nd International Scientific Conference, Trakai, Lithuania, 3–5 October 2018; Kaunas University of Technology: Kaunas, Lithuania, 2018. Pt. II. pp. 839–843. Available online: https://transportmeans.ktu.edu/wp-content/uploads/sites/307/2018/02/Transport-means-II-A4-2018-09-25.pdf (accessed on 25 March 2023).
- Gubarevych, O.; Goolak, S.; Golubieva, S. Classification of Defects, Systematization and Selection of Methods for Diagnosing the Stator Windings Insulation of Asynchronous Motors. Rev. Roum. Sci. Techn.–Électrotechn. et Énerg 2022, 67, 445–450. [Google Scholar]
- Choudhary, A.; Goyal, D.; Shimi, S.L.; Akula, A. Condition Monitoring and Fault Diagnosis of Induction Motors: A Review. Arch. Comput. Methods Eng. 2019, 26, 1221–1238. [Google Scholar] [CrossRef]
- Rauf1, A.; Usman, M.; Butt, A.; Ping, Z. Health Monitoring of Induction Motor Using Electrical Signature Analysis. J. Dong Hua Univ. 2022, 39, 265–271. [Google Scholar] [CrossRef]
- Gundewar, S.K.; Kane, P.V. Condition Monitoring and Fault Diagnosis of Induction Motor. J. Vib. Eng. Technol. 2021, 9, 643–674. [Google Scholar] [CrossRef]
- Gubarevych, O.; Gerlici, J.; Gorobchenko, O.; Kravchenko, K.; Zaika, D. Analysis of the features of application of vibration diagnostic methods of induction motors of transportation infrastructure using mathematical modeling. Diagnostyka 2023, 24, 2023111. [Google Scholar] [CrossRef]
- AlShorman, O.; Alkahatni, F.; Masadeh, M.; Irfan, M.; Glowacz, A.; Althobiani, F.; Kozik, J.; Glowacz, W. Sounds and acoustic emission-based early fault diagnosis of induction motor. A review study. Adv. Mech. Eng. 2021, 13, 1–19. [Google Scholar] [CrossRef]
- Yatsugi, K.; Pandarakone, S.E.; Mizuno, Y.; Nakamura, H. Common Diagnosis Approach to Three-Class Induction Motor Faults Using Stator Current Feature and Support Vector Machine. IEEE Access 2023, 11, 24945–24952. [Google Scholar] [CrossRef]
- Abdelhak, G.; Sid Ahmed, B.; Djekidel, R. Fault diagnosis of induction motors rotor using current signature with different signal processing techniques. Diagnostyka 2022, 23, 2022201. [Google Scholar] [CrossRef]
- Wei, L.; Rong, X.; Wang, H.; Yu, S.; Zhang, Y. Method for Identifying Stator and Rotor Faults of Induction Motors Based on Machine Vision. Math. Probl. Eng. 2021, 2021, 6658648. [Google Scholar] [CrossRef]
- Vilhekar, T.G.; Ballal, M.S.; Suryawanshi, H.M. Application of Multiple Parks Vector Approach for Detection of Multiple Faults in Induction Motors. J. Power Electron. 2017, 17, 972–982. [Google Scholar] [CrossRef]
- Wei, S.; Zhang, X.; Xu, Y.; Fu, Y.; Ren, Z.; Li, F. Extended Park’s vector method in early inter-turn short circuit fault detection for the stator windings of offshore wind doubly-fed induction generators. IET Gener. Transm. Distrib. 2020, 14, 3905–3912. [Google Scholar] [CrossRef]
- Gerlici, J.; Goolak, S.; Gubarevych, O.; Kravchenko, K.; Kamchatna-Stepanova, K.; Toropov, A. Method for Determining the Degree of Damage to the Stator Windings of an Induction Electric Motor with an Asymmetric Power System. Symmetry 2022, 14, 1305. [Google Scholar] [CrossRef]
- Sheikh, M.A.; Bakhsh, S.T.; Irfan, M.; bin Mohd Nor, N.; Nowakowski, G. A Review to Diagnose Faults Related to Three-Phase Industrial Induction Motors. J. Fail. Anal. Prev. 2022, 22, 1546–1557. [Google Scholar] [CrossRef]
- Gubarevych, O.; Goolak, S.; Melkonova, I.; Yurchenko, M. Structural diagram of the built-in diagnostic system for electric drives of vehicles. Diagnostyka 2022, 23, 2022406. [Google Scholar] [CrossRef]
- Sarkar, S.; Das, S.; Purkait, P. Wavelet and SFAM based classification of induction motor stator winding short circuit faults and incipient insulation failures. In Proceedings of the IEEE 1st International Conference on Condition Assessment Techniques in Electrical Systems (CATCON), Kolkata, India, 6–8 December 2013; pp. 237–242. Available online: http://toc.proceedings.com/21152webtoc.pdf (accessed on 25 March 2023).
- Spyropoulos, D.V.; Mitronikas, E.D. Induction motor stator fault diagnosis technique using Park vector approach and complex wavelets. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 1730–1734. [Google Scholar]
- Gyftakis, K.N.; Cardoso, A.J.M.; Antonino-Daviu, J.A. Introducing the Filtered Park’s and Filtered Extended Park’s Vector Approach to detect broken rotor bars in induction motors independently from the rotor slots number. Mech. Syst. Signal Process. 2017, 93, 30–50. [Google Scholar] [CrossRef]
- Goolak, S.; Riabov, I.; Tkachenko, V.; Kondratieva, L. Concerning the Diagnosis of Asymmetric Modes in the Traction Induction Drive of the Electric Locomotive. In Proceedings of the 2022 IEEE 3rd KhPI Week on Advanced Technology (KhPIWeek), Kharkiv, Ukraine, 3–7 October 2022; pp. 1–6. [Google Scholar]
- Chaouch, A.; Chouitek, M.; Mohamed Reda, M.A.; Belaid, M. Current Park’s Vector Pattern Technique for Diagnosis of Broken Rotor Bars Fault in Saturated Induction Motor. J. Electr. Eng. Technol. 2023. [Google Scholar] [CrossRef]
- Messaoudi, M.; Flah, A.; Alotaibi, A.A.; Althobaiti, A.; Sbita, L.; El-Bayeh, C.Z. Diagnosis and fault detection of rotor bars in squirrel cage induction motors using combined Park’s vector and extended Park’s vector approaches. Electronics 2022, 11, 380. [Google Scholar] [CrossRef]
- Goolak, S.; Riabov, I.; Gorobchenko, O.; Yurchenko, V.; Nezlina, O. Improvement of the model of an asynchronous traction motor of an electric locomotive by taking into account power losses. Prz. Elektrotechnicznythis 2022, 98, 1–10. [Google Scholar] [CrossRef]
- Gubarevych, O.; Golubieva, S.; Melkonova, I. Comparison of the results of simulation modeling of an asynchronous electric motor with the calculated electrodynamic and energy characteristics. Przegląd Elektrotechniczny 2022, 98, 61–66. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gubarevych, O.; Gerlici, J.; Kravchenko, O.; Melkonova, I.; Melnyk, O. Use of Park’s Vector Method for Monitoring the Rotor Condition of an Induction Motor as a Part of the Built-In Diagnostic System of Electric Drives of Transport. Energies 2023, 16, 5109. https://doi.org/10.3390/en16135109
Gubarevych O, Gerlici J, Kravchenko O, Melkonova I, Melnyk O. Use of Park’s Vector Method for Monitoring the Rotor Condition of an Induction Motor as a Part of the Built-In Diagnostic System of Electric Drives of Transport. Energies. 2023; 16(13):5109. https://doi.org/10.3390/en16135109
Chicago/Turabian StyleGubarevych, Oleg, Juraj Gerlici, Oleksandr Kravchenko, Inna Melkonova, and Olha Melnyk. 2023. "Use of Park’s Vector Method for Monitoring the Rotor Condition of an Induction Motor as a Part of the Built-In Diagnostic System of Electric Drives of Transport" Energies 16, no. 13: 5109. https://doi.org/10.3390/en16135109
APA StyleGubarevych, O., Gerlici, J., Kravchenko, O., Melkonova, I., & Melnyk, O. (2023). Use of Park’s Vector Method for Monitoring the Rotor Condition of an Induction Motor as a Part of the Built-In Diagnostic System of Electric Drives of Transport. Energies, 16(13), 5109. https://doi.org/10.3390/en16135109





