An Overview of Active Control Techniques for Vortex Rope Mitigation in Hydraulic Turbines
Abstract
:1. Introduction
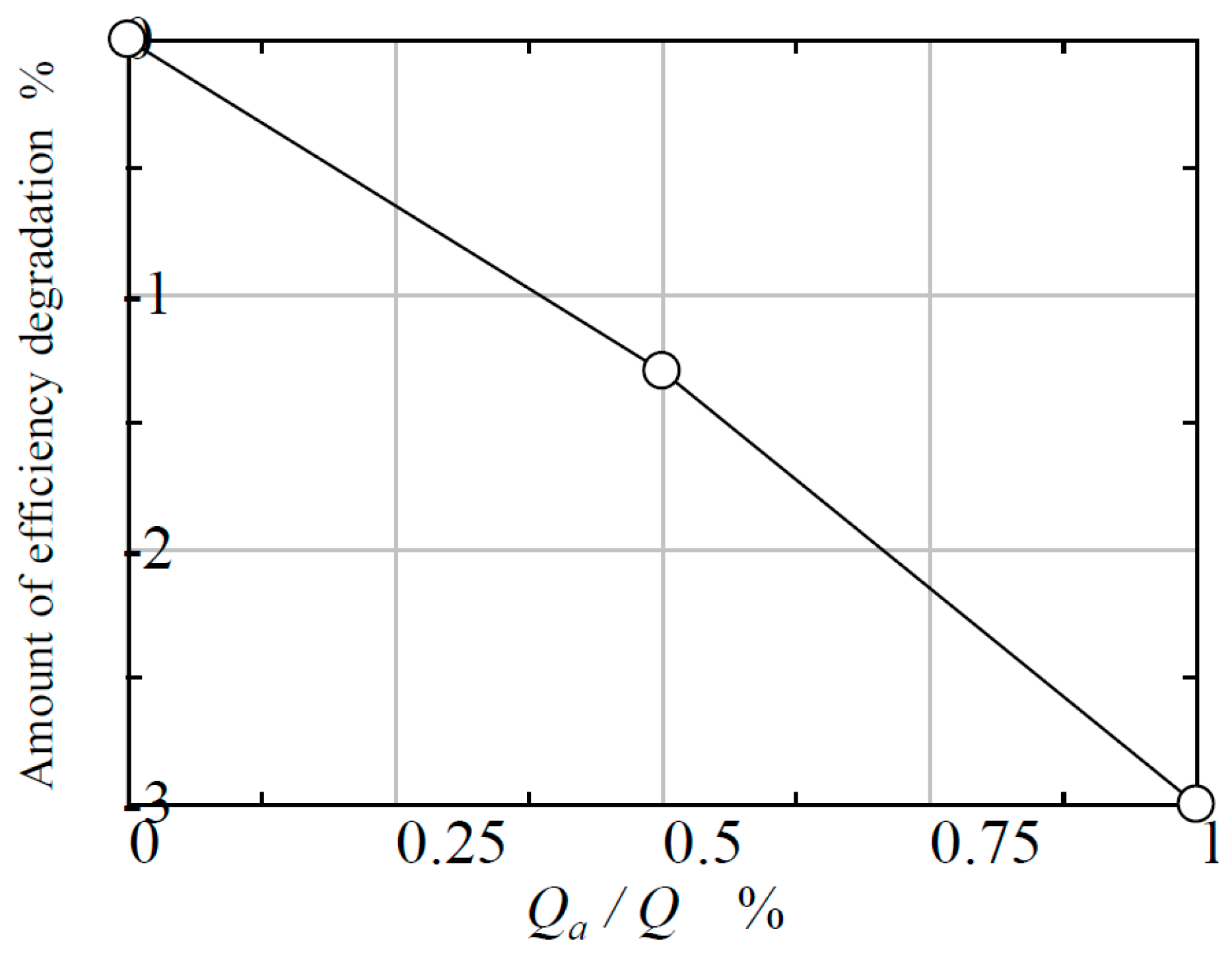
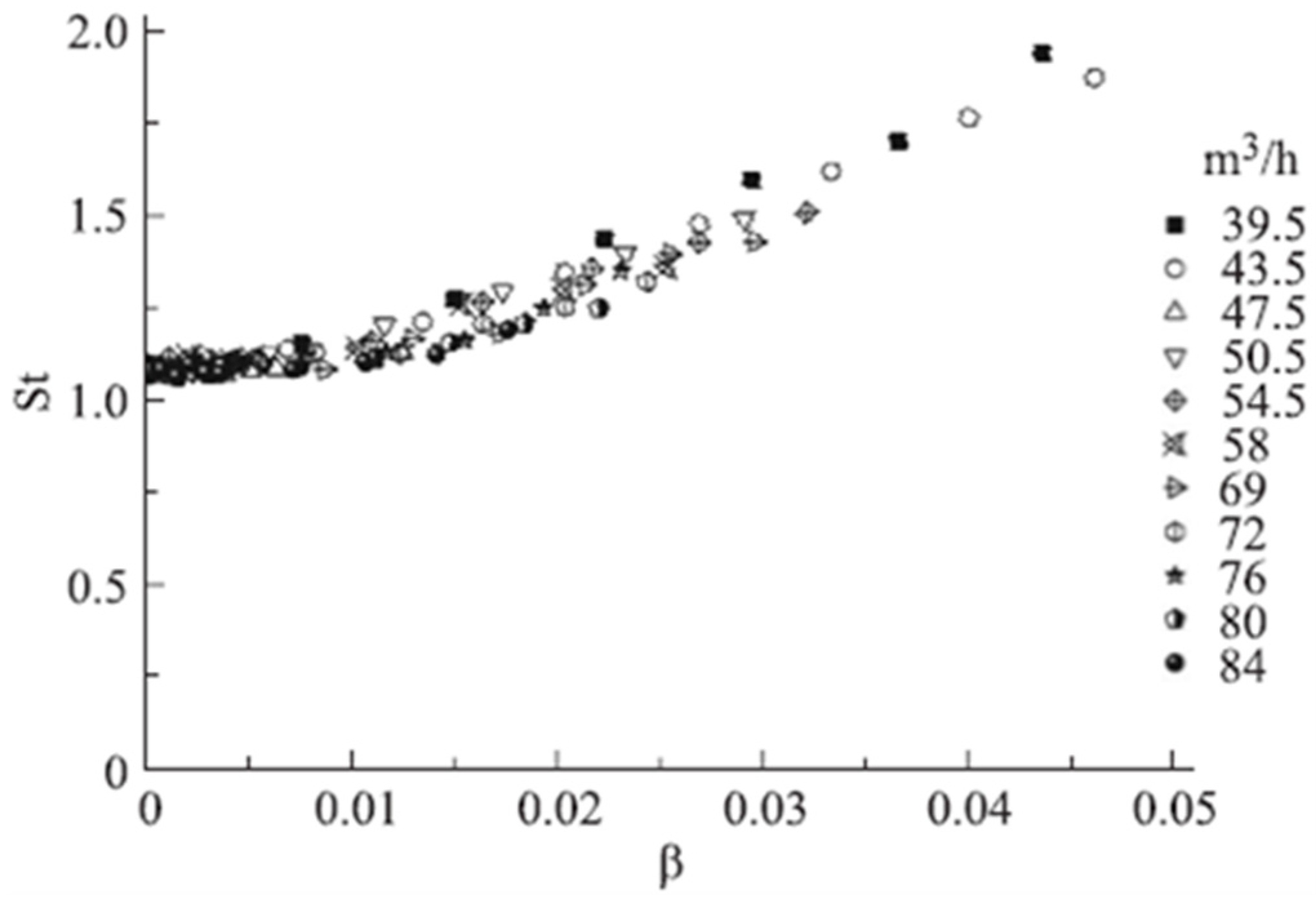
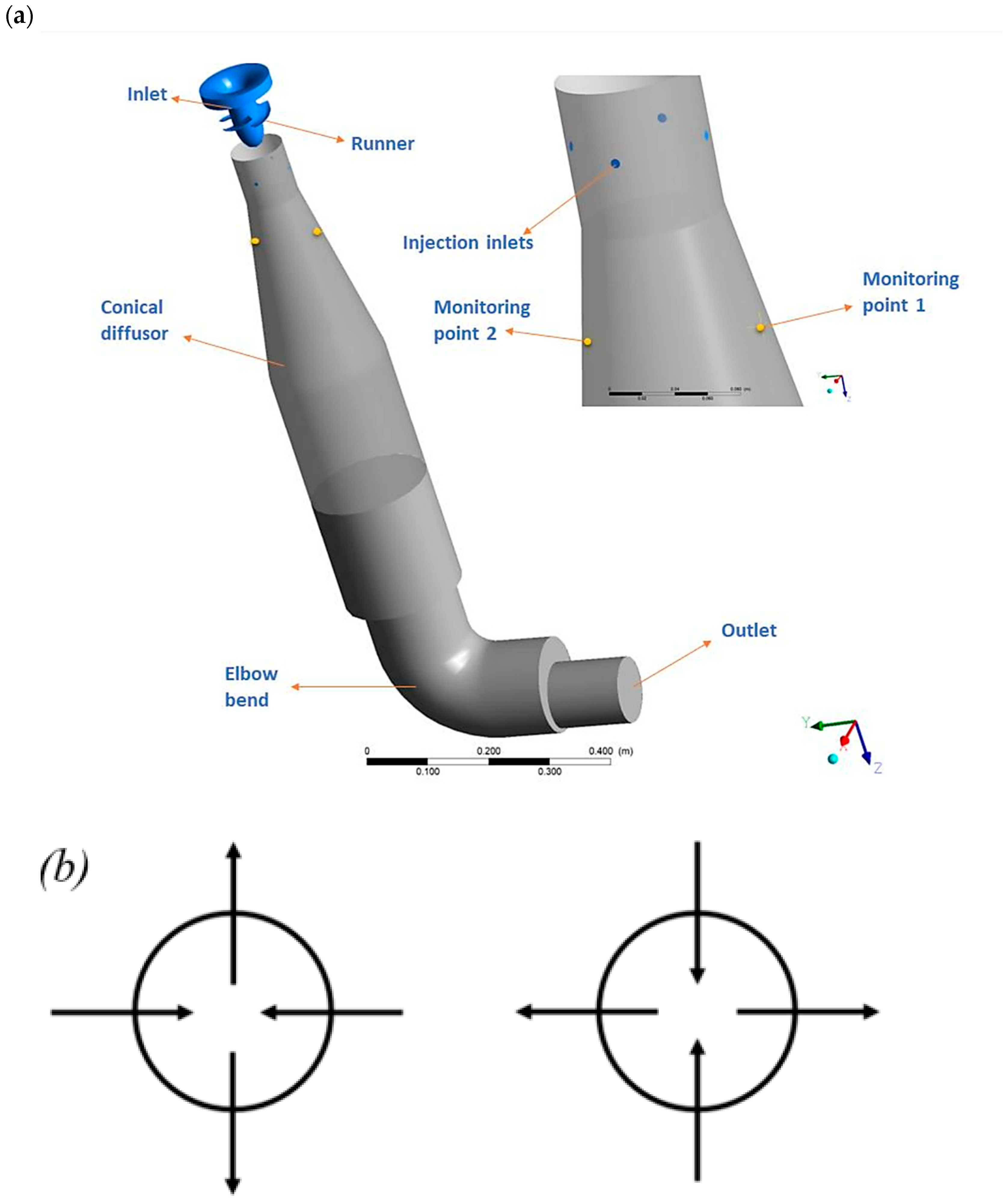
2. Air addition
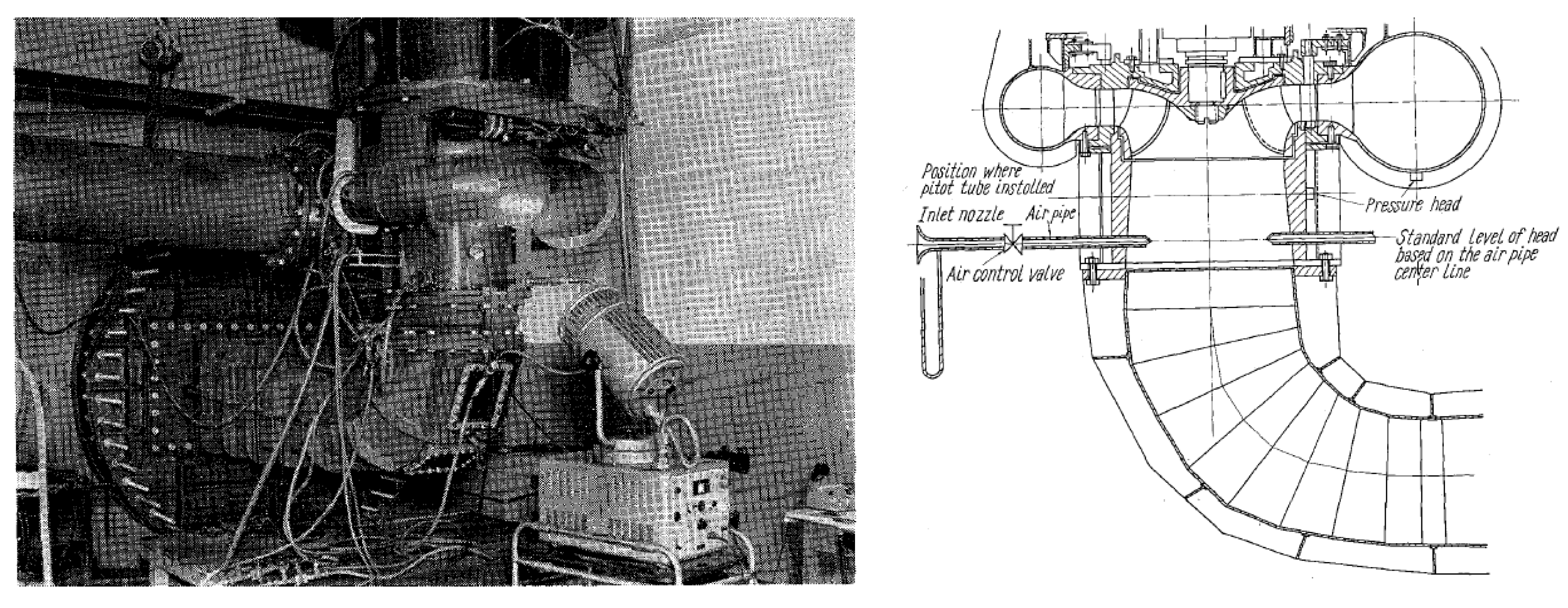
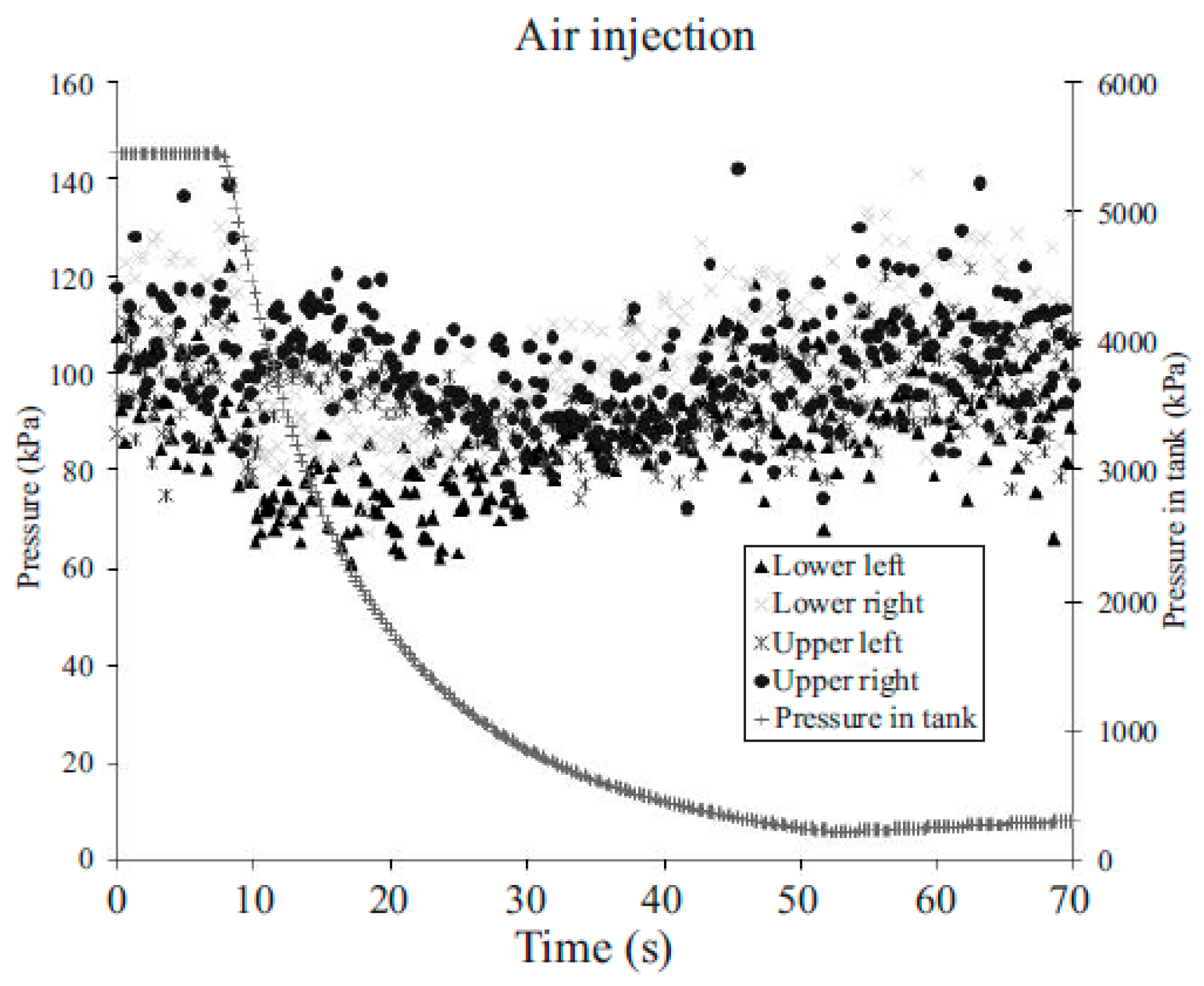
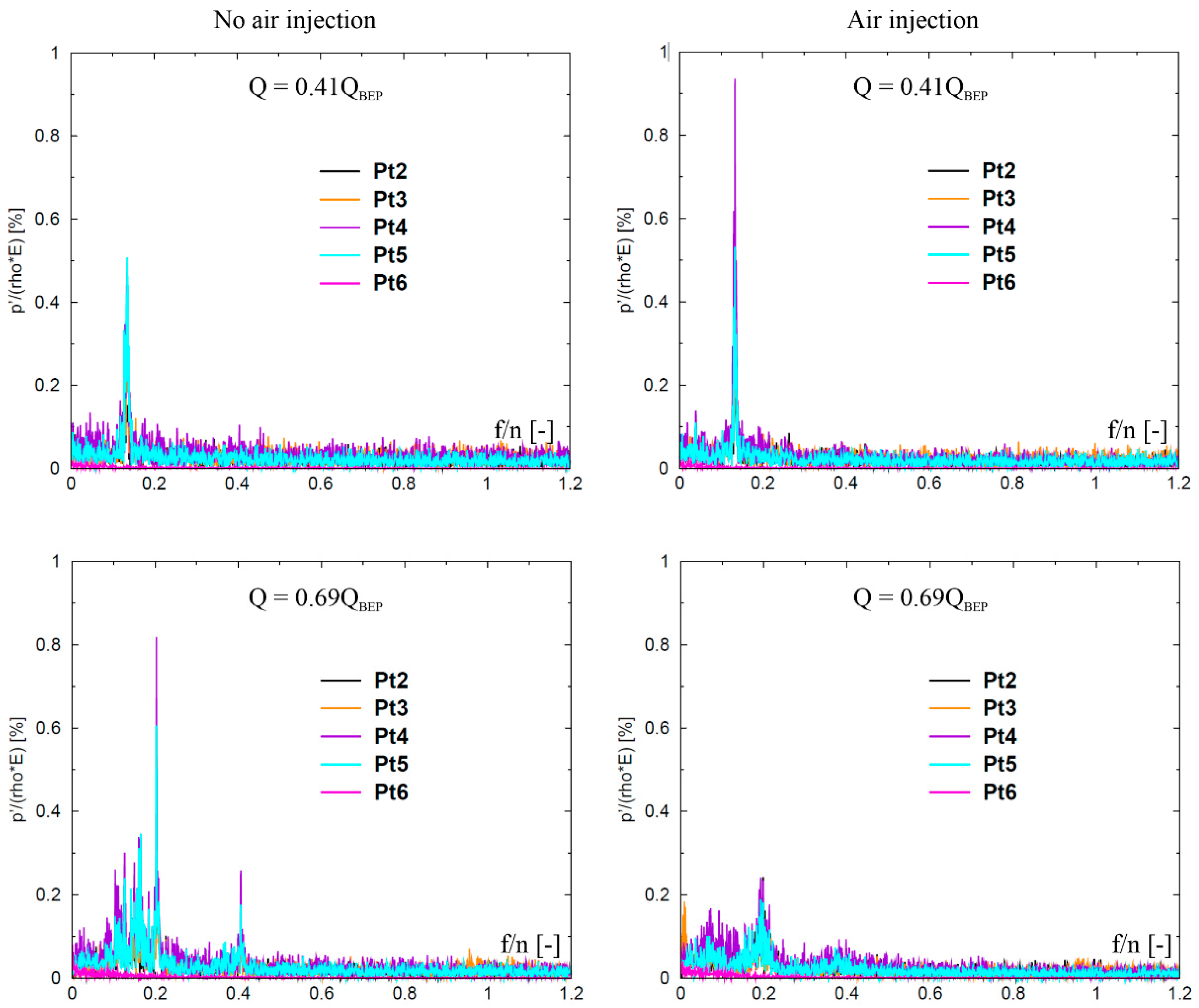
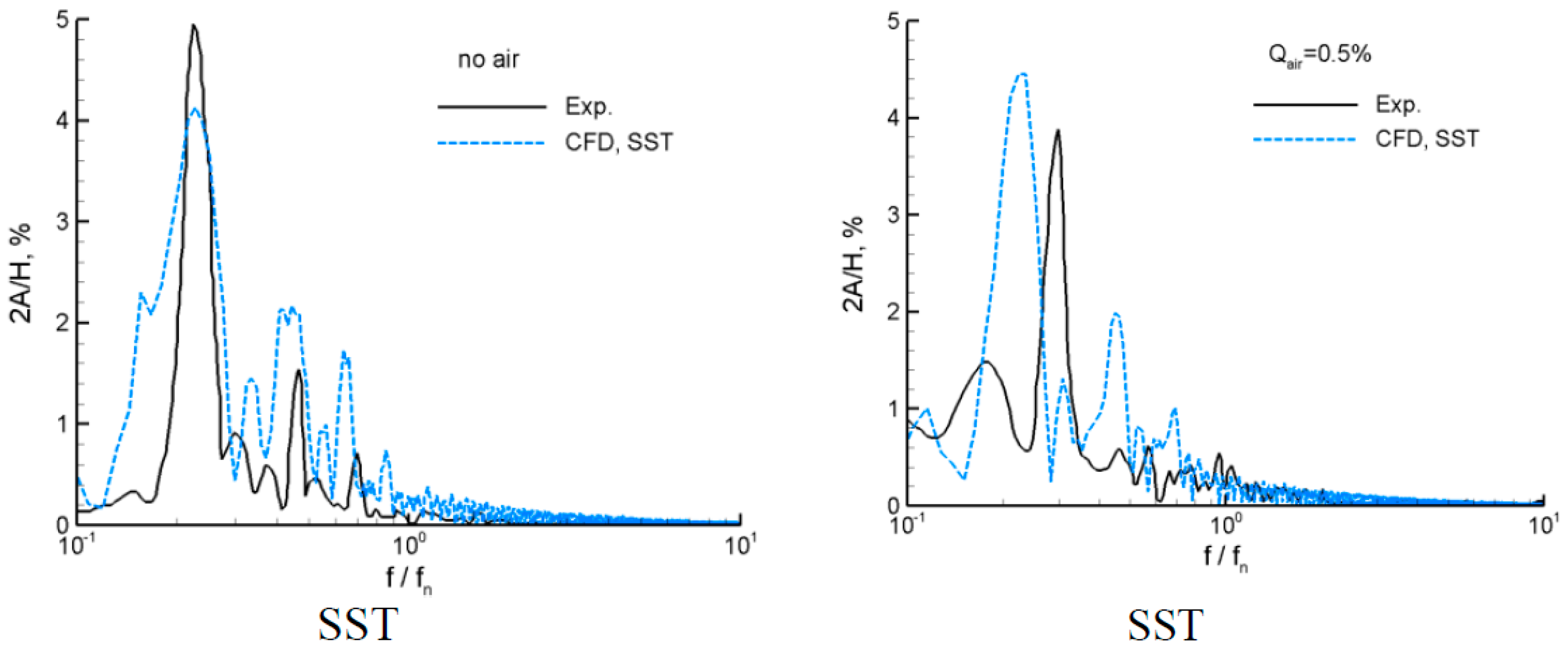
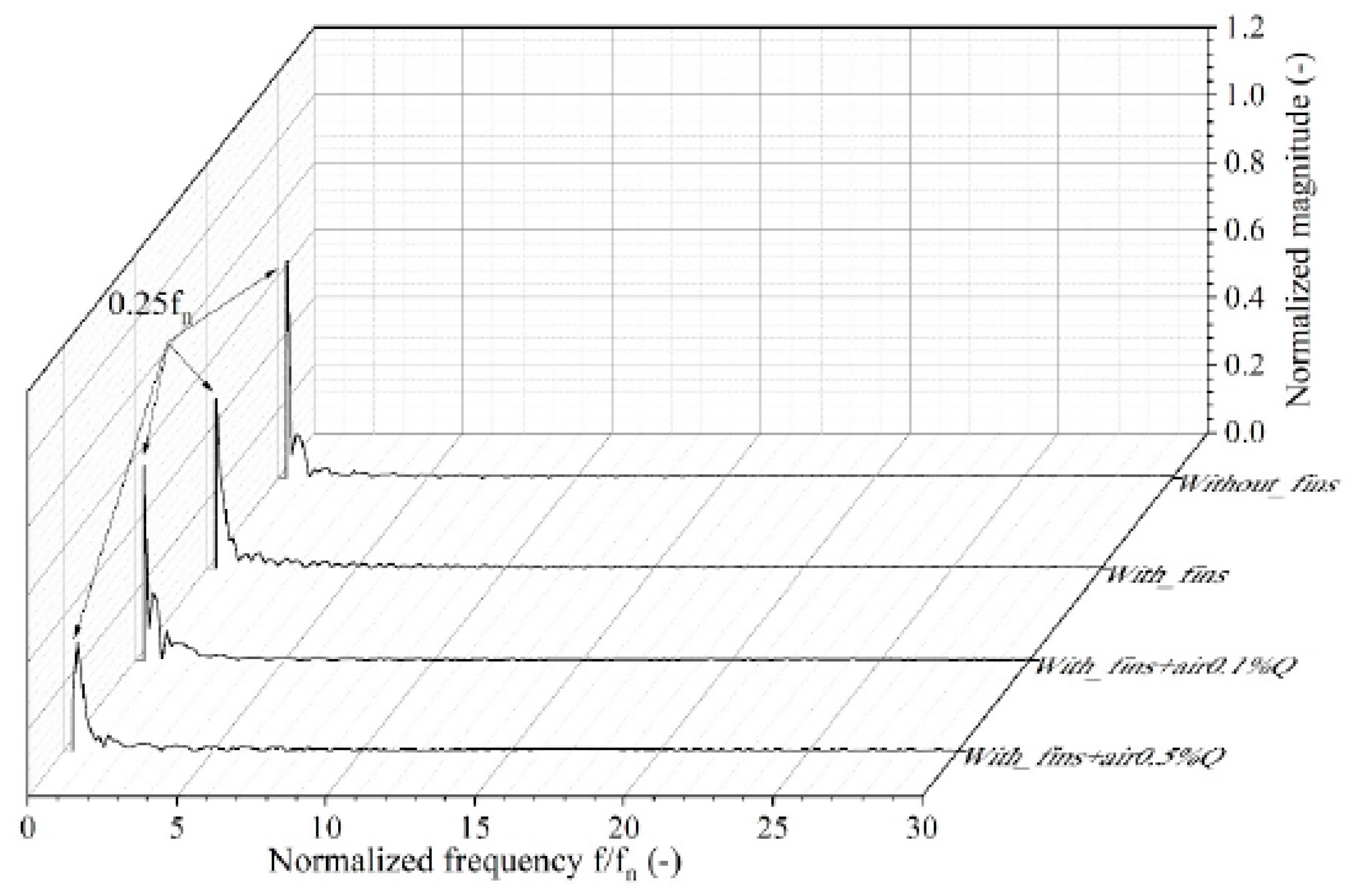
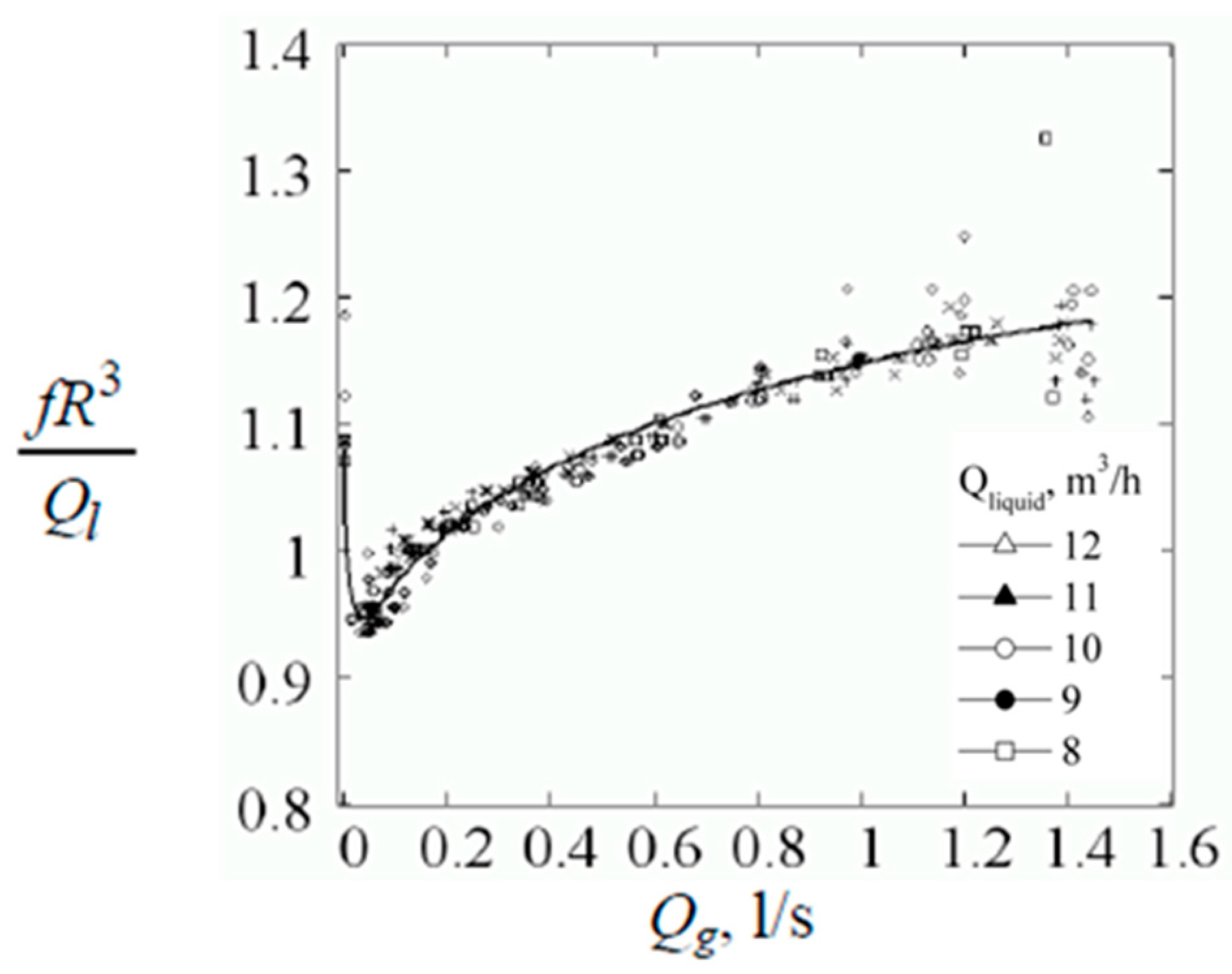
2.1. Experimental Works
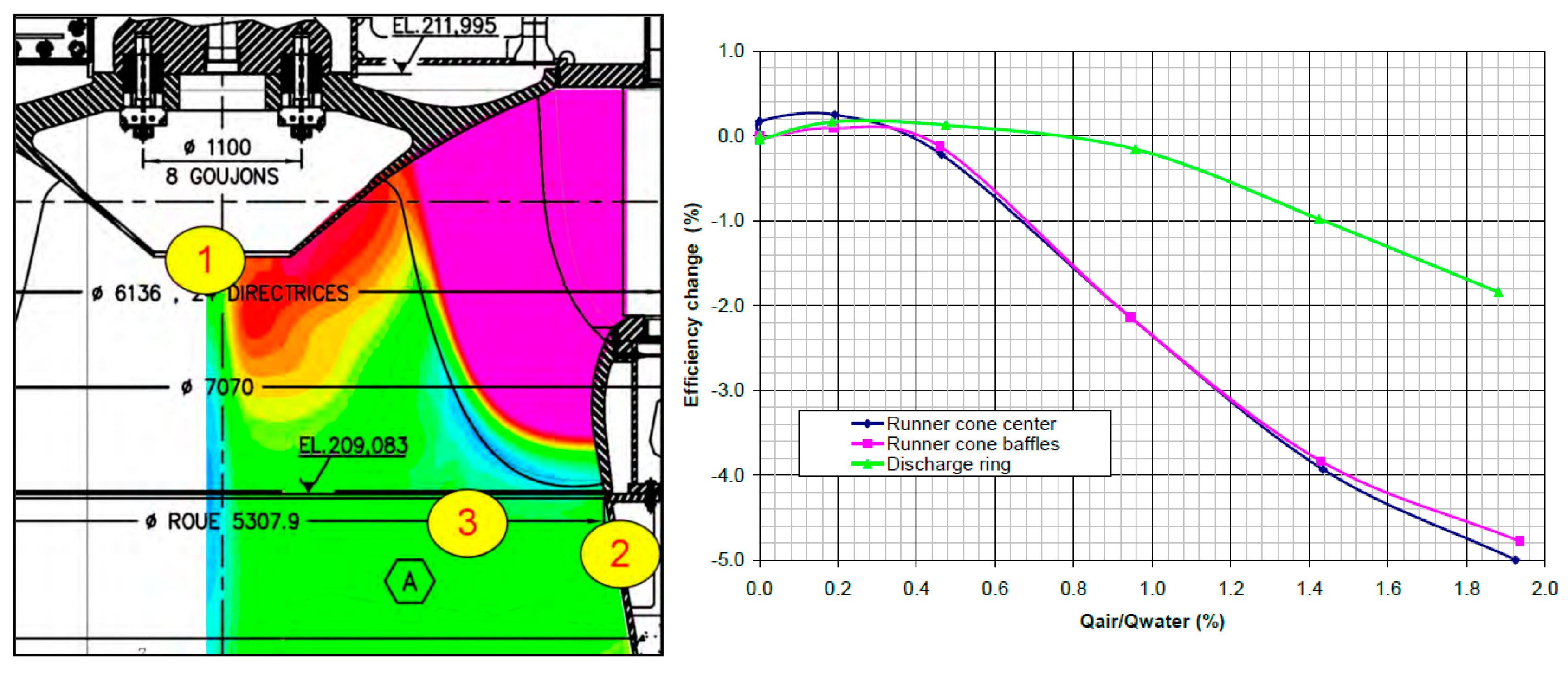
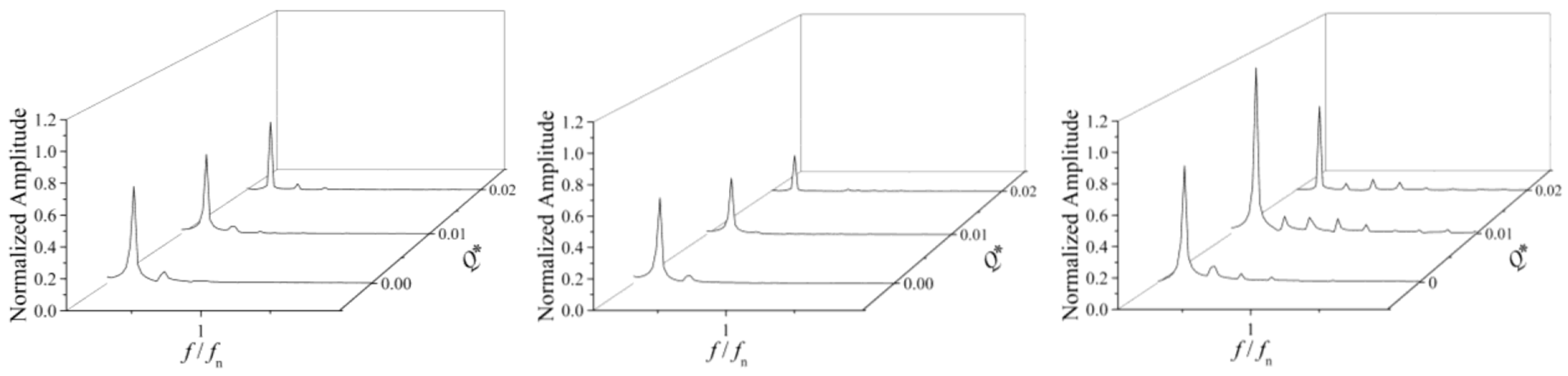
2.2. Numerical Work
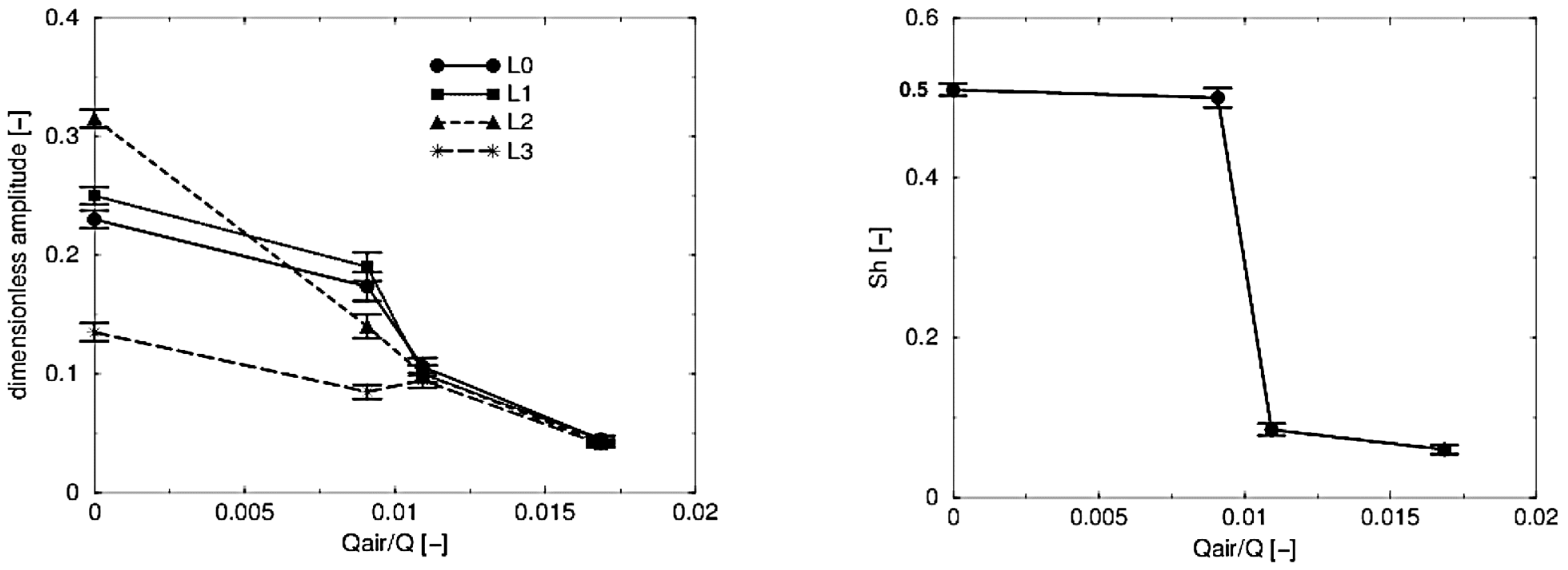
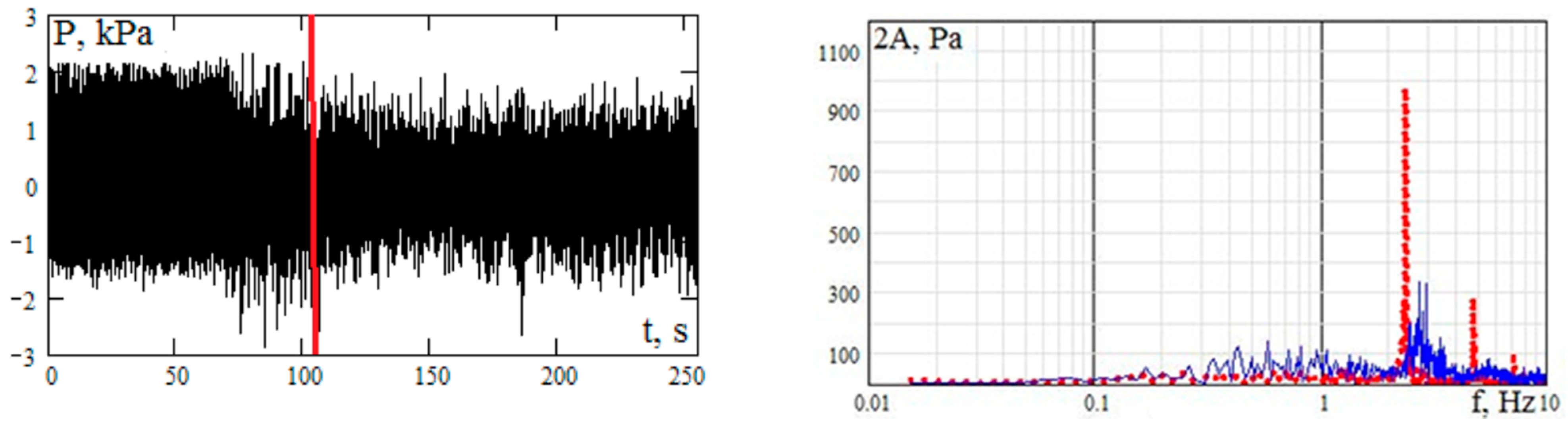
3. Auxiliary Fluid Jets
3.1. Tangential Injection
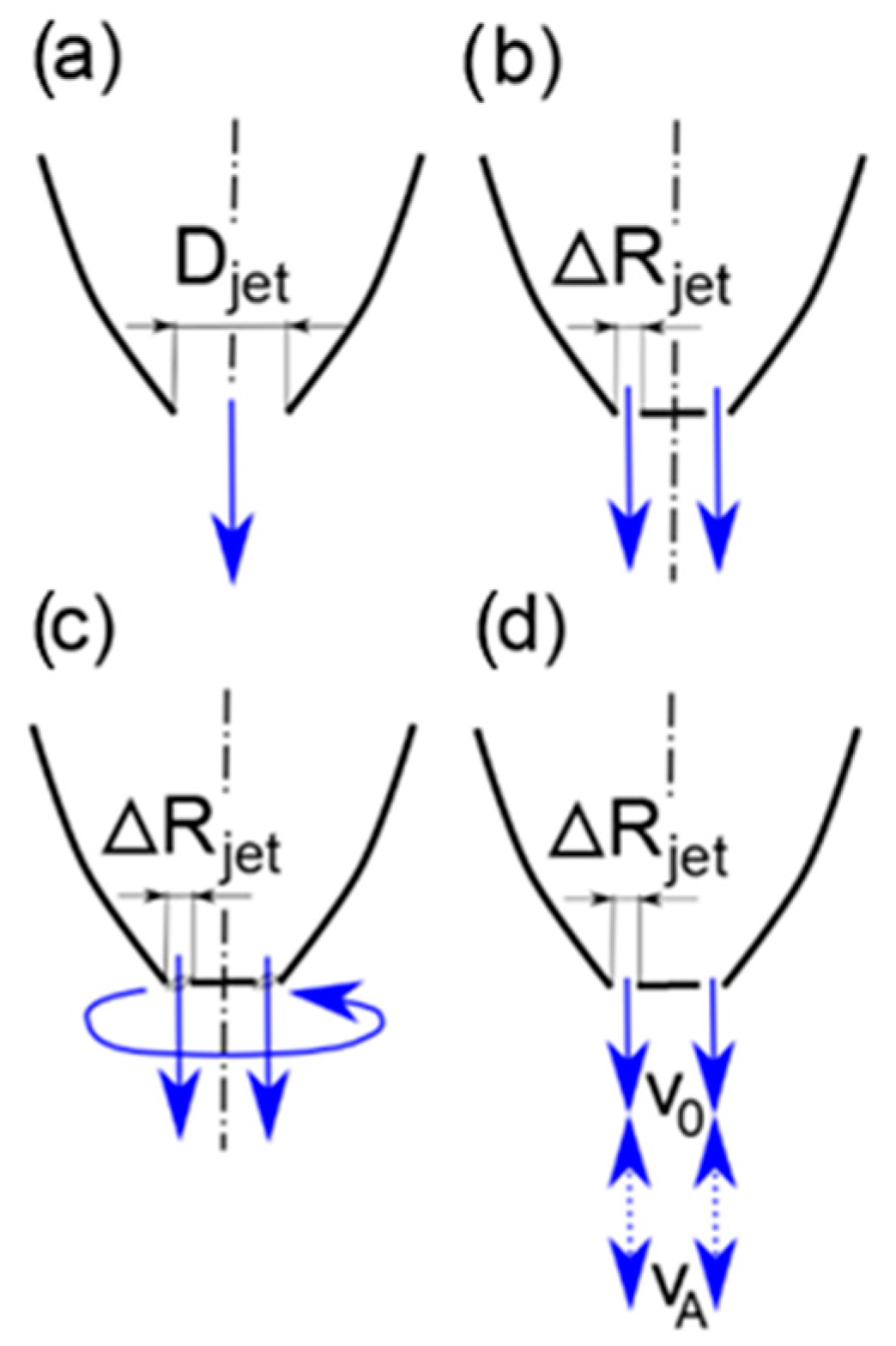
3.2. Axial Injection
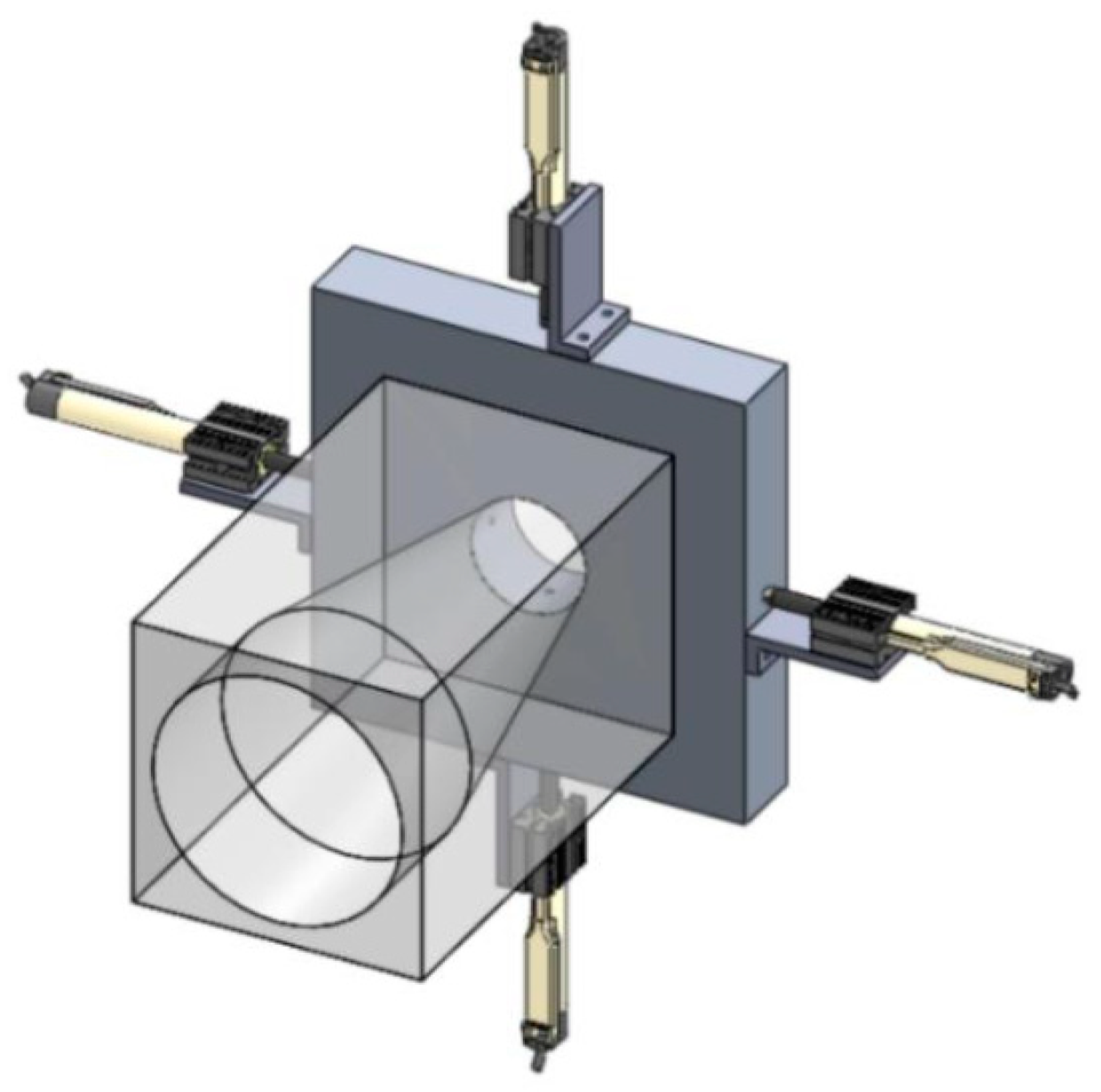
3.3. Periodic Perturbation
3.4. Control Based on the Results of Theoretical Framework of LSA
4. Summary and Perspective
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kishore, T.S.; Patro, E.R.; Harish, V.S.K.V.; Haghighi, A.T. A Comprehensive Study on the Recent Progress and Trends in Development of Small Hydropower Projects. Energies 2021, 14, 2882. [Google Scholar] [CrossRef]
- Nishi, M.; Liu, S. An Outlook on the Draft-Tube-Surge Study. Int. J. Fluid Mach. Syst. 2013, 6, 33–48. [Google Scholar] [CrossRef] [Green Version]
- Jonsson, P.P.; Mulu, B.G.; Cervantes, M.J. Experimental Investigation of a Kaplan Draft Tube–Part II: Off-Design Conditions. Appl. Energy 2012, 94, 71–83. [Google Scholar] [CrossRef]
- Liang, H.; Maxworthy, T. An Experimental Investigation of Swirling Jets. J. Fluid Mech. 2005, 525, 115–159. [Google Scholar] [CrossRef]
- Syred, N. A Review of Oscillation Mechanisms and the Role of the Precessing Vortex Core (PVC) in Swirl Combustion Systems. Prog. Energy Combust. Sci. 2006, 32, 93–161. [Google Scholar] [CrossRef]
- Żywica, G.; Bagiński, P.; Breńkacz, Ł. Dynamic State Assessment of the Water Turbine with the Power of 600 KW. Diagnostyka 2013, 14, 65–70. [Google Scholar]
- March, P. Hydraulic and Environmental Performance of Aerating Turbine Technologies; Electric Power Research Institute: Palo Alto, CA, USA, 2011; pp. 19–21. [Google Scholar]
- Rheingans, W.J. Power Swings in Hydroelectric Power Plants. J. Fluids Eng. 1940, 62, 171–177. [Google Scholar] [CrossRef]
- Masoodi, F.A.; Goyal, R. Efficacy of Ancillary Fluid Injection Technique for Mitigation of Vortex Rope in Hydraulic Turbines: A Review. Mater. Today Proc. 2021, 47, 3043–3053. [Google Scholar] [CrossRef]
- Kumar, S.; Cervantes, M.J.; Gandhi, B.K. Rotating Vortex Rope Formation and Mitigation in Draft Tube of Hydro Turbines—A Review from Experimental Perspective. Renew. Sustain. Energy Rev. 2021, 136, 110354. [Google Scholar] [CrossRef]
- Muhirwa, A.; Cai, W.-H.; Su, W.-T.; Liu, Q.; Binama, M.; Li, B.; Wu, J. A Review on Remedial Attempts to Counteract the Power Generation Compromise from Draft Tubes of Hydropower Plants. Renew. Energy 2020, 150, 743–764. [Google Scholar] [CrossRef]
- Wang, L.; Cui, J.; Shu, L.; Jiang, D.; Xiang, C.; Li, L.; Zhou, P. Research on the Vortex Rope Control Techniques in Draft Tube of Francis Turbines. Energies 2022, 15, 9280. [Google Scholar] [CrossRef]
- Tanasa, C.; Bosioc, A.; Stuparu, A.; Muntean, S.; Susan-Resiga, R. A Perspective Review of Passive Techniques Applied to Control the Swirling Flow Instabilities from The Conical Diffuser of Hydraulic Turbines. Appl. Mech. Rev. 2023, 1–89. [Google Scholar] [CrossRef]
- Susan-Resiga, R.; Vu, T.C.; Muntean, S.; Ciocan, G.D.; Nennemann, B. Jet Control of the Draft Tube Vortex Rope in Francis Turbines at Partial Discharge. In Proceedings of the 23rd IAHR Symposium on Hydraulic Machinery and Systems, Yokohama, Japan, 17–21 October 2006; ResearchGate: Berlin, Germany, 2006; pp. 67–80. [Google Scholar]
- Tănasă, C.; Bosioc, A.; Muntean, S.; Susan-Resiga, R. A Novel Passive Method to Control the Swirling Flow with Vortex Rope from the Conical Diffuser of Hydraulic Turbines with Fixed Blades. Appl. Sci. 2019, 9, 4910. [Google Scholar] [CrossRef] [Green Version]
- Urban, O.; Kurková, M.; Pochylý, F. Control of Swirling Flow in a Diffuser Using Various Installations. AIP Conf. Proceeding 2023, 2672, 020020. [Google Scholar]
- Imamura, H.; Kurokawa, J.; Matsui, J.; Kikuchi, M. Others Suppression of Cavitating Flow in Inducer by J-Groove. In Proceedings of the Fifth Intemational Symposium on Cavitation (CAV2003), Osaka, Japan, 1–4 November 2003. [Google Scholar]
- Kurokawa, J.; Imamura, H.; Choi, Y.-D. Effect of J-Groove on the Suppression of Swirl Flow in a Conical Diffuser. J. Fluids Eng. 2010, 132, 071101. [Google Scholar] [CrossRef]
- Biela, V.; Beltran, H. Draft Tube Fins. Procedings of the 19th IAHR symposium on Hydraulic Machinery and Cavitation, Singapore, 9–11 September 1998; pp. 454–461. [Google Scholar]
- Sentyabov, A.; Minakov, A.; Platonov, D.; Dekterev, D.; Zakharov, A.; Semenov, G. Numerical Investigation of the Influence of Special Structures On Suppression of Pressure Pulsations in The Draft Tube of a High-Head Hydraulic Turbine. J. Eng. Phys. Thermophys. 2019, 92, 1489–1500. [Google Scholar] [CrossRef]
- Dörfler, P.; Sick, M.; Coutu, A. Flow-Induced Pulsation and Vibration in Hydroelectric Machinery: Engineer’s Guidebook for Planning, Design and Troubleshooting; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
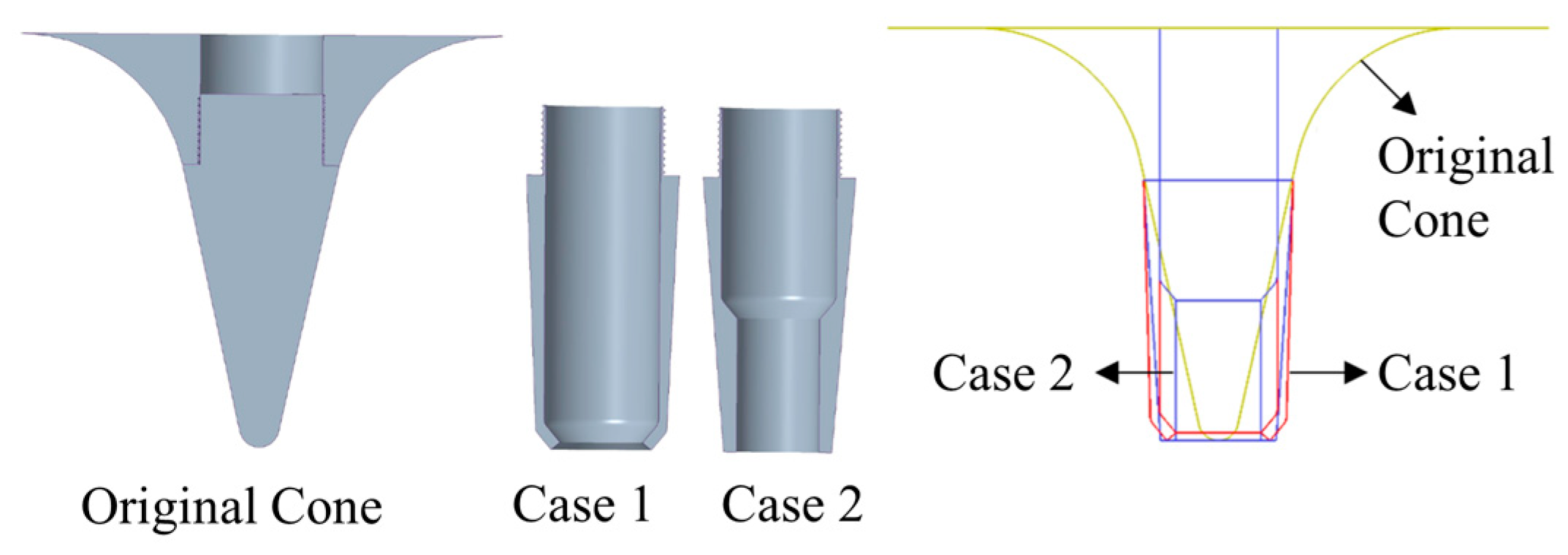
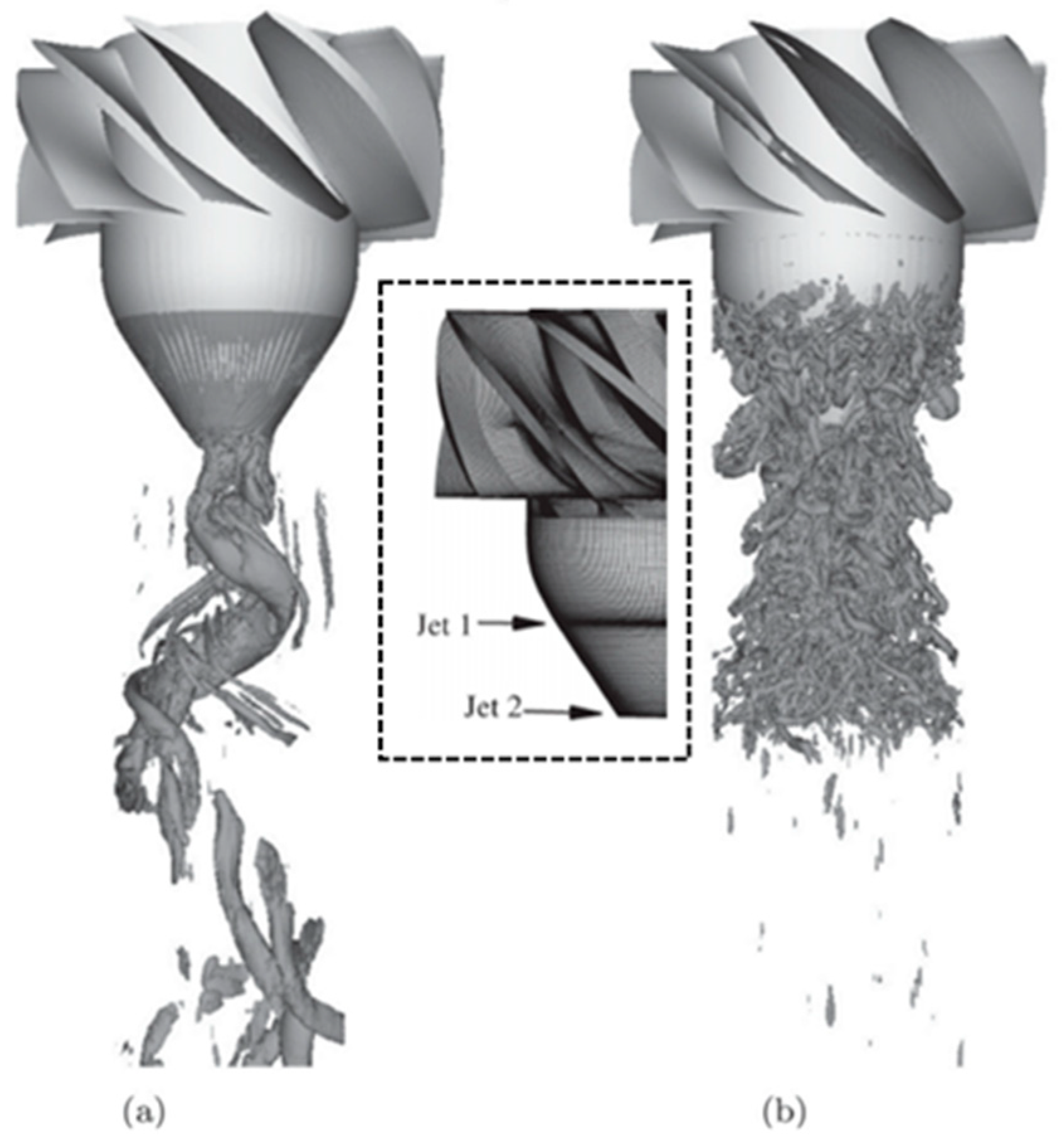
- Lückoff, F.; Naster, M.; Müller, J.; Sieber, M.; Litvinov, I.; Oberleithner, K. Impact of Runner Crown Shape Modifications on the Onset of the Precessing Vortex Core. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Chennai, India, 23–24 July 2022; IOP Publishing: Chiyoda City, Tokyo, 2022; Volume 1079, p. 012051. [Google Scholar]
- Qian, Z.; Li, W.; Huai, W.; Wu, Y. The Effect of Runner Cone Design on Pressure Oscillation Characteristics in a Francis Hydraulic Turbine. Proc. Inst. Mech. Eng. Part J. Power Energy 2012, 226, 137–150. [Google Scholar] [CrossRef]
- Li, Y.; Liu, H.; Lin, Y.; Li, W.; Gu, Y. Design and Test of a 600-KW Horizontal-Axis Tidal Current Turbine. Energy 2019, 182, 177–186. [Google Scholar] [CrossRef]
- Joy, J.; Raisee, M.; Cervantes, M.J. A Novel Guide Vane System Design to Mitigate Rotating Vortex Rope in High Head Francis Model Turbine. Int. J. Fluid Mach. Syst. 2022, 15, 188–209. [Google Scholar] [CrossRef]
- Murakami, M. Vibration of Water Turbine When Air Is Admitted to Its Draft Tube: Experimental Study. Bull. JSME 1958, 1, 298–304. [Google Scholar] [CrossRef] [Green Version]
- Nakanishi, K.; Ueda, T. Air Supply into Draft Tube of Francis Turbine. Fuji Electr. Rev. 1964, 10, 81–91. [Google Scholar]
- Casanova García, F.; Mantilla Viveros, C.A. Experimental Analysis of the Vibration on the Draft Tube of a Francis Hydraulic Turbine during Operation at Different Power Levels. Rev. Fac. Ing. Univ. Antioq. 2010, 55, 90–98. [Google Scholar]
- Papillon, B.; Sabourin, M.; Couston, M.; Deschenes, C. Methods for Air Admission in Hydroturbines. In Proceedings of the XXIst IAHR Symposium on Hydraulic Machinery and Systems, Lausanne, Switzerland, 9–12 September 2002; pp. 6–11. [Google Scholar]
- Papillon, B.; Sabourin, M.; Segoufin, C.; Gaudin, E. The Technical Challenges of Dissolved Oxygen Enhancement EPRI. In EPRI-DOE Conference on Environmentally-Enhanced Hydropower Turbines: Technical Papers; U.S. Department of Energy Office of Scientific and Technical Information: Oak Ridge, TN, USA, 2011; Volume 49, p. 072008. [Google Scholar] [CrossRef] [Green Version]
- Türkmenoğlu, V. The Vortex Effect of Francis Turbine in Electric Power Generation. Turk. J. Electr. Eng. Comput. Sci. 2013, 21, 26–37. [Google Scholar] [CrossRef]
- Muntean, S.; Susan-Resiga, R.F.; Campian, V.C.; Dumbrava, C.; Cuzmos, A. In Situ Unsteady Pressure Measurements on the Draft Tube Cone of the Francis Turbine with Air Injection over an Extended Operating Range. UPB Sci. Bull. Ser. D 2014, 76, 173–180. [Google Scholar]
- Nakashima, T.; Matsuzaka, R.; Miyagawa, K.; Yonezawa, K.; Tsujimoto, Y. Study on Flow Instability and Countermeasure in a Draft Tube with Swirling Flow. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 032007. [Google Scholar] [CrossRef]
- Nakashima, T.; Matsuzaka, R.; Miyagawa, K.; Yonezawa, K.; Tsujimoto, Y. Study on Flow Instability and Countermeasure in a Draft Tube with Swirling Flow. Int. J. Fluid Mach. Syst. 2015, 8, 230–239. [Google Scholar] [CrossRef] [Green Version]
- Skripkin, S.G.; Kuibin, P.A.; Shtork, S.I. The Effect of Air Injection on the Parameters of Swirling Flow in a Turbine-99 Draft Tube Model. Tech. Phys. Lett. 2015, 41, 638–640. [Google Scholar] [CrossRef]
- Tănasă, C.; Muntean, S.; Bosioc, A.I.; Susan-Resiga, R.; Ciocan, T. Influence of the Air Admission on the Unsteady Pressure Field in a Decelerated Swirling Flow. UPB Sci. Bull. Ser. D 2016, 78, 161–170. [Google Scholar]
- Unterluggauer, J.; Maly, A.; Doujak, E. Investigation on the Impact of Air Admission in a Prototype Francis Turbine at Low-Load Operation. Energies 2019, 12, 2893. [Google Scholar] [CrossRef] [Green Version]
- Platonov, D.; Minakov, A.; Dekterev, D.; Maslennikova, A. An Experimental Investigation of the Air Injection Effect on the Vortex Structure and Pulsation Characteristics in the Francis Turbine. Int. J. Fluid Mach. Syst. 2020, 13, 103–113. [Google Scholar] [CrossRef]
- Bucur, D.M.; Dunca, G.; Bunea, F.; Calinoiu, C. Aeration Process Influence over the Operation of a Small Hydro Turbine—Generator Unit. In Proceedings of the 2017 10th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 23–25 March 2017; IEEE: Bucharest, Romania, 2017; pp. 746–751. [Google Scholar]
- Bunea, F.; Ciocan, G.D.; Bucur, D.M.; Dunca, G.; Nedelcu, A. Hydraulic Turbine Performance Assessment with Implementation of an Innovative Aeration System. Water 2021, 13, 2459. [Google Scholar] [CrossRef]
- Qian, Z.; Yang, J.; Huai, W. Numerical Simulation and Analysis of Pressure Pulsation in Francis Hydraulic Turbine with Air Admission. J. Hydrodyn. 2007, 19, 467–472. [Google Scholar] [CrossRef]
- Chirkov, D.V.; Shcherbakov, P.K.; Cherny, S.G.; Skorospelov, V.A.; Turuk, P.A. Numerical Investigation of the Air Injection Effect on the Cavitating Flow in Francis Hydro Turbine. Thermophys. Aeromechanics 2017, 24, 691–703. [Google Scholar] [CrossRef]
- Chirkov, D.; Scherbakov, P.; Skorospelov, V.; Cherny, S.; Zakharov, A. Numerical Simulation of Air Injection in Francis Turbine. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 022043. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, M.; Hajidavalloo, E.; Behbahani-Nejad, M. Investigation on Combined Air and Water Injection in Francis Turbine Draft Tube to Reduce Vortex Rope Effects. J. Fluids Eng. 2019, 141, 051301. [Google Scholar] [CrossRef]
- Luo, X.; Yu, A.; Ji, B.; Wu, Y.; Tsujimoto, Y. Unsteady Vortical Flow Simulation in a Francis Turbine with Special Emphasis on Vortex Rope Behavior and Pressure Fluctuation Alleviation. Proc. Inst. Mech. Eng. Part J. Power Energy 2017, 231, 215–226. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, R.; Yu, A.; Lu, L.; Luo, X. Suppression of Vortex Rope Oscillation and Pressure Vibrations in Francis Turbine Draft Tube Using Various Strategies. J. Hydrodyn. 2021, 33, 534–545. [Google Scholar] [CrossRef]
- Luo, X.; Yu, A.; Yu, W.; Wang, L.; Xu, H. Pressure Oscillation Suppression by Air Admission in a Francis Turbine Draft Tube. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 022008. [Google Scholar] [CrossRef]
- Zhang, R.; Yu, A.; Nishi, M.; Luo, X. Numerical Investigation of Pressure Fluctuation and Cavitation inside a Francis Turbine Draft Tube with Air Admission through a Fin. J. Phys. Conf. Ser. 2021, 1909, 012017. [Google Scholar] [CrossRef]
- Kim, S.-J.; Cho, Y.; Kim, J.-H. Effect of Air Injection on the Internal Flow Characteristics in the Draft Tube of a Francis Turbine Model. Processes 2021, 9, 1182. [Google Scholar] [CrossRef]
- Shahzer, M.A.; Kim, S.-J.; Cho, Y.; Kim, J.-H. Effect of Air Injection Holes Intrusiveness on Internal Flow Phenomena of a Draft Tube Inside a Francis Turbine Model. KSFM J. Fluid Mach. 2022, 25, 5–12. [Google Scholar] [CrossRef]
- Sun, L.; Li, Y.; Guo, P.; Xu, Z. Numerical Investigation of Air Admission Influence on the Precessing Vortex Rope in a Francis Turbine. Eng. Appl. Comput. Fluid Mech. 2023, 17, 2164619. [Google Scholar] [CrossRef]
- Sun, L.; Guo, P.; Wu, L. Numerical Investigation of Alleviation of Undesirable Effect of Inter-Blade Vortex with Air Admission for a Low-Head Francis Turbine. J. Hydrodyn. 2020, 32, 1151–1164. [Google Scholar] [CrossRef]
- Pejovi, S. Air Influence on Stability of Real and Theoretical Hydraulic System. Sci. Rev. Serbian Sci. Soc. Belgrade 1996, 16, 23–38. [Google Scholar]
- Dörfler, P.K. Dissolved-Gas Influence on the Francis Part-Load Oscillation. IOP Conf. Ser. Earth Environ. Sci. 2019, 405, 012015. [Google Scholar] [CrossRef]
- Skripkin, S.; Zuo, Z.; Tsoy, M.; Kuibin, P.; Liu, S. Oscillation of Cavitating Vortices in Draft Tubes of a Simplified Model Turbine and a Model Pump–Turbine. Energies 2022, 15, 2965. [Google Scholar] [CrossRef]
- Kuibin, P.A.; Pylev, I.M.; Zakharov, A.V. Two-Phase Models Development for Description of Vortex-Induced Pulsation in Francis Turbine. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 022001. [Google Scholar] [CrossRef]
- Alekseenko, S.V.; Kuibin, P.A.; Okulov, V.L.; Shtork, S.I. Helical Vortices in Swirl Flow. J. Fluid Mech. 1999, 382, 195–243. [Google Scholar] [CrossRef]
- Litvinov, I.V.; Shtork, S.I.; Kuibin, P.A.; Alekseenko, S.V.; Hanjalic, K. Experimental Study and Analytical Reconstruction of Precessing Vortex in a Tangential Swirler. Int. J. Heat Fluid Flow 2013, 42, 251–264. [Google Scholar] [CrossRef]
- Shtork, S.I.; Alekseenko, S.; Okulov, V.L.; Kuibin, P.A. Vortex Precession in a Gas-Liquid Flow. Heat Transf. Res. 2010, 41, 465–478. [Google Scholar] [CrossRef]
- Zhang, R.-K.; Mao, F.; Wu, J.-Z.; Chen, S.-Y.; Wu, Y.-L.; Liu, S.-H. Analysis and Control of Part-Load Unsteady Flow in Francis Turbine’s Draft Tube. In Proceedings of the Volume 6: Turbo Expo 2007, Parts A and B; ASMEDC, Montreal, QC, Canada, 1 January 2007; Volume 47950, pp. 1647–1658. [Google Scholar]
- Nishi, M.; Yoshida, K.; Yano, M.; Okamoto, M.; Miyagawa, K.; Liu, S. A Preliminary Study on the Swirling Flow in a Conical Diffuser with Jet Issued at the Center of the Inlet; ResearchGate: Berlin, Germany, 2007; pp. 24–26. [Google Scholar]
- Seybert, T. Injection Nozzle Geometries Pursuant to the Reduction of Draft Tube Surge in Hydroelectric Pump-Turbines. Master’s Thesis, Pennsylvania State University, University Park, State College, PA, USA, Applied Research Lab, Setagaya City, Tokyo, Japan, 1978. [Google Scholar]
- Cassidy, J.J. Experimental Study and Analysis of Draft-Tube Surging. In BUR Reclam REP HYD-591 May 1969; Bureau of Reclamation: Washington, DC, USA, 1969; p. 31. [Google Scholar]
- Gupta, K.; Lilley, D.G.; Syred, N. Swirl Flows; Abacus Press: Kent, UK, 1984. [Google Scholar]
- Francke, H.H. Increasing Hydro Turbine Operation Range and Efficiencies Using Water Injection in Draft Tubes. Ph.D. Thesis, Norwegian University of Science and Technology, Norvay, Trondheim, 2010. [Google Scholar]
- Susan-Resiga, R.; Muntean, S.; Bosioc, A.; Stuparu, A.; Milos, T.; Baya, A.; Bernad, S.; Anton, L.E. Swirling Flow Apparatus and Test Rig for Flow Control in Hydraulic Turbines Discharge Cone; ResearchGate: Berlin, Germany, 2007; Volume 52, pp. 203–216. [Google Scholar]
- Bosioc, A.I.; Tanasa, C.; Muntean, S.; Susan-Resiga, R. Pressure Recovery Improvement in a Conical Diffuser with Swirling Flow Using Water Jet Injection. In Romanian Academy, Series A: Mathematics, Physics, Technical Sciences, Information Science; ResearchGate: Berlin, Germany, 2010; ISSN 14549069. [Google Scholar]
- Ciocan, G.D.; Iliescu, M.S.; Vu, T.C.; Nennemann, B.; Avellan, F. Experimental Study and Numerical Simulation of the FLINDT Draft Tube Rotating Vortex. J. Fluids Eng. 2007, 129, 146–158. [Google Scholar] [CrossRef]
- Bosioc, A.I.; Tanasa, C.; Muntean, S.; Susan-Resiga, R.F. Unsteady Pressure Measurements and Numerical Investigation of the Jet Control Method in a Conical Diffuser with Swirling Flow. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012017. [Google Scholar] [CrossRef]
- Tǎnasǎ, C.; Bosioc, A.I.; Susan-Resiga, R.F.; Muntean, S. Experimental Investigations of the Swirling Flow in the Conical Diffuser Using Flow-Feedback Control Technique with Additional Energy Source. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 062043. [Google Scholar] [CrossRef]
- Štefan, D.; Rudolf, P.; Muntean, S.; Susan-Resiga, R. Proper Orthogonal Decomposition of Self-Induced Instabilities in Decelerated Swirling Flows and Their Mitigation Through Axial Water Injection. J. Fluids Eng. 2017, 139, 081101. [Google Scholar] [CrossRef]
- Bosioc, A.I.; Susan-Resiga, R.; Muntean, S.; Tanasa, C. Unsteady Pressure Analysis of a Swirling Flow With Vortex Rope and Axial Water Injection in a Discharge Cone. J. Fluids Eng. 2012, 134, 081104. [Google Scholar] [CrossRef]
- Muntean, S.; Susan-Resiga, R.; Bosioc, A.I. Numerical Investigation of the Jet Control Method for Swirling Flow with Precessing Vortex Rope; ResearchGate: Berlin, Germany, 2009; Volume 1, pp. 65–74. [Google Scholar]
- Muntean, S.; Susan-Resiga, R.; Bosioc, A.; Stuparu, A.; Baya, A.; Anton, L.E. Mitigation of Pressure Fluctuation in a Conical Diffuser with Precessing Vortex Rope Using Axial Jet Control Method; ResearchGate: Berlin, Germany, 2008. [Google Scholar]
- Susan-Resiga, R.; Muntean, S.; Hasmatuchi, V.; Ruprecht, A.; Sandor, B. Development of a Swirling Flow Control Technique for Francis Turbines Operated at Partial Discharge; ResearchGate: Berlin, Germany, 2007; Volume 200, pp. 625–637. [Google Scholar]
- Susan-Resiga, R.; Muntean, S. Decelerated Swirling Flow Control in the Discharge Cone of Francis Turbines. In Fluid Machinery and Fluid Mechanics; Xu, J., Wu, Y., Zhang, Y., Zhang, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 89–96. ISBN 978-3-540-89748-4. [Google Scholar]
- Litvinov, I.V.; Suslov, D.R.; Gorelikov, I.V.; Sadbakov, O.U.; Shtork, S.I. Swirl Number Analysis in the Air Hydro-Turbine Model. AIP Conf. Proc. 2018, 2027, 040057. [Google Scholar] [CrossRef]
- Litvinov, I.; Sharaborin, D.; Gorelikov, E.; Dulin, V.; Shtork, S.; Alekseenko, S.; Oberleithner, K. Modal Decomposition of the Precessing Vortex Core in a Hydro Turbine Model. Appl. Sci. 2022, 12, 5127. [Google Scholar] [CrossRef]
- Tănasă, C.; Susan-Resiga, R.; Muntean, S.; Bosioc, A.I. Flow-Feedback Method for Mitigating the Vortex Rope in Decelerated Swirling Flows. J. Fluids Eng. 2013, 135, 061304. [Google Scholar] [CrossRef]
- Bosioc, A.I.; Tănasă, C. Experimental Study of Swirling Flow from Conical Diffusers Using the Water Jet Control Method. Renew. Energy 2020, 152, 385–398. [Google Scholar] [CrossRef]
- Foroutan, H.; Yavuzkurt, S. Flow in the Simplified Draft Tube of a Francis Turbine Operating at Partial Load—Part II: Control of the Vortex Rope. J. Appl. Mech. 2014, 81, 061011. [Google Scholar] [CrossRef]
- Avellan, F. Flow Investigation in a Francis Draft Tube : The Flindt Project; ResearchGate: Berlin, Germany, 2000. [Google Scholar]
- Kirschner, O.; Schmidt, H.; Ruprecht, A.; Mader, R.; Meusburger, P. Experimental Investigation of Vortex Control with an Axial Jet in the Draft Tube of a Model Pump-Turbine. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012092. [Google Scholar] [CrossRef]
- Jafarzadeh Juposhti, H.; Maddahian, R.; Cervantes, M.J. Optimization of Axial Water Injection to Mitigate the Rotating Vortex Rope in a Francis Turbine. Renew. Energy 2021, 175, 214–231. [Google Scholar] [CrossRef]
- Cervantes, M.; Trivedi, C.; Dahlhaug, O.G.; Nielsen, T. Francis-99 Workshop 2: Transient Operation of Francis Turbines. J. Phys. Conf. Ser. 2017, 782, 011001. [Google Scholar] [CrossRef]
- Khullar, S.; Singh, K.M.; Cervantes, M.J.; Gandhi, B.K. Influence of Runner Cone Profile and Axial Water Jet Injection in a Low Head Francis Turbine at Part Load. Sustain. Energy Technol. Assess. 2022, 50, 101810. [Google Scholar] [CrossRef]
- Altimemy, M.; Attiya, B.; Daskiran, C.; Liu, I.-H.; Oztekin, A. Mitigation of Flow-Induced Pressure Fluctuations in a Francis Turbine Operating at the Design and Partial Load Regimes—LES Simulations. Int. J. Heat Fluid Flow 2019, 79, 108444. [Google Scholar] [CrossRef]
- Javadi, A.; Nilsson, H. Active Flow Control of the Vortex Rope and Pressure Pulsations in a Swirl Generator. Eng. Appl. Comput. Fluid Mech. 2017, 11, 30–41. [Google Scholar] [CrossRef] [Green Version]
- Rudolf, P.; Litera, J.; Alejandro Ibarra Bolanos, G.; Štefan, D. Manipulation of the Swirling Flow Instability in Hydraulic Turbine Diffuser by Different Methods of Water Injection. EPJ Web Conf. 2018, 180, 02090. [Google Scholar] [CrossRef]
- Tanasa, C.; Ciocan, T.; Muntean, S. Numerical Assessment of Pulsating Water Jet in the Conical Diffusers. AIP Conf. Proc. 2017, 1906, 050002. [Google Scholar] [CrossRef]
- Holmström, H.; Sundström, J.; Cervantes, M.J. Vortex Rope Mitigation with Azimuthal Perturbations: A Numerical Study. IOP Conf. Ser. Earth Environ. Sci. 2021, 774, 012144. [Google Scholar] [CrossRef]
- Holmström, H.; Sundström, J.; Cervantes, M.J. Vortex Rope Interaction with Radially Protruded Solid Bodies in an Axial Turbine: A Numerical Study. IOP Conf. Ser. Earth Environ. Sci. 2022, 1079, 012055. [Google Scholar] [CrossRef]
- Shiraghaee, S.; Sundström, J.; Raisee, M.; Cervantes, M.J. An Experimental Investigation on the Effects of Cylindrical Rods in a Draft Tube at Part Load Operation in Down-Scale Turbine. IOP Conf. Ser. Earth Environ. Sci. 2022, 1079, 012007. [Google Scholar] [CrossRef]
- Shiraghaee, S.; Sundström, J.; Raisee, M.; Cervantes, M.J. Mitigation of Draft Tube Pressure Pulsations by Radial Protrusion of Solid Bodies into the Flow Field: An Experimental Investigation. IOP Conf. Ser. Earth Environ. Sci. 2021, 774, 012004. [Google Scholar] [CrossRef]
- Blommaert, G.; Avellan, F.; Prenat, J.E.; Boyer, A. Active Control of Francis Turbine Operation Stability. In Proceedings of the 3rd ASME/JSME Joint Fluids Engineering Conference, San Francisco, CA, USA, 18–23 July 1999. [Google Scholar]
- Gallaire, F.; Ruith, M.; Meiburg, E.; Chomaz, J.-M.; Huerre, P. Spiral Vortex Breakdown as a Global Mode. J. Fluid Mech. 2006, 549, 71. [Google Scholar] [CrossRef] [Green Version]
- Oberleithner, K.; Sieber, M.; Nayeri, C.N.; Paschereit, C.O.; Petz, C.; Hege, H.-C.; Noack, B.R.; Wygnanski, I. Three-Dimensional Coherent Structures in a Swirling Jet Undergoing Vortex Breakdown: Stability Analysis and Empirical Mode Construction. J. Fluid Mech. 2011, 679, 383–414. [Google Scholar] [CrossRef] [Green Version]
- Oberleithner, K. On Turbulent Swirling Jets: Vortex Breakdown, Coherent Structures, and Their Control. Ph.D. Thesis, Technical University of Berlin, Berlin, Germany, 2012. [Google Scholar]
- Pasche, S.; Avellan, F.; Gallaire, F. Part Load Vortex Rope as a Global Unstable Mode. J. Fluids Eng. 2017, 139, 051102. [Google Scholar] [CrossRef]
- Pasche, S.; Avellan, F.; Gallaire, F. Optimal Control of Part Load Vortex Rope in Francis Turbines. J. Fluids Eng. 2019, 141, 081203. [Google Scholar] [CrossRef]
- Müller, J.S.; Lückoff, F.; Oberleithner, K. Guiding Actuator Designs for Active Flow Control of the Precessing Vortex Core by Adjoint Linear Stability Analysis. J. Eng. Gas Turbines Power 2019, 141, 041028. [Google Scholar] [CrossRef]
- Müller, J.S.; Lückoff, F.; Paredes, P.; Theofilis, V.; Oberleithner, K. Receptivity of the Turbulent Precessing Vortex Core: Synchronization Experiments and Global Adjoint Linear Stability Analysis. J. Fluid Mech. 2020, 888, A3. [Google Scholar] [CrossRef] [Green Version]
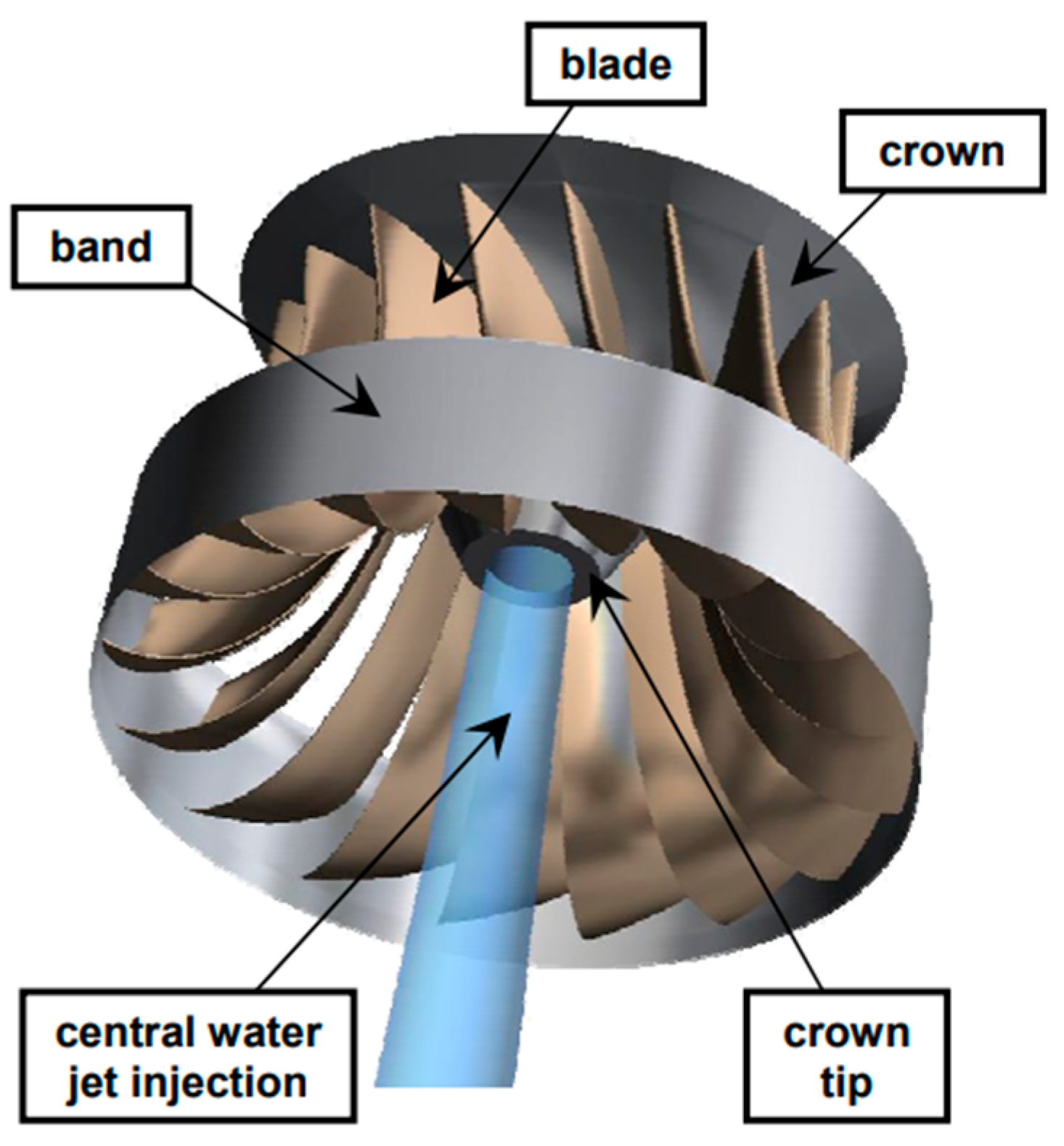
- Müller, J.; Lückoff, F.; Kaiser, T.; Oberleithner, K. On the Relevance of the Runner Crown for Flow Instabilities in a Francis Turbine. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Bristol, UK, 24 November 2022; IOP Publishing: Bristol, UK, 2022; Volume 1079, p. 012053. [Google Scholar]
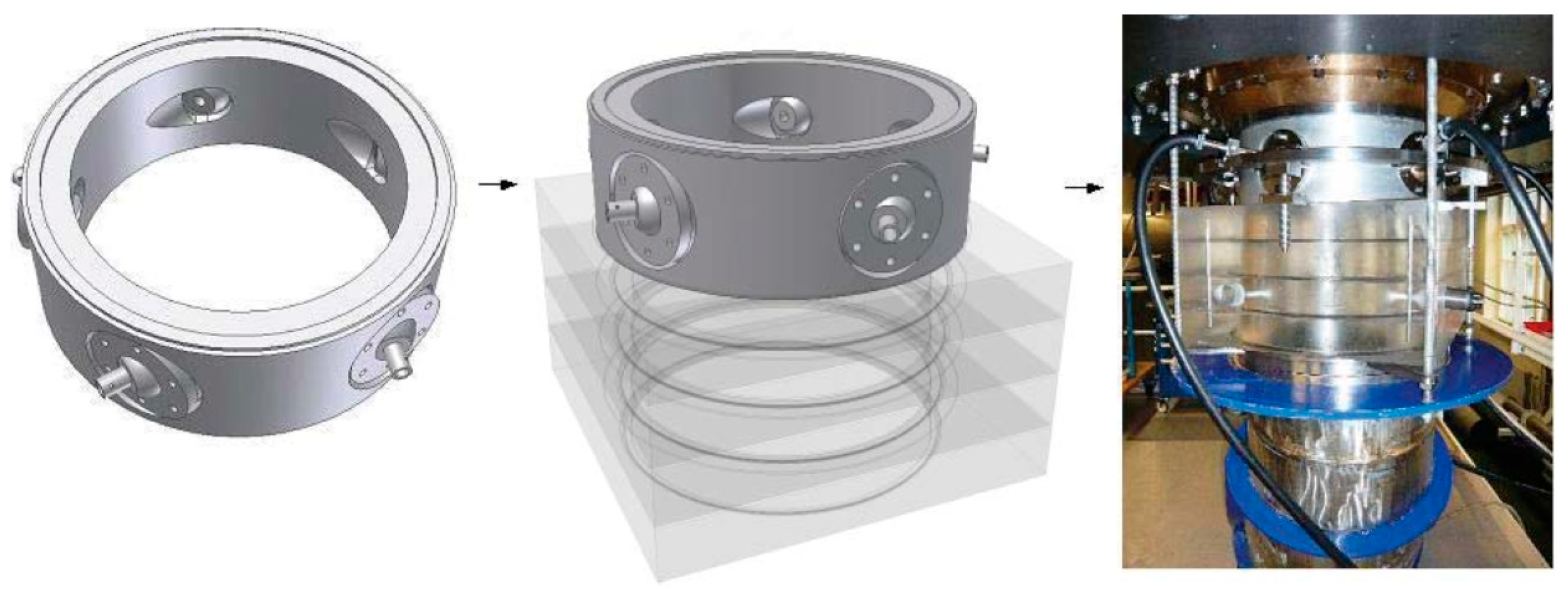
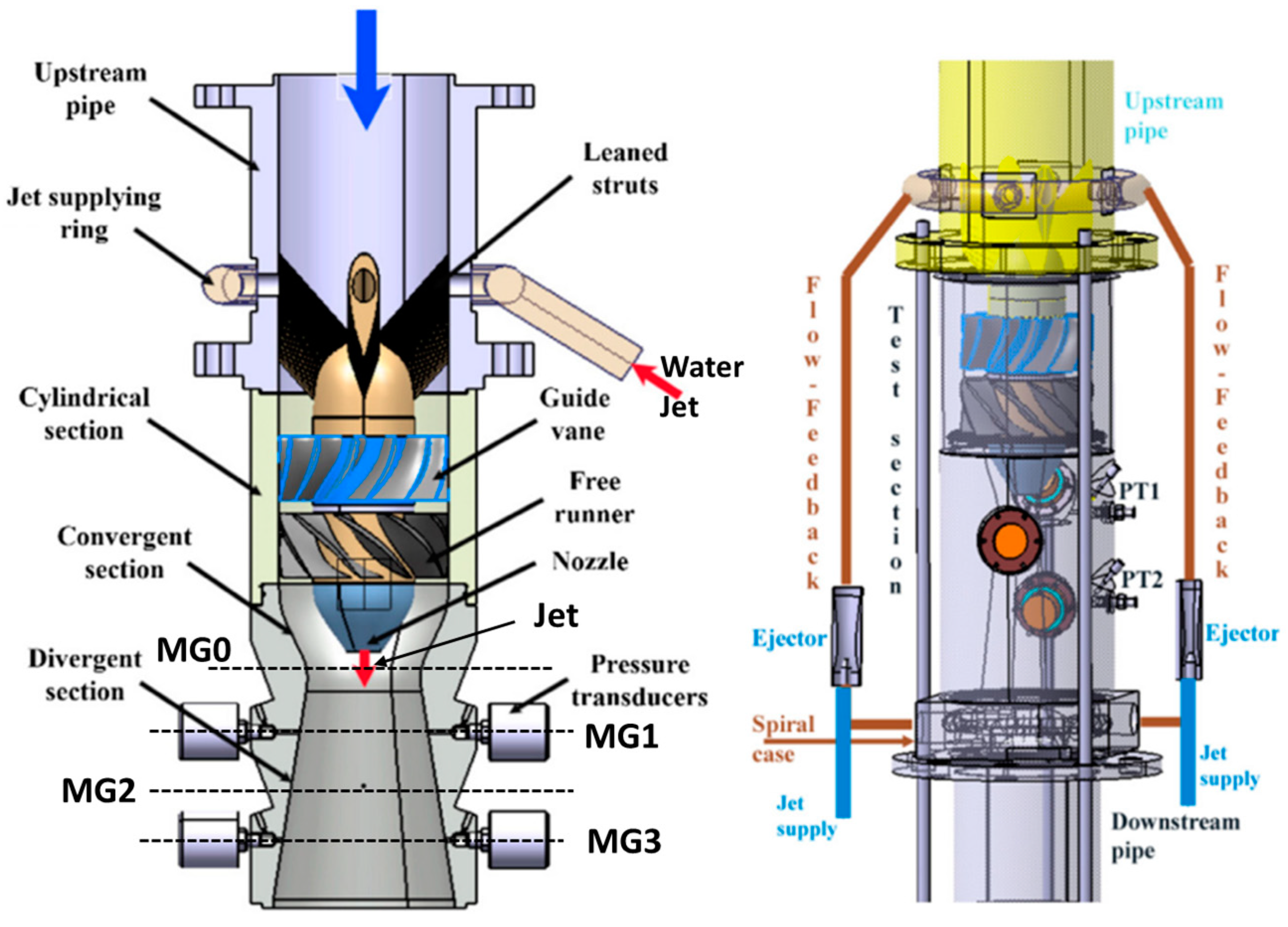
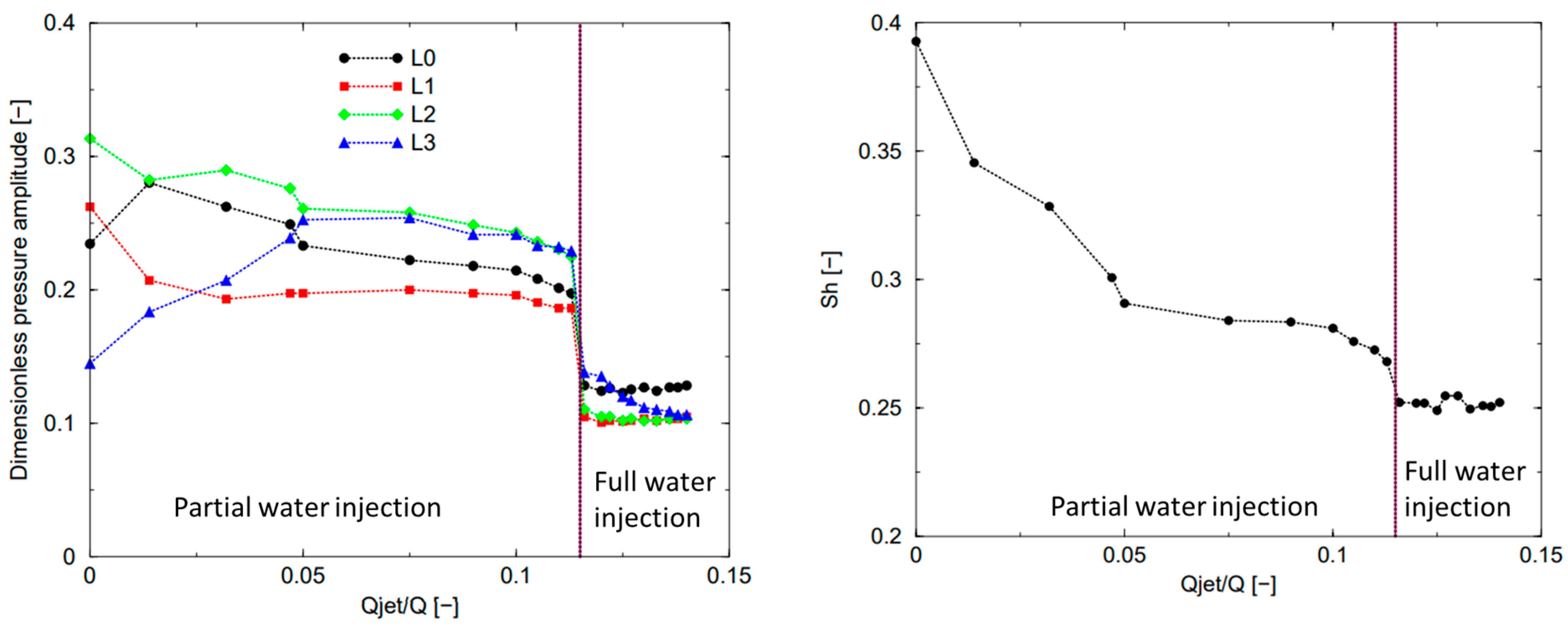
- Litvinov, I.; Suslov, D.; Tsoy, M.; Gorelikov, E.; Alekseenko, S.; Oberleithner, K. Active Control of the Vortex Induced Pressure Fluctuations in a Hydro Turbine Model via Axial and Radial Jets at the Crown Tip. Int. J. Fluid Mach. Syst. 2023. in press.
- Lückoff, F.; Sieber, M.; Paschereit, C.O.; Oberleithner, K. Characterization of Different Actuator Designs for the Control of the Precessing Vortex Core in a Swirl-Stabilized Combustor. J. Eng. Gas Turbines Power 2018, 140, 041503. [Google Scholar] [CrossRef]
- Lückoff, F.; Sieber, M.; Paschereit, C.O.; Oberleithner, K. Phase-Opposition Control of the Precessing Vortex Core in Turbulent Swirl Flames for Investigation of Mixing and Flame Stability. J. Eng. Gas Turbines Power 2019, 141, 111008. [Google Scholar] [CrossRef]
- Kuhn, P.; Moeck, J.P.; Paschereit, C.O.; Oberleithner, K. Control of the Precessing Vortex Core by Open and Closed-Loop Forcing in the Jet Core. In Volume 4B: Combustion, Fuels and Emissions; American Society of Mechanical Engineers: Seoul, Republic of Korea, 2016; p. V04BT04A036. [Google Scholar]
- Lückoff, F.; Sieber, M.; Paschereit, C.O.; Oberleithner, K. Characterization of Different Actuator Designs for the Control of the Precessing Vortex Core in a Swirl-Stabilized Combustor. In Volume 4A: Combustion, Fuels and Emissions; American Society of Mechanical Engineers: Charlotte, NC, USA, 2017; p. V04AT04A040. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shtork, S.; Suslov, D.; Skripkin, S.; Litvinov, I.; Gorelikov, E. An Overview of Active Control Techniques for Vortex Rope Mitigation in Hydraulic Turbines. Energies 2023, 16, 5131. https://doi.org/10.3390/en16135131
Shtork S, Suslov D, Skripkin S, Litvinov I, Gorelikov E. An Overview of Active Control Techniques for Vortex Rope Mitigation in Hydraulic Turbines. Energies. 2023; 16(13):5131. https://doi.org/10.3390/en16135131
Chicago/Turabian StyleShtork, Sergey, Daniil Suslov, Sergey Skripkin, Ivan Litvinov, and Evgeny Gorelikov. 2023. "An Overview of Active Control Techniques for Vortex Rope Mitigation in Hydraulic Turbines" Energies 16, no. 13: 5131. https://doi.org/10.3390/en16135131
APA StyleShtork, S., Suslov, D., Skripkin, S., Litvinov, I., & Gorelikov, E. (2023). An Overview of Active Control Techniques for Vortex Rope Mitigation in Hydraulic Turbines. Energies, 16(13), 5131. https://doi.org/10.3390/en16135131





