Evaluation of the Maturity of Urban Energy Internet Development Based on AHP-Entropy Weight Method and Improved TOPSIS
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
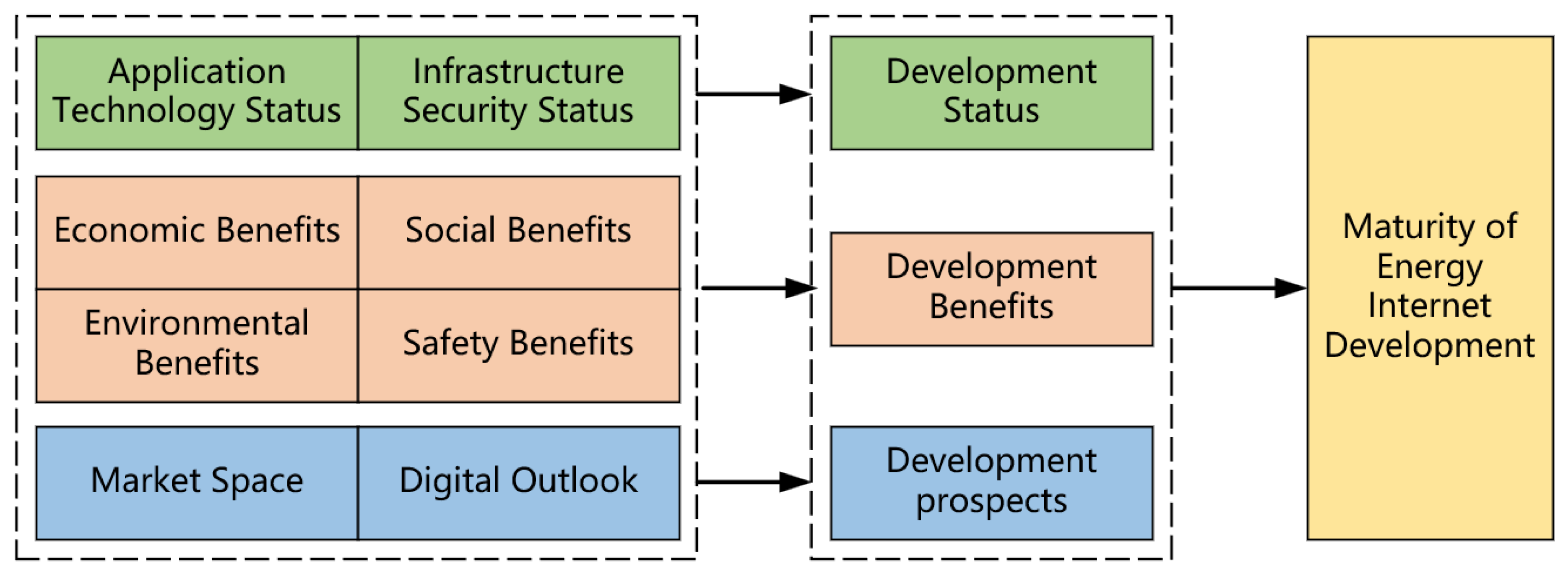
3.1. Indicator System Construction
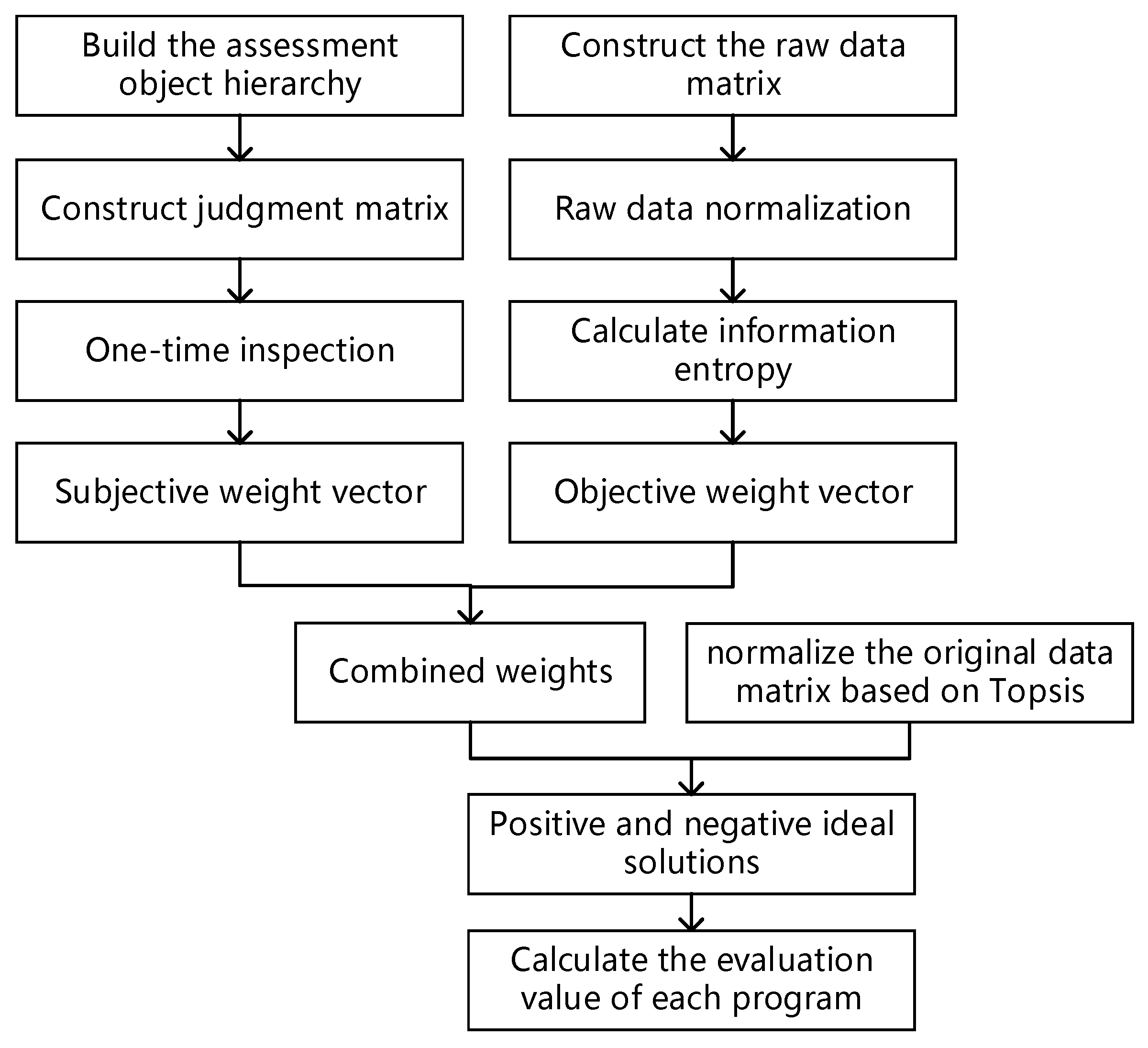
3.2. Combined Weight Calculation
3.3. Evaluation Model Construction
4. Results
4.1. Index Weight Calculation
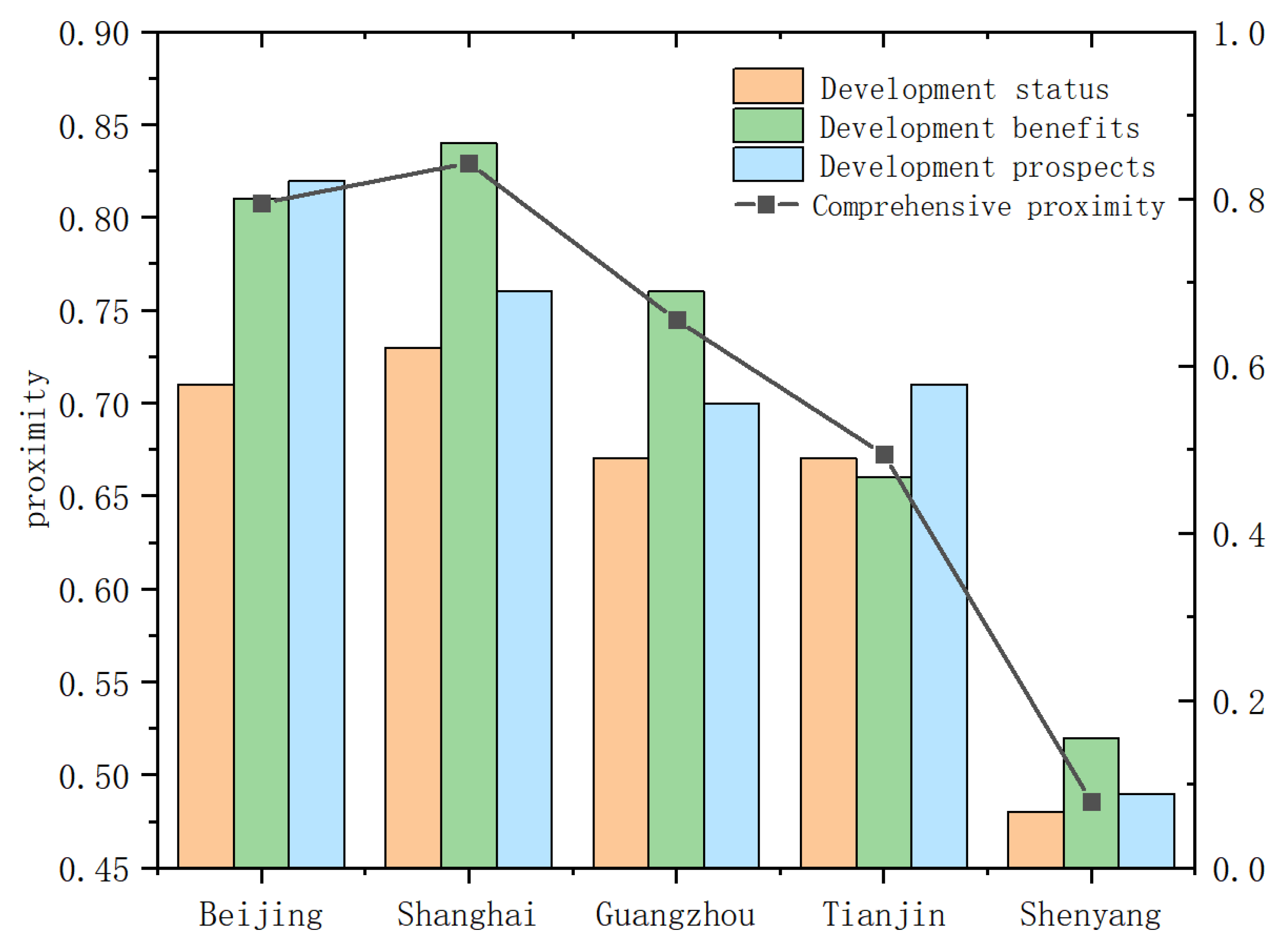
4.2. Evaluation Results of the Maturity of Energy Internet Development
4.3. Comparison of Methods
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yong, W.; Wang, J.; Xue, L.; Bie, Z. Water-energy collaborative optimization for regional energy Internet: Review and prospect. Autom. Electr. Power Syst. 2023, 5, 1–15. [Google Scholar]
- Li, S.; Yao, Y.; Liu, B. Optimal operation based on energy of comprehensive evaluation index system J. J. Guangxi Univ. Nat. Sci. Ed. 2022, 47, 1518–1531. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, Y.; Zhong, H.; Zhang, P.; Tan, Z.; Xia, Q. Research on the Mechanism and Method of Urban Energy Internet Trading Based on Value allocation and cost Allocation. J. Power Grid Technol. 2023, 47, 603–614. [Google Scholar] [CrossRef]
- Song, Z.; Cheng, M.; Niu, W.; Wang, Z.; Liu, J.; Ge, L. Key technologies and development trends of zero-carbon park optimization planning for Energy Internet. J. Electr. Power Constr. 2022, 43, 15–26. [Google Scholar]
- Pan, X.; Zhang, M.; Han, Z.; Hu, J.; Liu, J.; Ge, L. Optimal planning method of intelligent sensing equipment in zero-carbon parks for Energy Internet. J. Electr. Power Constr. 2022, 43, 47–55. [Google Scholar]
- Xu, W.; Han, W.; Jin, H.; Bo, Y.; Liu, H. Based on entropy method, comprehensive evaluation method of regional integrated energy system. J. Sci. Technol. 2022, 14, 66–69. [Google Scholar]
- Zhang, Y.; Ding, Z.; Xie, S.; Lin, J.; Shu, S. Review and Prospect of Research on Improving the Toughness of Distribution Networks Oriented to Energy Internet. J. Power Grid Technol. 2023, 47, 2054–2069. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Zhou, H.; Zong, X.; Sun, Y.; Xiong, J. An evaluation method of park integrated energy system planning considering the interaction of multiple indexes. J. Electr. Power Constr. 2022, 43, 98–110. [Google Scholar]
- Rong, S.; Wang, C.; He, C.; Ma, H.; Wang, T. Based on urban power distribution network planning optimization of Internet research. J. Electr. Power Sci. Technol. 2022, 37, 66–72. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Yang, Z.; Teng, X.; Du, W.; Wang, D. Summary of demonstration application of urban energy Internet: Status quo, experience and prospect. J. Autom. Electr. Power Syst. 2022, 46, 153–166. [Google Scholar]
- Li, X.; Li, C.; Ji, L. Construction of Energy Internet development index system based on Rough set and factor analysis. J. Sci. Technol. Manag. Res. 2018, 38, 75–83. [Google Scholar]
- Zhao, J.; Wang, Y.; Wang, D.; Mu, Y.; An, Q.; Deng, S. Research progress of energy Internet: Definition, index and research methods. J. Electr. Power Syst. Autom. 2018, 30, 1–14. [Google Scholar]
- Ma, J.; Lu, Y.; Yuan, W.; Wang, L.; Huang, W.; Yan, X. Research on evaluation system of Energy Internet. J. China Electr. Power 2018, 51, 38–42. [Google Scholar]
- Dong, X.; Su, Y.; Wu, J.; Wang, S.; Yin, H.; Zhang, Y.; Jiang, T. Scheme design and Engineering Demonstration of Active Distribution Network Supporting Urban Energy Internet. Proc. CSEE 2018, 38, 75–85. [Google Scholar] [CrossRef]
- Gui, X.; Zhao, X.; Qin, G.; Li, C.; Wei, C. Evaluation of Post-construction Effect of high standard basic farmland by entropy weight method and improved TOPSIS Model. J. Trans. Chin. Soc. Agric. Eng. 2017, 33, 238–249. [Google Scholar]
- Hu, S. Evaluation model of training program Maturity based on multi-level grey theory. J. Stat. Decis. 2018, 34, 177–180. (In Chinese) [Google Scholar]
- Wang, L.; Zhou, Z.; Wang, K.; Lu, C. Research on evaluation method of industrial system maturity. J. Eng. Sci. 2020, 22, 91–97. [Google Scholar]
- Wang, L.; Zhang, L.; Xu, C.; Wu, H. Research on User portrait and Maturity evaluation Model of park under the background of Energy Internet. J. China Electr. Power 2020, 53, 19–28. [Google Scholar]
- Xiao, C.; Tang, J.; Wang, X.; Peng, C. Research on the construction of evaluation index system of project organizational structure maturity. J. Constr. Econ. 2022, 43, 226–230. [Google Scholar]
- Xiang, Z.; Yang, G.; Wu, C. Optimization of management maturity evaluation criteria for power grid enterprises based on Performance excellence model. J. Shanghai Qual. 2022, 54–57. [Google Scholar]
- Jiang, Y.; Luo, X.; Liu, C. Construction and application of power grid construction project Maturity evaluation System based on AHP. J. Manag. Obs. 2018, 38, 26–30. [Google Scholar]
- Lin, J.; Xuan, J.; Lin, C. Research on Development Potential evaluation of urban energy Internet. J. Electr. Time 2020, 4, 18–21,26. [Google Scholar]
- Tan, Z.; Xue, F.; Fan, W.; De, G. Evaluation of rural energy Internet construction maturity based on cooperative game-cloud model. J. Smart Power 2022, 50, 9–14,22. [Google Scholar]
- Zhang, Z.; Zhi, R.; Ding, Z. Evaluation of Energy Internet development based on entropy weight matter element model. J. Nanjing Univ. Aeronaut. Astronaut. Soc. Sci. Ed. 2000, 22, 53–61. [Google Scholar]
- Zhang, L.; Zhou, D. Research on evaluation of provincial energy Internet development based on policy factors and variable weights. J. Tech. Econ. Manag. Res. 2020, 10, 3–7. [Google Scholar]
- Liu, K.; Zhu, C.; Luo, Y.; Zhong, M. Study on comprehensive benefit evaluation of Energy Internet in County Area—Based on G1-DEMATEL-CV method. J. Price Theory Pract. 2022, 147–151. [Google Scholar]
- Jiang, L.; Yuan, Y.; Wang, Z. Evaluation index and evaluation method of energy Internet in smart grid Innovation Demonstration Area. J. Electr. Power Syst. Autom. 2016, 28, 39–45. [Google Scholar]
- Jiang, H.; Gao, Y.; Li, J. Based on system dynamics of regional energy Internet comprehensive benefit analysis. J. Glob. Energy Internet 2019, 2, 16–26. [Google Scholar]
- Li, Y.; Nie, V.D.; Liu, C.; Zhao, K.; Song, Z. Evaluation of the Suitability of Energy Internet business Model Based on Decision Test Method and Evaluation Lab-network analysis. J. Mod. Electr. Power 2022, 39, 327–337. (In Chinese) [Google Scholar]
- Wen, D.; Kuo, T.; Yun, C.; Xu, Y.; Lan, M.; Zeng, M. Research on Comprehensive Energy System Evaluation Method Based on Game theory and Evidence Theory under Energy Internet. J. Intell. Electr. Power 2020, 48, 73–80. [Google Scholar]
- Xie, S.; Tian, M. Construction of business environment evaluation index system under “double cycle” pattern: A case study of coastal provinces. J. Bus. Econ. Res. 2021, 180–183. [Google Scholar]
- Nie, W.; Liu, L.; Fu, H.; Song, B. Evaluation mechanism and application of power infrastructure projects based on improved TOPSIS. J. Syst. Manag. 2021, 30, 1207–1214. [Google Scholar]
- Peng, T.; Wei, W.; Cui, C.; Xie, D. Comprehensive Value Evaluation Method of Power Grid Receiving User Assets Based on Double Entropy Correction Index Weighting. J. Mod. Electr. Power 2022, 39, 694–701. (In Chinese) [Google Scholar]
- Meng, X.; Chen, X.; Chen, J.; Yang, H. Application of combinatorial Weighting-Topsis in urban resilience assessment under flood disaster. J. Saf. Environ. 2023, 23, 1465–1473. [Google Scholar]
- Jiang, J.; Wang, X.; Wang, Y.; Fan, Q.; Gu, F.; Yin, Q. Study on the Comprehensive evaluation Method of sustainable remediation of contaminated site based on fuzzy comprehensive evaluation. J. Res. Environ. Sci. 2019, 36, 159–167. [Google Scholar]
- Shen, M.; Zhang, Q.; Zhang, C. Comprehensive evaluation method and application of regional integrated energy system at park level. J. Trans. Beijing Inst. Technol. Soc. Sci. 2022, 24, 52–65. [Google Scholar]
- Zeng, M.; Pan, T.; He, X.; Gong, C. Virtual power plant operation risk comprehensive evaluation method based on Bayesian feedback modified cloud model J/OL. Mod. Electr. Power 2021. [Google Scholar]
- Zu, H.; Shu, W.; Jinj, W.; Zhang, F. Research on Comprehensive Evaluation Method of CNC Machine Tool Based on RAMS. J. Mech. Eng. 2022, 58, 218–230. [Google Scholar]
- Hao, L.; Wu, J.; Wang, Z.; Zhang, Y. Research on comprehensive evaluation method of coordination level of source, network, load and storage in power system. J. Intell. Electr. Power 2021, 49, 12–18. [Google Scholar]
- Xiong, N.; Zhu, W.; Zhong, S.; Shu, J. Comprehensive Evaluation Method of Regional Distribution Network Based on Nonlinear Mapping and Kernel Principal Component Analysis. J. Mod. Electr. Power 2020, 37, 463–469. [Google Scholar]
- Liu, L.; Zhou, Z.; Shen, Y.; Ma, X. Selection of key indicators of Global Energy Internet Development Level. J. Electr. Power Syst. Autom. 2016, 28 (Suppl. 1), 198–201. [Google Scholar]
- Zhou, Z.; Zhang, M. Influencing factors and operating mechanism of market integration based on Explanatory Structural model technology J/OL. Soft Sci. 2022, 1–14. [Google Scholar]
- Huang, X.; Huang, D. Analysis of Value Co-creation ISM Model of engineering projects with Different Outcomes from Data-driven perspective. J. Chongqing Archit. 2022, 21, 43–46. [Google Scholar]
- Teng, Y.; Wu, S.; Fan, S.; Liu, Z. Study on the Mechanism of voluntary pro-environment Behavior of rural residents based on Interpretive structural model. J. Arid. Land Resour. Environ. 2022, 36, 34–40. [Google Scholar]
- Chen, C.-H. A Novel Multi-Criteria Decision-Making Model for Building Material Supplier Selection Based on Entropy-AHP Weighted TOPSIS. Entropy 2020, 22, 259. [Google Scholar] [CrossRef]
- Xu, S.; Xu, D.; Liu, L. Construction of regional informatization ecological environment based on the entropy weight modified AHP hierarchy model. Sustain. Comput. Inform. Syst. 2019, 22, 26–31. [Google Scholar] [CrossRef]
- Feng, G.; Lei, S.; Guo, Y.; Meng, B.; Jiang, Q. Optimization and Evaluation of Ventilation Mode in Marine Data Center Based on AHP-Entropy Weight. Entropy 2019, 21, 796. [Google Scholar] [CrossRef]
- Liu, Z.; Xie, Q.; Dai, L.; Wang, H. Research on comprehensive evaluation method of distribution network based on AHP-entropy weighting method. Front. Energy Res. 2022, 10, 975462. [Google Scholar] [CrossRef]
- Wu, G.; Duan, K.; Zuo, J.; Zhao, X.; Tang, D. Integrated Sustainability Assessment of Public Rental Housing Community Based on a Hybrid Method of AHP-Entropy Weight and Cloud Model. Sustainability 2017, 9, 603. [Google Scholar] [CrossRef]
- Xiao, K.; Tamborski, J.; Wang, X.; Feng, X.; Wang, S.; Wang, Q.; Lin, D.; Li, H. A coupling methodology of the analytic hierarchy process and entropy weight theory for assessing coastal water quality. Environ. Sci. Pollut. Res. 2022, 29, 31217–31234. [Google Scholar] [CrossRef]
- Fahim, A.; Tan, Q.; Naz, B.; Ain, Q.u.; Bazai, S.U. Sustainable Higher Education Reform Quality Assessment Using SWOT Analysis with Integration of AHP and Entropy Models: A Case Study of Morocco. Sustainability 2021, 13, 4312. [Google Scholar] [CrossRef]
- Qayyum, M.; Yuyuan, Y.; Bhatti, U.A.; Shijie, L. Evaluation of the one belt and one road (OBOR) in economic development and suggestions analysis based on SWOT analysis with weighted AHP and entropy methods. Multimed. Tools Appl. 2023, 82, 14985–15006. [Google Scholar] [CrossRef]
- Zeng, J.; Huang, G. Set pair analysis for karst waterlogging risk assessment based on AHP and entropy weight. Hydrol. Res. 2018, 49, 1143–1155. [Google Scholar] [CrossRef]
- Yang, S.; He, J. Analysis of Digital Economy Development Based on AHP-Entropy Weight Method. J. Sens. 2022, 2022, 1–8. [Google Scholar] [CrossRef]
- Chen, H.; Wan, Q.; Wang, Y. Refined Diebold-Mariano Test Methods for the Evaluation of Wind Power Forecasting Models. Energies 2014, 7, 4185–4198. [Google Scholar] [CrossRef]
- Shi, R.; Fan, X.; He, Y. Comprehensive Evaluation Index System for Wind Power Utilization Levels in Wind Farms in China. Renew. Sustain. Energy Rev. 2017, 69, 461–471. [Google Scholar] [CrossRef]
- Yu, S.; Song, Y. Organizational Performance Evaluation of Coal-Fired Power Enterprises Using a Hybrid Model. Energies 2022, 15, 3175. [Google Scholar] [CrossRef]
- Wang, Q.; Lu, C.; Xie, J.; Lu, J. Construction and Application of Electricity Market Transaction Compliance Index system—Construction of Electricity Transaction Compliance Index based on ANP-GRA-KL-TOPSIS method. J. Price Theory Pract. 2021, 79–83+193. [Google Scholar] [CrossRef]
- Ji, J.; Chen, J. Urban flood resilience assessment using RAGA-PP and KL-TOPSIS model based on PSR framework: A case study of Jiangsu province, China. Water Sci. Technol. 2022, 86, 3264–3280. [Google Scholar] [CrossRef]
- Hong, J.; Liu, J.; Xiang, Y. Urban energy Internet preliminary understanding and research prospects. J. Electr. Power Autom. Equip. 2017, 5, 15–25. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Mardani, A.; Turskis, Z.; Jusoh, A.; Nor, K.M. Development of TOPSIS Method to Solve Complicated Decision-Making Problems—An Overview on Developments from 2000 to 2015. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 645–682. [Google Scholar] [CrossRef]


| Levels | Key Elements |
|---|---|
| L1 | S1 |
| L2 | S2, S3, S4 |
| L3 | S5, S6, S7, S8, S9, S10, S11, S12 |
| L4 | S13, …, S35 |
| Tier 1 Indicators | Secondary Indicators | Tertiary Indicators | Description | |
|---|---|---|---|---|
| EI Development Evaluation Indicator System | Development status A1 | Infrastructural security B1 | Smart Grid Investment Scale C1 | Amount of investment in regional smart grids |
| Smart meter penetration rate C2 | Regional smart meter adoption share | |||
| Share of installed renewable energy C3 | Total installed renewable energy as a share of total regional installed capacity | |||
| Share of renewable energy generation C4 | Renewable energy generation as a share of total regional electricity generation | |||
| Core technologies B2 | New technology adoption rate C5 | Share of new technologies applied | ||
| Domestic replacement rate C6 | Proportion of self-developed equipment | |||
| Development benefits A2 | Economic benefits B3 | Operating income C7 | Annual profit amount | |
| Subsidy benefits C8 | Government subsidies for the year | |||
| Energy cost reduction rate C9 | Level of energy cost reduction from project construction | |||
| Operating cost reduction rate C10 | Level of operating cost reduction due to project construction | |||
| Social benefits B4 | User satisfaction C11 | Customer satisfaction with the provision of integrated energy services | ||
| Employment-led capacity C12 | Employment generated during the construction and application of the project | |||
| Environmental benefits B5 | Rate of change of pollutant emissions C13 | The effect of the project on the reduction of pollutant emissions after operation | ||
| Energy consumption reduction rate C14 | Level of energy reduction after project operation | |||
| Energy efficiency improvement rate C15 | Level of energy efficiency improvements after project operation | |||
| Safety benefits B6 | Reliability of energy supply C16 | Uptime for users | ||
| Grid Line Loss Ratio C17 | Average line loss ratio of the transmission network | |||
| Peak-to-valley differential rate C18 | Ratio of peak-to-valley difference to maximum load | |||
| Development prospects A3 | Market space B7 | Promoted adoption rate C19 | Integrated energy demonstration projects as a share of the market | |
| Industry chain driven level C20 | The pulling effect of the project on the upstream and downstream of the industry chain | |||
| User growth rate C21 | Level of growth in customers being provided with integrated energy services | |||
| Digital prospects B8 | Level of energy information integration C22 | Extent of integration with Internet IT applications | ||
| Project interconnectedness and shareability C23 | The extent to which distributed generation systems within the project share a wide area interconnection with all types of loads |
| Tier 1 Indicators | Weighting | Secondary Indicators | Weighting | Tertiary Indicators | Weighting | Ranking | |
|---|---|---|---|---|---|---|---|
| EI Development Maturity Evaluation Index System | Development status A1 | 0.3735 | Infrastructural security B1 | 0.1524 | Smart Grid Investment Scale C1 | 0.0337 | 12 |
| Smart meter penetration rate C2 | 0.0232 | 20 | |||||
| Share of installed renewable energy C3 | 0.0436 | 9 | |||||
| Share of renewable energy generation C4 | 0.0518 | 6 | |||||
| Core technologies B2 | 0.2211 | New technology adoption rate C5 | 0.1039 | 2 | |||
| Domestic replacement rate C6 | 0.1172 | 1 | |||||
| Development benefits A2 | 0.4251 | Economic benefits B3 | 0.0987 | Operating income C7 | 0.0327 | 14 | |
| Subsidy benefits C8 | 0.0066 | 23 | |||||
| Energy cost reduction rate C9 | 0.0392 | 11 | |||||
| Operating cost reduction rate C10 | 0.0202 | 22 | |||||
| Social benefits B4 | 0.0523 | User satisfaction C11 | 0.0293 | 17 | |||
| Employment-led capacity C12 | 0.0230 | 21 | |||||
| Environmental benefits B5 | 0.1321 | Pollutant emission reduction rate C13 | 0.0495 | 7 | |||
| Carbon emission reduction rate C14 | 0.0586 | 5 | |||||
| Energy efficiency improvement rate C15 | 0.0240 | 19 | |||||
| Safety benefits B6 | 0.1420 | Reliability of energy supply C16 | 0.0695 | 4 | |||
| Grid Line Loss Ratio C17 | 0.0331 | 13 | |||||
| Peak-to-valley differential rate C18 | 0.0394 | 10 | |||||
| Development prospects A3 | 0.2014 | Market space B7 | 0.0874 | Promoted adoption rate C19 | 0.0308 | 15 | |
| Industry chain driven level C20 | 0.0298 | 16 | |||||
| User growth rate C21 | 0.0268 | 18 | |||||
| Digital prospects B8 | 0.1140 | Level of energy information integration C22 | 0.0698 | 3 | |||
| Project interconnectedness and shareability C23 | 0.0442 | 8 |
| City | GRA-KL-TOPSIS Posting Progress | TOPSIS Posting Progress |
|---|---|---|
| Beijing | 0.7796 | 0.8215 |
| Shanghai | 0.7892 | 0.8452 |
| Guangzhou | 0.7338 | 0.6939 |
| Tianjin | 0.6204 | 0.6415 |
| Shenyang | 0.5193 | 0.4809 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhou, X.; Liu, H.; Chen, X.; Yan, Z.; Li, D.; Liu, C.; Wang, J. Evaluation of the Maturity of Urban Energy Internet Development Based on AHP-Entropy Weight Method and Improved TOPSIS. Energies 2023, 16, 5151. https://doi.org/10.3390/en16135151
Wang Y, Zhou X, Liu H, Chen X, Yan Z, Li D, Liu C, Wang J. Evaluation of the Maturity of Urban Energy Internet Development Based on AHP-Entropy Weight Method and Improved TOPSIS. Energies. 2023; 16(13):5151. https://doi.org/10.3390/en16135151
Chicago/Turabian StyleWang, Yongli, Xiangyi Zhou, Hao Liu, Xichang Chen, Zixin Yan, Dexin Li, Chang Liu, and Jiarui Wang. 2023. "Evaluation of the Maturity of Urban Energy Internet Development Based on AHP-Entropy Weight Method and Improved TOPSIS" Energies 16, no. 13: 5151. https://doi.org/10.3390/en16135151
APA StyleWang, Y., Zhou, X., Liu, H., Chen, X., Yan, Z., Li, D., Liu, C., & Wang, J. (2023). Evaluation of the Maturity of Urban Energy Internet Development Based on AHP-Entropy Weight Method and Improved TOPSIS. Energies, 16(13), 5151. https://doi.org/10.3390/en16135151








