Optimized Control of a Hybrid Water Pumping System Integrated with Solar Photovoltaic and Battery Storage: Towards Sustainable and Green Water-Power Supply
Abstract
1. Introduction
2. Materials and Methods
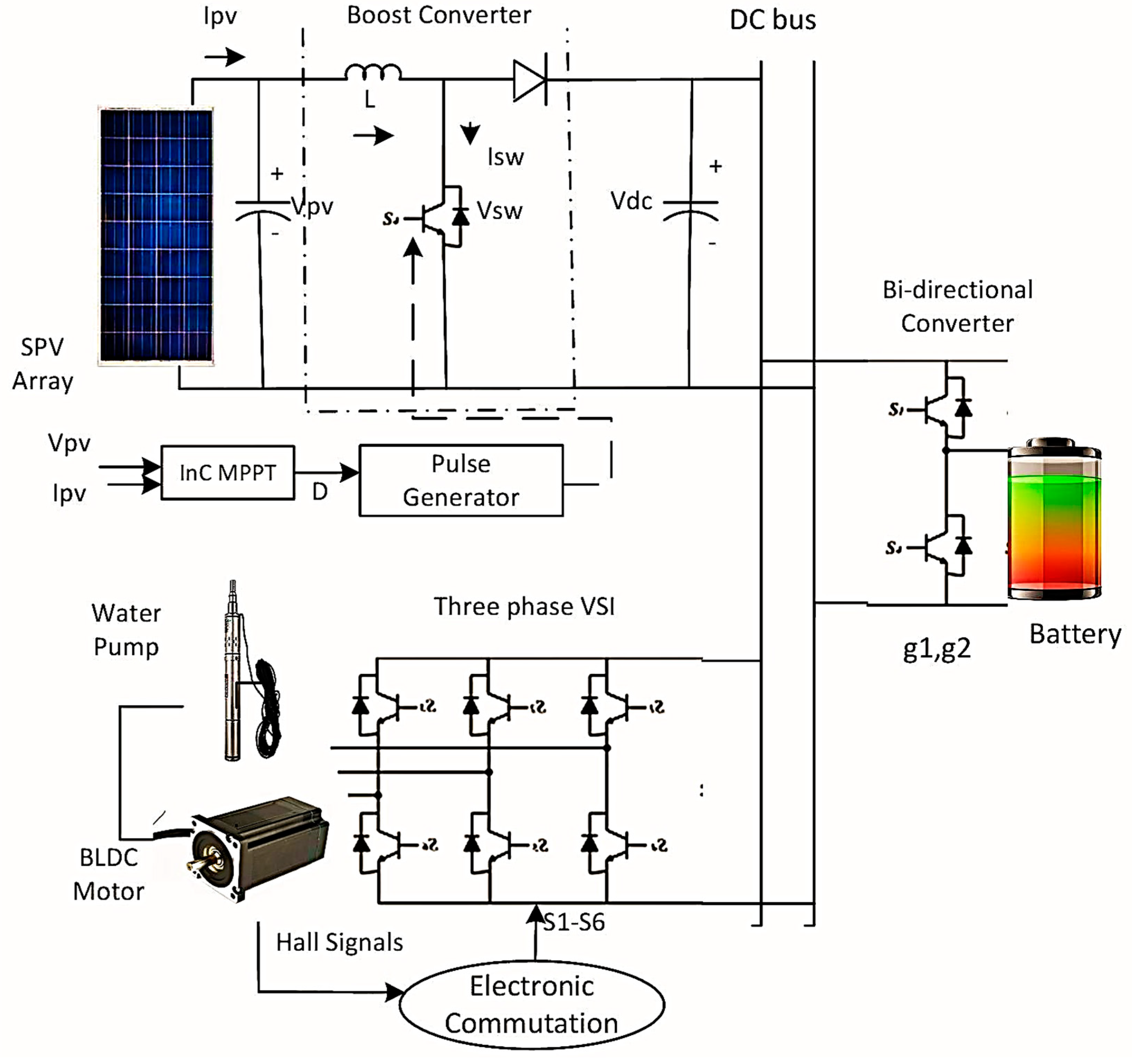
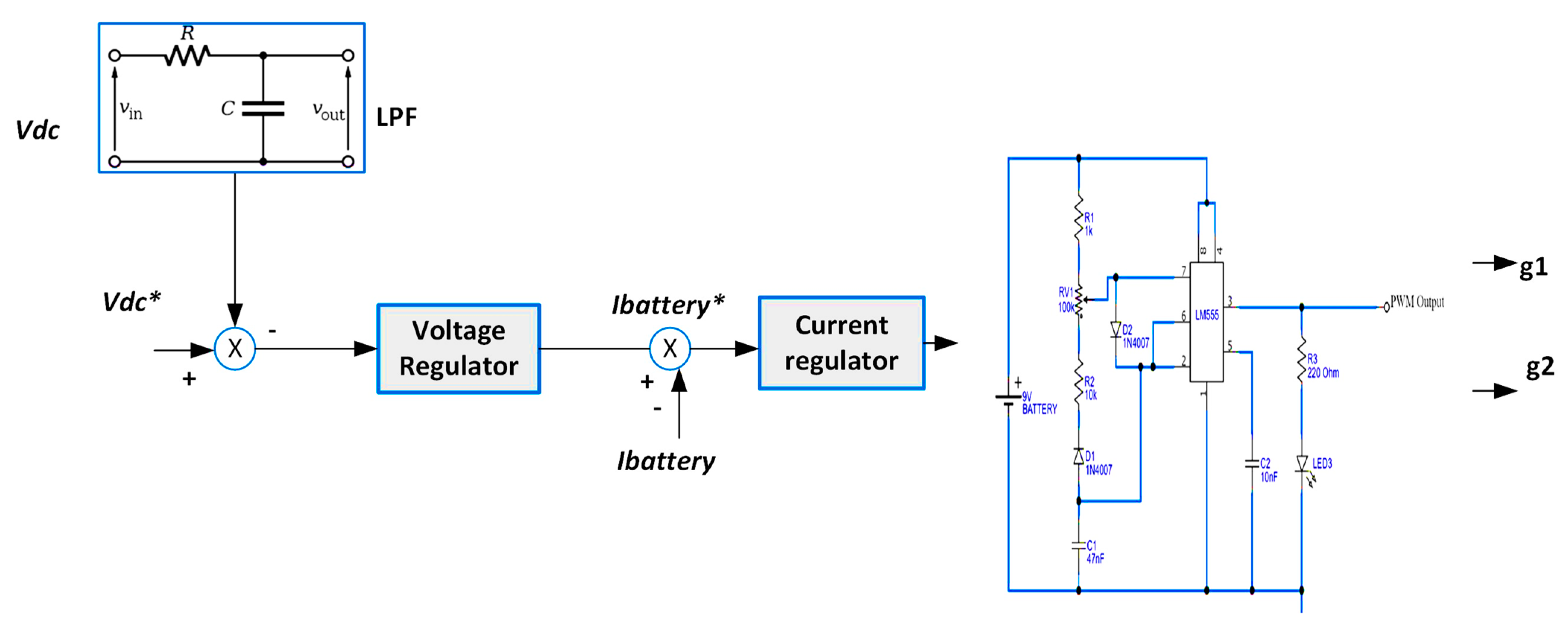
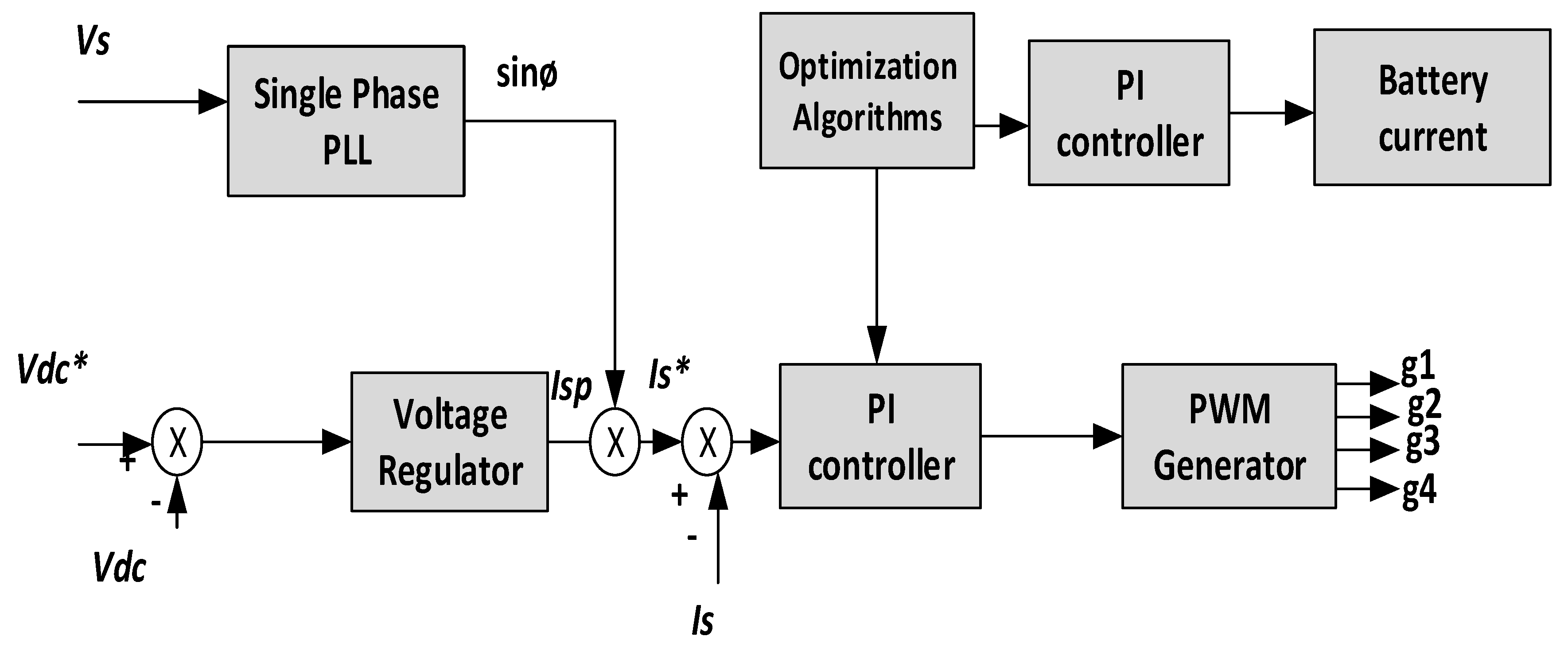
2.1. SPV Battery-Based Hybrid Water Pumping System
2.2. Electronic Commutation of the BLDC Motor
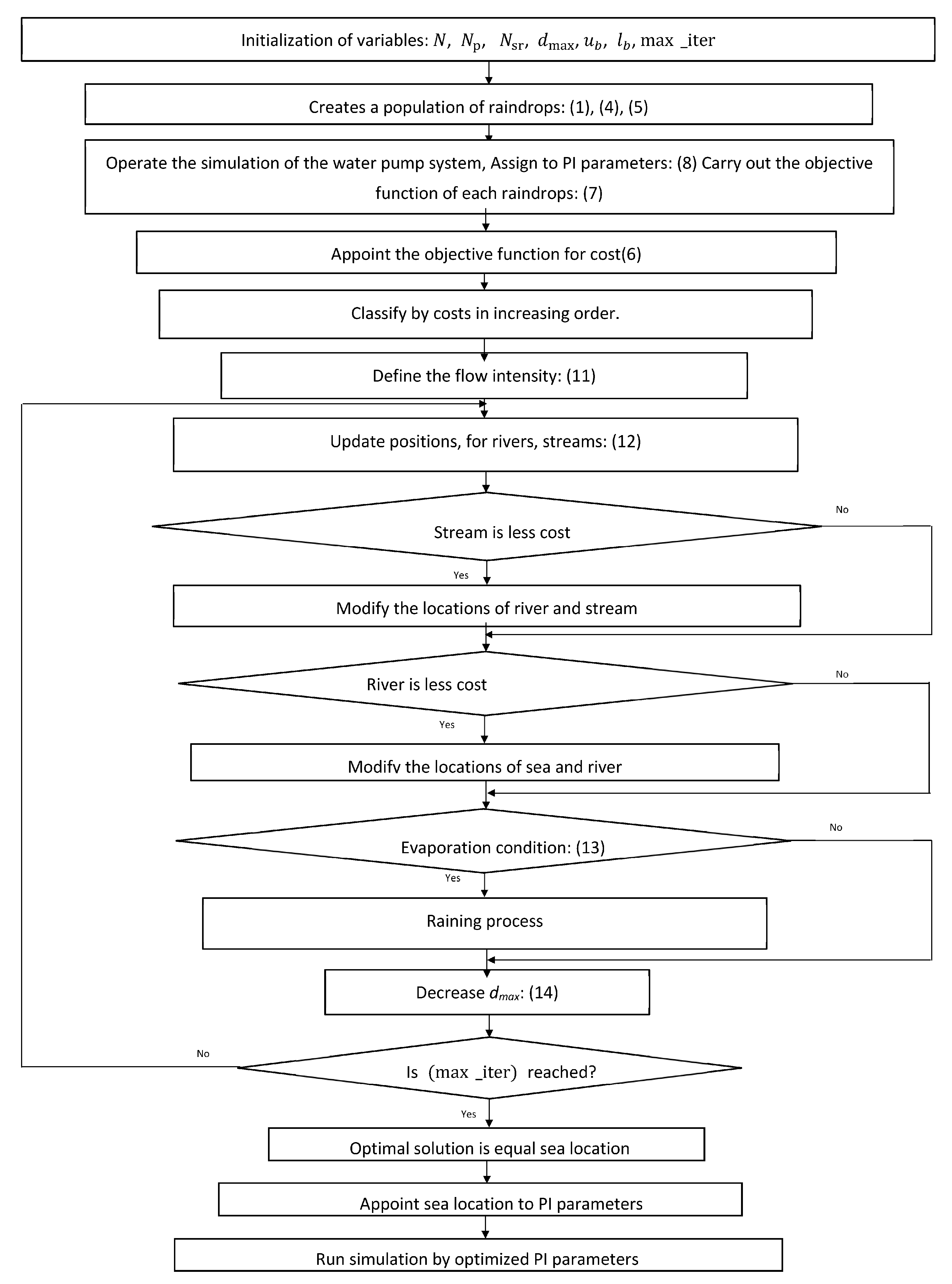
2.3. Water Cycle Algorithm for Optimization
| Parameters | Quantity |
|---|---|
| Number of variables | 4 |
| Number of iterations (Generations) | 100 |
| Population size | 50 |
| Rate of mutation | 0.01 |
| Rate of cross over | 0.8 |
| Parameters | Quantity |
|---|---|
| Dimension of search space | 4 |
| Number of iterations | 100 |
| Bacteria number (S) | 10 |
| Chemotactic steps number (Nc) | 5 |
| Limits the length of swim (Ns) and Reproduction steps number (Nre) | 4 |
| Probability for elimination/dispersion (Ped) and Elimination-dispersal number (Ned) | 2 |
| Parameters | Quantity |
|---|---|
| Condition constant of evaporation (dmax): | 10−16 |
| Rivers + sea (Nsr): | 4 |
| Iterations (max_iter) | 100 |
| Variables number (N) | 4 |
| Population number (Np) | 50 |
| Parameters | Quantity |
|---|---|
| Pole | 6 |
| Speed | 300 rpm |
| Stator resistance | 0.37 Ω |
| Stator inductance | 1.0 mH |
| Voltage constant | 34 VL/krpm |
| Parameters | Quantity |
|---|---|
| Peak Power | 1.92 kW |
| Open circuit voltage | 126 V |
| MPP voltage | 102 V |
| Short circuit current | 22.4 A |
| MPP current | 19 A |
| Parameters | Quantity |
|---|---|
| Boost inductor | 3 mH |
| Bus capacitor | 6000 µF |
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, R.; Singh, B. BLDC Motor Driven Solar PV Array Fed Water Pumping System Employing Zeta Converter. IEEE Trans. Ind. Appl. 2016, 52, 2315–2322. [Google Scholar] [CrossRef]
- Singh, B.; Kumar, R. Simple brushless DC motor drive for solar photovoltaic array fed water pumping system. IET Power Electron. 2016, 9, 1487–1495. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, B. Solar PV-battery based hybrid water pumping system using BLDC motor drive. In Proceedings of the 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Kar, B.N.; Samuel, P.; Pradhan, J.K.; Mallick, A. Grid-connected solar photovoltaic-fed brushless DC motor drive for water pumping system using colliding body optimization technique. Circuit World 2022. ahead of print. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, B. Grid interfaced solar PV based water pumping using brushless DC motor drive. In Proceedings of the IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Trivandrum, India, 14–17 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Jegha, A.D.G.; Subathra, M.S.P.; Kumar, N.M.; Ghosh, A. Optimally Tuned Interleaved Luo Converter for PV Array Fed BLDC Motor Driven Centrifugal Pumps Using Whale Optimization Algorithm—A Resilient Solution for Powering Agricultural Loads. Electronics 2020, 9, 1445. [Google Scholar] [CrossRef]
- Harsh, K.; Pandey, K.; Kumar, R.; Jangir, A.K. BLDC Motor Driven Water Pump Fed by Solar Photovoltaic Array using Boost Converter. Int. J. Eng. Res. Technol. 2020, 9, 635–639. [Google Scholar] [CrossRef]
- Ammar, A.; Hamraoui, K.; Belguellaoui, M.; Kheldoun, A. Performance Enhancement of Photovoltaic Water Pumping System Based on BLDC Motor under Partial Shading Condition. Eng. Proc. 2022, 14, 22. [Google Scholar] [CrossRef]
- Muralidhar, K.; Rajasekar, N. A review of various components of solar water-pumping system: Configuration, characteristics, and performance. Int. Trans. Electr. Energy Syst. 2021, 31, e13002. [Google Scholar] [CrossRef]
- Khiareddine, A.; Salah, C.K.; Mimouni, M.F. Power management of a photovoltaic/battery pumping system in agricultural experiment station. Solar Energy 2015, 112, 319–338. [Google Scholar] [CrossRef]
- Ding, F.; Li, P.; Huang, B.; Gao, F.; Ding, C.; Wang, C. Modeling and simulation of grid-connected hybrid photovoltaic/battery distributed generation system. In Proceedings of the CICED, Nanjing, China, 13–16 September 2010; pp. 1–10. [Google Scholar]
- Elgendy, M.A.; Atkinson, D.J.; Zahawi, B. Experimental investigation of the incremental conductance maximum power point tracking algorithm at high perturbation rates. Let Renew. Power Gener. 2016, 10, 133–139. [Google Scholar] [CrossRef]
- Singh, B.; Kumar, R. Solar photovoltaic array fed water pump driven by brushless DC motor using Landsman converter. Let Renew. Power Gener. 2016, 10, 474–484. [Google Scholar] [CrossRef]
- Sigarchian, S.G.; Malmquist, A.; Fransson, T. Modeling and Control Strategy of a Hybrid PV/Wind/Engine/Battery System to Provide Electricity and Drinkable Water for Remote Applications. Energy Procedia 2016, 57, 1401–1410. [Google Scholar] [CrossRef]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water cycle algorithm–A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110–111, 151–166. [Google Scholar] [CrossRef]
- Sadollaha, A.; Eskandar, H.; Lee, H.M.; Yoo, D.G.; Kim, J.H. Water cycle algorithm: A detailed standard code. SoftwareX 2016, 5, 37–43. [Google Scholar] [CrossRef]
- Almabrok, A.; Psarakis, M.; Dounis, A. Fast Tuning of the PID Controller in An HVAC System Using the Big Bang–Big Crunch Algorithm and FPGA Technology. Algorithms 2018, 11, 146. [Google Scholar] [CrossRef]
- Maghfiroh, H.; Saputro, J.S.; Hermanu, C.; Ibrahim, M.H.; Sujono, A. Performance Evaluation of Different Objective Function in PID Tuned by PSO in DC-Motor Speed Control. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1096, 012061. [Google Scholar] [CrossRef]
- Özdemir, M.T.; Öztürk, D. Comparative Performance Analysis of Optimal PID Parameters Tuning Based on the Optics Inspired Optimization Methods for Automatic Generation Control. Energies 2017, 10, 2134. [Google Scholar] [CrossRef]
- Teodorescu, R.; Liserre, M.; Rodriguez, P. Grid Converters for Photovoltaic and Wind Power Systems; John Wiley & Sons, Ltd. Publication: Hoboken, NJ, USA, 2011. [Google Scholar]
- Bakir, H.; Merabet, A.; Dhar, R.K.; Kulaksiz, A.A. Bacteria foraging optimisation algorithm based optimal control for doubly-fed induction generator wind energy system. IET Renew. Power Gener. 2020, 14, 1850–1859. [Google Scholar] [CrossRef]
- Hassan, L.H.; Haider, M.M.; Almurib, A.F.; Muttaqi, K.M.; Ganapathy, V.G. Optimization of power system stabilizers using participation factor and genetic algorithm. Int. J. Electr. Power 2014, 55, 668–679. [Google Scholar] [CrossRef]
- Kiehbadroudinezhad, M.; Merabet, A.; Abo-Khalil, A.G.; Salameh, T.; Ghenai, C. Intelligent and Optimized Microgrids for Future Supply Power from Renewable Energy Resources: A Review. Energies 2022, 15, 3359. [Google Scholar] [CrossRef]
- Kiehbadroudinezhad, M.; Merabet, A.; Rajabipour, A.; Cada, M.; Kiehbadroudinezhad, S.; Khanali, M.; Hosseinzadeh-Bandbafha, H. Optimization of wind/solar energy microgrid by division algorithm considering human health and environmental impacts for power-water cogeneration. Energy Convers. Manag. 2002, 252, 115064. [Google Scholar] [CrossRef]
- Kiehbadroudinezhad, M.; Rajabipour, A.; Cada, M.; Khanali, M. Modeling, design, and optimization of a cost-effective and reliable hybrid renewable energy system integrated with desalination using the division algorithm. Int. J. Energy Res. 2021, 45, 429–452. [Google Scholar] [CrossRef]
- Kiehbadroudinezhad, M.; Merabet, A.; Hosseinzadeh-Bandbafha, H. Optimization of Wind Energy Battery Storage Microgrid by Division Algorithm Considering Cumulative Exergy Demand for Power-Water Cogeneration. Energies 2021, 14, 3777. [Google Scholar] [CrossRef]
- Bakir, H.; Merabet, A.; Dhar, R.K.; Kulaksiz, A.A. Experimental evaluation of water cycle technique for control parameters optimization of double-fed induction generator-based wind turbine. Eng. Sci. Technol. Int. J. 2021, 24, 890–898. [Google Scholar] [CrossRef]
- Dhar, R.K.; Merabet, A.; Bakir, H.; Ghias, A.M.Y.M. Implementation of Water Cycle Optimization for Parametric Tuning of PI Controllers in Solar PV and Battery Storage Microgrid System. IEEE Syst. J. 2022, 16, 1751–1762. [Google Scholar] [CrossRef]


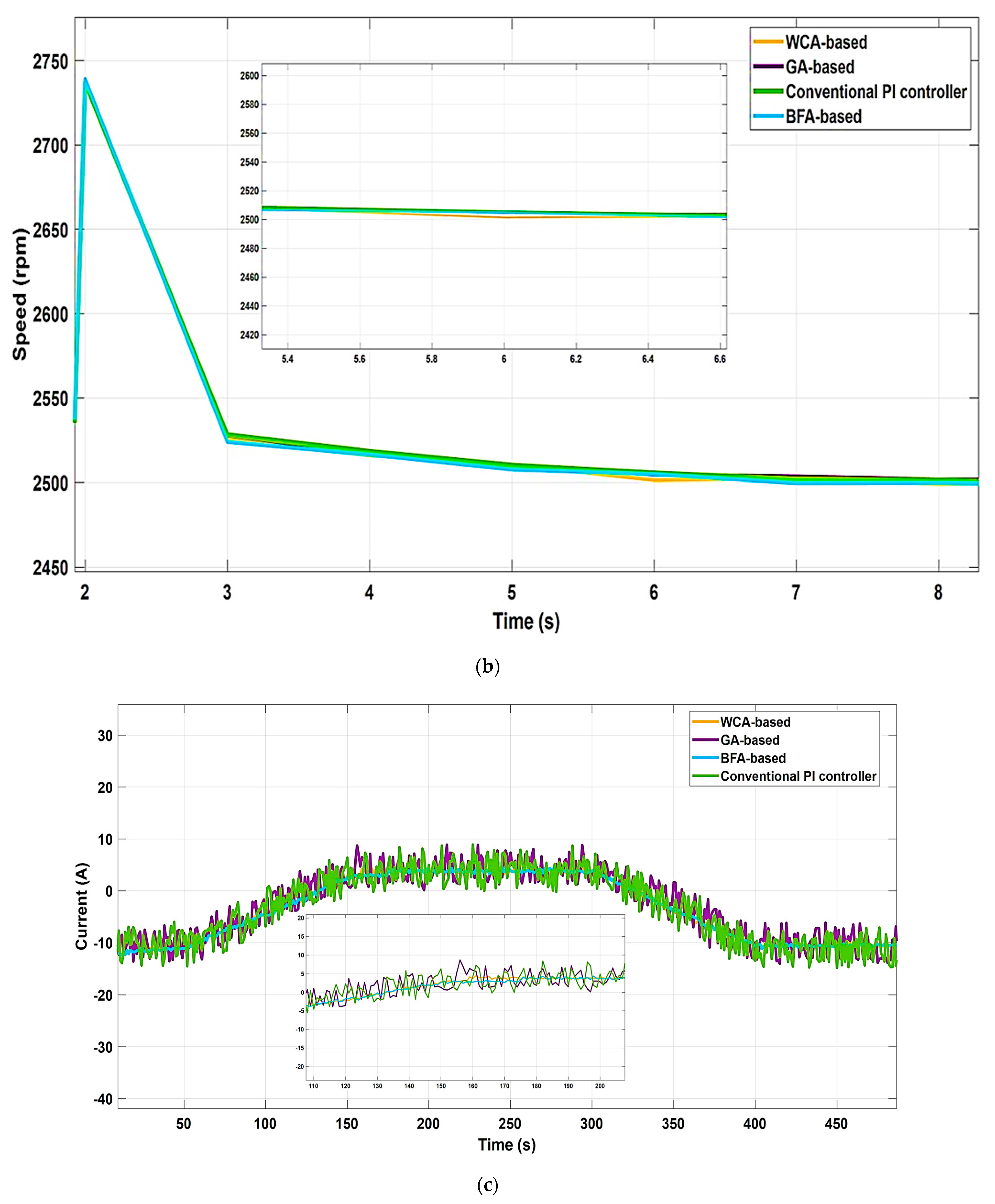
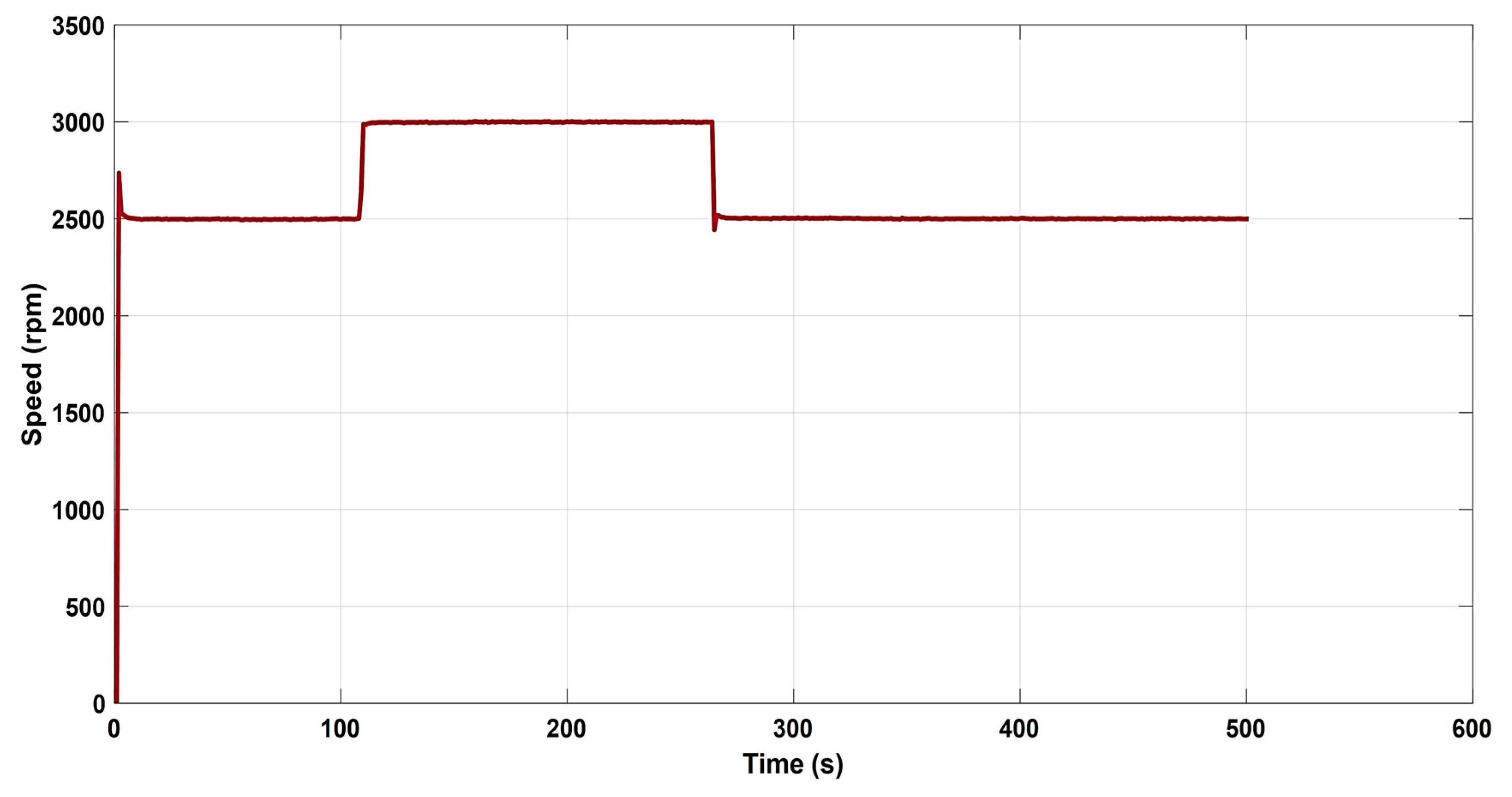
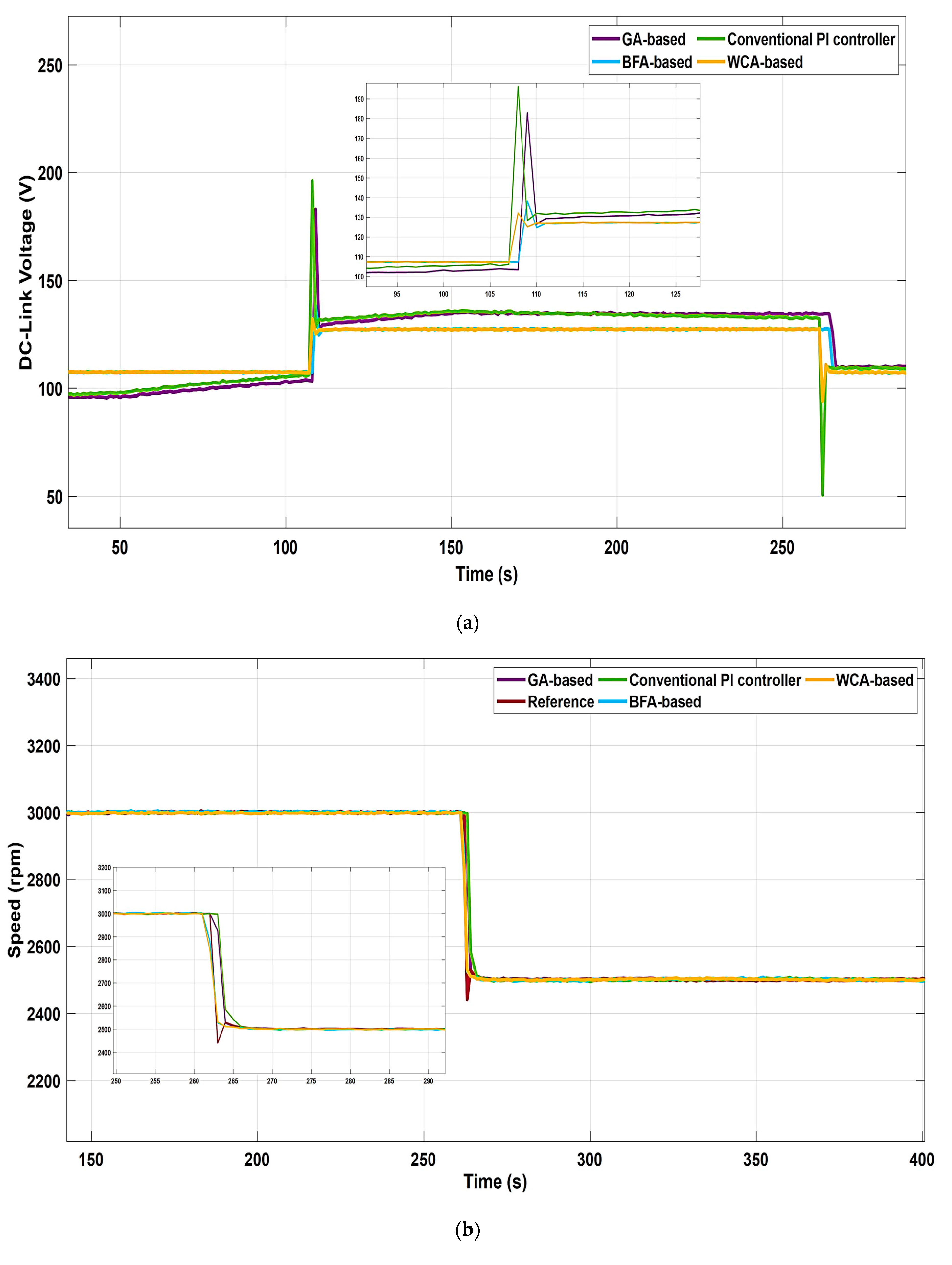
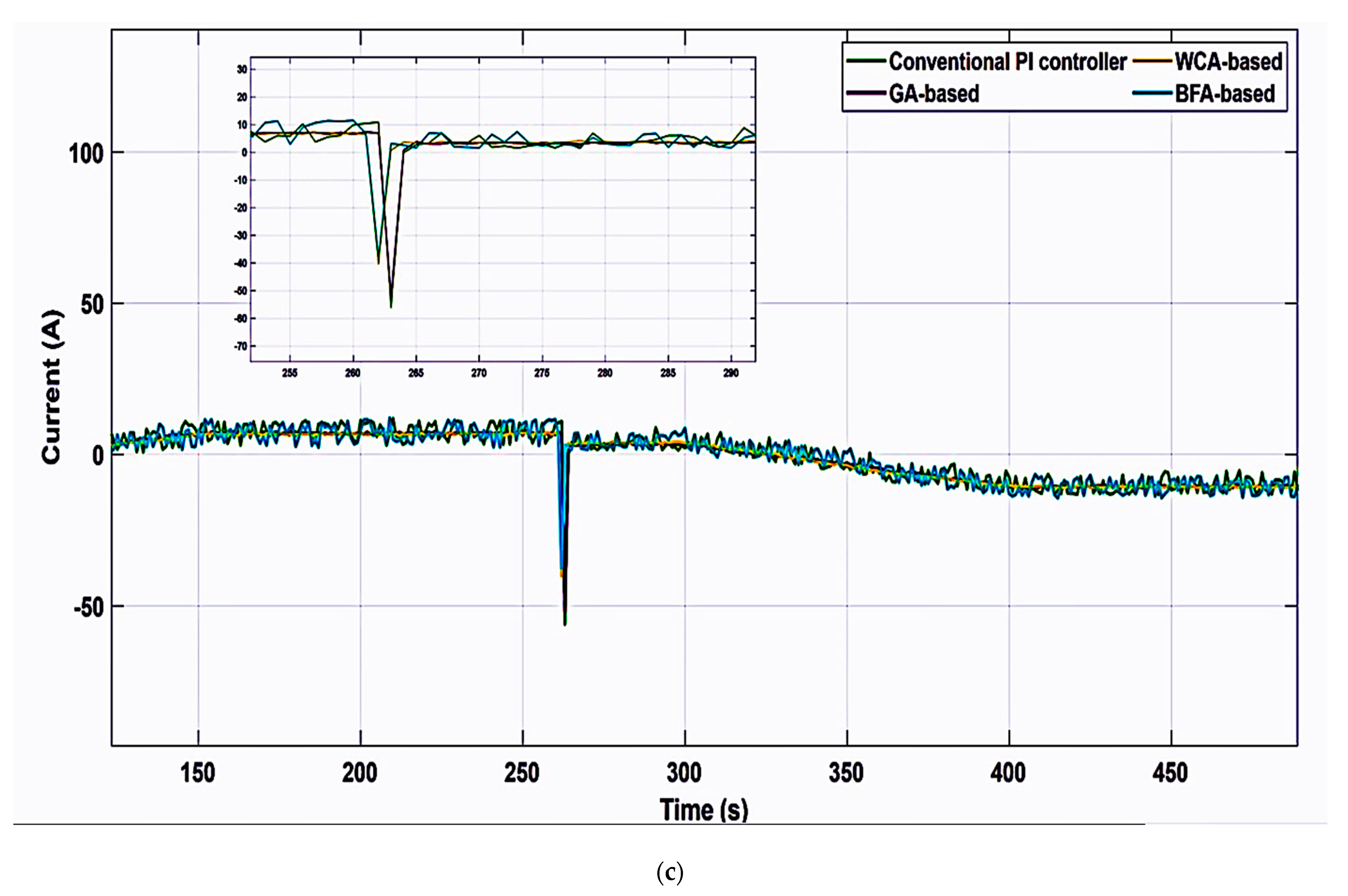
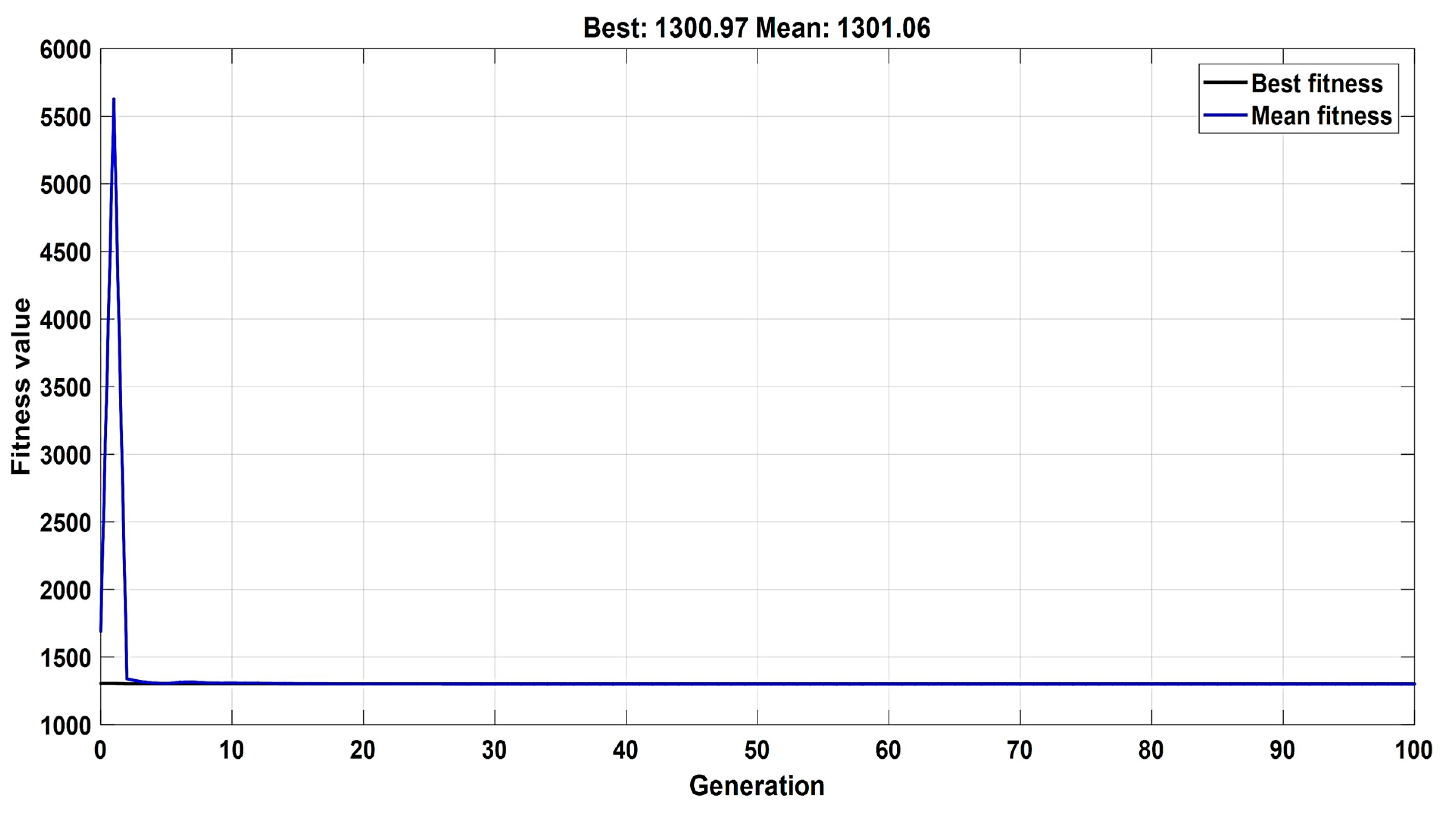
| Performance Tests | Gain Parameters (Control) | Genetic Algorithm Optimization Technique | Bacteria Foraging Algorithm Optimization Technique | Water Cycle Optimization Technique |
|---|---|---|---|---|
| ITSE | DC-link voltage controller () Battery current controller () | 0.9674, 0.3701 0.3350, 0.8347 | 0.9991, 0.0712 0.5805, 0.9347 | 0.9981, 0.0194 0.5643, 0.9555 |
| ISE | DC-link voltage controller () Battery current controller () | 0.9961, 0.0056 0.9756, 0.8414 | 0.9949, 0.0493 0.2099, 0.9861 | 0.9961, 0.0135 0.9766, 0.9834 |
| ITAE | DC-link voltage controller () Battery current controller () | 0.9707, 0.2124 0.3302, 0.9255 | 0.9943, 0.0259 0.4196, 0.9898 | 0.9649, 0.0046 0.5870, 0.9724 |
| IAE | DC-link voltage controller () Battery current controller () | 0.9815, 0 0.9693, 0.8278 | 0.9706, 0.0243 0.7482, 0.9421 | 0.9773, 0.0031 0.6111, 0.8928 |
| PI Block | Based Controller | Overshoot | Settling Time (s) | Peak Values |
|---|---|---|---|---|
| DC-link voltage (under variable speed) | Conventional | 45.12 | 112.5 | 195.2 |
| GA | 36.92 | 111.1 | 183.4 | |
| BFA | 9.80 | 110.8 | 138.2 | |
| WCA | 6.02 | 108.5 | 134.01 | |
| DC-link voltage (under constant speed) | Conventional | 8.90 | 160.5 | 113.3 |
| GA | 7.44 | 155.8 | 112.1 | |
| BFA | 3.202 | 153.04 | 111.09 | |
| WCA | 1.27 | 151.08 | 110.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakır, H.; Merabet, A.; Kiehbadroudinezhad, M. Optimized Control of a Hybrid Water Pumping System Integrated with Solar Photovoltaic and Battery Storage: Towards Sustainable and Green Water-Power Supply. Energies 2023, 16, 5209. https://doi.org/10.3390/en16135209
Bakır H, Merabet A, Kiehbadroudinezhad M. Optimized Control of a Hybrid Water Pumping System Integrated with Solar Photovoltaic and Battery Storage: Towards Sustainable and Green Water-Power Supply. Energies. 2023; 16(13):5209. https://doi.org/10.3390/en16135209
Chicago/Turabian StyleBakır, Hale, Adel Merabet, and Mohammadali Kiehbadroudinezhad. 2023. "Optimized Control of a Hybrid Water Pumping System Integrated with Solar Photovoltaic and Battery Storage: Towards Sustainable and Green Water-Power Supply" Energies 16, no. 13: 5209. https://doi.org/10.3390/en16135209
APA StyleBakır, H., Merabet, A., & Kiehbadroudinezhad, M. (2023). Optimized Control of a Hybrid Water Pumping System Integrated with Solar Photovoltaic and Battery Storage: Towards Sustainable and Green Water-Power Supply. Energies, 16(13), 5209. https://doi.org/10.3390/en16135209








