Advanced Machine Learning Techniques for Accurate Very-Short-Term Wind Power Forecasting in Wind Energy Systems Using Historical Data Analysis
Abstract
:1. Introduction
1.1. Need for Wind Energy Forecasting
1.2. Classification of Wind Energy Prediction
1.3. Forecasting Methods
2. Related Work
3. Materials and Methods
3.1. Data
3.2. Preprocessing
3.3. Attribute Selection
3.4. Outlier Removal
3.5. Exploratory Data Analysis
3.5.1. Wind Rose Analysis
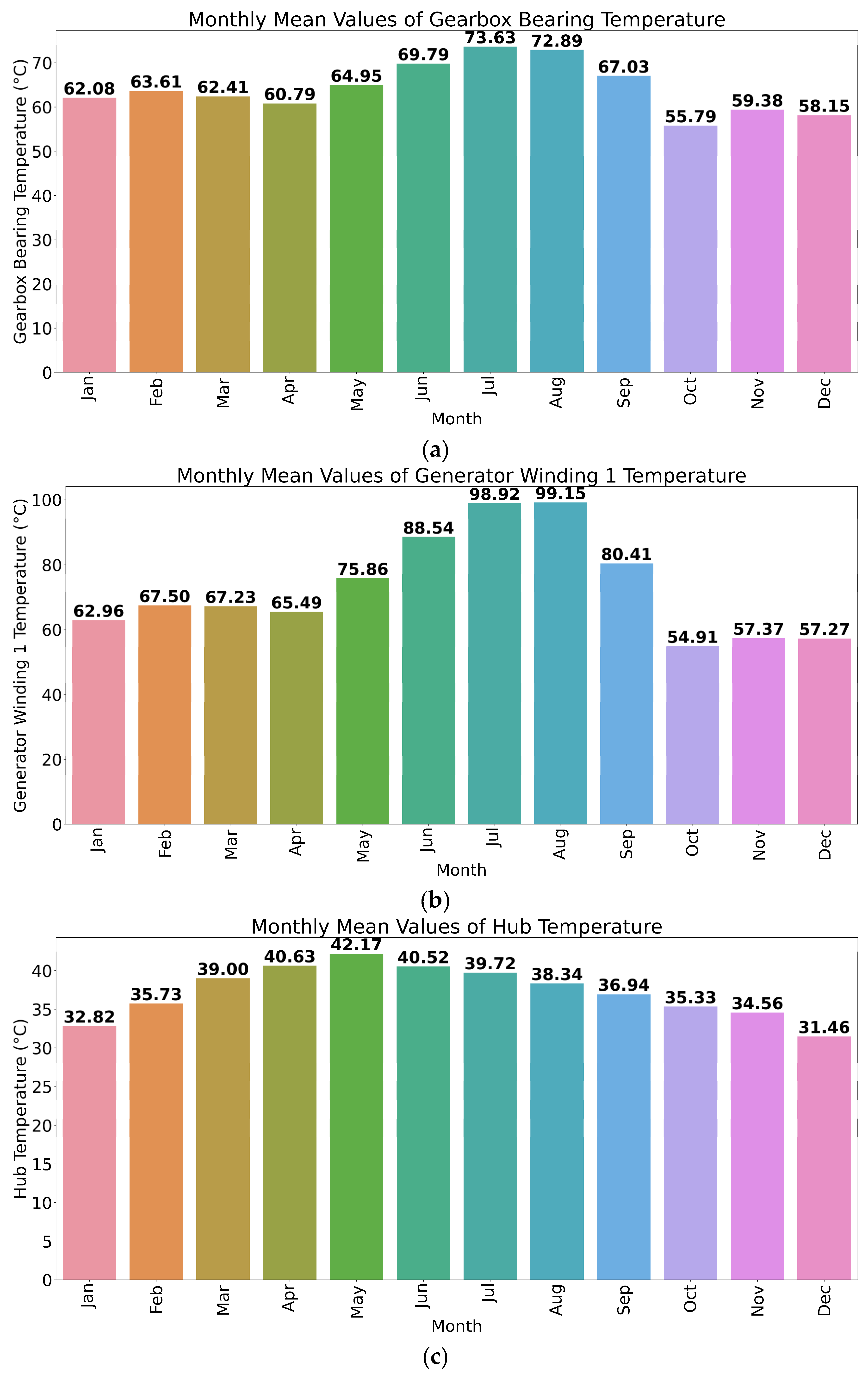
3.5.2. Dataset Insights
3.6. Machine Learning Algorithms
3.6.1. LightGBM
3.6.2. Random Forest
3.6.3. CatBoost
3.6.4. XGBoost
3.7. Results and Discussion
3.7.1. Hyperparameter Optimization
3.7.2. Prediction Model’s Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Harindintwali, J.D.; Yuan, Z.; Wang, M.; Wang, F.; Li, S.; Yin, Z.; Huang, L.; Fu, Y.; Li, L.; Chang, S.X.; et al. Technologies and perspectives for achieving carbon neutrality. Innovation 2021, 2, 100180. [Google Scholar] [CrossRef]
- Ahmad, T.; Zhang, D. A critical review of comparative global historical energy consumption and future demand: The story told so far. Energy Rep. 2020, 6, 1973–1991. [Google Scholar] [CrossRef]
- Kulkarni, S.H.; Anil, T.R.; Gowdar, R.D. Wind Energy Development in India and a Methodology for Evaluating Performance of Wind Farm Clusters. J. Renew. Energy 2016, 2016, 6769405. [Google Scholar] [CrossRef] [Green Version]
- Dang, T. Introduction, history, and theory of wind power. In Proceedings of the 41st North American Power Symposium, Starkville, MS, USA, 4–6 October 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Goudarzi, N.; Zhu, W.D. A review on the development of wind turbine generators across the world. Int. J. Dyn. Control 2013, 1, 192–202. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Li, Y.; Zheng, L.; Cui, L.; Li, S.; Li, W.; Cai, Y. Site selection of wind farms using GIS and multi-criteria decision making method in Wafangdian, China. Energy 2020, 207, 118222. [Google Scholar] [CrossRef]
- Gönül, Ö.; Duman, A.C.; Deveci, K.; Güler, Ö. An assessment of wind energy status, incentive mechanisms and market in Turkey. Eng. Sci. Technol. Int. J. 2021, 24, 1383–1395. [Google Scholar] [CrossRef]
- Wang, X.; Guo, P.; Huang, X. A Review of Wind Power Forecasting Models. Energy Procedia 2011, 12, 770–778. [Google Scholar] [CrossRef] [Green Version]
- Ramirez-Meyers, K.; Mann, W.N.; A Deetjen, T.; Johnson, S.C.; Rhodes, J.D.; Webber, M. How different power plant types contribute to electric grid reliability, resilience, and vulnerability: A comparative analytical framework. Prog. Energy 2021, 3, 033001. [Google Scholar] [CrossRef]
- Ragheb, M.; Ragheb, A.M. Wind Turbines Theory-The Betz Equation and Optimal Rotor Tip Speed Ratio. In Fundamental and Advanced Topics in Wind Power; IntechOpen: London, UK, 2011. [Google Scholar] [CrossRef] [Green Version]
- Barbosa de Alencar, D.; De Mattos Affonso, C.; Limão de Oliveira, R.C.; Moya Rodríguez, J.L.; Leite, J.C.; Reston Filho, J.C. Different Models for Forecasting Wind Power Generation: Case Study. Energies 2017, 10, 1976. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, A.; Javaid, N.; Mateen, A.; Awais, M.; Khan, Z.A. Short-Term Load Forecasting in Smart Grids: An Intelligent Modular Approach. Energies 2019, 12, 164. [Google Scholar] [CrossRef] [Green Version]
- Baer, F. Numerical weather prediction. In Advances in Computers; Zelkowitz, M.V., Ed.; Elsevier: Amsterdam, The Netherlands, 2000; Volume 52, pp. 91–157. [Google Scholar] [CrossRef]
- Pearre, N.S.; Swan, L.G. Statistical approach for improved wind speed forecasting for wind power production. Sustain. Energy Technol. Assess. 2018, 27, 180–191. [Google Scholar] [CrossRef]
- Hong, Y.-Y.; Rioflorido, C.L.P.P. A hybrid deep learning-based neural network for 24-h ahead wind power forecasting. Appl. Energy 2019, 250, 530–539. [Google Scholar] [CrossRef]
- Gallego, C.; Pinson, P.; Madsen, H.; Costa, A.; Cuerva, A. Influence of local wind speed and direction on wind power dynamics–Application to offshore very short-term forecasting. Appl. Energy 2011, 88, 4087–4096. [Google Scholar] [CrossRef] [Green Version]
- Hodge, B.-M.; Zeiler, A.; Brooks, D.; Blau, G.; Pekny, J.; Reklatis, G. Improved Wind Power Forecasting with ARIMA Models. Comput. Aided Chem. Eng. 2011, 29, 1789–1793. [Google Scholar] [CrossRef]
- Peiris, A.T.; Jayasinghe, J.; Rathnayake, U. Forecasting Wind Power Generation Using Artificial Neural Network: “Pawan Danawi”—A Case Study from Sri Lanka. J. Electr. Comput. Eng. 2021, 2021, 5577547. [Google Scholar] [CrossRef]
- Singh, U.; Rizwan, M. Enhancing wind power forecasting from meteorological parameters using machine learning models. J. Renew. Sustain. Energy 2022, 14, 063302. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, Z.Y.; Kong, W.; Meng, K. A Composite Anomaly Detection System for Data-Driven Power Plant Condition Monitoring. IEEE Trans. Ind. Inform. 2019, 16, 4390–4402. [Google Scholar] [CrossRef]
- Kim, J.; Afzal, A.; Kim, H.-G.; Dinh, C.T.; Park, S.G. Wind power forecasting based on hourly wind speed data in South Korea using machine learning algorithms. J. Mech. Sci. Technol. 2022, 36, 6107–6113. [Google Scholar] [CrossRef]
- Tyass, I.; Khalili, T.; Rafik, M.; Abdelouahed, B.; Raihani, A.; Mansouri, K. Wind Speed Prediction Based on Statistical and Deep Learning Models. Int. J. Renew. Energy Dev. 2023, 12, 288–299. [Google Scholar] [CrossRef]
- Navas, R.K.B.; Prakash, S.; Sasipraba, T. Artificial Neural Network based computing model for wind speed prediction: A case study of Coimbatore, Tamil Nadu, India. Phys. A Stat. Mech. Appl. 2019, 542, 123383. [Google Scholar] [CrossRef]
- Amroune, M. Support vector regression-bald eagle search optimizer-based hybrid approach for short-term wind power forecasting. J. Eng. Appl. Sci. 2022, 69, 107. [Google Scholar] [CrossRef]
- Li, L.-L.; Cen, Z.-Y.; Tseng, M.-L.; Shen, Q.; Ali, M.H. Improving short-term wind power prediction using hybrid improved cuckoo search arithmetic-Support vector regression machine. J. Clean. Prod. 2020, 279, 123739. [Google Scholar] [CrossRef]
- Liu, Z.; Li, X.; Zhao, H. Short-Term Wind Power Forecasting Based on Feature Analysis and Error Correction. Energies 2023, 16, 4249. [Google Scholar] [CrossRef]
- Xu, P.; Zhang, M.; Chen, Z.; Wang, B.; Cheng, C.; Liu, R. A Deep Learning Framework for Day Ahead Wind Power Short-Term Prediction. Appl. Sci. 2023, 13, 4042. [Google Scholar] [CrossRef]
- Miele, E.S.; Ludwig, N.; Corsini, A. Multi-Horizon Wind Power Forecasting Using Multi-Modal Spatio-Temporal Neural Networks. Energies 2023, 16, 3522. [Google Scholar] [CrossRef]
- Zhu, A.; Zhao, Q.; Wang, X.; Zhou, L. Ultra-Short-Term Wind Power Combined Prediction Based on Complementary Ensemble Empirical Mode Decomposition, Whale Optimisation Algorithm, and Elman Network. Energies 2022, 15, 3055. [Google Scholar] [CrossRef]
- Lin, W.-H.; Wang, P.; Chao, K.-M.; Lin, H.-C.; Yang, Z.-Y.; Lai, Y.-H. Wind Power Forecasting with Deep Learning Networks: Time-Series Forecasting. Appl. Sci. 2021, 11, 10335. [Google Scholar] [CrossRef]
- Dataset Link. Available online: https://www.kaggle.com/datasets/theforcecoder/wind-power-forecasting (accessed on 11 February 2023).
- Ayilara, O.F.; Zhang, L.; Sajobi, T.T.; Sawatzky, R.; Bohm, E.; Lix, L.M. Impact of missing data on bias and precision when estimating change in patient-reported outcomes from a clinical registry. Health Qual. Life Outcomes 2019, 17, 106. [Google Scholar] [CrossRef] [Green Version]
- Qiu, P.; Niu, Z. TCIC_FS: Total correlation information coefficient-based feature selection method for high-dimensional data. Knowl.-Based Syst. 2021, 231, 107418. [Google Scholar] [CrossRef]
- Mukaka, M.M. Statistics corner: A guide to appropriate use of correlation coefficient in medical research. Malawi Med. J. 2012, 24, 69–71. [Google Scholar]
- Gress, T.W.; Denvir, J.; Shapiro, J.I. Effect of Removing Outliers on Statistical Inference: Implications to Interpretation of Experimental Data in Medical Research. Marshall J. Med. 2018, 4, 84. [Google Scholar] [CrossRef] [Green Version]
- Hair, J.; Black, W.C.; Babin, B.J.; Anderson, R.E. Multivariate Data Analysis, 7th ed.; Pearson Educational International: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Byrne, B.M. Structural Equation Modeling with AMOS: Basic Concepts, Applications, and Programming; Routledge: New York, NY, USA, 2010. [Google Scholar]
- Irwanto, M.; Gomesh, N.; Mamat, M.; Yusoff, Y. Assessment of wind power generation potential in Perlis, Malaysia. Renew. Sustain. Energy Rev. 2014, 38, 296–308. [Google Scholar] [CrossRef]
- Liu, L.; Niu, M.; Zhang, C.; Shu, J. Light Gradient Boosting Machine-Based Link Quality Prediction for Wireless Sensor Networks. Wirel. Commun. Mob. Comput. 2022, 2022, 8278087. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Kanagarathinam, K.; Sankaran, D.; Manikandan, R. Machine learning-based risk prediction model for cardiovascular disease using a hybrid dataset. Data Knowl. Eng. 2022, 140, 102042. [Google Scholar] [CrossRef]
- Mahesh, T.R.; Kumar, V.V.; Muthukumaran, V.; Shashikala, H.K.; Swapna, B.; Guluwadi, S. Performance Analysis of XGBoost Ensemble Methods for Survivability with the Classification of Breast Cancer. J. Sensors 2022, 2022, 4649510. [Google Scholar] [CrossRef]















| Author(s) | Type of Forecasting | Method | Evaluation |
|---|---|---|---|
| Ying-Yi Hong et al. [15] | 24 h ahead wind power forecasting | Hybrid deep learning-based neural network | R2 = 0.8789 (summer), 0.8974 (fall), 0.9012 (spring) and 0.9125 (winter). |
| C. Gallego et al. [16] | 10 min forecasting | AR model, CPARX and TARSO models | CPARX (wind direction, wind speed) model—NRMSE ranged from 3.91 to 5.82. AR Model—NRMSE ranged from 3.96 to 6.03. TARSO (wind speed)—NRMSE ranged from 3.93 to 5.94. |
| Kim et al. [21] | Daily wind power generation (hourly) | ANN, kNN, RF, and SVR | R2 varied from 0.97 to 0.98. |
| Tyass et al. [22] | Medium-term forecasting | Forecasted the wind speed by combining the statistical SARIMA model with the deep neural network model. | MAPE ranged from 10.50% to 15.94% for LSTM model and 10.67% to 16.10 for SARIMA model. |
| R Kaja Bantha Navas et al. [23] | Medium-term forecasting | Developed the categorical regression (CATREG) model, multilayer perception neural network (MLPNN) model, and RBFNN model for predicting wind speed | MSE for MLPNN is 195.417, RBFNN is 3853.775, and for CATREG is 5598.937. |
| Amroune et al. [24] | Short-term wind power forecasting | Employed hybrid strategy that is based on support vector regression and the bald eagle search optimizer | R value 0.94574. |
| Ling-ling Li et al. [25] | Short-term wind power prediction | Developed the hybrid improved cuckoo search arithmetic—support vector regression machine (HICS-SVR) | The regression fitting degree of the HICS-SVR is obtained under the condition of 100 iterations, with an average of 0.87 and an optimal value of 0.98. |
| Liu, et al. [26] | Short-term wind power forecasting | Employed bidirectional long short-term memory network (BiLSTM) | For wind farm A, RMSE as 0.9518 and MAPE as 2.3593. For wind farm B, RMSE as 0.8537 and MAPE as 3.1740. |
| Xu, P et al. [27] | A day-ahead wind power short-term prediction model | Employed discrete wavelet transform—autoencoder—BiLSTM | MAPE as 10.94 for wind farm #1, 13.30 for wind farm #2, 12.01 for wind farm #3. |
| Miele et al. [28] | Multihorizon wind power forecasting model | A neural architecture based on stacked recurrent neural networks is proposed | The proposed model improved the XGBoost baseline with an average skill score of 25.1%. |
| Zhu et al. [29] | Ultra-short-term wind power combined prediction model | Complementary ensemble empirical mode decomposition and the Elman neural network model | The RMSE as 13.2642, MAE as 11.6409 and MAPE as 2.4158. |
| Lin et al. [30] | Employed deep learning algorithm-based medium-term prediction | Temporal convolutional network | MAPE as 5%. |
| Index | Count | Mean | Std | Min | 25% | 50% | 75% | Max |
|---|---|---|---|---|---|---|---|---|
| AmbientTemperatue | 93,817 | 28.77 | 4.37 | 0 | 25.63 | 28.34 | 31.66 | 42.41 |
| BearingShaftTemperature | 62,518 | 43.01 | 5.55 | 0 | 39.84 | 42.91 | 47.01 | 55.09 |
| Blade1PitchAngle | 41,996 | 9.75 | 20.64 | −43.16 | −0.94 | 0.39 | 8.10 | 90.14 |
| Blade2PitchAngle | 41,891 | 10.04 | 20.27 | −26.44 | −0.43 | 0.89 | 8.48 | 90.02 |
| Blade3PitchAngle | 41,891 | 10.04 | 20.27 | −26.44 | −0.43 | 0.89 | 8.48 | 90.02 |
| ControlBoxTemperature | 62,160 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| GearboxBearingTemperature | 62,540 | 64.23 | 10.46 | 0 | 57.87 | 64.83 | 71.08 | 82.24 |
| GearboxOilTemperature | 62,438 | 57.56 | 6.32 | 0 | 53.94 | 57.20 | 61.31 | 70.76 |
| GeneratorRPM | 62,295 | 1102.03 | 528.06 | 0 | 1029.81 | 1124.86 | 1515.40 | 1809.94 |
| GeneratorWinding1Temperature | 62,427 | 72.46 | 22.63 | 0 | 55.49 | 65.79 | 85.87 | 126.77 |
| GeneratorWinding2Temperature | 62,449 | 71.83 | 22.65 | 0 | 54.76 | 65.00 | 85.34 | 126.04 |
| HubTemperature | 62,406 | 36.90 | 5.18 | 0 | 33.94 | 37.00 | 40.01 | 48.00 |
| MainBoxTemperature | 62,507 | 39.55 | 5.73 | 0 | 35.81 | 39.49 | 43.36 | 54.25 |
| NacellePosition | 72,278 | 196.29 | 88.30 | 0 | 145 | 182 | 271 | 357 |
| ReactivePower | 94,748 | 88.13 | 116.60 | −203.18 | −0.43 | 35.88 | 147.36 | 403.71 |
| RotorRPM | 62,127 | 9.91 | 4.72 | 0 | 9.23 | 10.10 | 13.60 | 16.27 |
| TurbineStatus | 62,908 | 2280.43 | 358,603.39 | 0 | 2 | 2 | 2 | 65,746,528 |
| WindDirection | 72,278 | 196.29 | 88.30 | 0 | 145 | 182 | 271 | 357 |
| WindSpeed | 94,595 | 5.88 | 2.62 | 0 | 3.82 | 5.56 | 7.51 | 22.97 |
| ActivePower | 94,750 | 619.11 | 611.28 | −38.52 | 79.64 | 402.65 | 1074.59 | 1779.03 |
| Wind Power Category | Wind Speed (m/s) |
|---|---|
| Superb | >8.8 |
| Outstanding | 8 to 8.8 |
| Excellent | 7.5 to 8 |
| Good | 7 to 7.4 |
| Fair | 6.4 to 7 |
| Marginal | 5.6 to 6.3 |
| Poor | <5.6 |
| ML Algorithm | Training Set (25,202, 16) | Test Set (6301, 16) | ||||||
|---|---|---|---|---|---|---|---|---|
| MAE | MSE | RMSE | R-Squared | MAE | MSE | RMSE | R-Squared | |
| LightGBM | 6.034 | 118.21 | 10.87 | 0.999 | 7.01 | 248.44 | 15.7 | 0.999 |
| Random Forest | 2.34 | 27.94 | 5.28 | 0.999 | 6.462 | 268.13 | 16.37 | 0.999 |
| CatBoost | 6.339 | 88.44 | 9.404 | 0.999 | 7.781 | 191.57 | 13.84 | 0.999 |
| XGBoost | 9.692 | 307.66 | 17.54 | 0.999 | 10.431 | 415.85 | 20.39 | 0.998 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ponkumar, G.; Jayaprakash, S.; Kanagarathinam, K. Advanced Machine Learning Techniques for Accurate Very-Short-Term Wind Power Forecasting in Wind Energy Systems Using Historical Data Analysis. Energies 2023, 16, 5459. https://doi.org/10.3390/en16145459
Ponkumar G, Jayaprakash S, Kanagarathinam K. Advanced Machine Learning Techniques for Accurate Very-Short-Term Wind Power Forecasting in Wind Energy Systems Using Historical Data Analysis. Energies. 2023; 16(14):5459. https://doi.org/10.3390/en16145459
Chicago/Turabian StylePonkumar, G., S. Jayaprakash, and Karthick Kanagarathinam. 2023. "Advanced Machine Learning Techniques for Accurate Very-Short-Term Wind Power Forecasting in Wind Energy Systems Using Historical Data Analysis" Energies 16, no. 14: 5459. https://doi.org/10.3390/en16145459
APA StylePonkumar, G., Jayaprakash, S., & Kanagarathinam, K. (2023). Advanced Machine Learning Techniques for Accurate Very-Short-Term Wind Power Forecasting in Wind Energy Systems Using Historical Data Analysis. Energies, 16(14), 5459. https://doi.org/10.3390/en16145459






