Numerical Investigation of a Solar-Heating System with Solar-Tower Receiver and Seasonal Storage in Northern China: Dynamic Performance Assessment and Operation Strategy Analysis
Abstract
:1. Introduction
- The system’s dynamical performance was analyzed with a dynamic simulated method in typical-day or typical-operation modes, and the switch mechanism between multiple operation modes was revealed on a minute timescale;
- The system can reach a higher system performance with the proposed control strategies under different operation stages;
- The impacts of different heating operation strategies on the system performance were quantified. The performance indicators included the collection efficiency, storage efficiency, solar fraction of the system, and consumption of the circulation pump on the heating side.
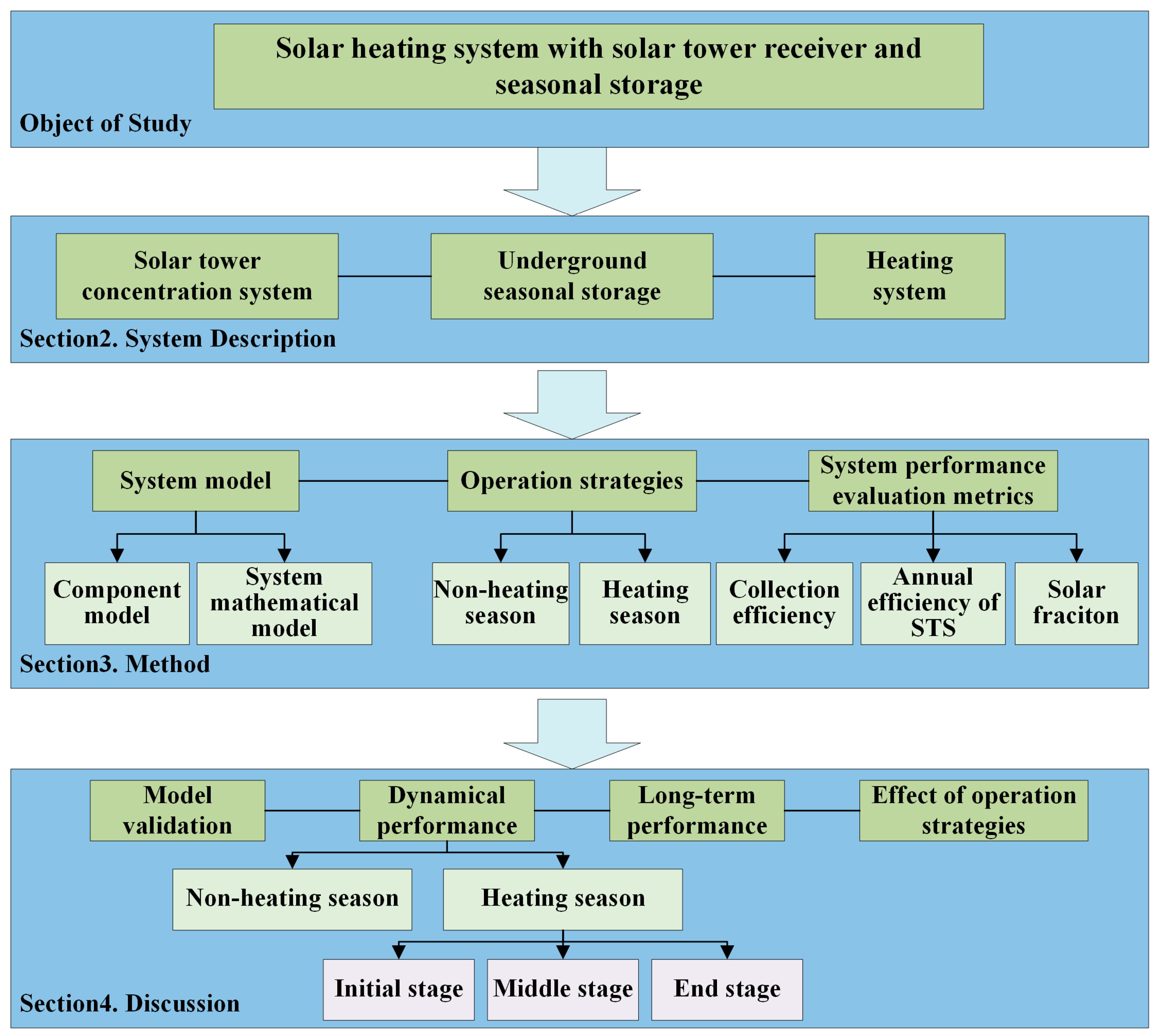
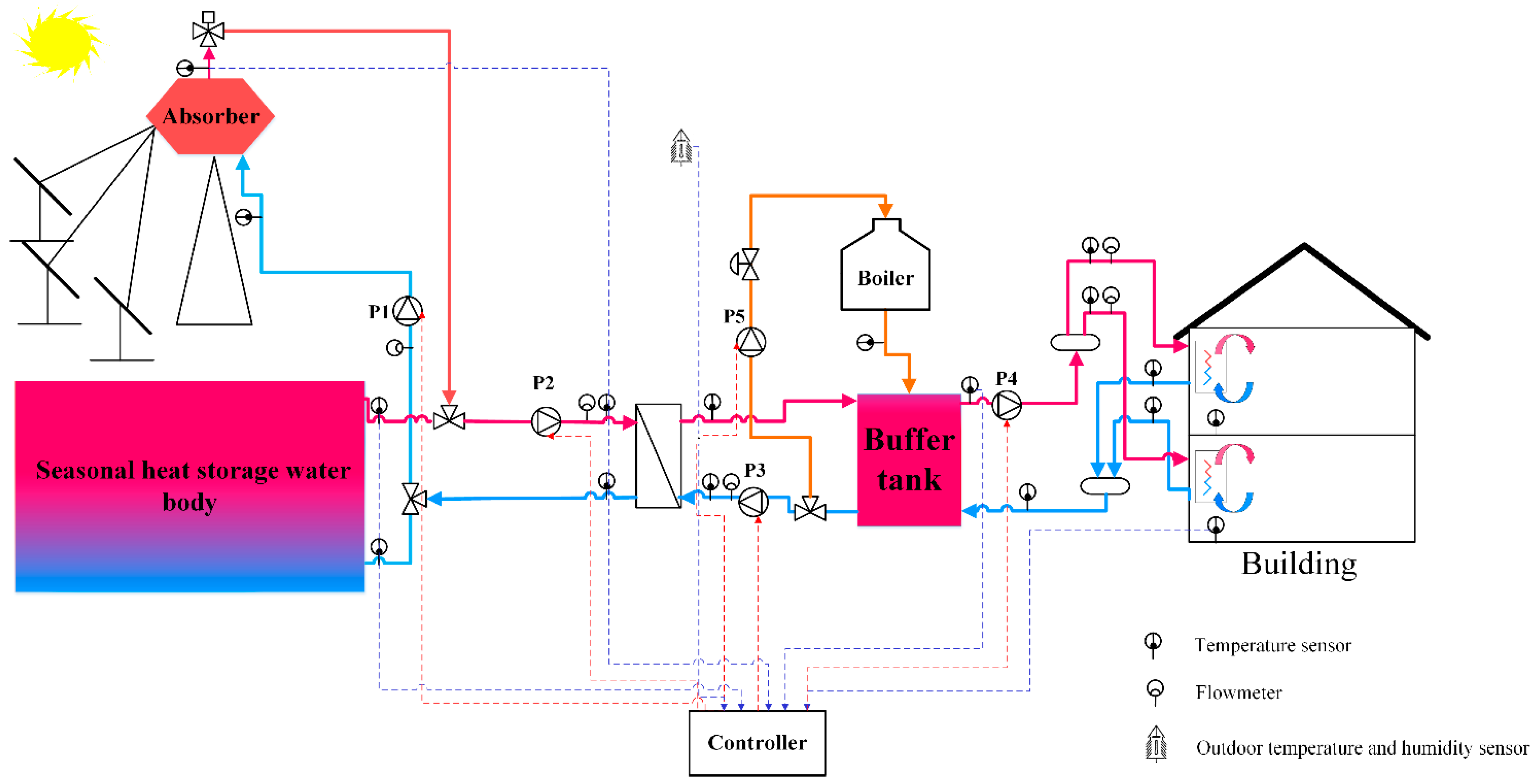
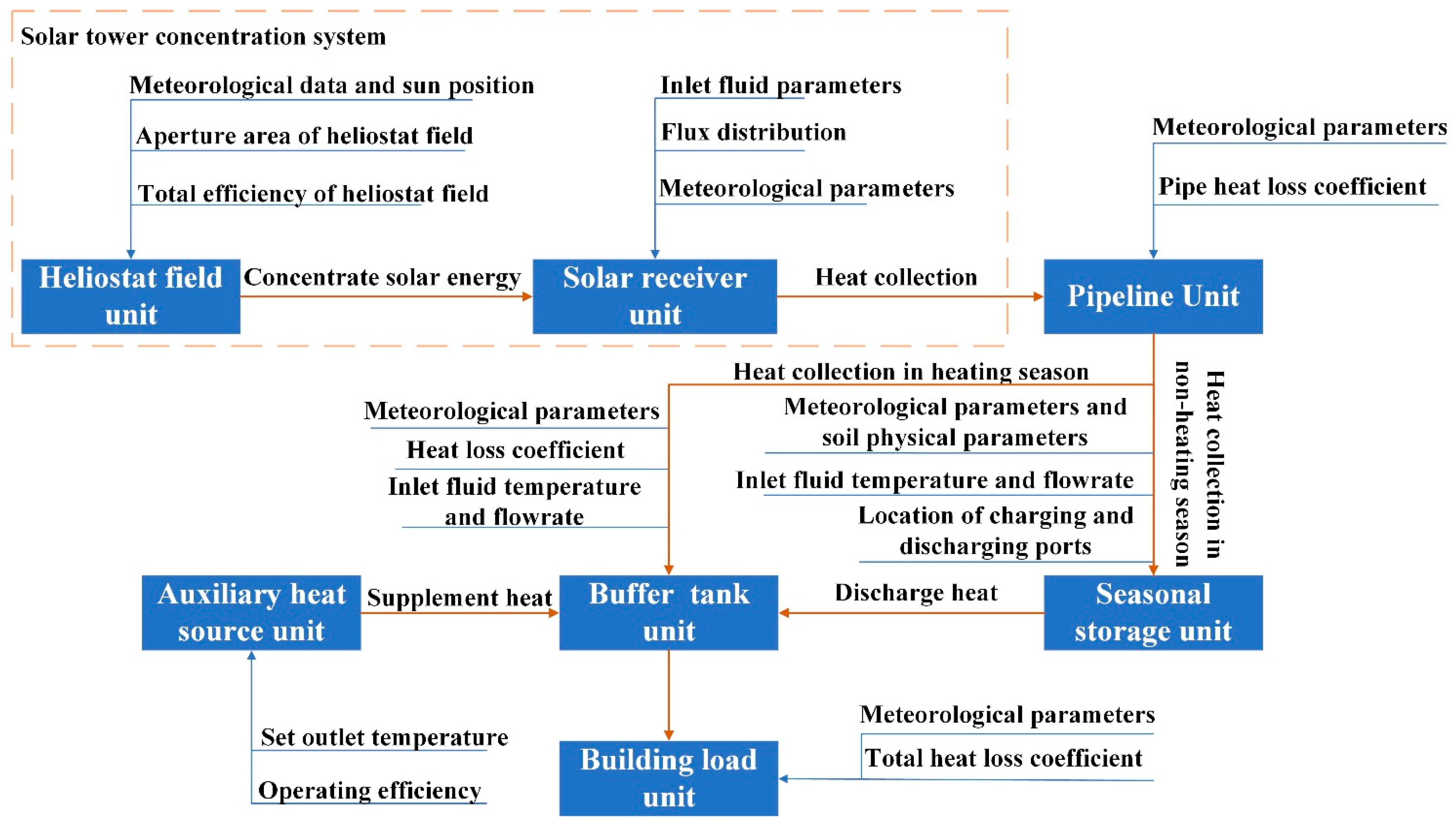
2. System Description
3. Methodology
3.1. System Model
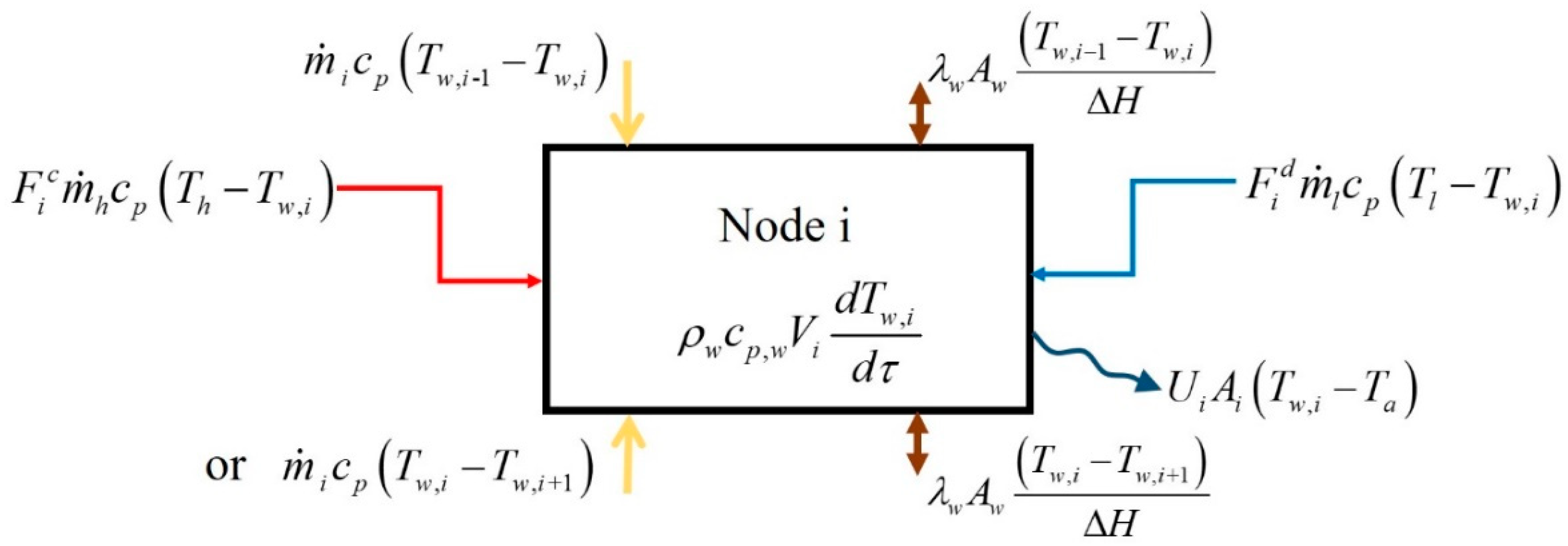
3.1.1. The Model of STS and the Solar-Receiver Model
3.1.2. Circulation-Pump Model
3.1.3. Buffer-Tank Model
3.1.4. Building-load model
3.1.5. Mathematical Model of the Whole System
3.2. Operation Strategies
3.2.1. Operation Strategy in the Non-Heating Season
3.2.2. Operation Strategy in the Heating Season
3.3. System Performance Evaluation Metrics
4. Discussion
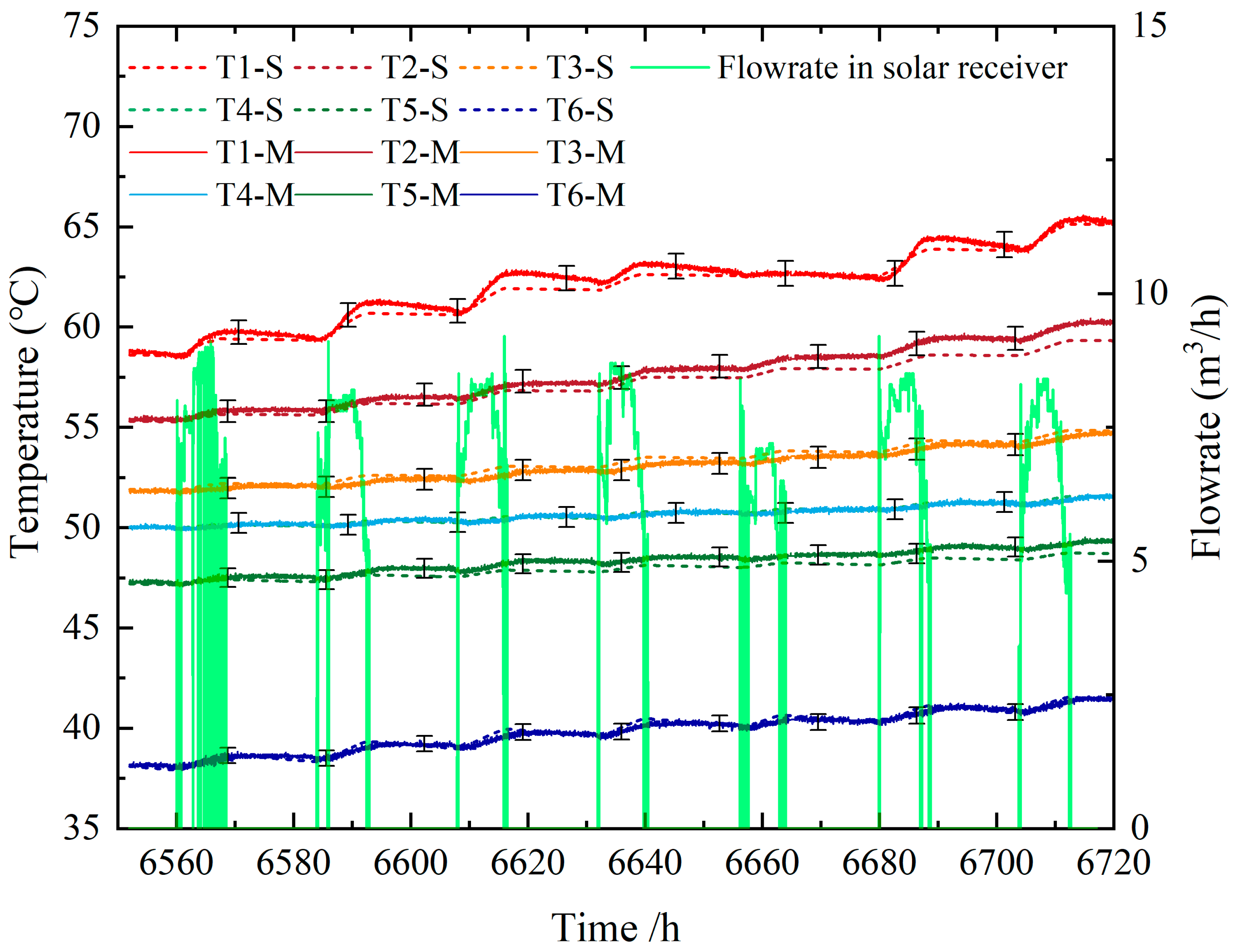
4.1. Model Validation
4.2. Dynamical Performance of the System
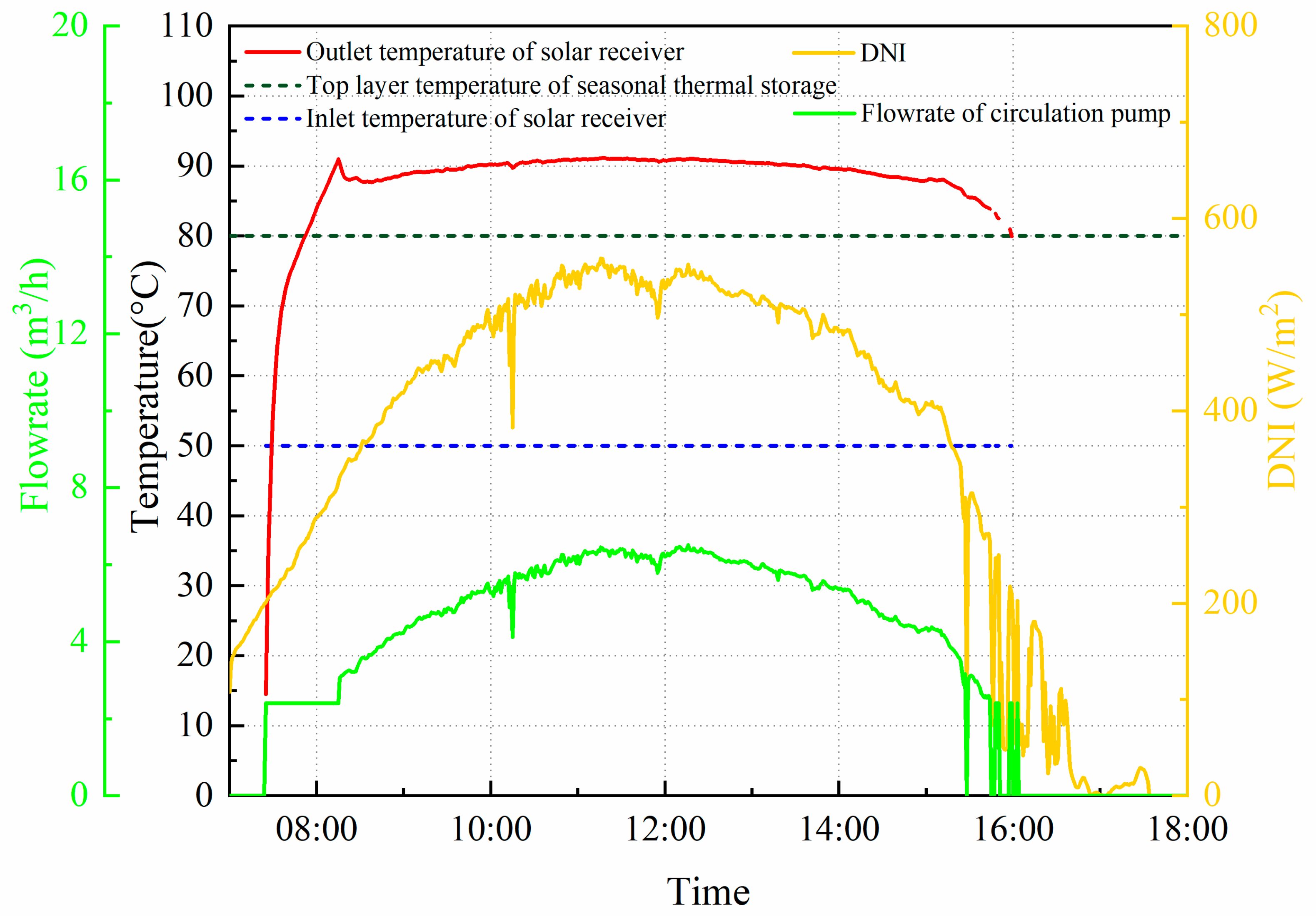
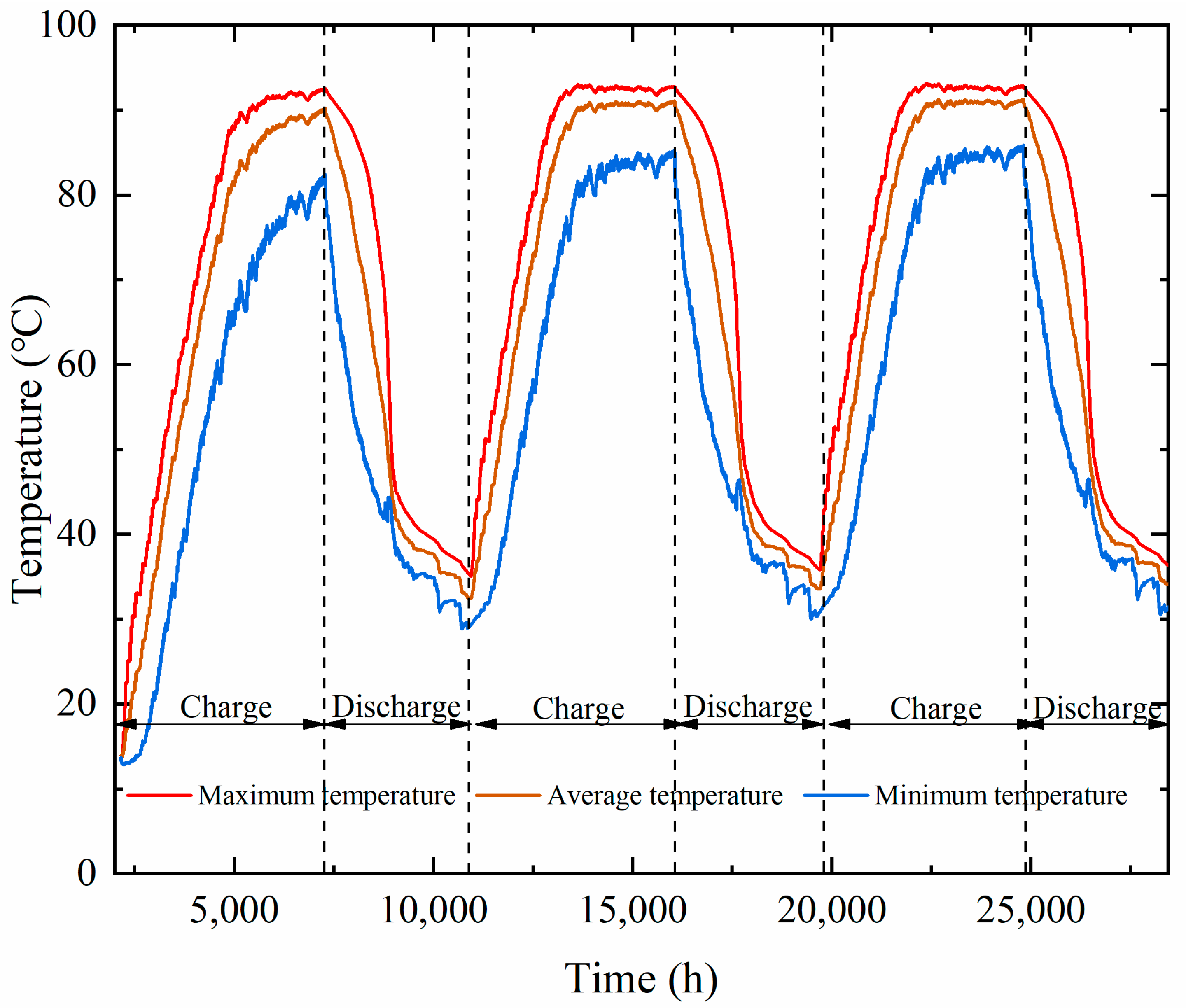
4.2.1. Dynamic Characteristic Analysis of Typical Working Conditions in the Non-Heating Season
4.2.2. Dynamic Characteristic Analysis of Typical Working Conditions in the Heating Season
- 1.
- In the initial stage of the heating season
- 2.
- In the middle stage of the heating season
- 3.
- At the end of the heating season
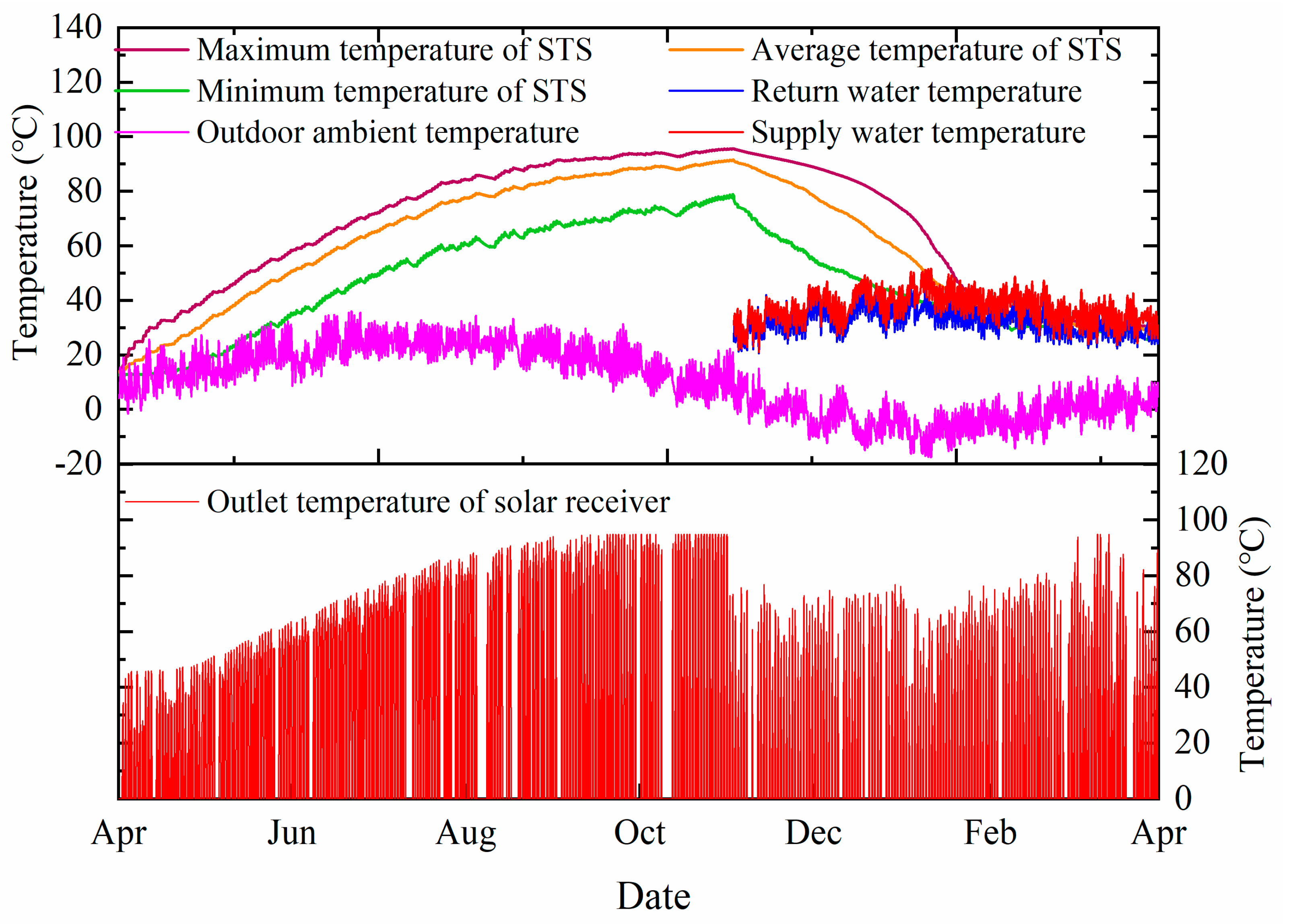
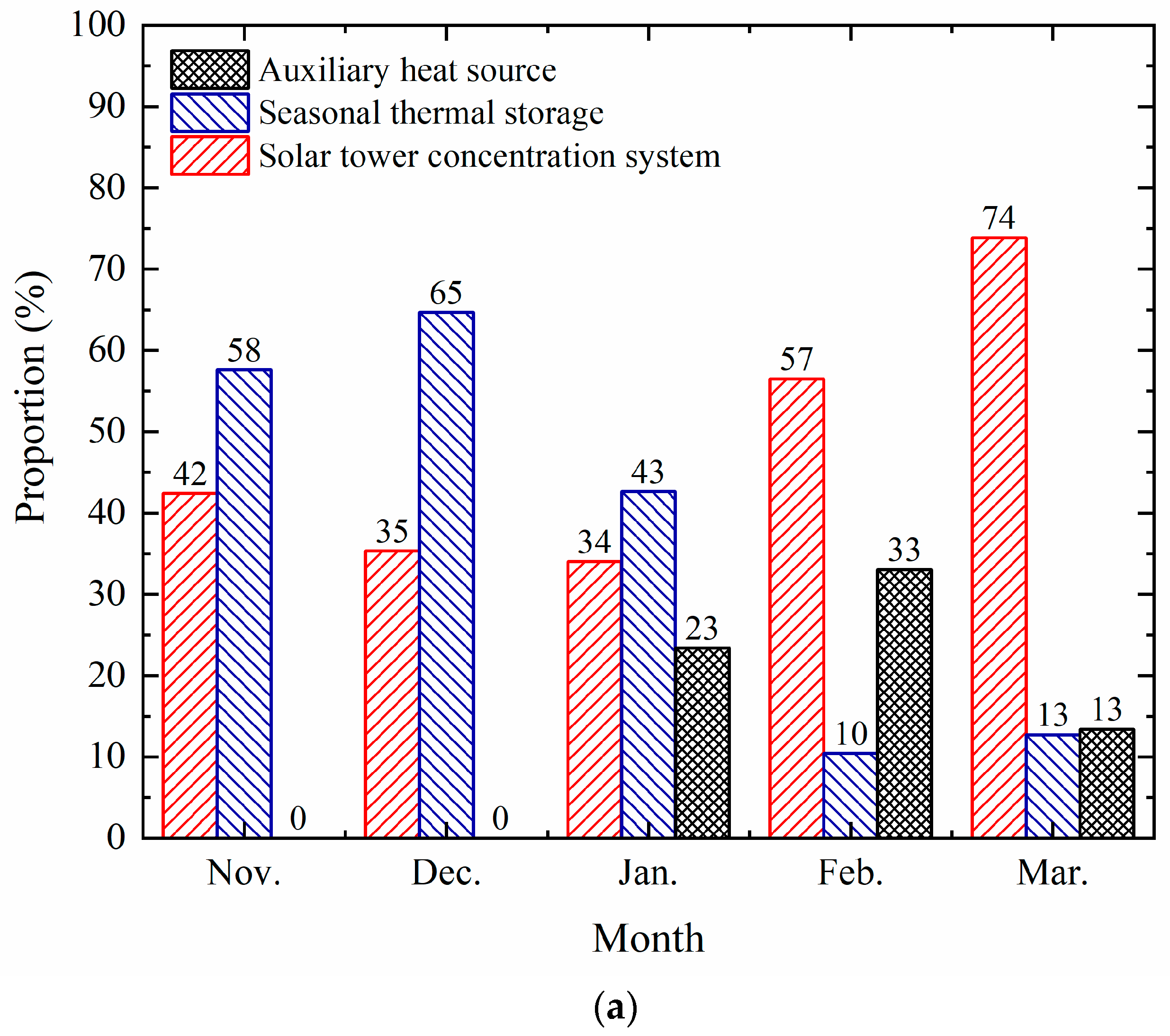
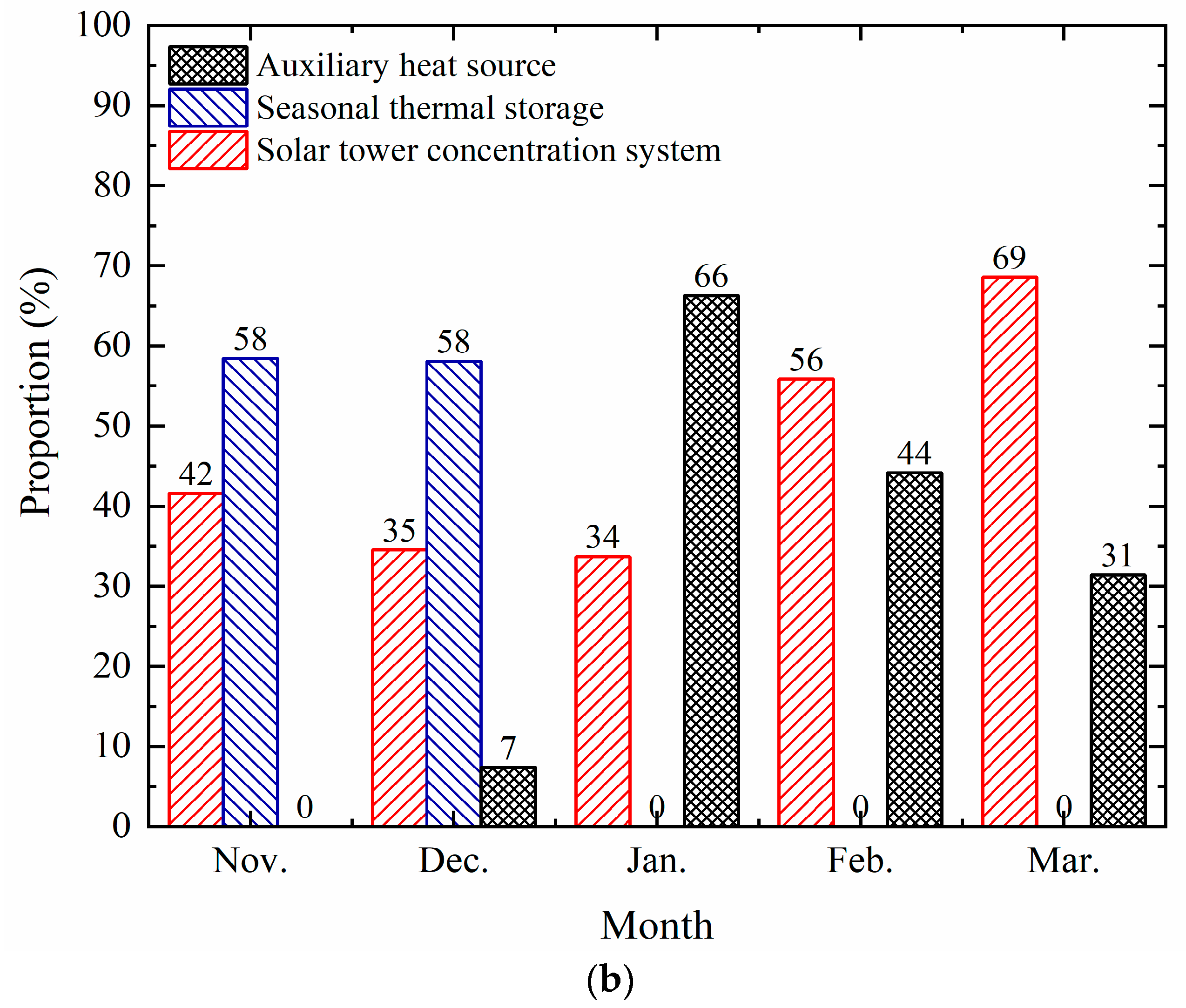
4.3. Long-Term Performance of the System
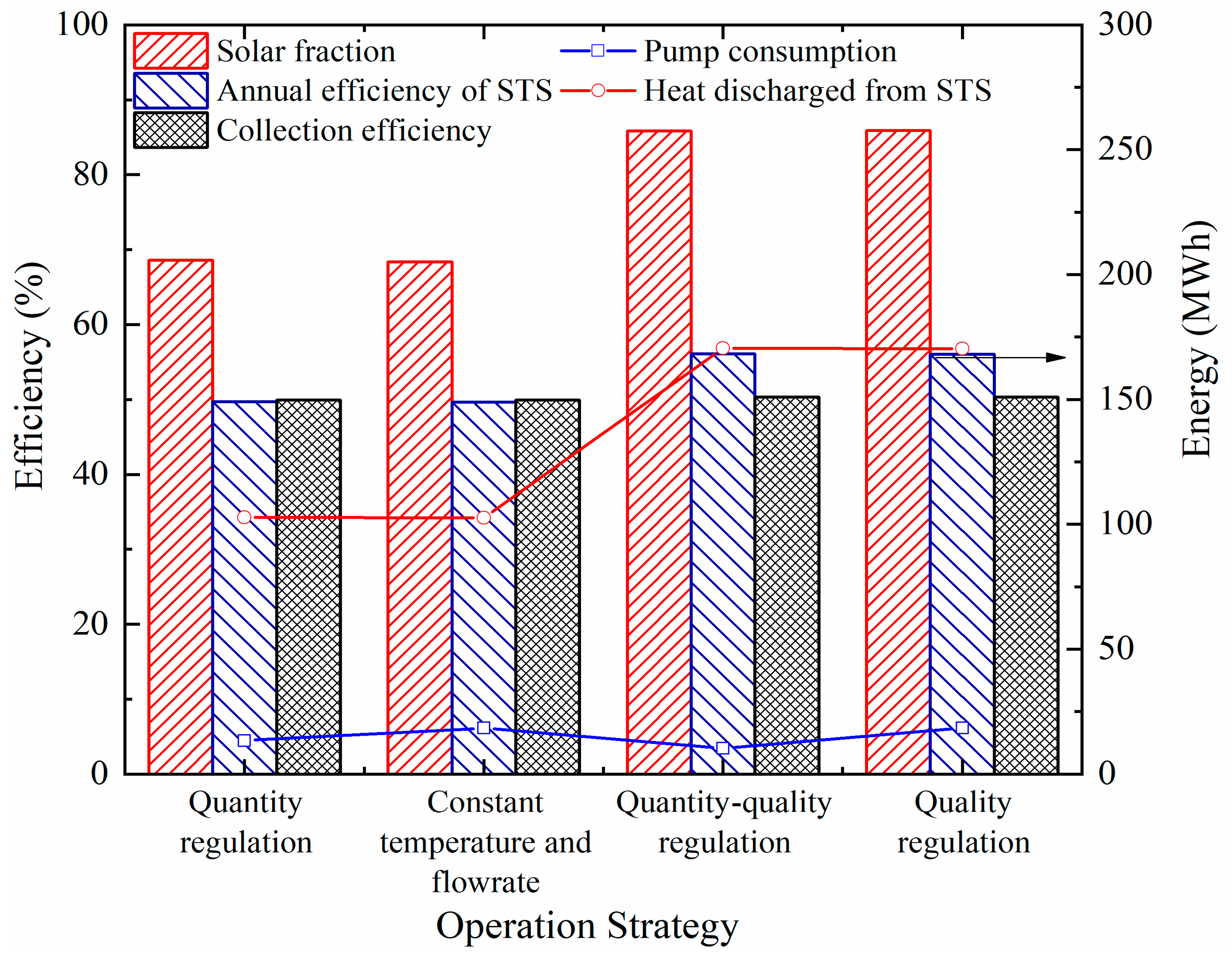
4.4. Effects of Operation Strategies
5. Conclusions
- (1)
- The solar-heating system with STS in our study had an outstanding performance at different time scales. Through the switching of multiple operation modes, the system can operate stably and continuously under fluctuations in solar radiation resources and the heat demand. The significant mismatch between the solar energy and heat load in northern China can be resolved;
- (2)
- The quality–quantity operation strategies are effective ways to improve the discharge efficiency of the STS and the system performance without a heat pump to utilize the thermal energy stored in the STS when the temperature of the STS is below the traditional heating-supply temperature. The annual solar fraction of the system could reach 85.9%, and the annual efficiency of the STS was 56.1%. The electricity consumption of the pump on the heating side could be significantly reduced by 44.6% compared with the quality control;
- (3)
- The solar fraction of the system was gradually improved. The solar fraction of the system reached 89.4% in the third year, which was 3.6% higher than that in the first year. Although the solar-tower collection system can improve the collection efficiency at a higher temperature, the operational temperature still affects the system performance, especially in the third year. Thus, reasonable control strategies for the whole system should be analyzed in different time dimensions, such as the long-term period;
- (4)
- In order to promote the development of solar-heating systems with STS, scientific design methods for system configuration and operation strategies need to be addressed in the future. Based on perfect forecasts of the weather and SDH loads, the development of optimized control strategies is the focus of future research.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Latin characters | |
| A | Area, m2 |
| C | Heat capacity, kJ/(h·k) |
| CAP | Effective lumped-heat capacity of building, kJ/K |
| Specific heat capacity, J/kg·K | |
| Control function | |
| F | Flowrate, m3/h |
| H | Height, m |
| Normal direct irradiance, W/m2 | |
| m | Mass flowrate, kg/h |
| M | Mass, kg |
| N | Number |
| P | Power, kJ/h |
| Q | Heat, J |
| T | Temperature, °C |
| Heat-loss coefficient, W/ (m2 °C) | |
| UA | Heat-loss coefficient of the building, kJ/(h·K) |
| V | Volume, m3 |
| Abbreviations | |
| STS | Seasonal thermal storage |
| SGHP | Solar and ground-source heat-pump system |
| DNI | Direct normal irradiance |
| SGSP | Salt-gradient solar pond |
| UGSTS | Underground seasonal thermal storage |
| SF | Solar fraction |
| RMSD | Root-mean-square deviation |
| ARE | Average relative error |
| MRE | Maximum relative error |
| Subscripts | |
| a | Ambient |
| abs | Effective heat absorption |
| aux | Auxiliary heat source |
| b | Buffer tank |
| col | Heat collected by solar receiver |
| charge | Charge into the STS |
| discharge | Heat discharged from the STS |
| exp | Experiment |
| h | Heat source/heliostat field |
| i | Natural numbers from 1 to n |
| in | Inflow |
| inc | Incident energy on the solar receiver |
| gain | Increment |
| l, load | Load side |
| max | Maximum |
| min | Minimum |
| out | Outflow |
| p | Pump |
| r | Room |
| rec | Receiver |
| Solar | Solar-tower concentration system |
| S, s | Seasonal storage |
| sim | Simulation |
| w | Water |
| Greek character | |
| Heat-exchange efficiency | |
| Density, kg/m³ | |
| Time, s | |
| Thermal conductivity, W/m/°C | |
References
- Annual Development Research Report on Building Energy Efficiency in China 2022; Tsinghua University Building Energy Efficiency Research Center: Beijing, China, 2022; pp. 1–23.
- Rghif, Y.; Zeghmati, B.; Bahraoui, F. Numerical Analysis of the Influence of Buoyancy Ratio and Dufour Parameter on Thermosolutal Convection in a Square Salt Gradient Solar Pond. Fluid Dyn. Mater. Process. 2022, 18, 1319–1329. [Google Scholar] [CrossRef]
- Rghif, Y.; Zeghmati, B.; Bahraoui, F. Modeling the Influences of a Phase Change Material and the Dufour Effect on Thermal Performance of a Salt Gradient Solar Pond. Int. J. Therm. Sci. 2021, 166, 106979. [Google Scholar] [CrossRef]
- Rghif, Y.; Bahraoui, F.; Zeghmati, B. Experimental and Numerical Investigations of Heat and Mass Transfer in a Salt Gradient Solar Pond under a Solar Simulator. Sol. Energy 2022, 236, 841–859. [Google Scholar] [CrossRef]
- Rghif, Y.; Colarossi, D.; Principi, P. Effects of Double-Diffusive Convection on Calculation Time and Accuracy Results of a Salt Gradient Solar Pond: Numerical Investigation and Experimental Validation. Sustainability 2023, 15, 1479. [Google Scholar] [CrossRef]
- Tosatto, A.; Dahash, A.; Ochs, F. Simulation-Based Performance Evaluation of Large-Scale Thermal Energy Storage Coupled with Heat Pump in District Heating Systems. J. Energy Storage 2023, 61, 106721. [Google Scholar] [CrossRef]
- Narula, K.; De Oliveira, F.; Villasmil, W.; Patel, M.K. Simulation Method for Assessing Hourly Energy Fl Ows in District Heating System with Seasonal Thermal Energy Storage. Renew. Energy 2020, 151, 1250–1268. [Google Scholar] [CrossRef]
- Ushamah, H.M.; Ahmed, N.; Elfeky, K.E.; Mahmood, M.; Qaisrani, M.A.; Waqas, A.; Zhang, Q. Techno-Economic Analysis of a Hybrid District Heating with Borehole Thermal Storage for Various Solar Collectors and Climate Zones in Pakistan. Renew. Energy 2022, 199, 1639–1656. [Google Scholar] [CrossRef]
- Kim, M.H.; Kim, D.; Heo, J.; Lee, D.W. Techno-Economic Analysis of Hybrid Renewable Energy System with Solar District Heating for Net Zero Energy Community. Energy 2019, 187, 115916. [Google Scholar] [CrossRef]
- Chu, S.; Sethuvenkatraman, S.; Goldsworthy, M.; Yuan, G. Techno-Economic Assessment of Solar Assisted Precinct Level Heating Systems with Seasonal Heat Storage for Australian Cities. Renew. Energy 2022, 201, 841–853. [Google Scholar] [CrossRef]
- Renaldi, R.; Friedrich, D. Techno-Economic Analysis of a Solar District Heating System with Seasonal Thermal Storage in the UK. Appl. Energy 2019, 236, 388–400. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Nielsen, E.; Fan, J.; Furbo, S. Thermal Behavior of a Combi-Storage in a Solar-Ground Source Heat Pump System for a Single-Family House. Energy Build. 2022, 259, 111902. [Google Scholar] [CrossRef]
- Maragna, C.; Rey, C.; Perreaux, M. A Novel and Versatile Solar Borehole Thermal Energy Storage Assisted by a Heat Pump. Part 1: System Description. Renew. Energy 2023, 208, 709–725. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Li, J.; Yang, M.; Yuan, G.; Bai, Y. Comparison of Control Strategies for a Solar Heating System with Underground Pit Seasonal Storage in the Non-Heating Season. J. Energy Storage 2019, 26, 100963. [Google Scholar] [CrossRef]
- Villasmil, W.; Troxler, M.; Hendry, R.; Schuetz, P.; Worlitschek, J. Control Strategies of Solar Heating Systems Coupled with Seasonal Thermal Energy Storage in Self-Sufficient Buildings. J. Energy Storage 2021, 42, 103069. [Google Scholar] [CrossRef]
- Wang, Y.; Rao, Z.; Liu, J.; Liao, S. An Optimized Control Strategy for Integrated Solar and Air-Source Heat Pump Water Heating System with Cascade Storage Tanks. Energy Build. 2020, 210, 109766. [Google Scholar] [CrossRef]
- Zhao, J.; Lyu, L.; Li, X. Numerical Analysis of the Operation Regulation in a Solar Heating System with Seasonal Water Pool Thermal Storage. Renew. Energy 2020, 150, 1118–1126. [Google Scholar] [CrossRef]
- Tian, Z.; Perers, B.; Furbo, S.; Fan, J. Annual Measured and Simulated Thermal Performance Analysis of a Hybrid Solar District Heating Plant with Flat Plate Collectors and Parabolic Trough Collectors in Series. Appl. Energy 2017, 205, 417–427. [Google Scholar] [CrossRef] [Green Version]
- Bai, Y.; Wang, Z.; Fan, J.; Yang, M.; Li, X.; Chen, L.; Yuan, G.; Yang, J. Numerical and Experimental Study of an Underground Water Pit for Seasonal Heat Storage. Renew. Energy 2020, 150, 487–508. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Li, J.; Chen, L.; Bai, Y.; Yang, M.; Guo, M.; Sun, F.; Yuan, G. Numerical and Experimental Study of a Concentrated Solar Thermal Receiver for a Solar Heating System with Seasonal Storage. Int. J. Energy Res. 2021, 45, 7588–7604. [Google Scholar] [CrossRef]
- GB/T18708-2002; Test Methods for Thermal Performance of Domestic Solar Water Heating System. General Administration of Quality Supervision, Inspection and Quarantine of the China: Beijing, China, 2002.
- University of Wisconsin-Madison. Volume 4: Mathematical Reference. In TRNSYS 17 Manual; Solar Energy Laboratory, University of Wisconsin-Madison: Madison, WI, USA, 2009. [Google Scholar]
- Pahud, D. Central solar heating plants with seasonal duct storage and short-term water storage: Design guidelines obtained by dynamic system simulations. Sol. Energy 2000, 69, 495–509. [Google Scholar] [CrossRef]
- Xiaoxia, L.; Zhifeng, W.; Jinping, L.; Yang, M.; Bai, Y.; Chen, L. Space Heating Management for Solar Heating System with Underground Pit Storage; Springer: Singapore, 2020; Volume III, ISBN 9789811395277. [Google Scholar]
- Ciampi, G.; Rosato, A.; Sibilio, S. Thermo-Economic Sensitivity Analysis by Dynamic Simulations of a Small Italian Solar District Heating System with a Seasonal Borehole Thermal Energy Storage. Energy 2018, 143, 757–771. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the Uncertainties in Experimental Results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef] [Green Version]

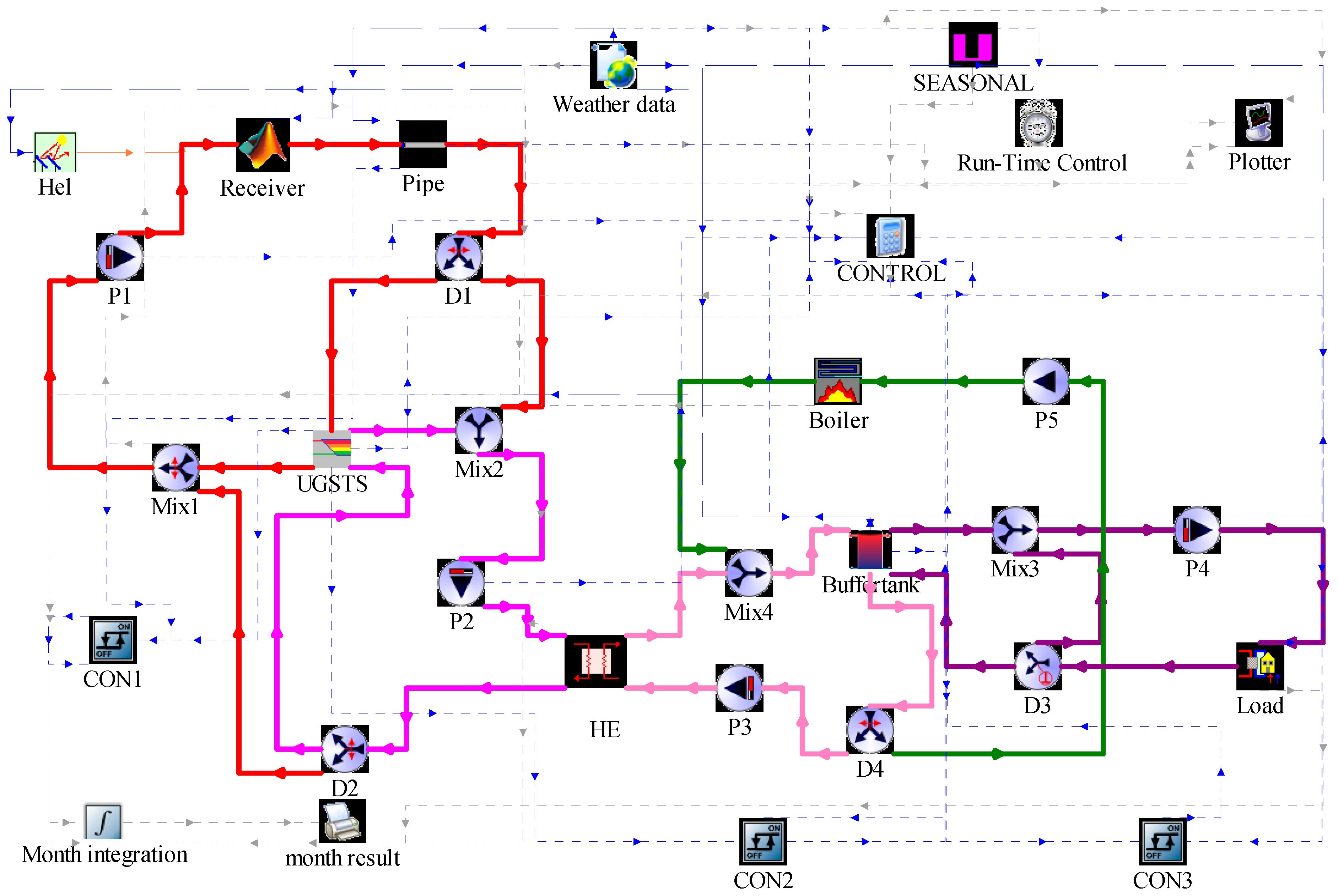








| Program | Property | Quantity | Unit |
|---|---|---|---|
| Location | Latitude | 40.23 N | ° |
| Longitude | 115.43 E | ° | |
| Heliostat field | Number of heliostats | 66 | |
| Area of heliostats | 11.2 | m2 | |
| Reflectivity | 0.9 | ||
| Solar receiver | Daylighting area | 4.76 | m2 |
| Buffer tank | Volume | 48 | m3 |
| Seasonal thermal storage | Volume | 3000 | m3 |
| Heat exchanger | Area | 30 | m2 |
| Project | Name | Type | Notes |
|---|---|---|---|
| Meteorological parameters | Weather data | Type 15-3 | Calling in typical annual meteorological data of Huailai obtained from the EnergyPlus website |
| Heliostat field | Hel | Type 394 | Calling in instantaneous efficiency of the heliostat field |
| Receiver | Receiver | Type 155 | Calling in structural parameters and mathematical models in MATLAB |
| Circulating pump | P (1~5) | Type 110 | Inputting of the power curve of each circulation pump |
| Underground seasonal thermal storage | UGSTS | Type 207 | Self-developed model |
| Buffer tank | Buffer tank | Type 531 | Measured heat-loss coefficient: 0.34 W/(m2·°C) |
| Operation control unit | CON (1~3) | Type 2b | Temperature-difference control |
| CONTROL | Calculator | Logical control | |
| Data display or output | Plotter | Type 65d | Display of results |
| Month result | Type 25c | Output of results | |
| Diversion valve | D (1~4) | Type 11f | Switch between different circulation routes |
| Mixing valve | M (1~4) | Type 11d | Switch between different circulation routes |
| Heat exchanger | HE | Type 5b | Counterflow, average heat-transfer coefficient: 100 W/K per m2 of collector area [23] |
| Building load | LOAD | Type 12c | Heat load per unit of heating area: 40 W/m2 |
| Heating season controller | SEASONAL | Type 14 | The heating season is from November 1st to April 1st of the following year |
| Auxiliary fuel boiler | Boiler | Type 700 | Rated power: 170 kW; boiler efficiency: 0.9 |
| Temperature-control diverter valve | D5 | Type 11b | The water-supply temperature can reach the set temperature by mixing the supply and return water |
| Location | RMSD (°C) | ARE (%) | MRE (%) |
|---|---|---|---|
| T1 (4.25 m from STS bottom) | 1.10 | 0.42 | 1.52 |
| T2 (3.45 m from STS bottom) | 1.54 | 0.75 | 1.85 |
| T3 (2.65 m from STS bottom) | 0.79 | 0.45 | 0.28 |
| T4 (1.85 m from STS bottom) | 0.32 | 0.03 | 0.57 |
| T5 (1.05 m from STS bottom) | 1.23 | 0.75 | 1.63 |
| T6 (0.25 m from STS bottom) | 0.50 | 0.12 | 0.92 |
| Inlet temperature of receiver | 1.12 | 2.49 | 6.0 |
| Outlet temperature of receiver | 3.01 | 2.57 | 9.8 |
| Measurement Device | Type | Range | Accuracy |
|---|---|---|---|
| Temperature sensor | PT100 | 0~100 °C | ±0.5 °C |
| Vortex flowmeter | HH-HYBLWGY-50 | 0~25 m3/h | ±1.0% |
| Parameter | Type of Data | Unit | Relative Error |
|---|---|---|---|
| Average inlet temperature of solar receiver | Measured | °C | 3.783% |
| Average outlet temperature of solar receiver | Measured | °C | 2.049% |
| Average flowrate | Measured | m3/h | 1.058% |
| Average temperature of STS | Measured | °C | 0.983% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Qiu, H.; Wang, Z.; Li, J.; Yuan, G.; Guo, X.; Jin, L. Numerical Investigation of a Solar-Heating System with Solar-Tower Receiver and Seasonal Storage in Northern China: Dynamic Performance Assessment and Operation Strategy Analysis. Energies 2023, 16, 5505. https://doi.org/10.3390/en16145505
Li X, Qiu H, Wang Z, Li J, Yuan G, Guo X, Jin L. Numerical Investigation of a Solar-Heating System with Solar-Tower Receiver and Seasonal Storage in Northern China: Dynamic Performance Assessment and Operation Strategy Analysis. Energies. 2023; 16(14):5505. https://doi.org/10.3390/en16145505
Chicago/Turabian StyleLi, Xiaoxia, Husheng Qiu, Zhifeng Wang, Jinping Li, Guobin Yuan, Xiao Guo, and Lifeng Jin. 2023. "Numerical Investigation of a Solar-Heating System with Solar-Tower Receiver and Seasonal Storage in Northern China: Dynamic Performance Assessment and Operation Strategy Analysis" Energies 16, no. 14: 5505. https://doi.org/10.3390/en16145505
APA StyleLi, X., Qiu, H., Wang, Z., Li, J., Yuan, G., Guo, X., & Jin, L. (2023). Numerical Investigation of a Solar-Heating System with Solar-Tower Receiver and Seasonal Storage in Northern China: Dynamic Performance Assessment and Operation Strategy Analysis. Energies, 16(14), 5505. https://doi.org/10.3390/en16145505





