Experimental and Numerical Studies on a Single Coherent Blade of a Vertical Axis Carousel Wind Rotor
Abstract
:1. Introduction
1.1. Movement of the Single Blade of the Carousel Wind Rotor
1.2. Procedure for Calculating Propelling Torque
2. Materials and Methods
2.1. Cross-Section of the Carousel Wind Rotor Blade
2.2. Wind Tunnel Test Conditions
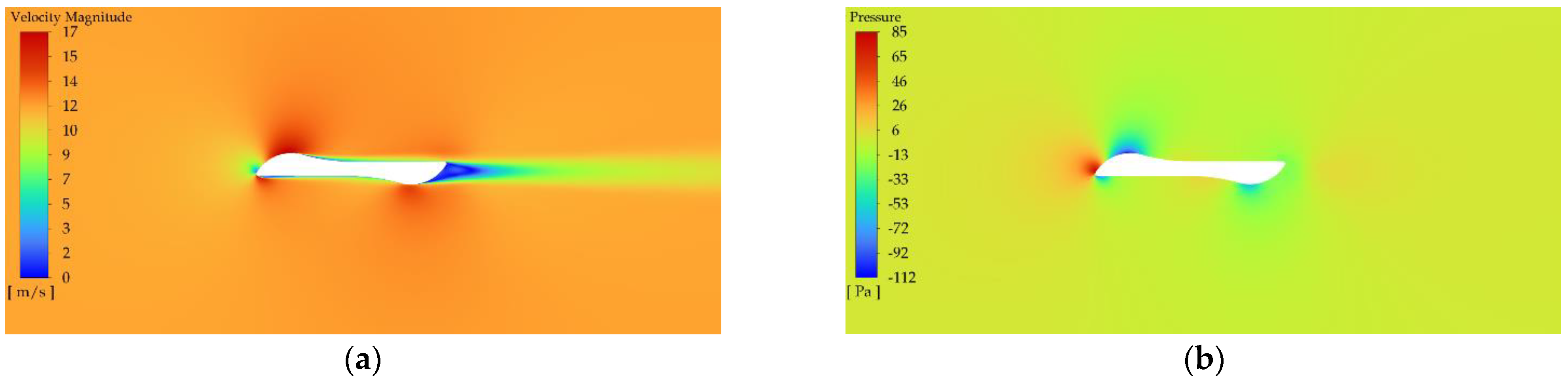
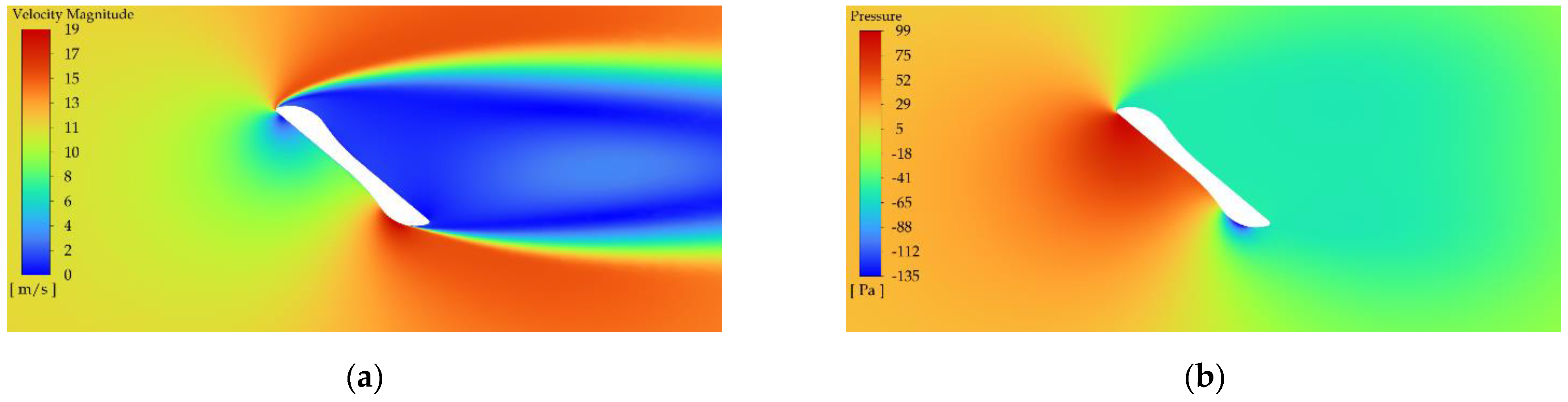
2.3. CFD Simulation
2.3.1. Governing Equations
2.3.2. Turbulence Model
2.3.3. Discrete Models and Assumptions for CFD Analysis
- First layer height = 0.01 mm
- Number of layers = 30
- Growth rate = 1.15
- Wind speed: W = 12.5 m/s was assumed as an average value from the wind profile
- Air density: ρ = 1.16 kg/m3
- Air viscosity: μ = 1.7894 × 10−5 kg/ms.
- Averaged Reynolds number: Re = 8.1 × 105
- Turbulence intensity of 8% was set at the inlet and outlet
- Hydraulic diameter was equal to 1 m
- Pressure-based solver was adopted
- The convergence of the numerical solution was obtained for both the mass and momentum residuals less than 10−3
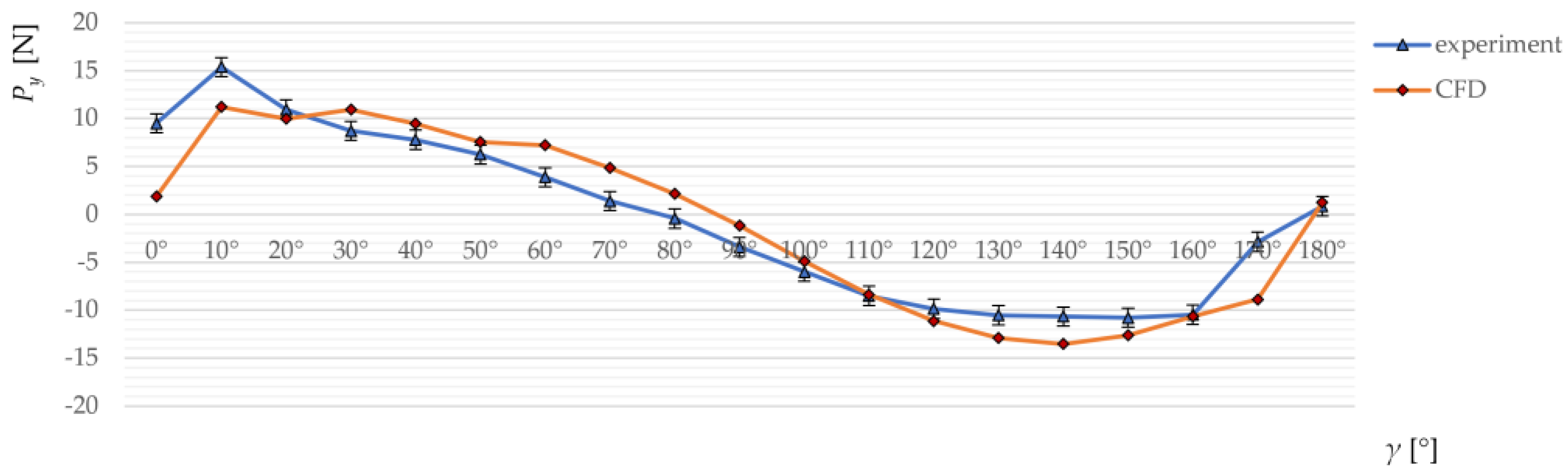
2.3.4. Validation of Numerical Solution
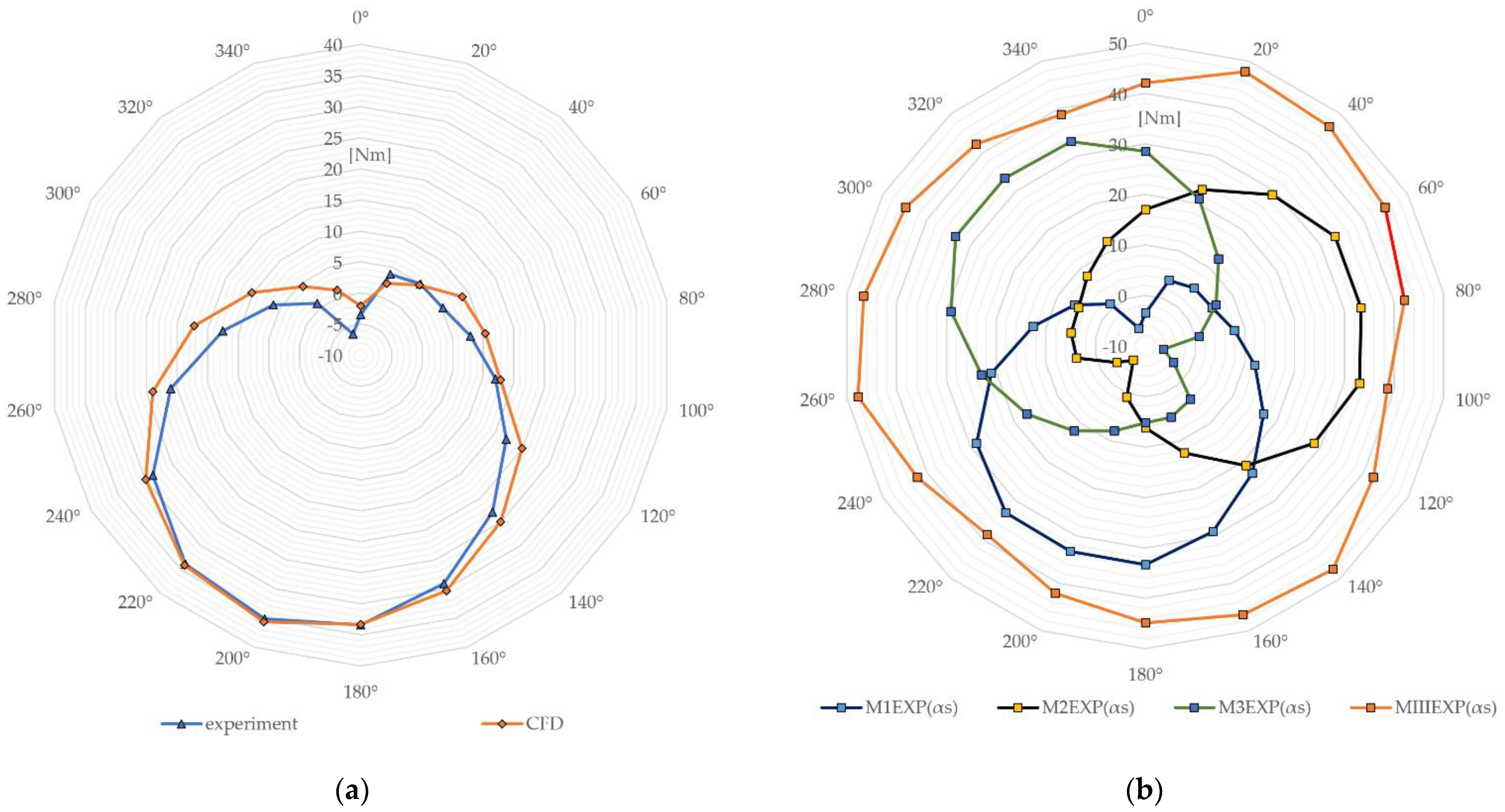
3. Results
Calculations of Propelling Torque for a Single Blade
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hau, E. Wind Turbines: Fundamentals, Technologies, Application, Economics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Ahmed, S. Wind Energy: Theory and Practice; PHI Learning Pvt. Ltd.: New Delhi, India, 2011; ISBN 9788120351639. [Google Scholar]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2001. [Google Scholar] [CrossRef]
- Eriksson, S.; Bernhoff, H.; Leijon, M. Evaluation of different turbine concepts for wind power. Renew. Sustain. Energy Rev. 2008, 12, 1419–1434. [Google Scholar] [CrossRef]
- Pope, K.; Dincer, I.; Naterer, G.F. Energy and exergy efficiency comparison of horizontal and vertical axis wind turbines. Renew. Energy 2010, 35, 2102–2113. [Google Scholar] [CrossRef]
- Darrieus, G. Turbine Having Its Rotating Shaft Transverse to the Flow of the Current. U.S. Patent 1835018, 8 December 1931. [Google Scholar]
- Mohan Kumar, P.; Sivalingam, K.; Lim, T.-C.; Ramakrishna, S.; Wei, H. Review on the Evolution of Darrieus Vertical Axis Wind Turbine: Large Wind Turbines. Clean Technol. 2019, 1, 205–223. [Google Scholar] [CrossRef] [Green Version]
- Gorelov, D.N. Energy characteristics of Darrieus rotor (review). Thermophys. Aeromech. 2010, 17, 301–308. [Google Scholar] [CrossRef]
- Islam, M.; Ting, D.S.K.; Fartaj, A. Aerodynamic models for Darrieus-type straight-bladed vertical axis wind turbines. Renew. Sustain. Energy Rev. 2008, 12, 1087–1109. [Google Scholar] [CrossRef]
- Gharib-Yosry, A.; Blanco-Marigorta, E.; Fernández-Jiménez, A.; Espina-Valdés, R.; Álvarez-Álvarez, E. Wind–Water Experimental Analysis of Small SC-Darrieus Turbine: An Approach for Energy Production in Urban Systems. Sustainability 2021, 13, 5256. [Google Scholar] [CrossRef]
- Wakui, T.; Tanzawa, Y.; Hashizume, T.; Nagao, T. Hybrid configuration of Darrieus and Savonius rotors for stand-alone wind turbine-generator systems. Electr. Eng. Jpn. 2005, 150, 13–22. [Google Scholar] [CrossRef]
- Mohan Kumar, P.; Surya, M.R.; Sivalingam, K.; Lim, T.-C.; Ramakrishna, S.; Wei, H. Computational Optimization of Adaptive Hybrid Darrieus Turbine: Part 1. Fluids 2019, 4, 90. [Google Scholar] [CrossRef] [Green Version]
- Savonius, S.J. The S-rotor and its applications. Mech. Eng. 1931, 53, 333–338. [Google Scholar]
- Kamoji, M.A.; Kedare, S.B.; Prabhu, S.V. Experimental investigations on single stage modified Savonius rotor. Appl. Energy 2009, 86, 1064–1073. [Google Scholar] [CrossRef]
- Moutsoglou, A.; Yan, W. Performance Tests of a Benesh Wind Turbine Rotor and a Savonius Rotor. Wind Eng. 1995, 19, 349–362. Available online: https://www.jstor.org/stable/43749592 (accessed on 3 May 2023).
- Van Bussel, G.; Mertens, S.; Polinder, H.; Sidler, H.F.A. The Development of Turby, a Small VAWT for the Built Environment. In Proceedings of the Global Windpower 2004 Conference, Chicago, IL, USA, 28–31 March 2004. [Google Scholar]
- Ghiasi, P.; Najafi, G.; Ghobadian, B.; Jafari, A.; Mazlan, M. Analytical Study of the Impact of Solidity, Chord Length, Number of Blades, Aspect Ratio and Airfoil Type on H-Rotor Darrieus Wind Turbine Performance at Low Reynolds Number. Sustainability 2022, 14, 2623. [Google Scholar] [CrossRef]
- Nader, N.A.; Jendoubi, A. Study of a Vertical Axis Wind Turbine for Low Speed Regions in Saudi Arabia. In Proceedings of the 5th International Conference of Fluid Flow, Heat and Mass Transfer (FFHMT’18), Niagara Falls, ON, Canada, 7–9 June 2018. [Google Scholar] [CrossRef]
- Ryś, J. Arrangement for Self-Positioning a Wing Motor in Wind’s Eye Position. Patent PAT.170515, 1993. Available online: https://api-ewyszukiwarka.pue.uprp.gov.pl/api/collection/32b800daa77c200e1dab609b1930bd92 (accessed on 9 April 2023). (In Polish).
- Ryś, J.; Augustyn, M. Homing a Wind Turbine Arrangement with a Horizontal Axis to the Rotation Wind Direction. Patent PAT.219834, 2015. Available online: https://api-ewyszukiwarka.pue.uprp.gov.pl/api/collection/05ac4a55973e657e16f2e877a94a9f07 (accessed on 9 April 2023). (In Polish).
- Rogowski, K.; Hansen, M.O.L.; Bangga, G. Performance Analysis of a H-Darrieus Wind Turbine for a Series of 4-Digit NACA Airfoils. Energies 2020, 13, 3196. [Google Scholar] [CrossRef]
- Ostowari, C.; Naik, D. Post-Stall Wind Tunnel Data for NACA 44XX Series Airfoil Sections; U.S. Department of Energy Office of Scientific and Technical Information: Oak Ridge, TN, USA, 1985. [CrossRef] [Green Version]
- Wind Engineering Laboratory. Available online: http://www.windlab.pl/en/ (accessed on 20 February 2023).
- Ryś, J.; Augustyn, M. Innovative construction of 3-component aerodynamic balance. Adv. Mater. Mach. Des.-Key Eng. Mater. 2013, 542, 171–177. [Google Scholar] [CrossRef]
- Augustyn, M.; Barski, M.; Chwał, M.; Stawiarski, A. Numerical and Experimental Determination of the Wind Speed Value Causing Catastrophe of the Scissor Lift. Appl. Sci. 2023, 13, 3528. [Google Scholar] [CrossRef]
- Flaga, A.; Kłaput, R.; Augustyn, M. Wind tunnel tests of two free-standing lighting protection masts in different arrangements with surroundings roof objects and roof conditions. Eng. Struct. 2016, 124, 539–548. [Google Scholar] [CrossRef]
- Lisowski, F.; Lisowski, E. Determination of Aerodynamic Drag Coefficients of Longitudinal Finned Tubes of LNG Ambient Air Vaporizers Using CFD and Experimental Methods. Appl. Sci. 2022, 12, 10865. [Google Scholar] [CrossRef]
- Augustyn, M. Propelling torque of the self-adjusting vertical-axis rotor. IOP Conf. Ser. Mater. Sci. Eng. 2020, 744, 012009. [Google Scholar] [CrossRef]
- Augustyn, M. A vertical-axis rotor as the adjusting system of a horizontal axis wind turbine. Tech. Trans. 2020, 117, 1–14. [Google Scholar] [CrossRef]
- Wen, J.; Zhou, L.; Zhang, H. Mode interpretation of blade number effects on wake dynamics of small-scale horizontal axis wind turbine. Energy 2023, 263, 125692. [Google Scholar] [CrossRef]
- Bhavsar, H.; Roy, S.; Niyas, H. Aerodynamic performance enhancement of the DU99W405 airfoil for horizontal axis wind turbines using slotted airfoil configuration. Energy 2023, 263, 125666. [Google Scholar] [CrossRef]
- Vedovelli, M.; Eltayesh, A.; Natili, F.; Castellani, F. Experimental and Numerical Investigation of the Effect of Blades Number on the Dynamic Response of a Small Horizontal-Axis Wind Turbine. Energies 2022, 15, 9134. [Google Scholar] [CrossRef]
- Intro to Governing Equations of Fluid Dynamics, 2020; ANSYS Inc.: Canonsburg, PA, USA, 2020; Available online: http://www.ansys.com (accessed on 6 May 2023).
- Menter, F.R. Zonal Two Equation k-ω Turbulence Models for Aerodynamic Flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics and Lasers Conference, Orlando, FL, USA, 6–9 July 1993. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Carraro, M.; De Vanna, F.; Zweiri, F.; Benini, E.; Heidari, A.; Hadavinia, H. CFD Modeling of Wind Turbine Blades with Eroded Leading Edge. Fluids 2022, 7, 302. [Google Scholar] [CrossRef]
- Meana-Fernández, A.; Fernández Oro, J.M.; Argüelles Díaz, K.M.; Galdo-Vega, M.; Velarde-Suárez, S. Application of Richardson extrapolation method to the CFD simulation of vertical-axis wind turbines and analysis of the flow field. Eng. Appl. Comput. Fluid Mech. 2019, 13, 359–376. [Google Scholar] [CrossRef] [Green Version]
- Gantasala, S.; Tabatabaei, N.; Cervantes, M.; Aidanpää, J.-O. Numerical Investigation of the Aeroelastic Behavior of a Wind Turbine with Iced Blades. Energies 2019, 12, 2422. [Google Scholar] [CrossRef] [Green Version]
- Wilcox, D.C. Formulation of the k-omega Turbulence Model Revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef] [Green Version]
- Chien, K.-Y. Predictions of Channel and Boundary-Layer Flows with a Low-Reynolds-Number Turbulence Model. AIAA J. 1982, 20, 33–38. [Google Scholar] [CrossRef]
- Ansys Fluent Theory Guide. Available online: https://www.afs.enea.it/project/neptunius/docs/fluent/html/th/node67.htm (accessed on 9 April 2023).
- Lisowski, F.; Lisowski, E. Influence of Longitudinal Fin Tubes Arrangement in LNG Ambient Air Vaporizers on the Wind Load. Energies 2022, 15, 405. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Xin, D.; Zhan, J. Improvement of Aerodynamic Performance of Savonius Wind Rotor Using Straight-Arc Curtain. Appl. Sci. 2020, 10, 7216. [Google Scholar] [CrossRef]



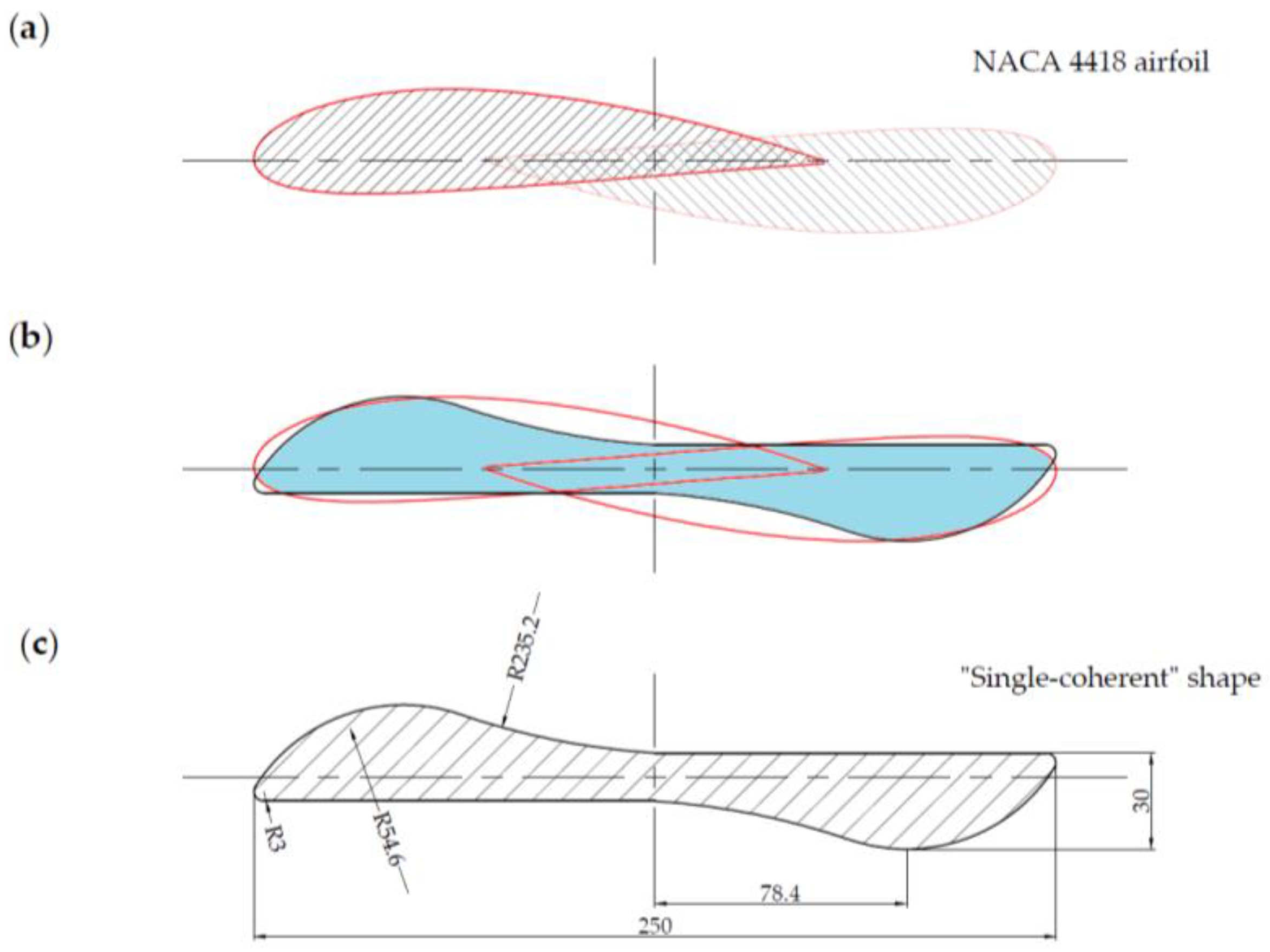


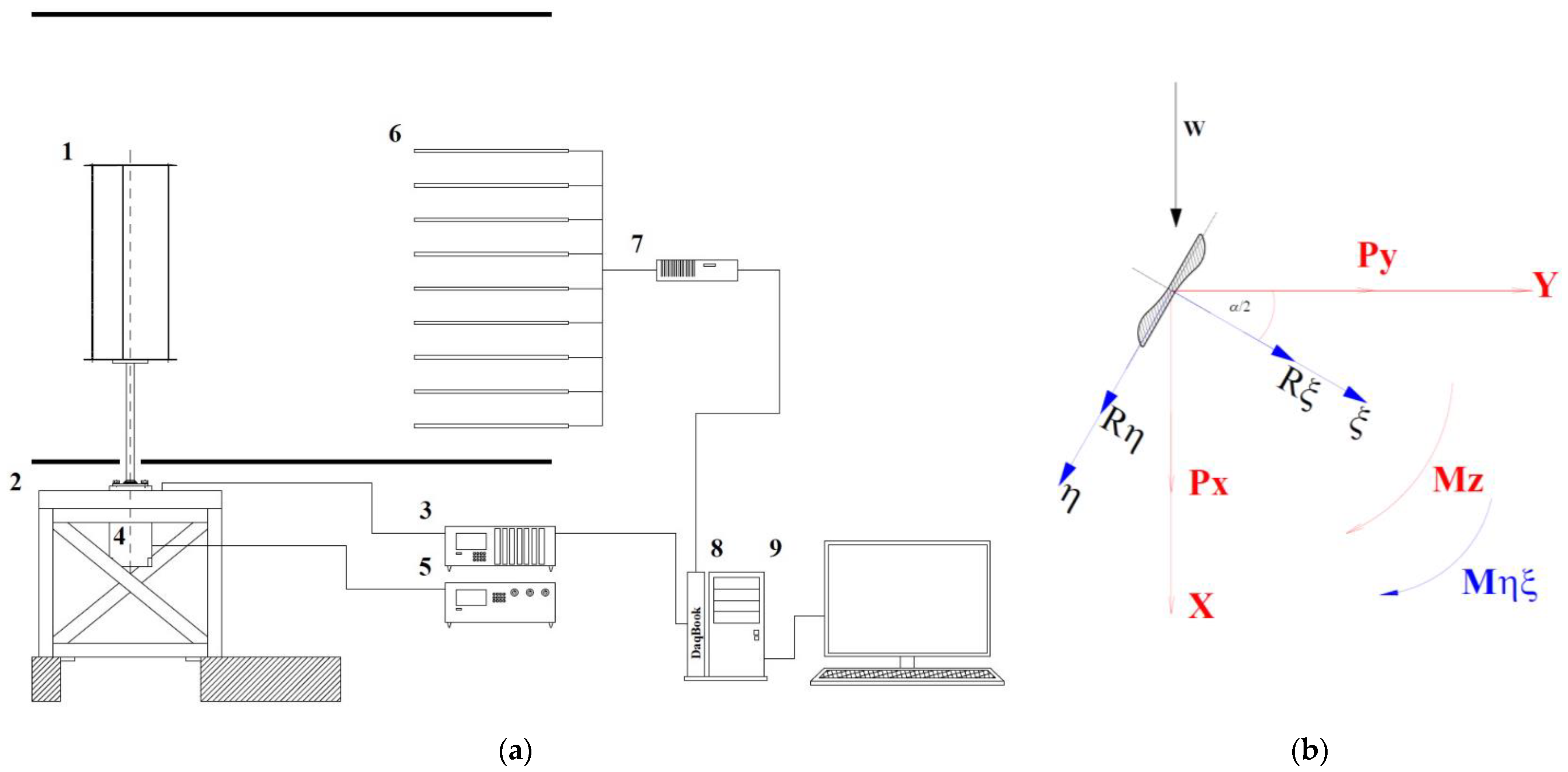
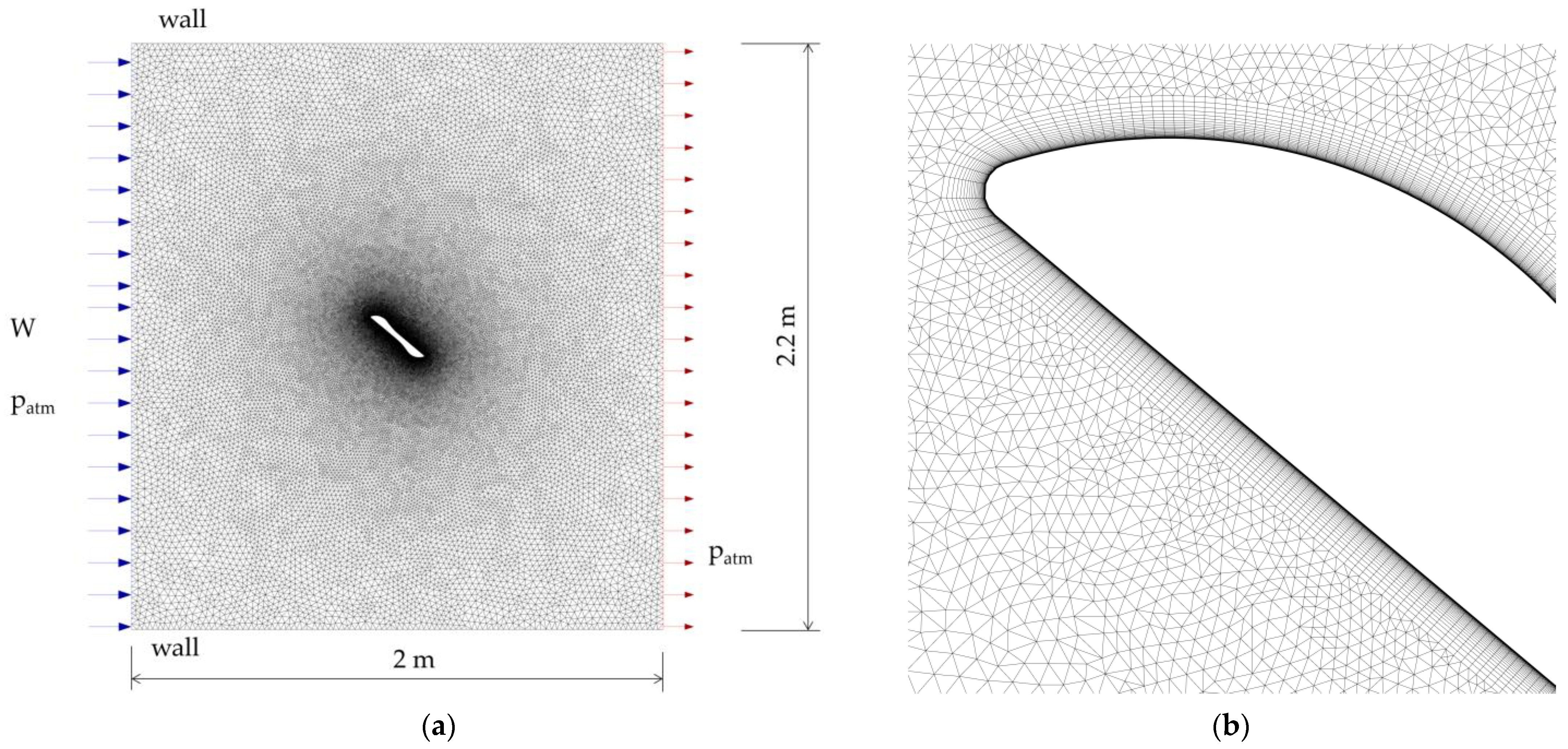

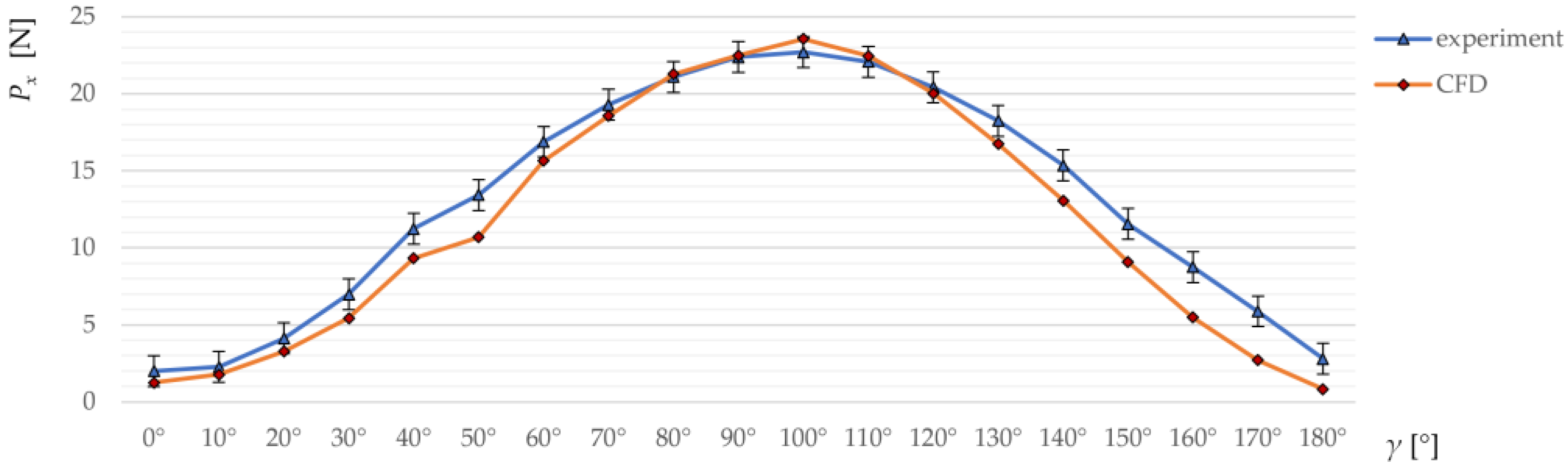





| Dimension Name | Value |
|---|---|
| width of the rotor blade [m] | aS = 0.250 |
| length of the blade [m] | bS = 0.044 |
| height of the rotor blade [m] | h = 0.625 |
| Parameter | Value |
|---|---|
| Geometric scale kD | 1:1 |
| Mean values of wind speed Wref [m/s] | 12.5 |
| Mean value of dynamic pressure qref [N/m2] | 96.4 |
| Mean turbulence intensity IW [%] | 8 |
| Number of considered wind directions | 18 (0°–180°) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Augustyn, M.; Lisowski, F. Experimental and Numerical Studies on a Single Coherent Blade of a Vertical Axis Carousel Wind Rotor. Energies 2023, 16, 5532. https://doi.org/10.3390/en16145532
Augustyn M, Lisowski F. Experimental and Numerical Studies on a Single Coherent Blade of a Vertical Axis Carousel Wind Rotor. Energies. 2023; 16(14):5532. https://doi.org/10.3390/en16145532
Chicago/Turabian StyleAugustyn, Marcin, and Filip Lisowski. 2023. "Experimental and Numerical Studies on a Single Coherent Blade of a Vertical Axis Carousel Wind Rotor" Energies 16, no. 14: 5532. https://doi.org/10.3390/en16145532






