A Distributed Control Scheme for Cyber-Physical DC Microgrid Systems
Abstract
:1. Introduction
- This article proposes a new distributed control technique for balanced voltage regulation and current sharing. The parameters of the proposed controller are adaptively determined using the fuzzy logic control scheme.
- The proposed distributed fuzzy logic control provides a nonlinear mapping between the voltage variation and current sharing error to determine the control reference to realize the control goals. A ramp control signal is presented to reduce the switching transients and ensure steady injection of the control signal.
- The stability assessment of the proposed control technique is conducted using the Lyapunov scheme to provide sufficient design conditions that assure the stability of the proposed controller. The proposed control technique is completely distributed; thus, it could be plugged and played.
2. Modeling of a Cyber-Physical DC μgrid System
2.1. Cyber System Modeling
2.2. Power System Modeling of the DC
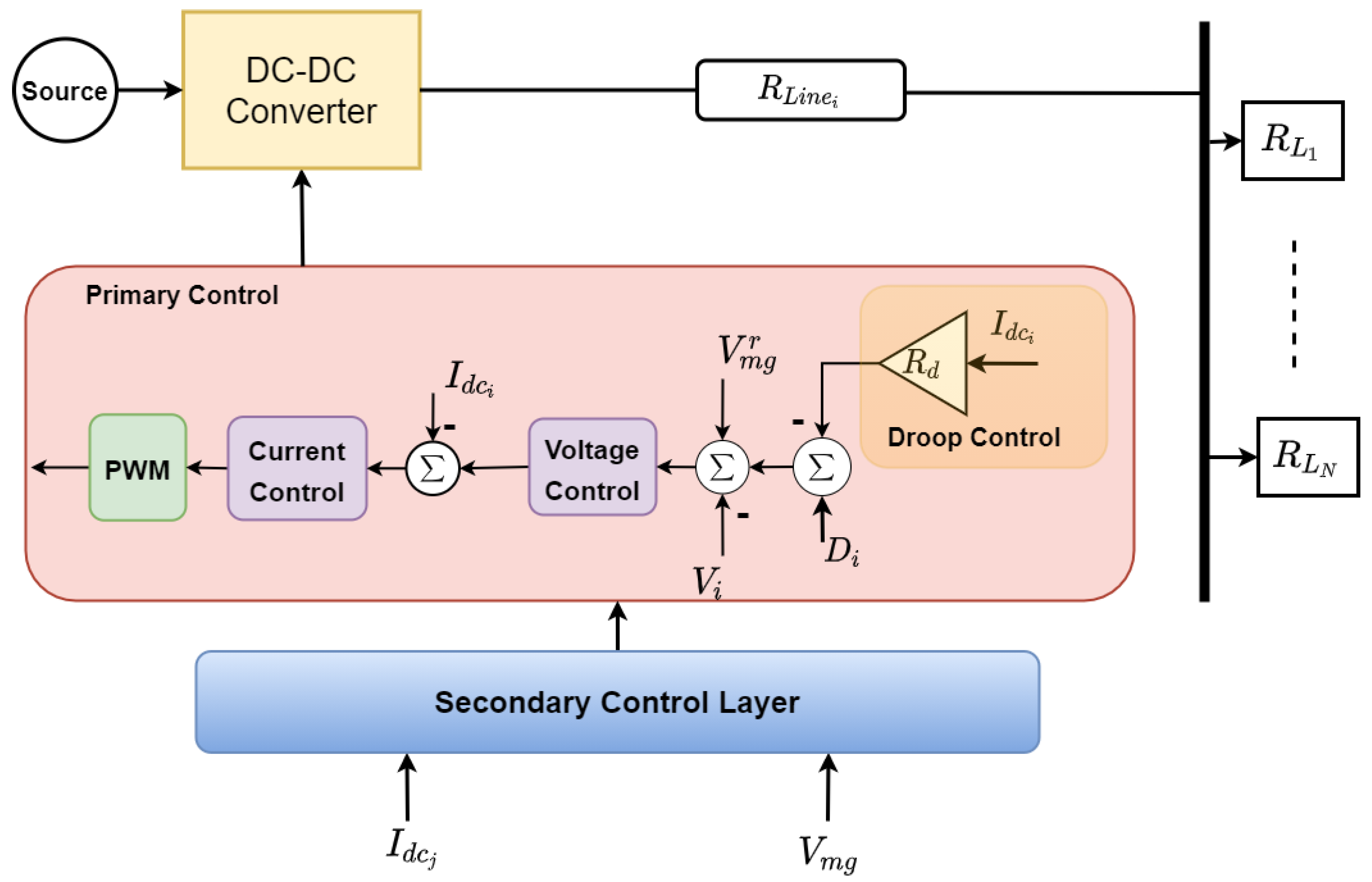
2.3. Primary Control in DC
2.4. Problem Formulation and Control Objectives
3. Proposed Controller Design
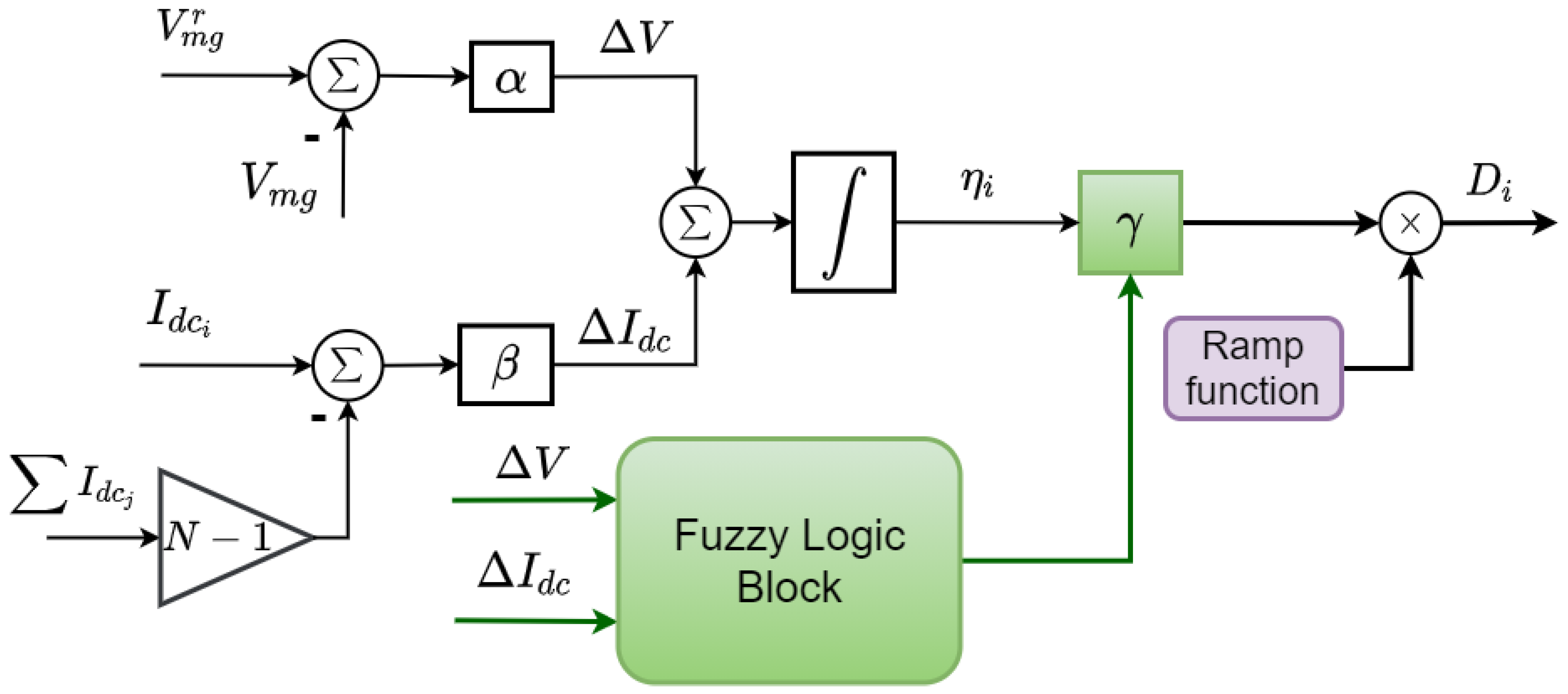
3.1. Distributed Secondary Controller
- Fuzzification: This transforms physical quantities into fuzzy sets consistent with the predefined membership functions. Linguistic variables are used to represent the membership functions.
- Inference engine: This consists of a database of the membership functions containing its input and output. It also contains the learning basis, which is a set of fuzzy rules that have been mapped using linguistic variables. The fuzzy output of the inference engine is based on the “If-then” mapping of the input fuzzy sets.
- Defuzzification: This transforms the fuzzy outputs into physical quantities that the system of interest can interpret.
3.2. Analysis of the Stability of the Proposed Controller
3.3. Overall Proposed Control Framework
4. Results and Discussion
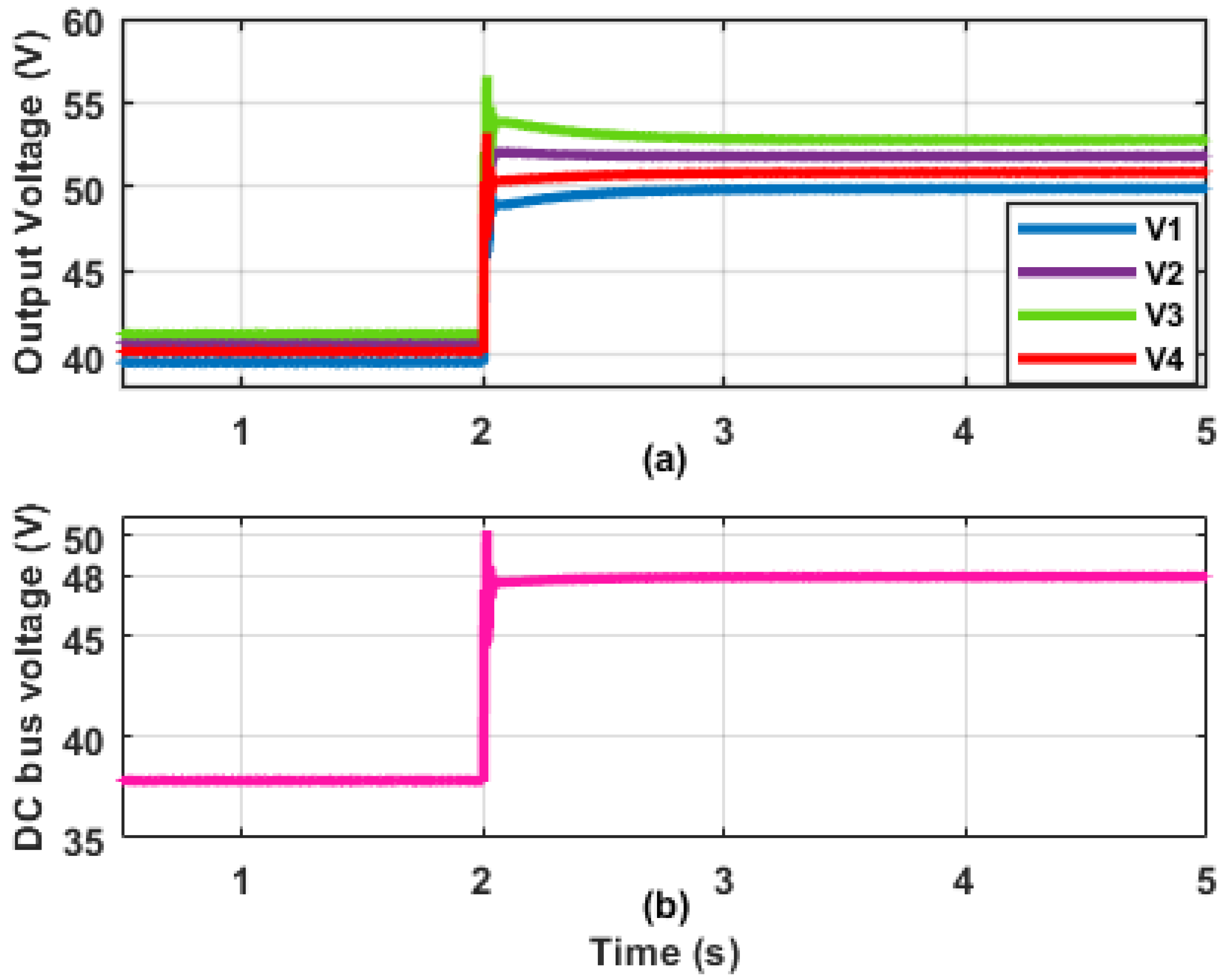
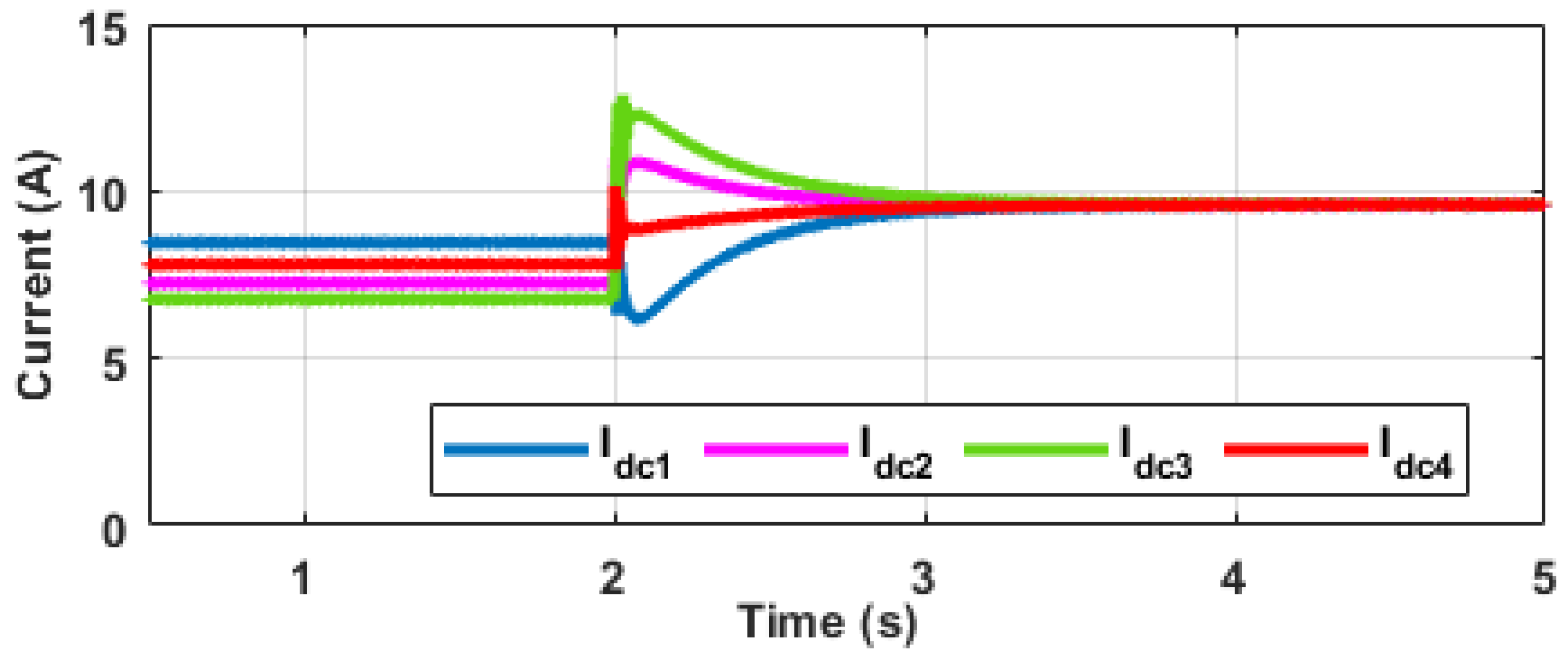
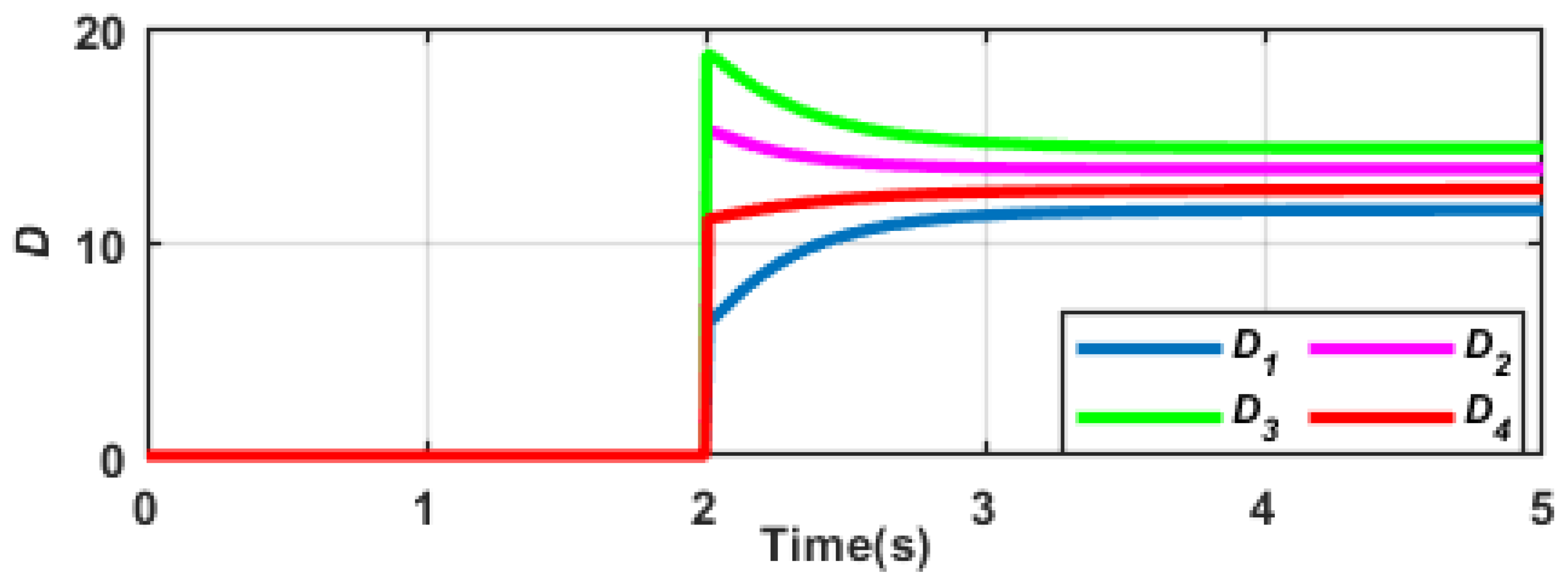
4.1. Scenario A: Realization of Control Objectives
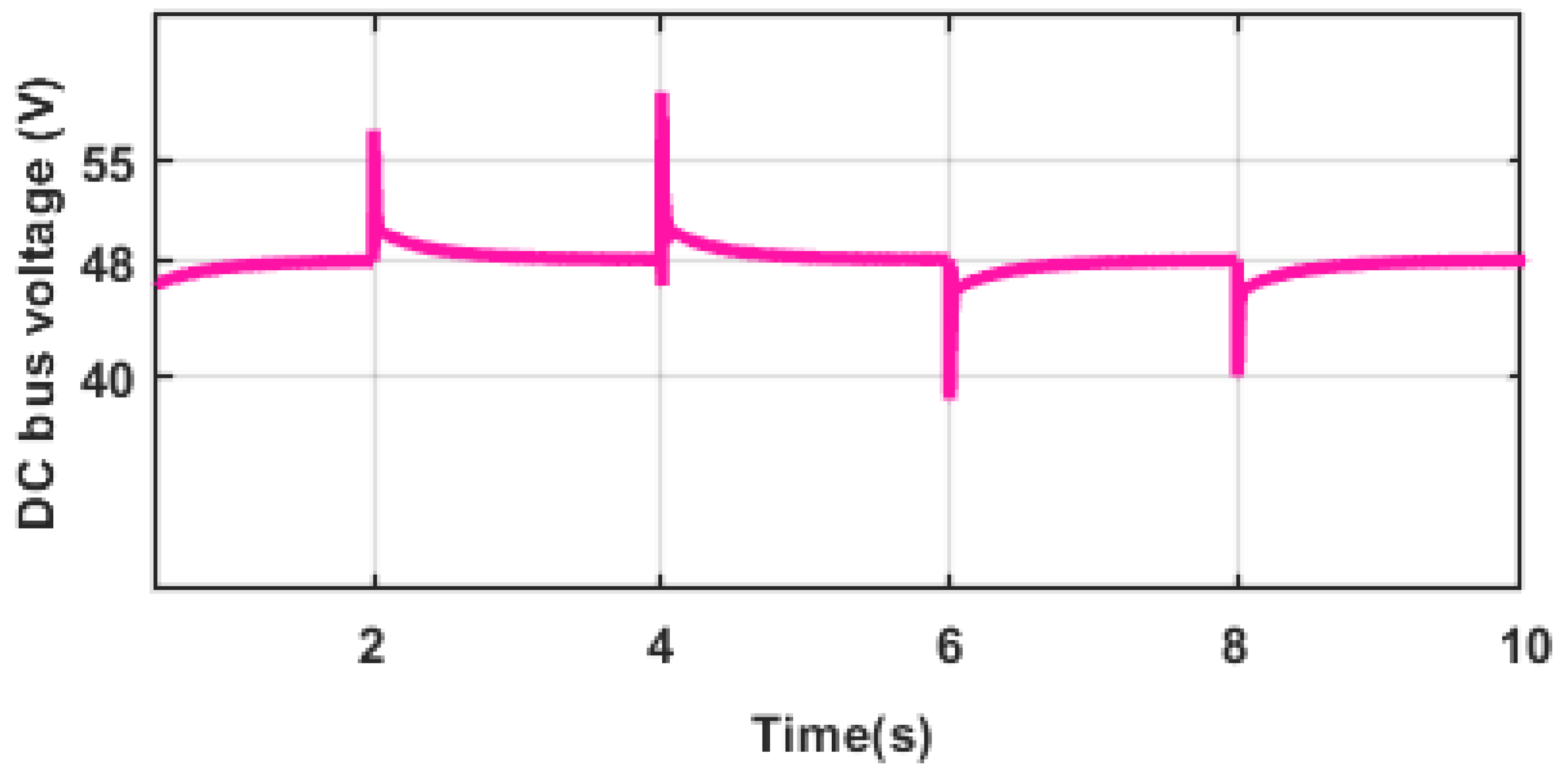
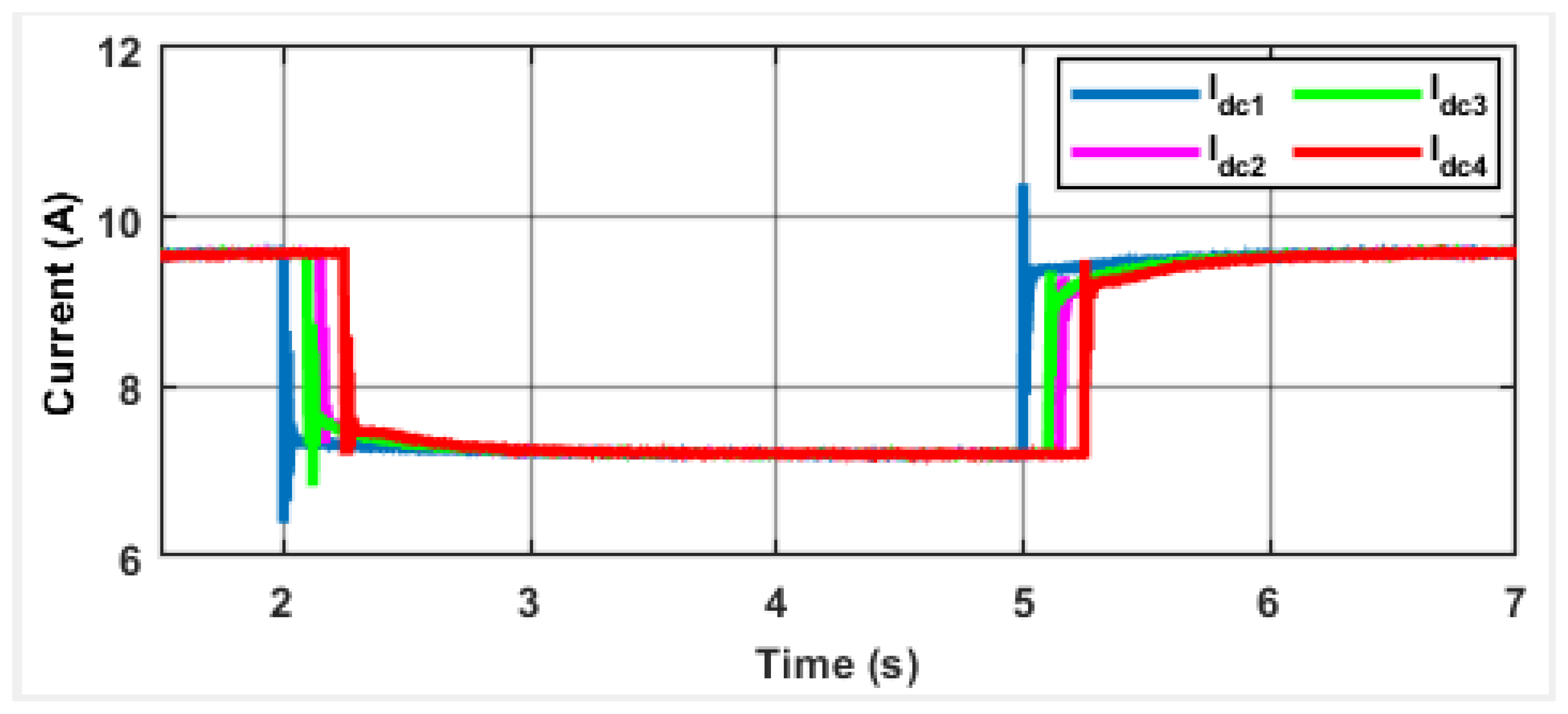
4.2. Scenario B: Plug-and-Play Ability
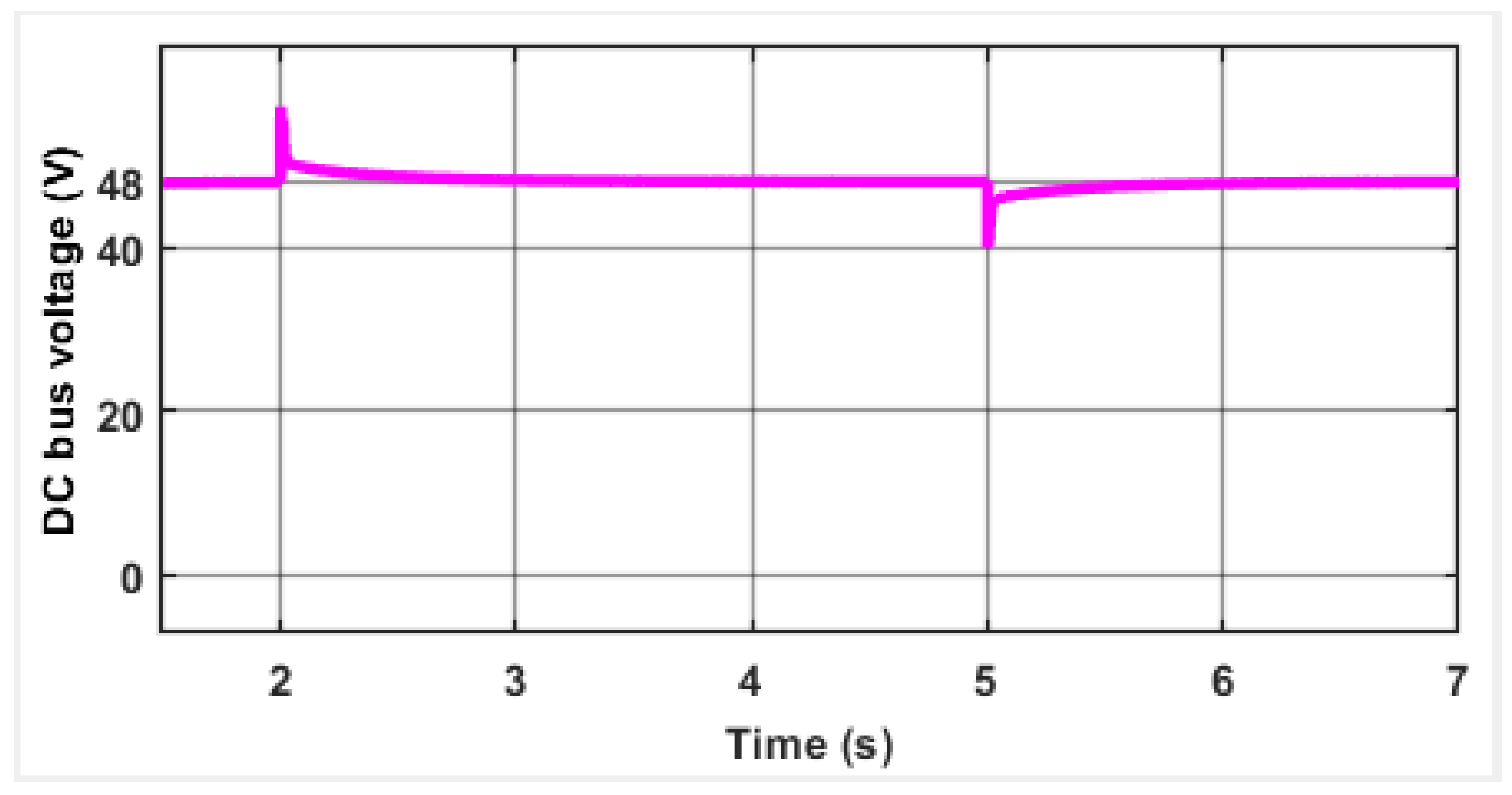
4.3. Scenario C: Robustness under Communication Time-Delay
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Primary | |
| Secondary | |
| 3C | Communication, Computation, and Control |
| AC | Alternating Current |
| CPSs | Cyber-Physical Systems |
| DC | Direct Current |
| DSs | Distributed Sources |
| HES | Hybrid Energy Systems |
| HIL | Hardware-In-Loop |
| LFC | Load Frequency Controller |
| MIMO | Multiple-Input, Multiple-Output |
| MPPT | Maximum Power Point Tracking |
| SOC | State-of-charge |
| WPS | Wind Power Systems |
| Microgrids |
References
- Khalil, S.M.; Bahsi, H.; Ochieng’Dola, H.; Korõtko, T.; McLaughlin, K.; Kotkas, V. Threat Modeling of Cyber-Physical Systems—A Case Study of a Microgrid System. Comput. Secur. 2023, 124, 102950. [Google Scholar] [CrossRef]
- Aluko, A.O.; Carpanen, R.P.; Dorrell, D.G.; Ojo, E.E. Real-Time Cyber Attack Detection Scheme for Standalone Microgrids. IEEE Internet Things J. 2022, 9, 21481–21492. [Google Scholar] [CrossRef]
- Mthukuse, N.; Onaolapo, A.K.; Aluko, A.; Dorrell, D.G. Review of cyberattack implementation, detection, and mitigation methods in cyber-physical systems. Energies 2023, 16, 5206. [Google Scholar] [CrossRef]
- Guo, J.; Liu, W.; Syed, F.R.; Zhang, J. Reliability assessment of a cyber-physical microgrid system in island mode. CSEE J. Power Energy Syst. 2019, 5, 46–55. [Google Scholar] [CrossRef]
- Adefarati, T.; Bansal, R.C. Reliability and economic evaluation of a microgrid power system. Energy Procedia 2017, 142, 43–48. [Google Scholar] [CrossRef]
- Aluko, A.O.; Carpanen, R.P.; Dorrell, D.G.; Ojo, E.E. Real-Time Dynamic Disturbance Estimation of Stand-Alone Microgrids Based on Unknown Input Observer for Frequency Regulation. In Proceedings of the IEEE PES/IAS PowerAfrica, Nairobi, Kenya, 23–27 August 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Shan, Y.; Hu, J.; Chan, K.W.; Islam, S. A Unified Model Predictive Voltage and Current Control for Microgrids with Distributed Fuzzy Cooperative Secondary Control. IEEE Trans. Ind. Inform. 2021, 17, 8024–8034. [Google Scholar] [CrossRef]
- Onaolapo, A.K.; Pillay Carpanen, R.; Dorrell, D.G.; Ojo, E.E. Reliability evaluation and financial viability of an electricity power micro-grid system with the incorporation of renewable energy sources and energy storage: A case study of KwaZulu-Natal, South Africa. IEEE Access 2021, 9, 159908–159924. [Google Scholar] [CrossRef]
- Adefarati, T.; Sharma, G.; Onaolapo, A.K.; Njepu, A.; Akindeji, K.T.; Oladejo, S.O.; Obikoya, G.D.; Adeyanju, I. Optimal design and techno-economic analysis of a grid-connected photovoltaic and battery hybrid energy system. Int. J. Eng. Res. Afr. (JERA) 2022, 60, 125–154. [Google Scholar] [CrossRef]
- Adefarati, T.; Obikoya, G.D.; Onaolapo, A.K.; Njepu, A. Design and analysis of a photovoltaic-battery-methanol-diesel power system. Int. Trans. Electr. Energy Syst. (ITEES) 2021, 31, e12800. [Google Scholar] [CrossRef]
- Adefarati, T.; Obikoya, G.D.; Sharma, G.; Onaolapo, A.K.; Akindeji, K.T. Design and Feasibility Analysis of Grid-Connected Hybrid Renewable Energy System: Perspective of Commercial Buildings. Energy Syst. 2023, 2023, 1–60. [Google Scholar] [CrossRef]
- Onaolapo, A.K.; Ojo, E.E. Effects of Upside Risk on Microgrids’ Reliability Considering the COVID-19 Pandemic. In Proceedings of the Southern African Universities Power Engineering Conference (SAUPEC), Johannesburg, South Africa, 24–26 January 2023; Volume 2023, pp. 1–6. [Google Scholar]
- Lin, P.; Zhang, C.; Zhang, X.; Iu, H.H.C.; Yang, Y.; Blaabjerg, F. Finite-time large signal stabilization for high power DC microgrids with exact offsetting of destabilizing effects. IEEE Trans. Ind. Electron. 2020, 68, 4014–4026. [Google Scholar] [CrossRef]
- Meng, L.; Shafiee, Q.; Trecate, G.F.; Karimi, H.; Fulwani, D.; Lu, X.; Guerrero, J.M. Review on control of DC microgrids and multiple microgrid clusters. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 928–948. [Google Scholar]
- Abhishek, A.; Ranjan, A.; Devassy, S.; Verma, B.K.; Ram, S.K.; Dhakar, A.K. Review of hierarchical control strategies for DC microgrid. IET Renew. Power Gener. 2020, 14, 1631–1640. [Google Scholar] [CrossRef]
- Bansal, R.C.; Bhatti, T.S. Small Signal Analysis of Isolated Hybrid Power Systems: Reactive Power and Frequency Control Analysis; Alpha Science International: Oxford, UK, 2008; pp. 1–240. [Google Scholar]
- Shrivastava, S.; Subudhi, B. Comprehensive review on hierarchical control of cyber-physical microgrid system. IET Gener. Transm. Distrib. 2020, 14, 6397–6416. [Google Scholar] [CrossRef]
- Liu, X.; Bansal, R.C. Integrating Multi-objective optimization with computational fluid dynamics to optimize boiler combustion process of a coal-fired power plant. Appl. Energy 2014, 114, 658–669. [Google Scholar] [CrossRef]
- Kumar, D.; Mathur, H.D.; Bhanot, S.; Bansal, R.C. Modeling and frequency control of community micro-grid under stochastic wind and solar sources. Int. J. Eng. Sci. Technol. (JESTECH) 2020, 23, 1084–1091. [Google Scholar] [CrossRef]
- Kumar, D.; Mathur, H.; Bhanot, S.; Bansal, R.C. Forecasting of solar and wind power using LSTM RNN for load frequency control in isolated microgrid. Int. J. Model. Simul. 2021, 41, 311–323. [Google Scholar] [CrossRef]
- Xing, L.; Guo, F.; Liu, X.; Wen, C.; Mishra, Y.; Tian, Y.C. Voltage Restoration and Adjustable Current Sharing for DC Microgrid with Time Delay via Distributed Secondary Control. IEEE Trans. Sustain. Energy 2020, 12, 1068–1077. [Google Scholar] [CrossRef]
- Anand, S.; Fernandes, B. Modified droop controller for paralleling of DC–DC converters in standalone DC system. IET Power Electron. 2012, 5, 782–789. [Google Scholar] [CrossRef]
- Wu, D.; Tang, F.; Dragicevic, T.; Guerrero, J.M.; Vasquez, J.C. Coordinated control based on bus-signaling and virtual inertia for islanded DC microgrids. IEEE Trans. Smart Grid 2015, 6, 2627–2638. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Guerrero, J.M.; Sun, K.; Vasquez, J.C. An improved droop control method for DC microgrids based on low bandwidth communication with DC bus voltage restoration and enhanced current sharing accuracy. IEEE Trans. Power Electron. 2013, 29, 1800–1812. [Google Scholar] [CrossRef] [Green Version]
- Lin, P.; Zhang, C.; Wang, P.; Xiao, J. A decentralized composite controller for unified voltage control with global system large-signal stability in DC microgrids. IEEE Trans. Smart Grid 2018, 10, 5075–5091. [Google Scholar] [CrossRef]
- Saafan, A.A.; Khadkikar, V.; El Moursi, M.S.; Zeineldin, H.H. A New Multiport DC-DC Converter for DC Microgrid Applications. IEEE Trans. Ind. Appl. 2023, 59, 601–611. [Google Scholar] [CrossRef]
- Wang, B.; Wang, Y.; Xu, Y.; Zhang, X.; Gooi, H.B.; Ukil, A.; Tan, X. Consensus-based Control of Hybrid Energy Storage System with a Cascaded Multiport Converter in DC Microgrids. IEEE Trans. Sustain. Energy 2019, 11, 2356–2366. [Google Scholar] [CrossRef]
- Yan, S.; Gu, Z.; Park, J.H.; Xie, X.; Dou, C. Probability-Density-Dependent Load Frequency Control of Power Systems with Random Delays and Cyber-Attacks via Circuital Implementation. IEEE Trans. Smart Grids 2022, 13, 4837–4847. [Google Scholar] [CrossRef]
- Yan, S.; Gu, Z.; Park, J.H.; Xie, X. Sampled Memory-Event-Triggered Fuzzy Load Frequency Control for Wind Power Systems Subject to Outliers and Transmission Delays. IEEE Trans. Cybern. 2023, 50, 4043–4053. [Google Scholar] [CrossRef] [PubMed]
- de Oliveira, R.C.; Tofoli, F.L.; de Morais, A.S. Novel Isolated Multiple-Input, Multiple-Output Multidirectional Converter for Modern Low-Voltage DC Power Distribution Architectures. Sustainability 2023, 15, 4582. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuña, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids—A general approach toward standardization. IEEE Trans. Ind. Electron. 2010, 58, 158–172. [Google Scholar] [CrossRef]
- Bansal, R.C. Automatic Reactive Power Control of Autonomous Hybrid Power Systems. Ph.D. Thesis, Indian Institutes of Technology, Delhi, India, 2003. [Google Scholar]
- Mbungu, N.T.; Ismail, A.A.; AlShabi, M.A.; Bansal, R.C.; ElNady, A.M.; Hamid, A.K. Control and estimation techniques applied to smart microgrids: A review. Renew. Sustain. Energy Rev. 2023, 179, 1–21. [Google Scholar] [CrossRef]
- Trip, S.; Cucuzzella, M.; Cheng, X.; Scherpen, J. Distributed averaging control for voltage regulation and current sharing in DC microgrids. IEEE Control Syst. Lett. 2018, 3, 174–179. [Google Scholar] [CrossRef] [Green Version]
- Aluko, A.; Swanson, A.; Jarvis, L.; Dorrell, D. Modeling and Stability Analysis of Distributed Secondary Control Scheme for Stand-Alone DC Microgrid Applications. Energies 2022, 15, 5411. [Google Scholar] [CrossRef]
- Aluko, A.; Buraimoh, E.; Oni, O.E.; Davidson, I.E. Advanced Distributed Cooperative Secondary Control of Islanded DC Microgrids. Energies 2022, 15, 3988. [Google Scholar] [CrossRef]
- Krishna Metihalli, B.; Narayana Sabhahit, J. Disturbance Observer Based Distributed Consensus Control Strategy of Multi-Agent System with External Disturbance in a Standalone DC Microgrid. Asian J. Control 2021, 23, 920–936. [Google Scholar] [CrossRef]
- Liu, X.K.; He, H.; Wang, Y.W.; Xu, Q.; Guo, F. Distributed hybrid secondary control for a DC microgrid via discrete-time interaction. IEEE Trans. Energy Convers. 2018, 33, 1865–1875. [Google Scholar] [CrossRef]
- Liu, X.K.; Wang, Y.W.; Lin, P.; Wang, P. Distributed supervisory secondary control for a DC microgrid. IEEE Trans. Energy Convers. 2020, 35, 1736–1746. [Google Scholar] [CrossRef]
- Sahoo, S.; Mishra, S. A distributed finite-time secondary average voltage regulation and current sharing controller for DC microgrids. IEEE Trans. Smart Grid 2017, 10, 282–292. [Google Scholar] [CrossRef]
- Guo, F.; Xu, Q.; Wen, C.; Wang, L.; Wang, P. Distributed secondary control for power allocation and voltage restoration in islanded DC microgrids. IEEE Trans. Sustain. Energy 2018, 9, 1857–1869. [Google Scholar] [CrossRef]
- Dong, M.; Li, L.; Nie, Y.; Song, D.; Yang, J. Stability analysis of a novel distributed secondary control considering communication delay in DC microgrids. IEEE Trans. Smart Grid 2019, 10, 6690–6700. [Google Scholar] [CrossRef]
- Bhargavi, K.; Jayalakshmi, N. Leader–Follower-Based Distributed Secondary Voltage Control for a Stand-alone PV and Wind-Integrated DC Microgrid System with EVs. J. Control Autom. Electr. Syst. 2020, 31, 233–246. [Google Scholar] [CrossRef]
- Deng, C.; Wang, Y.; Wen, C.; Xu, Y.; Lin, P. Distributed resilient control for energy storage systems in cyber–physical microgrids. IEEE Trans. Ind. Inform. 2020, 17, 1331–1341. [Google Scholar] [CrossRef]
- Aluko, A.O.; Carpanen, R.P.; Dorrell, D.G.; Ojo, E.E. Robust State Estimation Method for Adaptive Load Frequency Control of Interconnected Power System in a Restructured Environment. IEEE Syst. J. 2021, 15, 5046–5056. [Google Scholar] [CrossRef]
- Aluko, A.O.; Musumpuka, R.; Dorrell, D.G. Cyberattack-Resilient Secondary Frequency Control Scheme for Stand-Alone Microgrids. IEEE Trans. Ind. Electron. 2023, 70, 1622–1634. [Google Scholar] [CrossRef]
- Chandrasekar, A.; Sengupta, S.; Hingane, S.; Gururaja, C.; Pandit, S. Comparative Analysis of Model Predictive Control (MPC) and Conventional Control in Supervisory Controller of a Retrofit HEV; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2017; pp. 1–10. [Google Scholar] [CrossRef]


| NB | NS | Z | PS | PB | ||
| NB | B | B | M | M | M | |
| NS | B | B | S | M | M | |
| Z | B | S | S | S | B | |
| PS | M | M | S | B | B | |
| PB | M | M | M | B | B | |
| Description | Unit | Value |
|---|---|---|
| Rated Bus Voltage | 48 V | |
| Source Voltage | 100 V | |
| Sampling Frequency | 10 kHz | |
| Filter Inductance | 1 mH | |
| Filter Capacitance | 235 | |
| Line Resistance | 0.2 , 0.4 , 0.5 , 0.3 | |
| Load | 5 , 2.5 , 4 | |
| Control loop | ||
| Current Control | 0.05 | |
| 148 | ||
| Voltage Control | 0.248 | |
| 36 | ||
| Droop Resistance | 1 | |
| Control loop | ||
| Voltage Error Coefficient | 1.25 | |
| Current Error Coefficient | 7.5 | |
| Control Objective | S1 | S2 | S3 | S4 | Proposed |
|---|---|---|---|---|---|
| Voltage Regulation | 2 s | 1.72 s | 3 s | 1.3 s | ≤0.2 s |
| Current Sharing | 2.5 s | 2 s | 3.4 s | 1.5 s | 1 s |
| Implementation Complexity | simple | simple | simple | complex | complex |
| Robustness | low | moderate | moderate | high | very high |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Onaolapo, A.K.; Sharma, G.; Bokoro, P.N.; Aluko, A.; Pau, G. A Distributed Control Scheme for Cyber-Physical DC Microgrid Systems. Energies 2023, 16, 5611. https://doi.org/10.3390/en16155611
Onaolapo AK, Sharma G, Bokoro PN, Aluko A, Pau G. A Distributed Control Scheme for Cyber-Physical DC Microgrid Systems. Energies. 2023; 16(15):5611. https://doi.org/10.3390/en16155611
Chicago/Turabian StyleOnaolapo, Adeniyi K., Gulshan Sharma, Pitshou N. Bokoro, Anuoluwapo Aluko, and Giovanni Pau. 2023. "A Distributed Control Scheme for Cyber-Physical DC Microgrid Systems" Energies 16, no. 15: 5611. https://doi.org/10.3390/en16155611
APA StyleOnaolapo, A. K., Sharma, G., Bokoro, P. N., Aluko, A., & Pau, G. (2023). A Distributed Control Scheme for Cyber-Physical DC Microgrid Systems. Energies, 16(15), 5611. https://doi.org/10.3390/en16155611







