Experimental Investigation of Gas Transmission Pipeline Blockage Detection Based on Dynamic Pressure Method
Abstract
:1. Introduction
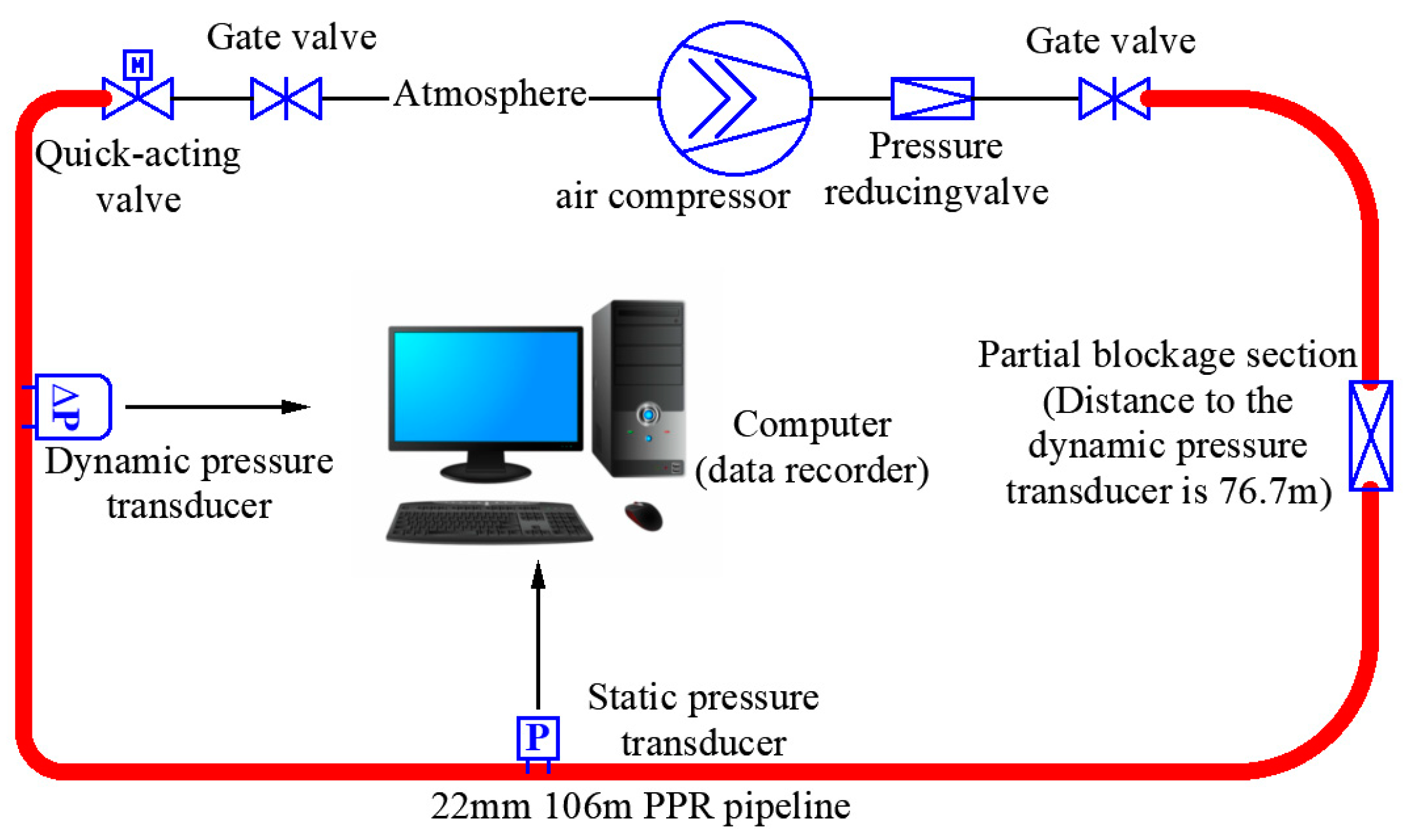
2. Materials and Methods
3. Results
3.1. Theory and Calculation
3.2. Results
4. Discussion
5. Conclusions
- (1)
- The blockage detection based on pressure wave method has the advantages of high detection accuracy, simple operation, short detection time, low cost;
- (2)
- It was suitable for complex plugging conditions and has good reliability and practicability;
- (3)
- The data selection method and model establishment and calculation method adopted in this paper are more accurate for blocking location, but the prediction model for blocking percentage needs to be reasonably optimized.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuan, Z.; Deng, Z.; Jiang, M.; Xie, Y.; Wu, Y. A modeling and analytical solution for transient flow in natural gas pipelines with extended partial blockage. Nat. Gas Sci. Eng. 2015, 22, 141–149. [Google Scholar] [CrossRef]
- Wang, L.; Sun, X.; Shen, S.; Wu, P.; Liu, T.; Liu, W.; Zhao, J.; Li, Y. Undrained triaxial tests on water-saturated methane hydrate-bearing clayey-silty sediments of the South China Sea. Can. Geotech. J. 2021, 58, 351–366. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Wu, P.; Shen, S.; Liu, T.; Leng, S.; Chang, Y.; Zhao, J. Physical and mechanical properties of the overburden layer on gas hydrate-bearing sediments of the South China Sea. J. Pet. Sci. Eng. 2020, 189, 107020. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Shen, S.; Liu, W.; Sun, X.; Liu, Y.; Zhao, J. Mechanical Behaviors of Gas Hydrate-bearing Clayey Sediments of the South China Sea. Environ. Geotec. 2022, 9, 210–222. [Google Scholar] [CrossRef]
- Zhang, X.; Lee, B.; Sa, J.; Kinnari, K.; Askvik, K.; Li, X.; Sum, A. Hydrate management in deadlegs: Effect of header temperature on hydrate deposition. Energy Fuels 2017, 31, 11802–11810. [Google Scholar] [CrossRef]
- Scott, S.L.; Satterwhite, L.A. Evaluation of the backpressure technique for blockage detection in gas flowlines. J. Energy Resour. Technol. 1998, 120, 27–31. [Google Scholar]
- Mazzotti, M.; Khazaali, M.; Bocchini, P.; Di Lullo, A.; Marzani, A. Restrictions and obstructions detection in pipe networks using incomplete and noisy flow and pressure steady-state measurements. Struct. Control Health Monit. 2022, 29, e2854. [Google Scholar]
- Koyama, H.; Watanabe, K.; Himmelblau, D.M. Identification of partial plugging in a gas-transport pipeline by an acoustic method. Appl. Acoust. 1993, 40, 1–19. [Google Scholar] [CrossRef]
- Pratap, V.; Rajendran, S.; Agrawal, R.K.; Indimath, S.S.; Reddy, B.P.; Balamurugan, S. Blockage Detection in Gas Pipelines to Prevent Failure of Transmission Line. J. Pipeline Syst. Eng. Pract. 2021, 12, 04021031. [Google Scholar] [CrossRef]
- Bello, O.; Virani, N.; Oyadiji, S.O. Identification of blockage in a pipe using modal analysis. In Proceedings of the ASME 2011 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference (IDETC/CIE), Washington, DC, USA, 28–31 August 2012; pp. 551–559. [Google Scholar]
- Duan, H.F.; Lee, P.J.; Ghidaoui, M.S.; Tuck, J. Transient wave-blockage interaction and extended blockage detection in elastic water pipelines. J. Fluids Struct. 2014, 46, 2–16. [Google Scholar] [CrossRef] [Green Version]
- Duan, H.F.; Lee, P.J. Transient-based frequency domain method for dead-end side branch detection in reservoir pipeline-valve systems. J. Hydraul. Eng. 2016, 142, 04015042. [Google Scholar] [CrossRef]
- Shi, W.; Yao, Y.; Cheng, S.; Shi, Z. Pressure transient analysis of acid fracturing stimulated well in multilayered fractured carbonate reservoirs: A field case in Western Sichuan Basin, China. J. Pet. Sci. Eng. 2019, 184, 106462. [Google Scholar] [CrossRef]
- Zhang, Y.; Duan, H.F.; Keramat, A.; Che, T.C. On the leak-induced transient wave reflection and dominance analysis in water pipelines. Mech. Syst. Signal Process. 2022, 167, 108512. [Google Scholar] [CrossRef]
- Duan, H.F.; Lee, P.J.; Ghidaoui, M.S.; Tung, Y.K. Extended blockage detection in pipelines by using the system frequency response analysis. J. Water Resour. Plan. Manag. 2012, 138, 55–62. [Google Scholar] [CrossRef]
- Lee, P.J.; Vítkovský, J.P.; Lambert, M.F.; Simpson, A.R.; Liggett, J.A. Discrete blockage detection in pipelines using the frequency response diagram: Numerical study. J. Hydraul. Eng. 2008, 134, 658–663. [Google Scholar] [CrossRef] [Green Version]
- Meniconi, S.; Brunone, B.; Ferrante, M. Water-hammer pressure waves interaction at cross-section changes in series in viscoelastic pipes. J. Fluids Struct. 2012, 33, 44–58. [Google Scholar] [CrossRef]
- Meniconi, S.; Duan, H.F.; Lee, P.J.; Brunone, B.; Ghidaoui, M.S.; Ferrante, M. Experimental investigation of coupled frequency and time-domain transient test–based techniques for partial blockage detection in pipelines. J. Hydraul. Eng. 2013, 139, 1033–1040. [Google Scholar] [CrossRef]
- Adewumi, M.; Eltohamie, E.; Solaja, A. Possible detection of multiple blockages using transients. J. Energy Resour. Technol. 2003, 125, 154–159. [Google Scholar] [CrossRef]
- Adeleke, N.; Ityokumbul, M.T.; Ademumi, M. Blockage detection and characterization in natural gas pipelines by transient pressure-wave reflection analysis. SPE J. 2013, 18, 355–365. [Google Scholar] [CrossRef]
- Stewart, N.; Jack, G. Pipeline blockage location by pressure wave analysis. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 13–16 November 2017. [Google Scholar]
- Chu, J.; Liu, Y.; Song, Y.; Yang, L.; Li, X.; Yan, K.; Zhao, J. Experimental platform for blockage detection and investigation using propagation of pressure pulse waves in a pipeline. Measurement 2020, 160, 107877. [Google Scholar] [CrossRef]
- Chu, J.; Yang, L.; Liu, Y.; Song, Y.; Yu, T.; Lv, X.; Li, Q.; Zhao, J. Pressure pulse wave attenuation model coupling waveform distortion and viscous dissipation for blockage detection in pipeline. Energy Sci. Eng. 2020, 8, 260–265. [Google Scholar] [CrossRef] [Green Version]
- Meng, Y.; Li, H.; Li, G.; Zhu, L.; Wei, N.; Lin, N. Investigation on propagation characteristics of the pressure wave in gas flow through pipes and its application in gas drilling. J. Nat. Gas Sci. Eng. 2015, 22, 163–171. [Google Scholar] [CrossRef]
- Chu, J.; Liu, Y.; Lv, X.; Li, Q.; Dong, H.; Song, Y.; Zhao, J. Experimental investigation on blockage predictions in gas pipelines using the pressure pulse wave method. Energy 2021, 230, 120897. [Google Scholar] [CrossRef]

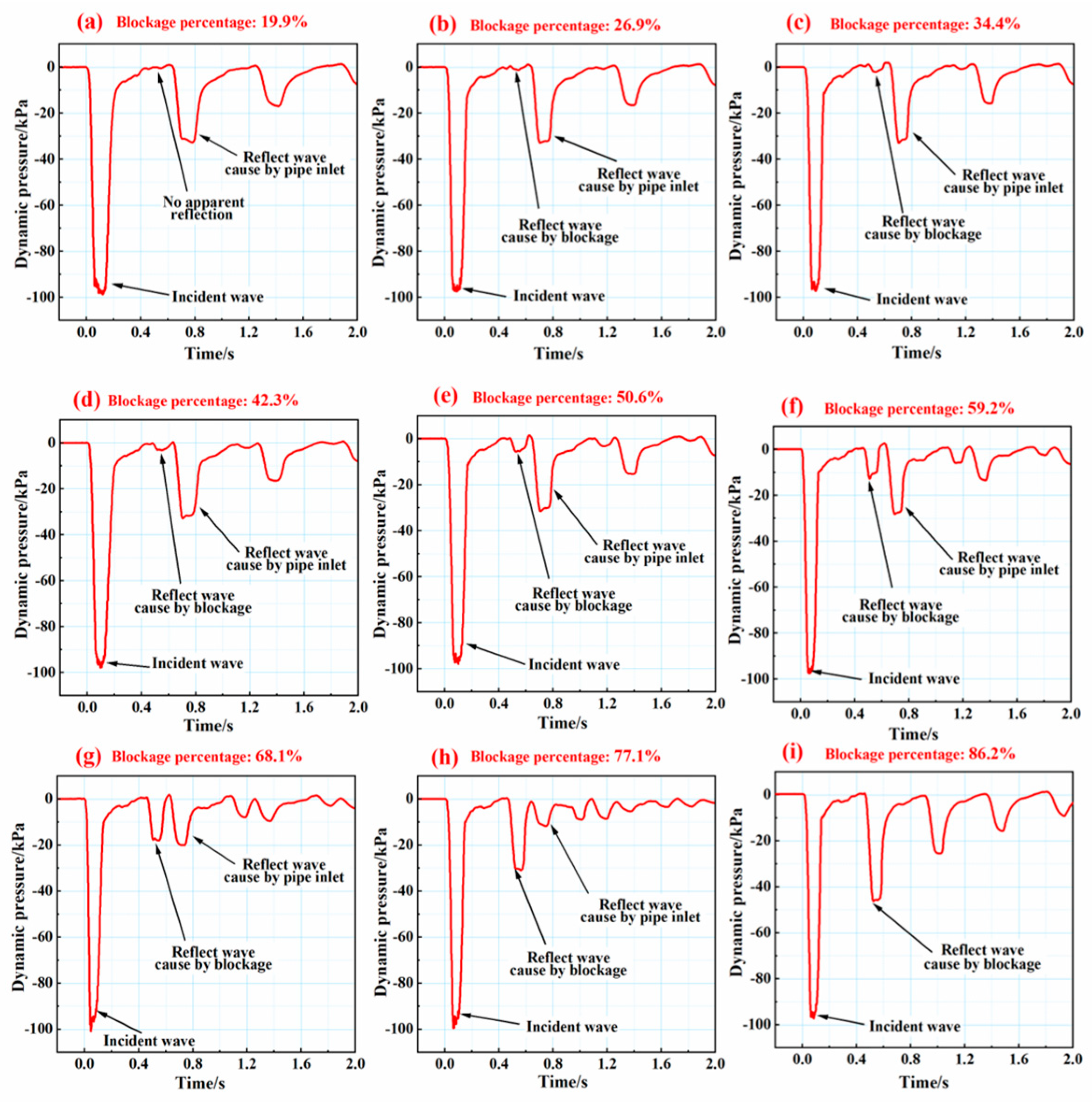
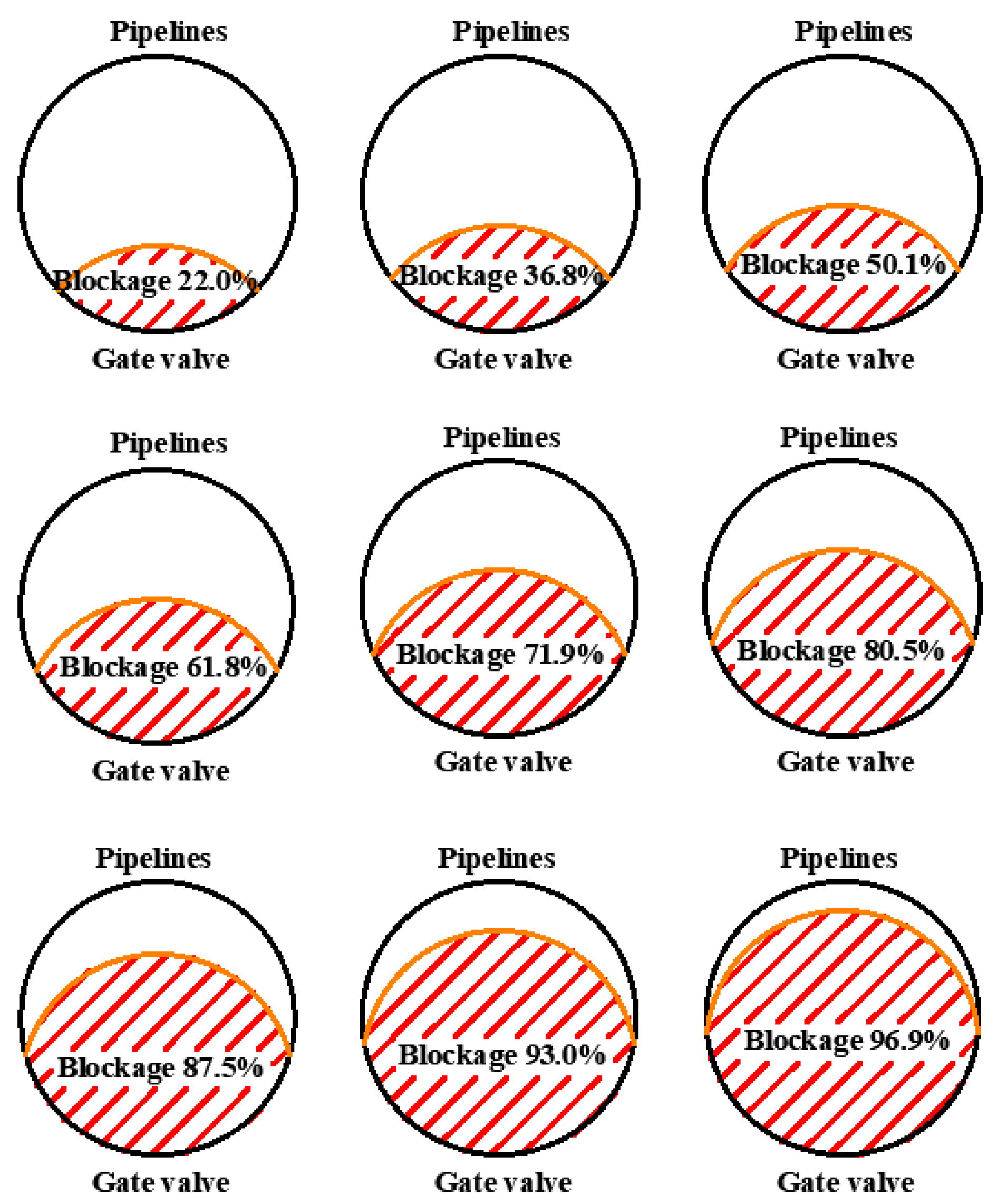
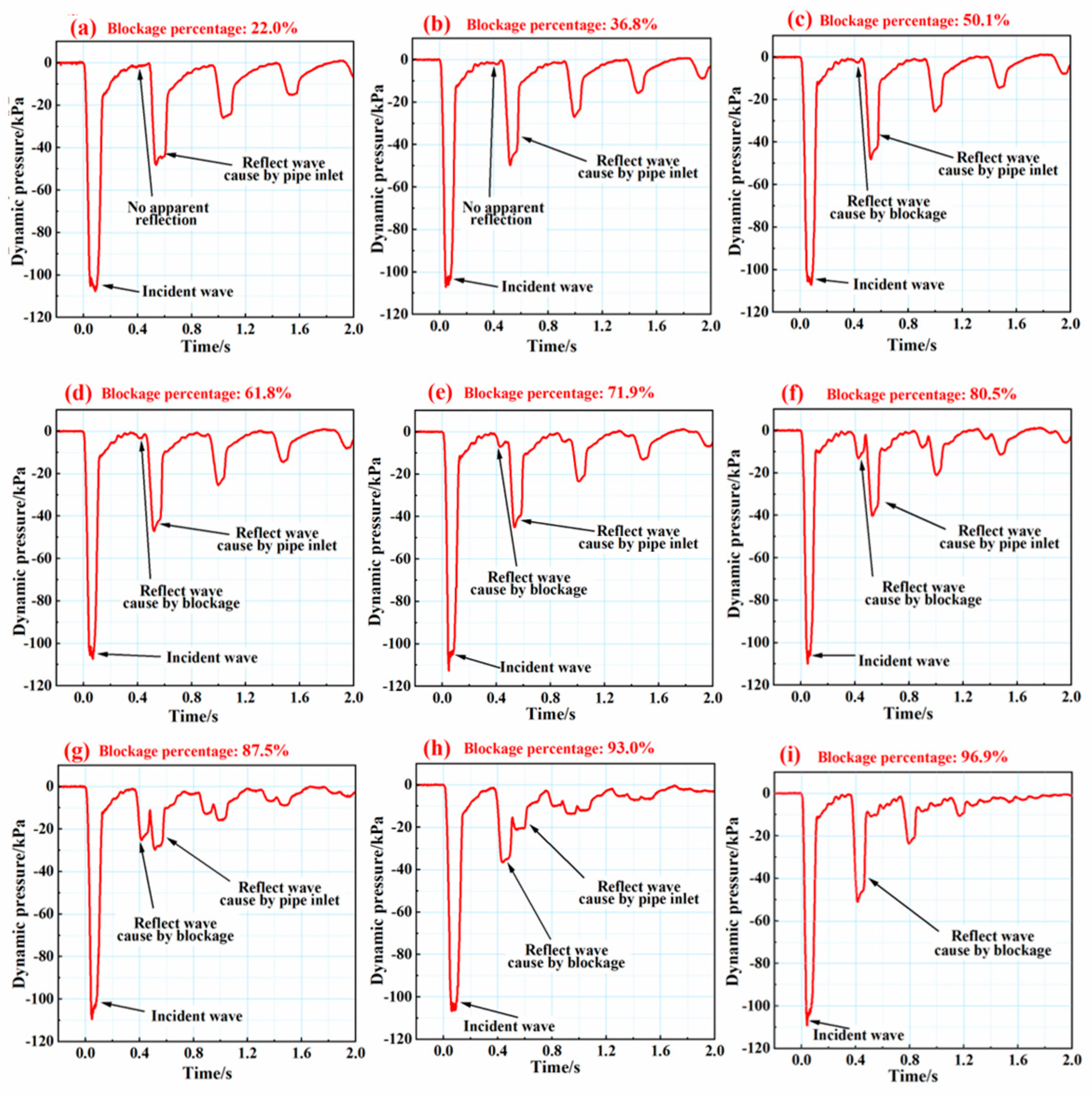
| Case | Blockage Location | Blockage Percentage | ||||
|---|---|---|---|---|---|---|
| Pred. (m) | Real. (m) | %Err | Pred. | Real. | %Err | |
| 1 | 61.4 | 59.4 | −3.4 | 48.1% | 50.1% | −4 |
| 2 | 60.2 | 59.4 | −1.5 | 51.2% | 61.8% | −20.6 |
| 3 | 62.3 | 59.4 | −4.9 | 61.2% | 71.9% | −17.5 |
| 4 | 61.9 | 59.4 | −4.2 | 70.1% | 80.5% | −14.8 |
| 5 | 60.7 | 59.4 | −2.3 | 81.7% | 87.5% | −7.1 |
| 6 | 61.1 | 59.4 | −2.8 | 88.7% | 93.0% | −4.8 |
| 7 | 60.5 | 59.4 | −1.9 | 93.6% | 96.9% | −3.6 |
| Case | Blockage Location | Blockage Percentage | ||||
|---|---|---|---|---|---|---|
| Pred. (m) | Real. (m) | %Err | Pred. | Real. | %Err | |
| 1 | 79.9 | 76.7 | −4.1 | 41.6% | 26.9% | 35.4 |
| 2 | 79.5 | 76.7 | −3.6 | 46.5% | 34.4% | 26.1 |
| 3 | 79.9 | 76.7 | −4.1 | 51.1% | 42.3% | 17.2 |
| 4 | 79.9 | 76.7 | −4.1 | 58.9% | 50.6% | 14.1 |
| 5 | 77.1 | 76.7 | −0.4 | 70.8% | 59.2% | 16.3 |
| 6 | 77.8 | 76.7 | −1.4 | 76.1% | 68.1% | 10.6 |
| 7 | 77.8 | 76.7 | −1.4 | 85.2% | 77.1% | 9.5 |
| 8 | 77.4 | 76.7 | −0.9 | 92.1% | 86.2% | 6.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, K.; Xu, D.; Wang, Q.; Chu, J.; Zhu, S.; Zhao, J. Experimental Investigation of Gas Transmission Pipeline Blockage Detection Based on Dynamic Pressure Method. Energies 2023, 16, 5620. https://doi.org/10.3390/en16155620
Yan K, Xu D, Wang Q, Chu J, Zhu S, Zhao J. Experimental Investigation of Gas Transmission Pipeline Blockage Detection Based on Dynamic Pressure Method. Energies. 2023; 16(15):5620. https://doi.org/10.3390/en16155620
Chicago/Turabian StyleYan, Kele, Dianqiang Xu, Qiong Wang, Jiawei Chu, Shengjie Zhu, and Jiafei Zhao. 2023. "Experimental Investigation of Gas Transmission Pipeline Blockage Detection Based on Dynamic Pressure Method" Energies 16, no. 15: 5620. https://doi.org/10.3390/en16155620
APA StyleYan, K., Xu, D., Wang, Q., Chu, J., Zhu, S., & Zhao, J. (2023). Experimental Investigation of Gas Transmission Pipeline Blockage Detection Based on Dynamic Pressure Method. Energies, 16(15), 5620. https://doi.org/10.3390/en16155620







