Thermohydraulic Efficiency of a Solar Air Heater in the Presence of Graded Aluminium Wire Mesh—A Combined Experimental–Numerical Study
Abstract
:1. Introduction
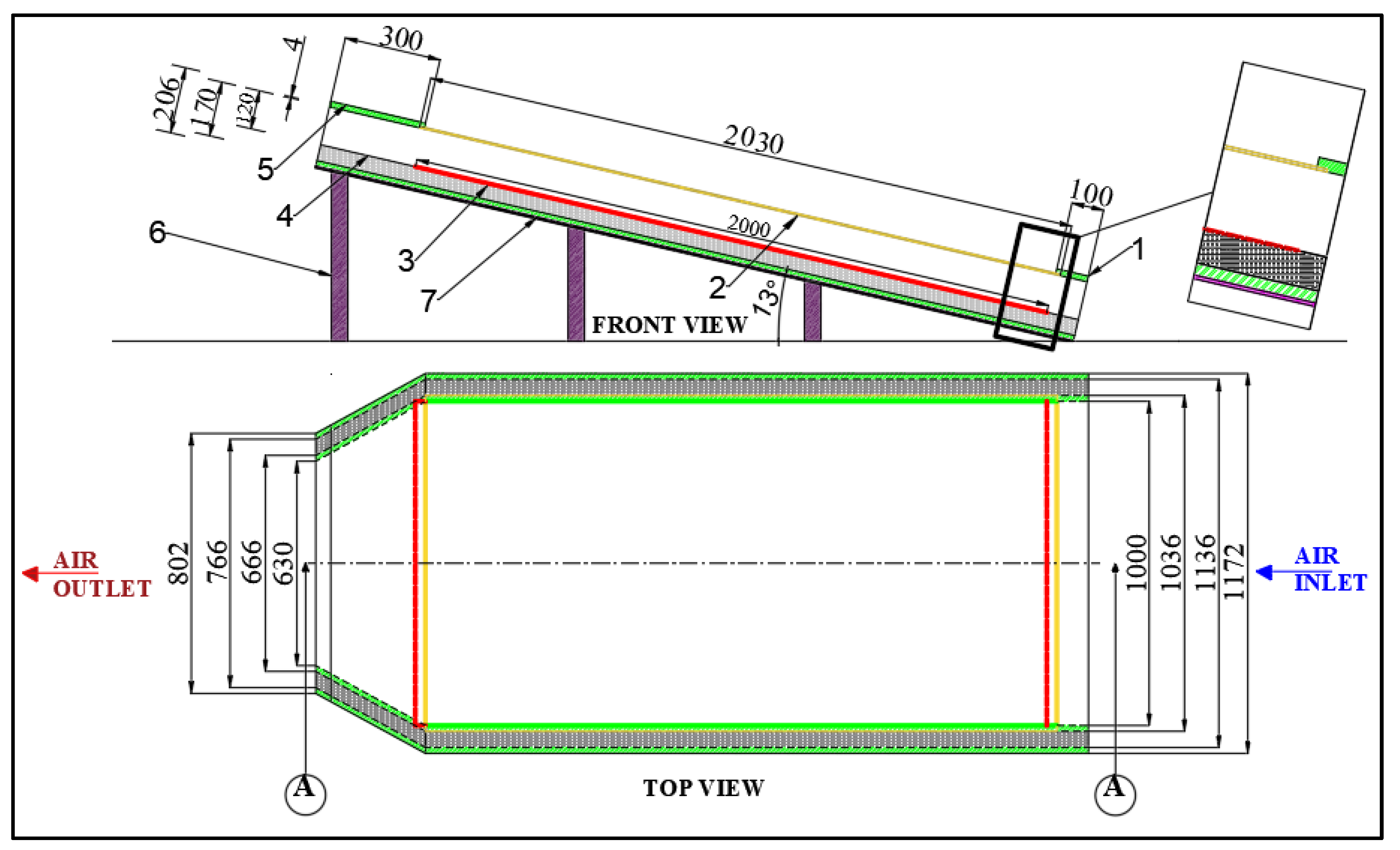
2. Materials and Methods
2.1. Measurement Procedure
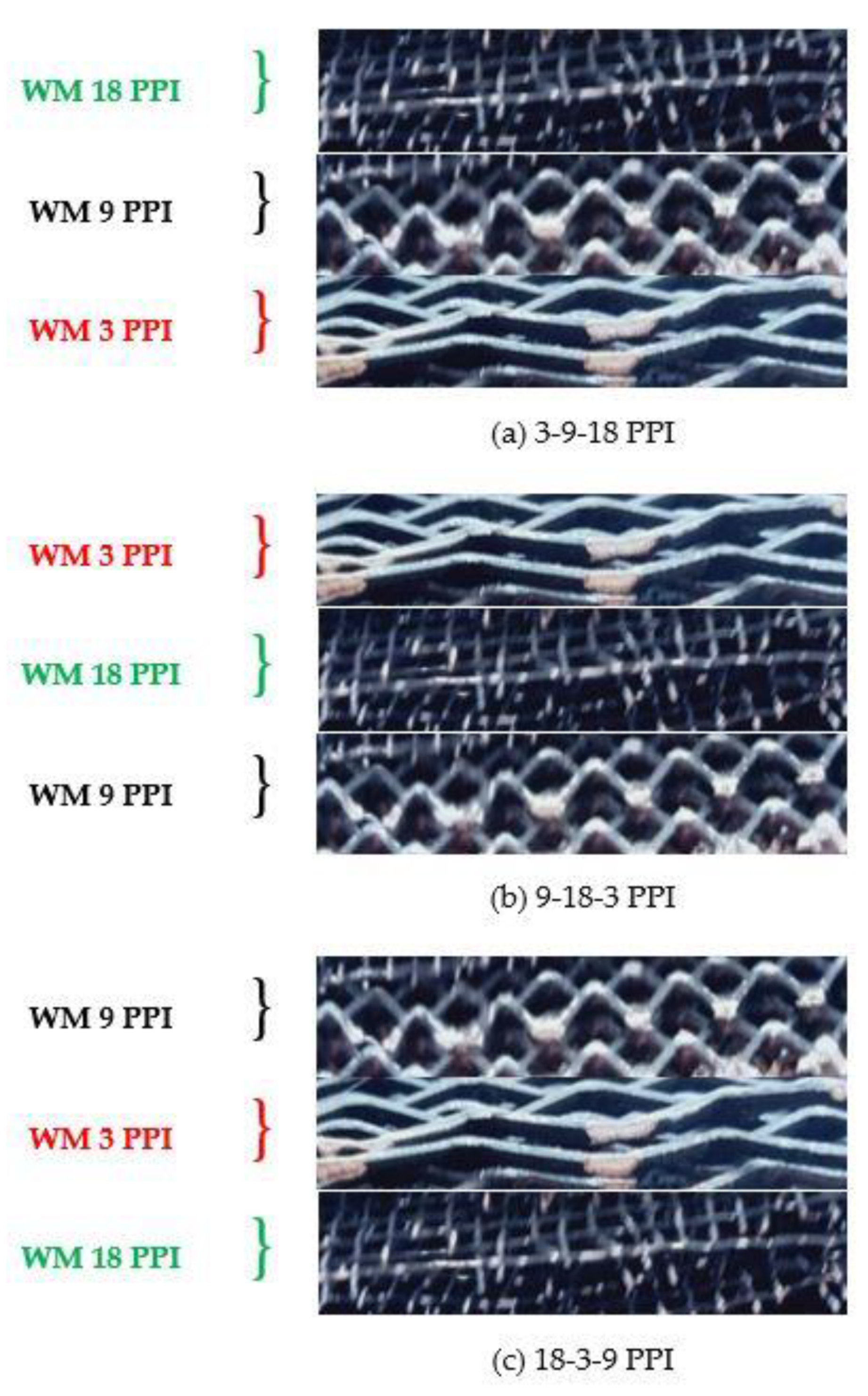
2.2. Details of Wire Mesh as a Porous Media in SAHs with Its Different Arrangement with Geometrical Parameters
2.3. Performance Paramaters of SAH
2.4. Uncertainties in Measurement
2.4.1. Uncertainty for Mass Flow Rate
2.4.2. Uncertainty for Thermal Efficiency
3. Computational Investigations
3.1. Governing Equations
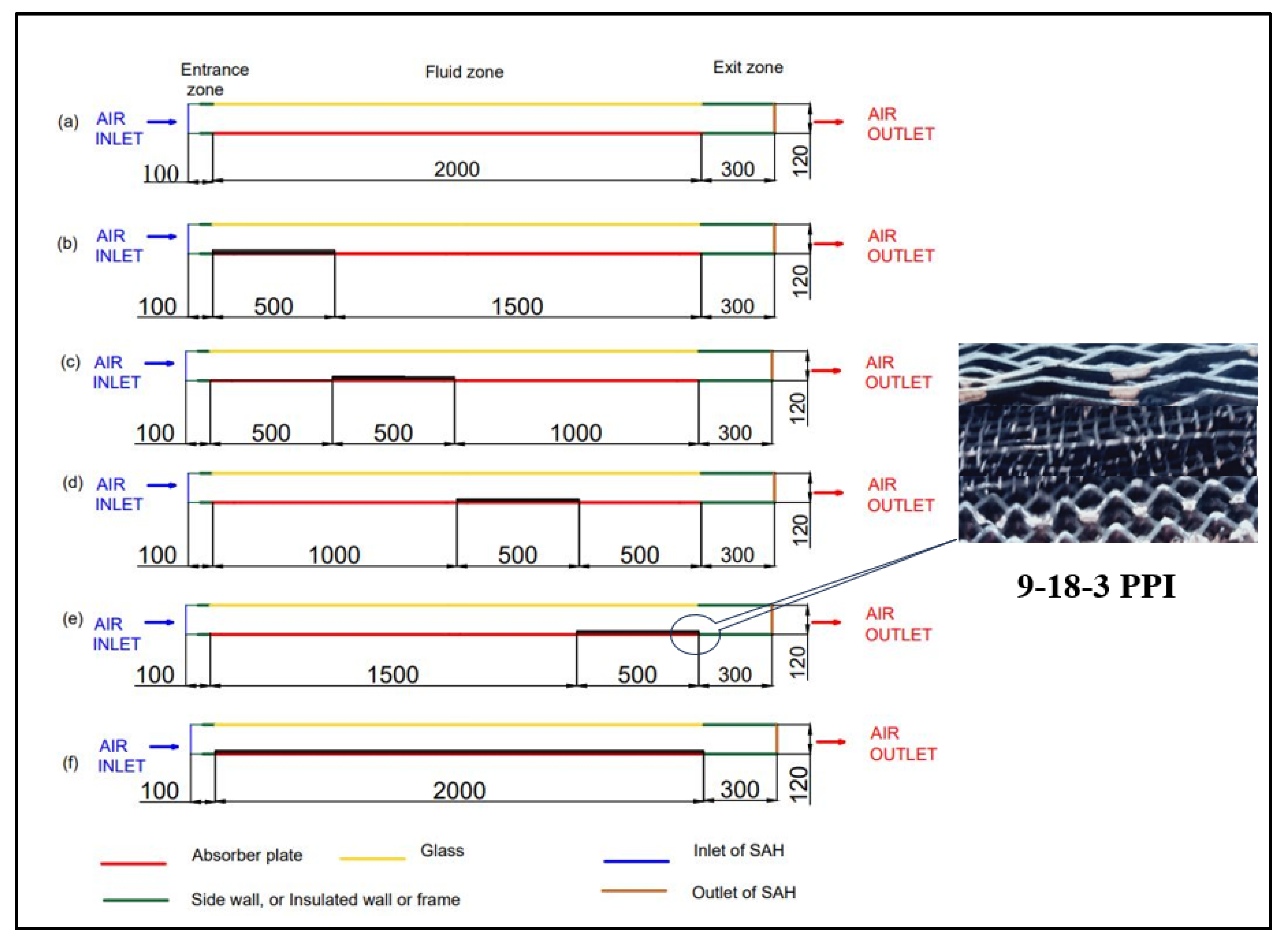
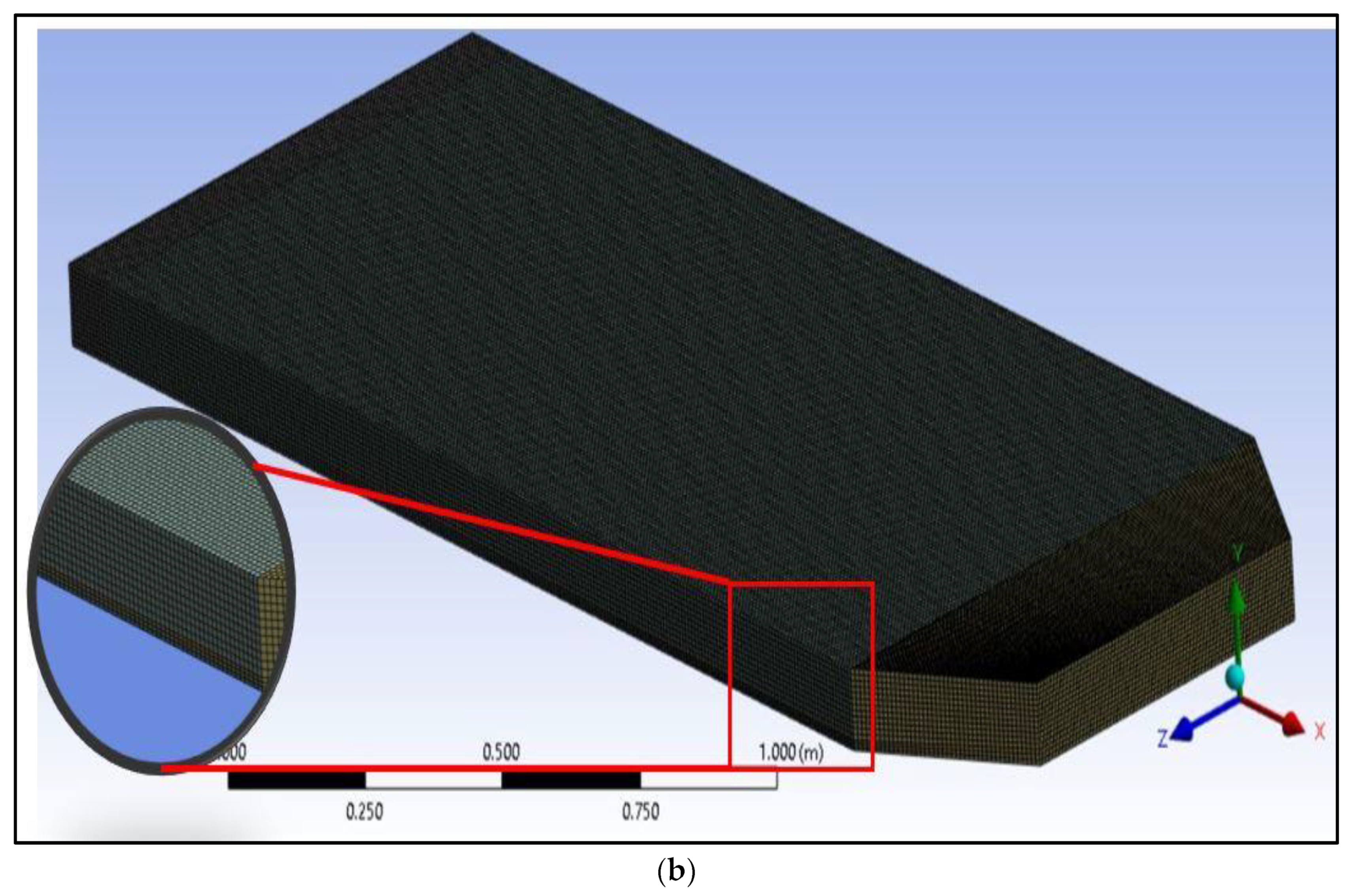
3.2. Details of Geometry, Mesh Generation, and Boundary Conditions
3.3. Computational Details
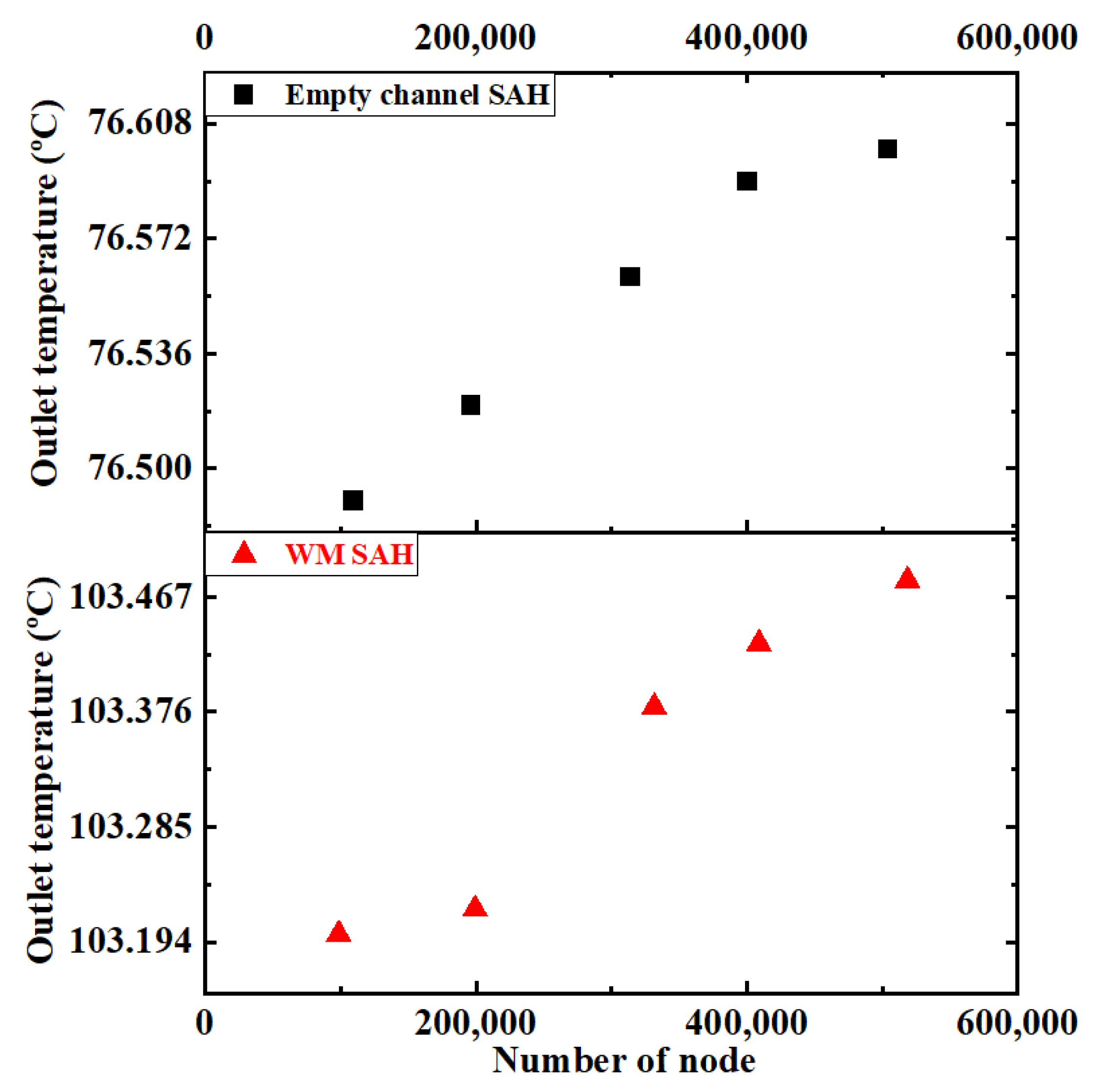
3.4. Grid-Independence Study
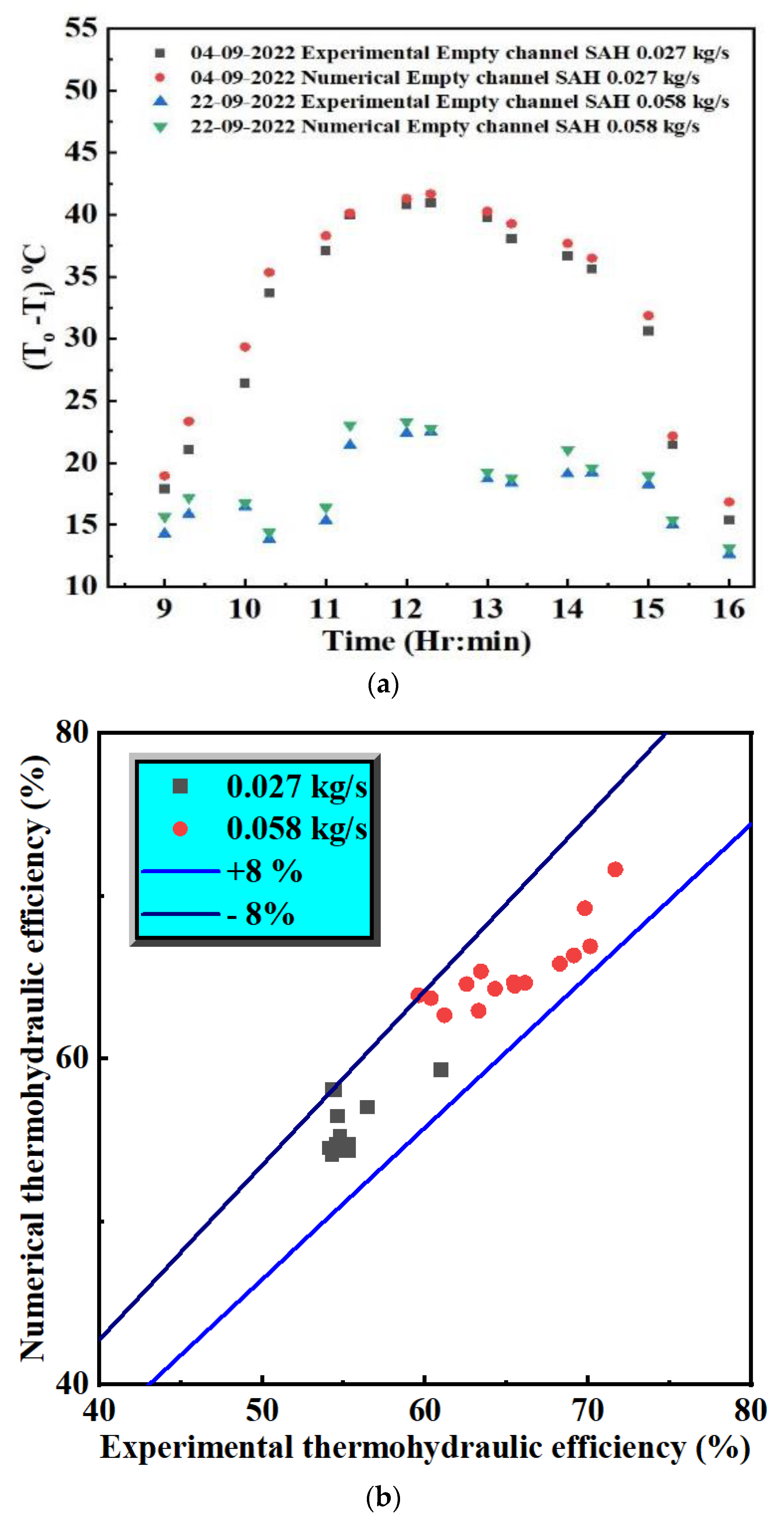
3.5. Validation of Numerical Study with Experimental Data
4. Results and Discussion
4.1. Numerical Results for Different Case Studies
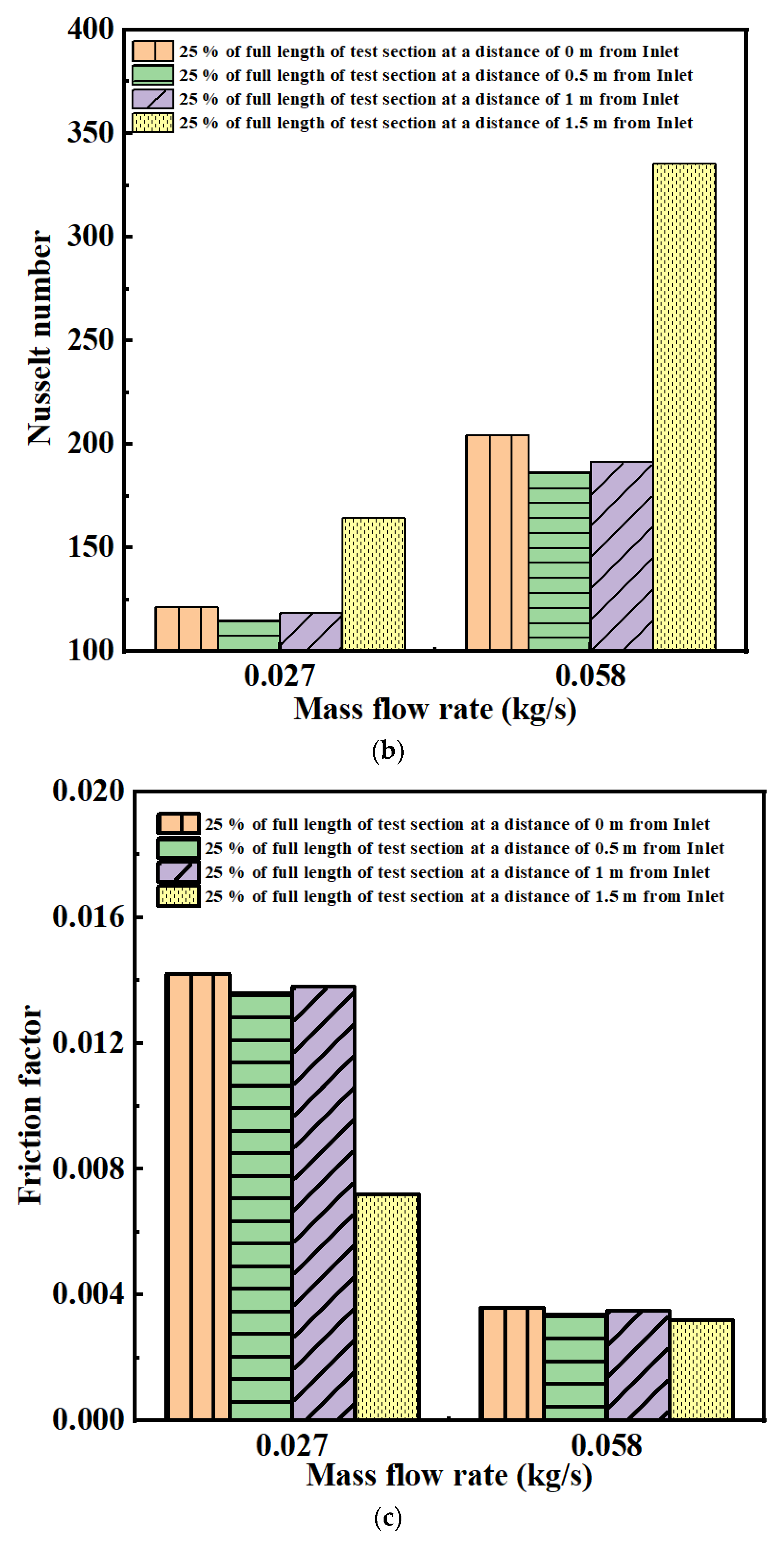
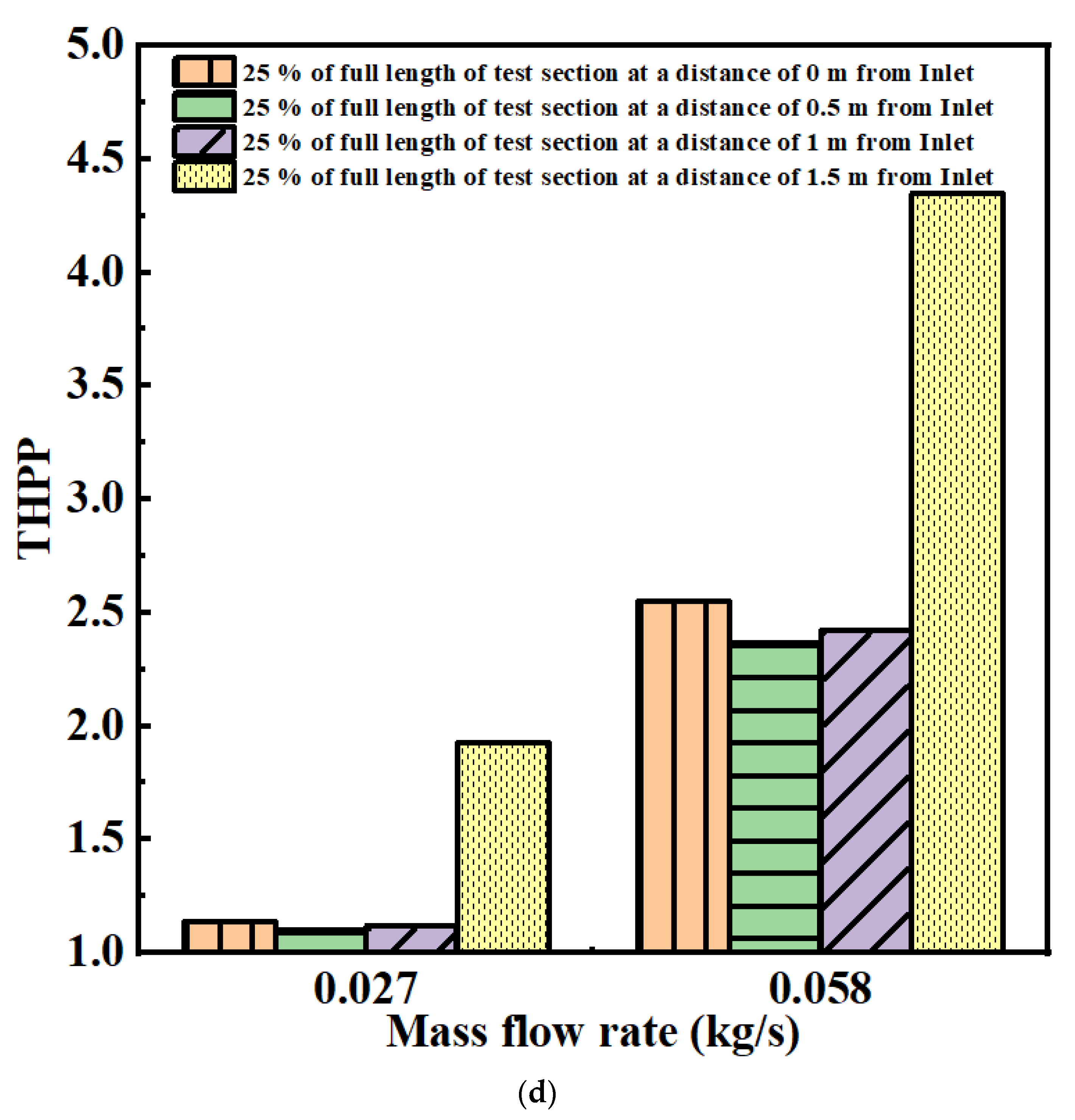
4.1.1. Comparative Study of Temperature Rise, Nusselt Number, Friction Factor, and THPP
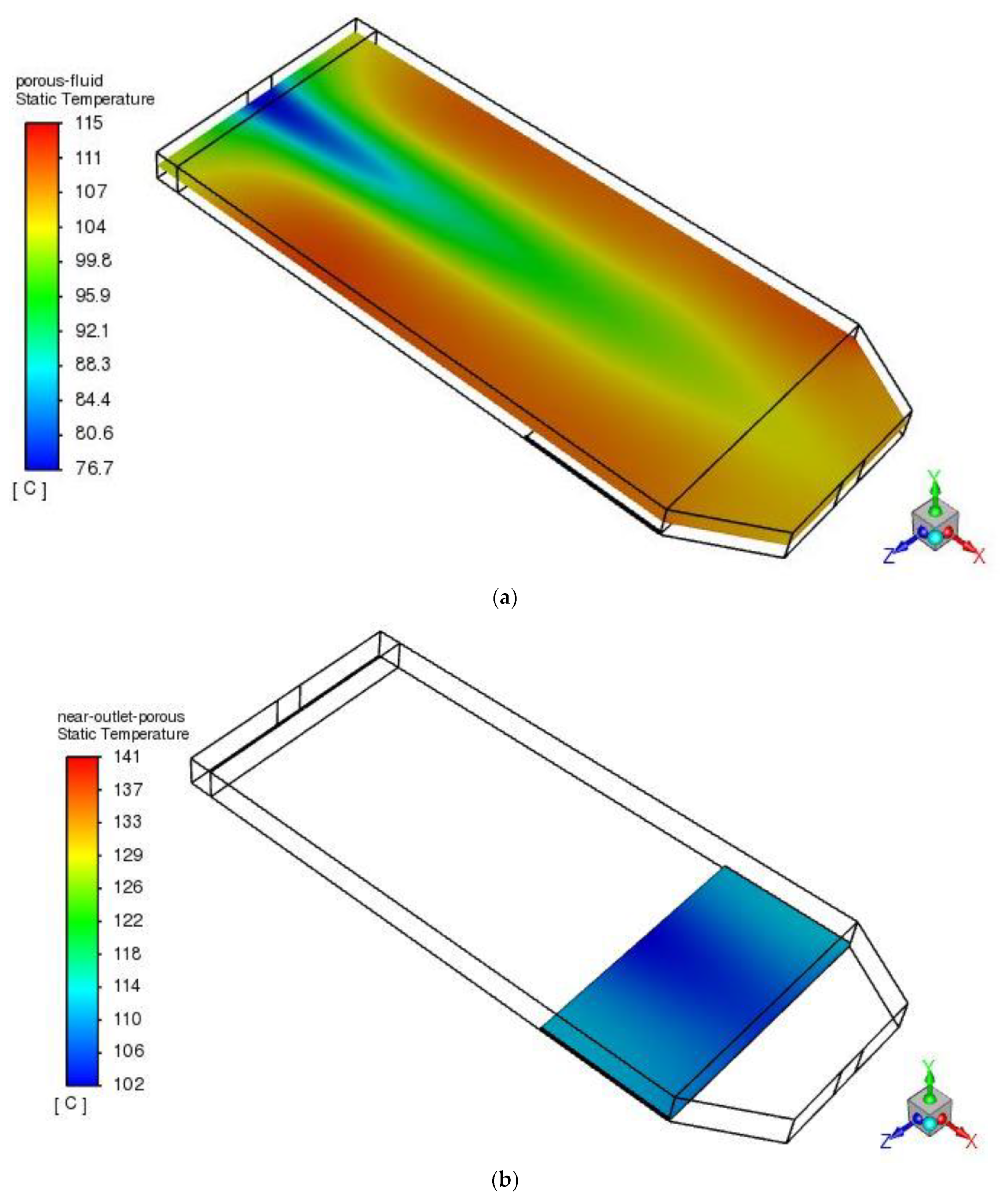
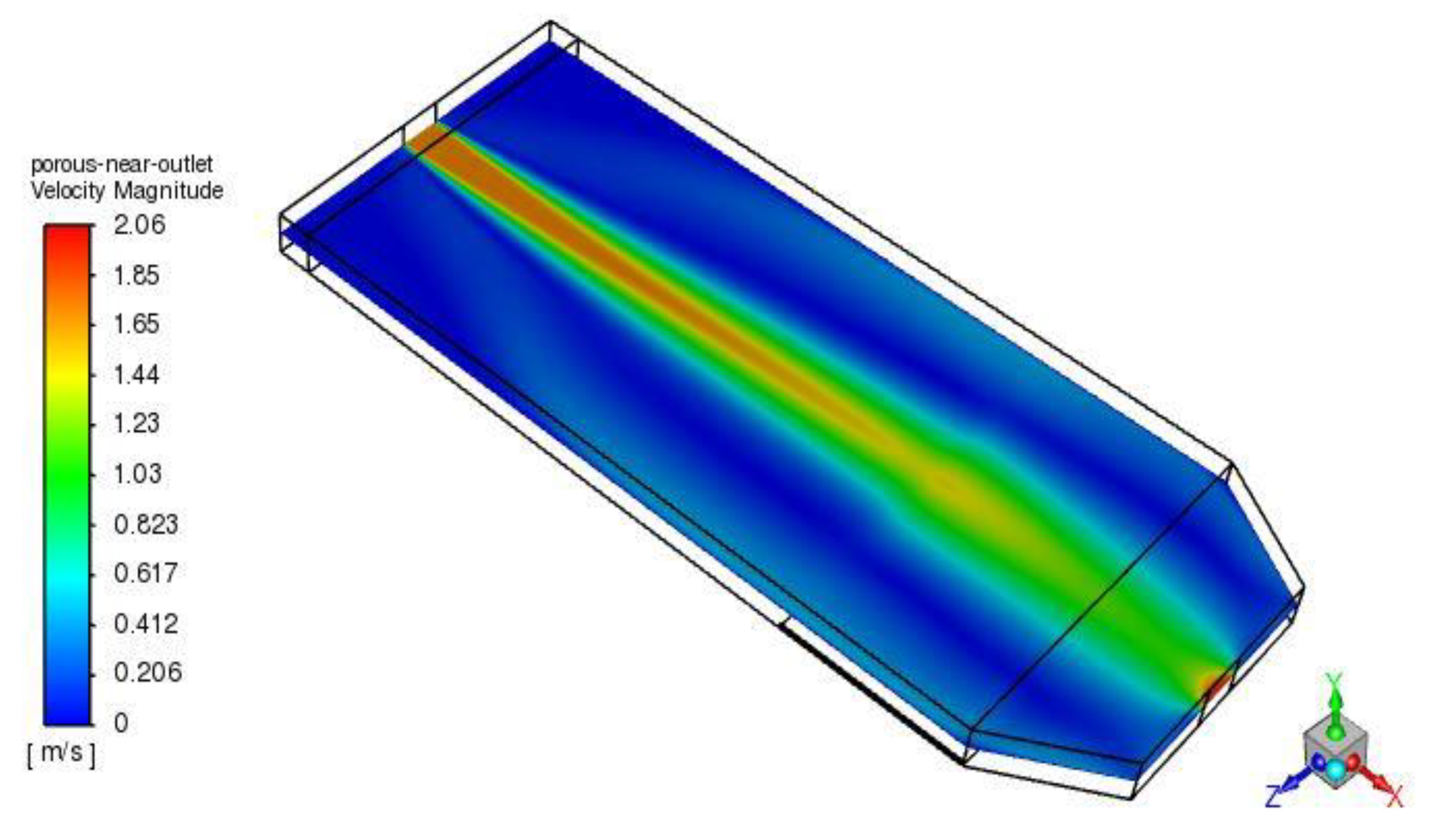
4.1.2. Temperature and Velocity Distribution in the 25% Length Case at a Distance 1.5 m from the Inlet for Single-Pass SAH
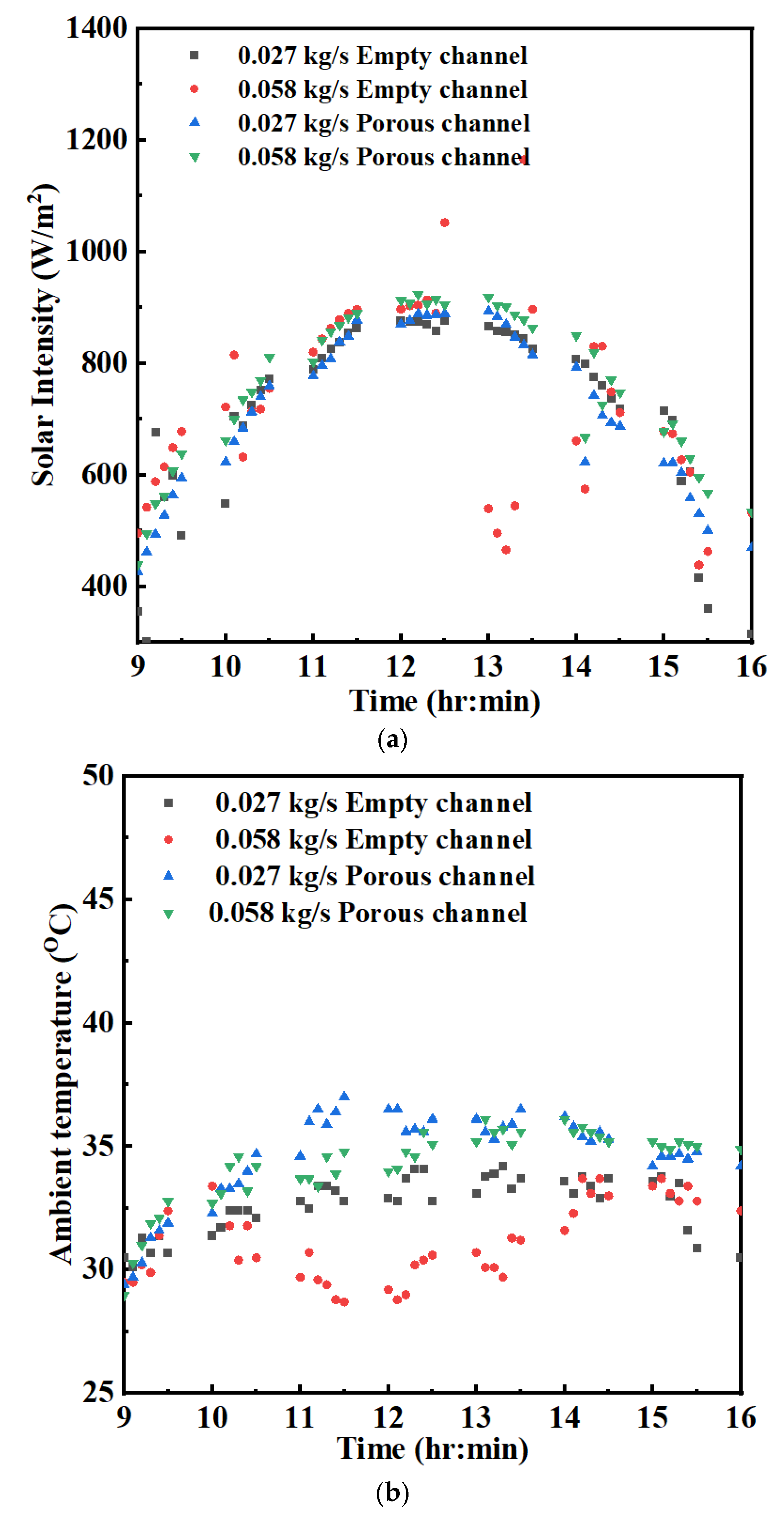
4.2. Experimental Results of Empty Channel and Porous SAH
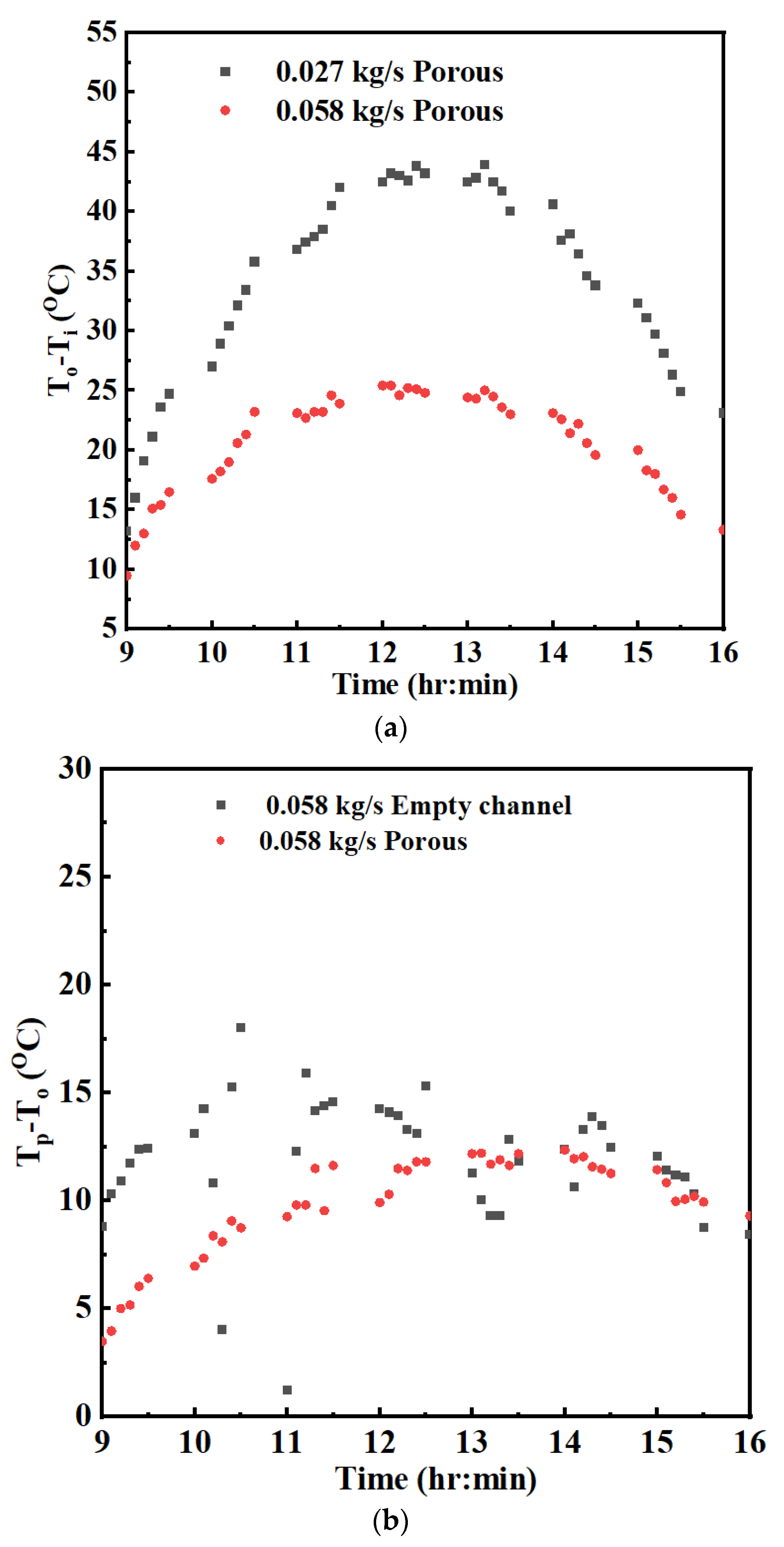
4.2.1. Thermal Performance of Porous Bed SAH
4.2.2. Comparison of Porous-Bed SAH with Empty-Channel SAH
5. Conclusions
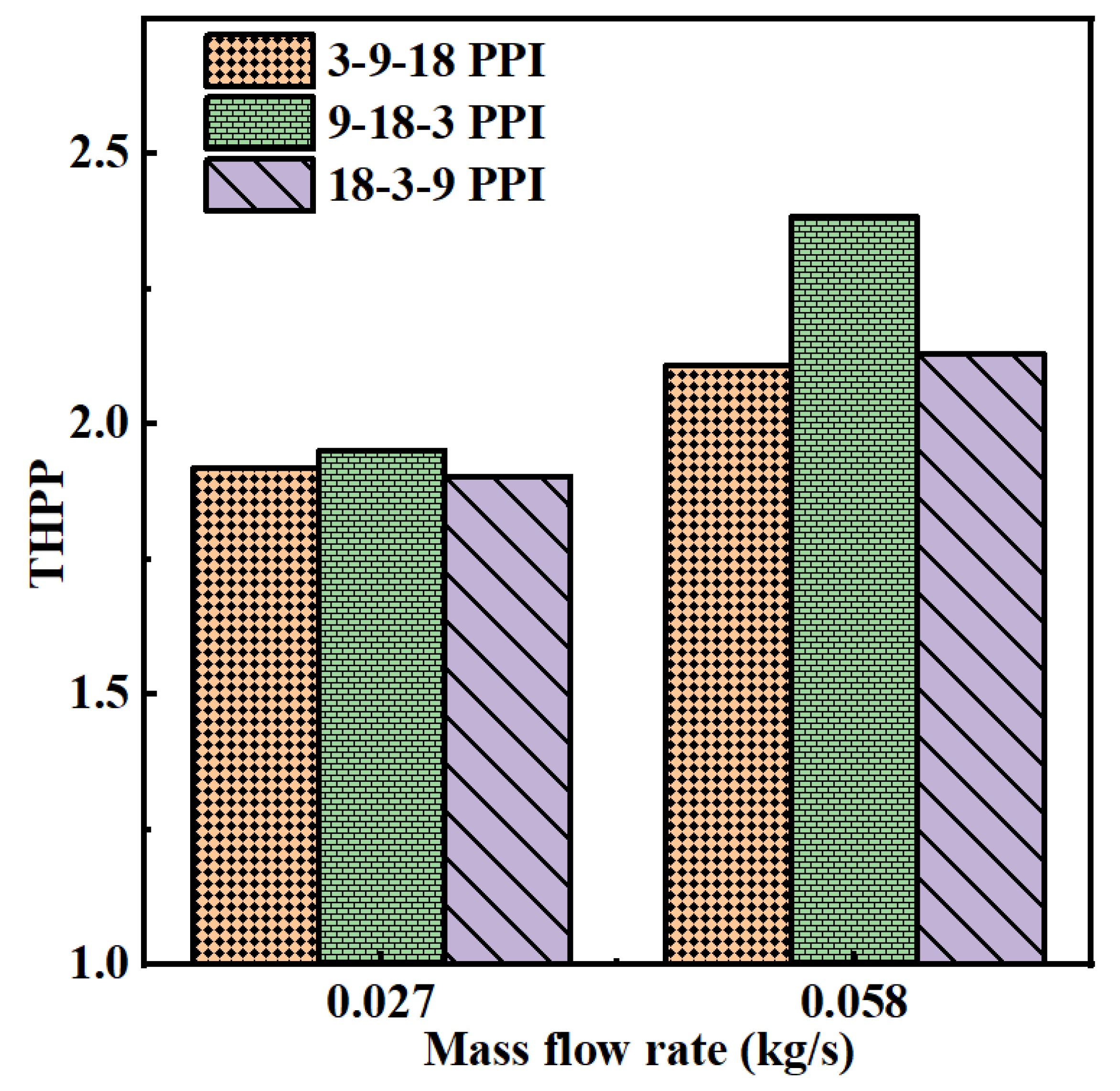
- For the full-length case, 9-18-3 PPI is the best suitable combination compared to Cases 3-9-18 and 18-3-9 PPI in terms of maximum outlet temperature, Nusselt number and THPP. Case 9-18-3 PPI has 7.62% and 7.22% higher average THPP than Case 3-9-18 and 18-3-9, respectively, for both the mass flow rate.
- The 25% length of the GWM of the full-length test section was kept at four different locations (i.e., 0, 0.5, 1, and 1.5 m from the inlet) in numerical analysis. The thermal performance was analysed with respect to temperature, Nusselt number, friction factor, and THPP at these four locations. It shows that the rise in the outlet temperature was nearly the same for all of the cases. The Nusselt number is higher in the WM of 25% of the length of the full-length test section than all other cases considered above as a result of the changes in the absorber plate temperature and bulk mean fluid temperature. The friction factor was lower and THPP was higher for the case of 25% of the length of the WM of the full-length test section among all of the other cases.
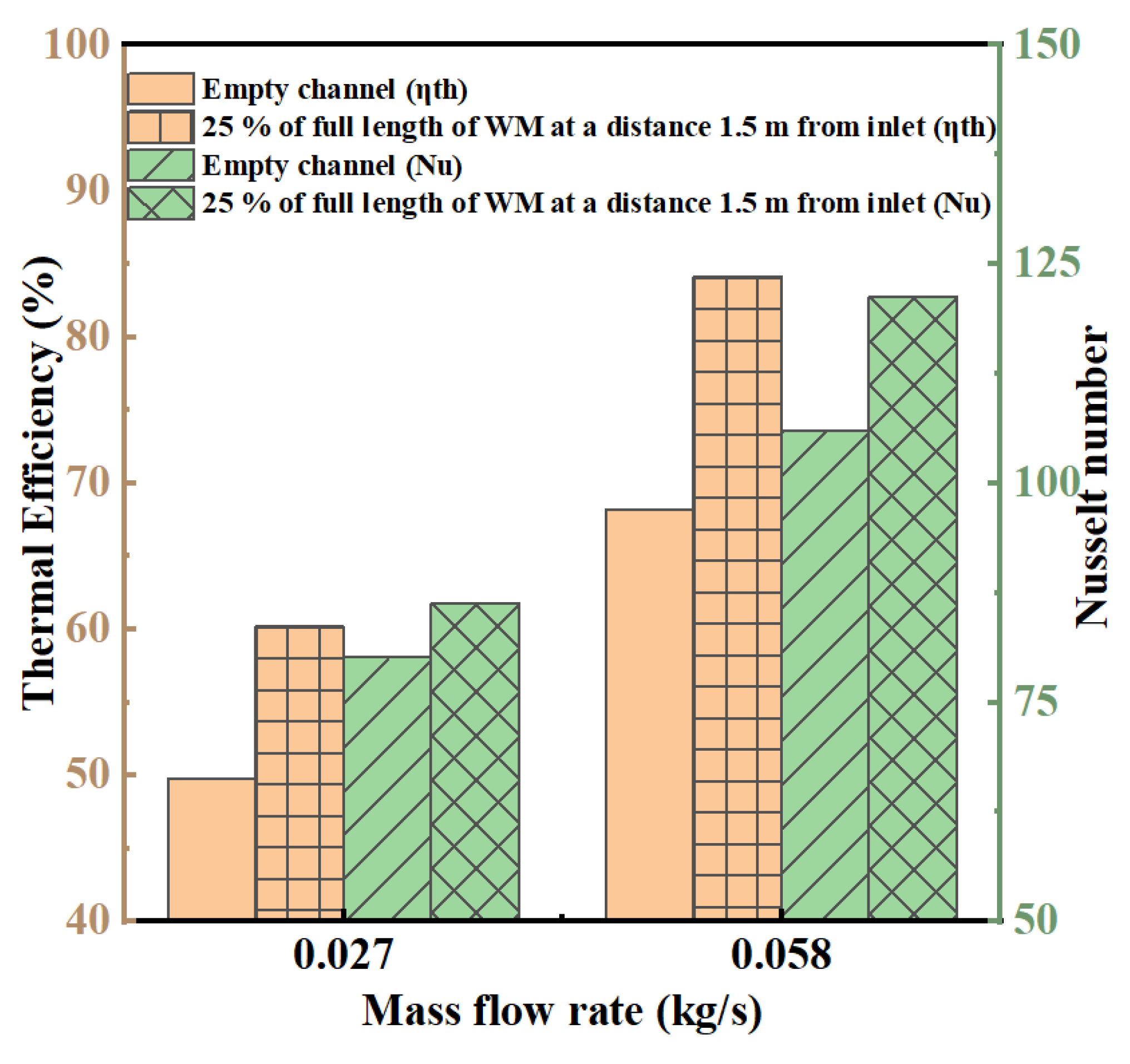
- The 25% length of the WM of the full-length test section at a distance 1.5 m from the inlet is more valuable than all other cases in terms of the overall performance of porous SAH. As the mass flow rate increases, thermal efficiency also increases. The enhancement in the thermal efficiency was 23.32% higher for 0.058 kg/s than the empty channel.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Af | Frontal area (m2) |
| AC | |
| Ap | Absorber plate area (m2) |
| ) | |
| Hydraulic diameter (m) | |
| D | Total height of the WM porous bed (m) |
| dw | Wire diameter (m) |
| f | Friction factor |
| H | Height of the inlet (m) |
| Convective heat transfer coefficient for top cover (W/m2 K) | |
| h | Heat transfer coefficient (W/m2K) |
| ) | |
| k | Thermal conductivity (W/m K) |
| Extinction coefficient | |
| L | Length of the absorber plate (m) |
| l | Height of the diamond WM (m) |
| ) | |
| Nu | Nusselt number |
| N | Pores per inch of wire mesh |
| n | Number of WM layers |
| Fan power | |
| Pflow | Flow pumping power |
| Pr | Prandtl number |
| Pt | Pitch of the WM (m) |
| Re | Reynolds number |
| ReP | Reynolds number of porous media |
| Useful heat gain, W | |
| rh | Hydraulic radius, m |
| T | |
| Vair | ) |
| W | Width of the inlet (m) |
| w | Pore of the diamond type WM (m) |
| Greek symbols | |
| Porosity of wire mesh (%) | |
| Pressure drops across the absorber plate (Pa) | |
| Fan efficiency (%) | |
| Motor efficiency (%) | |
| Thermal efficiency (%) | |
| Thermohydraulic efficiency (%) | |
| ) | |
| Relative density of the WM | |
| σ | Stefan–Boltzmann constant |
| ) | |
| Subscripts | |
| a | Ambient |
| b | Bulk mean fluid temperature |
| e | Empty channel |
| i | Inlet |
| o | Outlet |
| p | Absorber plate |
| Abbreviations | |
| CFD | Computational fluid dynamics |
| DAS | Data acquisition system |
| DC | Direct current |
| G I | Galvanized iron |
| GWM | Graded wire mesh |
| LTE | Local thermal equilibrium |
| MS | Mild steel |
| PVC | Polyvinyl chloride |
| PPI | Pores per inch |
| RNG | Re-normalization group |
| RTD | Resistance temperature detector |
| SAH | Solar air heater |
| THPP | Thermohydraulic performance parameter |
| WM | Wire mesh |
References
- Sukhatme, S.P.; Nayak, J.K. Solar Energy, 4th ed.; McGraw Hill: New York, NY, USA, 2018. [Google Scholar]
- Garg, H.P.; Prakash, J. Solar Energy Fundamentals and Applications, 1st ed.; Mc Graw Hill: New York, NY, USA, 2016. [Google Scholar]
- Yang, C.; Xu, Y.; Cai, X.; Zheng, Z.J. Effect of the Circumferential and Radial Graded Metal Foam on Horizontal Shell-and-Tube Latent Heat Thermal Energy Storage Unit by Choun Yang. Sol. Energy 2021, 226, 225–235. [Google Scholar] [CrossRef]
- Jadhav, P.H.; Gnanasekaran, N.; Mobedi, M. Analysis of Functionally Graded Metal Foams for the Accomplishment of Heat Transfer Enhancement under Partially Filled Condition in a Heat Exchanger. Energy 2023, 263, 125691. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Reddy, K.S. Lecture Notes in Mechanical Engineering Numerical Heat Transfer and Fluid Flow Select Proceedings of NHTFF 2018; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Trilok, G.; Gnanasekaran, N.; Mobedi, M. Various Trade-Off Scenarios in Thermo-Hydrodynamic Performance of Metal Foams Due to Variations in Their Thickness and Structural Conditions. Energies 2021, 14, 8343. [Google Scholar] [CrossRef]
- Trilok, G.; Srinivas, K.E.S.; Harikrishnan, D.; Gnanasekaran, N.; Mobedi, M. Correlations and Numerical Modeling of Stacked Woven Wire-Mesh Porous Media for Heat Exchange Applications. Energies 2022, 15, 2371. [Google Scholar]
- Liu, G.; Li, Y.; Wei, P.; Xiao, T.; Meng, X.; Yang, X. Thermo-Economic Assessments on a Heat Storage Tank Filled with Graded Metal Foam. Energies 2022, 15, 7213. [Google Scholar] [CrossRef]
- Abdulla, A.; Reddy, K.S. Comparative Study of Single and Multi-Layered Packed-Bed Thermal Energy Storage Systems for CSP Plants. Appl. Sol. Energy 2017, 53, 276–286. [Google Scholar] [CrossRef]
- Du, S.; Li, Z.Y.; He, Y.L.; Li, D.; Xie, X.Q.; Gao, Y. Experimental and Numerical Analysis of the Hydraulic and Thermal Performances of the Gradually-Varied Porous Volumetric Solar Receiver. Sci. China Technol. Sci. 2020, 63, 1224–1234. [Google Scholar] [CrossRef]
- Saedodin, S.; Zamzamian, S.A.H.; Nimvari, M.E.; Wongwises, S.; Jouybari, H.J. Performance Evaluation of a Flat-Plate Solar Collector Filled with Porous Metal Foam: Experimental and Numerical Analysis. Energy Convers. Manag. 2017, 153, 278–287. [Google Scholar] [CrossRef]
- Farhan, A.A.; Obaid, Z.A.H.; Hussien, S.Q. Analysis of Exergetic Performance for a Solar Air Heater with Metal Foam Fins. Heat Transf.-Asian Res. 2020, 49, 3190–3204. [Google Scholar] [CrossRef]
- Taha, S.Y.; Farhan, A.A. Performance Augmentation of a Solar Air Heater Using Herringbone Metal Foam Fins: An Experimental Work. Int. J. Energy Res. 2021, 45, 2321–2333. [Google Scholar] [CrossRef]
- Anirudh, K.; Dhinakaran, S. Numerical Study on Performance Improvement of a Flat-Plate Solar Collector Filled with Porous Foam. Renew. Energy 2020, 147, 1704–1717. [Google Scholar] [CrossRef]
- Chiou, J.P.; El-Wakil, M.M.; Duffie, J.A. A Slit-and -Expanded Aluminum-Foil Matrix Solar Collector. Sol. Energy 1965, 9, 73–80. [Google Scholar] [CrossRef]
- Sharma, S.P.; Saini, J.S.; Varma, H.K. Thermal Performance of Packed-Bed Solar Air Heaters. Sol. Energy 1991, 47, 59–67. [Google Scholar] [CrossRef]
- Ahmad, A.; Saini, J.S.; Varma, H.K. Thermohydraulic Performance of Packed-Bed Solar Air Heaters; Elsevier: Amsterdam, The Netherlands, 1996; Volume 37. [Google Scholar]
- Varshney, L.; Saini, J.S. Heat Transfer and Friction Factor Correlations for Rectangular Solar Air Heater Duct Packed with Wire Mesh Screen Matrices; Elsevier: Amsterdam, The Netherlands, 1998; Volume 62. [Google Scholar]
- Thakur, N.S.; Saini, J.S.; Solanki, S.C. Heat Transfer and Friction Factor Correlations for Packed Bed Solar Air Heater for a Low Porosity System. Sol. Energy 2003, 74, 319–329. [Google Scholar] [CrossRef]
- Mittal, M.K.; Varshney, L. Optimal Thermohydraulic Performance of a Wire Mesh Packed Solar Air Heater. Sol. Energy 2006, 80, 1112–1120. [Google Scholar] [CrossRef]
- Singh, O.K.; Panwar, N.L. Effects of Thermal Conductivity and Geometry of Materials on the Temperature Variation in Packed Bed Solar Air Heater. J. Therm. Anal. Calorim. 2013, 111, 839–847. [Google Scholar] [CrossRef]
- Chouksey, V.K.; Sharma, S.P. Investigations on Thermal Performance Characteristics of Wire Screen Packed Bed Solar Air Heater. Sol. Energy 2016, 132, 591–605. [Google Scholar] [CrossRef]
- Sharma, S.P.; Chauksey, V.K.; Kumar, A.; Behura, A.K.; Kumar, R. Wire Screen Matrices Packed Bed Solar Air Heater Performance—An Exergetic and Energetic Approach. Appl. Sci. 2017, 4, 90–108. [Google Scholar]
- Adnan Abed, Q.; Badescu, V.; Ciocanea, A.; Soriga, I.; Bureţea, D. Models for New Corrugated and Porous Solar Air Collectors under Transient Operation. J. Non-Equilib. Thermodyn. 2017, 42, 79–97. [Google Scholar] [CrossRef]
- Devecioğlu, A.G.; Oruc, V.; Tuncer, Z. Energy and Exergy Analyses of a Solar Air Heater with Wire Mesh-Covered Absorber Plate. Int. J. Exergy 2018, 26, 3–20. [Google Scholar] [CrossRef]
- Ghritlahre, H.K.; Prasad, R.K. Investigation of Thermal Performance of Unidirectional Flow Porous Bed Solar Air Heater Using MLP, GRNN, and RBF Models of ANN Technique. Therm. Sci. Eng. Prog. 2018, 6, 226–235. [Google Scholar] [CrossRef]
- Rajarajeswari, K.; Alok, P.; Sreekumar, A. Simulation and Experimental Investigation of Fluid Flow in Porous and Non-Porous Solar Air Heaters. Sol. Energy 2018, 171, 258–270. [Google Scholar] [CrossRef]
- Sözen, A.; Şirin, C.; Khanlari, A.; Tuncer, A.D.; Gürbüz, E.Y. Thermal Performance Enhancement of Tube-Type Alternative Indirect Solar Dryer with Iron Mesh Modification. Sol. Energy 2020, 207, 1269–1281. [Google Scholar] [CrossRef]
- Jalil, J.M.; Ali, S.J. Thermal Investigations of Double Pass Solar Air Heater with Two Types of Porous Media of Different Thermal Conductivity. Eng. Technol. J. 2021, 39, 79–88. [Google Scholar] [CrossRef]
- Sözen, A.; Kazancıoğlu, F.Ş.; Tuncer, A.D.; Khanlari, A.; Bilge, Y.C.; Gungor, A. Thermal Performance Improvement of an Indirect Solar Dryer with Tube-Type Absorber Packed with Aluminum Wool. Sol. Energy 2021, 217, 328–341. [Google Scholar] [CrossRef]
- Omojaro, A.P.; Aldabbagh, L.B.Y. Experimental Performance of Single and Double Pass Solar Air Heater with Fins and Steel Wire Mesh as Absorber. Appl. Energy 2010, 87, 3759–3765. [Google Scholar] [CrossRef]
- Aldabbagh, L.B.Y.; Egelioglu, F.; Ilkan, M. Single and Double Pass Solar Air Heaters with Wire Mesh as Packing Bed. Energy 2010, 35, 3783–3787. [Google Scholar] [CrossRef]
- Nowzari, R.; Mirzaei, N.; Aldabbagh, L.B.Y. Finding the Best Configuration for a Solar Air Heater by Design and Analysis of Experiment. Energy Convers. Manag. 2015, 100, 131–137. [Google Scholar] [CrossRef]
- Nowzari, R.; Aldabbagh, L.B.Y. Experimental Study on a Solar Air Heater with Various Perforated Covers. Sadhana-Acad. Proc. Eng. Sci. 2017, 42, 1585–1593. [Google Scholar] [CrossRef] [Green Version]
- Kesavan, S.; Arjunan, T.V.; Vijayan, S. Thermodynamic Analysis of a Triple-Pass Solar Dryer for Drying Potato Slices. J. Therm. Anal. Calorim. 2019, 136, 159–171. [Google Scholar] [CrossRef]
- Prasad, S.B.; Saini, J.S.; Singh, K.M. Investigation of Heat Transfer and Friction Characteristics of Packed Bed Solar Air Heater Using Wire Mesh as Packing Material. Sol. Energy 2009, 83, 773–783. [Google Scholar] [CrossRef]
- Nowzari, R.; Saygin, H.; Aldabbagh, L.B.Y. Evaluating the Performance of a Modified Solar Air Heater with Pierced Cover and Packed Mesh Layers. J. Sol. Energy Eng. Trans. ASME 2021, 143, 011006. [Google Scholar] [CrossRef]
- Güler, H.Ö.; Sözen, A.; Tuncer, A.D.; Afshari, F.; Khanlari, A.; Şirin, C.; Gungor, A. Experimental and CFD Survey of Indirect Solar Dryer Modified with Low-Cost Iron Mesh. Sol. Energy 2020, 197, 371–384. [Google Scholar] [CrossRef]
- Ranake Vinayak Data Loggers, Wireless Data Logger, Chart Recorder, Manufacturer, India. Available online: https://www.sunsuiprocess.com/ (accessed on 23 November 2022).
- Cengel, Y.A. Heat Transfer a Practical Approach; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Singh, S. Utilising Fractional Porous Interface for High Thermal Performance of Serpentine Wavy Channel Solar Air Heater. Appl. Therm. Eng. 2022, 205, 118044. [Google Scholar] [CrossRef]
- Azad, R.; Bhuvad, S.; Lanjewar, A. Study of Solar Air Heater with Discrete Arc Ribs Geometry: Experimental and Numerical Approach. Int. J. Therm. Sci. 2021, 167, 107013. [Google Scholar] [CrossRef]
- Saravanan, A.; Murugan, M.; Reddy, M.S.; Ranjit, P.S.; Elumalai, P.V.; Kumar, P.; Sree, S.R. Thermo-Hydraulic Performance of a Solar Air Heater with Staggered C-Shape Finned Absorber Plate. Int. J. Therm. Sci. 2021, 168, 107068. [Google Scholar] [CrossRef]
- Kumar, D.; Layek, A. Nusselt Number and Friction Characteristics of Solar Air Heater Roughened with Novel Twisted V-Shaped Staggered Ribs Using Liquid Crystal Thermography. Renew. Energy 2022, 201, 651–666. [Google Scholar] [CrossRef]
- Holman, J.P. Experimental Methods for Engineers, 6th ed.; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- El-khawajah, M.F.; Aldabbagh, L.B.Y.; Egelioglu, F. The Effect of Using Transverse Fins on a Double Pass Flow Solar Air Heater Using Wire Mesh as an Absorber. Sol. Energy 2011, 85, 1479–1487. [Google Scholar] [CrossRef]
- Singh, S. Experimental and Numerical Investigations of a Single and Double Pass Porous Serpentine Wavy Wiremesh Packed Bed Solar Air Heater. Renew. Energy 2020, 145, 1361–1387. [Google Scholar] [CrossRef]
- Yadav, S.; Saini, R.P. Numerical Investigation on the Performance of a Solar Air Heater Using Jet Impingement with Absorber Plate. Sol. Energy 2020, 208, 236–248. [Google Scholar] [CrossRef]
- Diganjit, R.; Gnanasekaran, N.; Mobedi, M. Numerical Study for Enhancement of Heat Transfer Using Discrete Metal Foam with Varying Thickness and Porosity in Solar Air Heater by LTNE Method. Energies 2022, 15, 8952. [Google Scholar] [CrossRef]
- Parsa, H.; Saffar-Avval, M.; Hajmohammadi, M.R. 3D Simulation and Parametric Optimization of a Solar Air Heater with a Novel Staggered Cuboid Baffles. Int. J. Mech. Sci. 2021, 205, 106607. [Google Scholar] [CrossRef]
- Zhao, Z.; Luo, L.; Qiu, D.; Wang, Z.; Sundén, B. On the Solar Air Heater Thermal Enhancement and Flow Topology Using Differently Shaped Ribs Combined with Delta-Winglet Vortex Generators. Energy 2021, 224, 119944. [Google Scholar] [CrossRef]
- Ansys Fluent R2 Student Version; Ansys, Inc.: Canonsburg, PA, USA, 2022.
- Avila-Marin, A.L.; Fernandez-Reche, J.; Martinez-Tarifa, A. Modelling Strategies for Porous Structures as Solar Receivers in Central Receiver Systems: A Review. Renew. Sustain. Energy Rev. 2019, 111, 15–33. [Google Scholar] [CrossRef]
- Anirudh, K.; Dhinakaran, S. Performance Improvement of a Flat-Plate Solar Collector by Inserting Intermittent Porous Blocks. Renew. Energy 2020, 145, 428–441. [Google Scholar] [CrossRef]
- Jadhav, P.H.; Gnanasekaran, N. Optimum Design of Heat Exchanging Device for Efficient Heat Absorption Using High Porosity Metal Foams. Int. Commun. Heat Mass Transf. 2021, 126, 105475. [Google Scholar] [CrossRef]
- Howell, J.R.; Siegel, R. Thermal Radiation Heat Transfer; Taylor and Francis: Abingdon, UK, 2002. [Google Scholar]
- Gill, R.S.; Hans, V.S.; Singh, R.P. Optimization of Artificial Roughness Parameters in a Solar Air Heater Duct Roughened with Hybrid Ribs. Appl. Therm. Eng. 2021, 191, 116871. [Google Scholar] [CrossRef]
- Tian, J.; Kim, T.; Lu, T.J.; Hodson, H.P.; Queheillalt, D.T.; Sypeck, D.J.; Wadley, H.N.G. The Effects of Topology upon Fluid-Flow and Heat-Transfer within Cellular Copper Structures. Int. J. Heat Mass Transf. 2004, 47, 3171–3186. [Google Scholar] [CrossRef]
- Gupta, M.K.; Kaushik, S.C. Performance Evaluation of Solar Air Heater Having Expanded Metal Mesh as Artificial Roughness on Absorber Plate. Int. J. Therm. Sci. 2009, 48, 1007–1016. [Google Scholar] [CrossRef]
- Nidhul, K.; Yadav, A.K.; Anish, S.; Arunachala, U.C. Efficient Design of an Artificially Roughened Solar Air Heater with Semi-Cylindrical Side Walls: CFD and Exergy Analysis. Sol. Energy 2020, 207, 289–304. [Google Scholar] [CrossRef]
- Koholé, Y.W.; Fohagui, F.C.V.; Tchuen, G. Flat-Plate Solar Collector Thermal Performance and Optimal Operation Mode by Exergy Analysis and Numerical Simulation. Arab. J. Sci. Eng. 2021, 46, 1877–1897. [Google Scholar] [CrossRef]
- Patel, Y.M.; Jain, S.V.; Lakhera, V.J. Thermo-Hydraulic Performance Analysis of a Solar Air Heater Roughened with Discrete Reverse NACA Profile Ribs. Int. J. Therm. Sci. 2021, 167, 107026. [Google Scholar] [CrossRef]
- Nidhul, K.; Yadav, A.K.; Anish, S.; Arunachala, U.C. Thermo-Hydraulic and Exergetic Performance of a Cost-Effective Solar Air Heater: CFD and Experimental Study. Renew. Energy 2022, 184, 627–641. [Google Scholar] [CrossRef]
- Debnath, S.; Das, B.; Randive, P. Energy and Exergy Analysis of Plain and Corrugated Solar Air Collector: Effect of Seasonal Variation. Int. J. Ambient. Energy 2022, 43, 2796–2807. [Google Scholar] [CrossRef]
- Kothandaraman, C.P. Heat and Mass Transfer Data Book, 9th ed.; New Age International Publishers: Chennai, India, 2018; ISBN 978-93-86649-30-0. [Google Scholar]
- Hu, J.; Sun, X.; Xu, J.; Li, Z. Numerical Analysis of Mechanical Ventilation Solar Air Collector with Internal Baffles. Energy Build. 2013, 62, 230–238. [Google Scholar] [CrossRef]
- Hung, T.C.; Huang, T.J.; Lee, D.S.; Lin, C.H.; Pei, B.S.; Li, Z.Y. Numerical Analysis and Experimental Validation of Heat Transfer Characteristic for Flat-Plate Solar Air Collector. Appl. Therm. Eng. 2017, 111, 1025–1038. [Google Scholar] [CrossRef]
- Hu, J.; Guo, M.; Guo, J.; Zhang, G.; Zhang, Y. Numerical and Experimental Investigation of Solar Air Collector with Internal Swirling Flow. Renew. Energy 2020, 162, 2259–2271. [Google Scholar] [CrossRef]
- Jia, B.; Yang, L.; Zhang, L.; Liu, B.; Liu, F.; Li, X. Optimizing Structure of Baffles on Thermal Performance of Spiral Solar Air Heaters. Sol. Energy 2021, 224, 757–764. [Google Scholar] [CrossRef]
- Kansara, R.; Pathak, M.; Patel, V.K. Performance Assessment of Flat-Plate Solar Collector with Internal Fins and Porous Media through an Integrated Approach of CFD and Experimentation. Int. J. Therm. Sci. 2021, 165, 106932. [Google Scholar] [CrossRef]
- Bai, X.; Kuwahara, F.; Mobedi, M.; Nakayama, A. Forced Convective Heat Transfer in a Channel Filled with a Functionally Graded Metal Foam Matrix. J. Heat Transf. 2018, 140, 111702. [Google Scholar] [CrossRef]
- Gupta, C.L.; Garg, H.P. Performance Studies on Solar Air Heaters. Sol. Energy 1967, 11, 25–31. [Google Scholar] [CrossRef]
- Gill, R.S.; Singh, S.; Singh, P.P. Low Cost Solar Air Heater. Energy Convers. Manag. 2012, 57, 131–142. [Google Scholar] [CrossRef]

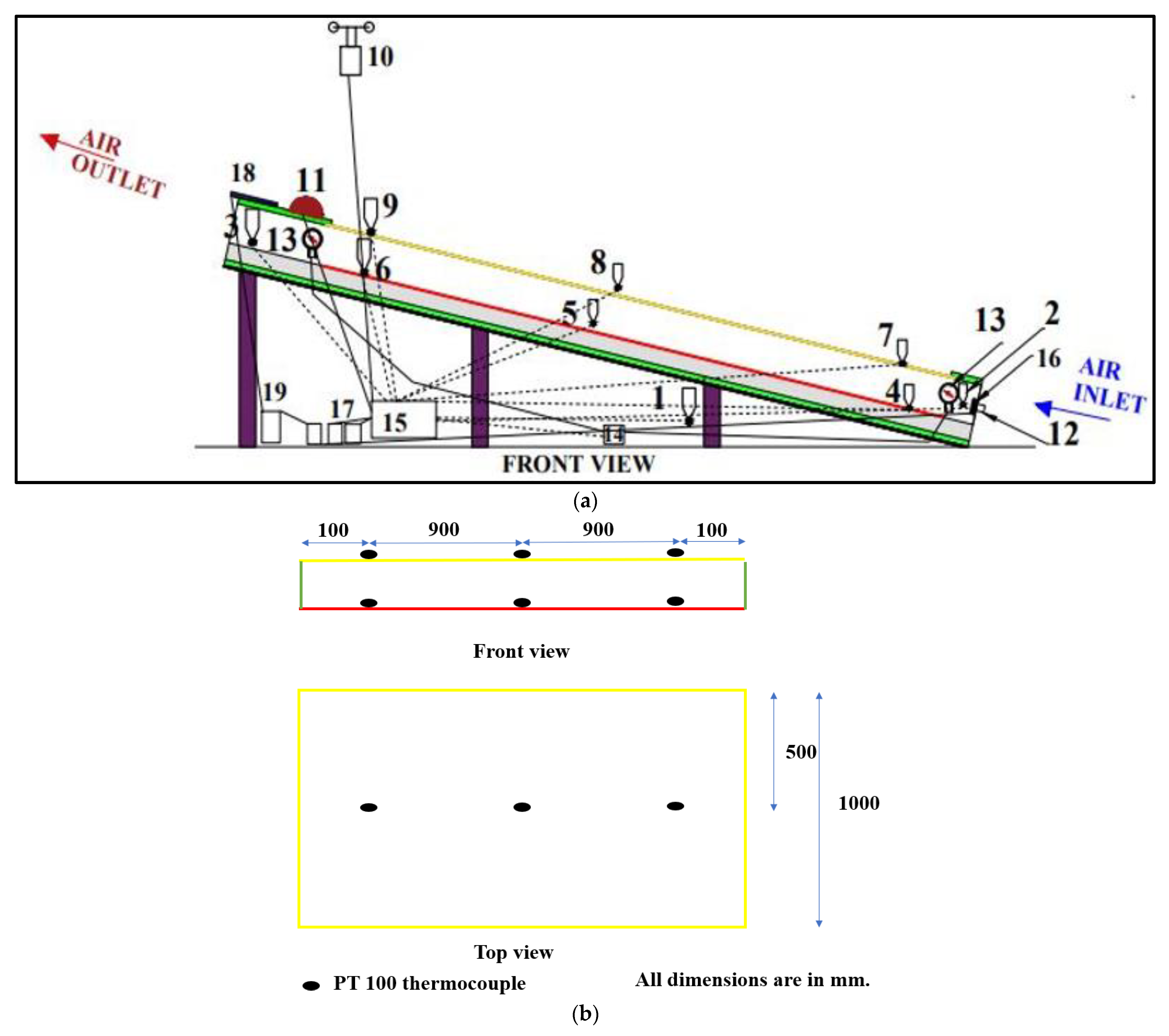





| Sr. No | Name of the Product, Quantity | Purpose | Make and Model | Accuracy | Range | Resolution |
|---|---|---|---|---|---|---|
| 1 | Solar pyranometer, 1 | To measure the intensity of solar radiation. | Pyra 300 V | ±5 W/m2 | 0–1800 W/m2 | 0.1 W/m2 |
| 2 | PT 100 RTD, 9 | At different positions to measure the temperatures of glazing (3), absorber (3), inlet air, outlet air, ambient | Heatron Industrial Heaters Class 1/3 | ±1 °C | 0–800 °C | 0.001 °C |
| 3 | Vane probe anemometer, 1 | To measure the velocity inside the duct | Mextech AM 4208 | ±2% | 0.4–45 m/s | 0.1 m/s |
| 4 | Differential pressure transmitter, 1 | To connect across the test section and to measure the pressure drop inside the duct | Sensocon Series 211 | ±5% | 0.5% | 0.25% |
| 5 | Universal data logger 16 Channel, 1 | To record the temperatures, pressure drop, velocity, and solar intensity for every 10 min | Sunsui Make DL-35-16 | For RTD ±0.2% or ±0.5 °C | For RTD 0–400 °C | For RTD 0.1 °C |
| 6 | Wind speed Sensor, 1 | To measure the wind speed | Sunsui Make-OC ANE-01, | ±2% | 0.3 to 60 m/s | 0.1 m/s |
| 7 | Measuring tape, 1 | To measure the length, width, and height of the parts of the SAH | Venus-Stylo | ±0.001 m | 0 to 3 m | 0.001 m |
| 8 | Flat scale rule, 1 | To measure the length | S.K. | ±0.001 m | 0 to 0.015 m | 0.001 m |
| 9 | Vernier Caliper, 1 | To measure the length | Kristeel-Shinwa | ±0.01 m | 0 to 0.015 m | 0.01 m |
| Type of Wire Mesh | Diamond or Expanded Metal Mesh | Diamond or Expanded Metal Mesh | Square Mesh |
|---|---|---|---|
| Pore per inch (PPI) | 3 | 9 | 18 |
| Wire diameter dw (mm) | 0.91 | 0.48 | 0.21 |
| Pitch Pt (mm) | 6.862 | 1.7 | 1.26 |
| Thickness of single-layer WM (mm) | 1.804 | 1.176 | 0.618 |
| 0.894 | 0.812 | 0.917 | |
| Viscous resistance (1/K) (m−2) | 2,546,508.718 | 34,898,955.12 | 30,116,606.43 |
| Inertial resistance (CF) (m−1) | 570.58 | 2560.5 | 1865 |
| Pt/dW | 7.54 | 3.54 | 6 |
| The number of layers used to achieve 5 mm thickness | 3 | 4 | 8 |
| 1/n | 0.37 | 0.31 | 0.14 |
| Uncertainty in Measurement | Uncertainty | Unit |
|---|---|---|
| Mass flow rate, | ±1.47%–1.028% | |
| Thermal efficiency, | ±3.48 | % |
| Properties | Aluminium | Toughened Glass | Polyvinyl Chloride Board Sheet (PVC) | Ceramic Wool | Air 47.5 °C |
|---|---|---|---|---|---|
| Density (ρ) kg/m3 | 2719 | 2500 | 0.55 | 64 | 1.1035 |
| Specific heat capacity (Cp) J/kg K | 871 | 670 | 900 | 1246 | 1005 |
| Thermal conductivity (k) W/m K | 202.4 | 0.7443 | 0.05 | 0.20 | 0.02805 |
| Dynamic viscosity (μ) Ns/m2 | - | - | - | - | 1.95 × 10−5 |
| Absorptivity | 0.95 | 0.06 | - | - | - |
| Emissivity | - | 0.88 | - | - | - |
| Transmissivity | - | 0.90 | - | - | - |
| Absorption coefficient | - | - | - | - | 1 |
| Refractive index | - | - | - | - | 1 |
| Momentum | Thermal | Radiation | |
|---|---|---|---|
| Absorber plate | Stationary wall No slip condition | Heat flux is flux absorbed by the absorber plate in W/m2 which is equal to the product of IT(τα) [50,65]. Absorber plate material is aluminium and wall thickness is 0.0005 m Bottom of the wall | Opaque BC type and absorptivity is 0.95 |
| Glass | Stationary wall No slip condition | Mixed [66,67,68] hw = 5.7 + (3.8 ) in W/m2 [68,69] Free stream temperatures are ambient temperature External emissivity is 0.88 External radiation temp is ambient temperature Wall thickness is 0.004 m | BC type—semi-transparent wall Absorptivity is 0.1 Transmissivity is 0.9 |
| Side wall and other walls | Stationary wall No slip condition | Heat flux is zero W/m2, i.e., adiabatic wall Wall Material is PVC Wall thickness is 0.018 m | BC type is opaque and does not participate in solar ray tracing |
| Inlet | Velocity magnitude as 1.7 and 3.6 m/s, with turbulent intensity as 4.9696 and 4.5247, respectively, and hydraulic diameter as 0.12 | Inlet temperature is obtained from experimental reading | Radiation condition is participating and factor is 1 |
| Outlet | Pressure outlet as zero and hydraulic diameter as 0.12 | Back flow temperature in the initial case same as inlet temperature | Radiation condition is participating and factor is 1 |
| Case | Number of Nodes | Outlet Temperature in °C | in Pa | % Deviation for |To| | |
|---|---|---|---|---|---|
| Empty channel SAH | 109,200 | 76.49 | 1.62 | 0.14 | 2.53 |
| 196,224 | 76.52 | 1.62 | 0.11 | 2.53 | |
| 314,160 | 76.56 | 1.63 | 0.05 | 3.16 | |
| 400,365 | 76.59 | 1.60 | 0.01 | 1.25 | |
| 504,192 | 76.60 | 1.58 | Baseline | ||
| WM SAH | 98,560 | 103.2 | 1.64 | 0.27 | 0.61 |
| 199,281 | 103.22 | 1.64 | 0.25 | 0.61 | |
| 331,500 | 103.38 | 1.64 | 0.097 | 0.61 | |
| 409,136 | 103.43 | 1.65 | 0.048 | 0 | |
| 518,500 | 103.48 | 1.65 | Baseline | ||
| Author Year and Ref. | Mass Flow Rate (kg/s) | Different Porous Absorbers | Thermal Efficiency (%) |
|---|---|---|---|
| Gupta and Garg 1967 [72] | 1.22 × 10−3 g/cm2 s | Aluminium expanded metal mesh with carbon black coating | 50 |
| Omojaro and Aldabbagh 2010 [31] | 0.012 to 0.038 | WM with longitudinal fins | Max. 59.62 |
| Aldabbagh et al., 2010 [32] | 0.012 to 0.038 | WM without absorber plate | Max. 45.93 |
| Singh and Panwar 2013 [21] | 0.02281 | Iron Brass Copper | 61.47, 64.42, 64.42 |
| Nowzari et al., 2015 [33] | 0.011, 0.032 | WM with different covers | 48 |
| Nowzari and Aldabbagh 2017 [34] | 0.011, 0.032 | Partially perforated cover with WM | 55 |
| Abed et al., 2017 [24] | 0.033 | U and V corrugated WM absorber | NM |
| Rajarajeswari et al., 2018 [27] | 0.01 to 0.055 | Cu WM | 15–88 |
| Gill et al., 2012 [73] | 0.011 to 0.020 m/s | Iron chips | 37.45 |
| Present study | 0.027 and 0.058 | Partially filled Al WM with different PPI and porosity | 35.8 to 69.5 for 0.027 kg/s and 53.8 to 84.12 for 0.058 kg/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diganjit, R.; Gnanasekaran, N.; Mobedi, M. Thermohydraulic Efficiency of a Solar Air Heater in the Presence of Graded Aluminium Wire Mesh—A Combined Experimental–Numerical Study. Energies 2023, 16, 5633. https://doi.org/10.3390/en16155633
Diganjit R, Gnanasekaran N, Mobedi M. Thermohydraulic Efficiency of a Solar Air Heater in the Presence of Graded Aluminium Wire Mesh—A Combined Experimental–Numerical Study. Energies. 2023; 16(15):5633. https://doi.org/10.3390/en16155633
Chicago/Turabian StyleDiganjit, Rawal, Nagaranjan Gnanasekaran, and Moghtada Mobedi. 2023. "Thermohydraulic Efficiency of a Solar Air Heater in the Presence of Graded Aluminium Wire Mesh—A Combined Experimental–Numerical Study" Energies 16, no. 15: 5633. https://doi.org/10.3390/en16155633
APA StyleDiganjit, R., Gnanasekaran, N., & Mobedi, M. (2023). Thermohydraulic Efficiency of a Solar Air Heater in the Presence of Graded Aluminium Wire Mesh—A Combined Experimental–Numerical Study. Energies, 16(15), 5633. https://doi.org/10.3390/en16155633







