Simple Discrete Control of a Single-Phase Voltage Source Inverter in a UPS System for Low Switching Frequency

Abstract

Previous research has shown that the inverter output voltage distortions are higher for low switching frequencies, and it is impossible to increase the controller gains because it will cause oscillations of the output voltage. The main reason is the real frequency domain characteristic of the PWM modulator and measuring traces, which can be modelled as switching periods delays. The thesis of this paper is that by using the control system that takes care of these delays, it is possible to decrease output voltage distortions for the standard loads for relatively low switching frequencies (e.g., 12,800 Hz). The Luenberger observer was implemented in the multi-input-multi-output passivity-based control of the system with the delay, in order to predict the state variables of the inverter. It is shown that state variable prediction is unnecessary for high switching frequencies (e.g., 51,200 Hz). The theory, simulations and breadboard verification, using the inverter model controlled with the real-time interface MicroLabBox, are presented.

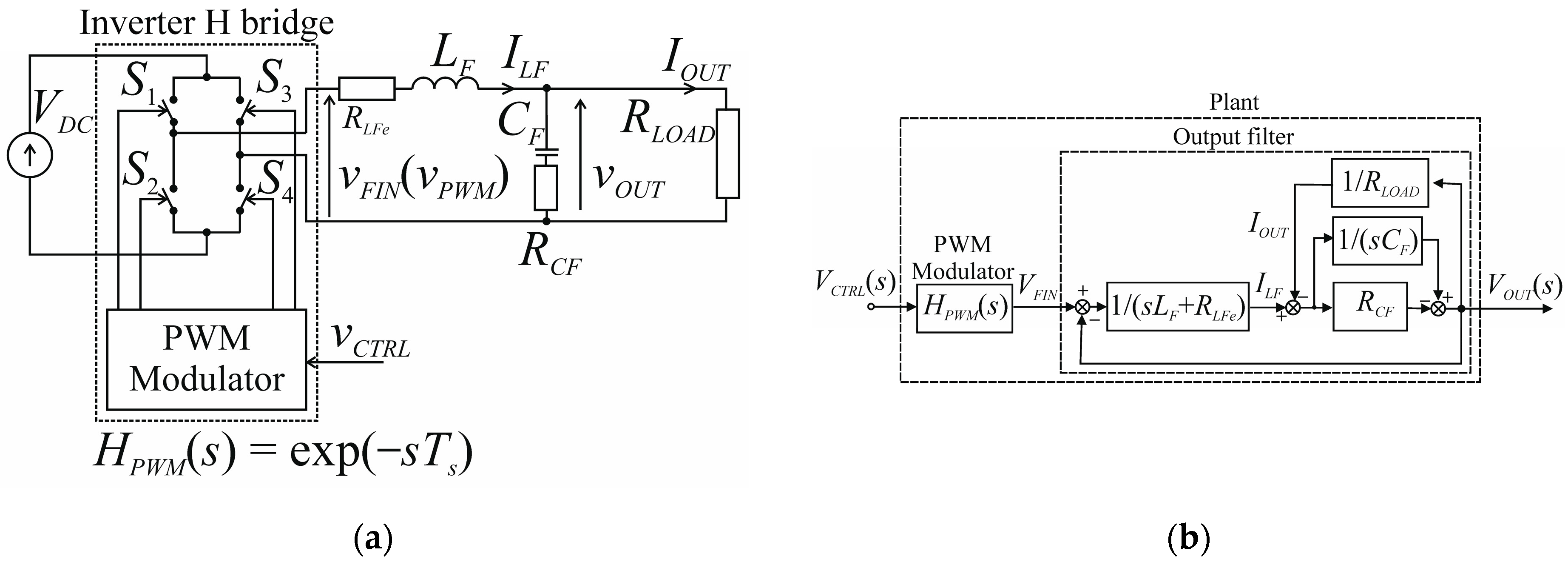
1. Introduction

The problem of controlling the voltage source inverter (VSI) is important in UPS systems. These systems should fill the requirements of the EN-62040-3 standard [1], in which the static and dynamic, linear and nonlinear loads are defined. To design such a control system, the inverter should be defined and modelled taking in care the properties of the output filter coil core [2,3,4]. Linear modelling in the operating point seems sufficient and is commonly used; however, there are many approaches (Section 2) to the nonlinearity of the inverter model [5,6,7]. Today, sophisticated control is only digital, so discrete models are required. It can be discretised from the continuous model or calculated as a discrete system from state equations [8]. The first parameter of the VSI is the capacitance C_F and ESR (equivalent serial resistance) R_CF of the output filter capacitor—typically MKP. The capacitance C_F is tens of μF and it is possible to assign a nominal value as real, whereas ESR is negligible. The inductance L_F of the output filter coil for a high-quality coil core (e.g., Sendust alloy powder [9]) can be assigned as equal to the nominal value. For a cheap coil core (iron powder [10]), the inductance L_F should be measured. In both cases of coil cores, the serial resistance R_LF, depending mainly on the power losses in the core, seriously increases with the increase in the magnetizing coil current and its frequency is equal to the switching frequency. The best solution is to measure this resistance. It should be summed with the other serial resistances. Switched-on bridge transistors have a resistance from 50 to 200 mΩ per transistor. Two are always conducting, and the resistance of the PCB traces and connectors is present. Altogether, the sum of serial resistances is called in the paper “equivalent serial resistance” R_LFe. The method for calculating the parameters of the VSI from its measured Bode plots enables the creation of the VSI model in the operating point [11,12,13]. The PWM modulator introduces one switching period delay. The feedback loop has galvanic isolation in all the voltage and current channels (the isolated amplifier in the output voltage channel, and transducers in the output and inductor channels), difference amplifiers, antialiasing filters, and analogue-to-digital converters. As it can be easily proved, the feedback loop operates efficiently (decreases the VSI output impedance) below the resonant frequency of the output filter [14]. This frequency is usually about 1 kHz. In this frequency range, the Bode plots of the feedback loop have been measured and successfully modelled in experimental models as the delay [15]. The PWM modulator and measuring trace can be modelled as a delay of two to three switching periods. The main thesis of this paper is that by using the control system that takes care of the delay, it is possible to decrease the output voltage distortions of standard loads for a low (≤12,800 Hz) switching frequency. The Luenberger observer [16,17,18,19] for the state variables for the multi-input-single-output control will be used. Section 2 presents the simple continuous model of the VSI. Section 3 describes the used modulation scheme for the three-level, double-edge PWM. Section 4 concerns the design of the output filter. Section 5 shows the method of discretizing the continuous model, while Section 6 presents the fully discrete model calculated directly from the state equations. Section 7 describes the identification of the VSI plant and the measuring traces of the VSI. Section 8 presents the theory of PBC control with the prediction of state variables and the simulations for different systems with a low switching frequency in control systems, with and without prediction. Section 9 presents MATLAB/Simulink simulations of the inverter. Section 10 shows breadboard verification. Section 11 presents the results of the simulation and the experimental verification. Section 12 is a discussion. Section 13 contains conclusions.

It is possible to assume that the equivalent serial resistance of the capacitor C_F is R_CF ≈ 0 (for parallel connected MKP metallized polyester capacitors in the experimental inverter, less than 10 mΩ). R_LFe is the equivalent serial resistance of the whole inverter—the serial resistance of the filter coil L_F, the switched-on transistors in the bridge and PCB traces. It was shown in [11,12,13] that R_LFe is much higher than the DC resistance of the coil, depending on the switching frequency (f_s = 1/T_s), the magnetizing coil current and, very strongly, on the coil core’s power losses. It was shown in [11,12,13] that the worst material is iron powder (e.g., Material Mix −26) and alloy powder (iron, silicon, aluminium); however, MS Sendust (previous name: Super MSS) is a very good material with a reasonable price [9,12].

$$K_{CTRL}(s)=\frac{V_{OUT}(s)}{V_{CTRL}(s)}=e^{-s{T}_s}{K}_{INV}=e^{-s{T}_s}\frac{V_{OUT}(s)}{V_{FIN}(s)}=e^{-s{T}_s}\frac{{\omega }_{F0}{}^2}{s^2+2{\xi }_{Fe}{\omega }_{F0}s+(1+\frac{R_{LFe}}{R_{LOAD}}){\omega }_{F0}{}^2},$$

(1)

where

$${\omega }_{F0}=\frac{1}{\sqrt{L_F{C}_F}}, {\xi }_{Fe}=\frac{1}{2}(R_{LFe}\sqrt{\frac{C_F}{L_F}}+\frac{1}{R_{LOAD}}\sqrt{\frac{L_F}{C_F}}).$$

(2)

A modification of this simple model is the quasi-continuous transfer function [20,21] of the inverter (including R_LOAD), which considers further ZOH discretization for the discrete control purpose (introducing the delay of half of T_s) and one T_s delay of the PWM modulator (3).

$$K_{CTRL}(s)=\exp (-s\frac{T_s}{2})\exp (-s{T}_s)F_{LC}(s)\approx (1-s\frac{T_s}{2})\frac{1-s\frac{T_s}{2}}{1+s\frac{T_s}{2}}\frac{{\omega }_{F0}{}^2}{s^2+2{\xi }_F{\omega }_{F0}s+(1+\frac{R_{LFe}}{R_{LOAD}}){\omega }_{F0}{}^2}$$

(3)

Modelling the load current as an independent disturbance or state variable has been the standard approach in inverter research for 40 years [22,23,24,25,26,27,28]. This allows the load impedance to be neglected in the state matrix. However, we are missing one feedback loop from the output voltage V_OUT to the load current I_OUT. After designing the control system, it is possible to check how the omission of this loop changes the real position of the poles of the closed-loop system (whether they do not go beyond the unit circle in the z plane). In [24] was shown how the omission of the load resistance shifts poles of the closed-loop system when using the Coefficient Diagram Method of the control [29,30,31].

2. Continuous Model of the Voltage Source Inverter

Creating the VSI model and its mathematical description is the basic subject of the VSI control design. In [5], the calculation of the nonlinear characteristic of the coil in the LC output filter and its influence on the adaptive control loop were shown. Depending on the inductor core material, its inductance and the equivalent serial resistance varies with the amplitude and the frequency of the magnetizing current [2,3,4].

The influence of the nonlinear characteristic of the inductor in the inverter output filter on the design of the adaptive control loop (with the calculation of the nonlinear inductance characteristic) was presented in [5]. The change in the coil’s inductance and its equivalent serial resistance as a function of the amplitude and the frequency of its magnetizing current depends on the core material [2,3,4]. The change in inductance is small, 5%, for iron–silicon–aluminium alloy powder materials (e.g., Sendust (MS)/Super-MSS™ [9]). The equivalent serial resistance resulting from power losses in the core, in the core operating point for this core material, is 3–5 times lower than for a cheaper iron-powder material mix −26 [12]. So, the coil core material has an impact on the VSI model. The state–space equations of the VSI with pulse width modulation (PWM) can be solved, resulting in the nonlinear (exponential) dependency of state–space variables on the duty ratio of pulses [8]. In [6], the approximation by the Fourier series of the nonlinear control law was presented. Hammerstein’s approach (decomposition of the input–output relationship, where dynamics are represented by a linear transfer function and nonlinearities are represented through the identified black box) to the nonlinear modelling of VSI was presented in [7]. The nonlinear modelling of VSI is a bit more accurate than models with linear approximation of the inverter in the operation point; however, the linear theory results in quite acceptable accordance with the experimental VSI verification. The linear theory enables the simple design of the VSI controller.

The continuous linear model of the single-phase inverter is just the output LC filter and the discrete PWM modulator that can be modelled as a delay with the switching period T_s. The PWM modulator is a digital circuit (e.g., microprocessor) in which we store the duty ratio of the output pulse, and these data are on the output of the modulator in the next period.

The state vector is assigned as $x={[v_{OUT}\hspace{0.33em}{i}_{LF}\hspace{0.33em}{i}_{OUT}]}^T$, the input vector (in the presented case, one variable) is $u=v_{FIN}$ and the output vector (in the presented case, one variable) is $y=v_{OUT}$. The PWM modulator transfer function is $H_{PWM}=\exp (-s{T}_s)$.

The state matrix, input matrix and output matrix are (4).

$$A=\left[\begin{array}{ccc}0& \frac{1}{C_F}& -\frac{1}{C_F}\\ -\frac{1}{L_F}& -\frac{R_{LFe}+R_{CF}}{L_F}& \frac{R_{CF}}{L_F}\\ 0& 0& 0\end{array}\right]\hspace{0.33em}, B=\left[\begin{array}{c}0\\ \frac{1}{L_F}\\ 0\end{array}\right], C=\left[\begin{array}{ccc}1& 0& 0\end{array}\right].$$

(4)

The continuous time-invariant state–space equation is (5).

$$\dot{x}=Ax+Bu$$

(5)

Finally, for R_CF ≈ 0, the transfer function of the control voltage and the disturbance (the output current) is (6).

$$V_{OUT}(s)=H_{PWM}\frac{{\omega }_{F0}{}^2}{s^2+s\frac{R_{LFe}}{L_F}+{\omega }_{F0}{}^2}{V}_{CTRL}(s)-\frac{(s{L}_F+R_{LFe}){\omega }_{F0}{}^2}{s^2+s\frac{R_{LFe}}{L_F}+{\omega }_{F0}{}^2}{I}_{OUT}(s)$$

(6)

The transfer control function of the VSI is (7).

$$K_{CTRL}(s)=\frac{V_{OUT}(s)}{V_{CTRL}(s)}=\exp (-s{T}_s)K_{INV}=\exp (-s{T}_s)\frac{V_{OUT}(s)}{V_{FIN}(s)}=\exp (-s{T}_s)\frac{{\omega }_{F0}{}^2}{s^2+s\frac{R_{LFe}}{L_F}+{\omega }_{F0}{}^2}$$

(7)

where the output impedance of the VSI with the open loop, that is, the disturbance transfer function, is (7).

$$Z_{OUT}(s)=-\frac{V_{OUT}(s)}{I_{OUT}(s)}=\frac{(s{L}_F+R_{LFe}){\omega }_{F0}{}^2}{s^2+s\frac{R_{LFe}}{L_F}+{\omega }_{F0}{}^2}$$

(8)

3. Modulation Scheme

The two-leg H bridge enables two or three levels of single-phase modulation. The three-level modulation results in a much lower level of harmonics than the two levels, in the sinusoidal modulated PWM waveform for the low modulation coefficient [32]. Each microprocessor that can be used to control VSI has the possibility of two-edge modulation that results in lower low-order harmonics than single-edge modulation. There are different modulation schemes—algorithms for driving the transistors in the H bridge in the three-level, two-edge single-phase modulation [32,33,34]. The best for control purposes is the first PWM scheme, in which it is possible to control the output waveform when it crosses the zero value. The transistors of a (two-leg) H-bridge (Figure 1a and Figure 2a) in the first modulation scheme (Figure 3), are switched with the frequency f_s. The current flows through the serial connection of two switches on the diagonal of the bridge (S₁ and S₄ or S₃ and S₂, Figure 1a and Figure 2a) and the output PWM waveform, which has a double 2f_s frequency is a coincidence of switching on two transistors. The control of the switches is described by Equations (9)–(12) and is presented in Figure 3. T_ON is the switching-on time. The double-output switching frequency enables one to design an output filter with the lower values of the filter parameters without increasing the switching frequency of transistors. For k = 1 to (f_s/f_m):

$$S_1:T_{ON}(k)/T_s=0.5M\sin (k\frac{2\pi }{f_s/f_m})+0.5M$$

(9)

$$S_2:NOT(S_1)$$

(10)

$$S_3:T_{ON}(k)/T_s=0.5M\sin ((k\frac{2\pi }{f_s/f_m})+\pi )+0.5M$$

(11)

$$S_4:NOT(S_3)$$

(12)

4. Design of the Output Filter

The VSI model was based on the output L_FC_F filter. The restriction of the output voltage ripple amplitude (13) 0.5V_OUTripplepp of up to 3% determines the value of the product of L_FC_F (14). Calculating the quotient L_F/C_F is more ambiguous [8,32,35]. One of the solutions is creating the “cost function” F_cost (14) as a sum of absolute values of reactive power in the filter components [8,32,35,36,37]. However, the reactive power of an inductor is sometimes weighted two-times higher than that of the capacitor [36,37], because the reduced L_F value decreases the VSI output impedance for the low frequency and improves the VSI dynamic properties. The presented design of the filter (17) is based on the minimization of the “cost function”, with the same weights for both absolute values of reactive powers of the inductor and capacitor [8,35,38]. The case of a single-phase, H-bridge, three-level inverter was presented. The L_F and C_F values depend on the load R_LOAD and the switching frequency f_s.

$${\left.0.5V_{OUTripplepp}\right|}_{\max }\le 3\%V_{OUTh1}$$

(13)

From (13)

$$L_F{C}_F\ge \frac{1}{f_s}$$

(14)

The cost function F_cost (15).

$$F_{\cos \mathrm{t}}={\omega }_m{L}_F{I}_{LFh1RMS}^2+{\omega }_m{C}_F{V}_{OUTh1RMS}^2={\omega }_m{L}_F{I}_{LFh1RMS}^2+{\omega }_m\frac{1}{f_s{L}_F}{V}_{OUTh1RMS}^2$$

(15)

$$\frac{\partial F_{\cos \mathrm{t}}}{\partial L_F}=0$$

(16)

The particular values of L_F and C_F from (14) and (16)

$$L_F\approx \frac{1}{f_s}{R}_{LOAD}, C_F\approx \frac{1}{f_s}\frac{1}{R_{LOAD}}$$

(17)

Similar output filter calculations are the result of calculations presented in [39].

When the effective switching frequency of the V_FIN is equal to 51,200 Hz (the double-switching frequency f_s = 25,600 Hz of the bridge transistors, Figure 3), R_LOAD = 50 Ω, the result from (17) is L_F = 1 mH, C_F = 0.4 μF; let us use C_F = 1 μF. The feedback is always delayed by at least one switching frequency period T_s = 39 μs (f_s = 25,600 Hz) in the digital PWM modulator. It is possible to assume that the inductor current is constant during one switching period and there is a resistive load. If the amplitude of the output current I_LFmax is 5 A and the load is fully decreased in the maximum of output sinusoidal voltage, the increase in the output voltage will be ΔV_OUT = T_sI_LFmax/C_F = 195 V. Such an instant increase in the output voltage is unacceptable (and saturates the control unit of VSI which can lead to further oscillations of the output voltage) and the C_F value should be increased to 50 μF. In this case, the increase in the output voltage ΔV_OUT = 4 V is acceptable. The presented values, about 1 mH and 50 μF, are typical for the low-output-power VSI.

5. Discretizing the Continuous Model of the VSI

Contemporary VSI is controlled using microprocessors or other digital devices (e.g., FPGA). The simplest approach is to discretize the continuous model of the inverter without delays K_INV = V_OUT(s)/V_FIN(s). The approximation of the transformation s = (ln z)/T_s should be used. The bilinear transform (Tustin) s = (2/T_s)(z − 1)/(z + 1) gives the results most similar to the exact logarithmical transformation of the left half plane s into the unity circle in the plane z. The MATLAB c2d function with, e.g., the ‘Tustin’ discretization method can be used (18) and (19).

$$K_{INV}(s)=\frac{V_{OUT}(s)}{V_{FIN}(s)}=tf([{\omega }_{F0}{}^2],[1\hspace{0.33em}\hspace{0.33em}2{\xi }_{Fe}{\omega }_{F0}\hspace{0.33em}{\omega }_{F0}{}^2]);$$

(18)

$$K_{INVc2d}(z)=c2d(K_{INV},T_s,‘tustin’);$$

(19)

Finally, Equation (20) introduces the PWM modulator delay.

$$K_{CTRLc2d}(z)=z^{-1}{K}_{INVc2d}(z);$$

(20)

All the discretisation methods introduce the delay (it was taken care of in model (3)). The disadvantage of this method is the same result for the single- or double-edged modulation, while the double-edged modulation introduces an additional delay (the voltage pulse T_OFF time when the transistor is switched off depends on the previous pulse) and a lower THD.

6. The Discrete Model of the VSI

The discrete model of the VSI is created as a linearized solution of the state–space equation of the inverter for a particular method (e.g., single- or double-edged) of PWM [8,32,38,40]. For a multidimensional MIMO system with r inputs, n state variables and p outputs, using the solution of state equations for $x(t)\hspace{0.33em}\in \hspace{0.33em}{R}^n,$ $u(t)\hspace{0.33em}\in \hspace{0.33em}{R}^r,$ $y(t)\hspace{0.33em}\in \hspace{0.33em}{R}^p,$ initial variable conditions x(t₀) and control conditions u(t₀), where x = [v_OUT i_LF i_OUT]^T, u = v_FIN, y = v_OUT, it is possible to solve state–space Equation (5).

The general solution in one switching period for 0 ≤ t ≤T_s is (21).

$$x(t)=e^{A(t-t_0)}x(k{T}_s)+{\displaystyle \underset{t_0}{\overset{t}{\int }}{e}^{A(t-\tau )}Bu(\tau )d\tau }$$

(21)

The solution of Equation (21) can be solved in the particular sectors of the switching period T_s for the double-edged PWM [32]. To linearize the solution of the equation the linear approximation (22) is used.

$$e^{A{T}_{ONk}/2}=I+A{T}_{ONk}/2+A^2{T}_{ONk}^2/4\dots \approx I+A{T}_{ONk}/2$$

(22)

Finally, the linearized state space equations are (23)–(25).

$$x((k+1)T_s)=e^{A{T}_s}x(k{T}_s)+e^{A{T}_s/2}B{V}_{DC}{T}_{ON}(k{T}_s)$$

(23)

$$x_{k+1}=A_D{x}_k+G_D{T}_{ONk}$$

(24)

$$y_k=C_{\mathrm{D}}{x}_k$$

(25)

The discrete state A_D and control G_D matrixes are (26)–(28).

$$A_D=e^{A{T}_s}=\Phi (T_s)={\left.L^{-1}[{(sI-A)}^{-1}]\right|}_{t=T_s}$$

(26)

$$G_D=e^{A{T}_s/2}B{V}_{DC}=\Phi (T_s/2)B{V}_{DC}$$

(27)

$$A_D=\Phi (T_s)=\left[\begin{array}{ccc}{\varphi }_{11}& {\varphi }_{12}& {\varphi }_{13}\\ {\varphi }_{21}& {\varphi }_{22}& {\varphi }_{23}\\ {\varphi }_{31}& {\varphi }_{32}& {\varphi }_{33}\end{array}\right],\hspace{0.33em}{G}_D=\left[\begin{array}{c}{g}_{11}\\ g_{21}\\ g_{31}\end{array}\right],\hspace{0.33em}{C}_D=C$$

(28)

where

$${\xi }_F=\frac{1}{2}{R}_{LFe}\sqrt{\frac{C_F}{L_F}}; {\omega }_{F0}=\frac{1}{\sqrt{L_F{L}_F}},$$

$${\varphi }_{11}=[\cos \left({\omega }_{F0}{T}_s\right)+{\xi }_F\sin \left({\omega }_{F0}{T}_s\right)]\exp (-{\xi }_F{\omega }_{F0}{T}_s),$$

$${\varphi }_{12}=\frac{1}{{\omega }_{F0}{C}_F}\sin ({\omega }_{F0}{T}_s)\exp (-{\xi }_F{\omega }_{F0}{T}_s),$$

$${\phi }_{13}=-{\phi }_{12}+R_{LFe}({\phi }_{11}-1),$$

$${\varphi }_{21}=-\frac{C_F}{L_F}{\phi }_{12},$$

$${\varphi }_{22}=[\cos ({\omega }_{F0}{T}_s)-{\xi }_F\sin ({\omega }_{F0}{T}_s)]\exp (-{\xi }_F{\omega }_{F0}{T}_s),$$

$${\varphi }_{23}=1-{\phi }_{11}; {\varphi }_{31}=0; {\varphi }_{32}=0\hspace{0.33em}{\varphi }_{33}=1,$$

$$g_{11}=V_{DC}{\omega }_{F0}\sin ({\omega }_{F0}{T}_s/2)\exp (-{\xi }_F{\omega }_{F0}{T}_s/2),$$

$$g_{21}=\frac{V_{DC}}{L_F}[\cos ({\omega }_{F0}{T}_s/2)-{\xi }_F\sin ({\omega }_{F0}{T}_s/2)]\exp (-{\xi }_F{\omega }_{F0}{T}_s/2),$$

$$g_{31}=0.$$

The control transfer function and the output impedance of VSI can be expressed as (29)

$$\begin{array}{l}{V}_{OUT}(z)=z^{-1}\frac{g_{11}+({\phi }_{12}{g}_{21}-{\phi }_{22}{g}_{11})z^{-1}}{1-z({\phi }_{11}+{\phi }_{22})z^{-1}+({\phi }_{11}{\phi }_{22}-{\phi }_{12}{\phi }_{21})z^{-2}}{T}_{ON}(z)+\\ z^{-1}\frac{{\phi }_{13}+({\phi }_{12}{\phi }_{23}-{\phi }_{13}{\phi }_{22})z^{-1}}{1-z({\phi }_{11}+{\phi }_{22})z^{-1}+({\phi }_{11}{\phi }_{22}-{\phi }_{12}{\phi }_{21})z^{-2}}{I}_O(z)\end{array}$$

(29)

The delay with one T_s that exists in (29) is the feature of the double-edged modulation. The time between two consecutive pulses depends on the previous switching period control. For single-edged modulation, this delay is absent [32].

The gain of the VSI, with double-edged PWM and a digital modulator inserting a switching period delay T_s, is given by (30), (31):

$$K_{CTRL}=\frac{V_{OUT}(z)}{V_{CRTL}(z)}=z^{-1}{K}_{INV}=z^{-1}\frac{a_1{z}^{-1}+a_2{z}^{-2}}{1+b_1{z}^{-1}+b_2{z}^{-2}},$$

(30)

where

$$a_1=\frac{T_s}{V_{DC}}{g}_{11}; a_2=\frac{T_s}{V_{DC}}({\phi }_{12}{g}_{21}-{\phi }_{22}{g}_{11})\hspace{0.33em}; b_1=-({\phi }_{11}+{\phi }_{22}); b_2={\phi }_{11}{\phi }_{22}-{\phi }_{12}{\phi }_{21}.$$

(31)

For high switching frequencies (e.g., 51,200 kHz), the difference between the discretized control transfer function and the discrete transfer function is low.

7. Measuring Bode Plots of the Inverter and Measuring Traces

To design the control of the VSI, its parameters should be known to define the VSI model. Additionally, Bode plots of the measuring traces should be appointed. The inverter bridge with the output filter can have parameters different from the nominal [11,12,13]. The parameter values depend mainly on the coil core material in the filter. For an iron powder core, the inductance L_F seriously changes; for the Super MSS, it is almost constant. The power losses in the core cause an increase in the equivalent serial resistance R_LFe. Inductance L_F and the equivalent serial resistance R_LFe should be measured in the chosen VSI operating point. The fundamental frequency f_m = 50 Hz was set to be constant. Three switching frequencies were checked in the experimental VSI: f_s = 12,800 Hz, 25,600 Hz or 51,200 Hz (the frequency of the voltage pulses on the coil in the presented PWM scheme is double 2f_s, Figure 3). The DC supply voltage V_DC, the load resistance R_LOAD and the switching frequency f_s were assigned for the selected operating point. The generated test signal V_CTRL (Figure 4) was the sum of the fundamental harmonic and the excitation signal, that is, the n-th harmonic of the fundamental harmonic (32) [11,12,13].

For k = 1 to f_s/f_m

$$V_{CTRL}(k)=round(M·floor\left(\frac{1}{2}\frac{f_{COMP}}{f_s}\right)(A\sin (k\frac{2\pi }{f_s/f_m})+(1-A)\sin (nk\frac{2\pi }{f_s/f_m})))$$

(32)

where M is the modulation depth (typically M = 0.9, to avoid distortions of the fundamental harmonic), f_COMP is the input frequency of the PWM unit comparator (in STM32F407VG microprocessor f_COMP = 84 MHz), A is the relative amplitude of the fundamental harmonic (A = 0.9–0.95) and k = 1…(f_s/f_m). The switching frequency f_s is always a harmonic of the fundamental frequency f_m = 50 Hz. The reference waveform is represented by f_s/50 samples of the sinusoidal reference per the fundamental period T_m = 20 ms. The number of samples of the n-th harmonic—the excitation—is equal to f_s/(n50) in one fundamental period. For the minimum number of ten samples per period of the generated harmonics, in the case of f_s = 12,800 Hz: n_max = 25, f_s = 25,600 Hz: n_max = 50 and f_s = 51,200 Hz: n_max = 100. Finally, n_max = 100 was used for f_s = 12,800, 25,600 and 51,200 Hz because it has a high attenuation over the 25th harmonics (for L_F = 1 mH, C_F = 51 μF, the output filter resonant frequency was 705 Hz, below the 25th harmonic) and the error in the measurement of the harmonics close to the 100th harmonic is not practically important. The MKP-type VSI output capacitor C_F = 51 μF was the same as in the experimental inverter. The accuracy of appointing the maximum gain is better for the lower-frequency step grid [13]. For lower damping, the frequency step grid should possibly be lower; for high damping, finding the maximum on the Bode plot will be always inaccurate. For the calculation of the L_F and R_LFe parameters, the maximum value of the damping coefficient should be ξ_F² < (1 + R_LFe/R_LOAD)/2 for R_LOAD >> R_LFe. The amplitude of the measured fundamental harmonic should be initially adjusted to 50–75% of the ADC range (the used 13-bit bipolar analogue-to-digital converter ADC has a range of −4095 to 4095; the required amplitude of the fundamental harmonic should be 2000–3000 units). The complex test signal v_CTRL (35) is generated in the DAC/ADC units from −floor(0.5f_COMP/f_s) to floor(0.5f_COMP/f_s). It should be checked that for a complex test signal with an excitation component frequency near the VSI filter resonant frequency, the measured value is inside the range of ADC. The amplitude of excitation |h_nIN| = 1 − A should have a value of 5 to 10%. It was shown [41] that the lowest comparator frequency is f_COMP = 68 MHz for f_s = 25,600 Hz and the double-edged PWM modulation, for which there were no additional distortions caused by the insufficient resolution of the generated waveform (in STM32F407VG, there is f_COMP = 84 MHz). The main assumption is that the fundamental harmonic is not attenuated in the inverter and it is delayed as all the components of the test signal (the T_s delay in the PWM modulator is not present in the relative calculations because it concerns the whole signal).

The values of the input and output excitations are compared, respectively, with the fundamental harmonic in the input and output. Such a solution solves the problem of the different units in the VSI output (volts) and PWM modulator input test signal (in ADC units). The amplitudes and phases of the excitation harmonic components (33) of the input and output complex signals are calculated using the fft transform [14].

For n = 1…n_max

$$\begin{array}{l}{K}_{INV}(j2\pi f_n)=\\ =\frac{\left|V_{OUT}(n{f}_m)\right|/\left|V_{OUT}(f_m)\right|}{\left|V_{CTRL}(n{f}_n)\right|/\left|V_{CTRL}(f_m)\right|}\exp (j\{[\arg (V_{OUT}(n{f}_m))-\arg (V_{OUT}(f_m))]-[\arg (V_{CTRL}(n{f}_m))-\arg (V_{CTRL}(f_m))]\})\end{array}$$

(33)

The magnitude Bode plot is (34)

$$\left|K_{INV}(n{f}_n)\right|=20\log \frac{\left|V_{OUT}(n{f}_m)\right|/\left|V_{OUT}(f_m)\right|}{\left|V_{CTRL}(n{f}_n)\right|/\left|V_{CTRL}(f_m)\right|}$$

(34)

The phase Bode plot is (35)

$$\arg (n{f}_m)=[\arg (V_{OUT}(n{f}_m))-\arg (V_{OUT}(f_m))]-[\arg (V_{CTRL}(n{f}_m))-\arg (V_{CTRL}(f_m))]$$

(35)

The switching frequency f_s and the load R_LOAD are parameters which should be kept constant during one measurement series. The measured row data series—magnitudes and phases of the inverter together with the measurement trace—are sent to PC where the previously measured magnitudes (dB) and phases (degrees) of the measurement trace are subtracted from the corresponding row data. From the magnitude Bode plot, the damping coefficient ζ_F (36), the inductance L_F (37) and the serial equivalent resistance R_LFe (38) can be calculated [14] for the assumption R_LOAD >> R_LFe.

$${\xi }_F\approx \sqrt{\frac{1}{2}[1-\sqrt{(1-\frac{1}{|K_{INV}{|}_{\max }{}^2})}]}$$

(36)

$$L_F=\frac{1-2{\xi }_F{}^2}{{{\omega }_{\max }}^2{C}_F}, \mathrm{for} {\xi }_F{}^2<0.5$$

(37)

$$R_{LFe}=(2{\xi }_F\frac{{{\omega }_{\max }}^2}{\sqrt{1-2{\xi }_F{}^2}}-\frac{1}{R_{LOAD}{C}_F})\frac{1-2{\xi }_F{}^2}{{{\omega }_{\max }}^2{C}_F} \mathrm{for} R_{LOAD}>\frac{\sqrt{1-2{\xi }_F{}^2}}{2{\xi }_F{\omega }_{\max }{C}_F} \mathrm{and} {\xi }_F{}^2<0.5$$

(38)

The error (41) in the calculation of the damping coefficient ξ_F was caused by the Δω_max error of appointing ω_max (39), (40).

$${\omega }_{\max }{}^2=(1-2{\xi }_F{}^2){\omega }_{F0}{}^2$$

(39)

$$\Delta {\xi }_F=\frac{\partial {\xi }_F}{\partial {\omega }_{\max }}\Delta {\omega }_{\max }=-\frac{1}{\sqrt{2{\omega }_{F0}{}^2}}\frac{{\omega }_{\max }}{\sqrt{{\omega }_{F0}{}^2-{\omega }_{\max }{}^2}}\Delta {\omega }_{\max }$$

(40)

$$\Delta {\xi }_F=-\frac{1}{2}\frac{1-2{\xi }_F{}^2}{{\xi }_F}\frac{\Delta {\omega }_{\max }}{{\omega }_{\max }}$$

(41)

The measured serial equivalent inductance error is low, and approximately can be assigned ΔL_F ≈ 0 (43) because the component errors cancel each other out (42).

$$\Delta L_F=\frac{\partial L_F}{\partial {\xi }_{Fe}}\Delta {\xi }_F+\frac{\partial L_F}{\partial {\omega }_{\max }}\Delta {\omega }_{\max }=-4\frac{{\xi }_F}{{{\omega }_{\max }}^2{C}_F}\Delta {\xi }_F-2\frac{1-2{\xi }_F{}^2}{{{\omega }_{\max }}^3{C}_F}\Delta {\omega }_{\max }$$

(42)

$$\Delta L_F\approx 0$$

(43)

The error of the serial equivalent resistance R_LFe (45) depends on the damping coefficient ξ_F and Δω_max that is equal to 0.5 frequency grid.

$$\Delta R_{LFe}=\frac{\partial R_{LFe}}{\partial {\xi }_F}\Delta {\xi }_F+\frac{\partial R_{Fe}}{\partial L_F}\Delta L_F\approx 2\sqrt{\frac{L_F}{C_F}}\Delta {\xi }_F$$

(44)

$$\left|\Delta R_{LFe}\right|=\sqrt{\frac{L_F}{C_F}}\frac{1-2{\xi }_F{}^2}{{\xi }_F}\frac{\Delta {\omega }_{\max }}{{\omega }_{\max }}$$

(45)

Figure 5 presents the error of R_LFe as a function of the damping coefficient ξ_F and frequency resolution Δf_max. This error ΔR_LFe (for L_F = 1 mH, C_F = 51 μF) is serious, up to 1.5 Ω, for the low damping coefficient, which is the case of a low resolution for Δf_max = 50 Hz (frequency step grid 100 Hz). The full real value of R_LFe is 1 to 2 Ω for the 1 mH coil DC resistance of about 0.2 Ω, the MOSFET bridge transistors with R_DS = 0.2 Ω (there are always two serially connected transistors conducting), and the coil core made of Sendust magnetic material [9] with a low power loss. So, ΔR_LFe = 1.5 Ω is unacceptable and the frequency step grid should be decreased.

Figure 6 presents the Bode plots of two experimental inverters. It can be noticed that in both cases, these frequency domain characteristics can be approximated in the frequency range up to the corner frequency of the output filter (for L_F = 1 mH, C_F = 51 μF, it is 705 Hz) as the simple delay with two switching periods T_s. This approximation (46) of the measuring trace transfer function for f < 1000 Hz will be used in the simulations.

$$K_{TRACE}(s)\approx e^{-s2T_s} \mathrm{for}\omega < 2\mathrm{\pi }1000 [1/\mathrm{s}]$$

(46)

8. The Prediction of the State Variables

It was shown that the transfer function of the measurement trace and the PWM modulator can be approximated with a simple delay (2T_s is the measuring trace and T_s is the PWM modulator). For the high switching frequency (51,200 Hz and more) this delay is not so important for the design of the control loop [42]. For the lower switching frequency, one of the solutions can be the prediction of the state variable at the next sampling instant [43]. The full-order state Luenberger observer [18,19] will be used. It is quite convenient because we do not need to know exactly the transfer function of the measurement traces.

The discrete state space equations for state variables $x={[v_{OUT}\hspace{0.33em}{i}_{LF}\hspace{0.33em}{i}_{OUT}]}^T$ and output variable y(k) = v_OUT(k) were described in (26), (27). The predicted state variables at the next sampling instant are (47).

$$\widehat{x}(k+1)=A_{\mathrm{D}}\widehat{x}(k)+G_{\mathrm{D}}{T}_{ON}(k)+L[y(k)-C_{\mathrm{D}}\widehat{x}(k)]$$

(47)

L is discretized observer gain matrix.

The error system is obtained from (48):

$$e(k+1)=(A_{\mathrm{D}}-L{C}_{\mathrm{D}})[x(k)-\widehat{x}(k)]=(A_{\mathrm{D}}-L{C}_{\mathrm{D}})e(k),$$

(48)

For three state variables:

$$L={[\begin{array}{ccc}{l}_1& l_2& l_3\end{array}]}^T$$

The characteristic equation of the observer is (49).

$$\det (z1-A_{\mathrm{D}}+L{C}_{\mathrm{D}})=0$$

(49)

According to the principle of separation of estimation and pole placement of the “separation theorem”, the roots of the characteristic equation of the observer (49) are independent of the closed-feedback-loop control system. However, the observer eigenvalues should enable a faster convergence to zero of the observation error than that of other transient processes in a closed-loop system. Better observer dynamics are obtained if the roots of their characteristic Equation (49) are closer to zero on the z-plane (their absolute value is lower) than the roots of the characteristic equation without estimation $\det (z1-A_{\mathrm{D}})=0$. E.g., in [44], the observer poles are selected to be about 0.8 times closer to the origin than the open-loop poles at the same phase angle. In [45], the Luenberger observer was designed with its dynamics three times faster than the fastest pole of the plant.

The characteristic equation of the open-loop system with the estimation is (50), (51).

$$\det \left[\begin{array}{ccc}z-{\phi }_{11}+l_1& -{\phi }_{12}& -{\phi }_{13}\\ -{\phi }_{21}+l_2& z-{\phi }_{22}& -{\phi }_{23}\\ 0+l_3& 0& z-1\end{array}\right]=0$$

(50)

$$\begin{array}{l}1+z^{-1}[-1-{\phi }_{11}-{\phi }_{22}+l_1]+z^{-2}[{\phi }_{22}+{\phi }_{11}+{\phi }_{11}{\phi }_{22}-{\phi }_{12}{\phi }_{21}-(1+{\phi }_{22})l_1+{\phi }_{12}{l}_2+{\phi }_{13}{l}_3]\\ z^{-3}[-{\phi }_{11}{\phi }_{22}+{\phi }_{12}{\phi }_{21}+l_1{\phi }_{22}-{\phi }_{12}{l}_2+({\phi }_{12}{\phi }_{23}-{\phi }_{13}{\phi }_{22})l_3]=0\end{array}$$

(51)

Manabe presented the coefficient diagram method (CDM) [29,30,31] to design a controller where coefficients of the closed-loop characteristic equation are calculated from the Manabe standard form. They depend on the time constant τ of the closed-loop system. Relation (52) is the discretized characteristic equation of the closed-loop system.

$$P(z^{-1})={\displaystyle \sum _{i=0}^n{p}_{zi}}(\tau /T_s)z^{-i}$$

(52)

The experimental work [20] showed that for the values of L_F = 1 mH, C_F = 51 μF, and a switching frequency of f_s = 12,800 to 51,200 Hz, the best results of control were for τ/T_s = 5 to 8. So, let us assign p_zi(τ/T_s) for the lower τ/T_s for the characteristic equation of the observer, which fills the requirement that the observer should be faster than the closed-loop system (the further adjustment—individual decreasing gains from τ/T_s = 1, leads to gains of observer τ/T_s equal to about 7 to avoid system oscillations). Equation (53) should be solved to obtain the gains l_i of the observer for the assigned τ/T_s.

$$\left[\begin{array}{ccc}1& 0& 0\\ -1-{\phi }_{22}& {\phi }_{12}& {\phi }_{13}\\ {\phi }_{22}& -{\phi }_{12}& {\phi }_{12}{\phi }_{23}-{\phi }_{13}{\phi }_{22}\end{array}\right]\left[\begin{array}{c}{l}_1\\ l_2\\ l_3\end{array}\right]=\left[\begin{array}{c}{p}_{z1}+1+{\phi }_{11}+{\phi }_{22}\\ p_{z2}-{\phi }_{22}-{\phi }_{11}-{\phi }_{11}{\phi }_{22}+{\phi }_{12}{\phi }_{21}\\ p_{z3}+{\phi }_{11}{\phi }_{22}-{\phi }_{12}{\phi }_{21}\end{array}\right]$$

(53)

Table 1. The gains of the observer and absolute values of the roots of its characteristic equation for the switching frequency f_s = 12,800 Hz and relative time constants τ/T_s from 1 to 7 for L_F = 1 mH, C_F = 51 μF, R_LFe = 1 Ω.

τ/Ts, fs	pz0	pz1	pz2	pz3	l1	l2	l3	Abs (Root1)	Abs (Root2)	Abs (Root3)
1, 12.8 k	1	0.043	0.015	−0.007	2.852	−7.780	−9.215	0.211	0.211	0.152
2, 12.8 k	1	−0.866	0.396	−0.082	1.943	−3.194	−3.930	0.459	0.459	0.389
3, 12.8 k	1	−1.456	0.846	−0.189	1.353	−1.392	−1.764	0.595	0.595	0.5332
4, 12.8 k	1	−1.805	1.196	−0.287	1.004	−0.719	−0.917	0.678	0.678	0.624
5, 12.8 k	1	−2.029	1.458	−0.368	0.780	−0.427	−0.531	0.732	0.732	0.686
6, 12.8 k	1	−2.184	1.657	−0.435	0.626	−0.284	−0.335	0.772	0.772	0.730
7, 12.8 k	1	−2.297	1.812	−0.490	0.513	−0.207	−0.223	0.801	0.801	0.764

presents the gains of the observer in the absolute values of the roots of its characteristic equation for the low switching frequency f_s = 12,800 Hz and relative time constants τ/T_s from 1 to 6. The roots of the characteristic equation of the observer for the lower τ/T_s are closer to zero for the z-plane in Manabe CDM. This research concerns the comparison of operating at a low switching frequency f_s = 12,800 Hz and operating at a high switching frequency f_s = 51,200 Hz, because of the higher values of the switching frequency when the prediction is not necessary (the delay in the inverter system is low).

In [10,20,42,46] the passivity-based control for the voltage source inverters was presented. When the supplied energy in a system exceeds the stored energy, the system is passive. The passive system is stable—this is the idea of PBC. The energy in an inverter is stored in the components of the output filter—the filter coil and the filter capacitor–and can be described by the Hamiltonian function (54) H(x) (sometimes H(x) is called a Lyapunov function [47]).

$$H(x)=\frac{1}{2}(L_F{i}_{LF}{}^2+C_F{v}_{OUT}{}^2)$$

(54)

The discrete control law of PBC for the predicted values of state variables is (55), (56), from [42].

$${\widehat{v}}_{CTRL}(k+1)=-R_i{\widehat{i}}_{LF}(k+1)+(R_i+R_{LF}){\widehat{i}}_{LFref}(k+1)+L_F\frac{{\widehat{i}}_{LFref}(k+1)-{\widehat{i}}_{LFref}(k)}{T_c}+v_{OUTref}(k+1)$$

(55)

$${\widehat{i}}_{LFref}(k+1)=K_v[v_{OUTref}(k+1)-{\widehat{v}}_{OUT}(k+1)]+C_F\frac{v_{OUTref}(k+1)-v_{OUTref}(k)}{T_c}+{\widehat{i}}_{OUT}(k+1)$$

(56)

where:

$${\widehat{v}}_{OUT}(k+1)={\phi }_{11}{v}_{OUT}(k)+{\phi }_{12}{i}_{LF}(k)+{\phi }_{13}{i}_{OUT}(k)+g_{11}\frac{{\widehat{v}}_{CTRL}(k)}{V_{DC}}{T}_s+l_1[v_{OUT}(k)-{\widehat{v}}_{OUT}(k)]$$

(57)

$${\widehat{i}}_{LF}(k+1)={\phi }_{21}{v}_{OUT}(k)+{\phi }_{22}{i}_{LF}(k)+{\phi }_{23}{i}_{OUT}(k)+g_{12}\frac{{\widehat{v}}_{CTRL}(k)}{V_{DC}}{T}_s+l_2[v_{OUT}(k)-{\widehat{v}}_{OUT}(k)]$$

(58)

$${\widehat{i}}_{OUT}(k+1)=i_{OUT}(k)+l_3[v_{OUT}(k)-{\widehat{v}}_{OUT}(k)]$$

(59)

The state–space Equations (57)–(59) are different from (47) because predicted space variables are not directly used in the equations. Using the predicted variables (47) is the typical approach [48]. But our C_D = [1 0 0], and the output variable is dependent only on the output voltage. So, the measured values of the variables were used directly in (57)–(59) because there was no other way of implementing them in the prediction procedure.

The important problem in PBC is the choice of the current gain R_i and the voltage gain K_v. It was shown in [14,26,47] that the bottom limits of gains are R_LFe + R_i > 0 and K_v > 0. The upper limits of R_i and K_v gains are a result of the limitation of the control voltage v_CTRL possible speed. The higher values of the gains cause saturation of the PWM modulator but do not always cause oscillations. Sometimes, slightly increasing the gains over these limits can decrease the distortions of the output voltage for the nonlinear load. But it should be remembered that during saturation, the feedback loop does not work. The derivative of the control voltage in one switching cycle should be lower than the maximum increase in the output PWM signal that is equal to V_DC/T_s.

We can assume that d(v_OUTref)/dt ≈ 0 in one sampling period. The control law without prediction is (60) and (61):

$$v_{CTRL}(k{T}_s)=-R_i{i}_{LF}(k{T}_s)+(R_i+R_{LFe})i_{LFref}(k{T}_s)+L_F\frac{d{i}_{LFref}(k{T}_s)}{dt}+v_{OUTref}(k{T}_s)$$

(60)

$$i_{LFref}(k{T}_s)=K_v[v_{OUTref}(k{T}_s)-v_{OUT}(k{T}_s)]+C_F\frac{d{v}_{OUTref}(k{T}_s)}{dt}+i_{OUT}(k{T}_s)$$

(61)

From (61) for the resistive load R_LOAD:

$$i_{LFref}(k{T}_s)\approx K_v{v}_{OUTref}(k{T}_s)+(\frac{1}{R_{LOAD}}-K_v)v_{OUT}(k{T}_s)$$

(62)

Let us assume the operation with the load R_LOAD = ∞.

$$\frac{d{i}_{LFref}(k{T}_s)}{dt}\approx -K_v\frac{d{v}_{OUT}(k{T}_s)}{dt}$$

(63)

The absolute value of the derivative of v_CTRL for the load R_LOAD = ∞ is (64).

$$\left|\frac{d{v}_{CTRL}(k{T}_s)}{dt}\right|\approx K_v{L}_F\frac{d^2{v}_{OUT}(k{T}_s)}{d{t}^2}+K_v(R_i+R_{LFe})\frac{d{v}_{OUT}(k{T}_s)}{dt}+R_i\frac{d{i}_{LF}(k{T}_s)}{dt}$$

(64)

In one switching cycle

$${\left.\frac{d{i}_{LF}(k{T}_s)}{dt}\right|}_{\max ,\min }\approx \pm \frac{V_{DC}}{L_F}, {\left.\frac{d{v}_{OUT}(k{T}_s)}{dt}\right|}_{\max }\approx \frac{i_{LF}}{C_F}, {\left.\frac{d^2{v}_{OUT}(k{T}_s)}{d{t}^2}\right|}_{\max }\approx {\left.\frac{d}{dt}(\frac{i_{LF}}{C_F})\right|}_{\max }\approx \pm \frac{V_{DC}}{L_F{C}_F}$$

(65)

Finally, the absolute value of the derivative of v_CTRL for the load R_LOAD = ∞ is (66).

$${\left|\frac{d{v}_{CTRL}(k{T}_s)}{dt}\right|}_{\max }\approx K_v[L_F+(R_i+R_{LFe})T_s]\frac{V_{DC}}{L_F{C}_F}+R_i\frac{V_{DC}}{L_F}$$

(66)

The upper limits of R_i and K_v gains are (67).

$$K_v[L_F+(R_i+R_{LFe})T_s]\frac{1}{L_F{C}_F}+\frac{R_i}{L_F}<f_s$$

(67)

Figure 7a,b presents the graphic visualisation of Equation (67), adequately for f_s = 12,800 and 51,200 Hz, while omitting the delays. When the left side of this equation is lower than the switching frequency, the gains are in the allowable range. The curves of equality of the left side of Equation (67) and the switching frequency—the border values of gains—are presented in Figure 7c for f_s = 12,800 and 51,200 Hz. Taking values of the R_i and K_v gains from these curves below them, we can be sure that there will be no oscillations in the output voltage. However, it is possible to check experimentally higher values of the gains to decrease the error of the control. The presented values of gains are valid for Simulink simulation because we do not need to scale the voltage and currents. We only divide all the measured variables by the V_DC that is on the input of the inverter because the input of the modulator is inside +1/−1. The other problem is the modulation index. The lower this index, the higher the dynamics of the modulator. However, in real inverters, the modulation index should be close to unity. Equation (67) does not consider the modulation index M value because the maximum carrier-slope increase does not depend on M. Equation (67) is calculated for R_LOAD = ∞, the worst case being that the restrictions of the K_v value for the existing load resistance will be slightly lower. The higher value of the gains, the lower the output voltage error and the lower the THD coefficient. That is why it is possible to obtain much lower THD for higher switching frequencies.

9. Simulation of the Inverter with the Delay in the Measurement Traces

Figure 8 presents the output voltage waveform of the open-loop inverter with the nonlinear rectifier load R = 100 Ω and C = 430 μF.

Figure 9a presents the simulation model without the delays in the measuring traces for the low switching frequency f_s = 12,800 Hz. Figure 9b,c presents the output voltage, output current and the control voltage waveforms for L_F = 1 mH, R_LFe = 1 Ω, C_F = 51 μF, f_s = 12,800 Hz, the nonlinear rectifier load R = 100 Ω and C = 430 μF, the modulation index M = 0.7, and the PBC control (60) and (61) without prediction. In Figure 9b, K_v = 0.3, and R_i = 4 from the border line from Figure 7b (THD = 2.69%). However, it is possible to increase the gains K_v = 0.5, R_i = 25 (Figure 9c) whilst accepting some oscillations of the control voltage, in order to decrease distortions (THD = 1.04%). In the simulated measurement traces (Figure 8a) there are only ZOH modules simulating the analogue-to-digital converters (ADCs).

In Figure 10a, the 2T_s delays in each of the measuring traces were added to make the simulation model more similar to the experimental model (Figure 6c,d) for f_s = 12,800 Hz. The gains K_v and R_i of PBC were reduced from the border values K_v = 0.3 and R_i = 4 (Figure 10b) to 0.1 and 4 (Figure 10c) to decrease the output voltage oscillations. The controller architecture was the same as in Figure 9a. The controller works wrongly because the output voltage distortions are higher than in the open-loop inverter (Figure 8), which is ridiculous.

As shown in Figure 11a, the inputs of the PBC controller (55), (56) were predicted (57)–(59). The gains of the observer l₁, l₂, l₃ were initially calculated for τ/T_s = 1 (Table 1) and then reduced to 0.285, −0.778 and −0.092 (the highest values for which there were no oscillations of the output voltage for the particular gains) and the gains K_v and R_i were adjusted to 0.1 and 4. In all the cases, the coefficient of the control quality was the THD of the output voltage.

To show the influence of delays in the measurement traces (depending on the switching frequency) for the higher switching frequency (51,200 Hz), Figure 12 presents the results of the simulation of the inverter with delays of 2T_s in the measuring traces and the PBC controller, without prediction, for f_s = 51,200 Hz. It can be seen that the THD is very low (0.87%), and there is no need to use the observer. Let us compare the shape of the output current waveforms from Figure 11b and Figure 12. The current in Figure 12 is forced to increase immediately even if there are 2T_s delays, owing to possible higher controller gains.

Table 2. The gains of PBC, gains of the Luenberger observer, and the THD of the simulated inverter output voltage for cases, are presented in Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12.

	Kv	Ri	l1	l2	l3	THD
Open loop, fs = 12,800 Hz	-	-	-	-	-	4.63%
No additional delay, PBC without prediction, fs = 12,800 Hz	0.5	25	-	-	-	1.04%
Additional delay 2Ts, PBC without prediction, fs = 12,800 Hz	0.1	4	-	-	-	5.19%
Additional delay 2Ts, PBC with prediction, fs = 12,800 Hz	0.1	4	0.285	−0.778	−0.092	2.80%
Additional delay 2Ts, PBC without prediction, fs = 51,200 Hz	0.6	25	-	-	-	0.87%

presents the results (THD) of the control in simulations.

10. The Experimental Verification of Output Voltage Distortions

Real-time interface (RTI1202 with FPGA—MicroLabBox) with MATLAB 2021b (with the dSpace RTI Electric Motor Control Blockset libraries) is the best choice for experimental verification of the previous SIMULINK simulations [46]. The main trouble of the microprocessor-based (or FPGA-based) control is scaling the measurement trace gain. In the case of the RTI, all the signals can be displayed on a PC monitor using ControlDesk 7.5 (dSpace 2021b) software, and the gains in the Simulink blocks can be adjusted. All the output voltage, output current and inductor current waveform amplitudes (for the modulation coefficient M = 1, the specified sinusoidal output voltage amplitude and the chosen load resistor) should be equal to the specified value 0.5 because the reference output voltage waveform is 0.5 sin (2π50t). The range of the input values of the PWM block was equal to 0–1. Two sinusoidal waveforms shifted mutually 180 degrees in the phase, with the zero level shifted by 0.5 and a maximum amplitude of 0.5 as the inputs of the PWM block to realize the PWM scheme from Figure 3. For a modulation index of M = 0.7, the output voltage scaling gain was −1.5 (it should be reversed), and the output and inductor currents have gains of 2.7. The measured signals were shifted by small constant values to adjust their zero-crossing level. The next step was to divide the current measurements by the load resistance (for the nominal load, scaling was 50 Ω). Experimental verification using RTI is sufficient; however, a further design step is to create software for the microprocessor. This is the reason why the architecture of the RTI1202 software is based on interrupts from the PWM unit, like in the microprocessor. The trigger line 1 events from an EMC multichannel PWM block are handled by an ADC class 1 hardware interrupt block (HWINT), connected to the input port of a function-call subsystem (Figure 13a). The function-call subsystem (Figure 13b) contains all the components of the inverter control loop, such as the EMC multichannel PWM block, the ADC class 1 block and the PBC controller, with amplifiers of all the measured signals. The sample time of all the blocks is inherited from the PWM block triggering event (it can be set only in this block). The experimental inverter bridge transistors are driven with four DIO class 1 3.3 V digital outputs: a noninverted channel 1 (corresponds to S1 from Figure 2) and channel 2 (S3 in Figure 2), and an inverted channel 3 (S2 in Figure 2) and channel 4 (S4). The dead time between switching off and on two transistors in the same leg of the bridge is equal to 500 ns for the Si-MOSFET transistors (IRFP360) and is implemented in IR2184-integrated circuits in the experimental inverter. The output voltage, output current and inductor current are measured via ADC Class 1 channel 1, with a single conversion (−10–+10 V input range) after the trigger event from the PWM block.

Figure 14 presents the same waveforms from the experimental inverter as Figure 8 and Figure 10, Figure 11 and Figure 12 for simulation. The gains and the distortions (THD) of the output signal are presented in

Table 3. The gains of PBC, gains of the Luenberger observer and THD of the experimental inverter output voltage for cases are presented in Figure 14.

	Kv	Ri	l1	l2	l3	THD
Open loop, fs = 12,800 Hz	-	-	-	-	-	6.35%
PBC without prediction, fs = 12,800 Hz	0.1	4	-	-	-	7.63%
PBC with prediction, fs = 12,800 Hz	0.2	9	0.285	−0.778	−0.138	4.09%
Additional delay 2Ts, PBC without prediction, fs = 51,200 Hz	0.3	30	-	-	-	1.73%

. Figure 15 presents the tested experimental inverter with MicroLabBox (rti1202).

11. Results

Comparing Table 2 and Table 3, it can be seen that the distortions are 1 to 2% higher in the experimental verification than in the simulations. The reason could be the ripple output voltage in the experimental VSI. The controller gains in the simulations and the experimental inverter were adjusted from the initial values from the border lines in Figure 7c to obtain the lowest THD of the VSI output voltage without oscillations. However, in both cases of the simulation and the experimental verification, it was shown that for the low switching frequency (12,800 Hz), a lack of prediction in the control system can cause higher distortions of the output voltage than in the case of the open loop. For the high switching frequency (51,200 Hz), no prediction is required. Similar results in simulations and experimental verification prove that the approximation of the measuring trace Bode plots in the bandpass 0–1000 Hz, with delays equal to 2T_s, is appropriate.

12. Discussion

The simulations and the breadboard verification showed that the measurement traces can be modelled as the delay with some switching periods and even using the MISO control (e.g., PBC) is insufficient for a low switching frequency (about 10 kHz). However, this control is perfect for a high switching frequency (about 50 kHz). For a low switching frequency, the delay in the measurement traces causes oscillations of the output voltage even for the low gains of the controller (below the border curve in Figure 7c, because the reason for these oscillations is not considered there). The distortions of the output voltage can be higher than without any instantaneous control. The high switching frequency allows for an increase in the controller gains and decreases the output voltage distortions. Using the prediction of the state variables is the solution for a low switching frequency, e.g., using the state equations with the Luenberger observer. In this way, calculations of the variables are more flexible for the different delays in the measurement traces. The whole time, the theoretical discrete model of the inverter was used. The gains of the Luenberger observer are initially calculated using the coefficient diagram method for the different delays of the closed-loop observer. Initially, one switching period delay of the observer was taken into the calculation of the initial gains and then the gains of the observer were experimentally decreased to obtain the lowest-output voltage distortions. Finally, the adjusted observer dynamics were comparable with the gains of the observer with about seven switching period delays. It can be concluded that for a low switching frequency (about 10 kHz) the observer is necessary because of delays in the measuring traces. The best results can be obtained without the prediction for a high switching frequency (about 50 kHz). The observer is the additional subsystem of the control loop and should be treated as a necessary evil, because it can cause some instability. The gains of the PBC controller were adjusted to the lowest distortions of the output voltage. In some cases, it was able to increase gains over the borderline of gains from Figure 7c and to accept small oscillations in the control voltage. Further increases in the controller gains increase the output voltage distortions.

13. Conclusions

Most of the measuring traces in the inverters have Bode plots that, in the range up to the corner frequency of the output filter, can be modelled as a delay equal to some switching periods. The only possibility for the low-output voltage distortion operation of a MISO instantaneous control loop with a low switching frequency (e.g., 10 kHz), in a real device with delays in the measuring traces, is to use an observer, e.g., the simple Luenberger type. The work with a high switching frequency (e.g., 50 kHz) makes this prediction unnecessary, because the delay in the measuring traces usually depends on the switching frequency, and the prediction unnecessarily complicates the control loop, even increasing the distortions.