A Multiphysics-Multiscale Model for Particle–Binder Interactions in Electrode of Lithium-Ion Batteries
Abstract
1. Introduction
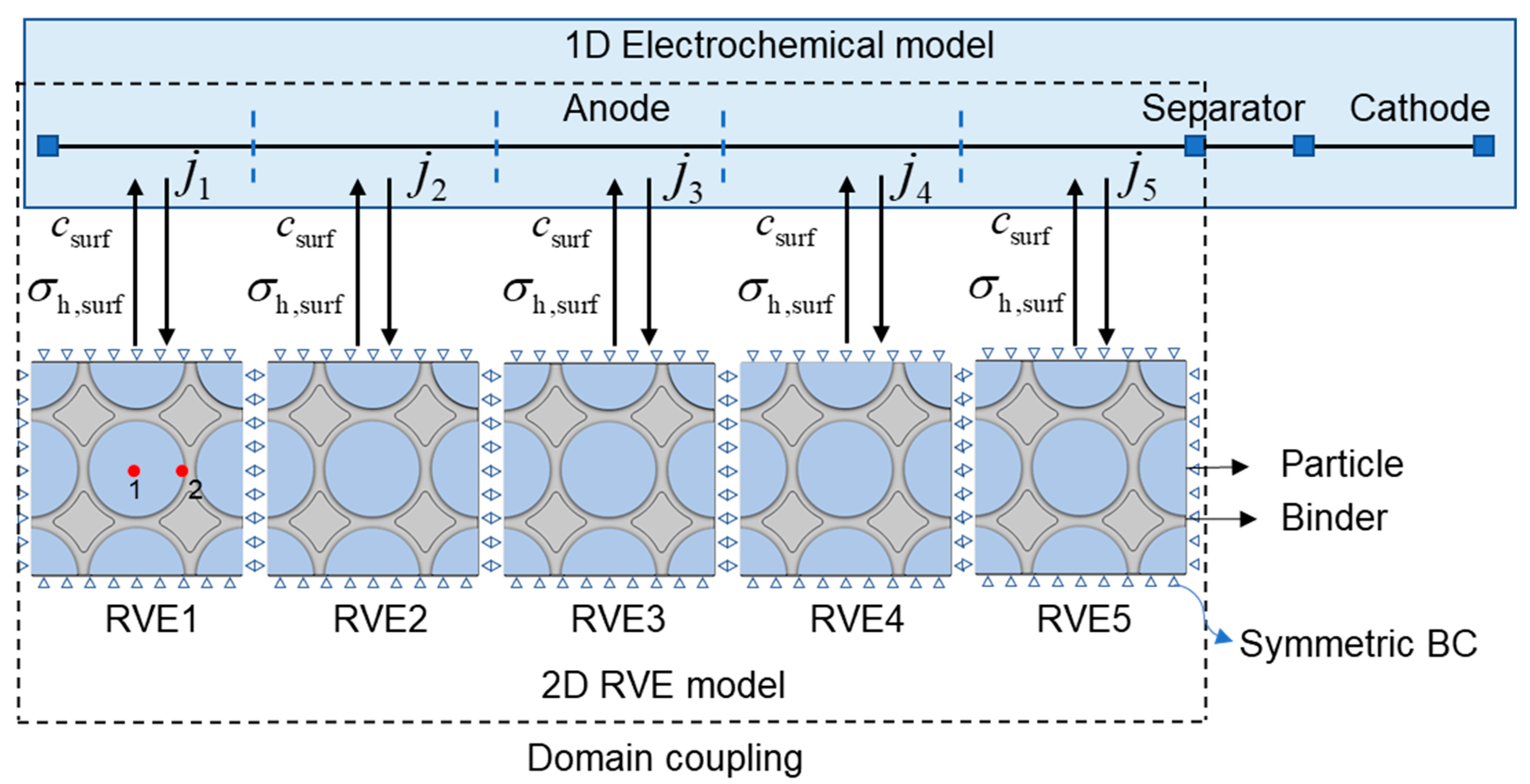
2. Multiphysics–Multiscale Computational Methodology
2.1. Electrochemistry at Electrode Level
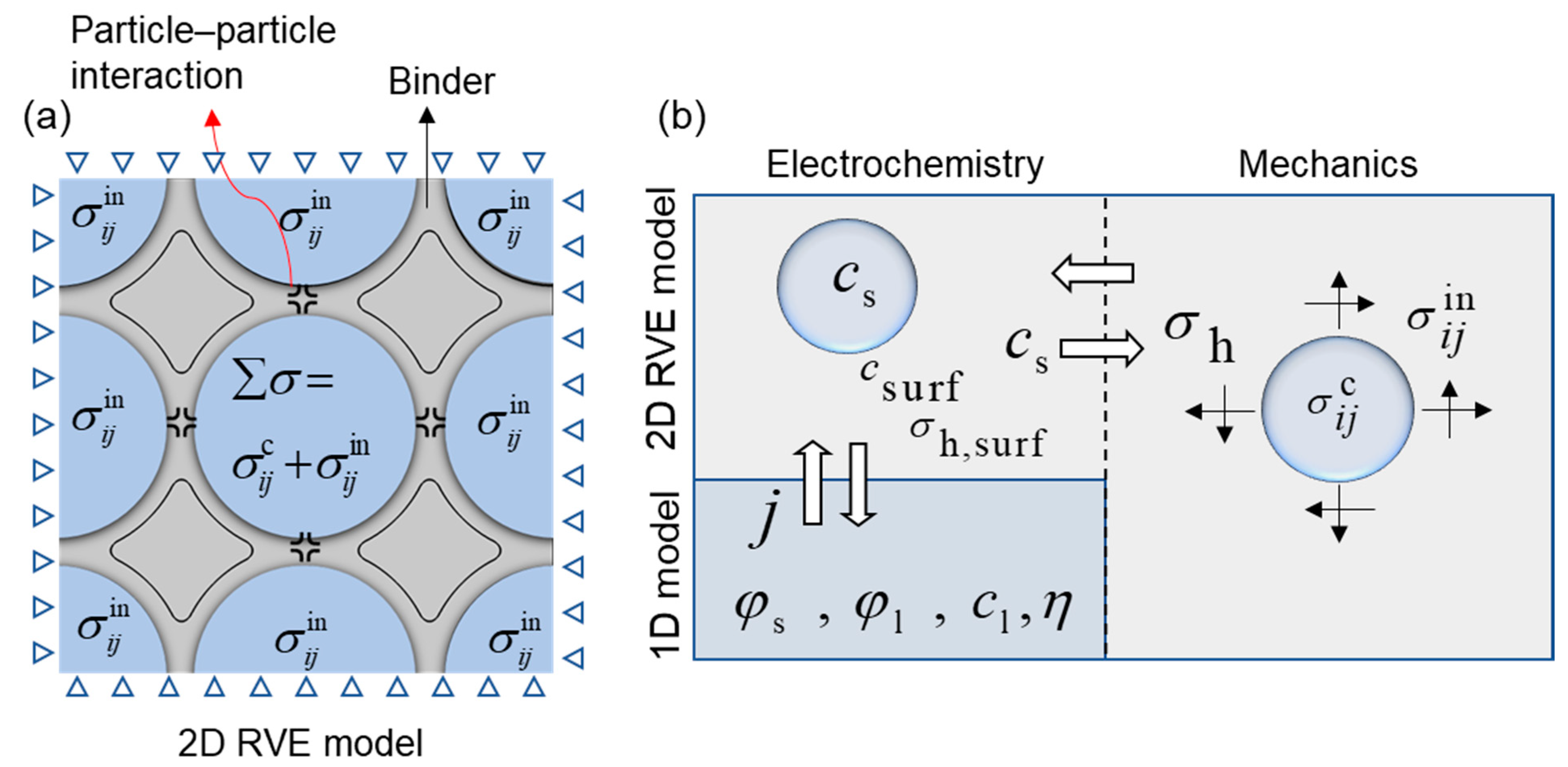
2.2. Particle Level
2.2.1. Stress-Enhanced Diffusion
2.2.2. Mechanics
3. Numerical Solution of Stress
4. Results and Discussion
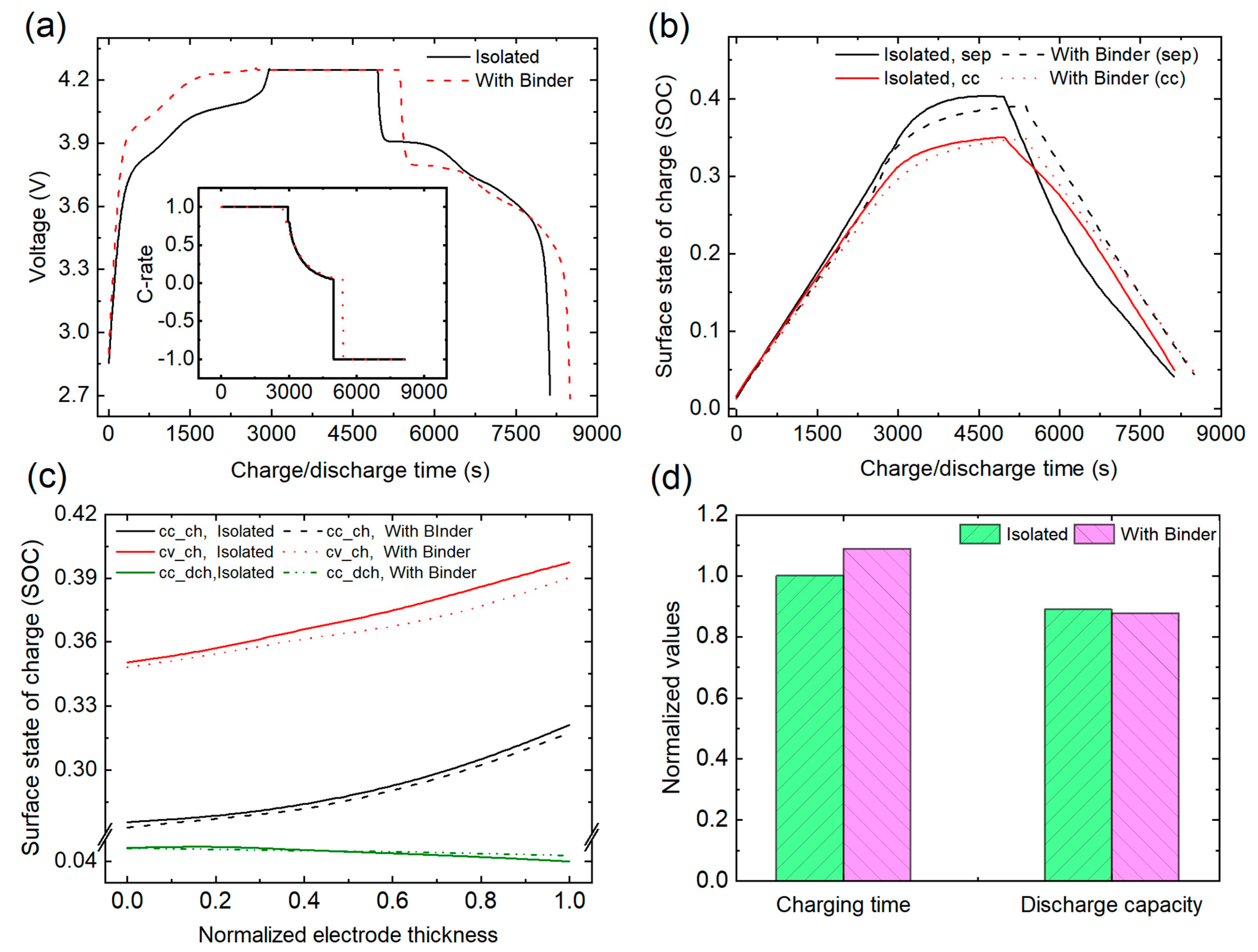
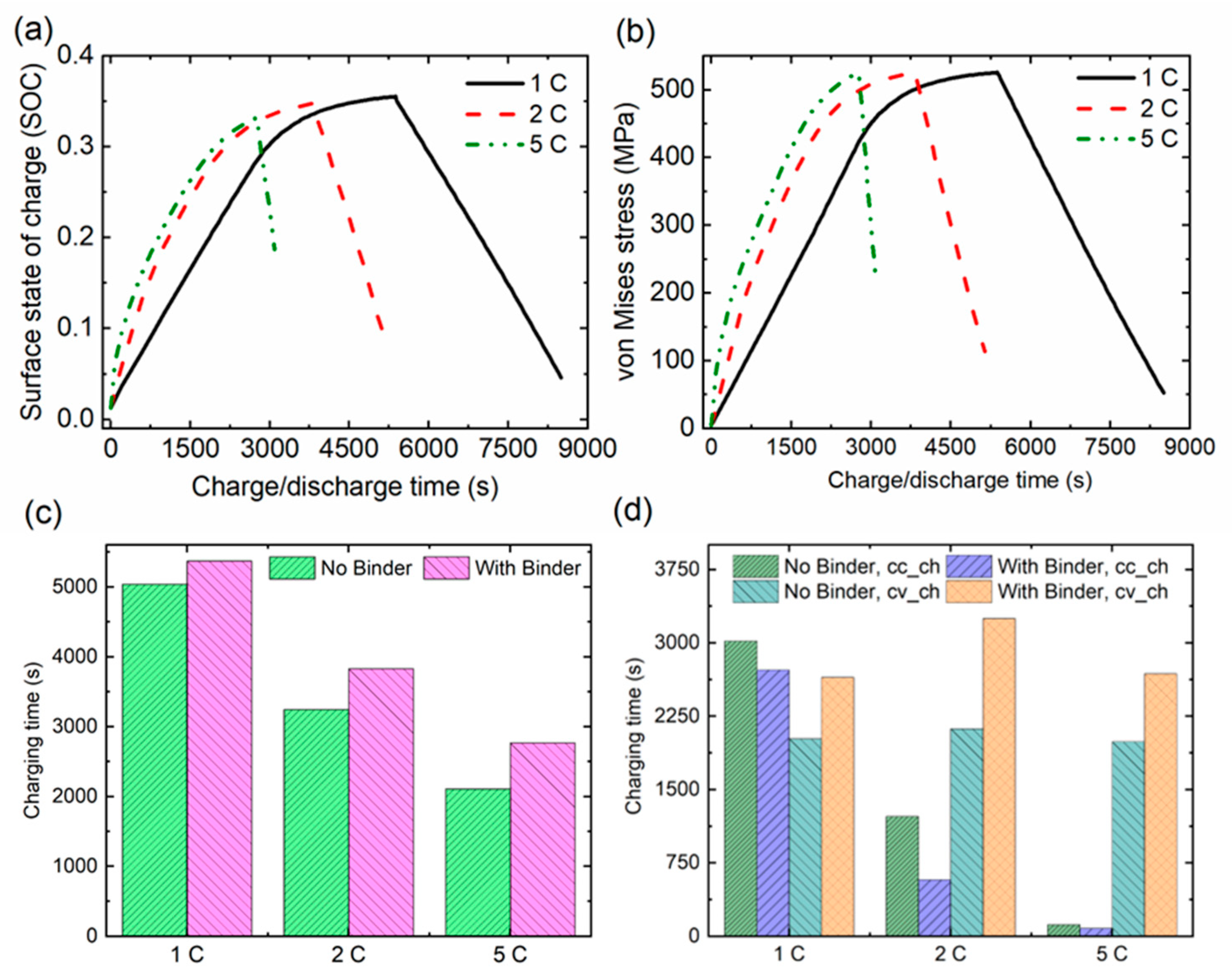
4.1. Electrochemical Results
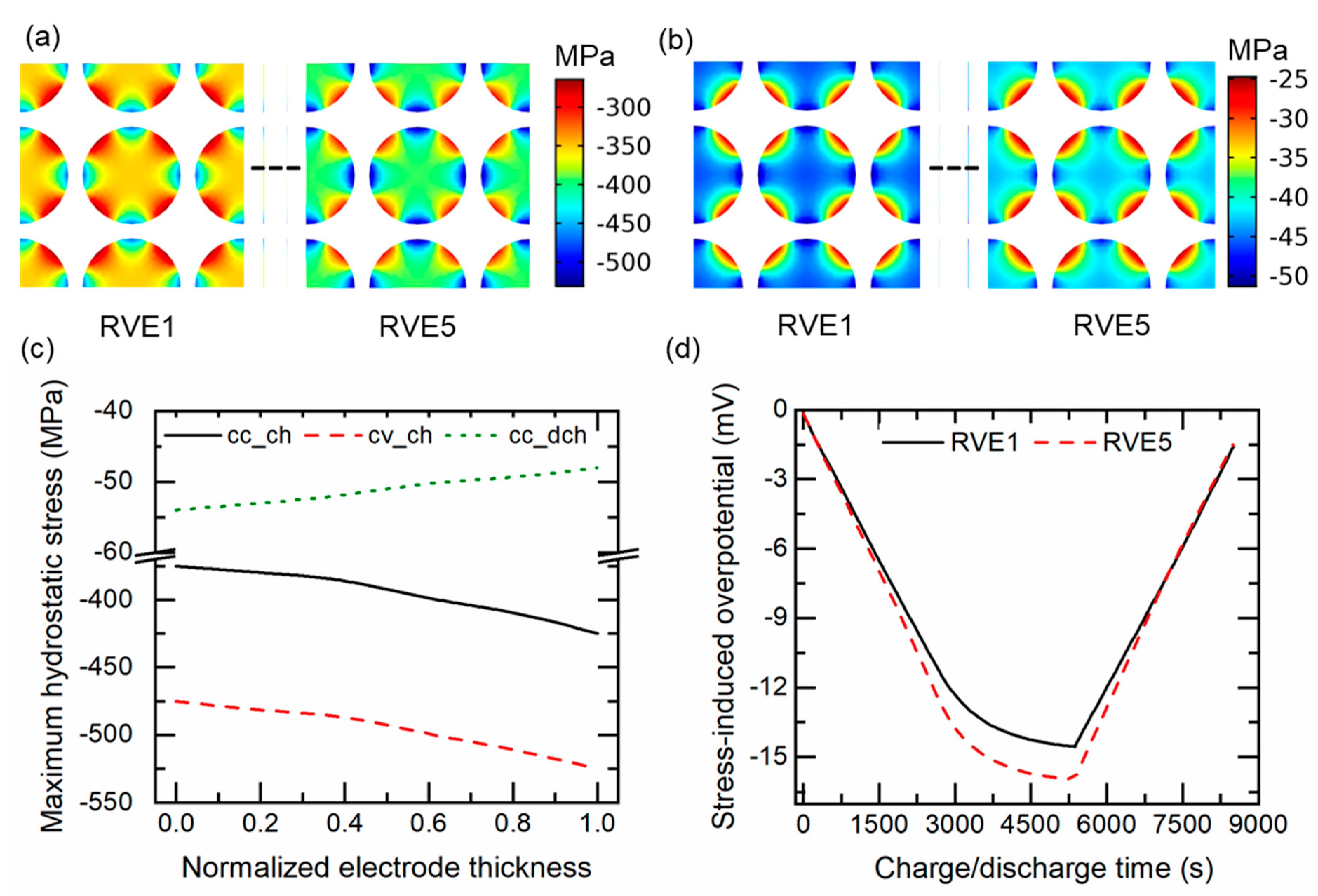
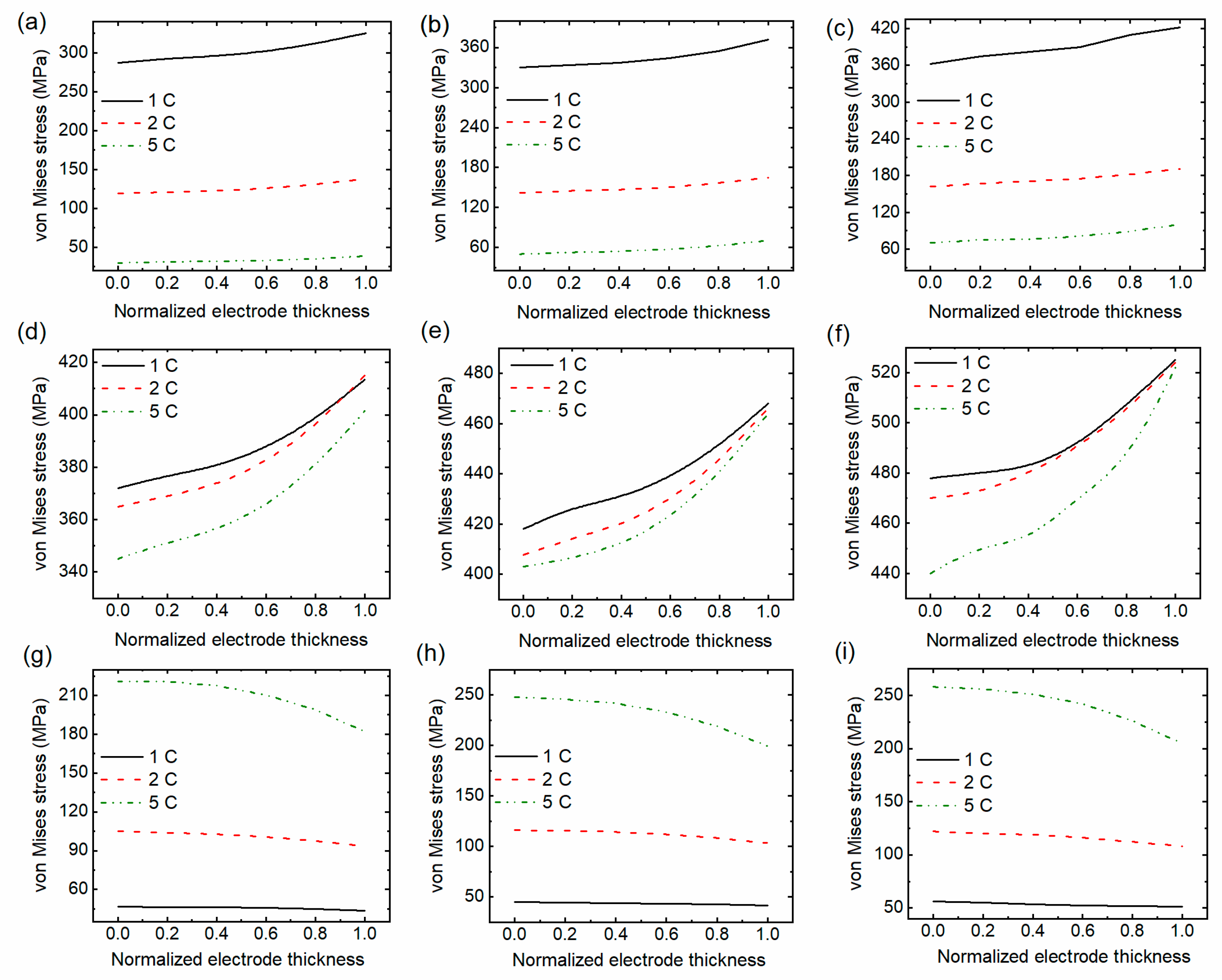
4.2. Stress Analysis
4.2.1. Effect of Binder Modulus
4.2.2. Effect of Charging Rates
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhuo, M.; Offer, G.; Marinescu, M. Degradation Model of High-Nickel Positive Electrodes: Effects of Loss of Active Material and Cyclable Lithium on Capacity Fade. J. Power Sources 2023, 556, 232461. [Google Scholar] [CrossRef]
- Jiao, X.; Wang, Y.; Chen, Y.; Wang, J.; Xiong, S.; Song, Z.; Xu, X.; Liu, Y. Insight of Electro-Chemo-Mechanical Process inside Integrated Configuration of Composite Cathode for Solid-State Batteries. Energy Storage Mater. 2023, 61, 102864. [Google Scholar] [CrossRef]
- Gao, X.; Li, S.; Xue, J.; Hu, D.; Xu, J. A Mechanistic and Quantitative Understanding of the Interactions between SiO and Graphite Particles. Adv. Energy Mater. 2023, 13, 2202584. [Google Scholar] [CrossRef]
- Li, D.; Guo, H.; Jiang, S.; Zeng, G.; Zhou, W.; Li, Z. Microstructures and Electrochemical Performances of TiO2-Coated Mg–Zr Co-Doped NCM as a Cathode Material for Lithium-Ion Batteries with High Power and Long Circular Life. New J. Chem. 2021, 45, 19446–19455. [Google Scholar] [CrossRef]
- Ali, Y.; Iqbal, N.; Lee, S. Inhomogeneous Stress Development at the Multiparticle Electrode of Lithium-ion Batteries. Int. J. Energy Res. 2021, 45, 14788–14803. [Google Scholar] [CrossRef]
- Chen, Z.; Christensen, L.; Dahn, J.R. Large-Volume-Change Electrodes for Li-Ion Batteries of Amorphous Alloy Particles Held by Elastomeric Tethers. Electrochem. Commun. 2003, 5, 919–923. [Google Scholar] [CrossRef]
- Yan, X.; Wang, Y.; Yu, T.; Chen, H.; Zhao, Z.; Guan, S. Polyimide Binder by Combining with Polyimide Separator for Enhancing the Electrochemical Performance of Lithium Ion Batteries. Electrochim. Acta 2016, 216, 1–7. [Google Scholar] [CrossRef]
- Liu, G.; Zheng, H.; Song, X.; Battaglia, V.S. Particles and Polymer Binder Interaction: A Controlling Factor in Lithium-Ion Electrode Performance. J. Electrochem. Soc. 2012, 159, A214. [Google Scholar] [CrossRef]
- Bucci, G.; Swamy, T.; Bishop, S.; Sheldon, B.W.; Chiang, Y.-M.; Carter, W.C. The Effect of Stress on Battery-Electrode Capacity. J. Electrochem. Soc. 2017, 164, A645–A654. [Google Scholar] [CrossRef]
- Tomaszewska, A.; Chu, Z.; Feng, X.; O’Kane, S.; Liu, X.; Chen, J.; Ji, C.; Endler, E.; Li, R.; Liu, L.; et al. Lithium-Ion Battery Fast Charging: A Review. eTransportation 2019, 1, 100011. [Google Scholar] [CrossRef]
- Zhu, G.L.; Zhao, C.Z.; Huang, J.Q.; He, C.; Zhang, J.; Chen, S.; Xu, L.; Yuan, H.; Zhang, Q. Fast Charging Lithium Batteries: Recent Progress and Future Prospects. Small 2019, 15, 1805389. [Google Scholar]
- Iqbal, N.; Ali, Y.; Lee, S. Analysis of Mechanical Failure at the Interface between Graphite Particles and Polyvinylidene Fluoride Binder in Lithium-Ion Batteries. J. Power Sources 2020, 457, 228019. [Google Scholar] [CrossRef]
- Ali, Y.; Iqbal, N.; Lee, S. Simultaneous Effect of Particle Size and Location on Stress Development in the Electrodes of Lithium-ion Batteries. Int. J. Energy Res. 2020, 44, 12145–12157. [Google Scholar] [CrossRef]
- Takahashi, K.; Higa, K.; Mair, S.; Chintapalli, M.; Balsara, N.; Srinivasan, V. Mechanical Degradation of Graphite/PVDF Composite Electrodes: A Model-Experimental Study. J. Electrochem. Soc. 2016, 163, A385–A395. [Google Scholar] [CrossRef]
- Baboo, J.P.; Yatoo, M.A.; Dent, M.; Hojaji Najafabadi, E.; Lekakou, C.; Slade, R.; Hinder, S.J.; Watts, J.F. Exploring Different Binders for a LiFePO4 Battery, Battery Testing, Modeling and Simulations. Energies 2022, 15, 2332. [Google Scholar] [CrossRef]
- Singh, G.; Bhandakkar, T.K. Analytical Investigation of Binder’s Role on the Diffusion Induced Stresses in Lithium Ion Battery through a Representative System of Spherical Isolated Electrode Particle Enclosed by Binder. J. Electrochem. Soc. 2017, 164, A608–A621. [Google Scholar] [CrossRef]
- Mendoza, H.; Roberts, S.A.; Brunini, V.E.; Grillet, A.M. Mechanical and Electrochemical Response of a LiCoO2 Cathode Using Reconstructed Microstructures. Electrochim. Acta 2016, 190, 1–15. [Google Scholar] [CrossRef]
- Trembacki, B.L.; Noble, D.R.; Brunini, V.E.; Ferraro, M.E.; Roberts, S.A. Mesoscale Effective Property Simulations Incorporating Conductive Binder. J. Electrochem. Soc. 2017, 164, E3613–E3626. [Google Scholar] [CrossRef]
- Huang, P.; Gao, L.T.; Guo, Z.-S. Elastoplastic Model for Chemo-Mechanical Behavior of Porous Electrodes Using Image-Based Microstructure. Int. J. Solids Struct. 2022, 254–255, 111903. [Google Scholar] [CrossRef]
- Foster, J.M.; Huang, X.; Jiang, M.; Chapman, S.J.; Protas, B.; Richardson, G. Causes of Binder Damage in Porous Battery Electrodes and Strategies to Prevent It. J. Power Sources 2017, 350, 140–151. [Google Scholar] [CrossRef]
- Rahani, E.K.; Shenoy, V.B. Role of Plastic Deformation of Binder on Stress Evolution during Charging and Discharging in Lithium-Ion Battery Negative Electrodes. J. Electrochem. Soc. 2013, 160, A1153–A1162. [Google Scholar] [CrossRef]
- Wu, W.; Xiao, X.; Wang, M.; Huang, X. A Microstructural Resolved Model for the Stress Analysis of Lithium-Ion Batteries. J. Electrochem. Soc. 2014, 161, A803. [Google Scholar] [CrossRef]
- Rieger, B.; Schlueter, S.; Erhard, S.V.; Jossen, A. Strain Propagation in Lithium-Ion Batteries from the Crystal Structure to the Electrode Level. J. Electrochem. Soc. 2016, 163, A1595–A1606. [Google Scholar] [CrossRef]
- Iqbal, N.; Ali, Y.; Lee, S. Mechanical Degradation Analysis of a Single Electrode Particle with Multiple Binder Connections: A Comparative Study. Int. J. Mech. Sci. 2020, 188, 105943. [Google Scholar] [CrossRef]
- Iqbal, N.; Ali, Y.; Lee, S. Chemo-Mechanical Response of Composite Electrode Systems with Multiple Binder Connections. Electrochim. Acta 2020, 364, 137312. [Google Scholar] [CrossRef]
- Liu, P.; Xu, R.; Liu, Y.; Lin, F.; Zhao, K. Computational Modeling of Heterogeneity of Stress, Charge, and Cyclic Damage in Composite Electrodes of Li-Ion Batteries. J. Electrochem. Soc. 2020, 167, 040527. [Google Scholar] [CrossRef]
- Wang, H.; Nadimpalli, S.P.V.; Shenoy, V.B. Inelastic Shape Changes of Silicon Particles and Stress Evolution at Binder/Particle Interface in a Composite Electrode during Lithiation/Delithiation Cycling. Extrem. Mech. Lett. 2016, 9, 430–438. [Google Scholar] [CrossRef]
- Gao, X.; He, P.; Ren, J.; Xu, J. Modeling of Contact Stress among Compound Particles in High Energy Lithium-Ion Battery. Energy Storage Mater. 2019, 18, 23–33. [Google Scholar] [CrossRef]
- Xiao, J.; Li, H.; Zhang, H.; He, S.; Zhang, Q.; Liu, K.; Jiang, S.; Duan, G.; Zhang, K. Nanocellulose and Its Derived Composite Electrodes toward Supercapacitors: Fabrication, Properties, and Challenges. J. Bioresour. Bioprod. 2022, 7, 245–269. [Google Scholar] [CrossRef]
- Deng, W.-N.; Li, Y.-H.; Xu, D.-F.; Zhou, W.; Xiang, K.-X.; Chen, H. Three-Dimensional Hierarchically Porous Nitrogen-Doped Carbon from Water Hyacinth as Selenium Host for High-Performance Lithium–Selenium Batteries. Rare Met. 2022, 41, 3432–3445. [Google Scholar] [CrossRef]
- Deng, W.; Xu, Y.; Zhang, X.; Li, C.; Liu, Y.; Xiang, K.; Chen, H. (NH4)2Co2V10O28·16H2O/(NH4)2V10O25·8H2O Heterostructure as Cathode for High-Performance Aqueous Zn-Ion Batteries. J. Alloys Compd. 2022, 903, 163824. [Google Scholar] [CrossRef]
- Zhou, W.; Zeng, G.; Jin, H.; Jiang, S.; Huang, M.; Zhang, C.; Chen, H. Bio-Template Synthesis of V2O3@Carbonized Dictyophora Composites for Advanced Aqueous Zinc-Ion Batteries. Molecules 2023, 28, 2147. [Google Scholar] [CrossRef] [PubMed]
- Wen, X.; Luo, J.; Xiang, K.; Zhou, W.; Zhang, C.; Chen, H. High-Performance Monoclinic WO3 Nanospheres with the Novel NH4+ Diffusion Behaviors for Aqueous Ammonium-Ion Batteries. Chem. Eng. J. 2023, 458, 141381. [Google Scholar] [CrossRef]
- Song, Y.C.; Soh, A.K.; Zhang, J.Q. On Stress-Induced Voltage Hysteresis in Lithium Ion Batteries: Impacts of Material Property, Charge Rate and Particle Size. J. Mater. Sci. 2016, 51, 9902–9911. [Google Scholar] [CrossRef]
- Liu, B.; Jia, Y.; Li, J.; Jiang, H.; Yin, S.; Xu, J. Multiphysics Coupled Computational Model for Commercialized Si/Graphite Composite Anode. J. Power Sources 2020, 450, 227667. [Google Scholar] [CrossRef]
- Sethuraman, V.A.; Srinivasan, V.; Bower, A.F.; Guduru, P.R. In Situ Measurements of Stress-Potential Coupling in Lithiated Silicon. J. Electrochem. Soc. 2010, 157, A1253. [Google Scholar] [CrossRef]
- Lu, Y.; Chang, L.; Song, Y.; He, L.; Ni, Y. Effect of Plasticity on Voltage Decay Studied by a Stress Coupled Phase Field Reaction Model. Extrem. Mech. Lett. 2021, 42, 101152. [Google Scholar] [CrossRef]
- Lu, B.; Song, Y.; Zhang, Q.; Pan, J.; Cheng, Y.T.; Zhang, J. Voltage Hysteresis of Lithium Ion Batteries Caused by Mechanical Stress. Phys. Chem. Chem. Phys. 2016, 18, 4721–4727. [Google Scholar] [CrossRef]
- Cannarella, J.; Leng, C.Z.; Arnold, C.B. On the Coupling between Stress and Voltage in Lithium-Ion Pouch Cells. In Energy Harvesting and Storage: Materials, Devices, and Applications V; SPI: Baltimore, MD, USA, 2014; Volume 9115, p. 91150K. [Google Scholar]
- Zhang, X.; Shyy, W.; Marie Sastry, A. Numerical Simulation of Intercalation-Induced Stress in Li-Ion Battery Electrode Particles. J. Electrochem. Soc. 2007, 154, A910. [Google Scholar] [CrossRef]
- Ai, W.; Kraft, L.; Sturm, J.; Jossen, A.; Wu, B. Electrochemical Thermal-Mechanical Modelling of Stress Inhomogeneity in Lithium-Ion Pouch Cells. J. Electrochem. Soc. 2020, 167, 013512. [Google Scholar] [CrossRef]
- Wu, B.; Lu, W. Mechanical-Electrochemical Modeling of Agglomerate Particles in Lithium-Ion Battery Electrodes. J. Electrochem. Soc. 2016, 163, A3131–A3139. [Google Scholar] [CrossRef]
- Christensen, J.; Newman, J. Stress Generation and Fracture in Lithium Insertion Materials. J. Solid State Electrochem. 2006, 10, 293–319. [Google Scholar] [CrossRef]
- Gao, Y.F.; Zhoua, M. Strong Stress-Enhanced Diffusion in Amorphous Lithium Alloy Nanowire Electrodes. J. Appl. Phys. 2011, 109, 014310. [Google Scholar] [CrossRef]
- Bower, A.F.; Guduru, P.R.; Sethuraman, V.A. A Finite Strain Model of Stress, Diffusion, Plastic Flow, and Electrochemical Reactions in a Lithium-Ion Half-Cell. J. Mech. Phys. Solids 2011, 59, 804–828. [Google Scholar] [CrossRef]
- Kim, S.; Wee, J.; Peters, K.; Huang, H.Y.S. Multiphysics Coupling in Lithium-Ion Batteries with Reconstructed Porous Microstructures. J. Phys. Chem. C 2018, 122, 5280–5290. [Google Scholar] [CrossRef]
- Gao, X.; Lu, W.; Xu, J. Modeling Framework for Multiphysics-Multiscale Behavior of Si–C Composite Anode. J. Power Sources 2020, 449, 227501. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Liu, B.; Yin, S.; Xu, J. Integrated Computation Model of Lithium-Ion Battery Subject to Nail Penetration. Appl. Energy 2016, 183, 278–289. [Google Scholar] [CrossRef]
- Xu, R.; Zhao, K. Mechanical Interactions Regulated Kinetics and Morphology of Composite Electrodes in Li-Ion Batteries. Extrem. Mech. Lett. 2016, 8, 13–21. [Google Scholar] [CrossRef]
- Xu, R.; Scalco De Vasconcelos, L.; Zhao, K. Computational Analysis of Chemomechanical Behaviors of Composite Electrodes in Li-Ion Batteries. J. Mater. Res. 2016, 31, 2715–2727. [Google Scholar] [CrossRef]
- Wu, B.; Lu, W. A Consistently Coupled Multiscale Mechanical–Electrochemical Battery Model with Particle Interaction and Its Validation. J. Mech. Phys. Solids 2019, 125, 89–111. [Google Scholar] [CrossRef]
- Kashkooli, A.G.; Farhad, S.; Lee, D.U.; Feng, K.; Litster, S.; Babu, S.K.; Zhu, L.; Chen, Z. Multiscale Modeling of Lithium-Ion Battery Electrodes Based on Nano-Scale X-ray Computed Tomography. J. Power Sources 2016, 307, 496–509. [Google Scholar] [CrossRef]
- Pannala, S.; Turner, J.A.; Allu, S.; Elwasif, W.R.; Kalnaus, S.; Simunovic, S.; Kumar, A.; Billings, J.J.; Wang, H.; Nanda, J. Multiscale Modeling and Characterization for Performance and Safety of Lithium-Ion Batteries. J. Appl. Phys. 2015, 118, 072017. [Google Scholar] [CrossRef]
- Richardson, G.; Denuault, G.; Please, C.P. Multiscale Modelling and Analysis of Lithium-Ion Battery Charge and Discharge. J. Eng. Math. 2012, 72, 41–72. [Google Scholar] [CrossRef]
- Liu, B.; Wang, X.; Chen, H.S.; Chen, S.; Yang, H.; Xu, J.; Jiang, H.; Fang, D.N. A Simultaneous Multiscale and Multiphysics Model and Numerical Implementation of a Core-Shell Model for Lithium-Ion Full-Cell Batteries. J. Appl. Mech. Trans. ASME 2019, 86, 041005. [Google Scholar] [CrossRef]
- Cheng, Y.T.; Verbrugge, M.W. Evolution of Stress within a Spherical Insertion Electrode Particle under Potentiostatic and Galvanostatic Operation. J. Power Sources 2009, 190, 453–460. [Google Scholar] [CrossRef]
- Iqbal, N.; Ali, Y.; Lee, S. Debonding Mechanisms at the Particle-Binder Interface in the Li-Ion Battery Electrode. J. Electrochem. Soc. 2020, 167, 060515. [Google Scholar] [CrossRef]
- Lin, X.; Park, J.; Liu, L.; Lee, Y.; Lu, W.; Sastry, A.M. A Comprehensive Capacity Fade Model and Analysis for Li-Ion Batteries. J. Electrochem. Soc. 2013, 160, A1701–A1710. [Google Scholar] [CrossRef]
- Xiao, X.; Wu, W.; Huang, X. A Multi-Scale Approach for the Stress Analysis of Polymeric Separators in a Lithium-Ion Battery. J. Power Sources 2010, 195, 7649–7660. [Google Scholar] [CrossRef]
- Lee, S.; Yang, J.; Lu, W. Debonding at the Interface between Active Particles and PVDF Binder in Li-Ion Batteries. Extrem. Mech. Lett. 2016, 6, 37–44. [Google Scholar] [CrossRef]
- Wang, X.; de Vasconcelos, L.S.; Chen, K.; Perera, K.; Mei, J.; Zhao, K. In Situ Measurement of Breathing Strain and Mechanical Degradation in Organic Electrochromic Polymers. ACS Appl. Mater. Interfaces 2020, 12, 50895. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Chen, K.; de Vasconcelos, L.S.; He, J.; Shin, Y.C.; Mei, J.; Zhao, K. Mechanical Breathing in Organic Electrochromics. Nat. Commun. 2020, 11, 211. [Google Scholar] [CrossRef] [PubMed]


| Parameter | Negative | Positive | Separator |
|---|---|---|---|
| Electrode thickness | 90 | 52 | 70 |
| Particle radius | 5–20 | 8 | |
| Active material volume fraction | 0.471 [59] | 0.297 [59] | |
| Conductivity | 100 | 3.8 | |
| Diffusion coefficient | 3.9 × 10−14 | 1 × 10−13 | |
| Initial electrolyte concentration | 1000 | 1000 | 1000 |
| Electrolyte diffusivity | 7.5 × 10−11 [22] | 7.5 × 10−11 | 7.5 × 10−11 |
| Charge transfer coefficient | 0.5 | 0.5 | |
| Reaction rate constant | 2 × 10−11 [22] | 2 × 10−11 | |
| Elastic modulus | 12 [60] | 10 [60] | |
| Elastic modulus of PVDF binder | 2 | 2 | 50 MPa [60] |
| Poisson’s ratio | 0.3 [61] | 0.3 | |
| Partial molar volume | 3.64 × 10−6 [61] | 4.17 × 10−6 [22] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, Y.; Shah, I.; Khan, T.A.; Iqbal, N. A Multiphysics-Multiscale Model for Particle–Binder Interactions in Electrode of Lithium-Ion Batteries. Energies 2023, 16, 5823. https://doi.org/10.3390/en16155823
Ali Y, Shah I, Khan TA, Iqbal N. A Multiphysics-Multiscale Model for Particle–Binder Interactions in Electrode of Lithium-Ion Batteries. Energies. 2023; 16(15):5823. https://doi.org/10.3390/en16155823
Chicago/Turabian StyleAli, Yasir, Imran Shah, Tariq Amin Khan, and Noman Iqbal. 2023. "A Multiphysics-Multiscale Model for Particle–Binder Interactions in Electrode of Lithium-Ion Batteries" Energies 16, no. 15: 5823. https://doi.org/10.3390/en16155823
APA StyleAli, Y., Shah, I., Khan, T. A., & Iqbal, N. (2023). A Multiphysics-Multiscale Model for Particle–Binder Interactions in Electrode of Lithium-Ion Batteries. Energies, 16(15), 5823. https://doi.org/10.3390/en16155823









