Improvement of a Hybrid Solar-Wind System for Self-Consumption of a Local Object with Control of the Power Consumed from the Grid
Abstract
:1. Introduction
2. Literature Review and Problem Statement
- to substantiate the structure of the system with the control of power which is consumed from the grid and the implementation mechanism;
- to study the possibility of compensating for deviations in the load schedule relative to the calculated and actual generation of RES relative to the forecast. To substantiate the mechanism of the calculated curve SoC(t) formation with the correction of the value of consumed power by the deviation of the actual value of the SoC;
- to formulate algorithms for the control system functioning;
- to refine the energy processes model “24 h” in the system, taking into account the peculiarities of the implementation of control and the error in estimating the value of the SoC. To explore the possibilities of the proposed solutions in different weather conditions.
3. Materials and Methods of Research
4. Research Results
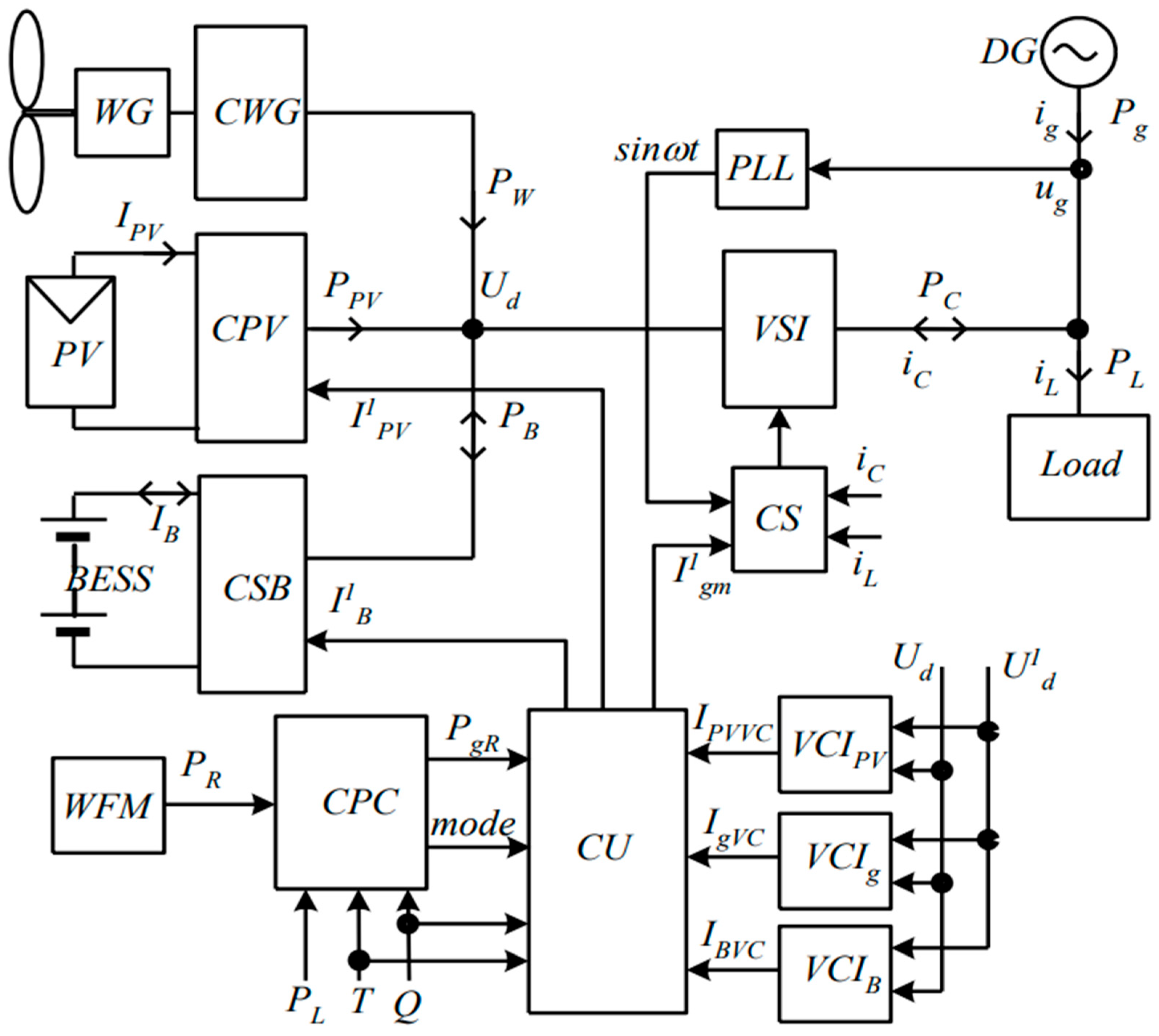
4.1. Structure of PV-WG System
- -
- the PV generation control. Ensures the maintenance of the setting value of the PV current I1PV in the MPPT mode or from the proportional-integral (PI) controller VCIPV when regulating the PV generation [20];
- -
- the BESS charge control. Ensures the maintenance of the set current value I1B from the PI-controller of the VCIB or a fixed value from the CU;
- -
- the current of the grid Ig control (setting the power consumed from the grid). Ensures the maintenance of the set current value at the PCC, taking into account the phase currents of the inverter iCa,b,c and the load iLa,b,c [2,20]. This is provided by the CS inverter control system with a phase-locked loop (PLL). At the same time, in the PCC a power factor is maintained close to 1. The setting of the current amplitude I1gm is provided by the PI—controller VCIg or from the CU.
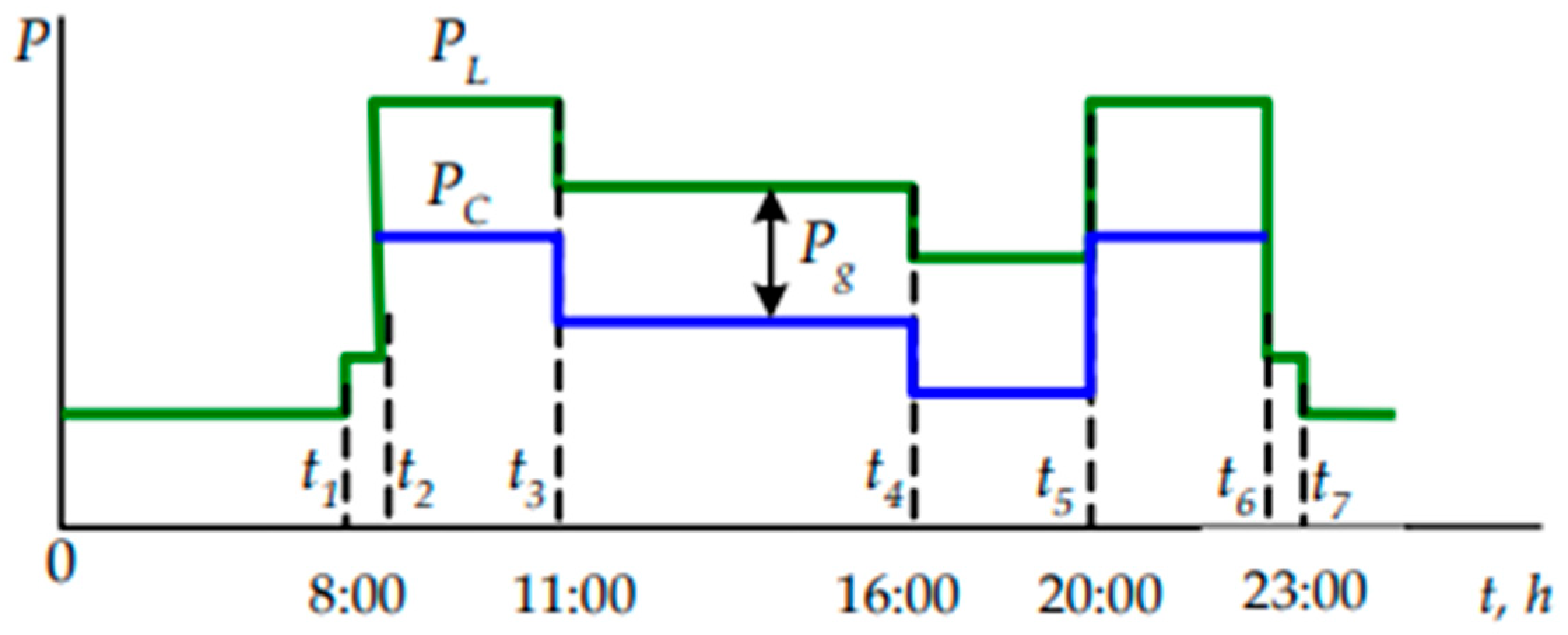
4.2. Setting the Value of the Power Consumed from the Grid and Correcting Its Value
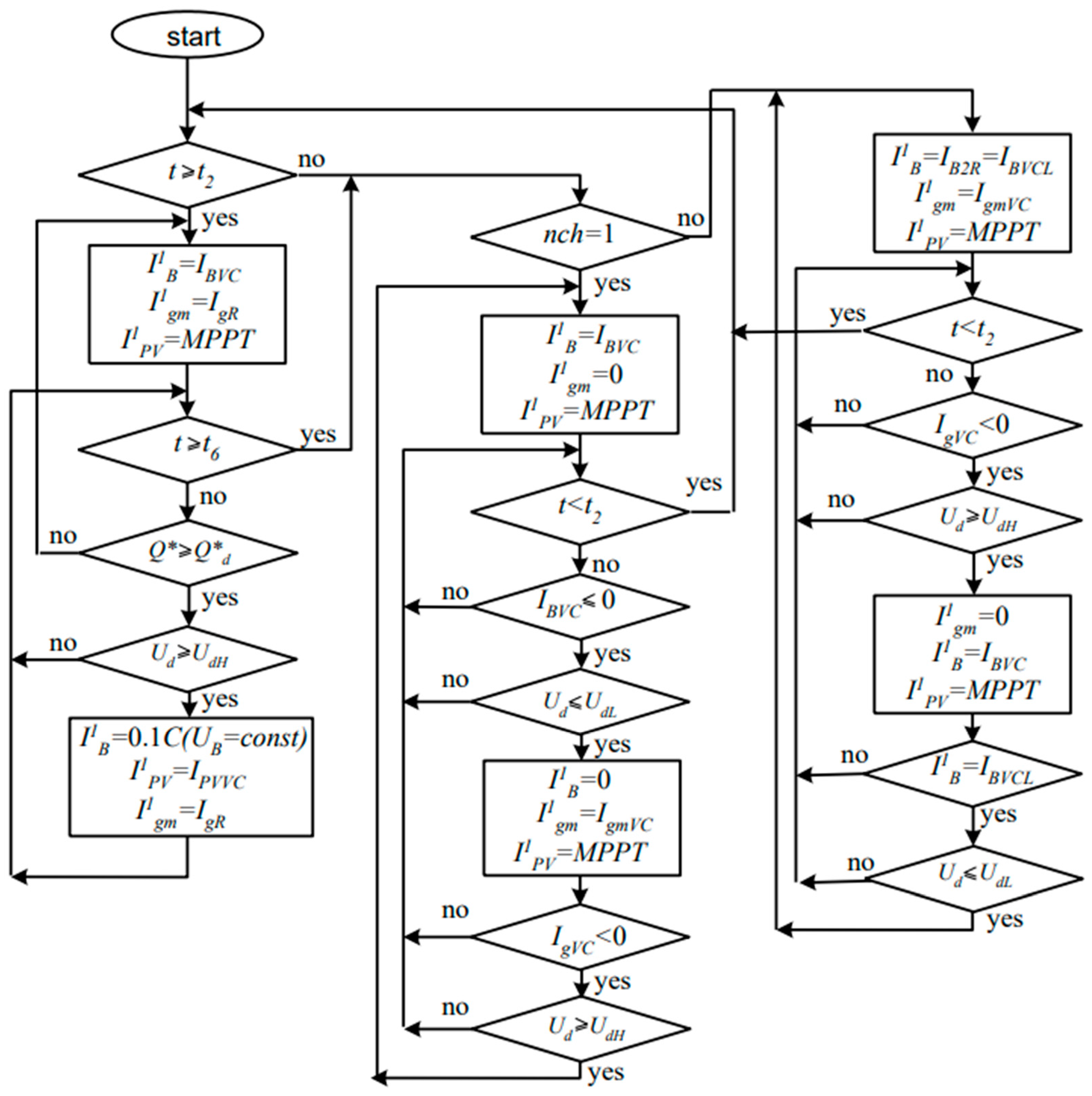
4.3. System: Operation Modes
- -
- interval (t2, t3). PV works in MPPT mode and PR = PRM. BESS current is set by VCIB→I1B. Reference of the current amplitude in PCC I1gm = Pg/3Ug (Ug—phase voltage) is calculated and fed to the input of the unit of the current reference of the grid inverter.
- -
- interval (t3, t5). At Q* < Q*d, the mode of operation is saved. At Q* ≥ Q*d, the BESS current is determined using its characteristic of charge IB(Q*). If the given value I1B> IB(Q*), then VCIB turns into saturation. Excess energy, which cannot accept the BESS, leads to an increase in voltage Ud on input VSI above the taken value U1d. When the switching threshold is reached UdH = (U1d+ ΔU) VCIPV is turned on and reduces I1PV (PPV). That is, we have a second condition for switching controllers while excluding the impact of transients [2]. If PC→0 and Q* ≥ Q*d VCI1gm is used, which provides regulation (reduction) Pg at maximum RES generation. That is, the full use of the RES energy is ensured.
- -
- interval (t5, t6). PC56 = (PL − Pg56) = PB + PRM·ηC. The value is given Pg56 (I1gm), PV is in the MPPT mode, and the BESS current is set by VCIB.
- -
- interval (t6, t2). A prerequisite is the charge of the BESS at PR·ηC ≥ PL. The value Q*6 ≥ Q*MIN and the night charge of the battery is carried out up to the value Q*2R, determined by the forecast for the night Q*2n = (Q*6 + ΔQ*62) and next day Q*2+1. A higher value is accepted.
- (a)
- value PRM·ηC > PL, and the value of the charge current exceeds the required value, accordingly Pg = 0;
- (b)
- value PRM·ηC > PL, and the value of the charge current is less than the required value. This involves consumption from the grid Pg > 0. A similar situation is with PRM·ηC ≤ PL.
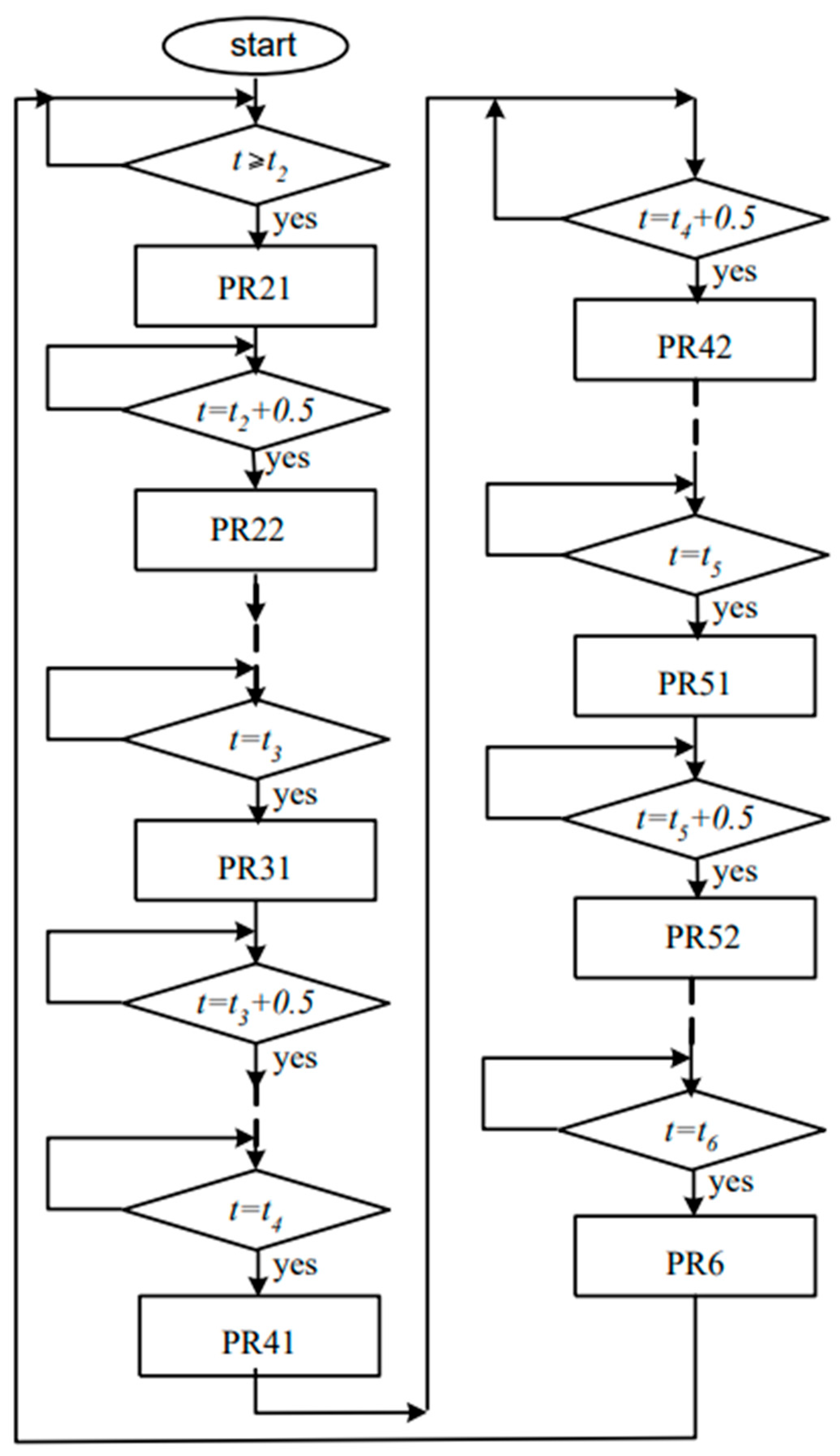
4.4. Algorithm for Changing the Structure of the Control System and Parameters Calculation
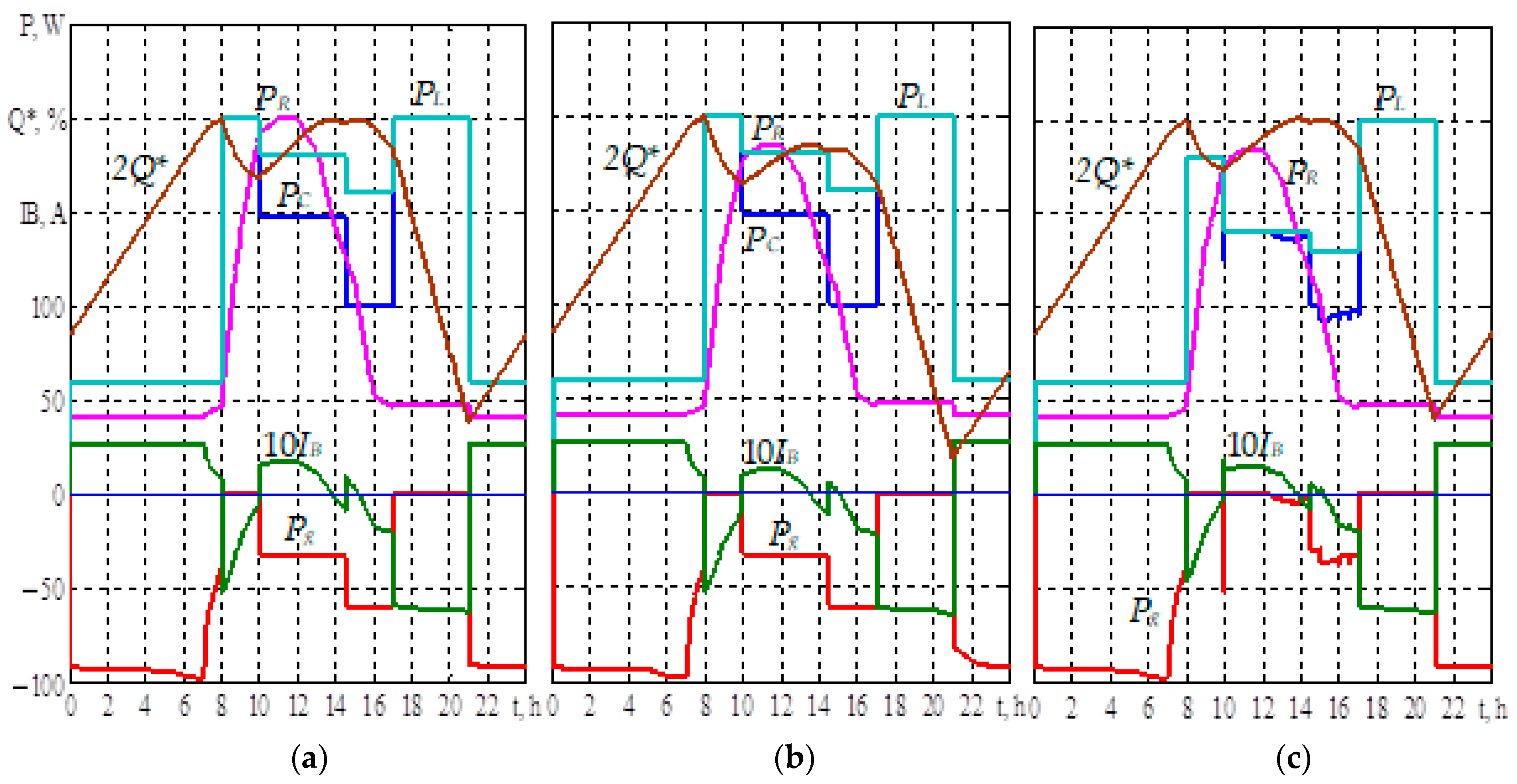
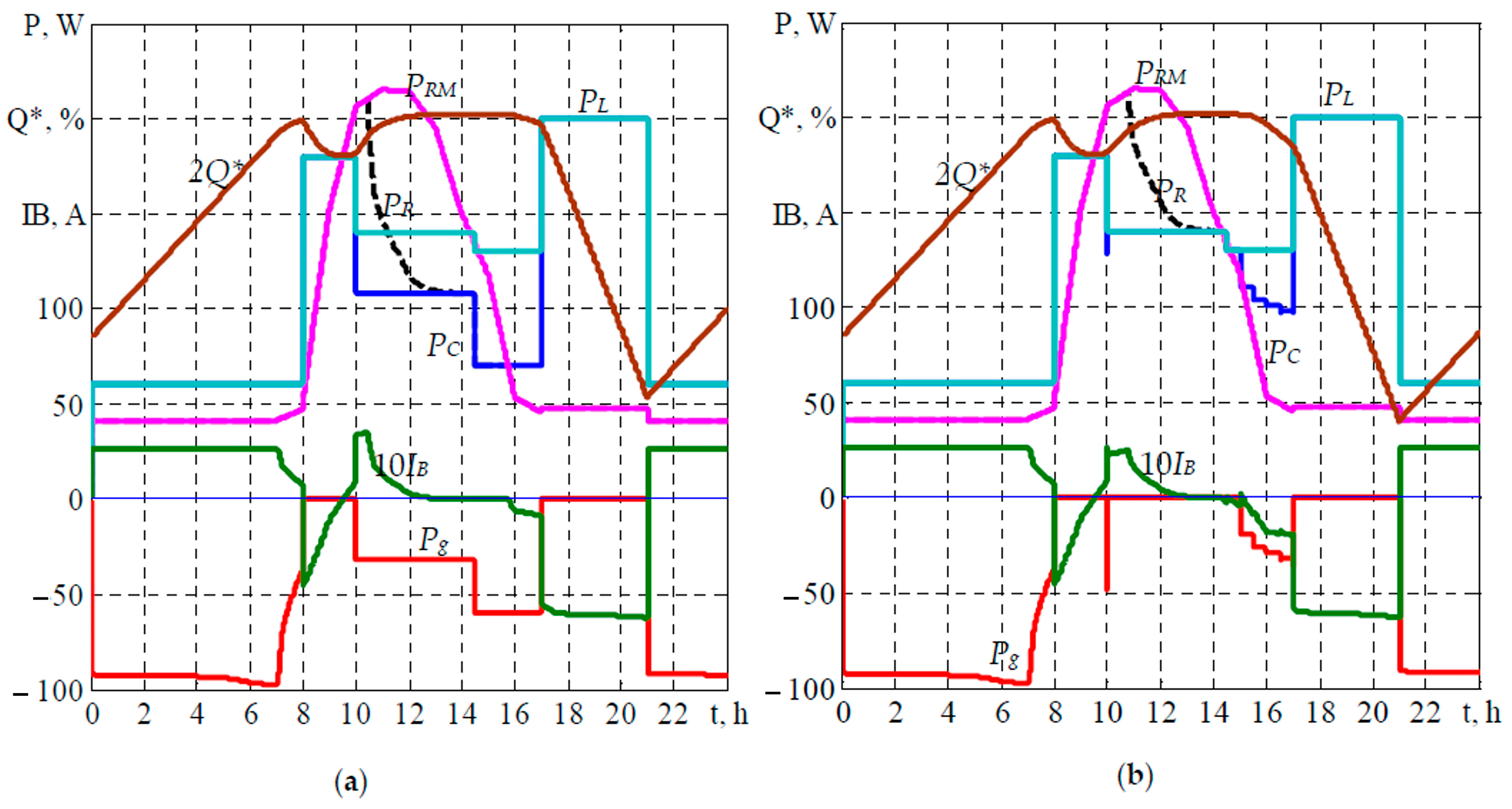
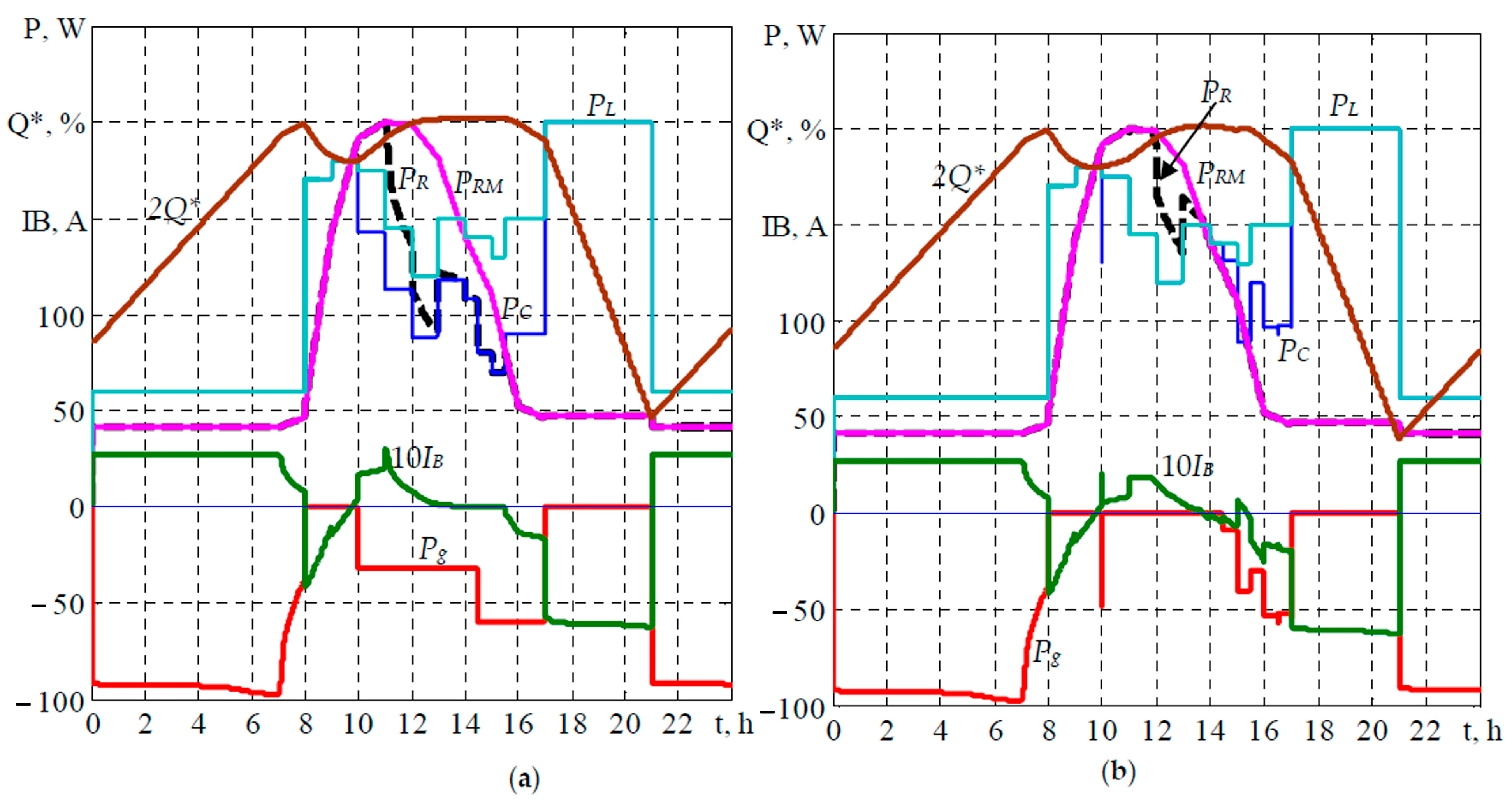
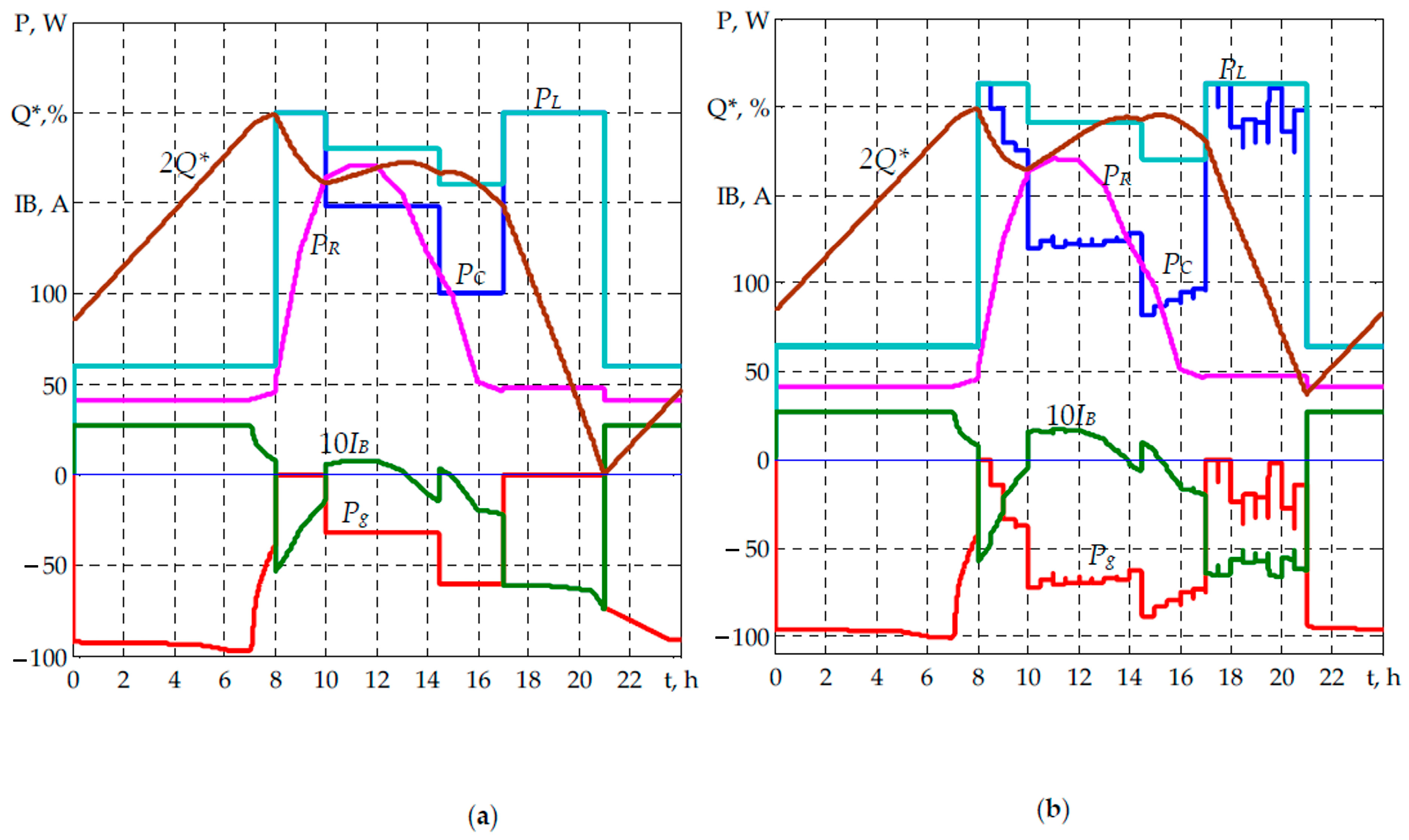
5. 24 h Simulation of Energy Processes
6. Simulation Results
7. Discussion of the Research Results
- -
- the control with the setting of the power consumption from the grid based on the short-term forecast of the RES, using the correction of the taken power value by the deviation of the measured value of the SoC relative to the calculated SoC schedule. The SoC schedule is calculated at the beginning of the day in accordance with the calculated load schedule and the forecast of RES generation. This provides an additional reduction in electricity consumption from the grid and an increase in the degree of RES energy utilization at a load below the calculation and the generation of RES, which is different from the forecast;
- -
- taking into account the peculiarities of the implementation of the night charge of the BESS and the WG generation in the implementation of various scenarios;
- -
- use of the measured value of the load power to exclude the energy generation into the grid and the exclusion of the PV power regulation at the low generation of RES, as well as the implementation of the power reference in the evening peak.
- -
- modeling with an assessment of the reduction in electricity costs for the average monthly generation RES and the calculated load was carried out with the generation of RES corresponding to the forecast;
- -
- the implementation of the correction of the value of power consumption on the deviation of the actual and calculated SoC assumes a high degree of SoC measurement and requires detailed study;
- -
- when simulation the solution with correction, the load deviation from the calculated value and the PV generation with a proportional change in PPV during the day was taken into account when the measured SoC value deviated to ±5%.
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| PV | photovoltaic battery |
| WG | wind generator |
| RES | renewable energy source |
| BESS | battery energy storage system |
| LO | local object |
| PV-WG | grid-connected solar-wind system |
| DG | distribution grid |
| PCC | point of common coupling |
| MPPT | maximum power point tracking |
| WFM | wi-Fi unit |
| CPC | unit of the calculation of parameters and setting of modes |
| CPV | PV voltage converter |
| CSB | battery voltage converter |
| CWG | WG converter |
| VSI | multifunctional grid inverter |
| SoC(t) | state of charge of BESS |
| DoD | depth of discharge of BESS |
| CU | control unit |
| PLL | phase-locked loop |
| PPV | PV power generation (W) |
| PW | power generation of the wind generator (W) |
| PL | load power (W) |
| Pg | power consumption from the grid (W) |
| PPVR | rate (installed) power of the photovoltaic battery (W) |
| PWR | rate (installed) power of wind generator (W) |
| Ud | DC link voltage (V) |
| UB | battery voltage (V) |
| Ug | grid voltage (V) |
| IB | current of battery (A) |
| Ig | current at point of common coupling with a grid (A) |
| IPV | current of photovoltaic battery (A) |
| WPV | energy generation of photovoltaic battery (Wh) |
| WW | energy generation of wind generator (Wh) |
| WR | total energy generation of photovoltaic battery and wind generator (Wh) |
| WB | BESS energy capacity (Wh) |
| Wg | consumption of the energy from the grid (Wh) |
| WL | energy consumed by the load (Wh) |
| WPVAVD | average value of energy, generated by PV battery per day (Wh) |
| WWA VD | average value of energy, generated by wind generator per day (Wh) |
| CB or QR | capacity of the BESS or rated state of charge (Ah) |
| Q* | state of charge of BESS (%) |
| Q*d | state of BESS charge when switching to the mode of constant voltage charge (%) |
| ηC | overall efficiency of converter and inverter (p.u.) |
| ηB | efficiency of the BESS (p.u.) |
| mP | coefficient of PV battery power recalculation (p.u.) |
| m | coefficient of wind power recalculation (p.u.) |
| kE | coefficient of the cost reduction for the energy from the grid (p.u.) |
| t, t1, t2.… t7 | time and time points for load schedule [h] |
| Td | day tariff rate (p.u.) |
| Tn | night tariff rate (p.u.) |
References
- Luthander, R.; Widén, J.; Nilsson, D.; Palm, J. Photovoltaic self-consumption in buildings: A review. Appl. Energy 2015, 142, 80–94. [Google Scholar] [CrossRef] [Green Version]
- Shavolkin, O.; Shvedchykova, I.; Kolcun, M.; Medved’, D. Improvement of the Grid-Tied Solar-Wind System with a Storage Battery for the Self-Consumption of a Local Object. Energies 2022, 15, 5114. [Google Scholar] [CrossRef]
- Ramoji, S.K.; Rath, B.B.; Kumar, D.V. Optimum Design of a Hybrid PV/Wind Energy System Using Genetic Algorithm (GA). IOSR J. Eng. 2014, 4, 38–48. [Google Scholar] [CrossRef]
- Yang, B.; Guo, Y.; Xiao, X.; Tian, P. 2Bi-level Capacity Planning of Wind-PV-Battery Hybrid Generation System Considering Return on Investment. Energies 2020, 13, 3046. [Google Scholar] [CrossRef]
- Menniti, D.; Pinnarelli, A.; Sorrentino, N. A Method to Improve Microgrid RELIABILITY by optimal Sizing PV/Wind Plants and Storage Systems. In Proceedings of the CIRED 2009—The 20th International Conference and Exhibition on Electricity Distribution—Part 2, Prague, Czech Republic, 8–11 June 2009; p. 1. [Google Scholar] [CrossRef] [Green Version]
- Shavolkin, O.; Shvedchykova, I.; Kolcun, M.; Medved’, D. Variant of Implementation of a Grid-Tied Solar-Wind System with a Storage Battery for Self-Consumption of Local Object. In Proceedings of the 2022 IEEE 8th International Conference on Energy Smart Systems (ESS), Kyiv, Ukraine, 12–14 October 2022; pp. 184–189. [Google Scholar] [CrossRef]
- Zsiborács, H.; Pintér, G.; Vincze, A.; Birkner, Z.; Baranyai, N.H. Grid balancing challenges illustrated by two European examples: Interactions of electric grids, photovoltaic power generation, energy storage and power generation forecasting. Energy Rep. 2021, 7, 3805–3818. [Google Scholar] [CrossRef]
- Wynn, S.L.L.; Boonraksa, T.; Boonraksa, P.; Pinthurat, W.; Marungsri, B. Decentralized Energy Management System in Microgrid Considering Uncertainty and Demand Response. Electronics 2023, 12, 237. [Google Scholar] [CrossRef]
- Shavolkin, O.; Gerlici, J.; Shvedchykova, I.; Kravchenko, K. Solar–Wind System for the Remote Objects of Railway Transport Infrastructure. Energies 2022, 15, 6546. [Google Scholar] [CrossRef]
- Forecast Solar. Available online: https://forecast.solar/ (accessed on 1 July 2023).
- Iyengar, S.; Sharma, N.; Irwin, D.; Shenoy, P.; Ramamritham, K. SolarCast—An Open WEB service for predicting Solar Power Generation in Smart Homes. In Proceedings of the 1st ACM Conference on Embedded Systems for Energy-Efficient Buildings, BuildSys, Memphis, TN, USA, 3–6 November 2014; pp. 174–175. [Google Scholar] [CrossRef]
- Iyengar, S.; Sharma, N.; Irwin, D.; Shenoy, P.; Ramamritham, K. A Cloud-Based Black-Box Solar Predictor for Smart Homes. ACM Trans. Cyber-Physical Syst. 2017, 1, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Barelli, L.; Bidini, G.; Bonucci, F.; Castellini, L.; Castellini, S.; Ottaviano, A.; Zuccati, A. Dynamic Analysis of a Hybrid Energy Storage System (H-ESS) Coupled to a Photovoltaic (PV) Plant. Energies 2018, 11, 396. [Google Scholar] [CrossRef] [Green Version]
- Shavolkin, O.; Shvedchykova, I.; Romanchenko, J.; Marchenko, R.; Yakymets, S. Installed Power of the Grid-Tied Photovoltaic System with Battery for Self-Consumption of the Local Object. In Proceedings of the 2022 IEEE 4th International Conference on Modern Electrical and Energy System (MEES), Kremenchuk, Ukraine, 20–23 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Ouédraogo, S.; Faggianelli, G.A.; Notton, G.; Duchaud, J.L.; Voyant, C. Impact of electricity tariffs and energy management strategies on PV/Battery microgrid performances. Renew. Energy 2022, 199, 816–825. [Google Scholar] [CrossRef]
- Schram, W.L.; Lampropoulos, L.; van Sark, W.G. Photovoltaic systems coupled with batteries that are optimally sized for household self-consumption: Assessment of peak shaving potential. Appl. Energy 2018, 223, 69–81. [Google Scholar] [CrossRef]
- Shavelkin, A.A.; Gerlici, J.; Shvedchykova, I.O.; Kravchenko, K.; Kruhliak, H.V. Management of power consumption in a photovoltaic system with a storage battery connected to the network with multi-zone electricity pricing to supply the local facility own needs. Electr. Eng. Electromechanics 2021, 2, 36–42. [Google Scholar] [CrossRef]
- Zeng, H.; Yang, R.; Zhao, C.; Cheng, C. Topologies and control strategies of multi-functional grid-connected inverters for power quality enhancement: A comprehensive review. Renew. Sustain. Energy Rev. 2013, 24, 223–270. [Google Scholar] [CrossRef]
- Vigneysh, T.; Kumarappan, N. Grid interconnection of renewable energy sources using multifunctional grid-interactive converters: A fuzzy logic based approach. Electr. Power Syst. Res. 2017, 151, 359–368. [Google Scholar] [CrossRef]
- Shavolkin, O.; Shvedchykova, I. Improvement of the multifunctional converter of the photoelectric system with a storage battery for a local object with connection to a grid. In Proceedings of the 2020 IEEE KhPI Week on Advanced Technology, KhPIWeek 2020, Kharkiv, Ukraine, 5–10 October 2020; pp. 287–292. [Google Scholar] [CrossRef]
- Guerrero-Martinez, M.A.; Milanes-Montero, M.I.; Barrero-Gonzalez, F.; Miñambres-Marcos, V.M.; Romero-Cadaval, T.; Gonzalez-Romera, E. A Smart Power Electronic Multiconverter for the Residential Sector. Sensors 2017, 17, 1217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abdelrahman, O.A.; Ahmed, M.H.; Mohamed, M.A.; Mohamed, N.S.; Mohamed, R.E. Energy management of photovoltaic-battery system connected with the grid. J. Energy Storage 2022, 55, 105865. [Google Scholar] [CrossRef]
- 24-Hour Simulation of a Vehicle to Grid (V2G) System. Available online: https://www.mathworks.com/help/physmod/sps/ug/24-hour-simulation-of-a-vehicle-to-grid-v2g-system.html (accessed on 1 July 2023).
- Simplified Model of a Small Scale Micro-Grid. Available online: https://www.mathworks.com/help/physmod/sps/ug/simplified-model-of-a-small-scale-micro-grid.html (accessed on 1 July 2023).
- Singh, M.; Singh, O. Phasor Solution of a Micro-Grid to Accelerate Simulation Speed. In Proceedings of the 2nd International Conference on Advanced Computing and Software Engineering (ICACSE-2019), Sultanpur, India, 11 April 2019; pp. 546–550. Available online: https://ssrn.com/abstract=3351025 (accessed on 1 July 2023).
- Chola, R.; Singh, S.B. A Case Study on 24-h Simulation of V2G System. In Advances in Renewable Energy and Sustainable Environment; Lecture Notes in Electrical, Engineering; Dewan, L.C., Bansal, R., Kumar Kalla, U., Eds.; Springer: Singapore, 2021; Volume 667. [Google Scholar] [CrossRef]
- Photovoltaic Geographical Information System. Available online: https://re.jrc.ec.europa.eu/pvg_tools/en/tools.html#SA (accessed on 1 July 2023).
- Data Sheet. Lithium Iron Phosphate Battery (LiFePO4) 12.8 V 150 Ah. Available online: https://www.eco-greenenergy.com/wp-content/uploads/2021/12/EGE-LiFePO4-Battery-12.8V150Ahd.pdf (accessed on 1 July 2023).
- Shepherd, C.M. Design of Primary and Secondary Cells. P. 2. An equation describing battery discharge. J. Electrochem. Soc. 1965, 112, 657–664. [Google Scholar] [CrossRef]
- Tremblay, O.; Dessaint, L.A.; Dekkiche, A.I. A Generic Battery Model for the Dynamic Simulation of Hybrid Electric Vehicles. In Proceedings of the Vehicle Power and Propulsion Conference (VPPC 2007), Arlington, TX, USA, 9–12 September 2007; pp. 284–289. [Google Scholar]
- Shavolkin, O.; Shvedchykova, I.; Lishchuk, V.; Stanovskyi, Y. Improving a model of the hybrid photovoltaic system with a storage battery for local object’s self-consumption involving the setting of power consumed from the grid. East.-Eur. J. Enterp. Technol. 2023, 3, 6–16. [Google Scholar] [CrossRef]
| Indicators | January | February | March | April | May | June | July | August | September | October | November | December |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| kE3 | 2.58 | 3.82 | 5.95 | 11.83 | 15.56 | 14.44 | 22.66 | 9.22 | 7.6 | 4.1 | 2.42 | 2.83 |
| kE2 | 2.06 | 2.98 | 4.68 | 9.04 | 12.48 | 11.34 | 17.84 | 7.15 | 5.84 | 3.23 | 1.93 | 2.25 |
| kE1 | 1.78 | 2.39 | 3.77 | 6.64 | 10.68 | 8.98 | 14.2 | 5.43 | 4.34 | 2.61 | 1.68 | 1.93 |
| Q*2R, % | 100 | 100 | 60 | 36 | 20 | 28 | 20 | 44 | 50 | 75 | 100 | 100 |
| Pg34, W | 120 | 32 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 126 | 96 |
| Pg45, W | 80 | 60 | 90 | 30 | 37 | 29 | 19 | 33 | 40 | 121 | 84 | 73 |
| P*LAV, p.u. | 1 | 1 | 0.877 | 0.877 | |||||||||||||
| P*PV, p.u. | 0.9 | 1 | 1.1 | 0.9 | 1.1 | 0.9 | 1 | 1.1 | 0.9 | 1 | 1.1 | ||||||
| Q1M, p.u. | - | - | - | 1 | 1 | - | - | - | 0.95 | 1 | 1.05 | 0.95 | 1 | 1.05 | 0.95 | 1 | 1.05 |
| kE3 | 3.85 | 3.82 | 3.82 | 3.48 | 4.24 | 3.46 | 3.46 | 3.47 | 4.22 | 4.42 | 4.5 | 4.41 | 4.61 | 4.67 | 4.43 | 4.67 | 4.75 |
| kE2 | 3 | 2.98 | 2.98 | 2.73 | 3.28 | 2.67 | 2.67 | 2.67 | 3.2 | 3.34 | 3.4 | 3.34 | 3.48 | 3.52 | 3.35 | 3.51 | 3.57 |
| kE1 | 2.53 | 2.39 | 2.39 | 2.34 | 2.56 | 2.16 | 2.16 | 2.16 | 2.46 | 2.54 | 2.57 | 2.54 | 2.61 | 2.63 | 2.54 | 2.63 | 2.66 |
| Q*2, % | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Q*6, % | 10 | 20 | 20 | 20 | 20 | 25 | 25 | 25 | 21.5 | 20 | 20 | 21 | 21 | 20 | 21.5 | 20 | 20 |
| P*PV, p.u. | 0.9 | 1.0 | 1.1 | |||
| Correction | − | + | − | + | − | + |
| kE3 | 3.52 | 4.225 | 3.52 | 4.545 | 3.522 | 4.635 |
| kE2 | 2.727 | 3.229 | 2.728 | 3.453 | 2.728 | 3.515 |
| kE1 | 2.2 | 2.49 | 2.2 | 2.61 | 2.201 | 2.643 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shavolkin, O.; Shvedchykova, I.; Kolcun, M.; Medveď, D. Improvement of a Hybrid Solar-Wind System for Self-Consumption of a Local Object with Control of the Power Consumed from the Grid. Energies 2023, 16, 5851. https://doi.org/10.3390/en16155851
Shavolkin O, Shvedchykova I, Kolcun M, Medveď D. Improvement of a Hybrid Solar-Wind System for Self-Consumption of a Local Object with Control of the Power Consumed from the Grid. Energies. 2023; 16(15):5851. https://doi.org/10.3390/en16155851
Chicago/Turabian StyleShavolkin, Olexandr, Iryna Shvedchykova, Michal Kolcun, and Dušan Medveď. 2023. "Improvement of a Hybrid Solar-Wind System for Self-Consumption of a Local Object with Control of the Power Consumed from the Grid" Energies 16, no. 15: 5851. https://doi.org/10.3390/en16155851
APA StyleShavolkin, O., Shvedchykova, I., Kolcun, M., & Medveď, D. (2023). Improvement of a Hybrid Solar-Wind System for Self-Consumption of a Local Object with Control of the Power Consumed from the Grid. Energies, 16(15), 5851. https://doi.org/10.3390/en16155851






