Heating Strategies for Efficient Combined Inductive and Convective Heating of Profiles
Abstract
1. Introduction
2. Materials and Methods
2.1. Experiments
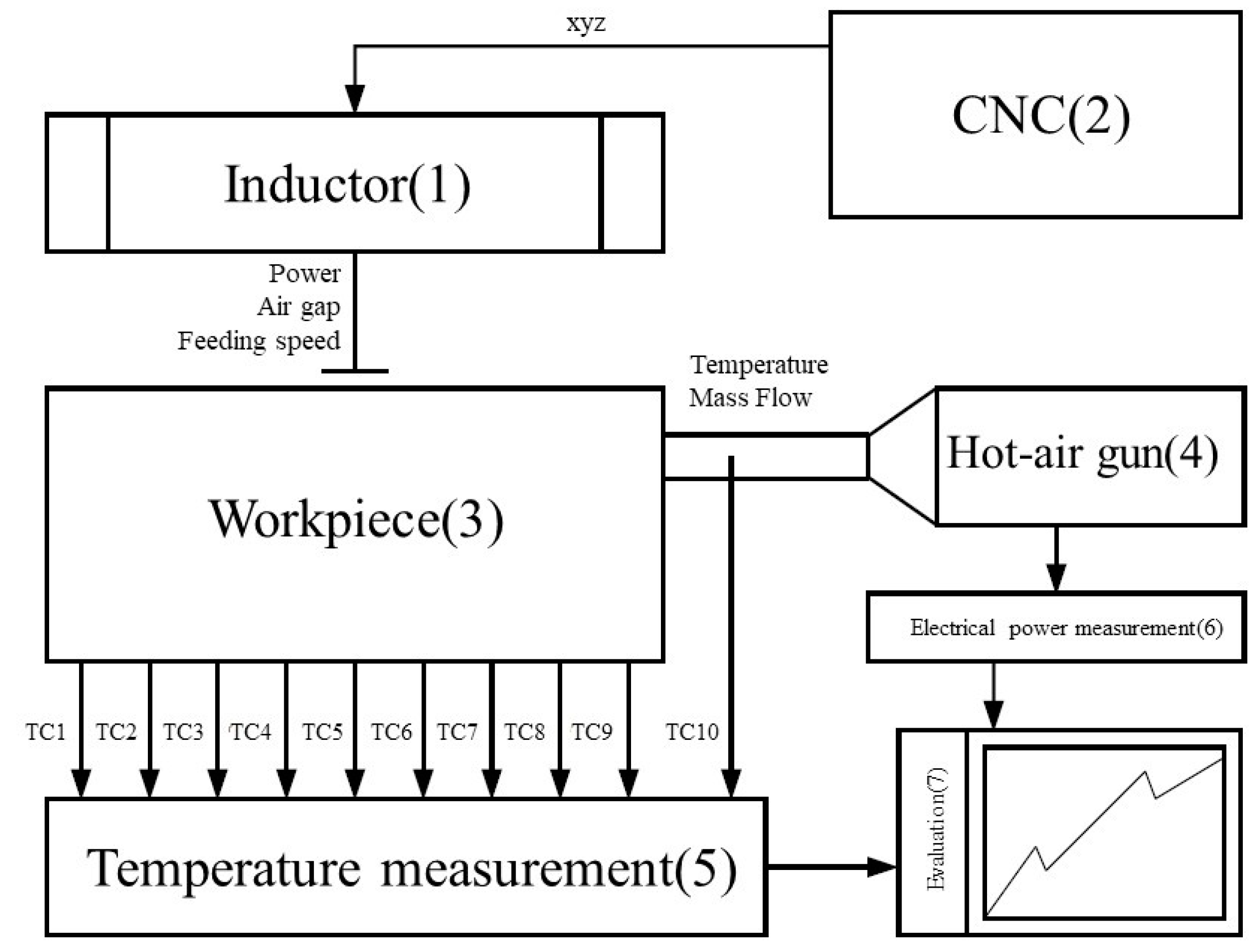
2.1.1. Structure of the Test Rig
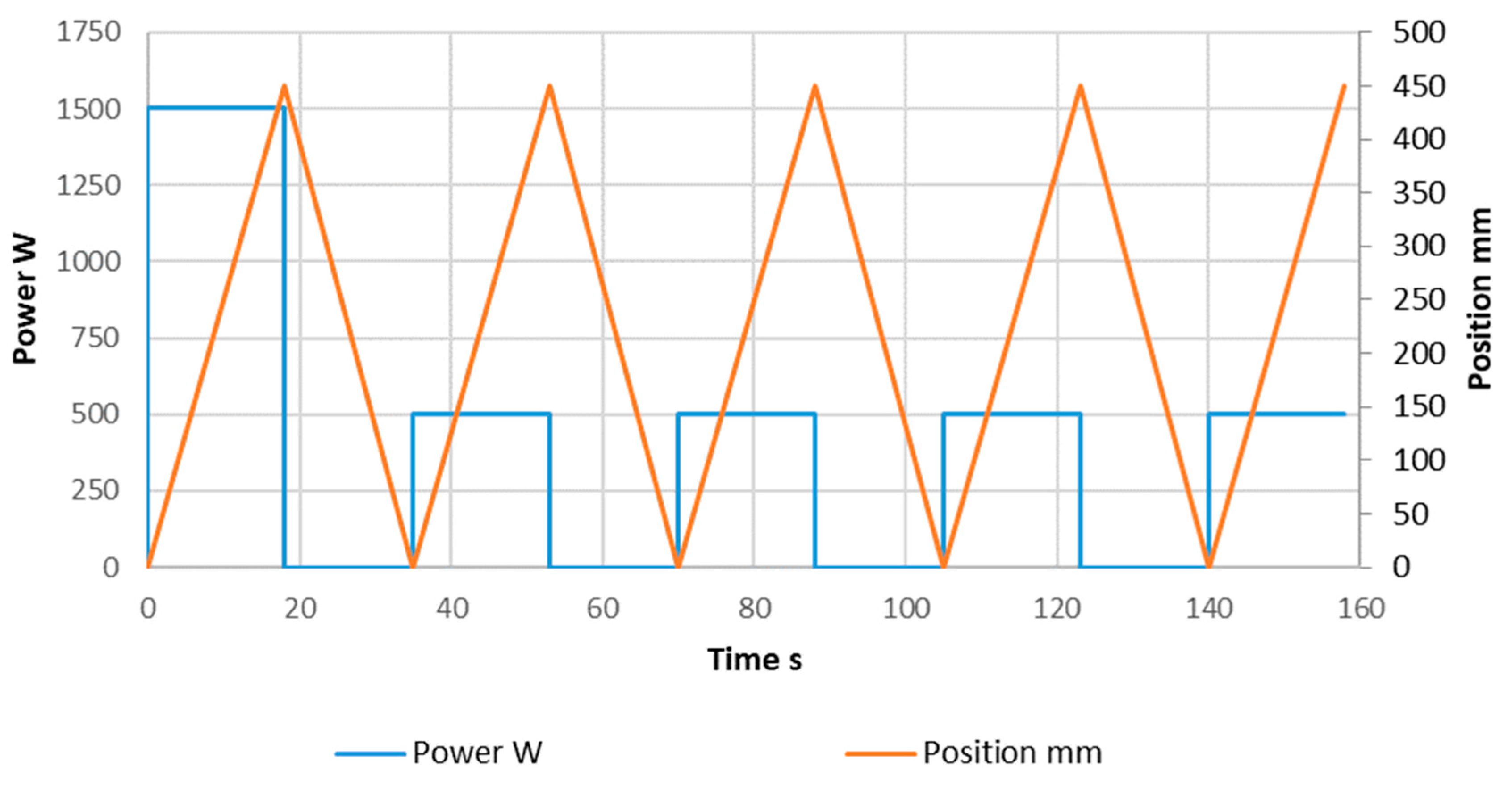
2.1.2. Execution of the Experiments
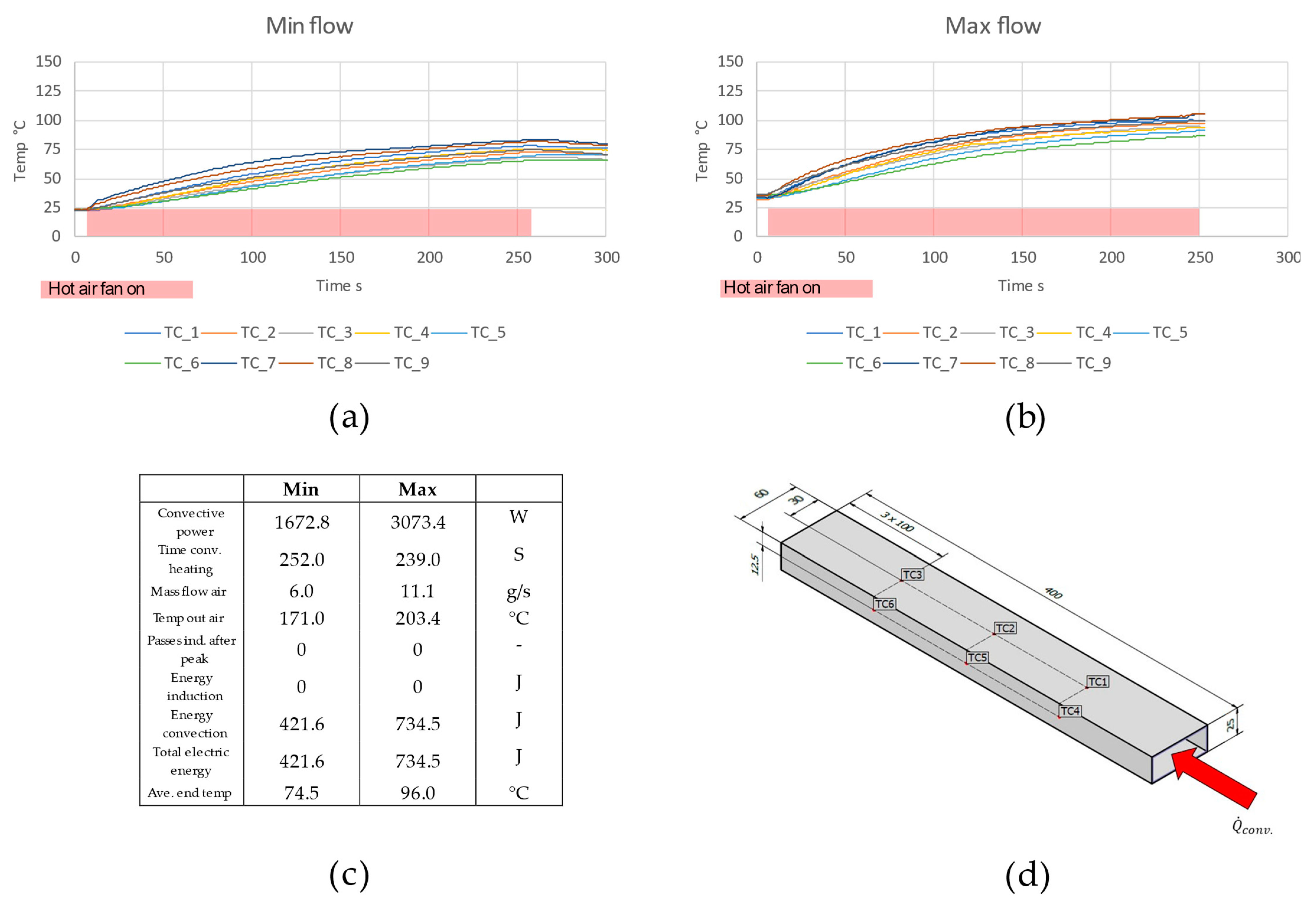
- Pure convection heating with minimal mass flow of the heat gun (~6 g/s);
- Pure convection heating with maximum mass flow of the heat gun (~12 g/s);
- Combination of induction and convection with minimal mass flow (~6 g/s);
- Combination of induction and convection with max mass flow (~12 g/s).
2.2. Simulation
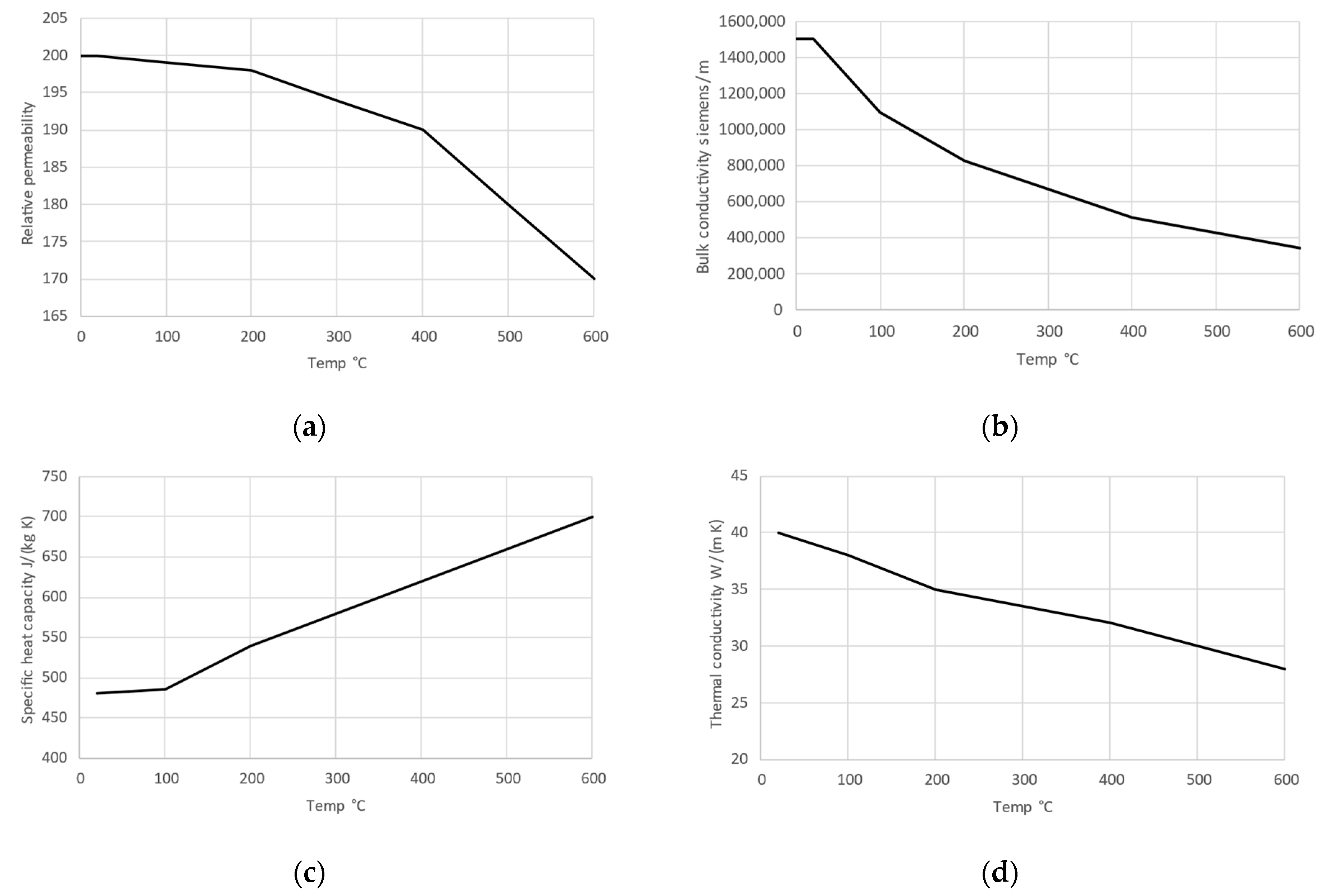
2.2.1. Mathematical Description
- The current flowing through the inductor coil;
- The geometry of the coil;
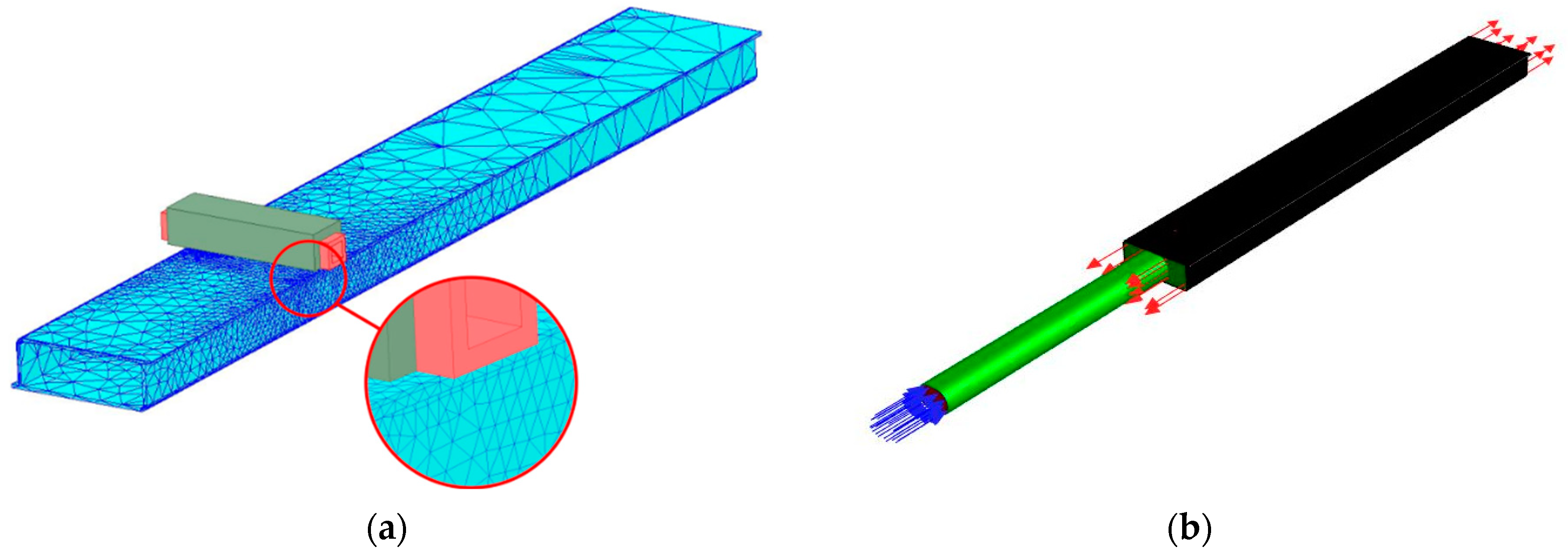
2.2.2. Execution of Simulation
3. Results
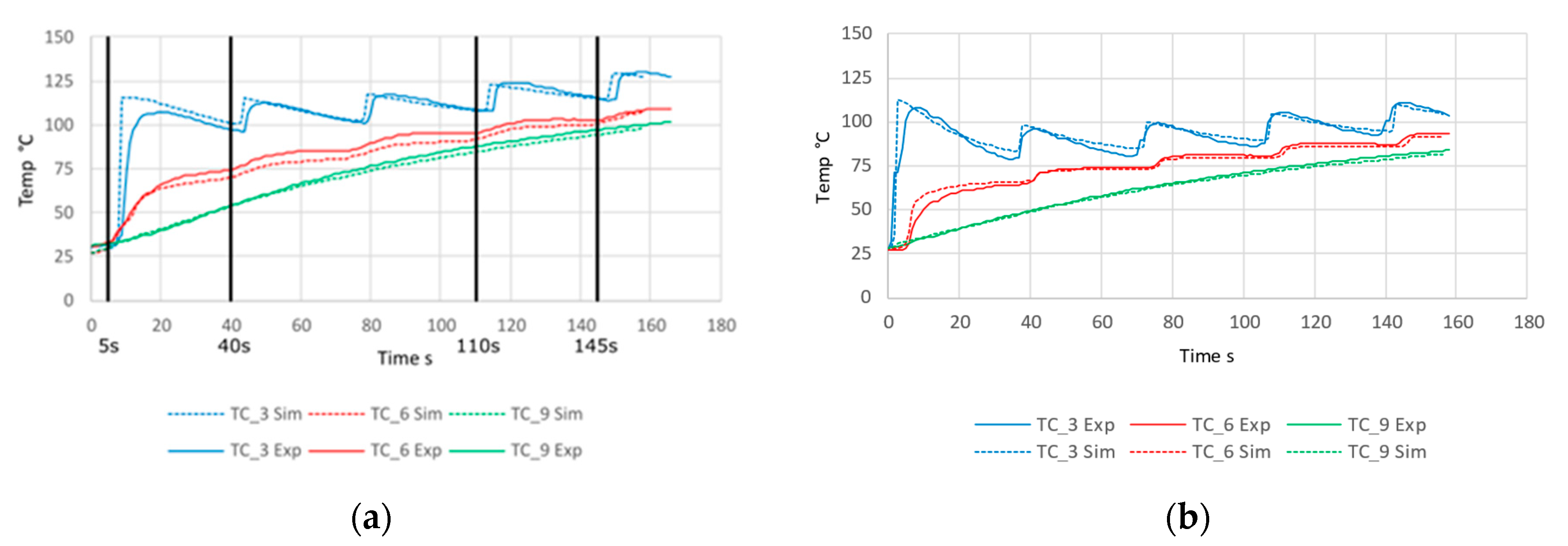
3.1. Experimental Results
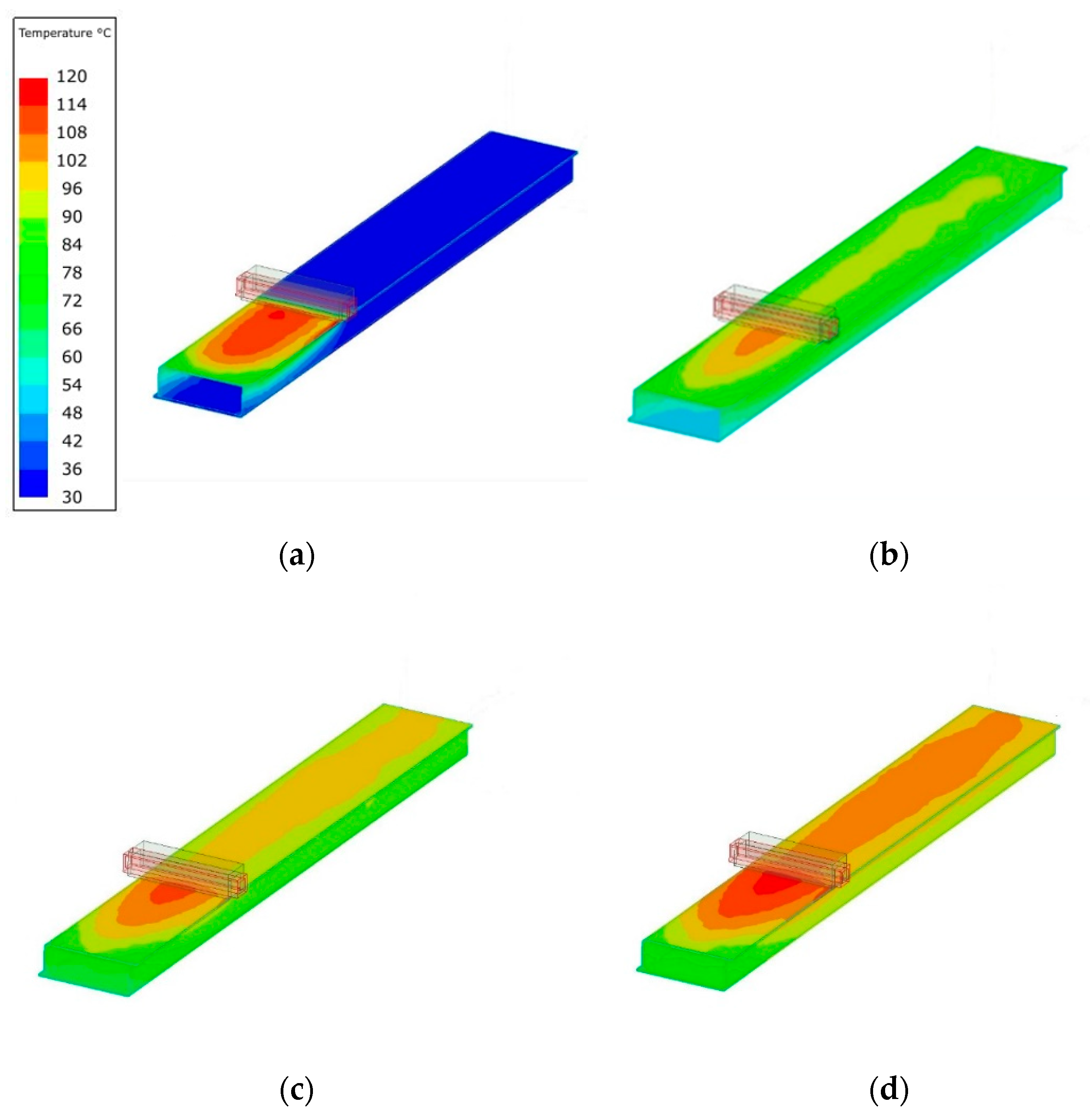
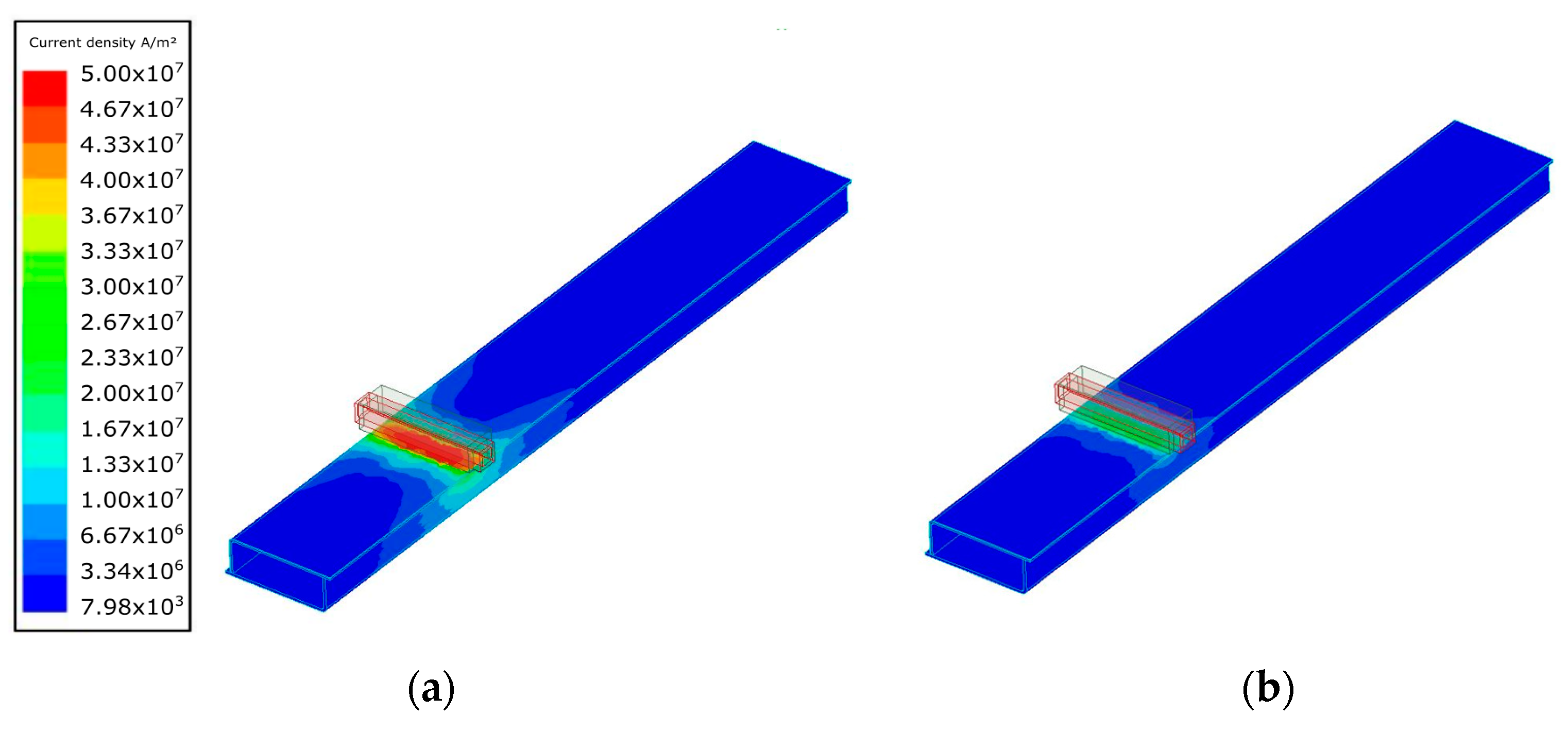
3.2. Simulation Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rudnev, V.; Loveless, D.; Raymond, L.C. Imprimerie noubelle associ-ation ouvriere. In Handbook of Induction Heating; CRC Press: Paris, France, 2017. [Google Scholar]
- Lehner, G. Elektromagnetische Feldtheorie; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Benkowsky, G.; Härten, I.; Glühen, S.; Löten, S. Grundlagen und Praktische Anleitungen für Induktionserwärmungsverfahren, Insbesondere auf dem Gebiet der Hochfrequenzerwärmung, 5th ed.; Verl. Technik: Berlin, Germany, 1990. [Google Scholar]
- Lucia, O.; Maussion, P.; Dede, E.J.; Burdio, J.M. Induction Heating Technology and Its Applications: Past Developments, Current Technology, and Future Challenges. IEEE Trans. Ind. Electron. 2014, 61, 2509–2520. [Google Scholar] [CrossRef]
- Davies, E.J. Conduction and Induction Heating; IET: Hertfordshire, UK, 1990. [Google Scholar]
- Rudnev, V. Metals HandBook VOL 4—Heat Treating; Amazon Publishing: Seattle, WA, USA, 1991. [Google Scholar]
- Rudnev, V. Systematic Analysis of Induction Coil Failures: Part 4: Coil Copper Electromagnetic Edge Effect; 2006; pp. 27–28. Available online: https://www.inductoheat.com/wp-content/uploads/sites/11/2019/08/133-1.pdf (accessed on 9 January 2023).
- Plumed, E.; Lope, I.; Acero, J. Induction Heating Adaptation of a Different-Sized Load With Matching Secondary Inductor to Achieve Uniform Heating and Enhance Vertical Displacement. IEEE Trans. Power Electron. 2021, 36, 6929–6942. [Google Scholar] [CrossRef]
- Huang, M.-S.; Huang, Y.-L. Effect of multi-layered induction coils on efficiency and uniformity of surface heating. Int. J. Heat Mass Transf. 2010, 53, 2414–2423. [Google Scholar] [CrossRef]
- Shih, S.-Y.; Nian, S.-C.; Huang, M.-S. Comparison between single- and multiple-zone induction heating of largely curved mold surfaces. Int. Commun. Heat Mass Transf. 2016, 75, 24–35. [Google Scholar] [CrossRef]
- Xiao, Y.; Han, Y.; Zhao, D.-F.; Wang, L.-M.; Xu, D. Temperature gradient control of frequency conversion heating for a thick-walled pipe based on energy transfer. Int. J. Heat Mass Transf. 2023, 201, 123589. [Google Scholar] [CrossRef]
- Bui, H.-T.; Hwang, S.-J. Modeling a working coil coupled with magnetic flux concentrators for barrel induction heating in an injection molding machine. Int. J. Heat Mass Transf. 2015, 86, 16–30. [Google Scholar] [CrossRef]
- Gao, K.; Qin, X.; Wang, Z.; Zhu, S.; Gan, Z. Effect of magnetizer geometry on the spot induction heating process. J. Mater. Process. Technol. 2016, 231, 125–136. [Google Scholar] [CrossRef]
- Sun, J.; Li, S.; Qiu, C.; Peng, Y. Numerical and experimental investigation of induction heating process of heavy cylinder. Appl. Therm. Eng. 2018, 134, 341–352. [Google Scholar] [CrossRef]
- Thosdeekoraphat, T.; Tanthai, K.; Lhathum, K.; Kotchapradit, S.; Santalunai, S.; Thongsopa, C. The Design of a Large-Scale Induction Heating Power Source for Organic Waste Digesters to Produce Fertilizer. Energies 2023, 16, 2123. [Google Scholar] [CrossRef]
- Fu, X.; Wang, B.; Tang, X.; Ji, H.; Zhu, X. Study on induction heating of workpiece before gear rolling process with different coil structures. Appl. Therm. Eng. 2017, 114, 1–9. [Google Scholar] [CrossRef]
- Tobias, V. (PMT/T1), Induktive Erwärmung von Formplatinen für die Warmumformung: Dissertation an der Fakultät für Maschinenbau der Technischen Universität Chemnitz; Institut für Werkzeugmaschinen und Produktionsprozesse: Chemnitz, Germany, 2016. [Google Scholar]
- Bao, L.; Liu, W.; Wang, B.; Li, H.; You, X.; Zhou, Q.; Liu, M.; Gao, S. Experimental investigation on partition controllable induction heating-hot stamping process of high-strength boron alloyed steel plates with designable temperature patterns. J. Mater. Res. Technol. 2020, 9, 13963–13976. [Google Scholar] [CrossRef]
- Wang, J.; Yi, B.; Zhang, C.; Zhou, H.; Shu, Y. Experiments of double curvature plate bending with induction heating and processing parameters investigation by computational analysis. Ocean. Eng. 2019, 192, 106596. [Google Scholar] [CrossRef]
- Zhu, B.; Meng, L.; Zeng, X.; Hu, Q.; Liu, X.; Xu, G.; Wang, D. Laser cladding high-performance maraging-steel coatings on bainitic cross wing rails assisted with in-situ induction heating: Microstructure and performance. J. Mater. Process. Technol. 2023, 313, 117886. [Google Scholar] [CrossRef]
- Li, L.; Mi, G.; Wang, C. A comparison between induction pre-heating and induction post-heating of laser-induction hybrid welding on S690QL steel. J. Manuf. Process. 2019, 43, 276–291. [Google Scholar] [CrossRef]
- Fan, W.; Tan, H.; Zhang, F.; Feng, Z.; Wang, Y.; Hu, Y.; Lin, X.; Huang, W. Effect of synchronous induction heating on residual stress for laser-based directed energy deposition of thin-walled structures. Mater. Today Commun. 2023, 35, 105702. [Google Scholar] [CrossRef]
- Kawakami, H.; Llave, Y.; Fukuoka, M.; Sakai, N. CFD analysis of the convection flow in the pan during induction heating and gas range heating. J. Food Eng. 2013, 116, 726–736. [Google Scholar] [CrossRef]
- Elsaady, W.; Moughton, C.; Nasser, A.; Lacovides, H. Coupled numerical modelling and experimental analysis of domestic induction heating systems. Appl. Therm. Eng. 2023, 227, 120170. [Google Scholar] [CrossRef]
- Park, S.M.; Jang, E.; Joo, D.; Lee, B.K. Power Curve-Fitting Control Method with Temperature Compensation and Fast-Response for All-Metal Domestic Induction Heating Systems. Energies 2019, 12, 2915. [Google Scholar] [CrossRef]
- Mouallem, J.; Hickey, J.-P. Induction heating of dispersed metallic particles in a turbulent flow. Int. J. Multiph. Flow 2020, 132, 103414. [Google Scholar] [CrossRef]
- Cao, L.-X.; Yin, T.; Jin, M.-X.; He, Z.-Z. Flexible circulated-cooling liquid metal coil for induction heating. Appl. Therm. Eng. 2019, 162, 114260. [Google Scholar] [CrossRef]
- Gerhardter, H.; Prieler, R.; Schluckner, C.; Knoll, M.; Hochenauer, C.; Mühlböck, M.; Tomazic, P.; Schroettner, H. Modelling convective heat transfer to non-spherical particles. Powder Technol. 2019, 343, 245–254. [Google Scholar] [CrossRef]
- Haimbaugh, R.E. Practical Induction Heat Treating; ASM International: Materials Park, OH, USA, 2015. [Google Scholar]
- Barglik, J.; Smagór, A.; Smalcerz, A.; Desisa, D.G. Induction Heating of Gear Wheels in Consecutive Contour Hardening Process. Energies 2021, 14, 3885. [Google Scholar] [CrossRef]
- Ansys Inc. Ansys Maxwell, Release 2020 R2. Available online: https://www.ansys.com/products/electronics/ansys-maxwell (accessed on 1 August 2023).
- Ansys Inc. Ansys Fluent, Release 2020 R2. Available online: https://www.ansys.com/products/fluids/ansys-fluent (accessed on 1 August 2023).
- Menter, F.R.; Kuntz, M.; Langstry, R. Ten Years of Industrial Experience with the SST Turbulance Model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6 July 1993; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1993. [Google Scholar]
- Feurhuber, M.; Magno, M.; Miranda, M.; Hochenauer, C. CFD investigations of steam penetration, air-removal and condensation inside hollow loads and cavities. Appl. Therm. Eng. 2019, 147, 1070–1082. [Google Scholar] [CrossRef]






| Profile | Set Power | Current in Coil | Frequency |
|---|---|---|---|
| Rectangular profile | 1500 W | 678.4 A | 15 kHz |
| 500 W | 329.6 A | 15 kHz | |
| Angled profile | 1500 W | 646.4 A | 15 kHz |
| 500 W | 329.6 A | 15 kHz |
| Steel | Copper | Air | ||
|---|---|---|---|---|
| Relative permittivity | 1 | 1 | - | - |
| Relative permeability | Temp. dep. | 0.999991 | - | - |
| Bulk conductivity | Temp. dep. | 58,000,000 | - | S/m |
| Mass density | 7500 | 8933 | 1.225 | kg/m3 |
| Specific heat capacity | Temp. dep. | - | 1006.43 | J/(kg K) |
| Thermal conductivity | Temp. dep. | - | 0.0242 | W/(m K) |
| Viscosity | - | - | 1.79 × 10−5 | kg/(m s) |
| Experiment | Profile | Convective Power | Time Conv. Heating | Mass Flow Air | Passes Ind. after Peak | Energy Induction | Energy Convection | Total Electric Energy | Ave. End Temp |
|---|---|---|---|---|---|---|---|---|---|
| W | s | 10−3 | - | J | J | J | J | ||
| Flow min. | Rectangle | 1672.8 | 252 | 6.0 | 0 | 0 | 421.5 | 421.5 | 74.5 |
| Flow max. | Rectangle | 3073.4 | 239 | 11.1 | 0 | 0 | 734.5 | 734.5 | 96.0 |
| Comb. min. | Rectangle | 1821.7 | 153 | 6.6 | 4 | 62.2 | 278.7 | 340.9 | 97.0 |
| Comb. max. | Rectangle | 3288.2 | 185 | 11.8 | 5 | 71.1 | 608.3 | 679.4 | 121.7 |
| Flow min. | Angled | 1651.7 | 308 | 5.9 | 0 | 0 | 508.7 | 508.7 | 82.8 |
| Flow max. | Angled | 3535.3 | 191 | 11.1 | 0 | 0 | 675.5 | 675.5 | 101.0 |
| Comb. min. | Angled | 1753.5 | 210 | 6.3 | 6 | 62.2 | 368.2 | 430.4 | 103.1 |
| Comb. max. | Angled | 1430.6 | 219 | 12.4 | 6 | 80 | 751.3 | 831.3 | 117.0 |
| TC2 | TC5 | TC8 | |
|---|---|---|---|
| Fluent finer | 0.3086 K | 0.3576 K | 0.1147 K |
| Maxw. finer | 0.3765 K | 0.4864 K | 0.0966 K |
| Both finer | 0.3180 K | 0.2080 K | 0.1823 K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gergely, R.; Hochenauer, C. Heating Strategies for Efficient Combined Inductive and Convective Heating of Profiles. Energies 2023, 16, 5895. https://doi.org/10.3390/en16165895
Gergely R, Hochenauer C. Heating Strategies for Efficient Combined Inductive and Convective Heating of Profiles. Energies. 2023; 16(16):5895. https://doi.org/10.3390/en16165895
Chicago/Turabian StyleGergely, Raphael, and Christoph Hochenauer. 2023. "Heating Strategies for Efficient Combined Inductive and Convective Heating of Profiles" Energies 16, no. 16: 5895. https://doi.org/10.3390/en16165895
APA StyleGergely, R., & Hochenauer, C. (2023). Heating Strategies for Efficient Combined Inductive and Convective Heating of Profiles. Energies, 16(16), 5895. https://doi.org/10.3390/en16165895





