Optimal Power Flow in Distribution Network: A Review on Problem Formulation and Optimization Methods †
Abstract
1. Introduction
- Through a comprehensive analysis of the model development and optimization methods for the optimal power flow problem in distribution power systems, this study provides a profound understanding and valuable references for solving this problem. Therefore, it establishes a solid theoretical framework for promoting the application and advancement of optimal power flow solutions in distribution power systems, thus making notable contributions to this field.
- A detailed discussion of the power flow and component models necessary for implementing the various applications mentioned above is provided.
- Furthermore, future opportunities and challenges for the application of OPF in DN are identified.
2. Problem Formulation
2.1. Impact of DG in DN
2.2. Generator Modeling
2.2.1. Stochastic Model
2.2.2. Forecasting Model
2.3. Demand Response
2.4. Power Flow Model
- Various models have been proposed from the grid perspective to enhance and optimize power system operations. These models include the superconducting cable model, voltage regulator model, flexible loop converter, and energy router model. Each model serves a specific purpose, such as improving transmission efficiency, voltage regulation, and interconnection between microgrids. In [32], the zero-resistance characteristic of superconducting material was considered, and the superconducting magnet parameters were introduced to reflect the superconducting properties. The modeling of the superconducting cable was constructed using a nonlinear inductance, current source, and leakage resistance to model the cable as an element within the circuit analysis. Voltage regulators play a crucial role in maintaining stable power transmission by adjusting the voltage levels of transformers. These devices ensure that voltage remains within the desired range, mitigating potential issues associated with voltage fluctuations. The power flow calculation method proposed in [21] considers the influence of distributed generation and voltage regulators. The method adds the power equation of distributed generation to the power flow equation of the system and uses the three-phase power injection method in the calculation, which overcomes the convergence problem that traditional power flow calculation methods face. In [33], the modeling of step voltage regulators (svrs) was achieved by assuming that the svr is an ideal component and by modeling it as a three-phase element. The series impedance of the single-phase autotransformer of the svr wes assumed to be zero. The Virtual Power Plant (VPP) model was proposed in [34], which allows for the integration of distributed energy resources as a virtual unit and can participate in the energy market. To interconnect microgrids, power routers must be used. In [35], a stable model for PRs was proposed based on the steady-state power flow calculation model. The line structure in the hybrid AC/DC distribution system based on PR is divided into eight types according to the bus type at both ends of the line and the line type. The power transaction between microgrids relies on energy routers, as proposed by [36]. The energy router is modeled using the port-bus incidence matrix by expressing the energy router using nodal currents and by applying constraints such as Kirchhoff’s current law (KCL) and Kirchhoff’s voltage law (KVL) before embedding it into the existing power system power flow model.
- The flexible closed-loop converter, constructed using power electronic devices, can achieve DC transmission and can solve the impact of closing AC load loop on the power grid, providing ideas for the closed-loop control of distribution networks. According to [37], there are four operational modes for the flexible closed-loop converter: closed-loop operation mode, power flow transfer mode, circulating current limiting mode, and power flow control mode. The power flow transfer and power flow control modes involve solving the power flow equations. In the power flow transfer mode, when a line of a substation fails or stops operating due to maintenance, the closed-loop controller transfers the remaining load to another line. In the power flow control mode, the closed-loop controller outputs adjustable voltage amplitudes and phases according to the power demand of the secondary power supply line, such as load balancing and minimum line loss, and inserts it into the line for the control of four-quadrant power flow.
- From the regional perspective, a Community Load Aggregator (CLA) is established. In some studies, a whole residential area is considered to be a node. Ref. [38] established the CLA model by integrating and modeling the residential load, electric vehicle load, and communication load in a community. The model is divided into static and dynamic loads, where static loads refer to the residential and communication loads that have relatively stable characteristics, while dynamic loads refer to the electric vehicle load, which has significant time-varying characteristics and requires optimized scheduling strategies.
- For a single node, the Soft Opening Point (SOP) model and the State of Charge (SOC) model are established. Ref. [39] modeled SOP and estimated the loss of SOP with the least square estimator. To describe the status of energy storage of a single nodal DG, Ref. [40] used SOC. The formula was used to determine the SOC of a battery based on the battery’s charging and discharging power, charging and discharging efficiency, rated capacity, and calculation time interval.
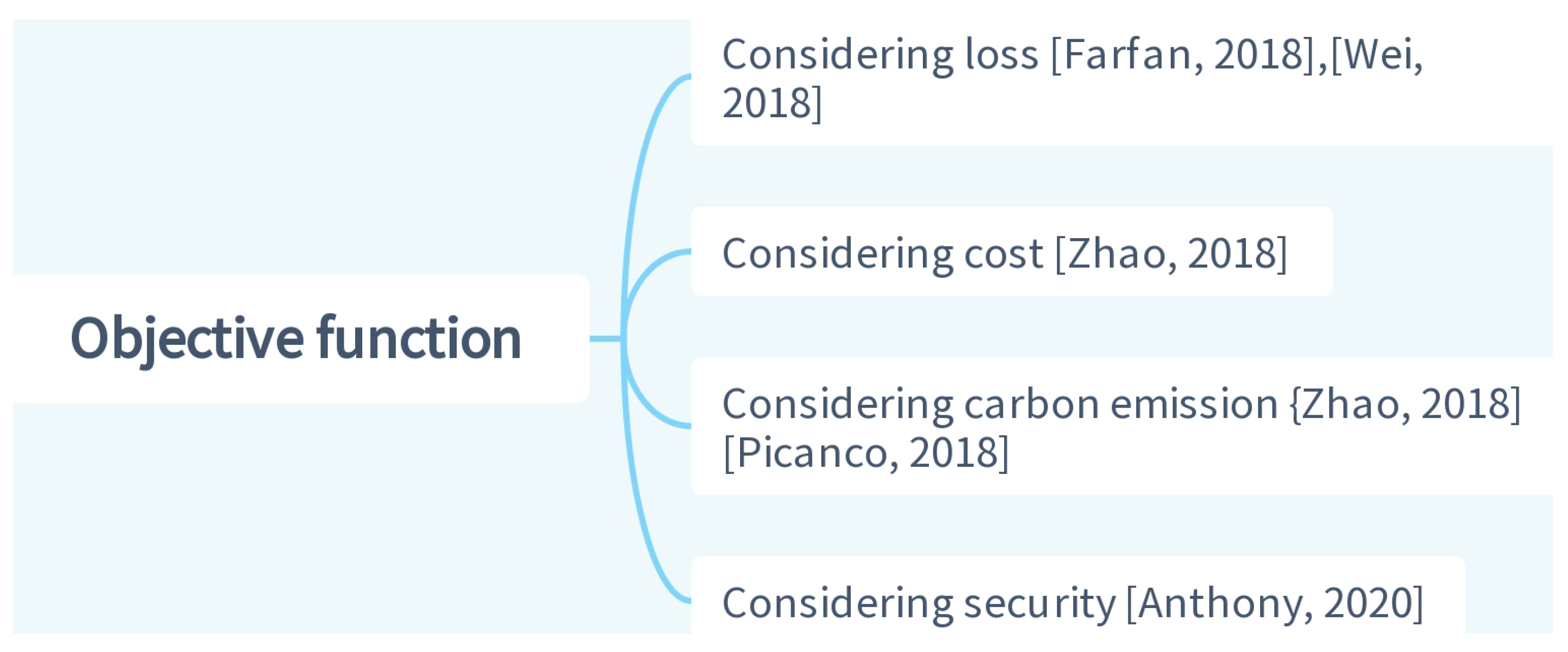
2.5. Objective Function
3. Optimization Methods
3.1. Mathematical Approach
3.1.1. Quadratic Programming
3.1.2. Alternating Direction Method of Multipliers
- Ref. [62] discussed Harmonic Optimal Power Flow (HOPF) problems that involve harmonic coupling factors. To efficiently solve these problems, they employed SDP optimization techniques. SDP is an effective approach for handling non-convex and nonlinear constraints, particularly for complex power system models that incorporate significant harmonic components. The authors used SDP to optimize the power flow and to ensure voltage stability even under harmonic conditions. Additionally, by incorporating harmonic coupling factors into the HOPF problem, they were able to achieve higher accuracy in their power flow solutions under harmonic scenarios.
- Ref. [41] improved the convergence speed of ADMM by proposing an adaptive scheme to improve the convergence of the ADMM on the component-based dual decomposition of the AC OPF. The proposed method incorporates a local curvature approximation scheme with underlying parameter update steps inspired by the local residual balancing scheme to automatically tune the penalty parameters locally without central oversight.
- Ref. [63] iteratively applied ADMM and the Sequential SOCP algorithm (SSA) with ADMM for optimal gas power flow and SSA for OPF and optimal gas flow.
- Ref. [64] made improvements by proposing a new penalty factor selection method. This method can achieve better optimization results by designing a smaller penalty factor while keeping the voltage deviation and the relative objective function value small and dynamically adjusting the step size parameter at each iteration cycle, which can improve the convergence speed and stability of the algorithm.
3.1.3. Mixed Integer Linear Programming
3.1.4. Semi-Definite Programming
- Ref. [69] established an SDP-OPF model which focuses on branch current and branch power flows rather than nodal injections. To perform convex relaxation of power flow equations, new variables were introduced to define branch currents and voltages. Ref. [33] reduced the complexity of OPF model with a sparse decomposition technique. Then, to further reduce the complexity of the optimization problem, it was transformed into a first-order semi-definite-constrained nonlinear minimization problem which was solved using a branch flow Semi-Definite Programming relaxation method.
- Ref. [70] replaced the nonlinear terms with new variables. The original AC-OPF problem was transformed into a “graph + relaxation”-based SDP problem. Ref. [71], based on [70], further proposed an intermediate variable that turns the general OPF problem into a mixed-integer SDP model. Ref. [72] combined SDP-OPF with the Branch Injection Model OPF (BIM-OPF) and then added constraints for nodal voltage, P, Q, and voltage angle to ensure the convex relationship of the model.
3.1.5. Second-Order Cones
- Ref. [75] improved the SOCP algorithm by introducing relaxation variables to simplify the power flow equations and by deriving a SOCP optimization problem, also considering the stochastic model, resulting in a chance-constrained optimal power flow model based on the SOCP algorithm.
- In the field of optimization, combining different models can often lead to further improvements. For instance, Ref. [76] introduced the SDP framework for modeling and the SOCP method for solving. The SDP framework leverages generalized matrix inequalities to handle problems with quadratic cost functions and arbitrary inequality constraints, while the use of the SOCP method for solving ensures high efficiency and universality.Similarly, the approach in [18] is a second-order method based on Robust Optimization (RO) and solved using the Column-and-Constraint Generation (C&CG) algorithm. This approach transforms the model into a problem of normal state optimization and corrective dispatch confirmation, enabling the variables and constraints involved in corrective dispatch to be introduced into normal state optimization. This yields a tight and efficient representation, resulting in accurate solutions. By utilizing different optimization frameworks in conjunction with one another, the resulting solution can be more robust, efficient, and flexible in handling complex problems.
- In [77], the authors proposed a mixed-integer SOCP model that comprises two significant parts. The first part involves the minimization of generation cost with Conditional Value at Risk (CVaR) as the constraint function. CVaR is a risk measure commonly used in finance and risk management that captures the expected loss beyond a certain confidence level. In this approach, CVaR is utilized as a constraint function to ensure the system’s stability while minimizing the generation cost. The second part of the model is the complete optimization model, which consists of multiple constraint conditions. The constraints ensure that the system operates within specific parameters, such as generator output limits, transmission line capacity, and demand balance. By using a mixed-integer SOCP model and by incorporating the CVaR constraint function, the optimization solution can simultaneously address the issues of cost and risk in power systems.
- In [78], the problem addressed is how to maximize economic, environmental, and reliability objectives under PV uncertainty. To solve this problem, the authors decomposed the original problem into multiple sub-problems. For each storage node, they used a SOCP model to solve the investment and operation problem. Then, they combined all the sub-problems using the Benders decomposition method. The Benders decomposition method is a powerful technique for solving large-scale optimization problems, particularly in cases where the problem structure is separable. This approach can achieve efficient and accurate solutions by solving each sub-problem independently and then by integrating the results of each sub-problem.
3.1.6. Multi-Level OPF
3.1.7. Other Mathematical OPF Models
- Other mathematical models are also used in power system optimization. For example, in [84], Model Predictive Control (MPC) was used to predict future energy demand and renewable energy generation, and these predictions were used to schedule the active distribution network, minimizing overall costs while increasing consumption of renewable energy. In [85], two indices were introduced: Power Stability Index (PSI) and Power Loss Index (PLI). PLI uses the reactive power values of all nodes to determine the optimal placement location for a Distribution Static Synchronous Compensator (D-STATCOM), while PSI determines the optimal placement location for a D-STATCOM by considering the stable voltage values of nodes. In [86], a Gaussian mixture model was established to describe the complementarity of power flows amongst AC/DC lines, which is a probabilistic distribution model obtained by linearly combining several Gaussian distributions. The Expectation-Maximum (EM) algorithm was used to estimate the parameters of the Gaussian mixture model. In [87], the C&CG algorithm was adopted. This algorithm was used to transform two-stage robust optimization problems into a master problem and subproblems and was iteratively solved using the CPLEX solver. In [88], Generalized Generation Distribution Factor (GGDF) was adopted to replace the voltage and angle variables in the general DC OPF model.
- Another approach to power system optimization is to use graph-theory-based methods. In [89], a minimum-spanning-tree-based approach was used, taking into account the measurement cost of each measurement in the optimization. In [90], the traditional minimum spanning tree algorithm was modified by incorporating microgrids as vertices and by connecting them with their corresponding load nodes. In [91], an Equivalent Network Approximation (ENApp) algorithm was proposed, which can be solved through reduced network equivalents and the augmented Lagrangian multiplier method. Building on [91], in [92], the impact and properties of communication network topology on the cooperative operation between microgrids were discussed. It was concluded that the network topology has a significant effect on the performance of the OPF algorithm and an efficient communication network topology can improve the algorithm’s performance and convergence speed, enabling microgrids to achieve optimal operation quickly.
- Some articles have established a sensitivity index for determining the optimal placement of DGs. For example, in [93], a DG placement optimization method was proposed based on a sensitive index algorithm. This method evaluates the sensitivity of each node in the power distribution grid to voltage and determines the optimal placement of DGs according to this sensitivity index to improve voltage and to minimize power losses. In [17], the Sensitivity Sequence Energy Algorithm (SSEA) was relied upon to adjust loads. The algorithm estimates the sensitivity of the flow based on a sensitivity matrix and calculates an implicit representation of reactive power based on energy scheduled for each management period. The energy scheduling was adjusted by translating some of the demand response strategies into load adjustment strategies in each management period. Additionally, corresponding power scheduling decisions can be made for each management period.
- Ref. [94] proposed a smart power distribution system for both residential and industrial applications. The system utilizes decentralized methods to determine optimized real and reactive power set points for inverters that provide auxiliary services such as voltage support and harmonic filtering. The entire distribution system is divided into multiple zones, and controllers that make use of local measurements to calculate the optimized power points are deployed in each zone. These controllers also communicate with each other to share information and to create a cohesive system-level strategy. The system is built to be scalable and flexible, easily adjusting to various applications and system sizes. By employing decentralized optimization techniques, the suggested system efficiently distributes the workload, ensures power quality, and maintains the stability and reliability of the distribution system.
- The paper in [95] presented a decentralized algorithm for reducing allocation costs and optimizing the deployment of DERs. The algorithm consists of two steps: first, a distributed optimization model calculates the allocation amount of each DER; second, local information exchange among allocation agents enables quick convergence on the optimal allocation scheme. The goal is to improve system efficiency while reducing allocation costs. Through decentralization, the algorithm can handle large-scale systems with multiple DERs and can maintain scalability and flexibility. The algorithm’s fast convergence speed makes it suitable for real-time applications.
- The paper in [96] proposed a modular structure for addressing the OPF problem in distribution networks. The structure consists of two parts: the first part solves the OPF problem using a gradient-descent algorithm, while the second part sends signals to devices in the distribution network, such as BESS, to control their power output.
- In [97], the authors proposed a method for integrating and coordinating multiple energy sources to optimize the energy flow system. The proposed method uses a unified energy pathway approach to model and analyze all the energy sources, treating them as a single integrated system comprising all energy sources and transmission lines in a unified model. By considering all energy sources and transmission lines together, this unified approach enables efficient optimization of the energy flow system. The authors devised an optimization algorithm that coordinates the operation of diverse energy sources while considering the constraints and uncertainties associated with each source.
- The paper in [98] introduced a hierarchical distributed algorithm designed for solving large-scale mixed-integer convex problems. The algorithm presented in [98] employed an enhanced Generalized Benders Decomposition (GBD) technique, aiming to ensure computational efficiency and to effectively handle intricate problems. The algorithm’s ability to optimize integer variables is useful for optimization problems in the energy and power systems domain.
- The paper in [99] presented a hardware implementation of an optimal power flow (OPF) algorithm for distribution networks using decentralized measurements. The algorithm was based on the MATPOWER OPF and optimizes power flow in the network using a decentralized approach. In [100], the cost optimization problem of energy storage systems was solved using Gurobi. The paper in [101] addressed the analysis and management needs of large-scale integrated transmission and distribution networks through the implementation of an integrated power flow algorithm. The algorithm in [101] was optimized through the utilization of an adaptive Lavenberg–Marquardt method and an incomplete LU decomposition. An improved DC OPF model with linear constraints was constructed. An adaptive interior point method was proposed to solve the problem based on branch loss. This approach provides an efficient solution for the operation and planning of integrated transmission and distribution networks, taking into account technical and economic aspects.
- In [102], a comprehensive optimization model was proposed to model active distribution networks, and the primal-dual interior point method was used to solve the optimization problem. The approach offers a promising solution for optimal operation and planning of distribution systems, considering both technical and economic aspects. The paper in [103] proposed the use of topology adjustment as a means to optimize the power generation of offshore wind farms. The proposed approach focuses on optimizing the power output of wind turbines and reducing transmission losses by making adjustments to the network topology. An efficient solution to the optimization problem is achieved through the utilization of the interior point method. The proposed approach shows promise in improving the performance and efficiency of offshore wind power generation systems.
3.2. Heuristic Approach
3.2.1. Sunflower Algorithm
3.2.2. Particle Swarm Algorithm
- To improve the PSO algorithm, several researchers have proposed different variations of the algorithm. For instance, Ref. [106] proposed an adaptive weight updating mechanism and an early stopping strategy to improve the algorithm’s performance and to reduce computation time. Likewise, another study [107] proposed an Enhanced PSO (EPSO) approach, which incorporates various heuristic operators, inertia weight adjustment, and chaotic mapping mechanisms. These enhancements were introduced to improve the overall performance of the traditional PSO algorithm. The study aimed to optimize the algorithm by introducing additional features and mechanisms. A study by [108] presented an improved PSO algorithm that enhances the analysis capability of each optimization direction by dividing the single-particle vector into sub-vectors. This partitioning approach was introduced to improve the algorithm’s ability to analyze and optimize individual dimensions separately. The algorithm utilizes a regionally coordinated control structure for intelligent distribution networks. It incorporates the energy generated via controllable distributed generators and energy storage systems and takes into account the charging and discharging process of the energy storage system. This holistic approach aims to optimize the coordination and utilization of energy resources within the distribution network. In another research paper [109], a framework was proposed to enhance the performance of Performance Index Optimization (PIO). This framework introduced the utilization of Power Management Unit (PMU) data, leading to the development of the PMU-PIO algorithm. The incorporation of PMU data aimed to improve the accuracy and effectiveness of the optimization process in the PIO algorithm. The PSO-PIO algorithm combines the strengths of both approaches to achieve more efficient and accurate optimization results.
- Several articles focus on using multi-objective optimization methods with the PSO algorithm to solve complex optimization problems. For instance, Ref. [110] improved the traditional Network-Structured Multi-Objective Particle Swarm Optimization (NS-MOPSO) algorithm by introducing crowding distance as a feasibility evaluation criterion. The paper also proposed a new weight coefficient updating strategy and a solution set pruning strategy to better manage the solution set size and to maintain its global optimality. Furthermore, the algorithm uses Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) to calculate the optimal solution for multi-objective problems. Similarly, Ref. [111] presented an improved version of the Multi-Objective Particle Swarm Optimization (MOPSO) algorithm for solving problems in electrical distribution systems. The algorithm coordinates transformer tap settings, capacitor bank injection, and DG active power output to minimize power flow losses and voltage deviations.In another study, Ref. [112] introduced the Pareto Entropy-based Multi-Objective Particle Swarm Optimization (PE-MOPSO) algorithm to solve optimal control problems in distribution networks. The PE-MOPSO algorithm is based on an elite strategy in the multi-objective PSO algorithm, which addresses the problem of non-uniform distribution of non-dominated solutions in the traditional MOPSO algorithm. Additionally, the algorithm introduces a region-updating strategy to balance the trade-off between global and local searches. The research paper in [113] introduced an enhanced version of the Multi-Objective Particle Swarm Optimization (MOPSO) algorithm known as Competitive Multi-Objective Particle Swarm Optimizer (CMOPSO). The Improved CMOPSO algorithm improves upon the traditional Particle Swarm Algorithm by incorporating an archive strategy that utilizes an adaptive grid. During the iteration process, the paper proposes updates to the position and velocity of each particle using different equations. These enhancements aim to improve the overall performance and optimization capabilities of the CMOPSO algorithm.Finally, in [114], a multi-objective optimization algorithm based on PSO is presented. This algorithm aims to minimize two objective functions concurrently. By utilizing different weighting factors and random coefficients, the algorithm calculates the velocity and displacement of each particle in order to search for the global optimal point during iterations. Through this approach, the algorithm aims to achieve superior solutions by efficiently exploring the solution space and by balancing between the two conflicting objectives.
- Ref. [115] improves upon the traditional PSO algorithm by applying it to the distribution network reconfiguration problem and by optimizing multiple objective functions such as power loss and the voltage level of the system.
- The research paper [116] introduces a novel hybrid algorithm called Hybrid Firefly and Particle Swarm Optimization (HFPSO). This algorithm combines the Firefly Algorithm (FA) with PSO to leverage their respective strengths. By incorporating the velocity concept from PSO and the brightness concept from FA, a mixed velocity is obtained and used to update the position of fireflies. This combination enables the algorithm to benefit from the fast convergence speed of PSO, while also mitigating the risk of getting trapped in local optima, which is a common issue in FA. The HFPSO algorithm provides a promising approach for optimization problems by effectively combining the advantages of both FA and PSO.
3.2.3. Genetic Algorithm
- Several papers have proposed improvements to GA algorithms to optimize power systems and control mechanisms. For instance, Ref. [119] combined GA with an N-R method to obtain the necessary reactive power factor that minimizes power losses across different PV-BESS connection schemes in a distribution network. Similarly, Ref. [120] used a combination of GA and a FBS power flow method to optimally place BESS in a unidirectional power distribution network. The authors used mathematical modeling and heuristic algorithms to quickly evaluate different scenarios and to determine the optimal placement of BESS. In another study, Ref. [121] proposed a GA algorithm that uses a search algorithm based on spanning trees during the selection operation to filter out invalid configuration combinations effectively. Another improvement was proposed in [122], where an improved GA based on dynamic weighting was presented. The paper considered both the weight of active power loss and grid voltage to achieve better coordination and more efficient solutions. In [123], a method to preserve the optimal solution from disruption caused by genetic crossover and mutation was proposed. This was achieved by incorporating an elitism selection mechanism. This mechanism ensures that the best solution discovered so far is preserved in the population, even if it is not improved in the current generation. By including elitism, the algorithm can prevent the loss of favorable solutions and can maintain the progress made towards finding the optimal solution. This enhances the effectiveness and robustness of the Genetic Algorithm in solving optimization problems.
- Various variants of GA algorithms have been applied to optimize OPF models, aiming to enhance performance and optimize capabilities. For example, in [124], the Non-dominated Sorting Genetic Algorithm II (NSGA-II) is utilized as a foundation, with several improvements proposed to enhance its performance. NSGA-II is a multi-objective Genetic Algorithm known for maintaining the diversity of Pareto-optimal solution sets. The paper introduced strategies such as an elite strategy, crowding distance comparison, and crowding distance control to further augment the algorithm.In another study [125], the Immune Genetic Algorithm (IGA) was employed to determine the optimal allocation and sizing of shunt capacitor banks in distribution networks while considering technical constraints. In this approach, chromosomes represent potential solutions, and a fitness function is employed to assess the quality of each chromosome. Genetic operators are employed to generate fresh populations, promoting the search for the global optimal solution. The fitness function is then used to evaluate the best solution obtained through IGA.Furthermore, in [126], a Multi-Objective Genetic Algorithm (MOGA) was employed to simultaneously optimize multiple objective functions. MOGA, which is a multi-objective variant of the original GA, offers improved optimization performance and the ability to effectively handle problems involving multiple objectives.
3.2.4. Other Heuristic Approaches
- Apart from the previously mentioned algorithms, there are several other heuristic optimization algorithms that have been utilized for OPF problems. For instance, Ref. [127] used the Increasing Population size Covariance Matrix Adaptation Evolution Strategy (IPOP-CMA-ES) algorithm, which is a type of optimization algorithm that introduces a new start trigger and can increase population size for Covariance Matrix Adaptation Evolution Strategy (CMA-ES). The IPOP-CMA-ES algorithm has the ability to cover a large search space in a shorter time, which results in faster convergence to global optimal solutions. In another study, Ref. [128] proposed improvements to the Water Cycle Algorithm (WCA). These improvements include including non-dominated sorting, a new solution type called “sea”, and a phase-based strategy for raindrop generation. Moreover, Ref. [129] used the Flower Pollination Algorithm (FPA) to optimize the optimal capacity and location of PV distributed generation to minimize power loss on the distribution grid. In another study, Ref. [130] used the Grey Wolf Optimization (GWO) algorithm to determine the optimal placement and size of PV stations in rural unbalanced distribution networks to minimize losses and to reduce the imbalance. The algorithm uses a set of randomly generated grey wolf populations to estimate the prey’s position using alpha, beta, and gamma wolves, and to optimize the objective function and position with the corresponding wolf population to obtain the optimal PV placement. Additionally, Ref. [131] introduced a modified heuristic function for updating the positions of teachers and students in Teaching Learning-Based Optimization (TLBO). The new function called the Weighted Parameter and Resonance Frequency Heuristic Function, defines a weighted parameter based on a concept similar to the resonance frequency. Furthermore, Ref. [132] used a heuristic multi-objective coordinated search algorithm based on the Multi-Objective Harmony Search (MOHS) algorithm to solve the problem of optimizing and dispatching DGs and obtained a set of Pareto optimal solutions. Finally, Ref. [133] proposed improvements to the Cuckoo Search algorithm by introducing a parameter that balances global and local random walks and by using the Levy distribution to describe the step size of the random walk. The Mantegna equation and gamma function were also used to generate random numbers, resulting in an improved trade-off between convergence time and global optimum.
- Some of the articles proposed improvements based on other articles. For instance, in [134], an improved version of the Whale Optimization Algorithm (WOA) was proposed based on the original WOA proposed in [135]. This improved version introduced a nonlinear update factor to increase the diversity of the population and to improve speed and accuracy. Similarly, in [136], an improved Multi-objective Bees Algorithm (BA) was proposed based on the BA proposed in [137,138]. This improved version incorporated both crowding distance and fuzzy mechanism to manage the size of solutions and to select non-dominating solutions in the algorithm. Moreover, in [139], an improved version of the Sine Cosine Algorithm (SCA) was proposed based on the original SCA proposed in [140]. The improvement involved the use of different operators to update position variables in the optimization problem, such as mutation operation to enhance exploration performance and to improve exploitation performance by targeting the position.
3.3. Machine Learning Approach
- Ref. [145] NN in this paper is designed as a deep recurrent NN that has more hidden layers than a simple recurrent NN. The additional layers enable the network to learn more complex historical and temporal information and to provide a more compact representation of the input–output relationship.
- Ref. [146] applies an Artificial Neural Network (ANN) to control the direct and quadrature axis currents of D-STATCOM improving the damping performance of power systems. The nonlinear characteristics of the ANN controller make it more adaptable to different operating conditions. In addition, by optimizing the parameters of the NN such as gain constants, the control performance and stability of D-STATCOM can be further improved.
- Ref. [147] overcomes the long convergence time of a conventional NN by updating the weight of the NN model with Lavenberg–Marquardt and Bayesian Regularization.
- Supervised learning is another approach to dealing with the OPF problems. For instance, in [1], supervised learning was used to map the solutions of linear OPF to nonlinear control variables using a two-node approximation of radial networks with a radial basis function network. Similarly, in [148], a Message Passing Graph Convolution OPF (MPGCN-OPF) model based on graph convolution and message passing interface was proposed. This approach utilizes the property of graph convolution feature mapping and collects, aggregates, and updates the feature matrix from neighboring nodes through information passing. The performance of this approach was found to be better than Deep Neural Network (DNN) models in terms of the loss function and performance evaluation parameters, and it has been validated through accurate predictions.Moreover, in [149], a data-driven approach was used to combine Support Vector Regression (SVR) and Ridge regression (RR) to minimize the linearization error of the power flow model. The accuracy of the model was improved by considering the covariance of the input data and using Principal Component Analysis (PCA) to reduce the impact of data collinearity. This data-driven approach was found to be effective for solving OPF problems.
- Multiple methods of deep reinforcement learning have been applied in the field of power system optimization. For example, Double Deep Q-learning has been used in [150,151], where two NNs are used for optimization simultaneously.Another method called Soft Actor-Critic (SAC), has been used in [152], where it was combined with Multi-Agent Reinforcement Learning techniques such as DDPG to solve the OPF problem. In [153], the optimal power flow problem over multiple time periods was described as a Markov process to control PV and WT output, thus avoiding local optima. Additionally, in [154], Deep Deterministic Policy Gradient (DDPG) was employed to solve dynamic OPF problems by describing the problem over multiple time periods as a Markov process and by utilizing active and reactive outputs of PV generation and an energy storage system as control actions. The algorithm then used deep learning to train the agent for decision-making.Similarly, in [155], the DDPG algorithm was used to solve the optimal control problem in the ADN, which is a Markov Decision Process. DDPG is a policy gradient method consisting of two neural networks—an actor and a critic—both based on DNNs. The critic network learns a Q-function that estimates the expected future rewards of state–action pairs. DDPG can handle continuous action spaces without discretization and learn deterministic policies that are more efficient and less noisy.
- A power flow model can also be added to the ML solution. Ref. [156] combines an exact nonlinear AC power flow model and an approximate linear power flow model to reflect the system’s response under uncertainty and proposed a data-drive AC-OPF model.
3.4. Mixed Approach
4. Discussion
4.1. Further Exploiting Uncertainty of DG
4.2. Distributed Optimization
4.3. Combination of OPF with Electricity Market
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ADMM | Alternating Direction Method of Multipliers |
| ADN | Active Distribution Network |
| ANN | Artificial Neural Network |
| ANN-PDIPM-T | Artificial Neural Network-Primal-Dual Interior Point Method-Temperature |
| BA | Bees Algorithm |
| BJM-OPF | Branch Injection Model OPF |
| OPF | Optimal Power Flow |
| DG | Distributed Generator |
| DN | Distribution Network |
| D-STATCOM | Distribution Static Synchronous Compensator |
| BESS | Battery Energy Storage System |
| BIM | Bus Injection Model |
| CVaR | Conditional Value at Risk |
| C&CG | Column-and-Constraint Generation |
| CB | Capacitor Banks |
| CLA | Community Load Aggregator |
| COPF | Coupled OPF |
| CMA-ES | Covariance Matrix Adaptation Evolution Strategy |
| CMOPSO | Competitive Multi-Objective Particle Swarm Optimizer |
| DDPG | Deep Deterministic Policy Gradient |
| DNN | Deep Neural Network |
| DRL | Deep Reinforcement Learning |
| DSO | Distribution System Operator |
| EA | Evolutionary Algorithm |
| EDC | Enhanced DC |
| EM | Expectation-Maximum |
| ENApp | Equivalent Network Approximation |
| ENS | Energy Not Supplied |
| EPSO | Enhanced PSO |
| EV | Electric Vehicle |
| FA | Firefly Algorithm |
| FBS | Forward/Backward Sweep |
| FPA | Flower Pollination Algorithm |
| GA | Genetic Algorithm |
| GBD | Generalized Benders Decomposition |
| GGDF | Generalized Generation Distribution Factors |
| GWO | Grey Wolf Optimization |
| HFPSO | Hybrid Firefly and Particle Swarm Optimization |
| HOPF | Harmonic Optimal Power Flow |
| IGA | Immune Genetic Algorithm |
| IPOP-CMA-ES | Increasing Population size Covariance Matrix Adaptation Evolution Strategy |
| IPSO | Intelligent Single Particle Optimization |
| LF | Loss Factor |
| LMP | Local Marginal Price |
| MILP | Mixed Integer Linear Programming |
| MIQP | Mixed Integer Quadratic Programming |
| ML | Machine Learning |
| MOGA | Multi-Objective GA |
| MOHS | Multi-Objective Harmonic Search |
| MOPSO | Multi-Objective Particle Swarm Optimization |
| MPC | Model Predictive Control |
| MPGCN-OPF | Message Passing Graph Convolution OPF |
| N-R | Newton–Raphson |
| NMF | Non-negative Matrix Factorization |
| NN | Neural Network |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm II |
| NS-MOPSO | Network-Structured Multi-Objective Particle Swarm Optimization |
| OPF | Optimal Power Flow |
| PCA | Principal Component Analysis |
| PE-MOPSO | Pareto Entropy-Based Multi-Objective Particle Swarm Optimization |
| PIO | Performance Index Optimization |
| PLI | Power Loss Index |
| PMU | Power Management Unit |
| PR | Power Router |
| PSI | Power Stability Index |
| PSO | Particle Swarm Optimization |
| PTDF | Power Transfer Distribution Factors |
| PV | Photovoltaic Cell |
| QCP | Quadratic Constraint Programming |
| QP | Quadratic Programming |
| RB | Reactor Banks |
| RO | Robust Optimization |
| RR | Ridge Regression |
| SAC | Soft Actor–Critic |
| SCA | Sine Cosine Algorithm |
| SCIG | Squirrel Cage Induction Generator |
| SDP | Semi-Definite Programming |
| SFO | Sunflower Optimization |
| SOC | State Of Charge |
| SOCP | Second-Order Conic Programming |
| SOP | Soft Opening Point |
| SRSM | Spectral Regularized Similarity Matching |
| SSA | Sequential SOCP algorithm |
| SSEA | Sensitivity Sequence Energy Algorithm |
| SVG | Static Var Generator |
| SVM | Support Vector Machines |
| svr | step-voltage regulators |
| SVR | Support Vector Regression |
| TLBO | Teaching Learning-Based Optimization |
| TOPSIS | Technique for Order of Preference by Similarity to Ideal Solution |
| TOU | Time of Use |
| WCA | Water Cycle Algorithm |
| WOA | Whale Optimization Algorithm |
| WT | Wind Turbine |
References
- Sadnan, R.; Dubey, A. Learning optimal power flow solutions using linearized models in power distribution systems. In Proceedings of the 2021 IEEE 48th Photovoltaic Specialists Conference (PVSC), Fort Lauderdale, FL, USA, 20–25 June 2021; pp. 1586–1590. [Google Scholar]
- Farfan-Ramirez, S.; Gutierrez-Alcaraz, G.; Perez-Hernandez, G. Two lossy multi-period optimal power flow formulations with renewable energy and storage. In Proceedings of the 2018 North American Power Symposium (NAPS), Fargo, ND, USA, 9–11 September 2018; pp. 1–6. [Google Scholar]
- Zheng, P.; Cheng, N.; Huang, X. Carbon reduction assessment of electric vehicle aggregation participating in distribution network dispatching based on v2g technology. In Proceedings of the 2022 4th International Conference on Smart Power & Internet Energy Systems (SPIES), Beijing, China, 27–30 October 2022; pp. 1563–1568. [Google Scholar]
- Ma, T.; Zhang, T. Research on reactive power and voltage characteristics analysis and reactive power configuration strategy of active distribution network. In Proceedings of the 2019 12th International Conference on Intelligent Computation Technology and Automation (ICICTA), Xiangtian, China, 19–27 August 2019; pp. 108–111. [Google Scholar]
- Verma, R.; Padhy, N.P. Optimal power flow based dr in active distribution network with reactive power control. IEEE Syst. J. 2022, 16, 3522–3530. [Google Scholar] [CrossRef]
- Oi, L.; Wu, K.; Wang, Y.; Jing, X.; Cui, C.; Zhao, R. Research on dynamic optimized operation strategy of distribution network considering demand response. In Proceedings of the 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 4–7 June 2020; pp. 901–906. [Google Scholar]
- Vaishya, S.R.; Abhyankar, A.R.; Kumar, P. A novel loss sensitivity based linearized opf and lmp calculations for active balanced distribution networks. IEEE Syst. J. 2023, 17, 1340–1351. [Google Scholar] [CrossRef]
- Shah, C.; Wies, R. Algorithms for optimal power flow in isolated distribution networks using different battery energy storage models. In Proceedings of the 2020 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 17–20 February 2020; pp. 1–5. [Google Scholar]
- Veeraganti, S.D.; Mohammed Imran, A. Optimal placement and sizing of dg and d-statcom in a distribution system: A review. In Proceedings of the 2022 International Virtual Conference on Power Engineering Computing and Control: Developments in Electric Vehicles and Energy Sector for Sustainable Future (PECCON), Chennai, India, 5–6 May 2022; pp. 1–13. [Google Scholar]
- Verma, A.; Thakur, R. A review on methods for optimal placement of distributed generation in distribution network. In Proceedings of the 2022 Interdisciplinary Research in Technology and Management (IRTM), Kolkata, India, 24–26 February 2022; pp. 1–8. [Google Scholar]
- Mylonas, C.; Karagiannopoulos, S.; Aristidou, P.; Shchetinin, D.; Hug, G. Comparison of optimal power flow formulations in active distribution grids. In Proceedings of the 12th Mediterranean Conference on Power Generation, Transmission, Distribution and Energy Conversion (MEDPOWER 2020), Paphos, Cyprus, 9–12 November 2020; Volume 2020, pp. 378–383. [Google Scholar]
- Charles, P.; Mehazzem, F.; Soubdhan, T. A review on optimal power flow problems: Conventional and metaheuristic solutions. In Proceedings of the 2020 2nd International Conference on Smart Power & Internet Energy Systems (SPIES), Bangkok, Thailand, 5 July 2020; pp. 577–582. [Google Scholar]
- Papadimitrakis, M.; Giamarelos, N.; Stogiannos, M.; Zois, E.; Livanos, N.; Alexandridis, A. Metaheuristic search in smart grid: A review with emphasis on planning, scheduling and power flow optimization applications. Renew. Sustain. Energy Rev. 2021, 145, 111072. [Google Scholar] [CrossRef]
- Maneesha, A.; Swarup, K. A survey on applications of Alternating Direction Method of Multipliers in smart power grids. Renew. Sustain. Energy Rev. 2021, 152, 111687. [Google Scholar] [CrossRef]
- Shin, B.H.; Oh, G.D.; Kim, S.C.; Jung, K.H. Power flow and economics analysis for rmu-based low-voltage distribution networks operation. In Proceedings of the CIRED 2021—The 26th International Conference and Exhibition on Electricity Distribution, Online, 20–23 September 2021; Volume 2021, pp. 2432–2436. [Google Scholar]
- Meegoda, M.; Balasooriya, B.; Dharmapriya, E.; Kumara, J.; Amarasinghe, P.A.G.M.; Abeygunawardane, S.K. Impact of solar PV systems on the reliability of power distribution systems. In Proceedings of the 2020 Moratuwa Engineering Research Conference (MERCon), Moratuwa, Sri Lanka, 28–30 July 2020; pp. 560–565. [Google Scholar]
- Fernández, J.; Grijalva, S. Implicit reactive power flow representation to support distribution system der energy scheduling. In Proceedings of the 2022 North American Power Symposium (NAPS), Salt Lake City, UT, USA, 9–11 October 2022; pp. 1–5. [Google Scholar]
- Huang, H.; Zhou, M.; Zhang, S.; Zhang, L.; Li, G.; Sun, Y. Exploiting the operational flexibility of wind integrated hybrid AC/DC power systems. IEEE Trans. Power Syst. 2021, 36, 818–826. [Google Scholar] [CrossRef]
- Li, B.; Zhang, X.; Wang, K.; Zhang, Y.; Zhu, Z.; Liu, J. Cooperative optimal scheduling of interconnected transmission-distribution-micro power system. In Proceedings of the 2022 12th International Conference on Power, Energy and Electrical Engineering (CPEEE), Scopus Shiga, Japan, 25–27 February 2022; pp. 215–219. [Google Scholar]
- Ammar, M.; Sharaf, A.M. Optimized use of pv distributed generation in voltage regulation: A probabilistic formulation. IEEE Trans. Ind. Inform. 2019, 15, 247–256. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, S.; Mo, W.; Wang, Y.; Li, G.; Chen, G. Power flow calculation for distribution network with distributed generations and voltage regulators. In Proceedings of the 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 4–7 June 2020; pp. 662–667. [Google Scholar]
- Biswas, B.D.; Kamalasadan, S. Alternative sdp relaxed optimal power flow formulation for radial distribution networks. In Proceedings of the 2022 IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE), Trivandrum, India, 2–5 January 2022; pp. 1–6. [Google Scholar]
- Yuan, H.; Li, F.; Wei, Y.; Zhu, J. Novel linearized power flow and linearized opf models for active distribution networks with application in distribution lmp. IEEE Trans. Smart Grid 2018, 9, 438–448. [Google Scholar] [CrossRef]
- Heidari-Akhijahani, A.; Safdarian, A.; Vrakopoulou, M. A linear ac power flow model for unbalanced multi-phase distribution networks based on current injection equations. IEEE Trans. Power Syst. 2021, 36, 3806–3809. [Google Scholar] [CrossRef]
- Campos, A.C.D.; Pinto, R.S.; Filho, M.O.D.L.; Unsihuay-Vila, C. A linear AC three-phase optimal power flow model for active distribution networks and microgrids. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies Conference—Latin America (ISGT Latin America), Lima, Peru, 15–17 September 2021; pp. 1–5. [Google Scholar]
- Li, H.; Yan, X.; Yan, J.; Zhang, A.; Zhang, F. A three-phase unbalanced linear power flow solution with pv bus and zip load. IEEE Access 2019, 7, 138879–138889. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, N.; Kang, C.; Xia, Q. A state-independent linear power flow model with accurate estimation of voltage magnitude. IEEE Trans. Power Syst. 2017, 32, 3607–3617. [Google Scholar] [CrossRef]
- Sepúlveda, S.; Ruíz, A.G.; Mora-Flórez, J.J. Optimal power flow for three-phase unbalanced active distribution networks with delta connections. In Proceedings of the 2022 IEEE ANDESCON, Barranquilla, Colombia, 16–19 November 2022; pp. 1–6. [Google Scholar]
- Feng, K.; Wu, Z.; Li, P.; Hu, M. Optimal active and reactive power coordinated dispatch in unbalanced distribution networks. In Proceedings of the 2020 International Conference on Smart Grids and Energy Systems (SGES), Perth, Australia, 23–26 November 2020; pp. 385–389. [Google Scholar]
- Giraldo, J.S.; Vergara, P.P.; López, J.C.; Nguyen, P.H.; Paterakis, N.G. A novel linear optimal power flow model for three-phase electrical distribution systems. In Proceedings of the 2020 International Conference on Smart Energy Systems and Technologies (SEST), Istanbul, Turkey, 7–9 September 2020; pp. 1–6. [Google Scholar]
- Yang, Z.; Zhong, H.; Bose, A.; Zheng, T.; Xia, Q.; Kang, C. A linearized opf model with reactive power and voltage magnitude: A pathway to improve the mw-only dc opf. IEEE Trans. Power Syst. 2018, 33, 1734–1745. [Google Scholar] [CrossRef]
- Zhang, Z.; Cheng, R.; He, X.; Huang, J.; Zhang, Z.; Zhang, A.; Ren, L. Research on optimal power flow control of closed-loop distribution network with superconducting cable. In Proceedings of the 2020 Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 28–30 March 2020; pp. 555–559. [Google Scholar]
- Bazrafshan, M.; Gatsis, N.; Zhu, H. Optimal power flow with step-voltage regulators in multi-phase distribution networks. IEEE Trans. Power Syst. 2019, 34, 4228–4239. [Google Scholar] [CrossRef]
- Wang, J.; Du, W.; Yang, D.; Liu, G.; Chen, H. An optimal scheduling method of virtual power plant cluster considering generation-grid-load-storage coordination. In Proceedings of the 2021 6th Asia Conference on Power and Electrical Engineering (ACPEE), Chongqing, China, 8–11 April 2021; pp. 1048–1052. [Google Scholar]
- Li, P.; Sheng, W.; Duan, Q. Optimal power flow calculation method for AC/DC hybrid distribution network based on power router. In Proceedings of the 2021 6th Asia Conference on Power and Electrical Engineering (ACPEE), Chongqing, China, 8–11 April 2021; pp. 1694–1699. [Google Scholar]
- Miao, J.; Zhang, N.; Kang, C.; Wang, J.; Wang, Y.; Xia, Q. Steady-state power flow model of energy router embedded ac network and its application in optimizing power system operation. IEEE Trans. Smart Grid 2018, 9, 4828–4837. [Google Scholar] [CrossRef]
- Zhang, Y.; Mao, Z.; Liu, J.; Xu, H. Research on optimal power flow by interior point method for ac distribution network with flexible loop converters. In Proceedings of the 2022 7th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 23–26 September 2022; pp. 257–263. [Google Scholar]
- Wang, H.; Li, Y.; Shi, S.; Zhou, Y.; Lei, T.; Feng, D.; Fang, C.; Liu, Z. Optimal power scheduling strategy in residential distribution network based on multi-dimensional network integration. In Proceedings of the 2021 Power System and Green Energy Conference (PSGEC), Shanghai, China, 13–16 May 2021; pp. 85–90. [Google Scholar]
- Ivic, D.R.; Stefanov, P.C. An extended control strategy for weakly meshed distribution networks with soft open points and distributed generation. IEEE Access 2021, 9, 137886–137901. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, W.; Hou, H.; Yuan, Z.; Xu, I. Research on optimal dispatching strategy of multi-terminal dc distribution network. In Proceedings of the 2022 China International Conference on Electricity Distribution (CICED), Changsha, China, 7–8 September 2022; pp. 525–529. [Google Scholar]
- Mhanna, S.; Verbič, G.; Chapman, A.C. Adaptive admm for distributed AC optimal power flow. IEEE Trans. Power Syst. 2019, 34, 2025–2035. [Google Scholar] [CrossRef]
- Wei, W.; Wang, J.; Wu, L. Distribution optimal power flow with real-time price elasticity. IEEE Trans. Power Syst. 2018, 33, 1097–1098. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, Z.; Hao, J.; Wang, S.; Wang, X.; Xie, H.; Li, X. A multi-objective power flow optimization model of electric and thermal distribution network using the power flow method. In Proceedings of the 2022 9th International Forum on Electrical Engineering and Automation (IFEEA), Zhuhai, China, 4–6 November 2022; pp. 687–690. [Google Scholar]
- Picanco, A.F.; Oliveira, A.P. Reactive optimal power flow in the temperature-dependent power flow using interior point method with artificial neural network. In Proceedings of the Mediterranean Conference on Power Generation, Transmission, Distribution and Energy Conversion (MEDPOWER 2018), Dubrovnik, Croatia, 12–15 November 2018; pp. 1–6. [Google Scholar]
- Anthony, I.O.; Mokryani, G.; Zubo, R.H.; Ezechukwu, O.A.; Ivry, P. Distribution network reconfiguration considering security-constraint and multi-dg configurations. In Proceedings of the 2020 55th International Universities Power Engineering Conference (UPEC), Torino, Italy, 1–4 September 2020; pp. 1–6. [Google Scholar]
- Sanam, J.; Sowjanya, M.L.; Pujitha, D.; Chaithanya, S.; Deepika, B.M. Optimal reactive power sizing in distribution systems to optimize the voltage profile and power loss using fbs based esa algorithm. In Proceedings of the 2020 IEEE 17th India Council International Conference (INDICON), Delhi, India, 10–13 December 2020; pp. 1–6. [Google Scholar]
- Kumar, P.; Vaishya, S.R.; Abhyankar, A.R. A linearized optimal power flow framework for a balanced active distribution network. In Proceedings of the 2019 8th International Conference on Power Systems (ICPS), Jaipur, India, 20–22 December 2019; pp. 1–6. [Google Scholar]
- Li, X.; Xia, Q. Stochastic optimal power flow with network reconfiguration: Congestion management and facilitating grid integration of renewables. In Proceedings of the 2020 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Chicago, IL, USA, 12–15 October 2020; pp. 1–5. [Google Scholar]
- Moutis, P.; Hug, G.; Kar, S. Resistive-aware linear approximations for solving the optimal power flow problem for distribution networks. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019; pp. 1959–1963. [Google Scholar]
- Tabarez, J.E.; Barnes, A.K.; Mate, A.; Bent, R.W. Fault current-constrained optimal power flow on unbalanced distribution networks. In Proceedings of the 2022 IEEE PES Innovative Smart Grid Technologies—Asia (ISGT Asia), Singapore, 1–5 November 2022; pp. 205–209. [Google Scholar]
- Zhong, R.; Teng, Y.; Wang, X.; Zhu, Y.; Zhang, H. Probabilistic optimal power flow calculation of AC/DC hybrid distribution network with photovoltaic power and electric vehicles. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–8 November 2018; pp. 20–27. [Google Scholar]
- Levis, C.; Phan-Tan, C.-T.; Hill, M. Multi-objective optimal active and reactive power dispatch for centrally controlled distributed pv systems. In Proceedings of the 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, UK, 4–7 September 2018; pp. 1–6. [Google Scholar]
- Gao, F.; Zhu, Z. Multi objective optimal method for new energy power grid considering maximum demand response. In Proceedings of the 2022 7th Asia Conference on Power and Electrical Engineering (ACPEE), Hangzhou, China, 15–17 April 2022; pp. 654–658. [Google Scholar]
- Chen, G.; Wang, Z.; Qian, F.; Jia, D.; Yu, H.; Kang, T. Optimal strategy for centralized regulation of distributed power supply in medium-voltage distribution network. In Proceedings of the 2022 5th International Conference on Energy, Electrical and Power Engineering (CEEPE), Chongqing, China, 22–24 April 2022; pp. 569–573. [Google Scholar]
- Franco, J.F.; Ochoa, L.F.; Romero, R. AC OPF for smart distribution networks: An efficient and robust quadratic approach. IEEE Trans. Smart Grid 2018, 9, 4613–4623. [Google Scholar] [CrossRef]
- Wu, C.; Gu, W.; Zhou, S.; Chen, X. Coordinated optimal power flow for integrated active distribution network and virtual power plants using decentralized algorithm. IEEE Trans. Power Syst. 2021, 36, 3541–3551. [Google Scholar] [CrossRef]
- Jha, R.R.; Dubey, A. Exact distribution optimal power flow (d-opf) model using convex iteration technique. In Proceedings of the 2019 IEEE Power& Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar]
- Pham, V.N.; Do, D.Q.; Nguyen, Q.D.; Nguyen, T.T. Optimal dg placement for power loss minimization in radial power distribution networks using mixed-integer quadratic programming method based on modified distflow. In Proceedings of the 2022 6th International Conference on Green Technology and Sustainable Development (GTSD), Nha Trang City, Vietnam, 29–30 July 2022; pp. 166–171. [Google Scholar]
- Javadi, M.S.; Gouveia, C.S.; Carvalho, L.M.; Silva, R. Optimal power flow solution for distribution networks using quadratically constrained programming and mccormick relaxation technique. In Proceedings of the 2021 IEEE International Conference on Environment and Electrical Engineering and 2021 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Bari, Italy, 7–10 September 2021; pp. 1–6. [Google Scholar]
- Peng, Q.; Low, S.H. Distributed optimal power flow algorithm for radial networks, i: Balanced single phase case. IEEE Trans. Smart Grid 2018, 9, 111–121. [Google Scholar] [CrossRef]
- Biswas, B.D.; Hasan, M.S.; Kamalasadan, S. Decentralized distributed convex optimal power flow model for power distribution system based on alternating direction method of multipliers. IEEE Trans. Ind. Appl. 2023, 59, 627–640. [Google Scholar] [CrossRef]
- Zhang, D.; Miao, S.; Yang, W.; Tu, Q. Harmonic optimal power flow considering harmonic coupling factors. In Proceedings of the 2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28–30 May 2021; pp. 1–6. [Google Scholar]
- Wang, C.; Wei, W.; Wang, J.; Bai, L.; Liang, Y.; Bi, T. Convex optimization based distributed optimal gas-power flow calculation. IEEE Trans. Sustain. Energy 2018, 9, 1145–1156. [Google Scholar] [CrossRef]
- Korompili, A.; Pandis, P.; Monti, A. Distributed OPF algorithm for system-level control of active multi-terminal DC distribution grids. IEEE Access 2020, 8, 136638–136654. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Q.; Li, J.; Peng, Y. Research on reactive power optimization configuration of distribution network based on small hydroelectric generating units. In Proceedings of the 2022 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 24–26 June 2022; pp. 534–539. [Google Scholar]
- Keshani, A.; Rafiei, A.; Mazaheri, H.; Pourghaderi, M. Optimal allocation and utilization of battery energy storage systems in electric power distribution network for peak shaving and loss reduction: A case study in Iran. In Proceedings of the CIRED Porto Workshop 2022: E-Mobility and Power Distribution Systems, Porto, Portugal, 2–3 June 2022; Volume 2022, pp. 279–283. [Google Scholar]
- Guo, Z.; Wei, W.; Chen, L.; Dong, Z.; Mei, S. Parametric distribution optimal power flow with variable renewable generation. IEEE Trans. Power Syst. 2022, 37, 1831–1841. [Google Scholar] [CrossRef]
- Biswas, B.D.; Kamalasadan, S. Semidefinite program based optimal power flow formulation with voltage regulators in multiphase distribution networks. In Proceedings of the 2022 IEEE Power & Energy Society General Meeting (PESGM), Denver, CO, USA, 17–21 July 2022; pp. 1–5. [Google Scholar]
- Chowdhury, M.M.-U.-T.; Kamalasadan, S. An angle included optimal power flow (OPF) model for power distribution network using second order cone programming (SOCP). In Proceedings of the 2020 IEEE Industry Applications Society Annual Meeting, Online, 10–16 October 2020; pp. 1–7. [Google Scholar]
- Liu, Y.; Li, J.; Wu, L.; Ortmeyer, T. Chordal relaxation based acopf for unbalanced distribution systems with ders and voltage regulation devices. IEEE Trans. Power Syst. 2018, 33, 970–984. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Wu, L. Coordinated optimal network reconfiguration and voltage regulator/der control for unbalanced distribution systems. IEEE Trans. Smart Grid 2019, 10, 2912–2922. [Google Scholar] [CrossRef]
- Usman, M.; Cervi, A.; Coppo, M.; Bignucolo, F.; Turri, R. Cheap conic OPF models for low-voltage active distribution networks. IEEE Access 2020, 8, 99691–99708. [Google Scholar] [CrossRef]
- Fan, Y.; Feng, L.; Li, G. Dynamic optimal power flow in distribution networks with wind/pv/storage based on second-order cone programming. In Proceedings of the 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 4–7 June 2020; pp. 1136–1142. [Google Scholar]
- Jin, Y.; Moduo, Y.; Zong, M.; Duan, R.; Lu, C. Research on optimal power flow of active distribution network based on soft open point. In Proceedings of the 11th International Conference on Renewable Power Generation—Meeting Net Zero Carbon (RPG 2022), Shanghai, China, 14–15 October 2022; Volume 2022, pp. 60–64. [Google Scholar]
- Liang, Y.; Tang, S.; Tian, H.; Wang, Z.; Li, X.; Li, G.; Bie, Z. A chance-constrained optimal power flow model based on second-order cone. In Proceedings of the 2020 4th International Conference on HVDC (HVDC), Xi’an, China, 6–9 November 2020; pp. 1195–1200. [Google Scholar]
- Ogundairo, O.; Kamalasadan, S.; Biju, K. Integrated transmission and distribution optimal power flow simulation using linear decision approach. In Proceedings of the 2022 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, Indiea, 14–17 December 2022; pp. 1–6. [Google Scholar]
- Cai, X.; Chen, M.; Lin, K.; Lyu, J.; Zhang, S.; Cheng, H. Optimal dispatch of active distribution network for solar power accommodation based on conditional value at risk. In Proceedings of the 2021 China International Conference on Electricity Distribution (CICED), Changsha, China, 7–8 September 2022; pp. 642–646. [Google Scholar]
- Nick, M.; Cherkaoui, R.; Paolone, M. Optimal planning of distributed energy storage systems in active distribution networks embedding grid reconfiguration. IEEE Trans. Power Syst. 2018, 33, 1577–1590. [Google Scholar] [CrossRef]
- Ansari, M.; Ansari, M.; Valinejad, J.; Asrari, A. Optimal daily operation in smart grids using decentralized bi-level optimization considering unbalanced optimal power flow. In Proceedings of the 2020 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 6–7 February 2020; pp. 1–6. [Google Scholar]
- Ni, S.; Zhang, L.; Wu, G.; Shi, P.; Zheng, J. Multi-objective bi-level optimal dispatch method of active distribution network considering dynamic reconfigurations. In Proceedings of the 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 4–7 June 2020; pp. 2077–2082. [Google Scholar]
- Qiao, F.; Yuan, L. Improved energy management scheme in active distribution network with grid-tied microgrids. In Proceedings of the 2021 International Conference on Advanced Technology of Electrical Engineering and Energy (ATEEE), Qingdao, China, 24–26 December 2021; pp. 93–98. [Google Scholar]
- Arnold, D.B.; Sankur, M.D.; Negrete-Pincetic, M.; Callaway, D.S. Model-free optimal coordination of distributed energy resources for provisioning transmission-level services. IEEE Trans. Power Syst. 2018, 33, 817–828. [Google Scholar] [CrossRef]
- Lahon, R.; Gupta, C.P.; Fernandez, E. Power flow coordination among smart migrogrids: A game theory approach. In Proceedings of the 2022 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 28 February–1 March 2022; pp. 1–6. [Google Scholar]
- Sheng, H.; Wang, C.; Li, B.; Liang, J.; Yang, M.; Dong, Y. Multi-timescale active distribution network scheduling considering demand response and user comprehensive satisfaction. IEEE Trans. Ind. Appl. 2021, 57, 1995–2005. [Google Scholar] [CrossRef]
- Sinha, S.; Roshan, R.; Alam, M.A.; Banerjee, S. Optimal placement of d-statcom for reduction of power loss and improvement of voltage profile using power stability and power loss indices in a radial distribution system. In Proceedings of the 2019 IEEE 5th International Conference for Convergence in Technology (I2CT), Bombay, India, 29–31 March 2019; pp. 1–4. [Google Scholar]
- Zhang, L.; Tong, B.; Wang, Z.; Tang, W.; Shen, C. Optimal configuration of hybrid AC/DC distribution network considering the temporal power flow complementarity on lines. IEEE Trans. Smart Grid 2022, 13, 3857–3866. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, P. Optimal exploitation of mobile emergency generator and distributed energy resource for improving the resilience of incremental power distribution system under extreme grid faults. In Proceedings of the 2021 IEEE International Conference on Electrical Engineering and Mechatronics Technology (ICEEMT), Qingdao, China, 2–4 July 2021; pp. 470–476. [Google Scholar]
- Contreras, J.M.P.; Gutierrez-Alcaraz, G.; Hinojosa, V. Comparative study of optimal power flow solution using DC and generalized generation distribution factor formulations. In Proceedings of the 2018 IEEE PES Transmission & Distribution Conference and Exhibition—Latin America (T&-LA), Lima, Peru, 18–21 September 2018; pp. 1–5. [Google Scholar]
- Chen, R.; Zhou, M.; Zhang, P.; Li, X.; Fang, H.; Chen, Y. An optimal configuration of multiple measurements in distribution network based on graph theory. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 1–5. [Google Scholar]
- Chen, Q.; Hao, W.; Zeng, P. Research on optimal planning of distribution network with multi-microgrids based on the improved minimum spanning tree algorithm. In Proceedings of the 2022 Asian Conference on Frontiers of Power and Energy (ACFPE), Chengdu, China, 21–23 October 2022; pp. 7–12. [Google Scholar]
- Sadnan, R.; Dubey, A. Distributed optimization using reduced network equivalents for radial power distribution systems. IEEE Trans. Power Syst. 2021, 36, 3645–3656. [Google Scholar] [CrossRef]
- Gray, N.; Sadnan, R.; Bose, A.; Dubey, A. Effects of communication network topology on distributed optimal power flow for radial distribution networks. In Proceedings of the 2021 North American Power Symposium (NAPS), College Station, TX, USA, 14–16 November 2021; pp. 1–6. [Google Scholar]
- Moloi, K.; Hamam, Y.; Jordaan, J.A. Optimal location of dgs into the power distribution grid for voltage and power improvement. In Proceedings of the 2020 IEEE PES/IAS PowerAfrica, Online, 25–28 August 2020; pp. 1–5. [Google Scholar]
- Komathi, C.; Durga Devi, S.; Thirupura Sundari, K.; Sahithya, T. Smart power distribution system for residential and industrial applications. In Proceedings of the 2020 International Conference on Power, Energy, Control and Transmission Systems (ICPECTS), Chennai, India, 10–11 December 2020; pp. 1–4. [Google Scholar]
- Wang, Y.; Ge, X.; Dai, H.; Wang, G.; Wang, F. Optimal dispatching strategy for virtual power plants based on distributed optimization considering network constraints. In Proceedings of the 2022 IEEE IAS Global Conference on Emerging Technologies (GlobConET), Arad, Romania, 20–22 May 2022; pp. 869–874. [Google Scholar]
- Hanif, S.; Alam, M.J.E.; Bhatti, B. A modular optimal power flow method for integrating new technologies in distribution grids. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar]
- Chen, L.; Lu, Y.; Wang, L.; Du, J.; Xu, C.; Sun, W.; Song, X. Optimal power flow of distribution network considering comprehensive flexibility resources. In Proceedings of the 2022 China International Conference on Electricity Distribution (CICED), Changsha, China, 7–8 September 2022; pp. 643–648. [Google Scholar]
- Chai, Y.; Liu, Y.; Bai, L.; Wang, C.; Guo, L.; Wang, Z.; Xue, Y. Hierarchical Distributed Optimal Power Flow of HV and MV Distribution Networks with Continuous and Discrete Devices. IEEE Trans. Power Syst. 2023, 38, 1009–1021. [Google Scholar] [CrossRef]
- Palaniappan, R.; Molodchyk, O.; Rehtanz, C. Hardware implementation of an optimal power flow algorithm in a distribution network with decentralised measurements. In Proceedings of the CIRED 2020 Berlin Workshop (CIRED 2020), Berlin, Germany, 22–23 September 2020; Volume 2020, pp. 580–583. [Google Scholar]
- Xiangyu, Z.; Jing, L.; Yao, M.; Wenxiu, D.; Hedong, Z. Optimal control and configuration of energy storage devices in regional distribution network with renewable energy sources. In Proceedings of the 2022 IEEE 2nd International Conference on Digital Twins and Parallel Intelligence (DTPI), Beijing, China, 26 October–13 November 2022; pp. 1–5. [Google Scholar]
- Ma, X.; Li, Z.; Cui, J.; Lv, L.; Chen, Y. Optimal power flow algorithm for large-scale integrated transmission and distribution networks. In Proceedings of the 2021 International Conference on Power System Technology (POWERCON), Online, 8–9 December 2021; pp. 2–7. [Google Scholar]
- Blasi, T.M.; Fernandes, T.S.P.; Aoki, A.R.; Tabarro, F.H. Multiperiod optimum power flow for active distribution networks with provisioning of ancillary services. IEEE Access 2021, 9, 110371–110395. [Google Scholar] [CrossRef]
- Yan, J.; Huang, L.; Ying, F.; Wang, Q.; Liu, Y. Topology adjustment and optimal flow power based power control for offshore wind power. In Proceedings of the 2021 11th International Conference on Power and Energy Systems (ICPES), Shanghai, China, 18–20 December 2021; pp. 696–700. [Google Scholar]
- Shaheen, A.M.; Elattar, E.E.; El-Sehiemy, R.A.; Elsayed, A.M. An improved sunflower optimization algorithm-based monte carlo simulation for efficiency improvement of radial distribution systems considering wind power uncertainty. IEEE Access 2021, 9, 2332–2344. [Google Scholar] [CrossRef]
- Shaheen, M.A.M.; Hasanien, H.M.; Mekhamer, S.F.; Talaat, H.E.A. Optimal power flow of power systems including distributed generation units using sunflower optimization algorithm. IEEE Access 2019, 7, 109289–109300. [Google Scholar] [CrossRef]
- Mendoza, G.E.; Vacas, V.M.; Ferreira, N.R. Optimal capacitor allocation and sizing in distribution networks using particle swarm optimization algorithm. In Proceedings of the 2018 Workshop on Communication Networks and Power Systems (WCNPS), Brasilia, Brazil, 7–9 November 2018; pp. 1–5. [Google Scholar]
- Liu, B.; Shi, L.; Yao, Z. Multi-objective optimal reactive power dispatch for distribution network considering pv generation uncertainty. In Proceedings of the 10th Renewable Power Generation Conference (RPG 2021), Online, 14–15 October 2021; Volume 2021, pp. 503–509. [Google Scholar]
- Gu, X.; Xu, X.; Yu, Z.; Huang, S.; Lu, B. Power flow optimization of intelligent distribution network with distributed energy resources. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 3452–3457. [Google Scholar]
- Tatipally, S.; Ankeshwarapu, S.; Maheswarapu, S. Swarm intelligence methods for optimal network reconfiguration of distribution system. In Proceedings of the 2022 IEEE International Power and Renewable Energy Conference (IPRECON), Kollam, India, 16–18 December 2022; pp. 1–6. [Google Scholar]
- Ni, S.; Zheng, J. Generator-grid-load-storage coordinated optimal dispatch considering CO2 emission in active distribution network. In Proceedings of the 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 22–24 October 2021; pp. 1838–1843. [Google Scholar]
- Sidea, D.O.; Picioroaga, I.I.; Tudose, A.M.; Bulac, C.; Tristiu, I. Multi-objective particle swarm optimization applied on the optimal reactive power dispatch in electrical distribution systems. In Proceedings of the 2020 International Conference and Exposition on Electrical and Power Engineering (EPE), Iaşi, Romania, 22–23 October 2020; pp. 413–418. [Google Scholar]
- Zhou, S.; Zhou, Y.; Wei, Y.; Kang, L.; Zhang, X. Multi-objective optimal control for distribution network loop-closing operation using pe-mopso algorithm. In Proceedings of the 2021 6th International Conference on Smart Grid and Electrical Automation (ICSGEA), Kunming, China, 29–30 May 2021; pp. 387–391. [Google Scholar]
- Meng, Q.; Lei, D.; Wang, L.; Shi, Y.; Ma, Z. Optimal control of reactive power and voltage in active distribution network based on source-grid-load interaction. In Proceedings of the 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 4–7 June 2020; pp. 376–380. [Google Scholar]
- Han, C.; Song, S.; Yoo, Y.; Lee, J.; Jang, G.; Yoon, M. Optimal operation of soft-open points for high penetrated distributed generations on distribution networks. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019—ECCE Asia), Busan, Republic of Korea, 27–30 May 2019; pp. 806–812. [Google Scholar]
- Sellami, R.; Neji, R.; Bouktir, T. Enhancing radial distribution network performance by optimal reconfiguration with PSO algorithm. In Proceedings of the 2019 16th International Multi-Conference on Systems, Signals & Devices (SSD), Istanbul, Turkey, 21–24 March 2019; pp. 180–186. [Google Scholar]
- Shaheen, M.A.M.; Mekhamer, S.F.; Hasanien, H.M.; Talaat, H.E.A. Optimal power flow of power systems using hybrid firefly and particle swarm optimization technique. In Proceedings of the 2019 21st International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 17–19 December 2019; pp. 232–237. [Google Scholar]
- Kumar, C.; Manojkumar, R.; Ganguly, S.; Liserre, M. Power loss minimization in smart transformer based meshed hybrid distribution network. In Proceedings of the IECON 2020 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 1670–1675. [Google Scholar]
- Gopu, P.; Naaz, S.; Aiman, K. Optimal placement of distributed generation using genetic algorithm. In Proceedings of the 2021 International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 19–20 February 2021; pp. 1–6. [Google Scholar]
- Amraj, N.; Boonrach, N.; Bhumkittipich, K. Optimal Allocation and Sizing of Photovoltaic-Battery Energy Storage Systems in Distribution Network for Power Loss Minimization. In Proceedings of the 2021 International Conference on Power, Energy and Innovations (ICPEI), Nakhon Ratchasime, Thailand, 20–21 October 2021; pp. 33–36. [Google Scholar]
- Guerrero, S.; Barrera-Singaña, C.; Valenzuela, A.; Rojas, S.Y.; Muñoz, J.M.; Jaramillo, M. Optimal location of battery storage systems to minimize losses in the distribution system considering power quality indicators. In Proceedings of the 2023 IEEE IAS Global Conference on Renewable Energy and Hydrogen Technologies (GlobConHT), Male, Maldives, 11–12 March 2023; pp. 1–6. [Google Scholar]
- Gautam, M.; Bhusal, N.; Benidris, M.; Louis, S.J. A spanning tree-based genetic algorithm for distribution network reconfiguration. In Proceedings of the 2020 IEEE Industry Applications Society Annual Meeting, Detroit, MI, USA, 10–16 October 2020; pp. 1–6. [Google Scholar]
- Sun, L.; Zhuo, F.; Yang, Z.; Yi, H.; Yin, X. Optimal voltage/var control of PV inverters in distribution network based on genetic algorithm. In Proceedings of the 2021 IEEE 1st International Power Electronics and Application Symposium (PEAS), Shanghai, China, 12–15 November 2021; pp. 1–5. [Google Scholar]
- Haowen, L.; Yi, L.; Xiaochun, X.; Dong, L.; Yuhui, H.; Xiaofei, W. Optimal configuration of high penetration rate DGS considering bi-directional power flow. In Proceedings of the 2018 China International Conference on Electricity Distribution (CICED), Tianjin, China, 17–19 September 2018; pp. 2307–2312. [Google Scholar]
- Liu, J.; Lu, Y.; Lv, G.; Du, J. Research on access point and capacity optimization of distributed generation in distribution power grid. In Proceedings of the 2021 China International Conference on Electricity Distribution (CICED), Shanghai, China, 7–9 April 2021; pp. 718–721. [Google Scholar]
- Mujezinović, A.; Turković, N.; Dautbašić, N.; Dedović, M.M.; Turković, I. Use of integer genetic algorithm for optimal allocation and sizing of the shunt capacitor banks in the radial distribution networks. In Proceedings of the 2019 18th International Symposium INFOTEH-JAHORINA (INFOTEH), East Sarajevo, Bosnia and Herzegovina, 20–22 March 2019; pp. 1–6. [Google Scholar]
- Ma, C.; Duan, Q.; Wang, H.; Mu, Y. Multi-objective dynamic network reconstruction method for active distribution network including distributed generation and electric vehicles. In Proceedings of the 2022 5th International Conference on Energy, Electrical and Power Engineering (CEEPE), Chongqing, China, 22–24 April 2022; pp. 612–617. [Google Scholar]
- Yin, M.; Li, K. Optimal allocation of distributed generations with SOP in distribution systems. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar]
- El-Ela, A.A.A.; El-Sehiemy, R.A.; Abbas, A.S. Optimal placement and sizing of distributed generation and capacitor banks in distribution systems using water cycle algorithm. IEEE Syst. J. 2018, 12, 3629–3636. [Google Scholar] [CrossRef]
- Prasetyo, T.; Sarjiya, S.; Putranto, L.M. Optimal sizing and siting of PV-based distributed generation for losses minimization of distribution using flower pollination algorithm. In Proceedings of the 2019 International Conference on Information and Communications Technology (ICOIACT), Yogyakarta, Indonesia, 24–25 July 2019; pp. 779–783. [Google Scholar]
- Kandpal, B.; Kumari, D.; Kumar, J.; Verma, A. Optimal PV placement in village distribution network considering loss minimization and unbalance. In Proceedings of the 2019 International Conference on Computing, Power and Communication Technologies (GUCON), New Delhi, India, 27–28 September 2019; pp. 566–571. [Google Scholar]
- Gupta, S.; Rawat, M.S.; Gupta, T.N. Optimal placement and sizing of various c-rate type of bess for minimizing reverse power flow in radial distribution network. In Proceedings of the 2022 2nd International Conference on Emerging Frontiers in Electrical and Electronic Technologies (ICEFEET), Patna, India, 24–25 June 2022; pp. 1–6. [Google Scholar]
- Zhou, J.; Wang, B.; Wu, J.; Lu, Y.; Zheng, M.; Wu, Z.; Ma, K. Research on multi-objective optimal dispatching and low voltage of distributed generation in rural distribution network. In Proceedings of the 2021 IEEE 4th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 18–20 June 2021; Volume 4, pp. 1131–1136. [Google Scholar]
- Venkatasivanagaraju, S.; Rao, M. Loss minimization and optimal power flow for long term and short-term real-time forecasting system using cuckoo search algorithm. In Proceedings of the 2022 Second International Conference on Artificial Intelligence and Smart Energy (ICAIS), Coimbatore, India, 23–25 February 2022; pp. 805–810. [Google Scholar]
- Liu, Z.; Liang, H. Optimal scheduling of distribution network based on improved whale algorithm. In Proceedings of the 2022 IEEE 5th International Conference on Automation, Electronics and Electrical Engineering (AUTEEE), Shenyang, China, 18–20 November 2022; pp. 987–990. [Google Scholar]
- Baimakhanov, O.; Saukhimov, A.; Ceylan, O. Whale optimization algorithm based optimal operation of power distribution systems. In Proceedings of the 2022 57th International Universities Power Engineering Conference (UPEC), Istanbul, Turkey, 30 August–2 September 2022; pp. 1–6. [Google Scholar]
- Anantasate, S.; Bhasaputra, P. A multi-objective bees algorithm for multi-objective optimal power flow problem. In Proceedings of the 8th Electrical Engineering/ Electronics, Computer, Telecommunications and Information Technology (ECTI) Association of Thailand—Conference 2011, Khon Kaen, Thailand, 17–19 May 2011; pp. 852–856. [Google Scholar]
- Yuanyuan, S.; Bo, W.; Peng, W.; Xiuguang, L. Optimization scheduling method of power grid energy-saving based on fuzzy decision. In Proceedings of the 2021 6th International Symposium on Computer and Information Processing Technology (ISCIPT), Changsha, China, 11–13 June 2021; pp. 321–324. [Google Scholar]
- Khatri, P.; Thapa, K.B.; Khanal, A. Artificial bee colony algorithm based dg units siting and sizing based on loadability improvement of distribution feeder of nepal. In Proceedings of the 2022 International Conference on Electrical, Computer and Energy Technologies (ICECET), Prague, Czech Republic, 20–22 July 2022; pp. 1–6. [Google Scholar]
- Sidea, D.O.; Picioroagă, I.I.; Tudose, A.M.; Podar, C.; Anton, N.; Bulac, C. Optimal reactive power dispatch considering load variation in distribution networks using an improved sine-cosine algorithm. In Proceedings of the 2022 International Conference and Exposition on Electrical And Power Engineering (EPE), Iasi, Romania, 20–22 October 2022; pp. 499–504. [Google Scholar]
- Mahmoud, B.G.; Aleem, S.H.A.; Sayed, M. Sine-cosine algorithm for optimal capacitor allocation in distribution systems operating under non-sinusoidal conditions. In Proceedings of the 2021 International Conference on Electrical, Communication, and Computer Engineering (ICECCE), Kuala Lumpur, Malaysia, 12–13 June 2021; pp. 1–6. [Google Scholar]
- Fu, X.; Guo, Q.; Sun, H. Statistical machine learning model for stochastic optimal planning of distribution networks considering a dynamic correlation and dimension reduction. IEEE Trans. Smart Grid 2020, 11, 2904–2917. [Google Scholar] [CrossRef]
- Vongvilasack, P.; Premrudeepreechacharn, S.; Ngamsanroaj, K. The application of machine learning for the voltage and reactive power control in power distribution network. In Proceedings of the 2022 19th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Prachuap Khiri Khan, Thailand, 24–27 May 2022; pp. 1–6. [Google Scholar]
- Bramm, A.; Eroshenko, S. Optimal reconfiguration of distribution network with solar power plants. In Proceedings of the 2021 Ural-Siberian Smart Energy Conference (USSEC), Novosibirsk, Russia, 13–15 November 2021; pp. 1–5. [Google Scholar]
- Simonovska, A.; Bassi, V.; Givisiez, A.G.; Ochoa, L.F.; Alpcan, T. An electrical model-free optimal power flow for pv-rich low voltage distribution networks. In Proceedings of the 2022 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Novi Sad, Serbia, 10–12 October 2022; pp. 1–5. [Google Scholar]
- Zeng, P.; Li, H.; He, H.; Li, S. Dynamic energy management of a microgrid using approximate dynamic programming and deep recurrent neural network learning. IEEE Trans. Smart Grid 2019, 10, 4435–4445. [Google Scholar] [CrossRef]
- Elende, A.A.; GebreMichael, M.G. Distribution network optimization by optimal sizing and placement of d-statcom using teaching and learning based optimization algorithm. In Proceedings of the 2021 IEEE Southern Power Electronics Conference (SPEC), Kigali, Rwanda, 6–9 December 2021; pp. 1–8. [Google Scholar]
- Mahto, D.K.; Saini, V.K.; Mathur, A.; Kumar, R.; Saxena, A. Data driven approach for optimal power flow in distribution network. In Proceedings of the 2021 5th International Conference on Information Systems and Computer Networks (ISCON), Mathura, Uttar Pradesh, India, 22–23 October 2021; pp. 1–6. [Google Scholar]
- Mahto, D.K.; Saini, V.K.; Mathur, A.; Kumar, R.; Verma, S. MPGCN-OPF: A message passing graph convolution approach for optimal power flow for distribution network. In Proceedings of the 2022 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 14–17 December 2022; pp. 1–6. [Google Scholar]
- Li, P.; Wu, W.; Wang, X.; Xu, B. A data-driven linear optimal power flow model for distribution networks. IEEE Trans. Power Syst. 2023, 38, 956–959. [Google Scholar] [CrossRef]
- Cao, D.; Hu, W.; Xu, X.; Huang, Q.; Chen, Z. Double deep q-learning based approach for power flow optimization in distribution networks. In Proceedings of the 2020 Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 29–31 May 2020; pp. 514–518. [Google Scholar]
- Gao, Z.; Zheng, Z.; Wu, J.; Qi, L.; Li, W.; Yang, Y. Reactive power optimization of distribution network based on deep reinforcement learning and multi agent system. In Proceedings of the 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 22–24 October 2021; pp. 1052–1057. [Google Scholar]
- Li, W.; Huang, W.; Zhu, T.; Wu, M.; Yan, Z. Deep reinforcement learning based continuous volt-var optimization in power distribution systems with renewable energy resources. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23–25 December 2021; pp. 682–686. [Google Scholar]
- Hu, D.; Peng, Y.; Yang, J.; Deng, Q.; Cai, T. Deep reinforcement learning based coordinated voltage control in smart distribution network. In Proceedings of the 2021 International Conference on Power System Technology (POWERCON), Haikou, China, 8–9 December 2021; pp. 1030–1034. [Google Scholar]
- Liu, X.; Fan, B.; Tian, J. Deep reinforcement learning based approach for dynamic optimal power flow in active distribution network. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 1951–1956. [Google Scholar]
- Tahir, Y.; Khan, M.F.N.; Sajjad, I.A.; Martirano, L. Optimal control of active distribution network using deep reinforcement learning. In Proceedings of the 2022 IEEE International Conference on Environment and Electrical Engineering and 2022 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Prague, Czech Republic, 28 June–1 July 2022; pp. 1–6. [Google Scholar]
- Duan, C.; Fang, W.; Jiang, L.; Yao, L.; Liu, J. Distributionally robust chance-constrained approximate ac-opf with wasserstein metric. IEEE Trans. Power Syst. 2018, 33, 4924–4936. [Google Scholar] [CrossRef]
- Ivic, D.; Stefanov, P. Control strategy for dc soft open points in large-scale distribution networks with distributed generators. CSEE J. Power Energy Syst. 2022, 8, 732–742. [Google Scholar]
- Karagiannopoulos, S.; Aristidou, P.; Hug, G. Data-driven local control design for active distribution grids using off-line optimal power flow and machine learning techniques. IEEE Trans. Smart Grid 2019, 10, 6461–6471. [Google Scholar] [CrossRef]
- Xu, G.; Qiao, C.; Wang, X.; Wu, H.; Yang, S.; Ma, L.; Zhang, Q.; Pang, G. A multi-layer optimized configuration method for energy storage device and compensation device on long-chain power distribution line. In Proceedings of the 2021 8th International Conference on Electrical and Electronics Engineering (ICEEE), Antalya, Turkey, 9–11 April 2021; pp. 150–154. [Google Scholar]
- Guo, X.; Chen, Q.; Liang, W.; Wang, S.; Wang, Y.; Qin, Y. Intelligent optimization algorithm of active distribution network based on load storage cooperative optimization of source network. In Proceedings of the 2021 IEEE 4th International Conference on Automation, Electronics and Electrical Engineering (AUTEEE), Shenyang, China, 19–21 November 2021; pp. 355–360. [Google Scholar]
- Liu, J.; Huang, X.; Li, Z. Multi-time scale optimal power flow strategy for medium-voltage DC power grid considering different operation modes. J. Mod. Power Syst. Clean Energy 2020, 8, 46–54. [Google Scholar] [CrossRef]
- Yang, Q.; Junqiang, W.; Leiyang, S. Optimal scheduling of distribution network considering reactive power auxiliary service in market environment. In Proceedings of the 18th International Conference on AC and DC Power Transmission (ACDC 2022), Online, 2–3 July 2022; Volume 2022, pp. 1381–1387. [Google Scholar]
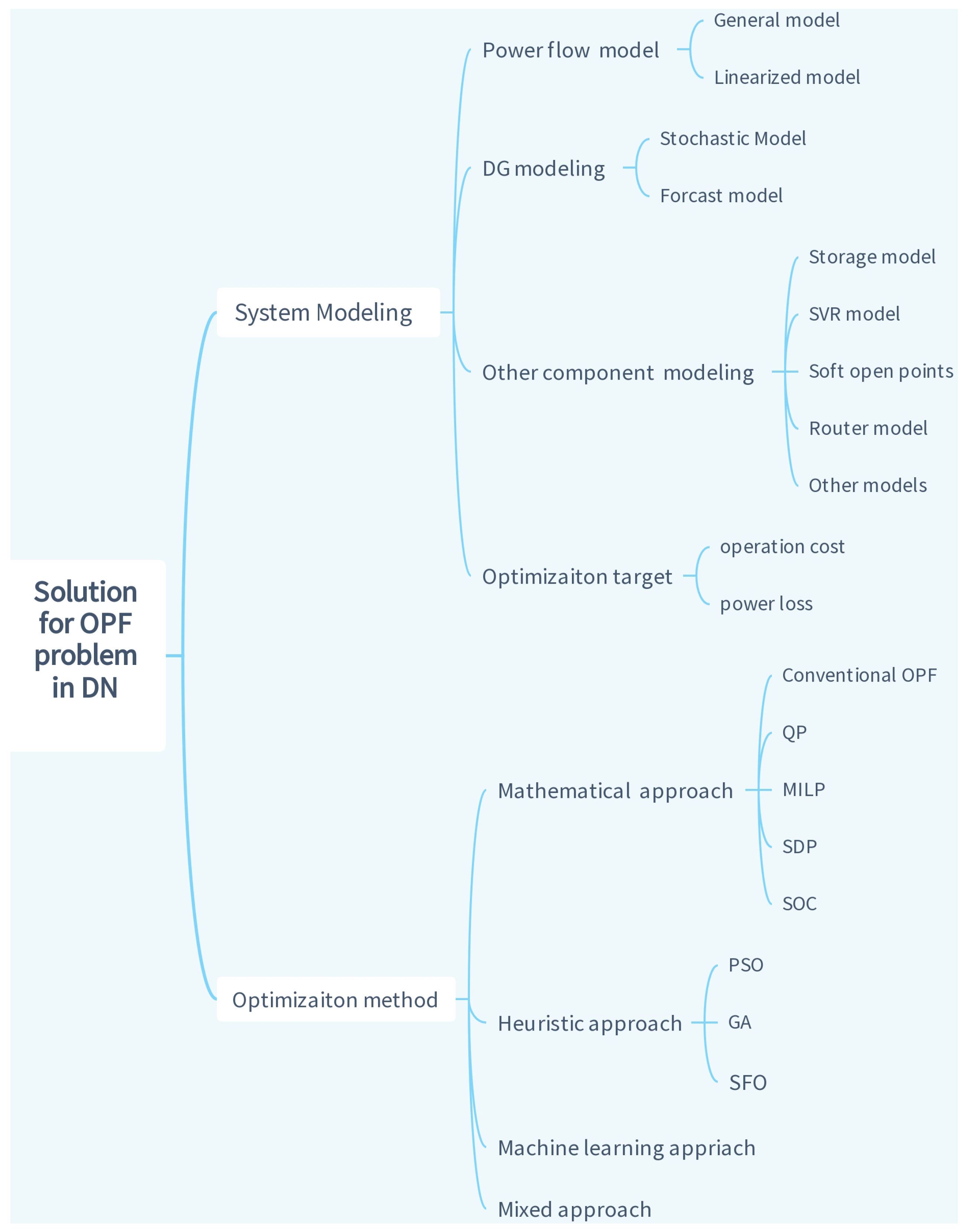


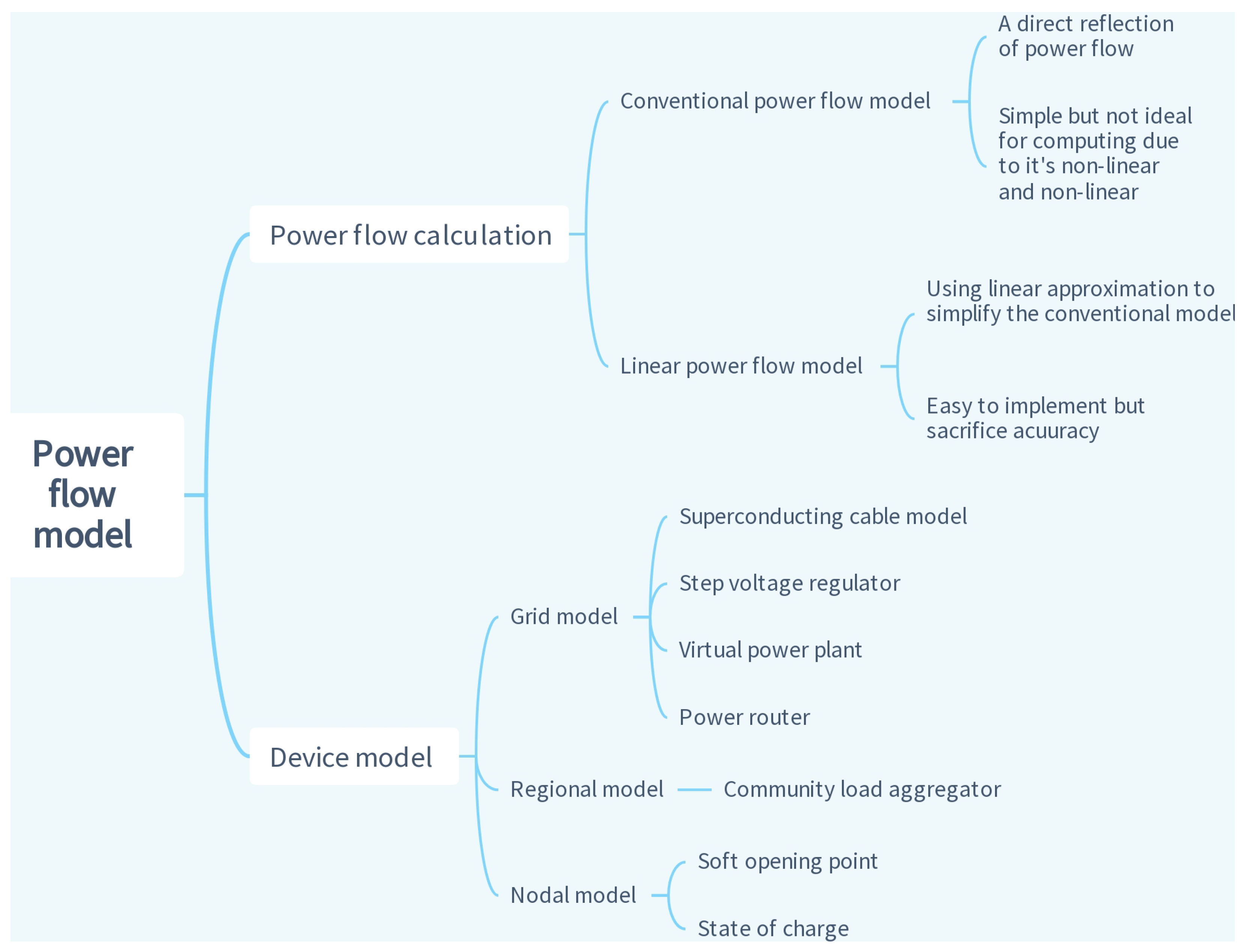
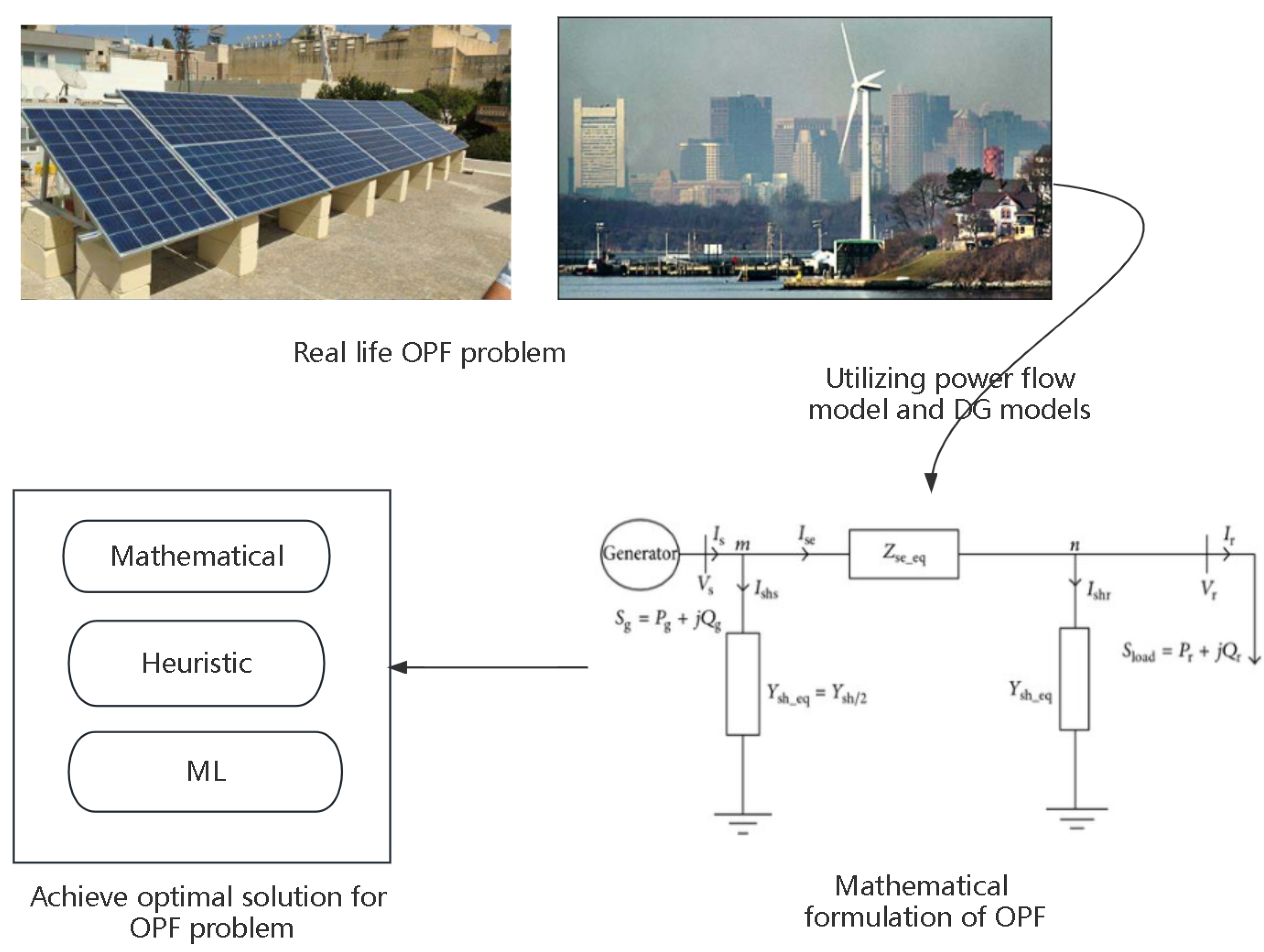
| Method | Advantages | Limitations |
|---|---|---|
| Conventional [51,52,53,54] | Simple and easy to understand/implement; Efficient computation | Can only handle linear constraints and variables; Cannot handle certain nonlinear constraints; Results may be local optima |
| MILP [30,66,67] | Handles discrete variables and logical constraints; High flexibility | Computational complexity for large-scale problems; Difficulties in solving non-convex problems |
| ADMM [41,62,63,64] | Handles structured constraints; Suitable for large-scale problems; Convergence guaranteed | Limited by sparsity; Requires proper problem decomposition; Parameter tuning required |
| QP [55,56,57,58] | Widely used; Efficient solution algorithms | Unable to handle certain nonlinear constraints; Computational complexity for large-scale problems |
| SOCP [18,73,74,75,76,77,78] | Handles some nonlinear and convex constraints; Efficient solution | Requires higher modeling requirements for the problem; Not suitable for general non-convex problems |
| SDP [22,33,68,69,70,71,72] | Capable of representing a wide range of constraints and variables; Precise convex optimization solution | Higher computational complexity; Suitable for medium-sized problems |
| Method | Advantages | Limitations |
|---|---|---|
| SFO [104,105] | Strong global optimization capability. | High computational complexity, especially for large-scale problems. Requires parameter tuning and appropriate convergence criteria. Lack of maturity compared to GA and PSO. |
| GA [117,118,119,120,121,122,123,124,125] | Widely applicable to various optimization problems. Can handle both discrete and continuous variables. Suitable for problems with multiple constraints and uncertainties. | Relatively slower convergence speed, especially for complex problems. May converge to local optima. High complexity for large-scale problems. |
| PSO [106,107,108,109,110,111,112,113,114,115,116] | Powerful global search capability. Suitable for optimization problems with constraints. Can handle high-dimensional problems. | Performance may degrade for complex problems. Requires parameter tuning and appropriate convergence criteria. May become trapped in optima when multiple exist. |
| Type | Method | # | Loss Reduced (%) | Compared to | Simulation Platform | Computation Time (s) |
|---|---|---|---|---|---|---|
| Mathematic | QP | [56] | 7.9 | Conventional OPF | MATLAB | 0.0750 |
| ADMM | [56] | - | - | MATLAB | 2.1030 | |
| MILP | [34] | 2.42 | No optimization | MATLAB | - | |
| Conventional OPF | [54] | 30.0 | CPLEX | - | ||
| Heuristic | PSO | [114] | 25.4 | - | - | |
| IPOP-CMA-ES | [127] | 62.9 | MATLAB | 24.9000 | ||
| GA | [127] | 61.6 | MATLAB | 9.1000 | ||
| PSO | [127] | 62.8 | MATLAB | 12.9000 | ||
| SCA | [139] | 25.8 | MATLAB | - | ||
| ML | DDQN | [150] | 18.4 | - | - | |
| DDPG | [154] | 64.4 | - | - | ||
| NN | [157] | 45.3 | - | - | ||
| ANN | [147] | - | - | - | 0.0095 |
| Comparison Factor | Mathematical | Heuristic | Machine Learning |
|---|---|---|---|
| Interpretability | High | Medium | Low |
| Accuracy | High | Medium-High | Medium-High |
| Scalability | Medium-High | Medium-High | High |
| Computational Complexity | High | Medium-High | Low-Medium |
| Data Requirement | Low | Low-Medium | High |
| Algorithm Tuning Requirement | High | Medium | Low-Medium |
| Robustness | High | Low-Medium | Medium-High |
| Applicability | Complex Problems | Medium-Complex Problems | Complex Problems |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Sun, Y.; Zou, Y.; Zheng, F.; Liu, S.; Zhao, B.; Wu, M.; Cui, H. Optimal Power Flow in Distribution Network: A Review on Problem Formulation and Optimization Methods. Energies 2023, 16, 5974. https://doi.org/10.3390/en16165974
Yang C, Sun Y, Zou Y, Zheng F, Liu S, Zhao B, Wu M, Cui H. Optimal Power Flow in Distribution Network: A Review on Problem Formulation and Optimization Methods. Energies. 2023; 16(16):5974. https://doi.org/10.3390/en16165974
Chicago/Turabian StyleYang, Cheng, Yupeng Sun, Yujie Zou, Fei Zheng, Shuangyu Liu, Bochao Zhao, Ming Wu, and Haoyang Cui. 2023. "Optimal Power Flow in Distribution Network: A Review on Problem Formulation and Optimization Methods" Energies 16, no. 16: 5974. https://doi.org/10.3390/en16165974
APA StyleYang, C., Sun, Y., Zou, Y., Zheng, F., Liu, S., Zhao, B., Wu, M., & Cui, H. (2023). Optimal Power Flow in Distribution Network: A Review on Problem Formulation and Optimization Methods. Energies, 16(16), 5974. https://doi.org/10.3390/en16165974