Review of Voltage Control Strategies for DC Microgrids
Abstract
:1. Introduction
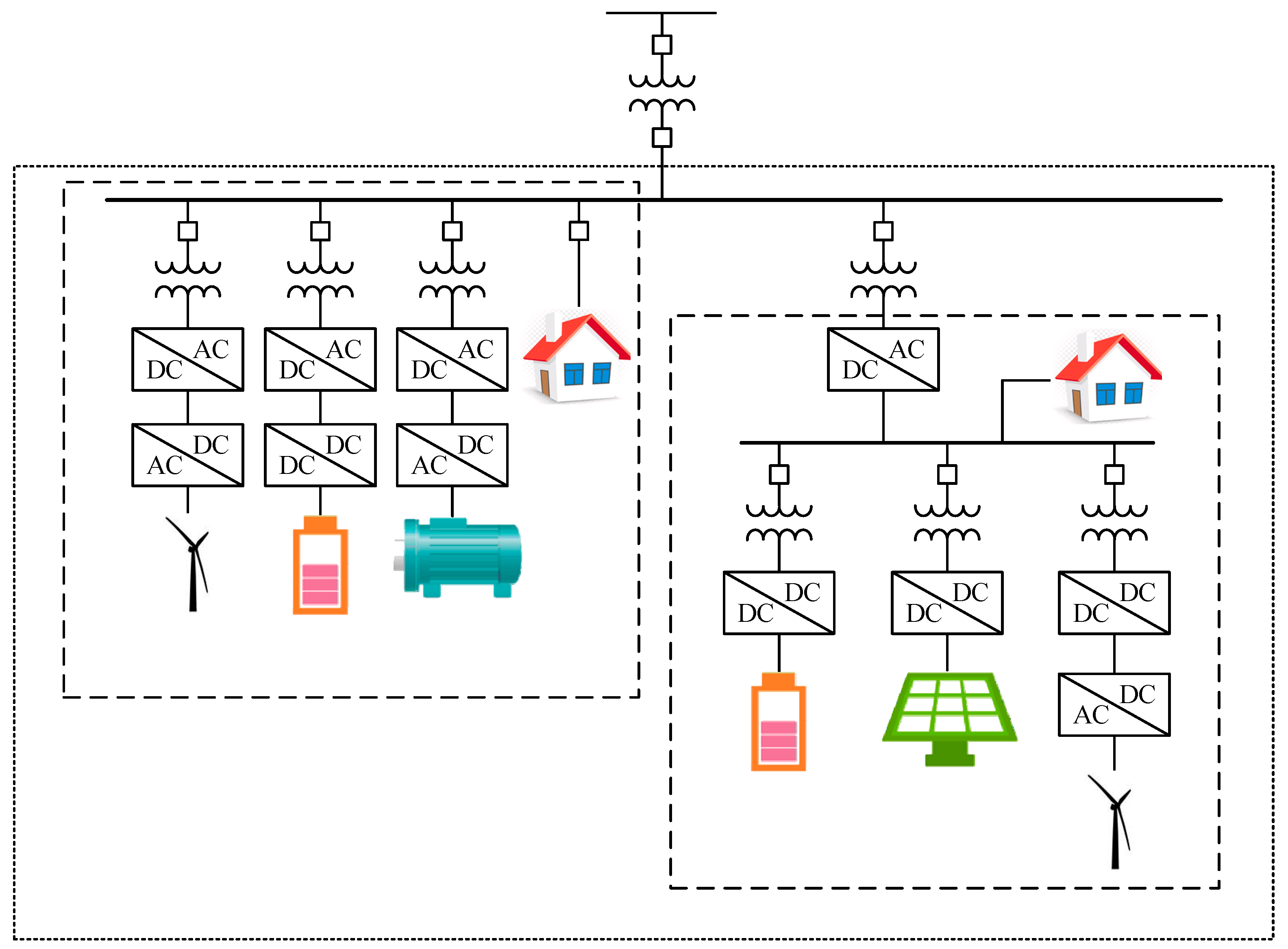
2. Basic Structure and Operation Control of MGs
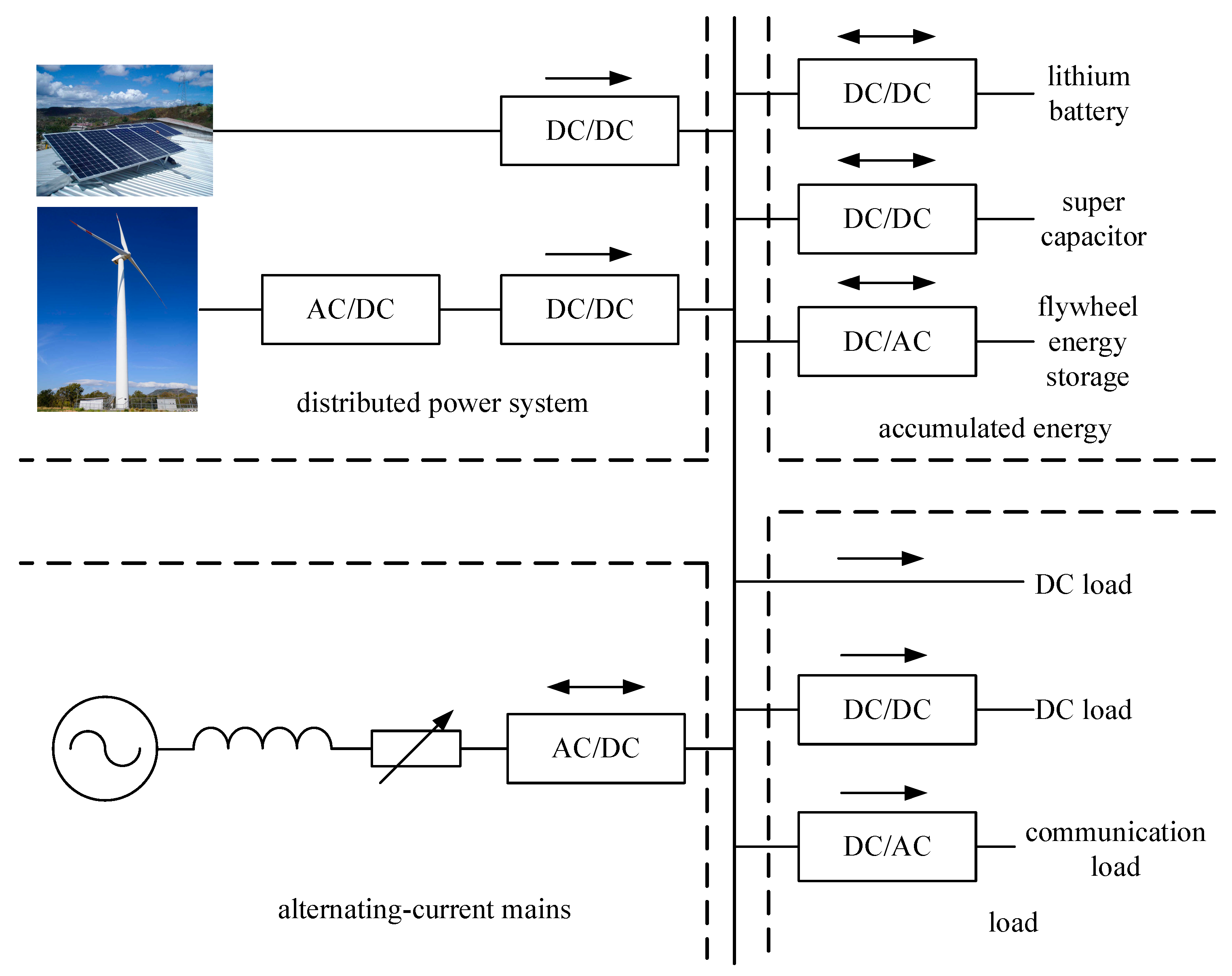
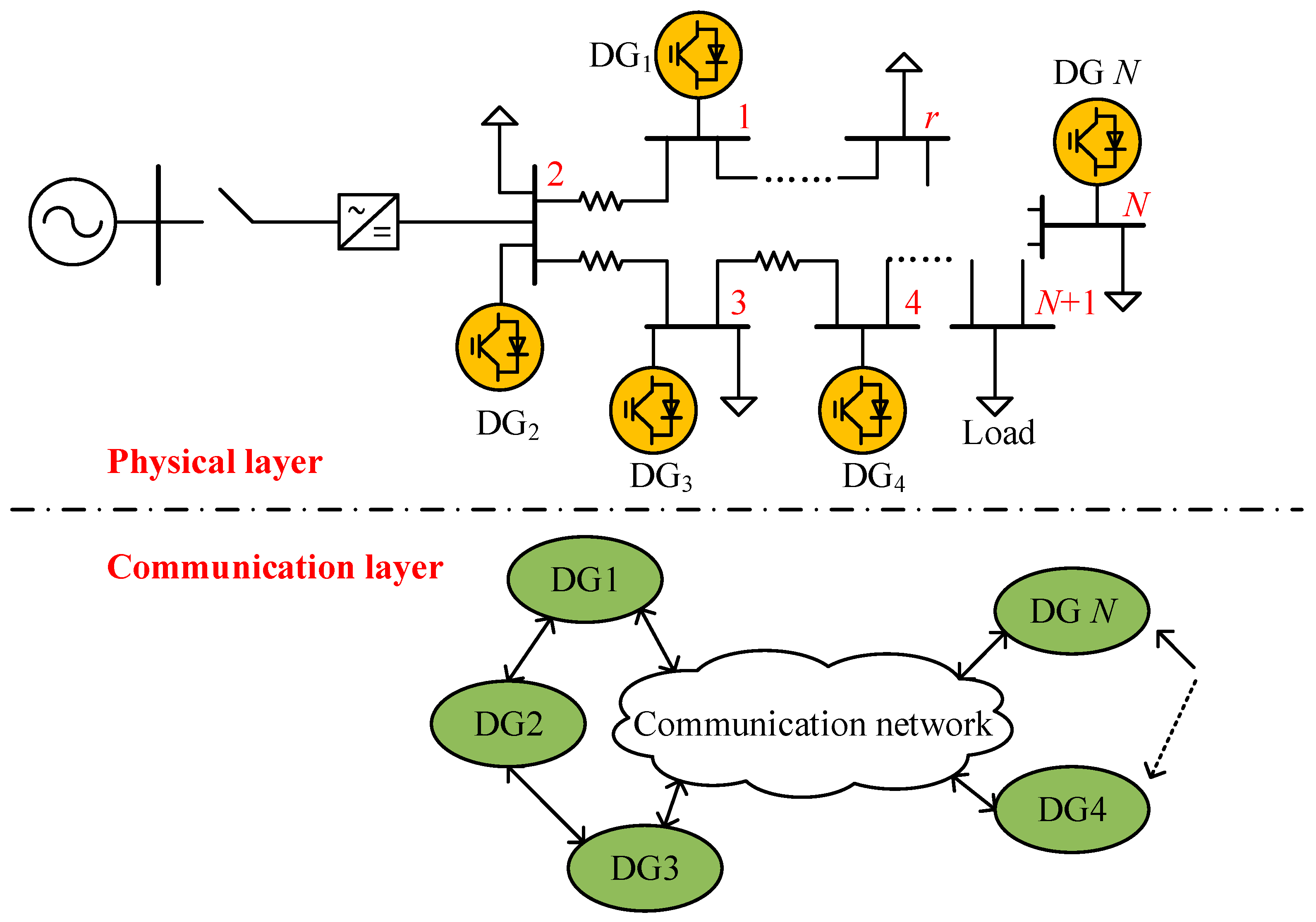
2.1. Basic Structure of MGs
2.2. Operation Control of MGs
- (1)
- Control under the grid-connected operation mode
- (2)
- Control under the island-like mode of operation
3. Research Status of Stability Control of DC MGs
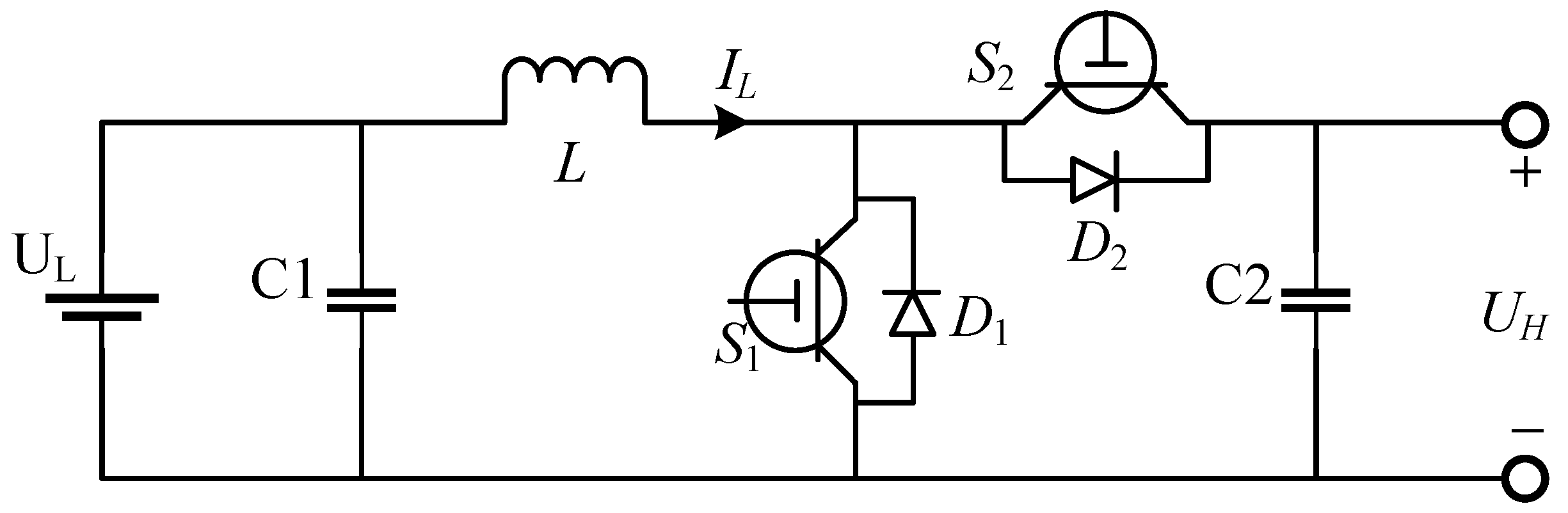
3.1. Research on Transient Control Strategy of DC MGs
3.2. Research on Stability of DC MGs
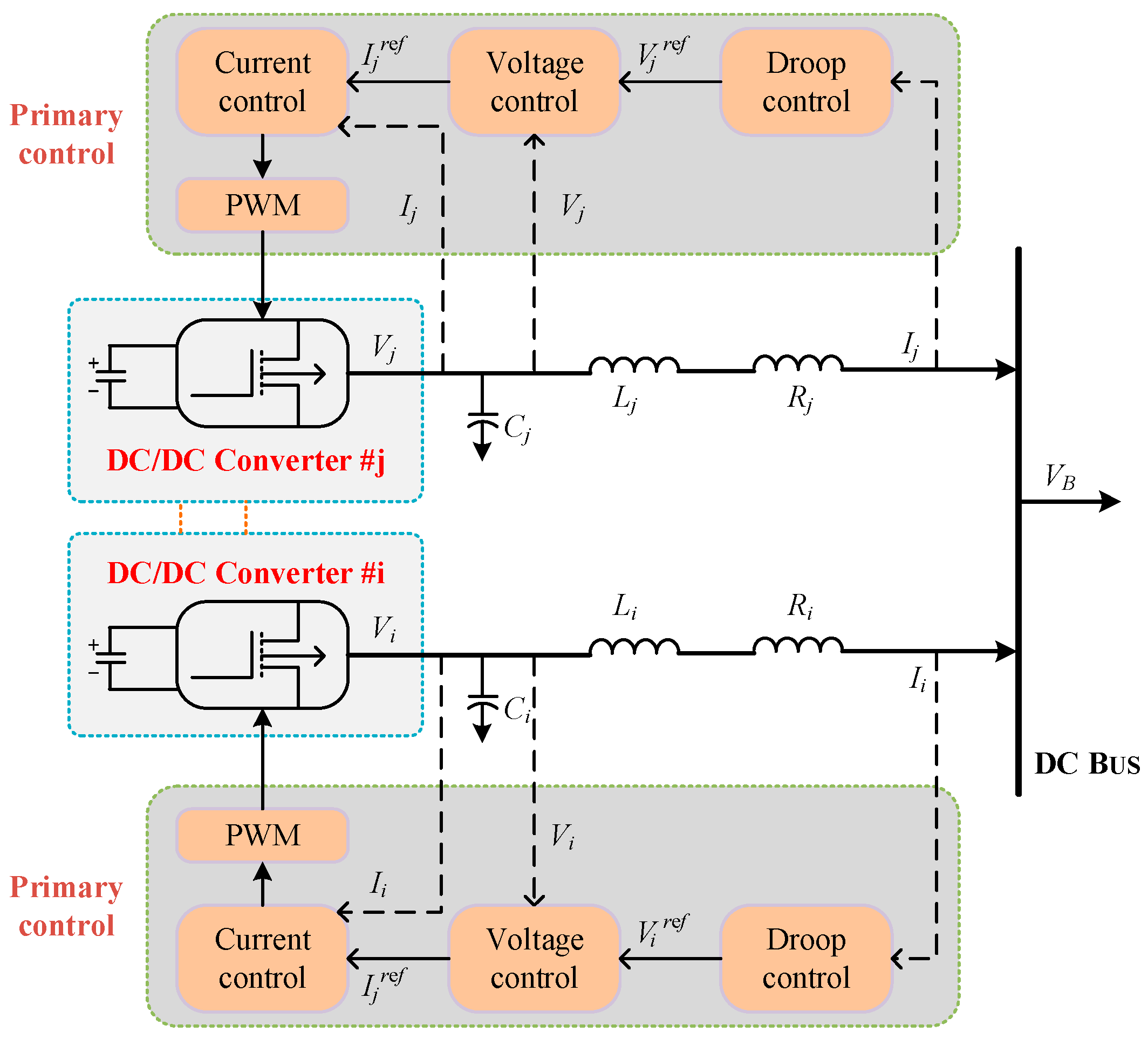
3.2.1. Small-Signal Stability Analysis
3.2.2. Large-Signal Stability Analysis
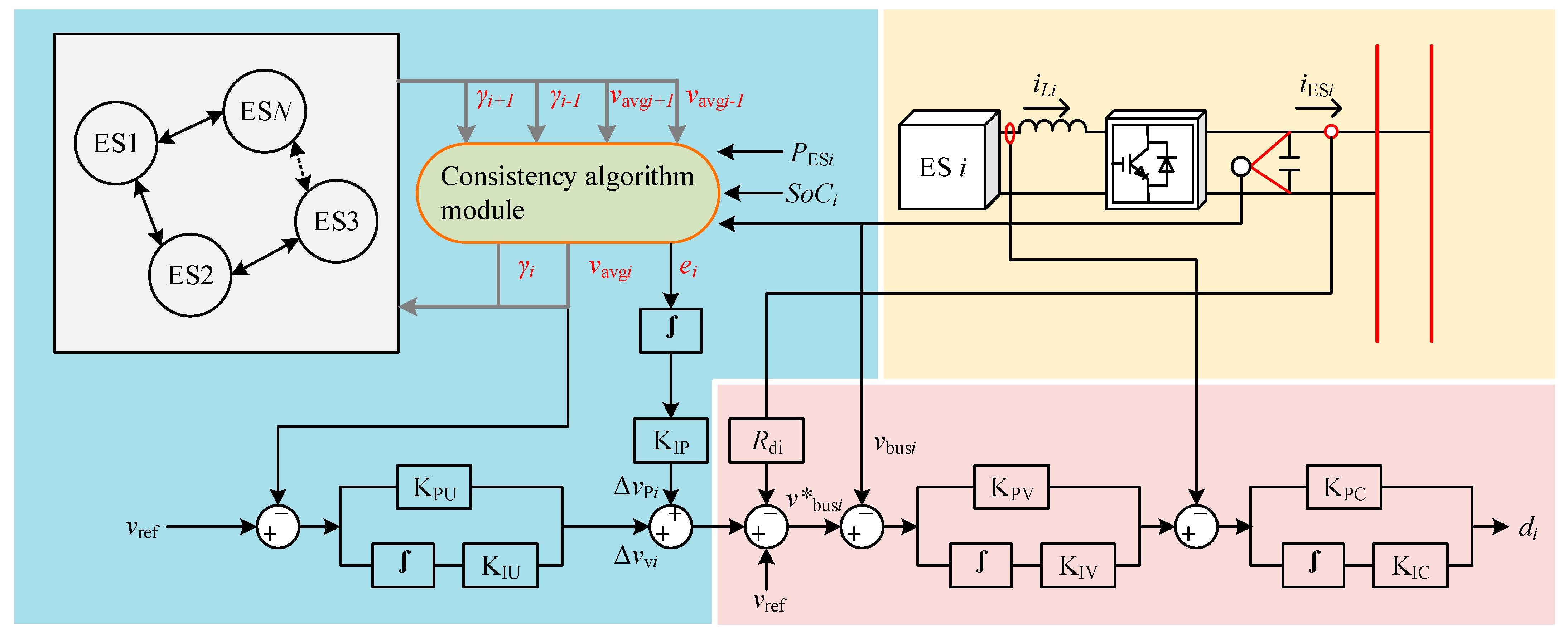
4. Application of Consistency Algorithm in DC MGs
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, Y.; Zhang, G.; Hu, W.; Huang, Q.; Chen, Z.; Blaabjerg, F. Meta-learning based voltage control strategy for emergency faults of active distribution networks. Appl. Energy 2023, 349, 121399. [Google Scholar] [CrossRef]
- Zhu, L.; Meng, X.; Wang, L.; Zhang, N.; Wang, H. Voltage Control Strategy for Low-Voltage Distribution Network with Distributed Energy Storage Participating in Regulation under Low-Carbon Background. Sustainability 2023, 15, 9943. [Google Scholar] [CrossRef]
- He, Y.; Li, L.; Qian, H.; Yao, S. Multi-layer Voltage Control Strategy for DC Microgrid without Communication. J. Phys. Conf. Ser. 2023, 2488, 012050. [Google Scholar] [CrossRef]
- Zhi, C.Y. Analysis of Voltage Control Strategies for DC Microgrid with Multiple Types of Energy Storage Systems. Electronics 2023, 12, 1661. [Google Scholar]
- Li, Z.; Zhu, X.; Ye, Q.; Tian, S.; Xiang, H. Single Loop Voltage Control Strategy Based on Model Predictive Control for NPC-UPS. J. Phys. Conf. Ser. 2023, 2418, 012045. [Google Scholar] [CrossRef]
- Lu, Y.Y.; Chen, L. Research on bus voltage control strategy of DC side of wind power grid-connected inverter. In Proceedings of the 2022 34th Chinese Control and Decision Conference (CCDC), Hefei, China, 15–17 August 2022; pp. 129–134. [Google Scholar]
- Liu, Y.; Mao, Q.; Yang, Q.; Dong, R.; Zhu, R.; Jiang, H. Research on Variable Voltage Control Strategy of Capacitor Energy Storage with High Speed On-Off Valve. pp. 91–101. 2020. Available online: https://www.researchgate.net/profile/Liu-Yudong-3/publication/357670824_Research_on_Variable_Voltage_Control_Strategy_of_Capacitor_Energy_Storage_with_High_Speed_On-Off_Valve/links/61d8f4e1b8305f7c4b2c55b5/Research-on-Variable-Voltage-Control-Strategy-of-Capacitor-Energy-Storage-with-High-Speed-On-Off-Valve.pdf (accessed on 30 October 2020).
- Engineering—Industrial Engineering. Studies from Xi’an Jiaotong University Have Provided New Data on Industrial Engineering (Dc Voltage Control Strategy of Three-terminal Medium-voltage Power Electronic Transformer-based Soft Normally Open Points). J. Eng. 2020, 67, 3684. [Google Scholar]
- Ma, J.; Ye, H.; Li, Z.; Han, P.; Lin, Z.; Shi, J. Research on Source-Network Coordination Voltage Control Strategy of Photovoltaic Power Plant Considering the Stability of Inverter Port Voltage. E3S Web Conf. 2019, 143, 359–365. [Google Scholar] [CrossRef]
- Shu, X. A New Neutral Point Voltage Control Strategy for NPC Three Level Inverters. Advanced Science and Industry Research Center. In Proceedings of the 2018 2nd International Conference on Electrical Engineering and Automation (ICEEA2018), Chengdu China, 25–26 March 2019; Advanced Science and Industry Research Center: Science and Engineering Research Center: Paris, French, 2018; pp. 23–26. [Google Scholar]
- Zhai, J.; Lin, X.; Zhang, Y. Reactive power and voltage control strategy based on dynamic and adaptive segment for DG inverter. IOP Conf. Ser. Earth Environ. Sci. 2017, 136, 70–77. [Google Scholar] [CrossRef]
- Zhou, Y. DC Voltage Control Strategy Based on Active Disturbance Rejection Control for Active Power Filter. In Proceedings of the 2017 29th Chinese Control And Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 1285–1290. [Google Scholar]
- Liu, C.-R.; Li, H.-F.; Li, G.-Y.; Wu, M.-H. An Additional DC Voltage Control Strategy for Modular Multilevel Converter. In Proceedings of the 2016 2nd International Conference on Sustainable Energy and Environmental Engineering (SEEE 2016), Xiamen, China, 18–19 December 2016; DEStech Publications: Lancaster, PA, USA, 2016; pp. 73–81. [Google Scholar]
- Yao, X.; Lu, Y.; Jin, Z.; Zhang, B. A Novel Neutral Point Voltage Control Strategy for Three-Level NPC APF Based on SVPWM. MATEC Web Conf. 2015, 22, 168–173. [Google Scholar] [CrossRef]
- He, Z. Safety Voltage Control Strategy for High Voltage Ride-Through of Doubly Fed Induction Generator (DFIG). In Proceedings of the 2015 International Power, Electronics and Materials Engineering Conference, Dalian, China, 16–17 May 2015; Atlantis Press: Paris, French, 2015; pp. 580–584. [Google Scholar]
- Zhao, J.; Hu, X.; Lv, X.; Zhang, X. A coordinated voltage control strategy for a Doubly-Fed Induction Generator (DFIG) wind farm system, IFSA. In Electronics and Electrical Engineering: Proceedings of the 2014 Asia-Pacific Electronics and Electrical Engineering Conference (EEEC 2014), 27–28 December 2014, Shanghai, China; CRC Press: Boca Raton, FL, USA, 2014; pp. 49–52. [Google Scholar]
- Redfern, M.A. Automatic Compensation Voltage Control Strategy for On-Load Tap Changer Transformers with Distributed Generations. Tsinghua University, Chinese Society for Electrical Engineering, IEEE Beijing Section, The Institution of Engineering and Technology(IET), Science China Press, Myongji University. In Proceedings of the 2011 International Conference on Advanced Power System Automation and Protection (APAP 2011), Beijing, China, 16–20 October 2011; pp. 796–800. [Google Scholar]
- Liu, Q.; Liu, Q.; Liu, D.; Liao, Y. Research on On-Line Coordinated Control Strategy to Improve the Voltage Vulnerability after Disturbance. J. Electron. Sci. Technol. 2014, 12, 1–6. [Google Scholar]
- Zhou, S.; Wu, H.; Zhao, G.; Li, L. Optimization control strategy for single-phase permanent magnet generator based on voltage ripple. High Technol. Lett. 2013, 19, 429–436. [Google Scholar]
- Zirkohi, M.M.; Fateh, M.M.; Shoorehdeli, M.A. Type-2 Fuzzy Control for a Flexible-joint Robot Using Voltage Control Strategy. Int. J. Autom. Comput. 2013, 10, 242–255. [Google Scholar] [CrossRef]
- Fateh, M.M.; Fateh, S. A Precise Robust Fuzzy Control of Robots Using Voltage Control Strategy. Int. J. Autom. Comput. 2013, 10, 64–72. [Google Scholar] [CrossRef]
- Hu, C.; Wang, H.; Zhou, J.; Shi, Y.; Luo, S.; Fan, H.; Lu, H. Multi-DC-DC droop dynamic compensation control strategy based on the robust residual generator. Proc. Chin. Soc. Electr. Eng. 2021, 41, 1410–1421+1547. [Google Scholar]
- Ma, W. Research on Small Disturbance Stability of DC MG; Anhui University of Science and Technology: Huainan, China, 2019. [Google Scholar]
- Yang, D.; Ding, Z.; Cao, W. Small disturbance stability analysis of DC MG based on sag control. Electr. Technol. 2019, 7, 20–26. [Google Scholar]
- Tabari, M.; Yazdani, A. A mathematical model for stability analysis of a DC distribution system for power system integration of plug-in electric vehicles. IEEE Trans. Veh. Technol. 2021, 64, 1729–1738. [Google Scholar] [CrossRef]
- Shamsi, P.; Fahimi, B. Stability assessment of a DC distribution network in a hybrid micro-grid application. IEEE Trans. Smart Grid 2017, 5, 527–2534. [Google Scholar] [CrossRef]
- Hu, H. Island Small Signal Stability Analysis and Grid-Connected Hierarchical Control Strategy of DC MG; Zhejiang University: Hangzhou, China, 2017. [Google Scholar]
- Middlebrook, R.D. Transformerless DC-to-DC converters with large conversion ratios. IEEE Trans. Power Electron. 2018, 3, 484–488. [Google Scholar] [CrossRef]
- Zhu, X.; Meng, X. Stability analysis and active damping control of DC MG. High Volt. Technol. 2020, 46, 1670–1681. [Google Scholar]
- Guo, L.; Zhang, S.; Li, X.; Li, Y.; Wang, C.; Feng, Y. Stability Analysis and Damping Enhancement Based on Frequency-Dependent Virtual Impedance for DC MGs. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 5, 338–350. [Google Scholar] [CrossRef]
- Guo, L.; Feng, Z.; Li, X.; Wang, C.; Li, Y. Stability analysis and damping control method of DC MG. Proc. CSEE 2021, 4, 927–936. [Google Scholar]
- Xie, W.; Han, M.; Cao, W.; Guerrero, J.; Vasquez, J. System-Level Large-Signal Stability Analysis of Droop-Controlled DC Microgrids. IEEE Trans. Power Electron. 2021, 36, 4224–4236. [Google Scholar] [CrossRef]
- Xie, W.; Han, M.; Yan, W.; Wang, C.; Yuan, D. Stability Control Strategy for DC Micro-grid Considering Constant Power Load. In Proceedings of the 2019 IEEE Third International Conference on DC MGs (ICDCM), Matsue, Japan, 20–23 May 2019; pp. 1–6. [Google Scholar]
- Xie, W.; Han, M.; Cao, W.; Guerrero, J.M.; Vasquez, J.C. Virtual Resistance Trade-off Design for DCMG Grid-Forming Converters Considering Static and Large-Signal Dynamic Constraints. IEEE Trans. Power Electron. 2019, 36, 5582–5593. [Google Scholar] [CrossRef]
- Kabalan, M.; Singh, P.; Niebur, D. Large signal Lyapunov-based stability studies in MGs: A review. IEEE Trans. Smart Grid 2020, 8, 2287–2295. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, C.; Wen, C.; Wang, P. A Novel Composite Nonlinear Controller for Stabilization of Constant Power Load in DC MG. IEEE Trans. Smart Grid 2019, 10, 752–761. [Google Scholar] [CrossRef]
- Hart, P.; Lesieutre, B. Energy function for a grid-tied, droop-controlled inverter. In Proceedings of the 2014 North American Power Symposium (NAPS), Pullman, WA, USA, 7–9 September 2014; pp. 1–6. [Google Scholar]
- Kabalan, M.; Singh, P.; Niebur, D. Large signal stability analysis of a DC/AC droop controlled inverter connected to an infinite bus. In Proceedings of the 2019 North American Power Symposium (NAPS), Charlotte, NC, USA, 13–15 October 2019; pp. 1–6. [Google Scholar]
- Berkovich, Y.; Ioinovici, A. Large-signal stability-oriented design of boost-type regulators in discontinuous conduction mode. IGCAS 2001. In Proceedings of the 2001 IEEE International Symposium on Circuits and Systems (Cat. No.O1CH37196), Sydney, Australia, 6–9 May 2001; Volume 2, pp. 5–8. [Google Scholar]
- Berkovich, Y.; Ioinovici, A. Large-signal stability-oriented design of boost regulators based on a Lyapunov criterion with nonlinear integral. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2022, 49, 1610–1619. [Google Scholar] [CrossRef]
- Gong, T.; Xie, X.; Rong, H.; Wang, W. Research on vehicle electronic stability control strategy based on phase plane method. Traffic Inf. Saf. 2019, 37, 83–90. [Google Scholar]
- Rivetta, C.; Williamson, G.A. Large-signal analysis and control of buck converters loaded by DC-DC converters. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; Volume 5, pp. 3675–3680. [Google Scholar]
- Rivetta, C.H.; Williamson, G.A.; Fahimi, B. Analysis and control of a buck DC-DC converter operating with constant power load in sea and undersea vehicles. IEEE Trans. Ind. Appl. 2020, 42, 559–572. [Google Scholar] [CrossRef]
- Griffo, A.; Wang, J. Large Signal Stability Analysis of ‘More Electric’ Aircraft Power Systems with Constant Power Loads. IEEE Trans. Aerosp. Electron. Syst. 2022, 48, 477–489. [Google Scholar] [CrossRef]
- Li, L.; Sun, Y.; Liu, Z.; Hou, X.; Shi, G.; Su, M. A Decentralized Control With Unique Equilibrium Point for Cascaded-Type MG. IEEE Trans. Sustain. Energy 2019, 10, 324–326. [Google Scholar] [CrossRef]
- Mathew, P.; Madichetty, S.; Mishra, S.A. Multilevel Distributed Hybrid Control Scheme for Islanded DC MGs. IEEE Syst. J. 2019, 13, 4200–4207. [Google Scholar] [CrossRef]
- Deng, S.; Chen, L.; Zheng, T.; Yang, L.; Mei, S. Distributed control strategy of active power in MG considering system delay. Power Grid Technol. 2019, 43, 1536–1542. [Google Scholar]
- Wu, C.; Lin, S.; Xia, C.; Guan, L. Distributed optimal dispatching of MG cluster based on model predictive control. Power Grid Technol. 2020, 44, 530–538. [Google Scholar]
- Lv, P.; Zhao, J.; Su, D.; Chen, G. Distributed dynamic economic dispatch of independent MG based on consistency theory. Power Syst. Autom. 2019, 43, 22–44. [Google Scholar]
- Gao, Y.; Ai, Q.; Wang, J. Coherent cooperative control of AC/DC hybrid MG group in a multi-agent system. High Volt. Technol. 2019, 44, 2372–2377. [Google Scholar]
- Nasirian, V.; Moayedi, S.; Davoudi, A.; Lewis, F. Distributed Cooperative Control of DC MGs. IEEE Trans. Power Electron. 2020, 30, 2288–2303. [Google Scholar] [CrossRef]
- Xie, G.; Zhang, Y. A summary of the research on the consistency of coordinated control of multi-intelligent systems. Comput. Appl. Res. 2021, 28, 2035–2039. [Google Scholar]
- Yang, L.M.; Lu, Q. More actions are needed to support the biomass power industry in developing countries. J. Clean. Prod. 2021, 278, 123554. [Google Scholar] [CrossRef]
- Yadav, A.K. Human health risk assessment in opencast coal mines and coal-fired thermal power plants surrounding area due to inhalation. Environ. Chall. 2021, 3, 100074. [Google Scholar] [CrossRef]
- Long, H.; Fan, X.; Liu, S. Research status of distributed consistency algorithm for the multi-intelligent system. Comput. Eng. Appl. 2022, 49, 36–42+81. [Google Scholar]
- Jadbabaie, A.; Jie, L.; Morse, A.S. Coordination of groups of mobile autonomous agents using nearest-neighbor rules. IEEE Trans. Autom. Control 2020, 48, 988–1001. [Google Scholar] [CrossRef]
- Lin, X.; Boyd, S. Fast linear iterations for distributed averaging. In Proceedings of the 42nd IEEE International Conference on Decision and Control (IEEE Cat. No.03CH37475), Maui, HI, USA, 9–12 December 2003; Volume 5, pp. 4997–5002. [Google Scholar]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2021, 49, 1520–1533. [Google Scholar] [CrossRef]
- Boyd, S.; Ghosh, A.; Prabhakar, B.; Shah, D. Randomized gossip algorithms. IEEE Trans. Oninform. Theory 2020, 52, 2508–2530. [Google Scholar] [CrossRef]
- Shuai, L.; Yi, G.; Fang, J.; Li, H. Average consensus with weighting matrix design for quantized communication on directed switching graphs. Int. J. Adapt. Control Signal Process. 2019, 27, 519–540. [Google Scholar]
- Kim, Y.; Mesbahi, M. On Maximizing the Second Smallest Eigenvalue of a State-Dependent GraphLaplacian. IEEE Trans. Autom. Control 2019, 51, 116–120. [Google Scholar] [CrossRef]
- Zhang, B.; Chang, D.; Li, Z.; Ma, D. On convergence rate for multi-agent consensus: A community detection algorithm. In Proceedings of the 32nd Youth Academic Annual Conference of Chinese Association of Automation(YAC), Hefei, China, 19–21 May 2017; pp. 72–77. [Google Scholar]
- Kokiopoulou, E.; Frossard, P. Accelerating Distributed Consensus Using Extrapolation. IEEE Signal Process. Lett. 2021, 14, 665–668. [Google Scholar] [CrossRef]
- Aysal, T.C.; Oreshkin, B.N.; Coates, M.J. Accelerated Distributed Average Consensus via Localized NodeState Prediction. IEEE Trans. Signal Process. 2019, 57, 1563–1576. [Google Scholar] [CrossRef]
- Yin, C.; Tron, R.; Terzis, A.; Vidal, R. Accelerated corrective consensus: Converge to the exact average at a faster rate. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 3417–3422. [Google Scholar]
- Spanos, D.P.; Olfati-Saber, R.; Murray, R.M. Dynamic consensus on mobile networks. In Proceedings of the 2005 IFAC World Congress, Prague, Czech Republic, 3–8 July 2005. [Google Scholar]
- Freeman, R.A.; Yang, P.; Lynch, K.M. Stability and Convergence Properties of Dynamic Average Consensus Estimators. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 338–343. [Google Scholar]
- Lv, Z.; Wu, Z.; Dou, X.; Hu, M.; Zhao, B. Adaptive sag control of isolated DC MG based on discrete consistency. Proc. CSEE 2021, 35, 4397–4407. [Google Scholar]
- Lv, Z.; Su, C.; Wu, Z.; Dou, X.; Li, H. Distributed secondary regulation strategy and communication topology optimization of isolated island MG. J. Electrotech. Sci. 2021, 32, 209–219. [Google Scholar]
- Su, C.; Wu, Z.; Lu, Z.; Yang, Y.; Dou, X. Distributed secondary power optimization control of isolated MG. Power Grid Technol. 2022, 40, 2689–2697. [Google Scholar]
- Shi, M.; Chen, X.; Zhou, J.; Chen, Y.; Wen, J. Distributed Optimal Control of Energy Storages in a DC MG with Communication Delay. IEEE Trans. Smart Grid 2020, 11, 2033–2042. [Google Scholar] [CrossRef]
- Shyam, A.B.; Anand, S.; Sahoo, S.R. Effect of Communication Delay on Consensus Based SecondaryControllers in DC MG. IEEE Trans. Smart Grid 2021, 68, 3202–13212. [Google Scholar]
- Sahoo, S.; Mishra, S. An Adaptive Event-Triggered Communication-Based Distributed SecondaryControl for DC MGs. IEEE Trans. Smart Grid 2018, 9, 6674–6683. [Google Scholar] [CrossRef]
- Han, R.; Aldana, N.L.D.; Meng, L.; Guerrero, J.; Sun, Q. Droop-free distributed control with event-triggered communication in DC micro-grid. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 1160–1166. [Google Scholar]
- Zhang, Z.; Chow, M.Y. Convergence Analysis of the Incremental Cost Consensus Algorithm Under Different Communication Network Topologies in a Smart Grid. IEEE Trans. Power Syst. 2020, 27, 1761–1768. [Google Scholar] [CrossRef]
- Behjati, H.; Davoudi, A.; Lewis, F. Modular DC-DC Converters on Graphs: Cooperative Control. IEEE Trans. Power Electron. 2019, 29, 6725–6741. [Google Scholar] [CrossRef]
- Prabhakaran, P.; Goyal, Y.; Agarwal, V. A Novel Communication-Based Average Voltage RegulationScheme for a Droop Controlled DC MG. IEEE Trans. Smart Grid 2019, 10, 1250–1258. [Google Scholar] [CrossRef]
- Sahoo, S.; Zhang, C.; Pullaguram, D.R.; Mishra, S.; Wu, J.; Senroy, N. Investigation of distributed cooperative control for DCMGs in different communication mediums. Energy Procedia 2019, 142, 2218–2223. [Google Scholar] [CrossRef]
- Sahoo, S.; Peng, J.C.-H.; Mishra, S.; Dragicevic, T. Distributed Screening of Hijacking Attacks in DC MGs. IEEE Trans. Power Electron. 2020, 35, 7574–7582. [Google Scholar] [CrossRef]
- Sahoo, S.; Mishra, S.; Peng, C.H.; Dragicevic, T. A Stealth Cyber Attack Detection Strategy for DC MGs. IEEE Trans. Power Electron. 2019, 34, 8162–8174. [Google Scholar] [CrossRef]
- Sahoo, S.; Peng, C.H.; Devakumar, A.; Mishra, S.; Dragicevic, T. On Detection of False Data in Cooperative DC MGs-ADiscordant Element Approach. IEEE Trans. Ind. Electron. 2020, 67, 6562–6571. [Google Scholar] [CrossRef]
- Ji, L.; Liao, X.; Liu, Q. Group consistency analysis of multi-agent system with time delay. J. Phys. 2019, 61, 11–18. [Google Scholar]
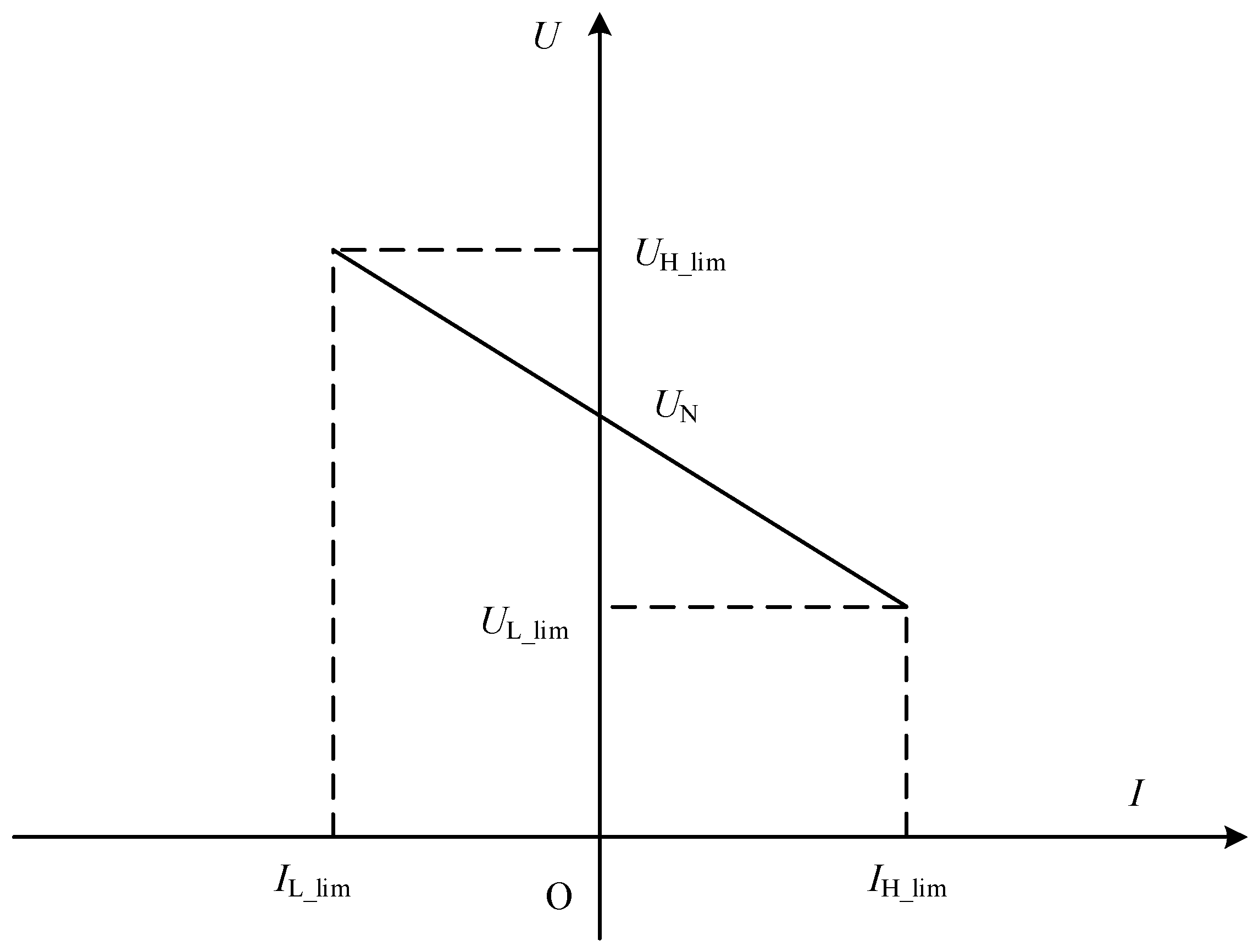

| Microsource | Output Voltage/V | Line Impedance/Ω |
|---|---|---|
| MGH1 | 400 | 0.3 + j3 |
| MGH2 | 400 | 0.2 + j2 |
| MGH3 | 400 | 0.1 + j1 |
| MGL1 | 48 | 0.3 + j3 |
| MGL2 | 48 | 0.2 + j2 |
| MGL3 | 48 | 0.1 + j1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.; Wang, L.; Wang, P. Review of Voltage Control Strategies for DC Microgrids. Energies 2023, 16, 6158. https://doi.org/10.3390/en16176158
Lu Z, Wang L, Wang P. Review of Voltage Control Strategies for DC Microgrids. Energies. 2023; 16(17):6158. https://doi.org/10.3390/en16176158
Chicago/Turabian StyleLu, Zhiye, Lishu Wang, and Panbao Wang. 2023. "Review of Voltage Control Strategies for DC Microgrids" Energies 16, no. 17: 6158. https://doi.org/10.3390/en16176158






