A New Method for Predicting the Gas Content of Low-Resistivity Shale: A Case Study of Longmaxi Shale in Southern Sichuan Basin, China
Abstract
:1. Introduction
2. Geology Settings
3. Data Selection and Methods
3.1. Data Selection
3.2. Methods
3.2.1. Grey Relational Analysis
- (1)
- Each independent variable is represented by a comparison sequence (Xi = xi(k)|k = 1, 2, n) and a reference sequence (Y = y(k)|k = 1, 2, m), while the dependent variable is represented by the reference sequence [24].
- (2)
- The comparison sequence and the reference sequence are normalized so that each independent variable and each dependent variable have values between 0 and 1.
- (3)
- The grey correlation coefficient i(k) of each element in each comparison sequence is calculated, based on this information. The calculation formula is as follows:
- (4)
- The average grey correlation coefficient, or the degree of grey correlation ri between each independent variable and each dependent variable, is computed for each comparison series. Below is the calculating formula:
3.2.2. Multiple Linear Regression
3.2.3. Prediction of Shale Gas Content Based on the Resistivity Method
3.2.4. Random Forest Regression
- (1)
- The dataset is divided into the independent variable matrix and the dependent variable vector (label).
- (2)
- The same number of samples is pulled from the initial data set, using put-back to create various subsets of the unordered data set [32].
- (3)
- A decision tree is obtained for each subgroup by using label-supervised learning to identify a certain number of ideal features (shown by the red line in Figure 2).
- (4)
- The decision trees of each subset are combined to obtain random forests.
- (5)
- The prediction results of each decision tree are added and averaged to determine the predicted value.
3.2.5. Method Process
4. Results and Discussion
4.1. Prediction Effect Analysis Based on Multiple Linear Regression
4.2. Prediction Effect Analysis Based on Resistivity Method
4.3. Prediction Effect Analysis Based on Random Forest Regression
5. Conclusions
- (1)
- The gray-correlation multiple linear regression method could not fully include the relationship between the gas content of the two types of low-resistivity shales and the logging series, and the accuracy of the prediction results was low.
- (2)
- The inclusion of pyrite and over-mature organic matter into the water-content-saturation prediction model was more consistent with the low-resistivity shale petrophysical model. However, the free-gas and adsorbed-gas fugitive forms were not fully defined and the existing free-gas volume and adsorbed-gas volume models could not accurately predict the total shale-gas content, resulting in high prediction results.
- (3)
- The random forest algorithm comprehensively learned the relationship between the gas content of low-resistivity shale and each logging series. the correlation between the predicted gas content and the measured gas content reached 0.95, which supported the extension of this application in the study area.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Ro | the resistivity of shale with 100% water content (ohm·m) |
| Rw | resistivity of formation water (ohm·m) |
| Vclay/Vsh | argillaceous content |
| Rsh | resistivity of clay (ohm·m) |
| Vom | organic matter volume ratio |
| Rom | resistivity of organic matter (ohm·m) |
| Vpy | pyrite volume ratio |
| Rpy | resistivity of pyrite (ohm·m) |
| S | mineralization (g/L) |
| T/t | temperature of formation (°C) |
| ρb/ρr | density of shale (g/cm3) |
| ρom | density of organic matter (g/cm3) |
| P | formation pressure (MPa) |
| Tsc | ground standard temperature, the value of 273.15 K |
| Psc | ground standard pressure, the value of 0.101 MPa |
| α | coefficient of formation pressure |
| Phydrostatic | formation pressure in the hydrostatic situation (MPa) |
| ρw | density of water, the value of 1.0 × 103 kg/m3 |
References
- Kokkinos, N.C.; Nkagbu, D.C.; Marmanis, D.I.; Dermentzis, K.I.; Maliaris, G. Evolution of Unconventional Hydrocarbons: Past, Present, Future, and Environmental Footprint. J. Eng. Sci. Technol. Rev. 2022, 15, 15–24. [Google Scholar] [CrossRef]
- Zhong, G.; Xie, B.; Zhou, X. Shale Gas Logging Evaluation Method—A Case Study of Southern Sichuan Basin. J. Lithol. Reserv. 2015, 27, 96–102. [Google Scholar]
- Cui, R.; Sun, J.; Liu, X. Study on main controlling factors of low resistivity shale. J. Geophys. Geochem. Explor. 2022, 46, 150–159. [Google Scholar]
- Sun, J.; Xiong, Z.; Luo, H. Low resistivity genesis analysis and logging evaluation of Lower Paleozoic shale gas reservoirs in Yangtze area. J. China Univ. Pet. (Nat. Sci. Ed.) 2018, 42, 47–56. [Google Scholar]
- Yin, S.; Ding, W.; Huang, C. Logging evaluation of gas saturation in unsaturated tight sandstone reservoirs. J. Gas Earth Sci. 2016, 27, 156–165. [Google Scholar]
- Xia, H.; Liu, C.; Wang, H. Shale gas content logging evaluation method. J. Spec. Reserv. 2019, 26, 1–6. [Google Scholar]
- Li, Y.; Hu, Z.; Cai, C.; Liu, X.; Duan, X.; Chang, J.; Li, Y.; Mu, Y.; Zhang, Q.; Zeng, S.; et al. Evaluation method of water saturation in shale: A comprehensive review. J. Mar. Pet. Geol. 2021, 128, 105017. [Google Scholar] [CrossRef]
- De, S.; Sengupta, D. An advanced well log and an effective methodology to evaluate water saturation of the organic-rich Cambay shale. J. Nat. Resour. Res. 2020, 30, 1719–1731. [Google Scholar] [CrossRef]
- Zhu, L.; Ma, Y.; Cai, J.; Zhang, C.; Wu, S.; Zhou, X. Key factors of marine shale conductivity in southern China—Part I: The influence factors other than the porosity. J. Pet. Sci. Eng. 2021, 20, 35. [Google Scholar] [CrossRef]
- Wen, K.; Yan, J.P.; Zhong, G.H.; Jing, C.; Tang, H.M.; Wang, M.; Wang, J. A new method for shale gas evaluation of Wufeng-Longmaxi Formations in Changning area, southern Sichuan. J. Lithol. Reserv. 2022, 34, 95–105. [Google Scholar]
- Li, X. Research on the application of big data technology in oilfield development. J. China Manag. Informatiz. 2022, 25, 113–115. [Google Scholar]
- Luo, S.; Xu, T.; Wei, S. Prediction method and application of shale reservoirs core gas content based on machine learning. J. Appl. Geophys. 2022, 204, 104741. [Google Scholar] [CrossRef]
- Chen, Y.; Deng, X.; Wang, X. Application of a PSO-SVM algorithm for predicting the TOC content of a shale gas reservoir: A case study in well Z in the Yuxi area. J. Geophys. Prospect. Pet. 2021, 60, 652–663. [Google Scholar]
- Ye, S.; Cao, J.; Wu, S. Prediction method of total organic carbon content based on deep belief nets. J. Prog. Geophys. 2018, 33, 2490–2497. [Google Scholar]
- Zhong, Z.; Carr, T.R.; Wu, X.; Wang, G. Application of a convolutional neural network in permeability prediction: A case study in the Jacksonburg-Stringtown oil field, West Virginia, USA. Geophysics 2019, 84, 363–373. [Google Scholar] [CrossRef]
- Rong, J.; Zheng, Z.; Luo, X.; Li, C.; Li, Y.; Wei, X.; Wei, Q.; Yu, G.; Zhang, L.; Lei, Y. Machine learning method for TOC prediction: Taking wufeng and longmaxi shales in the Sichuan Basin, Southwest China as an example. Geofluids 2021, 2021, 6794213. [Google Scholar] [CrossRef]
- Wang, X.; Chen, S.; Yang, Y. High-precision seismic prediction of gas content in shale reservoirs based on convolutional neural network algorithm. In Proceedings of the 2022 Chinese Petroleum Geophysical Prospecting Academic Annual Conference Proceedings, Xi’an, China, 16–18 November 2022; pp. 176–179. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, H.; Zhou, Y. Paleogeomorphic characteristics of the Wufeng-Longmaxi Formation in the Dazu block of western Chongqing and their influence on the development of high-quality shale. J. Cent. South Univ. (Nat. Sci. Ed.) 2022, 53, 3628–3640. [Google Scholar]
- Li, J.B.; Yang, Q.D.; Liu, C.S.; Tan, D.Y.; Li, Z.F. Reconstruction of Sichuan Basin by large-scale strike-slip faults. In Proceedings of the 2022 Annual Chinese Petroleum Geophysical Prospecting Academic Conference, Xi’an, China, 16–18 November 2022; pp. 542–545. [Google Scholar] [CrossRef]
- Wang, X. Influential Factors and Gas-Bearing Evaluation of Marine Low-Resistivity Shale Development in Southern Sichuan; China University of Petroleum: Beijing, China, 2020. [Google Scholar] [CrossRef]
- Sun, S.; Dong, D.; Li, Y. Hydrocarbon geological characteristics and accumulation controlling factors of continental shale in Da’anzhai Member of Jurassic Ziliujing Formation in Sichuan Basin. J. Oil Gas Geol. 2021, 42, 124–135. [Google Scholar]
- Zhao, K.; Mou, K. Discussion on shale reservoir evaluation methods based on grey correlation analysis and principal component analysis. J. Geol. Explor. 2022, 12, 1–13. [Google Scholar]
- Wang, P. Application of grey theory in coal seam gas content analysis. J. Innov. Appl. Sci. Technol. 2022, 12, 75–78. [Google Scholar] [CrossRef]
- Cai, Z.; Zhu, Z. Research on the Integration of Big Data and Manufacturing Industry Based on Entropy Weight-Grey Correlation Method—A Case Study of Beijing-Tianjin-Hebei Region. J. Hunan Univ. Financ. Econ. 2022, 38, 18–28. [Google Scholar]
- Chen, J. Regression analysis of urban fire frequency and meteorological factors. J. Sci. Technol. Innov. 2022, 35, 17–20. [Google Scholar]
- Wang, Y.; Geng, J.; Zhou, Y. Spatio-temporal variation of eco-environmental quality and its response to climate change and human activities in northern China. J. Mapp. Bull. 2022, 8, 14–21+35. [Google Scholar] [CrossRef]
- Wang, L.; Li, S.; Liu, X. Well logging evaluation of water saturation in low-resistivity shale of Wufeng-Longmaxi Formation in Sichuan Basin. J. Sci. Technol. Eng. 2022, 22, 6456–6462. [Google Scholar]
- Zhang, B. Study on Logging Characterization Method of Shale Reservoir Parameters; China University of Geosciences: Beijing, China, 2017. [Google Scholar] [CrossRef]
- Yang, A.; Firdaus, G.; Heidari, Z. Electrical resistivity and chemical properties of kerogen isolated from organic-rich mudrocks. Geophysics 2016, 81, 24–26. [Google Scholar]
- Ji, W.M.; Zhu, M.F.; Song, Y. Evolution characterization of marine shale gas occurrence state in South China. J. Cent. South Univ. (Sci. Technol.) 2022, 53, 3590–3602. [Google Scholar] [CrossRef]
- Yao, D.; Yang, J.; Zhan, X. Feature Selection Algorithm Based on Random Forest. J. Jilin Univ. Technol. Ed. 2014, 44, 142–146. [Google Scholar]
- Ganaie, M.A.; Tanveer, M.; Suganthan, P.N.; Snasel, V. Oblique and rotation double random forest. Neural Netw. 2022, 153, 496–517. [Google Scholar] [CrossRef]
- Seokhyun, C.; Young, W.P.; Taesu, C. A mathematical programming approach for integrated multiple linear regression subset selection and validation. Pattern Recognit. 2020, 108, 107565. [Google Scholar]
- Senger, K.; Birchall, T.; Betlem, P.; Ogata, K.; Ohm, S.; Olaussen, S.; Paulsen, R.S. Resistivity of reservoir sandstones and organic-rich shales on the Barents Shelf: Implications for interpreting CSEM data. Geosci. Front. 2021, 12, 101063. [Google Scholar] [CrossRef]
- Kethireddy, N.; Heidari, Z.; Chen, H. Quantifying the Effect of Kerogen on Resistivity Measurements in Organic-Rich Mudrocks. Petrophysics 2014, 55, 25–28. [Google Scholar]
- Zhang, M.H.; Wei, J.; Bian, H.D. Slope stability analysis method based on machine learning-a case study of 618 slopes in China. J. Earth Sci. Environ. 2022, 44, 1083–1095. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, J.; Gong, J.; Xia, Z. Gas content calculation model of shale gas reservoir. J. Lithol. Reserv. 2015, 27, 5–14. [Google Scholar]
- Zhe, W.; Peng, J.; Xu, X.L.; Wang, B.L.; Zhu, Y.J.; Li, D.D. Sample and feature selecting based ensemble learning for imbalanced problems. Appl. Soft Comput. 2021, 6, 54–58. [Google Scholar]
- Song, Y.J.; Tang, X.M. Generalized effective medium resistivity model for low resistivity reservoir. J. Sci. China (Ser. D Earth Sci.) 2008, 8, 144–158. [Google Scholar] [CrossRef]
- Ran, B. Elastic and resistivity anisotropy of compacting shale: Joint effective medium modeling and field observations. J. Seg Tech. Program Expand. Abstr. 2010, 29, 2580–2584. [Google Scholar]
- Pridmore, D.F.; Shuey, R.T. The electrical resistivity of galena, pyrite, and chalcopyrite. J. Phys. Chem. 1976, 62, 758–759. [Google Scholar]


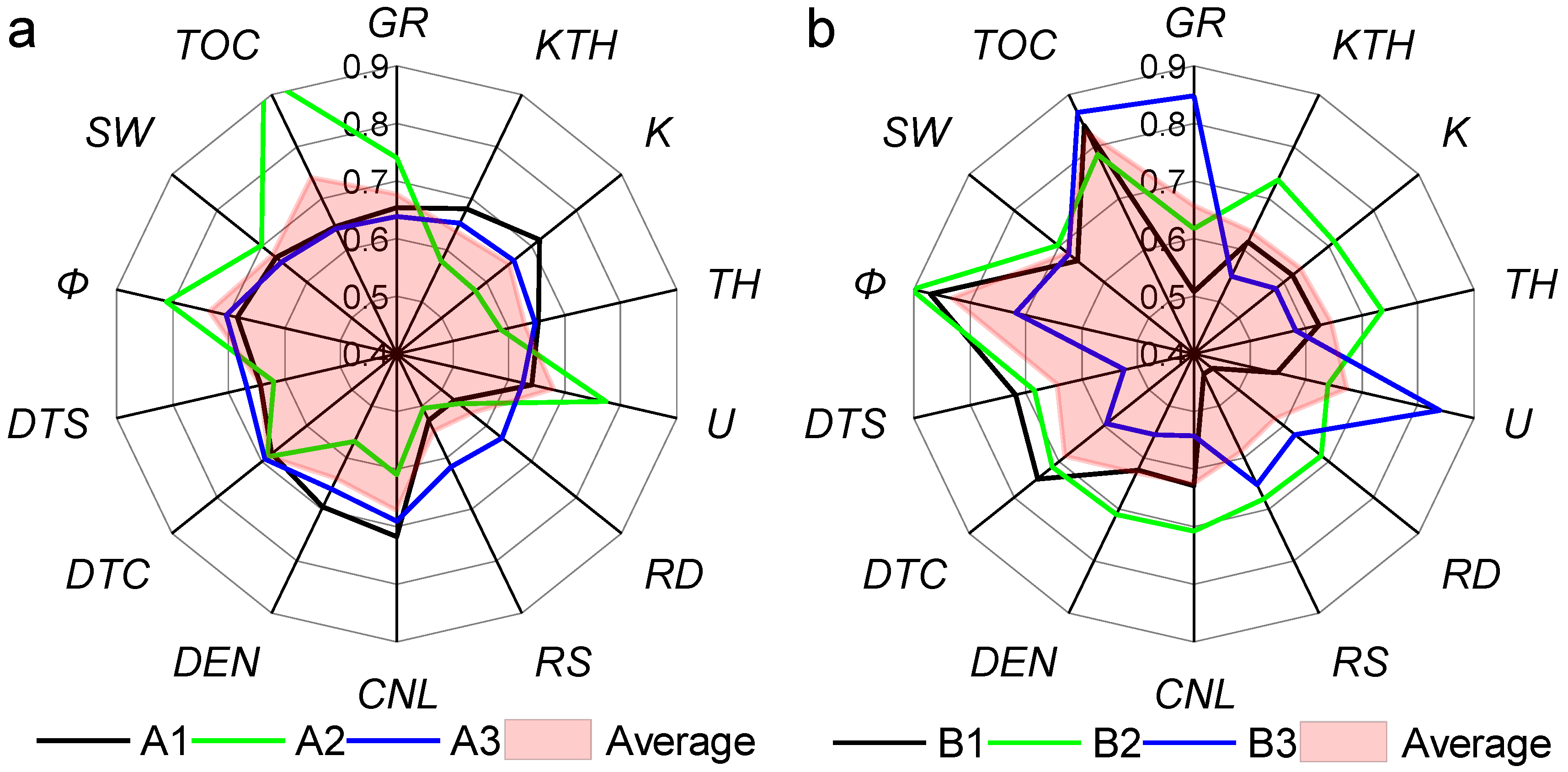






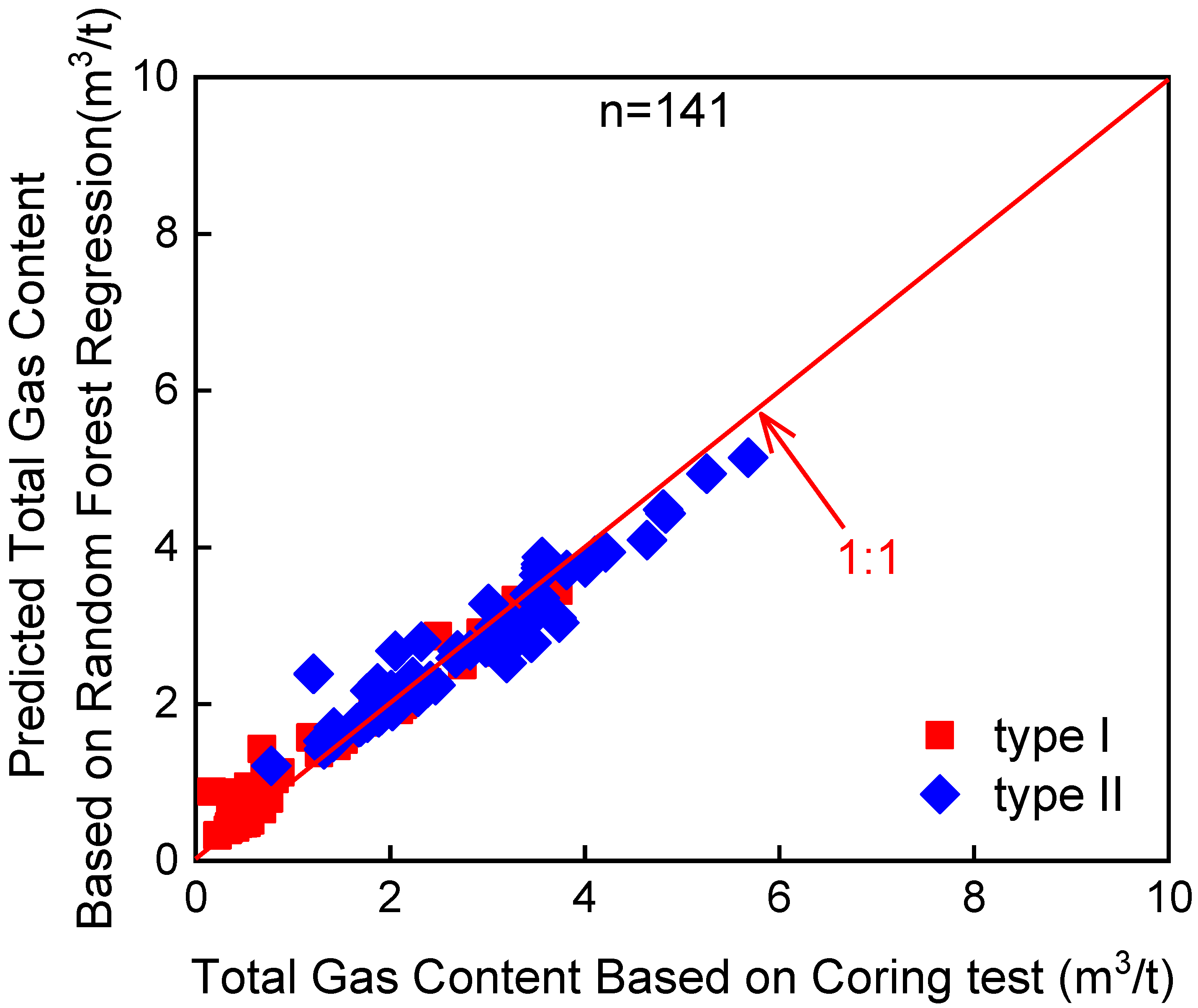
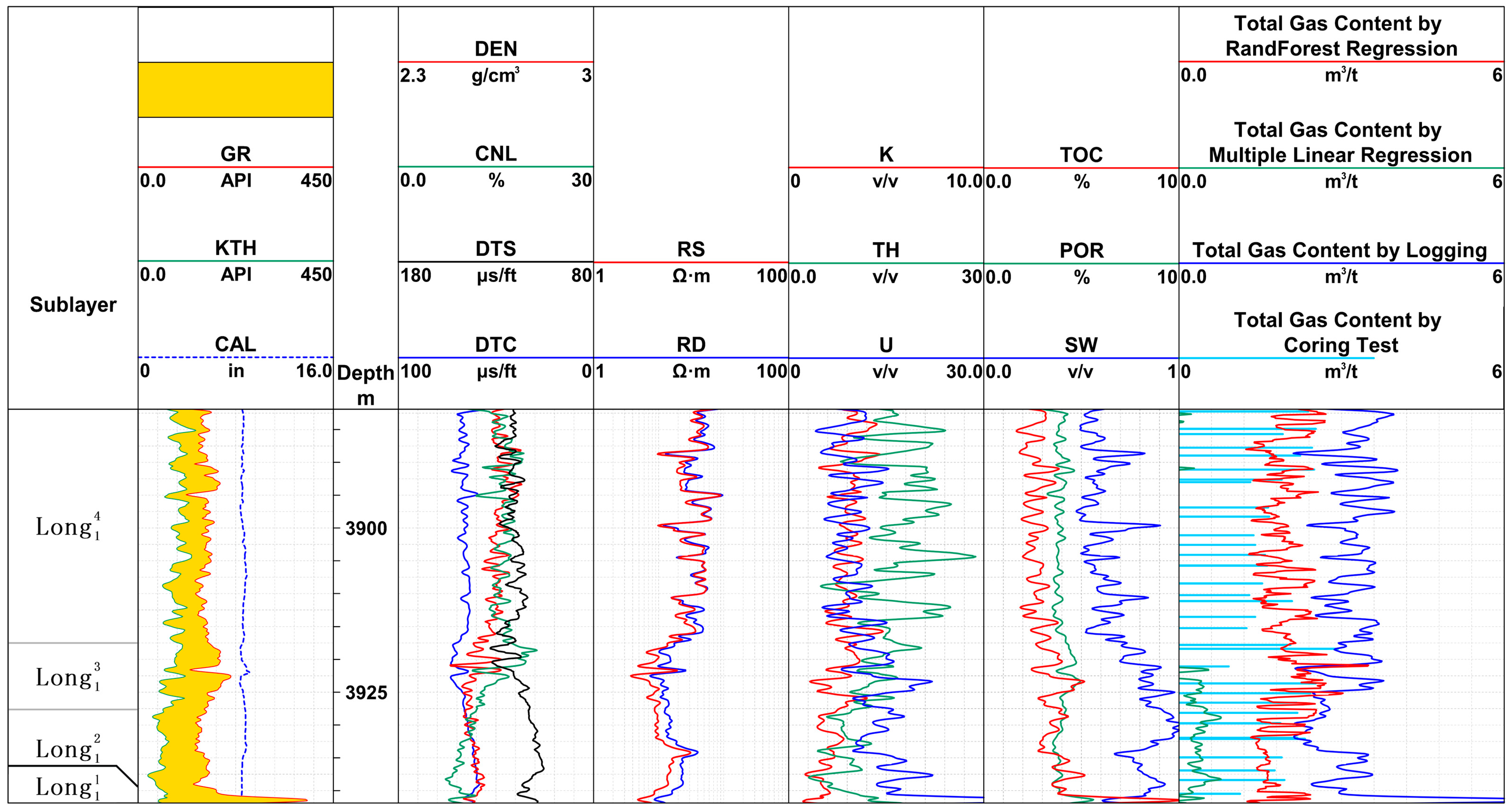

| Type | Well Name | Vitrinite Reflectivity (%) | Water Saturation (%) | Pressure Coefficient | Mineralization (g/L) |
|---|---|---|---|---|---|
| type Ⅰ | A1 | 3.52 | 55.00~83.30 (69.38) | 1.68 | 23.35 |
| A2 | 3.80 | 59.19~89.90 (72.93) | 0.50 | 23.57 | |
| A3 | 3.47 | 39.95~78.73 (64.07) | 1.95 | 24.65 | |
| A4 | 3.50 | 27.90~89.50 (63.82) | 1.00 | 23.94 | |
| type Ⅱ | B1 | 3.60 | 33.70~56.84 (46.60) | 2.00 | 24.83 |
| B2 | 3.52 | 56.93~70.78 (62.97) | 2.05 | 25.85 | |
| B3 | 3.39 | 32.07~78.39 (59.01) | 1.90 | 25.69 | |
| B4 | 4.59 | 54.63~62.62 (59.10) | 1.00 | 24.28 |
| Model | Equation | Characteristics |
|---|---|---|
| Modified Simandoux | Applied to shaly sandstone | |
| Total shale | ||
| Waxman–Smits | ||
| Dual-water | Modified from the Waxman–Smits model; water in reservoirs is divided into irreducible water and free water. | |
| Indonesian | Considering the total porosity-containing organic matter is currently the most suitable model for shale. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, X.; Wu, Y.; Jiang, Z.; Hu, Z.; Tang, X.; Zhang, Y.; Wang, X.; Chen, W. A New Method for Predicting the Gas Content of Low-Resistivity Shale: A Case Study of Longmaxi Shale in Southern Sichuan Basin, China. Energies 2023, 16, 6169. https://doi.org/10.3390/en16176169
Duan X, Wu Y, Jiang Z, Hu Z, Tang X, Zhang Y, Wang X, Chen W. A New Method for Predicting the Gas Content of Low-Resistivity Shale: A Case Study of Longmaxi Shale in Southern Sichuan Basin, China. Energies. 2023; 16(17):6169. https://doi.org/10.3390/en16176169
Chicago/Turabian StyleDuan, Xianggang, Yonghui Wu, Zhenxue Jiang, Zhiming Hu, Xianglu Tang, Yuan Zhang, Xinlei Wang, and Wenyi Chen. 2023. "A New Method for Predicting the Gas Content of Low-Resistivity Shale: A Case Study of Longmaxi Shale in Southern Sichuan Basin, China" Energies 16, no. 17: 6169. https://doi.org/10.3390/en16176169
APA StyleDuan, X., Wu, Y., Jiang, Z., Hu, Z., Tang, X., Zhang, Y., Wang, X., & Chen, W. (2023). A New Method for Predicting the Gas Content of Low-Resistivity Shale: A Case Study of Longmaxi Shale in Southern Sichuan Basin, China. Energies, 16(17), 6169. https://doi.org/10.3390/en16176169







