Temperature Control of a Chemical Reactor Based on Neuro-Fuzzy Tuned with a Metaheuristic Technique to Improve Biodiesel Production
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of Industrial Plant
2.2. PI Controller
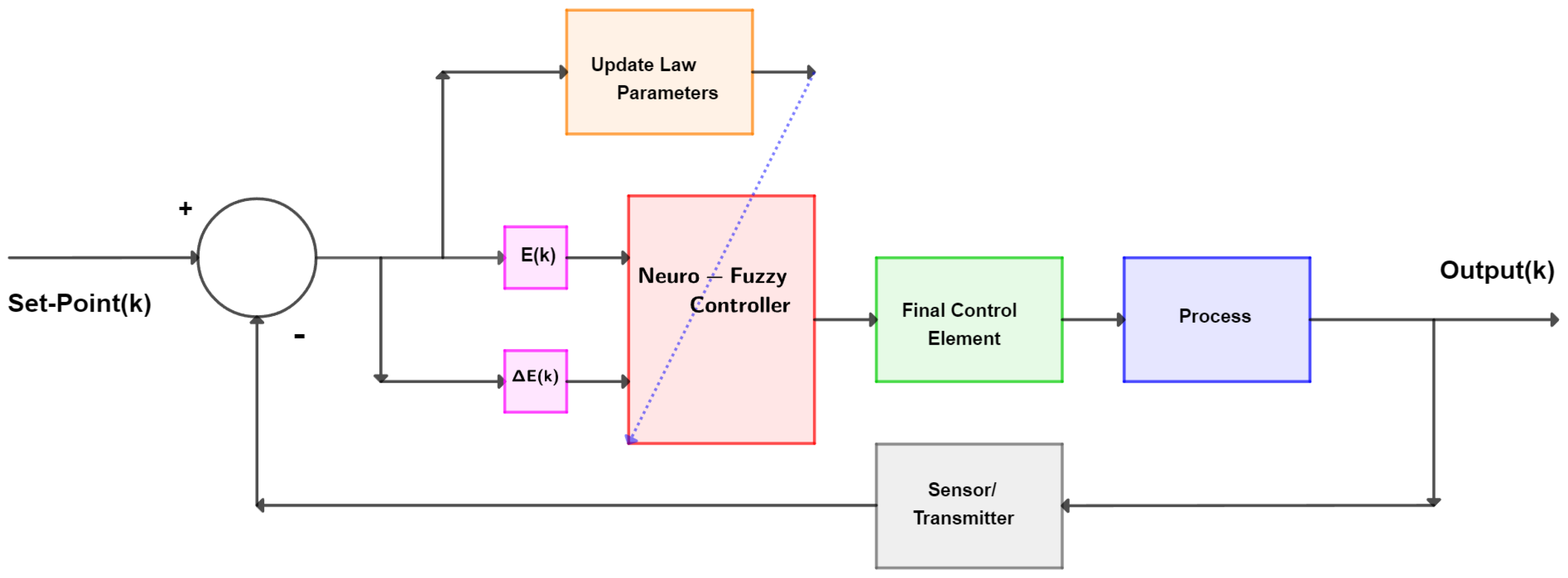
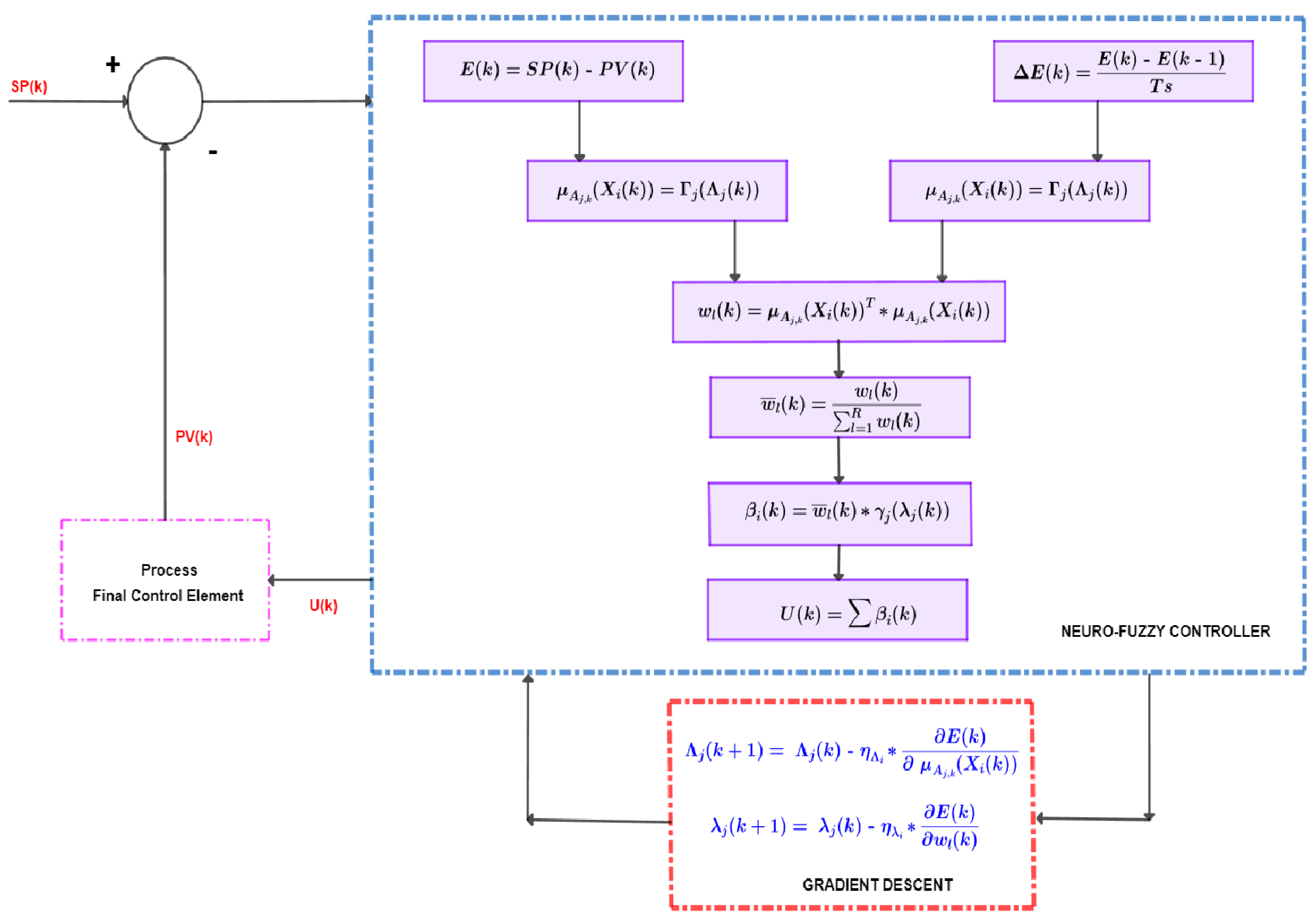
2.3. Neuro-Fuzzy Controller
2.4. Tuning NFC Parameters with DE
2.5. Validation Method
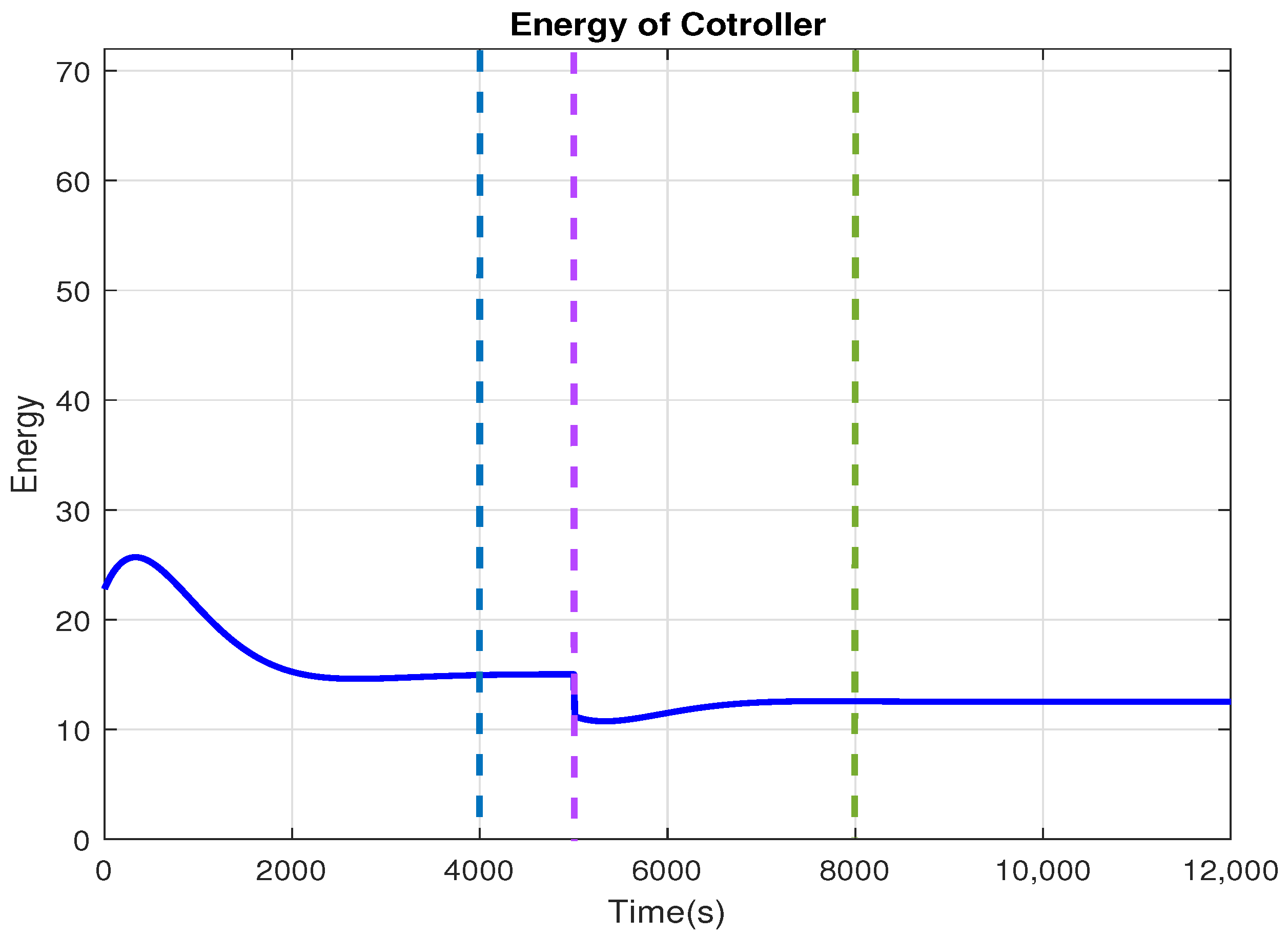
3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Z.; Dong, R.; Lan, G.; Yuan, T.; Tan, D. Diesel particulate filter regeneration mechanism of modern automobile engines and methods of reducing PM emissions: A review. Environ. Sci. Pollut. Res. 2023, 30, 39338–39376. [Google Scholar] [CrossRef]
- Benbellil, M.A.; Lounici, M.S.; Loubar, K.; Tazerout, M. Investigation of natural gas enrichment with high hydrogen participation in dual fuel diesel engine. Energy 2022, 243, 122746. [Google Scholar] [CrossRef]
- Bai, X.; Chen, H.; Oliver, B.G. The health effects of traffic-related air pollution: A review focused the health effects of going green. Chemosphere 2022, 289, 133082. [Google Scholar] [CrossRef]
- Mahbub, N.; Gemechu, E.; Zhang, H.; Kumar, A. The life cycle greenhouse gas emission benefits from alternative uses of biofuel coproducts. Sustain. Energy Technol. Assess. 2019, 34, 173–186. [Google Scholar] [CrossRef]
- Espootin, S.; Sameti, M.; Zaker, S. Biodiesel from fish waste oil: Synthesis via supercritical methanol and thermodynamic optimization. Clean Energy 2021, 5, 187–195. [Google Scholar] [CrossRef]
- Masera, O.; Rivero, J.C.S. Promoting a Sustainable Energy Transition in Mexico: The Role of Solid Biofuels. Bioenergy Res. 2022, 15, 1691–1693. [Google Scholar] [CrossRef]
- Balance Nacional de Energía: Producción de Energía Primaria. Available online: https://sie.energia.gob.mx/bdiController.do?action=cuadro&cvecua=IE11C01. (accessed on 14 July 2022).
- Orozco-Ramírez, Q.; Cohen-Salgado, D.; Arias-Chalico, T.; García, C.A.; Martínez-Bravo, R.; Masera, O. Production and market barriers of solid forest biofuels in Mexico From the enterprises’ perspective. Madera Bosques 2022, 28, 1–15. [Google Scholar]
- Sosa-Rodríguez, F.S.; Vazquez-Arenas, J. The biodiesel market in Mexico: Challenges and perspectives to overcome in Latin-American countries. Energy Convers. Manag. 2021, 12, 100149. [Google Scholar] [CrossRef]
- Macías-Alonso, M.; Hernández-Soto, R.; Carrera-Rodríguez, M.; Salazar-Hernández, C.; Mendoza-Miranda, J.M.; Villegas-Alcaraz, J.F.; Marrero, J.G. Obtention of biodiesel through an enzymatic two-step process. Study of its performance and characteristic emissions. RSC Adv. 2022, 12, 23747–23753. [Google Scholar] [CrossRef] [PubMed]
- Boly, M.; Sanou, A. Biofuels and food security: Evidence from Indonesia and Mexico. Energy Policy 2022, 163, 112834. [Google Scholar] [CrossRef]
- Yaqoob, H.; Teoh, Y.H.; Sher, F.; Farooq, M.U.; Jamil, M.A.; Kausar, Z.; Sabah, N.U.; Shah, M.F.; Rehman, H.Z.U.; Rehman, A.U. Potential of waste cooking oil biodiesel as renewable fuel in combustion engines: A review. Energies 2021, 14, 2565. [Google Scholar] [CrossRef]
- Rezaei, M.; Sameti, M.; Nasiri, F. An enviro-economic optimization of a hybrid energy system from biomass and geothermal resources for low-enthalpy areas. Energy Clim. Chang. 2021, 2, 100040. [Google Scholar] [CrossRef]
- Borase, R.P.; Maghade, D.; Sondkar, S.; Pawar, S. A review of PID control, tuning methods and applications. Int. J. Dyn. Control. 2021, 9, 818–827. [Google Scholar] [CrossRef]
- Aboelhassan, A.; Abdelgeliel, M.; Zakzouk, E.E.; Galea, M. Design and Implementation of model predictive control based PID controller for industrial applications. Energies 2020, 13, 6594. [Google Scholar] [CrossRef]
- Pacco, H.C. Simulation of temperature control and irrigation time in the production of tulips using Fuzzy logic. Procedia Comput. Sci. 2022, 200, 1–12. [Google Scholar] [CrossRef]
- Azad, A.S.; Rahaman, M.S.A.; Watada, J.; Vasant, P.; Vintaned, J.A.G. Optimization of the hydropower energy generation using Meta-Heuristic approaches: A review. Energy Rep. 2020, 6, 2230–2248. [Google Scholar] [CrossRef]
- Han, H.; Liu, H.; Li, J.; Qiao, J. Cooperative fuzzy-neural control for wastewater treatment process. IEEE Trans. Ind. Inform. 2020, 17, 5971–5981. [Google Scholar] [CrossRef]
- Pezeshki, Z.; Mazinani, S.M. Comparison of artificial neural networks, fuzzy logic and neuro fuzzy for predicting optimization of building thermal consumption: A survey. Artif. Intell. Rev. 2019, 52, 495–525. [Google Scholar] [CrossRef]
- Al Andzar, M.F.; Puriyanto, R.D. PID Control for Temperature and Motor Speed Based on PLC. Signal Image Process. Lett. 2019, 1, 7–13. [Google Scholar] [CrossRef]
- Giwa, A.; Ogunware, M.A. Modelling, simulation and control of a reactive distillation process for biodiesel production. ABUAD J. Eng. Res. Dev. 2018, 1, 49–60. [Google Scholar]
- Ajeni, M.O.; Heath, W.P.; Poupard, E. Modelling for Control of Biodiesel Microreactors. IFAC-Pap. 2021, 54, 312–317. [Google Scholar] [CrossRef]
- Adokiye, T.; Gunorubon, A.J.; Kenkugile, D.K. Modeling and Control of a Biodiesel Transesterification Reactor. Adv. Chem. Eng. Sci. 2020, 10, 210–224. [Google Scholar] [CrossRef]
- Farhat, Y.; Rhili, F.E.; Atig, A.; Zribi, A.; Ben Abdennour, R. Stability analysis strategy for the adaptive neural control system: A practical validation via a transesterification reactor. Iran. J. Sci. Technol. Trans. Electr. Eng. 2021, 45, 1395–1409. [Google Scholar] [CrossRef]
- Yassin, F.; Ali, Z.; Asma, A.; Ridha, B.A. Enhancement neural control scheme performance using PSO adaptive rate: Experimentation on a transesterification reactor. J. Vib. Control. 2022, 29, 3769–3782. [Google Scholar] [CrossRef]
- Shoelarta, S.; Ngatin, A.; Pia, R.B. Controlled microwave to boost biodiesel transesterification in continuous reactor. Proc. Aip Conf. Proc. 2020, 2197, 030002. [Google Scholar]
- Stanescu, R.C.; Leahu, C.I.; Soica, A. Aspects Regarding the Modelling and Optimization of the Transesterification Process through Temperature Control of the Chemical Reactor. Energies 2023, 16, 2883. [Google Scholar] [CrossRef]
- Tipsuwanporn, V.; Intajag, S.; Witheephanich, K.; Koetsam-ang, N.; Samiamag, S. Neuro-fuzzy controller design for industrial process controls. In Proceedings of the SICE 2004 Annual Conference, Sapporo, Japan, 4–6 August 2004; Volume 2, pp. 1656–1661. [Google Scholar]
- Ljung, L. System Identification Theory for User; Prentice-Hall: Englewood Cliffs, NJ, USA, 1987. [Google Scholar]
- Bortolet, P.; Palm, R. Identification, modeling and control by means of Takagi-Sugeno fuzzy systems. In Proceedings of the 6th International Fuzzy Systems Conference, Barcelona, Spain, 1–5 July 1997; Volume 1, pp. 515–520. [Google Scholar] [CrossRef]
- de Campos Souza, P.V. Fuzzy neural networks and neuro-fuzzy networks: A review the main techniques and applications used in the literature. Appl. Soft Comput. 2020, 92, 106275. [Google Scholar] [CrossRef]
- Cabrera, S.A.; Rojas–Moreno, A. Implementation of a Distributed Control System. In Proceedings of the 2022 IEEE XXIX International Conference on Electronics, Electrical Engineering and Computing (INTERCON), Lima, Peru, 11–13 August 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Huba, M.; Hypiusová, M.; Ťapák, P.; Vrancic, D. Active Disturbance Rejection Control for DC Motor Laboratory Plant Learning Object. Information 2020, 11, 151. [Google Scholar] [CrossRef]
- Liu, Y.; Lotero, E.; Goodwin, J.G.; Mo, X. Transesterification of poultry fat with methanol using Mg–Al hydrotalcite derived catalysts. Appl. Catal. Gen. 2007, 331, 138–148. [Google Scholar] [CrossRef]








| Parameter | Description | Range |
|---|---|---|
| Parameter of the membership functions ( and ) | Describe the functions in the first layer of NFC | must respect the relation (26) and (27), |
| Learning rate constants | Weight variations updated during learning | |
| Initial weights | The weights are used to calculate the output and also are updated through the training of NN, but different initial values can also produce different behaviors |
| Run | Objective Function | ITAE | TVU |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
| 9 | |||
| 10 | |||
| Mean | |||
| Standard deviation |
| Controller | ITAE | TVU |
|---|---|---|
| PID | 7.8770 | 32.0287 |
| Neuro-Fuzzy with Metaheuristics (best ITAE) | 4.0733 | 28.7059 |
| Neuro-Fuzzy with Metaheuristics (best TVU) | 8.1657 | 25.7697 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maya-Rodriguez, M.C.; Carvajal-Mariscal, I.; López-Muñoz, R.; Lopez-Pacheco, M.A.; Tolentino-Eslava, R. Temperature Control of a Chemical Reactor Based on Neuro-Fuzzy Tuned with a Metaheuristic Technique to Improve Biodiesel Production. Energies 2023, 16, 6187. https://doi.org/10.3390/en16176187
Maya-Rodriguez MC, Carvajal-Mariscal I, López-Muñoz R, Lopez-Pacheco MA, Tolentino-Eslava R. Temperature Control of a Chemical Reactor Based on Neuro-Fuzzy Tuned with a Metaheuristic Technique to Improve Biodiesel Production. Energies. 2023; 16(17):6187. https://doi.org/10.3390/en16176187
Chicago/Turabian StyleMaya-Rodriguez, Mario C., Ignacio Carvajal-Mariscal, Raúl López-Muñoz, Mario A. Lopez-Pacheco, and René Tolentino-Eslava. 2023. "Temperature Control of a Chemical Reactor Based on Neuro-Fuzzy Tuned with a Metaheuristic Technique to Improve Biodiesel Production" Energies 16, no. 17: 6187. https://doi.org/10.3390/en16176187
APA StyleMaya-Rodriguez, M. C., Carvajal-Mariscal, I., López-Muñoz, R., Lopez-Pacheco, M. A., & Tolentino-Eslava, R. (2023). Temperature Control of a Chemical Reactor Based on Neuro-Fuzzy Tuned with a Metaheuristic Technique to Improve Biodiesel Production. Energies, 16(17), 6187. https://doi.org/10.3390/en16176187







