Directions of Application of Phasor Measurement Units for Control and Monitoring of Modern Power Systems: A State-of-the-Art Review
Abstract
1. Introduction
- To determine the scope of PMU application in the conditions of a modern EPS;
- Characterized by a high degree of uncertainty in the course of normal and transient processes due to a significant proportion of stochastic generation sources.
- Section 2 provides general information about ultrasound and the directions for the development of algorithms for estimating the parameters of the electrical mode. This section allows you to identify the key features and directions for the development of a PMU;
- Section 3 is devoted to the consideration of the use of PMUs in the task of assessing the state of the EPS, which is the main one for monitoring and controlling normal and transient electrical modes;
- Section 4 provides an analysis of modern trends for the task of the relay protection of the EPS;
- In Section 5, the use of PMUs for the emergency management of EPS modes is considered;
- Section 6 presents the results of a review of the methods of optimal PMU placement in the EPS.
2. Development of Algorithms for Determining the Parameters of the Electric Mode Used in PMUs
- DFT and its modifications;
- Sinusoidal approximation algorithms;
- Hilbert transform (HT);
- Taylor series approximation;
- The Prony method.
3. The Use of PMUs for the Task of State Estimation
3.1. Classical WLSM SE, Expanded by PMU Data
- A single set of measurements is used in one procedure, which increases the accuracy of the initial data and can improve the accuracy of the assessment.
- The advantages of the accuracy of the PMU data, their synchronization, and linking to the moment of time will be partially lost due to their use in conjunction with classical telemetry;
- There is no certainty in the choice of weight coefficients;
- As the dimension of the problem increases, modern approaches to the SE aim to solve this problem, but it may persist, for example, when searching for bad data, analyzing observability, and searching for topological errors;
- Depending on the formulation of the problem, there may be some difficulties associated with taking into account currents, the angle of the base node, and measurements of voltage angles;
- The implementation of this approach will require the modification of existing SE programs, both in terms of introducing new types of measurements, and ensuring optimal design characteristics.
3.2. Linear SE WLSM Based Only on PMUs
- Increases the speed of operation and reliability of obtaining a solution due to the exclusion of the iterative process;
- Only high precision measurements are involved;
- The matrices used in the calculations do not change as long as the repair scheme of the network and the composition of measurements are preserved;
- All measurements have a timestamp, which can be taken into account at the preprocessing stage.
- For the correct operation of the SE algorithm and the associated search for bad data, an ultrasound redundancy PMU is required, which is extremely rare in practice.
3.3. Two-Level WLSM SE Based on the PMU Framework
- With a certain framework, the remaining network can be divided into islands, in each of which an independent SE is performed, which significantly speeds up the calculations.
- Measurements are evaluated in groups, which reduces the efficiency of the algorithm to reduce the overall error of the measurement set;
- The PMU should be arranged in a certain way, which is difficult to achieve given the variety of the repair schemes of the network.
3.4. Two-Level WLSM SE with Post-Processing Stage
- The approach can have all the advantages of a linear SE with a sufficient level of observability of the PMU network and the correct choice of weighting coefficients for the measurements;
- Instead of classical measurements with reduced accuracy, a state vector obtained at the stage of solving the iterative SE problem is added as the estimated parameters, which is better than adding traditional measurements directly;
- The existing software for the SE and processes based on the results of its calculations is preserved. In this case, the transfer of these processes to a linear SE can be done after a sufficient number of calculations have been performed by the power company, guaranteeing the best result for the new algorithm in comparison with existing SE modules.
- Post-processing is performed much more often than the first stage, which means that in most calculations, it contains outdated information; moreover, it is obtained on the basis of traditional measurements, which contain a large error in comparison with the vector measurements;
- There is no certainty in the choice of weight coefficients; this problem requires careful study to properly account for heterogeneous information.
3.5. Two-Level SE WLSM Performed at the Facility and in the Dispatch Center
- Parallelization of the SE process at the level of objects where the PMU is installed, due to its execution for each voltage class of each object in isolation;
- Only the results of the SE performed at the facility can be transmitted to the dispatcher center level; there is no need to transfer a complete set of data from the PMU;
- Switch states can be clarified at the object level and incorrect measurements can be rejected;
- At the object level, the resistances of the elements do not participate; the SE is performed for each voltage class based on the first Kirchhoff law as well as the calculation of the weighted average voltage.
- With the SE at the object level, the redundancy is insignificant, which worsens the quality of evaluation;
- It is required that all objects of the dispatch center model are observed by the PMU;
- At the object level, it is required that the PMU provide measurements of the currents of absolutely all connections in the object of the voltage classes under consideration;
- There are problems with finding bad data in the circuit variety; for example, if one voltage level of an object is modeled by a node with two branches, then bad data in the measurement of such an object cannot be identified since both measurements can relate to it with the same probability.
3.6. Transition to Linear SE
3.7. Features of Linear SE
3.8. Increasing the Redundancy of Measurements of the Classical Iterative SE
3.9. Selection of Weighting Coefficients for PMUs
- Measuring transformers;
- Measuring instruments;
- Update delays (dead zones caused by the nature of the transmission of measurements to dispatch centers).
- Be taken for an immutable network scheme,
- Have the same composition of measurements;
- Does not contain gross errors.
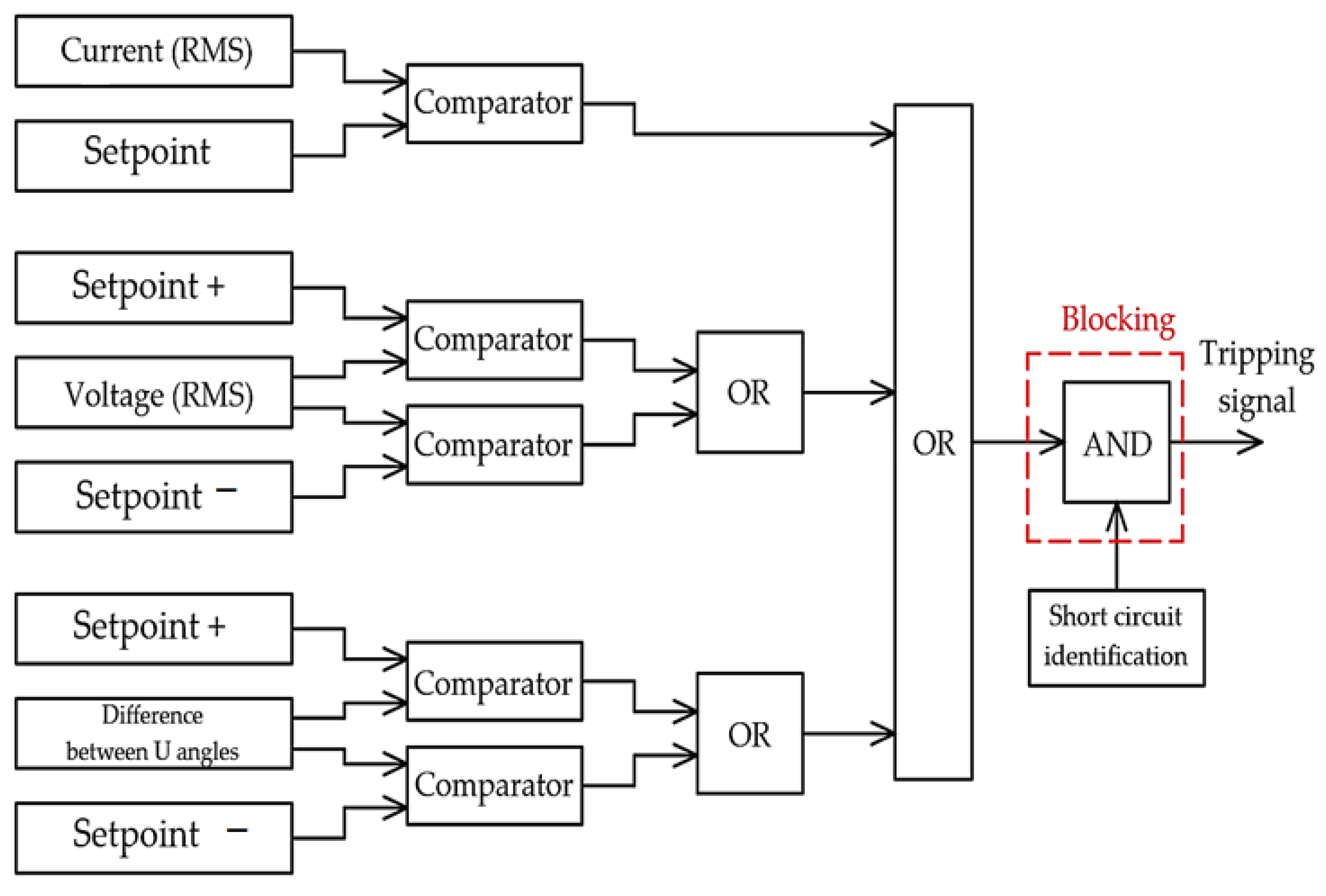
4. The Use of PMUs for Relay Protection
4.1. Classification of Directions of Development of Protection Functions with PMUs
- Providing the existing protections of power system elements with new properties: expanding the properties of the traditional differential protections of lines, motors, generators, tires, and busbars; increasing the sensitivity of remote protections during swings by clarifying the protection response zone; perfecting swing blocking (SB) functions; selectively triggering overcurrent protections (OPs) by fixing the direction of the short-circuit power flow and reducing the response time due to the control of the U vectors; protecting the generators (from loss of excitation, etc.) by tracking the movement of the vector in its operation mode according to the P−Q diagram;
- Adaptive protections that adapt to the conditions of changing the mode and network scheme. Basically, these are step-by-step protections with relative selectivity, the setpoint or characteristic of which depends on circuit-mode changes in the power system;
- Protection with a wide coverage of the protected area (due to coverage of communication channels and PMUs)—WAMPAC (Wide Area Monitoring Protection and Control).
- Centralization of the protection and automation functions in one decision-making device with action on the actuators of power system facilities through digital communication channels;
- Protections based on the analysis of trends in vector changes on the complex plane or the shape of current and voltage curves (Continuous Point-On-Wave, or CPOW technology). Mathematical apparatus: application of the DWT wavelet transform and application of AI machine learning methods.
4.2. Solutions in the Field of Integration of PMUs into Traditional Protection Algorithms
- The use of PMUs as part of existing, traditional protection algorithms.
- The use of algorithms based on new principles of damage detection, which are different from traditional ones.
4.3. Solutions in the Field of New Principles of Damage Detection
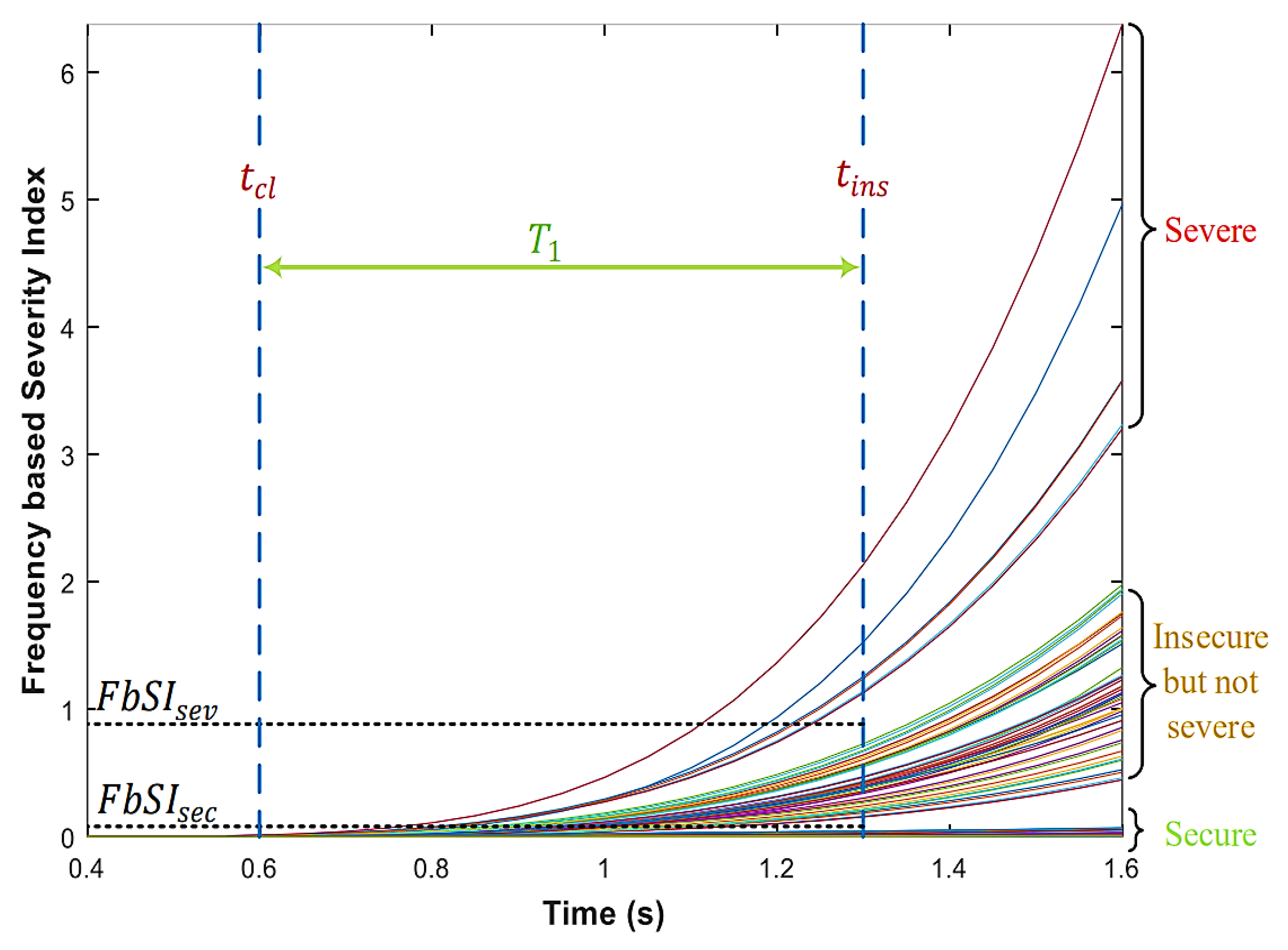
5. The Use of PMUs for Emergency Control
5.1. Phasor Measurements and AFLS
5.2. Phasor Measurements and AESM
5.3. Phasor Measurements in the Problem of Identification and Advanced Network Division
5.4. Phasor Measurements in the Problem of Identification and Damping of Electromechanical Oscillations
5.5. Phasor Measurements in the Problem of Identification and Damping of Electromechanical Oscillations
5.6. Phasor Measurements in the Problem of Identification and Classification of Emergency Events
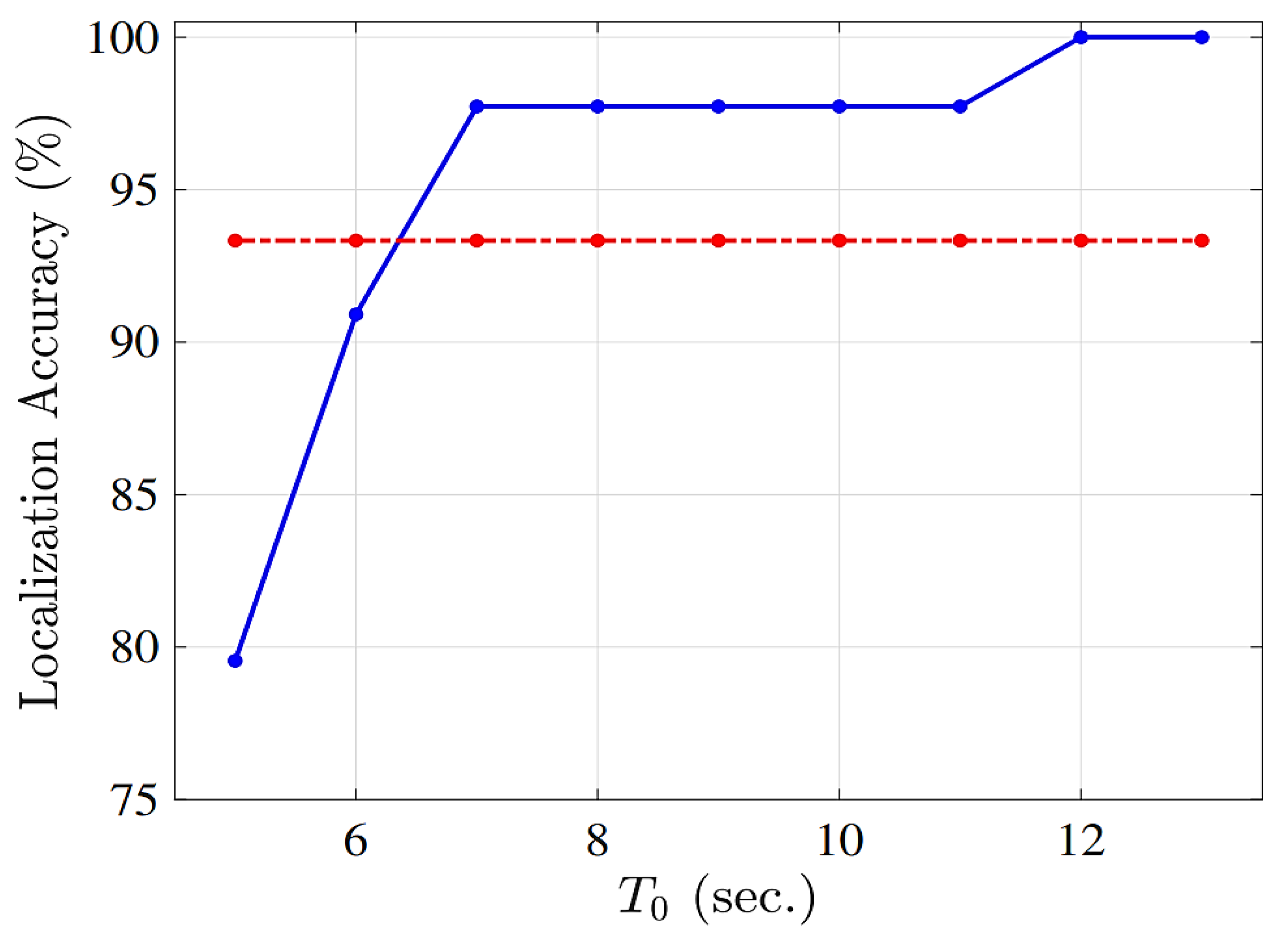
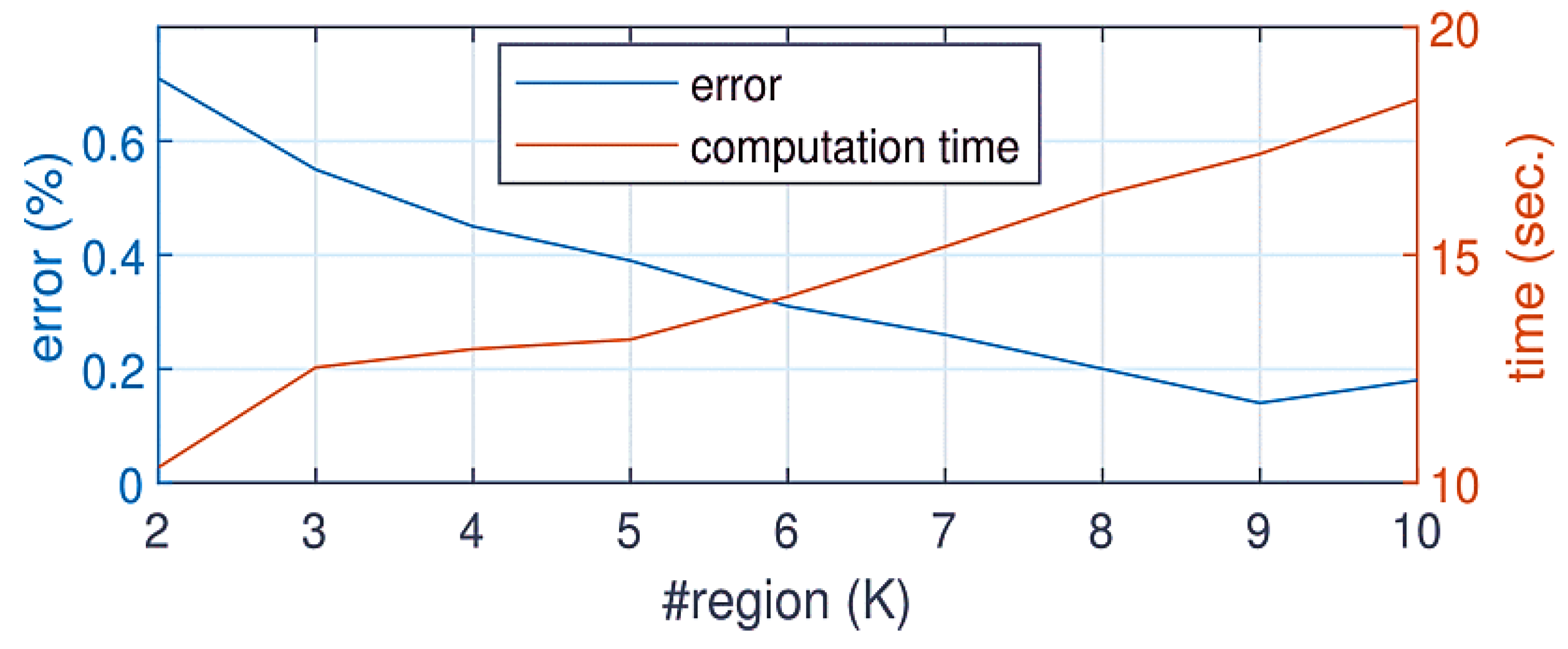
6. Determining the Optimal Installation Locations for PMUs
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AESM | Automatic elimination of asynchronous mode |
| AER | Automatic excitation regulator |
| AFLS | Automatic frequency load shedding |
| AI | Artificial intelligence |
| ANN | Artificial neural networks |
| APDC | Advanced phasor data concentrato |
| AVR | Automatic voltage regulator |
| CLTL | Cross-lingual transfer learning |
| DFT | Discrete Fourier transformation |
| DS | Digital substation |
| DT | Decision tree |
| DWT | Discrete wavelet transform |
| ECA | Emergency control automatics |
| ECS | Electrical centre of swings |
| EPS | Electric power substation |
| FACTS | Flexible alternating current transmission system |
| FFNN | Feedforward neural network |
| HT | Hilbert transformation |
| IEEE | Institute of electronic and electrical engineers |
| iNNE | Isolation using Nearest Neighbor Ensemble |
| kNN | K-nearest neighbor method |
| LR | Lock-out relay |
| LSM | Least square method |
| MC-CNN | Multi-channel convolutional neural network |
| MLP | Multilayer perceptron |
| MLR | Multinomial logistic regression |
| OOSPD | Out-of-step protection device |
| OP | Overcurrent protection |
| PMU | Phasor measurement unit |
| POW | Point of Wave |
| PS | Power system |
| PSS | Power system stabilizer |
| RES | Renewable energy resources |
| SB | Swing blocking |
| SC | Short circuit |
| SCADA | Supervisory control and data acquisition system |
| SC-CNN | Single channel convolutional neural network |
| SKNNO | kNN method with reinforcement |
| SE | State estimation |
| SCB | Static capacitor bank |
| SVM | Support vector machine |
| SLE | System of linear equations |
| WAMPAC | Wide Area Monitoring Protection and Control |
| WLSM | Weighted least squares method |
References
- Liu, D.; Zhang, X.; Tse, C.K. Effects of High Level of Penetration of Renewable Energy Sources on Cascading Failure of Modern Power Systems. IEEE J. Emerg. Sel. Top. Circuits Syst. 2022, 12, 98–106. [Google Scholar] [CrossRef]
- Hu, J.; Liu, X.; Shahidehpour, M.; Xia, S. Optimal Operation of Energy Hubs with Large-Scale Distributed Energy Resources for Distribution Network Congestion Management. IEEE Trans. Sustain. Energy 2021, 12, 1755–1765. [Google Scholar] [CrossRef]
- Xu, S.; Liu, H.; Bi, T.; Martin, K.E. A High-Accuracy Phasor Estimation Algorithm for PMU Calibration and Its Hardware Implementation. IEEE Trans. Smart Grid 2020, 11, 3372–3383. [Google Scholar] [CrossRef]
- Plamanescu, R.; Albu, M.; Gheorghe, S.; Bugnar, S.; Coroiu, M. PMU Cloud-based Applications for Power Systems Insight. In Proceedings of the 2019 54th International Universities Power Engineering Conference (UPEC), Bucharest, Romania, 3–6 September 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Baudette, M.; Vanfretti, L.; Del-Rosario, G.; Ruíz-Alvarez, A.; Domínguez-García, J.L.; Al-Khatib, I. Validating a real-time PMU-based application for monitoring of sub-synchronous wind farm oscillations. In Proceedings of the ISGT 2014, Washington, DC, USA, 19–22 February 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, X.; Nair, N.-K.C. Review on D-PMU based applications for active electricity distribution system. In Proceedings of the 2020 IEEE International Conference on Power Systems Technology (POWERCON), Bangalore, India, 14–16 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, X.; Lu, N.; Luo, H. Optimization Based Distribution Network Fault Location Method Using PMU Information. In Proceedings of the 2022 China International Conference on Electricity Distribution (CICED), Changsha, China, 7–8 September 2022; pp. 1361–1365. [Google Scholar] [CrossRef]
- Hou, Y.; Fang, T.; Shi, F.; Zhang, H. Parameter estimation method of distribution network based on PMU measurement data. In Proceedings of the 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 4–7 June 2020; pp. 1620–1625. [Google Scholar] [CrossRef]
- Alinejad, B.; Akbari, M.; Kazemi, H. PMU-based distribution network load modelling using Harmony Search Algorithm. In Proceedings of the 2012 17th Conference on Electrical Power Distribution, Tehran, Iran, 2–3 May 2012; pp. 1–6. [Google Scholar]
- Mogharbel, B.; Fan, L.; Miao, Z. Least squares estimation-based synchronous generator parameter estimation using PMU data. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Satsuk, E.; Zhukov, A.; Dubinin, D.; Ivanov, I.; Murzin, A. Analytical Approach to Phasor-based Line Parameter Estimation Verified Through Real PMU Data. In Proceedings of the 2022 International Conference on Smart Grid Synchronized Measurements and Analytics (SGSMA), Split, Croatia, 24–26 May 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Chowdhury, S.D.; Senroy, N. PMU data based online parameter estimation of synchronous generator. In Proceedings of the 2016 IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Rahman, K.M.J.; Munnee, M.M.; Khan, S. Largest blackouts around the world: Trends and data analyses. In Proceedings of the 2016 IEEE International WIE Conference on Electrical and Computer Engineering (WIECON-ECE), Pune, India, 19–21 December 2016; pp. 155–159. [Google Scholar] [CrossRef]
- Phadke, A.G. Synchronized phasor measurements-a historical overview. In Proceedings of the IEEE/PES Transmission and Distribution Conference and Exhibition, Yokohama, Japan, 6–10 October 2002; Volume 1, pp. 476–479. [Google Scholar] [CrossRef]
- Xu, S.; Liu, H.; Bi, T. Field PMU Test and Calibration Method—Part I: General Framework and Algorithms for PMU Calibrator. J. Mod. Power Syst. Clean Energy 2022, 10, 1507–1518. [Google Scholar] [CrossRef]
- Castello, P.; Ferrero, R.; Pegoraro, P.A.; Toscani, S. Effect of Unbalance on Positive-Sequence Synchrophasor, Frequency, and ROCOF Estimations. IEEE Trans. Instrum. Meas. 2018, 67, 1036–1046. [Google Scholar] [CrossRef]
- Wen, H.; Teng, Z.; Wang, Y.; Yang, Y. Optimized Trapezoid Convolution Windows for Harmonic Analysis. IEEE Trans. Instrum. Meas. 2013, 62, 2609–2612. [Google Scholar] [CrossRef]
- Derviškadić, A.; Romano, P.; Paolone, M. Iterative-Interpolated DFT for Synchrophasor Estimation: A Single Algorithm for P- and M-Class Compliant PMUs. IEEE Trans. Instrum. Meas. 2018, 67, 547–558. [Google Scholar] [CrossRef]
- Romano, P.; Paolone, M. Enhanced Interpolated-DFT for Synchrophasor Estimation in FPGAs: Theory, Implementation, and Validation of a PMU Prototype. IEEE Trans. Instrum. Meas. 2014, 63, 2824–2836. [Google Scholar] [CrossRef]
- Romano, P.; Paolone, M. An enhanced interpolated-modulated sliding DFT for high reporting rate PMUs. In Proceedings of the 2014 IEEE International Workshop on Applied Measurements for Power Systems Proceedings (AMPS), Aachen, Germany, 24–26 September 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Belega, D.; Petri, D. Accuracy of synchrophasor measurements provided by the sine-fit algorithms. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012; pp. 921–926. [Google Scholar] [CrossRef]
- Balestrieri, E.; De Vito, L.; Rapuano, S.; Slepicka, D. Estimating the Uncertainty in the Frequency Domain Characterization of Digitizing Waveform Recorders. IEEE Trans. Instrum. Meas. 2012, 61, 1613–1624. [Google Scholar] [CrossRef]
- Karimi-Ghartemani, M.; Ooi, B.-T.; Bakhshai, A. Application of Enhanced Phase-Locked Loop System to the Computation of Synchrophasors. IEEE Trans. Power Deliv. 2011, 26, 22–32. [Google Scholar] [CrossRef]
- Yang, H.; Tu, Y.; Peng, Y. Comparative analysis of phase difference estimation methods based on Hilbert transform with or without endpoint effect. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 2963–2967. [Google Scholar] [CrossRef]
- Martin, K.E.; Hamai, D.; Adamiak, M.G.; Anderson, S.; Begovic, M. Exploring the IEEE Standard C37.118–2005 Synchrophasors for Power Systems. IEEE Trans. Power Deliv. 2008, 23, 1805–1811. [Google Scholar] [CrossRef]
- de la O Serna, J.A. Dynamic phasor estimates for power system oscillations and transient detection. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; p. 7. [Google Scholar] [CrossRef]
- Frigo, G.; Derviškadić, A.; Zuo, Y.; Bach, A.; Paolone, M. Taylor-Fourier PMU on a Real-Time Simulator: Design, Implementation and Characterization. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- de la O Serna, J.A. Synchrophasor Estimation Using Prony’s Method. IEEE Trans. Instrum. Meas. 2013, 62, 2119–2128. [Google Scholar] [CrossRef]
- Toscani, S.; Muscas, C.; Pegoraro, P.A. Design and Performance Prediction of Space Vector-Based PMU Algorithms. IEEE Trans. Instrum. Meas. 2017, 66, 394–404. [Google Scholar] [CrossRef]
- Al-Othman, A.K.; Irving, M.R. A comparative study of two methods for uncertainty analysis in power system State estimation. IEEE Trans. Power Syst. 2005, 20, 1181–1182. [Google Scholar] [CrossRef]
- Tarali, A.; Abur, A. Bad data detection in two-stage state estimation using phasor measurements. In Proceedings of the 2012 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Berlin, Germany, 14–17 October 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Chen, J.; Abur, A. Improved bad data processing via strategic placement of PMUs. In Proceedings of the IEEE Power Engineering Society General Meeting 2005, San Francisco, CA, USA, 16 June 2005; pp. 2759–2763. [Google Scholar] [CrossRef]
- Göl, M.; Abur, A. LAV Based Robust State Estimation for Systems Measured by PMUs. IEEE Trans. Smart Grid 2014, 5, 1808–1814. [Google Scholar] [CrossRef]
- Göl, M.; Abur, A. A Hybrid State Estimator for Systems with Limited Number of PMUs. IEEE Trans. Power Syst. 2015, 30, 1511–1517. [Google Scholar] [CrossRef]
- Kolosok, I.N.; Korkina, E.S.; Mahnitko, A.E. Detection of systematic errors in PMU measurements by the power system state estimation methods. In Proceedings of the 2015 56th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 14 October 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Zhang, J.; Welch, G.; Bishop, G.; Huang, Z. A Two-Stage Kalman Filter Approach for Robust and Real-Time Power System State Estimation. IEEE Trans. Sustain. Energy 2014, 5, 629–636. [Google Scholar] [CrossRef]
- Ghahremani, E.; Kamwa, I. Dynamic State Estimation in Power System by Applying the Extended Kalman Filter with Unknown Inputs to Phasor Measurements. IEEE Trans. Power Syst. 2011, 26, 2556–2566. [Google Scholar] [CrossRef]
- Zivanovic, R.; Cairns, C. Implementation of PMU technology in state estimation: An overview. In Proceedings of the IEEE. AFRICON ′96, Stellenbosch, South Africa, 27 September 1996; Volume 2, pp. 1006–1011. [Google Scholar] [CrossRef]
- Manousakis, N.M.; Korres, G.N. Optimal PMU Placement for Numerical Observability Considering Fixed Channel Capacity—A Semidefinite Programming Approach. IEEE Trans. Power Syst. 2016, 31, 3328–3329. [Google Scholar] [CrossRef]
- Gao, Z.; Li, J. Optimal PMU Placement Considering Data Integrity Attack. In Proceedings of the 2022 IEEE 16th International Conference on Compatibility, Power Electronics, and Power Engineering (CPE-POWERENG), Birmingham, UK, 29 June–1 July 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Zhou, M.; Centeno, V.A.; Thorp, J.S.; Phadke, A.G. An Alternative for Including Phasor Measurements in State Estimators. IEEE Trans. Power Syst. 2006, 21, 1930–1937. [Google Scholar] [CrossRef]
- Phadke, A.G.; Thorp, J.S.; Nuqui, R.F.; Zhou, M. Recent developments in state estimation with phasor measurements. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009; pp. 1–7. [Google Scholar] [CrossRef]
- Yang, T.; Sun, H.; Bose, A. Transition to a Two-Level Linear State Estimator—Part I: Architecture. IEEE Trans. Power Syst. 2011, 26, 46–53. [Google Scholar] [CrossRef]
- Yang, T.; Sun, H.; Bose, A. Transition to a Two-Level Linear State Estimator—Part II: Algorithm. IEEE Trans. Power Syst. 2011, 26, 54–62. [Google Scholar] [CrossRef]
- Joshi, P.M.; Verma, H. Synchrophasor measurement applications and optimal PMU placement: A review. Electr. Power Syst. Res. 2021, 199, 107428. [Google Scholar] [CrossRef]
- Zhu, J.; Abur, A. Effect of Phasor Measurements on the Choice of Reference Bus for State Estimation. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–5. [Google Scholar] [CrossRef]
- D’Antona, G.; Davoudi, M. Effect of Phasor Measurement Unit on power State Estimation considering parameters uncertainty. In Proceedings of the 2012 IEEE International Workshop on Applied Measurements for Power Systems (AMPS) Proceedings, Aachen, Germany, 26–28 September 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Mokeev, A.V.; Piskunov, S.A. Expanding the Field of Synchronized Phasor Measurements Application in Power Systems. In Proceedings of the 2021 International Siberian Conference on Control and Communications (SIBCON), Kazan, Russia, 13–15 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Patil, G.C.; Thosar, A.G. Application of synchrophasor measurements using PMU for modern power systems monitoring and control. In Proceedings of the 2017 International Conference on Computation of Power, Energy Information and Commuincation (ICCPEIC), Melmaruvathur, India, 22–23 March 2017; pp. 754–760. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, G.; Jabr, R.A. Robust Detection of Cyber Attacks on State Estimators Using Phasor Measurements. IEEE Trans. Power Syst. 2017, 32, 2468–2470. [Google Scholar] [CrossRef]
- Ahmad, F.A.; Habiballah, I.O.; Shahriar, M.S. Inclusion of Phasor Measurement Units in Least Measurement Rejected State Estimator. In Proceedings of the 2018 Australasian Universities Power Engineering Conference (AUPEC), Auckland, New Zealand, 27–30 November 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Ghosh, P.K. Complete and incomplete PMU observablity for hybrid state estimation. In Proceedings of the 2017 International Conference on Computation of Power, Energy Information and Commuincation (ICCPEIC), Melmaruvathur, India, 22–23 March 2017; pp. 867–870. [Google Scholar] [CrossRef]
- Kumar, J.; Rai, J.N.; Hasan, N. Use of Phasor Measurement Unit (PMU) for large scale power system state estimation. In Proceedings of the 2012 IEEE 5th India International Conference on Power Electronics (IICPE), Delhi, India, 6–8 December 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Abur, A.; Gomez-Exposito, A. Power System State Estimation: Theory and Implementation; CRC Press: Boca Raton, FL, USA, 2004; Volume 24. [Google Scholar] [CrossRef]
- De la Villa Jaén, A.; Martínez, J.B.; Gómez-Expósito, A.; Vázquez, F.G. Tuning of Measurement Weights in State Estimation: Theoretical Analysis and Case Study. IEEE Trans. Power Syst. 2018, 33, 4583–4592. [Google Scholar] [CrossRef]
- Baltensperger, R.; Loosli, A.; Sauvain, H.; Zima, M.; Andersson, G.; Nuqui, R. An implementation of two-stage hybrid state estimation with limited number of PMU. In Proceedings of the 10th IET International Conference on Developments in Power System Protection (DPSP 2010), Manchester, UK, 29 March–1 April 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Zhong, S.; Abur, A. Auto tuning of measurement weights in WLS state estimation. IEEE Trans. Power Syst. 2004, 19, 2006–2013. [Google Scholar] [CrossRef]
- Zhang, L.; Abur, A. State estimator tuning for PMU measurements. In Proceedings of the 2011 North American Power Symposium, Boston, MA, USA, 4–6 August 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Standart 56947007-29.120.70.241-2017; Technical Requirements for Microprocessor-Based Relay Protection. FGC UES, PJSC Standard; Date of Changes Introduction: 11.12.2019; FSK-Rosseti PAO: Moscow, Russia, 2017; 357p.
- Ramesh, L.; Chowdhury, S.P.; Chowdhury, S. Wide area monitoring protection and control—A comprehensive application review. In Proceedings of the 10th International Conference on Developments in Power System Protection (DPSP 2010), Managing the Change, Manchester, UK, 29 March–1 April 2010; IET: London, UK; pp. 1–4. [Google Scholar] [CrossRef]
- Khederzadeh, M. Wide-area protection in smart grids. In Proceedings of the 11th IET International Conference on Developments in Power Systems Protection (DPSP 2012), Birmingham, UK, 23–26 April; IET: London, UK, 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Leibovich, P.; Issouribehere, F.; Barbero, J. Design and Implementation of a low-cost PMU: Validation by tests and perfor-mance during 2019 Argentinean blackout. In Proceedings of the IEEE Power & Energy Society General Meeting (PESGM 2021), Washington, DC, USA, 26–29 July 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Chavez, J.J.; Kumar, N.V.; Azizi, S.; Guardado, J.L.; Rueda, J.; Palensky, P.; Terzija, V.; Popov, M. PMU-voltage drop based fault locator for transmission backup protection. Electr. Power Syst. Res. 2021, 196, 107188. [Google Scholar] [CrossRef]
- Motavalian, A.R.; Moadabi, N.; Gharehpetian, G.B. Reliability Assessment of Power System Backup Protection in Smart Grid Control Center Using Phasor Measurement Units (PMU). Renew. Energy Power Qual. J. 2013, 11, 404–410. [Google Scholar] [CrossRef]
- Karthick, S.; Lakshmi, K. Wide area backup protection scheme for power transmission lines using PMU. Int. Res. J. Eng. Technol. IRJET 2015, 2, 273–281. [Google Scholar]
- Jena, M.K.; Samantaray, S.R.; Panigrahi, B.K. Supervisory control based wide area back-up protection scheme for power transmission network. In Proceedings of the National Power Systems Conference (NPSC 2016), Bhubaneswar, India, 19–21 December 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Saran, A. Comparison between overcurrent relay and devel-oped PMU based protection. In Proceedings of the North American Power Symposium (NAPS 2013), Manhattan, KS, USA, 22–24 September 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Rao, J.G.; Pradhan, A.K. Application of synchrophasor data for fault detection during power swing. In Proceedings of the International Conference on Energy, Automation and Signal, Bhubaneswar, India, 28–30 December 2011; pp. 1–5. [Google Scholar] [CrossRef]
- Ariff, M.A.M.; Pal, B.C. Adaptive Protection and Control in the Power System for Wide-Area Blackout Prevention. IEEE Trans. Power Deliv. 2016, 31, 1815–1825. [Google Scholar] [CrossRef]
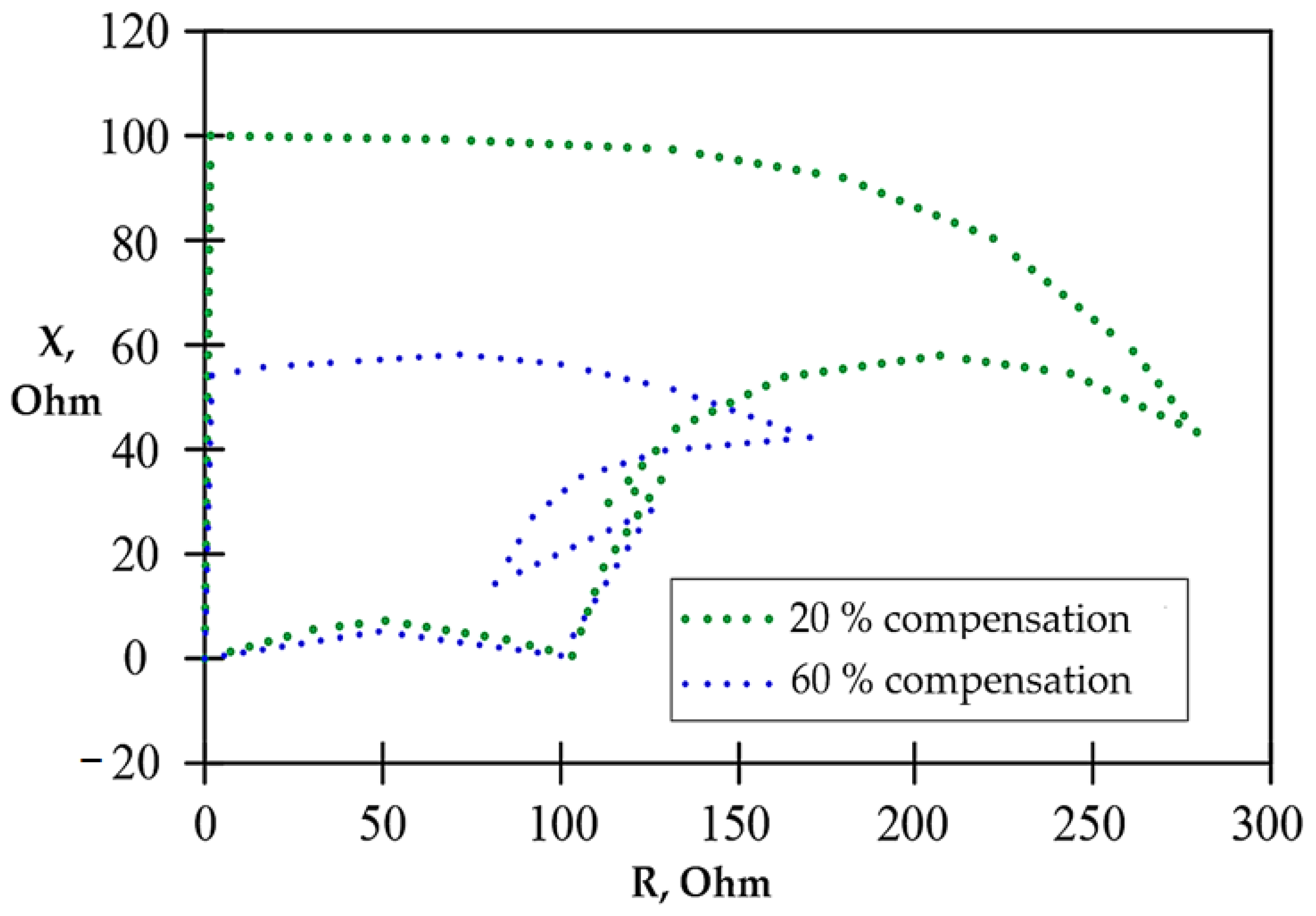
- Keramat, M.M.; Fazaeli, M.H. The New Adaptive Protection Method for the Compensated Transmission Lines with the Series Capacitor in a High Share of Wind Energy Resources by Using PMU Data. In Proceedings of the 7th Iran Wind Energy Conference (IWEC 2021), Shahrood, Iran, 17–18 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Sarangi, S.; Pradhan, A.K. Apply PMU data for Zone-2 setting of series compensated line. In Proceedings of the International Conference on Energy, Automation and Signal, Bhubaneswar, India, 28–30 December 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Pal, D.; Mallikarjuna, B.; Reddy, R.J.; Reddy, M.J.B.; Mohanta, D.K. Synchrophasor Assisted Adaptive Relaying Methodology to Prevent Zone-3 Mal-Operation During Load Encroachment. IEEE Sens. J. 2017, 17, 7713–7722. [Google Scholar] [CrossRef]
- Naeini, E.; Vaseghi, B.; Mahdavian, M. Modified Transmission Line Protection Scheme in the Presence of SCC. J. Electr. Eng. Technol. 2017, 12, 533–540. [Google Scholar] [CrossRef][Green Version]
- Chunju, F.; Shengfang, L.; Weiyong, Y.; Li, K.K. Study on adaptive relay protection scheme based on phase measurement unit (PMU). In Proceedings of the Eighth IEE International Conference on Developments in Power System Protectio, Amsterdam, The Netherlands, 5–8 April 2004; IET: London, UK, 2004; pp. 36–39. [Google Scholar] [CrossRef]
- Yang, Z.; Liao, W.; Zhang, Q.; Bak, C.L.; Chen, Z. Fault Coordination Control for Converter-Interfaced Sources Compatible With Distance Protection During Asymmetrical Faults. IEEE Trans. Ind. Electron. 2023, 70, 6941–6952. [Google Scholar] [CrossRef]
- Bi, T.; Sui, J.; Yu, H.; Yang, Q. Adaptive loss of field protection based on phasor measure-ments. In Proceedings of the IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Senapati, S.; Das Bhattacharya, K.; Das, J.K. Application of phasor measurement unit in adaptive protection for loss of excitation in a generator. In Proceedings of the 6th IEEE Power India International Conference (PIICON 2014), Delhi, India, 5–7 December 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Desai, J.P.; Makwana, V.H. Phasor Measurement Unit Incorporated Adaptive Out-of-step Protection of Synchronous Generator. J. Mod. Power Syst. Clean Energy 2021, 9, 1032–1042. [Google Scholar] [CrossRef]
- Dragomir, I.-M.; Iliescu, S.S. Synchrophasors Applications in Power System Monitoring, Protection and Control. In Proceedings of the 2015 20th International Conference on Control Systems and Computer Science, Bucharest, Romania, 27–29 May 2015; pp. 978–983. [Google Scholar] [CrossRef]
- Skok, S.; Frlan, K.; Ugarkovic, K. Detection and Protection of Distributed Generation from Island Operation by Using PMUs. Energy Procedia 2017, 141, 438–442. [Google Scholar] [CrossRef]
- Xu, M.; Meng, T.; Zou, G.; Zhang, J.; Lin, X.; Yang, J. A centralized protection and control scheme for microgrid. In Proceedings of the 2015 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC 2015), Brisbane, QLD, Australia, 15–18 November 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Follum, J.; Miller, L.; Etingov, P.; Kirkham, H.; Riepnieks, A.; Fan, X.; Ellwein, E. Phasor or Waveforms: Considerations for Choosing Measurements to Match Your Application; Pacific Northwest Report; Pacific Northwest National Laboratory: Richland, WA, USA, 2021; 43p. [Google Scholar]
- Galvez, C.; Abur, A. Fault Location in Meshed and Active Power Distribution Networks. In Proceedings of the IEEE Madrid PowerTech, Madrid, Spain, 28 June–2 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Chusovitin, P.V.; Vershinin, A.B. Emergency control system for angular stability based on PMU data. In Proceedings of the 2021 4th International Youth Scientific and Technical Conference on Relay Protection and Automation (RPA), Moscow, Russia, 21–22 October 2021; pp. 1–9. [Google Scholar] [CrossRef]
- Yang, Y.; Shu, H. Power system stability analysis and control based on PMU. In Proceedings of the 2011 International Conference on Computer Science and Service System (CSSS), Nanjing, China, 27–29 June 2011; pp. 3376–3379. [Google Scholar] [CrossRef]
- Li, H.; Xie, X.; Tong, L.; Wu, J.; Luo, J. Implement of On-line Transient Stability Control Pre-decision in Wide-Area Measurement System in Jiangsu Power Network. In Proceedings of the 2005 IEEE/PES Transmission & Distribution Conference & Exposition: Asia and Pacific, Dalian, China, 18 August 2005; pp. 1–4. [Google Scholar] [CrossRef]
- Das, H.P.; Pradhan, A.K. Development of a micro-phasor measurement unit for distribution system applications. In Proceedings of the 2016 National Power Systems Conference (NPSC), Bhubaneswar, India, 19–21 December 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Boussadia, F.; Belkhiat, S. A new adaptive underfrequency load shedding scheme to improve frequency stability in electric power system. J. Eur. Des Systèmes Autom. 2021, 54, 263–271. [Google Scholar] [CrossRef]
- Eissa, M.M.; Ali, A.A.; Abdel-Latif, K.; Al-Kady, A.F. A frequency control technique based on decision tree concept by managing thermostatically controllable loads at smart grids. Int. J. Electr. Power Energy Syst. 2019, 108, 40–51. [Google Scholar] [CrossRef]
- Shekari, T.; Gholami, A.; Aminifar, F.; Sanaye-Pasand, M. An Adaptive Wide-Area Load Shedding Incorporating Power System Real-Time Limitations. IEEE Syst. J. 2018, 12, 759–767. [Google Scholar] [CrossRef]
- Zhu, Q. A Deep End-to-End Model for Transient Stability Assessment with PMU Data. IEEE Access 2018, 6, 65474–65487. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, S.; Wang, J. A power system out-of-step splitting control system based on wide area information and an on-line searching scheme of optimal splitting section. Int. J. Electr. Power Energy Syst. 2021, 126, 106587. [Google Scholar] [CrossRef]
- Nguyen, N.-V.; Shin, V.; Shevlyakov, G. Power system state estimation with fusion method. In Proceedings of the 2nd International Conference on Computer and Automation Engineering (ICCAE), Singapore, 26–28 February 2010; pp. 71–76. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Y. A Novel Out-of-Step Splitting Protection Based on the Wide Area Information. IEEE Trans. Smart Grid 2017, 1, 41–51. [Google Scholar] [CrossRef]
- Aghamohammadi, M.; Abedi, M. DT based intelligent predictor for out of step condition of generator by using PMU data. Int. J. Electr. Power Energy Syst. 2018, 99, 95–106. [Google Scholar] [CrossRef]
- Ivankovi, I.; Kuzle, I.; Holjevac, N. Wide Area Information-Based Transmission System Centralized Out-of-Step Protection Scheme. Energies 2017, 10, 633. [Google Scholar] [CrossRef]
- Tealane, M.; Kilter, J.; Popov, M.; Bagleybter, O.; Klaar, D. Online Detection of Out-of-Step Condition Using PMU-Determined System Impedances. IEEE Access 2022, 10, 14807–14818. [Google Scholar] [CrossRef]
- Deshmukh, B.; Biswal, S.; Lal, D.K. Synchronous Generator Out-of-Step Protection Based on Savitzky-Golay Filtering Technique. In Proceedings of the 2021 Emerging Trends in Industry 4.0 (ETI 4.0), Raigarh, India, 19–21 May 2021; pp. 1–3. [Google Scholar] [CrossRef]
- Zare, H.; Alinejad-Beromi, Y.; Yaghobi, H. Intelligent prediction of out-of-step condition on synchronous generators because of transient instability crisis. Int. Trans. Electr. Energy Syst. 2018, 29, 2686. [Google Scholar] [CrossRef]
- Mahdi, M.; Genc, V.M.I. A Real-Time Self-Healing Methodology Using Model- and Measurement-Based Islanding Algorithms. IEEE Trans. Smart Grid 2019, 10, 1195–1204. [Google Scholar] [CrossRef]
- Shukla, A.; Dutta, S.; Sadhu, P.K. An island detection approach by μ-PMU with reduced chances of cyber-attack. Int. J. Electr. Power Energy Syst. 2021, 126, 106599. [Google Scholar] [CrossRef]
- Chatterjee, S.; Roy, B. Bagged tree based anti-islanding scheme for multi-DG microgrids. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 2273–2284. [Google Scholar] [CrossRef]
- Tang, Y.; Li, F.; Zheng, C.; Wang, Q.; Wu, Y. PMU Measurement-Based Intelligent Strategy for Power System Controlled Islanding. Energies 2018, 11, 143. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, J.; Chen, Q.; Xia, M. Distribution Network Topology Error Identification Method Based on D-PMU and Branch State Function. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 821–826. [Google Scholar] [CrossRef]
- Meng, Y.; Yu, Z.; Lu, N.; Shi, D. Time Series Classification for Locating Forced Oscillation Sources. IEEE Trans. Smart Grid 2021, 12, 1712–1721. [Google Scholar] [CrossRef]
- Baltas, G.; Lai, N.-B.; Tarraso, A.; Marin, L.; Blaabjerg, F.; Rodriguez, P. AI-Based Damping of Electromechanical Oscillations by Using Grid-Connected Converter. Front. Energy Res. 2021, 9, 598436. [Google Scholar] [CrossRef]
- Mukherjee, S.; Chakrabortty, A.; Bai, H.; Darvishi, A.; Fardanesh, B. Scalable Designs for Reinforcement Learning-Based Wide-Area Damping Control. IEEE Trans. Smart Grid 2021, 12, 2389–2401. [Google Scholar] [CrossRef]
- Abdulrahman, I.; Radman, G. Wide-Area-Based Adaptive Neuro-Fuzzy SVC Controller for Damping Interarea Oscillations. Can. J. Electr. Comput. Eng. 2018, 41, 133–144. [Google Scholar] [CrossRef]
- Mejia-Ruiz, G.E.; Cárdenas-Javier, R.; Paternina MR, A.; Rodríguez-Rodríguez, J.R.; Ramirez, J.M.; Zamora-Mendez, A. Coordinated Optimal Volt/Var Control for Distribution Networks via D-PMUs and EV Chargers by Exploiting the Eigensystem Realization. IEEE Trans. Smart Grid 2021, 12, 2425–2438. [Google Scholar] [CrossRef]
- Liu, H.; Su, J.; Yang, Y.; Qin, Z.; Li, C. Compatible Decentralized Control of AVR and PSS for Improving Power System Stability. IEEE Syst. J. 2021, 15, 2410–2419. [Google Scholar] [CrossRef]
- Alkhalaf, S. Modeling the Automatic Voltage Regulator (AVR) Using Artificial Neural Network. In Proceedings of the 2019 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 2–4 February 2019; pp. 570–575. [Google Scholar] [CrossRef]
- Bliznyuk, D.; Berdin, A.; Kovalenko, P.; Dekhtiar, S.; Gerasimov, A. Defining the damping properties of synchronous generator using disturbance measurements. In Proceedings of the 2017 9th International Conference on Information Technology and Electrical Engineering (ICITEE), Phuket, Thailand, 12–13 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Pierrou, G.; Wang, X. An Online Network Model-Free Wide-Area Voltage Control Method Using PMUs. IEEE Trans. Power Syst. 2021, 36, 4672–4682. [Google Scholar] [CrossRef]
- Huang, Q.; Huang, R.; Hao, W.; Tan, J.; Fan, R.; Huang, Z. Adaptive Power System Emergency Control Using Deep Reinforcement Learning. IEEE Trans. Smart Grid 2020, 11, 1171–1182. [Google Scholar] [CrossRef]
- Moiseichenkov, A.N.; Senyuk, M.D.; Kovalenko, P.Y.; Dmitrieva, A.A. The Technique of Calculating a Steam Turbine Power for Characterization of The Turbine Fast Valving. In Proceedings of the 2021 International Conference on Electrotechnical Complexes and Systems (ICOECS), Ufa, Russia, 16–18 November 2021; pp. 79–82. [Google Scholar] [CrossRef]
- Senyuk, M.; Safaraliev, M.; Gulakhmadov, A.; Ahyoev, J. Application of the Conditional Optimization Method for the Synthesis of the Law of Emergency Control of a Synchronous Generator Steam Turbine Operating in a Complex-Closed Configuration Power System. Mathematics 2022, 10, 3979. [Google Scholar] [CrossRef]
- Senyuk, M.D.; Moiseichenkov, A.N.; Kovalenko, P.Y.; Dmitrieva, A.A. Adaptive Algorithm for Steam Turbine Fast Valving Based on the Equal Area Criterion and Synchrophasor Measurements. In Proceedings of the 2021 International Conference on Electrotechnical Complexes and Systems (ICOECS), Ufa, Russia, 16–18 November 2021; pp. 68–73. [Google Scholar] [CrossRef]
- Beryozkina, S.; Senyuk, M.; Berdin, A.; Dmitrieva, A.; Dmitriev, S.; Erokhin, P. The Accelerate Estimation Method of Power System Parameters in Static and Dynamic Processes. IEEE Access 2022, 10, 61522–61529. [Google Scholar] [CrossRef]
- Pavlovski, M.; Alqudah, M.; Dokic, T.; Hai, A.A.; Kezunovic, M.; Obradovic, Z. Hierarchical Convolutional Neural Networks for Event Classification on PMU Measurements. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar] [CrossRef]
- Hai, A.A.; Dokic, T.; Pavlovski, M.; Mohamed, T.; Saranovic, D.; Alqudah, M.; Kezunovic, M.; Obradovic, Z. Transfer Learning for Event Detection from PMU Measurements with Scarce Labels. IEEE Access 2021, 9, 127420–127432. [Google Scholar] [CrossRef]
- Shahsavari, A.; Farajollahi, M.; Stewart, E.M.; Cortez, E.; Mohsenian-Rad, H. Situational Awareness in Distribution Grid Using Micro-PMU Data: A Machine Learning Approach. IEEE Trans. Smart Grid 2019, 10, 6167–6177. [Google Scholar] [CrossRef]
- Shi, J.; Foggo, B.; Yu, N. Power System Event Identification Based on Deep Neural Network with Information Loading. IEEE Trans. Power Syst. 2021, 36, 5622–5632. [Google Scholar] [CrossRef]
- Duan, N.; Stewart, E.M. Frequency Event Categorization in Power Distribution Systems Using Micro PMU Measurements. IEEE Trans. Smart Grid 2020, 11, 3043–3053. [Google Scholar] [CrossRef]
- Grando, F.L.; Lazzaretti, A.E.; Moreto, M.; Lopes, H.S. Fault Classification in Power Distribution Systems using PMU Data and Machine Learning. In Proceedings of the 20th International Conference on Intelligent System Application to Power Systems (ISAP), Istanbul, Turkey, 10–14 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Ahmed, A.; Sajan, K.S.; Srivastava, A.; Wu, Y. Anomaly Detection, Localization and Classification Using Drifting Synchrophasor Data Streams. IEEE Trans. Smart Grid. 2021, 12, 3570–3580. [Google Scholar] [CrossRef]
- Shrivastava, D.; Siddiqui, S.; Verma, K. A new synchronized data-driven-based comprehensive approach to enhance real-time situational awareness of power system. Int. Trans. Electr. Energy Syst. 2021, 31, e12887. [Google Scholar] [CrossRef]
- Huang, T.; Freris, N.M.; Kumar, P.R.; Xie, L. A Synchrophasor Data-Driven Method for Forced Oscillation Localization Under Resonance Conditions. IEEE Trans. Power Syst. 2020, 35, 3927–3939. [Google Scholar] [CrossRef]
- Papadopoulos, P.N.; Papadopoulos, T.A.; Chrysochos, A.I.; Milanović, J.V. Measurement Based Method for Online Characterization of Generator Dynamic Behaviour in Systems with Renewable Generation. IEEE Trans. Power Syst. 2018, 33, 6466–6475. [Google Scholar] [CrossRef]
- Kim, D.-I.; Wang, L.; Shin, Y.-J. Data Driven Method for Event Classification via Regional Segmentation of Power Systems. IEEE Access 2020, 8, 48195–48204. [Google Scholar] [CrossRef]
- Li, H.; Ma, Z.; Weng, Y. A Transfer Learning Framework for Power System Event Identification. IEEE Trans. Power Syst. 2022, 37, 4424–4435. [Google Scholar] [CrossRef]
- Nuqui, R.F.; Phadke, A.G. Phasor measurement unit placement techniques for complete and incomplete observability. IEEE Trans. Power Del. 2005, 20, 2381–2388. [Google Scholar] [CrossRef]
- Singh, B.; Pal, C.; Vinter, R.B. Measurement placement in distribution system state estimation. IEEE Trans. Power Syst. 2009, 24, 668–675. [Google Scholar] [CrossRef]
- Peng, Y.; Wu, Z.; Fang, C.; Zheng, S.; Zhao, J. Optimal PMU Placement in Distribution Networks for Improving State Estimation Accuracy and Fault Observability. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23–25 December 2021; pp. 1413–1418. [Google Scholar] [CrossRef]
- Khalafi, Z.; Dehghani, M.; Goel, L.; Li, W. Observability reliability evaluation in power systems considering data uncertainty. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Esmaili, M.; Ghamsari-Yazdel, M. Voltage Stability-Constrained Optimal Simultaneous Placement of PMUs and Channels Enhancing Measurement Reliability and Redundancy. IEEE Power Energy Technol. Syst. J. 2017, 4, 32–39. [Google Scholar] [CrossRef]
- Dua, D.; Dambhare, S.; Gajbhiye, R.K.; Soman, S.A. Optimal Multistage Scheduling of PMU Placement: An ILP Approach. IEEE Trans. Power Deliv. 2008, 23, 1812–1820. [Google Scholar] [CrossRef]
- Rakpenthai, C.; Premrudeepreechacharn, S.; Uatrongjit, S.; Watson, N.R. An Optimal PMU Placement Method Against Measurement Loss and Branch Outage. IEEE Trans. Power Deliv. 2007, 22, 101–107. [Google Scholar] [CrossRef]
- Devendran, V.S.; Jasni, J.; Radzi, M.A.M.; Azis, N. Optimal Placement of PMU for Complete Observability of Power System Considering Zero Injection and Islanding Condition. In Proceedings of the 2020 IEEE International Conference on Power and Energy (PECon), Penang, Malaysia, 7–8 December 2020; pp. 107–112. [Google Scholar] [CrossRef]
- Manda, S.; Balakrishna, K.; Sriharibabu, A. Linear programming method to find the minimal placements of phasor measuring units for power system state estimation. In Proceedings of the 2017 International Conference on Power and Embedded Drive Control (ICPEDC), Chennai, India, 16–18 March 2017; pp. 360–364. [Google Scholar] [CrossRef]
- Aminifar, F.; Lucas, C.; Khodaei, A.; Fotuhi-Firuzabad, M. Optimal Placement of Phasor Measurement Units Using Immunity Genetic Algorithm. IEEE Trans. Power Deliv. 2009, 24, 1014–1020. [Google Scholar] [CrossRef]
- Dixit, A.; Jain, S.K. Genetic algorithm based optimal placement of phasor measurement units for harmonic source identification. In Proceedings of the 2016 7th India International Conference on Power Electronics (IICPE), Patiala, India, 17–19 November 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Geramian, S.S.; Abyane, H.A.; Mazlumi, K. Determination of optimal PMU placement for fault location using genetic algorithm. In Proceedings of the 2008 13th International Conference on Harmonics and Quality of Power, Wollongong, NSW, Australia, 28 September–1 October 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Tarif, T.; Ladjici, A.A.; Chabane, Y. Optimal PMU placement for small-signal stability assessment using Genetic algorithm. In Proceedings of the 2018 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Algiers, Algeria, 28–31 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Rammal, Z.A.; Daher, N.A.; Kanaan, H.; Mougharbel, I.; Saad, M. Optimal PMU placement for reverse power flow detection. In Proceedings of the 2018 4th International Conference on Renewable Energies for Developing Countries (REDEC), Beirut, Lebanon, 1–2 November 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Dalawai, P.P.; Abhyankar, A.R. Placement of PMUs for complete and incomplete observability using search technique. In Proceedings of the 2013 Annual IEEE India Conference (INDICON), Mumbai, India, 13–15 December 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Babu, R.; Bhattacharyya, B. Optimal placement of phasor measurement unit using binary particle swarm optimization in connected power network. In Proceedings of the 2015 IEEE UP Section Conference on Electrical Computer and Electronics (UPCON), Allahabad, India, 4–6 December 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Mishra, S.K.; Swain, K.B.; Cherukuri, M. Optimal Placement of Phasor Measurement Unit Using Quantum Particle Swarm Optimization. In Proceedings of the 2021 1st International Conference on Power Electronics and Energy (ICPEE), Bhubaneswar, India, 2–3 January 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Patel, M.; Talati, S. Optimal PMU Placement by Improved Cuckoo & PSO Method. In Proceedings of the 2021 International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 19–20 February 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Tawfik, A.S.; Abdallah, E.N.; Youssef, K.H. Optimal placement of phasor measurement units using binary bat algorithm. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 559–564. [Google Scholar] [CrossRef]
- Tawfik, N.M.; El-Amary, N.H.; Nasrat, L. Phasor Measurement Unit Optimal Allocation Utilizing Discrete Water Cycle Optimization. In Proceedings of the 2023 5th International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russia, 16–18 March 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Jaiswal, V.; Thakur, S.S.; Mishra, B. Optimal placement of PMUs using Greedy Algorithm and state estimation. In Proceedings of the 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Rigatos, G.; Zervos, N.; Siano, P.; Wira, P.; Abbaszadeh, M. Nonlinear Optimal Control for Steam-Turbine Power Generation. In Proceedings of the2018 5th International Symposium on Environment-Friendly Energies and Applications (EFEA), Rome, Italy, 24–26 September 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Senyuk, M.; Safaraliev, M.; Kamalov, F.; Sulieman, H. Power System Transient Stability Assessment Based on Machine Learning Algorithms and Grid Topology. Mathematics 2023, 11, 525. [Google Scholar] [CrossRef]
- Senyuk, M.; Rajab, K.; Safaraliev, M.; Kamalov, F. Evaluation of the Fast Synchrophasors Estimation Algorithm Based on Physical Signals. Mathematics 2023, 11, 256. [Google Scholar] [CrossRef]
- Senyuk, M.; Beryozkina, S.; Gubin, P.; Dmitrieva, A.; Kamalov, F.; Safaraliev, M.; Zicmane, I. Fast Algorithms for Estimating the Disturbance Inception Time in Power Systems Based on Time Series of Instantaneous Values of Current and Voltage with a High Sampling Rate. Mathematics 2022, 10, 3949. [Google Scholar] [CrossRef]
- IEEE Std C37.242-2021; IEEE Guide for Synchronization, Calibration, Testing, and Installation of Phasor Measurement Units (PMUs) for Power System Protection and Control. Revision of IEEE Std C37.242-2013; IEEE Standards Association: Piscataway, NJ, USA, 2021; pp. 1–98. [CrossRef]





| Direction | Possible Solutions | Prerequisites |
|---|---|---|
| Emergency control | Development of adaptive algorithms implementing emergency control based on machine learning methods capable of forming an optimal impact on the EPS at the pace of the transition process | An increase in the rate of transient processes due to a decrease in the inertia of the EPS |
| Relay protection | Development of adaptive relay protection systems that provide selective shutdown of a damaged element of the EPS in the presence of a significant share of RES | Increasing the stochasticity of normal and transient processes of EPS |
| SE | Increasing the speed and accuracy of condition assessments | The need to increase the speed and accuracy of the assessment of the state |
| Optimal PMU placement | Development of complex algorithms for optimal PMU placement for emergency control and condition assessment tasks | The need to reduce the load of communication channels from PMU to APDC, ensuring the observability of the EPS |
| Development of algorithms for determining synchrophasors | Development of accelerated methods for determining a synchrophasors with a delay of less than a period of industrial frequency | An increase in the rate of transient processes due to a decrease in the inertia of the EPS |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pazderin, A.; Zicmane, I.; Senyuk, M.; Gubin, P.; Polyakov, I.; Mukhlynin, N.; Safaraliev, M.; Kamalov, F. Directions of Application of Phasor Measurement Units for Control and Monitoring of Modern Power Systems: A State-of-the-Art Review. Energies 2023, 16, 6203. https://doi.org/10.3390/en16176203
Pazderin A, Zicmane I, Senyuk M, Gubin P, Polyakov I, Mukhlynin N, Safaraliev M, Kamalov F. Directions of Application of Phasor Measurement Units for Control and Monitoring of Modern Power Systems: A State-of-the-Art Review. Energies. 2023; 16(17):6203. https://doi.org/10.3390/en16176203
Chicago/Turabian StylePazderin, Andrey, Inga Zicmane, Mihail Senyuk, Pavel Gubin, Ilya Polyakov, Nikita Mukhlynin, Murodbek Safaraliev, and Firuz Kamalov. 2023. "Directions of Application of Phasor Measurement Units for Control and Monitoring of Modern Power Systems: A State-of-the-Art Review" Energies 16, no. 17: 6203. https://doi.org/10.3390/en16176203
APA StylePazderin, A., Zicmane, I., Senyuk, M., Gubin, P., Polyakov, I., Mukhlynin, N., Safaraliev, M., & Kamalov, F. (2023). Directions of Application of Phasor Measurement Units for Control and Monitoring of Modern Power Systems: A State-of-the-Art Review. Energies, 16(17), 6203. https://doi.org/10.3390/en16176203









