Design and Implementation of Self-Limiting Two-Stage LC Oscillators Using Cascade Structure of Monolithic CCIIs as Active Elements
Abstract
:1. Introduction
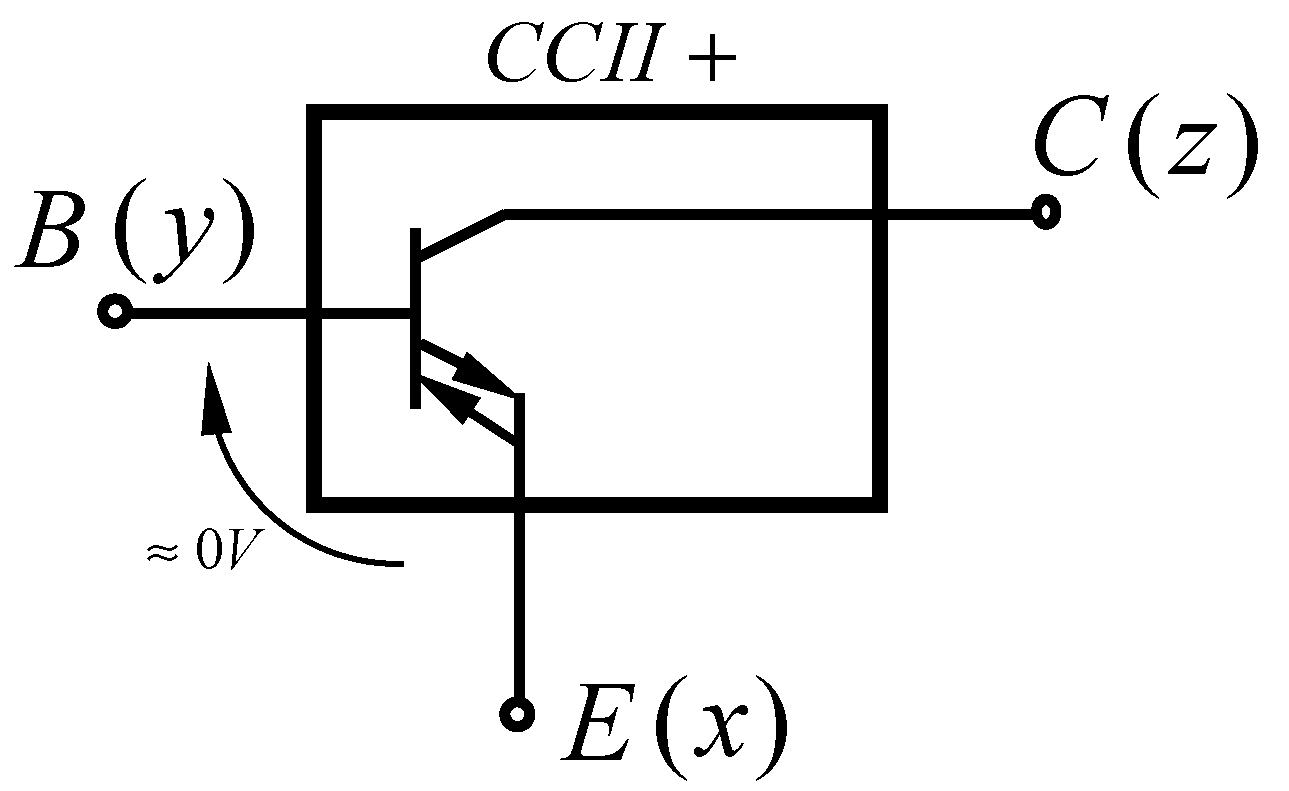
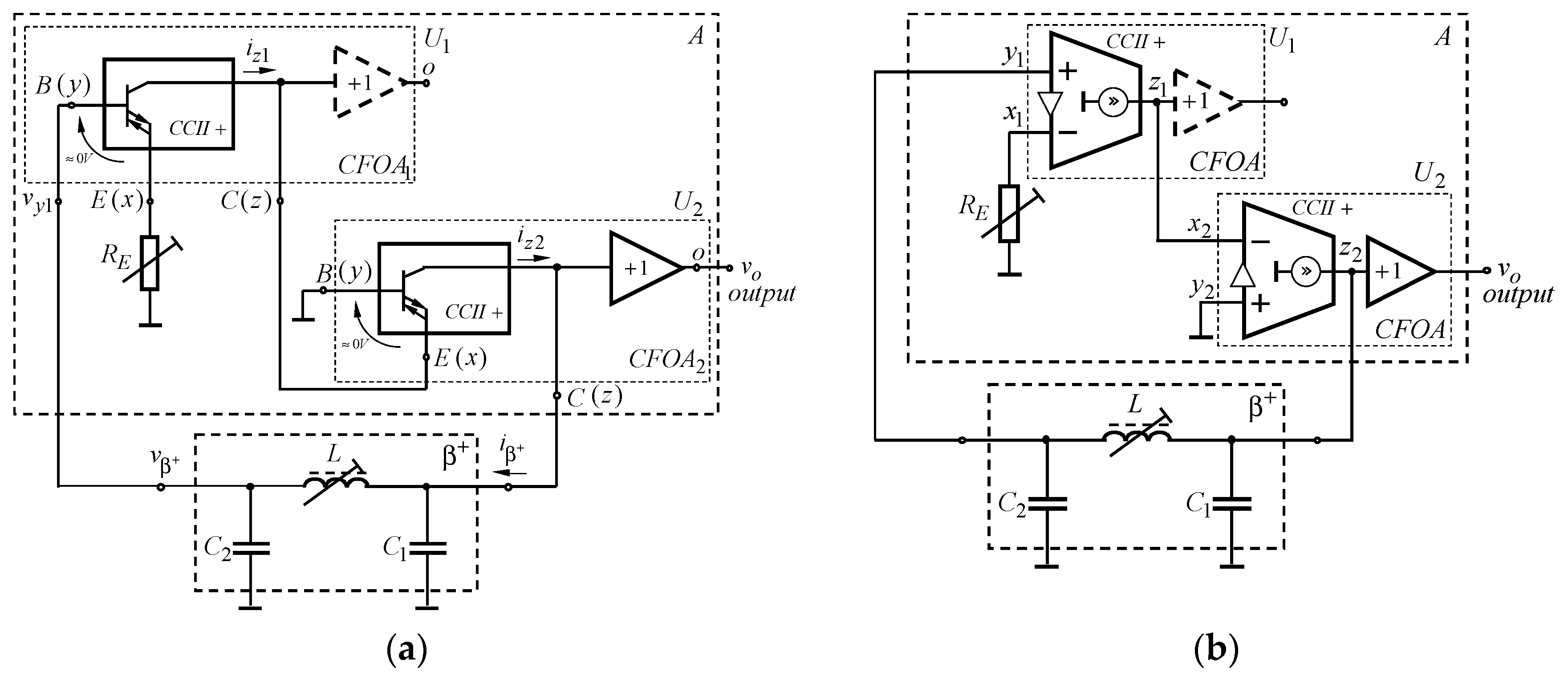
2. Structure of the Monolithic CCIIs
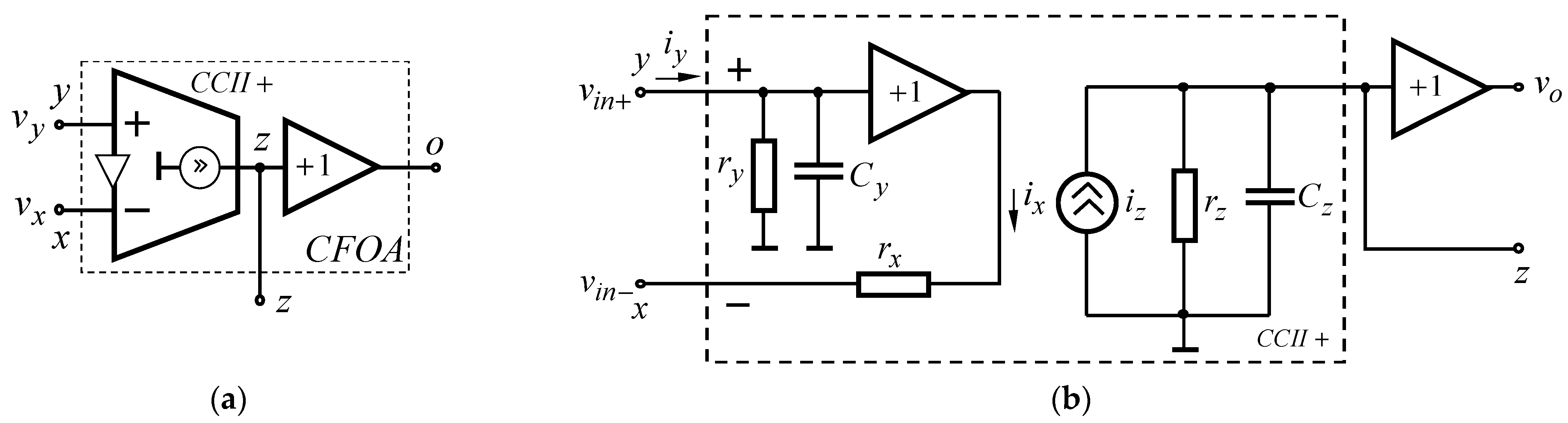
3. Theoretical Analysis of the Proposed Electronic Circuits
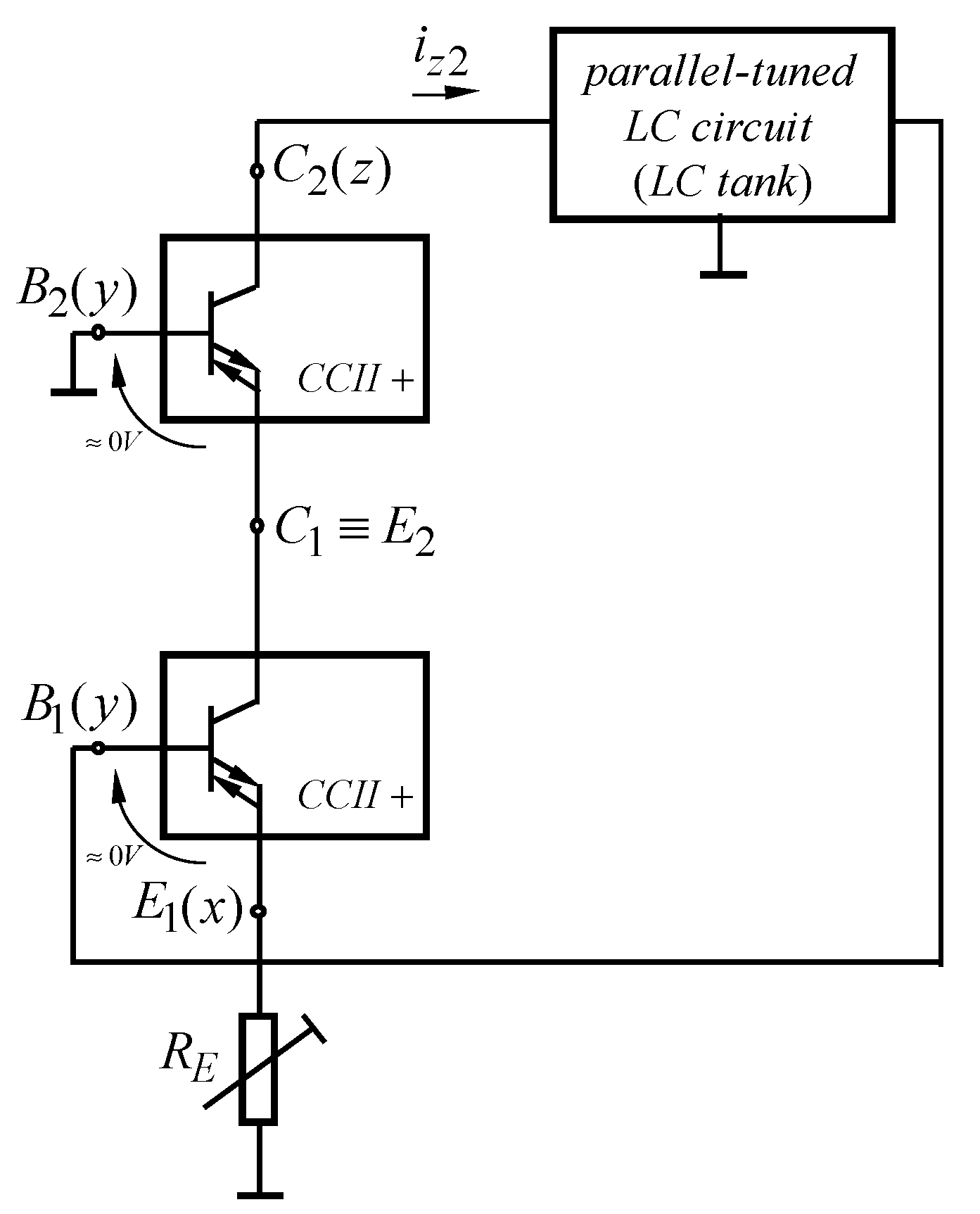
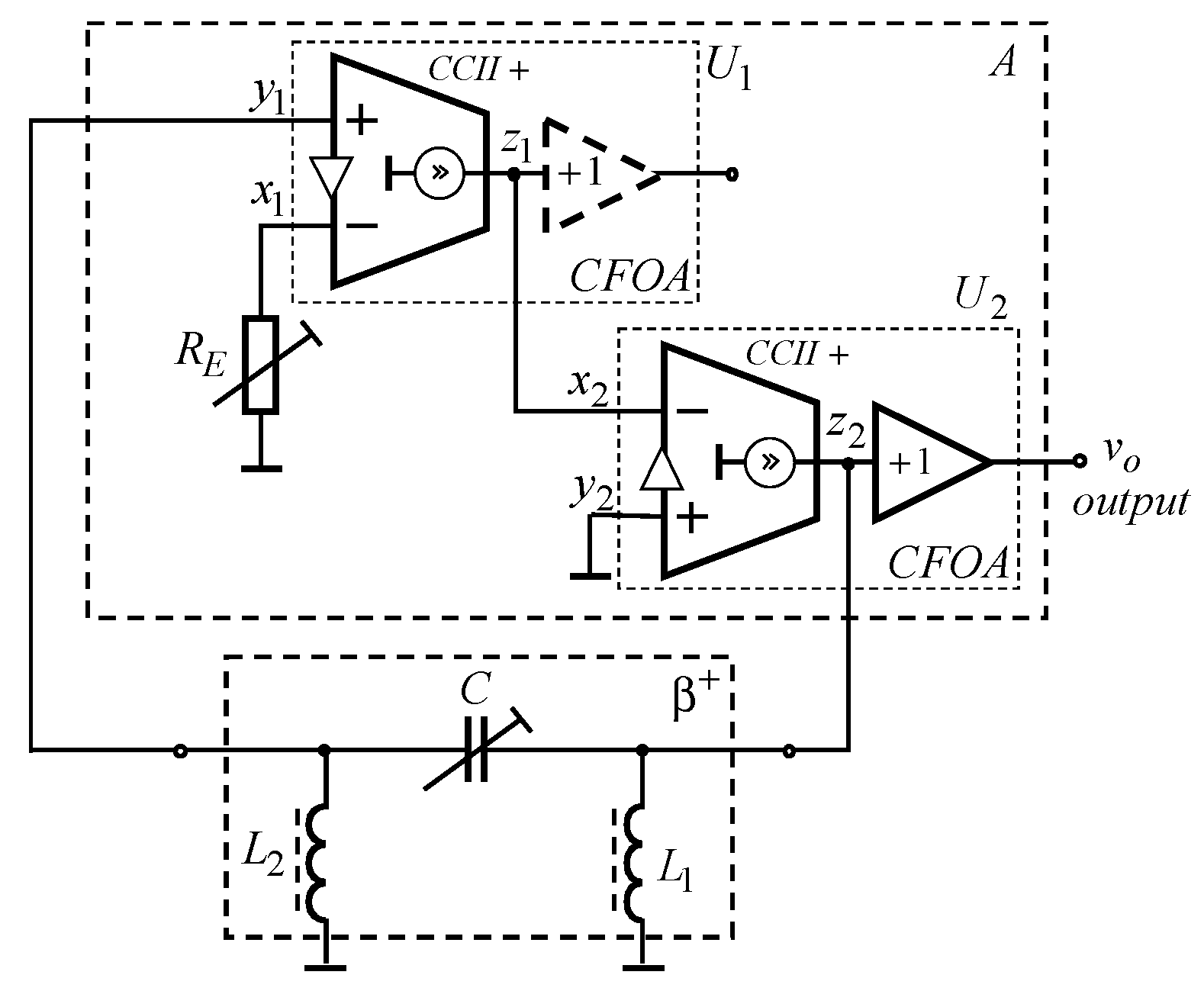
3.1. Structure of the Electronic Circuits
3.2. Circuit Analysis
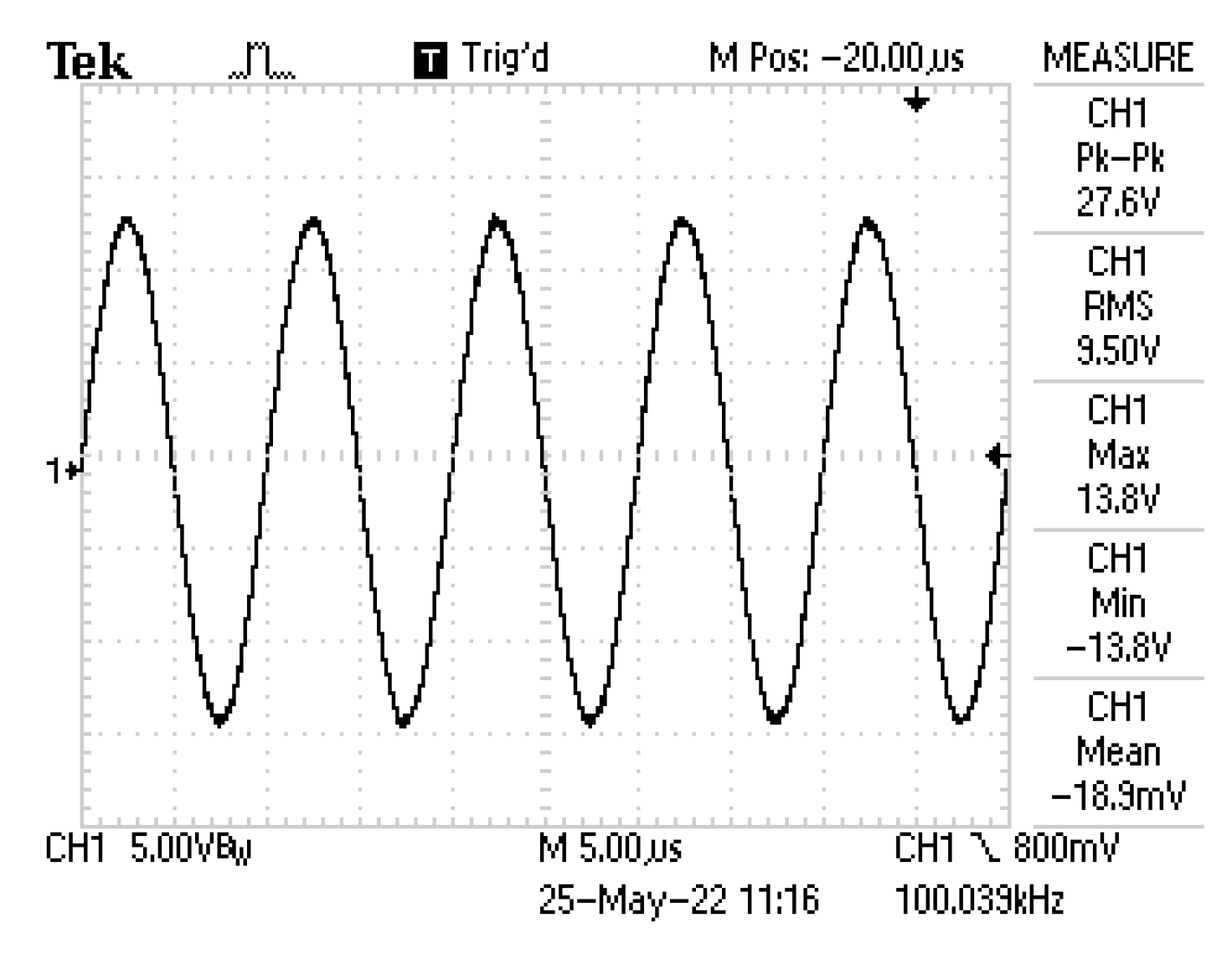
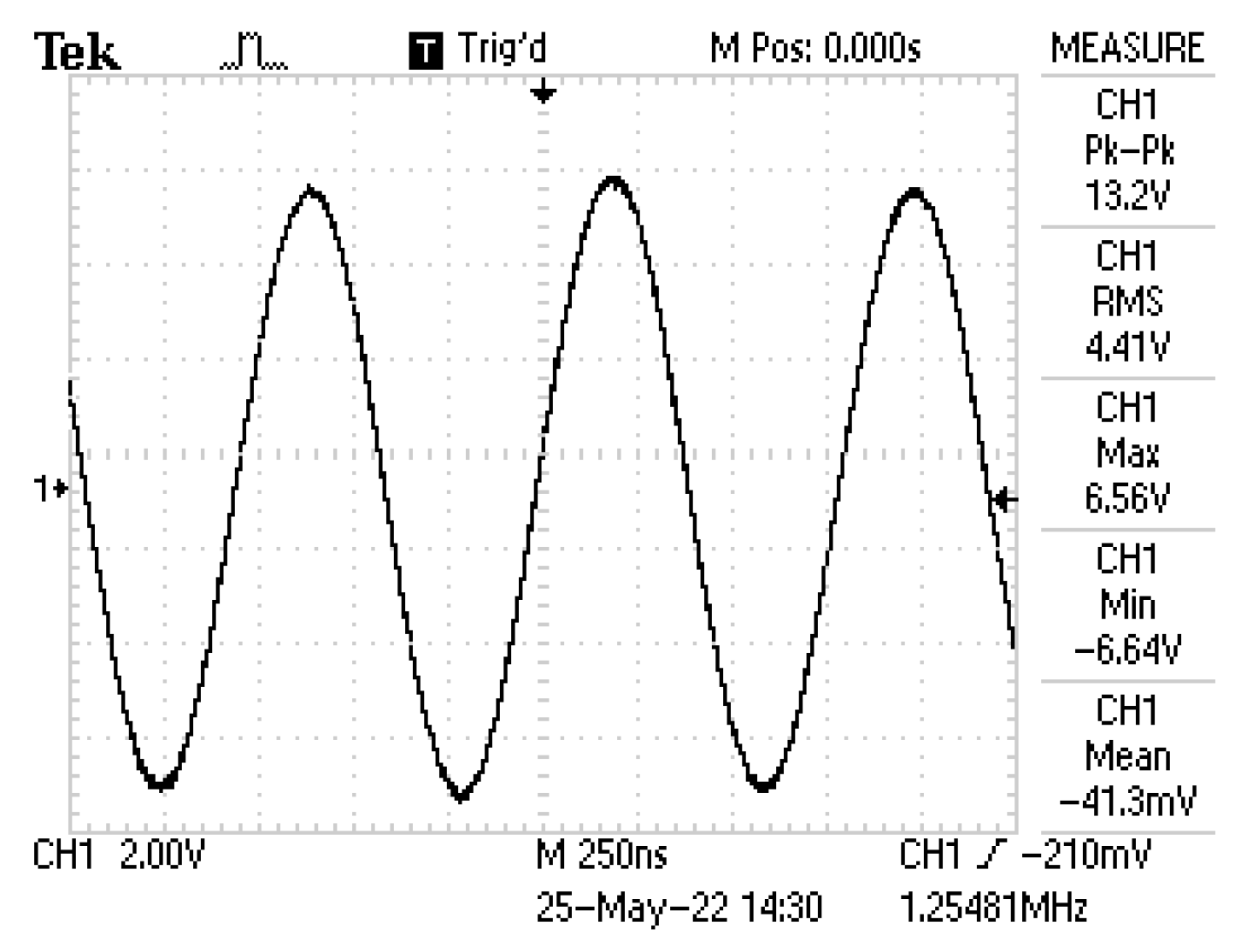
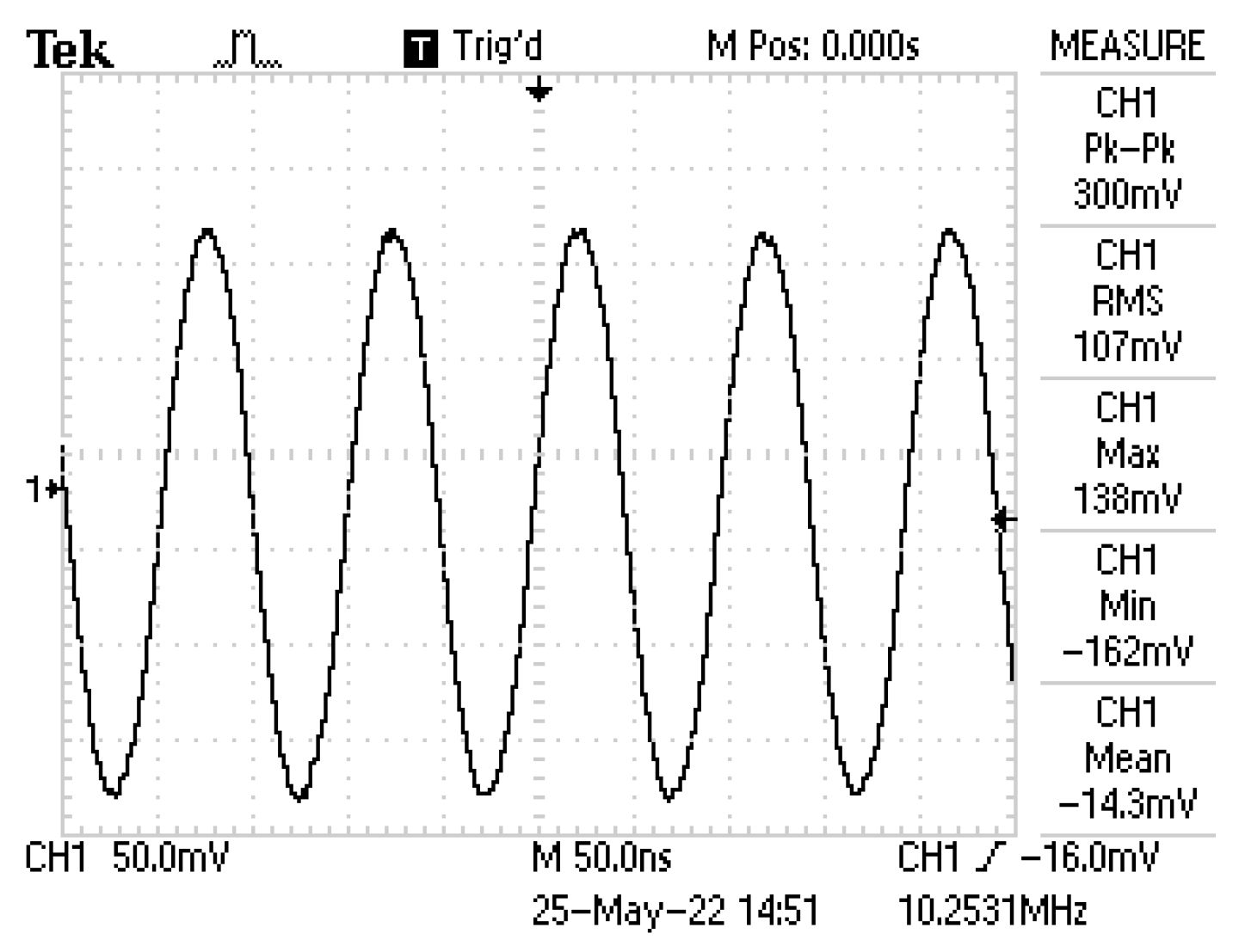
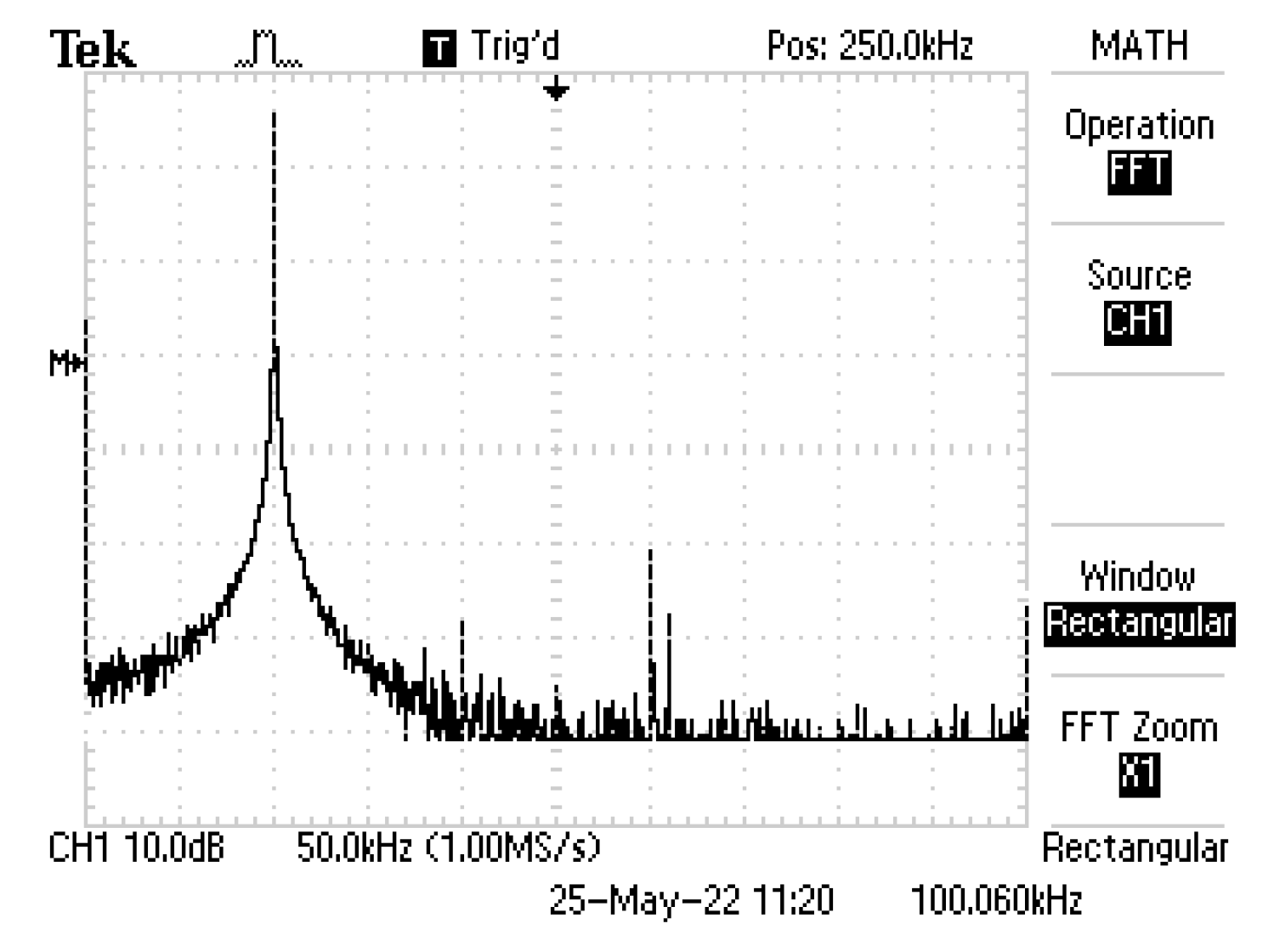
4. Simulation and Experimental Results
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Radfar, M.; Green, M.M. An LC voltage-Controlled Oscillator with Supply Sensitivity Compensation Method. In Proceedings of the IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017. [Google Scholar]
- Chaharboor, M.; Ghonoodi, H. Improved resonator phase shift in passive and active coupled LC Quadrature Oscillator. In Proceedings of the Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 2–4 May 2017. [Google Scholar]
- Rathore, T.S. Synthesis and classification of LC oscillators. In Proceedings of the 2nd International Conference on Communication Systems, Computing and IT Applications (CSCITA), Mumbai, India, 7–8 April 2017. [Google Scholar]
- Proano, E.; Navarro, M.; Sanchez, A.; Benitez, D.S. On the Design of Active LC Oscillators Using Small-Signal Model Network Analysis. In Proceedings of the IEEE Colombian Conference on Communications and Computing (COLCOM), Medellin, Colombia, 16–18 May 2018. [Google Scholar]
- Kira, A.; Elsayed, M.Y.; Allidina, K.; Chodavarapu, V.P.; El-Gamal, M.N. A 6.89-MHz 143-nW MEMS Oscillator Based on a 118-dB? Tunable Gain and Duty-Cycle CMOS TIA. Electronics 2021, 10, 21. [Google Scholar] [CrossRef]
- Salem, S.B.; Saied, A.B.; Masmoudi, D.S. High-performance Current-Controlled Quadrature Oscillator Using an optimized CCII. J. Microelectron. Electron. Compon. Mater. 2016, 46, 91–99. [Google Scholar]
- Mishra, S.K.; Upadhyay, D.K.; Gupta, M. Compact design of fractional order LC oscillator. In Proceedings of the URSI Asia-Pacific Radio Science Conference (AP-RASC), New Delhi, India, 9–15 March 2019. [Google Scholar]
- Agrawal, D.; Maheshwari, S. An active-C Current-Mode Universal First Order Filter and Oscillator. J. Circuits Syst. Comput. 2019, 28, 13. [Google Scholar] [CrossRef]
- Jaikla, W.; Adhan, S.; Suwanjan, P.; Kumngern, M. Current/Voltage Controlled Quadrature Sinusoidal Oscillators for Phase Sensitive Detection Using Commercially Available IC. Sensors 2020, 20, 5. [Google Scholar] [CrossRef]
- Garinto, D.; Syahriar, A.; Budiyanto, S. A Novel Op-Amp Based LC Oscillator for Wireless Communications. In Proceedings of the 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020. [Google Scholar]
- Mohsen, M.; Said, L.A.; Elwakil, A.S.; Madian, A.H.; Radwan, A.G. Extracting Optimized Bio-Impedance Model Parameters Using Different Topologies of Oscillators. IEEE Sens. J. 2020, 20, 9947–9954. [Google Scholar] [CrossRef]
- Maheshwari, S. Realization Approach for Sinusoidal Signal Generation and Circuit with Easy Control. J. Circuits Syst. Comput. 2020, 29, 2. [Google Scholar] [CrossRef]
- Stornelli, V.; Barile, G.; Pantoli, L.; Scarsella, M.; Ferri, G.; Centurelli, F.; Tommasino, P.; Trifiletti, A. A New VCII Application: Sinusoidal Oscillators. J. Low Power Electron. Appl. 2021, 11, 3. [Google Scholar] [CrossRef]
- Borah, S.S.; Singh, A.; Ghosh, M.; Ranjan, A. Electronically tunable higher-order quadrature oscillator employing CDBA. Microelectron. J. 2021, 108, 104985. [Google Scholar] [CrossRef]
- Altuntas, E.; Toker, A. Realization of voltage and current mode KHN biquads using CCCIIs. Int. J. Electron. Commun. 2002, 56, 45–49. [Google Scholar] [CrossRef]
- Sedra, A.; Smith, K. A second-generation current conveyor and its applications. IEEE Trans. Circuit Theory 1970, 17, 132–134. [Google Scholar] [CrossRef]
- Barthélemy, H.; Gies, V.; Meillère, S.; Vauché, R.; Kussener, E.; Fourniol, M. CMOS voltage and current feedback opamps: A comparison between two similar topologies. Int. J. Electron. Lett. 2021, 9, 187–202. [Google Scholar] [CrossRef]
- Tietze, V.; Schenk, C. Operational Amplifiers. Signal Generators. In Electronic Circuits, 2nd ed.; Springer-Verlag: New York, NY, USA, 2008; Chapter 5 and Chapter 14; pp. 483–586, 843–867. [Google Scholar]
- Sedra, A.; Smith, K.; Carusone, T.; Gaudet, V. Oscillators. In Microelectronic Circuits, 8th ed.; Oxford University Press: Oxford, UK, 2020; Chapter 15; pp. 1066–1107. [Google Scholar]
- Seifart, M. Signalgeneratoren. In Analoge Schaltungen, 6 Auflage; Verlag Technik: Berlin, Germany, 2003; Chapter 18; pp. 460–484. [Google Scholar]
- Pandiev, I. Development of Self-Limiting LC Oscillators Using Cascade Structure of Monolithic CCIIs. In Proceedings of the 2023 30th International Conference on Mixed Design of Integrated Circuits and System (MIXDES), Kraków, Poland, 29–30 June 2023; pp. 148–153. [Google Scholar] [CrossRef]
- Yuce, E. Fully integrable mixed-mode universal biquad with specific application of the CFOA. Int. J. Electron. Commun. 2010, 64, 304–309. [Google Scholar] [CrossRef]
- Yuce, E.; Minaei, S. A first-order fully cascadable current-mode universal filter composed of dual output CCIIs and a grounded capacitor. J. Circuits Syst. Comput. 2016, 25, 1–15. [Google Scholar] [CrossRef]
- Kumar, A.; Paul, S. Current mode first order universal filter and multiphase sinusoidal oscillator. Int. J. Electron. Commun. 2017, 81, 37–49. [Google Scholar] [CrossRef]
- Safari, L.; Yuce, E.; Minaei, S. A new ICCII based resistor-less current-mode first-order universal filter with electronic tuning capability. Microelectron. J. 2017, 67, 101–110. [Google Scholar] [CrossRef]
- Kamphoefner, F.J. Feedback in Very-High-Frequency and Ultra-High-Frequency Oscillators. Proc. IRE 1950, 38, 630–632. [Google Scholar] [CrossRef]
- Oakes, J.B. Analysis of Junction Transistor Audio Oscillator Circuits. Proc. IRE 1954, 42, 1235–1238. [Google Scholar] [CrossRef]
- Bell, D.L.T.; Li, R.C.M. Surface-Acoustic-Wave Resonators. Proc. IEEE 1976, 64, 711–721. [Google Scholar] [CrossRef]
- Parker, T.E.; Montress, G.K. Precision surface-acoustic-wave (SAW) oscillators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1988, 35, 342–364. [Google Scholar] [CrossRef]
- Pasternak, M. Overtone Oscillator for SAW Gas Detectors. IEEE Sens. J. 2006, 6, 1497–1501. [Google Scholar] [CrossRef]
- Montress, G.K.; Parker, T.E.; Andres, D. Review of SAW oscillator performance. In Proceedings of the IEEE Ultrasonics Symposium, Cannes, France, 31 October 1994–3 November 1994; Volume 1, pp. 43–54. [Google Scholar] [CrossRef]
- Savov, V.; Georgiev, Z.; Todorov, T. Analysis and synthesis of perturbed Duffing oscillators. Int. J. Circuits Theory Appl. 2006, 34, 281–306. [Google Scholar] [CrossRef]
- Vidal, E.; Poveda, A.; Ismail, M. Describing functions and oscillators. IEEE Circuits Devices Mag. 2001, 17, 7–11. [Google Scholar] [CrossRef]
- Fabre, A.; Saaid, O.; Wiest, F.; Boucheron, C. Current controlled bandpass filter based on translinear conveyors. Electron. Lett. 1995, 31, 1727–1728. [Google Scholar] [CrossRef]
- Fabre, A. Dual translinear voltage/current convertor. Electron. Lett. 1983, 19, 1030–1031. [Google Scholar] [CrossRef]
- 60 MHz 2000 V/μs Monolithic op amp AD844—Datasheet. Analog Devices, Norwood, MA, USA, 2017. Available online: https://www.analog.com/en/products/ad844.html (accessed on 13 July 2023).
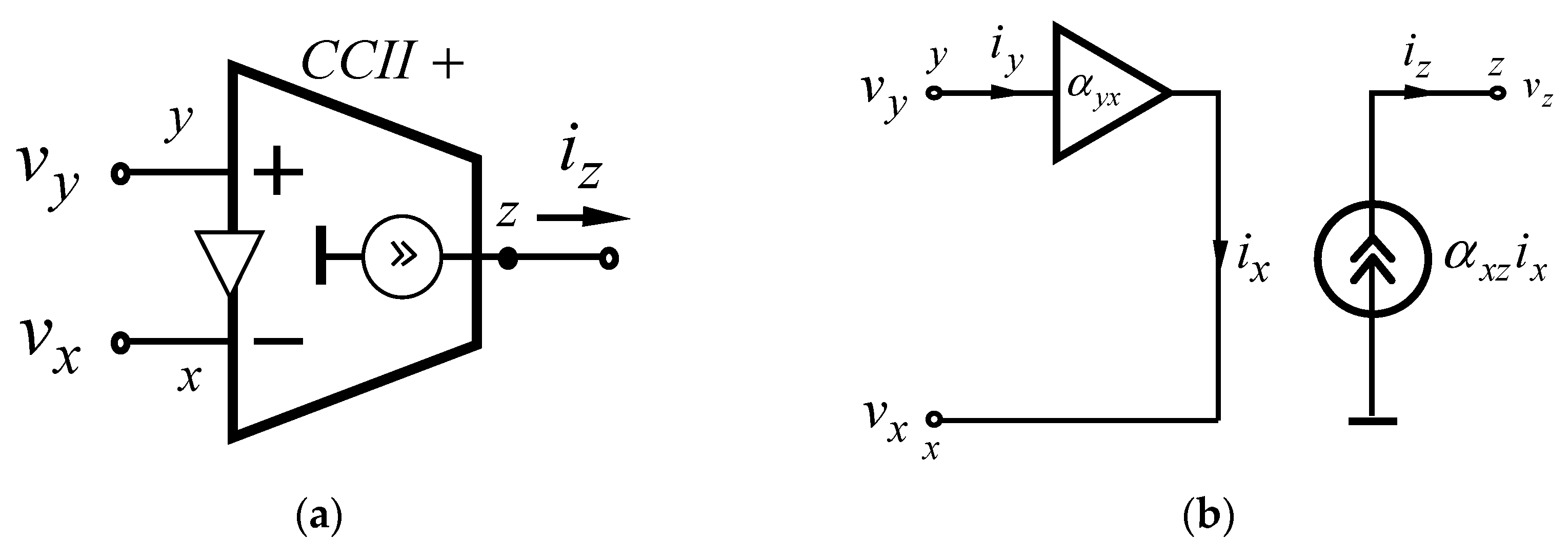



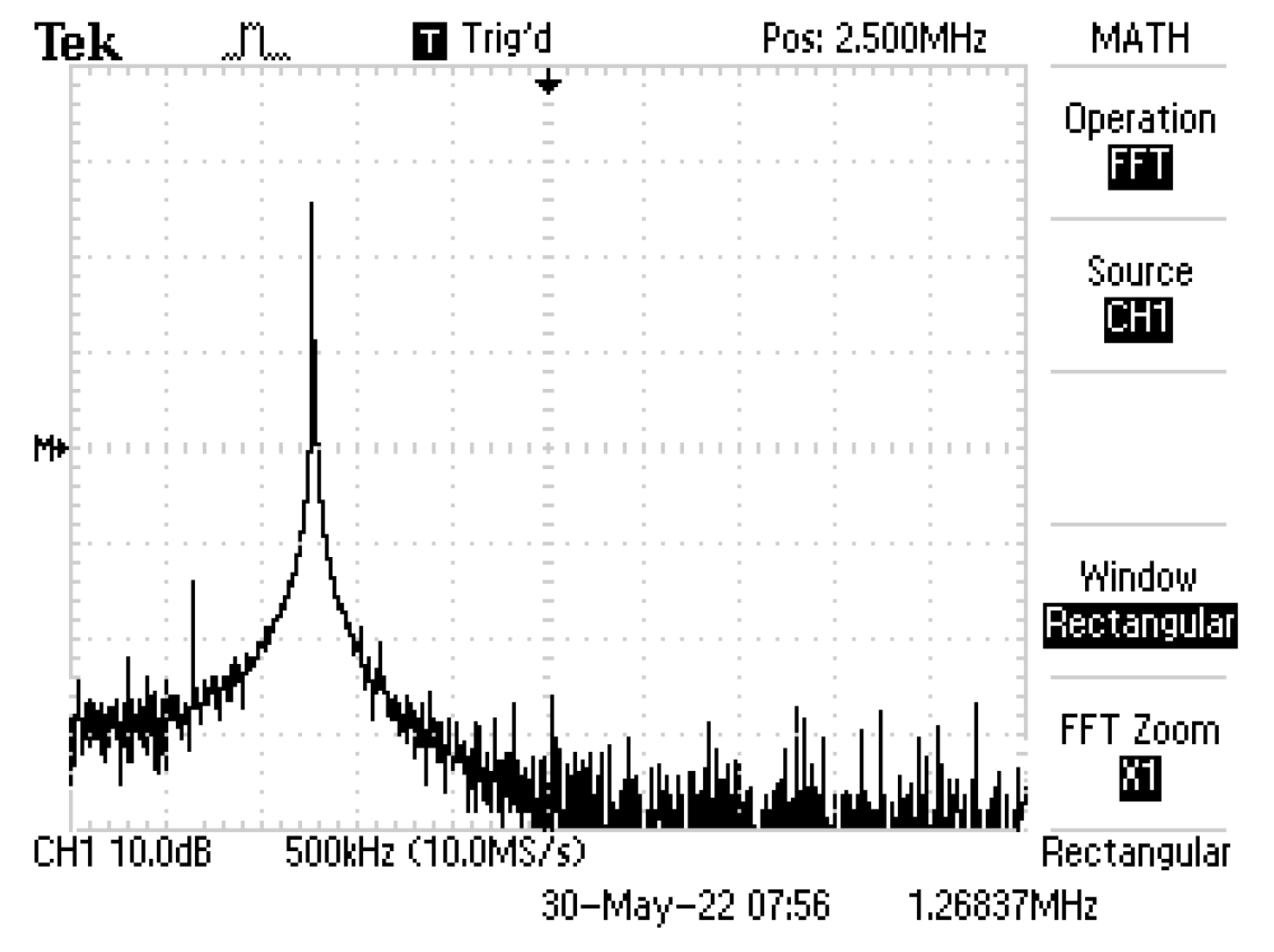
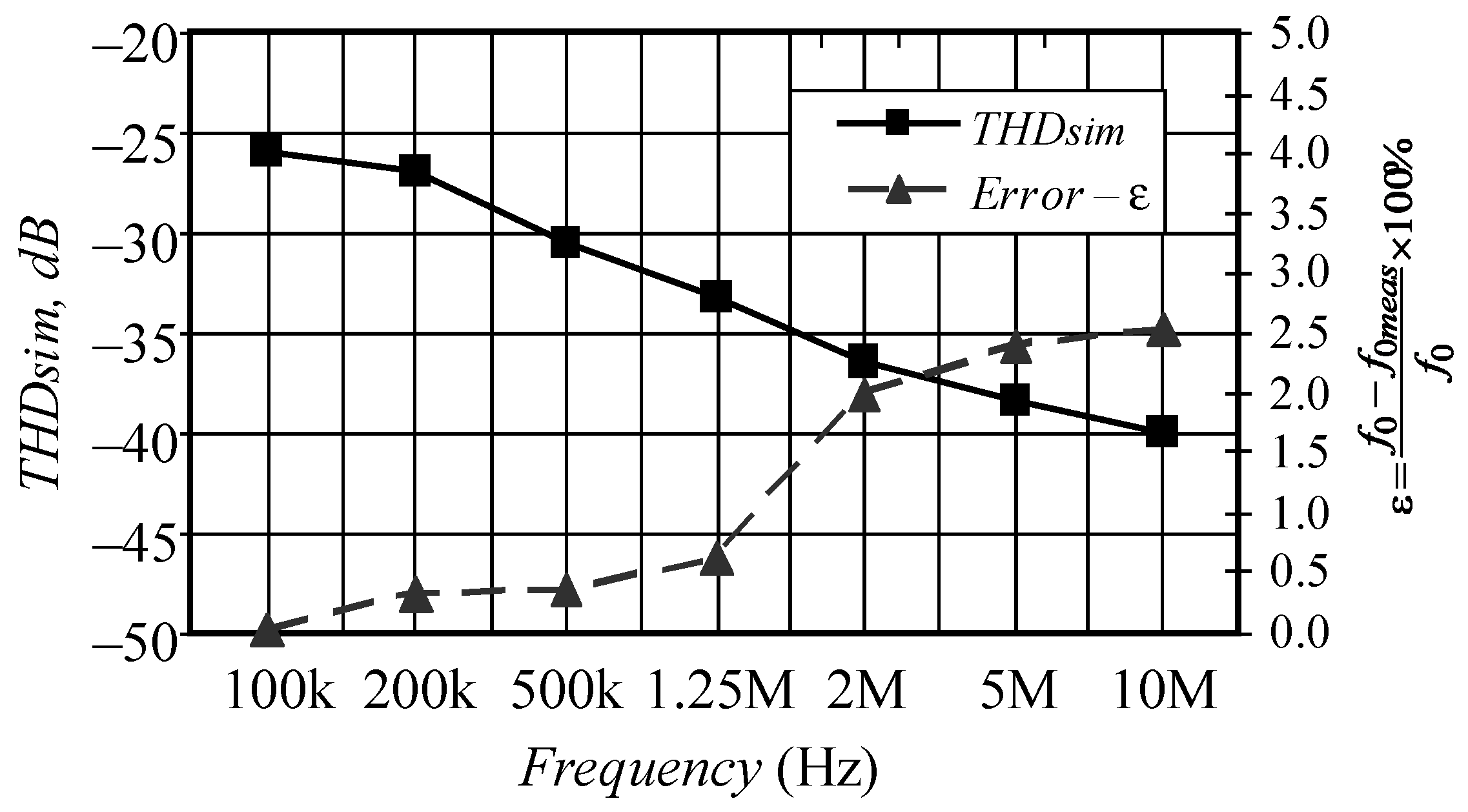
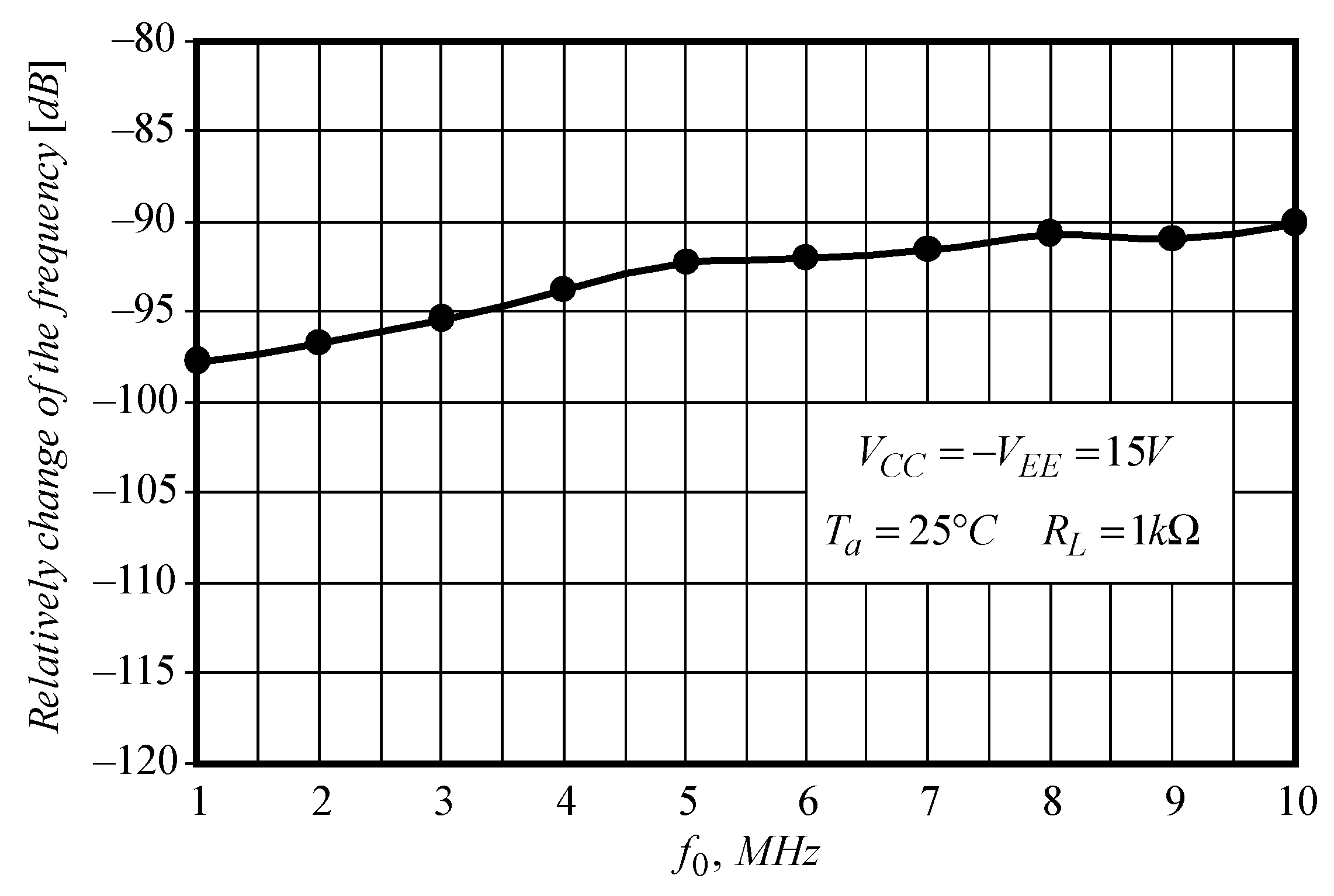
| Parameter | This Work | Three-Point Oscillators Refs. [18,19,20] | Ref. [13] | Ref. [11] | Ref. [10] | Ref. [14] | Ref. [24] |
|---|---|---|---|---|---|---|---|
| Number of active components | 2 CFOAs with available pin Z | Single transistor or two BJTs or MOSFETs | 2 CFOAs with available pin Z | 1 CFOA with available pin Z | 1 VFOA connected as a buffer | 4 CFOAs | Two dual-X multiple output second generation current conveyors (DXMOCCIIs) and 1 MOSFET |
| Number of passive components | One variable resistor to adjust the amplitude; LC tank | One current source, current mirrors, or several resistors; LC tank | 2 resistors and 2 capacitors | 2 resistors and 1 capacitor | LC tank | 5 or 6 Resistors and 5 or 6 Capacitors | 4 resistors and 3 capacitors |
| Power supply voltage | ±(5–10) V | 5–10 Vtyp | ±5 V | ±9 V | ±5 V | ±5 V | ±1.25 V |
| Supply current | 5–8 mA | 2–5 mAtyp | 14 mA | 3–5 mAtyp | 2–5 mAtyp | up to 10 mA | 100 μA |
| Nonlinearity distortion | up to 5% | 1–3% | 5.6% | <1% | <5% | up to 3.8% | 1.79% |
| Stability factor | – | – | >1 | , where n > 1 | >1 | ||
| Phase noise | – | – | – | – | 2/ω0 | 1/2ω0 | |
| Frequency of oscillation | up to 10 MHz | typically from 0.1 MHz up to several GHz | 1 MHz | up to 1 kHz | 107 kHz | 98.65 kHz/127.1 kHz | 5.28 MHz |
| Tunability of amplitude and frequency | Yes (independent adjustment) | Yes | Yes (amplitude vs. frequency tuning dependence) | Yes (amplitude vs. frequency tuning dependence) | Yes (without tuning the amplitude of the output signal) | Yes (tuning the frequency with voltage; two values of the f0 and the amplitude for both signals is 5 V) | Yes (the frequency of oscillation can be tuned without disturbing the condition of oscillation.) |
| Output impedance | Very low (output buffer) | Relatively high output impedance (without voltage follower) | High output impedance | Very low (output buffer) | Very low (the parameters of the load can change the Q-factor) | Very low (the parameters of the load at Vo1 can change the Q-factor) | Relatively high output impedance (current-mode sinusoidal six-phase oscillator output signals) |
| Technology | Bipolar | BJTs or MOSFETs | Bipolar | Bipolar | BJTs or MOSFETs | Bipolar | 0.25 μm CMOS process |
| Year | 2023 | last publication is found 2020 | 2021 | 2020 | 2020 | 2021 | 2017 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandiev, I. Design and Implementation of Self-Limiting Two-Stage LC Oscillators Using Cascade Structure of Monolithic CCIIs as Active Elements. Energies 2023, 16, 6226. https://doi.org/10.3390/en16176226
Pandiev I. Design and Implementation of Self-Limiting Two-Stage LC Oscillators Using Cascade Structure of Monolithic CCIIs as Active Elements. Energies. 2023; 16(17):6226. https://doi.org/10.3390/en16176226
Chicago/Turabian StylePandiev, Ivaylo. 2023. "Design and Implementation of Self-Limiting Two-Stage LC Oscillators Using Cascade Structure of Monolithic CCIIs as Active Elements" Energies 16, no. 17: 6226. https://doi.org/10.3390/en16176226
APA StylePandiev, I. (2023). Design and Implementation of Self-Limiting Two-Stage LC Oscillators Using Cascade Structure of Monolithic CCIIs as Active Elements. Energies, 16(17), 6226. https://doi.org/10.3390/en16176226






