Long-Term Voltage Stability Bifurcation Analysis and Control Considering OLTC Adjustment and Photovoltaic Power Station
Abstract
:1. Introduction
2. Long-Term Voltage Stability Bifurcation Analysis Based on Matcont
2.1. Brief Introduction of the Hopf Bifurcation Theory
2.2. Model of the 3-Bus System with OLTC and PV
2.3. The Equilibrium Point Curves
2.4. Impact of Load Power Disturbance on Long-Term Voltage Stability
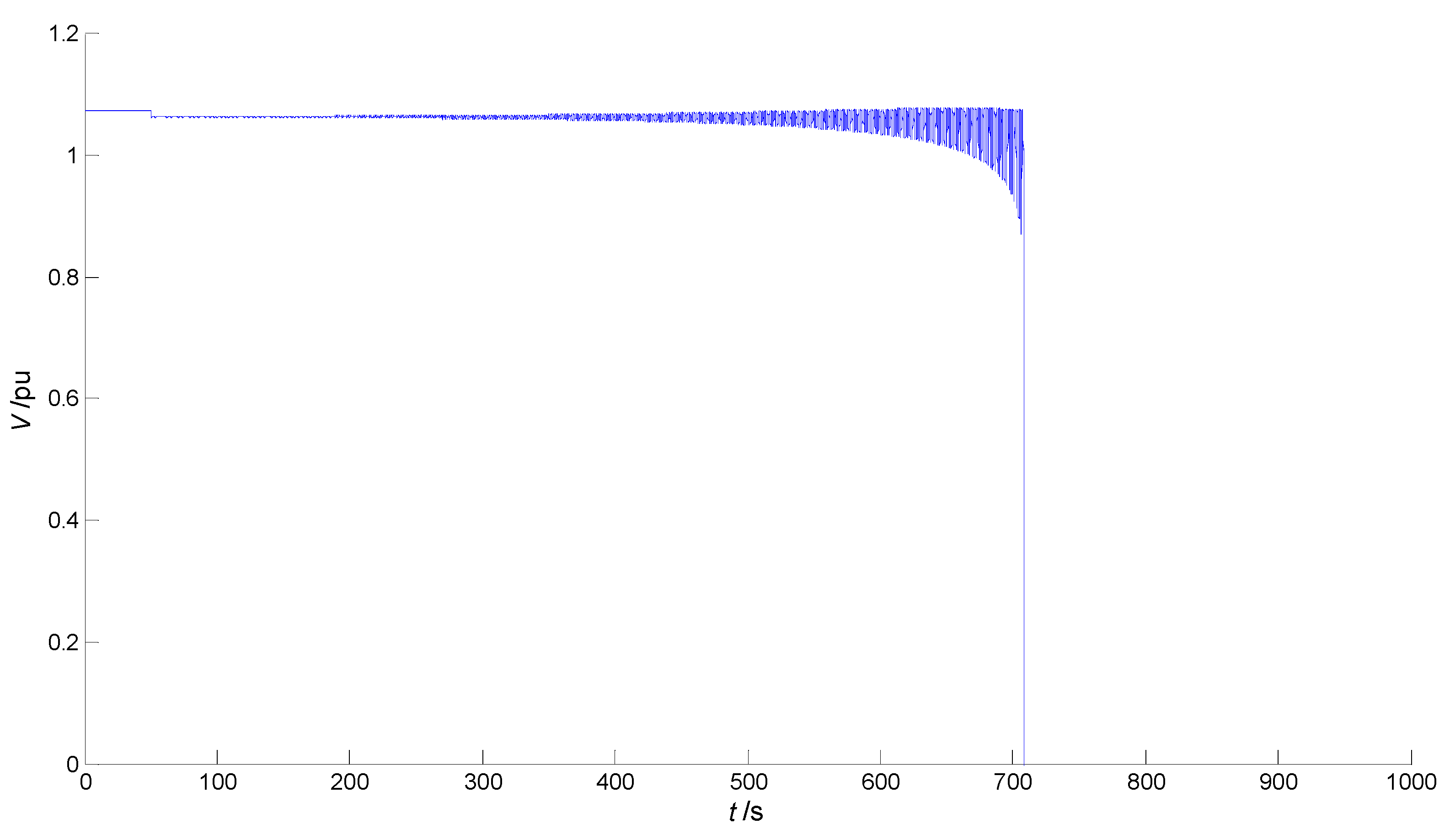
2.4.1. Sudden Increase in the Reactive Load Q1—Long-Term Voltage Collapse
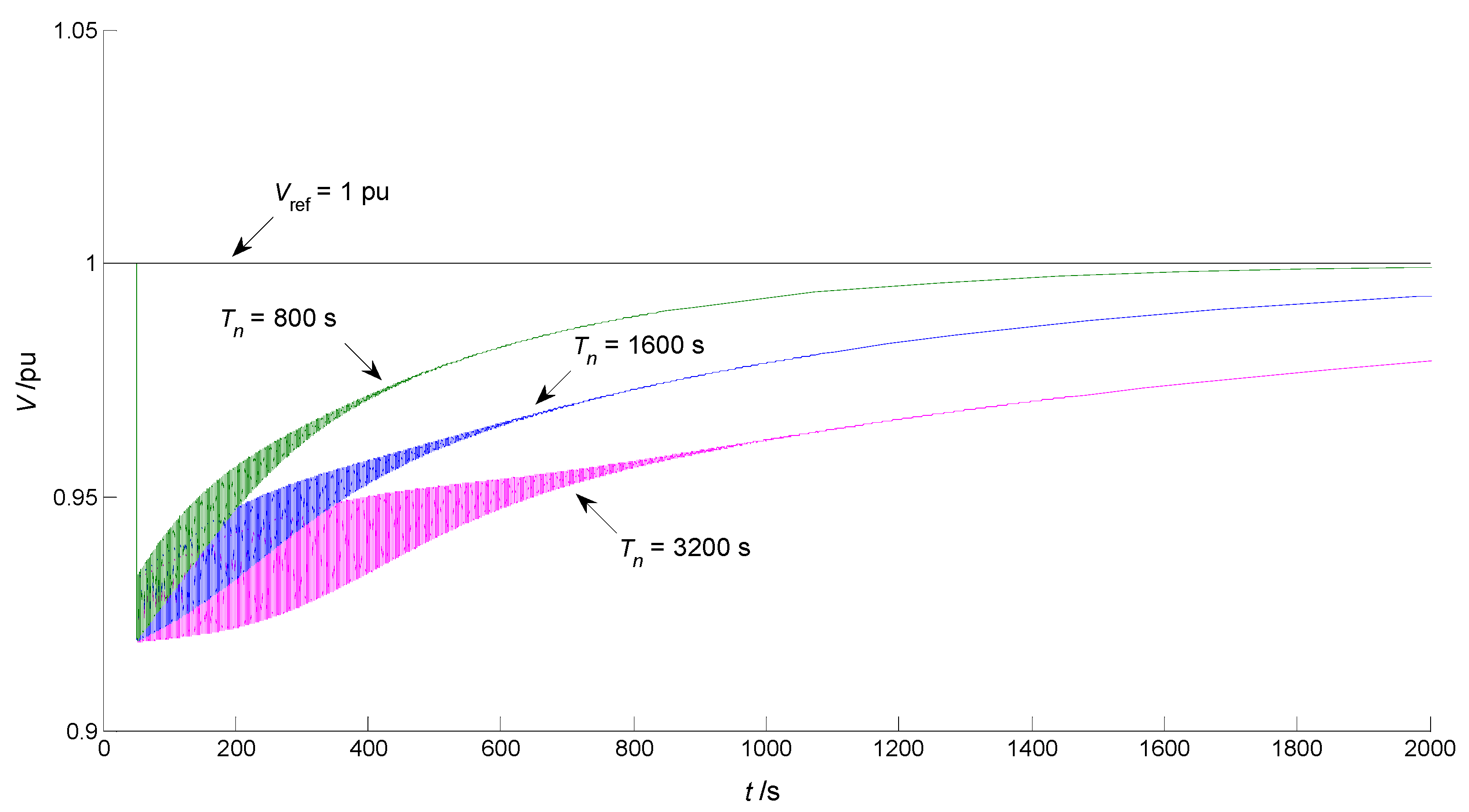
2.4.2. Impact of OLTC’s Time Constant—Key Influencing Factor Investigation
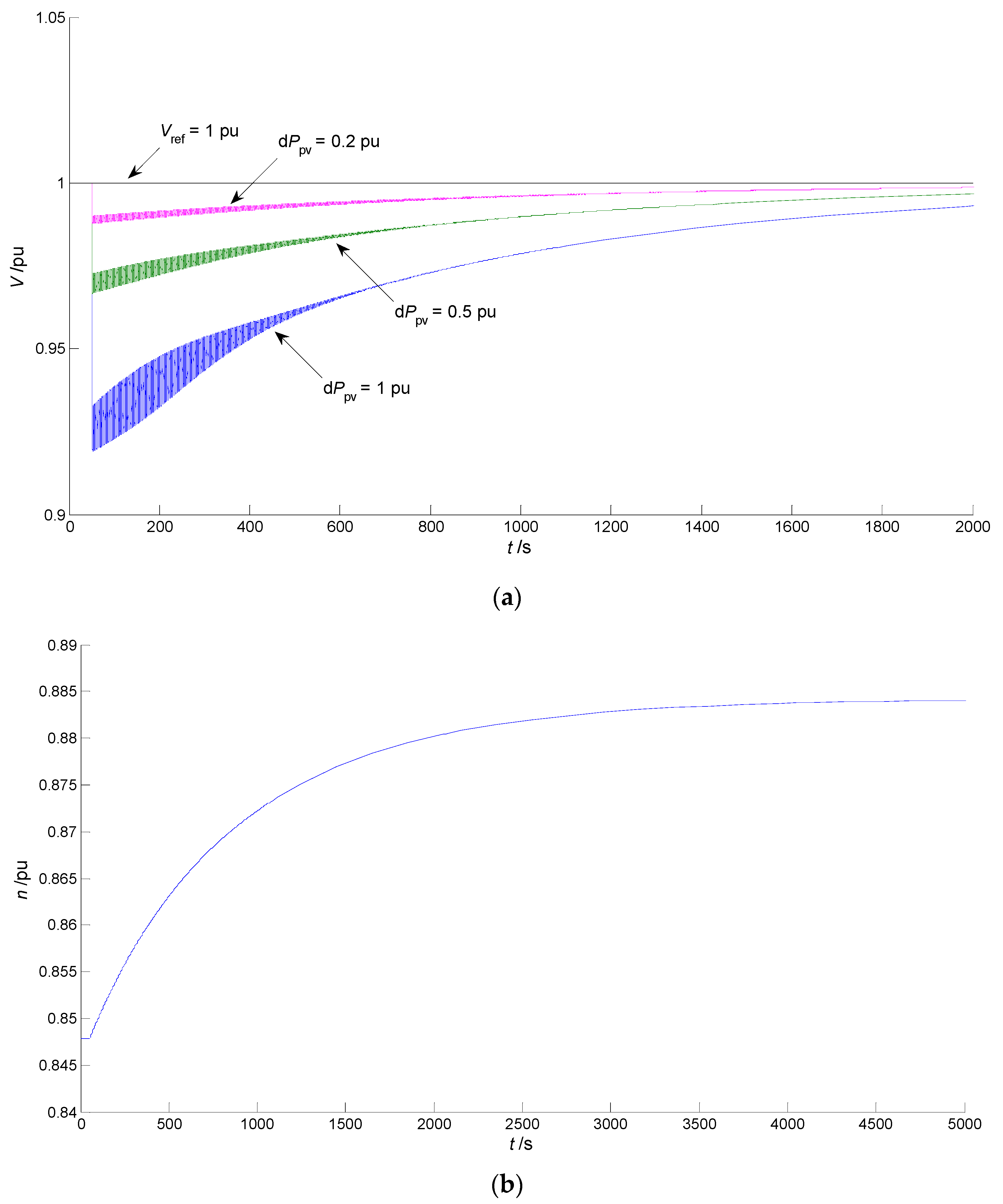
2.5. Impact of PV Power Disturbance on Long-Term Voltage Stability
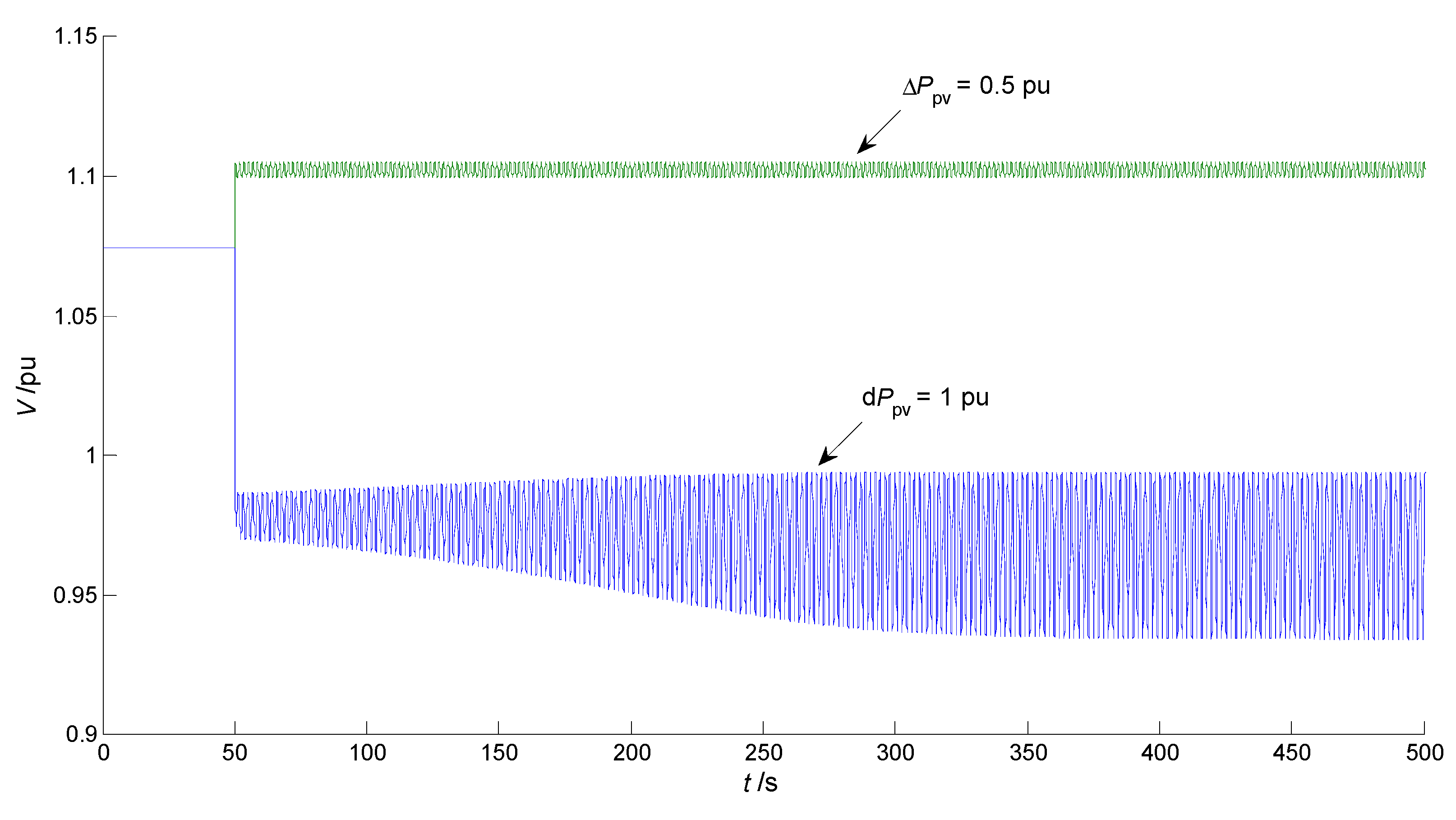
2.5.1. Sudden Drop of PV Power—Long-Term Voltage Recovery
2.5.2. Sudden Increase in PV Power—Long-Term Voltage Collapse
2.5.3. Impact of OLTC’s Time Constant—Key Influencing Factor Investigation
3. Comparison with the PV Grid-Connected 3-Bus System without OLTC
4. Design of the Index and Control Methods for Preventing Long-Term Voltage Collapse
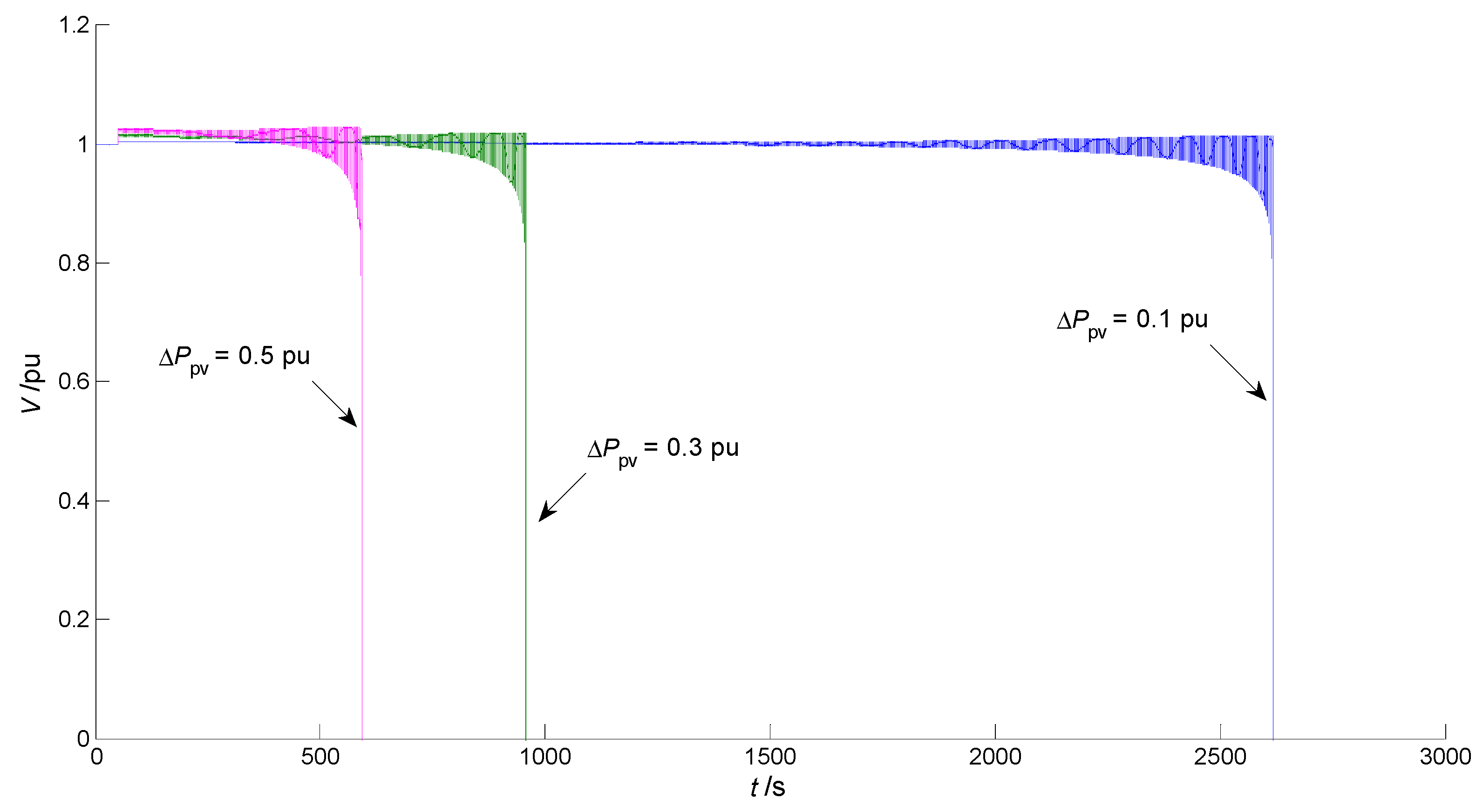
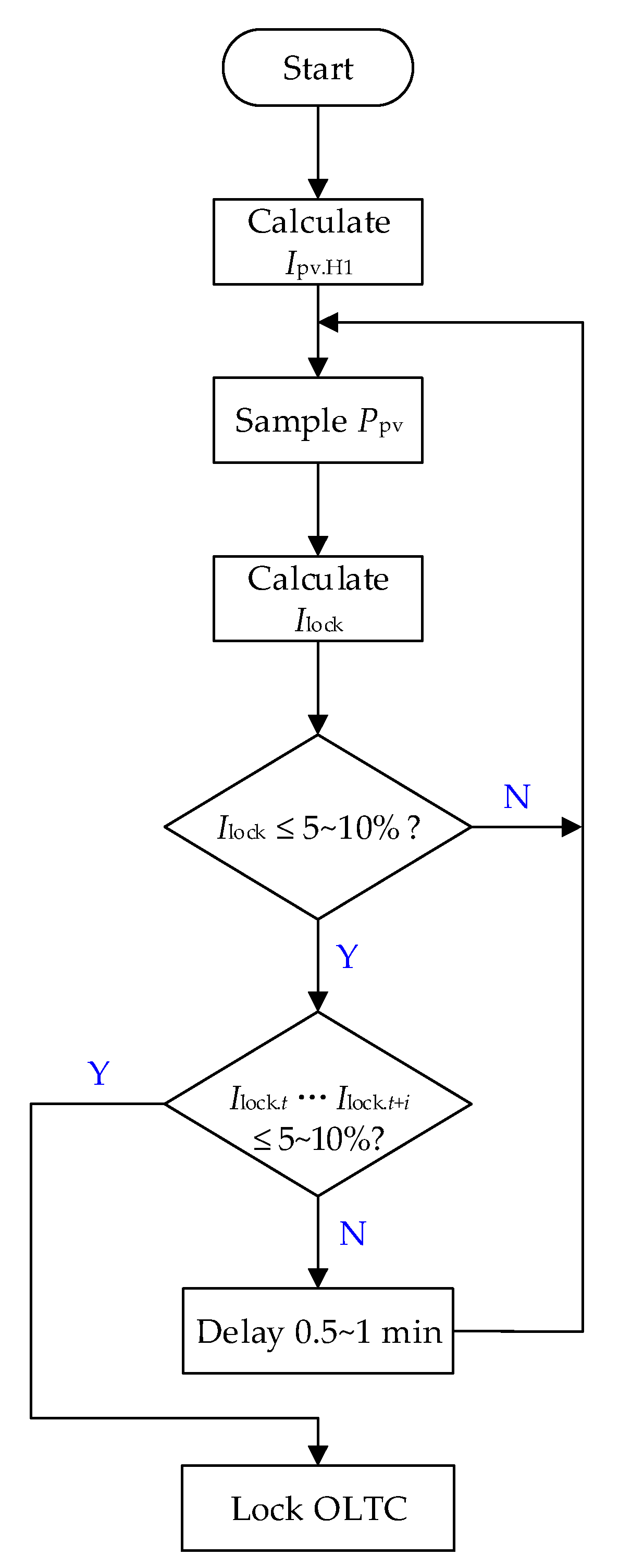
4.1. Prevention of Voltage Collapse Caused by a Sudden Increase in PV Power
4.2. Prevention of Voltage Collapse Caused by a Sudden Increase in Load Power
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, X.; Zhao, Q.; Zhang, Y.; Sun, L. Integrated energy production unit: An innovative concept and design for energy transition toward low-carbon development. CSEE J. Power Energy Syst. 2021, 7, 1133–1139. [Google Scholar]
- Guo, J.; Ma, S.; Wang, T.; Jing, Y.; Hou, W.; Xu, H. Challenges of developing a power system with a high renewable energy proportion under China’s carbon targets. iEnergy 2022, 1, 12–18. [Google Scholar]
- Landera, Y.G.; Zevallos, O.C.; Neves, F.A.S.; Neto, R.C.; Prada, R.B. Control of PV systems for multimachine power system stability improvement. IEEE Access 2022, 10, 45061–45072. [Google Scholar]
- Sajadi, A.; Rañola, J.A.; Kenyon, R.W.; Hodge, B.M.; Mather, B. Dynamics and stability of power systems with high shares of grid-following inverter-based resources: A tutorial. IEEE Access 2023, 11, 29591–29613. [Google Scholar]
- Campanhol, L.B.G.; Silva, S.A.O.D.; Oliveira, A.A.D.; Bacon, V.D. Power flow and stability analyses of a multifunctional distributed generation system integrating a photovoltaic system with unified power quality conditioner. IEEE Trans. Power Electr. 2018, 34, 6241–6256. [Google Scholar]
- Kawabe, K.; Ota, Y.; Yokoyama, A.; Tanaka, K. Novel dynamic voltage support capability of photovoltaic systems for improvement of short-term voltage stability in power systems. IEEE Trans. Power Syst. 2017, 32, 1796–1804. [Google Scholar]
- Li, S.; Wei, Z.; Ma, Y. Fuzzy load-shedding strategy considering photovoltaic output fluctuation characteristics and static voltage stability. Energies 2018, 11, 779. [Google Scholar]
- Rahman, S.; Saha, S.; Islam, S.N.; Arif, M.T.; Mosadeghy, M.; Haque, M.E.; Oo, A.M.T. Analysis of power grid voltage stability with high penetration of solar PV systems. IEEE Trans. Ind. Appl. 2021, 57, 2245–2257. [Google Scholar]
- Li, S.; Lu, Y.; Ge, Y. Static voltage stability zoning analysis based on a sensitivity index reflecting the influence degree of photovoltaic power output on voltage stability. Energies 2023, 16, 2808. [Google Scholar]
- General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China; Standardization Administration of the People’s Republic of China. Code on Security and Stability for Power System (GB 38755–2019); Standards Press of China: Beijing, China, 2019; p. 13.
- Khoshkhoo, H.; Yari, S.; Pouryekta, A.; Ramachandaramurthy, V.K.; Guerrero, J.M. A remedial action scheme to prevent mid/long-term voltage instabilities. IEEE Syst. J. 2021, 15, 923–934. [Google Scholar]
- Islam, S.R.; Sutanto, D.; Muttaqi, K.M. Coordinated decentralized emergency voltage and reactive power control to prevent long-term voltage instability in a power system. IEEE Trans. Power Syst. 2015, 30, 2591–2603. [Google Scholar]
- Sun, Q.; Cheng, H.; Song, Y. Bi-Objective reactive power reserve optimization to coordinate long- and short-term voltage stability. IEEE Access 2018, 6, 13057–13065. [Google Scholar]
- Matavalam, A.R.R.; Singhal, A.; Ajjarapu, V. Monitoring long term voltage instability due to distribution & transmission interaction using unbalanced μPMU & PMU measurements. IEEE Trans. Smart Grid. 2020, 11, 873–883. [Google Scholar]
- Matavalam, A.R.R.; Ajjarapu, V. Long term voltage stability Thevenin index using voltage locus method. In Proceedings of the 2014 IEEE PES General Meeting, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar]
- Wang, C.; Ju, P.; Wu, F.; Lei, S.; Pan, X. Long-term voltage stability-constrained coordinated scheduling for gas and power grids with uncertain wind power. IEEE Trans. Sustain. Energy 2022, 13, 363–377. [Google Scholar]
- Dharmapala, K.D.; Rajapakse, A.; Narendra, K.; Zhang, Y. Machine learning based real-time monitoring of long-term voltage stability using voltage stability indices. IEEE Access 2020, 8, 222544–222555. [Google Scholar]
- Cai, H.; Ma, H.; Hill, D.J. A data-based learning and control method for long-term voltage stability. IEEE Trans. Power Syst. 2020, 35, 3203–3212. [Google Scholar]
- Yang, H.; Qiu, R.C.; Tong, H. Reconstruction residuals based long-term voltage stability assessment using autoencoders. J. Mod. Power Syst. Clean Energy 2020, 8, 1092–1093. [Google Scholar]
- Peng, Z.; Hu, G.; Han, Z. Dynamic analysis of the power system voltage stability affected by OLTC. Proc. CSEE 1999, 19, 61–65, 78. [Google Scholar]
- Sun, Y.; Wang, Z. Modeling of OLTC and its impact on the voltage stability. Autom. Electr. Power Syst. 1998, 22, 10–13. [Google Scholar]
- Londero, R.R.; Affonso, C.d.M.; Vieira, J.P.A. Long-term voltage stability analysis of variable speed wind generators. IEEE Trans. Power Syst. 2015, 30, 439–447. [Google Scholar]
- Munkhchuluun, E.; Meegahapola, L. Impact of the solar photovoltaic (PV) generation on long-term voltage stability of a power network. In Proceedings of the 2017 IEEE Innovative Smart Grid Technologies-Asia (ISGT-Asia), Auckland, New Zealand, 4–7 December 2017; pp. 1–6. [Google Scholar]
- Li, S.; Wei, Z.; Sun, G.; Gao, P.; Xiao, J. Voltage stability bifurcation of large-scale grid-connected PV system. Electr. Power Autom. Equip. 2016, 36, 17–23. [Google Scholar]
- Li, S.; Wei, Z.; Ma, Y.; Cheng, J. Prediction and control of Hopf bifurcation in a large-scale PV grid-connected system based on an optimised support vector machine. J. Eng. 2017, 14, 2666–2671. [Google Scholar] [CrossRef]
- Canizares, C.A.; Mithulananthan, N.; Milano, F.; Reeve, J. Linear performance indices to predict oscillatory stability problems in power systems. IEEE Trans. Power Syst. 2004, 19, 1104–1114. [Google Scholar] [CrossRef]
- Cutsem, T.V.; Vournas, C. Bifurcations. In Voltage Stability of Electric Power Systems; Springer: New York, NY, USA, 1998; pp. 153–160. [Google Scholar]
- Wang, Y.; Chen, H.; Zhou, R. A nonlinear controller design for SVC to improve power system voltage stability. Int. J. Electr. Power Energy Syst. 2000, 22, 463–470. [Google Scholar]
- Jing, Z.; Xu, D.; Chang, Y.; Chen, L. Bifurcations, chaos, and system collapse in a three node power system. Int. J. Electr. Power Energy Syst. 2003, 25, 443–461. [Google Scholar]
- Tamimi, B.; Cañizares, C.; Bhattacharya, K. System stability impact of large-scale and distributed solar photovoltaic generation: The case of Ontario, Canada. IEEE Trans. Sustain. Energy 2013, 4, 680–688. [Google Scholar] [CrossRef]
- Li, S.; Wei, Z.; Sun, G.; Wang, Z. Stability research of transient voltage for multi-machine power systems integrated large-scale PV power plant. Acta Energiae Solaris Sin. 2018, 39, 3356–3362. [Google Scholar]
- Bao, L.; Duan, X.; He, Y. Analysis of the effect of OLTC on the voltage stability through time domain simulation. J. Huazhong Univ. Sci. Tech. 2000, 28, 61–63. [Google Scholar]
- Duan, X.; He, Y.; Chen, D. Dynamic analysis of the relation between on-load tap changer and voltage stability. Autom. Electr. Power Syst. 1995, 19, 14–19. [Google Scholar]






| Em/pu | Pm/pu | M/pu | D/pu | E0/pu | Ym/pu | θm/rad | Y0/pu | θ0/rad | C/pu | Tn/s | Vref/pu | Sbase |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.3 | 0.05 | 1 | 5 | −0.0872 | 20 | −0.0872 | 12 | 1600 | 1 | 100 MVA |
| T/s | kpω | kqω | kpV | kqV | kqV2 | P0/pu | Q0/pu | P1/pu | Tp/s | Tq/s | k |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 8.5 | 0.4 | −0.03 | 0.3 | −2.8 | 2.1 | 0.6 | 1.3 | 1.2 | 10 | 10 | 0.2 |
| The Content of Comparison | With OLTC | Without OLTC |
|---|---|---|
| Bifurcation type of point H1 | SHB | UHB |
| Reactive load Q1 of H1 (pu) | 10.3418 pu | 11.1309 pu |
| Voltage amplitude of H1 (pu) | 1 pu (Vref) | 1.0744 pu |
| Sudden small increase of Q1 | Long-term voltage collapse | Long-term voltage collapse |
| Sudden drop of Ppv | Long-term voltage recovery | Long-term voltage oscillation instability (Oscillation amplitude ≥ 5%) |
| Sudden increase of Ppv | Long-term voltage collapse | Long-term voltage oscillation without instability (Oscillation amplitude << 5%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Zhang, C.; Zuo, J. Long-Term Voltage Stability Bifurcation Analysis and Control Considering OLTC Adjustment and Photovoltaic Power Station. Energies 2023, 16, 6383. https://doi.org/10.3390/en16176383
Li S, Zhang C, Zuo J. Long-Term Voltage Stability Bifurcation Analysis and Control Considering OLTC Adjustment and Photovoltaic Power Station. Energies. 2023; 16(17):6383. https://doi.org/10.3390/en16176383
Chicago/Turabian StyleLi, Sheng, Can Zhang, and Jili Zuo. 2023. "Long-Term Voltage Stability Bifurcation Analysis and Control Considering OLTC Adjustment and Photovoltaic Power Station" Energies 16, no. 17: 6383. https://doi.org/10.3390/en16176383





