A Bidirectional Grid-Tied ZVS Three-Phase Converter Based on DPWM and Digital Control
Abstract
:1. Introduction
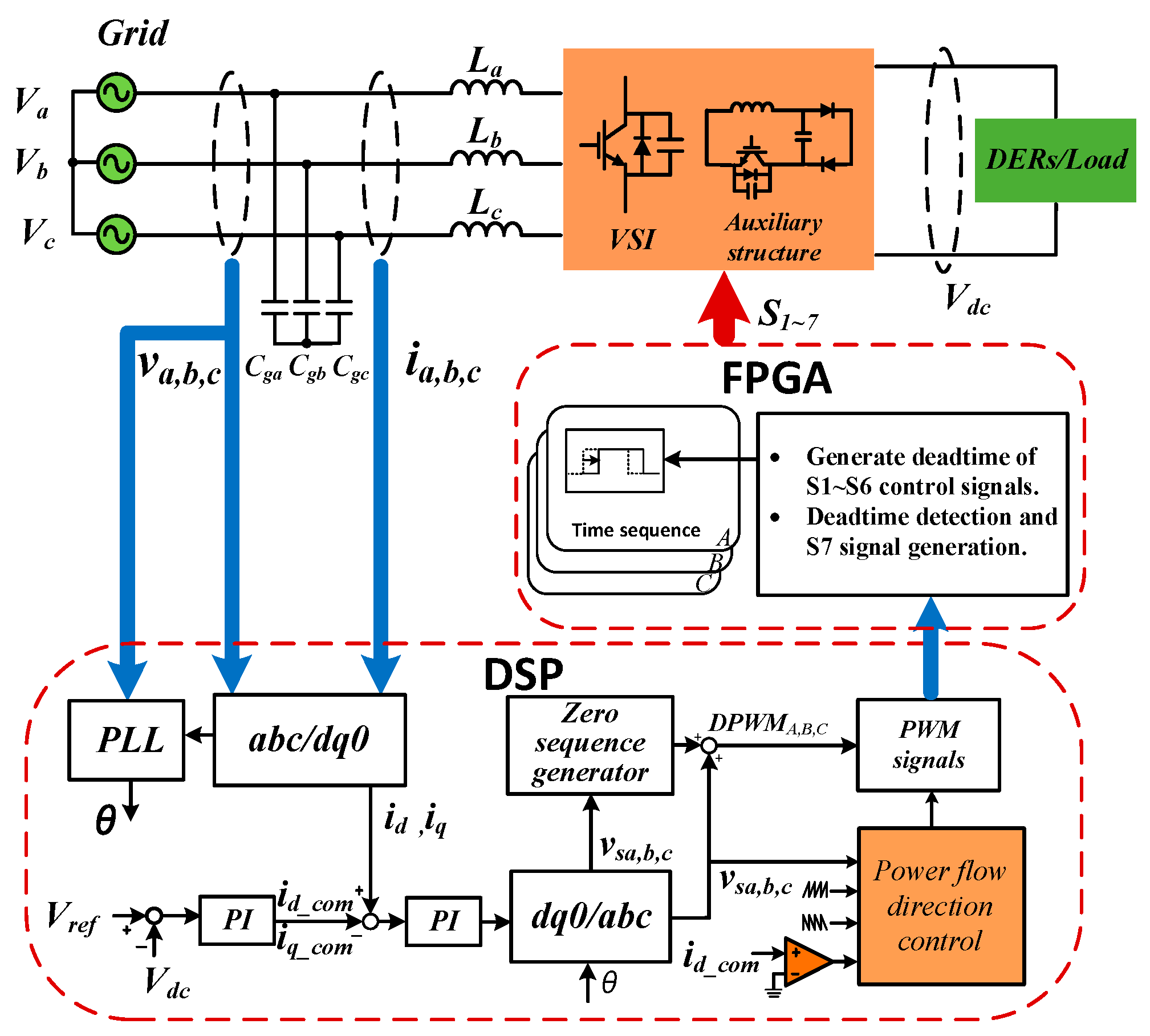
2. Proposed Bidirectional ZVS Three-Phase Converter
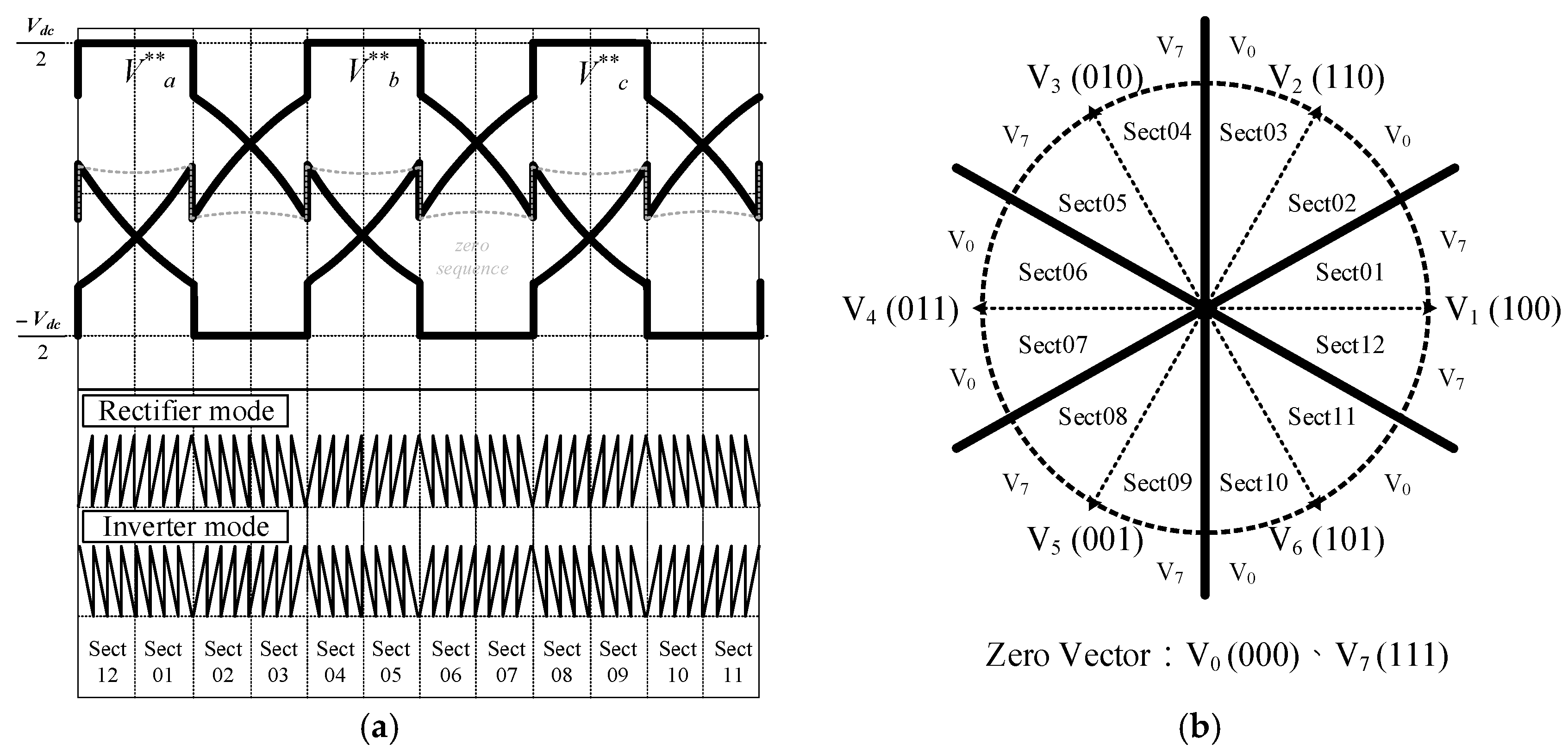
2.1. Proposed Circuit Topology and PWM Strategy
- Rectifier Mode
- B.
- Inverter Mode
- (1)
- The main switches S1–S6 and auxiliary switch S7 are considered ideal switches with their anti-paralleled diodes (body diodes). The body diodes of switches S1~S7 are named D1~D7, respectively.
- (2)
- All of the parasitic capacitances Cr1–Cr7 are in parallel with the switches S1–S7, respectively. Suppose Cr1 = Cr2 = ⋯ = Cr6.
- (3)
- The clamping capacitor Cc possesses a substantial capacitance, resulting in a minor voltage ripple across it. As a consequence, the voltage vCc can be treated akin to a voltage source.
- (4)
- The operational frequency of the converter is significantly higher than the resonant frequency of the LC filter on the AC side.
- (5)
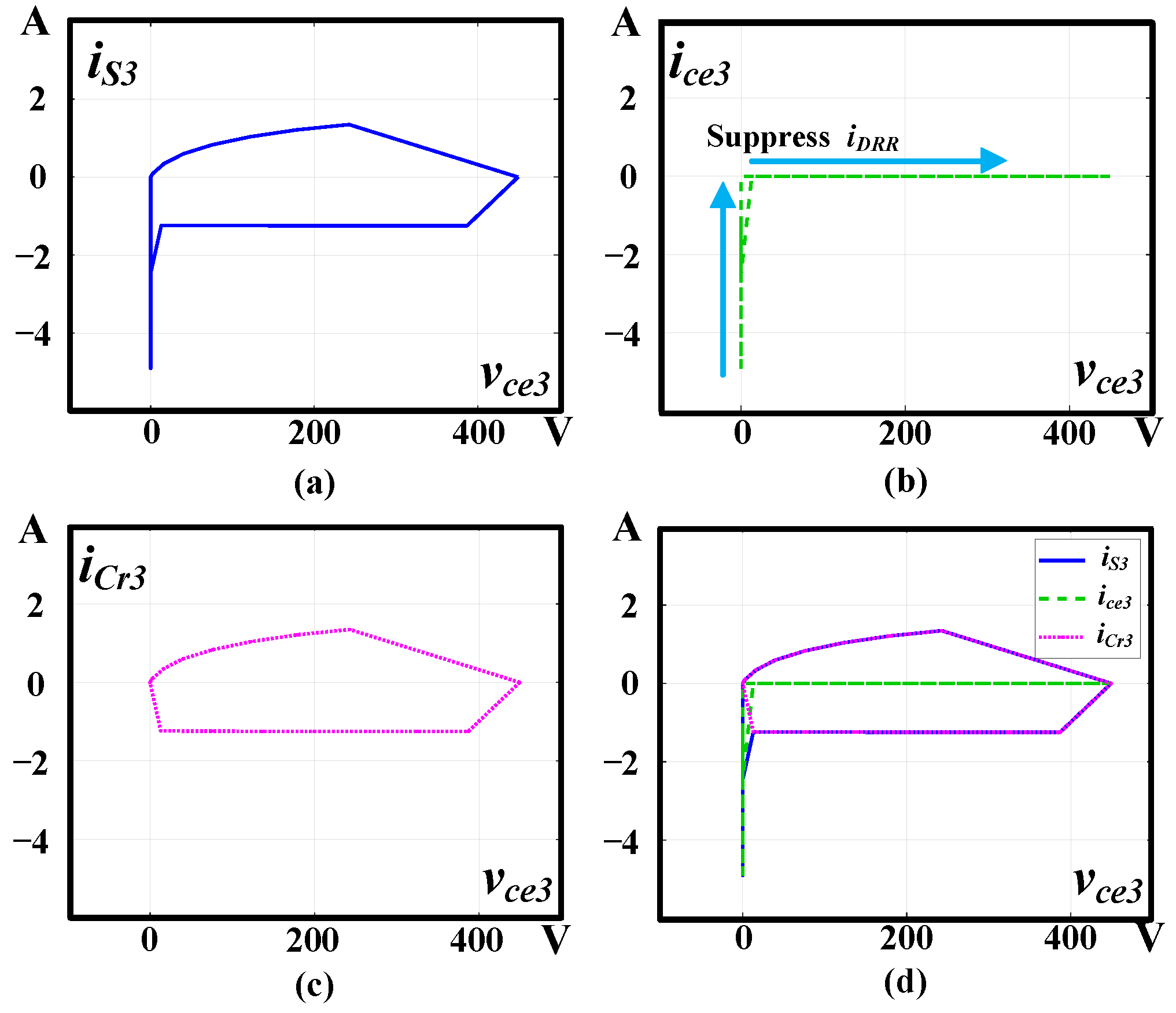
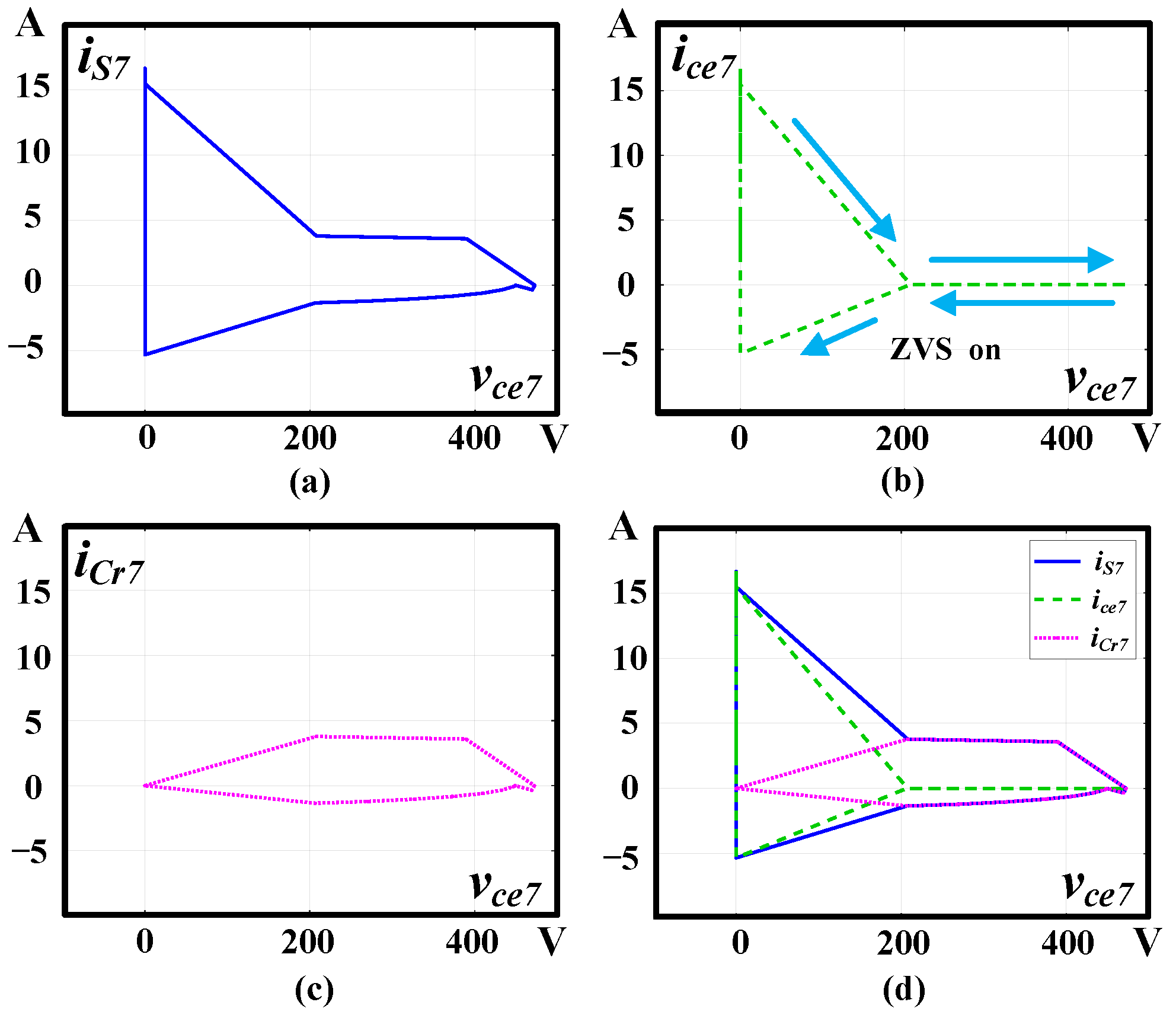
- The current isx, where x belongs to the set {1, 2, …, 7}, characterizes the switch current incorporating the parasitic capacitor current. Meanwhile, the current icex, with x also within the set {1, 2, …, 7}, represents the switch current after eliminating the parasitic capacitor contribution. The voltage vcex, x∈{1, 2, …, 7}, represents the switch voltage. vcr denotes the resonant capacitor voltage.
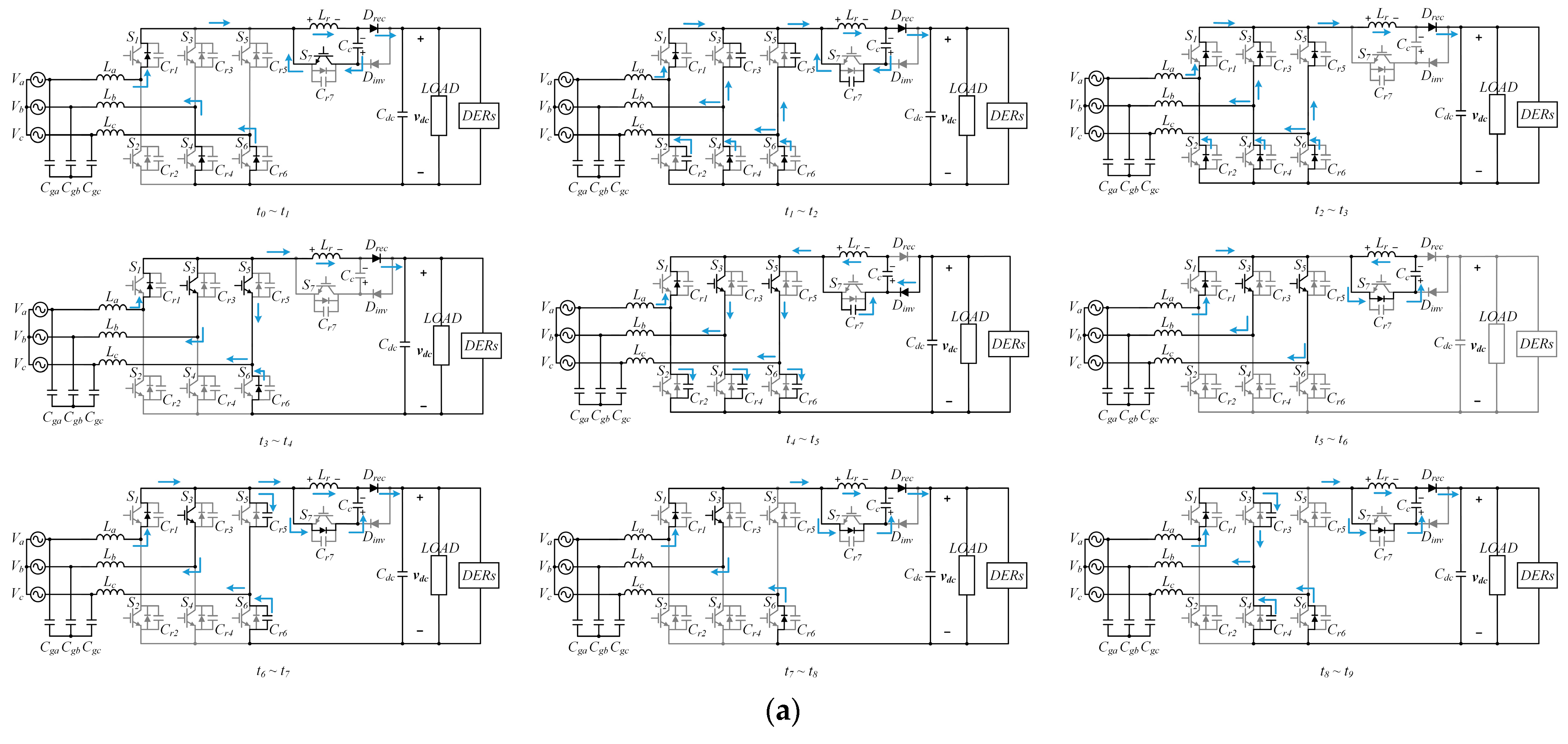
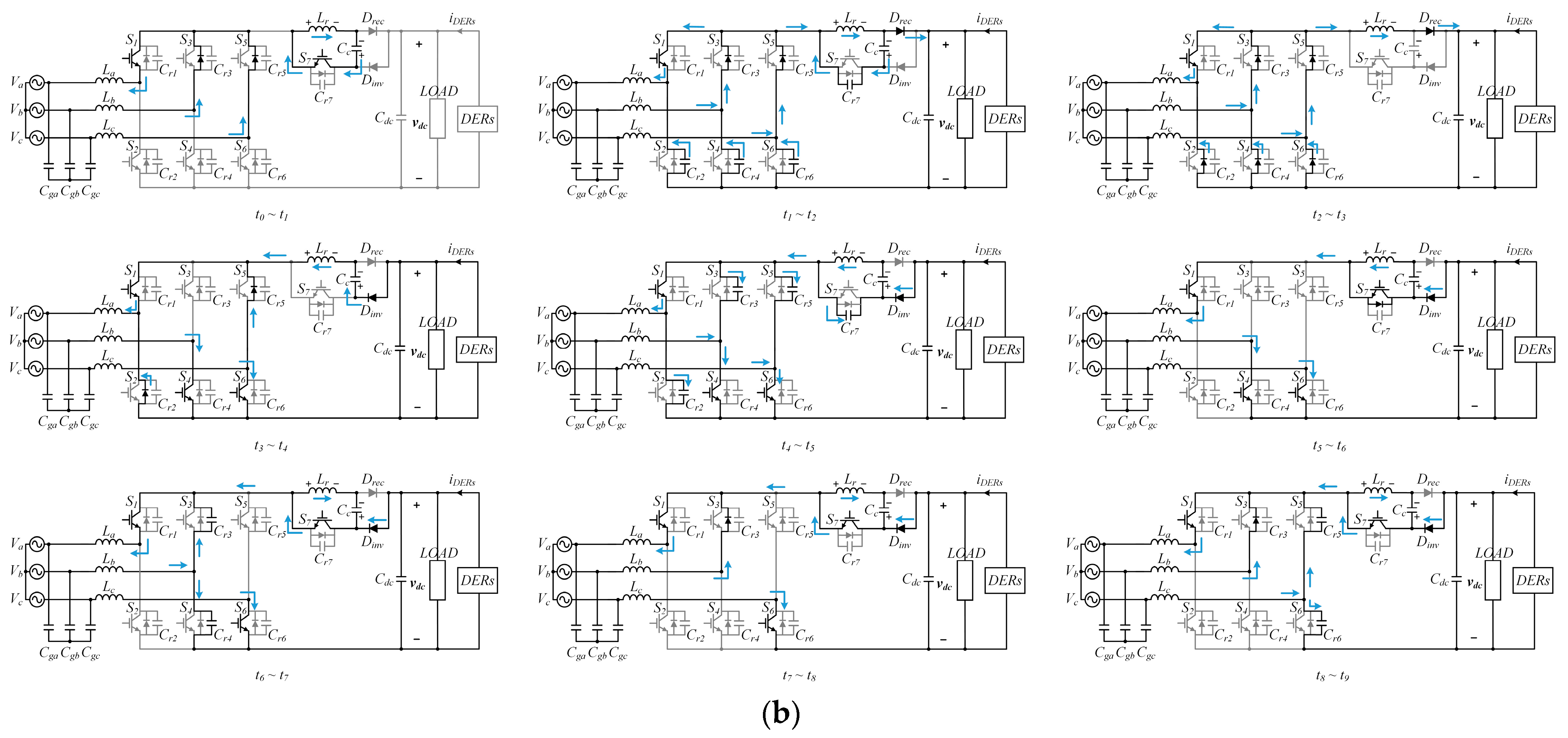
2.2. Rectifier Mode Operation
2.3. Inverter Mode Operation
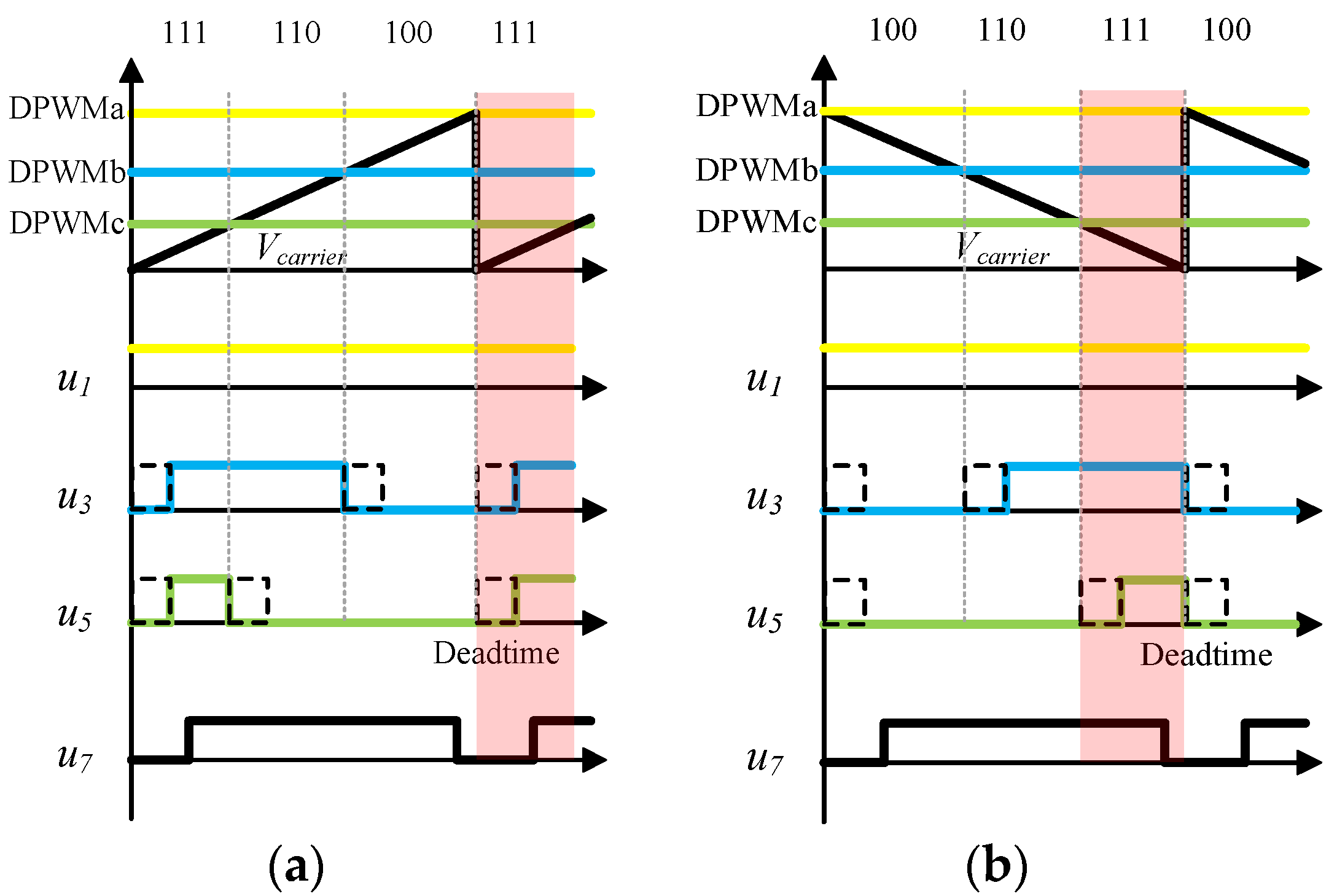
2.4. Control Scheme
2.5. Circuit Design
2.6. Controller Design
3. Simulation Results
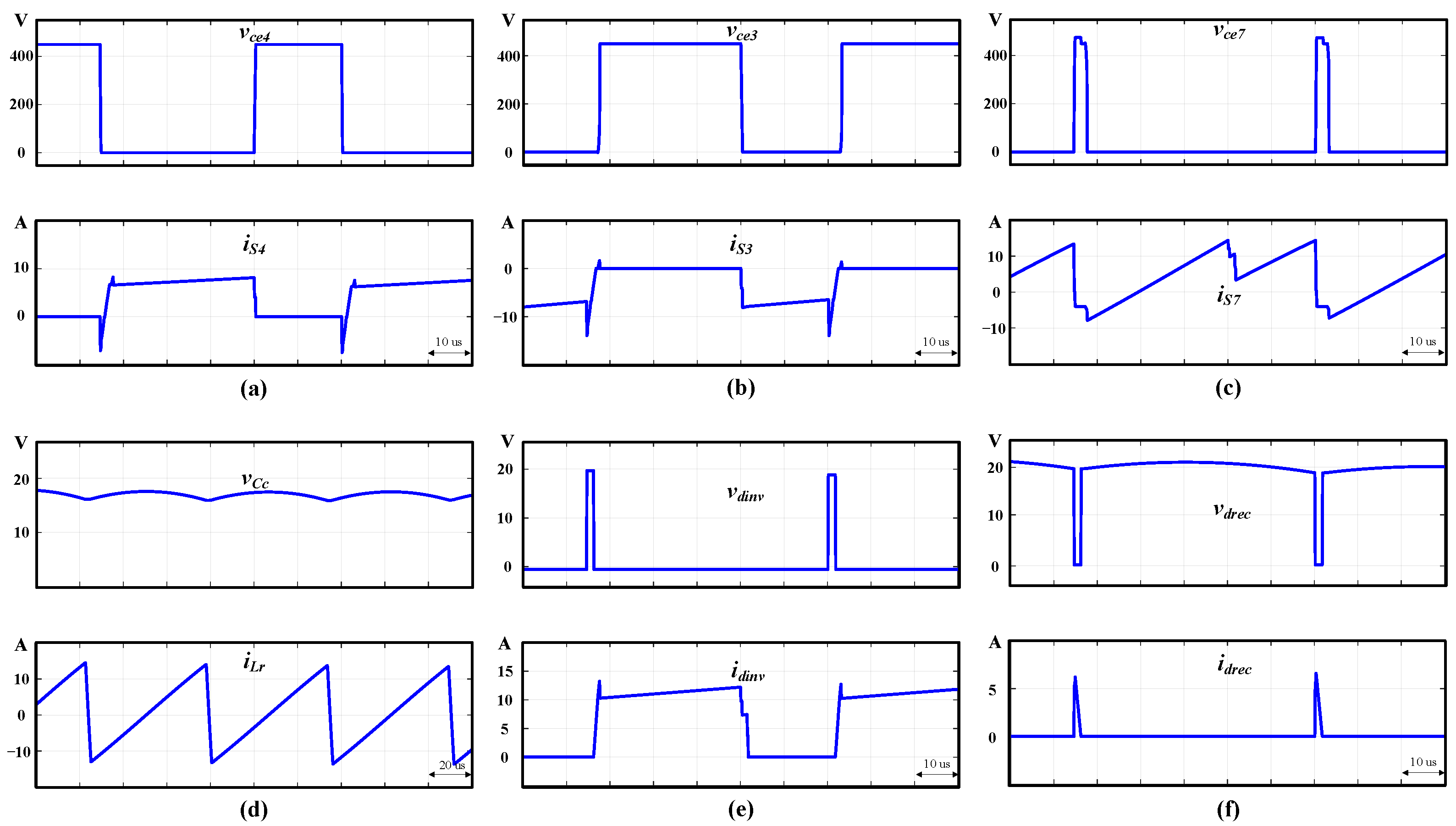
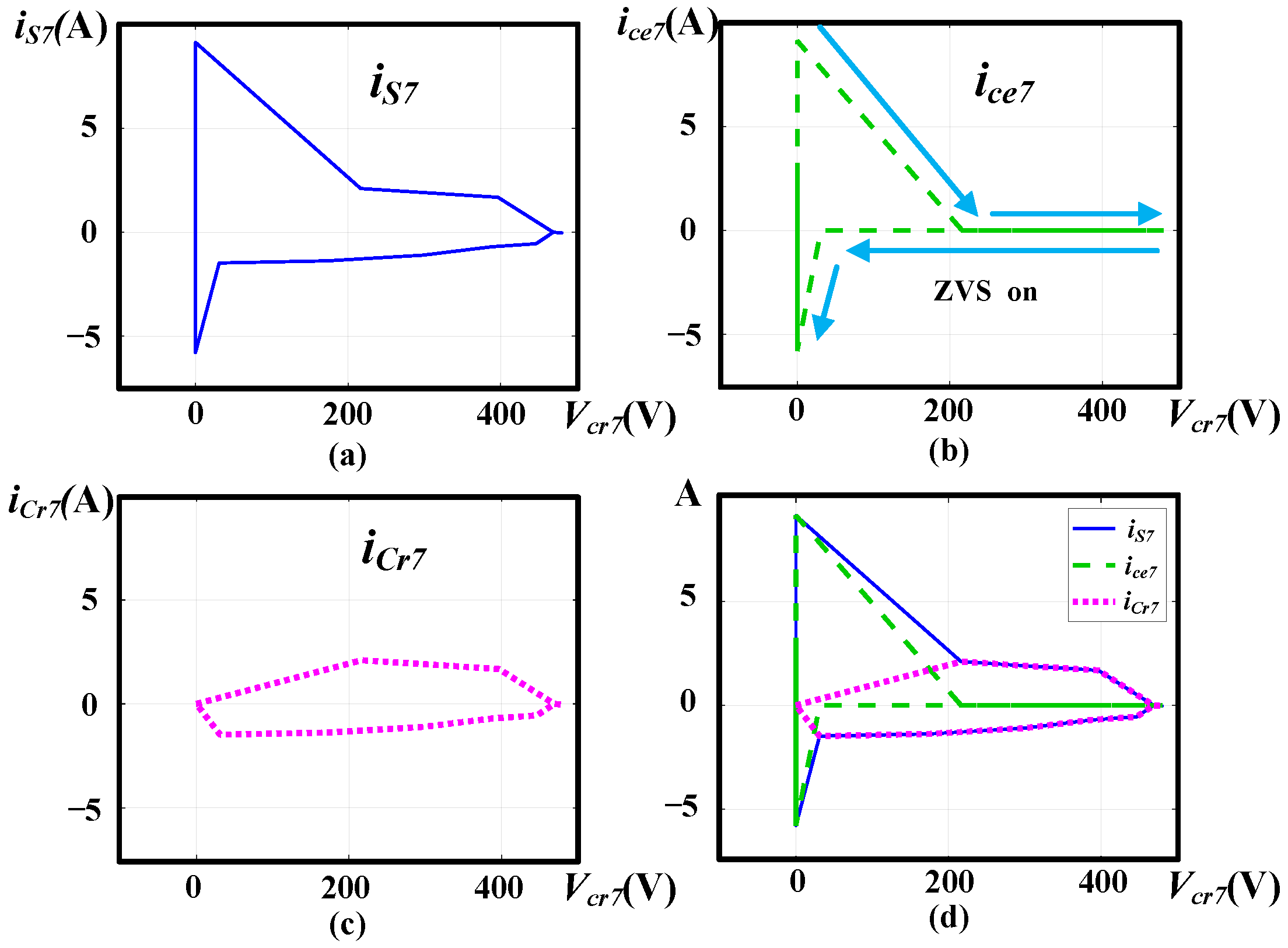
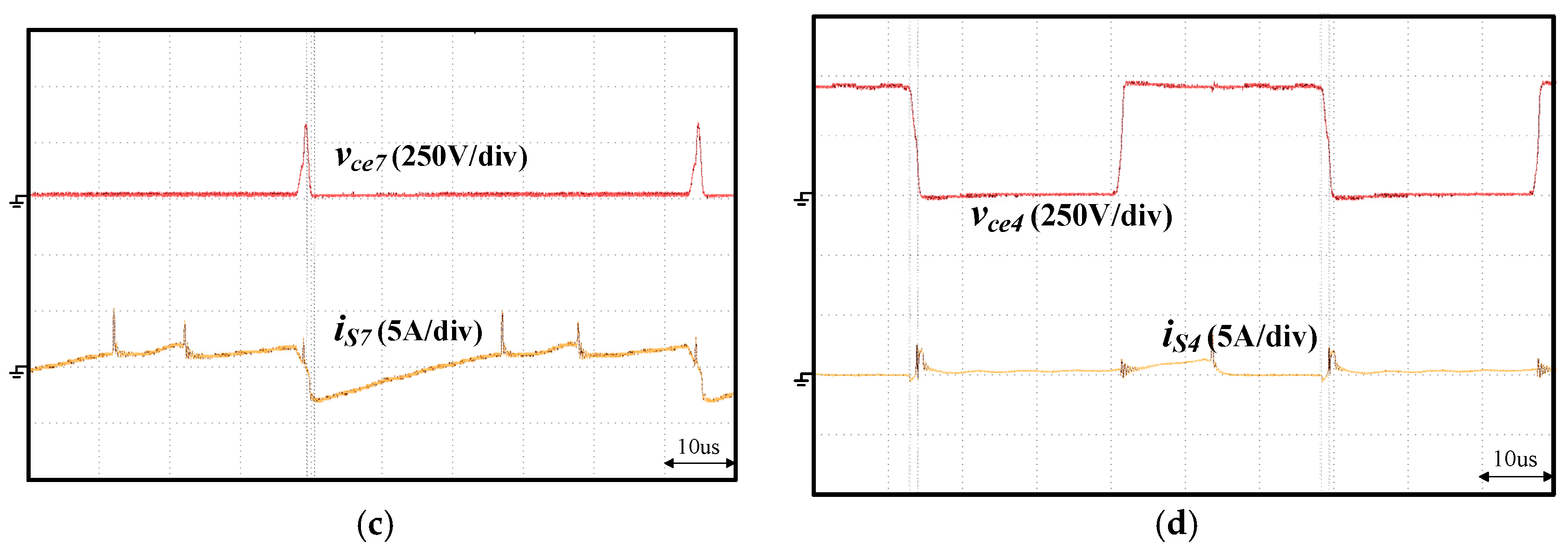
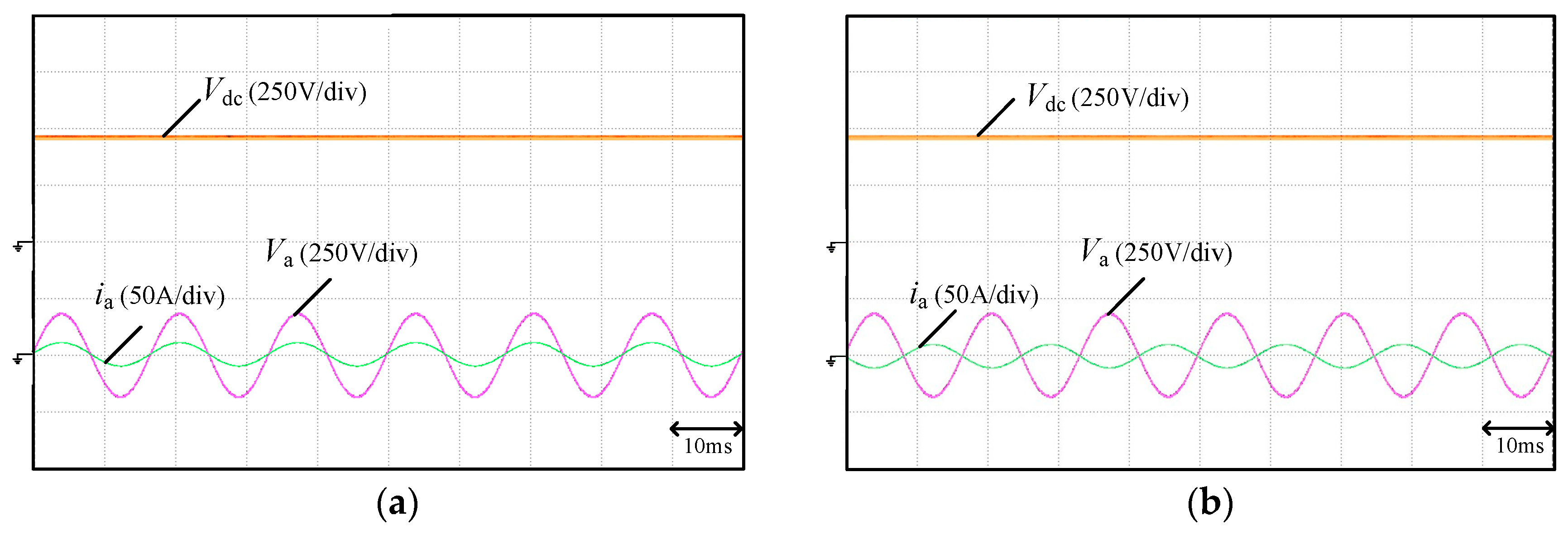
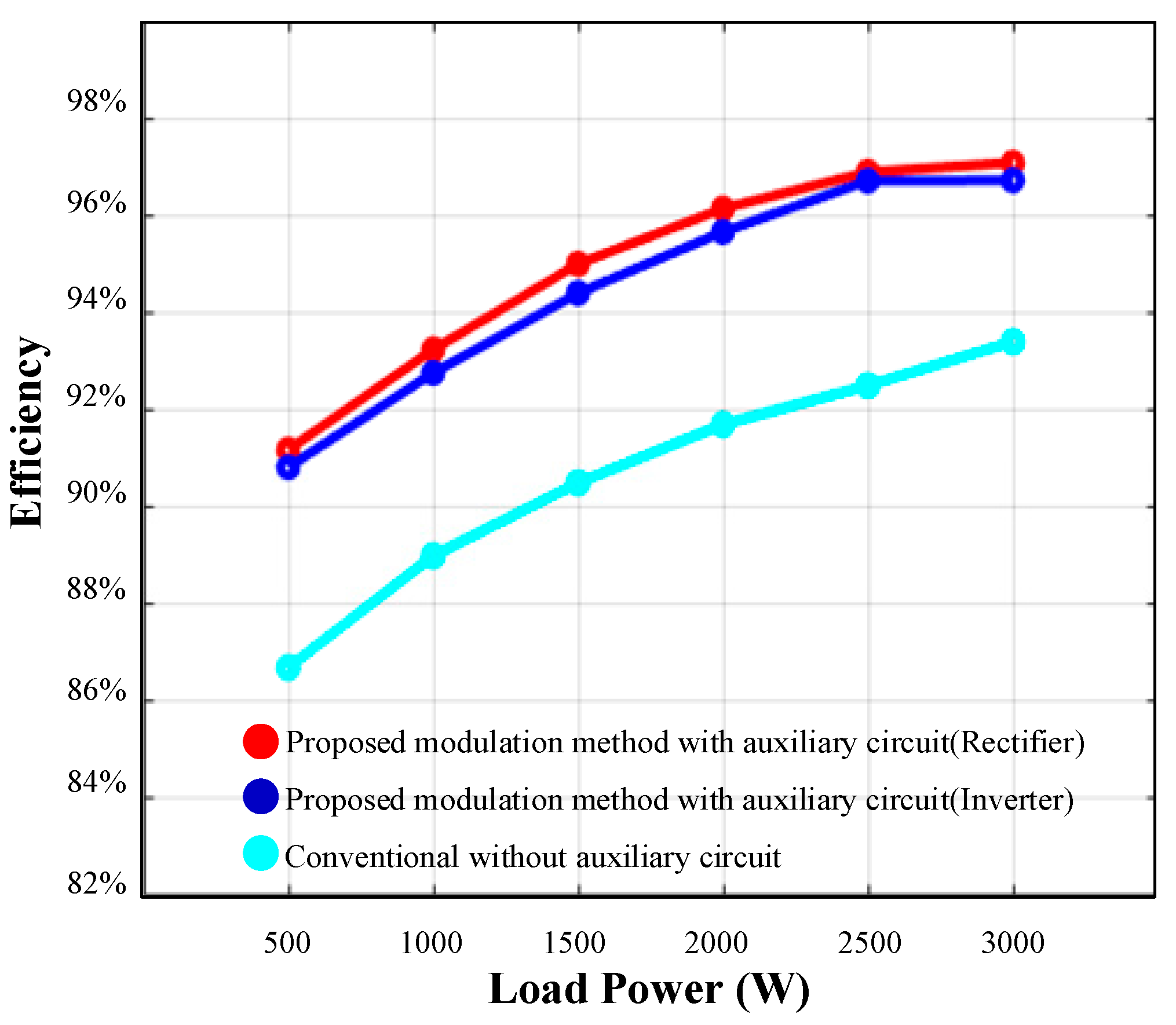
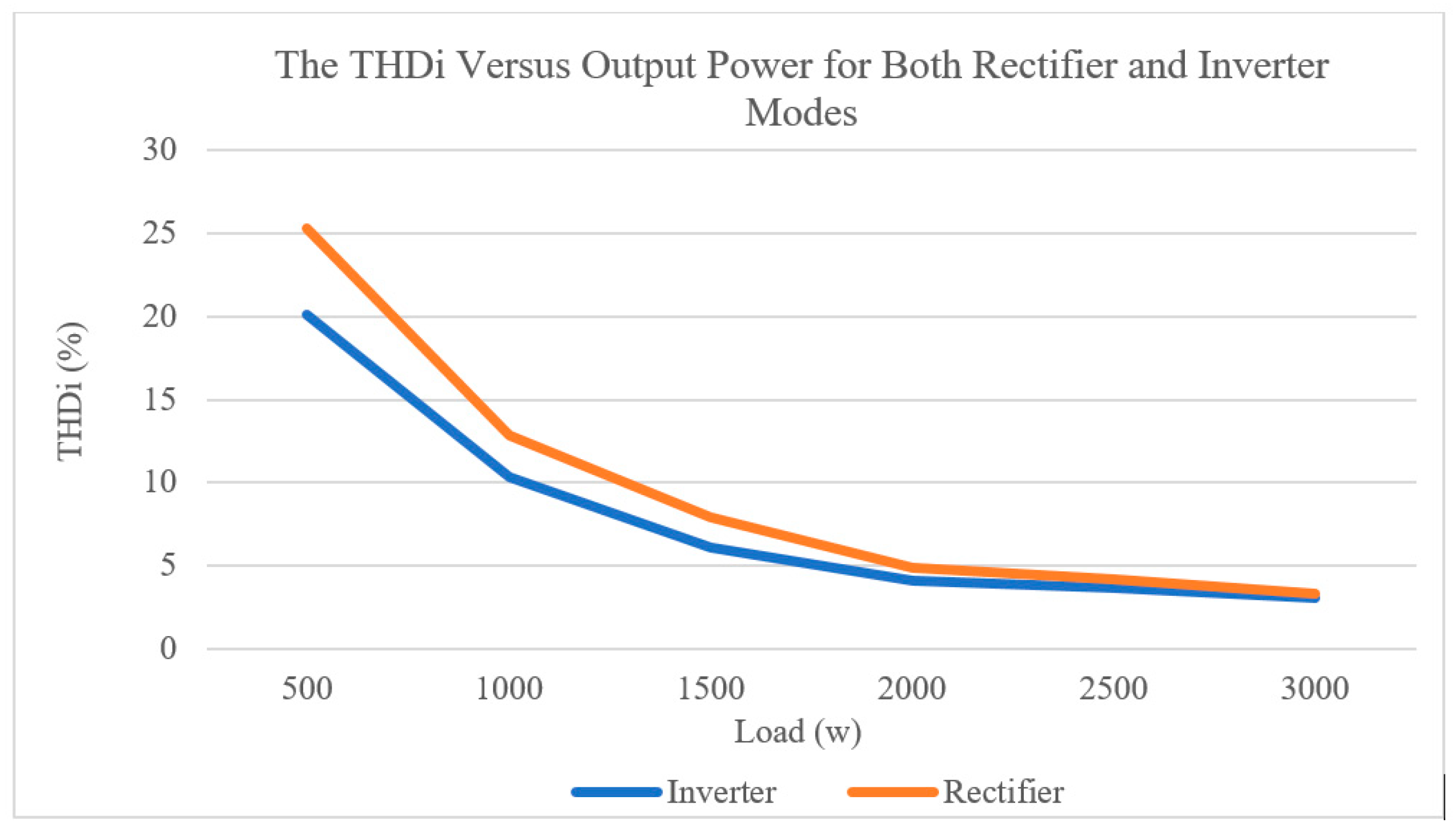
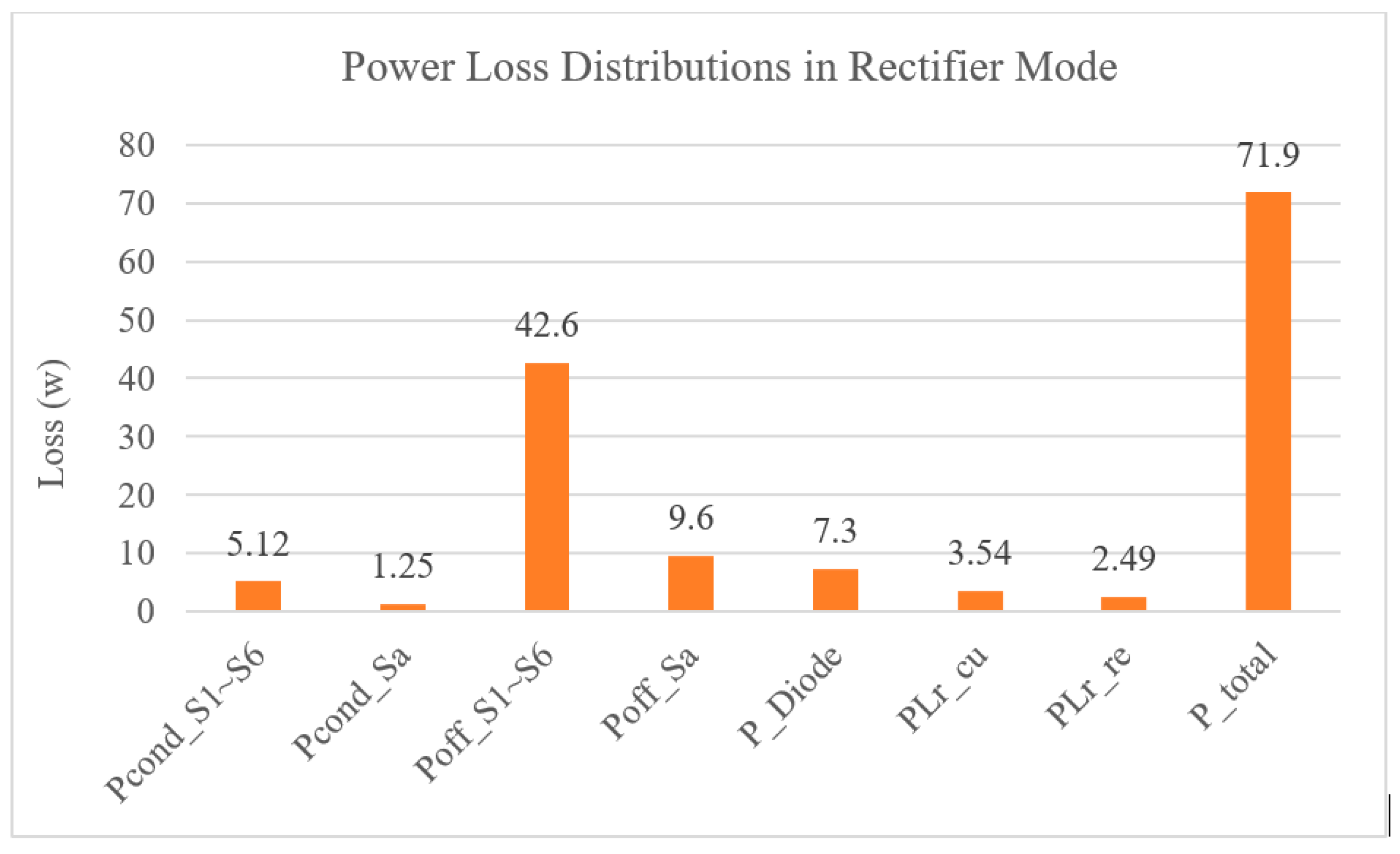
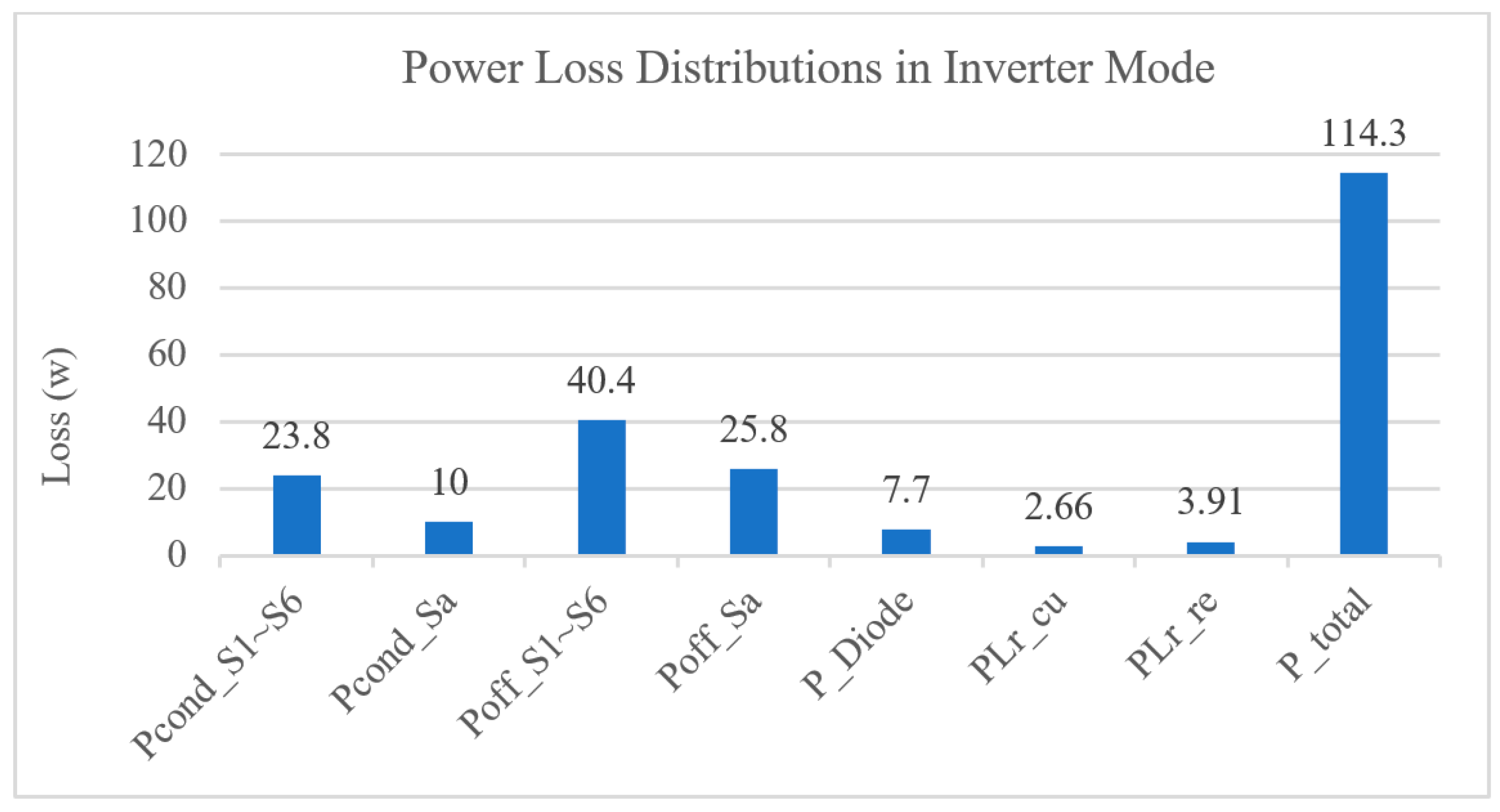
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, Z.; Liu, Z.; Lee, F.C.; Li, Q. Critical-Mode-Based Soft-Switching Modulation for High-Frequency Three-Phase Bidirectional AC–DC Converters. IEEE Trans. Power Electron. 2019, 34, 3888–3898. [Google Scholar] [CrossRef]
- Li, R.; Ma, Z.; Xu, D. A ZVS Grid-Connected Three-Phase Inverter. IEEE Trans. Power Electron. 2012, 27, 3595–3604. [Google Scholar] [CrossRef]
- Bellar, M.D.; Wu, T.-S.; Tchamdjou, A.; Mahdavi, J.; Ehsani, M. A review of soft-switched dc-ac converters. IEEE Trans. Ind. Appl. 1998, 34, 847–860. [Google Scholar] [CrossRef]
- Nakaoka, M.; Yonemori, H.; Yurugi, K. Zero-voltage soft-switched PDM three phase AC-DC active power converter operating at unity power factor and sinewave line current. In Proceedings of the IEEE Power Electronics Specialist Conference, Seattle, WA, USA, 20–24 June 1993; pp. 787–794. [Google Scholar]
- Yonemori, H.; Fukuda, H.; Nakaoka, M. Advanced three-phase ZVS-PWM active power rectifier with new resonant DC link and its digital control scheme. In Proceedings of the Fifth International Conference on Power Electronics and Variable-Speed Drives, London, UK, 26–28 October 1994; pp. 608–613. [Google Scholar]
- Mao, H.; Lee, C.Y.; Boroyevich, D.; Hiti, S. Review of high performance three-phase power-factor correction circuits. IEEE Trans. Ind. Electron. 1997, 44, 437–446. [Google Scholar]
- Xu, D.; Feng, B.; Li, R.; Mino, K.; Umida, H. A Zero Voltage Switching SVM (ZVS–SVM) Controlled Three-Phase Boost Rectifier. IEEE Trans. Power Electron. 2007, 22, 978–986. [Google Scholar] [CrossRef]
- Li, R.; Ma, K.; Xu, D. A Novel Minimum Voltage Active Clamping SVM (MVAC-SVM) Controlled Three-Phase PFC. In Proceedings of the Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Exposition, Washington, DC, USA, 15–19 February 2009; pp. 1879–1885. [Google Scholar]
- Divan, D.M. The resonant dc link converter—A new concept in static power conversion. IEEE Trans. Ind. Appl. 1989, 25, 317–325. [Google Scholar] [CrossRef]
- Divan, D.M.; Skibinski, G. Zero-switching-loss inverters for high power applications. IEEE Trans. Ind. Appl. 1989, 25, 634–643. [Google Scholar] [CrossRef]
- Venkataramanan, G.; Divan, D.M. Pulse width modulation with resonant DC link converters. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Seattle, WA, USA, 7–12 October 1990; Volume 2, pp. 984–990. [Google Scholar]
- He, J.; Mohan, N. Parallel resonant DC link circuit-a novel zero switching loss topology with minimum voltage stresses. IEEE Trans. Power Electron. 1991, 6, 687–694. [Google Scholar] [CrossRef]
- Chen, Y.-T. A new quasi-parallel resonant DC link for soft-switching PWM inverters. IEEE Trans. Power Electron. 1998, 13, 427–435. [Google Scholar] [CrossRef]
- Jafar, J.J.; Fernandes, B.G. A new quasi-resonant DC-link PWM inverter using single switch for soft switching. IEEE Trans. Power Electron. 2002, 17, 1010–1016. [Google Scholar] [CrossRef]
- Mezaroba, M.; Martins, D.C.; Barbi, I. A ZVS PWM Half-Bridge Voltage Source Inverter with Active Clamping. IEEE Trans. Ind. Electron. 2007, 54, 2665–2672. [Google Scholar] [CrossRef]
- Gurunathan, R.; Bhat, A.K.S. Zero-Voltage Switching DC Link Single-Phase Pulsewidth-Modulated Voltage Source Inverter. IEEE Trans. Power Electron. 2007, 22, 1610–1618. [Google Scholar] [CrossRef]
- Li, R.; Xu, D. A Zero-Voltage Switching Three-Phase Inverter. IEEE Trans. Power Electron. 2014, 29, 1200–1210. [Google Scholar]
- Du, C.; Xu, D.; He, N.; Zhu, N. Modeling and Optimization of a Zero-Voltage Switching Inverter for High Efficiency and Miniaturization. IEEE Trans. Power Electron. 2017, 32, 150–163. [Google Scholar] [CrossRef]
- Shi, K.; Deng, J.; Xu, D. A General Pulse Width Modulation Method for Zero-Voltage-Switching Active-clamping Three- phase Power Converters: Edge Aligned Pulse Width Modulation (EA-PWM). IEEE Open J. Power Electron. 2020, 1, 250–259. [Google Scholar] [CrossRef]
- Wu, Y.; He, N.; Chen, M.; Xu, D. Generalized Space-Vector-Modulation Method for Soft-Switching Three-Phase Inverters. IEEE Trans. Power Electron. 2021, 36, 6030–6045. [Google Scholar] [CrossRef]
- He, N.; Zhu, Y.; Zhao, A.; Xu, D. Zero-Voltage-Switching Sinusoidal Pulsewidth Modulation Method for Three-Phase Four-Wire Inverter. IEEE Trans. Power Electron. 2019, 34, 7192–7205. [Google Scholar] [CrossRef]
- Chen, J.; Sha, D.; Zhang, J. Current Ripple Prediction and DPWM-Based Variable Switching Frequency Control for Full ZVS Range Three-Phase Inverter. IEEE Trans. Ind. Electron. 2021, 68, 1412–1422. [Google Scholar] [CrossRef]
- Fan, B.; Wang, Q.; Burgos, R.; Ismail, A.; Boroyevich, D. Adaptive Hysteresis Current Based ZVS Modulation and Voltage Gain Compensation for High-Frequency Three-Phase Converters. IEEE Trans. Power Electron. 2021, 36, 1143–1156. [Google Scholar] [CrossRef]
- Chen, J.; Han, Y.; Han, Q.; Liu, Q. A DPWM-Based Quasi-Constant Switching Frequency Control for Full ZVS Range Three-Phase Inverter with Reactive Power Transfer Capability. IEEE Trans. Ind. Electron. 2022, 70, 4912–4921. [Google Scholar] [CrossRef]
- Bagawade, S.; Pahlevani, M.; Jain, P. Novel Soft-Switched Three-Phase Inverter with Output Current Ripple Cancellation. IEEE Trans. Power Electron. 2023, 38, 1232–1248. [Google Scholar] [CrossRef]
- Hava, A.M.; Kerkman, R.J.; Lipo, T.A. Simple analytical and graphical methods for carrier-based PWM-VSI drives. IEEE Trans. Power Electron. 1999, 14, 49–61. [Google Scholar] [CrossRef]


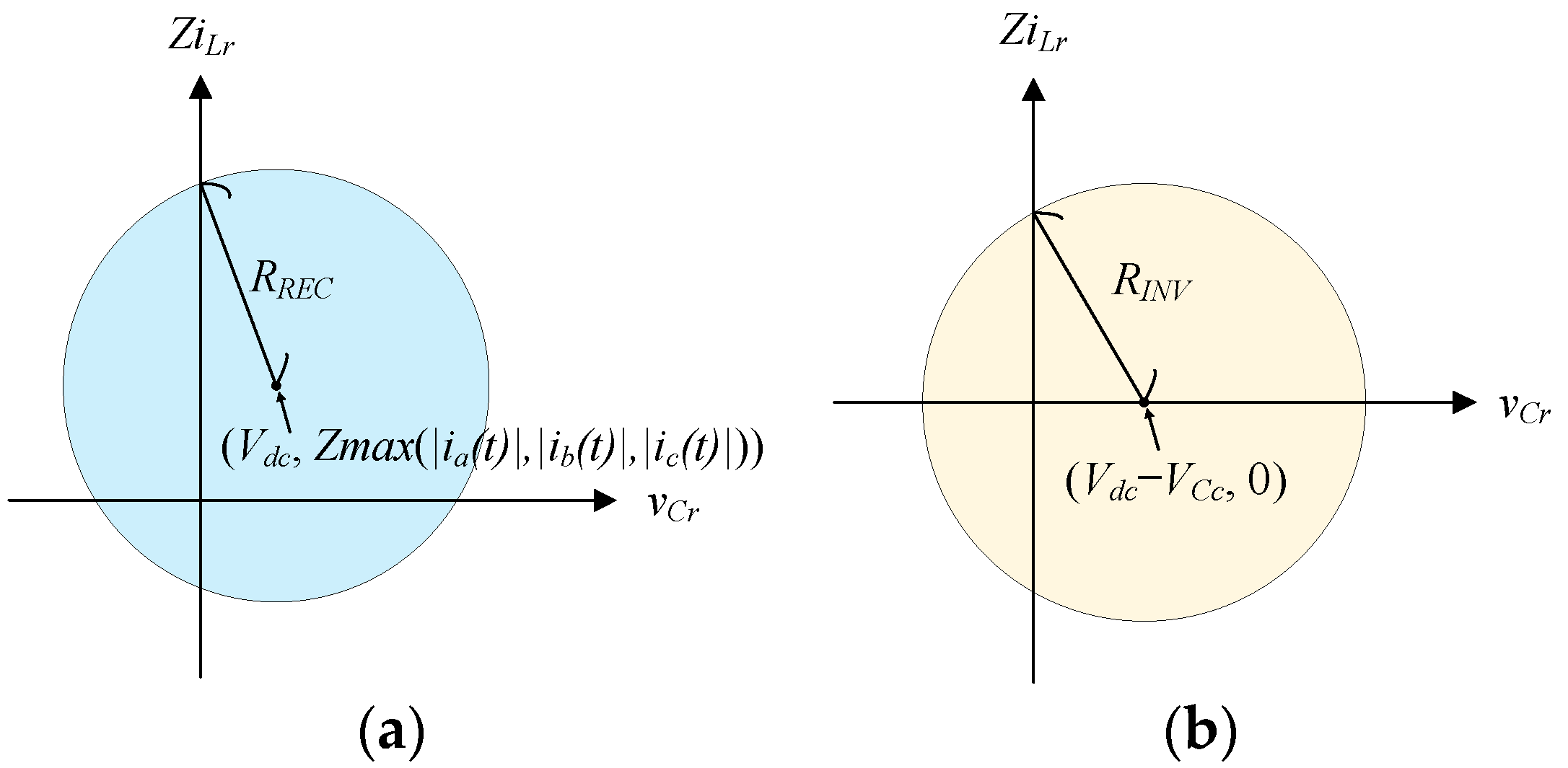









| Structure | Extra Elements (Structure) | Switching Frequency (fs) | Switch Voltage Stress on Main and Auxiliary Switches | Switch Current Stress on Main/Auxiliary Switches | Filter Design | Bidirectional Operation |
|---|---|---|---|---|---|---|
| [7] Rectifier | LC + switch (3ϕ/3w) | Fixed | Vdc + Vcc ≈ Vdc | Low/Low | LC | None |
| [8] Rectifier | LC + switch (3ϕ/3w) | Fixed | Vdc | Low/High | LC | None |
| [2] Inverter | LC + switch (3ϕ/3w) | Fixed | Vdc | Low/High | LC | None |
| [17] Inverter | LC + switch (3ϕ/3w) | Fixed | Vdc + Vcc ≈ Vdc | Low/Low | LC | None |
| [19] BTB | LC + switch (3ϕ/4w) | Fixed | Vdc + Vcc ≈ Vdc | Low/Low | LC | None |
| [20] Inverter | LC + switch (3ϕ/3w) | Fixed | Vdc + Vcc ≈ Vdc | Low/Low | LC | None |
| [21] Inverter | LC + switch (3ϕ/4w) | Fixed | Vdc + Vcc ≈ Vdc | Low/Low | LC | None |
| [22] Inverter | None (3ϕ/3w) | Variable | Vdc | High/X | LCL | None |
| [1] Converter | None (3ϕ/3w) | Variable | Vdc | High/X | LCL | √ |
| [23] Inverter | None (3ϕ/3 or 4w) | Variable | Vdc | High/X | LCL | None |
| [24] Inverter | None (3ϕ/3w) | Variable (quasi-constant) | Vdc | High/X | LCL | None (inverter full ZVS range) |
| [25] Inverter | 3 passive filters (current ripple cancellation) (3ϕ/3w) | Variable | Vdc | High/X | Transformer, L and C | None |
| Proposed converter | LC + switch + D (3ϕ/3w) | Fixed | Vdc + Vcc ≈ Vdc | Low/High | LC | √ |
| Sector | Vector |
|---|---|
| 1 | 111 → 110 → 100 → 111 |
| 2 | 000 → 100 → 110 → 000 |
| 3 | 000 → 010 → 110 → 000 |
| 4 | 111 → 110 → 010 → 111 |
| 5 | 111 → 011 → 010 → 111 |
| 6 | 000 → 010 → 011 → 000 |
| 7 | 000 → 001 → 011 → 000 |
| 8 | 111 → 011 → 001 → 111 |
| 9 | 111 → 101 → 001 → 111 |
| 10 | 000 → 001 → 101 → 000 |
| 11 | 000 → 100 → 101 → 000 |
| 12 | 111 → 101 → 100 → 111 |
| Sector | Vector |
|---|---|
| 1 | 111 → 100 → 110 → 111 |
| 2 | 000 → 110 → 100 → 000 |
| 3 | 000 → 110 → 010 → 000 |
| 4 | 111 → 010 → 110 → 111 |
| 5 | 111 → 010 → 011 → 111 |
| 6 | 000 → 011 → 010 → 000 |
| 7 | 000 → 011 → 001 → 000 |
| 8 | 111 → 001 → 011 → 111 |
| 9 | 111 → 001 → 101 → 111 |
| 10 | 000 → 101 → 001 → 000 |
| 11 | 000 → 101 → 100 → 000 |
| 12 | 111 → 100 → 101 → 111 |
| Parameters | Value | Unit |
|---|---|---|
| AC grid line voltage (rms) | 220 | V |
| DC link voltage, Vdc | 450 | V |
| Switching frequency, fs | 18 | kHz |
| Three-phase inductors, La,b,c | 2 | mH |
| Three-phase capacitors Cga,b,c | 22 | μF |
| DC-link capacitor, Cdc | 2200 | μF |
| Parasitic capacitance, Cr | 2 | nF |
| Resonant inductor, Lr | 40 | μH |
| Clamping capacitor, Cc | 100 | μF |
| Power rating, Prate | 3 | kW |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Y.-H.; Lin, F.-J.; Zhou, Y.; Lai, W.-R.; Huang, X.-S. A Bidirectional Grid-Tied ZVS Three-Phase Converter Based on DPWM and Digital Control. Energies 2023, 16, 6453. https://doi.org/10.3390/en16186453
Liao Y-H, Lin F-J, Zhou Y, Lai W-R, Huang X-S. A Bidirectional Grid-Tied ZVS Three-Phase Converter Based on DPWM and Digital Control. Energies. 2023; 16(18):6453. https://doi.org/10.3390/en16186453
Chicago/Turabian StyleLiao, Yi-Hung, Faa-Jeng Lin, Ying Zhou, Wei-Rong Lai, and Xuan-Sheng Huang. 2023. "A Bidirectional Grid-Tied ZVS Three-Phase Converter Based on DPWM and Digital Control" Energies 16, no. 18: 6453. https://doi.org/10.3390/en16186453
APA StyleLiao, Y.-H., Lin, F.-J., Zhou, Y., Lai, W.-R., & Huang, X.-S. (2023). A Bidirectional Grid-Tied ZVS Three-Phase Converter Based on DPWM and Digital Control. Energies, 16(18), 6453. https://doi.org/10.3390/en16186453







