Dynamic Pro-Active Eco-Driving Control Framework for Energy-Efficient Autonomous Electric Mobility
Abstract
:1. Introduction
1.1. Literature Review
1.2. Motivations and Contributions
- Proposing a pro-active algorithm that considers the IPV state data in the reference speed planning;
- Improving existing analytical energy consumption parameterization;
- Considering both the up and downstream of the signalized intersection.
2. Materials and Methods
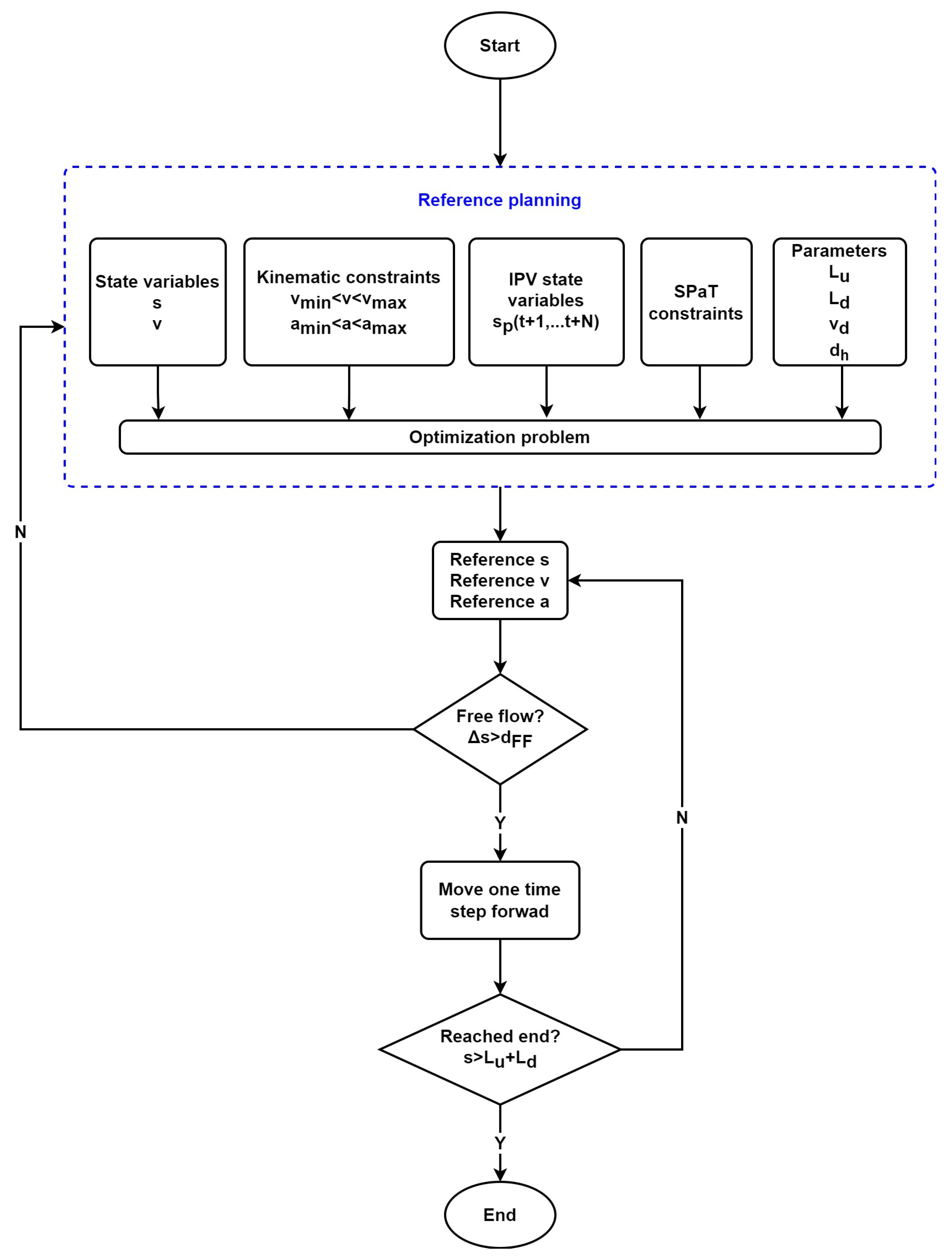
2.1. Eco-PPCC Logic
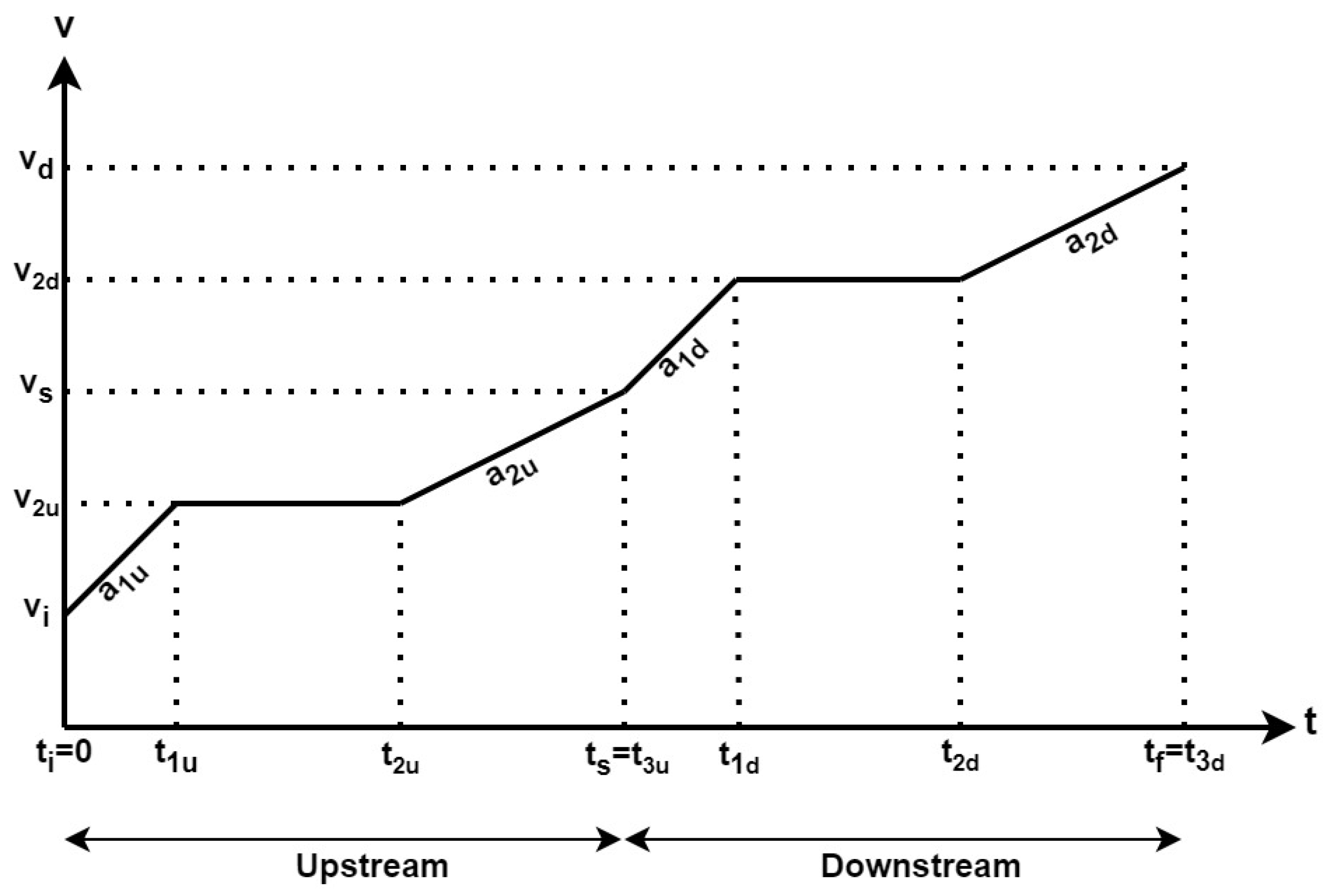
2.2. Reference Trajectory Planning
2.3. Analytical Parameterization
- Cruise (C): Maintaining a constant speed throughout the entire trajectory without any variations;
- Accelerate (A): Increasing or decreasing speed consistently at a fixed rate throughout the entire trajectory;
- Cruise–accelerate (C-A): Initially, cruising at a steady speed for a portion of the trajectory, followed by accelerating or decelerating at a constant rate for the remaining trajectory section;
- Accelerate–cruise (A-C): Initially, applying a constant acceleration or deceleration rate for a portion of the trajectory and maintaining a constant speed for the remaining section;
- Accelerate–cruise–accelerate (A-C-A): In the beginning, constant acceleration or deceleration occurs over a portion of the trajectory. It is followed by a phase of cruising at a constant speed. Finally, there is another phase of constant acceleration or deceleration occurs over the remaining trajectory section;
2.4. Parameterized Objective Function
2.5. Human Driver Simulation
3. Results and Discussions
3.1. Calibration
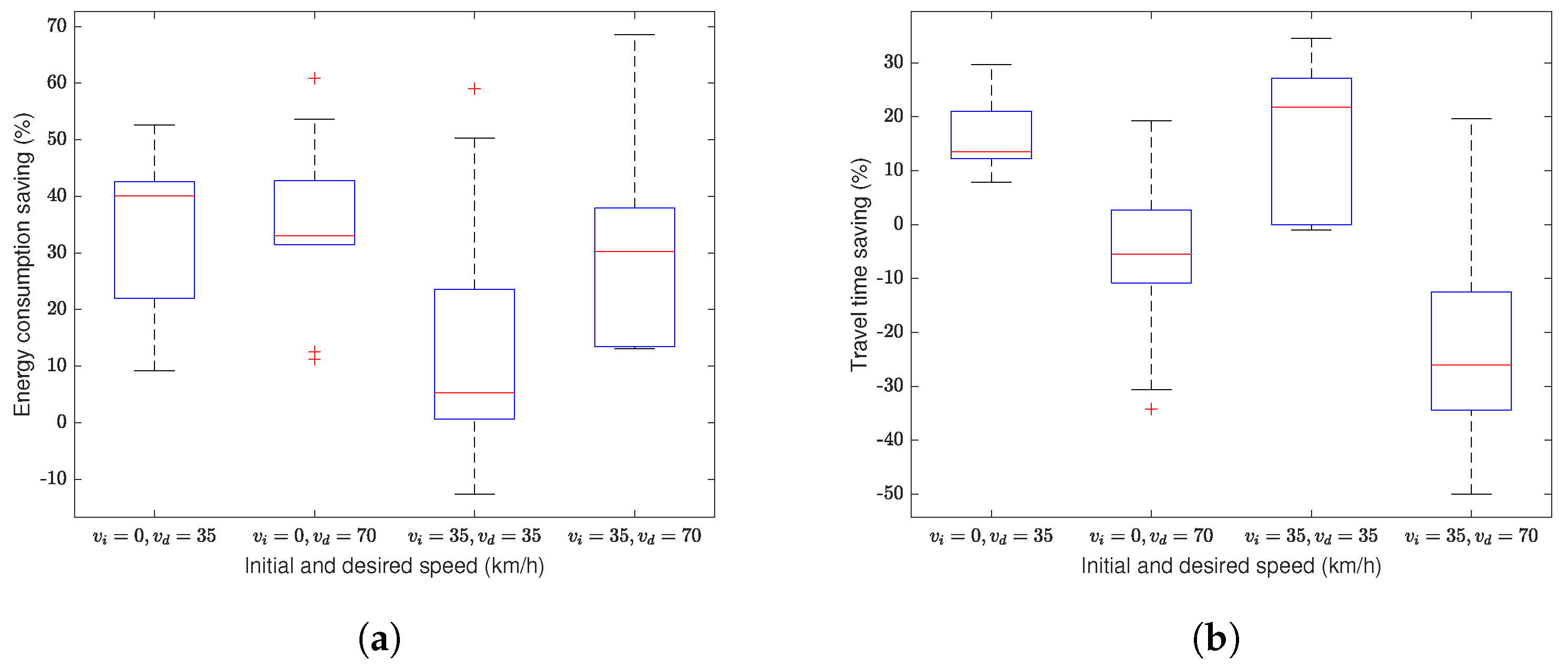
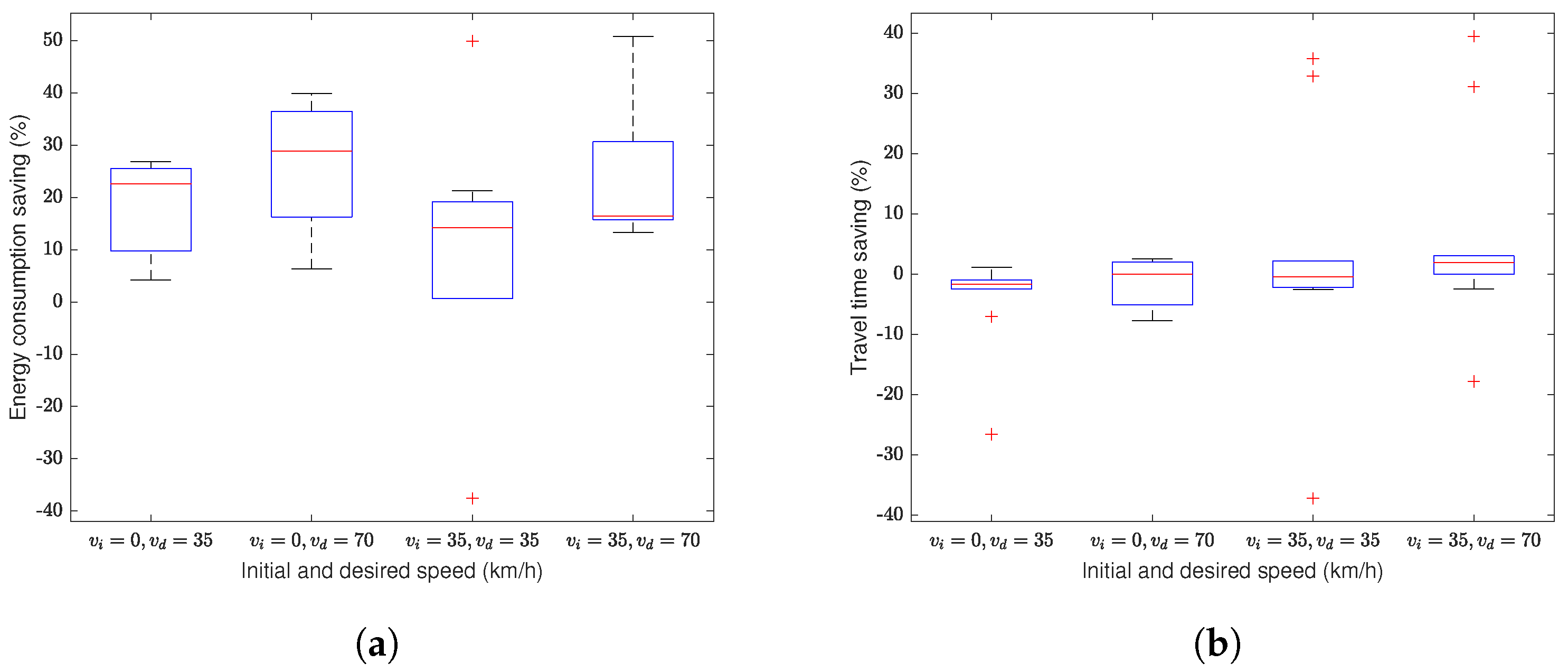
3.2. Eco-PPCC Framework Performance
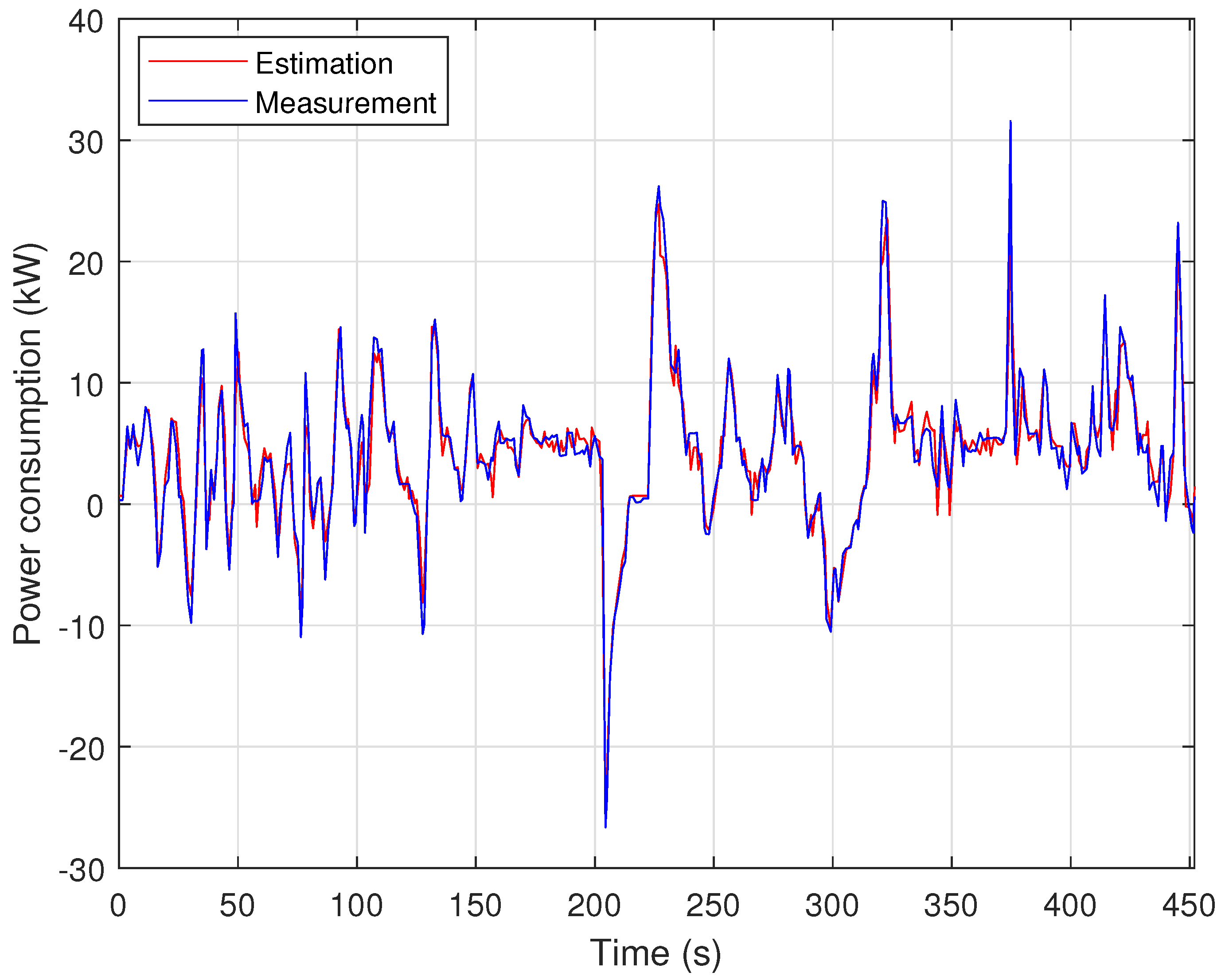
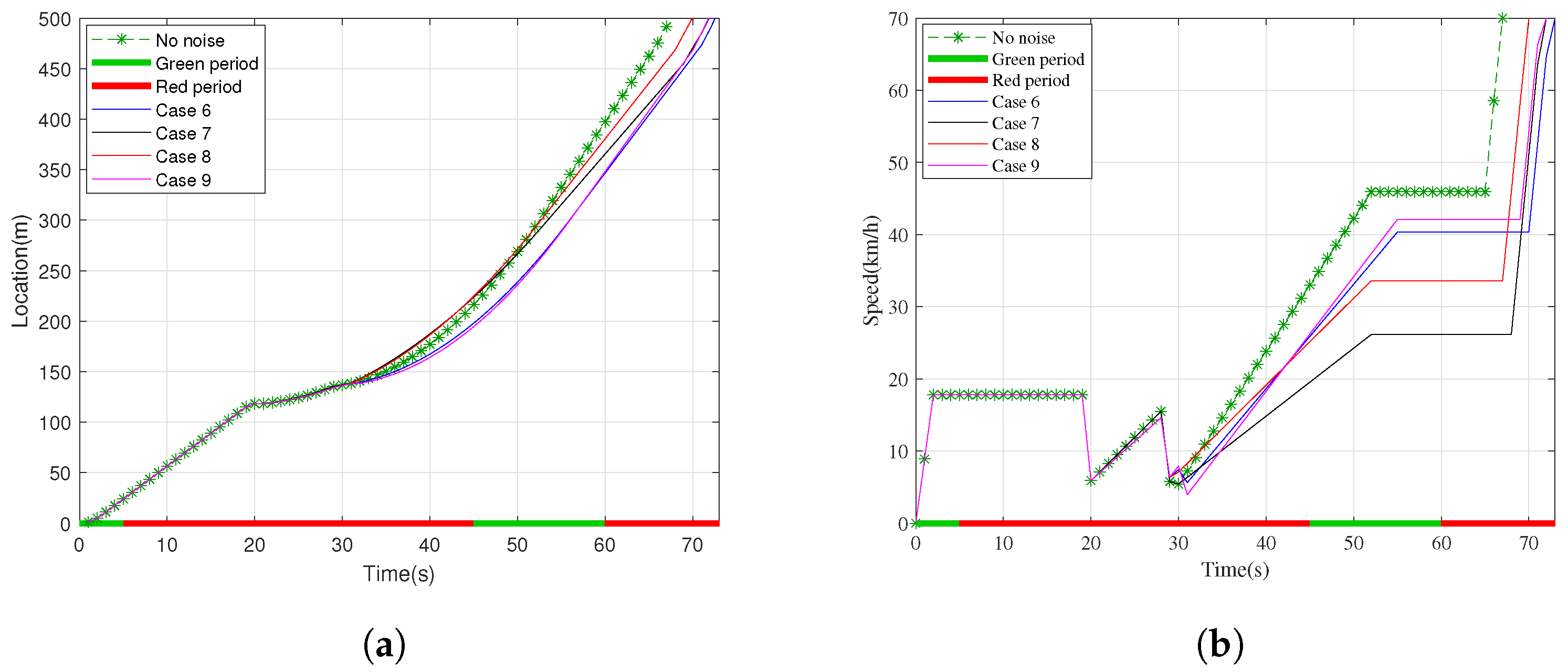
3.3. Eco-PPCC Framework Resilience in Presence of Noise
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hao, P.; Wu, G.; Boriboonsomsin, K.; Barth, M.J. Eco-approach and departure (EAD) application for actuated signals in real-world traffic. IEEE Trans. Intell. Transp. Syst. 2018, 20, 30–40. [Google Scholar] [CrossRef]
- De Nunzio, G.; Gomes, G.; Canudas-de Wit, C.; Horowitz, R.; Moulin, P. Speed advisory and signal offsets control for arterial bandwidth maximization and energy consumption reduction. IEEE Trans. Control Syst. Technol. 2016, 25, 875–887. [Google Scholar] [CrossRef]
- Nie, Z.; Farzaneh, H. Real-time dynamic predictive cruise control for enhancing eco-driving of electric vehicles, considering traffic constraints and signal phase and timing (SPaT) information, using artificial-neural-network-based energy consumption model. Energy 2022, 241, 122888. [Google Scholar] [CrossRef]
- Han, J.; Sciarretta, A.; Ojeda, L.L.; De Nunzio, G.; Thibault, L. Safe-and eco-driving control for connected and automated electric vehicles using analytical state-constrained optimal solution. IEEE Trans. Intell. Veh. 2018, 3, 163–172. [Google Scholar] [CrossRef]
- Hooker, J.N. Optimal driving for single-vehicle fuel economy. Transp. Res. Part A Gen. 1988, 22, 183–201. [Google Scholar] [CrossRef]
- Hellström, E.; Åslund, J.; Nielsen, L. Design of an efficient algorithm for fuel-optimal look-ahead control. Control Eng. Pract. 2010, 18, 1318–1327. [Google Scholar] [CrossRef]
- Weißmann, A.; Görges, D.; Lin, X. Energy-optimal adaptive cruise control combining model predictive control and dynamic programming. Control Eng. Pract. 2018, 72, 125–137. [Google Scholar] [CrossRef]
- Asadi, B.; Vahidi, A. Predictive cruise control: Utilizing upcoming traffic signal information for improving fuel economy and reducing trip time. IEEE Trans. Control Syst. Technol. 2010, 19, 707–714. [Google Scholar] [CrossRef]
- HomChaudhuri, B.; Vahidi, A.; Pisu, P. Fast model predictive control-based fuel efficient control strategy for a group of connected vehicles in urban road conditions. IEEE Trans. Control Syst. Technol. 2016, 25, 760–767. [Google Scholar] [CrossRef]
- Liu, B.; Sun, C.; Wang, B.; Liang, W.; Ren, Q.; Li, J.; Sun, F. Bi-level convex optimization of eco-driving for connected Fuel Cell Hybrid Electric Vehicles through signalized intersections. Energy 2022, 252, 123956. [Google Scholar] [CrossRef]
- Kamal, M.A.S.; Mukai, M.; Murata, J.; Kawabe, T. Model predictive control of vehicles on urban roads for improved fuel economy. IEEE Trans. Control Syst. Technol. 2012, 21, 831–841. [Google Scholar] [CrossRef]
- Meng, X.; Cassandras, C.G. Eco-driving of autonomous vehicles for nonstop crossing of signalized intersections. IEEE Trans. Autom. Sci. Eng. 2020, 19, 320–331. [Google Scholar] [CrossRef]
- Li, S.E.; Xu, S.; Huang, X.; Cheng, B.; Peng, H. Eco-departure of connected vehicles with V2X communication at signalized intersections. IEEE Trans. Veh. Technol. 2015, 64, 5439–5449. [Google Scholar] [CrossRef]
- Kamalanathsharma, R.K.; Rakha, H.A. Leveraging connected vehicle technology and telematics to enhance vehicle fuel efficiency in the vicinity of signalized intersections. J. Intell. Transp. Syst. 2016, 20, 33–44. [Google Scholar] [CrossRef]
- Jiang, H.; Hu, J.; An, S.; Wang, M.; Park, B.B. Eco approaching at an isolated signalized intersection under partially connected and automated vehicles environment. Transp. Res. Part C Emerg. Technol. 2017, 79, 290–307. [Google Scholar] [CrossRef]
- Nie, Z.; Farzaneh, H. Role of Model Predictive Control for Enhancing Eco-Driving of Electric Vehicles in Urban Transport System of Japan. Sustainability 2021, 13, 9173. [Google Scholar] [CrossRef]
- Li, M.; Boriboonsomsin, K.; Wu, G.; Zhang, W.B.; Barth, M. Traffic energy and emission reductions at signalized intersections: A study of the benefits of advanced driver information. Int. J. Intell. Transp. Syst. Res. 2009, 7, 49–58. [Google Scholar]
- Mahler, G.; Vahidi, A. An optimal velocity-planning scheme for vehicle energy efficiency through probabilistic prediction of traffic-signal timing. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2516–2523. [Google Scholar] [CrossRef]
- Wu, X.; He, X.; Yu, G.; Harmandayan, A.; Wang, Y. Energy-optimal speed control for electric vehicles on signalized arterials. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2786–2796. [Google Scholar] [CrossRef]
- Tang, T.Q.; Yi, Z.Y.; Zhang, J.; Wang, T.; Leng, J.Q. A speed guidance strategy for multiple signalized intersections based on car-following model. Phys. A Stat. Mech. Its Appl. 2018, 496, 399–409. [Google Scholar] [CrossRef]
- Yang, H.; Almutairi, F.; Rakha, H. Eco-driving at signalized intersections: A multiple signal optimization approach. IEEE Trans. Intell. Transp. Syst. 2020, 22, 2943–2955. [Google Scholar] [CrossRef]
- Ma, F.; Yang, Y.; Wang, J.; Li, X.; Wu, G.; Zhao, Y.; Wu, L.; Aksun-Guvenc, B.; Guvenc, L. Eco-driving-based cooperative adaptive cruise control of connected vehicles platoon at signalized intersections. Transp. Res. Part D Transp. Environ. 2021, 92, 102746. [Google Scholar] [CrossRef]
- Wang, S.; Lin, X. Eco-driving control of connected and automated hybrid vehicles in mixed driving scenarios. Appl. Energy 2020, 271, 115233. [Google Scholar] [CrossRef]
- Sun, C.; Guanetti, J.; Borrelli, F.; Moura, S.J. Optimal eco-driving control of connected and autonomous vehicles through signalized intersections. IEEE Internet Things J. 2020, 7, 3759–3773. [Google Scholar] [CrossRef]
- He, X.; Liu, H.X.; Liu, X. Optimal vehicle speed trajectory on a signalized arterial with consideration of queue. Transp. Res. Part C Emerg. Technol. 2015, 61, 106–120. [Google Scholar] [CrossRef]
- Biggs, D.; Akcelik, R. Energy-related model of instantaneous fuel consumption. Traffic Eng. Control 1986, 27, 320–325. [Google Scholar]
- Xiang, X.; Zhou, K.; Zhang, W.B.; Qin, W.; Mao, Q. A closed-loop speed advisory model with driver’s behavior adaptability for eco-driving. IEEE Trans. Intell. Transp. Syst. 2015, 16, 3313–3324. [Google Scholar] [CrossRef]
- Chen, P.; Yan, C.; Sun, J.; Wang, Y.; Chen, S.; Li, K. Dynamic eco-driving speed guidance at signalized intersections: Multivehicle driving simulator based experimental study. J. Adv. Transp. 2018, 2018, 6031764. [Google Scholar] [CrossRef]
- Kamal, M.A.S.; Mukai, M.; Murata, J.; Kawabe, T. Ecological vehicle control on roads with up-down slopes. IEEE Trans. Intell. Transp. Syst. 2011, 12, 783–794. [Google Scholar] [CrossRef]
- Wan, N.; Vahidi, A.; Luckow, A. Optimal speed advisory for connected vehicles in arterial roads and the impact on mixed traffic. Transp. Res. Part C Emerg. Technol. 2016, 69, 548–563. [Google Scholar] [CrossRef]
- Mousa, S.R.; Ishak, S.; Mousa, R.M.; Codjoe, J. Developing an eco-driving application for semi-actuated signalized intersections and modeling the market penetration rates of eco-driving. Transp. Res. Rec. 2019, 2673, 466–477. [Google Scholar] [CrossRef]
- Guo, L.; Gao, B.; Gao, Y.; Chen, H. Optimal energy management for HEVs in eco-driving applications using bi-level MPC. IEEE Trans. Intell. Transp. Syst. 2016, 18, 2153–2162. [Google Scholar] [CrossRef]
- Han, J.; Vahidi, A.; Sciarretta, A. Fundamentals of energy efficient driving for combustion engine and electric vehicles: An optimal control perspective. Automatica 2019, 103, 558–572. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, T.Q.; Yan, Y.; Qu, X. Eco-driving control for connected and automated electric vehicles at signalized intersections with wireless charging. Appl. Energy 2021, 282, 116215. [Google Scholar] [CrossRef]
- Dong, S.; Chen, H.; Gao, B.; Guo, L.; Liu, Q. Hierarchical energy-efficient control for CAVs at multiple signalized intersections considering queue effects. IEEE Trans. Intell. Transp. Syst. 2021, 23, 11643–11653. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, K. Online predictive connected and automated eco-driving on signalized arterials considering traffic control devices and road geometry constraints under uncertain traffic conditions. Transp. Res. Part B Methodol. 2021, 145, 80–117. [Google Scholar] [CrossRef]
- Deng, K.; Fang, T.; Feng, H.; Peng, H.; Löwenstein, L.; Hameyer, K. Hierarchical eco-driving and energy management control for hydrogen powered hybrid trains. Energy Convers. Manag. 2022, 264, 115735. [Google Scholar] [CrossRef]
- Dong, H.; Zhuang, W.; Chen, B.; Yin, G.; Wang, Y. Enhanced eco-approach control of connected electric vehicles at signalized intersection with queue discharge prediction. IEEE Trans. Veh. Technol. 2021, 70, 5457–5469. [Google Scholar] [CrossRef]
- Hesami, S.; De Cauwer, C.; Vafaeipour, M.; Rombaut, E.; Vanhaverbeke, L.; Coosemans, T. Bi-layer eco-driving control design of autonomous electric vehicles in presence of signalized intersections and preceding vehicles. Intell. Transp. Syst. 2023; submitted. [Google Scholar]
- Hesami, S.; De Cauwer, C.; Rombaut, E.; Vanhaverbeke, L.; Coosemans, T. Energy-Optimal Speed Control for Autonomous Electric Vehicles Up-and Downstream of a Signalized Intersection. World Electr. Veh. J. 2023, 14, 55. [Google Scholar] [CrossRef]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Gipps, P.G. A behavioural car-following model for computer simulation. Transp. Res. Part B Methodol. 1981, 15, 105–111. [Google Scholar] [CrossRef]
- Asamer, J.; Graser, A.; Heilmann, B.; Ruthmair, M. Sensitivity analysis for energy demand estimation of electric vehicles. Transp. Res. Part D Transp. Environ. 2016, 46, 182–199. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, C.; Liu, H.X. Spatiotemporal intersection control in a connected and automated vehicle environment. Transp. Res. Part C Emerg. Technol. 2018, 89, 364–383. [Google Scholar] [CrossRef]
- Papoulis, A.; Unnikrishna Pillai, S. Probability, Random Variables and Stochastic Processes; McGraw-Hill: Boston, MA, USA, 2002. [Google Scholar]
- Jia, D.; Ngoduy, D. Platoon based cooperative driving model with consideration of realistic inter-vehicle communication. Transp. Res. Part C Emerg. Technol. 2016, 68, 245–264. [Google Scholar] [CrossRef]



| Notation | Description | Notation | Description |
|---|---|---|---|
| Upstream length | Downstream length | ||
| L | Total length | m | Vehicle’s mass |
| Air density | Aerodynamic drag coefficient | ||
| Vehicle’s frontal area | g | Gravitational acceleration | |
| Friction coefficient | Road grade | ||
| Elevation difference in upstream | Elevation difference in downstream | ||
| Auxiliary power consumption | Drivetrain efficiency | ||
| Recuperation efficiency | E | Energy consumption | |
| Start of green light interval | End of green light interval | ||
| Min. inter-vehicle safe distance | Safe time headway | ||
| Dynamic inter-vehicle safe distance | Lower speed limit | ||
| Upper-speed limit | Lower acceleration limit | ||
| Upper-acceleration limit | Initial speed | ||
| Desired speed | Initial time | ||
| Final time | Time of passing the intersection | ||
| s | Controlled vehicle’s location | v | Controlled vehicle’s speed |
| a | Controlled vehicle’s acceleration | IPV’s location | |
| IPV’s speed | N | IPV’s upcoming data horizon | |
| Gipps min. safe distance | Gipps desired speed | ||
| Gipps max. acceleration | Gipps max. deceleration | ||
| Gipps IPV’s max. deceleration | Gipps reaction time |
| Strategy | |||
|---|---|---|---|
| C | 0 | ||
| A | 0 | 0 | |
| C–A | 0 | + | − |
| A–C | |||
| A–C–A |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Vehicle’s mass: m | 1270 (kg) | Frontal area: | 2.38 (m2) |
| Gravitational acceleration: g | (m/s2) | Air density: | (kg/m3) |
| Friction coefficient: | Air drag coefficient: | ||
| Drivetrain efficiency: | Regenerative efficiency: | ||
| Min. speed: | 0 (km/h) | Max. speed: | 70 (km/h) |
| Min. acceleration: | (m/s2) | Max. acceleration: | (m/s2) |
| Value | m | m | m |
|---|---|---|---|
| Case 1 | Case 2 | Case 3 | |
| m | m | m | |
| s | s | s | |
| kWh | kWh | kWh | |
| Case 4 | Case 5 | Case 6 | |
| m | m | m | |
| s | s | s | |
| kWh | kWh | kWh | |
| Case 7 | Case 8 | Case 9 | |
| m | m | m | |
| s | s | s | |
| kWh | kWh | kWh |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hesami, S.; Vafaeipour, M.; De Cauwer, C.; Rombaut, E.; Vanhaverbeke, L.; Coosemans, T. Dynamic Pro-Active Eco-Driving Control Framework for Energy-Efficient Autonomous Electric Mobility. Energies 2023, 16, 6495. https://doi.org/10.3390/en16186495
Hesami S, Vafaeipour M, De Cauwer C, Rombaut E, Vanhaverbeke L, Coosemans T. Dynamic Pro-Active Eco-Driving Control Framework for Energy-Efficient Autonomous Electric Mobility. Energies. 2023; 16(18):6495. https://doi.org/10.3390/en16186495
Chicago/Turabian StyleHesami, Simin, Majid Vafaeipour, Cedric De Cauwer, Evy Rombaut, Lieselot Vanhaverbeke, and Thierry Coosemans. 2023. "Dynamic Pro-Active Eco-Driving Control Framework for Energy-Efficient Autonomous Electric Mobility" Energies 16, no. 18: 6495. https://doi.org/10.3390/en16186495
APA StyleHesami, S., Vafaeipour, M., De Cauwer, C., Rombaut, E., Vanhaverbeke, L., & Coosemans, T. (2023). Dynamic Pro-Active Eco-Driving Control Framework for Energy-Efficient Autonomous Electric Mobility. Energies, 16(18), 6495. https://doi.org/10.3390/en16186495







