Analysis of Ice Formation during Start-Up of PEM Fuel Cells at Subzero Temperatures Using Experimental and Simulative Methods
Abstract
:1. Introduction
2. Literature Research
3. Novel Approach of This Study
4. Theoretical Formulation
- Gas mixtures obey the ideal gas law
- All gases are assumed to be incompressible
- Laminar flow due to small pressure gradients and small flow velocities
- Water exists in the aggregate states gaseous, liquid and solid and is present in dissolved form in the membrane
- Negligible gas crossover through the membrane
- Membrane consists of pure Nafion
- Convective transport of liquid water is negligible in the porous cell layers compared to transport by capillary forces
- The electrochemistry obeys the Butler-Volmer model
- The movement of ice lenses in the porous cell layers is neglected and ice is assumed to be immobile
- The gas diffusion layers are isotropic and homogeneous
- Constant temperature of the coolant over the length of the bipolar plate
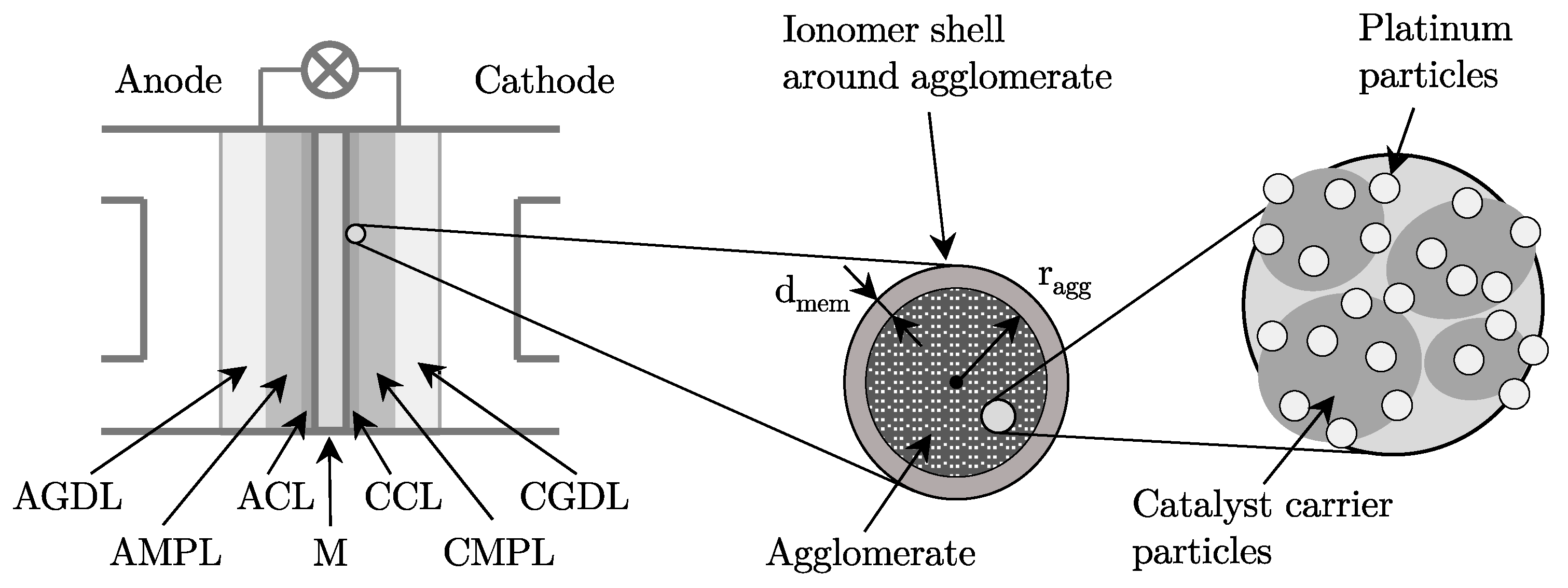
4.1. Modeling of the Gas Transport
4.2. Transport of Liquid Water
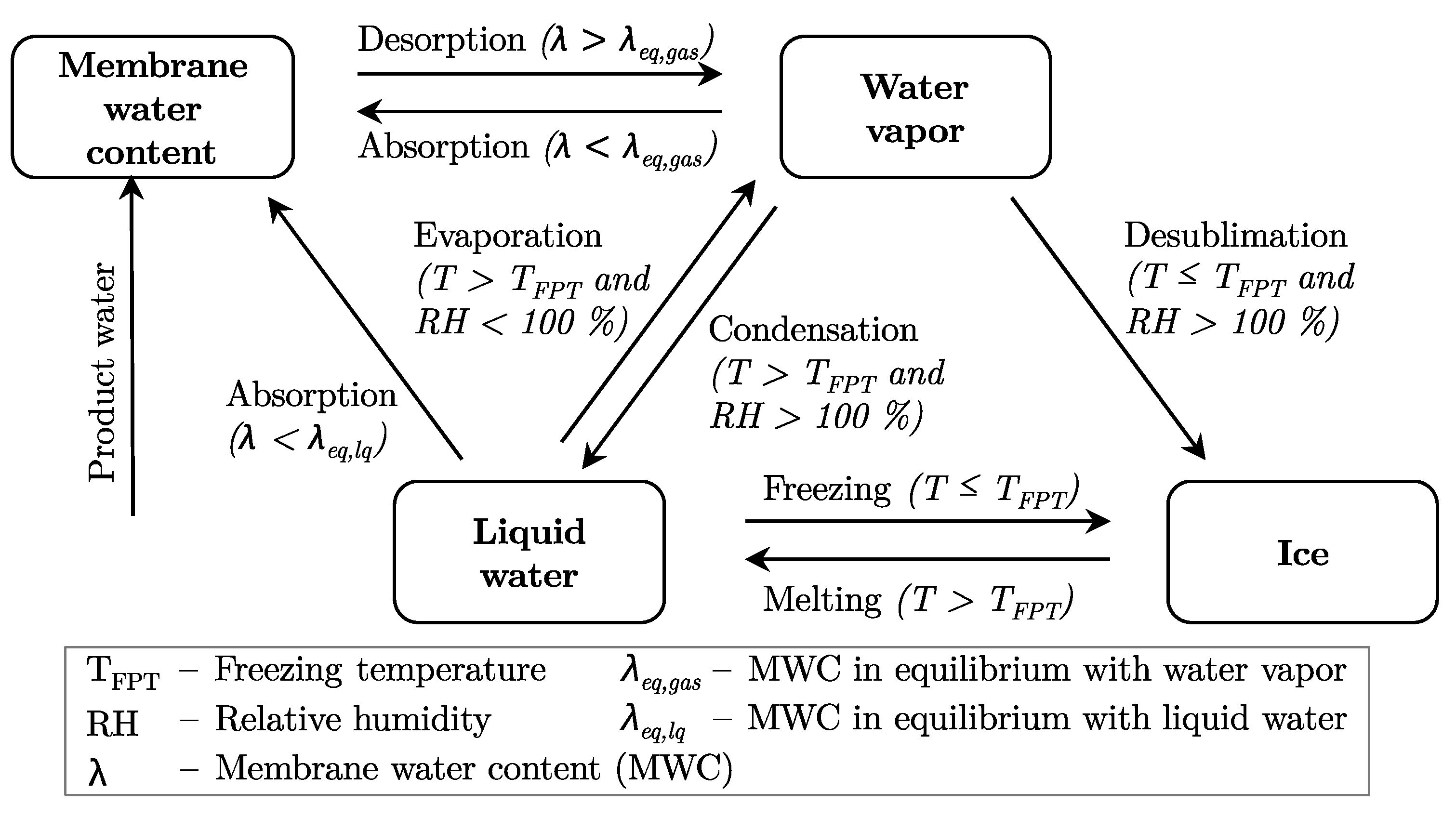
4.3. Modeling of Ice Formation
4.4. Phase Change Physics
4.5. Membrane Model
4.6. Electro-Chemistry Model
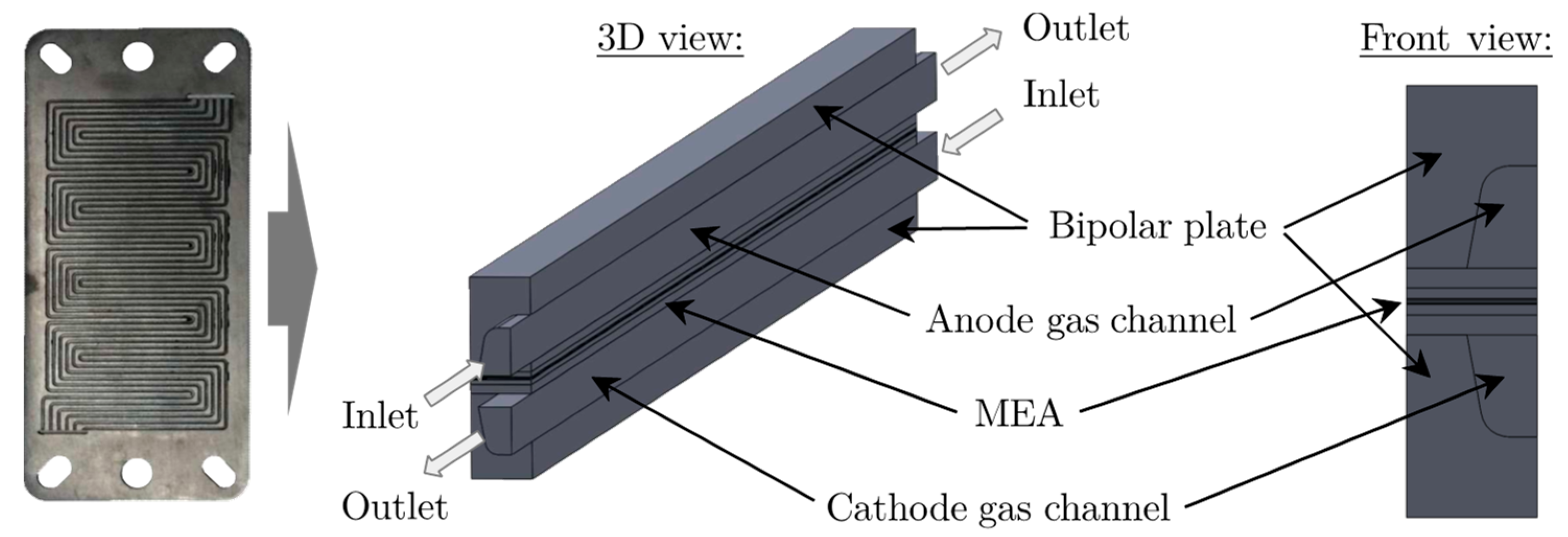
5. Experimental Setup
5.1. Steady State Measurements
5.2. Transient Frost Start Measurements
6. Results and Discussion
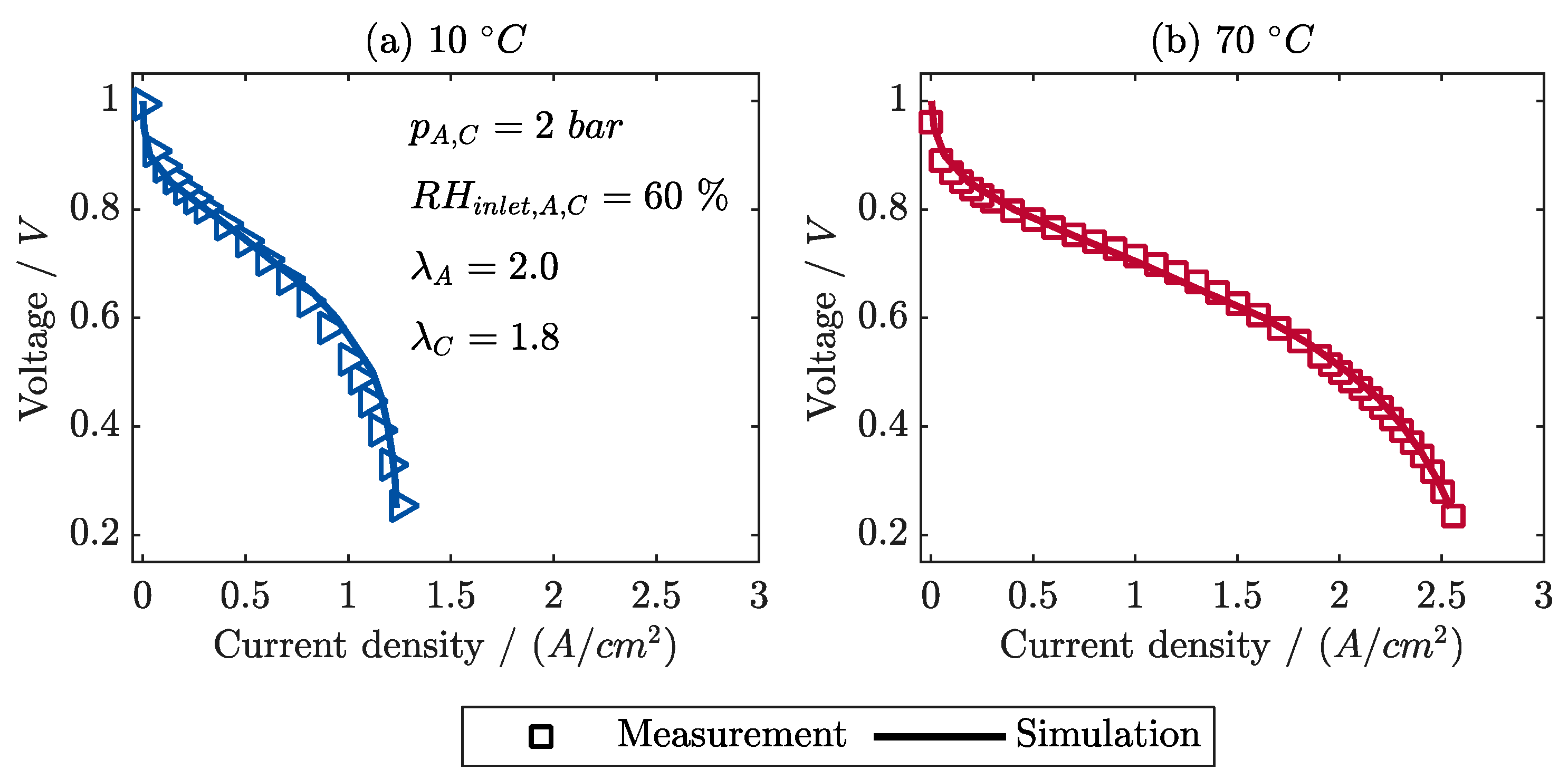
6.1. Model Validation with Steady Measurements
6.2. Model Validation with Transient Measurements
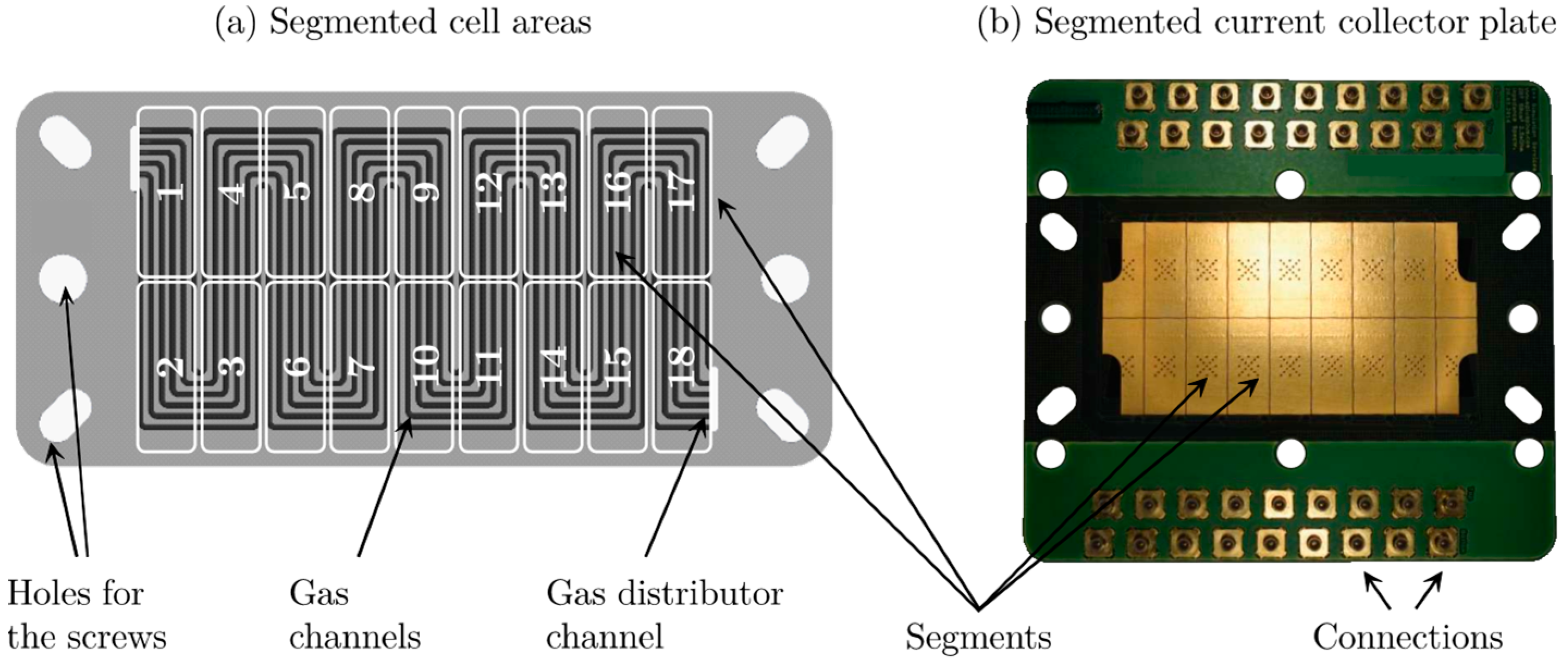
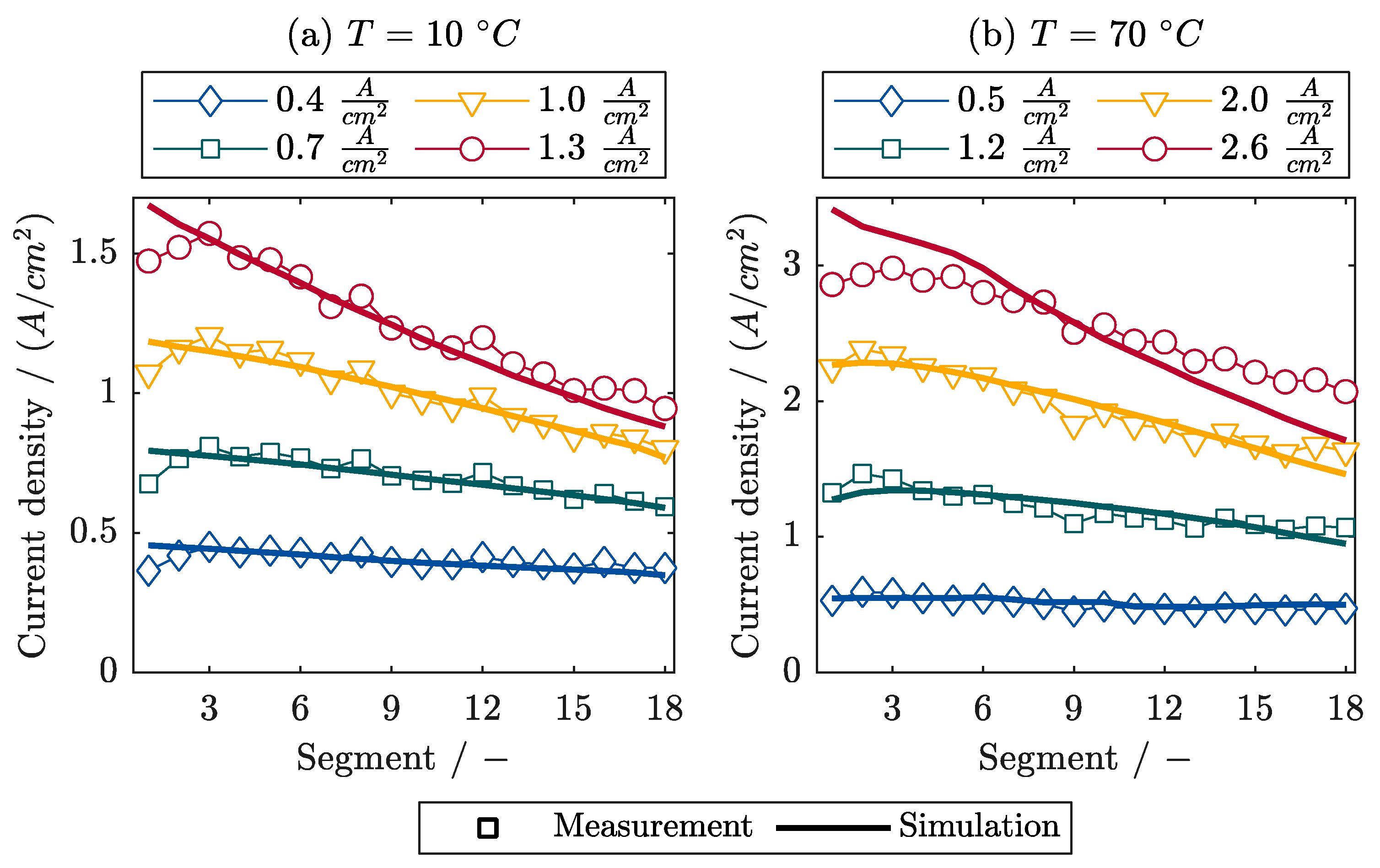
6.2.1. Segmented Current Densities during Frost Start
6.2.2. Segmented High Frequency Resistances during Frost Start
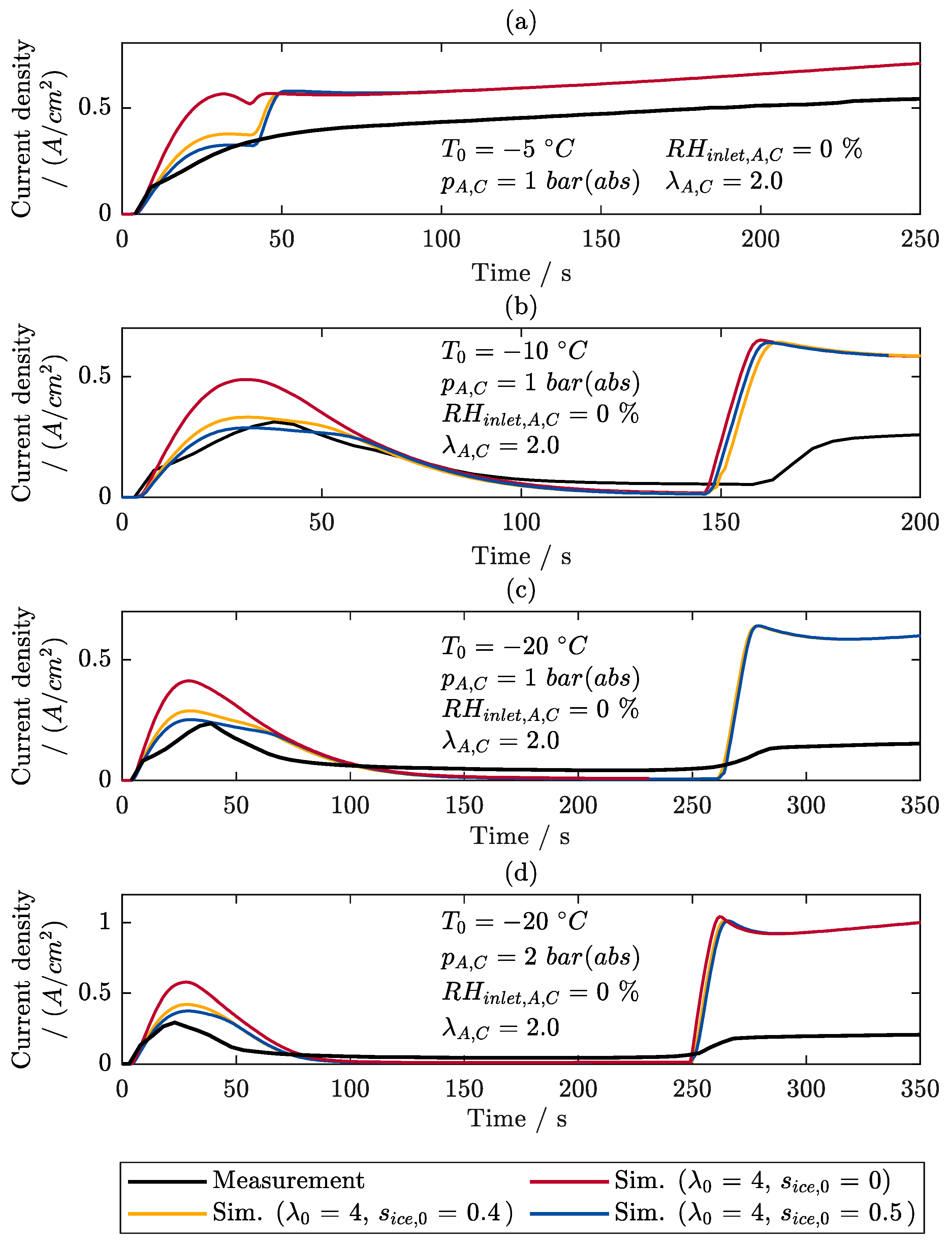
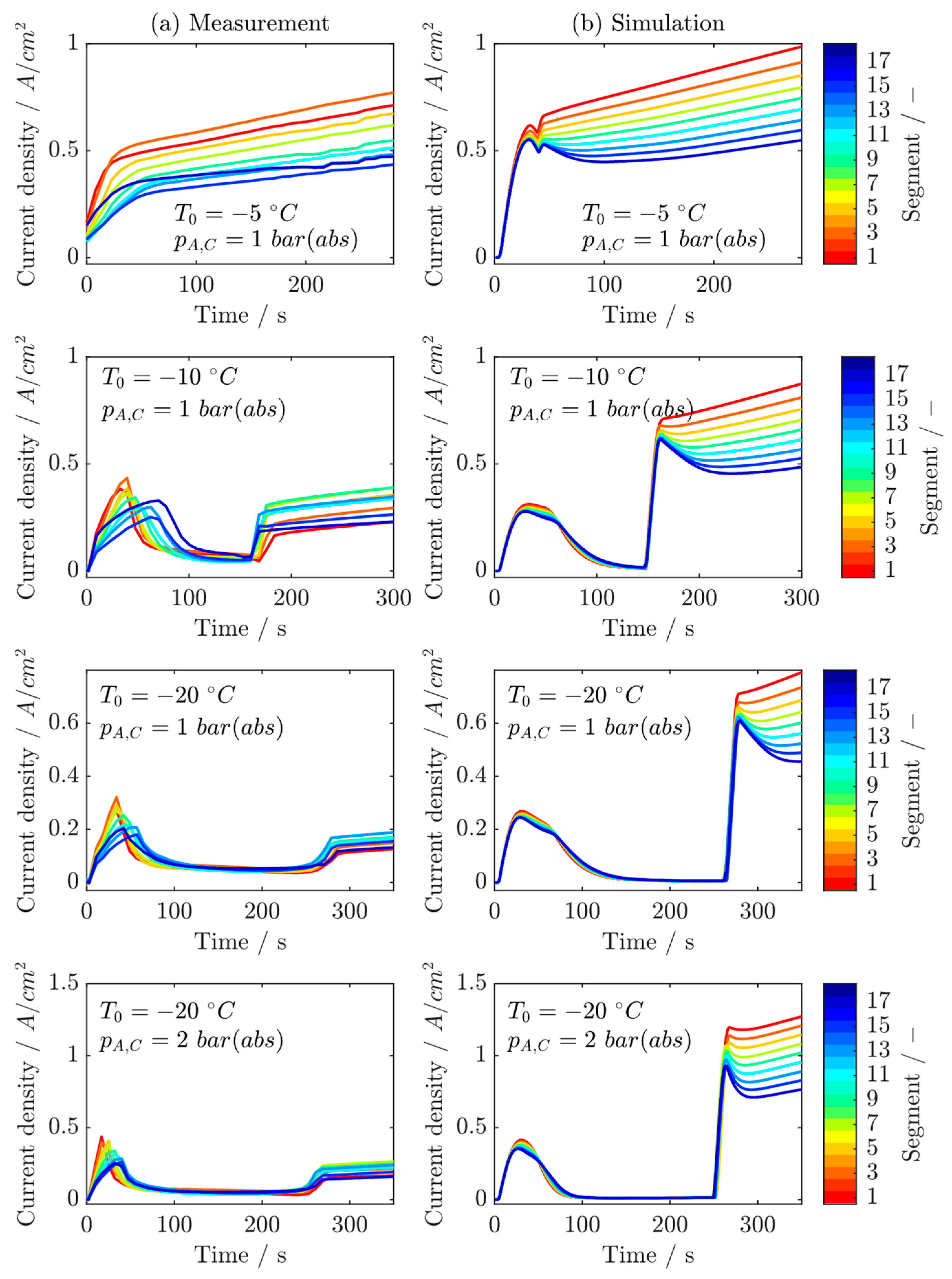
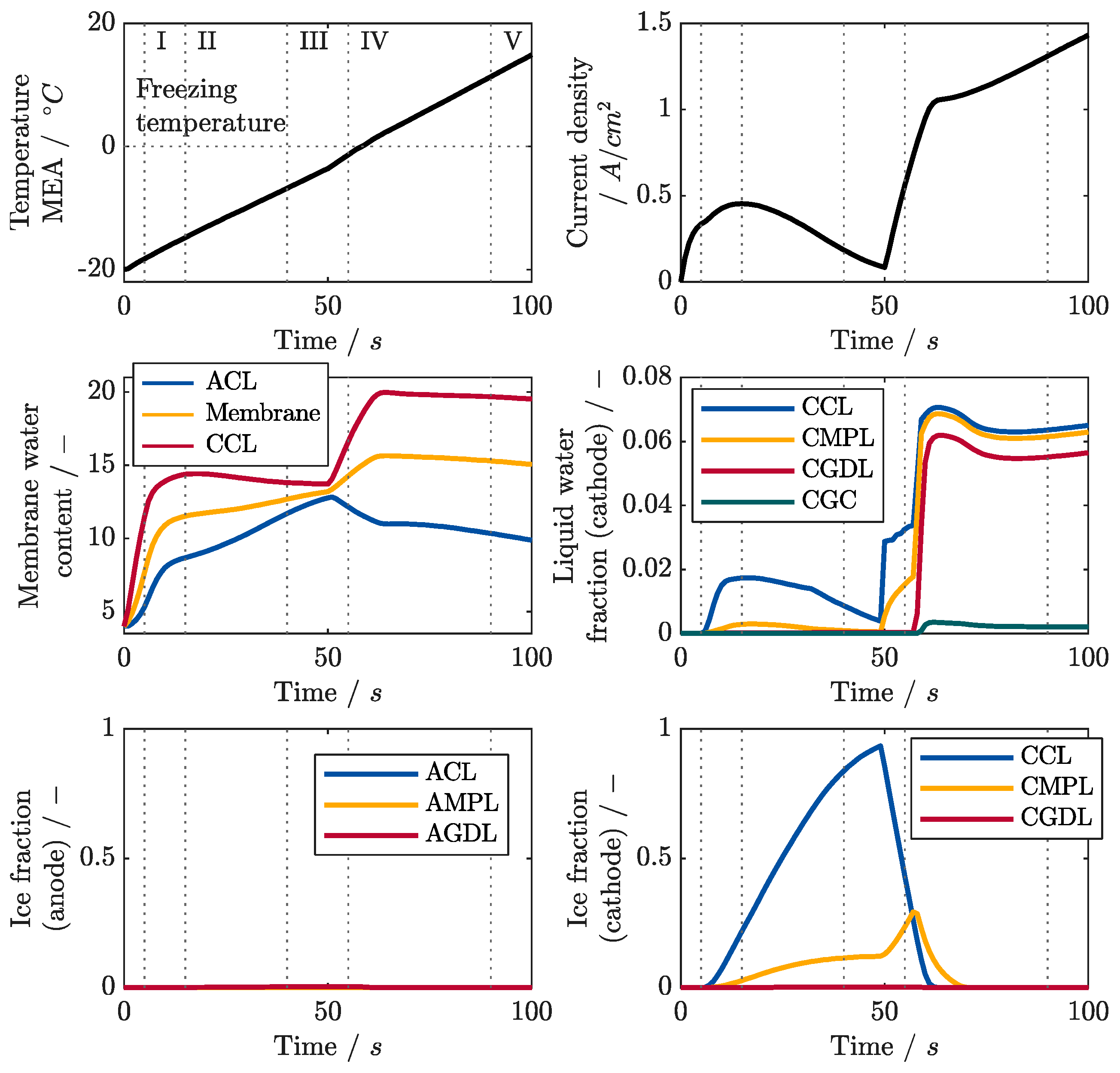
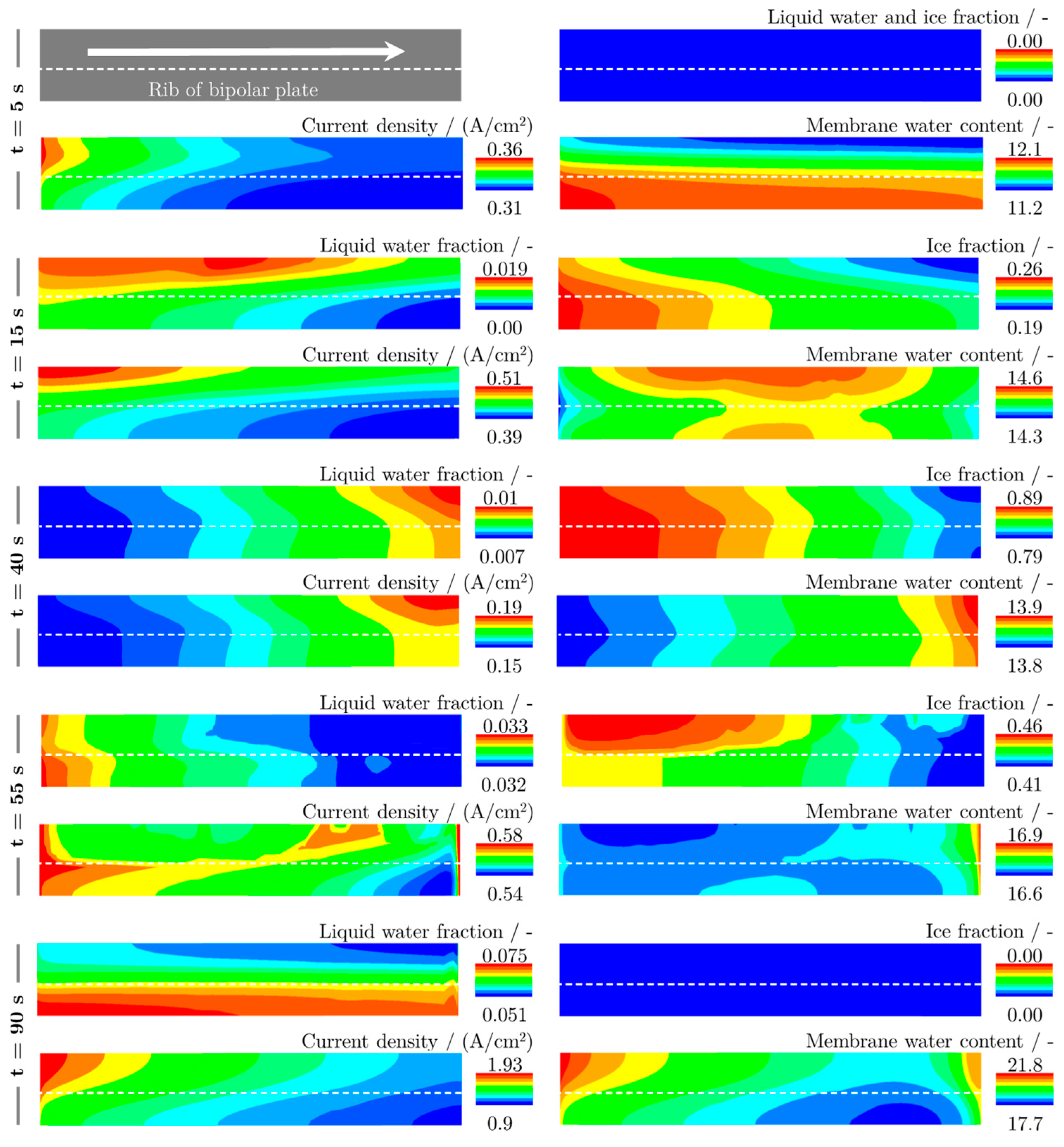
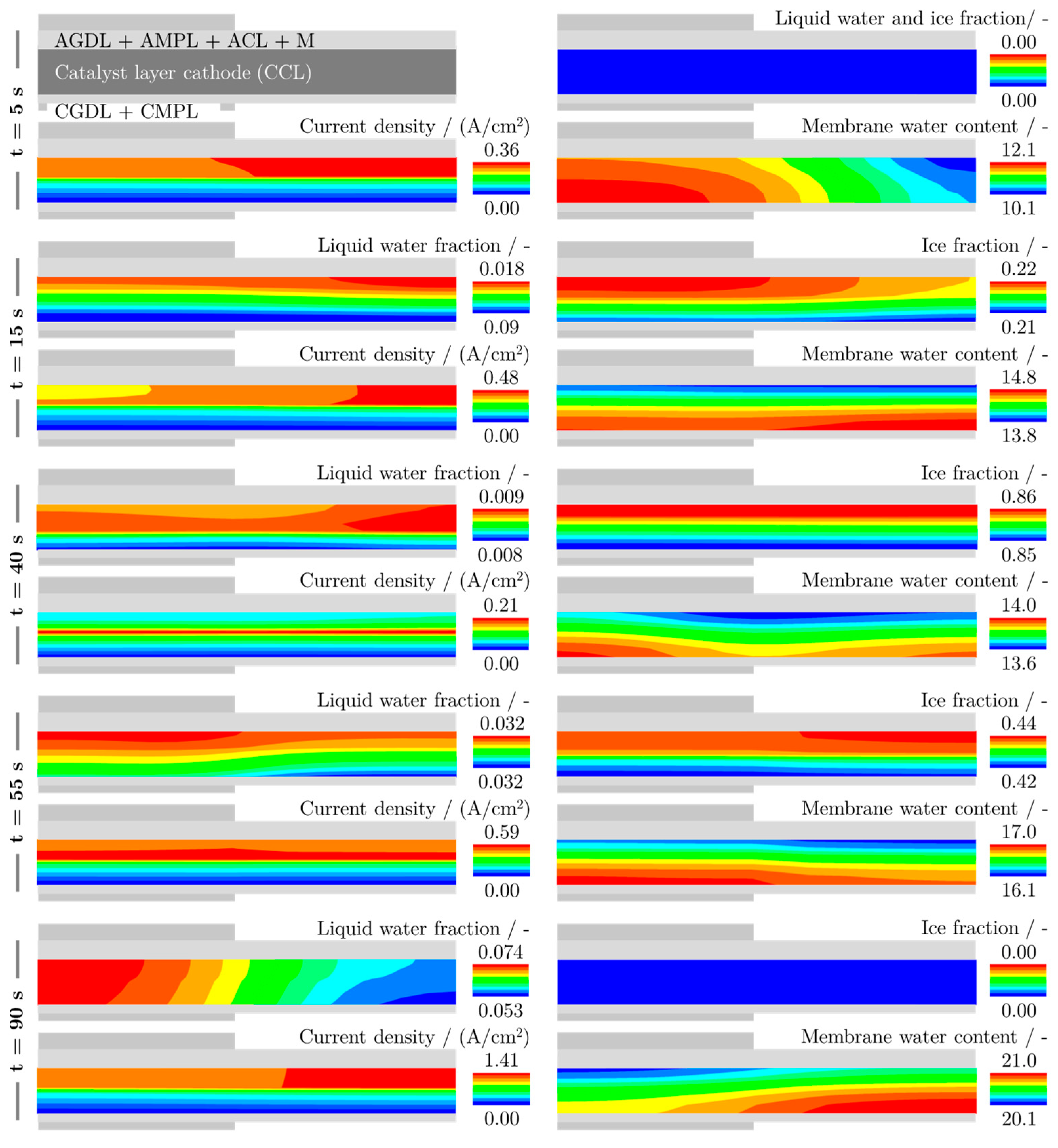
6.3. Locally Resolved Analysis of the Frost Start Process
7. Conclusions
- The polarization curves and local current densities are calculated in very good agreement with the measurements.
- The measurements show that most of the ice forms near the inlet of the cathode, so that the location where the maximum current density is produced shifts from there to the rear regions of the cell during the ice formation phase.
- After the freezing point is exceeded, most of the liquid water is produced in the regions near the cathode inlet due to melting, resulting in the highest current densities being produced in the middle regions of the cell.
- Ice lenses formed between the membrane and the CCL cause local delaminations that increase the internal resistances of the cell. The increase is particularly strong in the center of the cell since the cell is less stiff there than at the edges.
- The measurement of local HFRs is a suitable method to detect the local formation of ice lenses.
- The comparisons between the measurements and the simulations show that the model can determine the behavior of the cells very well at temperatures below the freezing point. Therefore, it can be applied for the investigations in the second part of this study.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Entire gas pressure | Pa | |
| Partial pressure species i | Pa | |
| Temperature | K | |
| Mass fraction species i | - | |
| Molar fraction species i | - | |
| Partial volumes | m3 | |
| Activity species i | - | |
| Molar mass species i | kg mol−1 | |
| Electrical potential | V | |
| Protonic potential | V | |
| Gas velocity | m s−1 | |
| Density gas mixture | kg m−3 | |
| Density liquid water | kg m−3 | |
| Density ice | kg m−3 | |
| Dry density ionomer | kg m−3 | |
| Membrane water content | - | |
| Equilibrium membrane water content humid gas | - | |
| Equilibrium membrane water content liquid water | - | |
| Liquid water fraction | - | |
| Ice fraction | - | |
| Relative humidity | - | |
| Saturation vapor pressure | Pa | |
| Proton current density | A m−2 | |
| Concentration species i | mol m−3 | |
| Protonic conductivity membrane | S m−1 | |
| Electric conductivity | S m−1 | |
| Pore volume | m3 | |
| Freezing point temperature | K | |
| Effective porosity | - | |
| Pressure loss in porous media | Pa | |
| Viscosity gas mixture | Pa s | |
| Viscosity liquid water | Pa s | |
| Unit matrix | - | |
| Absolute permeability gas mixture | m2 | |
| Absolute permeability liquid water | m2 | |
| Relative permeability | m2 | |
| Binary diffusion coefficients species i | m2 s−1 | |
| Effective diffusion coefficients | m2 s−1 | |
| Diffusion coefficient liquid water | m2 s−1 | |
| Diffusion coefficient solved water in membrane | m2 s−1 | |
| Tortuosity | - | |
| Capillary pressure | Pa | |
| Sorption constant gas mixture | - | |
| Sorption constant liquid water | - | |
| Charge transfer coefficient | - | |
| Electrochemical valence | - | |
| Local overvoltage anode | V | |
| Local overvoltage cathode | V | |
| Open circuit voltage | V | |
| Reference exchange current density HOR | A cm−2 | |
| Reference exchange current density ORR | A cm−2 | |
| Contact angle | ° | |
| Faraday’s constant | A s mol−1 | |
| Equivalent mass ionomer | kg mol−1 | |
| Ionomer fraction in CLs | - | |
| Freezing constant | s−1 | |
| Melting constant | s−1 | |
| Evaporation constant | s−1 | |
| Condensation constant | s−1 | |
| Desublimation constant | s−1 | |
| Specific melting enthalpy | J kg−1 K−1 | |
| Surface stress water | N m−1 | |
| Standard reaction enthalpy | J mol−1 | |
| Standard reaction entropy | J mol−1 K−1 | |
| Thiele modulus | - | |
| Effectivity factor agglomerate | - | |
| Time | s | |
| Pore radius | m | |
| Effective platinum surface ratio | - | |
| Platinum amount | kg m−2 | |
| Thickness catalyst layer cathode | m | |
| Overall gas constant | J mol−1 K−1 | |
| Thickness ionomer film agglomerate | m | |
| Effective specific surface agglomerate | m2 m−3 | |
| Radius agglomerate | m | |
| Local reaction rate ORR | s−1 | |
| High frequency resistance | cm2 | |
| Activation energy HOR | J mol−1 | |
| Activation energy ORR | J mol−1 | |
| Activation energy proton conductivity | J mol−1 | |
| Activation energy oxygen diffusion in ionomer | J mol−1 | |
| Henry’s coefficient | Pa m3 mol−1 | |
| Gas to liquid water velocity ratio | - | |
| Mass source | kg m−3 s−1 | |
| Mass source species i | kg m−3 s−1 | |
| Mass source liquid water | kg m−3 s−1 | |
| Mass source ice | kg m−3 s−1 | |
| Mass source solved water | kg m−3 s−1 | |
| Charge source HOR | A m−3 | |
| Charge source ORR | A m−3 | |
| Mass source species i due to reaction | kg m−3 s−1 | |
| Mass source evaporation / condensation | kg m−3 s−1 | |
| Mass source freezing / melting | kg m−3 s−1 | |
| Mass source desublimation | kg m−3 s−1 | |
| Mass source sorption | kg m−3 s−1 |
Appendix A
| Symbol | Parameter | Value | Unit |
|---|---|---|---|
| Thickness membrane | 15 | µm | |
| Thickness ACL | 9 | µm | |
| Thickness CCL | 12.5 | µm | |
| Thickness AMPL | 75 | µm | |
| Thickness CMPL | 75 | µm | |
| Thickness AGDL | 135 | µm | |
| Thickness CGDL | 135 | µm | |
| Overall gas constant | 8.3141 | J mol−1 K−1 | |
| Faraday’s constant | 96485.34 | A s mol−1 | |
| Equivalent weight ionomer | 1.1 [87] | kg mol−1 | |
| Dry density ionomer | 1920 [88] | kg m−3 | |
| Ionomer fraction in CLs | 0.5 | - | |
| Reference exchange current density HOR | 10 | A m−2 | |
| Effective specific agglomerate surface area | 3.6 × 105 [80] | m2 m−3 | |
| Platinum loading | 0.4 [80] | mg cm−2 | |
| Effective Pt surface ratio | 0.75 [80] | - | |
| Radius of agglomerate | 2.5 [80] | nm | |
| Pore radius | 3.89 × 10−5 [58] | m | |
| Contact angle | 100 [58] | ° | |
| Specific melting enthalpy | 333.55 [89] | kJ kg−1 | |
| Transfer coefficient | 0.5 [59] | - | |
| Transfer coefficient | 0.5 [59] | - | |
| Transfer coefficient | 0.5 [69] | - | |
| Transfer coefficient | 0.5 [69] | - | |
| Electrochemical valence | 2 [69] | - | |
| Electrical conductivity cell layers | 450 [85] | S m−1 | |
| Density liquid water | 997 [90] | kg m−3 | |
| Density ice | 916.7 [90] | kg m−3 | |
| Density platinum | 2.145 × 104 [80] | kg m−3 | |
| Standard reaction enthalpy | −237.13 [73] | kJ mol−1 | |
| Standard reaction entropy | −163.343 [73] | kJ mol−1 | |
| Standard pressure | 1 × 105 | Pa | |
| Standard temperature | 298.15 | K | |
| Liquid equilibrium membrane water content | 22 [74] | - | |
| Porosity cell layers | 0.7, 0.6, 0.85 | - | |
| Tortuosity cell layers | 3.0 | - | |
| Henry’s coefficient oxygen in ionomer | 2.2089 × 104 [91] | Pa m3 mol−1 | |
| Activation energy reaction anode | 168.4 [59] | J mol−1 | |
| Activation energy reaction cathode | 950.2 [59] | J mol−1 |
References
- Töpler, J.; Lehmann, J. Wasserstoff und Brennstoffzelle; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Peters, R. (Ed.) Brennstoffzellensysteme in der Luftfahrt; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Amamou, A.A.; Kelouwani, S.; Boulon, L.; Agbossou, K. A Comprehensive Review of Solutions and Strategies for Cold Start of Automotive Proton Exchange Membrane Fuel Cells. IEEE Access 2016, 4, 4989–5002. [Google Scholar] [CrossRef]
- Balliet, R.J. Modeling Cold Start in a Polymer-Electrolyte Fuel Cell; University of California: Berkeley, CA, USA, 2010. [Google Scholar]
- Oszcipok, M.; Riemann, D.; Kronenwett, U.; Kreideweis, M.; Zedda, M. Statistic analysis of operational influences on the cold start behaviour of PEM fuel cells. J. Power Sources 2005, 145, 407–415. [Google Scholar] [CrossRef]
- Al-Baghdadi, M.A.; Sadiq, R. Mechanical behaviour of membrane electrode assembly (MEA) during cold start of PEM fuel cell from subzero environment temperature. Int. J. Energy Environ. 2015, 6, 107. [Google Scholar]
- Mao, L.; Wang, C.-Y.; Tabuchi, Y. A Multiphase Model for Cold Start of Polymer Electrolyte Fuel Cells. J. Electrochem. Soc. 2007, 154, B341. [Google Scholar] [CrossRef]
- Cho, E.; Ko, J.-J.; Ha, H.Y.; Hong, S.-A.; Lee, K.-Y.; Lim, T.-W.; Oh, I.-H. Characteristics of the PEMFC Repetitively Brought to Temperatures below 0 °C. J. Electrochem. Soc. 2003, 150, A1667. [Google Scholar] [CrossRef]
- Cho, E.; Ko, J.-J.; Ha, H.Y.; Hong, S.-A.; Lee, K.-Y.; Lim, T.-W.; Oh, I.-H. Effects of Water Removal on the Performance Degradation of PEMFCs Repetitively Brought to <0 °C. J. Electrochem. Soc. 2004, 151, A661. [Google Scholar]
- St-Pierre, J.; Roberts, J.; Colbow, K.; Campbell, S.; Nelson, A. PEMFC operational and design strategies for Sub zero environments, Journal of New Materials for Electrochemical Systems. J. New Mat. Electrochem. Syst. 2005, 8, 163–176. [Google Scholar]
- Oszcipok, M.; Zedda, M.; Riemann, D.; Geckeler, D. Low temperature operation and influence parameters on the cold start ability of portable PEMFCs. J. Power Sources 2006, 154, 404–411. [Google Scholar] [CrossRef]
- Mukundan, R.; Lujan, R.; Davey, J.R.; Spendelow, J.S.; Hussey, D.S.; Jacobson, D.L.; Arif, M.; Borup, R. Ice Formation in PEM Fuel Cells Operated Isothermally at Sub-Freezing Temperatures. ECS Trans. 2009, 25, 345–355. [Google Scholar] [CrossRef]
- Thompson, E.L.; Jorne, J.; Gu, W.; Gasteiger, H.A. PEM Fuel Cell Operation at −20 °C. II. Ice Formation Dynamics, Current Distribution, and Voltage Losses within Electrodes. J. Electrochem. Soc. 2008, 155, B887. [Google Scholar] [CrossRef]
- Liphardt, L.; Suematsu, K.; Grundmeier, G. Kinetic studies of cathode degradation on PEM fuel cell short stack level undergoing freeze startups with different states of residual water and current draws. Int. J. Hydrogen Energy 2020, 46, 4399–4406. [Google Scholar] [CrossRef]
- Sabawa, J.P.; Bandarenka, A.S. Degradation mechanisms in polymer electrolyte membrane fuel cells caused by freeze-cycles: Investigation using electrochemical impedance spectroscopy. Electrochim. Acta 2019, 311, 21–29. [Google Scholar] [CrossRef]
- Takahashi, T.; Kokubo, Y.; Murata, K.; Hotaka, O.; Hasegawa, S.; Tachikawa, Y.; Nishihara, M.; Matsuda, J.; Kitahara, T.; Lyth, S.M.; et al. Cold start cycling durability of fuel cell stacks for commercial automotive applications. Int. J. Hydrogen Energy 2022, 47, 41111–41123. [Google Scholar] [CrossRef]
- Hishinuma, Y.; Chikahisa, T.; Kagami, F.; Ogawa, T. The Design and Performance of a PEFC at a Temperature Below Freezing. JSME Int. J. Ser. B 2004, 47, 235–241. [Google Scholar] [CrossRef]
- Hou, J.; Yi, B.; Yu, H.; Hao, L.; Song, W.; Fu, Y.; Shao, Z. Investigation of resided water effects on PEM fuel cell after cold start. Int. J. Hydrogen Energy 2007, 32, 4503–4509. [Google Scholar] [CrossRef]
- Yan, Q.; Toghiani, H.; Lee, Y.-W.; Liang, K.; Causey, H. Effect of sub-freezing temperatures on a PEM fuel cell performance, startup and fuel cell components. J. Power Sources 2006, 160, 1242–1250. [Google Scholar] [CrossRef]
- Tajiri, K.; Tabuchi, Y.; Wang, C.-Y. Isothermal Cold Start of Polymer Electrolyte Fuel Cells. J. Electrochem. Soc. 2007, 154, B147. [Google Scholar] [CrossRef]
- Xie, X.; Zhang, G.; Zhou, J.; Jiao, K. Experimental and theoretical analysis of ionomer/carbon ratio effect on PEM fuel cell cold start operation. Int. J. Hydrogen Energy 2017, 42, 12521–12530. [Google Scholar] [CrossRef]
- Hottinen, T.; Himanen, O.; Lund, P. Performance of planar free-breathing PEMFC at temperatures below freezing. J. Power Sources 2006, 154, 86–94. [Google Scholar] [CrossRef]
- Xie, X.; Wang, R.; Jiao, K.; Zhang, G.; Zhou, J.; Du, Q. Investigation of the effect of micro-porous layer on PEM fuel cell cold start operation. Renew. Energy 2018, 117, 125–134. [Google Scholar] [CrossRef]
- Schießwohl, E.; von Unwerth, T.; Seyfried, F.; Brüggemann, D. Experimental investigation of parameters influencing the freeze start ability of a fuel cell system. J. Power Sources 2009, 193, 107–115. [Google Scholar] [CrossRef]
- Tang, W.; Lin, R.; Weng, Y.; Zhang, J.; Ma, J. The effects of operating temperature on current density distribution and impedance spectroscopy by segmented fuel cell. Int. J. Hydrogen Energy 2013, 38, 10985–10991. [Google Scholar] [CrossRef]
- Cleghorn, S.J.; Derouin, C.R.; Wilson, M.S.; Gottesfeld, S. A printed curcuit board approach to measuring current distribution in a fuel cell. J. Appl. Electrochem. 1998, 28, 663–672. [Google Scholar] [CrossRef]
- Stumper, J.; Campbell, S.A.; Wilkinson, D.P.; Johnson, M.C.; Davis, M. In-situ methods for the determination of current distributions in PEM fuel cells. Electrochim. Acta 1998, 43, 3773–3783. [Google Scholar] [CrossRef]
- Wieser, C.; Helmbold, A.; Gülzow, E. A new technique for two-dimensional current distribution measurements in electrochemical cells. J. Appl. Electrochem. 2000, 30, 803–807. [Google Scholar] [CrossRef]
- Pérez, L.C.; Brandão, L.; Sousa, J.M.; Mendes, A. Segmented polymer electrolyte membrane fuel cells—A review. Renew. Sustain. Energy Rev. 2010, 15, 169–185. [Google Scholar] [CrossRef]
- Brett, D.J.L.; Atkins, S.; Brandon, N.P.; Vesovic, V.; Vasileiadis, N.; Kucernak, A. Localized Impedance Measurements along a Single Channel of a Solid Polymer Fuel Cell. Electrochem. Solid-State Lett. 2003, 6, A63. [Google Scholar] [CrossRef]
- Gerteisen, D.; Mérida, W.; Kurz, T.; Lupotto, P.; Schwager, M.; Hebling, C. Spatially Resolved Voltage, Current and Electrochemical Impedance Spectroscopy Measurements. Fuel Cells 2011, 11, 339–349. [Google Scholar] [CrossRef]
- Hakenjos, A.; Hebling, C. Spatially resolved measurement of PEM fuel cells. J. Power Sources 2005, 145, 307–311. [Google Scholar] [CrossRef]
- Hakenjos, A.; Zobel, M.; Clausnitzer, J.; Hebling, C. Simultaneous electrochemical impedance spectroscopy of single cells in a PEM fuel cell stack. J. Power Sources 2006, 154, 360–363. [Google Scholar] [CrossRef]
- Liu, D.; Lin, R.; Feng, B.; Han, L.; Zhang, Y.; Ni, M.; Wu, S. Localised electrochemical impedance spectroscopy investigation of polymer electrolyte membrane fuel cells using Print circuit board based interference-free system. Appl. Energy 2019, 254, 113712. [Google Scholar] [CrossRef]
- Liu, D.; Lin, R.; Feng, B.; Yang, Z. Investigation of the effect of cathode stoichiometry of proton exchange membrane fuel cell using localized electrochemical impedance spectroscopy based on print circuit board. Int. J. Hydrogen Energy 2019, 44, 7564–7573. [Google Scholar] [CrossRef]
- Jiao, K.; Alaefour, I.E.; Karimi, G.; Li, X. Simultaneous measurement of current and temperature distributions in a proton exchange membrane fuel cell during cold start processes. Electrochim. Acta 2011, 56, 2967–2982. [Google Scholar] [CrossRef]
- Lin, R.; Weng, Y.; Li, Y.; Lin, X.; Xu, S.; Ma, J. Internal behavior of segmented fuel cell during cold start. Int. J. Hydrogen Energy 2014, 39, 16025–16035. [Google Scholar] [CrossRef]
- Lin, R.; Weng, Y.; Lin, X.; Xiong, F. Rapid cold start of proton exchange membrane fuel cells by the printed circuit board technology. Int. J. Hydrogen Energy 2014, 39, 18369–18378. [Google Scholar] [CrossRef]
- FHaimerl, F.; Sabawa, J.P.; Dao, T.A.; Bandarenka, A.S. Spatially Resolved Electrochemical Impedance Spectroscopy of Automotive PEM Fuel Cells. ChemElectroChem 2022, 9, 428. [Google Scholar]
- Lin, R.; Ren, Y.; Lin, X.; Jiang, Z.; Yang, Z.; Chang, Y. Investigation of the internal behavior in segmented PEMFCs of different flow fields during cold start process. Energy 2017, 123, 367–377. [Google Scholar] [CrossRef]
- Zhu, Y.; Lin, R.; Jiang, Z.; Zhong, D.; Wang, B.; Shangguan, W.; Han, L. Investigation on cold start of polymer electrolyte membrane fuel cells with different cathode serpentine flow fields. Int. J. Hydrogen Energy 2019, 44, 7505–7517. [Google Scholar] [CrossRef]
- Zhu, Y.; Lin, R.; Han, L.; Jiang, Z.; Zhong, D. Investigation on cold start of polymer electrolyte membrane fuel cells stacks with diverse cathode flow fields. Int. J. Hydrogen Energy 2020, 46, 5580–5592. [Google Scholar] [CrossRef]
- Yang, X.; Sun, J.; Meng, X.; Sun, S.; Shao, Z. Cold start degradation of proton exchange membrane fuel cell: Dynamic and mechanism. Chem. Eng. J. 2023, 455, 140823. [Google Scholar] [CrossRef]
- Jiao, K.; Alaefour, I.E.; Karimi, G.; Li, X. Cold start characteristics of proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2011, 36, 11832–11845. [Google Scholar] [CrossRef]
- Yang, X.; Meng, X.; Sun, J.; Song, W.; Sun, S.; Shao, Z. Study on internal dynamic response during cold start of proton exchange membrane fuel cell with parallel and serpentine flow fields. J. Power Sources 2023, 561, 232609. [Google Scholar] [CrossRef]
- Liang, J.; Fan, L.; Miao, T.; Xie, X.; Wang, Z.; Chen, X.; Gong, Z.; Zhai, H.; Jiao, K. Cold start mode classification based on the water state for proton exchange membrane fuel cells. J. Mater. Chem. A 2022, 10, 20254–20264. [Google Scholar] [CrossRef]
- Tang, T.; Heinke, S.; Thüring, A.; Tegethoff, W.; Köhler, J. A spatially resolved fuel cell stack model with gas–liquid slip phenomena for cold start simulations. Int. J. Hydrogen Energy 2017, 42, 15328–15346. [Google Scholar] [CrossRef]
- Yang, Z.; Jiao, K.; Wu, K.; Shi, W.; Jiang, S.; Zhang, L.; Du, Q. Numerical investigations of assisted heating cold start strategies for proton exchange membrane fuel cell systems. Energy 2021, 222, 119910. [Google Scholar] [CrossRef]
- Bahr, M.; Gößling, S.; Schmitz, M. FC COLD START: PEM Fuel Cell Cold Start Simulation (Abschlussbericht FVV-Forschungsvorhaben); Forschungsvereinigung Verbrennungskraftmaschinen e.V.: Frankfurt am Main, Germany, 2023. [Google Scholar]
- Fink, C.; Gößling, S.; Karpenko-Jereb, L.; Urthaler, P. CFD Simulation of an Industrial PEM Fuel Cell with Local Degradation Effects. Fuel Cells 2020, 20, 431–452. [Google Scholar] [CrossRef]
- Zhang, Q.; Tong, Z.; Tong, S.; Cheng, Z. Research on water and heat management in the cold start process of proton exchange membrane fuel cell with expanded graphite bipolar plate. Energy Convers. Manag. 2021, 233, 113942. [Google Scholar] [CrossRef]
- Wei, L.; Liao, Z.; Suo, Z.; Chen, X.; Jiang, F. Numerical study of cold start performance of proton exchange membrane fuel cell with coolant circulation. Int. J. Hydrogen Energy 2019, 44, 22160–22172. [Google Scholar] [CrossRef]
- Ko, J.; Ju, H. Comparison of numerical simulation results and experimental data during cold-start of polymer electrolyte fuel cells. Appl. Energy 2012, 94, 364–374. [Google Scholar] [CrossRef]
- Ko, J.; Ju, H. Effects of cathode catalyst layer design parameters on cold start behavior of polymer electrolyte fuel cells (PEFCs). Int. J. Hydrogen Energy 2012, 38, 682–691. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X. Three-dimensional multiphase modeling of cold start processes in polymer electrolyte membrane fuel cells. Electrochim. Acta 2009, 54, 6876–6891. [Google Scholar] [CrossRef]
- Liao, Z.; Wei, L.; Dafalla, A.M.; Suo, Z.; Jiang, F. Numerical study of subfreezing temperature cold start of proton exchange membrane fuel cells with zigzag-channeled flow field. Int. J. Heat Mass Transf. 2020, 165, 120733. [Google Scholar] [CrossRef]
- Gwak, G.; Ko, J.; Ju, H. Numerical investigation of cold-start behavior of polymer-electrolyte fuel-cells from subzero to normal operating temperatures—Effects of cell boundary and operating conditions. Int. J. Hydrogen Energy 2014, 39, 21927–21937. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X. Effects of various operating and initial conditions on cold start performance of polymer electrolyte membrane fuel cells. Int. J. Hydrogen Energy 2009, 34, 8171–8184. [Google Scholar] [CrossRef]
- Yao, L.; Peng, J.; Zhang, J.-B.; Zhang, Y.-J. Numerical investigation of cold-start behavior of polymer electrolyte fuel cells in the presence of super-cooled water. Int. J. Hydrogen Energy 2018, 43, 15505–15520. [Google Scholar] [CrossRef]
- Ko, J.; Kim, W.-G.; Lim, Y.-D.; Ju, H. Improving the cold-start capability of polymer electrolyte fuel cells (PEFCs) by using a dual-function micro-porous layer (MPL): Numerical simulations. Int. J. Hydrogen Energy 2013, 38, 652–659. [Google Scholar] [CrossRef]
- Ko, J.; Ju, H. Numerical evaluation of a dual-function microporous layer under subzero and normal operating temperatures for use in automotive fuel cells. Int. J. Hydrogen Energy 2014, 39, 2854–2862. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X. Cold start analysis of polymer electrolyte membrane fuel cells. Int. J. Hydrogen Energy 2010, 35, 5077–5094. [Google Scholar] [CrossRef]
- Guo, Q.; Luo, Y.; Jiao, K. Modeling of assisted cold start processes with anode catalytic hydrogen–oxygen reaction in proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2013, 38, 1004–1015. [Google Scholar] [CrossRef]
- Yao, L.; Ma, F.; Peng, J.; Zhang, J.; Zhang, Y.; Shi, J. Analysis of the Failure Modes in the Polymer Electrolyte Fuel Cell Cold-Start Process—Anode Dehydration or Cathode Pore Blockage. Energies 2020, 13, 256. [Google Scholar] [CrossRef]
- Wei, L.; Dafalla, A.M.; Jiang, F. Effects of reactants/coolant non-uniform inflow on the cold start performance of PEMFC stack. Int. J. Hydrogen Energy 2020, 45, 13469–13482. [Google Scholar] [CrossRef]
- Jo, A.; Lee, S.; Kim, W.; Ko, J.; Ju, H. Large-scale cold-start simulations for automotive fuel cells. Int. J. Hydrogen Energy 2015, 40, 1305–1315. [Google Scholar] [CrossRef]
- Wei, L.; Liao, Z.; Dafalla, A.M.; Suo, Z.; Jiang, F. Effects of Endplate Assembly on Cold Start Performance of Proton Exchange Membrane Fuel Cell Stacks. Energy Technol. 2021, 9, 2100092. [Google Scholar] [CrossRef]
- Luo, Y.; Guo, Q.; Du, Q.; Yin, Y.; Jiao, K. Analysis of cold start processes in proton exchange membrane fuel cell stacks. J. Power Sources 2013, 224, 99–114. [Google Scholar] [CrossRef]
- Meng, H. A PEM fuel cell model for cold-start simulations. J. Power Sources 2007, 178, 141–150. [Google Scholar] [CrossRef]
- Meng, H.; Ruan, B. Numerical studies of cold-start phenomena in PEM fuel cells: A review. Int. J. Energy Res. 2010, 35, 2–14. [Google Scholar] [CrossRef]
- Hakenjos, A.; Tüber, K.; Schumacher, J.; Hebling, C. Characterising PEM Fuel Cell Performance Using a Current Distribution Measurement in Comparison with a CFD Model. Fuel Cells 2004, 4, 185–189. [Google Scholar] [CrossRef]
- ANSYS Inc. Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2021. [Google Scholar]
- Scholz, H. Modellierung und Untersuchung von Flutungsphänomenen in Niedertemperatur-PEM-Brennstoffzellen; AutoUni—Schriftenreihe Ser v.82; Logos Verlag: Berlin, Germany, 2015. [Google Scholar]
- Schmitz, M.; Welker, F.; Tinz, S.; Bahr, M.; Gössling, S.; Kaimer, S.; Pischinger, S. Comprehensive investigation of membrane sorption and CFD modeling of a tube membrane humidifier with experimental validation. Int. J. Hydrogen Energy 2023, 48, 8596–8612. [Google Scholar] [CrossRef]
- Wu, H.; Li, X.; Berg, P. On the modeling of water transport in polymer electrolyte membrane fuel cells. Electrochim. Acta 2009, 54, 6913–6927. [Google Scholar] [CrossRef]
- Dullien, F.A.L. Porous Media: Fluid Transport and Pore Structure; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Motupally, S.; Becker, A.J.; Weidner, J.W. Diffusion of Water in Nafion 115 Membranes. J. Electrochem. Soc. 2000, 147, 3171–3177. [Google Scholar] [CrossRef]
- Song, G.-H.; Meng, H. Numerical modeling and simulation of PEM fuel cells: Progress and perspective. Acta Mech. Sin. 2013, 29, 318–334. [Google Scholar] [CrossRef]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymer Electrolyte Fuel Cell Model. J. Electrochem. Soc. 1991, 138, 2334–2342. [Google Scholar] [CrossRef]
- Sun, W.; Peppley, B.A.; Karan, K. An improved two-dimensional agglomerate cathode model to study the influence of catalyst layer structural parameters. Electrochim. Acta 2005, 50, 3359–3374. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, K.S.; Mishler, J.; Cho, S.C.; Adroher, X.C. A review of polymer electrolyte membrane fuel cells: Technology, applications, and needs on fundamental research. Appl. Energy 2011, 88, 981–1007. [Google Scholar] [CrossRef]
- Xing, L.; Liu, X.; Alaje, T.; Kumar, R.; Mamlouk, M.; Scott, K. A two-phase flow and non-isothermal agglomerate model for a proton exchange membrane (PEM) fuel cell. Energy 2014, 73, 618–634. [Google Scholar] [CrossRef]
- Marr, C.; Li, X. Composition and performance modelling of catalyst layer in a proton exchange membrane fuel cell. J. Power Sources 1999, 77, 17–27. [Google Scholar] [CrossRef]
- Suzuki, T.; Kudo, K.; Morimoto, Y. Model for investigation of oxygen transport limitation in a polymer electrolyte fuel cell. J. Power Sources 2013, 222, 379–389. [Google Scholar] [CrossRef]
- Vetter, R.; Schumacher, J.O. Experimental parameter uncertainty in proton exchange membrane fuel cell modeling. Part I: Scatter in material parameterization. J. Power Sources 2019, 438, 227018. [Google Scholar] [CrossRef]
- Verein Deutscher Ingenieure, VDI-Wärmeatlas. 11., Bearb. Und Erw. AUFL; Springer eBook Collection, ed.; Springer Vieweg: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Meng, H. A three-dimensional PEM fuel cell model with consistent treatment of water transport in MEA. J. Power Sources 2006, 162, 426–435. [Google Scholar] [CrossRef]
- Satterfield, M.B.; Majsztrik, P.W.; Ota, H.; Benziger, J.B.; Bocarsly, A.B. Mechanical properties of Nafion and titania/Nafion composite membranes for polymer electrolyte membrane fuel cells. J. Polym. Sci. Part B Polym. Phys. 2006, 44, 2327–2345. [Google Scholar] [CrossRef]
- CRC Handbook of Chemistry and Physics: A Ready-Reference Book of Chemical and Physical Data, 80th ed.; CRC Press: Boca Raton, FL, USA, 1999.
- Haynes, W.M. (Ed.) CRC Handbook of Chemistry and Physics: A Ready-Reference Book of Chemical and Physical Data, 97th ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Bernardi, D.M.; Verbrugge, M.W. Mathematical model of a gas diffusion electrode bonded to a polymer electrolyte. AIChE J. 1991, 37, 1151–1163. [Google Scholar] [CrossRef]

| Name | Equation or Literature Source | Unit |
|---|---|---|
| Effective porosity | - | |
| Absolute permeability | (cf. [85]) | m2 |
| Relative permeability | m2 | |
| Viscosity gas mixture | (cf. [86]) | kg m−1 s−1 |
| Viscosity liquid water | (cf. [86]) | kg m−1 s−1 |
| Surface stress water | (cf. [86]) | N m−1 |
| Effectivity factor | [80] | - |
| Thiele modulus | [80] | - |
| Specific surface Pt particle | [80] | m2 kg−1 |
| Source of hydrogen | kg m−3 s−1 | |
| Source of oxygen | kg m−3 s−1 | |
| Source of water | kg m−3 s−1 | |
| Exchange current density (A) | A m−2 | |
| Exchange current density (C) | A m−2 |
| Name | Equation | Unit |
|---|---|---|
| Mass source | kg m−3 s−1 | |
| Hydrogen source | kg m−3 s−1 | |
| Oxygen source | kg m−3 s−1 | |
| Water source | kg m−3 s−1 | |
| Liquid water source | kg m−3 s−1 | |
| Ice source | kg m−3 s−1 | |
| Membrane water source | kg m−3 s−1 |
| Symbol | Parameter | Value | Unit |
|---|---|---|---|
| Reference exchange current density ORR | 3.4265 × 10−4 | A m−2 | |
| Thickness ionomer film on agglomerate | 27.5 | nm | |
| Activation energy proton conductivity | 104 | J mol−1 | |
| Activation energy oxygen diffusion in ionomer | 10.22 | J mol−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmitz, M.; Bahr, M.; Gößling, S.; Pischinger, S. Analysis of Ice Formation during Start-Up of PEM Fuel Cells at Subzero Temperatures Using Experimental and Simulative Methods. Energies 2023, 16, 6534. https://doi.org/10.3390/en16186534
Schmitz M, Bahr M, Gößling S, Pischinger S. Analysis of Ice Formation during Start-Up of PEM Fuel Cells at Subzero Temperatures Using Experimental and Simulative Methods. Energies. 2023; 16(18):6534. https://doi.org/10.3390/en16186534
Chicago/Turabian StyleSchmitz, Maximilian, Matthias Bahr, Sönke Gößling, and Stefan Pischinger. 2023. "Analysis of Ice Formation during Start-Up of PEM Fuel Cells at Subzero Temperatures Using Experimental and Simulative Methods" Energies 16, no. 18: 6534. https://doi.org/10.3390/en16186534
APA StyleSchmitz, M., Bahr, M., Gößling, S., & Pischinger, S. (2023). Analysis of Ice Formation during Start-Up of PEM Fuel Cells at Subzero Temperatures Using Experimental and Simulative Methods. Energies, 16(18), 6534. https://doi.org/10.3390/en16186534