Revitalization Modelling of a Mature Oil Field with Bottom-Type Aquifer into Geothermal Resource—Reservoir Engineering and Techno-Economic Challenges
Abstract
:1. Introduction
2. Materials and Methods
2.1. Organic Rankine Cycle
2.2. Well Completion
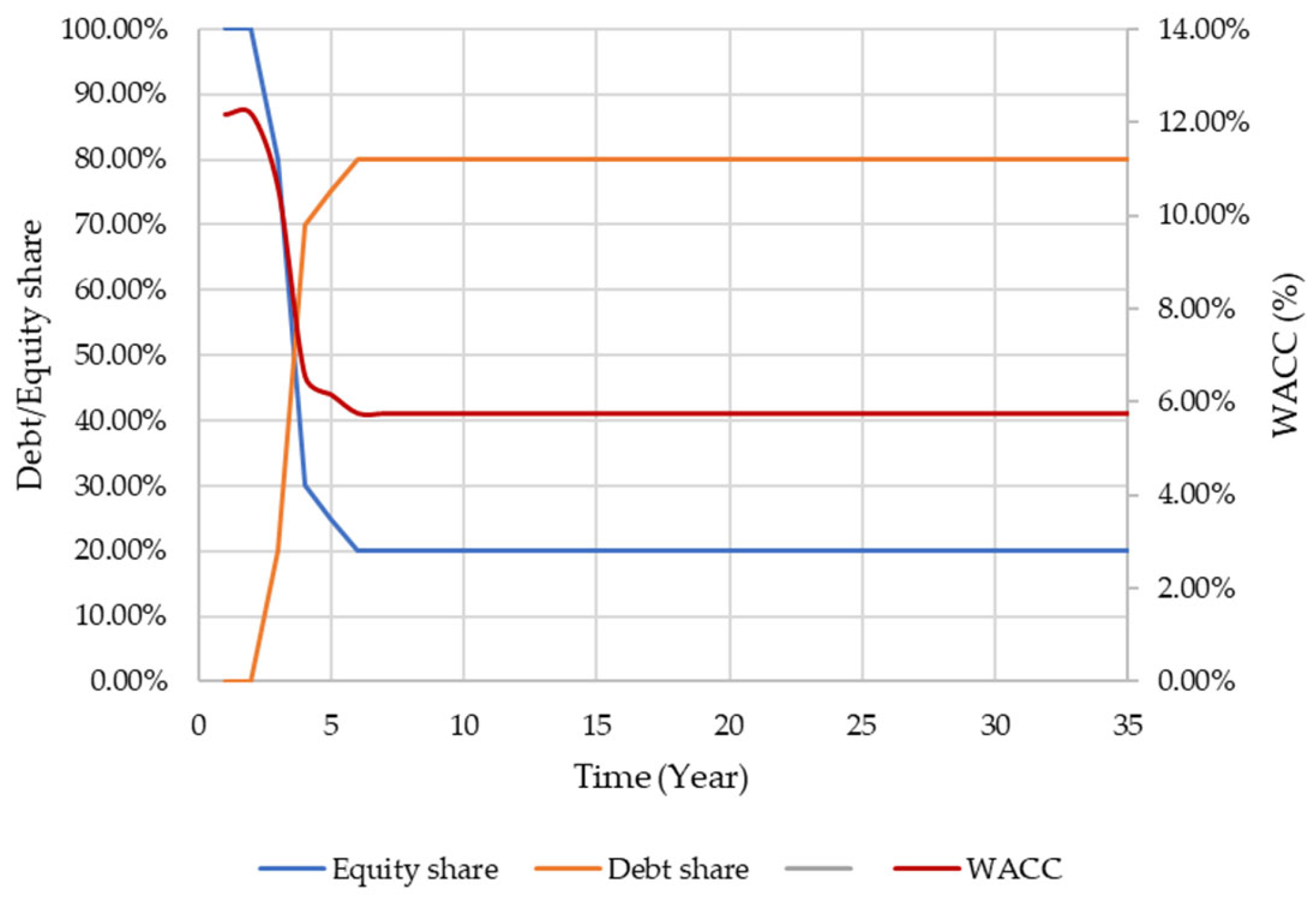
2.3. Economic Evaluation
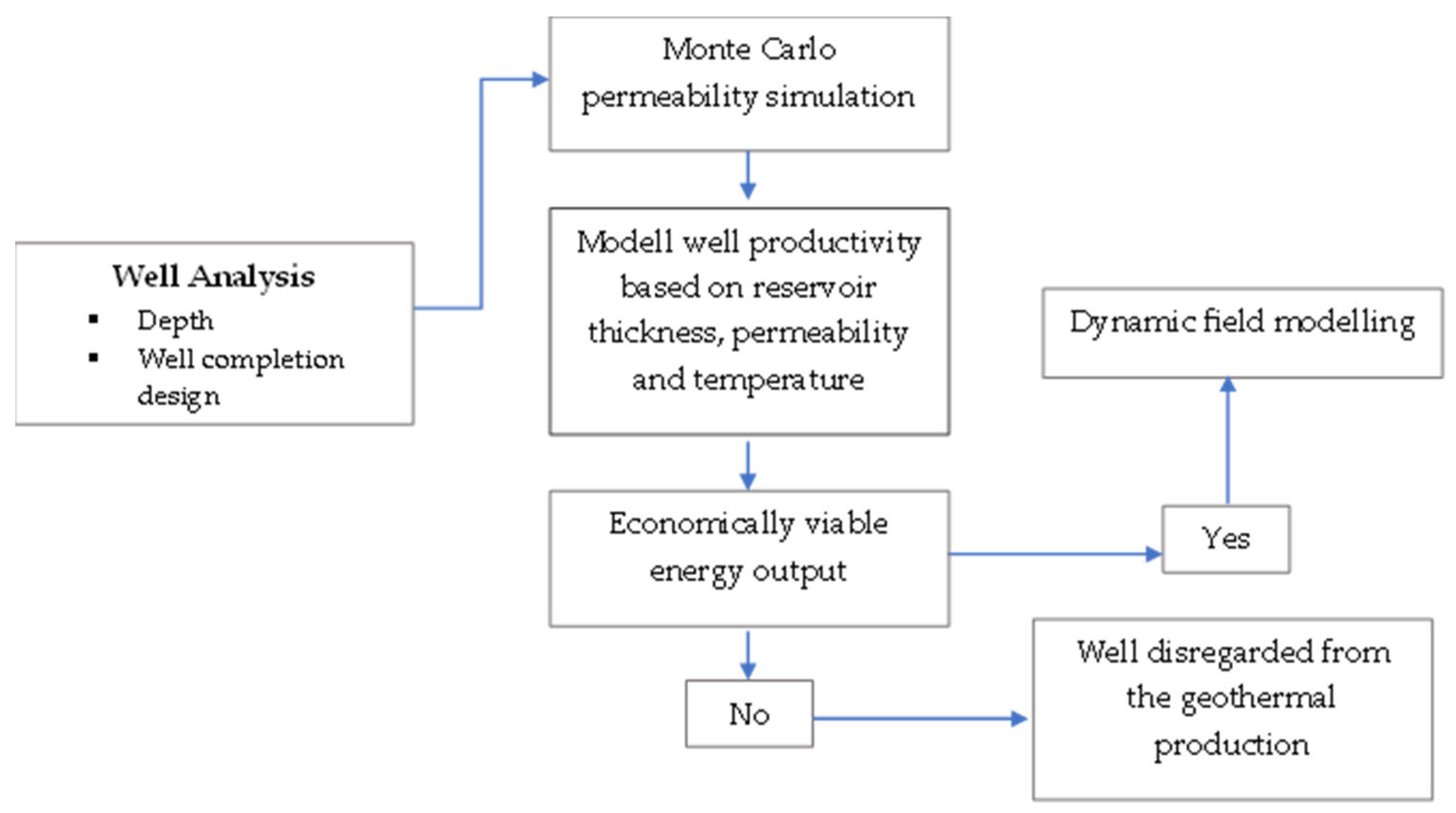
2.4. Selection of Mature Oil Fields for Geothermal Production
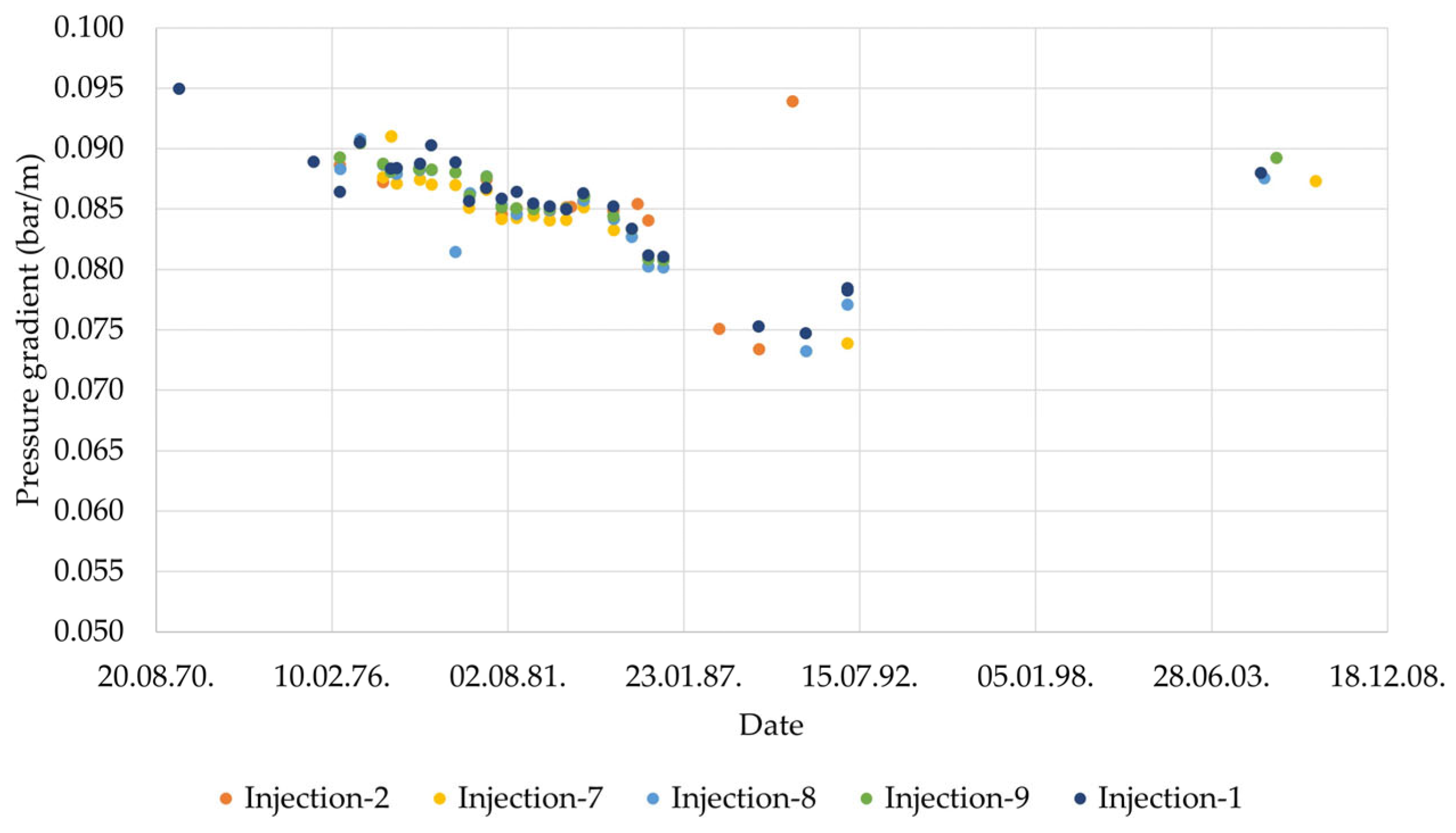
2.5. Geothermal Brine Flow through Existing Well Completion
3. Results and Discussion
- the thickness of the geothermal reservoir accessed by a single well;
- the permeability of the reservoir;
- the gas–liquid ratio of the aquifer.
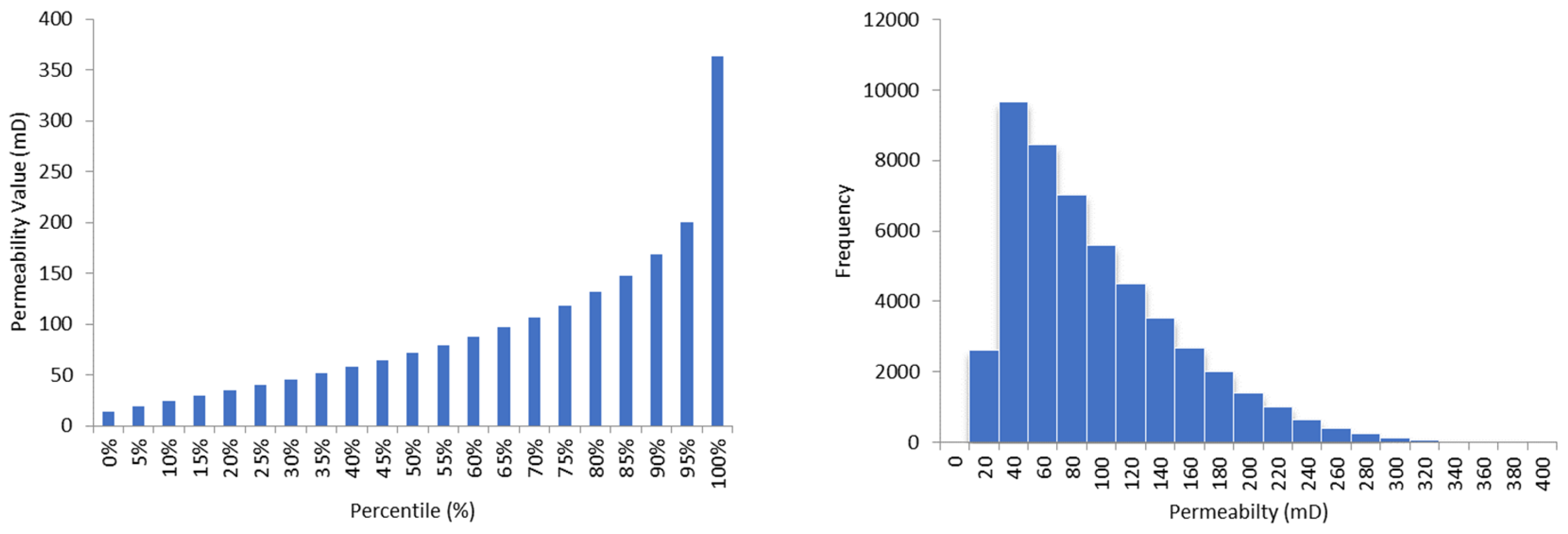
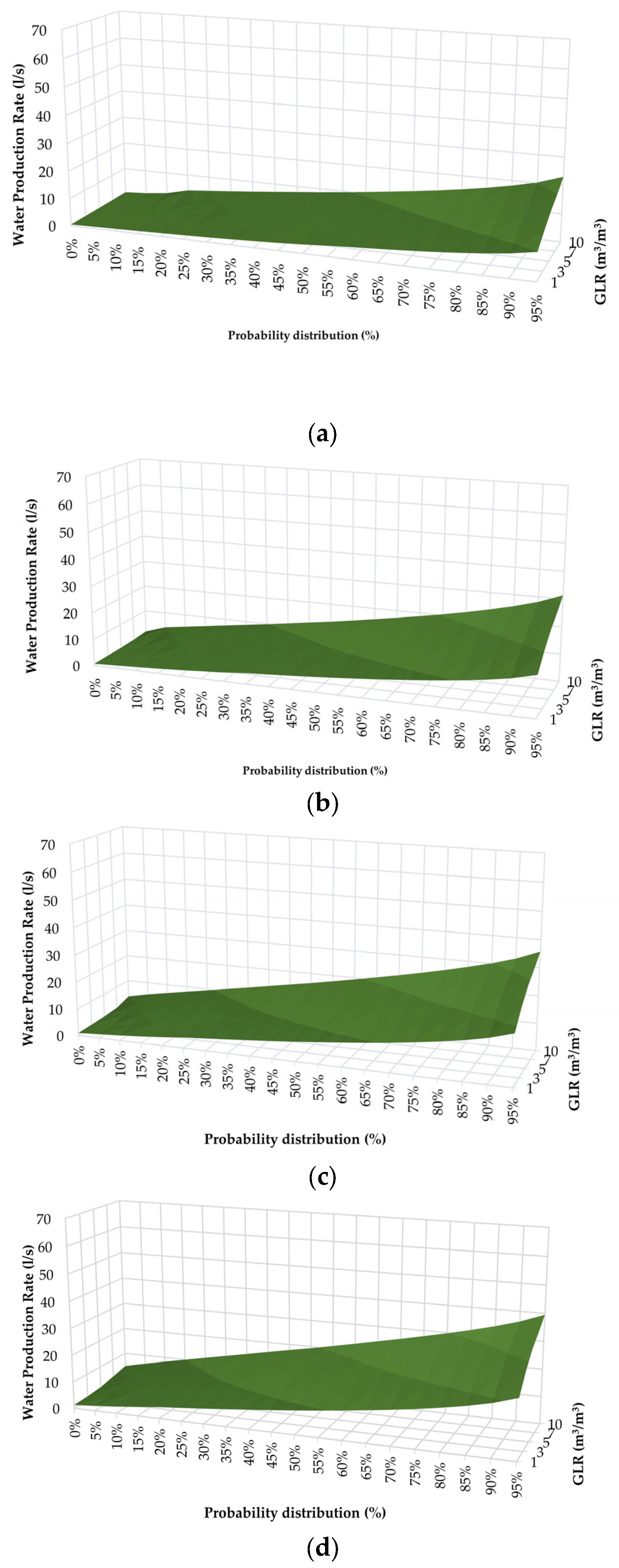
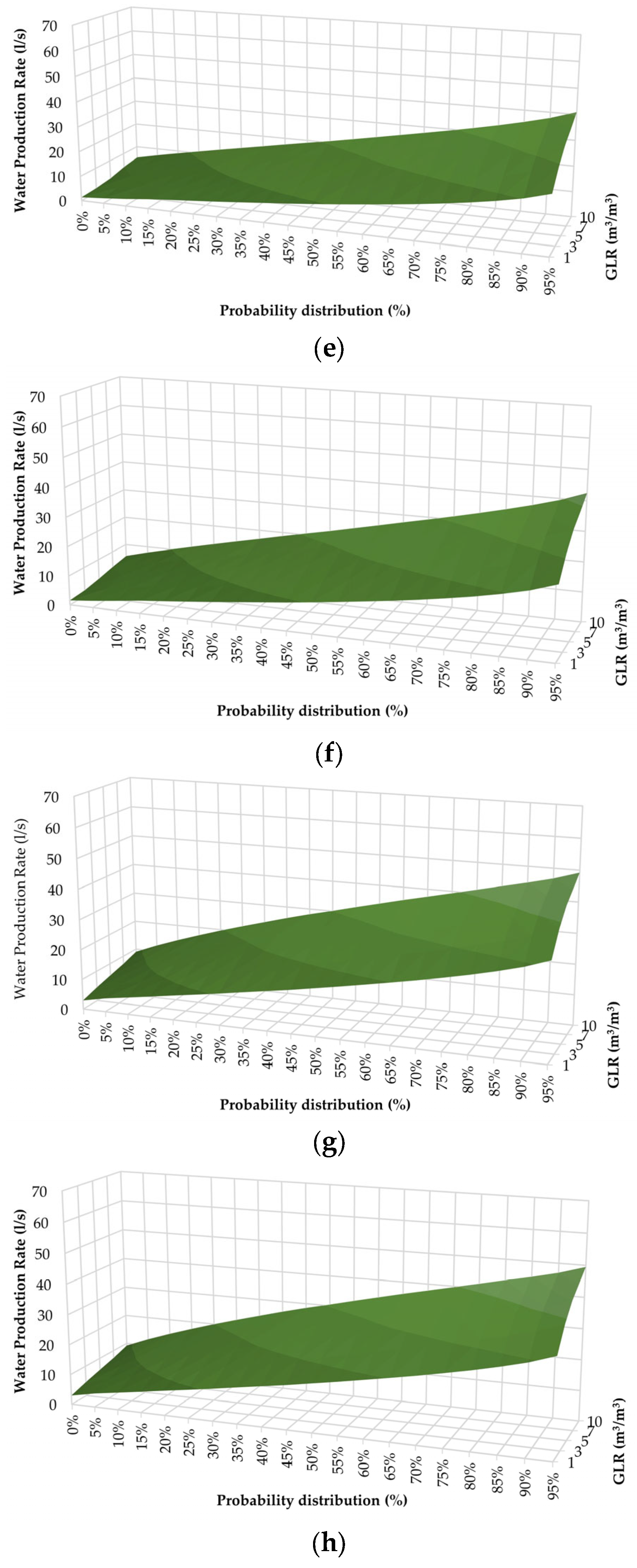
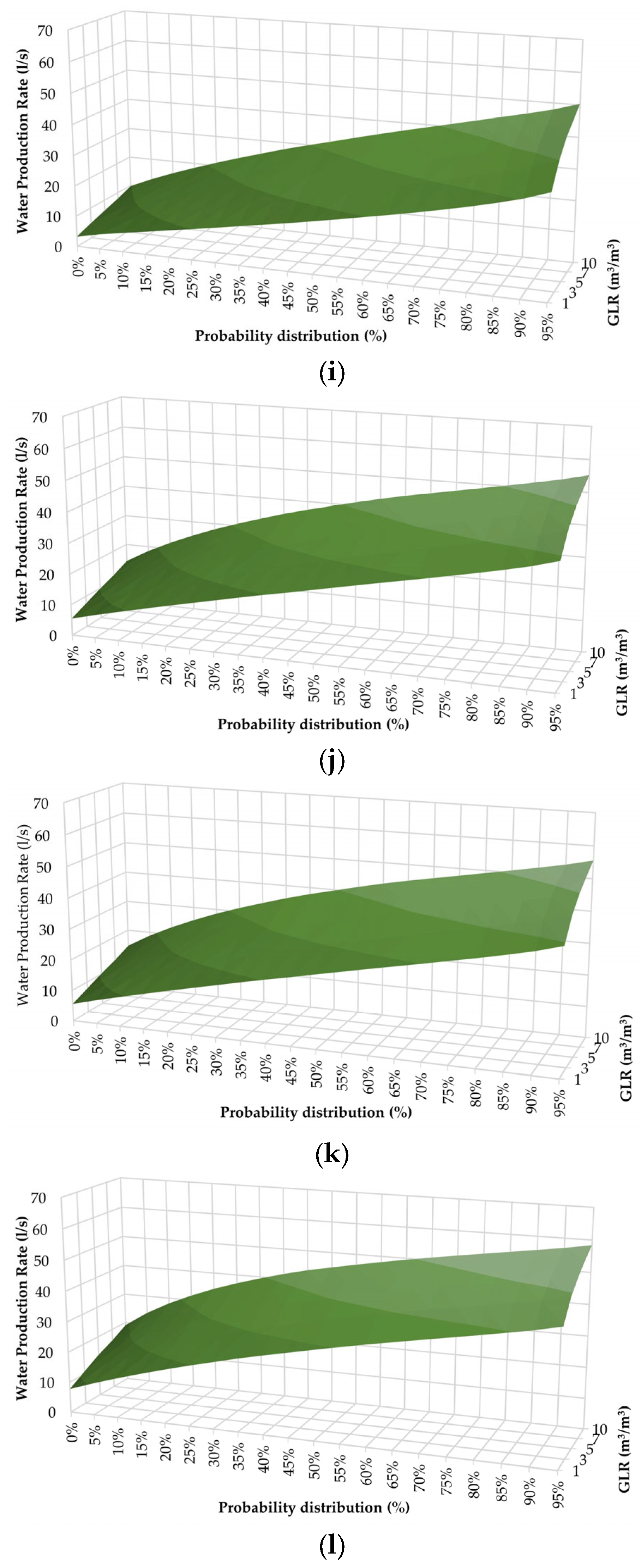
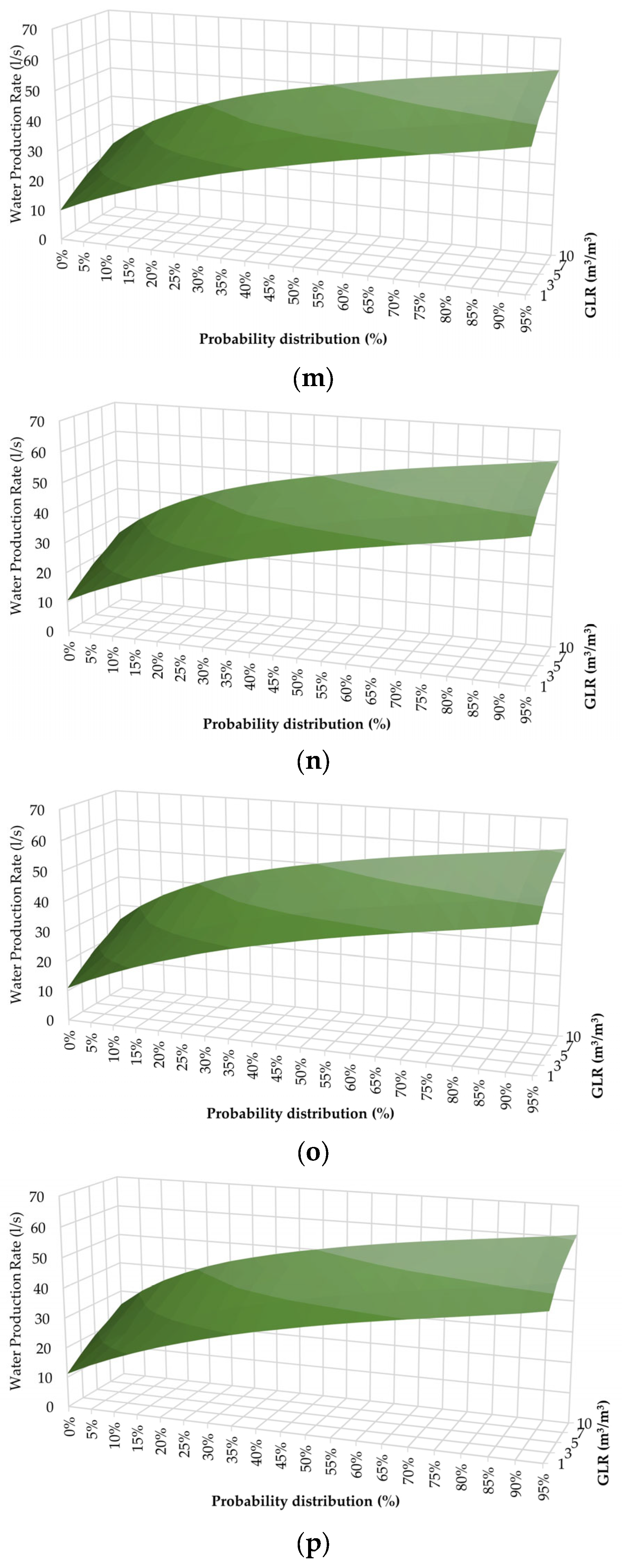
3.1. Permeability Probability Distribution
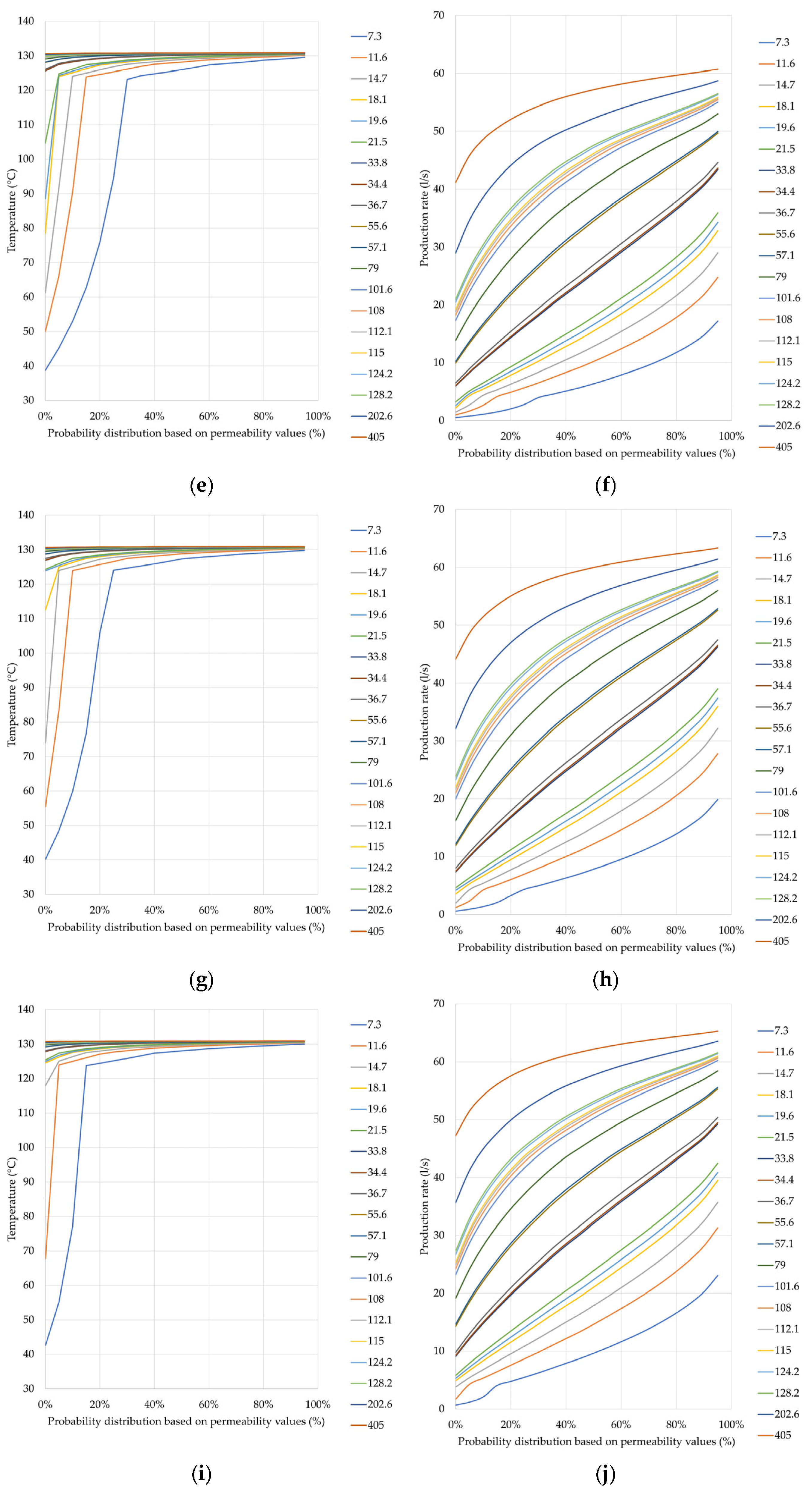
3.2. Sensitivity Analysis of Brine Flow Considering Well Completion Constraints
3.3. Assessment of the Techno-Economic Potential on a Well Basis
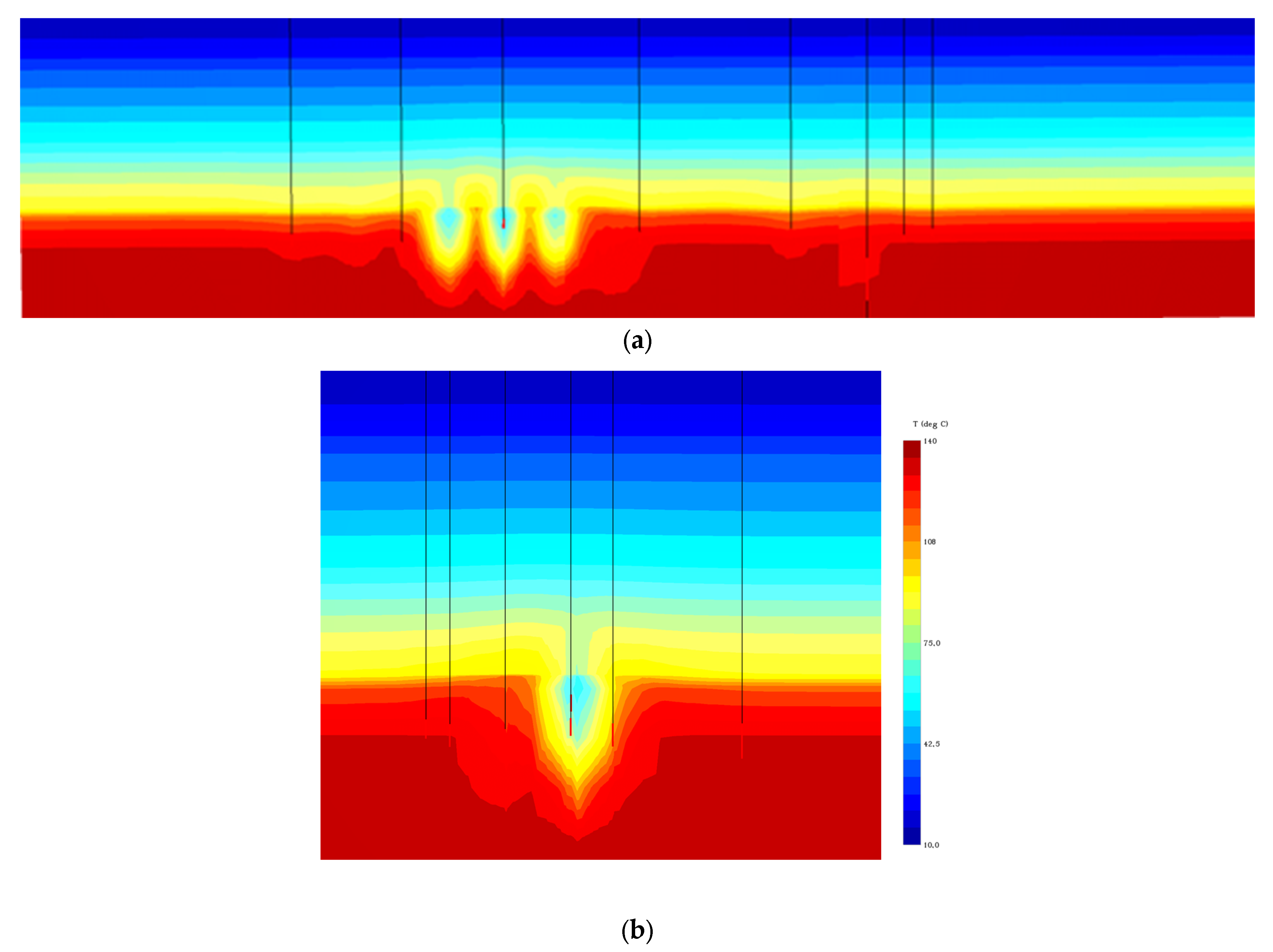
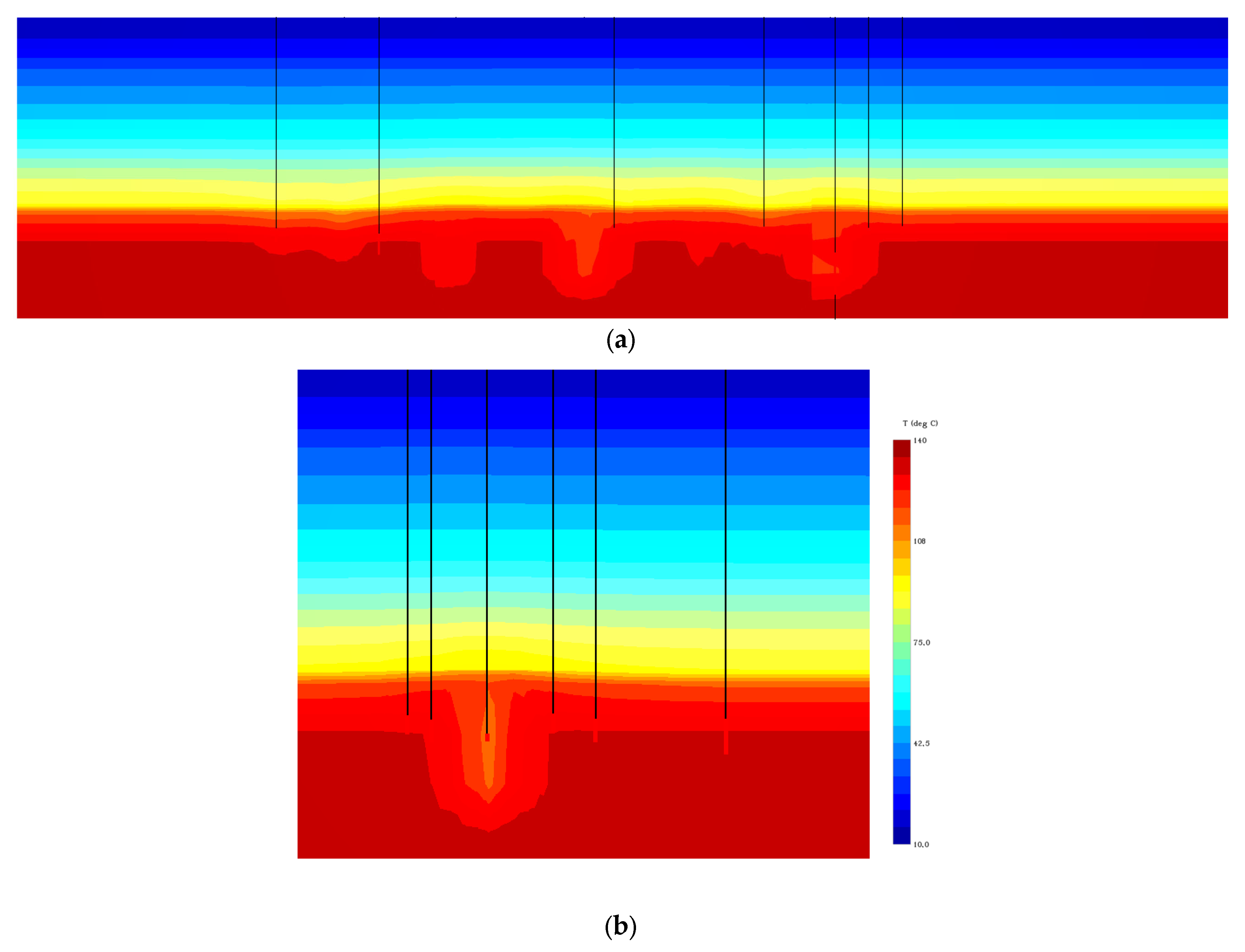
3.4. Reservoir Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IRENA. Renewable Capacity Statistics 2023; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2023. [Google Scholar]
- Sveinbjornsson, B.M.; Thorhallsson, S. Cost and effectiveness of geothermal drilling. In Proceedings of the SIMS 53rd Conference, Reykjavik, Iceland, 4–6 October 2012. [Google Scholar]
- Augustine, C.; Tester, J.W.; Anderson, B. A Comparison of Geothermal with Oil and Gas Well Drilling Costs. In Proceedings of the Thirty-First Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, CA, USA, 30 January–1 February 2006. [Google Scholar]
- Lukawski, M.Z.; Anderson, B.J.; Augustine, C.; Capuano, L.; Beckers, K.F.; Livesay, B.; Tester, J.W. Cost Analysis of Oil, Gas, and Geothermal Well Drilling. J. Pet. Sci. Eng. 2014, 118, 1–14. [Google Scholar] [CrossRef]
- Kaplanoğlu, M.A.; Baba, A.; Akkurt, G.G. Use of Abandoned Oil Wells in Geothermal Systems in Turkey. Geomech. Geophys. Geo-Energy Geo-Resour. 2019, 6, 1. [Google Scholar] [CrossRef]
- Wang, S.; Yan, J.; Li, F.; Hu, J.; Li, K. Exploitation and Utilization of Oilfield Geothermal Resources in China. Energies 2016, 9, 798. [Google Scholar] [CrossRef]
- Leitch, A.L.; Haley, B.; Hastings-Simon, S. Can the Oil and Gas Sector Enable Geothermal Technologies? Socio-Technical Opportunities and Complementarity Failures in Alberta, Canada. Energy Policy 2019, 125, 384–395. [Google Scholar] [CrossRef]
- Nadkarni, K.; Lefsrud, L.; Schiffner, D.; Banks, J. Converting Oil Wells to Geothermal Resources: Roadmaps and Roadblocks for Energy Transformation. Energy Policy 2022, 161, 112705. [Google Scholar] [CrossRef]
- Mahmoodpour, S.; Singh, M.; Mahyapour, R.; Tangirala, S.K.; Bär, K.; Sass, I. Numerical Simulation of Thermo-Hydro-Mechanical Processes at Soultz-Sous-Forêts. Energies 2022, 15, 9285. [Google Scholar] [CrossRef]
- Singh, M.; Mahmoodpour, S.; Ershadnia, R.; Soltanian, M.R.; Sass, I. Comparative Study on Heat Extraction from Soultz-Sous-Forêts Geothermal Field Using Supercritical Carbon Dioxide and Water as the Working Fluid. Energy 2023, 266, 126388. [Google Scholar] [CrossRef]
- Fridleifsson, I.B. Geothermal Energy for the Benefit of the People. Renew. Sustain. Energy Rev. 2001, 5, 299–312. [Google Scholar] [CrossRef]
- Lund, J.W.; Toth, A.N. Direct utilization of Geothermal Energy 2020 Worldwide Review. In Proceedings of the World Geothermal Congress 2020+1, Reykjavik, Iceland, 24–27 October 2021. [Google Scholar]
- Di Pippo, R. Geothermal Power Plants, Principles, Applications, Case Studies and Environmental Impact. Elements of Thermodynamics; Butterworth-Heinemann: Waltham, MA, USA, 2016; pp. 715–726. [Google Scholar] [CrossRef]
- Lindal, B. Industrial and other applications of geothermal energy. In Geothermal Energy; UNESCO: New York, NY, USA, 1973; pp. 135–148. [Google Scholar]
- Hranić, J.; Raos, S.; Leoutre, E.; Rajšl, I. Two-Stage Geothermal Well Clustering for Oil-to-Water Conversion on Mature Oil Fields. Geosciences 2021, 11, 470. [Google Scholar] [CrossRef]
- Kurnia, J.C.; Shatri, M.S.; Putra, Z.A.; Zaini, J.; Caesarendra, W.; Sasmito, A.P. Geothermal Energy Extraction Using Abandoned Oil and Gas Wells: Techno-Economicand Policy Review. Int. J. Energy Res. 2021, 46, 28–60. [Google Scholar] [CrossRef]
- Westphal, D.; Weijermars, R. Economic Appraisal and Scoping of Geothermal Energy Extraction Projects Using Depleted Hydrocarbon Wells. Energy Strategy Rev. 2018, 22, 348–364. [Google Scholar] [CrossRef]
- Li, K.; Sun, W. Modified Method for Estimating Geothermal Resources in Oil and Gas Reservoirs. Math. Geosci. 2014, 47, 105–117. [Google Scholar] [CrossRef]
- Nian, Y.-L.; Cheng, W.-L. Insights into Geothermal Utilization of Abandoned Oil and Gas Wells. Renew. Sustain. Energy Rev. 2018, 87, 44–60. [Google Scholar] [CrossRef]
- Wang, K.; Yuan, B.; Ji, G.; Wu, X. A Comprehensive Review of Geothermal Energy Extraction and Utilization in Oilfields. J. Pet. Sci. Eng. 2018, 168, 465–477. [Google Scholar] [CrossRef]
- Caulk, R.; Tomac, I. Reuse of Abandoned Oil and Gas Wells for Geothermal Energy Production. Renew. Energy 2017, 112, 388–397. [Google Scholar] [CrossRef]
- Macenić, M.; Kurevija, T. Revitalization of Abandoned Oil and Gas Wells for a Geothermal Heat Exploitation by Means of Closed Circulation: Case Study of the Deep Dry Well Pčelić-1. Interpretation 2018, 6, SB1–SB9. [Google Scholar] [CrossRef]
- Bu, X.; Ma, W.; Li, H. Geothermal Energy Production Utilizing Abandoned Oil and Gas Wells. Renew. Energy 2012, 41, 80–85. [Google Scholar] [CrossRef]
- Davis, A.; Michaelides, E.E. Geothermal Power Production from Abandoned Oil Wells. Energy 2009, 34, 866–872. [Google Scholar] [CrossRef]
- Gharibi, S.; Mortezazadeh, E.; Bodi, S.J.H.A.; Vatani, A. Feasibility Study of Geothermal Heat Extraction from Abandoned Oil Wells Using a U-Tube Heat Exchanger. Energy 2018, 153, 554–567. [Google Scholar] [CrossRef]
- Wang, K.; Liu, J.; Wu, X. Downhole Geothermal Power Generation in Oil and Gas Wells. Geothermics 2018, 76, 141–148. [Google Scholar] [CrossRef]
- Santos, L.; Taleghani, A.D.; Elsworth, D. Repurposing Abandoned Wells for Geothermal Energy: Current Status and Future Prospects. Renew. Energy 2022, 194, 1288–1302. [Google Scholar] [CrossRef]
- Liu, X.; Falcone, G.; Alimonti, C. A Systematic Study of Harnessing Low-Temperature Geothermal Energy from Oil and Gas Reservoirs. Energy 2018, 142, 346–355. [Google Scholar] [CrossRef]
- Dickson, M.H.; Fanelli, M. Small Geothermal Resources: A Review. Energy Sources 1994, 16, 349–376. [Google Scholar] [CrossRef]
- Lee, K.C. Classification of Geothermal Resources by Exergy. Geothermics 2001, 30, 431–442. [Google Scholar] [CrossRef]
- Rybach, L. Classification of Geothermal Resources by Potential. Geotherm. Energy Sci. 2015, 3, 13–17. [Google Scholar] [CrossRef]
- Muffler, P.; Cataldi, R. Methods for Regional Assessment of Geothermal Resources. Geothermics 1978, 7, 53–89. [Google Scholar] [CrossRef]
- Williams, C.F.; Reed, M.J.; Robert, H.M. A Review of Methods Applied by the U.S. Geological Survey in the Assessment of Identified Geothermal Resources; Open-File Report 2008–1296; U.S. Geological Survey: Reston, VA, USA, 2008; 30p. [Google Scholar]
- Muffler, L.J.P. Assesment of Geothermal Resources of the United States. Geol. Surv. Circ. 1978, 790, 163. [Google Scholar]
- Song, J.; Loo, P.; Teo, J.; Markides, C.N. Thermo-Economic Optimization of Organic Rankine Cycle (ORC) Systems for Geothermal Power Generation: A Comparative Study of System Configurations. Front. Energy Res. 2020, 8. [Google Scholar] [CrossRef]
- Astolfi, M.; Romano, M.C.; Bombarda, P.; Macchi, E. Binary ORC (Organic Rankine Cycles) Power Plants for the Exploitation of Medium–Low Temperature Geothermal Sources—Part A: Thermodynamic Optimization. Energy 2014, 66, 423–434. [Google Scholar] [CrossRef]
- DiPippo, R. Second Law Assessment of Binary Plants Generating Power from Low-Temperature Geothermal Fluids. Geothermics 2004, 33, 565–586. [Google Scholar] [CrossRef]
- Hijriawan, M.; Pambudi, N.A.; Biddinika, M.K.; Wijayanto, D.S.; Kuncoro, I.W.; Rudiyanto, B.; Wibowo, K.M. Organic Rankine Cycle (ORC) in Geothermal Power Plants. J. Phys. 2019, 1402, 044064. [Google Scholar] [CrossRef]
- Milora, S.L.; Tester, J.W. Geothermal Energy as a Source of Electric Power; MIT: New York, NY, USA, 1976; p. 186. [Google Scholar]
- Matanović, D. Cijevne Alatke pri Opremanju i Održavanju Bušotina (Tubulars in Completion and Workover Operations); Faculty of Mining, Geology and Petroleum Engineering, University of Zagreb: Zagreb, Croatia, 1999. [Google Scholar]
- Zarrouk, S.J.; McLean, K. Geothermal Wells. In Geothermal Well Test Analysis; Elsevier: London, UK, 2019; pp. 39–61. [Google Scholar] [CrossRef]
- Renpu, W. Well Completion Mode Selection. In Advanced Well Completion Engineering, 3rd ed.; Elsevier: Waltham, MA, USA, 2011; pp. 75–116. [Google Scholar] [CrossRef]
- Teodoriu, C.; Falcone, G. Comparing Completion Design in Hydrocarbon and Geothermal Wells: The Need to Evaluate the Integrity of Casing Connections Subject to Thermal Stresses. Geothermics 2009, 38, 238–246. [Google Scholar] [CrossRef]
- Kipsang, C. Cost Model for Geothermal Wells. In Proceedings of the World Geothermal Congress, Melbourne, Australia, 19–25 April 2015. [Google Scholar]
- Lukawski, M.Z.; Silverman, R.; Tester, J.W. Uncertainty Analysis of Geothermal Well Drilling and Completion Costs. Geothermics 2016, 64, 382–391. [Google Scholar] [CrossRef]
- Franc-Dąbrowska, J.; Mądra-Sawicka, M.; Milewska, A. Energy Sector Risk and Cost of Capital Assessment—Companies and Investors Perspective. Energies 2021, 14, 1613. [Google Scholar] [CrossRef]
- Simshauser, P. The Cost of Capital for Power Generation in Atypical Capital Market Conditions. Econ. Anal. Policy 2014, 44, 184–201. [Google Scholar] [CrossRef]
- Sharpe, W.F. Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk. J. Financ. 1964, 19, 425–442. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. The Capital Asset Pricing Model: Theory and Evidence. J. Econ. Perspect. 2004, 18, 25–46. [Google Scholar] [CrossRef]
- Horvathova, J.; Mokrišova, M. Application of CAPM for the Evaluation of Cost of Equity. 2014. Available online: https://exclusiveejournal.sk/files/4-2014/3-horvathova-mokrisova.pdf (accessed on 15 May 2023).
- Energy Development Strategy of the Republic of Croatia until 2030 with a Look at 2050. 2020. Available online: https://narodne-novine.nn.hr/clanci/sluzbeni/2020_03_25_602.html (accessed on 25 April 2023).
- Velić, J.; Malvić, T.; Cvetković, M.; Vrbanac, B. Reservoir Geology, Hydrocarbon Reserves and Production in the Croatian Part of the Pannonian Basin. Geol. Croat. 2012, 65, 91–101. [Google Scholar] [CrossRef]
- Lučić, D.; Saftić, B.; Krizmanić, K.; Prelogović, E.; Britvić, V.; Mesić, I.; Tadej, J. The Neogene Evolution and Hydrocarbon Potential of the Pannonian Basin in Croatia. Mar. Pet. Geol. 2001, 18, 133–147. [Google Scholar] [CrossRef]
- INA. Elaborat o Rezervama Polja Beničanci (Reserves Study of Beničanci Field); Original documentation provided by CHA; INA: Zagreb, Croatia, 1990. [Google Scholar]
- Pleić, M.; Futivić, I. 3D Seismic Interpretation of the Beničanci Oil Field. Naftaplin 2002, 19, 17–25. [Google Scholar]
- Malvić, T. Kriging, Cokriging or Stochastical Simulations, and the Choice between Deterministic or Sequential Approaches. Geol. Croat. 2008, 61, 37–47. [Google Scholar] [CrossRef]
- INA—Industrija Nafte, d.d. Elaborat o Rezervama Ugljikovodika Eksploatacijskog Polja Beničanci (Reserves Study of Beničanci Hydrocarbon Field); Original documentation provided by CHA; INA: Zagreb, Croatia, 2017. [Google Scholar]
- Croatian Meteorological and Hydrological Service. 2021. Available online: https://meteo.hr/klima.php?section=klima_podaci¶m=k1&Grad=osijek (accessed on 15 April 2023).
- Petroleum Experts. PROSPER User’s Manual; Scantron: Eagan, MN, USA, 2013. [Google Scholar]
- Poulsen, S.E.; Balling, N.; Nielsen, S.B. A Parametric Study of the Thermal Recharge of Low Enthalpy Geothermal Reservoirs. Geothermics 2015, 53, 464–478. [Google Scholar] [CrossRef]
- Zhao, Z. On the Heat Transfer Coefficient between Rock Fracture Walls and Flowing Fluid. Comput. Geotech. 2014, 59, 105–111. [Google Scholar] [CrossRef]
- Kędzierski, P.; Nagórski, Z.; Niezgoda, T. Determination of Local Values of Heat Transfer Coefficient in Geothermal Models with Internal Functions Method. Renew. Energy 2016, 92, 506–516. [Google Scholar] [CrossRef]
- Kolo, I.; Sousa, R.; Zhang, T. Heat Transmission in a Geothermal Wellbore: Modelling and Application. 2014. In Proceedings of the 19th Australasian Fluid Mechanics Conference, Melbourne, Australia, 8–11 December 2014. [Google Scholar]
- Barić, G. Organic Geochemistry in the Rationalization of Oil and Gas Exploration and Production. Geol. Croat. 1996, 49, 191–195. Available online: https://hrcak.srce.hr/61166 (accessed on 10 June 2023).
- Predovan, M.; Blecich, P. Thermodynamic Analysis of a 17.5 MW Geothermal Power Plant Operating with Binary Organic Rankine Cycle. Int. Sci. J. Mach. Technol. Mater. 2021, 15, 49–52. Available online: https://stumejournals.com/journals/mtm/2021/2/49 (accessed on 1 May 2023).
- Beckers, K.F.; McCabe, K. GEOPHIRES v2.0; OSTI OAI; US Department of Energy Office of Scientific and Technical Information: Washington, DC, USA, 2020. [Google Scholar] [CrossRef]
- Wall, A.M.; Dobson, P.F.; Thomas, H. Geothermal Costs of Capital: Relating Market Valuation to Project Risk and Technology. Geotherm. Resour. Counc. Trans. 2017, 41, 45–61. [Google Scholar]
- Kustra, A.; Lorenc, S. Financial Balance Analysis of Geothermal Companies in Poland Based on Managerial Cash Flows. Energies 2021, 14, 7885. [Google Scholar] [CrossRef]
- Davaux, M.; Ungemach, P.; Antics, M.; Naville, C. Geothermal derisking. How to learn and succeed from failure stories. In Proceedings of the European Geothermal Congress, Den Haag, The Netherlands, 11–14 June 2019. [Google Scholar]
- Pruess, K.; Oldenburg, C.; Moridis, G. TOUGH2 Use’s Guide, Version 2; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2012.
- Jelić, K. Thermodynamic Characteristics of Sedimentary Complex of SW Part of Pannonian Basin (in Croatian: Termodinamicke Osobine Sedimentnog Kompleksa Jugozapadnog Dijela Panonskog Bazena). Ph.D. Thesis, Faculty of Mining, Geology and Petroleum Engineering, University of Zagreb, Zagreb, Croatia, 1979. [Google Scholar]
- Jelić, K.; Kevrić, I.; Krasić, O. Temperatura i Toplinski Tok u Tlu Hrvatske. In Proceedings of the First Croatian Geological Congress, Zagreb, Croatia, 18–21 October 1995; pp. 245–249. [Google Scholar]
- Mahmoodpour, S.; Singh, M.; Turan, A.; Bär, K.; Sass, I. Simulations and Global Sensitivity Analysis of the Thermo-Hydraulic-Mechanical Processes in a Fractured Geothermal Reservoir. Energy 2022, 247, 123511. [Google Scholar] [CrossRef]
- Mahmoodpour, S.; Singh, M.; Bär, K.; Sass, I. Thermo-Hydro-Mechanical Modeling of an Enhanced Geothermal System in a Fractured Reservoir Using Carbon Dioxide as Heat Transmission Fluid—A Sensitivity Investigation. Energy 2022, 254, 124266. [Google Scholar] [CrossRef]
- Zayed, M.E.; Shboul, B.; Yin, H.; Zhao, J.; Zayed, A.A.A. Recent Advances in Geothermal Energy Reservoirs Modeling: Challenges and Potential of Thermo-Fluid Integrated Models for Reservoir Heat Extraction and Geothermal Energy Piles Design. J. Energy Storage 2023, 62, 106835. [Google Scholar] [CrossRef]
- Schulte, D.O.; Arnold, D.; Geiger, S.; Demyanov, V.; Sass, I. Multi-Objective Optimization under Uncertainty of Geothermal Reservoirs Using Experimental Design-Based Proxy Models. Geothermics 2020, 86, 101792. [Google Scholar] [CrossRef]







| Unit | |||
|---|---|---|---|
| Mean geothermal reservoir depth | m | 2199.06 | |
| Reservoir temperature at the mean reservoir depth | °C | 135.78 | |
| Average reservoir thickness | m | 148.66 | |
| Reservoir pressure—bottom of the reservoir | bar | 211.31 | |
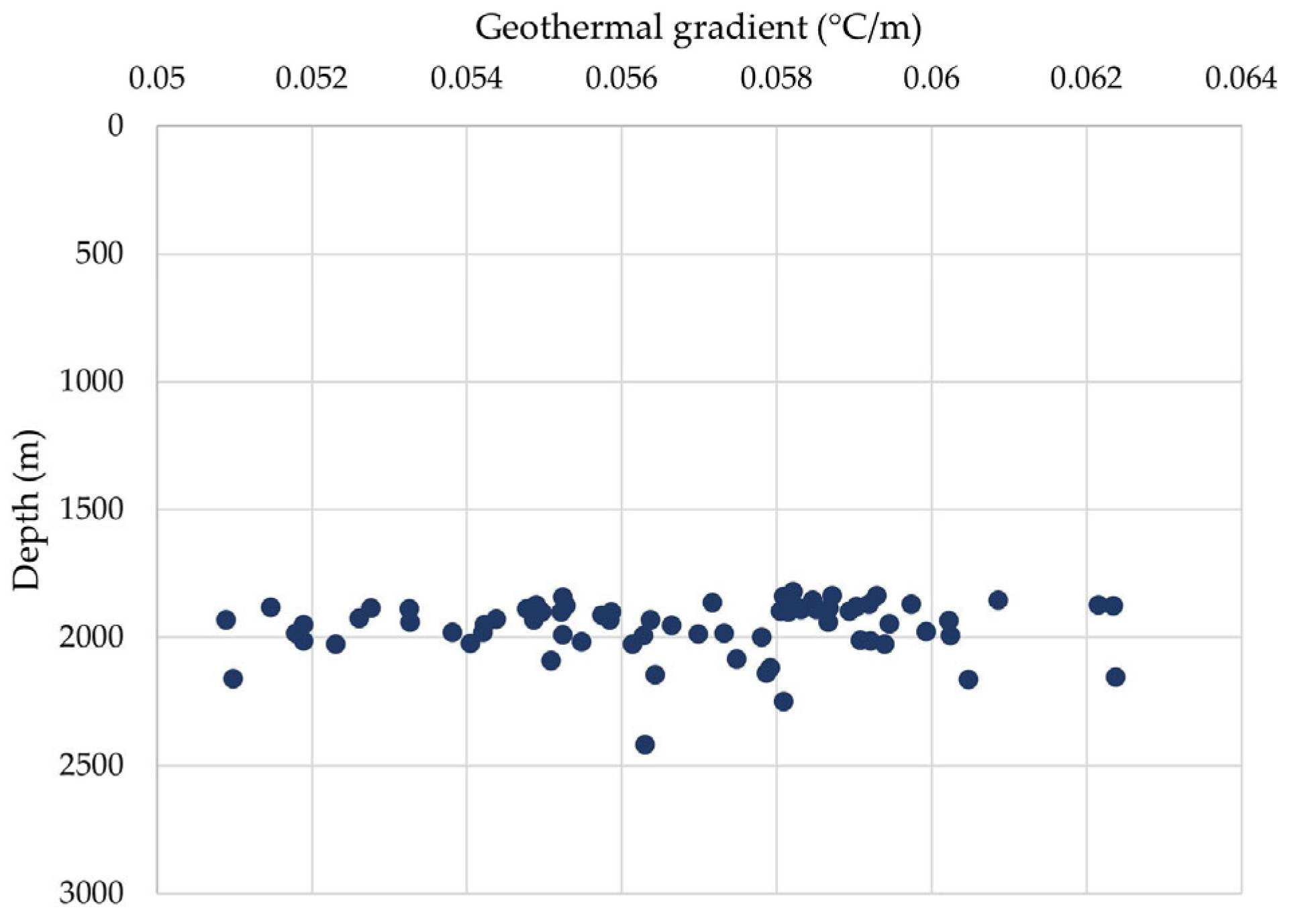
| Geothermal gradient | °C/m | 0.0567 | |
| Pressure gradient | bar/m | 0.0961 |
| Median | Minimum | Maximum | Standard Deviation | |
|---|---|---|---|---|
| Permeability (mD) | 71.62 | 14.50 | 363.22 | 57.54 |
| Production Rate (L/s) | Max. Production Temperature (°C) | Max. Electricity Generation (MW) | Increase in Production Rate (%) | Increase in Max. Production Temperature (%) | Increase in Electricity Generation (%) |
|---|---|---|---|---|---|
| 17 | 129.40 | 0.37 | |||
| 18 | 129.60 | 0.39 | 5.56% | 0.15% | 5.13% |
| 19 | 129.80 | 0.41 | 5.26% | 0.15% | 4.88% |
| 20 | 130.00 | 0.44 | 5.00% | 0.15% | 6.82% |
| 21 | 130.10 | 0.46 | 4.76% | 0.08% | 4.35% |
| 22 | 130.20 | 0.48 | 4.55% | 0.08% | 4.17% |
| 23 | 130.40 | 0.51 | 4.35% | 0.15% | 5.88% |
| 24 | 130.50 | 0.53 | 4.17% | 0.08% | 3.77% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuschl, M.; Kurevija, T. Revitalization Modelling of a Mature Oil Field with Bottom-Type Aquifer into Geothermal Resource—Reservoir Engineering and Techno-Economic Challenges. Energies 2023, 16, 6599. https://doi.org/10.3390/en16186599
Tuschl M, Kurevija T. Revitalization Modelling of a Mature Oil Field with Bottom-Type Aquifer into Geothermal Resource—Reservoir Engineering and Techno-Economic Challenges. Energies. 2023; 16(18):6599. https://doi.org/10.3390/en16186599
Chicago/Turabian StyleTuschl, Martina, and Tomislav Kurevija. 2023. "Revitalization Modelling of a Mature Oil Field with Bottom-Type Aquifer into Geothermal Resource—Reservoir Engineering and Techno-Economic Challenges" Energies 16, no. 18: 6599. https://doi.org/10.3390/en16186599
APA StyleTuschl, M., & Kurevija, T. (2023). Revitalization Modelling of a Mature Oil Field with Bottom-Type Aquifer into Geothermal Resource—Reservoir Engineering and Techno-Economic Challenges. Energies, 16(18), 6599. https://doi.org/10.3390/en16186599







