Robust Nonlinear Control of a Wind Turbine with a Permanent Magnet Synchronous Generator
Abstract
:1. Introduction
- 1.
- Unknown wind velocity, which is estimated based on measurements of the produced power.
- 2.
- Parameter variations and uncertainties in the WT model, which are estimated using HOSM estimators.
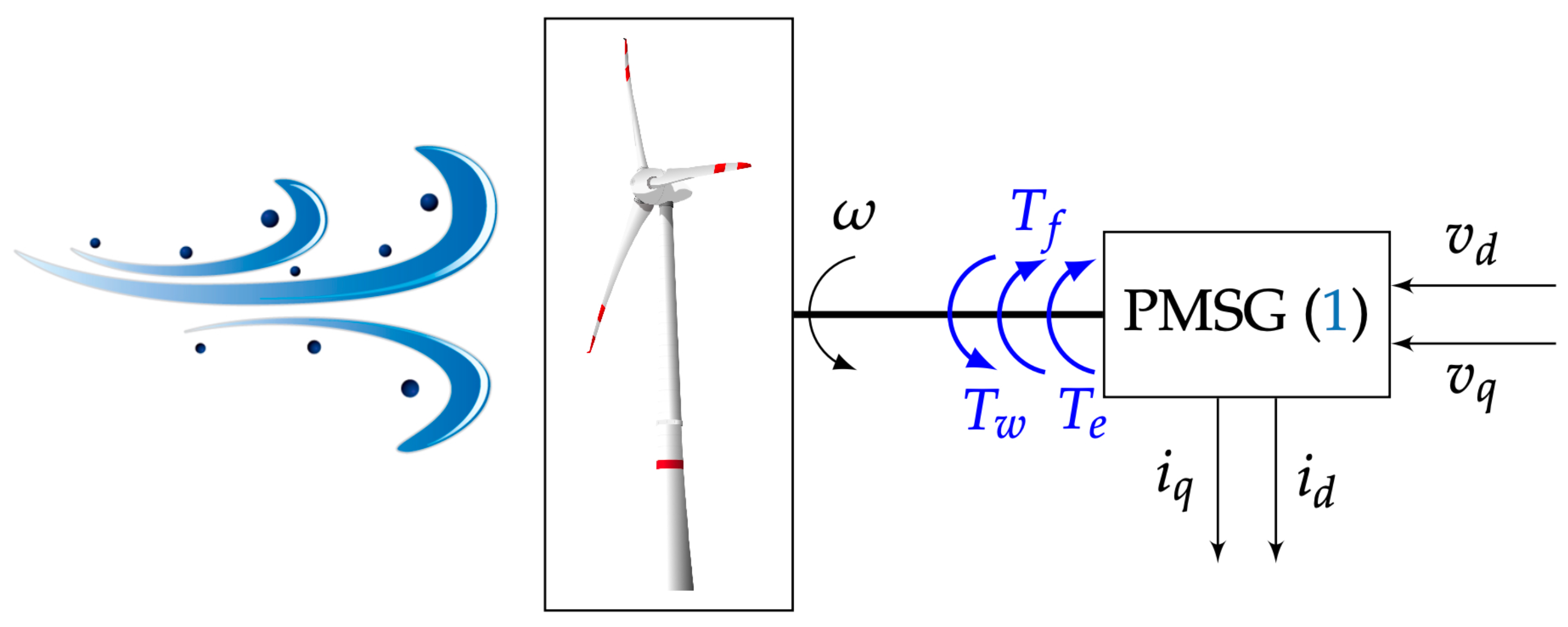
2. Mathematical Model of a WT
3. Design of the Dynamic Controller for the Tracking of the Angular Velocity Reference
3.1. Design of the Wind Velocity Estimator
3.2. Design of the Dynamic Controller for the Tracking of the Angular Velocity Reference
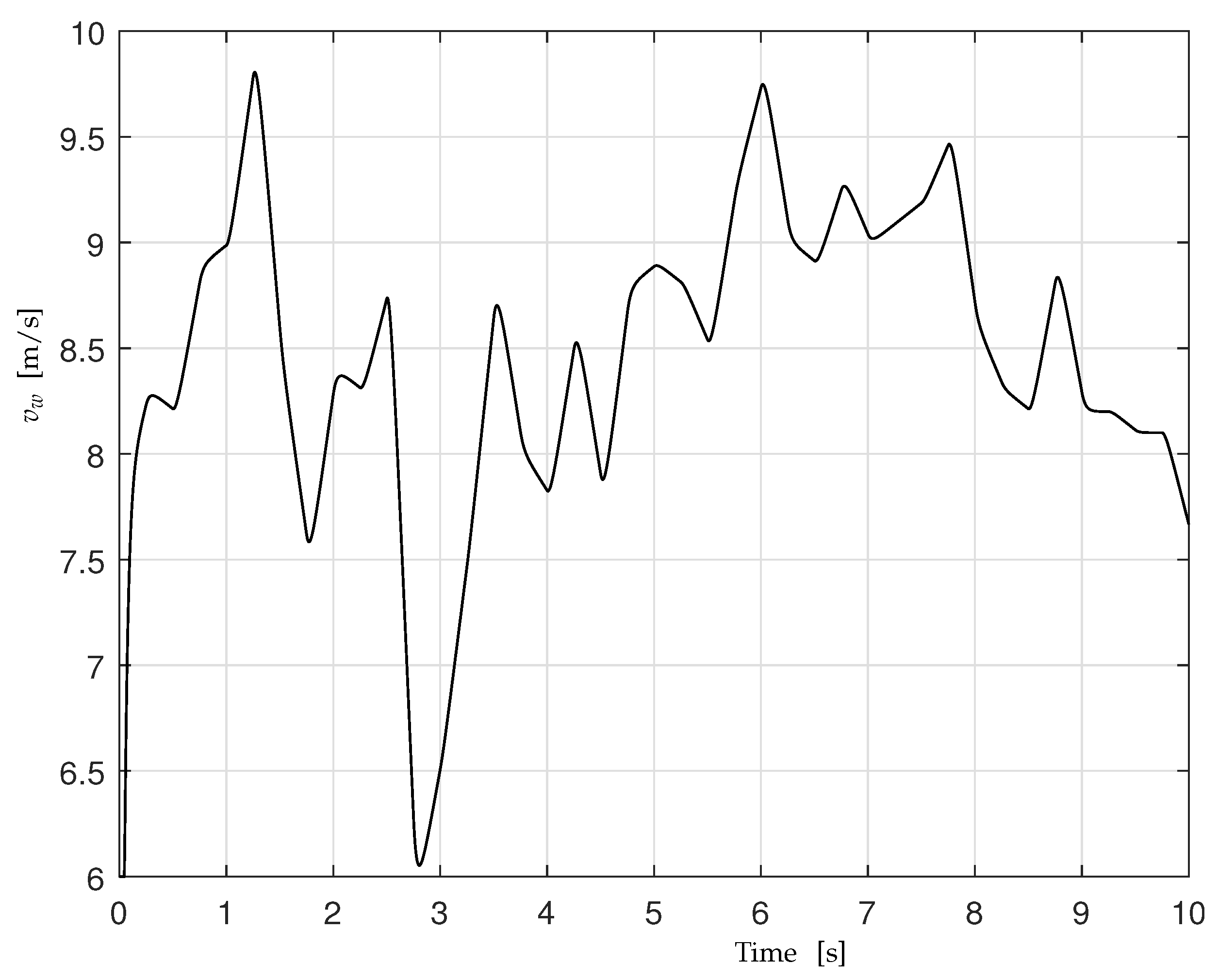
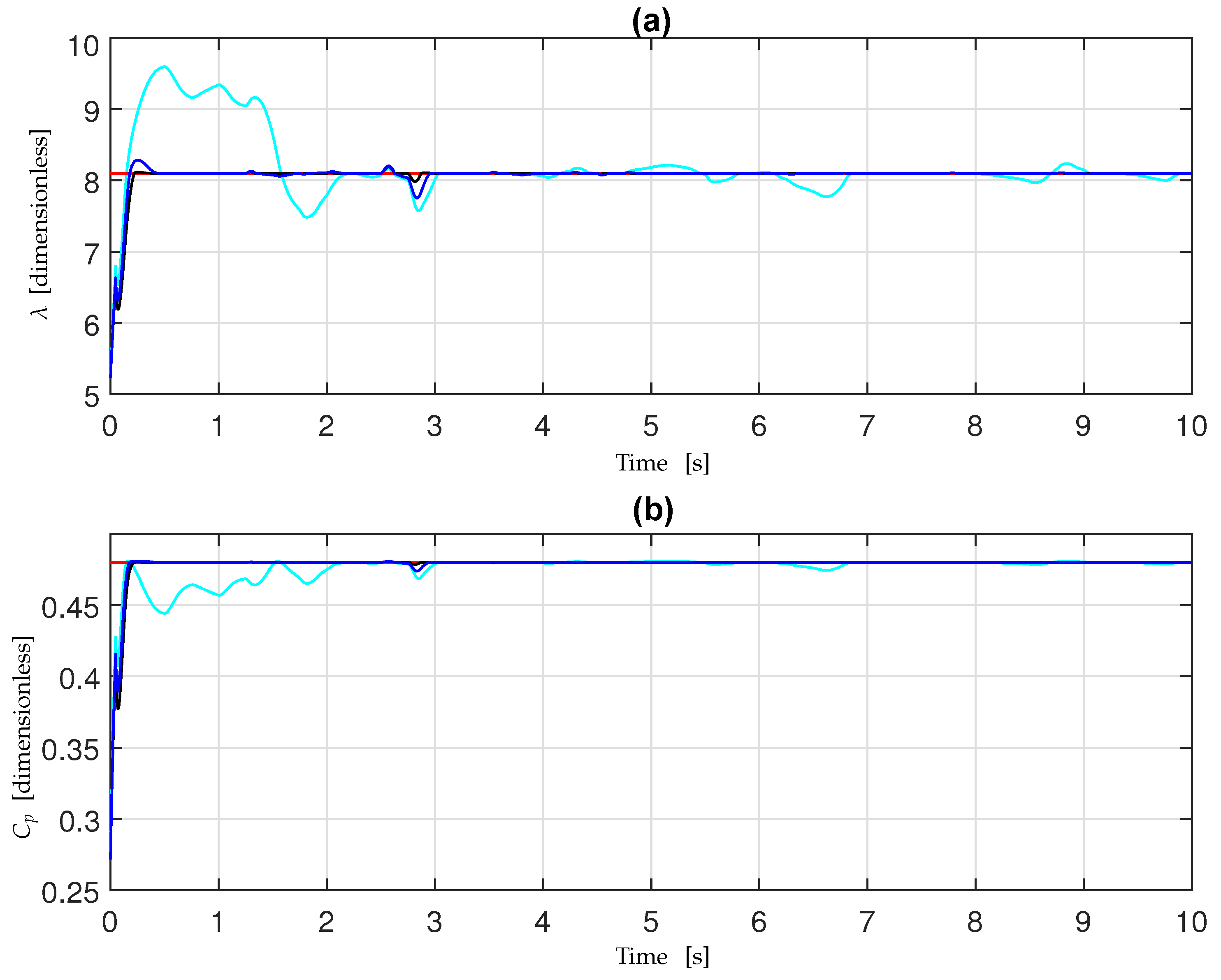
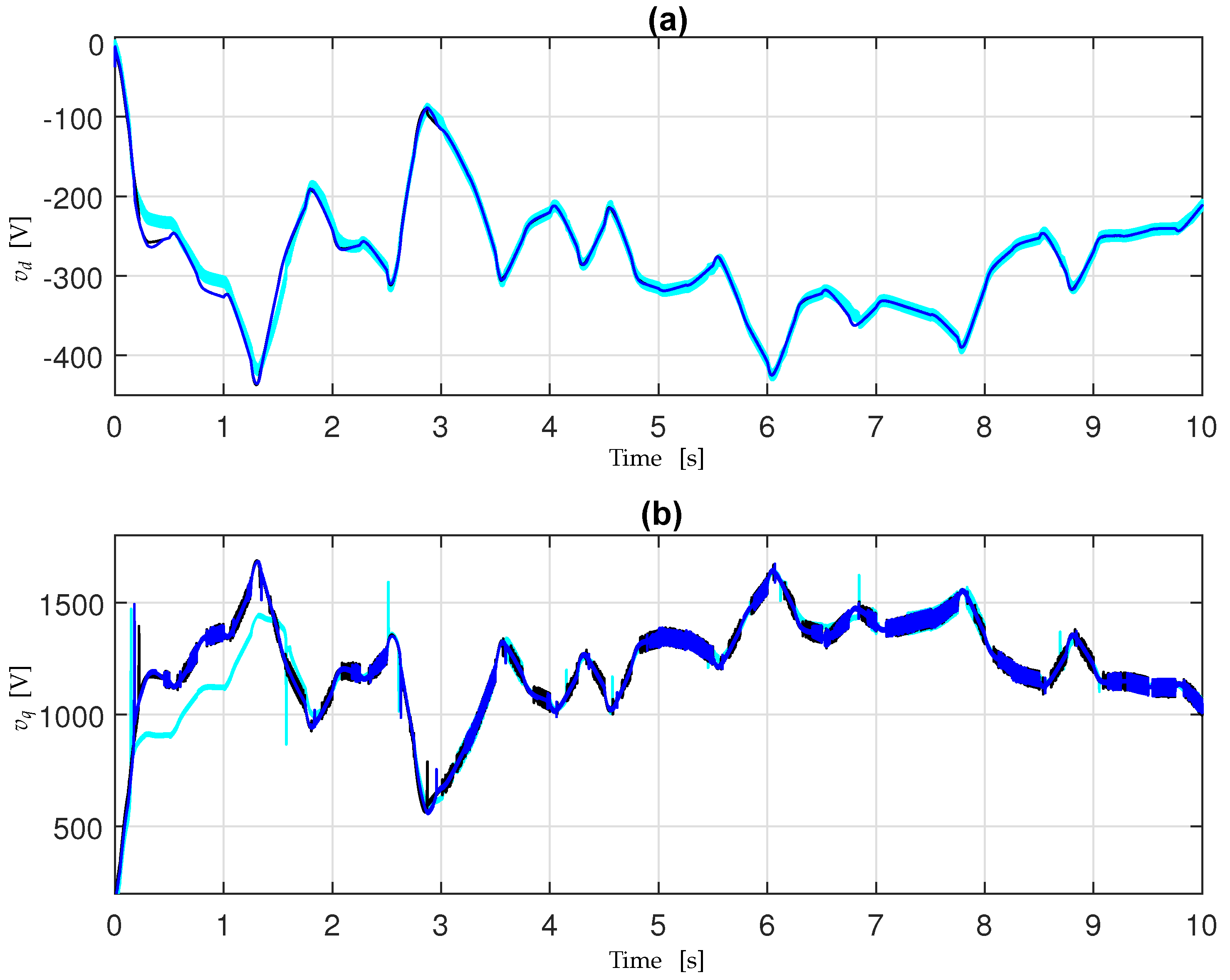
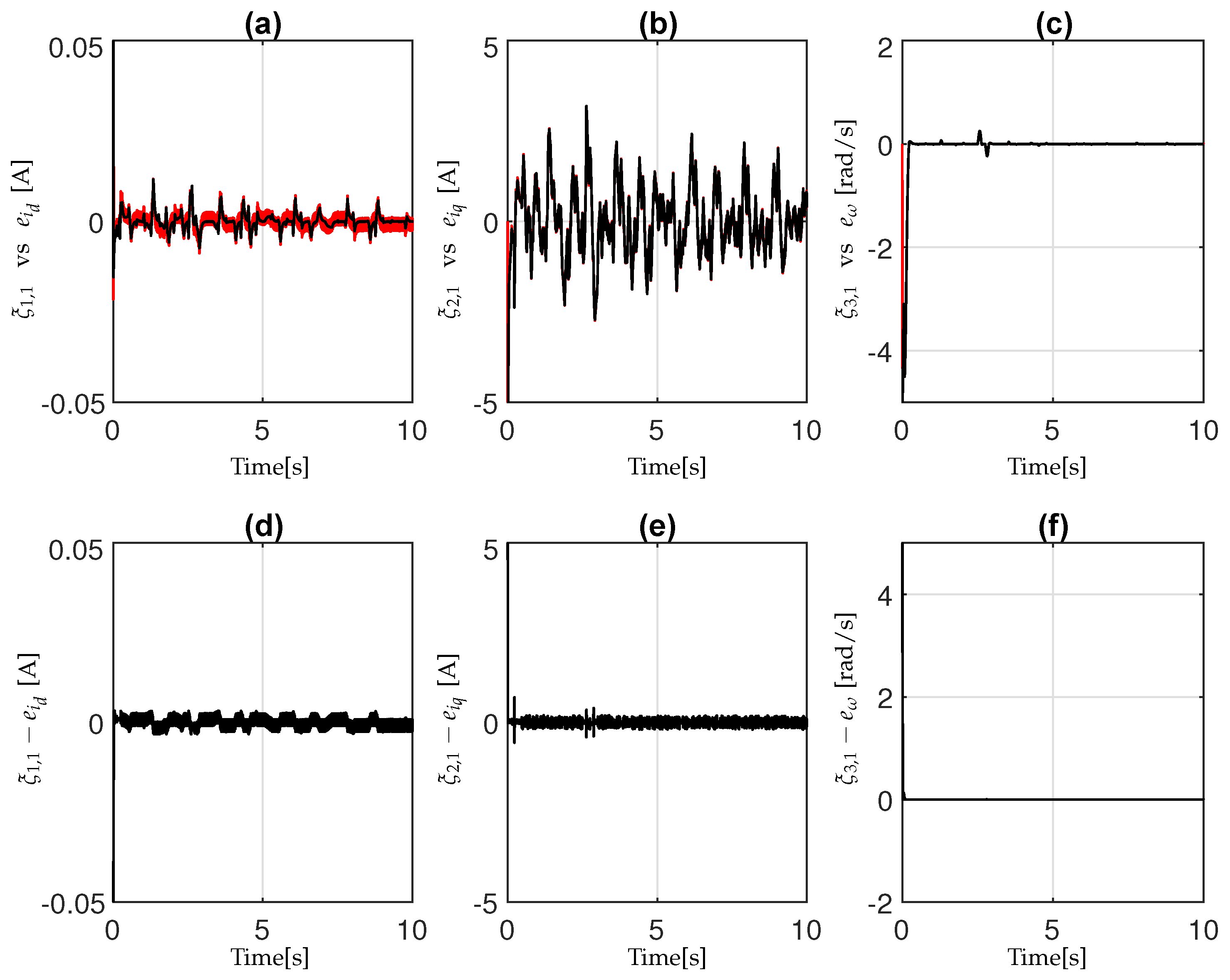
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, P.; Han, D. Effective wind speed estimation study of the wind turbine based on deep learning. Energy 2022, 247, 123491. [Google Scholar] [CrossRef]
- Avendano-Valencia, L.D.; Abdallah, I.; Chatzi, E. Virtual fatigue diagnostics of wake-affected wind turbine via Gaussian process regression. Renew. Energy 2021, 170, 539–561. [Google Scholar] [CrossRef]
- Mohammadi, E.; Rasoulinezhad, R.; Moschopoulos, G. Using a Supercapacitor to Mitigate Battery Microcycles Due to Wind Shear and Tower Shadow Effects in Wind-Diesel Microgrids. IEEE Trans. Smart Grid 2020, 11, 3677–3689. [Google Scholar] [CrossRef]
- Benmahdjoub, M.A.; Mezouar, A.; Ibrahim, M.; Boumediene, L.; Saidi, Y.; Atallah, M. Accurate Estimation of Effective Wind Speed for Wind Turbine Control Using Linear and Nonlinear Kalman Filters. Arab. J. Sci. Eng. 2023, 48, 6765–6781. [Google Scholar] [CrossRef]
- Amato, F.; Guignard, F.; Walch, A.; Mohajeri, N.; Scartezzini, J.L.; Kanevski, M. Spatio-temporal estimation of wind speed and wind power using extreme learning machines: Predictions, uncertainty and technical potential. Stoch. Environ. Res. Risk Assess. 2022, 36, 2049–2069. [Google Scholar] [CrossRef] [PubMed]
- Bhowmik, S.; Spee, R.; Enslin, J.H.R. Performance Optimization for Doubly Fed Wind Power Generation Systems. IEEE Trans. Ind. Appl. 1999, 35, 949–958. [Google Scholar] [CrossRef]
- Utkin, V.I. Sliding Modes in Control and Optimization; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Pourebrahim, R.; Shotorbani, A.M.; Márquez, F.P.G.; Tohidi, S.; Mohammadi-Ivatloo, B. Robust Control of a PMSG-Based Wind Turbine Generator Using Lyapunov Function. Energies 2021, 14, 1712. [Google Scholar] [CrossRef]
- Mousavi, Y.; Bevan, G.; Kucukdemiral, I.B.; Fekih, A. Sliding mode control of wind energy conversion systems: Trends and applications. Renew. Sustain. Energy Rev. 2022, 167, 112734. [Google Scholar] [CrossRef]
- Rajendran, S.; Jena, D. Backstepping Sliding Mode Control of a Variable Speed Wind Turbine for Power Optimization. J. Mod. Power Syst. Clean Energy 2015, 3, 402–410. [Google Scholar] [CrossRef]
- Corradini, M.L.; Ippoliti, G.; Orlando, G. A Sliding Mode Pitch Controller for Wind Turbines Operating in High Wind Speeds Region. In Proceedings of the International Conference on Control, Decision and Information Technologies, Barcelona, Spain, 5–7 April 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Gajewski, P.; Pieńkowski, K. Analysis of Sliding Mode Control of Variable Speed Wind Turbine System with PMSG. In Proceedings of the International Symposium on Electrical Machines (SME), Naleczow, Poland, 18–21 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Ardjal, A.; Mansouri, R.; Bettayeb, M. Fractional sliding mode control of wind turbine for maximum power point tracking. Trans. Inst. Meas. Control 2018, 41, 447–457. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Shu, H.; Dong, J.; Jiang, L. Robust sliding—Mode control of wind energy conversion systems for optimal power extraction via nonlinear perturbation observers. Appl. Energy 2018, 210, 711–723. [Google Scholar] [CrossRef]
- Mohammad, J.M.; Afef, F. A Sliding Mode Approach to Enhance the Power Quality of Wind Turbines Under Unbalanced Voltage Conditions. IEEE/CAA J. Autom. Sin. 2019, 2, 566–574. [Google Scholar] [CrossRef]
- Fridman, L.; Moreno, J.; Iriarte, R. Sliding Modes after the first Decade of the 21st Century: State of the Art. Lect. Notes Control Inf. Sci. 2011, 412, 113–149. [Google Scholar]
- Emelyanov, S.V.; Korovin, S.K.; Levantovsky, L.V. Higher Order Sliding Regimes in the Binary Control Systems. Sov. Phys. 1986, 31, 291–293. [Google Scholar]
- Edwards, C.; Spurgeon, S.K. Sliding Mode Control: Theory and Application; Taylor and Francis Ltd.: London, UK, 1999. [Google Scholar]
- Bartolini, G.; Pisano, A.; Usai, E. First and Second Derivative Estimation by Sliding Mode Technique. J. Signal Process. 2000, 4, 167–176. [Google Scholar]
- Fridman, L.; Levant, A. Higher Order Sliding Modes, Sliding Mode Control in Engineering; Marcel Dekker: New York, NY, USA, 2002; pp. 53–101. [Google Scholar]
- Floquet, T.; Barbot, J.P. Super Twisting Algorithm based Step–by–Step Sliding Mode Observers for Nonlinear Systems with Unknown Inputs. Int. J. Syst. Sci. 2007, 10, 803–815. [Google Scholar] [CrossRef]
- Levant, A. Higher–Order Sliding Modes, Differentiation and Output Feedback Control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Fridman, L.; Shtessel, Y.; Edwards, C.; Yan, X.G. Higher–Order Sliding–Mode Observer for State Estimation and Input Reconstruction in Nonlinear Systems. Int. J. Robust Nonlinear Control 2008, 18, 399–413. [Google Scholar] [CrossRef]
- Levant, A. Homogeneity Approach to High–Order Sliding Mode Design. Automatica 2005, 41, 823–830. [Google Scholar] [CrossRef]
- Basin, M.V.; Yu, P.; Shtessel, Y.B. Hypersonic Missile Adaptive Sliding Mode Control Using Finite-and Fixed-Time Observers. IEEE Trans. Ind. Electron. 2018, 65, 930–941. [Google Scholar] [CrossRef]
- Deng, H.; Li, Q.; Chen, W.; Zhang, G. High–Order Sliding Mode Observer Based OER Control for PEM Fuel Cell Air–Feed System. IEEE Trans. Energy Convers. 2018, 33, 232–244. [Google Scholar] [CrossRef]
- Kommuri, S.K.; Lee, S.B.; Veluvolu, K.C. Robust Sensors–Fault–Tolerance With Sliding Mode Estimation and Control for PMSM Drives. IEEE/ASME Trans. Mechatronics 2018, 23, 17–28. [Google Scholar] [CrossRef]
- Pan, Y.; Yang, C.; Pan, L.; Yu, H. Integral Sliding Mode Control: Performance, Modification, and Improvement. IEEE Trans. Ind. Inform. 2018, 14, 3087–3096. [Google Scholar] [CrossRef]
- Panathula, C.B.; Rosales, A.; Shtessel, Y.B.; Fridman, L.M. Closing Gaps for Aircraft Attitude Higher Order Sliding Mode Control Certification via Practical Stability Margins Identification. IEEE Trans. Control. Syst. Technol. 2018, 26, 2020–2034. [Google Scholar] [CrossRef]
- Liu, J.; Gao, Y.; Su, X.; Wack, M.; Wu, L. Disturbance Observer Based Control for Air Management of PEM Fuel Cell Systems via Sliding Mode Technique. IEEE Trans. Control Syst. Technol. 2018, 27, 1129–1138. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, J.; Sun, G.; Liu, M.; Wu, L. Fault Deviation Estimation and Integral Sliding Mode Control Design for Lipschitz Nonlinear Systems. Syst. Control Lett. 2019, 123, 8–15. [Google Scholar] [CrossRef]
- Van, M. An Enhanced Tracking Control of Marine Surface Vessels Based on Adaptive Integral Sliding Mode Control and Disturbance Observer. ISA Trans. 2019, in press. [CrossRef]
- Karim, B.; Sami, B.S.; Adnane, C. Higher Order Sliding mode control For PMSG in Wind power Conversion System. In Proceedings of the 2016 4th International Conference on Control Engineering & Information Technology (CEIT), Hammamet, Tunisia, 16–18 December 2016; pp. 1–6. [Google Scholar]
- Valenciaga, F.; Puleston, P.F. High-Order Sliding Control for a Wind Energy Conversion System Based on a Permanent Magnet Synchronous Generator. IEEE Trans. Energy Convers. 2008, 23, 860–867. [Google Scholar] [CrossRef]
- Barambones, O.; Gonzalez de Durana, J.M. Adaptive sliding mode control strategy for a wind turbine systems using a HOSM wind torque observer. In Proceedings of the IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016; pp. 1–610. [Google Scholar] [CrossRef]
- Barambones, O.; González de Durana, J.M. Second Order Sliding Mode Controller and Observer for a Wind Turbine System. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–6. [Google Scholar]
- Merabet, A. Adaptive Sliding Mode Speed Control for Wind Energy Experimental System. Energies 2018, 11, 2238. [Google Scholar] [CrossRef]
- Zine Laabidine, N.; Bossoufi, B.; El Kafazi, I.; El Bekkali, C.; El Ouanjli, N. Robust Adaptive Super Twisting Algorithm Sliding Mode Control of a Wind System Based on the PMSG Generator. Sustainability 2023, 15, 10792. [Google Scholar] [CrossRef]
- Matraji, I.; Al-Durra, A.; Errouissi, R. Design and experimental validation of enhanced adaptive second-order SMC for PMSG-based wind energy conversion system. Int. J. Electr. Power Energy Syst. 2018, 103, 21–30. [Google Scholar] [CrossRef]
- Zhang, C.; Plestan, F. Individual/collective blade pitch control of floating wind turbine based on adaptive second order sliding mode. Ocean Eng. 2021, 228, 108897. [Google Scholar] [CrossRef]
- Fdaili, M.; Essadki, A.; Kharchouf, I.; Nasser, T. An overall modeling of wind turbine systems based on DFIG using conventional sliding mode and second-order sliding mode controllers. In Proceedings of the 2019 International Conference on Wireless Technologies, Embedded and Intelligent Systems (WITS), Fez, Morocco, 3–4 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Zargham, F.; Mazinan, A.H. Super-twisting sliding mode control approach with its application to wind turbine systems. Energy Syst. 2019, 10, 211–229. [Google Scholar] [CrossRef]
- Bianchi, F.D.; Battista, H.N.D.; Mantz, R.J. Wind Turbine Control Systems: Principles, Modelling and Gain Scheduling Design; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Siegfried, H. Grid Integration of Wind Energy Conversion Systems; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Zaragoza, J.; Pou, J.; Arias, A.; Spiteri, C.; Robles, E.; Ceballos, S. Study and Experimental Verification of Control Tuning Strategies in a Variable Speed Wind Energy Conversion System. Renew. Energy 2011, 36, 1421–1430. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. A Lyapunov Approach to Second–Order Sliding Mode Controllers and Observers. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 2856–2861. [Google Scholar]
- Moreno, J.A. Lyapunov Approach for Analysis and Design of Second Order Sliding Mode Algorithms. In Sliding Modes after the First Decade of the 21st Century: State of the Art; Lecture Notes in Control and Information Sciences; Thoma, M., Allgöwer, F., Morari, M., Eds.; Springer: Berlin/Heidelberg Germany, 2011. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice–Hall: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]
- Clarke, F.H.; Ledyaev, Y.; Stern, R.J.; Wolenski, P.R. Nonsmooth Analysis and Control Theory; Springer: New York, NY, USA, 1998. [Google Scholar]
- Cortés, J. Discontinuous Dynamical Systems: A Tutorial on Solutions, Nonsmooth Analysis, and Stability. IEEE Control Syst. Mag. 2008, 28, 36–73. [Google Scholar]
- Introduction to Wind Speed Monitoring for Wind Turbines. 2021. Available online: https://www.windlogger.com/blogs/news/5116392-introduction-to-wind-speed-monitoring-for-wind-turbines (accessed on 30 July 2023).
- Corradini, M.L.; Ippoliti, G.; Orlando, G. Robust Control of Variable-Speed Wind Turbines Based on an Aerodynamic Torque Observer. IEEE Trans. Control Syst. Technol. 2013, 21, 1199–1206. [Google Scholar] [CrossRef]





| Rotor radius | 46.6 m | |
| Winding resistance | 0.821 | |
| Winding inductance | 1.5731 H | |
| Flux linkage | 5.8264 Wb | |
| p | Pole number | 26 |
| Mechanical inertia | 34.6 Kg m | |
| Coefficient of viscous friction | 1.5 Kg m/s | |
| Normal air density | 1.225 Kg/m |
| MAE | MSE | IAE | ISE | |
|---|---|---|---|---|
| Proposed controller (5) | 0.0132 | |||
| Proposed controller (5) | 0.0781 | |||
| without the HOSM estimators | ||||
| FOSM controller [52] | 0.0458 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acosta Lúa, C.; Bianchi, D.; Martín Baragaño, S.; Di Ferdinando, M.; Di Gennaro, S. Robust Nonlinear Control of a Wind Turbine with a Permanent Magnet Synchronous Generator. Energies 2023, 16, 6649. https://doi.org/10.3390/en16186649
Acosta Lúa C, Bianchi D, Martín Baragaño S, Di Ferdinando M, Di Gennaro S. Robust Nonlinear Control of a Wind Turbine with a Permanent Magnet Synchronous Generator. Energies. 2023; 16(18):6649. https://doi.org/10.3390/en16186649
Chicago/Turabian StyleAcosta Lúa, Cuauhtemoc, Domenico Bianchi, Salvador Martín Baragaño, Mario Di Ferdinando, and Stefano Di Gennaro. 2023. "Robust Nonlinear Control of a Wind Turbine with a Permanent Magnet Synchronous Generator" Energies 16, no. 18: 6649. https://doi.org/10.3390/en16186649






