Experimental Investigation of Fast−Charging Effect on Aging of Electric Vehicle Li−Ion Batteries

Abstract

A huge increase in fast−charging stations will be necessary for the transition to EVs. Nevertheless, charging a battery pack at a higher C−rate impacts its state of health, accelerating its degradation. The present paper proposes a different and innovative approach that considers the daily routine of an EV Li−ion battery based on a standard driving cycle, including charging phases when the depth of discharge is 90%. Through dynamic modeling of the EV battery system, the state of charge evolution is determined for different charging C−rates, considering both real discharging and charging current profiles. Finally, by applying a suitable post−processing procedure, aging test features are defined, each being related to a specific EV battery working mode, including charging at a particular C−rate, considering the global battery operation during its lifespan. It is demonstrated that, according to the implemented procedure, fast−charging cycles at 50 kW reduce battery lifespan by about 17% with respect to charge in a 22 kW three−phase AC column, in parity with the discharge rate. Thus, this work can provide a deep insight into the expected massive penetration of electric vehicles, providing an estimate of battery useful life based on charging conditions.

1. Introduction

The transportation sector represents one of the most significant sources of carbon dioxide emissions to date. In 2019, at the EU−27 level, 835 million tons of CO₂ were emitted by the transportation sector, representing about 21.5% of the total delivered CO₂ emissions [1]. Specifically, cars were responsible for more than 55% of the total CO₂ emissions in this sector [2]. Therefore, the road transportation industry is facing a transition from internal combustion engine vehicles to electric vehicles (EVs), aiming to reach EU targets to reduce CO₂ emissions, since EVs have proved to be the best alternative to counteract these problems.

In this framework, battery technology is a key point for this evolution [3] as the main component in terms of the performance, reliability, and affordability of hybrid and full−electric vehicles, thanks to recent technical and economic developments in battery and fast−charging technologies.

Specifically, Li−ion batteries represent a core technology among the different battery chemistries thanks to their high gravimetric energy density, volumetric energy density, and power density.

Currently, the long time needed for battery charging, safety, and the absence of abundant fast−charging stations (FCSs) are the major drawbacks highlighted by electric vehicle (EV) owners in accelerating the EV transition [4,5,6,7,8,9,10,11]. Essentially, EV owners urgently need FCSs to rapidly charge their EVs.

On the other hand, charging a battery pack at a higher C−rate impacts its state of health, increasing the cell degradation rate, mainly due to thermal, mechanical, and lithium plating effects [12]. Thus, an increase in the charging current shortens the charging time but accelerates battery degradation. To mitigate this issue, an EV battery fast−charging strategy should be developed through the hybridization of non−complex and low−cost current fast−charging strategies, e.g., by means of controller implementation for C−rate regulation based on an onboard cell degradation diagnosis solution [12].

Among the EU−27 member states, only 338,191 charging points were installed in 2022, of which 27,000 were for ultra−fast and high−power charging. The total number of charging points is targeted to increase to 3.9 million by 2030, while the number of charging points needed at the same date is assessed at 7 million [13]. This highlights how the infrastructure for EV charging still has to be developed and realized in a large part in the coming years, thus allowing the implementation of solutions and strategies to mitigate the impact on EV batteries. This will make electric mobility more competitive with respect to other alternatives.

Therefore, the research directions for upgrading BEV technologies involve solving the charging problem of BEVs and improving their application convenience while ensuring safety during the life of electric vehicles [14].

To this aim, it is crucial to assess, from a quantitative point of view, the impact of charging current on battery capacity loss rate in a typical operating routine, i.e., in parity with the discharging profile and maximum depth of discharge.

Some papers provide battery aging models developed for several applications, generally applied to operating conditions assessed in relation to specific sizing and integration conditions. For instance, [15] focuses on a Li−ion battery pack, proposing a semiempirical electrothermal aging model that accounts for calendar and cycle aging at different C−rates and temperatures, also considering vehicle−to−grid (V2G) services. Nevertheless, the model does not take into account any experiment based on the actual operating BEV mode, such as the driving cycle. The authors of [16] estimate the state of health (SoH) of lithium–iron–phosphate (LFP) cells, analyzing the ohmic resistance and peak value of the incremental capacity. The authors of [17] present a dynamic model of Li−ion batteries based on the battery equivalent circuit, incorporating electrothermal and aging aspects for electric vehicles. Other noteworthy studies on Li−ion battery aging models and prediction methods for state−of−health estimation are illustrated in [18,19,20,21,22]. Nevertheless, the accuracy of these models is often low or requires a long computational time [12].

To address these drawbacks, the present paper proposes a different and innovative approach that considers the daily routine of EV batteries based on a standard driving cycle, including charging phases upon achieving a 90% depth of discharge (DoD). Different charging C−rates are considered. As a matter of fact, such a novel approach aims to fill the gap with the different approaches presented in the literature on battery aging and battery state of health assessment, having a significant impact on battery economy, as illustrated in [23,24,25,26,27,28,29]. Through dynamic modeling of the EV battery system, the state of charge (SoC) evolution is determined for different charging C−rates, considering both real discharging and charging current profiles. Finally, by applying a suitable post−processing procedure, aging test features are defined, each being related to a specific EV battery working mode, including charging at a particular C−rate, considering the global battery operation during its lifespan. This approach is innovative and more accurate with respect to the state of the art, i.e., battery aging models developed over standard test conditions not related to real operation modes, then applied to operating conditions typical of specific applications.

The followed procedure is described in the following sections. Specifically, Section 2 provides a background on the battery aging phenomena and the parameters used to evaluate degradation. Moreover, it discusses the methodology applied to determine the cumulative distribution of cycle number per DoD class based on the SoC evolution, aiming to assess battery cycle aging. Section 3 addresses EV battery modeling and simulation over defined working profiles, taking into account both real discharging and charging current profiles. Section 4 deals with the methodology applied to design the accelerated aging tests and describes the test rig, while Section 5 presents the obtained numerical and experimental results.

2. Battery Degradation Theory

Battery degradation rate depends on several stress factors, such as charging, discharging, time, temperature, and its current state of life [30]. Thus, this process is considered nonlinear with respect to time and stress cycles, complicating the analysis of test outcomes and the predictive modeling of the aging process.

2.1. Aging Phenomena

Phenomena that lead to battery degradation typically consist of calendar aging and cycle aging [31,32,33,34].

Calendar aging reveals the degradation over time during resting periods, whose rate is affected by the temperature and the battery state of charge (SoC). Calendar aging L_cal can be expressed in (1) as a function of the time t, the average SoC, and the cell temperature (Tc):

L_cal = f (t, SoC, Tc)

(1)

Cycle aging represents the life lost due to the battery charging/discharging cycles. Referring to the i−th cycle, the cycle aging L_cyc is a function of its depth of discharge (DoD), its average SoC (SoC_i), and the average cell temperature T_c,i. Each cycle is modeled as a single independent stress event, allowing the evaluation of the accumulated degradation as the sum of the capacity reduction produced by each cycle [35]. The cycle aging L_cyc can be then expressed as follows (2):

$$L_{cyc}={\sum }_{i=1}^N{z}_i\mathrm{f}(\mathrm{Do}{\mathrm{D}}_{\mathrm{i}},\mathrm{So}{\mathrm{C}}_{\mathrm{i}},{\mathrm{T}}_{\mathrm{c},\mathrm{i}})$$

(2)

where N corresponds to the identified number of cycles, and $z_i$ indicates whether cycle i is a full− or half−cycle and is used to include the rainflow cycle counting (RFC) algorithm.

Thus, calendar aging and cycle aging are linear degradation processes with respect to the number of cycles and battery aging, and L_b,tot can be expressed as the sum of these two contributions, as indicated by (3).

$$L_{b,tot}={\sum }_{i=1}^N{z}_i\mathrm{f}(\mathrm{Do}{\mathrm{D}}_{\mathrm{i}},\mathrm{So}{\mathrm{C}}_{\mathrm{i}},{\mathrm{T}}_{\mathrm{c},\mathrm{i}})+\mathrm{f}(\mathrm{t},\mathrm{SoC},\mathrm{Tc})$$

(3)

Moreover, it is highlighted that when all cycles are equal, the average temperature and SoC of a single cycle are the same as those of the entire operation; therefore, the temperature and SoC inputs of L_cal and L_cyc are the same.

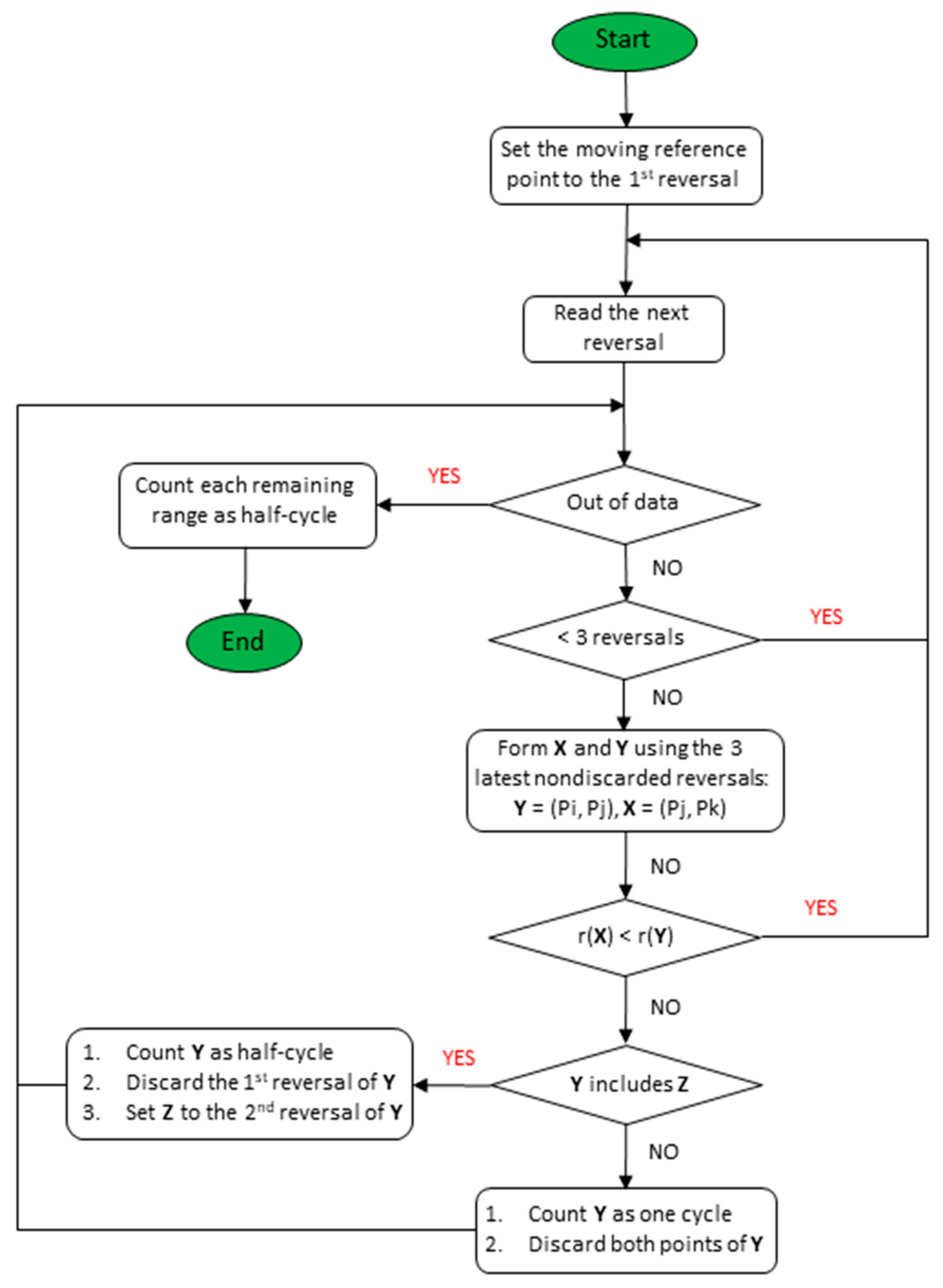
2.2. Rainflow Cycle Counting

This algorithm is widely used in material fatigue stress analysis to count cycles and quantify their depths. It has also been extensively applied to battery life assessment when subjected to complex charging/discharging cycles [36,37,38,39,40,41,42,43,44,45,46]. In fact, the damage accumulated in an object subjected to cyclical changes is studied by means of fatigue analysis since the number of cycles that break the considered object depends on the cycle amplitude [47].

The RFC method identifies cycles from local extrema in the load profile as a function of cycle amplitude. In Li−ion battery life estimation, SoC represents the load. A set of SoC−time curves is determined; then, the entire coordinate system is rotated 90 degrees clockwise, and the time coordinate axis is vertically downward [48]. The procedure is detailed according to [47].

Initially, RFC reduces the battery SoC history into a sequence of reversals. Reversals are defined as the local minima and maxima corresponding to the changed load sign. Each reversal is imagined as a source of water that “drips” down the roof.

RFC counts cycles by considering a moving reference point of the sequence, according to the ASTM standard [49], as described below:

• Count the number of half−cycles by looking for terminations in the flow occurring when either:
  • It reaches the end of the time history;
  • It merges with a flow that started at an earlier reversal;
  • It encounters a trough of greater magnitude.
• Assign a magnitude to each half−cycle corresponding to the stress difference between its start and termination.
• Pair up half−cycles of equal magnitude (but in opposite sense) to count the number of complete cycles. Generally, some residual half−cycles are present. Concerning Li−ion batteries, the most relevant cycles for degradation are those with more than 2% DoD [50]. Hence, the cycles at a lower DoD are not considered in this work. Figure 1 shows an example of RFC operation on a generic load time history.

It is evident from Figure 1 that E−F is counted as one cycle because its amplitude is completely within F−G. All the other segments are computed as half−cycles. For the sake of clarity, Figure 2 depicts the operating flow chart of the RFC algorithm according to the ASTM standard. The algorithm counts cycles by considering a moving reference point of the data sequence, Z, and a moving ordered three−point subset with the following characteristics:

• The first and second points are collectively called Y;
• The second and third points are collectively called X;
• In both X and Y, the points are sorted from earlier to later in time, although not necessarily consecutive;
• The range of X, denoted by r(X), corresponds to the absolute value of the difference between the amplitude of the first point and the amplitude of the second point. The range r(Y) is equally defined.

The RFC algorithm for the analysis presented in this work is customized by authors considering the cycle amplitude, a parameter that gives reliable results when applied to batteries. This is also experimentally validated by authors on LiFePO₄ cells, as reported in [44].

2.3. Battery State of Health

State of health (SOH) is a widely used index to estimate battery aging. It is defined as the capacity loss over a certain period because of calendar and cycle aging and can be expressed (in p.u.) as:

$$\mathrm{SOH}=\frac{Q_{max}}{Q_r}$$

(4)

where $Q_{max}$ is the maximum charge available of the battery at a certain period, and $Q_r$ is the rated capacity of the fresh cell.

Generally, Li−ion batteries for transport applications are considered at the end of life (EOL) when their capacity reaches 80% with respect to their initial rated capacity [51]. However, they can be reused in stationary applications for power smoothing, grid support, and storage. Such use is known as “second life”, and it is adopted to increase large−scale battery exploitation and reduce the environmental impact of the waste.

3. Dynamic Modeling

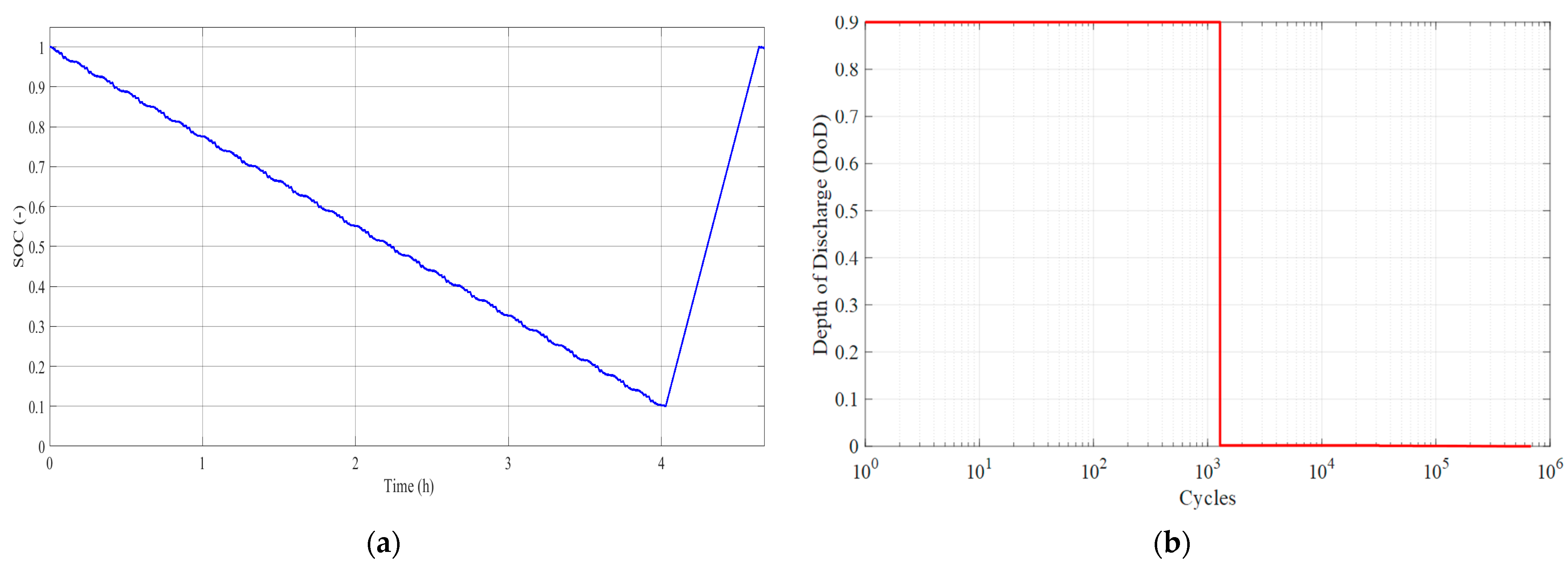
3.1. Input Data

To define the experimental procedure for the assessment of the Li−ion battery lifespan for battery electric vehicles (BEVs), the SC03 cycle has been selected, as reported in [20]. This cycle corresponds to a mileage of 5.763 km with a duration of about 600 s. Figure 3 shows the vehicle speed over time for the considered cycle and the corresponding battery current profile of the BEV, respectively.

3.2. Battery Modeling Description

To calculate the number of cycles through the RFC analysis, a dynamic model of the Li−ion battery of the considered BEV is realized. Specifically, the current profile of Figure 3b is used as input to the model to assess the battery SoC variation.

The dynamic model of a $Q$ (Ah) capacity battery was tuned by the authors of a previous research work [52]. Specifically, the open−circuit voltage ($V_{ocv}$) and the change in internal resistance ($R_{bat}^{int}$) during charging ($R_{int,ch}$) or discharge ($R_{int,dis}$) are used to determine battery behavior. Battery current ($I_{bat}$) and voltage ($V_{bat}$) can be expressed according to Equations (5) and (6):

$$I_{bat}=\frac{V_{ocv}-\sqrt{V_{ocv}^2-4R_{bat}^{int}P}}{2R_{bat}^{int}}$$

(5)

$$V_{bat}=V_{ocv}-R_{bat}^{int}{I}_{bat}$$

(6)

where $P$ is the power required/delivered to the battery, and

$$V_{ocv}=\left\{\begin{array}{c}{V}_{ocv,ch}=f_1\left({\mathrm{S}\mathrm{o}\mathrm{C}}_{ch}\right)\\ V_{ocv,dis}=f_2\left({\mathrm{S}\mathrm{o}\mathrm{C}}_{dis}\right)\end{array}\right.$$

(7)

$$R_{bat}^{int}=\left\{\begin{array}{c}{R}_{int,ch}=f_1\left({\mathrm{S}\mathrm{o}\mathrm{C}}_{ch}\right)\\ R_{int,dis}=f_2\left({\mathrm{S}\mathrm{o}\mathrm{C}}_{dis}\right)\end{array}\right.$$

(8)

The data from Equations (7) and (8) were experimentally determined by the authors and implemented in the model by using look−−up tables. The SoC and the battery voltage efficiency $\eta$ are instantaneously determined as follows (9):

$$\mathrm{S}\mathrm{o}\mathrm{C}={\mathrm{S}\mathrm{o}\mathrm{C}}_{ini}-\int \frac{\eta I_{bat}}{Q}dt$$

(9)

where $I_{bat}$ has a negative or positive sign during the charging/discharging process, respectively, and efficiency is determined as (10):

$$\eta =\left\{\begin{array}{c}{\eta }_{ch}=\frac{V_{ocv}}{V_{ocv}-I_{bat}{R}_{ch}}\\ {\eta }_{dis}=\frac{V_{ocv}-I_{bat}{R}_{dis}}{V_{ocv}}\end{array}\right.$$

(10)

where ${\mathrm{S}\mathrm{o}\mathrm{C}}_{ini}$ is the initial value of SoC, and Q (Ah) represents the battery capacity. The battery specifications refer to Renault ZoE [20]. Its nominal capacity corresponds to 22 kWh (55 Ah at 400 V). The ZoE battery is composed of two modules placed electrically in parallel. and each module is made up of 96 Li−−ion cells electrically connected in series. The DoD is set at 90%. Figure 4a depicts the measured open−−circuit voltages vs. the state of charge during charge and discharge for the studied Li−−ion cell, while Figure 4b illustrates the registered internal resistances vs. the state of charge during battery charge and discharge.

4. Experimental Activity: Materials and Methods

4.1. Aging Test Design

The experimental aging campaign was carried out on Panasonic NCR 18650 Li−ion batteries, typically employed in BEVs. The Panasonic NCR datasheet, listed in

Table 1. Main features of the considered Panasonic NCR 18650 Li−ion battery ([53]).

Parameter	Value
Nominal voltage	3.6 V
Nominal capacity (at 25 °C)	3350 mAh (typical)
Weight	47.5 g
Max discharge C−rate	2C
Max charge C−rate	0.7C
Voltage operating range	2.5 V–4.2 V

, is detailed in [53]. The maximum continuous discharge/charge currents are, respectively, 2C and 0.7C.

The aging procedure is sequentially designed as follows:

• Initial Battery Capacity Determination (BCD).
• Galvanostatic charge/discharge cycling was repeated 30 times up to 150 cycles and subsequently repeated 75 times up to 300 cycles. Every 30 cycles (until the battery reaches 150 cycles), BCD was performed to assess the capacity fade due to cycle aging. Subsequently, when the cell exceeded 150 cycles, BCD was carried out every 75 aging cycles until the battery reached the maximum number of aging cycles allowed by the manufacturer. The restricted cycling range of up to 150 cycles was chosen since the first aging cycles did not follow a linear relation with capacity fading.

BCD was performed by fixing the C−rate at 0.5C (corresponding to a current of 1.7 A) both in charge and discharge. A voltage range of 2.5−4.2 V was fixed, and the resting time between charge and discharge was 5 min. Furthermore, the charge was carried out as a constant current (CC) followed by a constant voltage (CV) process, maintaining the voltage during CV at 4.2 V until the cut−off current of 65 mA was reached. The cycling tests were realized by varying the charging C−rate while the discharge C−rate was fixed equal to 2C. The latter was chosen since it corresponded to the battery’s required current peak value over the considered driving cycle.

Specifically, two NCR cells were tested at 0.3C and 0.7C. These values correspond to a charge power of 22 kW (considering a three−phase AC urban charging column) and 50 kW (i.e., a DC fast−charging column), respectively.

The maximum number of cycles was fixed at 300 since the cell SOH exceeded the 80% threshold value, as presented in the aging tests performed by the manufacturer [53].

4.2. Experimental Section

This section illustrates the test rig and instrumentation used for the aging tests. Figure 5 depicts the battery test rig. The instruments to realize the aging tests were purchased from BioLogic^®. In detail, the galvanostat/potentiostat BioLogic SP−240 and its external booster HCV−3048 were used to perform the experiments.

5. Results and Discussion

5.1. Simulation and Rainflow Cycle Counting

The Renault ZoE battery was simulated through the implemented dynamic model described in Section 3.2. Figure 6 depicts the SoC variation over the chosen driving cycle of Figure 3a. It was assumed that the BEV starts with a fully charged battery (SoC equal to 1). Specifically, the simulation was performed by repeating the driving cycle since the battery SoC reached its minimum value (i.e., 0.1). Subsequently, the battery was completely charged to restore the initial condition. According to battery specifications (22 kWh as nominal capacity), the BEV can travel up to 160 km since the driving cycle was repeated 28 times.

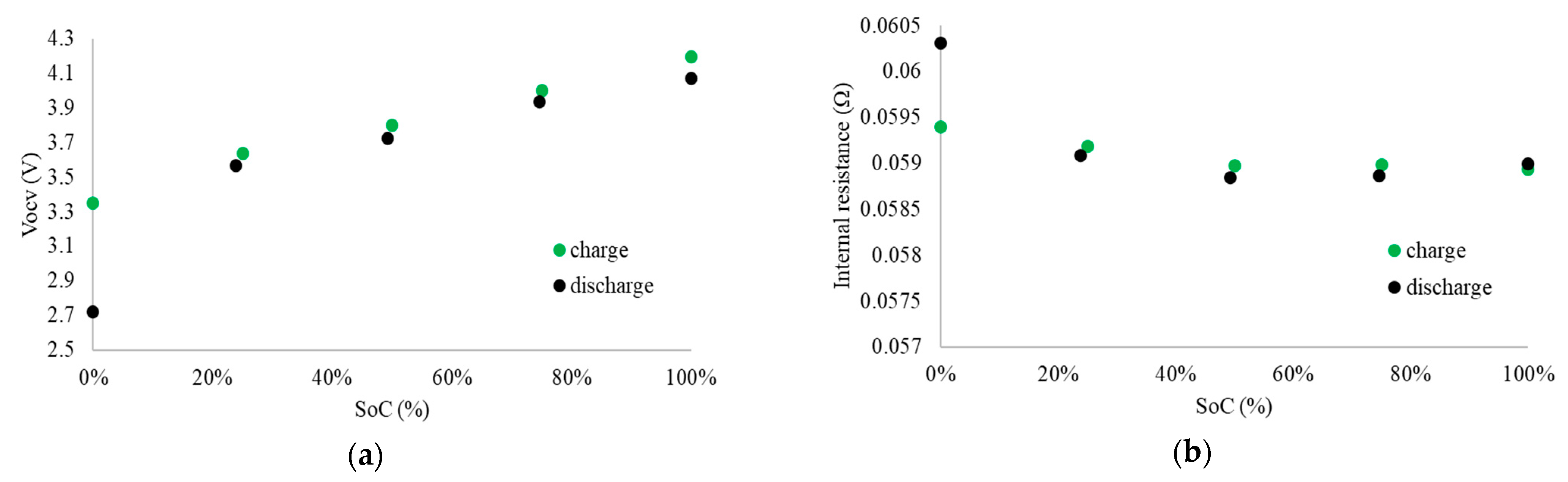
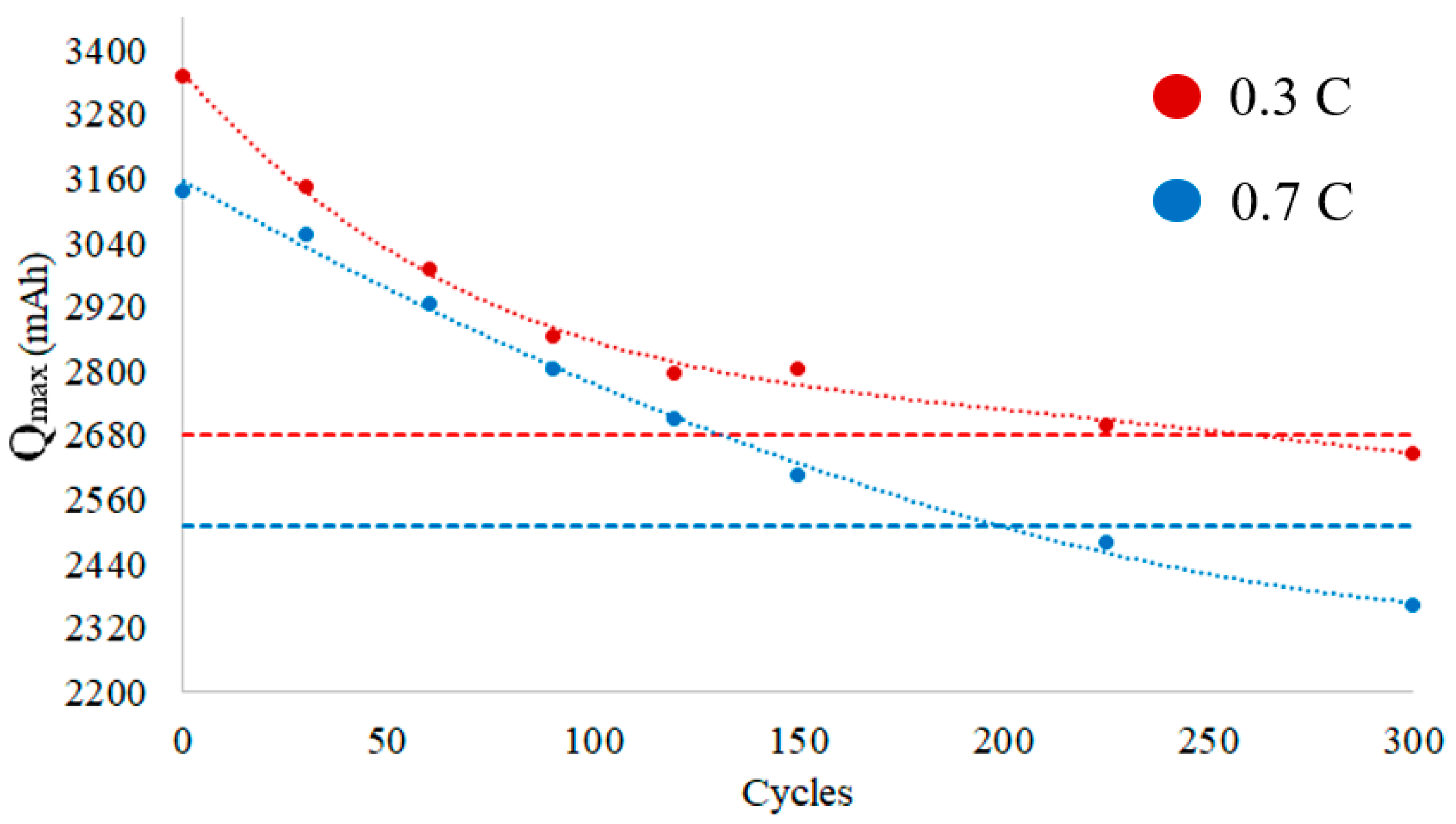
5.2. Experimental Results

As regards the experimental results to assess the battery life reduction when cycled at different C−rates (i.e., 0.3C and 0.7C, corresponding to 22 kW AC three−phase and DC fast−charging columns, respectively), the voltage and current trends over time are illustrated in Figure 7 and Figure 8 in reference to the 0.3C and 0.7C charging rates, respectively. It is shown that the voltage trend varies within the allowable range (i.e., from 2.5 V to 4.2 V, as suggested by the Li−ion cell manufacturer). According to the experimental campaign described in Section 4.2, battery capacity was measured for the fresh cell every 30 aging cycles until the battery reached 150 cycles. This was performed since the first aging cycles do not follow a linear relation with the capacity fading. Subsequently, battery capacity determination was performed every 75 cycles until the cell reached its end of life (300 cycles, as reported in the manufacturer’s datasheet).

Figure 9 illustrates the measured data in terms of the time variation of the battery maximum capacity ($Q_{max}\mathrm{i}\mathrm{n}\mathrm{E}\mathrm{q}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\left(4\right))$ for both experiments on NCR cells.

For both cells, SOH variation over time can be assessed according to Equation (4), dividing $Q_{max}$ by Q_r, i.e., the rated capacity of each fresh cell. Specifically, the red dotted line corresponds to the 80% SOH of the cell cycled at the 0.3 C−rate in the charging phase. The blue dotted line identifies the 80% SOH condition for the cell cycled at the 0.7 charging C−rate. It is emphasized that the results obtained from the experimental tests are in line with those presented in the NCR battery datasheet, although they refer to different cycling conditions, as indicated in [53]. Since the EOL for BEV batteries is identified at 80% SOH, it is evident that the NCR cell can last for about 210 cycles when charged at 0.7C (i.e., 2510 mAh of remaining useful capacity). On the other hand, by reducing the C−rate to 0.3C, the battery reaches 255 cycles (i.e., a remaining useful capacity of 2680 mAh).

Therefore, in parity with discharge rate (2C), it is highlighted that fast−charging cycles at 50 kW reduce the battery lifespan by about 17% with respect to the charge in a 22 kW three−phase AC column.

6. Conclusions

In the coming years, massive penetration of battery electric vehicles is expected. Since BEVs have a limited mileage range and the current charging columns require a long time to charge the vehicle, fast−charging stations are needed. Nevertheless, increasing the charging power contributes to reducing the battery pack lifespan.

To quantify such a reduction, this research work aimed to investigate the effect of different charge rates on NCR cells through experimental aging tests. The main contributions are the following:

• A dynamic battery model was developed to obtain the SoC variation over the considered driving cycle.
• A customized rainflow cycle counting algorithm was applied to the SoC profile to identify the DoD of each cycle for subsequent implementation on the experimental test rig.
• Galvanostatic charge/discharge cycling interspersed by battery capacity determination was carried out for two NCR cells, emulating the BEV charge at 22 kW and 50 kW, respectively.
• The experimentally obtained results are in line with the aging performed by the manufacturer.
• A battery lifespan reduction of about 17% is registered when the cell is discharged at a higher C−rate (i.e., 0.7C with respect to 0.3C).

Thus, this work can provide deep insight into the expected massive penetration of electric vehicles, providing an estimate of battery useful life based on users’ charging conditions.