Smart Sag Detection and Reactive Current Injection Control for a PV Microgrid under Voltage Faults
Abstract
:1. Introduction
- The NN control model effectively processes grid voltage data to accurately detect voltage sags and extract their distinctive characteristics. This initial feature ensures a comprehensive understanding of sag events.
- Subsequently, the NN model leverages this sag information to provide vital grid support through the precise injection of reactive current in compliance with grid code stipulations.
2. System Configuration and Modelling
2.1. PV Module’s Equivalent Circuit
2.2. Size of PV Array and MPPT
2.3. Control Strategy for Microgrid System
2.3.1. DC Boost Converter Control
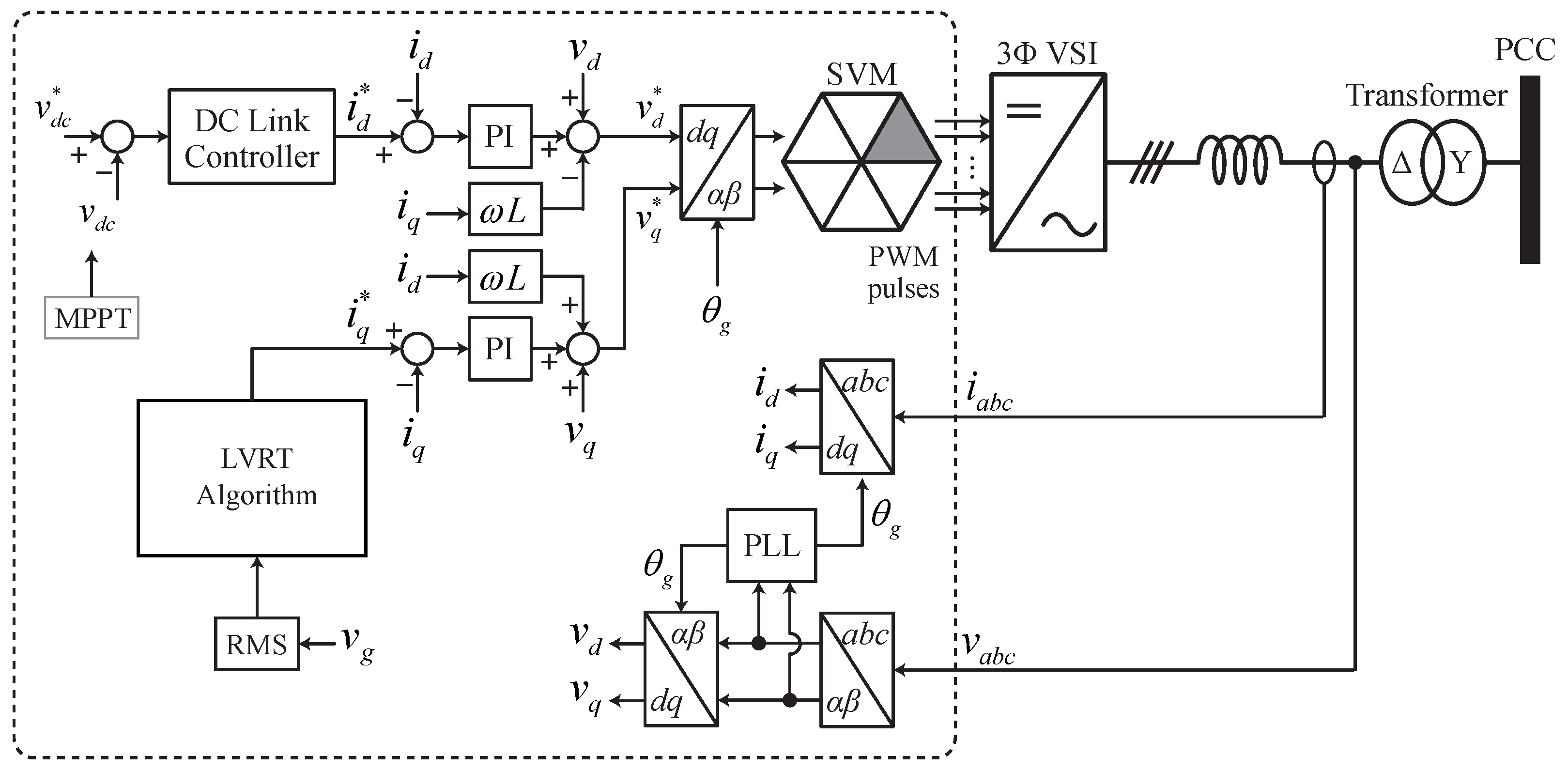
2.3.2. Control of the VSI
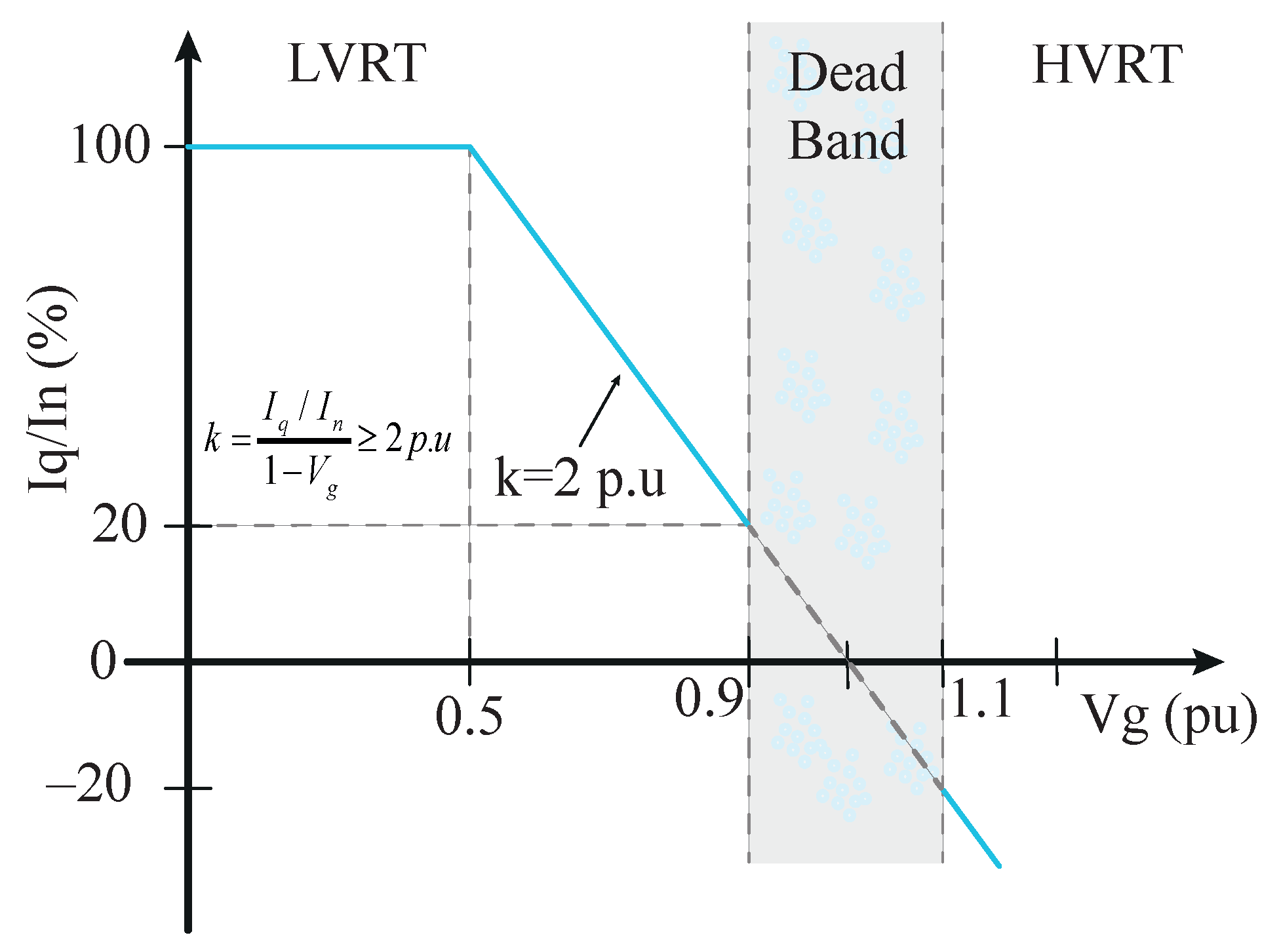
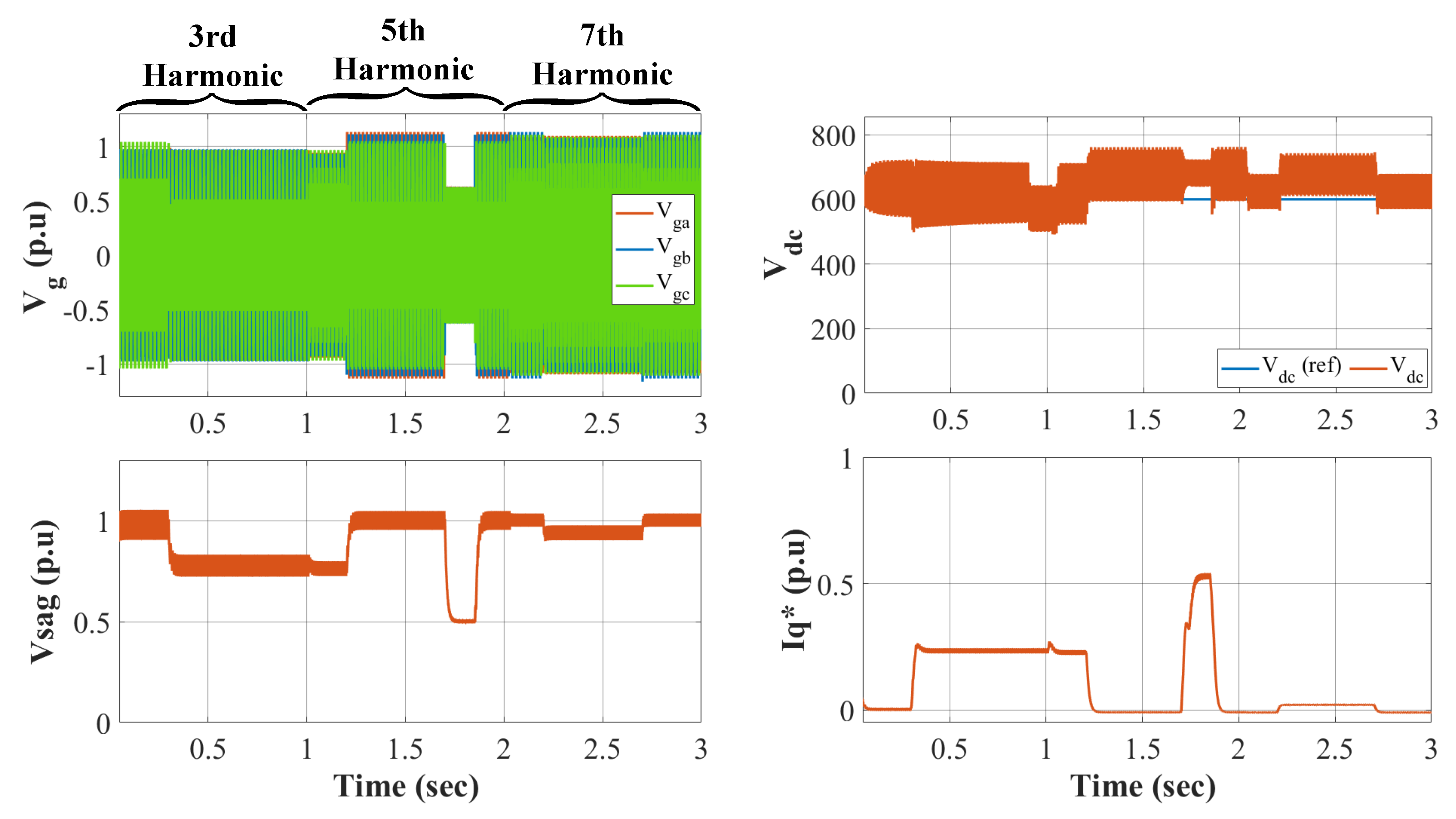
3. Ability of Low-Voltage Ride Through (LVRT)
3.1. Method of Fault Detection
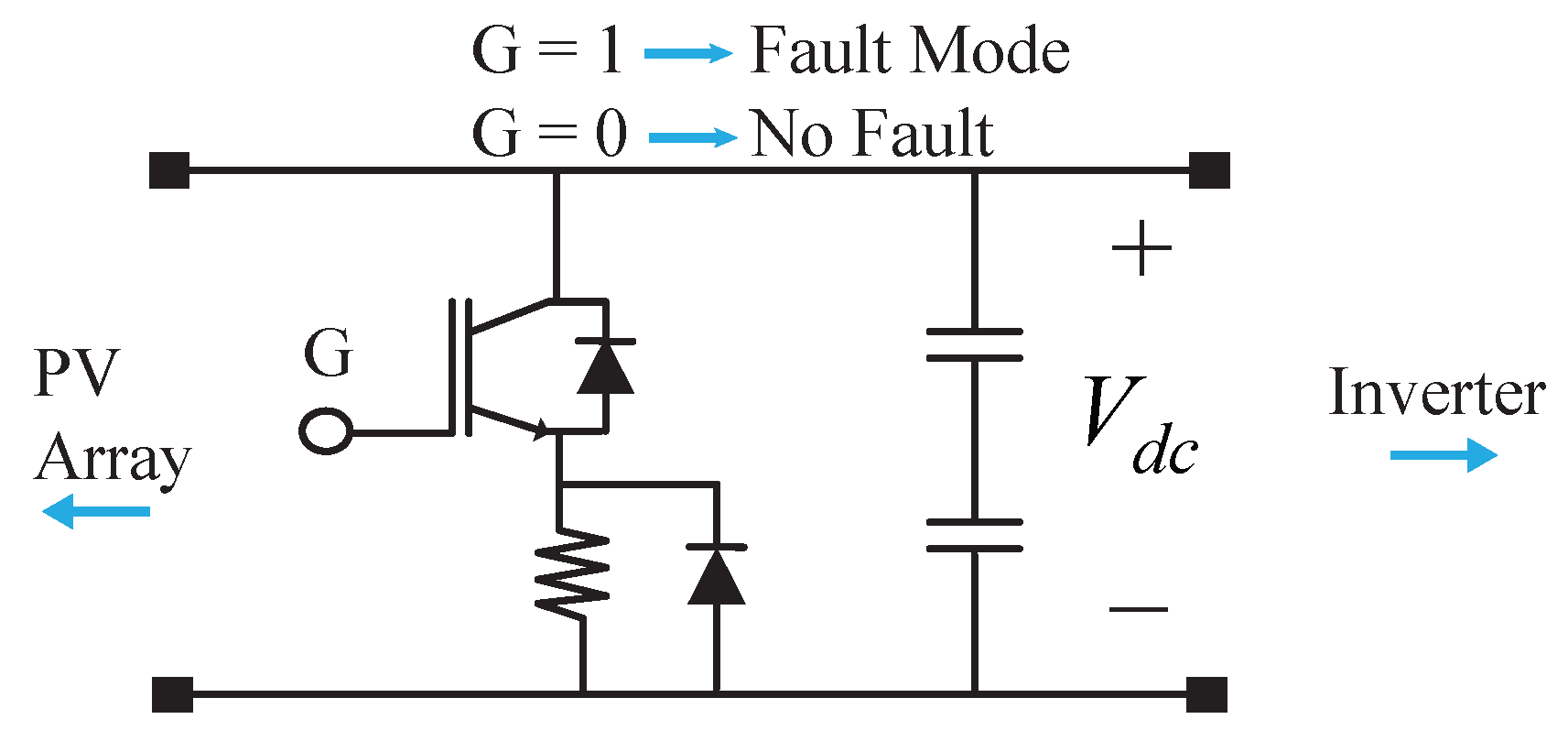
3.2. Control of DC Over-Voltage
3.3. Limiting of Excessive AC Current
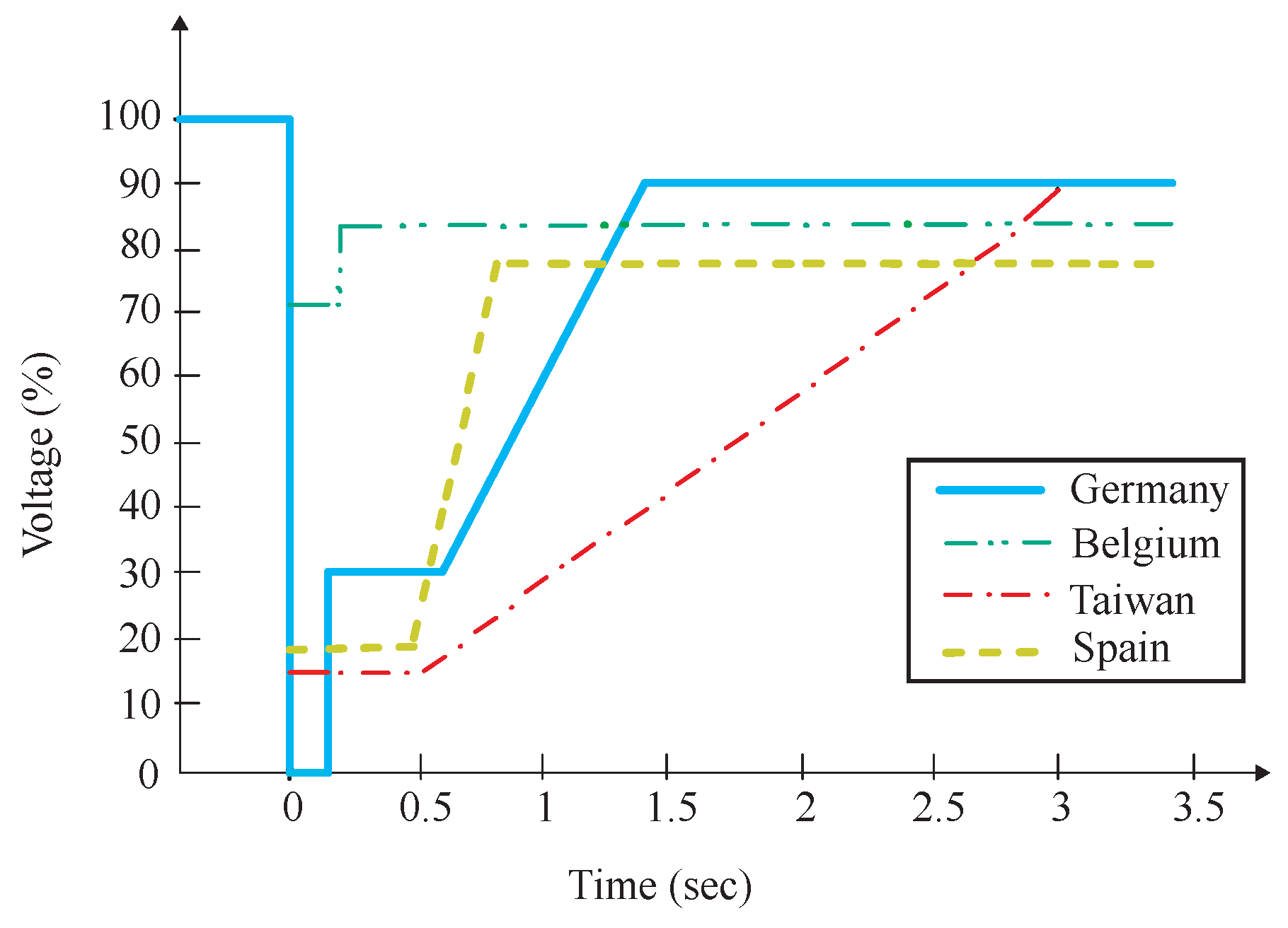
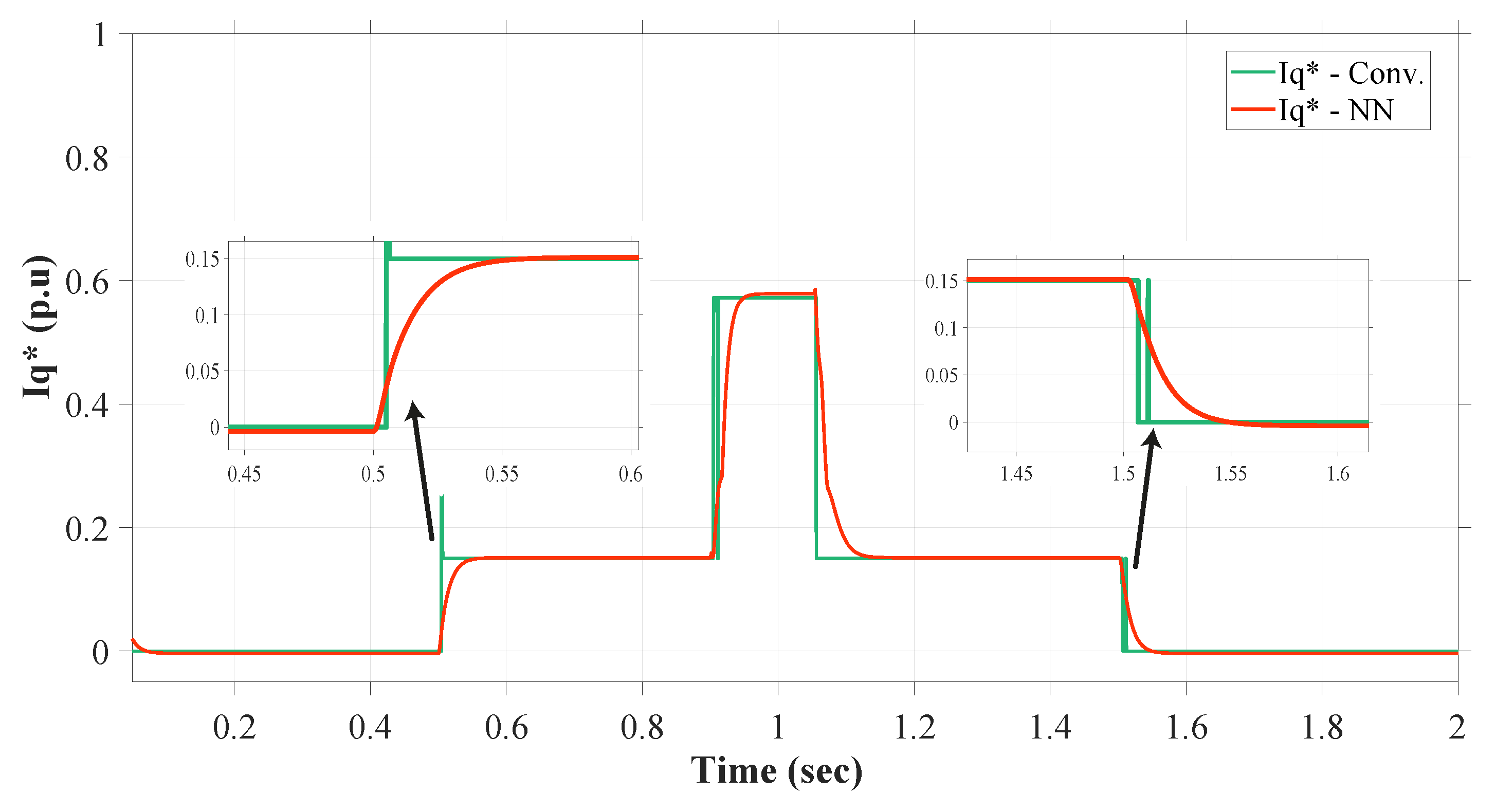
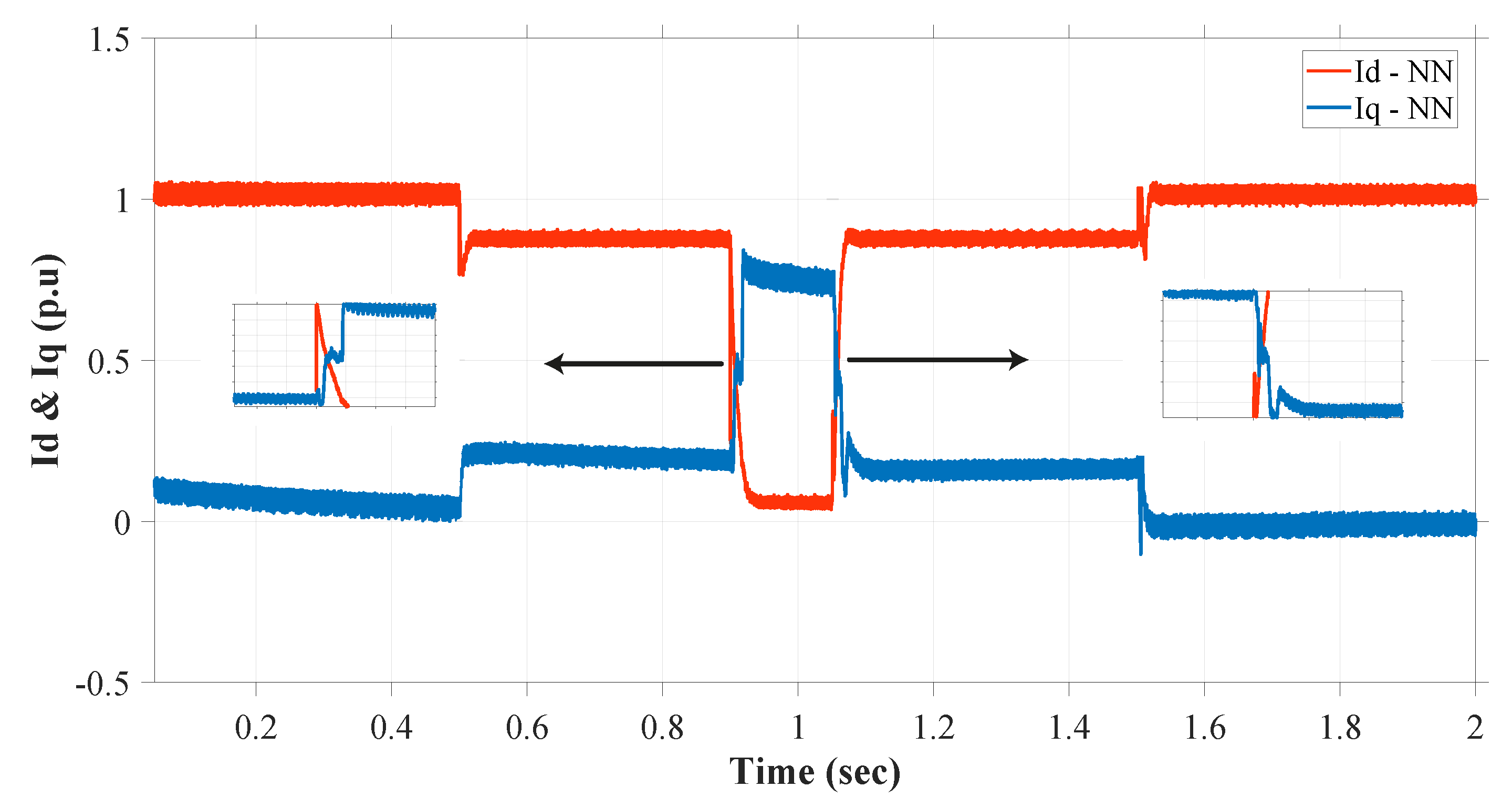
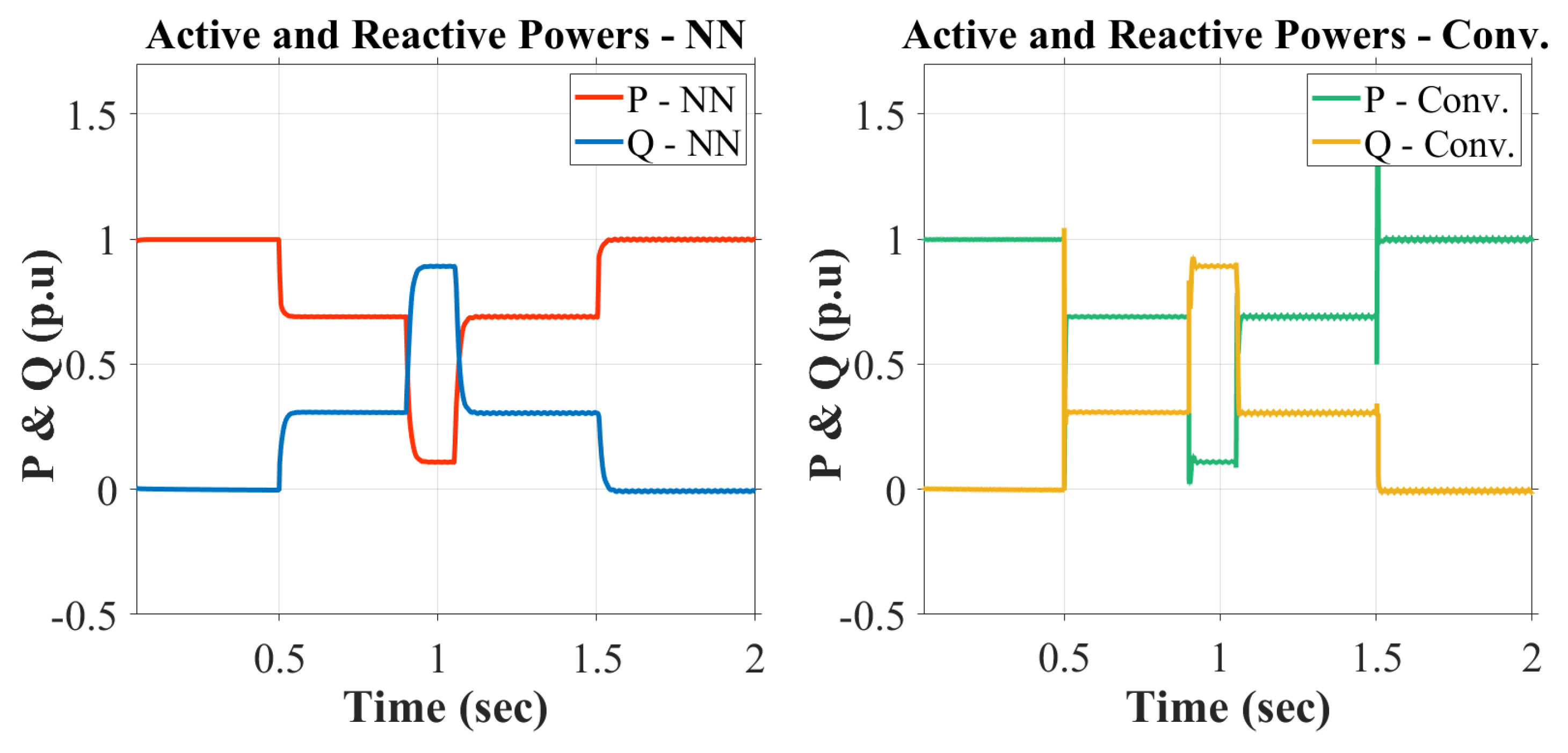
3.4. Reactive Current Injection
4. Proposed NN Controller
- Data Collection and Preprocessing: The initial step in building a neural network model, involves gathering voltage, current, and relevant parameter data from the grid system, cleaning and formatting it, and then normalizing or scaling to ensure consistent input. This process also encompasses selecting pertinent features, engineering new ones, and addressing imbalances if necessary. By organizing and enhancing the dataset, the neural network can better understand and learn from the data, ultimately leading to a more accurate and reliable model for detecting grid faults and predicting required reactive current injection.
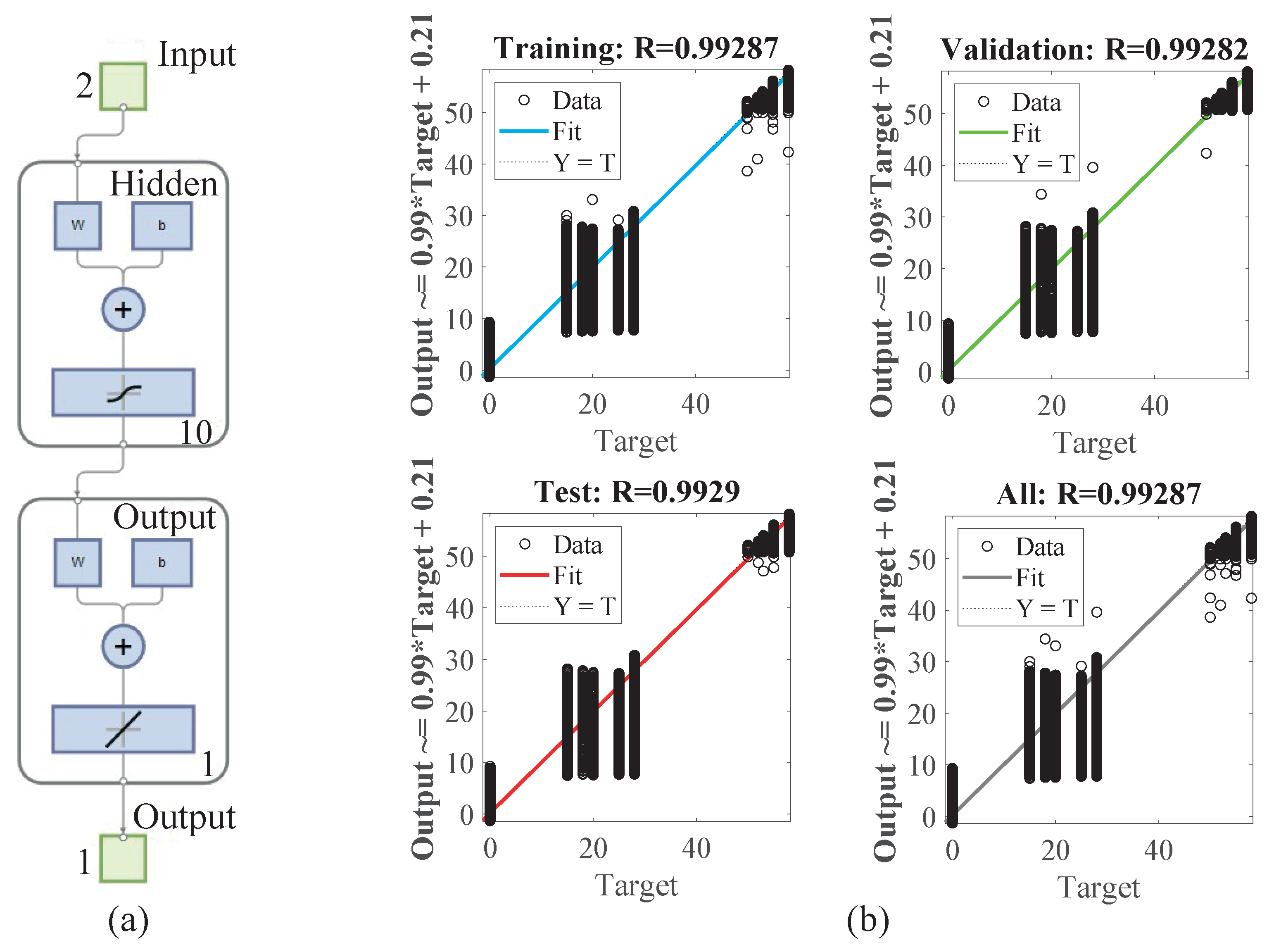
- NN Architecture: The second step involves labeling the collected data, distinguishing between grid fault instances labeled as “fault” and normal operation as “normal”. Then, the dataset is divided into distinct training, validation, and testing subsets to facilitate model training and evaluation. Finally, the architecture of the NN is designed (Figure 10a), encompassing multiple layers for input with 2 neurons (voltage and/or current), hidden layers with 10 neurons for feature extraction, and output layer with 1 neuron for fault detection and reactive current prediction. This architecture is structured to capture intricate relationships in the data and enable the network to perform the dual functions of detecting grid faults and predicting the requisite reactive current.

- Training and Evaluation: In the third step, the designed neural network (NN) is trained using the labeled training dataset, with a focus on developing an accurate loss function that considers fault detection accuracy and reactive current prediction. The NN’s weights are adjusted through back-propagation [32], and its performance is monitored using the validation set to prevent overfitting. After evaluating the trained neural network’s performance standards, achieving high accuracy entails the correlation coefficient (R) approaching a value of 1 [33], while minimizing the mean squared error (MSE) to approach a value close to 0. Next, the trained NN is rigorously evaluated using the separate testing dataset. This involves calculating performance metrics like accuracy, precision, recall, and mean absolute error (Figure 11a) for both fault detection and reactive current prediction. The evaluation results (Figure 10b and Figure 11b) offer insights into the model’s proficiency in simultaneously detecting grid faults and accurately predicting the reactive current required for stabilization.

- Integration into the Grid system: In the final step, the trained NN is integrated into the actual grid system, continuously gathering real-time voltage and current data. Then, the NN is utilized to predict grid fault occurrences and reactive current injection needs based on real-time data, thus enabling timely response to grid anomalies. After that, the model’s performance is monitored and refined as needed, ensuring its reliability and effectiveness over time. Eventually, it is confirmed that the NN’s reactive current injection complies with specified grid codes and regulations, ensuring that the predictions align with the required standards and maintaining grid stability and safety.
NN-Based Control
5. Results
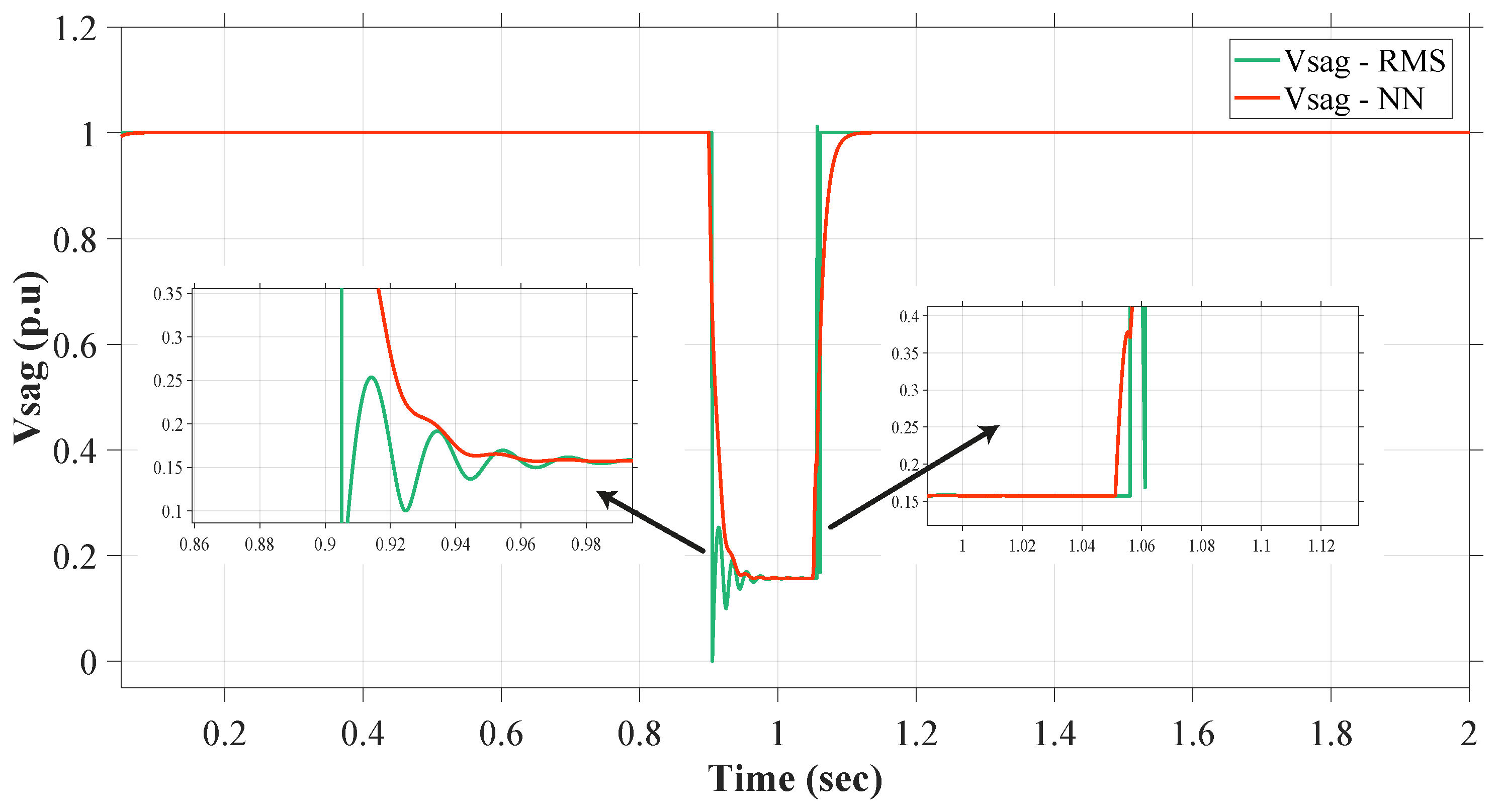
5.1. Case 1
5.2. Case 2
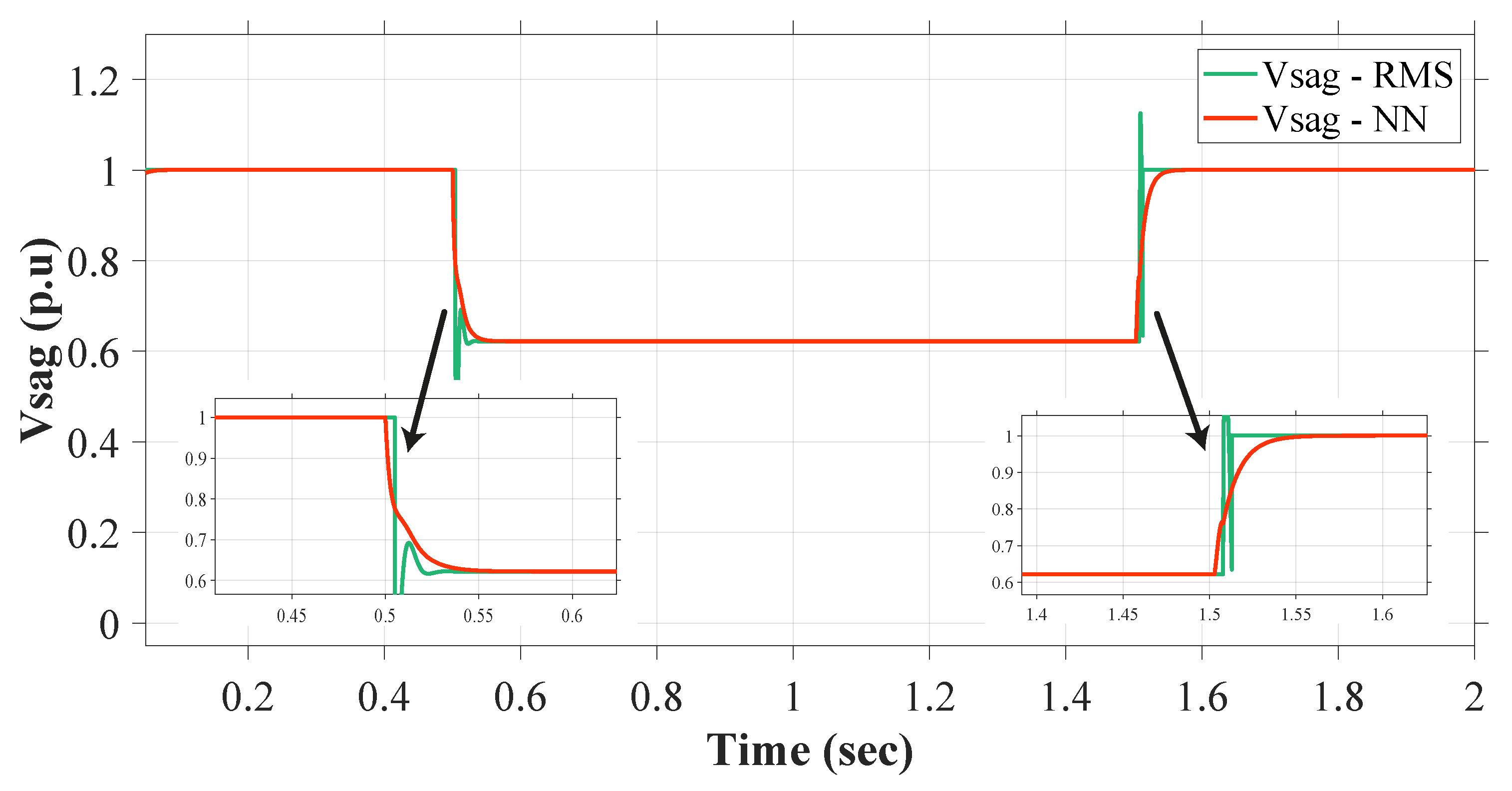
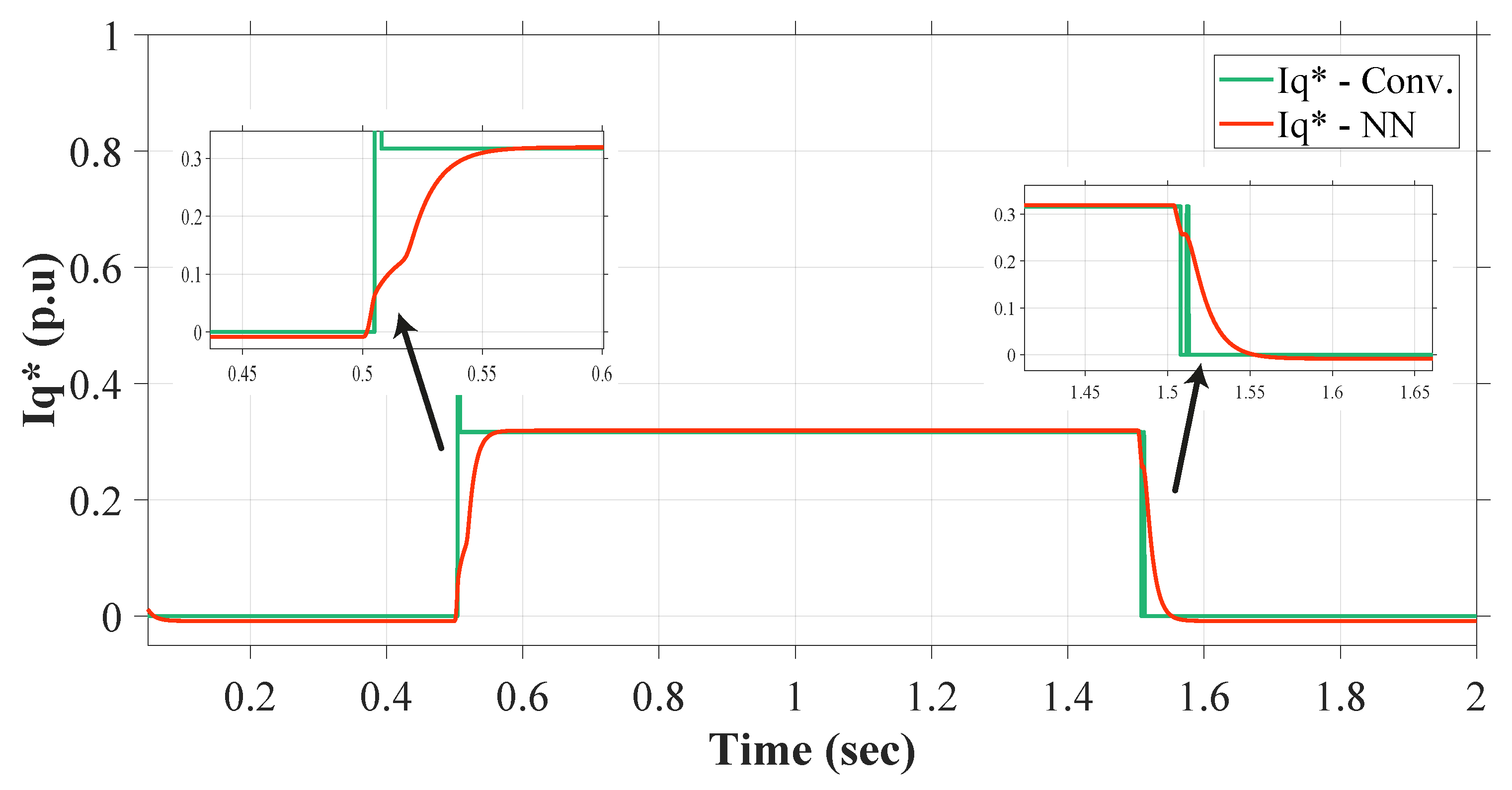
5.3. Case 3
5.4. Case 4
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GCPV | Grid-Connected Photovoltaic System |
| LVRT | Low-Voltage Ride Through |
| NN | Neural Network |
| RMS | Root Mean Square |
| DG | Distributed Generation |
| MPP | Maximum Power Point |
| PCC | Point of Common Coupling |
| PR | Proportional Resonant |
| PLL | Phase-Locked Loop |
| FCL | Fault-Current Limiters |
| CSS | Current Saturation Strategy |
| PSO | Partical Swarm Optimization |
| P&O | Perturb and Observe |
| VSI | Voltage Source Inverter |
| SRF | Synchronous Reference Frame |
| ANN | Artificial Neural Network |
| MSE | Mean Squared Error |
References
- Joshi, J.; Swami, A.; Jately, V.; Azzopardi, B. A comprehensive review of control strategies to overcome challenges during LVRT in PV systems. IEEE Access 2021, 9, 121804–121834. [Google Scholar] [CrossRef]
- Tang, C.; Chen, Y.; Chen, Y. PV power system With multi-mode operation and low-voltage ride-through capability. IEEE Trans. Ind. Electron. 2015, 62, 7524–7533. [Google Scholar] [CrossRef]
- Shetwi, A.; Sujod, M.; Blaabjerg, F. Low voltage ride-through capability control for single-stage inverter-based grid-connected photovoltaic power plant. Sol. Energy 2018, 159, 665–681. [Google Scholar] [CrossRef]
- Peter, M.; Ramon, Z.; Tek-Tjing, L. The role of inertia for grid flexibility under high penetration of variable renewables—A review of challenges and solutions. Renew. Sustain. Energy Rev. 2021, 147, 111223. [Google Scholar]
- Ding, G.; Gao, F.; Tian, H.; Ma, C.; Chen, M.; He, G.; Liu, Y. Adaptive DC-link voltage control of two-stage photovoltaic inverter during low voltage ride-through operation. IEEE Trans. Power Electron. 2016, 31, 4182–4194. [Google Scholar] [CrossRef]
- Zeng, D.; Guo, J.; Ding, M.; Geng, D. Fault ride-through capability enhancement by ADAPATIVE Voltage Support Control for inverter interfaced distributed generation. In Proceedings of the 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Changsha, China, 26–29 November 2015. [Google Scholar]
- Miret, J.; Castilla, M.; Camacho, A.; Vicuña, L.G.; Matas, J. Control scheme for photovoltaic three-phase inverters to minimize peak currents during unbalanced grid-voltage sags. IEEE Trans. Power Electron. 2012, 27, 4262–4271. [Google Scholar] [CrossRef]
- Yang, Y.; Blaabjerg, F.; Zou, Z. Benchmarking of Grid Fault modes in single-phase grid-connected photovoltaic systems. IEEE Trans. Ind. Appl. 2013, 49, 2167–2176. [Google Scholar] [CrossRef]
- Vasquez, J.C.; Mastromauro, R.A.; Guerrero, J.M.; Liserre, M. Voltage support provided by a droop-controlled multifunctional inverter. IEEE Trans. Ind. Electron. 2009, 56, 4510–4519. [Google Scholar] [CrossRef]
- Ding, K.; Cheng, K.W.E.; Xue, X.D.; Divakar, B.P.; Xu, C.D.; Che, Y.B.; Wang, D.H.; Dong, P. A novel detection method for voltage sags. In Proceedings of the 2nd International Conference on Power Electronics Systems and Applications, Hong Kong, China, 12–14 November 2006. [Google Scholar]
- Silvestre, S.; Chouder, A.; Karatepe, E. Automatic fault detection in Grid Connected PV systems. Sol. Energy 2013, 94, 119–127. [Google Scholar] [CrossRef]
- Naderi, S.; Negnevitsky, M.; Muttaqi, K. A Modified DC Chopper for Limiting the Fault Current and Controlling the DC-Link Voltage to Enhance Fault Ride-Through Capability of Doubly-Fed Induction-Generator-Based Wind Turbine. IEEE Trans. Ind. Appl. 2019, 55, 2021–2032. [Google Scholar] [CrossRef]
- Al-Durra, A.; Fayyad, Y.; Muyeen, S.; Blaabjerg, F. Fault Ride-through of a Grid-connected Photovoltaic System with Quasi Z Source Inverter. Electr. Power Components Syst. 2016, 44, 1786–1800. [Google Scholar] [CrossRef]
- Islam, M.; Muttaqi, K.; Sutanto, D. A Novel Saturated Amorphous Alloy Core Based Fault Current Limiter for Improving the Low Voltage Ride Through Capability of Doubly-Fed Induction Generator Based Wind Turbines. IEEE Trans. Ind. Appl. 2021, 57, 2023–2034. [Google Scholar] [CrossRef]
- Ramirez, D.; Martinez, S.; Platero, C.; Blazquez, F.; de Castro, R. Low-Voltage Ride-Through Capability for Wind Generators Based on Dynamic Voltage Restorers. IEEE Trans. Energy Convers. 2011, 26, 195–203. [Google Scholar] [CrossRef]
- Döşoğlu, M.; Basa Arsoy, A.; Güvenç, U. Application of STATCOM-supercapacitor for low-voltage ride-through capability in DFIG-based wind farm. Neural Comput. Appl. 2016, 28, 2665–2674. [Google Scholar] [CrossRef]
- Pal, A.; Pal, D.; Panigrahi, B.J. A Current Saturation Strategy for Enhancing the Low Voltage Ride-Through Capability of Grid-Forming Inverters. IEEE Trans. Circuits Syst. 2023, 70, 1009–1013. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, X.; Qin, C.; Xing, X.; Chen, Z. Improved Particle Swarm Optimization Based Selective Harmonic Elimination and Neutral Point Balance Control for Three-Level Inverter in Low-Voltage Ride-Through Operation. IEEE Trans. Ind. Inform. 2022, 18, 642–652. [Google Scholar] [CrossRef]
- Fu, X.; Li, S.; Fairbank, M.; Wunsch, D.C.; Alonso, E. Training Recurrent Neural Networks With the Levenberg–Marquardt Algorithm for Optimal Control of a Grid-Connected Converter. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1900–1912. [Google Scholar] [CrossRef]
- Hussain, A.; Sher, H.A.; Murtaza, A.H.; Al-Hadeed, K. Improved Voltage Controlled Three Phase Voltage Source Inverter Using Model Predictive Control for Standalone System. In Proceedings of the IECON (2018)-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018. [Google Scholar]
- Al-Shetwi, A.; Muhamad Zahim, S. Modeling and simulation of photovoltaic module with enhanced perturb and observe MPPT algorithm using Matlab/Simulink. ARPN J. Eng. Appl. Sci. 2016, 11, 12033–12038. [Google Scholar]
- Villalva, M.; Gazoli, J.; Filho, E. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Saravanan, S.; Ramesh Babu, N. Maximum power point tracking algorithms for photovoltaic system—A review. Renew. Sustain. Energy Rev. 2016, 57, 192–204. [Google Scholar] [CrossRef]
- Durusu, A.; Nakir, I.; Ajder, A.; Ayaz, R.; Akca, H.; Tanrioven, M. Performance Comparison of Widely-Used Maximum Power Point Tracker Algorithms under Real Environmental Conditions. Adv. Electr. Comput. Eng. 2014, 14, 89–94. [Google Scholar] [CrossRef]
- Usama, M.; Kim, J. Low-speed transient and steady-state performance analysis of IPMSM for nonlinear speed regulator with effective compensation scheme. Energies 2021, 14, 6679. [Google Scholar] [CrossRef]
- Usama, M.; Jaehong, K. Simplified model predicted current control method for speed control of non-silent permanent magnet synchronous motors. In Proceedings of the 3rd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 29–30 January 2020. [Google Scholar]
- Azit, A.; Sulaiman, S.; Hussein, Z.; Balakhrisnan, M.; Busrah, A.; Devaraju, P.; Mohamed, A.; Kumaran, R.; Ramasami, A.; Ismail, M. TNB Technical Guidebook on Grid-Interconnection of Photovoltaic Power Generation System to LV and MV Networks; Tenaga Nasional Berhad: Kuala Lumpur, Malaysia, 2012; pp. 1–38. [Google Scholar]
- Saeedul Islam, G.M.; Al-Durra, A.; Muyeen, S.M.; Tamura, J. Low voltage ride through capability enhancement of grid connected large scale photovoltaic system. In Proceedings of the IECON-37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011. [Google Scholar]
- Pannell, G.; Zahawi, B.; Atkinson, D.J.; Missailidis, P. Evaluation of the performance of a DC-link brake chopper as a DFIG low-voltage fault-ride-through device. IEEE Trans. Energy Convers. 2013, 28, 535–542. [Google Scholar] [CrossRef]
- Neumann, T.; Erlich, I. Modelling and control of photovoltaic inverter systems with respect to German grid code requirements. In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Hassan, Z.; Amir, A.; Selvaraj, J.; Rahim, N.A. A review on current injection techniques for low-voltage ride-through and grid fault conditions in grid-connected photovoltaic system. In Solar Energy; Elsevier: Amsterdam, The Netherlands, 2020; pp. 851–873. [Google Scholar]
- Akpolat, A.N.; Habibi, M.R.; Baghaee, H.R.; Dursun, E.; Kuzucuoglu, A.E.; Yang, Y.; Dragicevic, T.; Blaabjerg, F. Dynamic Stabilization of DC Microgrids Using ANN-Based Model Predictive Control. IEEE Trans. Energy Convers. 2022, 37, 999–1010. [Google Scholar] [CrossRef]
- Okwako, O.E.; Lin, Z.; Xin, M.; Premkumar, K.; Rodgers, A.J. Neural Network Controlled Solar PV Battery Powered Unified Power Quality Conditioner for Grid Connected Operation. Energies 2022, 15, 6825. [Google Scholar] [CrossRef]











| Parameters | Values |
|---|---|
| Max. power voltage | = 29 V |
| Max. power | = 213.15 W |
| Short-circuit current | = 7.84 A |
| Temp. coefficient of | = −0.367/C |
| Max. power current | = 7.35 A |
| Open-circuit voltage | = 36.3 V |
| Cells per module | = 60 |
| Temp. coefficient of | = 0.102/C |
| Parameters | Values |
|---|---|
| Grid voltage | = 25 kV |
| Grid frequency | = 50 Hz |
| DC-link voltage | = 600 V |
| resistance of filter | = 1.25 |
| inductance of filter | = 2.5 mH |
| Current loop PI | = 0.3, = 200 |
| Voltage loop PI | = 2, = 400 |
| transformer | 0.38/25 kV, 50 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, M.A.; Kim, J. Smart Sag Detection and Reactive Current Injection Control for a PV Microgrid under Voltage Faults. Energies 2023, 16, 6776. https://doi.org/10.3390/en16196776
Khan MA, Kim J. Smart Sag Detection and Reactive Current Injection Control for a PV Microgrid under Voltage Faults. Energies. 2023; 16(19):6776. https://doi.org/10.3390/en16196776
Chicago/Turabian StyleKhan, Muhammad Affan, and Jaehong Kim. 2023. "Smart Sag Detection and Reactive Current Injection Control for a PV Microgrid under Voltage Faults" Energies 16, no. 19: 6776. https://doi.org/10.3390/en16196776
APA StyleKhan, M. A., & Kim, J. (2023). Smart Sag Detection and Reactive Current Injection Control for a PV Microgrid under Voltage Faults. Energies, 16(19), 6776. https://doi.org/10.3390/en16196776







