Mechanical Ventilation Heat Recovery Modelling for AccuRate Home—A Benchmark Tool for Whole House Energy Rating in Australia
Abstract
:1. Introduction
- (1)
- With coupled mass and heat transfer theory, a model is developed to simulate mass and heat transfer of the bathroom ventilation system with heat recovery during and after showers;
- (2)
- The model is coded and implemented into the Chenath engine to evaluate it under the operation of the bathroom only and for the whole house;
- (3)
- With the updated Chenath engine, the effects of heat recovery mechanical ventilation on energy star rating are analysed under various operation conditions;
- (4)
- The maximum potential heat recovery energy is investigated under different climate zones.
2. Heat Recovery Model
2.1. Bathroom Heat Recovery Model
- (1)
- The bathroom air is mixed perfectly (i.e., incoming air instantly and uniformly mixes with the existing air in the bathroom);
- (2)
- After heat and mass transfer, the thermal performance of the mixed air can achieve uniformity immediately;
- (3)
- The temperature of the hot water on the base floor is assumed to be constant during the shower.
2.2. Kitchen Heat Recovery Model
2.3. Daily Space Heating Heat Recovery Model
- (1)
- The building recovery energy, including the energy recovery from the bathroom and kitchen, is used to pre-heat the supplied fresh air;
- (2)
- The total fresh airflow rate is assumed to be equal to the total exhaust air at the current calculating step;
- (3)
- The fresh air requirement for each conditioned zone is calculated based on its volume under the air change rate.
3. Case Study
3.1. Evaluation of the Bathroom Exhaust Air Thermal Performance Prediction Model
3.2. Comparison between the Existing Engine and New Engine by Case Study
- No heat recovery and no additional mechanical ventilation (C-EX);
- No heat recovery with all additional mechanical ventilation (C-N2, 5, 8, 11, 14, 17, 20, 23, and 26);
- Only the bathroom and kitchen with heat recovery with all additional mechanical ventilation (C-N3, 6, 9, 12, 15, 18, 21, 24, and 27);
- The whole-time heat recovery with all additional mechanical ventilation (C-N4, 7, 10, 13, 16, 19, 22, 25, and 28).
4. Conclusions
- (1)
- The simulation results show that this new proposed model can be used to estimate critical parameters, such as the turning point of the water film temperature and the final thermal performance of the exhaust air;
- (2)
- With the bathroom inlet air temperature and humidity given without turning on the air heater, only changing the air charge rate in the bathroom has little effect on drying the wet floor. It is necessary to install the additional air heater to achieve a higher efficiency of the floor water evaporation, which can be improved by about 24.7% under the airflow rate of 507.6 m3/h;
- (3)
- Although the heat recovery from the bathroom and kitchen is not significant due to the short operation time, the variation in the thickness of the water film on the bathroom floor plays a critical role in determining whether the wet floor can be dried and the time to remove all the floor water by ventilation. It is reasonable to suggest that the proposed detailed bathroom exhaust air thermal performance model can be used to determine the dehumidification endpoint;
- (4)
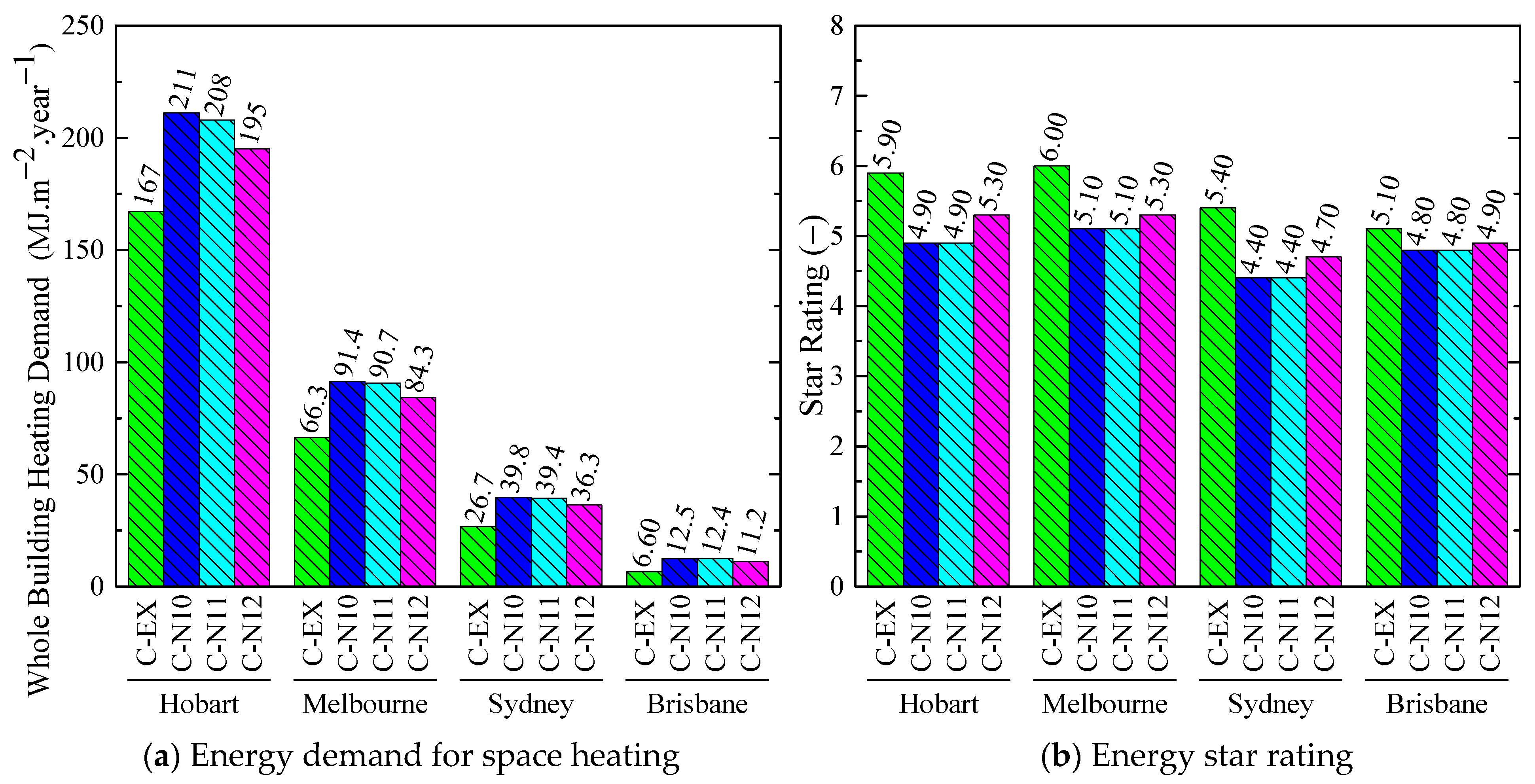
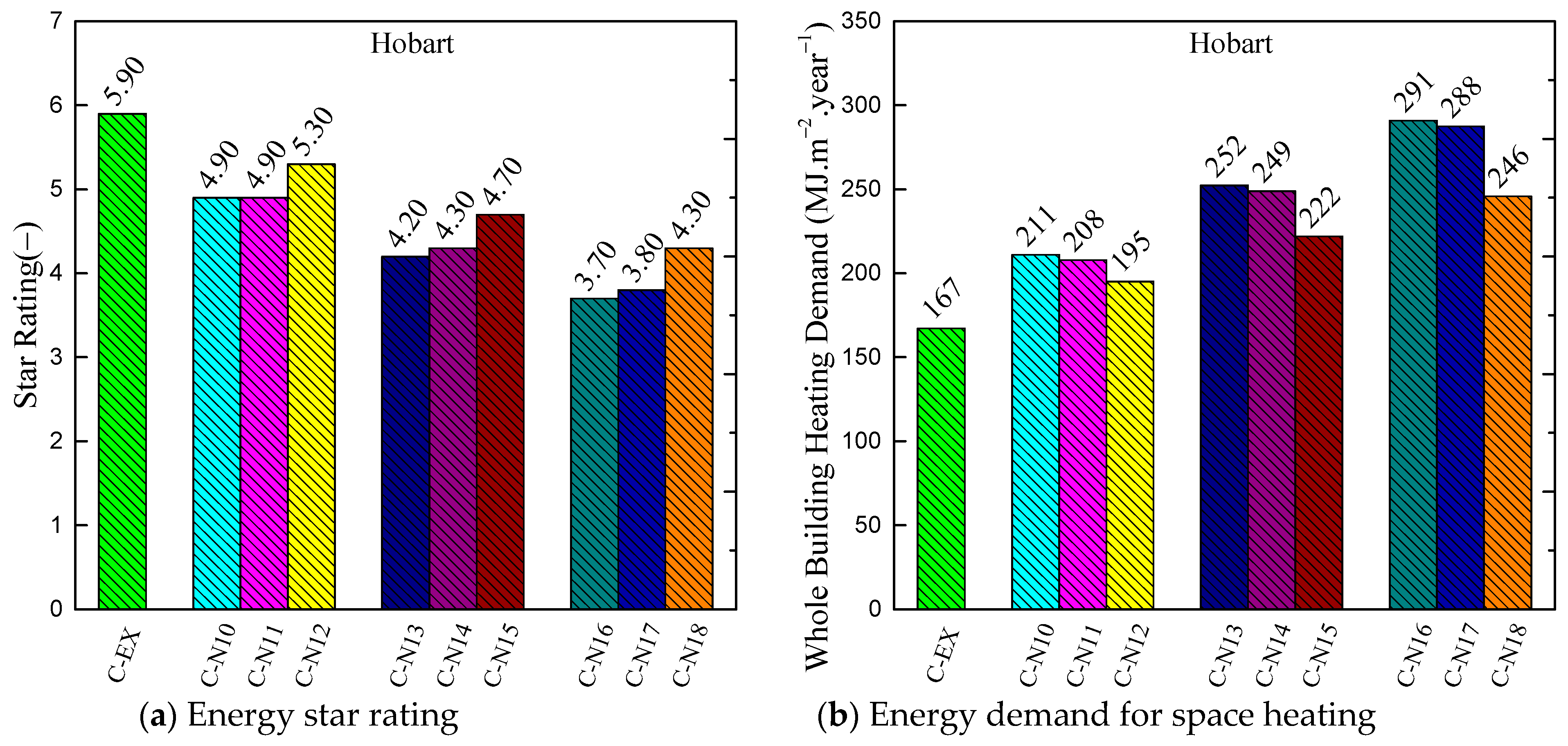
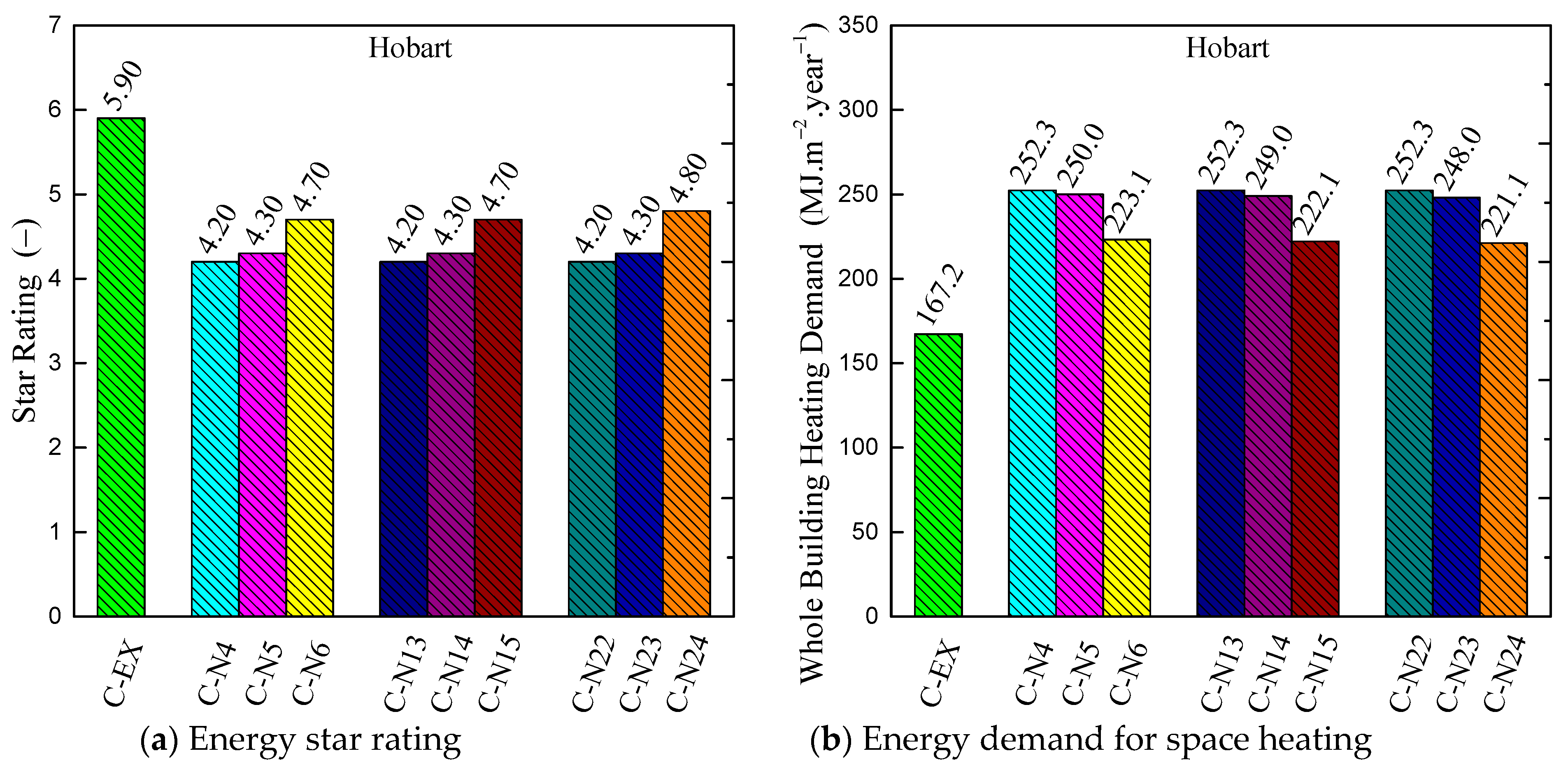
- The comparison study of the mechanical ventilation system with and without heat recovery shows the system without heat recovery increases the energy consumption due to the additional fresh air load. With the decrease in the average winter temperature of the city (from Brisbane to Hobart), the fresh air load becomes more and more large, and heat recovery becomes more and more important. The heat recovery can increase the house star rating up to 0.6 stars under the operation condition of C-N24 in Hobart. Compared with heat recovery in daily time, although the recovered energy from the bathroom and kitchen is smaller, it can still save about 3.3 MJ/(m2·year). It indicates the importance of considering the temperature difference between indoor and ambient environments when designing the heat recovery system under different climate zones.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| HVAC | Heating, ventilating, and air conditioning | H/C | heating and cooling |
| HDDs | Heating Degree Days | BESTEST | Building Energy Simulation Test |
| NatHERS | Nationwide House Energy Star Scheme | ε-NTU | Effectiveness–number of transfer units (NTU) |
| Chenath engine | A simulation engine for the AccuRate Home platform | ACH | Air Changes per Hour |
| Critical point time, s | The density of the wet air in the bathroom after the mixture process, kg/m3 | ||
| The volume of the bathroom, m3 | Gasification latent heat of water, J/kg | ||
| The airflow rate, m3/s | The thickness of the water on the floor in the last calculation step, m | ||
| h | Heat transfer coefficient, W/(m2·K) | The temperature of the water on the floor in the last calculation step, K | |
| Mass transfer coefficient, m/s | The exhaust air temperature in the last calculation step, K | ||
| Value of the Sherwood | The thickness of the water film, m | ||
| Qualitative length, m | Recovered energy at moisture removal time, J | ||
| Mass diffusivity of moisture, m2/s | Recovered energy at shower time, J | ||
| Nuchelt value | Total recovered energy from the bathroom, J | ||
| Conductive coefficient, W/(m·K) | Heat exchange efficiency | ||
| Area of shower space, m2 | Minimum heat capacity, J/k | ||
| Length of the shower space, m | Mass flow rate of working air, kg/s | ||
| Width of shower space, m | Temperature of the kitchen exhaust air, K | ||
| Re | Reynolds number | Recovered energy from kitchen, J | |
| Pr | The Prandtl number | Recovered energy at daily time, J | |
| Sc | Schmidt value | Total number of condition zones at current time step | |
| Dynamic viscosity, m2/s | Temperature of zone a, K | ||
| P1 | Working pressure in bathroom, Pa | The ambient temperature, K | |
| Tequ | Qualitative temperature, K | Extra energy consumption caused by the air heater, J | |
| Exhaust air temperature from the bathroom, K | Set temperature of outlet air of the air heater, K | ||
| Air temperature after the mixture process between the inlet air and the existing air in the bathroom, K | Inlet air temperature, K | ||
| The absolute air moisture content after the mixture process, kg/kg | n | Time steps | |
| The density of indoor wet air, kg/m3 | Air-specific heat at constant pressure after the mixture process, J/(kg·k) | ||
| The density of inlet wet air, kg/m3 | Hot water temperature on the floor, K | ||
| The initial absolute air moisture content for the bathroom air, kg/kg | Partial pressure of water vapour, Pa | ||
| The initial absolute air moisture content for the inlet air, kg/kg | Exhaust air temperature, K | ||
| The initial temperature for the bathroom air, K | Exhaust air absolute moisture content, kg/kg | ||
| The initial temperature for the inlet air, K | Time step, s | ||
| Saturation value, kg/kg | ψ | Relative humidity, % | |
| Mass diffusion flux, kg/(m2·s) | Subscripts | ||
| The molar gas constant of vapour | sup | Supplied fresh air | |
| The saturation pressure at the base of the water temperature, Pa | exbath | Exhaust air from the bathroom | |
| The density of the dry air in the bathroom, kg/kg | Number from 1 to 28 | Corresponding to each operating condition |
References
- Sun, J.; Zhu, D.; Yin, Y.; Li, X. Experimental investigation of the heating performance of refrigerant injection heat pump with a single-cylinder inverter-driven rotary compressor. J. Therm. Anal. Calorim. 2018, 133, 1579–1588. [Google Scholar] [CrossRef]
- Song, G.; Ai, Z.; Liu, Z.; Zhang, G. A systematic literature review on smart and personalized ventilation using CO2 concentration monitoring and control. Energy Rep. 2022, 8, 7523–7536. [Google Scholar] [CrossRef]
- Hu, J.; Liu, Z.; Ma, G.; Zhang, G.; Ai, Z. Air infiltration and related building energy consumption: A case study of office buildings in Changsha, China. J. Build. Eng. 2023, 74, 106859. [Google Scholar] [CrossRef]
- Zhang, L.Z.; Zelik, E.B. Total Heat Recovery: Heat and Moisture Recovery from Ventilation Air; Nova Science Publishers: Hauppauge, NY, USA, 2008. [Google Scholar]
- Zhang, L. Energy performance of independent air dehumidification systems with energy recovery measures. Energy 2006, 31, 1228–1242. [Google Scholar] [CrossRef]
- Zender–Świercz, E. A review of heat recovery in ventilation. Energies 2021, 14, 1759. [Google Scholar] [CrossRef]
- Tang, L.; Ai, Z.; Song, C.; Zhang, G.; Liu, Z. A strategy to maximally utilize outdoor air for indoor thermal environment. Energies 2021, 14, 3987. [Google Scholar] [CrossRef]
- Alhindawi, I.; Jimenez-Bescos, C. Computational Approach to Predict Thermal Comfort Levels at Summer Peak Conditions in Passive House Based on Natural Ventilation. J. Sustain. Dev. Energy Water Environ. Syst. 2022, 10, 1–21. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, Z.; Ai, Z.; Zhang, G. Performance evaluation of ventilative cooling systems for buildings under different control parameters and strategies. J. Build. Eng. 2023, 65, 105627. [Google Scholar] [CrossRef]
- Cuce, P.M.; Riffat, S. A comprehensive review of heat recovery systems for building applications. Renew. Sustain. Energy Rev. 2015, 47, 665–682. [Google Scholar] [CrossRef]
- Besant, R.; Simonson, C. Air-to-air exchangers. ASHRAE J. 2003, 45, 42. [Google Scholar]
- Besant, R.W.; Simonson, C.J. Air-to-air energy recovery. ASHRAE J. 2000, 42, 31–43. [Google Scholar]
- Dieckmann, J.; Roth, K.W.; Brodrick, J. Air-to-air energy recovery heat exchangers. ASHRAE J. 2003, 45, 57. [Google Scholar]
- Mardiana-Idayu, A.; Riffat, S. Review on heat recovery technologies for building applications. Renew. Sustain. Energy Rev. 2012, 16, 1241–1255. [Google Scholar] [CrossRef]
- Xu, Q.; Riffat, S.; Zhang, S. Review of heat recovery technologies for building applications. Energies 2019, 12, 1285. [Google Scholar] [CrossRef]
- Li, J.; Shao, S.; Wang, Z.; Xie, G.; Wang, Q.; Xu, Z.; Han, L.; Gou, X. A review of air-to-air membrane energy recovery technology for building ventilation. Energy Build. 2022, 265, 112097. [Google Scholar] [CrossRef]
- Nielsen, T.R. Simple tool to evaluate energy demand and indoor environment in the early stages of building design. Sol. Energy 2005, 78, 73–83. [Google Scholar] [CrossRef]
- Pekdogan, T.; Tokuç, A.; Ezan, M.A.; Başaran, T. Experimental investigation of a decentralized heat recovery ventilation system. J. Build. Eng. 2021, 35, 102009. [Google Scholar] [CrossRef]
- Larowski, A.; Taylor, M.A. Systematic Procedure for Selection of Heat Exchangers. Proc. Inst. Mech. Eng. Part A Power Process Eng. 1983, 197, 51–69. [Google Scholar] [CrossRef]
- Kuppan, T. Heat Exchanger Design Handbook; Marcel Dekker, Inc.: New York, NY, USA, 2000. [Google Scholar]
- Riffat, S.B.; Gillott, M.C. Performance of a novel mechanical ventilation heat recovery heat pump system. Appl. Therm. Eng. 2002, 22, 839–845. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, Y.; Zhu, L.; Wang, Q. Enhanced performance of heat recovery ventilator by airflow-induced film vibration (HRV performance enhanced by FIV). Int. J. Therm. Sci. 2010, 49, 2037–2041. [Google Scholar] [CrossRef]
- Li, B.; Wild, P.; Rowe, A. Performance of a heat recovery ventilator coupled with an air-to-air heat pump for residential suites in Canadian cities. J. Build. Eng. 2019, 21, 343–354. [Google Scholar] [CrossRef]
- Ribé, O.; Ruiz, R.; Quera, M.; Cadafalch, J. Analysis of the sensible and total ventilation energy recovery potential in different climate conditions. Application to the Spanish case. Appl. Therm. Eng. 2019, 149, 854–861. [Google Scholar] [CrossRef]
- Strand, A.; Kim, M.K. Comparative numerical energy analysis of decentralized ventilation adapting to local Norway climates. E3S Web Conf. 2022, 362, 11005. [Google Scholar] [CrossRef]
- Marsik, T.; Bickford, R.; Dennehy, C.; Garber-Slaght, R.; Kasper, J. Impact of Intake and Exhaust Ducts on the Recovery Efficiency of Heat Recovery Ventilation Systems. Energies 2021, 14, 351. [Google Scholar] [CrossRef]
- Crawley, D.B.; Lawrie, L.K.; Winkelmann, F.C.; Pedersen, C.O. EnergyPlus: A New-Generation Building Energy Simulation Program. In Proceedings of the Forum 2001: Solar Energy: The Power to Choose, Washington, DC, USA, 21–25 April 2001. [Google Scholar]
- Klein, S.A.; Beckman, W.A.; Duffie, J.A. TRNSYS—A transient simulation program. ASHRAE Trans. 1976, 82, 623–633. [Google Scholar]
- Davidsson, H.; Bernardo, R. Heat Loss for a Run-Around Hybrid Ventilation System with Heat Recovery. In Proceedings of the International Solar Energy Society, ISES Solar World Congress 2015, SWC 2015, Daegu, Republic of Korea, 8–12 November 2015; pp. 81–86. [Google Scholar]
- Nuernberger, S.; Lau, A. Modeling of ventilation air heat recovery and its impact in high-performance green buildings. In Proceedings of the Proceedings of SimBuild Conference 2004: 1st Conference of IBPSA-USA; Boulder, CO, USA, August 2004, Available online: https://publications.ibpsa.org/conference/paper/?id=simbuild2004_SB04T2C1 (accessed on 16 August 2023).
- Bojic, M. Mathematical model of heat recovery in a space-heating and ventilation system. Energy 1993, 18, 49–61. [Google Scholar] [CrossRef]
- Bojic, M.; Trnobransky, K. Influence of hot tool parameters on heat recovery in a space-heating and ventilation system. Energy 1995, 20, 1075–1079. [Google Scholar] [CrossRef]
- EnergyPlus™. EnergyPlus™ Documentation-Engineering Reference, Version 23.1.0; U.S. Department of Energy: Washington, DC, USA, 2023.
- Ren, Z.; Jian, A.; Law, A.; Godhani, A.; Chen, D. Development of a benchmark tool for whole of home energy rating for Australian new housing. Energy Build. 2023, 285, 112921. [Google Scholar] [CrossRef]
- Walsh, P.J.; Delsante, A.E. Calculation of the thermal behaviour of multi-zone buildings. Energy Build. 1983, 5, 231–242. [Google Scholar] [CrossRef]
- Ren, Z.; Chen, Z. Enhanced air flow modelling for AccuRate–A nationwide house energy rating tool in Australia. Build. Environ. 2010, 45, 1276–1286. [Google Scholar] [CrossRef]
- Delsante, A. A Validation of the ‘Accurate’ Simulation Engine Using Bestest; Report for the Australian Greenhouse Office by Commonwealth Scientific and Industrial Research Organisation (CSIRO), Report No. CMIT(C)-2004-152; Melbourne, Australia, April 2004. Available online: https://www.nathers.gov.au/sites/default/files/Validation%2520of%2520the%2520AccuRate%2520Simulation%2520Engine%2520Using%2520BESTEST_0.pdf (accessed on 16 August 2023).
- Ren, Z.; Chen, D.; James, M. Evaluation of a whole-house energy simulation tool against measured data. Energy Build. 2018, 171, 116–130. [Google Scholar] [CrossRef]
- Bai, H.; Liu, P.; Alonso, M.J.; Mathisen, H.M. A review of heat recovery technologies and their frost control for residential building ventilation in cold climate regions. Renew. Sustain. Energy Rev. 2022, 162, 112417. [Google Scholar] [CrossRef]
- Yang, S.-M.; Tao, W.-Q. Heat Transfer Theory, 4th ed.; Higher Education Publishing House: Beijing, China, 2006. [Google Scholar]
- Zhang, X. The Fifth Edition of Heat Transfer; China Building Industry Press: Beijing, China, 2007. [Google Scholar]
- Chen, G.; Wu, G. Experiment on heat pumps with exhaust heat recovery from kitchens. J. HVAC 2005, 35, 69–71. [Google Scholar]
- Eckert, E.R.; Drake, R.M., Jr. Analysis of Heat and Mass Transfer; McGraw-Hill: New York, NY, USA, 1987. [Google Scholar]
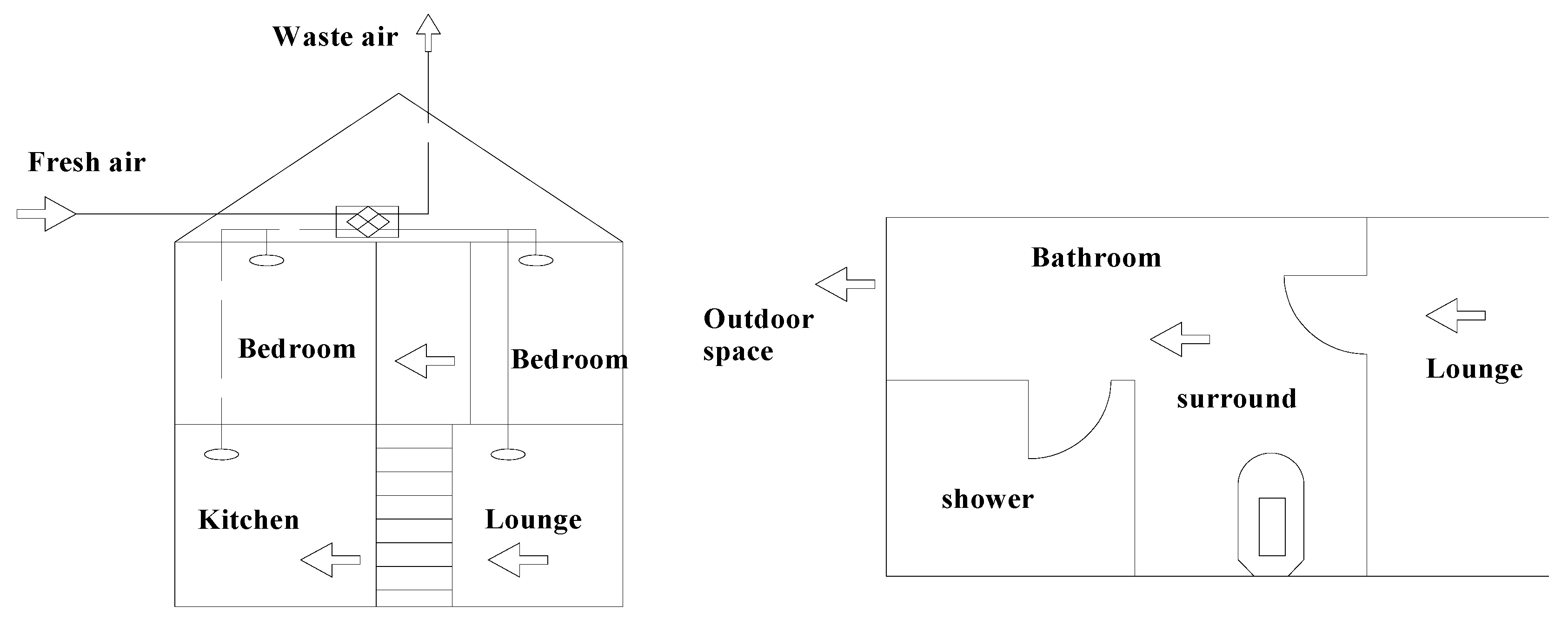

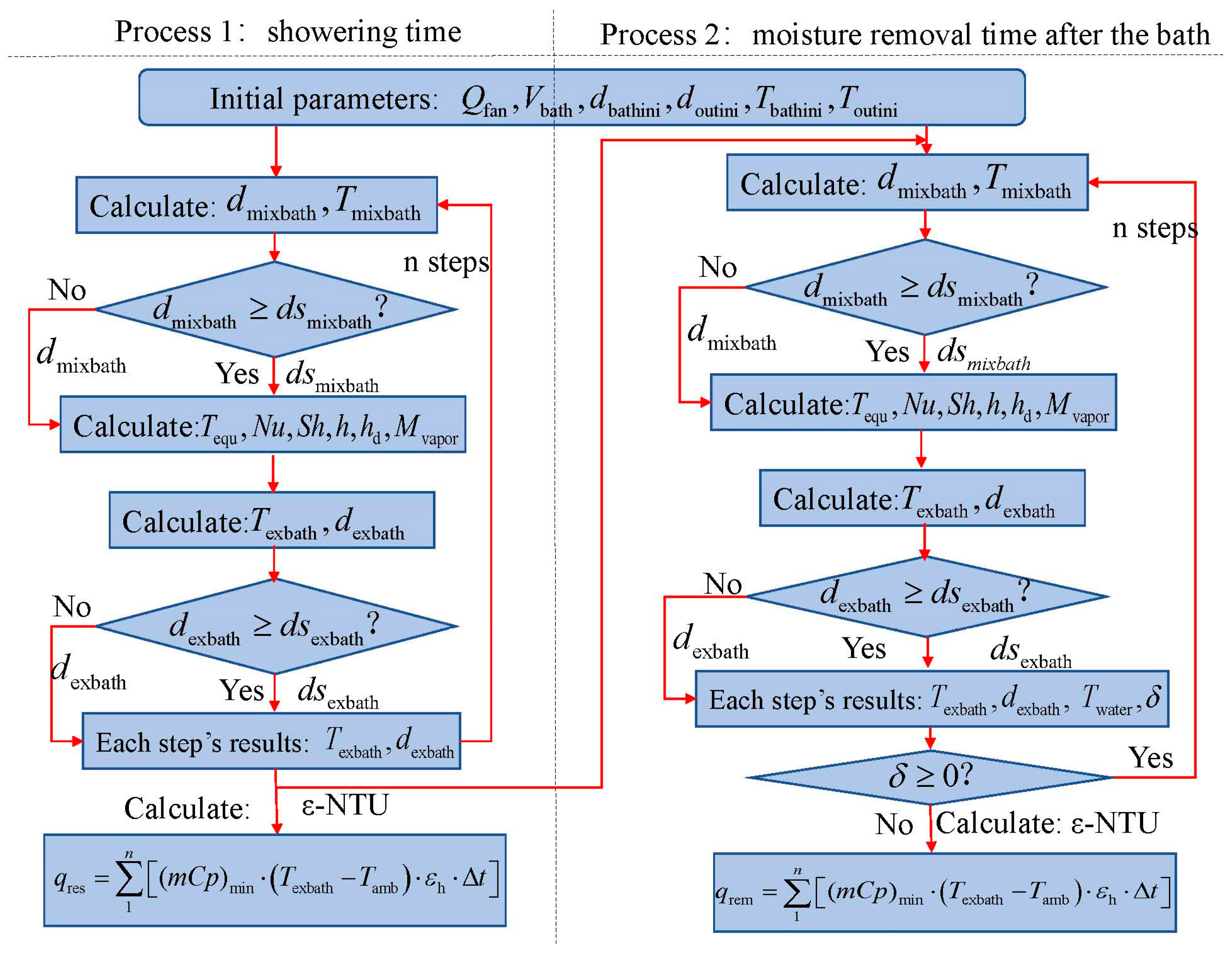
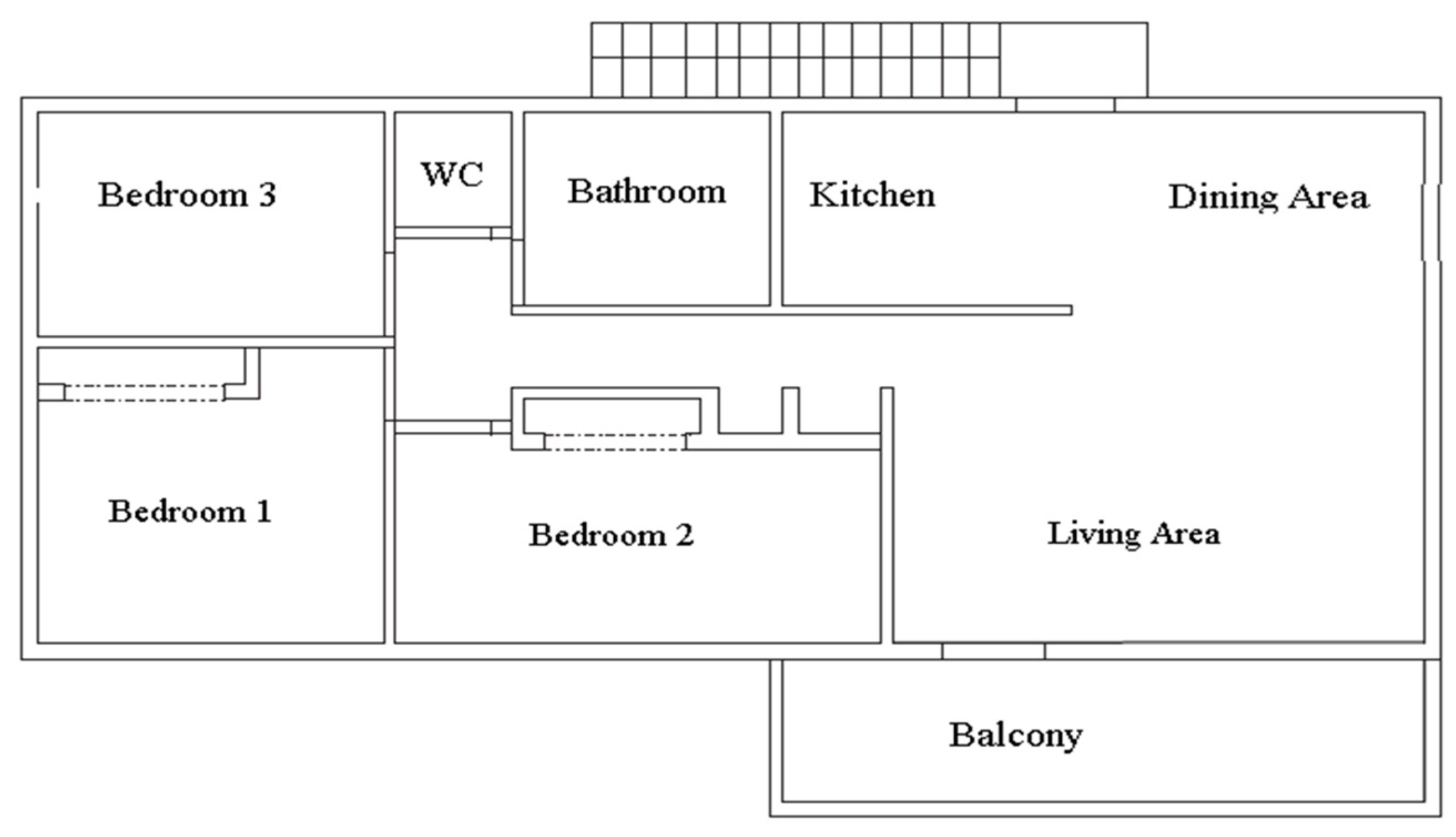
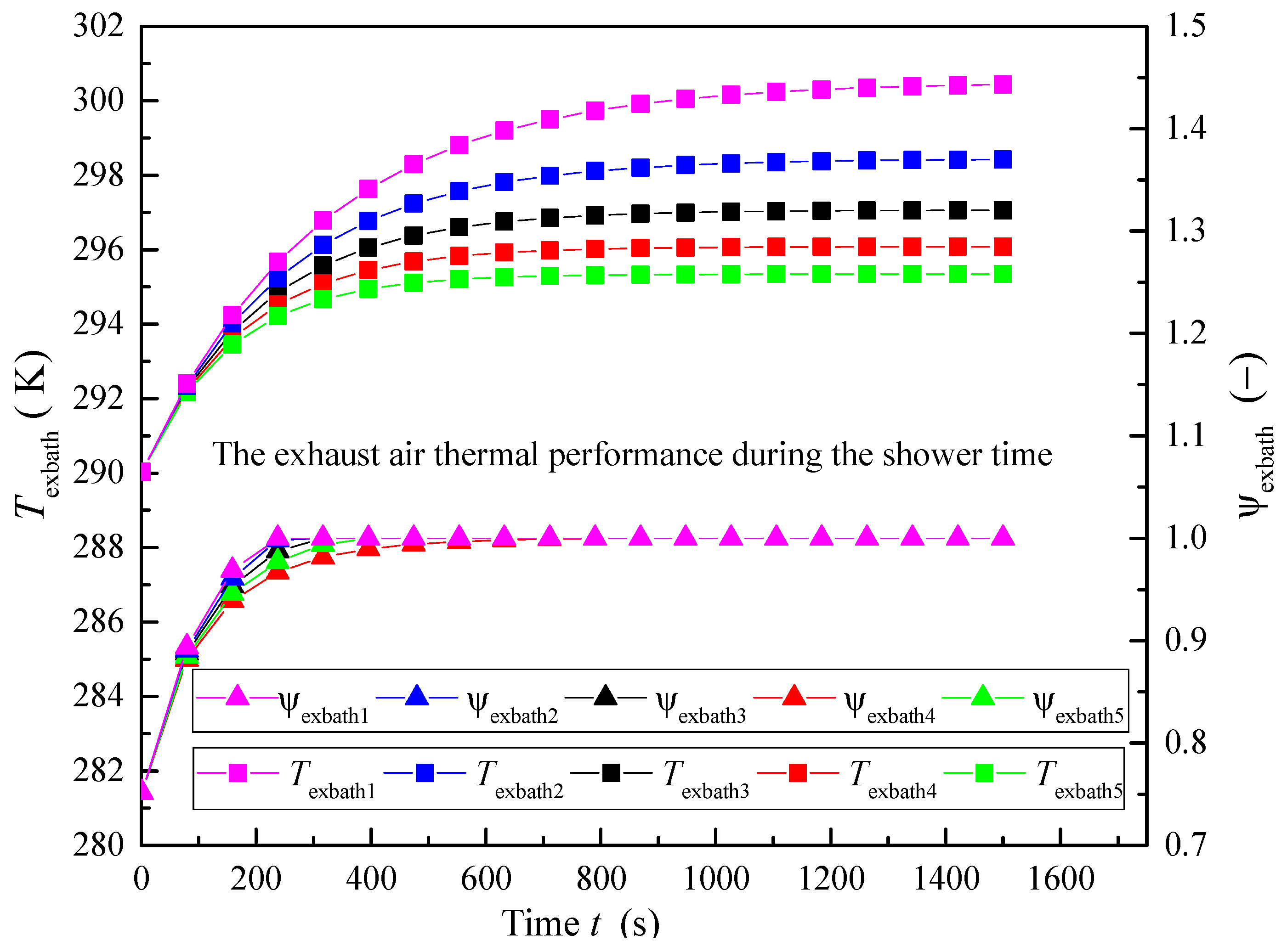
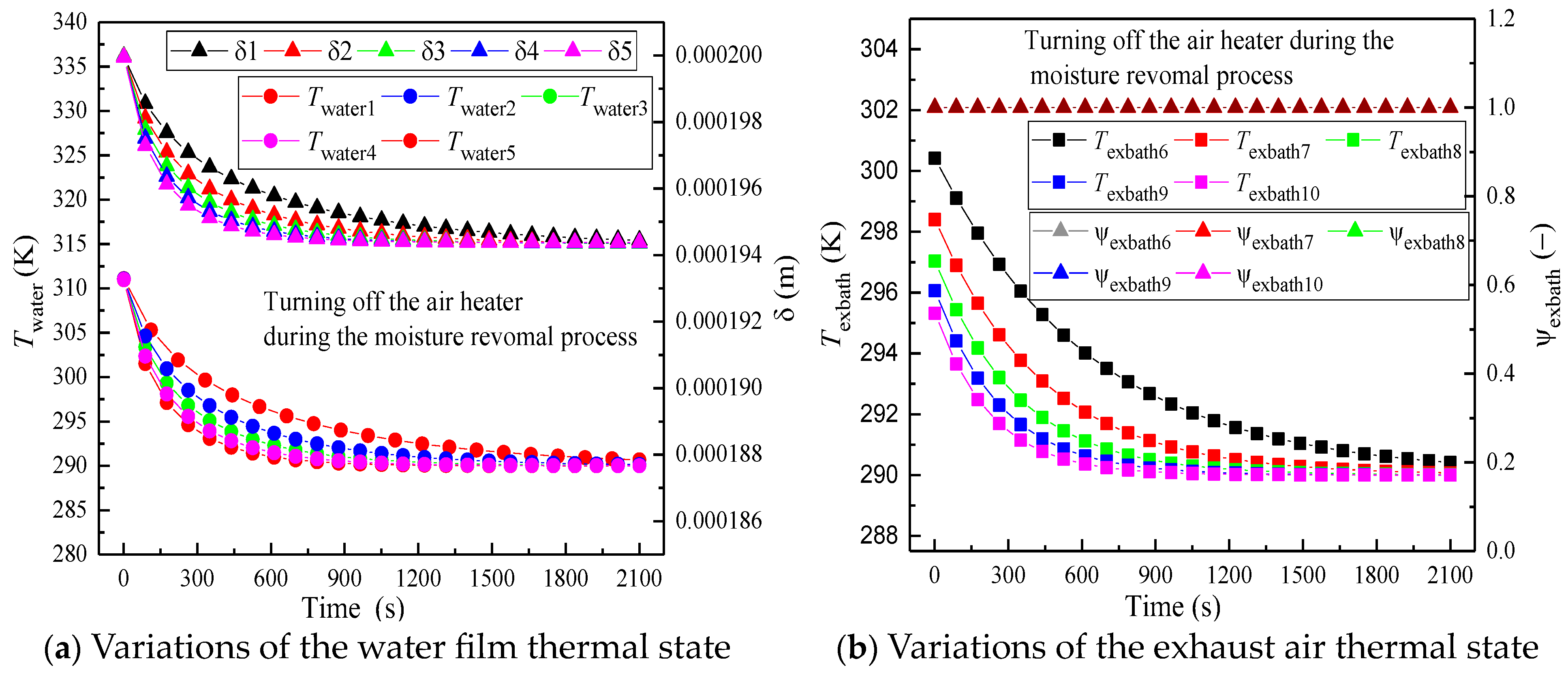
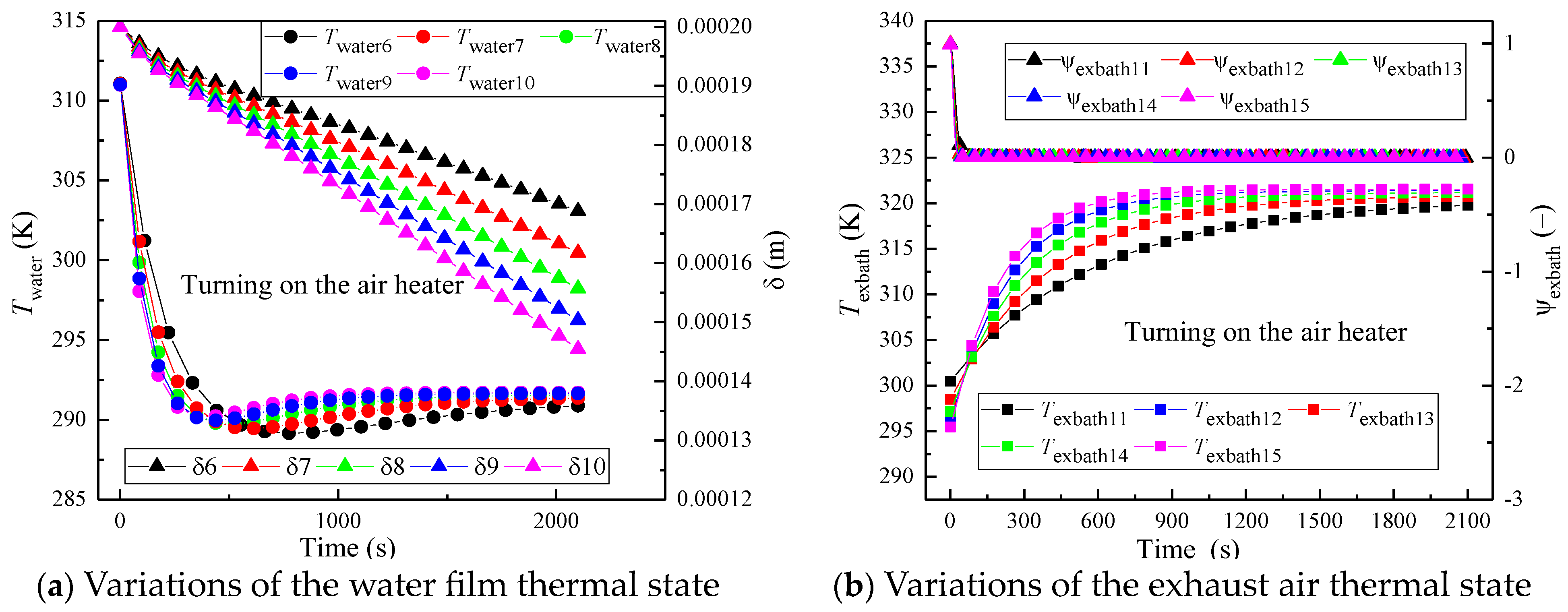
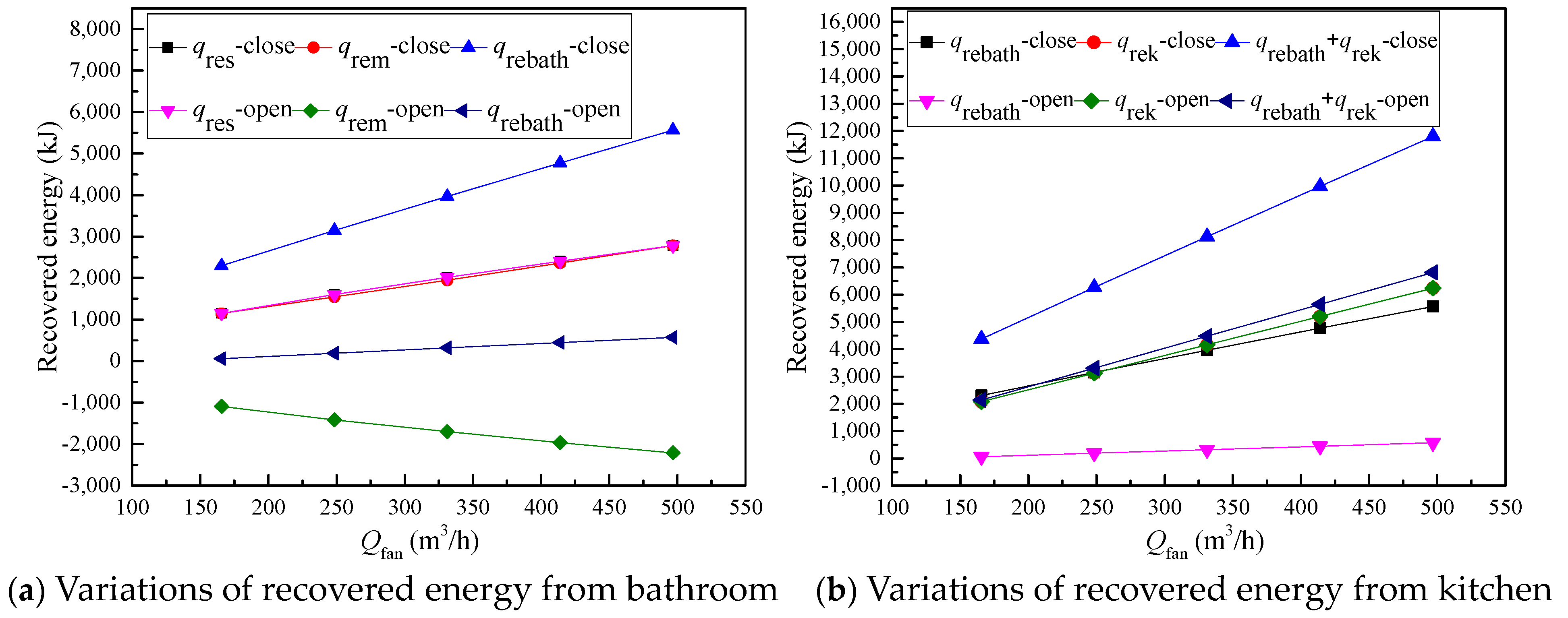

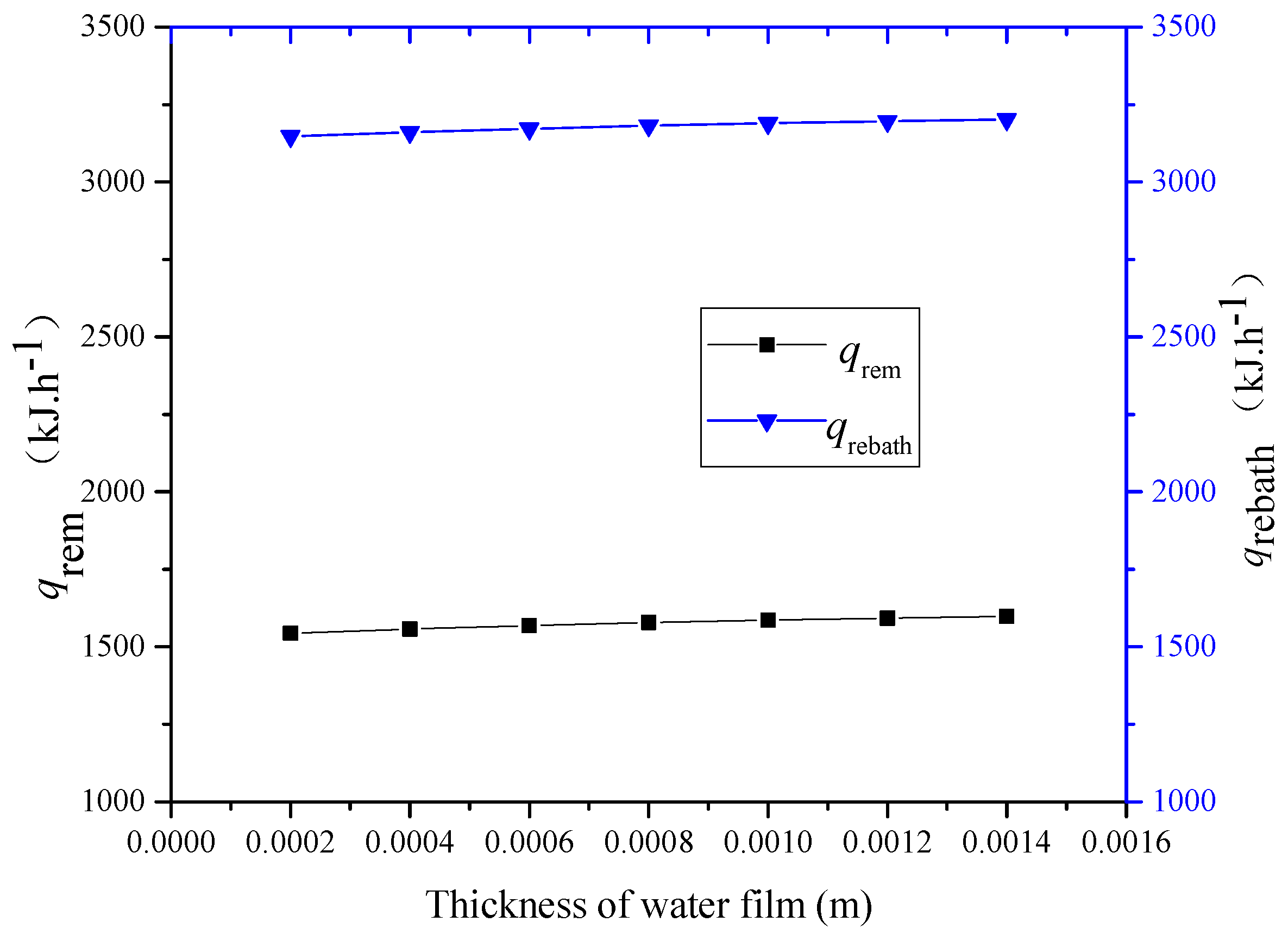
| Zone | Items | Units | Specification |
|---|---|---|---|
| bathroom | Temperature of the hot water on the bathroom base floor | K | 311.15 |
| Initial thickness of the water film | mm | 0.2 | |
| Geometry of shower space (W × L × H) | m | 0.9 × 0.9 × 2.0 | |
| Airflow rate of ventilation | m³/s | 0.046 | |
| - | 0.7 [33] | ||
| kitchen | Exhaust air temperature | K | 305 |
| Exhaust air relative humidity | - | 85% | |
| Airflow rate of ventilation | m³/s | 0.046 | |
| - | 0.7 | ||
| Daily heat recovery | - | 0.7 |
| Time | Qfan (m³/h) | Corresponding Parameters | ||||
|---|---|---|---|---|---|---|
| 1 | Shower | 169.2 | Texbath1, ψexbath1 | qres | qrebath | |
| 2 | 253.8 | Texbath2, ψexbath2 | ||||
| 3 | 338.4 | Texbath3, ψexbath3 | ||||
| 4 | 423 | Texbath4, ψexbath4 | ||||
| 5 | 507.6 | Texbath5, ψexbath5 | ||||
| 6 | Moisture removal process | Turning off the air heater | 169.2 | Texbath6, ψexbath6,Twater1, δ1 | qrem | |
| 7 | 253.8 | Texbath7, ψexbath7,Twater2, δ2 | ||||
| 8 | 338.4 | Texbath8, ψexbath8,Twater3, δ3 | ||||
| 9 | 423 | Texbath9, ψexbath9,Twater4, δ4 | ||||
| 10 | 507.6 | Texbath10, ψexbath10,Twater5, δ5 | ||||
| 11 | Turning on the air heater | 169.2 | Texbath11, ψexbath11,Twater6, δ6 | qrem | ||
| 12 | 253.8 | Texbath12, ψexbath12,Twater7, δ7 | ||||
| 13 | 338.4 | Texbath13, ψexbath13,Twater8, δ8 | ||||
| 14 | 423 | Texbath14, ψexbath14,Twater9, δ9 | ||||
| 15 | 507.6 | Texbath15, ψexbath15,Twater10, δ10 | ||||
| Operating Condition | Shower Process | Moisture Removal Process | Qfan (m3/s) | (kJ) | (kJ) | (kJ) | Recovered Energy Per Square Meter (kJ/m2·h) | ||
|---|---|---|---|---|---|---|---|---|---|
| Proposed Model | Fixed Temperature | Proposed Model | Fixed Temperature | ||||||
| C1-1 | on | off | on | off | 0.047 | 1151.92 | 1146.69 | 2298.62 | 77.92 |
| C1-2 | off | on | on | off | 0.047 | 1136.87 | 1091.79 | 2228.66 | 75.55 |
| C1-3 | off | on | off | on | 0.047 | 1136.87 | 1590.24 | 2727.11 | 92.44 |
| C2-1 | on | off | on | off | 0.0705 | 1603.77 | 1543.87 | 3147.64 | 106.70 |
| C2-2 | off | on | on | off | 0.0705 | 1704.68 | 1537.13 | 3241.81 | 109.89 |
| C2-3 | off | on | off | on | 0.0705 | 1704.68 | 2384.39 | 4089.07 | 138.61 |
| C3-1 | on | off | on | off | 0.094 | 2017.58 | 1949.43 | 3967.01 | 134.47 |
| C3-2 | off | on | on | off | 0.094 | 2272.08 | 1976.74 | 4248.83 | 144.03 |
| C3-3 | off | on | off | on | 0.094 | 2272.08 | 3177.98 | 5450.07 | 184.75 |
| C4-1 | on | off | on | off | 0.1175 | 2407.44 | 2363.28 | 4770.71 | 161.72 |
| C4-2 | off | on | on | off | 0.1175 | 2839.07 | 2415.16 | 5254.23 | 178.11 |
| C4-3 | off | on | off | on | 0.1175 | 2839.07 | 3970.99 | 6810.06 | 230.85 |
| C5-1 | on | off | on | off | 0.141 | 2781.34 | 2783.01 | 5564.35 | 188.62 |
| C5-2 | off | on | on | off | 0.141 | 3405.65 | 2853.33 | 6258.97 | 212.17 |
| C5-3 | off | on | off | on | 0.141 | 3405.65 | 4763.41 | 8169.06 | 276.92 |
| Operating Condition | Qfan (m3/s) | Thickness of Water Film (m) | (kJ) | (kJ) | (kJ) | Recovered Energy Per Square Meter (kJ/m2·h) |
|---|---|---|---|---|---|---|
| T1 | 0.0705 | 0.0002 | 1603.77 | 1543.87 | 3147.64 | 106.70 |
| CT2 | 0.0705 | 0.0004 | 1603.77 | 1557.12 | 3160.88 | 107.15 |
| CT3 | 0.0705 | 0.0006 | 1603.77 | 1568.50 | 3172.27 | 107.53 |
| CT4 | 0.0705 | 0.0008 | 1603.77 | 1577.93 | 3181.70 | 107.85 |
| CT5 | 0.0705 | 0.001 | 1603.77 | 1585.72 | 3189.49 | 108.12 |
| CT6 | 0.0705 | 0.0012 | 1603.77 | 1592.21 | 3195.97 | 108.34 |
| CT7 | 0.0705 | 0.0014 | 1603.77 | 1597.67 | 3201.44 | 108.52 |
| Operating Condition | Version of Engine | Heat Recovery | Airflow Rate m3/s | Daily Time Air Charge Rate (Times Per Hour) | |||
|---|---|---|---|---|---|---|---|
| Daily Time | Bathroom and Kitchen | Bathroom | Kitchen | ||||
| 1 | C-EX | Existing engine | Off | Off | - | - | - |
| 2 | C-N1 | New engine | Off | Off | 0.047 × 1 | 0.047 × 1 | 0.5 |
| 3 | C-N2 | New engine | Off | On | 0.047 × 1 | 0.047 × 1 | 0.5 |
| 4 | C-N3 | New engine | On | On | 0.047 × 1 | 0.047 × 1 | 0.5 |
| 5 | C-N4 | New engine | Off | Off | 0.047 × 1 | 0.047 × 1 | 1 |
| 6 | C-N5 | New engine | Off | On | 0.047 × 1 | 0.047 × 1 | 1 |
| 7 | C-N6 | New engine | On | On | 0.047 × 1 | 0.047 × 1 | 1 |
| 8 | C-N7 | New engine | Off | Off | 0.047 × 1 | 0.047 × 1 | 1.5 |
| 9 | C-N8 | New engine | Off | On | 0.047 × 1 | 0.047 × 1 | 1.5 |
| 10 | C-N9 | New engine | On | On | 0.047 × 1 | 0.047 × 1 | 1.5 |
| 11 | C-N10 | New engine | Off | Off | 0.047 × 1.5 | 0.047 × 1.5 | 0.5 |
| 12 | C-N11 | New engine | Off | On | 0.047 × 1.5 | 0.047 × 1.5 | 0.5 |
| 13 | C-N12 | New engine | On | On | 0.047 × 1.5 | 0.047 × 1.5 | 0.5 |
| 14 | C-N13 | New engine | Off | Off | 0.047 × 1.5 | 0.047 × 1.5 | 1 |
| 15 | C-N14 | New engine | Off | On | 0.047 × 1.5 | 0.047 × 1.5 | 1 |
| 16 | C-N15 | New engine | On | On | 0.047 × 1.5 | 0.047 × 1.5 | 1 |
| 17 | C-N16 | New engine | Off | Off | 0.047 × 1.5 | 0.047 × 1.5 | 1.5 |
| 18 | C-N17 | New engine | Off | On | 0.047 × 1.5 | 0.047 × 1.5 | 1.5 |
| 19 | C-N18 | New engine | On | On | 0.047 × 1.5 | 0.047 × 1.5 | 1.5 |
| 20 | C-N19 | New engine | Off | Off | 0.047 × 2 | 0.047 × 2 | 0.5 |
| 21 | C-N20 | New engine | Off | On | 0.047 × 2 | 0.047 × 2 | 0.5 |
| 22 | C-N21 | New engine | On | On | 0.047 × 2 | 0.047 × 2 | 0.5 |
| 23 | C-N22 | New engine | Off | Off | 0.047 × 2 | 0.047 × 2 | 1 |
| 24 | C-N23 | New engine | Off | On | 0.047 × 2 | 0.047 × 2 | 1 |
| 25 | C-N24 | New engine | On | On | 0.047 × 2 | 0.047 × 2 | 1 |
| 26 | C-N25 | New engine | Off | Off | 0.047 × 2 | 0.047 × 2 | 1.5 |
| 27 | C-N26 | New engine | Off | On | 0.047 × 2 | 0.047 × 2 | 1.5 |
| 28 | C-N27 | New engine | On | On | 0.047 × 2 | 0.047 × 2 | 1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Ren, Z.; Guo, J. Mechanical Ventilation Heat Recovery Modelling for AccuRate Home—A Benchmark Tool for Whole House Energy Rating in Australia. Energies 2023, 16, 6801. https://doi.org/10.3390/en16196801
Sun J, Ren Z, Guo J. Mechanical Ventilation Heat Recovery Modelling for AccuRate Home—A Benchmark Tool for Whole House Energy Rating in Australia. Energies. 2023; 16(19):6801. https://doi.org/10.3390/en16196801
Chicago/Turabian StyleSun, Jinfei, Zhengen Ren, and Jianxiang Guo. 2023. "Mechanical Ventilation Heat Recovery Modelling for AccuRate Home—A Benchmark Tool for Whole House Energy Rating in Australia" Energies 16, no. 19: 6801. https://doi.org/10.3390/en16196801
APA StyleSun, J., Ren, Z., & Guo, J. (2023). Mechanical Ventilation Heat Recovery Modelling for AccuRate Home—A Benchmark Tool for Whole House Energy Rating in Australia. Energies, 16(19), 6801. https://doi.org/10.3390/en16196801






